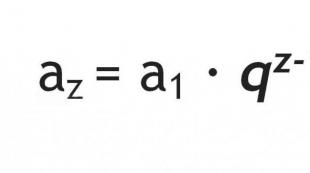Pesmi za otroke

Neskončno napredovanje geom. Geometrijsko napredovanje. Primer z rešitvijo. Formula za n-ti člen geometrijske progresije

Razmislimo o določeni seriji.

7 28 112 448 1792...

Popolnoma jasno je, da je vrednost katerega koli od njegovih elementov natanko štirikrat večja od prejšnjega. To pomeni, da je ta serija napredek.

Geometrijska progresija je neskončno zaporedje števil, katerega glavna značilnost je, da naslednje število dobimo iz prejšnjega z množenjem z določenim številom. To je izraženo z naslednjo formulo.

a z +1 =a z ·q, kjer je z številka izbranega elementa.

V skladu s tem je z ∈ N.

Obdobje, ko se v šoli preučuje geometrijsko napredovanje, je 9. razred. Primeri vam bodo pomagali razumeti koncept:

0.25 0.125 0.0625...

Na podlagi te formule je imenovalec napredovanja mogoče najti na naslednji način:

Niti q niti b z ne moreta biti nič. Prav tako vsak od elementov progresije ne sme biti enak nič.

V skladu s tem, če želite izvedeti naslednjo številko v nizu, morate zadnjo pomnožiti s q.

Če želite nastaviti to napredovanje, morate določiti njegov prvi element in imenovalec. Po tem je mogoče najti katerega koli od naslednjih členov in njihovo vsoto.

Sorte

Glede na q in a 1 je to napredovanje razdeljeno na več vrst:

Če sta tako a 1 kot q večja od ena, potem je takšno zaporedje geometrijska progresija, ki narašča z vsakim naslednjim elementom. Primer tega je predstavljen spodaj.

Primer: a 1 =3, q=2 - oba parametra sta večja od ena.

Potem lahko zaporedje številk zapišemo takole:

3 6 12 24 48 ...

Če |q| manjša od ena, kar pomeni, da je množenje z njo enakovredno deljenju, potem je progresija s podobnimi pogoji padajoča geometrijska progresija. Primer tega je predstavljen spodaj.

Primer: a 1 =6, q=1/3 - a 1 je večji od ena, q je manjši.

Potem lahko zaporedje številk zapišemo takole:

6 2 2/3 ... - vsak element je 3-krat večji od elementa, ki mu sledi.

Izmenično znamenje. Če q<0, то знаки у чисел последовательности постоянно чередуются вне зависимости от a 1 , а элементы ни возрастают, ни убывают.

Primer: a 1 = -3, q = -2 - oba parametra sta manjša od nič.

Potem lahko zaporedje številk zapišemo takole:

3, 6, -12, 24,...

Formule

Obstaja veliko formul za priročno uporabo geometrijskih progresij:

Z-term formula. Omogoča izračun elementa pod določeno številko brez izračuna prejšnjih številk.

primer:q = 3, a 1 = 4. Potrebno je prešteti četrti element napredovanja.

rešitev:a 4 = 4 · 3 4-1 = 4 · 3 3 = 4 · 27 = 108.

Vsota prvih elementov, katerih količina je enaka z. Omogoča izračun vsote vseh elementov zaporedja doa zvključno.

Ker (1-q) je v imenovalcu, potem (1 - q)≠ 0, zato q ni enak 1.

Opomba: če je q=1, bi bila progresija niz neskončno ponavljajočih se števil.

Vsota geometrijske progresije, primeri:a 1 = 2, q= -2. Izračunajte S5.

rešitev:S 5 = 22 - izračun po formuli.

Znesek, če |q| < 1 и если z стремится к бесконечности.

primer:a 1 = 2 , q= 0,5. Poiščite znesek.

rešitev:S z = 2 · = 4

S z = 2 + 1 + 0.5 + 0.25 + 0.125 + 0.0625 = 3.9375 4

Nekatere lastnosti:

Značilna lastnost. Če naslednji pogoj deluje za vsez, potem je podana številska serija geometrijska progresija:

a z 2 = a z -1 · az+1

Prav tako se kvadrat poljubnega števila v geometrijskem napredovanju najde tako, da seštejeta kvadrata poljubnih dveh drugih števil v danem nizu, če sta enako oddaljeni od tega elementa.

a z 2 = a z - t 2 + a z + t 2 , Kjet- razdalja med temi številkami.

Elementirazlikujejo v qenkrat.
Logaritmi elementov progresije prav tako tvorijo progresijo, vendar aritmetično, to je, da je vsak od njih večji od prejšnjega za določeno število.

Primeri nekaterih klasičnih problemov

Da bi bolje razumeli, kaj je geometrijsko napredovanje, lahko pomagajo primeri z rešitvami za 9. razred.

Pogoji:a 1 = 3, a 3 = 48. Poiščiq.

Rešitev: vsak naslednji element je večji od prejšnjega vq enkrat.Nekatere elemente je treba izraziti z drugimi z imenovalcem.

toreja 3 = q 2 · a 1

Pri zamenjaviq= 4

Pogoji:a 2 = 6, a 3 = 12. Izračunaj S 6.

rešitev:Če želite to narediti, samo poiščite q, prvi element in ga nadomestite s formulo.

a 3 = q· a 2 , torej,q= 2

a 2 = q · 1,Zato a 1 = 3

S 6 = 189

· a 1 = 10, q= -2. Poiščite četrti element napredovanja.

Rešitev: za to je dovolj, da četrti element izrazimo skozi prvi in skozi imenovalec.

a 4 = q 3· a 1 = -80

Primer aplikacije:

Stranka banke je položila depozit v višini 10.000 rubljev, pod pogoji katerega se stranki vsako leto doda 6% glavnice. Koliko denarja bo na računu po 4 letih?

Rešitev: začetni znesek je 10 tisoč rubljev. To pomeni, da bo leto po naložbi na računu znesek 10.000 + 10.000 · 0,06 = 10000 1,06

V skladu s tem bo znesek na računu po naslednjem letu izražen na naslednji način:

(10000 · 1,06) · 0,06 + 10000 · 1,06 = 1,06 · 1,06 · 10000

To pomeni, da se vsako leto znesek poveča za 1,06-krat. To pomeni, da je za ugotovitev zneska sredstev na računu po 4 letih dovolj najti četrti element progresije, ki je podan s prvim elementom, ki je enak 10 tisoč in imenovalcem, ki je enak 1,06.

S = 1,06 1,06 1,06 1,06 10000 = 12625

Primeri težav pri izračunu vsote:

Geometrična progresija se uporablja pri različnih problemih. Primer za iskanje vsote je lahko naveden na naslednji način:

a 1 = 4, q= 2, izračunajS 5.

Rešitev: vsi potrebni podatki za izračun so znani, le vstaviti jih je treba v formulo.

S 5 = 124

a 2 = 6, a 3 = 18. Izračunaj vsoto prvih šestih elementov.

rešitev:

V geom. napredovanje, vsak naslednji element je q-krat večji od prejšnjega, to pomeni, da izračunate vsoto, morate poznati elementa 1 in imenovalecq.

a 2 · q = a 3

q = 3

Podobno morate najtia 1 , vedoča 2 inq.

a 1 · q = a 2

a 1 =2

S 6 = 728.

>>Matematika: Geometrijsko napredovanje

Za udobje bralca je ta odstavek zgrajen natančno po istem načrtu, kot smo mu sledili v prejšnjem odstavku.

1. Osnovni pojmi.

Opredelitev.Številsko zaporedje, katerega vsi členi so različni od 0 in katerega vsak člen, začenši od drugega, dobimo iz prejšnjega člena tako, da ga pomnožimo z istim številom, imenujemo geometrijska progresija. V tem primeru se število 5 imenuje imenovalec geometrijskega napredovanja.

Geometrična progresija je torej numerično zaporedje (b n), ki ga ponavljajoče določajo razmerja

Ali je mogoče pogledati številsko zaporedje in ugotoviti, ali gre za geometrijsko napredovanje? Lahko. Če ste prepričani, da je razmerje med katerim koli članom zaporedja in prejšnjim članom konstantno, potem imate geometrijsko napredovanje.
Primer 1.

1, 3, 9, 27, 81,... .
b 1 = 1, q = 3.

Primer 2.

To je geometrijsko napredovanje, ki ima
Primer 3.

To je geometrijsko napredovanje, ki ima
Primer 4.

8, 8, 8, 8, 8, 8,....

To je geometrijska progresija, v kateri je b 1 - 8, q = 1.

Upoštevajte, da je tudi to zaporedje aritmetična progresija (glej primer 3 iz § 15).

Primer 5.

2,-2,2,-2,2,-2.....

To je geometrijska progresija, v kateri je b 1 = 2, q = -1.

Očitno je geometrijsko napredovanje naraščajoče zaporedje, če je b 1 > 0, q > 1 (glej primer 1), in padajoče zaporedje, če je b 1 > 0, 0.< q < 1 (см. пример 2).

Da bi označili, da je zaporedje (b n) geometrijsko napredovanje, je včasih primeren naslednji zapis:

Ikona nadomešča frazo "geometrijsko napredovanje".
Upoštevajte eno zanimivo in hkrati precej očitno lastnost geometrijskega napredovanja:
Če zaporedje je geometrijska progresija, potem je zaporedje kvadratov, tj. je geometrijsko napredovanje.
V drugi geometrijski progresiji je prvi člen enak in enak q 2.
Če v geometrijski progresiji zavržemo vse člene, ki sledijo b n , dobimo končno geometrijsko progresijo
V nadaljnjih odstavkih tega razdelka bomo obravnavali najpomembnejše lastnosti geometrijske progresije.

2. Formula za n-ti člen geometrijske progresije.

Razmislite o geometrijski progresiji imenovalec q. Imamo:

Ni težko uganiti, da enakost velja za vsako število n

To je formula za n-ti člen geometrijske progresije.

Komentiraj.

Če ste prebrali pomembno pripombo iz prejšnjega odstavka in jo razumeli, poskusite formulo (1) dokazati z metodo matematične indukcije, tako kot je bilo to storjeno za formulo za n-ti člen aritmetične progresije.

Prepišimo formulo za n-ti člen geometrijske progresije

in uvedemo zapis: Dobimo y = mq 2 ali, podrobneje,
Argument x je vsebovan v eksponentu, zato se ta funkcija imenuje eksponentna funkcija. To pomeni, da lahko geometrijsko progresijo obravnavamo kot eksponentno funkcijo, definirano na množici N naravnih števil. Na sl. 96a prikazuje graf funkcije sl. 966 - funkcijski graf V obeh primerih imamo ločene točke (z abscisami x = 1, x = 2, x = 3 itd.), ki ležijo na določeni krivulji (obe sliki prikazujeta isto krivuljo, le da sta različno locirani in upodobljeni v različnih merilih). Ta krivulja se imenuje eksponentna krivulja. Več podrobnosti o eksponentni funkciji in njenem grafu bomo obravnavali pri predmetu algebra za 11. razred.

Vrnimo se k primerom 1-5 iz prejšnjega odstavka.

1) 1, 3, 9, 27, 81,... . To je geometrijska progresija, za katero je b 1 = 1, q = 3. Ustvarimo formulo za n-ti člen
2) To je geometrijska progresija, za katero ustvarimo formulo za n-ti člen

To je geometrijsko napredovanje, ki ima Ustvarimo formulo za n-ti člen
4) 8, 8, 8, ..., 8, ... . To je geometrijska progresija, za katero je b 1 = 8, q = 1. Ustvarimo formulo za n-ti člen
5) 2, -2, 2, -2, 2, -2,.... To je geometrijska progresija, v kateri je b 1 = 2, q = -1. Ustvarimo formulo za n-ti člen

Primer 6.

Glede na geometrijsko progresijo

V vseh primerih rešitev temelji na formuli n-tega člena geometrijske progresije

a) Če v formulo za n-ti člen geometrijske progresije vnesemo n = 6, dobimo

b) Imamo

Ker je 512 = 2 9, dobimo n - 1 = 9, n = 10.

d) Imamo

Primer 7.

Razlika med sedmim in petim členom geometrijske progresije je 48, vsota petega in šestega člena progresije je prav tako 48. Poiščite dvanajsti člen te progresije.

Prva stopnja. Izdelava matematičnega modela.

Pogoje problema lahko na kratko zapišemo takole:

Z uporabo formule za n-ti člen geometrijske progresije dobimo:
Potem lahko drugi pogoj problema (b 7 - b 5 = 48) zapišemo kot

Tretji pogoj problema (b 5 + b 6 = 48) lahko zapišemo kot

Kot rezultat dobimo sistem dveh enačb z dvema spremenljivkama b 1 in q:

ki v kombinaciji z zgoraj napisanim pogojem 1) predstavlja matematični model problema.

Druga faza.

Delo s prevedenim modelom. Če izenačimo levi strani obeh enačb sistema, dobimo:

(obe strani enačbe smo delili z ničelnim izrazom b 1 q 4).

Iz enačbe q 2 - q - 2 = 0 najdemo q 1 = 2, q 2 = -1. Če nadomestimo vrednost q = 2 v drugo enačbo sistema, dobimo
Če zamenjamo vrednost q = -1 v drugo enačbo sistema, dobimo b 1 1 0 = 48; ta enačba nima rešitev.

Torej, b 1 =1, q = 2 - ta par je rešitev sestavljenega sistema enačb.

Zdaj lahko zapišemo geometrijsko progresijo, ki je obravnavana v nalogi: 1, 2, 4, 8, 16, 32, ... .

Tretja stopnja.

Odgovor na problemsko vprašanje. Izračunati morate b 12. Imamo

Odgovor: b 12 = 2048.

3. Formula za vsoto členov končne geometrijske progresije.

Naj bo podana končna geometrijska progresija

Označimo s S n vsoto njegovih členov, tj.

Izpeljimo formulo za iskanje tega zneska.

Začnimo z najpreprostejšim primerom, ko je q = 1. Potem je geometrijska progresija b 1 , b 2 , b 3 ,..., bn sestavljena iz n števil, ki so enaka b 1 , tj. napredovanje je videti kot b 1, b 2, b 3, ..., b 4. Vsota teh števil je nb 1.

Naj bo zdaj q = 1. Za iskanje S n uporabimo umetno tehniko: izvedemo nekaj transformacij izraza S n q. Imamo:

Pri izvajanju transformacij smo najprej uporabili definicijo geometrijske progresije, po kateri (glej tretjo vrstico sklepanja); drugič so seštevali in odštevali, zaradi česar se pomen izraza seveda ni spremenil (glej četrto vrstico sklepanja); tretjič, uporabili smo formulo za n-ti člen geometrijske progresije:

Iz formule (1) najdemo:

To je formula za vsoto n členov geometrijske progresije (za primer, ko je q = 1).

Primer 8.

Glede na končno geometrijsko progresijo

a) vsota pogojev napredovanja; b) vsota kvadratov njegovih členov.

b) Zgoraj (glej str. 132) smo že ugotovili, da če vse člene geometrijske progresije kvadriramo, dobimo geometrijsko progresijo s prvim členom b 2 in imenovalcem q 2. Nato bo vsota šestih členov novega napredovanja izračunana z

Primer 9.

Poiščite 8. člen geometrijskega napredovanja, za katerega

Pravzaprav smo dokazali naslednji izrek.

Numerično zaporedje je geometrijsko napredovanje, če in samo če je kvadrat vsakega od njegovih členov, razen prvega izreka (in zadnjega, v primeru končnega zaporedja), enak produktu predhodnega in naslednjih členov ( značilna lastnost geometrijske progresije).

Od Masterweb

22.09.2018 22:00

Geometrična progresija je poleg aritmetične progresije pomemben številski niz, ki se preučuje v šolskem tečaju algebre v 9. razredu. V tem članku si bomo ogledali imenovalec geometrijske progresije in kako njegova vrednost vpliva na njene lastnosti.

Opredelitev geometrijske progresije

Najprej dajmo definicijo te številske serije. Geometrična progresija je niz racionalnih števil, ki nastane z zaporednim množenjem prvega elementa s konstantnim številom, imenovanim imenovalec.

Na primer, števila v nizu 3, 6, 12, 24, ... so geometrijsko napredovanje, ker če pomnožite 3 (prvi element) z 2, dobite 6. Če pomnožite 6 z 2, dobite 12 in tako naprej.

Člani obravnavanega zaporedja so običajno označeni s simbolom ai, kjer je i celo število, ki označuje številko elementa v nizu.

Zgornjo definicijo napredovanja lahko v matematičnem jeziku zapišemo takole: an = bn-1 * a1, kjer je b imenovalec. To formulo je enostavno preveriti: če je n = 1, potem je b1-1 = 1 in dobimo a1 = a1. Če je n = 2, potem je an = b * a1 in spet pridemo do definicije zadevnega niza števil. Podobno razmišljanje je mogoče nadaljevati za velike vrednosti n.

Imenovalec geometrijske progresije

Število b popolnoma določa, kakšen znak bo imela celotna številska serija. Imenovalec b je lahko pozitiven, negativen ali večji ali manjši od ena. Vse zgornje možnosti vodijo do različnih zaporedij:

b > 1. Obstaja naraščajoča vrsta racionalnih števil. Na primer 1, 2, 4, 8, ... Če je element a1 negativen, se bo celotno zaporedje povečalo le v absolutni vrednosti, zmanjšalo pa se bo odvisno od predznaka števil.
b = 1. Pogosto se ta primer ne imenuje progresija, saj obstaja običajna serija enakih racionalnih števil. Na primer -4, -4, -4.

Formula za znesek

Preden preidemo na obravnavo specifičnih problemov z uporabo imenovalca obravnavane vrste napredovanja, je treba podati pomembno formulo za vsoto njegovih prvih n elementov. Formula je videti takole: Sn = (bn - 1) * a1 / (b - 1).

Ta izraz lahko dobite sami, če upoštevate rekurzivno zaporedje členov napredovanja. Upoštevajte tudi, da je v zgornji formuli dovolj poznati samo prvi element in imenovalec, da bi našli vsoto poljubnega števila členov.

Neskončno padajoče zaporedje

Zgoraj je bilo razloženo, kaj je to. Zdaj, ko poznamo formulo za Sn, jo uporabimo za to številsko vrsto. Ker se vsako število, katerega modul ne presega 1, nagiba k ničli, ko je povišano na velike potence, to je b∞ => 0, če je -1

Ker bo razlika (1 - b) vedno pozitivna, ne glede na vrednost imenovalca, je predznak vsote neskončno padajoče geometrijske progresije S∞ enolično določen s predznakom njenega prvega elementa a1.

Zdaj pa si oglejmo več problemov, kjer bomo pokazali, kako pridobljeno znanje uporabiti na določenih številkah.

Naloga št. 1. Izračun neznanih elementov progresije in vsote

Pri podani geometrijski progresiji je imenovalec progresije 2, njen prvi element pa 3. Čemu bosta enaka njen 7. in 10. člen in kakšna je vsota njenih sedmih začetnih elementov?

Pogoj problema je precej preprost in vključuje neposredno uporabo zgornjih formul. Torej, za izračun številke elementa n uporabimo izraz an = bn-1 * a1. Za 7. element imamo: a7 = b6 * a1, če nadomestimo znane podatke, dobimo: a7 = 26 * 3 = 192. Enako naredimo za 10. člen: a10 = 29 * 3 = 1536.

Uporabimo dobro znano formulo za vsoto in določimo to vrednost za prvih 7 elementov serije. Imamo: S7 = (27 - 1) * 3 / (2 - 1) = 381.

Problem št. 2. Določanje vsote poljubnih elementov progresije

Naj bo -2 enako imenovalcu geometrijske progresije bn-1 * 4, kjer je n celo število. Določiti je treba vsoto od vključno 5. do 10. elementa te serije.

Zastavljenega problema ni mogoče rešiti neposredno z znanimi formulami. Rešimo jo lahko z 2 različnima metodama. Za popolnost predstavitve teme predstavljamo oboje.

Metoda 1. Ideja je preprosta: izračunati morate dve ustrezni vsoti prvih členov in nato od enega odšteti drugega. Izračunamo manjši znesek: S10 = ((-2)10 - 1) * 4 / (-2 - 1) = -1364. Zdaj izračunamo večjo vsoto: S4 = ((-2)4 - 1) * 4 / (-2 - 1) = -20. Upoštevajte, da so bili v zadnjem izrazu sešteti samo 4 členi, saj je 5. že vključen v znesek, ki ga je treba izračunati glede na pogoje problema. Na koncu vzamemo razliko: S510 = S10 - S4 = -1364 - (-20) = -1344.

2. način. Pred zamenjavo števil in štetjem lahko dobite formulo za vsoto med m in n členom zadevne serije. Delamo popolnoma enako kot pri 1. metodi, le da najprej delamo s simboličnim prikazom zneska. Imamo: Snm = (bn - 1) * a1 / (b - 1) - (bm-1 - 1) * a1 / (b - 1) = a1 * (bn - bm-1) / (b - 1) . V nastali izraz lahko nadomestite znana števila in izračunate končni rezultat: S105 = 4 * ((-2)10 - (-2)4) / (-2 - 1) = -1344.

Naloga št. 3. Kaj je imenovalec?

Naj bo a1 = 2, poiščite imenovalec geometrijske progresije, pod pogojem, da je njegova neskončna vsota 3, in vemo, da je to padajoča vrsta števil.

Na podlagi pogojev problema ni težko uganiti, katero formulo je treba uporabiti za njegovo rešitev. Seveda za vsoto progresije, ki neskončno pada. Imamo: S∞ = a1 / (1 - b). Od koder izrazimo imenovalec: b = 1 - a1 / S∞. Ostaja, da nadomestimo znane vrednosti in dobimo zahtevano število: b = 1 - 2 / 3 = -1 / 3 ali -0,333 (3). Ta rezultat lahko kvalitativno preverimo, če se spomnimo, da pri tej vrsti zaporedja modul b ne sme presegati 1. Kot lahko vidite, |-1 / 3|

Naloga št. 4. Obnovitev niza številk

Naj sta podana 2 elementa številske serije, na primer 5. je enak 30, 10. pa 60. Iz teh podatkov je treba rekonstruirati celotno vrsto, saj vemo, da izpolnjuje lastnosti geometrijske progresije.

Za rešitev naloge morate najprej zapisati ustrezen izraz za vsak znani izraz. Imamo: a5 = b4 * a1 in a10 = b9 * a1. Zdaj delimo drugi izraz s prvim, dobimo: a10 / a5 = b9 * a1 / (b4 * a1) = b5. Od tu določimo imenovalec tako, da vzamemo peti koren razmerja členov, znanih iz izjave problema, b = 1,148698. Dobljeno število nadomestimo z enim od izrazov za znani element, dobimo: a1 = a5 / b4 = 30 / (1,148698)4 = 17,2304966.

Geometrična progresija je številsko zaporedje, katerega prvi člen ni nič, vsak naslednji člen pa je enak prejšnjemu členu, pomnoženemu z istim številom, ki ni nič.

Označena je geometrijska progresija b1,b2,b3, …, bn, … .

Razmerje katerega koli člena geometrijske napake in njegovega prejšnjega člena je enako istemu številu, to je b2/b1 = b3/b2 = b4/b3 = ... = bn/b(n-1) = b( n+1)/bn = …. To neposredno izhaja iz definicije aritmetične progresije. To število imenujemo imenovalec geometrijske progresije. Običajno je imenovalec geometrijske progresije označen s črko q.

Monotono in konstantno zaporedje

Eden od načinov podajanja geometrijske progresije je podajanje njenega prvega člena b1 in imenovalca geometrijske napake q. Na primer, b1=4, q=-2. Ta dva pogoja določata geometrijsko progresijo 4, -8, 16, -32, ….

Če je q>0 (q ni enak 1), potem je napredovanje monotono zaporedje. Na primer, zaporedje 2, 4,8,16,32, ... je monotono naraščajoče zaporedje (b1=2, q=2).

Če je imenovalec v geometrijski napaki q=1, bodo vsi členi geometrijske progresije med seboj enaki. V takih primerih pravijo, da je napredovanje stalno zaporedje.

Formula za n-ti člen geometrijske progresije

Da bi bilo številsko zaporedje (bn) geometrijska progresija, mora biti vsak njegov člen, začenši z drugim, geometrična sredina sosednjih členov. To pomeni, da je treba izpolniti naslednjo enačbo
(b(n+1))^2 = bn * b(n+2), za vsak n>0, kjer n pripada množici naravnih števil N.

Formula za n-ti člen geometrijske progresije je:

bn=b1*q^(n-1),

kjer n pripada množici naravnih števil N.

Formula za vsoto prvih n členov geometrijske progresije

Formula za vsoto prvih n členov geometrijske progresije ima obliko:

Sn = (bn*q - b1)/(q-1), kjer q ni enak 1.

Poglejmo preprost primer:

V geometrijski progresiji b1=6, q=3, n=8 poiščite Sn.

Za iskanje S8 uporabimo formulo za vsoto prvih n členov geometrijske progresije.

S8= (6*(3^8 -1))/(3-1) = 19.680.

Aritmetična in geometrijska progresija

Teoretične informacije

Teoretične informacije

	Aritmetična progresija	Geometrijsko napredovanje
Opredelitev	Aritmetična progresija a n je zaporedje, v katerem je vsak člen, začenši z drugim, enak prejšnjemu členu, dodanemu istemu številu d (d- razlika v napredovanju)	Geometrijsko napredovanje b n je zaporedje neničelnih števil, katerih vsak člen, začenši z drugim, je enak prejšnjemu členu, pomnoženemu z istim številom q (q- imenovalec napredovanja)
Formula ponovitve	Za vsako naravno n a n + 1 = a n + d	Za vsako naravno n b n + 1 = b n ∙ q, b n ≠ 0
Formula n-ti člen	a n = a 1 + d (n – 1)	b n = b 1 ∙ q n - 1 , b n ≠ 0
Značilna lastnost
Vsota prvih n členov

Primeri nalog s komentarji

1. vaja

V aritmetični progresiji ( a n) a 1 = -6, a 2

Po formuli n-tega člena:

a 22 = a 1+ d (22 - 1) = a 1+ 21 d

Po stanju:

a 1= -6, torej a 22= -6 + 21 d .

Treba je najti razliko napredovanj:

d = a 2 – a 1 = -8 – (-6) = -2

a 22 = -6 + 21 ∙ (-2) = - 48.

odgovor: a 22 = -48.

Naloga 2

Poiščite peti člen geometrijske progresije: -3; 6;....

1. metoda (z uporabo formule n-členov)

Po formuli za n-ti člen geometrijske progresije:

b 5 = b 1 ∙ q 5 - 1 = b 1 ∙ q 4.

Ker b 1 = -3,

2. metoda (z uporabo ponavljajoče se formule)

Ker je imenovalec napredovanja -2 (q = -2), potem:

b 3 = 6 ∙ (-2) = -12;

b 4 = -12 ∙ (-2) = 24;

b 5 = 24 ∙ (-2) = -48.

odgovor: b 5 = -48.

Naloga 3

V aritmetični progresiji ( a n ) a 74 = 34; a 76= 156. Poiščite petinsedemdeseti člen te progresije.

Za aritmetično progresijo ima karakteristična lastnost obliko .

Zato:

Zamenjajmo podatke v formulo:

Odgovor: 95.

Naloga 4

V aritmetični progresiji ( a n ) a n= 3n - 4. Poiščite vsoto prvih sedemnajstih členov.

Za iskanje vsote prvih n členov aritmetičnega napredovanja se uporabljata dve formuli:

Kateri od njih je bolj primeren za uporabo v tem primeru?

Po pogoju je znana formula za n-ti člen prvotne progresije ( a n) a n= 3n - 4. Takoj lahko najdete in a 1, In a 16 brez najdbe d. Zato bomo uporabili prvo formulo.

Odgovor: 368.

Naloga 5

V aritmetični progresiji ( a n) a 1 = -6; a 2= -8. Poiščite dvaindvajseti člen napredovanja.

Po formuli n-tega člena:

a 22 = a 1 + d (22 – 1) = a 1+ 21 d.

Pod pogojem, če a 1= -6, torej a 22= -6 + 21d. Treba je najti razliko napredovanj:

d = a 2 – a 1 = -8 – (-6) = -2

a 22 = -6 + 21 ∙ (-2) = -48.

odgovor: a 22 = -48.

Naloga 6

Zapisanih je več zaporednih členov geometrijske progresije:

Poiščite člen napredovanja, označen z x.

Pri reševanju bomo uporabili formulo za n-ti člen b n = b 1 ∙ q n - 1 za geometrijske progresije. Prvi člen napredovanja. Če želite najti imenovalec progresije q, morate vzeti katerega koli od danih členov progresije in ga deliti s prejšnjim. V našem primeru lahko vzamemo in delimo z. Dobimo, da je q = 3. Namesto n v formulo nadomestimo 3, saj je treba najti tretji člen dane geometrijske progresije.

Če nadomestimo najdene vrednosti v formulo, dobimo: