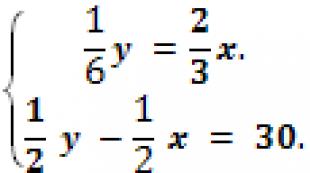ZGODOVINSKA REFERENCA

Kompleksna števila so bila uvedena v matematiko, da bi lahko vzeli kvadratni koren katerega koli realnega števila. To pa ni zadosten razlog za uvajanje novih števil v matematiko. Izkazalo se je, da če izvajate izračune po običajnih pravilih na izrazih, v katerih se pojavi kvadratni koren negativnega števila, lahko pridete do rezultata, ki ne vsebuje več kvadratnega korena negativnega števila. V XVI stoletju. Cardano je našel formulo za rešitev kubične enačbe. Izkazalo se je, da ko ima kubična enačba tri realne korenine, se kvadratni koren negativnega števila pojavi v formuli Cardano. Zato so kvadratne korene negativnih števil začeli uporabljati v matematiki in jih imenovali imaginarna števila - s tem so si tako rekoč pridobili pravico do nezakonitega obstoja. Gauss je dal polno državljansko pravico imaginarnim številom, ki jih je poimenoval kompleksna števila, podal geometrijsko razlago in dokazal temeljni izrek algebre, ki pravi, da ima vsak polinom vsaj en pravi koren.

1. POJEM KOMPLEKSNEGA ŠTEVILA

Rešitev številnih problemov v matematiki in fiziki se zmanjša na reševanje algebrskih enačb. Zato je preučevanje algebrskih enačb eno najpomembnejših vprašanj v matematiki. Želja, da bi bile enačbe rešljive, je eden glavnih razlogov za razširitev koncepta števila.

Torej za rešljivost enačb oblike X+A=B pozitivna števila niso dovolj. Na primer, enačba X+5=2 nima pozitivnih korenin. Zato morate vnesti negativna števila in ničlo.

Na množici racionalnih števil so rešljive algebraične enačbe prve stopnje, tj. enačbe oblike A · X+B=0 (A0). Vendar algebraične enačbe stopnje, višje od ena, morda nimajo racionalnih korenin. Takšni sta na primer enačbi X 2 =2, X 3 =5. Potreba po reševanju takih enačb je bila eden od razlogov za uvedbo iracionalnih števil. Racionalna in iracionalna števila tvorijo množico realnih števil.

Vendar realna števila niso dovolj za rešitev katere koli algebraične enačbe. Na primer, kvadratna enačba z realnimi koeficienti in negativnim diskriminantom nima realnih korenin. Najenostavnejša med njimi je enačba X 2 +1=0. Zato je treba množico realnih števil razširiti tako, da ji dodamo nova števila. Ta nova števila skupaj z realnimi števili tvorijo množico, ki jo imenujemo množica kompleksna števila.

Najprej ugotovimo, kakšno obliko morajo imeti kompleksna števila. Predpostavimo, da ima na množici kompleksnih števil enačba X 2 +1=0 koren. Ta koren označujemo s črko jaz torej jaz je kompleksno število tako, da jaz 2 = –1.

Pri realnih številih je treba uvesti operaciji seštevanja in množenja kompleksnih števil, da bi bila njihova vsota in produkt kompleksna števila. Potem še posebej za poljubna realna števila A in B izraz A + B jaz si lahko predstavljamo kot splošno predstavitev kompleksnega števila. Ime "kompleks" izhaja iz besede "kompozit": v obliki izraza A + B jaz .

Kompleksna števila imenujemo izrazi oblike A+B jaz , kjer sta A in B realni števili in jaz je neki lik tak, da jaz 2 = –1 in označeno s črko Z.

Število A imenujemo realni del kompleksnega števila A+B jaz, in število B je njen imaginarni del. številka jaz se imenuje imaginarna enota.

Na primer realni del kompleksnega števila 2+3 jaz je 2 in imaginarij je 3.

Za strogo definicijo kompleksnega števila je potrebno uvesti koncept enakosti teh števil.

Dve kompleksni števili A+B jaz in C+D jaz klical enakače in samo če je A=C in B=D, tj. ko sta njun realni in imaginarni del enaka.

2. GEOMETRIJSKA INTERPRETACIJA KOMPLEKSNEGA ŠTEVILA

Realna števila so geometrijsko predstavljena s točkami na številski premici. Kompleksno število A+B jaz lahko gledamo kot par realnih števil (A;B). Zato je naravno kompleksno število predstaviti kot točke v ravnini. V pravokotnem koordinatnem sistemu je kompleksno število Z=A+B· jaz je predstavljena z ravninsko točko s koordinatami (A;B), to točko pa označujemo z isto črko Z (slika 1). Očitno je korespondenca, pridobljena v tem primeru, ena proti ena. Omogoča interpretacijo kompleksnih števil kot točk na ravnini, na kateri je izbran koordinatni sistem. Ta koordinatna ravnina se imenuje kompleksna ravnina . Abscisa se imenuje prava os , Ker na njej so točke, ki ustrezajo realnim številom. Y-os se imenuje imaginarna os – vsebuje točke, ki ustrezajo namišljenim kompleksnim številom.

Nič manj pomembna in priročna je razlaga kompleksnega števila A+B jaz kot vektor, tj. vektorji z izhodiščem v točki

O(0;0) in se konča v točki M(A;B) (slika 2).

Korespondenca, vzpostavljena med množico kompleksnih števil na eni strani in množico točk ali vektorjev ravnine na drugi, omogoča, da so kompleksna števila točke ali vektorji.

3.MODUL KOMPLEKSNEGA ŠTEVILA

Naj bo kompleksno število Z=A+B· jaz . Konjugirano z Z imenujemo kompleksno število A-B jaz , ki ga označujemo z , tj.

A-B jaz .

Upoštevajte, da = A + B jaz , torej za vsako kompleksno število Z velja enakost =Z.

modul kompleksno število Z=A+B jaz klical število in je označena z , tj.

Iz formule (1) sledi, da je za vsako kompleksno število Z in =0, če in samo če je Z=0, tj. ko je A=0 in B=0. Dokažimo, da za poljubno kompleksno število Z veljajo formule:

4. SEŠTEVANJE IN MNOŽENJE KOMPLEKSNIH ŠTEVIL

vsota dve kompleksni števili A+B jaz in C+D jaz se imenuje kompleksno število (A+C ) + ( B+D)· jaz , tj. ( A+B jaz) + ( C+D jaz)=( A+C) + (B+D) jaz

delo dve kompleksni števili A+B jaz in C+D jaz se imenuje kompleksno število (A C – B D)+(A D+B C) jaz , tj.

(A + B jaz ) (C + D jaz )=(A C – B D) + (A D + B C) jaz

Iz formul sledi, da lahko seštevanje in množenje izvajamo po pravilih operacij s polinomi, če predpostavimo jaz 2 = -1. Operaciji seštevanja in množenja kompleksnih števil imata lastnosti realnih števil. Osnovne lastnosti:

Prenos nepremičnine:

Z 1 + Z 2 \u003d Z 2 + Z 1, Z 1 Z 2 \u003d Z 2 Z 1

Asociativna lastnost:

(Z 1 + Z 2) + Z 3 \u003d Z 1 + (Z 2 + Z 3), (Z 1 Z 2) Z 3 \u003d Z 1 (Z 2 Z 3)

Distribucijska lastnost:

Z 1 (Z 2 + Z 3) \u003d Z 1 Z 2 + Z 1 Z 3

Geometrična predstavitev vsote kompleksnih števil

Po definiciji seštevanja dveh kompleksnih števil je realni del vsote enak vsoti realnih delov členov, imaginarni del vsote je enak vsoti imaginarnih delov členov. Koordinate vsote vektorjev se določijo na enak način:

Vsota dveh vektorjev s koordinatami (A 1 ;B 1) in (A 2 ;B 2) je vektor s koordinatami (A 1 +A 2 ;B 1 +B 2). Zato morate za iskanje vektorja, ki ustreza vsoti kompleksnih števil Z 1 in Z 2, sešteti vektorja, ki ustrezata kompleksnima številoma Z 1 in Z 2 .

Primer 1: Poiščite vsoto in produkt kompleksnih števil Z 1 =2 - 3× jaz in

Z 2 \u003d -7 + 8 × jaz .

Z 1 + Z 2 \u003d 2 - 7 + (-3 + 8) × jaz = - 5 + 5× jaz

Z 1× Z 2 = (2 – 3× jaz )× (–7 + 8× jaz ) = –14 + 16× jaz + 21× jaz + 24 = 10 + 37× jaz

5. ODŠTEVANJE IN DELJENJE KOMPLEKSNIH ŠTEVIL

Odštevanje kompleksnih števil je inverzna operacija seštevanja: za katerokoli kompleksno število Z 1 in Z 2 obstaja in poleg tega samo eno, število Z, tako da:

Če obema deloma enačbe (–Z 2) prištejemo nasprotje števila Z 2:

Z + Z 2 + (-Z 2) \u003d Z 1 + (-Z 2), od koder

Pokliče se število Z \u003d Z 1 + Z 2 razlika števil Z 1 in Z 2 .

Deljenje je uvedeno kot obratno množenje:

Z × Z 2 \u003d Z 1

Če oba dela delimo z Z 2, dobimo:

Ta enačba kaže, da je Z 2 0

Geometrična predstavitev razlike kompleksnih števil

Razlika Z 2 - Z 1 kompleksnih števil Z 1 in Z 2 ustreza razliki vektorjev, ki ustrezata številoma Z 1 in Z 2 . Modul razlike dveh kompleksnih števil Z 2 in Z 1 je po definiciji modula dolžina vektorja Z 2 - Z 1 . Ta vektor sestavimo kot vsoto vektorjev Z 2 in (–Z 1) (slika 4). Tako je modul razlike dveh kompleksnih števil razdalja med točkama kompleksne ravnine, ki ustrezata tem številom.

Ta pomembna geometrijska razlaga modula razlike dveh kompleksnih števil omogoča uspešno uporabo preprostih geometrijskih dejstev.

Primer 2: Dana kompleksna števila Z 1 = 4 + 5 jaz in Z 2 = 3 + 4 jaz . Poiščite razliko Z 2 - Z 1 in količnik

Z 2 - Z 1 \u003d (3 + 4) jaz) – (4 + 5 jaz) = –1 – jaz

==

6. TRIGONOMETRIJSKA OBLIKA KOMPLEKSNEGA ŠTEVILA

Zapis kompleksnega števila Z kot A+B jaz klical algebrska oblika kompleksno število. Poleg algebrske oblike se uporabljajo tudi druge oblike zapisa kompleksnih števil.

Razmislite trigonometrična oblika zapis kompleksnega števila. Realni in imaginarni deli kompleksnega števila Z=A+B jaz so izraženi v smislu njegovega modula = r in argumenta j, kot sledi:

A= r cosj ; B= r sinj .

Število Z lahko zapišemo takole:

Z= r cosj + jaz sinj = r (cosj + jaz sinj)

Z = r (cosj + jaz sinj ) (2)

Ta vnos se imenuje trigonometrična oblika kompleksnega števila .

r = je modul kompleksnega števila.

Število j imenujemo argument kompleksnega števila.

Argument kompleksnega števila Z0 je vrednost kota med pozitivno smerjo realne osi in vektorjem Z, pri čemer velja, da je vrednost kota pozitivna, če je štetje v nasprotni smeri urinega kazalca, in negativno, če je v smeri urinega kazalca.

Pri številu Z=0 argument ni definiran in le v tem primeru je število podano le z modulom.

Kot je navedeno zgoraj = r =, lahko enakost (2) zapišemo kot

A+B jaz =· cosj + jaz · sinj , od koder z enačenjem realnega in imaginarnega dela dobimo:

cosj =, sinj = (3)

če sinj deli z cosj dobimo:

tgj= (4)

To formulo je bolj priročno uporabiti za iskanje argumenta j kot formule (3). Vendar niso vse vrednosti j, ki izpolnjujejo enakost (4), argumenti števila A + B jaz . Zato morate pri iskanju argumenta upoštevati, v kateri četrtini se nahaja točka A + B jaz .

7. LASTNOSTI MODULA IN ARGUMENTA KOMPLEKSNEGA ŠTEVILA

Z uporabo trigonometrične oblike je priročno najti produkt in količnik kompleksnih števil.

Naj bo Z 1 = r 1 ( cosj 1 +jaz sinj 1), Z 2 = r 2 ( cosj 2 +jaz sinj 2). Nato:

Z 1 Z 2 = r 1 r 2 =

= r 1 r 2 .

Tako lahko produkt kompleksnih števil, zapisanih v trigonometrični obliki, najdemo po formuli:

Z 1 Z 2 = r 1 r 2 (5)

Iz formule (5) sledi, da pri množenju kompleksnih števil se njihovi moduli pomnožijo in argumenti seštejejo.

Če je Z 1 \u003d Z 2, dobimo:

Z2=2= r 2 (cos2j +jaz sin2j)

Z 3 \u003d Z 2 Z \u003d r 2 ( cos2j +jaz sin2j ) r (cosj + jaz sinj )=

= r 3 ( cos3j +jaz sin3j)

Na splošno za katero koli kompleksno število Z=r (cosj + jaz sinj )0 in poljubno naravno število n velja formula:

Zn=[ r (cosj + jaz sinj )] n = r n (cosnj + jaz sinnj ),(6)

ki se imenuje De Moivrejeva formula.

Kvocient dveh kompleksnih števil, zapisanih v trigonometrični obliki, je mogoče najti po formuli:

[cos(j 1 – j 2) + jaz sin(j 1 - j 2)].(7)

= = cos(–j 2) + jaz greh (–j 2)

Uporaba formule 5

(cosj 1 + jaz sinj 1)× (cos(–j 2) + jaz sin(–j 2)) =

cos(j 1 – j 2) + jaz sin(j 1 - j 2).

Primer 3:

Število -8 zapišemo v trigonometrični obliki

8 = 8 (cos(p + 2p k ) + jaz sin(p + 2p k )), k О Z

Naj bo Z = r× (cosj + i×

r 3× (cos3j + i× sin3j ) = 8 (cos(p + 2p k ) + jaz sin(p + 2p k )), k О Z

Potem je 3j =p + 2p k , k О Z

j= , k О Z

Zato:

Z = 2 (cos() + jaz sin()), k О Z

k = 0,1,2...

k = 0

Z 1 = 2 (cos + jaz greh) = 2 ( jaz) = 1+× jaz

k = 1

Z 2 = 2 (cos( ​​​​+ ) + jaz sin( + )) = 2 (cosp + jaz sinp) = –2

k = 2

Z 3 = 2 (cos( ​​​​+ ) + jaz sin( + )) = 2 (cos + jaz sin) = 1–× jaz

Odgovor: Z 13 =; Z 2 \u003d -2

Primer 4:

Število 1 zapišemo v trigonometrični obliki

1 = 1 (cos(2p k ) + jaz sin(2p k )), k О Z

Naj bo Z = r× (cosj + i× sinj ), potem bo ta enačba zapisana kot:

r 4× (cos4j + i× sin4j ) = cos(2p k ) + jaz sin(2p k )), k О Z

4j = 2p k , k О Z

j = , k О Z

Z = cos+ i× greh

k = 0,1,2,3...

k = 0

Z1 = cos0+ i× sin0 = 1 + 0 = 1

k = 1

Z2 = cos + i× greh=0+ jaz = jaz

k = 2

Z 3 \u003d cosp + jaz sinp = -1 + 0 = -1

k = 3

Z4 = cos+ i× greh

Odgovor: Z 13 = 1

Z 24 = jaz

8. Potenciranje in izločanje korena

Formula 6 kaže, da dvig kompleksnega števila r (cosj + jaz sinj ) na pozitivno celo potenco z naravnim eksponentom, se njegov modul dvigne na potenco z enakim eksponentom, argument pa se pomnoži z eksponentom.

[ r (cosj + jaz sinj )] n = r n (cos nj + jaz greh nj )

številka Z klical koren stopnje n iz števila w (označeno z ), če je Z n =w .

Iz te definicije sledi, da je vsaka rešitev enačbe Z n = w je koren stopnje n od številke w. Z drugimi besedami, da bi izluščili koren stopnje n iz števila w je dovolj za rešitev enačbe Z n =w.Če je w =0, potem za kateri koli n enačba Z n = w ima samo eno rešitev Z= 0. Če je w 0, potem Z0 , in posledično lahko Z in w predstavimo v trigonometrični obliki

Z = r (cosj + jaz sinj ), w = p (prijetno + jaz siny)

Enačba Z n = w bo imela obliko:

r n (cos nj + jaz sin nj ) = p (udoben + jaz siny)

Dve kompleksni števili sta enaki, če in samo če sta njuna modula enaka in se njuna argumenta razlikujeta v členih, ki so večkratniki 2p. Zato je r n = p in nj = y + 2p k , kjer je kn Z ali r = in j= , kjer je kн Z .

Torej lahko vse rešitve zapišemo na naslednji način:

Z K =, kн Z (8)

Formula 8 se imenuje De Moivrejeva druga formula.

Torej, če je w 0, potem obstaja natanko n korenin stopnje n iz števila w: vse so vsebovane v formuli 8. Vse korenine stopnje n iz števila w imajo enak modul, vendar različne argumente, ki se razlikujejo v seštevku, ki je večkratnik števila. Iz tega sledi, da kompleksna števila, ki so korenine stopnje n iz kompleksnega števila w, ustrezajo točkam kompleksne ravnine, ki se nahajajo v ogliščih pravilnega n-kotnika, včrtanega v krog s polmerom s središčem v točki Z = 0.

Simbol nima enoznačnega pomena. Zato je treba pri njegovi uporabi jasno razumeti, kaj pomeni ta simbol. Na primer, z uporabo zapisa bi morali razmisliti o tem, da bi bilo jasno, da ta simbol pomeni par kompleksnih števil jaz in -jaz , ali enega, potem katerega.

Enačbe višjih potenc

Formula 8 določa vse korene dvočlenske enačbe stopnje n. Situacija je neizmerno bolj zapletena v primeru splošne algebraične enačbe stopnje n:

a n × Z n+ a n–1× Z n–1 +...+ a 1× Z 1 + a 0 = 0(9)

Kjer so a n ,..., a 0 podana kompleksna števila.

Pri predmetu višje matematike je dokazan Gaussov izrek: vsaka algebraična enačba ima vsaj en koren v množici kompleksnih števil. Ta izrek je leta 1779 dokazal nemški matematik Carl Gauss.

Na podlagi Gaussovega izreka lahko dokažemo, da lahko levo stran enačbe 9 vedno predstavimo kot produkt:

,

Kjer so Z 1 , Z 2 ,..., Z K nekatera različna kompleksna števila,

in a 1 ,a 2 ,...,a k so naravna števila in:

a 1 + a 2 + ... + a k = n

To pomeni, da so števila Z 1 , Z 2 ,..., Z K koreni enačbe 9. V tem primeru pravijo, da je Z 1 koren množice a 1 , Z 2 koren množice a 2 in tako naprej

Gaussov izrek in pravkar formulirani izrek dajeta rešitve o obstoju korenin, ne povesta pa nič o tem, kako najti te korenine. Če je korenine prve in druge stopnje mogoče zlahka najti, potem so za enačbe tretje in četrte moči formule okorne, za enačbe stopnje višje od četrte pa takšne formule sploh ne obstajajo. Odsotnost splošne metode ne preprečuje iskanja vseh korenin enačbe. Za reševanje enačbe s celimi koeficienti je pogosto uporaben naslednji izrek: celoštevilske korenine katere koli algebrske enačbe s celimi koeficienti so delitelji konstantnega člena.

Dokažimo ta izrek:

Naj bo Z = k celoštevilski koren enačbe

a n× Z n + a n–1× Z n–1 +...+ a 1× Z 1 + a 0 = 0

s celimi koeficienti. Potem

a n× k n + a n–1× k n–1 +...+ a 1× k 1 + a 0 = 0

a 0 = – k(a n× k n–1 + a n–1× k n–2 +...+ a 1)

Število v oklepaju je pod postavljenimi predpostavkami očitno celo število, kar pomeni, da je k delitelj števila a 0 .

9.KVADRATNA ENAČBA S KOMPLEKSNO NEZNANO

Razmislite o enačbi Z 2 = a, kjer je a dano realno število, Z je neznanka.

To je enačba:

Število a zapišemo v obliki a = (– 1)× (– a) = jaz 2× = jaz 2× () 2 . Nato bo enačba Z 2 = a zapisana v obliki: Z 2 - jaz 2×() 2 = 0

tiste. (Z- i× )(Z + i× ) = 0

Zato ima enačba dva korena: Z 1.2 = i×

Uveden koncept korena iz negativnega števila nam omogoča, da zapišemo korene poljubne kvadratne enačbe z realnimi koeficienti

a× Z 2 + b× Z + c = 0

Po znani splošni formuli

Z 1,2 = (10)

Torej, za vsak realni a(a0), b, c, lahko korenine enačbe najdemo s formulo 10. Še več, če je diskriminanta, tj. radikalni izraz v formuli 10

D \u003d b 2 - 4 × a × c

pozitivna, potem ima enačba a× Z 2 + b× Z + c = 0 dva realna različna korena. Če je D = 0, ima enačba a × Z 2 + b × Z + c = 0 en koren. Če D< 0, то уравнение a× Z 2 + b× Z + c = 0 имеет два различных комплексных корня.

Kompleksni koreni kvadratne enačbe imajo enake lastnosti kot znane lastnosti realnih korenov.

Oblikujmo glavne:

Naj sta Z 1 ,Z 2 korena kvadratne enačbe a× Z 2 + b× Z + c = 0, a0. Potem so lastnosti resnične:

Z 1 × Z 2 =

1. Za vse kompleksne Z je formula

a × Z 2 + b × Z + c \u003d a × (Z - Z 1) × (Z - Z 2)

Primer 5:

Z 2 - 6 Z + 10 \u003d 0

D \u003d b 2 - 4 a c

D \u003d 6 2 - 4 10 \u003d - 4

– 4 = jaz 2 ·4

Z 1,2 =

Odgovor: Z 1 \u003d Z 2 \u003d 3 + jaz

Primer 6:

3 Z 2 +2 Z + 1 = 0

D \u003d b 2 - 4 a c

D \u003d 4 - 12 \u003d - 8

D \u003d -1 8 \u003d 8 jaz 2

Z 1,2 = =

Odgovor: Z 1 \u003d Z 2 \u003d -

Primer 7:

Z 4 - 8 Z 2 - 9 = 0

t 2 - 8 t - 9 = 0

D \u003d b 2 - 4 a c \u003d 64 + 36 \u003d 100

t 1 \u003d 9 t 2 \u003d - 1

Z 2 \u003d 9 Z 2 \u003d - 1

Z 3,4 = jaz

Odgovor: Z 1,2 \u003d 3, Z 3,4 \u003d jaz

Primer 8:

Z 4 + 2 Z 2 - 15 \u003d 0

t 2 + 2 t - 15 \u003d 0

D \u003d b 2 - 4 a c \u003d 4 + 60 \u003d 64

t 1,2 = = = –14

t 1 \u003d - 5 t 2 \u003d 3

Z 2 \u003d - 5 Z 2 \u003d 3

Z 2 \u003d - 1 5 Z 3,4 \u003d

Z2 = jaz 2 ·5

Z 1,2 = jaz

Odgovor: Z 1,2 = jaz , Z 3,4 =

Primer 9:

Z 2 = 24 10 jaz

Naj bo Z = X + Y jaz

(X + Y jaz ) 2 = X 2 + 2 X Y jaz – Y2

X 2 + 2 X Y Y jaz – Y 2 = 24 10 jaz

(X 2 Y 2) + 2 X Y jaz = 24 10 jaz

pomnožite z X 2 0

X 4 - 24 X 2 - 25 = 0

t 2 - 24 t - 25 = 0

t 1 t 2 \u003d - 25

t 1 \u003d 25 t 2 \u003d - 1

X 2 \u003d 25 X 2 \u003d - 1 - ni rešitev

X 1 \u003d 5 X 2 \u003d - 5

Y 1 = - Y 2 =

Y 1 = - 1 Y 2 = 1

Z 1,2 \u003d (5 - jaz )

Odgovor: Z 1,2 \u003d (5 - jaz )

NALOGE:

(2 - Y) 2 + 3 (2 - Y) Y + Y 2 = 6

4 - 4 Y + Y 2 + 6 Y - 3 Y 2 + Y 2 = 6

-Y 2 + 2Y - 2 \u003d 0 / -1

Y 2 - 2Y + 2 = 0

D \u003d b 2 - 4 a c \u003d 4 - 8 \u003d - 4

– 4 = – 1 4 = 4 jaz 2

Y 1,2 = = = 1 jaz

Y 1 = 1– jaz Y 2 \u003d 1 + jaz

X 1 = 1 + jaz X 2 \u003d 1– jaz

Odgovor: (1 + jaz ; 1–jaz }

{1–jaz ; 1 + jaz }

Kvadratiramo

Če morate poimenovati razdaljo med dvema mestoma, lahko navedete eno samo številko v miljah, kilometrih ali drugih enotah linearne razdalje. Če pa morate opisati, kako priti iz enega mesta v drugo, potem morate dati več informacij kot le razdaljo med dvema točkama na zemljevidu. V tem primeru je vredno povedati o smeri, v katero se morate premakniti, in o tem.

Vrsta informacije, ki izraža enodimenzionalno dimenzijo, se v znanosti imenuje skalarna količina. Skalarji so števila, ki se uporabljajo v večini matematičnih izračunov. Na primer, masa in hitrost, ki ju ima predmet, sta skalarni količini.

Za uspešno analizo naravnih pojavov moramo delati z abstraktnimi objekti in metodami, ki lahko predstavljajo večdimenzionalne količine. Tukaj je treba opustiti skalarna števila v korist kompleksnih. Omogočajo izražanje dveh dimenzij hkrati.

Kompleksna števila je lažje razumeti, če so predstavljena grafično. Če ima črta določeno dolžino in smer, bo to grafična predstavitev. Splošno znan je tudi kot vektor.

Razlike med kompleksnimi in skalarnimi količinami

Takšne vrste števil, kot so cela, racionalna in realna števila, so otrokom poznane že v šoli. Vsi imajo enodimenzionalnost. Ravnost številske premice to grafično ponazarja. Po njej se lahko premikate gor ali dol, vendar bodo vsi "premiki" vzdolž te črte omejeni na vodoravno os. Enodimenzionalna, skalarna števila zadostujejo za štetje števila predmetov, izražanje teže ali merjenje enosmerne napetosti baterije. Ne morejo pa pomeniti nečesa bolj zapletenega. Skalarji ne morejo hkrati izraziti razdalje in smeri med dvema mestoma ali amplitude s fazo. Te vrste števil je treba predstaviti že v obliki večdimenzionalnega obsega vrednosti. Z drugimi besedami, potrebujemo vektorske količine, ki imajo lahko ne le velikost, ampak tudi smer širjenja.

Zaključek

Skalarno število je vrsta matematičnega predmeta, ki smo ga ljudje navajeni uporabljati v vsakdanjem življenju - to je temperatura, dolžina, teža itd. Kompleksno število je vrednost, ki vključuje dve vrsti podatkov.

Vektor je grafični prikaz kompleksnega števila. Videti je kot puščica z začetno točko ter določeno dolžino in smerjo. Včasih se beseda "vektor" uporablja v radijski tehniki, kjer izraža fazni premik med signali.

Pri preučevanju lastnosti kvadratne enačbe je bila postavljena omejitev - za diskriminanto, manjšo od nič, ni rešitve. Takoj je bilo določeno, da govorimo o nizu realnih števil. Radovedni um matematika bo zanimalo - kaj je skrivnost, ki jo vsebuje zadržek o resničnih vrednostih?

Sčasoma so matematiki predstavili koncept kompleksnih števil, kjer je pogojna vrednost drugega korena minus ena vzeta kot enota.

Zgodovinska referenca

Matematična teorija se razvija zaporedno, od enostavnega do zapletenega. Ugotovimo, kako je nastal koncept, imenovan "kompleksno število", in zakaj je to potrebno.

Že od nekdaj je osnova matematike običajen račun. Raziskovalci so poznali samo naravni niz vrednot. Seštevanje in odštevanje je bilo preprosto. Ko so ekonomski odnosi postajali bolj zapleteni, se je začelo uporabljati množenje namesto seštevanja istih vrednosti. Obstaja obratna operacija množenju - deljenje.

Koncept naravnega števila je omejil uporabo aritmetičnih operacij. Nemogoče je rešiti vse probleme deljenja na množici celih vrednosti. pripeljala najprej do koncepta racionalnih pomenov, nato pa do iracionalnih pomenov. Če je za racionalno mogoče navesti točno lokacijo točke na premici, potem je za iracionalno takšne točke nemogoče navesti. Interval lahko določite le približno. Zveza racionalnih in iracionalnih števil je tvorila realno množico, ki jo lahko predstavimo kot določeno črto v danem merilu. Vsak korak vzdolž črte je naravno število, med njimi pa so racionalne in iracionalne vrednosti.

Začelo se je obdobje teoretične matematike. Razvoj astronomije, mehanike, fizike je zahteval reševanje vse bolj zapletenih enačb. Na splošno so bile najdene korenine kvadratne enačbe. Pri reševanju kompleksnejšega kubičnega polinoma so znanstveniki naleteli na protislovje. Koncept kubnega korena iz negativnega je smiseln, toda za kvadratni koren dobimo negotovost. Poleg tega je kvadratna enačba le poseben primer kubične.

Leta 1545 je Italijan J. Cardano predlagal uvedbo koncepta imaginarnega števila.

To število je bil drugi koren iz minus ena. Izraz kompleksno število se je dokončno izoblikoval šele tristo let pozneje, v delih slovitega matematika Gaussa. Predlagal je formalno razširitev vseh zakonov algebre na imaginarno število. Realna premica se je razširila na ravnino. Svet je postal večji.

Osnovni pojmi

Spomnite se številnih funkcij, ki imajo omejitve glede realnega niza:

• y = arcsin(x), definiran v območju vrednosti med negativno in pozitivno.
• y = ln(x), je smiselno za pozitivne argumente.
• kvadratni koren y = √x, izračunan samo za x ≥ 0.

Če označimo i = √(-1), uvedemo tak koncept kot imaginarno število, to bo odstranilo vse omejitve iz domene definicije zgornjih funkcij. Izrazi, kot so y = arcsin(2), y = ln(-4), y = √(-5), so smiselni v nekem prostoru kompleksnih števil.

Algebraično obliko lahko zapišemo kot izraz z = x + i×y na množici realnih vrednosti x in y ter i 2 = -1.

Nov koncept odpravlja vse omejitve pri uporabi katere koli algebrske funkcije in po svojem videzu spominja na graf premice v koordinatah realnih in namišljenih vrednosti.

Kompleksno letalo

Geometrijska oblika kompleksnih števil nam omogoča vizualno predstavitev mnogih njihovih lastnosti. Na osi Re (z) označimo realne vrednosti x, na Im (z) - namišljene vrednosti y, nato pa bo točka z na ravnini prikazala zahtevano kompleksno vrednost.

Definicije:

• Re(z) - realna os.
• Im(z) - pomeni imaginarno os.
• z je pogojna točka kompleksnega števila.
• Številčno vrednost dolžine vektorja od ničelne točke do z imenujemo modul.
• Realna in namišljena os delita ravnino na četrtine. S pozitivno vrednostjo koordinat - I četrtina. Ko je argument realne osi manjši od 0, imaginarne osi pa je večja od 0 - II četrtina. Ko so koordinate negativne - III četrtina. Zadnje, četrto četrtletje vsebuje veliko pozitivnih realnih vrednosti in negativnih imaginarnih vrednosti.

Tako lahko na ravnini z vrednostma koordinat x in y vedno vizualiziramo točko kompleksnega števila. Simbol i je uveden, da loči realni del od imaginarnega.

Lastnosti

1. Ko je vrednost imaginarnega argumenta nič, dobimo samo število (z = x), ki se nahaja na realni osi in pripada realni množici.
2. V posebnem primeru, ko vrednost realnega argumenta postane nič, izraz z = i×y ustreza lokaciji točke na imaginarni osi.
3. Splošna oblika z = x + i×y bo za neničelne vrednosti argumentov. Pomeni lokacijo točke, ki označuje kompleksno število v eni od četrtin.

trigonometrični zapis

Spomnimo se polarnega koordinatnega sistema ter definicije sin in cos. Očitno je, da je s pomočjo teh funkcij mogoče opisati lokacijo katere koli točke na ravnini. Če želite to narediti, je dovolj, da poznate dolžino polarnega žarka in kot naklona na realno os.

Opredelitev. Vnos v obliki ∣z ∣, pomnožen z vsoto trigonometričnih funkcij cos(ϴ) in imaginarnega dela i ×sin(ϴ), imenujemo trigonometrično kompleksno število. Tukaj je oznaka naklonski kot glede na realno os

ϴ = arg(z) in r = ∣z∣, dolžina žarka.

Iz definicije in lastnosti trigonometričnih funkcij sledi zelo pomembna De Moivrova formula:

z n = r n × (cos(n × ϴ) + i × sin(n × ϴ)).

S to formulo je priročno rešiti številne sisteme enačb, ki vsebujejo trigonometrične funkcije. Še posebej, ko se pojavi naloga potenciranja.

Modul in faza

Za dokončanje opisa kompleksne množice predlagamo dve pomembni definiciji.

Poznavanje Pitagorovega izreka je enostavno izračunati dolžino žarka v polarnem koordinatnem sistemu.

r = ∣z∣ = √(x 2 + y 2), se tak zapis na kompleksnem prostoru imenuje "modul" in označuje razdaljo od 0 do točke na ravnini.

Kot nagiba kompleksnega žarka glede na realno premico ϴ običajno imenujemo faza.

Iz definicije je razvidno, da sta realni in imaginarni del opisana s cikličnimi funkcijami. namreč:

• x = r × cos(ϴ);
• y = r × sin(ϴ);

Nasprotno pa je faza povezana z algebraičnimi vrednostmi prek formule:

ϴ = arctan(x / y) + µ, je popravek µ uveden zaradi upoštevanja periodičnosti geometrijskih funkcij.

Eulerjeva formula

Matematiki pogosto uporabljajo eksponentno obliko. Števila kompleksne ravnine so zapisana kot izraz

z = r × e i × ϴ , kar izhaja iz Eulerjeve formule.

Takšen zapis je postal razširjen za praktično računanje fizikalnih količin. Oblika predstavitve v obliki eksponentnih kompleksnih števil je še posebej primerna za inženirske izračune, kjer je treba izračunati tokokroge s sinusoidnimi tokovi in ​​je treba poznati vrednost integralov funkcij z danim obdobjem. Sami izračuni služijo kot orodje pri načrtovanju različnih strojev in mehanizmov.

Definiranje operacij

Kot smo že omenili, vsi algebraični zakoni dela z osnovnimi matematičnimi funkcijami veljajo za kompleksna števila.

operacija vsote

Pri seštevanju kompleksnih vrednosti se seštevata tudi njihov realni in imaginarni del.

z = z 1 + z 2 , kjer sta z 1 in z 2 splošni kompleksni števili. S preoblikovanjem izraza po odprtju oklepajev in poenostavitvi zapisa dobimo pravi argument x \u003d (x 1 + x 2), namišljeni argument y \u003d (y 1 + y 2).

Na grafu je to videti kot seštevek dveh vektorjev v skladu z dobro znanim pravilom paralelograma.

operacija odštevanja

Šteje se, da je poseben primer seštevanja, ko je ena številka pozitivna, druga pa negativna, to je, da se nahaja v zrcalni četrtini. Algebraični zapis je videti kot razlika med realnimi in imaginarnimi deli.

z \u003d z 1 - z 2, ali ob upoštevanju vrednosti argumentov, podobno kot operacija seštevanja, dobimo za realne vrednosti \u200b\u200bx \u003d (x 1 - x 2) in namišljene y \u003d (y 1 - y 2).

Množenje v kompleksni ravnini

S pomočjo pravil za delo s polinomi izpeljemo formulo za reševanje kompleksnih števil.

Po splošnih algebrskih pravilih z=z 1 ×z 2 opišemo vsak argument in podamo podobne. Realne in imaginarne dele lahko zapišemo takole:

• x \u003d x 1 × x 2 - y 1 × y 2,
• y = x 1 × y 2 + x 2 × y 1.

Videti je lepše, če uporabimo eksponentna kompleksna števila.

Izraz izgleda takole: z = z 1 × z 2 = r 1 × e i ϴ 1 × r 2 × e i ϴ 2 = r 1 × r 2 × e i(ϴ 1+ ϴ 2) .

Delitev

Če obravnavamo operacijo deljenja kot obratno operacijo množenja, dobimo preprost izraz v eksponentni obliki. Delitev vrednosti z 1 z z 2 je rezultat delitve njihovih modulov in fazne razlike. Formalno je pri uporabi eksponentne oblike kompleksnih števil videti takole:

z \u003d z 1 / z 2 \u003d r 1 × e i ϴ 1 / r 2 × e i ϴ 2 \u003d r 1 / r 2 × e i (ϴ 1- ϴ 2) .

V obliki algebraičnega zapisa je operacija deljenja števil kompleksne ravnine zapisana nekoliko bolj zapleteno:

S pisanjem argumentov in izvajanjem polinomskih transformacij je enostavno dobiti vrednosti x \u003d x 1 × x 2 + y 1 × y 2, oziroma y \u003d x 2 × y 1 - x 1 × y 2, znotraj opisanega prostora pa je ta izraz smiseln, če je z 2 ≠ 0.

Izluščimo korenino

Vse našteto lahko uporabimo pri definiciji kompleksnejših algebrskih funkcij - dvig na poljubno potenco in inverz nanjo - ekstrakcija korena.

Z uporabo splošnega koncepta dviga na potenco n dobimo definicijo:

z n = (r × e i ϴ) n.

Z uporabo skupnih lastnosti ga lahko prepišemo v obliki:

z n = r n × e i ϴ n.

Dobili smo preprosto formulo za dvig kompleksnega števila na potenco.

Iz definicije diplome dobimo zelo pomembno posledico. Soda potenca imaginarne enote je vedno 1. Vsaka liha potenca imaginarne enote je vedno -1.

Zdaj pa preučimo inverzno funkcijo - pridobivanje korena.

Zaradi enostavnosti zapisa vzamemo n = 2. Kvadratni koren w kompleksne vrednosti z na kompleksni ravnini C se običajno šteje za izraz z = ±, ki velja za kateri koli realni argument, večji ali enak nič. Za w ≤ 0 rešitve ni.

Oglejmo si najenostavnejšo kvadratno enačbo z 2 = 1. Z uporabo formul kompleksnih števil prepišemo r 2 × e i 2ϴ = r 2 × e i 2ϴ = e i 0 . Iz zapisa je razvidno, da je r 2 = 1 in ϴ = 0, zato imamo edinstveno rešitev enako 1. Vendar je to v nasprotju s konceptom, da je z = -1, prav tako ustreza definiciji kvadratnega korena.

Ugotovimo, česa ne upoštevamo. Če se spomnimo trigonometričnega zapisa, potem obnovimo izjavo - s periodično spremembo faze ϴ se kompleksno število ne spremeni. Naj p označuje vrednost periode, potem imamo r 2 × e i 2ϴ = e i (0+ p) , od koder je 2ϴ = 0 + p ali ϴ = p / 2. Zato imamo e i 0 = 1 in e i p / 2 = -1. Dobili smo drugo rešitev, ki ustreza splošnemu razumevanju kvadratnega korena.

Torej, da bi našli poljuben koren kompleksnega števila, bomo sledili postopku.

• Zapišemo eksponentno obliko w= ∣w∣ × e i (arg (w) + pk) , k je poljubno celo število.
• Želeno število lahko predstavimo tudi v Eulerjevi obliki z = r × e i ϴ.
• Uporabimo splošno definicijo funkcije ekstrakcije korena r n *e i n ϴ = ∣w∣ × e i (arg (w) + pk) .
• Iz splošnih lastnosti enakosti modulov in argumentov zapišemo r n = ∣w∣ in nϴ = arg (w) + p×k.
• Končni zapis korena kompleksnega števila je opisan s formulo z = √∣w∣ × e i (arg (w) + pk) / n .
• Komentiraj. Vrednost ∣w∣ je po definiciji pozitivno realno število, zato je vsak potenčni koren smiseln.

Polje in konjugacija

Za zaključek podajamo dve pomembni definiciji, ki za reševanje aplikativnih problemov s kompleksnimi števili nista pomembni, a sta bistveni za nadaljnji razvoj matematične teorije.

Za izraza za seštevanje in množenje pravimo, da tvorita polje, če izpolnjujeta aksiome za kateri koli element kompleksne ravnine z:

1. S spremembo mest kompleksnih členov se kompleksna vsota ne spremeni.
2. Trditev drži – v kompleksnem izrazu lahko katero koli vsoto dveh števil nadomestimo z njuno vrednostjo.
3. Obstaja nevtralna vrednost 0, za katero velja z + 0 = 0 + z = z.
4. Za vsak z obstaja nasprotje - z, katerega dodatek daje nič.
5. Ko se mesta kompleksnih faktorjev zamenjajo, se kompleksni produkt ne spremeni.
6. Množenje poljubnih dveh števil lahko nadomestimo z njuno vrednostjo.
7. Obstaja nevtralna vrednost 1, množenje s katero ne spremeni kompleksnega števila.
8. Za vsak z ≠ 0 obstaja recipročna vrednost z -1, ki pri množenju daje 1.
9. Množenje vsote dveh števil s tretjino je enakovredno množenju vsakega od njiju s tem številom in seštevanju rezultatov.
10. 0 ≠ 1.

Števili z 1 = x + i×y in z 2 = x - i×y imenujemo konjugirana.

Izrek. Za konjugacijo velja izjava:

• Konjugacija vsote je enaka vsoti konjugiranih elementov.
• Konjugacija produkta je enaka produktu konjugacij.
• enako samemu številu.

V splošni algebri se takšne lastnosti imenujejo poljski avtomorfizmi.

Primeri

Če upoštevate zgornja pravila in formule za kompleksna števila, lahko z njimi enostavno upravljate.

Razmislimo o najpreprostejših primerih.

Naloga 1. S pomočjo enačbe 3y +5 x i= 15 - 7i določite x in y.

rešitev. Spomnimo se definicije kompleksnih enačb, nato pa 3y = 15, 5x = -7. Zato je x = -7/5, y = 5.

Naloga 2. Izračunajte vrednosti 2 + i 28 in 1 + i 135 .

rešitev. Očitno je, da je 28 sodo število, iz posledice definicije kompleksnega števila v potenci imamo i 28 = 1, kar pomeni, da je izraz 2 + i 28 = 3. Druga vrednost, i 135 = - 1, potem 1 + i 135 = 0.

Naloga 3. Izračunajte zmnožek vrednosti 2 + 5i in 4 + 3i.

rešitev. Iz splošnih lastnosti množenja kompleksnih števil dobimo (2 + 5i)X(4 + 3i) = 8 - 15 + i(6 + 20). Nova vrednost bo -7 + 26i.

Naloga 4. Izračunajte korene enačbe z 3 = -i.

rešitev. Obstaja več načinov za iskanje kompleksnega števila. Razmislimo o enem od možnih. Po definiciji je ∣ - i∣ = 1, faza za -i je -p / 4. Prvotno enačbo lahko prepišemo kot r 3 *e i 3ϴ = e - p/4+ pk , od koder je z = e - p / 12 + pk /3 , za poljubno celo število k.

Množica rešitev ima obliko (e - ip/12 , e ip /4 , e i 2 p/3).

Zakaj so potrebna kompleksna števila

Zgodovina pozna veliko primerov, ko znanstveniki med delom na teoriji sploh ne razmišljajo o praktični uporabi svojih rezultatov. Matematika je najprej igra uma, dosledno upoštevanje vzročno-posledičnih odnosov. Skoraj vse matematične konstrukcije so zmanjšane na reševanje integralnih in diferencialnih enačb, te pa se z nekaj približki rešujejo z iskanjem korenin polinomov. Tu se prvič srečamo s paradoksom imaginarnih števil.

Naravoslovci, ki rešujejo povsem praktične probleme, se zatekajo k rešitvam različnih enačb, odkrivajo matematične paradokse. Razlaga teh paradoksov vodi do popolnoma neverjetnih odkritij. Dvojna narava elektromagnetnih valov je en tak primer. Kompleksna števila igrajo ključno vlogo pri razumevanju njihovih lastnosti.

To pa je našlo praktično uporabo v optiki, radioelektroniki, energetiki in številnih drugih tehnoloških področjih. Drug primer, veliko težje razumljivi fizikalni pojavi. Antimaterija je bila napovedana na konici peresa. In šele po mnogih letih se začnejo poskusi, da bi ga fizično sintetizirali.

Ne smemo misliti, da takšne situacije obstajajo samo v fiziki. Nič manj zanimiva odkritja niso narejena v divjih živalih, pri sintezi makromolekul, med študijem umetne inteligence. In vse to je posledica širjenja naše zavesti, izogibanja preprostemu seštevanju in odštevanju naravnih vrednosti.

PredmetKompleksna števila in polinomi

Predavanje 22

§1. Kompleksna števila: osnovne definicije

Simbol vnesite razmerje
in se imenuje imaginarna enota. Z drugimi besedami,
.

Opredelitev. Izražanje oblike
, Kje
, imenujemo kompleksno število in število imenujemo realni del kompleksnega števila in označujejo
, številka - imaginarni del in označujejo
.

Iz te definicije sledi, da so realna števila tista kompleksna števila, katerih imaginarni del je enak nič.

Kompleksna števila je priročno predstaviti kot točke ravnine, na kateri je podan kartezični pravokotni koordinatni sistem, in sicer: kompleksno število
točka srečanja
in obratno. na osi
so prikazana realna števila in se imenuje realna os. Kompleksna števila oblike

se imenujejo čisto namišljeni. Prikazane so kot pike na osi.
, ki se imenuje imaginarna os. Ta ravnina, ki služi za predstavitev kompleksnih števil, se imenuje kompleksna ravnina. Kompleksno število, ki ni realno, tj. tako da
, včasih imenovano namišljeno.

Dve kompleksni števili naj bi bili enaki, če in samo če imata enake realne in imaginarne dele.

Seštevanje, odštevanje in množenje kompleksnih števil se izvaja po običajnih pravilih polinomske algebre, ob upoštevanju dejstva, da

. Operacijo deljenja lahko definiramo kot obratno operacijo množenja in lahko dokažemo edinstvenost rezultata (če je delitelj različen od nič). Vendar se v praksi uporablja drugačen pristop.

Kompleksna števila
in
se imenujejo konjugirane, na kompleksni ravnini pa so predstavljene s točkami, simetričnimi glede na realno os. Očitno je, da:

1)

;

2)
;

3)
.

Zdaj se razdeli na lahko storite na naslednji način:

.

Tega ni težko pokazati

,

kje simbol pomeni katero koli aritmetično operacijo.

Pustiti
neko namišljeno število in je realna spremenljivka. Produkt dveh binomov

je kvadratni trinom z realnimi koeficienti.

Zdaj, ko imamo na voljo kompleksna števila, lahko rešimo katero koli kvadratno enačbo
.Če, potem

in enačba ima dva kompleksna konjugirana korena

.

če
, potem ima enačba dva različna realna korena. če
, potem ima enačba dva enaka korena.

§2. Trigonometrična oblika kompleksnega števila

Kot je navedeno zgoraj, kompleksno število
priročno za prikaz s piko
. Takšno število lahko identificiramo tudi s polmernim vektorjem te točke
. S to interpretacijo se seštevanje in odštevanje kompleksnih števil izvaja po pravilih seštevanja in odštevanja vektorjev. Za množenje in deljenje kompleksnih števil je primernejša druga oblika.

Uvajamo na kompleksni ravnini
polarni koordinatni sistem. Kam pa potem
,
in kompleksno število
lahko zapišemo kot:

Ta oblika zapisa se imenuje trigonometrična (v nasprotju z algebraično obliko
). V tej obliki je številka se imenuje modul in - argument kompleksnega števila . Označeni so:
,

. Za modul imamo formulo

Argument števila je definiran dvoumno, vendar do izraza
,
. Vrednost argumenta, ki zadovoljuje neenakosti
, imenujemo glavni in označimo
. potem,
. Za glavno vrednost argumenta lahko dobite naslednje izraze:

,

številski argument
velja za nedefinirano.

Pogoj za enakost dveh kompleksnih števil v trigonometrični obliki ima obliko: moduli števil so enaki, argumenti pa se razlikujejo za večkratnik
.

Poiščite produkt dveh kompleksnih števil v trigonometrični obliki:

Torej, pri množenju števil se njihovi moduli pomnožijo, argumenti pa seštejejo.

Podobno je mogoče ugotoviti, da se pri deljenju moduli števil delijo, argumenti pa se odštejejo.

Če potenciranje razumemo kot večkratno množenje, lahko dobimo formulo za dvig kompleksnega števila na potenco:

Izpeljemo formulo za
- korenina potenco kompleksnega števila (ne zamenjujte z aritmetičnim korenom realnega števila!). Operacija ekstrakcije korena je inverzna operaciji potenciranja. Zato
je kompleksno število tako da
.

Pustiti
znano, in
potrebno najti. Potem

Iz enakosti dveh kompleksnih števil v trigonometrični obliki sledi, da

,
,
.

Od tod
(to je aritmetični koren!),

,
.

To je enostavno preveriti lahko le sprejme bistveno drugačne vrednosti, denimo, ko
. Končno imamo formulo:

,
.

Torej korenina stopnje iz kompleksnega števila ima različne vrednosti. Na kompleksni ravnini so te vrednosti pravilno nameščene na ogliščih -kotnik včrtan v krog s polmerom
s središčem na izvoru. "Prvi" koren ima argument
, se argumenti dveh "sosednjih" korenov razlikujejo za
.

Primer. Vzemimo kubni koren namišljene enote:
,
,
. Nato:

,

§1. Kompleksna števila

1°. Opredelitev. Algebrski zapis.

Definicija 1. Kompleksna števila imenujemo urejeni pari realnih števil in , če je zanje definiran koncept enakosti, operaciji seštevanja in množenja, ki zadoščata naslednjim aksiomom:

1) Dve številki
in
enako, če in samo če
,
, tj.

 , .

2) Vsota kompleksnih števil
in

in enaka
, tj.

+ = .

3) Zmnožek kompleksnih števil
in
številka se kliče
in enako , tj.

∙=.

Množica kompleksnih števil je označena C.

Formule (2), (3) za števila oblike
prevzame obrazec

od koder sledi, da operaciji seštevanja in množenja za števila oblike
sovpadajo s seštevanjem in množenjem za realna števila  kompleksno število oblike
se identificira z realnim številom .

Kompleksno število
klical imaginarna enota in označeno , tj.
Nato iz (3) 

Iz (2), (3)  kar pomeni

Izraz (4) se imenuje algebrski zapis kompleksno število.

V algebraični obliki imata operaciji seštevanja in množenja obliko:

Kompleksno število je označeno
, - pravi del, je imaginarni del, je čisto namišljeno število. Oznaka:
,
.

Definicija 2. Kompleksno število
klical konjugat s kompleksnim številom
.

Lastnosti kompleksne konjugacije.

1)

2)
.

3) Če
, To
.

4)
.

5)
je realno število.

Dokaz se izvede z neposrednim izračunom.

Definicija 3. številka
klical modul kompleksno število
in označeno
.

To je očitno
, in


. Tudi formule so očitne:
in
.

2°. Lastnosti operacij seštevanja in množenja.

1) Komutativnost:
,
.

2) Asociativnost:,
.

3) Distributivnost: .

Dokaz 1) - 3) je izveden z neposrednimi izračuni na podlagi podobnih lastnosti za realna števila.

4)
,
.

5) , C ! , ki izpolnjuje enačbo
. Takšna

6) ,C, 0, ! :
. Takšna dobimo tako, da enačbo pomnožimo z



.

Primer. Predstavljajte si kompleksno število
v algebraični obliki. Če želite to narediti, pomnožite števec in imenovalec ulomka s konjugatom imenovalca. Imamo:

3°. Geometrijska interpretacija kompleksnih števil. Trigonometrična in eksponentna oblika zapisa kompleksnega števila.

Naj bo na ravnini podan pravokotni koordinatni sistem. Potem
C točko na ravnini lahko povežemo s koordinatami
.(glej sliko 1). Očitno je, da je taka korespondenca ena proti ena. V tem primeru ležijo realna števila na abscisni osi, čisto imaginarna števila pa na ordinatni osi. Zato se imenuje abscisna os prava os in y-os − imaginarna os. Ravnina, na kateri ležijo kompleksna števila, se imenuje kompleksna ravnina.

Upoštevajte to in
so simetrični glede izvora in in so simetrični glede na Ox.

Vsako kompleksno število (tj. vsako točko na ravnini) lahko povežemo z vektorjem z začetkom v točki O in koncem v točki
. Korespondenca med vektorji in kompleksnimi števili je ena proti ena. Zato je vektor, ki ustreza kompleksnemu številu , označena z isto črko

D vektorska linija
ki ustreza kompleksnemu številu
, je enako
, in
,
.

Z uporabo vektorske interpretacije lahko vidimo, da vektor
− vsota vektorjev in , A
− vsota vektorjev in
.(glej sliko 2). Zato veljajo naslednje neenakosti:

Skupaj z dolžino vektor uvedemo kot med vektorjem in os Ox, šteto od pozitivne smeri osi Ox: če je štetje v nasprotni smeri urinega kazalca, se šteje, da je predznak kota pozitiven, če je v smeri urinega kazalca, pa negativen. Ta kotiček se imenuje argument kompleksnega števila in označeno
. Kotiček ni definiran enolično, ampak natančno
…. Za
argument ni definiran.

Formule (6) definirajo t.i trigonometrični zapis kompleksno število.

Iz (5) sledi, da če
in
to

, .

Od (5)
kaj po in Kompleksno število je enolično definirano. Obratno ne drži: namreč s kompleksnim številom njegov modul je edinstven in argument , zaradi (7), − z natančnostjo
. Iz (7) sledi tudi, da argument lahko najdemo kot rešitev enačbe

Vendar niso vse rešitve te enačbe rešitve (7).

Med vsemi vrednostmi argumenta kompleksnega števila je izbrana ena, ki se imenuje glavna vrednost argumenta in je označena
. Običajno je glavna vrednost argumenta izbrana bodisi v intervalu
, ali v intervalu

V trigonometrični obliki je priročno izvajati operacije množenja in deljenja.

1. izrek. Modul produkta kompleksnih števil in je enak produktu modulov, argument pa je enak vsoti argumentov, tj.

, A .

podobno

,

Dokaz. Pustiti , . Nato z neposrednim množenjem dobimo:

podobno

.■

Posledica(De Moivrejeva formula). Za
Moivrova formula velja

p primer. Naj Poiščemo geometrijsko lokacijo točke
. Iz izreka 1 sledi, da .

Zato morate za njegovo konstrukcijo najprej zgraditi točko , kar je obratno okoli enotskega kroga in nato poiščite točko, ki je nanj simetrična glede na os x.

Pustiti
, tj.
Kompleksno število
označeno
, tj. R Eulerjeva formula velja

Ker
, To
,
. Iz izreka 1
kaj pa funkcija
mogoče je delati kot z navadno eksponentno funkcijo, tj. enakosti so resnične

,
,
.

Od (8)
eksponentni zapis kompleksno število

, Kje
,

Primer. .

4°. Korenine potenco kompleksnega števila.

Razmislite o enačbi

, Z , n .

Pustiti
, rešitev enačbe (9) pa iščemo v obliki
. Nato dobi (9) obliko
, od koder to najdemo
,
, tj.

,
,
.

Tako ima enačba (9) korene

, .

Pokažimo, da je med (10) točno različne korenine. res,

se razlikujejo, saj njihovi argumenti so različni in se razlikujejo manj kot
. Nadalje,
, Ker
. podobno
.

Tako enačba (9) za
ima točno korenine
ki se nahajajo na vrhovih pravilne -kotnik včrtan v krog s polmerom s središčem pri T. O.

Tako je bilo dokazano

2. izrek. pridobivanje korenin potenco kompleksnega števila
vedno možno. Vse korenske vrednosti th stopnjo ki se nahaja na vrhu pravilnega -kotnik včrtan v krog s središčem na ničli in polmerom
. pri čemer,

Posledica. Korenine -te stopnje 1 so izražene s formulo

.

Produkt dveh korenov iz 1 je koren, 1 je koren - stopnja od enotnosti, korenina
:
.