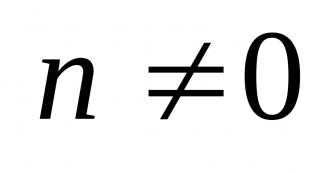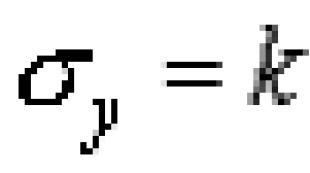amatai

Užduočių rūšys elastingumo teorijoje. Pagrindinės tamprumo teorijos lygtys. Tamprumo teorijos problemų tipai Kas yra klasikinės elastingumo teorijos tyrimo objektas

Rusijos valstybinis universitetas

naftos ir dujų juos. I. M. Gubkina

Techninės mechanikos katedra

SANTRAUKA

"Elastingumo teorija"

Užbaigė: Polyakov A. A.

Patikrintas: Evdokimov A.P.

Maskva 2011 m

elastingumo teorijos lygtis

1. Įvadas

Įtempių ir deformacijų būsenos kūno taške teorija

2.1 Streso teorija

2 Deformacijos teorija

3 Ryšys tarp tamprių kūnų įtemptos ir deformuotos būsenos

Pagrindinės tamprumo teorijos lygtys. Užduočių rūšys elastingumo teorijoje

1 Pagrindinės tamprumo teorijos lygtys

2 Tamprumo teorijos uždavinių tipai

4 Poslinkių tamprumo teorijos lygtys (Lame lygtys)

Tamprumo teorijos variaciniai principai

1 Galimų poslinkių principas (Lagrange principas)

2 Galimų būsenų principas (Castillano principas)

3 Ryšys tarp tikslaus sprendimo ir sprendimų, gautų remiantis Lagrange ir Castigliano principais

Naudotos literatūros sąrašas

1. Įvadas

Įtempių ir deformacijų teorijas sukūrė O. Koši. Jie išdėstyti 1822 m. Paryžiaus mokslų akademijai pateiktame darbe, kurio santrauka buvo paskelbta 1823 m. ir daugybė vėlesnių straipsnių. O. Koshi išvedė tris elementariojo tetraedro pusiausvyros lygtis, įrodė tangentinių įtempių poravimosi dėsnį, supažindino su pagrindinių ašių ir pagrindinių įtempių sąvokomis bei išvedė diferencines pusiausvyros lygtis (dažniausiai jos nėra išvedamos per įtempių stiprumą). medžiagos). Jis taip pat pristatė normaliųjų įtempių paviršių (Koši keturkampį), ant kurio yra spindulio vektorių galai, kurių kryptys sutampa su normaliųjų kryptimis į sritis, o reikšmė yra atvirkščiai proporcinga kvadratinei šaknei. absoliučios normaliojo įtempio vertės šioje srityje, ir buvo įrodyta, kad šis paviršius yra antros eilės paviršius, kurio centras yra ištakoje. Galimybė transformuoti normaliųjų įtempių paviršių į pagrindines ašis rodo, kad kiekviename taške yra trys viena kitai pagrindinės statmenos sritys.

Panašų šlyties įtempių paviršių pristatė rusų mechanikas G.V. Kolosovas 1933 m

Geometrinę įtempių būsenos erdvėje interpretaciją įtempių elipsoido pavidalu G. Lame'as ir B. Clapeyronas pateikė savo atsiminimuose, pateiktuose Paryžiaus mokslų akademijai 1828 m., o paskelbtuose 1833 m.

Geometrinį įtempių būsenos vaizdą plokštumoje vienai platformų, einančių per pagrindinę ašį, serijai įtempių apskritimo pavidalu, savo knygoje 1866 metais pasiūlė K. Kuhlmanas.

Bendram įtempių būsenos atveju labai aiškią geometrinę jos interpretaciją plokštumoje 1882 m. pateikė O. Mohr (vadinamoji apskritoji Mohro diagrama). Iš jos galima padaryti keletą svarbių išvadų apie pagrindinių įtempių kraštutinumai, sričių, kuriose tangentiniai įtempiai yra didžiausi, padėtis ir apie šių didžiausių šlyties įtempių vertes.

O. Cauchy pateikė deformacijų apibrėžimą, išvedė jų priklausomybę nuo poslinkių konkrečiu mažų deformacijų atveju (šios priklausomybės, kaip taisyklė, nėra išvestos medžiagų atsparumo eigoje), apibrėžė pagrindinių įtempių ir pagrindinės sąvokas. deformacijų, ir gautos įtempių komponentų priklausomybės nuo deformacijos komponentų, kaip izotropiniam ir anizotropiniam elastingam kūnui. Medžiagų atsparumo atveju dažniausiai nustatomos deformacijų komponentų priklausomybės nuo įtempių komponentų izotropiniam kūnui. Jie vadinami apibendrintu Huko dėsniu, nors, žinoma, šis pavadinimas yra savavališkas, nes R. Hukas nežinojo streso sąvokos.

Šiose priklausomybėse Cauchy pirmiausia įvedė dvi konstantas ir užrašė įtempių priklausomybes nuo deformacijų formoje

m, ,

Tačiau vėliau O. Koshi perėmė L. Navier koncepciją. Pagal ją tamprūs kūnai susideda iš molekulių, tarp kurių deformuojant atsiranda jėgos, veikiančios molekules jungiančių tiesių kryptimis ir proporcingos atstumų tarp molekulių pokyčiui. Tada tamprumo konstantų skaičius bendram anizotropinio kūno atveju yra 15, o izotropiniam kūnui gauname vieną elastinę konstantą. Šios hipotezės laikėsi S. Poissonas, o pradžioje – G. Lame'as ir B. Clapeyronas. Remdamasis juo, Puasonas nustatė, kad skersinės deformacijos koeficientas yra 1/4.

D. Greenas 1839 metais išvedė ryšį tarp deformacijų ir įtempių, nenaudodamas elastingų kūnų molekulinės sandaros hipotezės. Jis juos gavo remdamasis energijos tvermės principu, įvesdamas tampriojo potencialo sampratą ir parodė, kad naudojant šešių deformacijų komponentų tiesines priklausomybes nuo šešių įtempių dedamųjų, 21 iš 36 koeficientų yra nepriklausomi, t.y. anizotropinio kūno elastinių konstantų skaičius yra 21 Izotropiniam kūnui elastinių konstantų skaičius sumažinamas iki dviejų. Teorija, pagal kurią anizotropinio kūno tamprių konstantų skaičius yra 15, o izotropinio kūno – 1, kartais buvo vadinama „raric konstanta“ arba „viena konstanta“, o teorija, pagal kurią anizotropinio kūno elastinių konstantų skaičius yra 21, o izotropiniam 2 - "daugiakonstantinis" .

Ginčas tarp šių teorijų šalininkų paskatino fizikus imtis eksperimentinių tyrimų.

G. Wertheimas, remdamasis stiklinių ir metalinių vamzdžių vidinių tūrių ašiniu įtempimu matavimais, 1848 metais nustatė, kad skersinės deformacijos koeficientas nelygus 1/4. Jis manė, kad įvairioms medžiagoms jis skiriasi, tačiau daugeliui medžiagų jis buvo artimas 1/3.

IR AŠ. Kupfferis 1853 m., išbandydamas metalinių strypų įtempimą ir sukimą, taip pat nustatė, kad šlyties ir įtempimo modulių santykis neatitinka skersinės deformacijos, lygios 1/4.

1855 metais F. Neumanas išbandė stačiakampio skerspjūvio pavyzdžius lenkimui ir išmatavo dviejų sijos paviršių sukimosi kampus (skerspjūvis įgauna trapecijos formą). Dėl to jis parodė, kad skersinės deformacijos koeficientas nėra lygus 1/4. G. Kirchhoffas, F. Neumanno mokinys, priėjo prie tokios pat išvados, remdamasis 1859 m. atliktais apvalių žalvarinių strypų, iš vieno galo sandarių, o kitame sutelkta jėga apkrautų, sujungimo lenkimo ir sukimo bandymais. strypo posūkio kampo ir sekcijos sukimosi kampo matavimas .

Didelį eksperimentinį įvairių rūšių plieno skersinės deformacijos koeficientų tyrimą atliko vienas iš G. Kirchhoff mokinių M.F. Okatovas 1865–1866 m Rezultatai pateikti daktaro disertacijoje Iš pavienių kristalų išpjautų plonų prizmių sukimo ir lenkimo bandymus, taip pat kristalų gniuždomumo vienodo vienodo gniuždymo sąlygomis bandymus atliko V. Voigtas ir aprašė daugybėje savo straipsnių, vėliau. sujungta į 1910 metais išleistą knygą Jie patvirtino kelių konstantų teorijos teisingumą.

1984 m. mechanikas ir inžinierius Janas Rychlevskis atliko gilų Huko dėsnio anizotropiniams kūnams matematinės struktūros tyrimą, remdamasis jo pristatyta tampriosios savosios būsenos koncepcija. Visų pirma, jis parodė, kad 21 tamprumo konstanta reiškia šešis tikrus standumo modulius, 12 standumo skirstytuvų ir tris kampus.

2. Įtempių-įtempimų būsenos kūno taške teorija

1 Streso teorija

Vidinės jėgos veiksniai, atsirandantys apkraunant tamprų kūną, apibūdina tam tikros kūno dalies būklę, tačiau neatsako į klausimą, kuris skerspjūvio taškas yra labiausiai apkrautas, arba, kaip sakoma, pavojingas taškas. Todėl būtina atsižvelgti į kai kuriuos papildomus kiekius, apibūdinančius kūno būklę tam tikrame taške.

Jei kūnas, kuriam veikia išorinės jėgos, yra pusiausvyroje, tai vidinės pasipriešinimo jėgos atsiranda bet kurioje jo dalyje. Žymima vidine jėga, veikiančia elementariąją sritį , o normaliąja šiai sričiai per tada reikšmė

vadinama pilna įtampa.

Bendru atveju bendras įtempis nesutampa kryptimi su normaliu elementariajam plotui, todėl patogiau dirbti su jo komponentais išilgai koordinačių ašių -

Jei išorinė normalioji sutampa su bet kuria koordinačių ašimi, pavyzdžiui, su X ašimi, tada įtempių komponentai įgaus formą, o komponentas bus statmenas pjūviui ir vadinamas normaliu įtempimu, o komponentai bus pjūvio plokštuma ir vadinami šlyties įtempiais.

Norint lengvai atskirti įprastą ir šlyties įtempį, dažniausiai vartojami kiti pavadinimai: - normalus įtempis, - šlyties.

Išskirkime iš kūno, veikiant išorinėms jėgoms, be galo mažą gretasienį, kurio paviršiai lygiagretūs koordinačių plokštumoms, o kraštinės ilgis . Kiekviename tokio elementaraus gretasienio paviršiuje yra trys įtempių komponentai, lygiagrečiai koordinačių ašims. Iš viso šešiuose veiduose gauname 18 streso komponentų.

Normalūs įtempiai žymimi kaip , kur indeksas žymi normalų atitinkamam veidui (tai yra, jis gali paimti reikšmes). Šlyties įtempiai turi formą; čia pirmasis indeksas atitinka normalią vietą, kurioje veikia nurodytas šlyties įtempis, o antrasis nurodo ašį lygiagrečiai, į kurią nukreiptas šis įtempis (1 pav.).

1 pav. Normalūs ir šlyties įtempiai

Šioms įtampoms taikoma tokia ženklų taisyklė. Įprastas įtempis laikomas teigiamu įtempimu arba lygiaverčiu, kai jis sutampa su išorinės normalios kryptimi į vietą, kurioje jis veikia. Tangentinis įtempis laikomas teigiamu, jei vietoje, kurios normalioji sutampa su jai lygiagrečios koordinačių ašies kryptimi, jis nukreiptas į šią įtampą atitinkančią teigiamą koordinačių ašį.

Įtempių komponentai yra trijų koordinačių funkcijos. Pavyzdžiui, normalus įtempis taške su koordinatėmis gali būti pažymėtas

Tayke, kuris yra be galo mažu atstumu nuo nagrinėjamojo, įtampa iki be galo mažų pirmosios eilės gali būti išplėsta Taylor serijoje:

Platformoms, kurios yra lygiagrečios plokštumai, keičiasi tik x koordinatė ir prieaugiai. Todėl gretasienio paviršiuje, kuris sutampa su plokštuma, normalus įtempis bus Todėl iš 18 įtampos komponentų tik devyni yra nežinomi.

Tamprumo teorijoje įrodytas šlyties įtempių poravimosi dėsnis, pagal kurį išilgai dviejų viena kitai statmenų sričių šlyties įtempių dedamosios, statmenos šių sričių susikirtimo linijoms, yra lygios viena kitai:

Lygybės (2) lemia tai, kad iš devynių įtempių komponentų, apibūdinančių streso būseną kūno taške, lieka tik šeši:

Galima įrodyti, kad įtempiai (3) ne tik charakterizuoja kūno įtempimo būseną tam tikrame taške, bet ir lemia ją vienareikšmiškai. Šių įtempių derinys sudaro simetrišką matricą, vadinamą įtempių tenzoriumi:

(4)

Tenzorių padauginus iš skaliarinės reikšmės, gaunamas naujas tenzorius, kurio visi komponentai yra kartų didesni už pradinio tenzoriaus komponentus.

2 Deformacijos teorija

Veikiamas išorinių apkrovų elastingas kūnas keičia savo formą ir deformuojasi. Tokiu atveju kūno taškai užima naują padėtį. Tampraus kūno deformacijai nustatyti lyginame kūno taškų padėtis prieš ir po apkrovos.

Apsvarstykite neapkrauto kūno tašką ir jo naują padėtį po apkrovos. Vektorius vadinamas taško poslinkio vektoriumi (2 pav.).

2 pav. Taško judėjimo vektorius

Galimi du poslinkių tipai: viso kūno poslinkis be deformacijos – tokius poslinkius tiria teorinė mechanika kaip absoliučiai standaus kūno poslinkius, ir poslinkius, susijusius su kūno deformacija – tokius poslinkius tiria teorija. elastingumo.

Atitinkamai pažymėkime taško poslinkio vektoriaus projekcijas koordinačių ašyse. Jie yra lygūs skirtumui tarp atitinkamų taškų koordinačių ir :

ir yra koordinačių funkcijos:

Kūno deformaciją lemia skirtingų jo taškų poslinkių skirtumas. Be galo mažas gretasienis su briaunomis, iškirptomis iš elastingo kūno šalia savavališko taško, dėl įvairių jo taškų poslinkių deformuojasi taip, kad pakinta jo briaunų ilgis ir iškraipomi iš pradžių stačiakampiai tarp paviršių.

3.3 paveiksle pavaizduotos dvi šio gretasienio briaunos: ir briaunos ilgis lygus ir briauna

Po deformacijos taškai užima padėtį Šiuo atveju taškas gaus poslinkį, kurio komponentai brėžinio plokštumoje yra lygūs, o taškas, atskirtas nuo taško be galo mažu atstumu, gaus poslinkį, kurių komponentai dėl koordinatės pasikeitimo skirsis nuo taško poslinkio komponentų be galo maža reikšme

3 pav. Linijinės ir kampinės deformacijos

Taško poslinkio komponentai nuo taško poslinkio komponentų skirsis be galo maža verte dėl koordinatės pasikeitimo

Šonkaulio projekcijos ilgis ašyje po deformacijos:

Šonkaulio absoliutaus pailgėjimo projekcija ašyje

Santykinis pailgėjimas išilgai ašies

(6)

vadinama tiesine deformacija ašies kryptimi.

Panašiai tiesinės deformacijos pagal ašių kryptis ir

(7)

Apsvarstykite kampų pokytį tarp gretasienio kraštų (3 pav.). Šonkaulio sukimosi kampo plokštumoje liestinė

Dėl deformacijų a mažumo tiesinė deformacija gali būti nepaisoma dėl jos mažumo lyginant su vienetu, o tada

Panašiai galite nustatyti šonkaulio sukimosi kampą toje pačioje plokštumoje:

Stačiojo kampo iškraipymas vadinamas kampine deformacija ir apibrėžiamas kaip briaunų sukimosi kampų suma ir:

(8)

Tuo pačiu būdu nustatomos kampinės deformacijos dviejose kitose koordinačių plokštumose:

(9)

Formulės (6)-(9) pateikia šešias pagrindines linijinių ir kampinių deformacijų priklausomybes nuo poslinkio komponentų. Šios priklausomybės vadinamos Koši lygtimis:

(10)

Riboje, kai gretasienio kraštų ilgiai linkę į nulį, Koši santykiai nustato tiesines ir kampines deformacijas taško apylinkėse

Teigiamos tiesinės deformacijos atitinka pailgėjimus, o neigiamos – sutrumpėjimus. Poslinkio kampas laikomas teigiamu, kai kampas tarp teigiamų atitinkamų koordinačių ašių krypčių mažėja, o neigiamas – kitaip.

Panašiai kaip įtempių tenzorius, kūno deformuota būsena tam tikrame taške apibūdinama deformacijos tenzoriumi

(11)

Kaip ir įtempių tenzorius, deformacijos tenzorius yra simetriška matrica, kurią sudaro devyni komponentai, iš kurių šeši yra skirtingi.

2.3 Įtempių ir deformacijų ryšys elastingiems kūnams

Ryšys tarp streso ir įtampos yra fizinio pobūdžio. Apsiribojant mažomis deformacijomis, ryšys tarp įtempių ir deformacijų gali būti laikomas tiesiniu.

Bandant strypą tempiant (mechaniniai medžiagų bandymai bus išsamiai aptariami kitame skyriuje), nustatomas proporcingas ryšys tarp normalaus įtempio ir tiesinės deformacijos viena kryptimi, kuris vadinamas Huko dėsniu:

kur tamprumo konstanta vadinama išilginio tamprumo moduliu.

Tuo pačiu eksperimentiniu būdu buvo nustatytas ryšys tarp linijinių deformacijų išilgine ir skersine kryptimis:

čia – tiesinė deformacija skersine kryptimi, – antroji tamprumo konstanta, vadinama Puasono koeficientu.

Atliekant mechaninius gryno šlyties bandymus, buvo nustatytas tiesiogiai proporcingas ryšys tarp šlyties įtempių ir kampinės deformacijos šio įtempio veikimo plokštumoje, kuris buvo vadinamas Huko dėsniu šlyties atžvilgiu:

kur reikšmė yra trečioji tamprumo konstanta ir vadinama šlyties moduliu. Tačiau ši elastinė konstanta nėra nepriklausoma, nes susiję su pirmaisiais dviem

Norėdami nustatyti ryšį tarp deformacijų ir įtempimų, iš kūno pasirenkame be galo mažą gretasienį (1 pav.) ir atsižvelgiame į tik normalių įtempių veikimą. tai veda prie aukštesnio mažumo laipsnio deformacijų.

Nustatykime šonkaulio pailgėjimą lygiagrečiai įtempimui Veikiant šiam įtempimui pagal Huko dėsnį (3.12) atsiras santykinis briaunos pailgėjimas.

Įtempimas sukelia panašų pailgėjimą statmenai šonkauliui

o šonkaulio kryptimi - trumpinimas, kuris pagal (13) yra

arba, atsižvelgiant į deformacijos išraišką

Panašiai nustatomas santykinis šonkaulio sutrumpėjimas veikiant įtempimui

Remiantis jėgų veikimo nepriklausomumo principu, bendras santykinis briaunos pailgėjimas gali būti apibrėžiamas kaip pailgėjimų suma nuo kiekvieno įtempio veikimo:

Panašiai galima apibrėžti linijines deformacijas kitų dviejų ašių kryptimis:

Pagal Huko šlyties dėsnį (14), santykį tarp kampinių deformacijų ir šlyties įtempių galima pavaizduoti atskirai kiekvienai iš trijų plokštumų, lygiagrečių koordinačių plokštumoms:

Taigi gautos šešios formulės, išreiškiančios tiesinį ryšį tarp deformacijos ir įtempių komponentų izotropiniame elastingame kūne ir vadinamos apibendrintu Huko dėsniu:

(16)

3. Pagrindinės tamprumo teorijos lygtys. Užduočių rūšys elastingumo teorijoje

Pagrindinis tamprumo teorijos uždavinys – įtempių-įtempimų būsenos nustatymas pagal pateiktas kūno apkrovos ir fiksavimo sąlygas.

Įtempių ir deformacijų būsena nustatoma, jei įtempio tenzoriaus (-ių) ir poslinkio vektoriaus komponentai yra devynios funkcijos.

3.1 Pagrindinės tamprumo teorijos lygtys

Norint rasti šias devynias funkcijas, reikia užrašyti pagrindines elastingumo teorijos lygtis arba:

Diferencialinis Cauchies

(17)

kur yra Koši deformacijų tiesinės dalies tenzoriaus komponentai;

poslinkio išvestinės išilgai spindulio tenzoriaus komponentai.

Diferencialinės pusiausvyros lygtys

kur yra įtempių tenzoriaus komponentai; yra kūno jėgos projekcija į j ašį.

Huko dėsnis tiesiškai elastingam izotropiniam kūnui

kur yra Lame konstantos; izotropiniam kūnui. Čia yra normalūs ir šlyties įtempiai; atitinkamai deformacijos ir šlyties kampai.

Aukščiau pateiktos lygtys turi tenkinti Saint-Venant priklausomybes

Tamprumo teorijoje uždavinys išspręstas, jei tenkinamos visos pagrindinės lygtys.

2 Tamprumo teorijos uždavinių tipai

Kraštinės sąlygos kūno paviršiuje turi būti tenkinamos ir, priklausomai nuo ribinių sąlygų tipo, elastingumo teorijoje yra trijų tipų problemos.

Pirmasis tipas. Jėgos suteikiamos kūno paviršiui. Pasienio sąlygos

Antrasis tipas. Problemos, kai poslinkis nurodomas kūno paviršiuje. Pasienio sąlygos

Trečias tipas. Mišrios elastingumo teorijos problemos. Jėgos suteikiamos kūno paviršiaus daliai, poslinkis – kūno paviršiaus daliai. Pasienio sąlygos

Problemos, kai kūno paviršiuje nurodytos jėgos ar poslinkiai, tačiau reikia rasti įtempių-įtempimų būseną kūno viduje ir tai, kas nenurodyta paviršiuje, vadinamos tiesioginėmis problemomis. Jei vis dėlto kūno viduje nurodyti įtempiai, deformacijos, poslinkiai ir pan., ir reikia nustatyti, kas nenurodyta kūno viduje, taip pat poslinkius ir įtempimus kūno paviršiuje (tai yra rasti priežastys, sukėlusios tokią streso-įtempimo būseną)), tada tokios problemos vadinamos atvirkštinėmis.

4 Poslinkių tamprumo teorijos lygtys (Lame lygtys)

Norėdami nustatyti poslinkių elastingumo teorijos lygtis, rašome: diferencialinės pusiausvyros lygtis (18) Huko dėsnis tiesiškai elastingam izotropiniam kūnui (19)

Jei atsižvelgsime į tai, kad deformacijos išreiškiamos poslinkiais (17), rašome:

Taip pat reikėtų prisiminti, kad šlyties kampas yra susijęs su poslinkiais tokiu ryšiu (17):

(23)

Pakeitę išraišką (22) į pirmąją lygčių (19) lygtį, gauname, kad normalūs įtempiai

(24)

Atkreipkite dėmesį, kad žymėjimas u šiuo atveju nereiškia sumavimo per i.

Pakeitę išraišką (23) į antrąją lygčių (19) lygtį, gauname šlyties įtempius

(25)

Parašykime pusiausvyros lygtis (18) išplėstine forma, kai j = 1

(26)

Pakeitę (26) lygties išraiškas normaliuosius (24) ir tangentinius (25) įtempius, gauname

kur λ yra Lame konstanta, kuri nustatoma pagal išraišką:

Išreiškimą (28) pakeičiame lygtimi (27) ir rašome,

kur nustatoma pagal išraišką (22) arba išplėstine forma

Išreiškimą (29) padaliname iš G ir pridedame panašius terminus ir gauname pirmąją Lame lygtį:

(30)

kur yra Laplaso operatorius (harmoninis operatorius), kuris apibrėžiamas kaip

(31)

Panašiai galite gauti:

(32)

(30) ir (32) lygtis gali būti parašytos taip:

(33)

(33) arba (30) ir (32) lygtys yra Lame lygtys. Jei kūno jėgos yra lygios nuliui arba pastovios, tada

(34)

be to, žymėjimas šiuo atveju nereiškia sumavimo per i. Čia

Galima parodyti, kad toks poslinkių vaizdavimas harmonine funkcija paverčia Lame lygtis (33) tapatybe. Dažnai jos vadinamos Popkovičiaus-Grodskio sąlygomis. Keturios harmoninės funkcijos nėra būtinos, nes φ0 gali būti prilyginamas nuliui.

4. Tamprumo teorijos variaciniai principai.

1 Galimų poslinkių principas (Lagrange principas)

Lagranžo principas. Jei kūnas yra pusiausvyroje, išorinių ir vidinių jėgų poveikis bet kokiam galimam be galo mažam poslinkio prieaugiui yra lygus nuliui.

Naudojant Clapeyron teoremą, kad tampriai deformuotam kūnui keičiant poslinkį gauname Lagranžo principą

Deformuojamų kūnų mechanikoje galimi tokie poslinkiai, kurie tenkina išorinius ir vidinius kūno suvaržymus.

Išorinės jungtys yra tvirtinimo sąlygos, vidinės jungtys yra tęstinumo sąlyga.

Norint patenkinti vidinius apribojimus, būtina, kad poslinkio prieaugiai būtų nuolatinės vienos vertės koordinačių funkcijos.

Šioje formoje Lagranžo principas galioja bet kokiems deformuojamiems kūnams.

Dėl elastingų kūnų gauta, kad

(41)

Tada (40), atsižvelgiant į (41), gali būti parašytas kaip

(42)

kur W yra specifinė padermė ir

Čia U yra visos potencialios kūno energijos kitimas.

Pakeičiame išraišką (43) į (42) ir, kadangi jėgos nesikeičia, rašome, kad

(44)

(44) lygtis yra variacinė Lagranžo lygtis.

Jei jėgos yra konservatyvios, tai pirmieji du integralai reiškia išorinių jėgų potencialo kitimą pereinant iš nedeformuotos būsenos į deformuotą.

Išorinių jėgų potencialas

(45)

kur - galimas išorinių jėgų darbas pereinant iš nedeformuotos į deformuotą būseną apskaičiuojamas darant prielaidą, kad išorinės jėgos lieka nepakitusios. Bendra sistemos energija

Tada, atsižvelgiant į išraiškas (44) - (46), Lagranžo principas bus parašytas:

tai visos pusiausvyros padėtyje esančios sistemos energijos kitimas dėl galimų poslinkių yra lygus nuliui. Išraiška (47) yra variacinė Lagranžo lygtis, kai veikia tik konservatyvios jėgos.

Stabilios pusiausvyros padėtyje bendra energija P yra minimali,

Lagranžo principas yra minimalios energijos principas.

2 Galimų būsenų principas (Castillano principas)

Galimomis būsenomis vadinsime tas, kurios atitinka išorines ir vidines jėgas, tai yra tenkina pusiausvyros lygtis.

(57) lygtis rašo Castigliano principą. Esant galimiems kūno įtempimo būsenos pokyčiams, pokytis yra lygus integralui toje kūno paviršiaus dalyje, kurioje poslinkiai pateikiami iš galimų paviršiaus jėgų ir poslinkių sandaugų.

3 Ryšys tarp tikslaus sprendimo ir sprendimų, gautų remiantis Lagrange ir Castigliano principais

Remiantis Lagranžo principu, pasirenkant kai kurias funkcijas, ar jų aibę, o kadangi funkcijų rinkinys yra ribotas, gauname mažesnį sistemos laisvės laipsnių skaičių, taip sumažindami struktūros laisvės laipsnius. Tai reiškia, kad energijos prasme sprendimas yra griežtesnis nei tikslus.

Jei imsime integralines charakteristikas, tada apytikslis sprendimas yra griežtesnis integralas.

Sprendžiant šarnyrinės sijos apkrovimo skersine jėga tarpatramio viduryje uždavinį (1 pav.), apytikslis sprendimas duos mažesnį poslinkį veikiant jėgai, nei su tikslu.

tikslus sprendimas

Sprendžiant tą patį uždavinį naudojant Castigliano variacinį principą, kadangi netenkinama tęstinumo sąlyga, sistema gauna daugiau laisvės nei realybėje.

Tikslus sprendimas yra tarp šių dviejų apytikslių metodų (Lagrange ir Castigliano). Kartais skirtumas tarp gautų sprendinių būna nedidelis.

5. Naudotos literatūros sąrašas

1. Aleksandrovas A.V., Potapovas V.D. Tamprumo ir plastiškumo teorijos pagrindai. 400 puslapių Aukštoji mokykla 1990 m.

2. Veretimus D.K. Tamprumo teorijos pagrindai. I dalis. Streso teorija. Kurso "Elastingumo ir plastiškumo teorijos pagrindai" metodinis vadovas. 2005.-37s.

Veretimus D.K. Tamprumo teorijos pagrindai II dalis Deformacijų teorija. Įtemptos ir deformuotos būsenos ryšys Kurso "Elastingumo ir plastiškumo teorijos pagrindai" metodinis vadovas, 2005.-53psl.

Veretimus D.K. Tamprumo teorijos pagrindai.III dalis.Pagrindinės tamprumo teorijos lygtys.Elastingumo teorijos uždavinių rūšys. Kurso "Elastingumo ir plastiškumo teorijos pagrindai" metodinis vadovas, 2005.-45p.

Kūnuose ramybės būsenoje arba judant veikiant apkrovoms.

1. Elastingumo teorijos problema

Šios teorijos uždavinys – parašyti matematines lygtis, kurių sprendimas leidžia atsakyti į šiuos klausimus:

Kokios bus konkretaus kūno deformacijos, jei žinomose vietose jam bus taikomos tam tikros vertės apkrovos?
kokia bus įtampa kūne?

Klausimas, kūnas subyrės, atlaikys šias apkrovas, glaudžiai susijusias su elastingumo teorija, bet, griežtai tariant, nepriklauso jo kompetencijai.

Yra daug pavyzdžių – nuo deformacijų ir įtempių nustatymo apkrautoje sijoje ant atramų iki tų pačių parametrų apskaičiavimo orlaivio, raketos, povandeninio laivo korpuse, automobilio vaire tanko šarvuose, kai sviedinys pataiko, kalnų grandinėje klojant aditą, į daugiaaukščio namo karkasą ir pan.

Inžinerinių problemų atveju konstrukcijų įtempiai ir deformacijos skaičiuojami pagal supaprastintas teorijas, logiškai pagrįstas tamprumo teorija. Šios teorijos apima: medžiagų stiprumas, kurio užduotis yra strypų ir sijų skaičiavimas, taip pat įtempių, atsirandančių kietųjų kūnų kontaktinės sąveikos zonose, įvertinimas; konstrukcinė mechanika- strypų sistemų (pvz., tiltų) projektavimas ir apvalkalo teorija- nepriklausoma ir gerai išvystyta deformacijų ir įtempių mokslo šaka, kurios objektas yra plonasieniai apvalkalai - cilindrinės, kūginės, sferinės ir sudėtingos formos.

2. Pagrindinės tamprumo teorijos sampratos

Pagrindinės tamprumo teorijos sąvokos yra mažose plokštumose veikiantis įtempis, kurį mintyse galima nubrėžti kūne per duotą tašką P, taško P mažos kaimynystės deformacija ir paties taško P poslinkis. tiksliai įvedamas mechaninis įtempių tenzorius , mažas deformacijos tenzorius ir poslinkio vektorius tu aš. Trumpas žymėjimas , Kur indeksai aš, j paimkite reikšmes 1, 2, 3 (arba x, y, z) turėtų būti suprantama kaip matrica tokia forma:

Panašiai reikėtų suprasti ir trumpą tenzoriaus žymėjimą.

Jei fizinis kūno taškas M dėl deformacijos užėmė naują vietą erdvėje P ", tada poslinkio vektorius yra vektorius su komponentais (u x, u y, u z), arba trumpiau, tu aš. Mažųjų deformacijų teorijoje komponentai tu aš ir laikomi mažais kiekiais (griežtai kalbant, be galo maži). Tenzoriaus, kuris taip pat vadinamas, komponentai deformacijos tenzorius Koši arba tiesinės deformacijos tenzorius ir vektorius tu aš susijusios priklausomybės:

Iš paskutinio įrašo matyti, kad , Todėl deformacijos tenzorius pagal apibrėžimą yra simetriškas.

Jei tamprus kūnas, veikiamas išorinių jėgų, yra pusiausvyroje (t. y. visų jo taškų greičiai lygūs nuliui), tai bet kuri kūno dalis, kurią galima psichiškai nuo jo atskirti, taip pat yra pusiausvyroje. Iš kūno išgaunamas be galo mažas stačiakampis gretasienis, kurio paviršiai yra lygiagrečiai Dekarto sistemos koordinačių plokštumoms. Iš pusiausvyros sąlygos gretasieniui su briaunų dydžiais dx, dy, dz, Atsižvelgdami į jėgų pusiausvyros projekcijose sąlygas, galime gauti:

Panašiai gaunamos pusiausvyros lygtys, išreiškiančios visų gretasienį veikiančių jėgų pagrindinio momento lygybę iki nulio, sumažintos iki formos:

Ši lygybė reiškia, kad įtempių tenzorius yra simetriškas tenzorius ir nežinomų įtempių tenzoriaus komponentų skaičius sumažėja iki 6. Yra tik trys pusiausvyros lygtys, t.y. uždaviniui išspręsti neužtenka statikos lygčių. Išeitis yra išreikšti įtempius deformacijomis naudojant Huko dėsnio lygtis, o tada išreikšti deformacijas poslinkiais tu aš naudodami Koši formules ir pakeiskite rezultatą į pusiausvyros lygtį. Šiuo atveju gaunamos trys diferencinės pusiausvyros lygtys trijų nežinomų funkcijų atžvilgiu u x u y u z, tie. nežinomųjų skaičius atitiks lygčių skaičių. Šios lygtys vadinamos Navier-Cauchy lygtimis.

3. Ribinės sąlygos

Tamprumo teorijos uždavinių sprendimas redukuojamas iki diferencialinių lygčių sistemos integravimo dalinėse išvestinėse, kurios lemia tampriojo kūno elgesį vidiniuose taškuose. Šios lygtys papildytos kūną ribojančio paviršiaus sąlygomis. Šios sąlygos nustato išorinių paviršiaus jėgų arba taškų poslinkių kūno paviršiuje užduotis. Atsižvelgiant į tai, dažniausiai suformuluojama viena iš trijų ribinių verčių problemų tipų.

Pirmoji ribinės vertės problema- kinematinė. Kūno tūryje randami poslinkių komponentai, jie paviršiuje įgyja tam tikras vertes. Taigi, esant kūno paviršiaus būsenai, nustatomos paviršiaus lygtys ir poslinkių komponentų reikšmės.

Antroji ribinės vertės problema- statinis. Šiuo atveju kūno paviršiui netaikomi jokie judėjimo apribojimai, nustatomos paviršiaus lygtys, kurios nukreipia normalės kosinusus į paviršių ir paviršiaus apkrovos komponentų reikšmes.

Tuo atveju, kai kūno paviršius sutampa su koordinačių plokštumomis, ribinės sąlygos gali būti formuluojamos tiesiogiai įtempių prasme. Tada pakanka nurodyti paviršiaus lygtį ir nustatyti joje įtempių komponentų reikšmes.

Trečioji ribinės vertės problema- sumaišytas. Šiuo atveju vienoje kūno paviršiaus dalyje nustatomos kinematinės sąlygos, o kitoje – statinės.

Šios trys problemos neišsemia visų ribinių sąlygų įvairovės. Pavyzdžiui, kai kuriose paviršiaus srityse gali būti nurodyti ne visi trys poslinkio komponentai arba paviršiaus apkrovos komponentai.

4. Taip pat žr

Šaltiniai

Timošenko S. P., Goodyear J. Elastingumo teorija. M.: Nauka, 1979. 560 p.

ELASTINGUMO TEORIJA- kontinuumo mechanikos šaka, tirianti stovinčių ar judančių kūnų poslinkius, deformacijas ir įtempimus veikiant apkrovoms. Šios teorijos tikslas – išvesti matematines lygtis, kurių sprendimas leidžia atsakyti į tokius klausimus: kokia bus šio konkretaus kūno deformacija, jei jam žinomose vietose bus taikomos tam tikros vertės apkrovos? Kokia bus įtampa kūne? Klausimas, ar kūnas subyrės, ar atlaikys šias apkrovas, yra glaudžiai susijęs su elastingumo teorija, tačiau, griežtai tariant, nepriklauso šios teorijos kompetencijai.

Galimų pavyzdžių skaičius neribotas – nuo deformacijų ir įtempių nustatymo sijoje, gulinčioje ant atramų ir apkrautoje jėgomis, iki tų pačių verčių skaičiavimo orlaivio, laivo, povandeninio laivo konstrukcijoje, vagono vaire, šarvuose pataikius sviediniui, kalnų grandinėje einant pro aditą, daugiaaukščio pastato rėme ir pan. Čia reikia padaryti išlygą: konstrukcijos, susidedančios iš plonasienių elementų, skaičiuojamos pagal supaprastintas teorijas, logiškai remiantis elastingumo teorija; prie tokių teorijų priskiriama: medžiagų atsparumo apkrovoms teorija (garsusis „sopromatas“), kurios užduotis daugiausia yra skaičiuoti strypus ir sijas; konstrukcinė mechanika - strypų sistemų skaičiavimas (pavyzdžiui, tiltai); ir, galiausiai, apvalkalų teorija iš tikrųjų yra nepriklausoma ir labai išvystyta mokslo apie deformacijas ir įtempimus sritis, kurios tema yra svarbiausi konstrukciniai elementai - plonasieniai apvalkalai - cilindriniai, kūginiai, sferoidiniai. ir sudėtingesnių formų. Todėl tamprumo teorijoje dažniausiai laikomi kūnai, kurių esminiai matmenys per daug nesiskiria. Taigi nagrinėjamas tam tikros formos tamprus kūnas, kurį veikia žinomos jėgos.

Pagrindinės elastingumo teorijos sąvokos yra nedidelius plotus veikiantys įtempiai, kurie gali būti psichiškai atliekami kūne per tam tikrą tašką. M, nedidelės taško kaimynystės deformacijos M ir perkeliant patį tašką M. Tiksliau, streso tenzoriai s ij, mažos deformacijos tenzorius e ij ir poslinkio vektorius tu aš.

Trumpas pavadinimas s ij, kur indeksai i, j 1, 2, 3 reikšmės turėtų būti suprantamos kaip formos matrica:

Trumpasis tenzoriaus žymėjimas e ij.

Jei fizinis kūno taškas M dėl deformacijos užėmė naują vietą erdvėje M', tada poslinkio vektorius yra vektorius su komponentais ( u x u y u z), arba trumpai tu aš. Mažųjų deformacijų teorijoje komponentai tu aš ir e i laikomi mažais kiekiais (griežtai tariant, be galo maži). E tenzoriaus komponentai ij ir vektorius u ij yra susiję su Koši formulėmis, kurios turi tokią formą:

Matyti, kad e xy= e yx, ir, paprastai kalbant, el ij= e ji, todėl deformacijos tenzorius pagal apibrėžimą yra simetriškas.

Jei tamprus kūnas, veikiamas išorinių jėgų, yra pusiausvyroje (t. y. visų jo taškų greičiai lygūs nuliui), tai bet kuri kūno dalis, kurią galima psichiškai nuo jo atskirti, taip pat yra pusiausvyroje. Iš kūno išsiskiria mažas (griežtai tariant, be galo mažas) stačiakampis gretasienis, kurio paviršiai yra lygiagrečiai Dekarto sistemos koordinačių plokštumoms Oxyz(1 pav.).

Tegul gretasienio briaunos turi ilgius dx, dy, dz atitinkamai (čia, kaip įprasta dx yra skirtumas x ir kt.). Remiantis įtempių teorija, įtempio tenzoriaus komponentai veikia lygiagretaus vamzdžio paviršius, kurie žymimi:

ant slenksčio OADG:s xx, s xy, s xz

ant slenksčio OABC:s yx, s yy, s yz

ant slenksčio DABE:s zx, s zy, s zz

o komponentai su tais pačiais indeksais (pavyzdžiui, s xx) veikia statmenai veidui, o turintys skirtingus indeksus – ploto plokštumoje.

Priešingose pusėse to paties pavadinimo įtempių tenzoriaus komponentų reikšmės šiek tiek skiriasi, taip yra dėl to, kad jos yra koordinačių funkcijos ir kinta iš taško į tašką (visada, išskyrus žinomus paprasčiausius atvejus), o pokyčio mažumas yra susijęs su mažais gretasienio matmenimis, todėl galime manyti, kad jei ant ribos OABCįtampa s yy, tada ant ribos GDEFįtampa s yy+ds yy, o maža reikšmė ds yy būtent dėl savo mažumo jį galima nustatyti naudojant Taylor serijos išplėtimą:

(čia naudojamos dalinės išvestinės, nes įtempio tenzoriaus komponentai priklauso nuo x, y, z).

Panašiai visų paviršių įtempiai gali būti išreikšti s ij ir ds ij. Be to, norint pereiti nuo įtempių prie jėgų, reikia padauginti įtempio dydį iš vietos, kurioje jis veikia, ploto (pavyzdžiui, s yy+ds yy padauginti iš dx dz). Nustačius visas gretasienį veikiančias jėgas, galima, kaip tai daroma statikoje, užrašyti kūno pusiausvyros lygtį, tuo tarpu visose pagrindinio vektoriaus lygtyse liks tik terminai su išvestinėmis, nes patys įtempiai panaikina vienas kitą ir veiksnius dx dy dz sumažėja ir dėl to

Panašiai gaunamos pusiausvyros lygtys, išreiškiančios visų gretasienį veikiančių jėgų pagrindinio momento lygybę iki nulio, kurios redukuojamos į formą:

Šios lygybės reiškia, kad įtempių tenzorius yra simetriškas tenzorius. Taigi 6 nežinomiems komponentams s ij yra trys pusiausvyros lygtys, t.y. uždaviniui išspręsti neužtenka statikos lygčių. Išeitis – išreikšti kirčius s ij per deformacijas e ij naudojant Huko dėsnio lygtis, o tada deformacijos e ij išreikšti poslinkio prasme tu aš naudodami Koši formules ir pakeiskite rezultatą į pusiausvyros lygtis. Šiuo atveju gaunamos trys diferencinės pusiausvyros lygtys trijų nežinomų funkcijų atžvilgiu u x u y u z, t.y. nežinomųjų skaičius lygus lygčių skaičiui. Šios lygtys vadinamos Lame lygtimis

neatsižvelgiama į kūno jėgas (svorį ir kt.).

D yra Laplaso operatorius, t.y.

Dabar turime nustatyti kraštines kūno paviršiaus sąlygas;

Pagrindiniai šių sąlygų tipai yra šie:

1. Poslinkiai pateikti žinomoje kūno paviršiaus dalyje S 1, t.y. poslinkio vektorius yra lygus žinomam vektoriui su komponentais ( fx; f y; f z ):

u x = f(xyz)

tu y= f(xyz)

u z= f(xyz)

(fx, f m, fz yra žinomos koordinačių funkcijos)

2. Ant likusio paviršiaus S 2 yra pateiktos paviršiaus jėgos. Tai reiškia, kad įtempių pasiskirstymas kūno viduje yra toks, kad įtempių vertės prie pat paviršiaus, o ribinės - paviršiuje kiekvienoje elementarioje srityje sukuria įtempių vektorių, lygų žinomam išorinės apkrovos vektoriui su komponentais. ( F x ;Fy ; Fz) paviršiaus jėgos. Matematiškai tai parašyta taip: jei taške A paviršiaus, vienetinis normalusis vektorius šiam paviršiui turi komponentų n x, n m, nz tada šioje vietoje lygybės (nežinomų) komponentų s atžvilgiu ij:e ij, tada trims nežinomiesiems gauname šešias lygtis, tai yra, per daug apibrėžta sistema. Ši sistema turės sprendimą tik tuo atveju, jei bus įvykdytos papildomos sąlygos e ij. Šios sąlygos yra suderinamumo lygtys.

Šios lygtys dažnai vadinamos tęstinumo sąlygomis, o tai reiškia, kad jos užtikrina kūno tęstinumą po deformacijos. Ši išraiška yra perkeltinė, bet netiksli: šios sąlygos užtikrina ištisinio poslinkio lauko egzistavimą, jei deformacijų (ar įtempių) dedamąsias imame nežinomaisiais. Šių sąlygų nesilaikymas lemia ne tęstinumo pažeidimą, o problemos sprendimo nebuvimą.

Taigi, elastingumo teorija pateikia diferencialines lygtis ir ribines sąlygas, leidžiančias suformuluoti ribinių reikšmių uždavinius, kurių sprendimas suteikia pilną informaciją apie įtempių, deformacijų ir poslinkių pasiskirstymą nagrinėjamuose kūnuose. Tokių problemų sprendimo metodai yra labai sudėtingi, o geriausi rezultatai gaunami derinant analitinius metodus su skaitmeniniais metodais, naudojant galingus kompiuterius.

Vladimiras Kuznecovas

ELASTINGUMO TEORIJOS PAGRINDAI

AKSIMMETRINĖS ELASTINGUMO TEORIJOS PROBLEMOS

ELASTINGUMO TEORIJOS PAGRINDAI

Pagrindinės nuostatos, prielaidos ir žymėjimas Elementariojo gretasienio ir elementariojo tetraedro pusiausvyros lygtys. Normalus ir šlyties įtempis palei pasvirusią platformą

Pagrindinių įtempių ir didžiausių šlyties įtempių taške nustatymas. Įtempiai oktaedrinėse vietose Poslinkių samprata. Deformacijų ir poslinkių ryšiai. Giminaitis

tiesinė deformacija savavališka kryptimi Deformacijos suderinamumo lygtys. Huko dėsnis izotropiniam kūnui Plokštumos uždavinys stačiakampėse koordinatėse Plokštumos uždavinys polinėse koordinatėse

Galimi tamprumo teorijos uždavinių sprendimai. Poslinkių ir įtempimų problemų sprendimai Temperatūros lauko buvimas. Trumpos išvados apie skyrių PAPRASTOS AKSIMMETRINĖS UŽDUOTYS Lygtys cilindrinėse koordinatėse Lygtys cilindrinėse koordinatėse (tęsinys)

Storasienio sferinio indo deformacija Koncentruota jėga, veikianti plokštumą

Ypatingi tamprios pusės erdvės apkrovimo atvejai: vienoda apkrova apskritimo plote, apkrova apskritimo plote išilgai „pusrutulio“, atvirkštinė problema Absoliučiai standaus rutulio įdubimas į elastingą pusrutulį. erdvė. Rutuliukų elastingo griūties problema STORSIENIŲ VAMZDŽIAI

Bendra informacija. Vamzdžio elemento pusiausvyros lygtis Slėgio vienoje iš grandinių įtempių tyrimas. Tampriosios deformacijos stiprumo sąlygos Kompozitinių vamzdžių įtempiai. Daugiasluoksnių vamzdžių skaičiavimo samprata Skaičiavimo pavyzdžiai

PLOKŠTELĖS, MEMBRANOS Pagrindiniai apibrėžimai ir hipotezės

Plokštės lenkto vidurinio paviršiaus diferencialinė lygtis stačiakampėmis koordinatėmis Plokštės cilindrinis ir sferinis lenkimas

Lenkimo momentai apvalios plokštės ašiesimetriniam lenkimui. Apvalios plokštės lenkto vidurinio paviršiaus diferencialinė lygtis Kraštinės sąlygos apvaliose plokštėse. Didžiausi įtempimai ir deformacijos. stiprumo sąlygos. Šiluminiai įtempiai plokštėse

Jėgų membranose nustatymas. Grandinės jėgos ir įtampa. Apytikslis įlinkių ir įtempių nustatymas apskritose diafragmose Skaičiavimo pavyzdžiai Skaičiavimo pavyzdžiai (tęsinys)

1.1 Pagrindinės nuostatos, prielaidos ir simboliai

Tamprumo teorija skirta analitiniam elastingo kūno įtempių ir deformacijų būklės tyrimui. Tamprumo teorijos pagalba galima patikrinti sprendinius, gautus naudojant varžos prielaidas

medžiagų, ir nustatomos šių sprendimų pritaikymo ribos. Kartais tamprumo teorijos skyriai, kuriuose, kaip ir medžiagų atsparumo atveju, svarstomas detalės tinkamumo klausimas, tačiau naudojant gana sudėtingą matematinį aparatą (plokščių, apvalkalų, masyvų skaičiavimas), jie nurodomi kaip taikomoji elastingumo teorija.

Šiame skyriuje pateikiamos pagrindinės matematinės tiesinės elastingumo teorijos sąvokos. Matematikos taikymas fizikiniams reiškiniams aprašyti reikalauja jų schematizacijos. Matematinė elastingumo teorija uždaviniai sprendžiami taikant kuo mažiau prielaidų, o tai apsunkina sprendimui taikomus matematinius metodus. Tiesinė elastingumo teorija daro prielaidą, kad egzistuoja tiesinis ryšys tarp komponentų įtempių ir deformacijų. Daugeliui medžiagų (gumos, kai kurių rūšių ketaus) tokia priklausomybė, net ir esant nedidelėms deformacijoms, nepriimtina: diagrama σ - ε elastingumo ribose turi tokią pačią formą tiek apkraunant, tiek iškraunant, bet abiem atvejais jis yra kreivinis. Tiriant tokias medžiagas, būtina naudoti netiesinės elastingumo teorijos priklausomybes.

IN Matematinė tiesinė elastingumo teorija remiasi šiomis prielaidomis:

1. Apie terpės tęstinumą (tęstinumą). Šiuo atveju atominė medžiagos struktūra arba buvimasį bet kokias tuštybes neatsižvelgiama.

2. Apie natūralią būseną, kurios pagrindu neatsižvelgiama į pradinę kūno įtempį (deformuotą) būseną, susidariusią prieš taikant jėgos veiksmus, t.y., daroma prielaida, kad kūno apkrovos momentu deformacijos o įtempiai bet kuriame jo taške yra lygūs nuliui. Esant pradiniams įtempimams, ši prielaida galios, jei tik tiesinės tamprumo teorijos priklausomybės gali būti taikomos susidarantiems įtempiams (pradinių ir iš poveikių kylančių įtempių sumai).

3. Dėl homogeniškumo, kurio pagrindu daroma prielaida, kad kūno sudėtis visuose taškuose yra vienoda. Nors metalams ši prielaida nesuteikia didelių klaidų, betonui, atsižvelgiant į mažus kiekius, tai gali sukelti didelių klaidų.

4. Apie sferinę izotropiją, kurios pagrindu manoma, kad mechaninės medžiagos savybės visomis kryptimis yra vienodos. Metalo kristalai neturi šios savybės, tačiau visam metalui, susidedančiam iš daugybės mažų kristalų, galime manyti, kad ši hipotezė yra teisinga. Medžiagoms, turinčioms skirtingas mechanines savybes skirtingomis kryptimis, pavyzdžiui, sluoksniuotiems plastikams, buvo sukurta ortotropinių ir anizotropinių medžiagų elastingumo teorija.

5. Apie idealų elastingumą, kurio pagrindu daroma prielaida, kad pašalinus apkrovą visiškai išnyks deformacija. Kaip žinoma, realiuose kūnuose, veikiant bet kokiai apkrovai, atsiranda liekamoji deformacija. Todėl prielaida

6. Apie tiesinį ryšį tarp komponentų deformacijų ir pabrėžia.

7. Dėl deformacijų mažumo, kurio pagrindu daroma prielaida, kad santykinės tiesinės ir kampinės deformacijos yra mažos, palyginti su vienetu. Tokioms medžiagoms kaip guma arba elementams, tokiems kaip spyruoklės, buvo sukurta didelių tamprių deformacijų teorija.

Spręsdami elastingumo teorijos uždavinius, jie naudojasi sprendimo unikalumo teorema: jei nurodytos išorinio paviršiaus ir kūno jėgos yra pusiausvyroje, jos atitinka vieną bendrą įtempių ir poslinkių sistemą. Sprendimo unikalumo padėtis galioja, jei galioja tik prielaida apie natūralią kūno būseną (kitaip galimas begalinis sprendinių skaičius) ir tiesinio ryšio tarp deformacijų ir išorinių jėgų prielaida.

Sprendžiant elastingumo teorijos uždavinius, dažnai naudojamas Saint-Venant principas: jei išorinės jėgos, veikiančios nedidelę elastingo kūno atkarpą, pakeičiamos statiškai lygiaverte jėgų sistema, veikiančia tą pačią pjūvį (turinti tą patį pagrindinį vektorių ir tą patį pagrindinį momentą), tai šis pakeitimas sukels tik vietinių deformacijų pasikeitimą .

Taškuose, kurie yra pakankamai nutolę nuo išorinių apkrovų taikymo vietų, įtempiai mažai priklauso nuo jų taikymo būdo. Apkrova, kuri medžiagų atsparumo eigoje pagal Saint-Venant principą buvo schematiškai išreikšta jėgos arba koncentruoto momento forma, iš tikrųjų yra normali ir šlyties įtempiai vienaip ar kitaip pasiskirsto ant tam tikra kūno paviršiaus sritis. Šiuo atveju skirtingi įtempių pasiskirstymai gali atitikti tą pačią jėgą arba jėgų porą. Remiantis Saint-Venant principu, galima manyti, kad jėgų pokytis tam tikroje kūno paviršiaus dalyje beveik neturi įtakos įtempiams taškuose, esančiuose pakankamai dideliu atstumu nuo šių jėgų taikymo vietos (palyginti su apkrauto ploto linijiniai matmenys).

Tiriamos srities padėtis, pasirinkta kūne (1 pav.), nustatoma pagal normaliosios N krypties kosinusus į plotą pasirinktoje stačiakampių koordinačių ašių x, y ir z sistemoje.

Jei P yra vidinių jėgų, veikiančių taške A pasirinktą elementarųjį plotą, rezultatas, tada bendras įtempis p N šiame taške išilgai ploto su normaliuoju N yra apibrėžiamas kaip santykio riba

tokia forma:

Vektorius p N erdvėje gali būti išskaidytas į tris viena kitai statmenas dedamąsias.

2. Į dedamąsias σ N , τ N s ir τ N t kryptimis normalės į vietą (normalus įtempis) ir dvi viena kitai statmenas ašis s ir t (1b pav.), esančias aikštelės plokštumoje (tangentinė). pabrėžia). Pagal 1 pav., b

Jei kūno pjūvis arba plotas yra lygiagretus vienai iš koordinačių plokštumų, pavyzdžiui, y0z (2 pav.), tai trečioji koordinačių x ašis bus normali šiai sričiai ir įtempių komponentai turės žymėjimą σ x , τ xy ir τ xz .

Normalus įtempis yra teigiamas, jei jis yra tempiamas, ir neigiamas, jei jis yra gniuždomasis. Šlyties įtempio ženklas nustatomas pagal šią taisyklę: jei teigiamas (tempiamas) normalus įtempis išilgai aikštelės suteikia teigiamą projekciją, tada tangentinė

įtempis toje pačioje srityje laikomas teigiamu, jei jis taip pat suteikia teigiamą projekciją atitinkamoje ašyje; jei tempiamasis normalusis įtempis suteikia neigiamą projekciją, tai teigiamas šlyties įtempis taip pat turi duoti neigiamą projekciją atitinkamoje ašyje.

Ant pav. 3, pavyzdžiui, visos įtempių dedamosios, veikiančios elementariojo gretasienio paviršius, sutampančius su koordinačių plokštumomis, yra teigiami.

Norint nustatyti įtempių būseną tampriojo kūno taške, reikia žinoti trijų viena kitai statmenų sričių, einančių per šį tašką, bendruosius įtempius p N. Kadangi kiekvienas bendras įtempis gali būti suskaidytas į tris komponentus, įtempių būsena bus nustatyta, jei žinomi devyni įtempių komponentai. Šiuos komponentus galima parašyti kaip matricą

vadinama įtempių tenzoriaus komponentų matrica taške.

Kiekvienoje horizontalioje matricos eilutėje yra trys įtempių komponentai, veikiantys tą pačią sritį, nes pirmosios piktogramos (normalios pavadinimas) joms yra vienodos. Kiekviename vertikaliame tenzoriaus stulpelyje yra trys įtempiai, lygiagrečiai tai pačiai ašiai, nes antrieji ženklai (ašies, kuriai veikia lygiagrečiai, pavadinimas) yra vienodi.

1.2 Elementariojo gretasienio pusiausvyros lygtys

ir elementarus tetraedras

Įtempto tampriojo kūno taške A (su koordinatėmis x, y ir z) trimis tarpusavyje statmenomis plokštumų poromis paskirsime elementarųjį gretasienį, kurio briaunų dydžiai yra dx, dy ir dz (2 pav.). Kiekviename iš trijų viena kitai statmenų paviršių, esančių šalia taško A (arčiausiai koordinačių plokštumų), veiks trys įtempių komponentai - normalus ir du tangentiniai. Manome, kad jie yra teigiami išilgai taško A esančių paviršių.

Judant nuo paviršiaus, einančio per tašką A, į lygiagrečią paviršių, įtempiai keičiasi ir didėja. Pavyzdžiui, jei įtempių komponentai σ x \u003d f 1 (x, y, z), τ xy \u003d f 2 (x, y, z,), τ xz \u003d f 3 (x, y, z,) , tada išilgai lygiagrečio paviršiaus dėl tik vienos x koordinatės padidėjimo pereinant iš vieno paviršiaus į kitą,

įtempių komponentai Galima nustatyti įtempius visuose elementaraus gretasienio paviršiuose, kaip parodyta fig. 3.

Be įtempių, taikomų elementaraus gretasienio paviršiams, jį veikia kūno jėgos: svorio jėgos, inercinės. Šių tūrio vieneto jėgų projekcijas koordinačių ašyse pažymėkime X, Y ir Z. Jei visų normaliųjų, tangentinių ir tūrinių jėgų projekcijų x ašyje sumą prilyginsime nuliui,

veikiant elementarų gretasienį, tada sumažinus sandauga dxdydz gauname lygtį

Sudarę panašias lygtis jėgų projekcijoms į y ir z ašis, parašome tris diferencialines lygtis elementariojo gretasienio pusiausvyrai, gautai pagal Koši,

Kai gretasienio matmenys sumažinami iki nulio, jis virsta tašku, o σ ir τ yra įtempių komponentai išilgai trijų viena kitai statmenų sričių, einančių per tašką A.

Jei prilyginsime nuliui visų jėgų, veikiančių elementarųjį gretasienį, x c ašies atžvilgiu, lygiagrečią x ašiai ir einančių per jos svorio centrą, momentų sumą, gausime lygtį.

arba, atsižvelgiant į tai, kad antrasis ir ketvirtasis lygties nariai yra mažesnio laipsnio, palyginti su kitais, sumažinus dxdydz

τ yz - τ zy = 0 arba τ yz = τ zy.

Sudarę panašias momentų lygtis apie centrines ašis y c ir z c , gauname tris šlyties įtempių poravimosi dėsnio lygtis

τ xy = τ yx, τ yx = τ xy , τ zx = τ xz . (1.3)

Šis įstatymas suformuluotas taip: tangentiniai įtempiai, veikiantys viena kitai statmenas sritis ir nukreipti statmenai į sričių susikirtimo liniją, yra vienodo dydžio ir vienodo ženklo.

Taigi iš devynių tenzoriaus T σ matricos įtempių komponentų šeši yra poromis lygūs vienas kitam, ir norint nustatyti įtempių būseną taške, pakanka rasti tik šiuos šešis įtempių komponentus:

Tačiau nustatytos pusiausvyros sąlygos davė mums tik tris lygtis (1.2), iš kurių šešių nežinomųjų negalima rasti. Taigi tiesioginė įtempių būsenos taške nustatymo problema bendru atveju yra statiškai neapibrėžta. Norint atskleisti šį statinį neapibrėžtumą, reikia papildomų geometrinių ir fizinių priklausomybių.

Įpjaukime elementarųjį gretasienį taške A plokštuma, pasvirusi į jo paviršius; tegul normalioji N šiai plokštumai turi krypties kosinusus l, m ir n. Gauta geometrinė figūra (4 pav.) yra piramidė su trikampiu pagrindu – elementariu tetraedru. Darysime prielaidą, kad taškas A sutampa su koordinačių pradžia, o trys viena kitai statmenos tetraedro paviršiai sutampa su koordinačių plokštumomis.

Bus svarstomi įtempių komponentai, veikiantys šiuos tetraedro paviršius

teigiamas. Jie parodyti fig. 4. Pažymėkite , o bendrojo įtempio p N, veikiančio pasvirusį BCD tetraedro paviršių, projekcijas x, y ir z ašyse. Pasvirusio veido BCD plotas žymimas dF. Tada veido ABC plotas bus dFp, veido ACD - dFl ir veido ADB - dFt.

Tetraedro pusiausvyros lygtį sudarysime projektuodami visas jo paviršius veikiančias jėgas į x ašį; kūno jėgos projekcija į projekcijos lygtį neįtraukta, todėl

kokia yra aukštesnio laipsnio mažumo reikšmė, palyginti su paviršiaus jėgų projekcijomis:

Sudarę projekcijų lygtis jėgoms, veikiančioms tetraedrą y ir z ašyse, gauname dar dvi panašias lygtis. Dėl to turėsime tris elementariojo tetraedro pusiausvyros lygtis

Savavališkos formos erdvinį kūną padalinkime viena kitai statmenų plokštumų хОу, yОz ir хОz sistema (5 pav.) į keletą elementariųjų gretasienių. Kūno paviršiuje elementarus

tetraedra, (kreivinės paviršiaus atkarpos dėl savo mažumo gali būti pakeistos plokštumomis). Šiuo atveju p N reprezentuos paviršiaus apkrovą, o (1.4) lygtys susies šią apkrovą su kūno įtempiais σ ir τ, t.y., pavaizduos tamprumo teorijos uždavinio ribines sąlygas. Šiomis lygtimis apibrėžtos sąlygos vadinamos paviršiaus sąlygos.

Pažymėtina, kad elastingumo teorijoje išorinės apkrovos vaizduojamos normaliais ir tangentiniais įtempiais, taikomais pagal tam tikrą dėsnį su kūno paviršiumi sutampančiose srityse.

1.3 Normalūs ir šlyties įtempiai išilgai šlaito

svetainę

Panagrinėkime elementarųjį tetraedrą ABCD, kurio trys paviršiai lygiagrečios koordinačių plokštumoms, o normalusis N į ketvirtą paviršių sudaro kampus su koordinačių ašimis, kurių kosinusai lygūs l, m ir n (6 pav.). . Tarkime, kad yra pateiktos normaliųjų ir šlyties įtempių, veikiančių koordinačių plokštumose esančias sritis, dedamosios, ir nustatysime įtempius BCD srityje. Mes pasirenkame naują stačiakampių koordinačių ašių x 1, y 1 ir z 1 sistemą, kad x 1 ašis sutaptų su normaliąja N,

Pagrindinis tamprumo teorijos uždavinys – įtempių-įtempimų būsenos nustatymas pagal pateiktas kūno apkrovos ir fiksavimo sąlygas.

Įtempių ir deformacijų būsena nustatoma, jei randamos įtempio tenzoriaus () ir poslinkio vektoriaus komponentai, devynios funkcijos.

Pagrindinės tamprumo teorijos lygtys

Norint rasti šias devynias funkcijas, reikia užrašyti pagrindines elastingumo teorijos lygtis arba:

Diferencialinis Cauchies

kur yra Koši deformacijų tiesinės dalies tenzoriaus komponentai;

Poslinkio išvestinės išilgai spindulio tenzoriaus komponentai.

Diferencialinės pusiausvyros lygtys

kur yra įtempių tenzoriaus komponentai; yra kūno jėgos projekcija į j ašį.

Huko dėsnis tiesiškai elastingam izotropiniam kūnui

kur yra Lame konstantos; izotropiniam kūnui. Čia yra normalūs ir šlyties įtempiai; atitinkamai deformacijos ir šlyties kampai.

Aukščiau pateiktos lygtys turi tenkinti Saint-Venant priklausomybes

Tamprumo teorijoje uždavinys išspręstas, jei tenkinamos visos pagrindinės lygtys.

Užduočių rūšys elastingumo teorijoje

Kraštinės sąlygos kūno paviršiuje turi būti tenkinamos ir, priklausomai nuo ribinių sąlygų tipo, elastingumo teorijoje yra trijų tipų problemos.

Pirmasis tipas. Jėgos suteikiamos kūno paviršiui. Pasienio sąlygos

Antrasis tipas. Problemos, kai poslinkis nurodomas kūno paviršiuje. Pasienio sąlygos

Trečias tipas. Mišrios elastingumo teorijos problemos. Jėgos suteikiamos kūno paviršiaus daliai, poslinkis – kūno paviršiaus daliai. Pasienio sąlygos

Tiesioginės ir atvirkštinės tamprumo teorijos problemos

Tamprumo teorijos lygtys poslinkiuose (Lame lygtys)

Tamprumo poslinkiuose teorijos lygtims nustatyti rašome: diferencialinės pusiausvyros lygtis (18) Huko dėsnį tiesiškai tampriam izotropiniam kūnui (19)

Jei atsižvelgsime į tai, kad deformacijos išreiškiamos poslinkiais (17), rašome:

Taip pat reikėtų prisiminti, kad šlyties kampas yra susijęs su poslinkiais tokiu ryšiu (17):

Pakeitę išraišką (22) į pirmąją lygčių (19) lygtį, gauname, kad normalūs įtempiai

Atkreipkite dėmesį, kad žymėjimas u šiuo atveju nereiškia sumavimo per i.

Pakeitę išraišką (23) į antrąją lygčių (19) lygtį, gauname šlyties įtempius

Parašykime pusiausvyros lygtis (18) išplėstine forma, kai j = 1

Pakeitę (26) lygties išraiškas normaliuosius (24) ir tangentinius (25) įtempius, gauname

kur l yra Lame konstanta, kuri nustatoma pagal išraišką:

Išreiškimą (28) pakeičiame lygtimi (27) ir rašome,

kur nustatoma pagal išraišką (22) arba išplėstine forma

Išreiškimą (29) padaliname iš G ir pridedame panašius terminus ir gauname pirmąją Lame lygtį:

kur yra Laplaso operatorius (harmoninis operatorius), kuris apibrėžiamas kaip

Panašiai galite gauti:

(30) ir (32) lygtis gali būti parašytos taip:

(33) arba (30) ir (32) lygtys yra Lame lygtys. Jei kūno jėgos yra lygios nuliui arba pastovios, tada

be to, žymėjimas šiuo atveju nereiškia sumavimo per i. Čia

arba, atsižvelgiant į (31)

Pakeitę (22) į (34) ir atlikę transformacijas, gauname

ir dėl to

kur yra šią lygybę tenkinanti funkcija. Jeigu

taigi f yra harmoninė funkcija. Tai reiškia, kad tūrinė deformacija taip pat yra harmoninė funkcija.

Laikant ankstesnę prielaidą teisinga, harmoninį operatorių paimame iš Lame lygties i-osios eilutės

Jei kūno jėgos yra lygios nuliui arba pastovios, tada poslinkio komponentai yra biharmoninės funkcijos.

Egzistuoja įvairios dviharmoninių funkcijų vaizdavimo harmoninės atžvilgiu formos (tenkinančios Lame'o lygtis).

kur k = 1,2,3. Ir