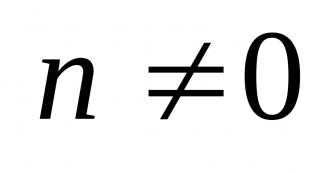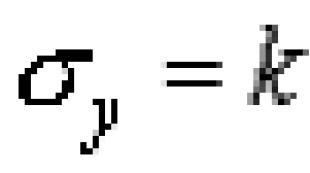Mat analizės funkcija. Matematinė analizė. Pažiūrėkite, kas yra „matematinė analizė“ kituose žodynuose
Sudarė Yu.V.Obrubovas
Kaluga – 2012 m
Įvadas į matematinę analizę.
Realūs skaičiai. Kintamieji ir konstantos.
Viena iš pagrindinių matematikos sąvokų yra numerį.
Iškviečiami teigiami skaičiai 1,2,3, ..., kurie gaunami skaičiuojant natūralus.
Skaičiai ... -3, -2, -1,0,1,2,3, ... vadinami sveikaisiais skaičiais. Skaičiai, kurie gali būti pavaizduoti kaip baigtinis dviejų sveikųjų skaičių santykis ( 
) yra vadinami racionalus.
Tai apima sveikuosius ir trupmeninius, teigiamus ir neigiamus skaičius. Vadinami skaičiai, kurie gali būti pavaizduoti kaip begalinės nesikartojančios trupmenos neracionalus.
Iracionaliųjų skaičių pavyzdžiai yra 
,
. Iracionaliųjų skaičių aibėje jie išskiria transcendentinis
numeriai. Tai skaičiai, kurie yra nealgebrinių operacijų rezultatas. Garsiausi iš jų yra skaičius 
ir ne lygiaverčių numerių 
. Vadinami racionalieji ir iracionalieji skaičiai galioja
. Tikrieji skaičiai žymimi taškais skaičių eilutėje. Kiekvienas skaičių ašies taškas atitinka vieną realųjį skaičių ir, atvirkščiai, kiekvieną realųjį skaičių atitinka vienas skaičiaus ašies taškas. Taigi tarp realiųjų skaičių ir skaičių linijos taškų buvo nustatytas vienas su vienu atitikimas. Dėl to terminus „skaičius a“ ir „taškas a“ galima vartoti pakaitomis.
Tiriant įvairius fizinius, ekonominius, socialinius procesus, dažnai tenka susidurti su dydžiais, reprezentuojančiais tiriamų reiškinių parametrų skaitines reikšmes. Kartu vieni jų keičiasi, o kiti išlaiko savo vertybes.
kintamasis
Vadinamas dydis, kuris įgauna įvairias skaitines reikšmes. Vadinamas dydis, kurio skaitinė reikšmė tam tikrame uždavinyje ar eksperimente nekinta pastovus.
Kintamieji paprastai žymimi lotyniškomis raidėmis 
ir nuolatinis 
.
kintamasis 
laikomas duotu, jei žinomas galimų reikšmių rinkinys. Ši aibė vadinama kintamojo diapazonu.
Yra įvairių skaitinio kintamojo reikšmių rinkinių.
intervalas
yra x reikšmių rinkinys, esantis tarp skaičių a ir b, o skaičiai a ir b nepriklauso nagrinėjamai aibei. Intervalas žymimas: (a,b);a segmentas
vadinamas x reikšmių rinkiniu, esančiu tarp skaičių a ir b, o skaičiai a ir b priklauso nagrinėjamai aibei. Atkarpa žymima ,a≤x≤b. Visų realiųjų skaičių aibė yra atviras intervalas. Žymima: (- ∞,+ ∞), -∞<х <+∞, R. Taško x kaimynystė
0
vadinamas savavališkas intervalas (а, b), kuriame yra taškas x 0, visi šio intervalo taškai tenkina nelygybę a ε
- taško a kaimynystė
yra intervalas, kurio centras yra taške a, tenkinantis nelygybę a–ε Funkcija yra viena iš pagrindinių matematinės analizės sąvokų. Tegul X ir Y yra savavališkos realiųjų skaičių aibės. Jei kiekvienam skaičiui x X pagal kokią nors taisyklę ar dėsnį priskiriamas unikalus tiksliai apibrėžtas tikrasis skaičius yY, tada jie sako, kad funkcija
su apibrėžimo X domenu ir reikšmių rinkiniu Y. Pažymėkite y \u003d f (x). Kintamasis x vadinamas argumentas
funkcijas. Funkcijos apibrėžime esminiai du punktai: apibrėžimo srities nuoroda ir atitikimo dėsnio nustatymas. Apibrėžimo sritis
arba egzistavimo sritis
Funkcija yra argumentų reikšmių rinkinys, kuriam funkcija egzistuoja, tai yra, ji turi prasmę. Keisti sritį
Funkcija vadinama y verčių rinkiniu, kurio reikia leistinoms x reikšmėms. Funkcijos nustatymo būdai.
Analitinis funkcijos apibrėžimo būdas. Taikant šį funkcijos nustatymo būdą, atitikimo dėsnis rašomas kaip formulė (analitinė išraiška), nurodanti kokiais matematiniais transformacijomis, naudojant žinomą argumento x reikšmę, galima rasti atitinkamą y reikšmę. Funkciją galima apibrėžti viena analitine išraiška visoje apibrėžimo srityje arba pateikti kelių analitinių išraiškų rinkinį. Pavyzdžiui: y \u003d sin (x 2 + 1) 2. Lentelinis funkcijos nustatymo būdas Dėl tiesioginio reiškinio ar proceso stebėjimo ar eksperimentinio tyrimo argumento x reikšmės ir atitinkamos y reikšmės išrašomos tam tikra tvarka. Šioje lentelėje apibrėžiama x funkcija y. Lentelinio funkcijos nurodymo būdo pavyzdys gali būti trigonometrinių funkcijų lentelės, logaritmų, datų ir valiutų kursų, temperatūros ir drėgmės lentelės ir kt. 3. Grafinis funkcijos nustatymo būdas. Grafinis funkcijos nustatymo būdas yra taškų (x, y) atvaizdavimas koordinačių plokštumoje, naudojant techninius prietaisus. Grafinis funkcijos nurodymo metodas matematinėje analizėje nenaudojamas, bet visada pasitelkiamas grafinis analitiškai pateiktų funkcijų iliustravimas. Viskas turi būti išdėstyta kuo paprasčiau, bet ne paprasčiau. Mūsų kelionė prasideda išgalvotu veikėju, kurį vadinsime John Doe. Tai vidutinis darbuotojas, kurį galima lengvai rasti bet kuriame pasaulio mieste. Beveik kiekvieną dieną Jonas atsibunda nuo garsių signalų ir važiuoja į darbą savo automobiliu. Jis liftu kyla į savo biurą, kur paleidžia kompiuterį ir įveda savo vartotojo vardą bei slaptažodį. Jonas daro visus šiuos dalykus net neįsivaizduodamas, kaip jie veikia. Galbūt jam būtų įdomu sužinoti, kaip yra išdėstyti ir veikia kasdien naudojami prietaisai ir įrenginiai, tačiau tam neturi nei laiko, nei jėgų. Automobilius, liftus, kompiuterius ir žadintuvus jis laiko visiškai skirtingais ir sudėtingais mechanizmais, kurie neturi nieko bendro. Anot Johno, norint suprasti, kaip kiekvienas iš jų veikia, reikia studijų metų. Kai kurie žmonės mato dalykus šiek tiek kitaip nei mūsų John Doe. Jie žino, kad liftų įrenginiuose esantys elektros varikliai labai panašūs į automobilių generatorius. Jie žino, kad programuojamas loginis valdiklis, valdantis elektros variklį, atsakingą už lifto judėjimą, yra labai panašus į John Doe darbo kompiuterį. Jie žino, kad iš esmės PLC, žadintuvas ir kompiuteris yra pagrįsti gana paprasta tranzistorių teorija. Tai, kas Johnui Doe ir paprastam žmogui atrodo neįtikėtinai sudėtinga, yra tai, kad įsilaužėlis dažniausiai naudoja paprastus mechaninius ir elektrinius principus. Problema yra ta, kaip šie principai taikomi. Pagrindinių principų abstrahavimas iš sudėtingų idėjų leidžia suprasti ir supaprastinti jas taip, kad atitiktų Alberto Einšteino improvizuotą patarimą, cituotą aukščiau. Daugelis iš mūsų skaičiavimus laiko sudėtingu dalyku. (John Doe įrenginio veikimo principą ir įvairių mechanizmų veikimą laiko tuo pačiu.) Matai krūvą sudėtingų, įmantrių dalykų. Norint juos suprasti, reikia daug laiko ir pastangų. O kas, jei pasakytume, kad matematinė analizė (skaičiavimas) nėra tokia sudėtinga, kaip atrodo iš pirmo žvilgsnio, kaip ir dauguma mechanizmų? Ar yra keletas pagrindinių principų, kuriuos turi suprasti kiekvienas, ir kai tik tai padarysite, turėsite naują požiūrį į pasaulį ir jo veikimą? Įprastą skaičiavimo vadovėlį sudaro apie tūkstantis puslapių. Tipiškas John Doe pamatys jame tūkstančius sunkiai suprantamų ir išstudijuojamų dalykų, o įsilaužėlis pamatys du pagrindinius principus (išvestinį ir integralą) ir 998 šių principų pavyzdžius. Kartu pabandysime išsiaiškinti, kokie yra šie principai. Remdamiesi Michaelo Starbirdo, Teksaso universiteto Ostine profesoriaus darbu, naudosime kasdienius, bet kam suprantamus pavyzdžius. Matematinė analizė atskleidžia ypatingą mūsų pasaulio grožį – grožį, kuris atsiranda, kai sugebi jį stebėti dinamiškai, o ne statiškai. Tikimės, kad viskas jums pasiseks. Prieš pradedant, norėčiau trumpai peržvelgti skaičiavimo atsiradimo istoriją, kurios šaknys glūdi labai kruopščioje pokyčių ir judėjimo analizėje. Zenono paradoksas Zenonas iš Elėjos yra filosofas, gyvenęs IV amžiuje prieš Kristų. Jis iškėlė keletą subtilių, bet gilių paradoksų, iš kurių du galiausiai paskatino skaičiavimo gimimą. Kad išspręstų Zenono paradoksus, žmonijai prireikė daugiau nei dviejų tūkstančių metų. Kaip galite įsivaizduoti, tai nebuvo lengva. Sunkumai daugiausia buvo susiję su begalybės idėja. Kokia yra begalybės problema matematiniu požiūriu? XVII amžiuje Izaokas Niutonas ir Gotfrydas Leibnicas sugebėjo išspręsti Zenono paradoksus ir sukurti matematinę analizę. Pažvelkime į šiuos paradoksus atidžiau, kad suprastume, kodėl aplink juos kilo tiek daug triukšmo. Rodyklė Įsivaizduokite, kaip strėlė skrenda oru. Galime labai užtikrintai pasakyti, kad rodyklė juda. Dabar apsvarstykite rodyklę tam tikru momentu. Ji nebejuda, o ilsisi. Bet mes tikrai žinome, kad strėlė juda, tai kaip ji gali būti ramybės būsenoje?! Tai yra šio paradokso esmė. Tai gali atrodyti kvaila, bet iš tikrųjų tai labai sudėtinga sąvoka, kurią reikėtų apsvarstyti matematiniu požiūriu. Vėliau išsiaiškinsime, kad susiduriame su momentinio kitimo greičio samprata, kurią susiesime su vieno iš dviejų matematinės analizės (skaičiavimo) principų – išvestinės – idėja. Tai leis mums apskaičiuoti rodyklės greitį tam tikru laiko momentu – to žmonija negalėjo padaryti daugiau nei du tūkstantmečius. Dichotomija Dar kartą pažiūrėkime į tą pačią rodyklę. Šį kartą įsivaizduokite, kad jis skrenda mūsų kryptimi. Zenonas tvirtino, kad neturėtume judėti, nes strėlė niekada negalėjo į mus pataikyti. Įsivaizduokite, kad po to, kai strėlė yra ore, ji turi įveikti pusę atstumo tarp lanko ir taikinio. Kai ji pasieks tam tikrą tašką pusiaukelėje, jai vėl reikės įveikti pusę atstumo – šį kartą tarp šio taško ir taikinio. Įsivaizduokite, jei taip darysime ir toliau. Taigi rodyklė nuolat nuskrenda pusę atstumo tarp atskaitos taško ir taikinio. Atsižvelgdami į tai, galime daryti išvadą, kad strėlė niekada negalės į mus pataikyti! Realiame gyvenime strėlė galiausiai pataikys į taikinį, todėl mums kyla klausimas, ką reiškia paradoksas. Kaip ir pirmojo paradokso atveju, vėliau svarstysime, kaip išspręsti šią problemą naudojant vieną iš matematinės analizės principų – integralą. Integralas leidžia žiūrėti į begalybės sąvoką kaip į matematinę funkciją. Pasak mokslininkų ir inžinierių, tai itin galingas įrankis. Du pagrindiniai skaičiavimo principai Dviejų pagrindinių matematinės analizės principų esmę galima parodyti pritaikius juos Zenono paradoksams spręsti. Darinys. Išvestinė yra metodas, kuris leis mums apskaičiuoti rodyklės greitį rodyklės paradokse. Tai darome analizuodami rodyklės padėtį nuosekliai mažėjančiais laiko intervalais. Tikslus rodyklės greitis paaiškės, kai laikas tarp matavimų pasirodys be galo mažas. Integralinis. Integralas yra metodas, kuris leis mums apskaičiuoti rodyklės padėtį dichotomijos paradokse. Tai padarysime analizuodami rodyklės greitį nuosekliai mažėjančiais laiko intervalais. Tikslią rodyklės padėtį sužinosime, kai laikas tarp matavimų pasirodys be galo mažas. Nesunku pastebėti kai kuriuos išvestinės ir integralo panašumus. Abi vertės apskaičiuojamos analizuojant strėlės padėtį arba greitį palaipsniui mažėjančiais laiko intervalais. Vėliau išsiaiškinsime, kad integralas ir išvestinė iš tikrųjų yra dvi to paties keraminio kondensatoriaus pusės. Kodėl turėtume studijuoti skaičiavimo pagrindus? Visi žinome Ohmo dėsnį, kuris sujungia srovę, įtampą ir varžą į vieną paprastą lygtį. Dabar pažvelkime į Omo dėsnį naudodami kondensatoriaus pavyzdį. Kondensatoriaus srovės stiprumas priklauso nuo įtampos ir laiko. Laikas šiuo atveju yra kritinis kintamasis ir į jį reikia atsižvelgti atliekant bet kokį dinaminį įvykį. Matematinė analizė leidžia suprasti ir įvertinti, kaip viskas keičiasi laikui bėgant. Kondensatoriaus atveju srovė lygi talpos padauginus voltus per sekundę arba i = C(dv/dt), kur: i - srovės stiprumas (momentinis); Šioje grandinėje kondensatoriuje nėra elektros srovės. Voltmetras parodys akumuliatoriaus įtampą, bet ampermetras nieko nerodys. Įtampa nepasikeis tol, kol potenciometras išliks nepažeistas. Šiuo atveju i = C(0/dt) = 0 amer. Bet kas atsitiks, jei pradėsime reguliuoti potenciometrą? Sprendžiant iš lygties, kondensatoriuje atsiras gautos srovės stiprumas. Ši srovė priklausys nuo įtampos pokyčio, kuris yra susijęs su potenciometro judėjimo greičiu. Šie grafikai rodo ryšį tarp įtampos kondensatoriuje, srovės ir greičio, kuriuo sukame potenciometrą. Iš pradžių tai darome lėtai. Padidėjus greičiui, pasikeičia įtampa, o tai savo ruožtu išprovokuoja staigų srovės padidėjimą. Visuose etapuose srovė kondensatoriuje yra proporcinga įtampos kitimo greičiui. Matematinė analizė, tiksliau, išvestinė, suteikia mums galimybę nustatyti pokyčio greitį, kad tiksliai žinotume kondensatoriaus srovės vertę tam tikru momentu. Panašiai galime apskaičiuoti ir Zenono strėlės momentinį greitį. Tai neįtikėtinai galingas įrankis, kuris turėtų būti jūsų arsenale. Medžiaga buvo parengta specialiai svetainei - pagal svetainės hackaday.com straipsnį P.S. Mano vardas Aleksandras. Tai mano asmeninis, nepriklausomas projektas. Labai džiaugiuosi, jei straipsnis patiko. Norite padėti svetainei? Tiesiog ieškokite žemiau skelbimo apie tai, ko neseniai ieškojote. Autorių teisių svetainė © – šios naujienos priklauso svetainei ir yra tinklaraščio intelektinė nuosavybė, saugoma autorių teisių įstatymų ir negali būti niekur naudojama be aktyvios nuorodos į šaltinį. Skaityti daugiau - "Apie autorystę" Ar jūs to ieškote? Galbūt tai yra tai, ko taip ilgai negalėjote rasti? MATEMATINĖ ANALIZĖ matematikos dalis, kurioje funkcijas o jų apibendrinimai tiriami metodu ribos. Ribos sąvoka glaudžiai susijusi su be galo mažo dydžio sąvoka, todėl galima teigti ir M. a. tiria funkcijas ir jų apibendrinimus begalinio mažumo metodu. Pavadinimas "M. a." - sutrumpinta senojo šios matematikos dalies pavadinimo modifikacija - "Begalinė analizė"; pastarasis išsamiau atskleidžia turinį, tačiau jis taip pat yra sutrumpintas (temą tiksliau apibūdintų pavadinimas „Analizė naudojant begalinius mažylius“). Klasikinėje M. ir. tyrimo (analizės) objektai pirmiausia yra funkcijos. „Pirmiausia“ todėl, kad M. a. lėmė galimybę jo metodais tirti sudėtingesnius darinius nei funkciniai, operatoriai ir kt. Gamtoje ir technikoje judesiai ir procesai aptinkami visur, to-rugiai aprašomi funkcijomis; gamtos reiškinių dėsniai taip pat dažniausiai apibūdinami funkcijomis. Taigi objektyvi svarba M. a. kaip mokymosi funkcijų priemonė. M. a. plačiąja šio termino prasme apima labai didelę matematikos dalį. Tai įeina diferencialinis, integralinis skaičiavimas, sudėtingų kintamųjų teorijos funkcijos, teorija įprastos diferencialinės lygtys, teorija dalinės diferencialinės lygtys, teorija integralinės lygtys, variacijų skaičiavimas, funkcinė analizė ir kai kurių kitų matematinių disciplinas. Modernus skaičių teorija Ir tikimybių teorija taikyti ir plėtoti metodus M. ir. Nepaisant to, terminas M. a. dažnai vartojami įvardyti tik teoriją jungiančius matematinės analizės pagrindus tikras numeris, ribų teorija, teorija eilės, diferencialiniai ir integraliniai skaičiavimai ir tiesioginiai jų pritaikymai, tokie kaip maksimumų ir minimumų teorija, teorija numanomos funkcijos, Furjė serija, Furjė integralai. Funkcija.Į M. a. išplaukia iš funkcijos apibrėžimo pagal Lobačevskį ir Dirichlet. Jei kiekvienam tam tikros F skaičių aibės skaičiui xz, pagal k.-l. įstatymas yra įtrauktas į sąrašą y, tada tai apibrėžia funkciją iš vieno kintamojo X. Funkcija apibrėžiama panašiai iš kintamųjų, kur x=(x 1 , ..., x n) -
n-matės erdvės taškas; taip pat apsvarstykite funkcijas iš taškų x=(x 1 , X 2 ,
...) kokios nors begalinės erdvės, kurios vis dėlto dažniau vadinamos funkcinėmis. elementarios funkcijos. Esminė vertė M. ir. žaisti elementarios funkcijos. Praktiškai jie daugiausia veikia su elementariomis funkcijomis, jie apytiksliai atitinka sudėtingesnio pobūdžio funkcijas. Elementariosios funkcijos gali būti laikomos ne tik realiomis, bet ir kompleksinėmis x, tada idėjos apie šias funkcijas tam tikra prasme tampa užbaigtos. Šiuo atžvilgiu svarbi M. a. šaka, vadinama. kompleksinio kintamojo funkcijų teorija arba teorija analitinės funkcijos. Tikras numeris. Funkcijos samprata iš esmės remiasi realaus (racionalaus ir neracionalaus) skaičiaus samprata. Jis galutinai susiformavo tik XIX amžiaus pabaigoje. Visų pirma, buvo sukurtas logiškai nepriekaištingas ryšys tarp skaičių ir geometrinių taškų. tiesi linija, nulėmusi formalų R. Dekarto idėjų pagrindimą (R. Dekartas, XVII a. vidurys), įvedusio į matematiką stačiakampes koordinačių sistemas ir funkcijų vaizdavimą jose grafikais. Riba.Į M. a. funkcijų tyrimo metodas yra . Atskirkite sekos ribą ir funkcijos ribą. Šios sąvokos galutinai susiformavo tik XIX amžiuje, nors kiti graikai apie jas suprato. mokslininkai. Pakanka pasakyti, kad Archimedas (III a. pr. Kr.) sugebėjo apskaičiuoti parabolės atkarpą procesu, kurį vadintume perėjimu iki ribos (plg. išsekimo metodas). Nuolatinės funkcijos. Svarbi funkcija, tirta M. a., forma nuolatinės funkcijos. Vienas iš galimų šios sąvokos apibrėžimų: funkcija y=f(x).iš vieno kintamojo X, nurodyta intervale ( a, b),
paskambino ištisinis taške X, Jeigu Funkcija tęsiasi intervale ( a, b),
jei jis yra ištisinis visuose savo taškuose; tada tai yra kreivė, ištisinė kasdienine to žodžio prasme. Išvestinė ir . Tarp tęstinių funkcijų reikėtų išskirti funkcijas, kurios turi išvestinė. Funkcijos išvestinė taške turi savo kitimo greitį šiame taške, ty ribą Jei turime taško, judančio išilgai y ašies, koordinates X, tada f "(x). yra momentinis taško greitis vienu metu X. Išvestinės f ženklu "(x) .
spręskite f (x) pokyčio pobūdį: jei f "(z)> 0 ( f"(x) <0
).
per intervalą ( c, d), tada funkcija / šiame intervale padidėja (sumažėja). Jei funkcija / taške x pasiekia vietinį ekstremumą (maksimumą arba minimumą) ir šiame taške turi išvestinę, tada pastaroji šiame taške yra lygi nuliui f "(x 0) \u003d 0. Lygybę (1) galima pakeisti lygiaverte lygybe kur yra begalinis kai, t.y., jei funkcija f taške turi išvestinę X, tada jo prieaugis šioje vietoje išskaidomas į du narius. Iš jų pirmasis yra nuo (proporcingas), antrasis - linkęs į nulį greičiau nei Vertė (2) ref. diferencialas funkcijos, atitinkančios prieaugį At mažas galima laikyti apytiksliai lygiomis dy: Minėti samprotavimai apie skirtumą būdingi M. a. Jie apima daugelio kintamųjų funkcijas ir funkcines funkcijas. Pavyzdžiui, jei funkcija iš kintamųjų turi tęstinumą daliniai dariniai taške x=(x 1 , ... , x n), tada jo padidėjimas
atitinkančius nepriklausomų kintamųjų priedus, galima parašyti kaip kur t.y. jei visi Čia pirmasis žodis (3) dešinėje yra diferencialas dz funkcijos f. Tai priklauso tiesiškai nuo ir antrasis narys linkęs į nulį greičiau nei Tebūnie tai duota (žr. Variacijų skaičiavimas) išplėstas iki funkcijų klasėms x(t) ,
turintis nuolatinę išvestinę intervale ir tenkinantis ribines sąlygas x( t0)\u003d x 0, x( t1)=x l , Kur x 0, x 1 - duoti skaičiai; toliau tegul yra funkcijos h(t) klasė ,
turintis nuolatinę išvestinę ir tokią, kad h( t0)=h(t1)=0. Aišku, jei Variacijų skaičiavime įrodyta, kad tam tikromis L sąlygomis funkcinės J(x) prieaugis gali būti parašytas kaip kur ir todėl antrasis narys dešinėje (4) linkęs į nulį greičiau nei ||h||, o pirmasis narys tiesiškai priklauso nuo. Pirmasis (4) narys vadinamas. funkcinio pokytis ir žymimas dJ( x, h). Integralinis. Kartu su vediniu ji esminę reikšmę turi M. a. Yra neapibrėžtieji ir apibrėžtieji integralai. Neapibrėžtas integralas yra glaudžiai susijęs su antiderivatine funkcija. Funkcija F(x). funkcijos f antidarinys intervale ( a, b), jei šiuo intervalu F"(x) =f(x). Funkcijos / apibrėžtasis integralas (Riemano) intervale [ a, b] yra riba Jei funkcija f yra teigiama ir tęstinė intervale [ a, b],
tada jo integralas šiame segmente yra lygus figūros plotui, kurį riboja kreivė y=f(x), ašis Oi ir tiesioginis x=a, x=b. Riemann integruojamų funkcijų klasėje yra visos nuolatinės [ a, b]funkcijos ir kai kurios nepertraukiamos funkcijos. Bet jie visi būtinai riboti. Neribotoms funkcijoms, kurios neauga labai greitai, taip pat tam tikroms funkcijoms, pateiktoms begaliniais intervalais, įvedama vadinamoji. netinkami integralai, reikalaujantis dvigubo praėjimo iki jų apibrėžimo ribos. Vieno kintamojo funkcijos Riemano integralo sąvoka apima daugelio kintamųjų funkcijas (žr. Daugialypis integralas). Kita vertus, M. poreikiai ir. paskatino integralo apibendrinimą visiškai kita kryptimi, prasme Lebesgue integralas ar bendriau Lebesgue-Stieltjes integralas.Šių integralų apibrėžime labai svarbu tam tikroms aibėms, vadinamoms išmatuojamomis, įvesti jų mato sąvoką ir, remiantis tuo, išmatuojamos funkcijos sąvoką. Išmatuojamoms funkcijoms įvestas Lebesgue-Stieltjes integralas. Šiuo atveju atsižvelgiama į daugybę skirtingų matų ir atitinkamas išmatuojamų aibių bei funkcijų klases. Tai leidžia pritaikyti tą ar tą integralą prie tam tikros konkrečios problemos. Niutono-Leibnizo formulė. Tarp išvestinės ir integralo yra ryšys, išreikštas Niutono - Leibnizo formule (teorema) Čia f(x) yra tęstinis [ a, b] funkcija, F(x) -
jos prototipas. Formulė ir Teiloras. Kartu su išvestine ir integralu svarbiausia matematinės analizės sąvoka (tyrimo įrankis). yra Taylor p Taylor serija. Jei funkcija f(x) , a paskambino jo Teiloro daugianario (n laipsniai). x-x 0: (Taylor formulė); o aproksimacijos paklaida linkęs į nulį ties greičiau negu Taigi funkcija f (x), esanti šalia taško x 0, gali būti bet kokiu tikslumu aproksimuota labai paprasta funkcija (polinomu), kuriai apskaičiuoti reikia tik aritmetikos. operacijos – sudėjimas, atimtis ir daugyba. Ypač svarbūs yra vadinamieji funkcijos, kurios yra analitinės tam tikroje kaimynystėje x 0 ir turi begalinį išvestinių skaičių, todėl šioje kaimynystėje jos gali būti pavaizduotos kaip begalinė Teiloro laipsnių eilutė: Taylor išplėtimas tam tikromis sąlygomis taip pat galimi daugelio kintamųjų funkcijoms, taip pat funkcijoms ir operatoriams. Istorinė nuoroda. Iki XVII a M. a. buvo įvairių konkrečių problemų sprendimų rinkinys; pavyzdžiui, integraliniame skaičiavime tai yra užduotys, skirtos figūrų plotams, kūnų su lenktomis ribomis tūriams, kintamos jėgos veikimui apskaičiuoti ir kt. Kiekviena užduotis ar konkreti problema buvo išspręsta savitu metodu, kartais sudėtingu ir sudėtingu (dėl M. a. priešistorės žr. straipsnį Begalinis skaičiavimas),
M. a. kaip vientisas ir sistemingas. visuma susiformavo I. Niutono (I. Niutonas), G. Leibnizo (G. Leibnicas), L. Eilerio (L. Eileris), J. Lagranžo (J. Lagranžas) ir kitų XVII a. XVIII a., o jo – ribų teoriją – pradžioje sukūrė O. Komi (A. Koši). 19-tas amžius Gili pradinių M. a sampratų analizė. buvo siejamas su plėtra XIX–XX a. aibių teorija, matų teorija, realaus kintamojo funkcijų teorija ir paskatino įvairius apibendrinimus. Lit.: La V a l l e - P u s s e n S.-J. e, Begalinių mažumų analizės kursas, vert. iš prancūzų k., 1-2 t., Maskva, 1933; Iljinas V. A., Poznyak E. G., Matematinės analizės pagrindai, 3 leidimas, 1 dalis, M., 1971; 2 leidimas, 2 dalis, M., 1980; Ir l ir N V. A., Sadovnichiy V. A., Seidov B. Kh., Matematinė analizė, M., 1979; K u d r i v e in L. D., Matematinė analizė, 2 leidimas, t. 1-2, M., 1973; Nikolsky S. M., Matematinės analizės kursas, 2 leidimas, t. 1-2, M., 1975; Uitteker E. T., W a t s o n J. N., Šiuolaikinės analizės kursas, vert. iš anglų kalbos, 1-2 dalis, 2 leidimas, M., 1962-63; F ir kht n gol'ts G. M., Diferencialinio ir integralinio skaičiavimo kursas, 7 leidimas, t. 1-2, M., 1970; 5 leidimas, 3 t., M., 1970 m. S. M. Nikolskis. Matematinė enciklopedija. - M.: Tarybinė enciklopedija. I. M. Vinogradovas. 1977–1985 m. MATEMATINĖ ANALIZĖ, matematikos šakų rinkinys, skirtas funkcijoms tirti diferencialinio skaičiavimo ir integralinio skaičiavimo metodais... Šiuolaikinė enciklopedija Matematikos šakų rinkinys, skirtas funkcijoms tirti diferencialinio ir integralinio skaičiavimo metodais. Terminas yra labiau pedagoginis nei mokslinis: universitetuose ir technikos mokyklose dėstomi matematinės analizės kursai ... Didysis enciklopedinis žodynas Anglų matematinė analizė; vokiečių kalba matematinė analizė. Matematikos šaka, skirta funkcijoms tirti diferencialinio ir integralinio skaičiavimo metodais. Antinazis. Sociologijos enciklopedija, 2009 ... Sociologijos enciklopedija Egzist., sinonimų skaičius: 2 matan (2) matematinė analizė (2) ASIS sinonimų žodynas. V.N. Trishin. 2013... Sinonimų žodynas MATEMATINĖ ANALIZĖ- MATEMATINĖ ANALIZĖ. Matematikos šakų rinkinys, skirtas matematinėms funkcijoms tirti diferencialinio ir integralinio skaičiavimo metodais. Metodų naudojimas M. ir. yra veiksminga priemonė sprendžiant svarbiausius ... Naujas metodinių terminų ir sąvokų žodynas (kalbų mokymo teorija ir praktika) matematinė analizė- — LT matematinė analizė Matematikos šaka, labiausiai susijusi su ribiniu procesu arba konvergencijos samprata; apima diferenciacijos teorijas,…… Techninis vertėjo vadovas Matematinė analizė- MATEMATINĖ ANALIZĖ, matematikos skyrių rinkinys, skirtas funkcijoms tirti diferencialinio skaičiavimo ir integralinio skaičiavimo metodais. … Iliustruotas enciklopedinis žodynas „...jeigu turėčiau sukurti mechanizmą, kurio vienintelis tikslas – sugriauti natūralų vaiko smalsumą ir jo meilę modeliavimui, vargu ar būčiau pasielgęs geriau nei tai jau buvo įgyvendinta – tiesiog neužtektų fantazijos. konkuruoti su tokiomis nejautriomis, nuobodžiomis idėjomis, kurias įkūnija šiuolaikiniai matematikos studijų metodai. Pagalvokite apie vaizduojamojo meno studijas taip: vaikai, darželyje negalima piešti. Vietoj to, išstudijuokime dažų gaminių chemiją, šviesos fiziką ir akies anatomiją. 12 metų tyrinėję šiuos aspektus, jei vaikai (tiksliau jau paaugliai) vis dar neapkenčia meno, gali pradėti piešti patys. Galiausiai jie dabar turi tvirtą pagrindą, kad pradėtų gerbti meną. Tiesa? Taip pat su poezija. Įsivaizduokite, kad studijuojate šią citatą (formulę): „Bet svarbiausia: būk ištikimas sau; Tada, kaip naktis po dienos, kitų neišduosi“. - Viljamas Šekspyras, Hamletas Tai elegantiškas būdas pasakyti „būk savimi“ (ir jei tai reiškia nepagarbiai rašyti apie matematiką, tebūnie). Bet jei matematikos pamokoje svarstytume poeziją, užuot ieškoję prasmės, skaičiuotume skiemenų skaičių, analizuotume jambinį pentametrą, žymėtume daiktavardžius, veiksmažodžius ir būdvardžius. Matematika ir poezija – tarsi skirtingi būdai tam pačiam dalykui paaiškinti, charakterizuoti. Formulės yra priemonė tikslui pasiekti, būdas išreikšti matematinę tiesą. Pamiršome, kad matematika operuoja idėjomis, o ne mechaninis manipuliavimas formulėmis, išreiškiančiomis šias idėjas. Štai ko aš nedarysiu: neperpasakosiu vadovėlių, kuriuos jau parašiau. Jei jums reikia atsakymų čia ir dabar, yra daugybė svetainių, vaizdo įrašų vadovėlių ir 20 minučių padėti. Vietoj to, įsisavinkime skaičiavimo pagrindus. Lygčių neužtenka – noriu įžvalgos akimirkų, kad tikrai pamatytum jų prasmę ir suprastum matematikos kalbą. Oficiali matematinė kalba yra tiesiog bendravimo būdas. Grafikai, informatyvi animacija ir paprasta kalba gali suteikti daugiau įžvalgos nei puslapis su nereikšmingais įrodymais. Manau, kad kiekvienas gali suprasti pagrindinius skaičiavimo principus. Nebūtina būti poetais, kad galėtume mėgautis Šekspyro kūriniais. Jums bus daug lengviau, jei išmanysite algebrą ir domitės matematika. Ne taip seniai skaitymas ir rašymas buvo specialiai apmokytų raštininkų darbas. Ir šiandien tai gali padaryti bet kuris 10 metų vaikas. Kodėl? Nes mes to tikimės. Lūkesčiai vaidina didžiulį vaidmenį plėtojant galimybes. Taigi tikėkitės, kad skaičiavimas bus tik dar vienas dalykas. Kai kurie žmonės nusileidžia iki smulkmenų (rašytojai/matematikai). Bet mes visi galime tiesiog grožėtis tuo, kas vyksta, ir bandyti tai suprasti. Norėčiau, kad visi įsisavintų pagrindines matematinės analizės sąvokas ir pasakytų „Oho!“. Tai buvo paprastas pavyzdys, bet ar supratote pagrindinę mintį? Paėmėme diską, padalijome ir šiek tiek kitaip sudėjome gabalus. Matematinė analizė parodė, kad diskas ir žiedas yra glaudžiai susiję vienas su kitu: diskas iš tikrųjų yra žiedų rinkinys. Tai labai populiari tema skaičiuojant: dideli dalykai susideda iš mažesnių dalykų. O kartais būtent su šiais mažais daiktais dirbti lengviau ir aiškiau. Daugelis skaičiavimo pavyzdžių yra pagrįsti fizika. Tai, žinoma, nuostabu, bet gali būti sunku jas suvokti: tiesą sakant, toli gražu ne visada įmanoma turėti omenyje įvairias fizikines formules, pavyzdžiui, objekto greičio formulę. Man patinka pradėti nuo paprastų vaizdinių pavyzdžių, nes taip veikia mūsų smegenys. Žiedas / apskritimas, kurį tyrinėjome – galite modeliuoti tą patį su keliais skirtingo skersmens vamzdžių gabalėliais: padalinti juos, sulygiuoti ir sudėti į grubų trikampį, kad įsitikintumėte, jog matematika tikrai veikia. Vargu ar tai pavyks padaryti naudojant paprastą fizinę formulę. Jaučiu, kaip pedantiški matematikai degina savo klaviatūras. Todėl įterpsiu tik keletą žodžių apie „griežtumą“. Ar žinote, kad mes nemokome skaičiavimo taip, kaip jį atrado Niutonas ar Leibnicas? Jie naudojo intuityvias idėjas „srautas“ ir „be galo mažas“, kurias pakeitė ribos, nes „Žinoma, tai veikia praktiškai. Bet ar tai veikia teoriškai? Sukūrėme sudėtingus mechaninius modelius, kad „tiksliai“ įrodytume skaičiavimus, tačiau tokių įrodymų procese praradome intuiciją. Į cukraus saldumą žiūrime smegenų chemijos požiūriu, užuot aiškinę jį mokslo kalba „Cukrus turi daug energijos. Valgyti." Nenoriu (ir negaliu) mokyti studentų skaičiavimo ar rengti mokslininkus. Bet ar būtų blogai, jei visi suprastų skaičiavimą tokiu „netiksliu“ lygiu, kuriuo jį suprato Niutonas? Kad tai pakeistų pasaulį ir tau, kaip kadaise jam? Per ankstyvas dėmesys tikslumui išsklaido mokinius ir apsunkina matematikos mokymąsi. Štai geras pavyzdys: skaičius e techniškai apibrėžiamas riba, tačiau jis buvo atrastas būtent intuityvaus spėjimo apie augimą pagalba. Natūralus logaritmas gali atrodyti kaip integralas arba laikas augti. Kurie paaiškinimai yra geriausi pradedantiesiems? Šiek tiek pieškime ranka, o pakeliui pasinerkime į chemiją. Laimingas kompiuteris. (P.S. Vienas malonus skaitytojas sukūrė animuotą powerpoint skaidrių demonstraciją, kuri padeda šią idėją pateikti vizualiau (geriau žiūrėti PowerPoint, ten bus matomos animacijos). Ačiū!) Pagal rusų kalbos žodyną analizė- tai mokslinio tyrimo metodas, kai atsižvelgiama į atskirus kažko aspektus, savybes, komponentus. Viena svarbiausių matematikos šakų vadinama matematinė analizė o dažnai net tik analizę. Iš karto kyla klausimas: kas tiksliai analizuojama matematine analize? Atsakymas aiškus - funkcijos analizuojamos. Funkcija(iš lotynų kalbos "funkcija" - įgyvendinimas) reiškia ryšį tarp kintamųjų skaitinių reikšmių. Kadangi analizė yra tyrimo metodas, kyla antras klausimas: koks tai metodas? Atsakymas suteikia antrąjį matematinės analizės pavadinimą - diferencialinis ir integralinis skaičiavimas. Skaičiavimas yra matematikos šaka, kuri nustato skaičiavimo taisykles. žodis" diferencialas“ kilęs iš lotyniško žodžio „diferenciacija“, t.y. skirtumas. žodis" integralas“ neturi tokios aiškios kilmės („integratorius“ – visuma; „integro“ – atstatyti), tačiau turi prasmę sujungti dalis į visumą, atkurti suskaidytus į skirtumus. Šis atsigavimas pasiekiamas naudojant sumavimas. Apibendrinkime pirmuosius rezultatus: · pagrindiniai objektai studijavo matematinėje analizėje yra funkcijos. · Funkcijos yra įvairių tipų priklausomybės tarp kintamųjų skaitinių reikšmių. · Matematinės analizės metodas yra diferenciacija– darbas su funkcijų reikšmių skirtumais ir integracija- sumų apskaičiavimas. Taigi, norėdami įvaldyti matematinę analizę, pirmiausia turite suprasti funkcijos sąvoką. Funkcija yra esminė matematinė sąvoka, nes funkcijos yra matematinis judėjimo ir pokyčių apibūdinimo būdas. Funkcija yra procesas. Svarbiausias judėjimo tipas yra mechaninis judėjimas tiesia linija. Judant matuojami atstumai, kuriuos nukeliauja objektas, tačiau to aiškiai neužtenka norint visapusiškai apibūdinti judėjimą. Tiek Achilas, tiek vėžlys gali judėti vienodu atstumu nuo pradžios taško, tačiau jų judėjimo greitis skiriasi, be to, greitis negali būti išmatuotas nematuojant laiko. Jau išnagrinėjus šį pavyzdį tampa aišku, kad judėjimui ir pokyčiams apibūdinti neužtenka vieno kintamojo. Intuityviai aišku, kad laikas keičiasi tolygiai, o atstumas gali keistis greičiau arba lėčiau. Judėjimas yra visiškai aprašytas, jei kiekvienu laiko momentu yra žinoma, kiek objektas nutolsta nuo pradžios taško. Taigi mechaninio judėjimo metu yra dviejų kintamųjų reikšmių atitikimas - laikas, kuris kinta nepriklausomai nuo nieko, ir atstumas, kuris priklauso nuo laiko. Šis faktas yra funkcijos apibrėžimo pagrindas. Šie du kintamieji nebėra vadinami laiku ir atstumu. Funkcijos apibrėžimas: funkcija – tai taisyklė ar įstatymas, įtraukiant kiekvieną nepriklausomo kintamojo reikšmę X
tam tikra priklausomo kintamojo reikšmė adresu
. Nepriklausomas kintamasis X
vadinamas argumentu, o priklausomu adresu
- funkcija. Kartais sakoma, kad funkcija yra ryšys tarp dviejų kintamųjų. Kaip įsivaizduoti, kas yra kintamasis? Kintamasis yra skaičių linija (liniuote arba skalė), kuria juda taškas (termometras arba adata su karoliuku). Funkcija yra pavarų mechanizmas su dviem langeliais x ir y. Šis mechanizmas leidžia montuoti lange X
bet kokia vertė, bet dėžutėje adresu
funkcijos reikšmė automatiškai atsiras krumpliaračių pagalba. 1 užduotis. Paciento temperatūra matuojama kas valandą. Yra funkcija - temperatūros priklausomybė nuo laiko. Kaip pristatyti šią funkciją? Atsakymas: lentelė ir grafikas. Funkcija yra nenutrūkstama, kaip ir judėjimas yra nenutrūkstamas, tačiau praktiškai šio tęstinumo nustatyti neįmanoma. Galite užfiksuoti tik atskirų argumentų ir funkcijų reikšmes. Tačiau teoriškai tęstinumą dar įmanoma apibūdinti. 2 užduotis. Galilėjus Galilėjus atrado, kad laisvai krintantis kūnas pirmąją sekundę nukeliauja atstumo vienetą, antrą – 3 vienetus, trečią – 5 vienetus ir tt Nustatykite laiko priklausomybę nuo atstumo. indikacija: Išveskite bendrą nuvažiuoto atstumo ir atstumo skaičiaus ryšio formulę. Funkcijų nustatymo būdai. Matematinės analizės uždaviniai. Perėjimas nuo vieno funkcijos vaizdavimo prie kito (funkcijos reikšmių skaičiavimas, apytikslių analitinių funkcijų konstravimas iš eksperimentinių skaitinių ir grafinių duomenų, funkcijų tyrimas ir braižymas). Matematinis funkcijos, kaip proceso, savybių tyrimas. 1 pavyzdys: greičio paieška pagal žinomą laiko kelio funkciją (diferencijavimą). 2 pavyzdys: Kelio radimas naudojant žinomą greičio ir laiko funkciją (integracija).Funkcija. Pagrindiniai apibrėžimai ir sąvokos.
Albertas Einšteinas
C - talpa, matuojama faradais;
dv - įtampos pokytis;
dt yra laiko pokytis. 
Pažiūrėkite, kas yra „MATEMATINĖ ANALIZĖ“ kituose žodynuose:
Na, viskas aišku, tad kokia yra tavo puiki idėja?
Bet matematika yra sunki!
Taigi, kas yra matematikos analizė?
Keletas pavyzdžių
Šiek tiek apie matematinį griežtumą (šio mokslo fanatikams)
|
kita paskaita ==>
Kūrybiškumas: sąsiuvinius tikrina x (kas?) mokytojas |
