Kortelės

Koks yra dviejų plokštumų statmenumo ženklas. Matematikos paskaita tema „Dviejų plokštumų statmenumo ženklas“. Kai plokštumos statmenos

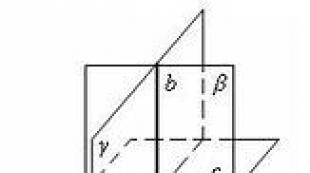
Jei viena iš dviejų plokštumų eina per tiesę, statmeną kitai plokštumai, tai duotosios plokštumos yra statmenos () (28 pav.)

α - plokštuma, V yra jai statmena tiesė, β – plokštuma, einanti per tiesę V, Ir Su yra tiesi linija, išilgai kurios susikerta plokštumos α ir β.

Pasekmė. Jei plokštuma yra statmena dviejų nurodytų plokštumų susikirtimo linijai, tai ji yra statmena kiekvienai iš šių plokštumų

1 užduotis. Įrodykite, kad per bet kurį erdvės tašką galima nubrėžti dvi skirtingas tieses, statmenas jam.

Įrodymas:

Pagal aksiomą aš yra taškas ne ant linijos A. Pagal 2.1 teoremą per tašką IN ir tiesioginis A galima nubrėžti plokštumą α. (29 pav.) Pagal 2.3 teoremą per tašką A plokštumoje α galima nubrėžti tiesę A. Pagal aksiomą C 1 yra taškas SU, nepriklausantis α. Pagal 15.1 teoremą per tašką SU ir tiesioginis A galima nubrėžti plokštumą β. Plokštumoje β pagal 2.3 teoremą per tašką a galima nubrėžti tiesę su A. Linijos in ir c turi tik vieną bendrą tašką A ir abu yra statmeni

2 užduotis. Dviejų vertikaliai stovinčių stulpų, atskirtų 3,4 m atstumu, viršutiniai galai sujungti skersiniu. Vieno stulpo aukštis 5,8 m, o kito 3,9 m Raskite skersinio ilgį.

AU= 5,8 m, BD= 3,9 m, AB- ? (30 pav.)

AE = AC - CE = AC - BD= 5,8–3,9 = 1,9 (m)

Pagal Pitagoro teoremą iš ∆ AEB mes gauname:

AB 2 \u003d AE 2 + EB 2 \u003d AE 2 + CD 2 \u003d ( 1,9) 2 + (3,4) 2 \u003d 15,17 (m 2)

AB== 3,9 (m)

Užduotys

Tikslas. Išmoks analizuoti santykinę objektų padėtį erdvėje paprasčiausiais atvejais, panaudoti planimetrinius faktus ir metodus sprendžiant stereometrinius uždavinius.

1. Įrodykite, kad per bet kurį erdvės tiesės tašką galima nubrėžti jam statmeną tiesę.

2. Tiesės AB, AC ir AD poromis statmenos. Raskite segmentą SD, jei:

1) AB = 3 cm , saulė= 7 cm, REKLAMA= 1,5 cm;

2) VD= 9 cm, REKLAMA= 5 cm, Saulė= 16 cm;

3) AB = c, BC = a, AD = d;

4) BD = c, BC = a, AD = d

3. Taškas A yra nutolęs a nuo lygiakraščio trikampio su kraštine viršūnių A. Raskite atstumą nuo taško A iki trikampio plokštumos.

4. Įrodykite, kad jei tiesė lygiagreti plokštumai, tai visi jos taškai yra vienodu atstumu nuo plokštumos.

5. Telefono laidas 15 m ilgio ištemptas nuo telefono stulpo, kur jis pritvirtintas 8 m aukštyje nuo žemės, iki namo, kur jis pritvirtintas 20 m aukštyje Raskite atstumą tarp namo ir stulpas, darant prielaidą, kad viela nenusvyra.

6. Iš taško į plokštumą nubrėžtos dvi pasvirosios, lygios 10 cm ir 17 cm Šių pasvirusių projekcijų skirtumas 9 cm Raskite pasvirųjų projekcijas.

7. Iš taško į plokštumą nubrėžiamos dvi pasvirosios linijos, kurių viena yra 26 cm didesnė už kitą. Įstrižų projekcijos yra 12 cm ir 40 cm Raskite įstrižus.

8. Iš taško į plokštumą nubrėžiamos dvi pasvirosios linijos. Raskite įstrižų ilgius, jei jie yra santykiu 1:2, o įstrižų projekcijos yra 1 cm ir 7 cm.

9. Iš taško į plokštumą nubrėžtos dvi pasvirosios linijos, lygios 23 cm ir 33 cm.

atstumas nuo šio taško iki plokštumos, jei pasvirojo santykio projekcijos yra 2:3.

10. Raskite atstumą nuo atkarpos AB vidurio iki plokštumos, kuri nekerta šios atkarpos, jei atstumas nuo taškų a ir B iki plokštumos yra: 1) 3,2 cm ir 5,3 cm; 7,4 cm ir 6,1 cm; 3) a ir c.

11. Išspręskite ankstesnį uždavinį, jei atkarpa AB kerta plokštumą.

12. 1 m ilgio atkarpa kerta plokštumą, jos galai atitraukti nuo plokštumos 0,5 m ir 0,3 m atstumu Raskite atkarpos projekcijos į plokštumą ilgį.

13. Iš taškų A ir B statmenai nuleidžiami į plokštumą. Raskite atstumą tarp taškų A ir B, jei statmenys yra 3 m ir 2 m, atstumas tarp jų pagrindų yra 2,4 m, o atkarpa AB nekerta plokštumos.

14. Iš taškų A ir B, esančių dviejose statmenose plokštumose, statmenys AC ir BD nuleidžiami į plokštumų susikirtimo liniją. Raskite atkarpos AB ilgį, jei: 1) AC = 6 m, BD = 7 m, CD = 6 m; 2) AC = 3 m, BD = 4 m, CD = 12 m; 3) AD = 4 m, BC = 7 m, CD = 1 m; 4) AD = BC = 5 m, CD = 1 m; 4) AC = a, BD = b, CD = c; 5) AD = a, BC = b, CD = c.

15. Iš lygiakraščio trikampio ABC viršūnių A ir B nutiesti trikampio plokštumos statmenys AA 1 ir BB 1. Raskite atstumą nuo viršūnės C iki atkarpos A 1 B 1 vidurio, jei AB \u003d 2 m, CA 1 \u003d 3 m, CB 1 \u003d 7 m, o atkarpa A 1 B 1 nesikerta su atkarpos plokštuma. trikampis

16. Iš stačiojo trikampio ABC smailiųjų kampų viršūnių A ir B statomi statmenai AA 1 ir BB 1 į trikampio plokštumą. Raskite atstumą nuo viršaus C iki atkarpos A 1 B 1 vidurio, jei A 1 C \u003d 4 m, AA 1 \u003d 3 m, CB 1 \u003d 6 m, BB 1 \u003d 2 m ir atkarpa A 1 B 1 nesikerta su trikampio plokštuma.

Statmenų plokštumų samprata

Kai susikerta dvi plokštumos, gauname 4$ dvikampius kampus. Du kampai yra $\varphi $, o kiti du yra $(180)^0-\varphi $.

1 apibrėžimas

Kampas tarp plokštumų yra mažiausias iš šių plokštumų suformuotų dvikampių kampų.

2 apibrėžimas

Dvi susikertančios plokštumos vadinamos statmenomis, jei kampas tarp šių plokštumų lygus $90^\circ$ (1 pav.).

1 pav. Statmenos plokštumos

Dviejų plokštumų statmenumo ženklas

1 teorema

Jei plokštumos tiesė yra statmena kitai plokštumai, tai šios plokštumos yra statmenos viena kitai.

Įrodymas.

Pateikiame plokštumas $\alpha $ ir $\beta $, kurios susikerta išilgai tiesės $AC$. Tegul tiesė $AB$, esanti plokštumoje $\alpha $, yra statmena plokštumai $\beta $ (2 pav.).

2 pav.

Kadangi tiesė $AB$ yra statmena plokštumai $\beta $, ji taip pat statmena tiesei $AC$. Papildomai nubrėžkime tiesę $AD$ plokštumoje $\beta $, statmeną tiesei $AC$.

Gauname, kad kampas $BAD$ yra dvikampio kampo tiesinis kampas, lygus $90^\circ$. Tai reiškia, kad pagal 1 apibrėžimą kampas tarp plokštumų yra lygus $90^\circ$, o tai reiškia, kad šios plokštumos yra statmenos.

Teorema įrodyta.

Iš šios teoremos išplaukia tokia teorema.

2 teorema

Jei plokštuma yra statmena tiesei, išilgai kurios susikerta dvi kitos plokštumos, tai ji taip pat yra statmena šioms plokštumoms.

Įrodymas.

Duotos dvi plokštumos $\alpha $ ir $\beta $, susikertančios išilgai tiesės $c$. Plokštuma $\gamma $ yra statmena tiesei $c$ (3 pav.)

3 pav

Kadangi tiesė $c$ priklauso plokštumai $\alpha $, o plokštuma $\gamma $ yra statmena tiesei $c$, tai pagal 1 teoremą plokštumos $\alpha $ ir $\gamma $ yra statmenos.

Kadangi tiesė $c$ priklauso plokštumai $\beta $, o plokštuma $\gamma $ yra statmena tiesei $c$, tai pagal 1 teoremą plokštumos $\beta $ ir $\gamma $ yra statmenos.

Teorema įrodyta.

Kiekvienai iš šių teoremų galioja ir priešingi teiginiai.

Užduočių pavyzdžiai

1 pavyzdys

Pateikiame stačiakampę dėžutę $ABCDA_1B_1C_1D_1$. Raskite visas statmenų plokštumų poras (5 pav.).

4 pav

Sprendimas.

Pagal stačiakampio ir statmenų plokštumų apibrėžimą matome šias aštuonias plokštumų poras, statmenas viena kitai: $(ABB_1)$ ir $(ADD_1)$, $(ABB_1)$ ir $(A_1B_1C_1)$, $(ABB_1) $ ir $(BCC_1) $, $(ABB_1)$ ir $(ABC)$, $(DCC_1)$ ir $(ADD_1)$, $(DCC_1)$ ir $(A_1B_1C_1)$, $(DCC_1)$ ir $(BCC_1)$, $(DCC_1)$ ir $(ABC)$.

2 pavyzdys

Duokime dvi viena kitai statmenas plokštumas. Iš vienos plokštumos taško statmenas nubrėžiamas į kitą plokštumą. Įrodykite, kad ši tiesė yra duotoje plokštumoje.

Įrodymas.

Duokime $\alpha $ ir $\beta $ statmenas plokštumoms ir susikertančias išilgai tiesės $c$. Iš plokštumos $\beta $ taško $A$ brėžiamas statmenas $AC$ plokštumai $\alpha $. Tarkime, kad $AC$ nėra $\beta $ plokštumoje (6 pav.).

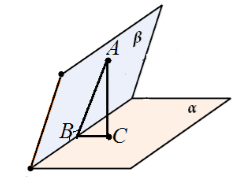
5 pav

Apsvarstykite trikampį $ABC$. Jis yra stačiakampis su stačiu kampu $ACB$. Taigi $\angle ABC\ne (90)^0$.

Tačiau, kita vertus, $\angle ABC$ yra šių plokštumų suformuoto dvikampio kampo tiesinis kampas. Tai yra, šių plokštumų suformuotas dvikampis kampas nėra lygus 90 laipsnių. Gauname, kad kampas tarp plokštumų nėra lygus $90^\circ$. Prieštaravimas. Taigi $AC$ yra $\beta $ plokštumoje.

Dviejų viena kitai statmenų plokštumų konstrukcija. Kaip žinoma, Plokštuma yra statmena, jei tiesė vienoje plokštumoje yra statmena kitai plokštumai. Todėl plokštuma, statmena duotajai plokštumai, gali būti nubrėžta per tiesę, statmeną tam tikrai plokštumai, arba statmeną tiesei, kuri yra tam tikroje plokštumoje.

Pavaizduota fig. 4.12 plokštumos (trikampio ABC plokštuma ir plokštuma P) yra viena kitai statmenos, nes plokštuma P yra statmena tiesei A1, esančiai trikampio plokštumoje. Parodytos plokštumos P, einančios per tiesę su projekcijomis m 2 n 2, m 1 n 1 ir statmenos trikampio projekcijų a 2 b 2 c 2, a 1 b 1 c 1 plokštumai, projekcijos. pav. 4.12.

Konstrukcija: 1. Nubrėžkite pagrindines plokštumos linijas, C1 - horizontalią, C2 - priekinę.

2. Per savavališką tašką E (esantį už trikampio ABC ribų) nubrėžkite tiesę EF, statmeną pagrindinėms plokštumos tiesėms (c 2 f 2 yra statmena c 2 2 2, o c 1 f 1 yra statmena 1 1 1 ).

3. Per tašką N nubrėžiame savavališką tiesę EM, susikertančią su EF, gauname dviejų susikertančių tiesių (EM X EF) pateiktą plokštumą P.

Taigi plokštuma P(ME X EF) yra statmena plokštumai Q(trikampis ABC).

Pažymėtina, kad viena kitai statmenoms plokštumoms bendroje padėtyje jų to paties pavadinimo pėdsakai niekada nėra statmeni. Bet jei viena iš nurodytų plokštumų (arba abi) yra bendrosios padėties plokštuma, tada vienos jų pėdsakų poros diagramoje esantis abipusis statmenumas rodo plokštumų statmenumą erdvėje.

18) Tiesią dviejų plokštumų susikirtimo liniją galima nustatyti pagal du bendrus jų taškus. Norėdami tai padaryti, nustatykite bet kurių dviejų vienos plokštumos tiesių susikirtimo taškus su kita plokštuma arba tiesės susikirtimo taškus kiekvienoje plokštumoje su kita plokštuma.

Statybos seka:

Dviejų plokštumų susikirtimo liniją galima rasti naudojant pagalbines pjovimo plokštumas sprendžiant. Paprastai pasirenkamos projekcijos plokštumos (dažnai horizontalios arba priekinės)

Pasirinkta savavališka sekanti pagalbinė horizontali plokštuma Ф1, kuri kerta nurodytas plokštumas išilgai tiesių (12 ir 34), kurios (n1 kertasi taške k)

Antroji skenanti horizontali plokštuma kerta duotąsias plokštumas taip pat išilgai horizontalių, jos savo ruožtu susikerta taške E

Tiesė KE yra duotųjų plokštumų susikirtimo linija.

Apsvarstykite šios problemos sprendimą plokščiame brėžinyje.

1-as sprendimo etapas Taškui M sukonstruoti buvo panaudota horizontaliai projektuojanti plokštuma - tarpinė ("), kurioje yra trikampio ABC kraštinė AB.

2-asis sprendimo etapas Nutiesiame tarpinės plokštumos (") ir DEK plokštumos susikirtimo liniją (brėžinyje ją pateikia taškai 1 ir 2).

3 sprendinio etapas Raskite tiesės 1 - 2 susikirtimo su tiese AB tašką M.

Rastas norimos sankirtos linijos vienas taškas M.

Taškui N sudaryti naudojama horizontaliai projektuojanti plokštuma  ("), kurioje yra trikampio ABC kraštinė AC.

Konstrukcijos panašios į ankstesnes.

Matomumas plokštumoje H apibrėžiamas naudojant horizontaliai konkuruojančius 4 ir 8 taškus

4 taškas yra virš taško 8 (4" ir 8"), todėl plokštumoje H trikampio DEK dalis, esanti link taško 4, apima trikampio ABC dalį, esančią nuo susikirtimo linijos link taško 8. Priekyje konkuruojančių taškų 6 ir 7 poros apibrėžiamas matomumas V plokštumoje.

Dviejų priekyje išsikišusių plokštumų sankirta (?)

Dviejų horizontaliai išsikišančių plokštumų sankirta (?)

19) Pjūvis yra objekto vaizdas, psichiškai išskaidytas viena ar keliomis plokštumomis, o objekto protinis išpjaustymas susijęs tik su šiuo pjūviu ir nekeičia kitų to paties objekto vaizdų. Skyriuje rodoma kas yra pjovimo plokštumoje ir kas yra už jos.

Priklausomai nuo pjovimo plokštumų skaičiaus, sekcija skirstoma į:

Paprasta (su viena pjovimo plokštuma)

Sudėtingas (su keliomis pjovimo plokštumomis)

Priklausomai nuo pjovimo plokštumos padėties horizontalios projekcijos plokštumos atžvilgiu, sekcijos skirstomos į:

HORIZONTALUS – pjovimo plokštuma lygiagreti horizontaliajai projekcijos plokštumai

VERTIKALI – pjovimo plokštuma statmena horizontaliai projekcijos plokštumai

SLANT - pjovimo plokštuma yra tam tikras nestatus kampas su horizontalia plokštuma =) vadinamas VERTIKALUS pjūvis priekinis jei pjovimo plokštuma lygiagreti priekinei projekcijos plokštumai. IR specializuotas jeigu pjovimo plokštuma lygiagreti profilio projekcijos plokštumai.

KOMPLEKSINIAI pjūviai yra ILGINIAI, jei pjovimo plokštumos nukreiptos išilgai objekto ilgio arba aukščio. IR TRANSVERSALUS, JEI pjovimo plokštumos nukreiptos stačiakampiai į objekto ilgį arba aukštį.

STEP – jei sekantinės plokštumos lygiagrečios viena kitai

POLILINIJAS – jei sekantinės plokštumos susikerta viena su kita.

LOCAL pjūviai naudojami vidinei objekto struktūrai atskleisti atskiroje ribotoje vietoje. LOCAL SECTION vaizde paryškintas kaip vientisa, banguota plona linija.

Pjūvių žymėjimas – pjovimo plokštumos padėtis rodoma atvira pjūvio linija. Pjūvio linijos pradžia ir pabaiga neturi kirsti atitinkamo vaizdo kontūro. Rodyklės, nurodančios žiūrėjimo kryptį, turi būti dedamos ant pradinio ir paskutinio potėpio.. Rodyklės turi būti uždėtos 2...3 mm atstumu nuo išorinio brūkšnio galo.

KOMPLEKŠINIAM PJOVYMUI atviros pjūvio linijos potėpiai atliekami ir pjūvio linijos vingiuose.

PRIE rodyklių, nurodančių žiūrėjimo kryptį, iš kampo išorės dedamos didžiosios rusiškos abėcėlės raidės. Raidžių pavadinimai priskiriami abėcėlės tvarka be pasikartojimų ir be praleidimų.

Pats pjūvis turėtų būti pažymėtas A-A tipo užrašu

Jei pjovimo plokštuma sutampa su objekto simetrijos plokštuma, o pjūvis atliekamas atitinkamo vaizdo vietoje projekcijos santykyje, tai atliekant horizontalius, frontalinius ir profilinius pjūvius, pjovimo vietos žymėti nereikia. plokštuma ir pjūvis nėra lydimas užrašo.

Jei objekto kontūrinė linija sutampa su simetrijos ašimi, tai ribą tarp vaizdo ir pjūvio nurodo banguota linija, kuri nubrėžiama taip, kad būtų išsaugotas krašto vaizdas.

Ši pamoka padės norintiems susidaryti idėją tema „Dviejų plokštumų statmenumo ženklas“. Jo pradžioje pakartosime dvikampio ir tiesinio kampo apibrėžimą. Tada apsvarstysime, kurios plokštumos vadinamos statmenomis, ir įrodysime dviejų plokštumų statmenumo kriterijų.

Tema: tiesių ir plokštumų statmena

Pamoka: Dviejų plokštumų statmenumo ženklas

Apibrėžimas. Dvikampis kampas – tai figūra, kurią sudaro dvi tai pačiai plokštumai nepriklausančios pusplokštumos ir jų bendra tiesė a (a – briauna).

Ryžiai. 1

Panagrinėkime dvi pusiau plokštumas α ir β (1 pav.). Jų bendra siena yra l. Ši figūra vadinama dvikampiu kampu. Dvi susikertančios plokštumos sudaro keturis dvikampius kampus su bendra briauna.

Dvikampis kampas matuojamas jo tiesiniu kampu. Mes pasirenkame savavališką tašką dvikampio kampo bendrojoje briaunoje l. Pusplokštumose α ir β iš šio taško brėžiame statmenus a ir b tiesei l ir gauname dvikampio kampo tiesinį kampą.

Tiesios linijos a ir b sudaro keturis kampus, lygius φ, 180° - φ, φ, 180° - φ. Prisiminkite, kad mažiausias iš šių kampų vadinamas kampu tarp linijų.

Apibrėžimas. Kampas tarp plokštumų yra mažiausias iš šių plokštumų suformuotų dvikampių kampų. φ - kampas tarp plokštumų α ir β, jei

Apibrėžimas. Dvi susikertančios plokštumos vadinamos statmenomis (abipusiomis statmenomis), jei kampas tarp jų yra 90°.

Ryžiai. 2

Kraštinėje l pasirenkamas savavališkas taškas M (2 pav.). Nubrėžkime dvi statmenas tieses MA = a ir MB = b į kraštinę l atitinkamai plokštumoje α ir plokštumoje β. Gavome kampą AMB. Kampas AMB yra dvikampio kampo tiesinis kampas. Jei kampas AMB yra 90°, vadinasi, plokštumos α ir β yra statmenos.

Tiesė b yra statmena tiesei l pagal konstrukciją. Tiesė b yra statmena tiesei a, nes kampas tarp plokštumų α ir β yra 90°. Gauname, kad tiesė b yra statmena dviem susikertančioms tiesėms a ir l iš plokštumos α. Vadinasi, tiesė b yra statmena plokštumai α.

Panašiai galima įrodyti, kad tiesė a yra statmena plokštumai β. Tiesė a yra statmena tiesei l pagal konstrukciją. Tiesė a yra statmena tiesei b, nes kampas tarp plokštumų α ir β yra 90°. Gauname, kad tiesė a yra statmena dviem susikertančioms tiesėms b ir l iš plokštumos β. Vadinasi, tiesė a yra statmena plokštumai β.

Jei viena iš dviejų plokštumų eina per tiesę, statmeną kitai plokštumai, tai tokios plokštumos yra statmenos.

Įrodykite:

Ryžiai. 3

Įrodymas:

Tegul plokštumos α ir β susikerta išilgai tiesės AC (3 pav.). Norėdami įrodyti, kad plokštumos yra viena kitai statmenos, turite sukurti tiesinį kampą tarp jų ir parodyti, kad šis kampas yra lygus 90 °.

Tiesė AB yra statmena plokštumai β, taigi ir tiesei AC, esančiai plokštumoje β.

Nubrėžkime tiesę AD, statmeną tiesei AC plokštumoje β. Tada BAD yra dvikampio kampo tiesinis kampas.

Tiesė AB yra statmena plokštumai β, taigi ir tiesei AD, esančiai plokštumoje β. Taigi tiesinis kampas BAD yra 90°. Vadinasi, plokštumos α ir β yra statmenos, o tai turėjo būti įrodyta.

Plokštuma, statmena tiesei, iš kurios susikerta dvi nurodytos plokštumos, yra statmena kiekvienai iš šių plokštumų (4 pav.).

Įrodykite: