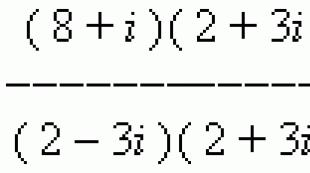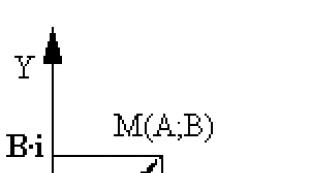ខ្សែដៃកៅស៊ូ

តើចំនួនកុំផ្លិចសម្រាប់អ្វី? §១. លេខស្មុគស្មាញ៖ និយមន័យមូលដ្ឋាន។ ដក និងចែកចំនួនកុំផ្លិច

ឯកសារយោងប្រវត្តិសាស្ត្រ

ចំនួនកុំផ្លិចត្រូវបានបញ្ចូលទៅក្នុងគណិតវិទ្យា ដើម្បីធ្វើឱ្យវាអាចយកឬសការេនៃចំនួនពិតណាមួយ។ ទោះជាយ៉ាងណាក៏ដោយ នេះមិនមែនជាហេតុផលគ្រប់គ្រាន់ដើម្បីណែនាំលេខថ្មីទៅក្នុងគណិតវិទ្យានោះទេ។ វាបានប្រែក្លាយថាប្រសិនបើអ្នកធ្វើការគណនាដោយយោងទៅតាមច្បាប់ធម្មតាលើកន្សោមដែលឫសការ៉េនៃចំនួនអវិជ្ជមានកើតឡើងនោះ អ្នកអាចទទួលបានលទ្ធផលដែលលែងមានឫសការ៉េនៃចំនួនអវិជ្ជមានទៀតហើយ។ នៅសតវត្សទី XVI ។ Cardano បានរកឃើញរូបមន្តសម្រាប់ដោះស្រាយសមីការគូប។ វាបានប្រែក្លាយថានៅពេលដែលសមីការគូបមានឫសពិតបី ឫសការ៉េនៃចំនួនអវិជ្ជមានកើតឡើងនៅក្នុងរូបមន្ត Cardano ។ ដូច្នេះឫសការ៉េនៃលេខអវិជ្ជមានបានចាប់ផ្តើមប្រើក្នុងគណិតវិទ្យា ហើយហៅពួកគេថាជាលេខស្រមើស្រមៃ - ដោយហេតុនេះ ពួកគេទទួលបានសិទ្ធិក្នុងការអត្ថិភាពខុសច្បាប់។ Gauss បានផ្តល់សិទ្ធិស៊ីវិលពេញលេញចំពោះលេខស្រមើស្រមៃ ដែលហៅថាលេខស្មុគស្មាញ ផ្តល់ការបកស្រាយធរណីមាត្រ និងបានបង្ហាញពីទ្រឹស្តីបទជាមូលដ្ឋាននៃពិជគណិត ដែលចែងថា គ្រប់ពហុនាមមានឫសពិតប្រាកដយ៉ាងហោចណាស់មួយ។

1. គំនិតនៃចំនួនស្មុគស្មាញមួយ។

ដំណោះស្រាយនៃបញ្ហាជាច្រើននៅក្នុងគណិតវិទ្យា និងរូបវិទ្យា ត្រូវបានកាត់បន្ថយទៅជាការដោះស្រាយសមីការពិជគណិត។ ដូច្នេះហើយ ការសិក្សាអំពីសមីការពិជគណិតគឺជាសំណួរដ៏សំខាន់បំផុតមួយនៅក្នុងគណិតវិទ្យា។ បំណងប្រាថ្នាដើម្បីធ្វើឱ្យសមីការអាចដោះស្រាយបានគឺជាហេតុផលចម្បងមួយសម្រាប់ការពង្រីកគំនិតនៃចំនួន។

ដូច្នេះសម្រាប់ភាពអាចរលាយបាននៃសមីការនៃទម្រង់ X+A=B ចំនួនវិជ្ជមានគឺមិនគ្រប់គ្រាន់ទេ។ ឧទាហរណ៍ សមីការ X+5=2 មិនមានឫសវិជ្ជមានទេ។ ដូច្នេះ អ្នកត្រូវបញ្ចូលលេខអវិជ្ជមាន និងលេខសូន្យ។

នៅលើសំណុំនៃលេខសនិទានភាព សមីការពិជគណិតនៃសញ្ញាប័ត្រទីមួយគឺអាចដោះស្រាយបាន ពោលគឺឧ។ សមីការនៃទម្រង់ A · X + B = 0 (A0) ។ ទោះយ៉ាងណាក៏ដោយ សមីការពិជគណិតនៃសញ្ញាបត្រខ្ពស់ជាងមួយអាចមិនមានឫសសនិទានទេ។ ឧទាហរណ៍ដូចជាសមីការ X 2 = 2, X 3 = 5 ។ តំរូវការដើម្បីដោះស្រាយសមីការបែបនេះគឺជាហេតុផលមួយសម្រាប់ការណែនាំចំនួនមិនសមហេតុផល។ លេខសនិទានភាព និងមិនសមហេតុផលបង្កើតជាសំណុំនៃចំនួនពិត។

ទោះជាយ៉ាងណាក៏ដោយ ចំនួនពិតប្រាកដមិនគ្រប់គ្រាន់ដើម្បីដោះស្រាយសមីការពិជគណិតណាមួយឡើយ។ ជាឧទាហរណ៍ សមីការការ៉េដែលមានមេគុណពិតប្រាកដ និងការរើសអើងអវិជ្ជមានមិនមានឫសគល់ពិតប្រាកដទេ។ សាមញ្ញបំផុតនៃពួកគេគឺសមីការ X 2 +1 = 0 ។ ដូច្នេះចាំបាច់ត្រូវពង្រីកសំណុំនៃចំនួនពិតដោយបន្ថែមលេខថ្មីទៅវា។ លេខថ្មីទាំងនេះរួមនឹងលេខពិតបង្កើតជាសំណុំដែលគេហៅថាសំណុំ លេខស្មុគស្មាញ។

ចូរយើងស្វែងយល់ជាមុនថាតើចំនួនកុំផ្លិចគួរមានទម្រង់បែបណា។ យើងសន្មត់ថានៅលើសំណុំនៃចំនួនកុំផ្លិច សមីការ X 2 +1=0 មានឫសគល់។ យើងសម្គាល់ឫសនេះដោយអក្សរ ខ្ញុំ ដូច្នេះ ខ្ញុំ គឺជាចំនួនកុំផ្លិច ខ្ញុំ 2 = –1.

ចំពោះចំនួនពិត មួយត្រូវតែណែនាំប្រតិបត្តិការនៃការបូក និងគុណនៃចំនួនកុំផ្លិច ដូច្នេះផលបូកនិងផលរបស់វាជាចំនួនកុំផ្លិច។ បន្ទាប់មក ជាពិសេសសម្រាប់ចំនួនពិតណាមួយ A និង B កន្សោម A + B ខ្ញុំ អាចត្រូវបានចាត់ទុកថាជាតំណាងទូទៅនៃចំនួនកុំផ្លិច។ ឈ្មោះ "ស្មុគស្មាញ" មកពីពាក្យ "សមាសធាតុ"៖ តាមទម្រង់នៃកន្សោម A + B ខ្ញុំ .

លេខស្មុគស្មាញ ត្រូវបានគេហៅថាកន្សោមនៃទម្រង់ A + B ខ្ញុំ ដែល A និង B គឺជាចំនួនពិត និង ខ្ញុំ គឺជាតួអង្គបែបនេះ ខ្ញុំ 2 = –1 ហើយតំណាងដោយអក្សរ Z ។

លេខ A ត្រូវបានគេហៅថាផ្នែកពិតនៃចំនួនកុំផ្លិច A+B ខ្ញុំ, ហើយលេខ B គឺជាផ្នែកស្រមើលស្រមៃរបស់វា។ ចំនួន ខ្ញុំ ត្រូវបានគេហៅថាឯកតាស្រមើលស្រមៃ។

ឧទាហរណ៍ ផ្នែកពិតនៃចំនួនកុំផ្លិច 2+3 ខ្ញុំ គឺ 2 ហើយការស្រមើលស្រមៃគឺ 3 ។

សម្រាប់និយមន័យយ៉ាងម៉ត់ចត់នៃចំនួនកុំផ្លិច ចាំបាច់ត្រូវណែនាំគោលគំនិតនៃសមភាពសម្រាប់លេខទាំងនេះ។

ចំនួនកុំផ្លិចពីរ A+B ខ្ញុំ និង C+D ខ្ញុំ ហៅ ស្មើប្រសិនបើ A=C និង B=D, i.e. នៅពេលដែលផ្នែកពិត និងការស្រមើលស្រមៃរបស់ពួកគេស្មើគ្នា។

2. ការបកស្រាយធរណីមាត្រនៃលេខស្មុគស្មាញមួយ។

ចំនួនពិតត្រូវបានតំណាងតាមធរណីមាត្រដោយចំណុចនៅលើបន្ទាត់លេខ។ លេខស្មុគស្មាញ A+B ខ្ញុំ អាចត្រូវបានមើលជាគូនៃចំនួនពិត (A; B) ។ ដូច្នេះ វាជាធម្មជាតិដែលតំណាងឱ្យចំនួនកុំផ្លិចជាចំណុចក្នុងយន្តហោះ។ នៅក្នុងប្រព័ន្ធកូអរដោណេចតុកោណ ចំនួនកុំផ្លិច Z=A+B· ខ្ញុំ ត្រូវបានតំណាងដោយចំណុចយន្តហោះដែលមានកូអរដោណេ (A; B) ហើយចំណុចនេះត្រូវបានតាងដោយអក្សរ Z ដូចគ្នា (រូបភាពទី 1) ។ ជាក់ស្តែងការឆ្លើយឆ្លងដែលទទួលបានក្នុងករណីនេះគឺមួយទៅមួយ។ វាធ្វើឱ្យវាអាចបកស្រាយលេខស្មុគ្រស្មាញជាចំណុចនៅលើយន្តហោះដែលប្រព័ន្ធកូអរដោនេត្រូវបានជ្រើសរើស។ យន្តហោះសម្របសម្រួលនេះត្រូវបានគេហៅថា យន្តហោះស្មុគស្មាញ . abscissa ត្រូវបានគេហៅថា អ័ក្សពិត , ដោយសារតែ នៅលើវាមានចំនុចដែលត្រូវនឹងចំនួនពិត។ អ័ក្ស y ត្រូវបានគេហៅថា អ័ក្សស្រមៃ - វាមានចំណុចដែលត្រូវនឹងចំនួនកុំផ្លិចដែលស្រមើលស្រមៃ។

មិនសំខាន់ និងងាយស្រួលនោះទេ គឺការបកស្រាយនៃចំនួនកុំផ្លិច A+B ខ្ញុំ ជាវ៉ិចទ័រ, i.e. វ៉ិចទ័រដែលមានប្រភពដើមនៅចំណុចមួយ។

O(0;0) និងបញ្ចប់នៅចំណុច M(A;B) (រូបភាពទី 2) ។

ការឆ្លើយឆ្លងដែលបានបង្កើតឡើងរវាងសំណុំនៃចំនួនកុំផ្លិច មួយនៅលើដៃមួយ និងសំណុំនៃចំណុច ឬវ៉ិចទ័រនៃយន្តហោះ ម្យ៉ាងវិញទៀតអនុញ្ញាតឱ្យចំនួនកុំផ្លិចទៅជាចំណុច ឬវ៉ិចទ័រ។

3.MODULE នៃលេខស្មុគស្មាញមួយ។

សូមឱ្យចំនួនកុំផ្លិច Z = A + B · ខ្ញុំ . ផ្សំ ជាមួយ Zត្រូវបានគេហៅថាចំនួនកុំផ្លិច A - B ខ្ញុំ ដែលត្រូវបានតំណាងដោយ , i.e.

ក-ខ ខ្ញុំ .

ចំណាំថា = A + B ខ្ញុំ ដូច្នេះសម្រាប់ចំនួនកុំផ្លិច Z យើងមានសមភាព = Z ។

ម៉ូឌុល ចំនួនកុំផ្លិច Z = A + B ខ្ញុំ ហៅ ចំនួនហើយត្រូវបានតំណាងដោយ , i.e.

ពីរូបមន្ត (1) វាធ្វើតាមថាសម្រាប់ចំនួនកុំផ្លិចណាមួយ Z និង =0 ប្រសិនបើ និងបានតែ Z = 0 ពោលគឺឧ។ នៅពេល A=0 និង B=0 ។ ចូរយើងបញ្ជាក់ថា សម្រាប់ចំនួនកុំផ្លិច Z ណាមួយ រូបមន្តមានសុពលភាព៖

4. ការបន្ថែមនិងគុណនៃចំនួនស្មុគស្មាញ

ផលបូក ចំនួនកុំផ្លិចពីរ A+B ខ្ញុំ និង C+D ខ្ញុំ ត្រូវបានគេហៅថា ចំនួនកុំផ្លិច (A+C ) + ( B+D) · ខ្ញុំ , i.e. ( A+B ខ្ញុំ) + ( C+D ខ្ញុំ)=( A+C)+(B+D) ខ្ញុំ

ការងារ ចំនួនកុំផ្លិចពីរ A+B ខ្ញុំ និង C+D ខ្ញុំ ត្រូវបានគេហៅថាចំនួនកុំផ្លិច (A C - B D) + (A D + B C) ខ្ញុំ , i.e.

(A + B ខ្ញុំ ) (គ + ឃ ខ្ញុំ )=(A C – B D) + (A D + B C) ខ្ញុំ

វាធ្វើតាមរូបមន្តដែលការបូក និងគុណអាចត្រូវបានអនុវត្តដោយយោងទៅតាមច្បាប់នៃប្រតិបត្តិការជាមួយពហុនាម ដោយសន្មត់ថា ខ្ញុំ ២=-១. ប្រតិបត្តិការនៃការបូក និងគុណនៃចំនួនកុំផ្លិច មានលក្ខណៈសម្បត្តិនៃចំនួនពិត។ លក្ខណៈសម្បត្តិមូលដ្ឋាន៖

ផ្ទេរទ្រព្យសម្បត្តិ៖

Z 1 + Z 2 \u003d Z 2 + Z 1, Z 1 Z 2 \u003d Z 2 Z 1

ទ្រព្យសម្បត្តិរួម៖

(Z 1 + Z 2) + Z 3 \u003d Z 1 + (Z 2 + Z 3), (Z 1 Z 2) Z 3 \u003d Z 1 (Z 2 Z 3)

ទ្រព្យសម្បត្តិចែកចាយ៖

Z 1 (Z 2 + Z 3) \u003d Z 1 Z 2 + Z 1 Z 3

តំណាងធរណីមាត្រនៃផលបូកនៃចំនួនកុំផ្លិច

យោងតាមនិយមន័យនៃការបន្ថែមចំនួនកុំផ្លិចចំនួនពីរ ផ្នែកពិតនៃផលបូកស្មើនឹងផលបូកនៃផ្នែកពិតនៃពាក្យ ផ្នែកស្រមើលស្រមៃនៃផលបូកស្មើនឹងផលបូកនៃផ្នែកស្រមើលស្រមៃនៃពាក្យ។ កូអរដោនេនៃផលបូកនៃវ៉ិចទ័រត្រូវបានកំណត់តាមវិធីដូចគ្នា៖

ផលបូកនៃវ៉ិចទ័រពីរដែលមានកូអរដោណេ (A 1 ;B 1) និង (A 2 ;B 2) គឺជាវ៉ិចទ័រដែលមានកូអរដោណេ (A 1 +A 2 ;B 1 +B 2)។ ដូច្នេះ ដើម្បីស្វែងរកវ៉ិចទ័រដែលត្រូវនឹងផលបូកនៃចំនួនកុំផ្លិច Z 1 និង Z 2 អ្នកត្រូវបន្ថែមវ៉ិចទ័រដែលត្រូវនឹងចំនួនកុំផ្លិច Z 1 និង Z 2 ។

ឧទាហរណ៍ 1៖ រកផលបូក និងផលនៃចំនួនកុំផ្លិច Z 1 = 2 − 3 × ខ្ញុំ និង

Z 2 \u003d −7 + 8 × ខ្ញុំ .

Z 1 + Z 2 \u003d 2 - 7 + (−3 + 8) × ខ្ញុំ = - 5 + 5 × ខ្ញុំ

Z 1 × Z 2 = (2 − 3 × ខ្ញុំ ) × (–៧ + ៨ × ខ្ញុំ ) = −14 + 16 × ខ្ញុំ + ២១ × ខ្ញុំ + 24 = 10 + 37 × ខ្ញុំ

5. ការដកនិងការបែងចែកនៃចំនួនស្មុគស្មាញ

ការដកលេខស្មុគ្រស្មាញគឺជាប្រតិបត្តិការបញ្ច្រាសនៃការបូក៖ សម្រាប់ចំនួនកុំផ្លិច Z 1 និង Z 2 មាន ហើយលើសពីនេះទៅទៀត មានតែលេខមួយប៉ុណ្ណោះ លេខ Z ដូចនេះ៖

ប្រសិនបើយើងបន្ថែមទៅផ្នែកទាំងពីរនៃសមភាព (–Z 2) ផ្ទុយពីលេខ Z 2៖

Z + Z 2 + (-Z 2) \u003d Z 1 + (-Z 2) មកពីណា

លេខ Z \u003d Z 1 + Z 2 ត្រូវបានហៅ ភាពខុសគ្នានៃលេខ Z 1 និង Z 2 ។

ការបែងចែកត្រូវបានណែនាំជាផលបញ្ច្រាសនៃគុណ៖

Z × Z 2 \u003d Z ១

ចែកផ្នែកទាំងពីរដោយ Z 2 យើងទទួលបាន៖

សមីការនេះបង្ហាញថា Z 2 0

តំណាងធរណីមាត្រនៃភាពខុសគ្នានៃចំនួនកុំផ្លិច

ភាពខុសគ្នា Z 2 - Z 1 នៃចំនួនកុំផ្លិច Z 1 និង Z 2 ត្រូវគ្នាទៅនឹងភាពខុសគ្នានៃវ៉ិចទ័រដែលត្រូវនឹងលេខ Z 1 និង Z 2 ។ ម៉ូឌុលនៃភាពខុសគ្នានៃចំនួនកុំផ្លិច Z 2 និង Z 1 តាមនិយមន័យនៃម៉ូឌុលគឺជាប្រវែងនៃវ៉ិចទ័រ Z 2 - Z 1 ។ យើងបង្កើតវ៉ិចទ័រនេះជាផលបូកនៃវ៉ិចទ័រ Z 2 និង (–Z 1) (រូបភាពទី 4) ។ ដូច្នេះ ម៉ូឌុលនៃភាពខុសគ្នានៃចំនួនកុំផ្លិច គឺជាចំងាយរវាងចំនុចនៃប្លង់ស្មុគស្មាញដែលត្រូវនឹងលេខទាំងនេះ។

ការបកស្រាយធរណីមាត្រដ៏សំខាន់នេះនៃម៉ូឌុលនៃភាពខុសគ្នានៃចំនួនកុំផ្លិចពីរធ្វើឱ្យវាអាចប្រើការពិតធរណីមាត្រសាមញ្ញដោយជោគជ័យ។

ឧទាហរណ៍ 2៖ ផ្តល់លេខកុំផ្លិច Z 1 = 4 + 5 ខ្ញុំ និង Z 2 = 3 + 4 ខ្ញុំ . ស្វែងរកភាពខុសគ្នា Z 2 - Z 1 និង quotient

Z 2 - Z 1 \u003d (3 + 4) ខ្ញុំ) - (៤ + ៥ ខ្ញុំ) = –1 – ខ្ញុំ

6. ទម្រង់ត្រីកោណមាត្រនៃចំនួនស្មុគស្មាញ

ការសរសេរចំនួនកុំផ្លិច Z ជា A+B ខ្ញុំ ហៅ ទម្រង់ពិជគណិត ចំនួនកុំផ្លិច។ បន្ថែមពីលើទម្រង់ពិជគណិត ទម្រង់ផ្សេងទៀតនៃការសរសេរលេខស្មុគស្មាញក៏ត្រូវបានប្រើប្រាស់ផងដែរ។

ពិចារណា ទម្រង់ត្រីកោណមាត្រ សញ្ញាណនៃចំនួនកុំផ្លិច។ ផ្នែកពិត និងស្រមើលស្រមៃនៃចំនួនកុំផ្លិច Z=A+B ខ្ញុំ ត្រូវបានបង្ហាញនៅក្នុងលក្ខខណ្ឌនៃម៉ូឌុលរបស់វា = r និងអាគុយម៉ង់ j ដូចខាងក្រោម:

A = r cosj ; B = r sinj ។

លេខ Z អាចសរសេរដូចនេះ៖

Z = r cosj + ខ្ញុំ sinj = r (cosj + ខ្ញុំ sinj)

Z = r (cosj + ខ្ញុំ sinj ) (2)

ធាតុនេះត្រូវបានគេហៅថា ទម្រង់ត្រីកោណមាត្រនៃចំនួនកុំផ្លិច .

r = គឺជាម៉ូឌុលនៃចំនួនកុំផ្លិច។

លេខ j ត្រូវបានគេហៅថា អាគុយម៉ង់ចំនួនកុំផ្លិច។

អាគុយម៉ង់នៃចំនួនកុំផ្លិច Z0 គឺជាតម្លៃនៃមុំរវាងទិសដៅវិជ្ជមាននៃអ័ក្សពិត និងវ៉ិចទ័រ Z ហើយតម្លៃនៃមុំត្រូវបានចាត់ទុកថាជាវិជ្ជមានប្រសិនបើការរាប់ច្រាសទ្រនិចនាឡិកា ហើយអវិជ្ជមានប្រសិនបើវាជាទ្រនិចនាឡិកា។

សម្រាប់លេខ Z=0 អាគុយម៉ង់មិនត្រូវបានកំណត់ទេ ហើយក្នុងករណីនេះលេខត្រូវបានផ្តល់ឱ្យដោយម៉ូឌុលរបស់វាតែប៉ុណ្ណោះ។

ដូចដែលបានរៀបរាប់ខាងលើ = r =, សមភាព (2) អាចត្រូវបានសរសេរជា

A+B ខ្ញុំ =· cosj + ខ្ញុំ · sinj ,ពីណាមក ដោយស្មើផ្នែកពិត និងការស្រមៃ យើងទទួលបាន៖

cosj =, ស៊ិនជ = (3)

ប្រសិនបើ ស៊ិនជចែកដោយ cosjយើងទទួលបាន:

tgj= (4)

រូបមន្តនេះងាយស្រួលប្រើដើម្បីស្វែងរកអាគុយម៉ង់ j ជាងរូបមន្ត (3)។ ទោះយ៉ាងណាក៏ដោយ មិនមែនតម្លៃទាំងអស់នៃ j ដែលបំពេញសមភាព (4) គឺជាអាគុយម៉ង់នៃលេខ A + B ខ្ញុំ . ដូច្នេះនៅពេលស្វែងរកអាគុយម៉ង់ អ្នកត្រូវយកទៅពិចារណាថាតើចំនុច A + B ស្ថិតនៅត្រីមាសណា ខ្ញុំ .

7. លក្ខណៈសម្បត្តិនៃម៉ូឌុល និងអាគុយម៉ង់នៃចំនួនស្មុគស្មាញ

ដោយប្រើទម្រង់ត្រីកោណមាត្រ វាងាយស្រួលក្នុងការស្វែងរកផលិតផល និងផលគុណនៃចំនួនកុំផ្លិច។

អនុញ្ញាតឱ្យ Z 1 = r 1 ( cosj ១ +ខ្ញុំ sinj 1), Z 2 = r 2 ( កូស ២ +ខ្ញុំ sinj ២).បន្ទាប់មក៖

Z 1 Z 2 = r 1 r 2 =

= r 1 r 2 .

ដូច្នេះផលគុណនៃចំនួនកុំផ្លិចដែលសរសេរក្នុងទម្រង់ត្រីកោណមាត្រអាចត្រូវបានរកឃើញដោយរូបមន្ត៖

Z 1 Z 2 = r 1 r 2 (5)

ពីរូបមន្ត (5) វាធ្វើតាមនោះ។ នៅពេលដែលចំនួនកុំផ្លិចត្រូវបានគុណ ម៉ូឌុលរបស់ពួកគេត្រូវបានគុណ ហើយអាគុយម៉ង់ត្រូវបានបន្ថែម។

ប្រសិនបើ Z 1 \u003d Z 2 នោះយើងទទួលបាន៖

Z2=2= r ២ (cos2j +ខ្ញុំ sin2j)

Z 3 \u003d Z 2 Z \u003d r 2 ( cos2j +ខ្ញុំ sin2j) r (cosj + ខ្ញុំ sinj) =

= r 3 ( cos3j +ខ្ញុំ sin3j)

ជាទូទៅសម្រាប់ចំនួនកុំផ្លិចណាមួយ។ Z=r (cosj + ខ្ញុំ sinj ) 0និងលេខធម្មជាតិណាមួយ n រូបមន្តមានសុពលភាព៖

Zn=[ r (cosj + ខ្ញុំ sinj )] n = r n (cosnj + ខ្ញុំ sinnj),(6)

ដែលត្រូវបានគេហៅថារូបមន្តរបស់ De Moivre ។

កូតានៃចំនួនកុំផ្លិចពីរដែលសរសេរក្នុងទម្រង់ត្រីកោណមាត្រអាចត្រូវបានរកឃើញដោយរូបមន្ត៖

[cos(j 1 ដល់ j 2) + ខ្ញុំ sin(j 1 - j 2)]។(7)

= = cos(–j 2) + ខ្ញុំអំពើបាប(–j ២)

ដោយប្រើរូបមន្ត 5

(cosj 1 + ខ្ញុំ sinj 1) × (cos(–j 2) + ខ្ញុំ sin(–j 2)) =

cos(j 1 ដល់ j 2) + ខ្ញុំ sin(j 1 - j 2)។

ឧទាហរណ៍ 3៖

យើងសរសេរលេខ -8 ក្នុងទម្រង់ត្រីកោណមាត្រ

8 = 8 (cos(p + 2p k) + ខ្ញុំ sin(p + 2p k )), k О Z

អនុញ្ញាតឱ្យ Z = r × (cosj + ខ្ញុំ ×

r 3 × (cos3j + ខ្ញុំ × sin3j) = 8 (cos(p + 2p k) + ខ្ញុំ sin(p + 2p k )), k О Z

បន្ទាប់មក 3j = p + 2p k, k О Z

j= , k О Z

ដូច្នេះ៖

Z = 2 (cos() + ខ្ញុំ sin()), k О Z

k = 0,1,2...

k = 0

Z 1 = 2 (cos + ខ្ញុំបាប) = 2 ( ខ្ញុំ) = 1+ × ខ្ញុំ

k = ១

Z 2 = 2 (cos( ) + ខ្ញុំ sin(+)) = 2 (cosp + ខ្ញុំ sinp) = -2

k = ២

Z 3 = 2 (cos( ) + ខ្ញុំ sin(+)) = 2 (cos + ខ្ញុំ sin) = 1–× ខ្ញុំ

ចម្លើយ៖ Z 13 =; Z 2 \u003d -2

ឧទាហរណ៍ទី ៤៖

យើងសរសេរលេខ 1 ក្នុងទម្រង់ត្រីកោណមាត្រ

1 = 1 (cos(2p k) + ខ្ញុំ sin(2p k )), k О Z

អនុញ្ញាតឱ្យ Z = r × (cosj + ខ្ញុំ × sinj) បន្ទាប់មកសមីការនេះនឹងត្រូវបានសរសេរជា៖

r 4 × (cos4j + ខ្ញុំ × sin4j) = cos(2p k) + ខ្ញុំ sin(2p k )), k О Z

4j = 2p k , k О Z

j = , k О Z

Z = cos+ ខ្ញុំ × អំពើបាប

k = 0,1,2,3...

k = 0

Z1 = cos0+ ខ្ញុំ × sin0 = 1 + 0 = 1

k = ១

Z2 = cos+ ខ្ញុំ × sin=0+ ខ្ញុំ = ខ្ញុំ

k = ២

Z 3 \u003d cosp + ខ្ញុំ sinp = -1 + 0 = -1

k = ៣

Z4 = cos+ ខ្ញុំ × អំពើបាប

ចម្លើយ៖ Z 13 = 1

Z 24 = ខ្ញុំ

8. និទស្សន្ត និងដកឫសគល់

រូបមន្ត 6 បង្ហាញថាការបង្កើនចំនួនកុំផ្លិច r (cosj + ខ្ញុំ sinj ) ទៅជាថាមពលចំនួនគត់វិជ្ជមានជាមួយនិទស្សន្តធម្មជាតិ ម៉ូឌុលរបស់វាត្រូវបានលើកឡើងទៅជាថាមពលដែលមាននិទស្សន្តដូចគ្នា ហើយអាគុយម៉ង់ត្រូវបានគុណដោយនិទស្សន្ត។

[ r (cosj + ខ្ញុំ sinj )] n = r n (cos nj + ខ្ញុំ sin nj)

ចំនួន Zហៅ ដឺក្រេឫស នពីលេខ w (តំណាងដោយ) ប្រសិនបើ Z n = w ។

ពីនិយមន័យនេះវាធ្វើតាមដំណោះស្រាយនីមួយៗនៃសមីការ Z n = wគឺជាឫសគល់នៃសញ្ញាបត្រ នពីលេខ w ម្យ៉ាងទៀត ដើម្បីស្រង់ឫសនៃសញ្ញាប័ត្រ នពីលេខ w វាគ្រប់គ្រាន់ដើម្បីដោះស្រាយសមីការ Z n =វ.ប្រសិនបើ w = 0 នោះសម្រាប់សមីការ n ណាមួយ។ Z n = wមានដំណោះស្រាយតែមួយគត់ Z= 0. ប្រសិនបើ w 0 បន្ទាប់មក Z0 ដូច្នេះហើយ Z និង w អាចត្រូវបានតំណាងជាទម្រង់ត្រីកោណមាត្រ

Z = r (cosj + ខ្ញុំ sinj ), w = p (កក់ក្ដៅ + ខ្ញុំ ខុស)

សមីការ Z n = w នឹងយកទម្រង់៖

r n (cos nj + ខ្ញុំ sin nj ) = p (កក់ក្ដៅ + ខ្ញុំ ខុស)

ចំនួនកុំផ្លិចពីរគឺស្មើគ្នាប្រសិនបើ និងលុះត្រាតែម៉ូឌុលរបស់ពួកគេស្មើគ្នា ហើយអាគុយម៉ង់របស់ពួកគេខុសគ្នានៅក្នុងពាក្យដែលគុណនឹង 2p ។ ដូច្នេះ r n = p និង nj = y + 2p k , ដែលជាកន្លែងដែល kн Z ឬ r = និង j= ដែលជាកន្លែងដែល kн Z ។

ដូច្នេះដំណោះស្រាយទាំងអស់អាចត្រូវបានសរសេរដូចខាងក្រោម:

Z K =, kн Z (8)

រូបមន្ត ៨ ត្រូវបានគេហៅថា រូបមន្តទីពីររបស់ De Moivre.

ដូច្នេះប្រសិនបើ w 0 នោះពិតជាមានឫស n នៃដឺក្រេ n ពីលេខ w៖ ពួកវាទាំងអស់មាននៅក្នុងរូបមន្ត 8 ។ ឫសនៃដឺក្រេទាំងអស់ នពីលេខ w មានម៉ូឌុលដូចគ្នា ប៉ុន្តែអាគុយម៉ង់ផ្សេងគ្នាខុសគ្នានៅក្នុង summand ដែលជាពហុគុណនៃចំនួន។ វាធ្វើតាមថាចំនួនកុំផ្លិចដែលជាឫសនៃដឺក្រេ n ពីចំនួនកុំផ្លិច w ត្រូវគ្នានឹងចំនុចនៃប្លង់ស្មុគស្មាញដែលមានទីតាំងនៅចំនុចកំពូលនៃ n-gon ធម្មតាដែលចារឹកក្នុងរង្វង់កាំដែលដាក់ចំកណ្តាលចំនុច។ Z = 0 ។

និមិត្តសញ្ញាមិនមានអត្ថន័យមិនច្បាស់លាស់ទេ។ ដូច្នេះនៅពេលប្រើវា មនុស្សម្នាក់គួរតែយល់ច្បាស់ពីអត្ថន័យនៃនិមិត្តសញ្ញានេះ។ ជាឧទាហរណ៍ ការប្រើសញ្ញាណ អ្នកគួរតែគិតអំពីការធ្វើឱ្យច្បាស់ថានិមិត្តសញ្ញានេះមានន័យថាជាគូនៃចំនួនកុំផ្លិច ខ្ញុំ និង – ខ្ញុំ ឬមួយ បន្ទាប់មកមួយណា។

សមីការនៃអំណាចខ្ពស់ជាង

រូបមន្ត 8 កំណត់ឫសទាំងអស់នៃសមីការពីររយៈពេលនៃដឺក្រេ n ។ ស្ថានការណ៍មានភាពស្មុគស្មាញជាងក្នុងករណីនៃសមីការពិជគណិតទូទៅនៃដឺក្រេ n:

a n × Z n+ a n–1× Z n–1 +...+ a 1× Z 1 + a 0 = 0(9)

ដែល n ,..., a 0 ត្រូវបានផ្តល់លេខកុំផ្លិច។

នៅក្នុងវគ្គសិក្សានៃគណិតវិទ្យាកម្រិតខ្ពស់ ទ្រឹស្តីបទរបស់ Gauss ត្រូវបានបង្ហាញឱ្យឃើញ៖ រាល់សមីការពិជគណិតមានឫសយ៉ាងតិចមួយនៅក្នុងសំណុំនៃចំនួនកុំផ្លិច។ ទ្រឹស្តីបទនេះត្រូវបានបញ្ជាក់ដោយគណិតវិទូជនជាតិអាឡឺម៉ង់ Carl Gauss ក្នុងឆ្នាំ ១៧៧៩។

ដោយផ្អែកលើទ្រឹស្តីបទ Gauss យើងអាចបង្ហាញថាផ្នែកខាងឆ្វេងនៃសមីការ 9 តែងតែអាចត្រូវបានតំណាងជាផលិតផលមួយ៖

ដែល Z 1 , Z 2 , ... , Z K គឺជាចំនួនកុំផ្លិចផ្សេងៗគ្នា។

និង a 1,a 2,...,a k គឺជាលេខធម្មជាតិ និង៖

a 1 + a 2 + ... + a k = n

នេះបញ្ជាក់ថាលេខ Z 1 , Z 2 , ... , Z K គឺជាឫសគល់នៃសមីការ 9 ។ ក្នុងករណីនេះពួកគេនិយាយថា Z 1 គឺជាឫសនៃគុណ a 1 , Z 2 គឺជាឫសនៃគុណ 2 និង ដូច្នេះនៅលើ។

ទ្រឹស្តីបទរបស់ Gauss និងទ្រឹស្តីបទទើបតែបង្កើតបានផ្តល់នូវដំណោះស្រាយអំពីអត្ថិភាពនៃឫស ប៉ុន្តែមិននិយាយអ្វីអំពីវិធីស្វែងរកឫសទាំងនេះទេ។ ប្រសិនបើឫសនៃដឺក្រេទី 1 និងទីពីរអាចត្រូវបានរកឃើញយ៉ាងងាយស្រួល នោះសម្រាប់សមីការនៃអំណាចទីបី និងទីបួន រូបមន្តគឺពិបាក ហើយសម្រាប់សមីការនៃដឺក្រេខ្ពស់ជាងរូបមន្តទី 4 មិនមានទាល់តែសោះ។ អវត្ដមាននៃវិធីសាស្រ្តទូទៅមិនរារាំងការស្វែងរកឫសគល់ទាំងអស់នៃសមីការនោះទេ។ ដើម្បីដោះស្រាយសមីការជាមួយមេគុណចំនួនគត់ ទ្រឹស្ដីខាងក្រោមជាញឹកញាប់មានប្រយោជន៍៖ ឫសចំនួនគត់នៃសមីការពិជគណិតដែលមានមេគុណចំនួនគត់គឺជាផ្នែកចែកនៃពាក្យថេរ។

ចូរយើងបង្ហាញទ្រឹស្តីបទនេះ៖

សូមឱ្យ Z = k ជាឫសចំនួនគត់នៃសមីការ

a n × Z n + a n–1 × Z n–1 +...+ a 1 × Z 1 + a 0 = 0

ជាមួយមេគុណចំនួនគត់។ បន្ទាប់មក

a n×k n + a n–1× k n–1 +...+ a 1× k 1 + a 0 = 0

a 0 = – k(a n× k n–1 + a n–1× k n–2 +…+ a 1)

លេខក្នុងតង្កៀប ក្រោមការសន្មត់ថាជាចំនួនគត់ ដែលមានន័យថា k គឺជាអ្នកចែកនៃលេខ a 0 ។

9. សមីការ quadratic ជាមួយនឹងភាពស្មុគស្មាញដែលមិនស្គាល់

ពិចារណាសមីការ Z 2 = a ដែល a គឺជាចំនួនពិតដែលបានផ្តល់ឱ្យ Z គឺមិនស្គាល់។

នេះគឺជាសមីការ៖

យើងសរសេរលេខ a ក្នុងទម្រង់ a = (– 1) × (– a) = ខ្ញុំ 2 × = ខ្ញុំ ២ × ( ) ២ . បន្ទាប់មកសមីការ Z 2 = a នឹងត្រូវបានសរសេរក្នុងទម្រង់៖ Z 2 - ខ្ញុំ 2 × ( ) 2 = 0

ទាំងនោះ។ (Z- ខ្ញុំ × )(Z + ខ្ញុំ × ) = 0

ដូច្នេះសមីការមានឫសពីរ៖ Z ១.២ = ខ្ញុំ ×

គំនិតដែលបានណែនាំនៃឫសពីចំនួនអវិជ្ជមានអនុញ្ញាតឱ្យយើងសរសេរឫសនៃសមីការការ៉េណាមួយជាមួយនឹងមេគុណពិតប្រាកដ

a× Z 2 + b × Z + c = 0

យោងទៅតាមរូបមន្តទូទៅដែលគេស្គាល់

Z 1,2 = (10)

ដូច្នេះ សម្រាប់ a(a0), b, c ឫសគល់នៃសមីការអាចត្រូវបានរកឃើញដោយរូបមន្ត 10។ លើសពីនេះ ប្រសិនបើការរើសអើង ពោលគឺឧ។ កន្សោមរ៉ាឌីកាល់នៅក្នុងរូបមន្ត 10

ឃ \u003d b 2 - 4 × a × គ

គឺវិជ្ជមាន បន្ទាប់មកសមីការ a × Z 2 + b × Z + c = 0 មានឫសគល់ពីរផ្សេងគ្នា។ ប្រសិនបើ D = 0 នោះសមីការ a × Z 2 + b × Z + c = 0 មានឫសមួយ។ ប្រសិនបើ D< 0, то уравнение a× Z 2 + b× Z + c = 0 имеет два различных комплексных корня.

ឫសស្មុគ្រស្មាញនៃសមីការ quadratic មានលក្ខណៈសម្បត្តិដូចគ្នាទៅនឹងលក្ខណៈសម្បត្តិដែលគេស្គាល់នៃឫសពិត។

ចូរយើងបង្កើតធាតុសំខាន់ៗ៖

ឱ្យ Z 1 ,Z 2 ជាឫសគល់នៃសមីការការ៉េ a× Z 2 + b × Z + c = 0, a0 ។ បន្ទាប់មកលក្ខណៈសម្បត្តិគឺពិត៖

Z 1 × Z 2 =

សម្រាប់ស្មុគស្មាញ Z ទាំងអស់ រូបមន្ត

a × Z 2 + b × Z + c \u003d a × (Z − Z 1) × (Z − Z 2)

ឧទាហរណ៍ 5៖

Z 2 - 6 Z + 10 \u003d 0

ឃ \u003d b 2 - 4 a គ

ឃ \u003d 6 2 - 4 10 \u003d - 4

– 4 = ខ្ញុំ 2 · ៤

Z 1,2 =

ចម្លើយ៖ Z 1 \u003d Z 2 \u003d 3 + ខ្ញុំ

ឧទាហរណ៍ ៦៖

3 Z 2 +2 Z + 1 = 0

ឃ \u003d b 2 - 4 a គ

ឃ \u003d 4 - 12 \u003d - 8

ឃ \u003d -1 8 \u003d ៨ ខ្ញុំ 2

Z 1,2 = =

ចម្លើយ៖ Z 1 \u003d Z 2 \u003d -

ឧទាហរណ៍ ៧៖

Z 4 − 8 Z 2 − 9 = 0

t 2 − 8 t − 9 = 0

ឃ \u003d b 2 - 4 a c \u003d 64 + 36 \u003d 100

t 1 \u003d 9 t 2 \u003d - 1

Z 2 \u003d 9 Z 2 \u003d - ១

Z 3.4 = ខ្ញុំ

ចម្លើយ៖ Z 1.2 \u003d 3, Z 3.4 \u003d ខ្ញុំ

ឧទាហរណ៍ ៨៖

Z 4 + 2 Z 2 - 15 \u003d 0

t 2 + 2 t - 15 \u003d 0

ឃ \u003d b 2 - 4 a c \u003d 4 + 60 \u003d 64

t 1,2 = = = −14

t 1 \u003d - 5 t 2 \u003d ៣

Z 2 \u003d - 5 Z 2 \u003d ៣

Z 2 \u003d - 1 5 Z 3.4 \u003d

Z2 = ខ្ញុំ 2 · ៥

Z 1,2 = ខ្ញុំ

ចម្លើយ៖ Z 1,2 = ខ្ញុំ , Z 3,4 =

ឧទាហរណ៍ ៩៖

Z 2 = 24 ១០ ខ្ញុំ

អនុញ្ញាតឱ្យ Z = X + Y ខ្ញុំ

(X + Y ខ្ញុំ ) 2 = X 2 + 2 X Y ខ្ញុំ យ២

X 2 + 2 X Y Y ខ្ញុំ យ ២ = ២៤ ១០ ខ្ញុំ

(X 2 Y 2) + 2 X Y ខ្ញុំ = ២៤ ១០ ខ្ញុំ

គុណនឹង X 20

X 4 − 24 X 2 − 25 = 0

t 2 − 24 t − 25 = 0

t 1 t 2 \u003d - 25

t 1 \u003d 25 t 2 \u003d - 1

X 2 \u003d 25 X 2 \u003d - 1 - គ្មានដំណោះស្រាយ

X 1 \u003d 5 X 2 \u003d - 5

Y 1 = − Y 2 =

Y 1 = − 1 Y 2 = 1

Z 1,2 \u003d (5 - ខ្ញុំ )

ចម្លើយ៖ Z 1,2 \u003d (5 - ខ្ញុំ )

ភារកិច្ច:

(2 − Y) 2 + 3 (2 − Y) Y + Y 2 = 6

4 − 4 Y + Y 2 + 6 Y − 3 Y 2 + Y 2 = 6

-Y 2 + 2Y - 2 \u003d 0 / -1

Y 2 − 2Y + 2 = 0

ឃ \u003d b 2 - 4 a c \u003d 4 - 8 \u003d - 4

– 4 = – 1 4 = 4 ខ្ញុំ 2

Y 1,2 = = = 1 ខ្ញុំ

Y 1 = 1– ខ្ញុំ យ 2 \u003d 1 + ខ្ញុំ

X 1 = 1 + ខ្ញុំ X 2 \u003d 1– ខ្ញុំ

ចម្លើយ៖ (១ + ខ្ញុំ ; 1–ខ្ញុំ }

{1–ខ្ញុំ ; 1 + ខ្ញុំ }

ចូរធ្វើការ៉េ

ប្រសិនបើអ្នកត្រូវការដាក់ឈ្មោះចម្ងាយរវាងទីក្រុងទាំងពីរ នោះអ្នកអាចផ្តល់លេខតែមួយជាម៉ាយ គីឡូម៉ែត្រ ឬឯកតាផ្សេងទៀតនៃចម្ងាយលីនេអ៊ែរ។ ទោះជាយ៉ាងណាក៏ដោយ ប្រសិនបើអ្នកត្រូវរៀបរាប់ពីរបៀបធ្វើដំណើរពីទីក្រុងមួយទៅទីក្រុងមួយទៀត នោះអ្នកត្រូវផ្តល់ព័ត៌មានបន្ថែមជាជាងចម្ងាយរវាងចំណុចពីរនៅលើផែនទី។ ក្នុងករណីនេះវាមានតម្លៃនិយាយអំពីទិសដៅដែលអ្នកត្រូវការផ្លាស់ទីនិងអំពី។

ប្រភេទនៃព័ត៌មានដែលបង្ហាញពីវិមាត្រមួយវិមាត្រត្រូវបានគេហៅថាបរិមាណមាត្រដ្ឋាននៅក្នុងវិទ្យាសាស្ត្រ។ មាត្រដ្ឋានគឺជាលេខដែលប្រើក្នុងការគណនាគណិតវិទ្យាភាគច្រើន។ ឧទាហរណ៍ ម៉ាស់ និងល្បឿនដែលវត្ថុមានគឺជាបរិមាណមាត្រដ្ឋាន។

ដើម្បីវិភាគបាតុភូតធម្មជាតិដោយជោគជ័យ យើងត្រូវធ្វើការជាមួយវត្ថុអរូបី និងវិធីសាស្រ្តដែលមានសមត្ថភាពតំណាងឱ្យបរិមាណពហុវិមាត្រ។ នៅទីនេះវាចាំបាច់ដើម្បីបោះបង់ចោលលេខមាត្រដ្ឋាននៅក្នុងការពេញចិត្តនៃស្មុគស្មាញ។ ពួកគេធ្វើឱ្យវាអាចបង្ហាញវិមាត្រពីរក្នុងពេលដំណាលគ្នា។

ចំនួនកុំផ្លិចងាយយល់នៅពេលដែលពួកវាត្រូវបានតំណាងជាក្រាហ្វិក។ ប្រសិនបើបន្ទាត់មានប្រវែង និងទិសដៅជាក់លាក់ នោះវានឹងជាតំណាងក្រាហ្វិក។ វាត្រូវបានគេស្គាល់ជាទូទៅថាជាវ៉ិចទ័រ។

ភាពខុសគ្នារវាងបរិមាណស្មុគ្រស្មាញ និងមាត្រដ្ឋាន

ប្រភេទនៃលេខដូចជាចំនួនគត់ សនិទានភាព និងពិតគឺធ្លាប់ស្គាល់ចំពោះកុមារពីសាលា។ ពួកគេទាំងអស់មានវិមាត្រតែមួយ។ ភាពត្រង់នៃបន្ទាត់លេខបង្ហាញពីក្រាហ្វិក។ អ្នកអាចផ្លាស់ទីឡើងលើ ឬចុះក្រោម ប៉ុន្តែ "ចលនា" ទាំងអស់នៅតាមបណ្តោយបន្ទាត់នេះនឹងត្រូវបានកំណត់ត្រឹមអ័ក្សផ្តេក។ លេខមាត្រដ្ឋានមួយវិមាត្រគឺគ្រប់គ្រាន់សម្រាប់រាប់ចំនួនធាតុ បង្ហាញទម្ងន់ ឬវាស់វ៉ុល DC នៃថ្ម។ ប៉ុន្តែពួកគេមិនអាចមានន័យថាអ្វីដែលស្មុគស្មាញជាងនេះទេ។ មាត្រដ្ឋានមិនអាចបង្ហាញចម្ងាយ និងទិសដៅក្នុងពេលដំណាលគ្នារវាងទីក្រុងពីរ ឬទំហំជាមួយដំណាក់កាល។ វាចាំបាច់ដើម្បីតំណាងឱ្យប្រភេទនៃលេខទាំងនេះរួចហើយនៅក្នុងទម្រង់នៃជួរពហុវិមាត្រនៃតម្លៃ។ ម្យ៉ាងវិញទៀត យើងត្រូវការបរិមាណវ៉ិចទ័រ ដែលអាចមិនត្រឹមតែមានរ៉ិចទ័រប៉ុណ្ណោះទេ ប៉ុន្តែក៏មានទិសដៅនៃការឃោសនាផងដែរ។

សេចក្តីសន្និដ្ឋាន

លេខមាត្រដ្ឋានគឺជាប្រភេទវត្ថុគណិតវិទ្យាដែលមនុស្សទម្លាប់ប្រើក្នុងជីវិតប្រចាំថ្ងៃ ពោលគឺសីតុណ្ហភាព ប្រវែង ទម្ងន់។ល។ ចំនួនកុំផ្លិច គឺជាតម្លៃដែលរួមបញ្ចូលទិន្នន័យពីរប្រភេទ។

វ៉ិចទ័រគឺជាតំណាងក្រាហ្វិកនៃចំនួនកុំផ្លិច។ វាមើលទៅដូចជាព្រួញដែលមានចំណុចចាប់ផ្តើម និងប្រវែង និងទិសដៅដែលបានកំណត់។ ជួនកាលពាក្យ "វ៉ិចទ័រ" ត្រូវបានប្រើនៅក្នុងវិស្វកម្មវិទ្យុ ដែលវាបង្ហាញពីការផ្លាស់ប្តូរដំណាក់កាលរវាងសញ្ញា។

នៅពេលសិក្សាលក្ខណៈសម្បត្តិនៃសមីការបួនជ្រុង ការដាក់កម្រិតមួយត្រូវបានកំណត់ - សម្រាប់អ្នករើសអើងតិចជាងសូន្យ គ្មានដំណោះស្រាយទេ។ វាត្រូវបានចែងភ្លាមៗថាយើងកំពុងនិយាយអំពីសំណុំនៃចំនួនពិត។ ចិត្តចង់ដឹងចង់ឃើញរបស់គណិតវិទូនឹងចាប់អារម្មណ៍ - តើអ្វីជាអាថ៌កំបាំងដែលមាននៅក្នុងការកក់ទុកអំពីតម្លៃពិត?

យូរ ៗ ទៅគណិតវិទូបានណែនាំគំនិតនៃចំនួនកុំផ្លិចដែលតម្លៃតាមលក្ខខណ្ឌនៃឫសទីពីរនៃដកមួយត្រូវបានគេយកជាឯកតា។

ឯកសារយោងប្រវត្តិសាស្ត្រ

ទ្រឹស្តីគណិតវិទ្យាមានការរីកចម្រើនជាបន្តបន្ទាប់ ពីសាមញ្ញទៅស្មុគស្មាញ។ ចូរយើងស្វែងយល់ថាតើគំនិតដែលហៅថា "ចំនួនកុំផ្លិច" កើតឡើងយ៉ាងដូចម្តេច ហើយហេតុអ្វីបានជាវាត្រូវការ។

តាំងពីបុរាណកាលមក មូលដ្ឋានគ្រឹះនៃគណិតវិទ្យាគឺជាគណនីធម្មតា។ អ្នកស្រាវជ្រាវបានដឹងតែសំណុំនៃតម្លៃធម្មជាតិប៉ុណ្ណោះ។ ការបូកនិងដកគឺសាមញ្ញ។ នៅពេលដែលទំនាក់ទំនងសេដ្ឋកិច្ចកាន់តែស្មុគ្រស្មាញ មេគុណបានចាប់ផ្តើមប្រើជំនួសឱ្យការបន្ថែមតម្លៃដូចគ្នា។ មានប្រតិបត្តិការបញ្ច្រាសទៅគុណ-ចែក។

គោលគំនិតនៃចំនួនធម្មជាតិកំណត់ការប្រើប្រាស់ប្រតិបត្តិការនព្វន្ធ។ វាមិនអាចទៅរួចទេក្នុងការដោះស្រាយបញ្ហាការបែងចែកទាំងអស់លើសំណុំនៃតម្លៃចំនួនគត់។ ទីមួយនាំឱ្យគំនិតនៃអត្ថន័យសមហេតុផល ហើយបន្ទាប់មកទៅកាន់អត្ថន័យមិនសមហេតុផល។ ប្រសិនបើសម្រាប់សនិទានភាព វាអាចបង្ហាញពីទីតាំងពិតប្រាកដនៃចំណុចនៅលើបន្ទាត់ នោះសម្រាប់ភាពមិនសមហេតុផល វាមិនអាចទៅរួចទេក្នុងការចង្អុលបង្ហាញចំណុចបែបនេះ។ អ្នកអាចប៉ាន់ស្មានចន្លោះពេលប៉ុណ្ណោះ។ ការរួបរួមនៃលេខសមហេតុសមផល និងអសមហេតុផលបានបង្កើតជាសំណុំពិត ដែលអាចត្រូវបានតំណាងជាបន្ទាត់ជាក់លាក់ជាមួយនឹងមាត្រដ្ឋានដែលបានផ្តល់ឱ្យ។ ជំហាននីមួយៗតាមបន្ទាត់គឺជាលេខធម្មជាតិ ហើយរវាងពួកវាគឺជាតម្លៃសមហេតុផល និងអសមហេតុផល។

យុគសម័យនៃទ្រឹស្តីគណិតវិទ្យាបានចាប់ផ្តើម។ ការអភិវឌ្ឍនៃតារាសាស្ត្រ មេកានិច រូបវិទ្យា ទាមទារដំណោះស្រាយនៃសមីការស្មុគស្មាញកាន់តែច្រើនឡើង។ ជាទូទៅ ឫសគល់នៃសមីការ quadratic ត្រូវបានរកឃើញ។ នៅពេលដោះស្រាយពហុនាមគូបដែលស្មុគស្មាញជាងនេះ អ្នកវិទ្យាសាស្ត្របានរត់ចូលទៅក្នុងភាពផ្ទុយគ្នា។ គំនិតនៃឫសគូបពីអវិជ្ជមានធ្វើឱ្យយល់បាន ប៉ុន្តែសម្រាប់ឫសការ៉េ ភាពមិនច្បាស់លាស់ត្រូវបានទទួល។ ជាងនេះទៅទៀត សមីការការ៉េគ្រាន់តែជាករណីពិសេសនៃគូបមួយប៉ុណ្ណោះ។

នៅឆ្នាំ 1545 ជនជាតិអ៊ីតាលី J. Cardano បានស្នើឡើងនូវគំនិតនៃចំនួនស្រមើលស្រមៃ។

លេខនេះគឺជាឫសទីពីរនៃដកមួយ។ ពាក្យថាចំនួនកុំផ្លិចត្រូវបានបង្កើតឡើងត្រឹមតែបីរយឆ្នាំក្រោយមកនៅក្នុងស្នាដៃរបស់គណិតវិទូដ៏ល្បីល្បាញ Gauss ។ គាត់បានស្នើឱ្យពង្រីកជាផ្លូវការនូវច្បាប់ទាំងអស់នៃពិជគណិតទៅជាលេខស្រមើលស្រមៃ។ បន្ទាត់ពិតប្រាកដបានពង្រីកទៅយន្តហោះ។ ពិភពលោកកាន់តែធំឡើង។

គំនិតជាមូលដ្ឋាន

រំលឹកឡើងវិញនូវមុខងារមួយចំនួនដែលមានការរឹតបន្តឹងលើសំណុំពិត៖

y = arcsin(x) ដែលកំណត់ក្នុងជួរតម្លៃរវាងអវិជ្ជមាន និងវិជ្ជមាន។
y = ln(x) មានន័យសម្រាប់អាគុយម៉ង់វិជ្ជមាន។
ឫសការ៉េ y = √x គណនាសម្រាប់តែ x ≥ 0 ។

ការបញ្ជាក់ i = √(-1) យើងណែនាំគំនិតបែបនេះជាលេខស្រមើលស្រមៃ វានឹងដកការរឹតបន្តឹងទាំងអស់ចេញពីដែននៃនិយមន័យនៃមុខងារខាងលើ។ កន្សោមដូចជា y = arcsin(2), y = ln(-4), y = √(-5) មានន័យក្នុងចន្លោះមួយចំនួននៃចំនួនកុំផ្លិច។

ទម្រង់ពិជគណិតអាចត្រូវបានសរសេរជាកន្សោម z = x + i × y នៅលើសំណុំនៃតម្លៃ x និង y ពិត ហើយ i 2 = -1 ។

គំនិតថ្មីដកការរឹតបន្តឹងទាំងអស់លើការប្រើប្រាស់មុខងារពិជគណិតណាមួយ ហើយនៅក្នុងរូបរាងរបស់វាប្រហាក់ប្រហែលនឹងក្រាហ្វនៃបន្ទាត់ត្រង់មួយនៅក្នុងកូអរដោណេនៃតម្លៃពិត និងការស្រមើលស្រមៃ។

យន្តហោះស្មុគស្មាញ

ទម្រង់ធរណីមាត្រនៃលេខស្មុគ្រស្មាញដោយមើលឃើញអនុញ្ញាតឱ្យយើងតំណាងឱ្យលក្ខណៈសម្បត្តិជាច្រើនរបស់ពួកគេ។ នៅលើអ័ក្ស Re(z) យើងសម្គាល់តម្លៃពិតនៃ x នៅលើ Im(z) - តម្លៃស្រមៃរបស់ y បន្ទាប់មកចំនុច z នៅលើយន្តហោះនឹងបង្ហាញតម្លៃស្មុគស្មាញដែលត្រូវការ។

និយមន័យ៖

Re(z) - អ័ក្សពិត។
Im(z) - មានន័យថា អ័ក្សស្រមើស្រមៃ។
z គឺជាចំណុចតាមលក្ខខណ្ឌនៃចំនួនកុំផ្លិច។
តម្លៃជាលេខនៃប្រវែងវ៉ិចទ័រពីចំណុចសូន្យទៅ z ត្រូវបានគេហៅថាម៉ូឌុល។
អ័ក្សពិត និងស្រមើស្រមៃ បែងចែកយន្តហោះទៅជាត្រីមាស។ ជាមួយនឹងតម្លៃវិជ្ជមាននៃកូអរដោនេ - I ត្រីមាស។ នៅពេលដែលអាគុយម៉ង់នៃអ័ក្សពិតមានតិចជាង 0 ហើយអ័ក្សស្រមើស្រមៃគឺធំជាង 0 - II ត្រីមាស។ នៅពេលដែលកូអរដោនេគឺអវិជ្ជមាន - ត្រីមាសទី III ។ ត្រីមាសចុងក្រោយ ត្រីមាសទីបួន មានគុណតម្លៃពិតវិជ្ជមានជាច្រើន និងតម្លៃស្រមើលស្រមៃអវិជ្ជមាន។

ដូច្នេះនៅលើយន្តហោះដែលមានតម្លៃកូអរដោនេ x និង y មនុស្សម្នាក់តែងតែអាចស្រមៃមើលចំណុចនៃចំនួនកុំផ្លិច។ និមិត្តសញ្ញាខ្ញុំត្រូវបានណែនាំដើម្បីបំបែកផ្នែកពិតចេញពីការស្រមើលស្រមៃ។

ទ្រព្យសម្បត្តិ

នៅពេលដែលតម្លៃនៃអាគុយម៉ង់ស្រមើលស្រមៃគឺសូន្យ យើងទទួលបានគ្រាន់តែជាលេខ (z = x) ដែលមានទីតាំងនៅលើអ័ក្សពិត ហើយជាកម្មសិទ្ធិរបស់សំណុំពិត។
ក្នុងករណីពិសេស នៅពេលដែលតម្លៃនៃអាគុយម៉ង់ពិតក្លាយជាសូន្យ កន្សោម z = i×y ត្រូវគ្នាទៅនឹងទីតាំងនៃចំនុចនៅលើអ័ក្សស្រមើស្រមៃ។
ទម្រង់ទូទៅ z = x + i × y នឹងសម្រាប់តម្លៃដែលមិនមែនជាសូន្យនៃអាគុយម៉ង់។ វាមានន័យថាទីតាំងនៃចំនុចដែលកំណត់ចំនួនកុំផ្លិចនៅក្នុងត្រីមាសមួយ។

សញ្ញាណត្រីកោណមាត្រ

រំលឹកឡើងវិញនូវប្រព័ន្ធកូអរដោណេប៉ូល និងនិយមន័យនៃ sin និង cos ។ វាច្បាស់ណាស់ថាដោយមានជំនួយពីមុខងារទាំងនេះវាអាចធ្វើទៅបានដើម្បីពិពណ៌នាអំពីទីតាំងនៃចំណុចណាមួយនៅលើយន្តហោះ។ ដើម្បីធ្វើដូចនេះវាគ្រប់គ្រាន់ដើម្បីដឹងពីប្រវែងនៃធ្នឹមប៉ូលនិងមុំទំនោរទៅនឹងអ័ក្សពិត។

និយមន័យ។ ធាតុនៃទម្រង់ ∣z ∣ គុណនឹងផលបូកនៃអនុគមន៍ត្រីកោណមាត្រ cos(ϴ) និងផ្នែកស្រមើលស្រមៃ i ×sin(ϴ) ត្រូវបានគេហៅថាចំនួនកុំផ្លិចត្រីកោណមាត្រ។ នៅទីនេះការរចនាគឺជាមុំទំនោរទៅអ័ក្សពិត

ϴ = arg(z) និង r = ∣z∣ ប្រវែងនៃធ្នឹម។

ពីនិយមន័យ និងលក្ខណៈសម្បត្តិនៃអនុគមន៍ត្រីកោណមាត្រ រូបមន្ត De Moivre ដ៏សំខាន់បំផុតដូចខាងក្រោម៖

z n = r n × (cos(n × ϴ) + i × sin(n × ϴ)) ។

ដោយប្រើរូបមន្តនេះ វាងាយស្រួលក្នុងការដោះស្រាយប្រព័ន្ធជាច្រើននៃសមីការដែលមានអនុគមន៍ត្រីកោណមាត្រ។ ជាពិសេសនៅពេលដែលភារកិច្ចនៃនិទស្សន្តកើតឡើង។

ម៉ូឌុលនិងដំណាក់កាល

ដើម្បីបញ្ចប់ការពិពណ៌នានៃសំណុំស្មុគស្មាញ យើងស្នើឱ្យនិយមន័យសំខាន់ពីរ។

ដោយដឹងពីទ្រឹស្តីបទពីថាហ្គោរ វាងាយស្រួលក្នុងការគណនាប្រវែងនៃធ្នឹមនៅក្នុងប្រព័ន្ធកូអរដោណេប៉ូឡា។

r = ∣z∣ = √(x 2 + y 2) សញ្ញាណបែបនេះនៅលើលំហស្មុគស្មាញត្រូវបានគេហៅថា "ម៉ូឌុល" ហើយកំណត់លក្ខណៈពីចម្ងាយពី 0 ទៅចំណុចមួយនៅលើយន្តហោះ។

មុំទំនោរនៃធ្នឹមស្មុគ្រស្មាញទៅបន្ទាត់ពិតϴត្រូវបានគេហៅថាជាទូទៅដំណាក់កាល។

វាអាចត្រូវបានគេមើលឃើញពីនិយមន័យដែលផ្នែកពិត និងការស្រមើលស្រមៃត្រូវបានពិពណ៌នាដោយប្រើមុខងាររង្វិល។ ពោលគឺ៖

x = r × cos(ϴ);
y = r × sin(ϴ);

ផ្ទុយទៅវិញ ដំណាក់កាលគឺទាក់ទងទៅនឹងតម្លៃពិជគណិតតាមរយៈរូបមន្ត៖

ϴ = arctan(x / y) + µ ការកែតម្រូវ µ ត្រូវបានណែនាំដើម្បីគិតគូរពីភាពទៀងទាត់នៃអនុគមន៍ធរណីមាត្រ។

រូបមន្តអយល័រ

គណិតវិទូតែងតែប្រើទម្រង់អិចស្ប៉ូណង់ស្យែល។ លេខនៃយន្តហោះស្មុគស្មាញត្រូវបានសរសេរជាកន្សោម

z = r × e i × ϴ ដែលធ្វើតាមរូបមន្តអយល័រ។

កំណត់ត្រាបែបនេះបានរីករាលដាលសម្រាប់ការគណនាជាក់ស្តែងនៃបរិមាណរូបវន្ត។ ទម្រង់នៃការតំណាងក្នុងទម្រង់នៃលេខស្មុគ្រស្មាញអិចស្ប៉ូណង់ស្យែលគឺងាយស្រួលជាពិសេសសម្រាប់ការគណនាវិស្វកម្ម ដែលវាចាំបាច់ដើម្បីគណនាសៀគ្វីជាមួយចរន្ត sinusoidal ហើយវាចាំបាច់ត្រូវដឹងពីតម្លៃនៃអាំងតេក្រាលនៃមុខងារជាមួយនឹងរយៈពេលដែលបានផ្តល់ឱ្យ។ ការគណនាដោយខ្លួនឯងបម្រើជាឧបករណ៍ក្នុងការរចនាម៉ាស៊ីន និងយន្តការផ្សេងៗ។

ការកំណត់ប្រតិបត្តិការ

ដូចដែលបានកត់សម្គាល់រួចមកហើយ ច្បាប់ពិជគណិតទាំងអស់នៃការធ្វើការជាមួយមុខងារគណិតវិទ្យាជាមូលដ្ឋានអនុវត្តចំពោះចំនួនកុំផ្លិច។

ប្រតិបត្តិការបូក

នៅពេលបន្ថែមតម្លៃស្មុគស្មាញ ផ្នែកពិត និងការស្រមើលស្រមៃរបស់ពួកគេក៏ត្រូវបានបន្ថែមផងដែរ។

z = z 1 + z 2 ដែល z 1 និង z 2 គឺជាចំនួនកុំផ្លិចទូទៅ។ ការបំប្លែងកន្សោម បន្ទាប់ពីបើកតង្កៀប និងសម្រួលសញ្ញាណ យើងទទួលបានអាគុយម៉ង់ពិតប្រាកដ x \u003d (x 1 + x 2) អាគុយម៉ង់ស្រមើលស្រមៃ y \u003d (y 1 + y 2) ។

នៅលើក្រាហ្វ នេះមើលទៅដូចជាការបន្ថែមវ៉ិចទ័រពីរ យោងទៅតាមច្បាប់ប៉ារ៉ាឡែលដ៏ល្បីល្បាញ។

ប្រតិបត្តិការដក

វាត្រូវបានគេចាត់ទុកថាជាករណីពិសេសនៃការបន្ថែម នៅពេលដែលលេខមួយគឺវិជ្ជមាន មួយទៀតគឺអវិជ្ជមាន នោះគឺមានទីតាំងនៅត្រីមាសកញ្ចក់។ ការសម្គាល់ពិជគណិតមើលទៅដូចជាភាពខុសគ្នារវាងផ្នែកពិត និងផ្នែកស្រមើលស្រមៃ។

z \u003d z 1 - z 2 ឬដោយគិតគូរពីតម្លៃនៃអាគុយម៉ង់ ស្រដៀងគ្នាទៅនឹងប្រតិបត្តិការបន្ថែម យើងទទួលបានតម្លៃពិត \u200b\u200bx \u003d (x 1 - x 2) និងការស្រមើលស្រមៃ y \u003d (y 1 - y 2) ។

គុណក្នុងប្លង់ស្មុគស្មាញ

ដោយប្រើក្បួនសម្រាប់ធ្វើការជាមួយពហុនាម យើងទទួលបានរូបមន្តសម្រាប់ដោះស្រាយចំនួនកុំផ្លិច។

ដោយអនុវត្តតាមច្បាប់ពិជគណិតទូទៅ z=z 1×z 2 យើងពណ៌នាអំពីអាគុយម៉ង់នីមួយៗ ហើយផ្តល់ឱ្យស្រដៀងគ្នា។ ផ្នែកពិត និងស្រមើស្រមៃអាចសរសេរដូចខាងក្រោម៖

x \u003d x 1 × x 2 - y 1 × y 2,
y = x 1 × y 2 + x 2 × y 1 ។

វាមើលទៅស្អាតជាងប្រសិនបើយើងប្រើលេខកុំផ្លិចអិចស្ប៉ូណង់ស្យែល។

កន្សោមមើលទៅដូចនេះ៖ z = z 1 × z 2 = r 1 × e i ϴ 1 × r 2 × e i ϴ 2 = r 1 × r 2 × e i(ϴ 1+ ϴ 2) ។

ការបែងចែក

នៅពេលពិចារណាប្រតិបត្តិការចែកជាបញ្ច្រាសនៃប្រតិបត្តិការគុណ យើងទទួលបានកន្សោមសាមញ្ញក្នុងទម្រង់អិចស្ប៉ូណង់ស្យែល។ ការបែងចែកតម្លៃនៃ z 1 ដោយ z 2 គឺជាលទ្ធផលនៃការបែងចែកម៉ូឌុលរបស់ពួកគេនិងភាពខុសគ្នានៃដំណាក់កាល។ ជាផ្លូវការ នៅពេលប្រើទម្រង់អិចស្ប៉ូណង់ស្យែលនៃចំនួនកុំផ្លិច វាមើលទៅដូចនេះ៖

z \u003d z 1 / z 2 \u003d r 1 × e i ϴ 1 / r 2 × e i ϴ 2 \u003d r 1 / r 2 × e i (ϴ 1- ϴ 2) ។

នៅក្នុងទម្រង់នៃការសម្គាល់ពិជគណិត ប្រតិបត្តិការនៃការបែងចែកលេខនៃយន្តហោះស្មុគស្មាញត្រូវបានសរសេរស្មុគស្មាញបន្តិច៖

ដោយការសរសេរអាគុយម៉ង់ និងអនុវត្តការបំប្លែងពហុនាម វាងាយស្រួលក្នុងការទទួលបានតម្លៃ x \u003d x 1 × x 2 + y 1 × y 2 រៀងគ្នា y \u003d x 2 × y 1 - x 1 × y 2, ទោះយ៉ាងណាក៏ដោយ ក្នុងចន្លោះដែលបានពិពណ៌នា កន្សោមនេះមានន័យ ប្រសិនបើ z 2 ≠ 0 ។

យើងដកឫស

ទាំងអស់ខាងលើអាចត្រូវបានអនុវត្តនៅក្នុងនិយមន័យនៃមុខងារពិជគណិតដែលស្មុគ្រស្មាញជាងមុន - បង្កើនអំណាចណាមួយ និងច្រាសមកវិញ - ស្រង់ឫស។

ដោយប្រើគំនិតទូទៅនៃការបង្កើនថាមពល n យើងទទួលបាននិយមន័យ៖

z n = (r × e i ϴ) n .

ដោយប្រើលក្ខណៈសម្បត្តិទូទៅ យើងអាចសរសេរវាឡើងវិញក្នុងទម្រង់៖

z n = r n × e i ϴ n ។

យើងទទួលបានរូបមន្តសាមញ្ញមួយសម្រាប់បង្កើនចំនួនកុំផ្លិចទៅជាថាមពលមួយ។

ពីនិយមន័យនៃសញ្ញាបត្រយើងទទួលបានលទ្ធផលសំខាន់ណាស់។ ថាមពលគូនៃឯកតាស្រមើលស្រមៃគឺតែងតែ 1. ថាមពលសេសណាមួយនៃឯកតាស្រមើលស្រមៃគឺតែងតែ -1 ។

ឥឡូវនេះសូមសិក្សាមុខងារបញ្ច្រាស - ស្រង់ឫស។

សម្រាប់ភាពសាមញ្ញនៃការសម្គាល់ យើងយក n = 2. ឫសការ៉េ w នៃតម្លៃស្មុគស្មាញ z នៅលើប្លង់ស្មុគស្មាញ C ជាធម្មតាត្រូវបានគេចាត់ទុកថាជាកន្សោម z = ± ដែលមានសុពលភាពសម្រាប់អាគុយម៉ង់ពិតប្រាកដណាមួយធំជាង ឬស្មើសូន្យ។ សម្រាប់ w ≤ 0 មិនមានដំណោះស្រាយទេ។

សូមក្រឡេកមើលសមីការការ៉េសាមញ្ញបំផុត z 2 = 1. ដោយប្រើរូបមន្តនៃចំនួនកុំផ្លិច យើងសរសេរឡើងវិញ r 2 × e i 2ϴ = r 2 × e i 2ϴ = e i 0 ។ វាអាចត្រូវបានគេមើលឃើញពីកំណត់ត្រាថា r 2 = 1 និង ϴ = 0 ដូច្នេះយើងមានដំណោះស្រាយតែមួយគត់ស្មើនឹង 1 ។ ប៉ុន្តែនេះផ្ទុយនឹងគំនិតដែល z = -1 ក៏ត្រូវគ្នាទៅនឹងនិយមន័យនៃឫសការ៉េផងដែរ។

ចូរយើងគិតពីអ្វីដែលយើងមិនយកទៅក្នុងគណនី។ ប្រសិនបើយើងរំលឹកឡើងវិញនូវសញ្ញាណត្រីកោណមាត្រ នោះយើងស្ដារសេចក្តីថ្លែងការណ៍ឡើងវិញ - ជាមួយនឹងការផ្លាស់ប្តូរតាមកាលកំណត់ក្នុងដំណាក់កាល ϴ ចំនួនកុំផ្លិចមិនផ្លាស់ប្តូរទេ។ ឲ្យ p កំណត់តម្លៃនៃរយៈពេល បន្ទាប់មកយើងមាន r 2 × e i 2ϴ = e i (0+ p) , wherece 2ϴ = 0 + p, ឬ ϴ = p / 2. ដូច្នេះហើយ យើងមាន e i 0 = 1 និង e i p / 2 = -1 ។ យើងទទួលបានដំណោះស្រាយទីពីរ ដែលត្រូវនឹងការយល់ដឹងទូទៅនៃឫសការ៉េ។

ដូច្នេះ ដើម្បីស្វែងរកឫសតាមអំពើចិត្តនៃចំនួនកុំផ្លិច យើងនឹងអនុវត្តតាមនីតិវិធី។

យើងសរសេរទម្រង់អិចស្ប៉ូណង់ស្យែល w= ∣w∣ × e i (arg (w) + pk), k គឺជាចំនួនគត់តាមអំពើចិត្ត។
លេខដែលចង់បានក៏អាចត្រូវបានតំណាងក្នុងទម្រង់អយល័រ z = r × e i ϴ ។
ចូរប្រើនិយមន័យទូទៅនៃអនុគមន៍ស្រង់ឫស r n *e i n ϴ = ∣w∣ × e i (arg (w) + pk) ។
ពីលក្ខណៈសម្បត្តិទូទៅនៃសមភាពនៃម៉ូឌុល និងអាគុយម៉ង់ យើងសរសេរ r n = ∣w∣ និង nϴ = arg (w) + p ×k ។
កំណត់ត្រាចុងក្រោយនៃឫសនៃចំនួនកុំផ្លិចត្រូវបានពិពណ៌នាដោយរូបមន្ត z = √∣w∣ × e i (arg (w) + pk) / n ។
មតិយោបល់។ តម្លៃ ∣w∣ តាមនិយមន័យ ជាចំនួនពិតវិជ្ជមាន ដូច្នេះឬសថាមពលណាមួយសមហេតុផល។

វាលនិងការរួមបញ្ចូលគ្នា

សរុបសេចក្តីមក យើងផ្តល់និយមន័យសំខាន់ៗចំនួនពីរ ដែលមានសារៈសំខាន់តិចតួចសម្រាប់ការដោះស្រាយបញ្ហាអនុវត្តជាមួយនឹងចំនួនកុំផ្លិច ប៉ុន្តែមានសារៈសំខាន់ក្នុងការអភិវឌ្ឍន៍បន្ថែមទៀតនៃទ្រឹស្តីគណិតវិទ្យា។

កន្សោមសម្រាប់ការបូក និងគុណត្រូវបានគេនិយាយថានឹងបង្កើតជាវាលមួយ ប្រសិនបើពួកវាបំពេញតាមអ័ក្សសម្រាប់ធាតុណាមួយនៃប្លង់ស្មុគស្មាញ z:

ពីការផ្លាស់ប្តូរកន្លែងនៃពាក្យស្មុគស្មាញ ផលបូកស្មុគស្មាញមិនផ្លាស់ប្តូរទេ។
សេចក្តីថ្លែងការណ៍គឺពិត - នៅក្នុងកន្សោមស្មុគស្មាញ ផលបូកនៃចំនួនពីរអាចត្រូវបានជំនួសដោយតម្លៃរបស់វា។
មានតម្លៃអព្យាក្រឹត 0 ដែល z + 0 = 0 + z = z គឺពិត។
សម្រាប់ z ណាមួយគឺផ្ទុយគ្នា - z បូកដែលផ្តល់ឱ្យសូន្យ។
នៅពេលដែលកន្លែងនៃកត្តាស្មុគ្រស្មាញត្រូវបានផ្លាស់ប្តូរផលិតផលស្មុគស្មាញមិនផ្លាស់ប្តូរទេ។
គុណនៃលេខទាំងពីរអាចត្រូវបានជំនួសដោយតម្លៃរបស់វា។
មានតម្លៃអព្យាក្រឹត 1 គុណដែលមិនផ្លាស់ប្តូរចំនួនកុំផ្លិច។
សម្រាប់រាល់ z ≠ 0 មានច្រាសនៃ z -1 ដែលនៅពេលគុណនឹងលទ្ធផល 1 ។
ការគុណផលបូកនៃចំនួនពីរដោយមួយភាគបីគឺស្មើនឹងការគុណលេខនីមួយៗដោយលេខនោះ ហើយបន្ថែមលទ្ធផល។
0 ≠ 1.

លេខ z 1 = x + i × y និង z 2 = x − i × y ត្រូវបានគេហៅថា conjugate ។

ទ្រឹស្តីបទ។សម្រាប់ការផ្សំ សេចក្តីថ្លែងការណ៍គឺពិត៖

ផលបូកនៃផលបូកគឺស្មើនឹងផលបូកនៃធាតុផ្សំ។
ការផ្សំនៃផលិតផលគឺស្មើនឹងផលិតផលនៃការភ្ជាប់គ្នា។
ស្មើនឹងលេខខ្លួនឯង។

នៅក្នុងពិជគណិតទូទៅ លក្ខណៈសម្បត្តិបែបនេះត្រូវបានគេហៅថា automorphisms វាល។

ឧទាហរណ៍

ដោយអនុវត្តតាមច្បាប់ និងរូបមន្តខាងលើសម្រាប់ចំនួនកុំផ្លិច អ្នកអាចធ្វើប្រតិបត្តិការលើពួកវាបានយ៉ាងងាយស្រួល។

ចូរយើងពិចារណាឧទាហរណ៍សាមញ្ញបំផុត។

កិច្ចការ 1 ។ដោយប្រើសមីការ 3y +5 x i = 15 − 7i កំណត់ x និង y ។

ដំណោះស្រាយ។ រំលឹកនិយមន័យនៃសមភាពស្មុគស្មាញ បន្ទាប់មក 3y = 15, 5x = -7 ។ ដូច្នេះ x = −7/5, y = 5 ។

កិច្ចការទី 2 ។គណនាតម្លៃ 2 + i 28 និង 1 + i 135 ។

ដំណោះស្រាយ។ ជាក់ស្តែង 28 គឺជាលេខគូ ពីលទ្ធផលនៃនិយមន័យនៃចំនួនកុំផ្លិចនៅក្នុងអំណាច យើងមាន i 28 = 1 ដែលមានន័យថាកន្សោមគឺ 2 + i 28 = 3 តម្លៃទីពីរ i 135 = - 1 បន្ទាប់មក 1 + i 135 = 0 ។

កិច្ចការទី 3 ។គណនាផលគុណនៃតម្លៃ 2+5i និង 4+3i ។

ដំណោះស្រាយ។ ពីលក្ខណៈសម្បត្តិទូទៅនៃការគុណនៃចំនួនកុំផ្លិច យើងទទួលបាន (2 + 5i) X (4 + 3i) = 8 - 15 + i (6 + 20) ។ តម្លៃថ្មីនឹងជា -7 + 26i ។

កិច្ចការទី 4 ។គណនាឫសនៃសមីការ z 3 = -i ។

ដំណោះស្រាយ។ មានវិធីជាច្រើនដើម្បីស្វែងរកចំនួនកុំផ្លិច។ ចូរយើងពិចារណាអំពីលទ្ធភាពមួយ។ តាមនិយមន័យ ∣ - i∣ = 1 ដំណាក់កាលសម្រាប់ -i គឺ -p / 4 ។ សមីការដើមអាចត្រូវបានសរសេរឡើងវិញជា r 3 * e i 3ϴ = e - p/4+ pk , whence z = e - p / 12 + pk /3 សម្រាប់ចំនួនគត់ k ។

សំណុំនៃដំណោះស្រាយមានទម្រង់ (e - ip/12, e ip /4, e i 2 p/3) ។

ហេតុអ្វីបានជាត្រូវការលេខស្មុគស្មាញ

ប្រវត្តិសាស្ត្រដឹងពីឧទាហរណ៍ជាច្រើន នៅពេលដែលអ្នកវិទ្យាសាស្ត្រ ខណៈពេលដែលកំពុងធ្វើការលើទ្រឹស្ដីមួយ មិនគិតពីការអនុវត្តជាក់ស្តែងនៃលទ្ធផលរបស់ពួកគេ។ ជាដំបូង គណិតវិទ្យាគឺជាល្បែងនៃចិត្ត ការប្រកាន់ខ្ជាប់យ៉ាងតឹងរ៉ឹងចំពោះទំនាក់ទំនងបុព្វហេតុ និងផល។ សំណង់គណិតវិទ្យាស្ទើរតែទាំងអស់ត្រូវបានកាត់បន្ថយទៅជាការដោះស្រាយសមីការអាំងតេក្រាល និងឌីផេរ៉ង់ស្យែល ហើយការប៉ាន់ស្មានទាំងនោះត្រូវបានដោះស្រាយដោយការស្វែងរកឫសគល់នៃពហុនាម។ នៅទីនេះដំបូងយើងជួបប្រទះភាពផ្ទុយគ្នានៃចំនួនស្រមើលស្រមៃ។

អ្នកវិទ្យាសាស្ត្រធម្មជាតិ ដោះស្រាយបញ្ហាជាក់ស្តែងទាំងស្រុង ងាកទៅរកដំណោះស្រាយនៃសមីការផ្សេងៗ រកឃើញភាពផ្ទុយគ្នានៃគណិតវិទ្យា។ ការបកស្រាយអំពីភាពផ្ទុយគ្នាទាំងនេះនាំទៅរកការរកឃើញដ៏អស្ចារ្យ។ ធម្មជាតិពីរនៃរលកអេឡិចត្រូម៉ាញ៉េទិចគឺជាឧទាហរណ៍មួយ។ លេខស្មុគស្មាញដើរតួនាទីយ៉ាងសំខាន់ក្នុងការយល់ដឹងអំពីលក្ខណៈសម្បត្តិរបស់វា។

នេះ, នៅក្នុងវេន, បានរកឃើញការអនុវត្តជាក់ស្តែងនៅក្នុងអុបទិក, វិទ្យុអេឡិចត្រូនិ, ថាមពលនិងវិស័យបច្ចេកវិទ្យាជាច្រើនទៀត។ ឧទាហរណ៍មួយទៀត ពិបាកយល់អំពីបាតុភូតរាងកាយ។ Antimatter ត្រូវបានព្យាករណ៍នៅចុងប៊ិច។ ហើយមានតែបន្ទាប់ពីជាច្រើនឆ្នាំព្យាយាមសំយោគវាដោយរាងកាយចាប់ផ្តើម។

គេមិនគួរគិតថាស្ថានភាពបែបនេះមានតែនៅក្នុងរូបវិទ្យាទេ។ មិនមានការរកឃើញគួរឱ្យចាប់អារម្មណ៍តិចជាងនេះត្រូវបានធ្វើឡើងនៅក្នុងសត្វព្រៃនៅក្នុងការសំយោគនៃ macromolecules ក្នុងអំឡុងពេលសិក្សានៃបញ្ញាសិប្បនិម្មិត។ ហើយទាំងអស់នេះគឺដោយសារតែការពង្រីកស្មារតីរបស់យើង ជៀសវាងការបូក និងដកតម្លៃធម្មជាតិដ៏សាមញ្ញ។

ប្រធានបទចំនួនកុំផ្លិច និងពហុនាម

ការបង្រៀន 22

§១. លេខស្មុគស្មាញ៖ និយមន័យមូលដ្ឋាន

និមិត្តសញ្ញា បញ្ចូលសមាមាត្រ
ហើយត្រូវបានគេហៅថាឯកតាស្រមើលស្រមៃ។ ក្នុងន័យផ្សេងទៀត,
.

និយមន័យ។ ការបង្ហាញទម្រង់
, កន្លែងណា
ត្រូវបានគេហៅថា ចំនួនកុំផ្លិច និងលេខ ហៅថាផ្នែកពិតនៃចំនួនកុំផ្លិច និងបញ្ជាក់
, ចំនួន - ផ្នែកស្រមើលស្រមៃ និងបញ្ជាក់
.

ពីនិយមន័យនេះវាដូចខាងក្រោមថាចំនួនពិតគឺជាចំនួនកុំផ្លិចដែលផ្នែកស្រមៃស្មើនឹងសូន្យ។

វាងាយស្រួលក្នុងការតំណាងឱ្យចំនួនកុំផ្លិចជាចំណុចនៃយន្តហោះដែលប្រព័ន្ធកូអរដោនេចតុកោណ Cartesian ត្រូវបានផ្តល់ឱ្យ ពោលគឺ៖ ចំនួនកុំផ្លិច
ចំណុចប្រកួត
និងច្រាសមកវិញ។ នៅលើអ័ក្ស
ចំនួនពិតត្រូវបានបង្ហាញ ហើយវាត្រូវបានគេហៅថាអ័ក្សពិត។ លេខស្មុគស្មាញនៃទម្រង់

ត្រូវបានគេហៅថាការស្រមើលស្រមៃសុទ្ធសាធ។ ពួកវាត្រូវបានបង្ហាញជាចំណុចនៅលើអ័ក្ស។
ដែលត្រូវបានគេហៅថាអ័ក្សស្រមើស្រមៃ។ យន្តហោះនេះដែលបម្រើឱ្យតំណាងឱ្យចំនួនកុំផ្លិចត្រូវបានគេហៅថាយន្តហោះស្មុគស្មាញ។ ចំនួនកុំផ្លិចដែលមិនមែនពិត ឧ. បែបនោះ។
ជួនកាលគេហៅថា ស្រមើស្រមៃ។

ចំនួនកុំផ្លិចពីរត្រូវបានគេនិយាយថាស្មើគ្នាប្រសិនបើវាមានផ្នែកពិតនិងស្រមើស្រមៃដូចគ្នា។

ការបូក ដក និងគុណនៃចំនួនកុំផ្លិចត្រូវបានអនុវត្តដោយយោងទៅតាមច្បាប់ធម្មតានៃពិជគណិតពហុធា ដោយគិតគូរពីការពិតដែលថា

. ប្រតិបត្តិការបែងចែកអាចត្រូវបានកំណត់ថាជាការបញ្ច្រាសនៃប្រតិបត្តិការគុណ ហើយគេអាចបញ្ជាក់ពីភាពឯកោនៃលទ្ធផល (ប្រសិនបើផ្នែកចែកខុសពីសូន្យ)។ ទោះយ៉ាងណាក៏ដោយនៅក្នុងការអនុវត្តវិធីសាស្រ្តផ្សេងគ្នាត្រូវបានប្រើ។

លេខស្មុគស្មាញ
និង
ត្រូវបានគេហៅថា conjugate នៅលើយន្តហោះស្មុគស្មាញដែលពួកគេត្រូវបានតំណាងដោយចំណុចស៊ីមេទ្រីអំពីអ័ក្សពិត។ វាច្បាស់ណាស់ថា:

1)

;

2)
;

3)
.

ឥឡូវបំបែក នៅលើ អាចត្រូវបានធ្វើដូចខាងក្រោម:

វាមិនមែនជាការលំបាកក្នុងការបង្ហាញថា

ដែលជាកន្លែងដែលនិមិត្តសញ្ញា តំណាងឱ្យប្រតិបត្តិការនព្វន្ធណាមួយ។

អនុញ្ញាតឱ្យ
ចំនួនស្រមើស្រមៃមួយចំនួន និង គឺជាអថេរពិតប្រាកដ។ ផលិតផលនៃលេខពីរ

គឺជាត្រីកោណមាត្រការ៉េដែលមានមេគុណពិត។

ឥឡូវនេះ យើងមានលេខកុំផ្លិច យើងអាចដោះស្រាយសមីការការ៉េណាមួយ។
.ប្រសិនបើ

ហើយសមីការមានឫសផ្សំស្មុគស្មាញពីរ

ប្រសិនបើ
បន្ទាប់មកសមីការមានឫសពិតពីរផ្សេងគ្នា។ ប្រសិនបើ
បន្ទាប់មកសមីការមានឫសដូចគ្នាពីរ។

§២. ទម្រង់ត្រីកោណមាត្រនៃចំនួនកុំផ្លិច

ដូចដែលបានរៀបរាប់ខាងលើចំនួនកុំផ្លិច
ងាយស្រួលតំណាងដោយចំណុច
. គេក៏អាចកំណត់អត្តសញ្ញាណលេខបែបនេះជាមួយនឹងវ៉ិចទ័រកាំនៃចំណុចនេះ។
. ជាមួយនឹងការបកស្រាយនេះ ការបូកនិងដកនៃចំនួនកុំផ្លិចត្រូវបានអនុវត្តដោយយោងទៅតាមច្បាប់នៃការបូក និងដកវ៉ិចទ័រ។ សម្រាប់ការគុណ និងចែកចំនួនកុំផ្លិច ទម្រង់មួយផ្សេងទៀតគឺងាយស្រួលជាង។

យើងណែនាំនៅលើយន្តហោះស្មុគស្មាញ
ប្រព័ន្ធកូអរដោណេប៉ូល។ បន្ទាប់មកកន្លែងណា
,
និងចំនួនកុំផ្លិច
អាចត្រូវបានសរសេរជា:

ទម្រង់នៃការសម្គាល់នេះត្រូវបានគេហៅថាត្រីកោណមាត្រ (ផ្ទុយពីទម្រង់ពិជគណិត
) នៅក្នុងទម្រង់នេះលេខ ត្រូវបានគេហៅថាម៉ូឌុលនិង - អាគុយម៉ង់ចំនួនកុំផ្លិច . ពួកគេត្រូវបានសម្គាល់:
,

. សម្រាប់ម៉ូឌុលយើងមានរូបមន្ត

អាគុយម៉ង់ចំនួនត្រូវបានកំណត់មិនច្បាស់លាស់ ប៉ុន្តែរហូតដល់មួយពាក្យ
,
. តម្លៃនៃអាគុយម៉ង់ដែលបំពេញវិសមភាព
ត្រូវបានគេហៅថា មេ និងតំណាង
. បន្ទាប់មក
. សម្រាប់តម្លៃចម្បងនៃអាគុយម៉ង់ អ្នកអាចទទួលបានកន្សោមខាងក្រោម៖

អាគុយម៉ង់លេខ
ចាត់ទុកថាមិនត្រូវបានកំណត់។

លក្ខខណ្ឌសម្រាប់សមភាពនៃចំនួនកុំផ្លិចពីរក្នុងទម្រង់ត្រីកោណមាត្រមានទម្រង់៖ ម៉ូឌុលនៃលេខគឺស្មើគ្នា ហើយអាគុយម៉ង់ខុសគ្នាដោយពហុគុណ
.

ស្វែងរកផលគុណនៃចំនួនកុំផ្លិចពីរក្នុងទម្រង់ត្រីកោណមាត្រ៖

ដូច្នេះនៅពេលគុណលេខ ម៉ូឌុលរបស់ពួកគេត្រូវបានគុណ ហើយអាគុយម៉ង់ត្រូវបានបន្ថែម។

ដូចគ្នានេះដែរ វាអាចត្រូវបានបង្កើតឡើងថា នៅពេលបែងចែក ម៉ូឌុលនៃលេខត្រូវបានបែងចែក ហើយអាគុយម៉ង់ត្រូវបានដក។

ការយល់ដឹងអំពីនិទស្សន្តជាគុណពហុគុណ យើងអាចទទួលបានរូបមន្តសម្រាប់បង្កើនចំនួនកុំផ្លិចទៅជាថាមពល៖

យើងទទួលបានរូបមន្តសម្រាប់
- ឫស th power នៃចំនួនកុំផ្លិច (មិនត្រូវច្រឡំជាមួយឫសនព្វន្ធនៃចំនួនពិតទេ!) ប្រតិបត្តិការដកឫសគឺបញ្ច្រាសនៃប្រតិបត្តិការនិទស្សន្ត។ នោះហើយជាមូលហេតុដែល
គឺជាចំនួនកុំផ្លិច បែបនោះ។
.

អនុញ្ញាតឱ្យ
ស្គាល់, និង
តម្រូវឱ្យត្រូវបានរកឃើញ។ បន្ទាប់មក

ពីសមភាពនៃចំនួនកុំផ្លិចពីរក្នុងទម្រង់ត្រីកោណមាត្រ វាធ្វើតាមនោះ។

,
,
.

ពីទីនេះ
(វាជាឫសនព្វន្ធ!)

,
.

វាងាយស្រួលក្នុងការផ្ទៀងផ្ទាត់វា។ អាចទទួលយកបាន។ តម្លៃខុសគ្នាជាសំខាន់ ឧទាហរណ៍ នៅពេលដែល
. ទីបំផុតយើងមានរូបមន្ត៖

,
.

ដូច្នេះឫស សញ្ញាប័ត្រទី ពីចំនួនកុំផ្លិចមាន តម្លៃខុសគ្នា។ នៅលើយន្តហោះស្មុគ្រស្មាញ តម្លៃទាំងនេះស្ថិតនៅត្រង់ចំណុចកំពូលយ៉ាងត្រឹមត្រូវ -gon ចារឹកក្នុងរង្វង់កាំ
ផ្តោតលើប្រភពដើម។ ឫស "ទីមួយ" មានអំណះអំណាង
អាគុយម៉ង់នៃឫស "អ្នកជិតខាង" ពីរខុសគ្នាដោយ
.

ឧទាហរណ៍។ ចូរយើងយកឫសគូបនៃឯកតាស្រមើលស្រមៃ៖
,
,
. បន្ទាប់មក៖

§១. លេខស្មុគស្មាញ

1° និយមន័យ។ ការសម្គាល់ពិជគណិត។

និយមន័យ ១. លេខស្មុគស្មាញហៅថាលំដាប់លេខពិត និង ប្រសិនបើគោលគំនិតនៃសមភាពត្រូវបានកំណត់សម្រាប់ពួកគេ ប្រតិបត្តិការនៃការបូក និងគុណដែលបំពេញនូវ axioms ខាងក្រោម៖

1) លេខពីរ
និង
ស្មើគ្នាប្រសិនបើ និងប្រសិនបើ
,
, i.e.


,
.

2) ផលបូកនៃចំនួនកុំផ្លិច
និង

និងស្មើ
, i.e.

+
=
.

3) ផលិតផលនៃចំនួនកុំផ្លិច
និង
លេខត្រូវបានហៅ
និងស្មើនឹង , i.e.

∙=.

សំណុំនៃចំនួនកុំផ្លិចត្រូវបានតំណាង គ.

រូបមន្ត (2), (3) សម្រាប់លេខនៃទម្រង់
យកទម្រង់

តើវាមកពីណាដែលប្រតិបត្តិការនៃការបូក និងគុណសម្រាប់លេខនៃទម្រង់
ស្របពេលជាមួយនឹងការបូក និងគុណសម្រាប់ចំនួនពិត  ចំនួនកុំផ្លិចនៃទម្រង់
ត្រូវបានកំណត់អត្តសញ្ញាណដោយចំនួនពិត .

លេខស្មុគស្មាញ
ហៅ ឯកតាស្រមើលស្រមៃនិងតំណាង , i.e.
បន្ទាប់មកពី (3) 

ពី (2), (3)  ដែលមានន័យថា

កន្សោម (៤) ត្រូវបានគេហៅថា ការសម្គាល់ពិជគណិតចំនួនកុំផ្លិច។

ក្នុងទម្រង់ពិជគណិត ប្រតិបត្តិការនៃការបូក និងគុណមានទម្រង់៖

ចំនួនកុំផ្លិចត្រូវបានចង្អុលបង្ហាញ
, - ផ្នែកពិត, គឺជាផ្នែកនៃក្តីស្រមៃ គឺជាចំនួនស្រមើស្រមៃសុទ្ធសាធ។ ការកំណត់:
,
.

និយមន័យ ២. លេខស្មុគស្មាញ
ហៅ រួមជាមួយនឹងចំនួនកុំផ្លិច
.

លក្ខណៈសម្បត្តិនៃការផ្សំស្មុគស្មាញ។

2)
.

3) ប្រសិនបើ
, នោះ។
.

4)
.

5)
គឺជាចំនួនពិត។

ភស្តុតាងត្រូវបានអនុវត្តដោយការគណនាដោយផ្ទាល់។

និយមន័យ ៣. ចំនួន
ហៅ ម៉ូឌុលចំនួនកុំផ្លិច
និងតំណាង
.

វាច្បាស់ណាស់។
, និង

. រូបមន្តក៏ច្បាស់ដែរ៖
និង
.

2° លក្ខណៈសម្បត្តិនៃប្រតិបត្តិការបូកនិងគុណ។

១) ទំនាក់ទំនង៖
,
.

2) សមាគម:,
.

៣) ការចែកចាយ៖

ភស្តុតាង 1) - 3) ត្រូវបានអនុវត្តដោយការគណនាដោយផ្ទាល់ដោយផ្អែកលើលក្ខណៈសម្បត្តិស្រដៀងគ្នាសម្រាប់ចំនួនពិត។

4)
,
.

5) , គ ! , បំពេញសមីការ
. បែប

6) ,គ, 0, ! :
. បែប ត្រូវបានរកឃើញដោយការគុណសមីការដោយ

.

ឧទាហរណ៍។ ស្រមៃមើលចំនួនកុំផ្លិច
ក្នុងទម្រង់ពិជគណិត។ ដើម្បីធ្វើដូចនេះគុណភាគយកនិងភាគបែងនៃប្រភាគដោយ conjugate នៃភាគបែង។ យើងមាន:

3°។ ការបកស្រាយធរណីមាត្រនៃចំនួនកុំផ្លិច។ ទម្រង់ត្រីកោណមាត្រ និងអិចស្ប៉ូណង់ស្យែលនៃការសរសេរចំនួនកុំផ្លិច។

អនុញ្ញាតឱ្យប្រព័ន្ធកូអរដោនេរាងចតុកោណត្រូវបានផ្តល់ឱ្យនៅលើយន្តហោះ។ បន្ទាប់មក
គមនុស្សម្នាក់អាចភ្ជាប់ចំណុចនៅលើយន្តហោះជាមួយនឹងកូអរដោនេ
.(សូមមើលរូបទី 1)។ វាច្បាស់ណាស់ថាការឆ្លើយឆ្លងបែបនេះគឺមួយទៅមួយ។ ក្នុងករណីនេះ លេខពិតស្ថិតនៅលើអ័ក្ស abscissa ហើយលេខស្រមើលស្រមៃសុទ្ធសាធស្ថិតនៅលើអ័ក្សកំណត់។ ដូច្នេះអ័ក្ស abscissa ត្រូវបានគេហៅថា អ័ក្សពិតនិងអ័ក្ស y − អ័ក្សស្រមៃ. យន្តហោះដែលលេខស្មុគ្រស្មាញកុហកត្រូវបានគេហៅថា យន្តហោះស្មុគស្មាញ.

ចំណាំថា និង
គឺស៊ីមេទ្រីអំពីប្រភពដើម និង និង គឺស៊ីមេទ្រីទាក់ទងនឹង Ox ។

ចំនួនកុំផ្លិចនីមួយៗ (ឧ. ចំណុចនីមួយៗនៅលើយន្តហោះ) អាចត្រូវបានភ្ជាប់ជាមួយវ៉ិចទ័រដែលមានការចាប់ផ្តើមនៅចំណុច O និងចុងបញ្ចប់នៅចំណុច
. ការឆ្លើយឆ្លងគ្នារវាងវ៉ិចទ័រ និងចំនួនកុំផ្លិចគឺពីមួយទៅមួយ។ ដូច្នេះវ៉ិចទ័រដែលត្រូវគ្នានឹងចំនួនកុំផ្លិច តំណាងដោយអក្សរដូចគ្នា។

ឃ បន្ទាត់វ៉ិចទ័រ
ដែលត្រូវគ្នានឹងចំនួនកុំផ្លិច
, គឺស្មើនឹង
, និង
,
.

ដោយប្រើការបកស្រាយវ៉ិចទ័រ គេអាចមើលឃើញថាវ៉ិចទ័រ
- ផលបូកនៃវ៉ិចទ័រ និង , ក
- ផលបូកនៃវ៉ិចទ័រ និង
.(សូមមើលរូបទី 2)។ ដូច្នេះ វិសមភាពខាងក្រោមគឺពិត៖

រួមជាមួយនឹងប្រវែង វ៉ិចទ័រ យើងណែនាំមុំ រវាងវ៉ិចទ័រ និងអ័ក្សអុក រាប់ពីទិសដៅវិជ្ជមាននៃអ័ក្សអុក៖ ប្រសិនបើការរាប់ច្រាសទ្រនិចនាឡិកា នោះសញ្ញានៃមុំត្រូវបានចាត់ទុកថាជាវិជ្ជមាន ប្រសិនបើតាមទ្រនិចនាឡិកា នោះអវិជ្ជមាន។ ជ្រុងនេះត្រូវបានគេហៅថា អាគុយម៉ង់ចំនួនកុំផ្លិចនិងតំណាង
. ជ្រុង មិនត្រូវបានកំណត់ជាក់លាក់ទេ ប៉ុន្តែមានភាពជាក់លាក់
…. សម្រាប់
អាគុយម៉ង់មិនត្រូវបានកំណត់ទេ។

រូបមន្ត (៦) កំណត់នូវអ្វីដែលហៅថា សញ្ញាណត្រីកោណមាត្រចំនួនកុំផ្លិច។

ពី (5) វាធ្វើតាមថាប្រសិនបើ
និង
នោះ។

,
.

ពី (5)
តើដោយអ្វី និង ចំនួនកុំផ្លិចត្រូវបានកំណត់តែមួយ។ ការសន្ទនាមិនពិត៖ ពោលគឺដោយចំនួនកុំផ្លិច ម៉ូឌុលរបស់វា។ គឺមានតែមួយគត់, និងអាគុយម៉ង់ , ដោយសារតែ (7), − ជាមួយនឹងភាពត្រឹមត្រូវ
. វាក៏ធ្វើតាមពី (7) ថាអាគុយម៉ង់ អាចរកបានជាដំណោះស្រាយចំពោះសមីការ

ទោះយ៉ាងណាក៏ដោយ មិនមែនគ្រប់ដំណោះស្រាយចំពោះសមីការនេះ គឺជាដំណោះស្រាយចំពោះ (7) នោះទេ។

ក្នុងចំណោមតម្លៃទាំងអស់នៃអាគុយម៉ង់នៃចំនួនកុំផ្លិច មួយត្រូវបានជ្រើសរើស ដែលត្រូវបានគេហៅថាតម្លៃសំខាន់នៃអាគុយម៉ង់ ហើយត្រូវបានតំណាង
. ជាធម្មតាតម្លៃចម្បងនៃអាគុយម៉ង់ត្រូវបានជ្រើសរើសក្នុងចន្លោះពេល
ឬក្នុងចន្លោះពេល

ក្នុងទម្រង់ត្រីកោណមាត្រ វាងាយស្រួលក្នុងការអនុវត្តប្រតិបត្តិការគុណ និងចែក។

ទ្រឹស្តីបទ ១.ម៉ូឌុលនៃផលិតផលនៃចំនួនកុំផ្លិច និង គឺស្មើនឹងផលិតផលនៃម៉ូឌុល ហើយអាគុយម៉ង់គឺស្មើនឹងផលបូកនៃអាគុយម៉ង់ i.e.

, ក.

ស្រដៀងគ្នា

ភស្តុតាង។អនុញ្ញាតឱ្យ, ។ បន្ទាប់មកដោយការគុណដោយផ្ទាល់យើងទទួលបាន៖

ស្រដៀងគ្នា

.■

ផលវិបាក(រូបមន្តរបស់ De Moivre) ។ សម្រាប់
រូបមន្តរបស់ Moivre មានសុពលភាព

ទំ ឧទាហរណ៍។ អនុញ្ញាតឱ្យស្វែងរកទីតាំងធរណីមាត្រនៃចំណុច
. វាធ្វើតាមទ្រឹស្ដី 1 នោះ។

ដូច្នេះ ដើម្បីសង់វាដំបូងអ្នកត្រូវតែសង់ចំណុច ដែលជាការបញ្ច្រាស អំពីរង្វង់ឯកតា ហើយបន្ទាប់មករកចំណុចស៊ីមេទ្រីទៅវាអំពីអ័ក្ស x ។

អនុញ្ញាតឱ្យ
, i.e.
លេខស្មុគស្មាញ
តំណាង
, i.e. ររូបមន្តអយល័រគឺត្រឹមត្រូវ។

ដោយសារតែ
, នោះ។
,
. ពីទ្រឹស្តីបទ ១
ចុះមុខងារវិញ?
វាអាចធ្វើទៅបានដើម្បីធ្វើការដូចទៅនឹងអនុគមន៍អិចស្ប៉ូណង់ស្យែលធម្មតា ពោលគឺឧ។ សមភាពគឺជាការពិត

,
,
.

ពី (8)
សញ្ញាណអិចស្ប៉ូណង់ស្យែលចំនួនកុំផ្លិច

, កន្លែងណា
,

ឧទាហរណ៍។ .

4° ឫស th power នៃចំនួនកុំផ្លិច។

ពិចារណាសមីការ

,
ជាមួយ ,
ន .

អនុញ្ញាតឱ្យ
ហើយដំណោះស្រាយនៃ Eq ។ (9) ត្រូវបានស្វែងរកក្នុងទម្រង់
. បន្ទាប់មក (9) យកទម្រង់
តើយើងរកឃើញពីណាមក
,
, i.e.

,
,
.

ដូច្នេះសមីការ (៩) មានឫសគល់

,
.

ចូរយើងបង្ហាញថាក្នុងចំណោម (10) មានពិតប្រាកដ ឫសផ្សេងៗ។ ពិតជា

គឺខុសគ្នា, ដោយសារតែ អំណះអំណាងរបស់ពួកគេគឺខុសគ្នា និងខុសគ្នាតិចជាង
. បន្ថែមទៀត
, ដោយសារតែ
. ស្រដៀងគ្នា
.

ដូច្នេះសមីការ (9) សម្រាប់
មានពិតប្រាកដ ឫស
ដែលមានទីតាំងនៅផ្នែកខាងលើនៃធម្មតា។ -gon ចារឹកក្នុងរង្វង់កាំ ផ្តោតលើ T.O.

ដូច្នេះវាត្រូវបានបង្ហាញឱ្យឃើញ

ទ្រឹស្តីបទ ២.ការទាញយកឫស th power នៃចំនួនកុំផ្លិច
តែងតែអាចធ្វើទៅបាន។ តម្លៃជា root ទាំងអស់។ កម្រិតនៃ ដែលមានទីតាំងនៅផ្នែកខាងលើនៃត្រឹមត្រូវ។ -gon បានចារឹកជារង្វង់ដោយកណ្តាលនៅសូន្យនិងកាំ
. ម្ល៉ោះហើយ