Күрделі сандары бар қатар. Күрделі терминдері бар қатар. Күшті кешенді қатарлар
1. Күрделі сандар. Күрделі сандарформаның сандары деп аталады x+iy,Қайда XЖәне у -нақты сандар, мен-ойша бірлік,теңдігімен анықталады i 2 =-1.Нақты сандар XЖәне сағсәйкес деп аталады жарамдыЖәне ойдан шығарылған бөліктеркүрделі сан z.Олар үшін белгілер енгізіледі: x=Rez; y=imz.
Геометриялық тұрғыдан алғанда әрбір күрделі сан z=x+iyнүктемен бейнеленген M (x; y)координаталық жазықтық xOy(Cурет 26). Бұл жағдайда ұшақ Хойкүрделі сандар жазықтығы деп аталады, немесе күрделі айнымалы z жазықтығы.
Полярлық координаттар rЖәне φ ұпай М, z күрделі санының кескіні деп аталады модульЖәне аргументкүрделі сан z; олар үшін белгілер енгізіледі: r=|z|, φ=Argz.
Жазықтықтың әрбір нүктесі бір-бірінен 2kπ (k - оң немесе теріс бүтін сан) айырмашылығы бар полярлық бұрыштың шексіз санына сәйкес келетіндіктен, Arg - z-тің шексіз мәнді функциясы.
Полярлық бұрыштың мәндері φ , ол –π теңсіздігін қанағаттандырады< φ ≤ π деп аталады басты маңыздылығы z аргументі және arg z мәнін белгілеңіз.
Келесіде белгілеу φ z аргументінің негізгі мәні үшін ғана сақтаңыз , анау. қояйық φ =argz,аргументтің барлық басқа мәндері үшін zтеңдігін аламыз
Arg z = arg z + 2kπ =φ + 2kπ.
z комплекс санының модулі мен аргументі және оның нақты және жорамал бөліктері арасындағы қатынастар формулалар арқылы белгіленеді.
x = r cos φ; y = r sin φ.
Аргумент zформуласымен де анықтауға болады
arg z = arctg (y / x) + C,
Қайда МЕН= 0 кезінде x > 0, МЕН x үшін = +π<0, сағ> 0; C \u003d - π кезінде x < 0, сағ< 0.
Ауыстыру xЖәне сағкүрделі сандардың жазылуында z = x+iyарқылы олардың өрнектері rЖәне φ , деп аталатынды аламыз Комплекс санның тригонометриялық түрі:
Күрделі сандар z 1 \u003d x 1 + iy 1Және z 2 \u003d x 2 + iy 2қарастырылады теңегер олардың нақты және жорамал бөліктері бөлек тең болса ғана:
z1 = z2, Егер x 1 = x 2, y 1 = y 2 .
Тригонометриялық түрде берілген сандар үшін, егер осы сандардың модульдері тең болса және аргументтер 2π-ге бүтін еселікпен ерекшеленсе, теңдік орын алады:
z 1 = z 2,Егер |z 1 | = |z 2 |Және Arg z 1 = Arg z 2 +2kπ.
Екі күрделі сан z = x+iyжәне z = x -iyтең нақты және қарама-қарсы жорамал бөлшектер деп аталады конъюгацияланған.Жалғасатын күрделі сандар үшін қатынастар
|z 1 | = |z 2 |; arg z 1 = -arg z 2,
(соңғы теңдік формасын беруге болады Arg z 1 + Arg z 2 = 2kπ).
Комплекс сандарға амалдар келесі ережелермен анықталады.

Қосу. Егер z 1 \u003d x 1 + iy 1, z 2 \u003d x 2 + iy 2, Бұл
Күрделі сандарды қосу ауыспалы және ассоциативті заңдарға бағынады:
![]()
Алу. Егер , Бұл
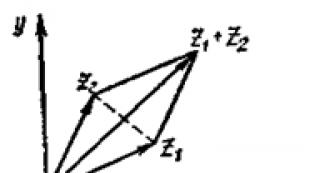
Күрделі сандарды қосу және азайтуды геометриялық түсіндіру үшін оларды жазықтықтағы нүктелер ретінде емес көрсету пайдалы. z,және векторлары: z саны = x + iyвектор арқылы берілген басы О нүктесінде (жазықтықтың «нөлдік» нүктесі – координаталар басы) және соңы нүктеде болады M(x; y).Содан кейін күрделі сандарды қосу және азайту векторларды қосу және азайту ережесі бойынша орындалады (27-сурет).
Векторларды қосу және алу амалдарының мұндай геометриялық интерпретациясы екінің қосындысы мен айырмасының модулі және теңсіздіктермен өрнектелген бірнеше күрделі сандардың қосындысы туралы теоремаларды орнатуды жеңілдетеді:
| |z 1 |-|z 2 | | ≤ |z 1 ±z 2 | ≤ |z 1 | + |z 2 | ,
Бұған қоса, мұны есте сақтау пайдалы екі күрделі санның айырмасының модулі z1 Және z2 z жазықтығында олардың кескіндері болып табылатын нүктелер арасындағы қашықтыққа тең:| |z 1 -z 2 |=d(z 1 ,z 2) .
Көбейту. Егер z 1 \u003d x 1 + iy 1, z 2 \u003d x 2 + iy 2. Бұл
z 1 z 2 \u003d (x 1 x 2 -y 1 y 2) + i (x 1 y 2 + x 2 y 1).
Осылайша, күрделі сандар биномдар ретінде көбейтіледі, i 2 саны -1-ге ауыстырылады.
ЕГЕР, онда
Осылайша, өнімнің модулі сомноэктелдердің модульдерінің көбейтіндісіне тең, ал туындының аргументі-факторлардың аргументтерінің қосындысы.Күрделі сандарды көбейту коммутативті, ассоциативті және дистрибутивтік (қосуға қатысты) заңдарға бағынады:
Бөлім.Алгебралық түрде берілген екі күрделі санның бөлімін табу үшін дивиденд пен бөлгішті бөлгішке қосылатын санға көбейту керек:

" Егер тригонометриялық түрде берілген, онда
Осылайша, Бөлімнің модулі дивиденд пен бөлгіштің модулінің бөліміне тең,А аргументжеке дивиденд пен бөлгіштің аргументтерінің айырмасына тең.
Экспоненциация. Егер z= , онда Ньютон биномдық формуласы бойынша
(Пнатурал сан); алынған өрнекте дәрежелерді ауыстыру қажет менолардың мағыналары:
i 2 \u003d -1; i 3 =i; i 4 =1; i 5 =1,…
және жалпы алғанда,
i 4k = 1; i 4k+1 =i; i 4k+2 = -1; i 4k+3 = -i .
Егер болса, онда
(Мұнда Поң бүтін немесе теріс бүтін сан болуы мүмкін).
Сондай-ақ,
(Де Мойвр формуласы).
Түбірді экстракциялау. Егер Пнатурал сан, онда күрделі санның n-ші түбірі zформула бойынша табылған n түрлі мәндері бар

мұндағы k=0, 1, 2, ..., n-1.
437.
(z 1 z 2)/z 3 болса, табыңыз z1 = 3 + 5i, z 2 = 2 + 3i, z 3 = 1+2i.
∆
438.
саны z= 2 + 5i.
∆ Комплекс санның модулін табыңыз: . Аргументтің негізгі мәнін табыңыз: . Сондықтан, ▲
439.
Комплексті тригонометриялық түрде көрсетіңіз
саны ![]()
∆ табу ![]() , ; , , яғни.
, ; , , яғни.
440.
Тригонометриялық формадағы комплексті көрсетіңіз
1, i, -1, -i сандары.
441.
Сандарды көрсету ,
,
тригонометриялық түрде, содан кейін күрделі санды табыңыз
z 1 /(z 2 z 3).
∆ табу
Демек,
442. Барлық мәндерді табыңыз.
∆ Комплекс санды тригонометриялық түрде жазамыз. Бізде бар , , . Демек,

Демек, , ,
443. Екілік теңдеуді шешіңіз ω 5 + 32i = 0.
∆ Теңдеуді түрдегі қайта жазайық ω 5 + 32i = 0. Сан -32iтригонометриялық түрде көрсетеді:
Егер k = 0содан кейін (A).
k=1,(B).
k=2,(С).
k=3,(D).
k=4,(Е).
Екі мүшелі теңдеудің түбірлері радиусы бар шеңберге сызылған дұрыс бесбұрыштың төбелеріне сәйкес келеді R=2бастапқыда орталықтандырылған (Cурет 28).
Жалпы, екімүшелі теңдеудің түбірлері ω n \u003d a,Қайда А-күрделі сан, регулярдың төбелеріне сәйкес n-гон центрі координат басында және радиусы ▲-ке тең шеңберге сызылған

444. Де Мойвр формуласын пайдаланып өрнектеңіз cos5φЖәне sin5 φарқылы cosφЖәне sinφ.
∆ Теңдіктің сол жағын Ньютон биномдық формуласы бойынша түрлендіреміз:
Теңдіктің нақты және қиял бөліктерін теңестіру қалады:
445. Күрделі сан берілген z=2-2i. Табу Rez, Imz, |z|, argz.
446. z = -12 + 5i.
447 . Моивр формуласы арқылы өрнекті есептеңіз (cos 2° + isin 2°) 45 .
448. Де Мойвр формуласы арқылы есептеңіз.
449. Комплекс санды тригонометриялық түрде көрсетіңіз
z = 1 + cos 20° + isin 20°.
450. Өрнекті бағалау (2 + 3i) 3 .
451.
Өрнекті бағалау 
452. Өрнекті бағалау
453. Комплекс санды тригонометриялық түрде көрсетіңіз 5-3i.
454. Комплекс санды тригонометриялық түрде көрсетіңіз -1 + i.
455.
Өрнекті бағалау 
456.
Өрнекті бағалау  тригонометриялық түрде алымдағы және бөлгіштегі көбейткіштерді бұрын ұсынған.
тригонометриялық түрде алымдағы және бөлгіштегі көбейткіштерді бұрын ұсынған.
457. Барлық мәндерді табыңыз
458.
Екілік теңдеуді шешіңіз ![]()
459. экспресс cos4φЖәне sin4φарқылы cosφЖәне sinφ.
460. Нүктелер арасындағы қашықтық екенін көрсетіңіз z1Және z2тең | z2-z1|.
∆ Бізде бар z 1 \u003d x 1 + iy 1, z 2 \u003d x 2 + iy 2, z 2 -z 1 \u003d (x 2 -x 1) + i (y 2 -y 1),қайда
анау. | z2-z1| берілген нүктелер арасындағы қашықтыққа тең. ▲
461. Қай түзу нүкте арқылы сипатталады z, мұндағы теңдеуді қанағаттандыру бірге-тұрақты комплекстік сан, ал R>0?
462.
Теңсіздіктердің геометриялық мағынасы қандай: 1) | z-c|
463. Теңсіздіктердің геометриялық мағынасы қандай: 1) Rez > 0; 2) мен з< 0 ?
2. Күрделі терминдер қатары. Күрделі сандардың тізбегін қарастырайық z 1 , z 2 , z 3 , ..., қайда z p \u003d x p + iy p (n \u003d 1, 2, 3, ...).тұрақты сан c = a + biшақырды шектеутізбектер z 1 , z 2 , z 3 , ..., егер кез келген ерікті аз сан үшін δ>0 саны бар N,мағынасы қандай z бсандармен n > Nтеңсіздікті қанағаттандырады \z n-бірге\< δ . Бұл жағдайда жазыңыз .
Күрделі сандар тізбегі шегінің болуының қажетті және жеткілікті шарты келесідей: сан c=a+biкүрделі сандар тізбегінің шегі болып табылады x 1 + iy 1, x 2 + iy 2, x 3 + iy 3, ...егер және тек егер,.
![]() (1)
(1)
мүшелері күрделі сандар деп аталады жинақтау,Егер nthүшін S n қатарының ішінара қосындысы n → ∞белгілі бір шекке ұмтылады. Әйтпесе, (1) қатары шақырылады дивергентті.
(1) қатар, егер нақты мүшелері бар қатарлар жинақталса ғана жинақталады
(2) Қатардың жинақтылығын зерттеңіз. Мүшелері шексіз кемімелі геометриялық прогрессияны құрайтын бұл қатар жинақталады; сондықтан күрделі мүшелері бар берілген қатар абсолютті жинақталады. ^

474. Қатардың жинақтылық ауданын табыңыз
19.4.1. Күрделі мүшелері бар сандық қатар.Жинақтаудың барлық негізгі анықтамалары, жинақты қатарлардың қасиеттері, күрделі қатарлардың жинақтылық критерийлері нақты жағдайдан ешқандай айырмашылығы жоқ.
19.4.1.1. Негізгі анықтамалар. Күрделі сандардың шексіз тізбегі берілсін z 1 , z 2 , z 3 , …, z n , … .Санның нақты бөлігі z n белгілейміз а n , ойдан шығарылған - б n
(анау. z n = а n + мен б n , n = 1, 2, 3, …).
Сандық қатар- жазба түрі.
Ішінарасомаларқатар: С 1 = z 1 , С 2 = z 1 + z 2 , С 3 = z 1 + z 2 + z 3 , С 4 = z 1 + z 2 + z 3 + z 4 , …,
С n = z 1 + z 2 + z 3 + … + z n , …
Анықтама.Егер шектеу болса С
үшін қатардың ішінара қосындыларының тізбегі  , бұл дұрыс күрделі сан, онда қатар жинақталады деп айтылады; саны С
қатардың қосындысын атаңыз және жазыңыз С
= z
1
+ z
2
+ z
3
+ … +
z
n
+ ... немесе
, бұл дұрыс күрделі сан, онда қатар жинақталады деп айтылады; саны С
қатардың қосындысын атаңыз және жазыңыз С
= z
1
+ z
2
+ z
3
+ … +
z
n
+ ... немесе  .
.
Жартылай қосындылардың нақты және жорамал бөліктерін табыңыз:
С n = z 1 + z 2 + z 3 + … + z n = (а 1 + мен б 1) + (а 2 + мен б 2) + (а 3 + мен б 3) + … + (а n + мен б n ) = (а 1 + а 2 + а 3 +…+ а n ) +
Мұндағы символдар  Және
Және  жартылай қосындының нақты және жорамал бөліктері көрсетіледі. Сандық реттілік оның нақты және жорамал бөліктерінен тұратын тізбектер жинақталған жағдайда ғана жинақталады. Осылайша, күрделі мүшелері бар қатар оның нақты және жорамал бөліктері арқылы құрылған қатар жинақталған жағдайда ғана жинақталады. Күрделі мүшелері бар қатарлардың жинақтылығын зерттеу әдістерінің бірі осы бекітуге негізделген.
жартылай қосындының нақты және жорамал бөліктері көрсетіледі. Сандық реттілік оның нақты және жорамал бөліктерінен тұратын тізбектер жинақталған жағдайда ғана жинақталады. Осылайша, күрделі мүшелері бар қатар оның нақты және жорамал бөліктері арқылы құрылған қатар жинақталған жағдайда ғана жинақталады. Күрделі мүшелері бар қатарлардың жинақтылығын зерттеу әдістерінің бірі осы бекітуге негізделген.
Мысал.Жинақтау қатарын зерттеңіз  .
.
Өрнектің бірнеше мәндерін жазып көрейік  : келесі мәндер кезеңді түрде қайталанады. Нақты бөліктер саны: ; ойдан шығарылған бөліктер қатары ; екі қатар да жинақталады (шартты), сондықтан бастапқы қатар жинақталады.
: келесі мәндер кезеңді түрде қайталанады. Нақты бөліктер саны: ; ойдан шығарылған бөліктер қатары ; екі қатар да жинақталады (шартты), сондықтан бастапқы қатар жинақталады.
19.4.1.2. Абсолютті конвергенция.
Анықтама.Қатар  шақырды абсолютті конвергенттіегер қатар жинақталса
шақырды абсолютті конвергенттіегер қатар жинақталса  , оның мүшелерінің абсолютті мәндерінен тұрады.
, оның мүшелерінің абсолютті мәндерінен тұрады.
Еркін мүшелері бар нақты сандық қатарлар сияқты, егер қатар жинақталатын болса, дәлелдеу оңай.  , онда қатар міндетті түрде жинақталады
, онда қатар міндетті түрде жинақталады  (
( , сондықтан қатардың нақты және елестетілген бөліктері арқылы құрылған қатар
, сондықтан қатардың нақты және елестетілген бөліктері арқылы құрылған қатар  , абсолютті жинақталады). Егер қатар
, абсолютті жинақталады). Егер қатар  жинақталады және қатар
жинақталады және қатар  алшақтайды, содан кейін қатар
алшақтайды, содан кейін қатар  шартты конвергентті деп аталады.
шартты конвергентті деп аталады.
Қатар  теріс емес мүшелері бар қатар болып табылады, сондықтан оның жинақтылығын зерттеу үшін барлық белгілі белгілерді (салыстыру теоремаларынан Коши интегралдық критерийіне дейін) пайдалануға болады.
теріс емес мүшелері бар қатар болып табылады, сондықтан оның жинақтылығын зерттеу үшін барлық белгілі белгілерді (салыстыру теоремаларынан Коши интегралдық критерийіне дейін) пайдалануға болады.
Мысал.Жинақтау қатарын зерттеңіз  .
.
Модульдер сериясын жасайық ():  . Бұл қатар жинақталады (Коши сынағы
. Бұл қатар жинақталады (Коши сынағы  ), сондықтан бастапқы қатар абсолютті жинақталады.
), сондықтан бастапқы қатар абсолютті жинақталады.
19.4. 1 . 3 . Жинақталған қатарлардың қасиеттері.Күрделі мүшелері бар жинақты қатарлар үшін нақты мүшелері бар қатарлардың барлық қасиеттері дұрыс:
Қатар жинақтылығының қажетті критерийі.
Жинақталған қатардың ортақ мүшесі ретінде нөлге ұмтылады
 .
.
Егер қатар жинақталса  , онда оның кез келген қалдығы жинақталады.Керісінше, қатардың кез келген қалдығы жинақталса, онда қатардың өзі жинақталады.
, онда оның кез келген қалдығы жинақталады.Керісінше, қатардың кез келген қалдығы жинақталса, онда қатардың өзі жинақталады.
Егер қатар жинақталса, одан кейінгі қалдығының қосындысыn
-ші мүшесі нөлге ұмтылады
 .
.
Жинақтаушы қатардың барлық мүшелері бірдей санға көбейтілсебірге , онда қатардың жинақтылығы сақталады, ал қосынды көбейтіледібірге .
Жинақталған жолдар (А
) Және (IN
) мүшені мүше бойынша қосуға және азайтуға болады; алынған қатар да жинақталады және оның қосындысы тең болады
 .
.
Егер жинақтаушы қатардың мүшелері ерікті түрде топтастырылса және жақшаның әрбір жұбындағы мүшелердің қосындыларынан жаңа қатар жасалса, онда бұл жаңа қатар да жинақталады және оның қосындысы бастапқы қатардың қосындысына тең болады. .
Егер қатар абсолютті жинақталса, онда оның мүшелерінің кез келген ауыстыруы үшін жинақтылық сақталады және қосынды өзгермейді.
Егер жолдар (А
) Және (IN
) олардың қосындыларына абсолютті жинақталады
 Және
Және
 , онда олардың ерікті мүшелер реті үшін көбейтіндісі де абсолютті жинақталады және оның қосындысы тең
, онда олардың ерікті мүшелер реті үшін көбейтіндісі де абсолютті жинақталады және оның қосындысы тең
 .
.
Көру белгісі В 1 + В 2 +…+ В n +…= (1), Қайда В n = u n + мен· v n (n = 1, 2, …) күрделі сандар (комплекс сандар тізбегі) деп аталады күрделі сандарға жақын.
Сандар В n (n = 1, 2, …) шақырды санның мүшелері, мүше В nшақырды қатардың ортақ мүшесі.
Сандарды теріңіз С n = В 1 + В 2 +…+ В n (2) (n = 1, 2, …) , деп аталады қатардың ішінара қосындылары (1).
Ақырлы немесе шексіз шек Стізбектер С nшақырды осы қатардың қосындысы.
Егер шектеу Сақырлы болса, онда қатар шақырылады жинақтау, егер шек шексіз болса немесе мүлде жоқ болса, онда қатар дивергентті.
Егер С(1) қатарларының қосындысын жазыңыз  .
.
Болсын  , А
, А  . Әлбетте σ
n =
u 1
+
u 2
+…+
u n ,
τ
n =
v 1
+
v 2
+…+
v n. Теңдікті қайдан білеміз
. Әлбетте σ
n =
u 1
+
u 2
+…+
u n ,
τ
n =
v 1
+
v 2
+…+
v n. Теңдікті қайдан білеміз
 (Сәрине) екі теңдікке тең
(Сәрине) екі теңдікке тең
 Және
Және
 . Демек, (1) қатардың жинақтылығы екі нақты қатардың жинақтылығына тең:
. Демек, (1) қатардың жинақтылығы екі нақты қатардың жинақтылығына тең:  Және
Және  . Сондықтан жинақталған сандық қатарлардың негізгі қасиеттері жинақталған күрделі қатарларға таралады.
. Сондықтан жинақталған сандық қатарлардың негізгі қасиеттері жинақталған күрделі қатарларға таралады.
Мысалы, күрделі қатарлар үшін Коши критерийі жарамды: (1) қатары, егер бар болса ғана жинақталады 
 , бұл барлығы үшінn
>
Нжәне кез келгенб= 1, 2, … теңсіздік.
, бұл барлығы үшінn
>
Нжәне кез келгенб= 1, 2, … теңсіздік.
Бұл критерий қатардың жинақтылығы үшін қажетті критерийді тікелей білдіреді: (1) қатарын жинақтау үшін оның ортақ мүшесі қажет және жеткіліктіВ n → 0 .
Жинақтаушы қатардың келесі қасиеттері дұрыс: жолдар болса
 Және
Және
 олардың сомасына жинақталадыСЖәнег, содан кейін жолдар
олардың сомасына жинақталадыСЖәнег, содан кейін жолдар
 Және
Және
 сомаларына сәйкесінше жинақталадыС
±
гжәне λС
.
сомаларына сәйкесінше жинақталадыС
±
гжәне λС
.
Күрделі сандардың абсолютті жинақты қатары.
Комплекс сандар қатары  (1) шақырылды абсолютті конвергенттіегер қатар жинақталса
(1) шақырылды абсолютті конвергенттіегер қатар жинақталса  (2).
(2).
Теорема.
Комплекс сандардың әрбір абсолютті жинақты қатары (1) жинақталады.
Дәлелдеу.
Әлбетте, бізге (1) қатар үшін қатарлардың жинақтылығының Коши критерийінің шарттары орындалатынын анықтау жеткілікті. Кез келгенін алыңыз  . (1) қатарларының абсолютті жинақтылығына байланысты (2) қатар жинақталады. Сондықтан, таңдалғандар үшін
. (1) қатарларының абсолютті жинақтылығына байланысты (2) қатар жинақталады. Сондықтан, таңдалғандар үшін 
 , бұл кез келген үшін n
>
НЖәне p=1,2,…теңсіздік қанағаттандырылады
, бұл кез келген үшін n
>
НЖәне p=1,2,…теңсіздік қанағаттандырылады  , Бірақ
, Бірақ 
 , және одан да көп, теңсіздік
, және одан да көп, теңсіздік  кез келген үшін n
>
НЖәне б=1,2,…
Демек, (1) қатар үшін күрделі қатардың жинақтылығының Коши критерийінің шарттары орындалады. Сондықтан (1) қатар жинақталады. Теорема дұрыс.
кез келген үшін n
>
НЖәне б=1,2,…
Демек, (1) қатар үшін күрделі қатардың жинақтылығының Коши критерийінің шарттары орындалады. Сондықтан (1) қатар жинақталады. Теорема дұрыс.
Теорема.
Күрделі сандар қатары үшін
 (1) абсолютті жинақтаушы, нақты қатардың абсолютті жинақталуы қажет және жеткілікті
(1) абсолютті жинақтаушы, нақты қатардың абсолютті жинақталуы қажет және жеткілікті
 (3) және
(3) және
 (4) , мұндаВ n
=
u n +
мен·
v n
(n
= 1, 2,…).
(4) , мұндаВ n
=
u n +
мен·
v n
(n
= 1, 2,…).
Дәлелдеу,
мынадай айқын теңсіздіктерге сүйенеді
 (5)
(5)
Қажеттілік.(1) қатар абсолютті жинақталсын, (3) және (4) қатарлары абсолютті жинақталатынын көрсетейік, яғни қатарлар жинақталады.  Және
Және  (6). (1) қатарларының абсолютті жинақтылығынан (2) қатар шығады.
(6). (1) қатарларының абсолютті жинақтылығынан (2) қатар шығады.  жинақталады, онда (5) теңсіздіктің сол жағының күшімен (6) қатар жинақталады, яғни (3) және (4) қатарлары абсолютті жинақталады.
жинақталады, онда (5) теңсіздіктің сол жағының күшімен (6) қатар жинақталады, яғни (3) және (4) қатарлары абсолютті жинақталады.
Адекваттылық.(3) және (4) қатарлары абсолютті жинақталсын, (1) қатардың да абсолютті жинақталатынын көрсетейік, яғни (2) қатары жинақталады. (3) және (4) қатарларының абсолютті жинақтылығынан (6) қатар жинақталатыны шығады, сондықтан қатарлар да жинақталады.  . Сондықтан (5) теңсіздіктің оң жағына байланысты (2) қатар жинақталады, яғни, (1) қатар абсолютті жинақталады.
. Сондықтан (5) теңсіздіктің оң жағына байланысты (2) қатар жинақталады, яғни, (1) қатар абсолютті жинақталады.
Сонымен, (1) күрделі қатардың абсолютті жинақтылығы (3) және (4) нақты сандар қатарларының абсолютті жинақтылығына тең. Сондықтан абсолютті жинақталған күрделі қатарлар нақты абсолютті жинақты сандық қатарлардың барлық негізгі қасиеттеріне бағынады. Атап айтқанда, абсолютті жинақталған күрделі қатар үшін оның мүшелерін ауыстыру туралы теорема жарамды, яғни, абсолютті жинақты қатардағы мүшелерді ауыстыру қатардың қосындысына әсер етпейді. Күрделі қатардың абсолютті жинақтылығын орнату үшін оң қатардың жинақтылығының кез келген критерийін қолдануға болады.
Коши белгісі.
(1) қатарында шек болсын
 , онда егерq
< 1 , то ряд (1) абсолютно сходится, если
q>1, содан кейін (1) қатары ажыратылады.
, онда егерq
< 1 , то ряд (1) абсолютно сходится, если
q>1, содан кейін (1) қатары ажыратылады.
Д'Аламбер белгісі.
Егер күрделі сандардың (1) қатары үшін шектеу болса
 , содан кейінq
< 1 этот ряд абсолютно сходится, а если
q> 1 болса, қатар алшақтайды.
, содан кейінq
< 1 этот ряд абсолютно сходится, а если
q> 1 болса, қатар алшақтайды.
Мысал.
Абсолютті жинақтылық қатарын зерттеңіз  , Мұнда
, Мұнда  .
.
Табайық
 . Әлбетте
. Әлбетте  =
=
 =
=
 . Сондықтан қатар абсолютті жинақты болады.
. Сондықтан қатар абсолютті жинақты болады.
Абсолютті жинақты қатарларды көбейтуге болады. Абсолют жинақты және жинақты қатардың көбейтіндісі жинақталады. Екі жинақтаушының көбейтіндісі ажыратылуы мүмкін.
Өлшемі: px
Әсерді келесі беттен бастау:
транскрипт
1 8 (S) тізбегінің күрделі сандар қатары S қатардың қосындысы деп аталады (46) a k қатары қатардың --ші қалдығы деп аталады (46) жинақталған k қатар S S r және lm r үшін сол ε > N, N: r< ε Для сходящегося ряда (46) необходимым и достаточным признаком его сходимости является критерий Коши: ряд (46) сходится тогда и только тогда, если ε >, N, N: a< ε p k k Необходимым условием сходимости ряда (46) является требование lm a Действительно, из сходимости ряда (46) следует, согласно критерию Коши, что ε >, N > бұл p үшін, одан S S шығады< ε Если сходится ряд ak k a (47) с действительными положительными членами, то очевидно, сходится и ряд (46), который в этом случае называется абсолютно сходящимся А для ряда (47) уже можно применить признаки Даламбера и Коши: ряд (47) сходится, если, начиная с a некоторого номера N соотношение l < a, N значит, сходится абсолютно ряд (46)), если a q <, N k ; и ряд (47) сходится (а,
2 9 Функциялар қатары және олардың қасиеттері Бірыңғай жинақтылық Вейерштрас теоремасы Бір мәнді функциялардың шексіз тізбегі ((Z)) күрделі жазықтықтың G облысында анықталсын Z ((Z)) U U түрінің өрнегі (48) функционалдық қатар деп аталады (48) қатары G облысында жинақталған деп аталады, егер Z G оған сәйкес сандар қатары жинақталса Егер (48) қатары G аймағында жинақталса, онда бұл аймақта бір-бірін анықтауға болады. G облысының әрбір нүктесіндегі мәні G аймағындағы сәйкес сандар қатарының (48) қосындысына тең болатын мәнді функция. Сонда G, > k () U k()< ε Заметим, что в общем случае N зависит и от ε и от Определение Если ε >, N(ε), N(ε): ε, N (ε,), N(ε,) : G k U k облысы< ε G, то ряд (48) называется равномерно сходящимся в k k Если остаток ряда обозначить r U, то тогда условие равномерной сходимости ряда (48) можем записать в виде: r < ε, N(ε), G Достаточным признаком равномерной сходимости ряда (48) является признак Вейерштрасса: Если всюду в области G члены функционального ряда (48) могут быть мажорированы членами некоторого абсолютно сходящегося числового ряда a, те
3 a U, G, (49) онда (48) қатар біркелкі жинақталады N Шынында, a қатары жинақталғандықтан, >< ε, U U a < ε при N, что и доказывает равномерную k k k k k k сходимость ряда (48) в области G Приведем некоторые теоремы о равномерно сходящихся рядах Они доказываются совершенно также, как соответствующие теоремы вещественного анализа и поэтому приведем их без доказательства Теорема 5 Если функции U непрерывны в области G, а ряд U сходится в этой области равномерно к функции, то также непрерывна в G Теорема 6 Если ряд (48) непрерывных функций U сходится равномерно в области G к функции, то интеграл от этой функции по любой кусочногладкой кривой, целиком лежащей в области G, можно вычислить путем почленного интегрирования ряда (48), те Теорема 7 Если члены d U d U сходящегося в области G ряда U имеют непрерывные производные в этой области и ряд U равномерно сходится в G, то данный ряд U можно почленно дифференцировать в области G, причем U U, где U - сумма ряда
4 Кешенді талдаудағы функционалдық қатарлар үшін нақты талдаудан белгілі функционалдық қатарды мүшелер бойынша дифференциалдау мүмкіндігі туралы теореманы айтарлықтай күшейтуге мүмкіндік беретін Вейерштрасс теоремасы бар.Оны айту және дәлелдеу алдында мынаны ескертеміз: l түзуінің бойымен біркелкі жинақталатын U қатары оның барлық мүшелерін l арқылы шектелген ϕ функциясына көбейткеннен кейін біркелкі қалатыны Шынында да, l түзуінде ϕ () теңсіздігі орындалсын.< M Тогда для остатков ρ и r рядов U и U ϕ справедливо соотношение ϕ U U r < M r ρ ϕ ε и, тк N, >Н:р< и одновременно с ним ρ < ε, то этим доказано M высказанное утверждение Если сумма данного ряда есть S, то сумма ряда, полученного после умножения на ϕ, очевидно будет ϕ S Теорема 8 (Вейерштрасса) Если члены ряда - аналитические в некоторой области G функции и этот ряд сходится в области G равномерно, то его сумма также является функцией аналитической в G, ряд можно почленно дифференцировать и полученный ряд F равномерно сходится к () F Выберем любую внутреннюю точку области G и построим круг столь малого радиуса с центром в этой точке, чтобы он целиком лежал внутри G (рис) В силу равномерной сходимости данного ряда в G, G ρ Рис он, в частности, равномерно сходится на окружности этого круга Пусть - любая точка на Умножим ряд () () () () () (5) на величину Полученный ряд
5 сонымен бірге оның қосындысына () () () () () жинақталады, өйткені (5) функциясы шектелген, өйткені бұл шеңбердің нүктелері үшін ρ шеңбердің радиусы (еске түсірейік: - мұнда тұрақты шама) Сонда , жоғарыда айтылғанға сәйкес, (5) қатарды мүшелер бойынша біріктіруге болады: () d () d () d d π π π π Функциялардың аналитикалық болуына байланысты оларға Коши формуласын қолдануға болады, негізінде оның () d π, (5) мәнін аламыз және (5) оң жағындағы қатардың қосындысы тең болады, демек, Tk нүктесінде π () d теңдігін аламыз - G облысының кез келген нүктесі, онда теореманың бірінші бөлігі дәлелденеді.қатар біркелкі жинақталатынын және оның қосындысы (k) (k) тең болатынын аламыз.
Дәрежелік қатар Абель теоремасы Жалпы функционалдық қатарлардың өте маңызды жағдайы дәрежелік қатарлар (), (53) - кейбір комплекс сандар және - күрделі жазықтықтың тұрақты нүктесі. қатар, алдыңғылардың жалпы теоремалары. қималарды қолдануға болады.Оларда анықталғандай, көптеген қасиеттер біркелкі жинақтылықтың салдары болып табылады.(53) дәрежелік қатардың жинақтылық облысын анықтау үшін келесі теорема маңызды болып шығады.9 теорема (Абель) Егер дәрежелік қатар (53) қандай да бір нүктеде жинақталады, содан кейін ол абсолютті және шартты қанағаттандыратын кез келген нүктеде, сонымен қатар шеңберде жинақталады.< ρ, радиусом ρ, меньшим < сходится равномерно, ряд Δ Выберем произвольную точку, удовлетворяющую условию < Обозначим q сходимости ряда следовательно M >, бұл M, q< В силу необходимого признака его члены стремятся к нулю при, отсюда () M M q M, Тогда, где q < (54) Ряд справа в (54) бесконечно убывающая геометрическая прогрессия со знаменателем q < Тогда из (54) следует сходимость и рассматриваемого ряда
7б< достаточно в силу признака Вейерштрасса (53) В круге построить сходящийся числовой ряд, можорирующий данный ряд в рассматриваемой области Очевидно, таковым является ряд ρ M, также представляющий собой сумму бесконечной геометрической прогрессии со знаменателем, меньшим единицы Из теоремы Абеля можно вывести ряд следствий, в известной мере аналогичным следствиям из теоремы Абеля в теории степенных рядов вещественного анализа Если степенной ряд (53) расходится в некоторой точке, то он расходится и во всех точках, удовлетворяющих неравенству >(53) қатары жинақталған нүктеден нүктеге дейінгі қашықтықтардың дәл жоғарғы шегі дәрежелік қатардың жинақтылық радиусы деп аталады, ал облыс.<, называется кругом сходимости степенного ряда В точках границы ряд может как сходиться так и расходиться Пример Найти область сходимости ряда Δ Находим радиус сходимости по признаку Даламбера lm () и наш ряд сходится в круге < При <, те, исследуется особо В этом случае и, значит, областью абсолютной сходимости является
8б< В круге любого радиуса ρ, меньшего чем радиус сходимости, степенной ряд (53) сходится равномерно 3 Внутри круга сходимости степенной ряд сходится к аналитической функции В самом деле, члены ряда u есть функции, аналитические на всей плоскости Z, ряд сходится в любой замкнутой подобласти круга сходимости Тогда по теореме Вейерштрасса сумма ряда есть аналитическая функция 4 Степенной ряд внутри круга сходимости можно почленно интегрировать и дифференцировать любое число раз, причем радиус сходимости полученных рядов равен радиусу сходимости исходного ряда 5 Коэффициенты степенного ряда (53) находятся по формулам! () () (55) Доказательство этого факта приводится методами, аналогичными методам вещественного анализа Ряд Тейлора Теорема Тейлора Нули аналитических функций Итак степенной ряд внутри круга сходимости определяет некоторую аналитическую функцию Возникает вопрос: можно ли функции, аналитической внутри некоторого круга, сопоставить степенной ряд, сходящийся в этом круге к данной функции? < Теорема 9 (Тейлора) Функция, аналитическая внутри круга, может быть представлена в этом круге сходящимся степенным рядом, причем этот ряд определен однозначно
9 ρ ρ шеңберінің ішіндегі ерікті нүктені таңдап алайық< и построим окружность ρ точке радиусом < с центром в ρ (рис), содержащую точку внутри Такое построение возможно для любой точки внутри этого круга Так как < ρ, а внутри круга < Рис аналитична, то по формуле Коши имеем π ρ () d (56) Преобразуем подынтегральное выражение: (57) <, то < Так как Поэтому второй сомножитель справа в (57) можно представить как сумму степенного ряда (прогрессии), ту которая первый член есть, а знаменатель прогрессии есть Так как, те () () (58) ρ, то ряд (58) сходится равномерно по, так как он мажорируется сходящимся числовым рядом Подставляя (58) в (56) и интегрируя почленно, получаем ρ (< ρ)
10 () d () ρ π () d () π ρ () белгілеуін енгізіп, (59) таңдалған нүктеде жинақталатын дәрежелік қатар ретінде қайта жазайық: (59) (6) () (6) Формуладағы (6), ρ төңірегін Коши теоремасының күшімен аймақта жатқан кез келген тұйық контурмен ауыстыруға болады.< и содержащим точку внутри Так как - произвольная точка данной области, то отсюда следует, что ряд (6) сходится к круге ρ < этот ряд сходится равномерно Итак, функция всюду внутри круга < аналитическая внутри круга <, причем в разлагается в этом круге в сходящийся степенной ряд Коэффициенты разложения (6) на основании формулы Коши для производных аналитической функции имеет вид () d () π ρ () ()! (6) Для доказательства единственности разложения (6) допустим, что имеет еще место формула разложения (), (6)
11 мұнда да бір коэффициент болады<, поэтому на основании формулы (55) Ряд (6) сходящимся в круге () () (6) Тем самым единственность определения коэффициентов доказана Разложение функции, аналитической в круге! <, что совпадает с, в сходящийся степенной ряд (6), часто называется разложением Тейлора, а сам ряд (6) Рядом Тейлора Доказанная теорема устанавливает взаимнооднозначное соответствие между функцией, аналитической в окрестности некоторой точки и степенным рядом с центром в этой точке, это означает эквивалентность конкретной аналитической функции, как функции бесконечное число раз дифференцируемой и функцией, представимой в виде суммы степенного ряда G и Заметим, наконец, что, если функция является аналитической в области G - внутренняя точка, то радиус сходимости ряда Тейлора () () () этой функции не меньше расстояния от точки до! границы области G (имеется в виду ближайшее расстояние) Пример Разложить в ряд Тейлора по степеням Δ Эта функция является аналитической на всей комплексной плоскости за исключением точек, Поэтому в круге < функция может быть ± разложена в ряд Тейлора При условии < выражение рассматриваться как сумма бесконечно убывающей прогрессии может q, q < Поэтому
12 , < Пример 3 Найти разложение в ряд Тейлора в круге < Определение по формуле (6) здесь довольно затруднительно Поэтому, представим π Так как < и <, то, используя геометрическую, получаем q q, Используя показательную форму чисел и находим окончательно 4 s π (63) Тк расстояние от центра разложения до ближайших особых точек (те до границы аналитичности) есть, то радиус сходимости ряда (63) есть Рис X Y
13 4 4 3 Мысал<, 4 3 < Ближайшей к центру разложения особой точкой является точка, до которой расстояние равно, поэтому В заключение приведем основные разложения: e (<)!! 3! cos! 4 3 4! ; (<)! ; s () m 3 3! 5 5! m m m!! (<) ()! ; m(m)(m)! ; l 3 3 () 4 (<) Если для аналитической функции (), то точка называется нулем аналитической функции В этом случае разложение функции в ряд Тейлора в окрестности точки имеет вид () () тк () Если в разложении функции окрестности точки и, следовательно, разложение имеет вид, в ряд Тейлора в,
14 онда () (), (64) нүктесі функцияның нөлі деп аталады. Егер, онда нөл ретті немесе еселік жай деп аталады Тейлор қатарының коэффициенттерінің формулаларынан, егер нүкте болатынын көреміз. ретінің нөлі, онда () () түрінде қайта жазуға болады, бірақ () () () [ () ] () ϕ, ϕ () (), () ϕ және жинақтылық шеңбері бұл қатар (64) сериясының қарама-қарсы мәлімдемесімен бірдей екені анық, мұнда пішіннің кез келген функциясы бүтін сан, ϕ () және реттік нөл нөлге тең және (±) 6-мысал Функция үшін нөл ретін табыңыз. 8 с Бөлгіштің дәрежесін кеңейтіңіз: 3 3! 8 5 5! ! 5! 3! 5 5! ϕ
15 5 ϕ, мұндағы ϕ, және ϕ және 3 функциясының нүктесі!, сондықтан 5 нүктесі! ϕ аналитикалық болып табылады - бастапқы Лоран қатары және оның жинақтылық облысы үшін 5-ші ретті нөл. Лоран қатарындағы аналитикалық функцияның ыдырауы () түріндегі қатарды қарастырайық, мұндағы күрделі жазықтықтың қозғалмайтын нүктесі, (65) Кейбір күрделі сандар.Оның жинақтылық ауданын белгілейік. Ол үшін (65) центрі қандай да бір радиусы бар нүктеде орналасқан пішінде көрсетеміз, атап айтқанда, ол нөлге немесе шексіздікке тең болуы мүмкін Шеңбердің ішінде жинақтау, бұл қатар күрделі айнымалының кейбір аналитикалық функциясына жинақталады, бұл (),< (67)
16 Айнымалылар қатарының жинақталу облысын анықтау үшін () () параметрін орнатыңыз. Сонда бұл қатар ауыстыруды орындайық пішінді қабылдайды - оның жинақтау шеңбері ішінде комплексі бар қандай да бір аналитикалық ϕ () функциясына жинақталатын қарапайым дәрежелік қатар. айнымалы Алынған дәрежелік қатардың жинақтылық радиусы r болсын Сонда ϕ,< r Возвращаясь к старой переменной и полагая ϕ () () (68), >r Бұдан шығатыны, қатардың жинақтылық облысы, r шеңберінен тыс аймақ, біз (69) () аламыз.<, то существует общая область сходимости этих рядов круговое кольцо r < <, в которой ряд (65) сходится к аналитической функции (), r < < (7) Так как ряды (67) и (68) являются обычными степенными рядами, то в указанной области функция обладает всеми свойствами суммы степенного ряда Это означает, что ряд Лорана сходится внутри своего кольца сходимости к некоторой функции, аналитической в данном кольце
17 Егер r > болса, онда (67) және (68) қатарларының жинақтылықтың ортақ облысы болмайды, осылайша бұл жағдайда (65) қатар ешбір жерде ешбір функцияға жинақталмайды. серия (7) және 7-мысал Кеңейту - серияның негізгі бөлігі (65) () a)< < ; б) >; V)< < называется правильной частью или в ряд Лорана в кольцах: Во всех кольцах функция регулярна (аналитична) и поэтому может быть представлена рядом Лорана (доказательство этого факта в следующем пункте) Перепишем функцию в виде а) Так как <, то второе слагаемое есть сумма убывающей геометрической прогрессии Поэтому () Здесь главная часть состоит из одного слагаемого < б) в этом случае, поэтому () 3
18 Бұл кеңейтімде тұрақты бөлік жоқ< в) Для случая < функцию также надо привести к сходящейся геометрической прогрессии, но со знаменателем Это даст: 3 Заметим, что в главной части этого разложения присутствует одно слагаемое Возникает вопрос: можно ли функции аналитической в некотором круговом кольце, сопоставить ряд Лорана, сходящийся к этой функции в данном кольце? На этот вопрос отвечает Теорема Функция, аналитическая в круговом кольце < <, однозначно представляется в этом кольце сходящимся рядом Лорана дробь На Рис 3 Δ Зафиксируем произвольную точку внутри данного кольца и контурами окружности и с центром в, радиусы которых удовлетворяют условиям < < < < < (рис 3) Согласно формуле Коши для многосвязной области имеем π () d () выполняется неравенство q, можно представить в виде d (7) Поэтому
19 (7) тармағында мүшелік интегралдауды жүзеге асырамыз, ол қатарлардың біркелкі жинақтылығының арқасында мүмкін болады, d π, (7) аламыз, мұндағы d π, (73) (7) π болады. π d d, (d үшін), (74) мұндағы d π (75) (75) интегралдау бағытын өзгертіп, аламыз
20 π () () d ()() d π, > (76) Дөңгелек сақинадағы (73) және (76) интегралдарының аналитикалық болуына байланысты< < в соответствии с теоремой Коши значения интегралов не изменятся при произвольной деформации контуров интегрирования в области аналитичности Это позволяет объединить формулы (73) и (76): π () d (), ±, ±, (77) где - произвольный замкнутый контур, лежащий в указанном кольце и содержащий точку внутри Возвратимся теперь к формуле (7), получим где коэффициенты () (), (78) () для всех определяются однообразной формулой (77) Так как - люба точка кольца < <, то отсюда следует, что ряд (78) сходится к внутри данного кольца причем в замкнутом кольце < < ряд сходится к равномерно Доказательство единственности разложения (78) опускаем Из полученных результатов следует, что областью сходимости ряда (78) Лорана является круговое кольцо < <, на границах которого имеется хотя бы по одной особой точке аналитической функции ряд (78), к которой сходится Замечание Формула (77) для определения коэффициентов разложения в ряд Лорана (78) не всегда практически удобна Поэтому часто прибегают к разложению рациональной дроби на простейшие с использованием геометрической прогрессии, а также используют разложение в ряд Тейлора элементарные функции Приведем примеры
21 8-мысал Лоран қатарын (дәрежесі барлар) Y Δ нүктесіндегі ()() нүктесіне жақын жерде кеңейтіңіз. Бұл жағдайда центрі нүктеде (4-сурет) орналасқан екі дөңгелек сақина саламыз: а) шеңбер « орталықсыз»< < ; Рис 4 X б) внешность круга >Ол осы сақиналардың әрқайсысында аналитикалық болып табылады және шекараларында ерекше нүктелер бар. Осы аймақтардың әрқайсысында өкілеттіктердегі функцияны кеңейтейік)< < ; ; [ () () () ] () < Этот ряд сходится, так как Так что ()() () () () (), ; >) Мұнда бізде 3 бар, () () () () () жинақты қатар, өйткені<
22 с Нәтижесінде ()() () () сол, 3, 3 9-мысал Лоран қатарындағы Δ функциясын нүктеге жақын жерде кеңейтіңіз Бізде:, s s s cos cos s s! cos 4 () () 3 4! 3! () 5! () (scos)!! 5
Тақырып Күрделі сандар қатары А түріндегі күрделі сандары бар k ak сандар қатарын қарастырайық, егер оның толық емес қосындыларының S тізбегі S a k k жинақталса, жиынтық деп аталады. Сонымен қатар, тізбектің шегі S
Тақырып Функционалды кешенді серия Анықтамасы. Егер k, N, N U k G бірден орындалса, G облысында жинақталады, онда қатар біркелкі деп аталады.Қатардың біркелкі жинақтылығының жеткілікті критерийі критерий болып табылады.
№37 ДӘРІС. Аналитикалық функциялар қатары. Дәрежелік қатардағы аналитикалық функцияның ыдырауы. Тейлор сериясы. Лоран қатары..Дәрежелік қатардағы аналитикалық функцияның кеңеюі.....Тейлор қатары.... 3.Аналитикалық қатардың кеңеюі.
Модуль Тақырыбы Функция қатарлары және қатарлары Тізбектер мен қатарлардың біркелкі жинақтылық қасиеттері Дәрежелік қатарлар Дәріс Функциялар тізбегі мен қатарларының анықтамалары Біркелкі
7-дәріс Тейлор және Лоран сериясы 7. Тейлор қатары Бұл бөлімде дәрежелік қатар және аналитикалық функция ұғымдары бір объектіні анықтайтынын көреміз: жинақтылықтың оң радиусы бар кез келген дәрежелік қатар.
Математикалық талдау Бөлім: Күрделі айнымалы функциялар теориясы Тақырыбы: Күрделі жазықтықтағы қатарлар Дәріс беруші Янушчик О.В. 217 9. Күрделі жазықтықтағы қатарлар 1. Сандық қатарлар реттілік болсын
5 Дәрежелік қатар 5 Дәрежелік қатар: анықтамасы, жинақтылық облысы (a + a) + a () + K + a () + K a) (, (5) түріндегі функция қатары сандар дәрежелік қатарлар деп аталады Сандар
Федералдық білім беру агенттігі Мәскеу мемлекеттік геодезия және картография университеті (MIIGAiK) ЖОҒАРЫ МАТЕМАТИКА курсы бойынша ӨЗІНДІК ЖҰМЫСТАРҒА АРНАЛҒАН ӘДІСТЕМЕЛІК НҰСҚАУЛАР МЕН ТАПСЫРМАЛАР
Функциялар қатары 7-8-дәрістер 1 Жинақталу облысы 1 Функциялары белгілі бір аралықта анықталған u () u () u () u (), 1 2 u () түріндегі қатар функционалды қатар деп аталады. Барлық нүктелердің жиынтығы
№38 ДӘРІС. Аналитикалық функцияның шексіздіктегі әрекеті. арнайы нүктелер. Функция қалдықтары..шексіздіктегі нүктенің маңайы.....Шексіздіктегі нүктенің маңайындағы Лоранның кеңеюі.... 3. Мінез
РЕСЕЙ ФЕДЕРАЦИЯСЫНЫҢ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ Н.И.Лобачевский атындағы Нижний Новгород мемлекеттік университеті Н.П.
Беларусь Республикасы Білім министрлігі Витебск мемлекеттік технологиялық университеті Тақырып. «Қатарлар» теориялық және қолданбалы математика кафедрасы. әзірлеген доц. Е.Б. Дунина. Негізгі
В.В. Жук, А.М. Камачкин 1 қуат сериясы. Жинақталу радиусы және жинақтылық интервалы. Конвергенцияның сипаты. Интеграция және дифференциация. 1.1 Жинақталу радиусы және жинақтылық интервалы. Функционалдық диапазон
Тақырып Лоран қатары және оның жинақтылық облысы. n C n n C n n n n C n n түріндегі қатарды қарастырайық, мұндағы күрделі жазықтықтың қозғалмайтын нүктесі, кейбір комплекс сандар. C n Бұл қатар Лоран сериясы деп аталады.
ДӘРІС N 7 .Күш
Математикалық талдау Бөлім: Сандық және функционалды қатар Тақырыбы: Дәрежелік қатар. Дәрежелік қатардағы функцияны кеңейту Оқытушы Рожкова С.В. 3 г 34. Қуат қатары
4 Аналитикалық функциялар қатары 4. Функционалдық тізбектер Ω C және f n болсын: Ω C. Функциялар тізбегі (f n ) f функциясына нүктелік жинақталады: Ω C, егер әрбір z Ω lim n f n(z) = f(z) болса.
Функционалдық қатар Функционалдық қатар оның қосындысы және функционалдық ауданы o нақты немесе күрделі сандардың Δ аймағында k (k 1) функцияларының тізбегі берілсін.
Дәрістерді доцент Мусина М.В.Дайындаған Анықтама Пішін өрнегі Сандық және функционалдық қатар Сандық қатар: негізгі ұғымдар (), мұндағы ол сандар қатары (немесе жай қатар) деп аталады Сандар, қатар мүшелері (тәуелді).
Сандық қатар Сандық тізбек Opr Сандық реттілік дегеніміз x натурал сандар жиынында анықталған сандық функция - x =, x =, x =, x =, тізбегінің ортақ мүшесі.
Ch Дәрежелік қатар a a a a a a a a () түріндегі қатар дәрежелік қатар деп аталады, мұндағы, a, тұрақтылар, қатардың коэффициенттері деп аталады.Кейде жалпы түрдегі дәрежелік қатар қарастырылады: a a (a) a () а) а (а) (), мұндағы
Дәріс 8 Сериялар және ерекше нүктелер. Лоран сериясы. Оқшауланған ерекше нүктелер. 6. Қатарлар және ерекше нүктелер 6.7. Лоран сериясының теоремасы (П. Лоран): f() функциясы r сақинасында аналитикалық болса< a < R r R то она может быть разложена
Федералдық білім беру агенттігі Жоғары кәсіби білім беру федералдық мемлекеттік оқу орны ОҢТҮСТІК ФЕДЕРАЛЫҚ УНИВЕРСИТЕТ Р.М.Гаврилова, Г.С.Костецкая әдістемелік
Тақырып 9 Дәрежелік қатарлар - бұл түрдегі функционалды қатар, ал сандар ... қатардың коэффициенттері және қатардың кеңею нүктесі., ..., ... R ... деп аталады. орталық Қуат қатары Дәрежелік қатардың жалпы мүшесі
4 Функциялар қатары 4 Негізгі анықтамалар Жалпы облысы X u), u (), K, u (),K (АНҚАУ Өрнегі u) + u () + K + u () + болатын шексіз функциялар тізбегі болсын.
Дәріс 3 Тейлор және Маклаурин сериялары Дәрежелік қатарларды қолдану Функцияларды дәрежелік қатарларға кеңейту Тейлор және Маклаурин қатарлары Қолданбалар үшін берілген функцияны дәрежелік қатарға кеңейте алу маңызды, сол функциялар
Дәріс 6 Функцияның дәрежелік қатардағы кеңеюі Кеңейтудің бірегейлігі Тейлор және Маклаурин қатарлары Кейбір элементар функциялардың дәрежелік қатарындағы кеңейту Дәрежелік қатарларды қолдану Алдыңғы дәрістерде
Металлургия факультеті Жоғары математика кафедрасы
Лоран сериясы Дәрежелік қатардың жалпы түрі z z 0 оң және теріс дәрежесін қамтитын қатарлар болып табылады. Тейлор қатарлары сияқты олар аналитикалық функциялар теориясында маңызды рөл атқарады.
Серия Сандық қатар Жалпы ұғымдар Def Егер әрбір натурал санға белгілі бір заң бойынша белгілі бір сан берілсе, онда нөмірленген сандар жиыны сандық тізбек деп аталады,
S A Lavrenchenko wwwlwrecekoru Дәріс Функционалдық қатар Функционалдық қатар туралы түсінік Бұрын біз сандар қатарын зерттедік, яғни қатардың мүшелері сандар болды.Енді біз функционалдық қатарларды зерттеуге көшеміз, яғни.
Тақырып Лоран қатары және оның жинақтылық облысы. C (z z) n = C (z z) n + n n n= n= z жазықтықтың C n комплексінің қозғалмайтын нүктесі болатын түрдегі қатар Лоран қатары деп аталады. C n (z z) n= - кейбір комплекс
Дәріс. функционалдық қатарлар. Функция қатарының анықтамасы Мүшелері х-тің функциясы болатын қатар функционалдық қатар деп аталады: u = u (x) + u + K+ u + K = x-ке х-тің белгілі бір мәнін берсек, біз
СЕРИЯЛАР ТЕОРИЯСЫ Қатар теориясы математикалық талдаудың ең маңызды құрамдас бөлігі болып табылады және теориялық және көптеген практикалық қолданбаларды табады. Сандық және функционалды қатарды ажырату.
Конвергенция радиусы Анықтама. Дәрежелік қатар дегеніміз c 0 + c (t a) + c 2 (t a) 2 + + c (t a) + = c (t a), () түріндегі функционалды қатар, мұндағы c 0, c, c 2,.. ., с, ... С қуат коэффициенттері деп аталады
МӘСКЕУ МЕМЛЕКЕТТІК АЗАМАТТЫҚ АВИАЦИЯ ТЕХНИКАЛЫҚ УНИВЕРСИТЕТІ В.М. Любимов, Е.А. Жукова, В.А. Ухова, Ю.А. Шуринов
82 4. 4-бөлім. Функционалдық және қуат сериясы 4.2. 3-сабақ 4.2. 3-сабақ 4.2.. Функцияның Тейлор кеңеюі АНЫҚТАМА 4.2.. y = f(x) функциясы кейбір маңайда шексіз дифференциалданатын болсын.
Дәріс. Қуат қатары. Гармоникалық талдау; қатары және Фурье түрлендіруі. Ортогоналдық қасиеті.8. Жалпы функционалды қатар.8.. Функциялардан жалтару U + U + U қатары функционалды қатар деп аталады, егер оның
Старков В.Н. Кіріспе лекцияға арналған материалдар 9-сұрақ. Дәрежелік қатардағы аналитикалық функциялардың декомпозициясы Анықтама. (((... (..., мұнда күрделі тұрақтылар (қатар коэффициенттері.)) түріндегі функционалды қатар
Sgups Жоғары математика кафедрасы типтік есептеуді жүзеге асыру бойынша нұсқаулықтар «Жолдар» Новосибирск 006 Кейбір теориялық ақпарат Сандық сериялар Let u ; u ; u ; ; u ; шексіз сан бар
E кәсіп. Тейлор қатарлары. Дәрежелік қатардың қосындысы Mat. талдау, қолданба. Математика, 3 семестр Функцияның дәрежелердегі дәрежелік қатарға ұлғаюын табыңыз, дәрежелер қатарының жинақтылық радиусын есептеңіз: A f()
Тараулар қатары Белгілі бір сандық қатар мүшелерінің қосындысының формальды белгіленуі Сандық қатар сандық қатар деп аталады Қосындылар S қатардың ішінара қосындылары деп аталады. S шегі болса, S, онда қатар.
Тәжірибе 8 Қалдық 8 Қалдықты анықтау 8 Қалдықты есептеу 8 Логарифмдік қалдық 8 Қалдықты анықтау
~ ~ FCF Комплекс айнымалы функциясының туындысы Коши-Риман шартының FCF FCF заңдылығы туралы түсінік Комплекс санның кескіні және формасы FCF формасы: мұнда екі айнымалының нақты функциясы нақты болады.
ЖОҒАРЫ МАТЕМАТИКА КУРСЫ БОЙЫНША ЕСЕПТІК ТАПСЫРМАЛАРҒА АРНАЛҒАН ӘДІСТЕМЕЛІК НҰСҚАУЛЫҚ «ҚАРАПАЙДЫ ДИФФЕРЕНЦИАЛДЫҚ ТЕҢДЕЛЕР ТІРЛІГІ ҚОС ИНТЕГРАЛДАР» ІІІ БӨЛІМ ТАҚЫРЫП ТІРИЯЛАРЫ Мазмұны Сериялар Сандық қатарлар Жинақталу және дивергенция
Федералдық білім беру агенттігі Архангельск мемлекеттік техникалық университетінің құрылыс факультеті СЕРИЯСЫ Өзіндік жұмыс тапсырмаларын орындауға арналған нұсқаулар Архангельск қ.
КҮРДЕЛІ АЙНЫмалы Операциялық ЕСЕП ФУНКЦИЯЛАР ТЕОРИЯСЫНЫҢ ЭЛЕМЕНТТЕРІ
Математикалық талдау 3-бөлім. Сандық және функционалды қатар. Бірнеше интегралдар. Өріс теориясы. оқулық N.D.Vysk MATI-RGTU им. Қ.Е. Циолковский атындағы жоғары математика кафедрасы МАТЕМАТИКАЛЫҚ ТАЛДАУ
Дәріс 3. Дедукциялар. Негізгі қалдық теоремасы f () функциясының оқшауланған сингулярлық а нүктесіндегі қалдығы шеңбер бойымен i оң бағытта қабылданған f () 2 интегралының мәніне тең комплекс сан.
Сандық және дәрежелік қатарлар Сабақ. Сандық сызықтар. Жол сомасы. Жинақтау критерийлері.Қатар қосындысын есептеңіз. 6 Шешім. Шексіз геометриялық прогрессияның мүшелерінің қосындысы q, мұндағы q прогрессияның бөлгіші.
S A Lavrenchenko wwwlawreceoru Дәріс Функцияларды Тейлор сериясы бойынша бейнелеу Бір пайдалы шектеу Соңғы дәрісте келесі стратегия әзірленді: функцияның бейнеленуінің жеткілікті шарты бойынша,
М.В.Дейкалова КЕШЕНДІ ТАЛДАУ Емтихан сұрақтары (МХ-21, 215 топ) Бірінші коллоквиум сұрақтары 1 1. Күрделі айнымалы функцияның нүктедегі дифференциалдануы. Коши Риманның шарттары (Д'Аламбер Эйлер).
Варианттық тапсырма Функцияның мәнін есептеп, жауабын алгебралық түрде беріңіз: a sh ; b l Шешімі а Тригонометриялық синус пен гиперболалық синус арасындағы қатынас формуласын қолданайық: ; sh -s алыңыз
Дәріс Сандық қатар Жинақталу белгілері Сан қатары Жинақталу белгілері Шексіз мүшелерден тұратын + + + + сандық тізбегінің шексіз өрнегі сандық қатар деп аталады.
4. Функционалдық қатар, жинақтылық ауданы Функционалдық қатардың жинақтылық ауданы () - бұл қатар жинақталатын аргумент мәндерінің жиыны. (2) функциясы қатардың жартылай қосындысы деп аталады;
3-дәріс Скалярлық теңдеуді шешуге арналған бар болу және бірегейлік теоремасы Есептің қойылымы Негізгі нәтиже Коши есебін қарастырайық d f () d =, () =
РЕСЕЙ ФЕДЕРАЦИЯСЫ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ ҚАЗАН МЕМЛЕКЕТТІК АРХИТЕКТУРА ЖӘНЕ ҚҰРЫЛЫС УНИВЕРСИТЕТІ Жоғары математика кафедрасы САНДЫҚ-ФУНКЦИЯЛЫҚ СЕРИЯ
(функционалдық қатар дәрежелік қатар жинақтау облысы жинақтылық интервалын табу реті - мысал жинақтау интервалының радиус мысалдары) Функциялардың шексіз тізбегі берілсін, Функционалдық
С.А.Лавренченко wwwlawrecekoru Дәріс Функцияларды дәрежелік қатармен көрсету Кіріспе Функцияларды дәрежелік қатармен көрсету келесі есептерді шешуде пайдалы: - функцияларды интегралдау.
E кәсіп. Қуат қатары. Тейлор сериялы төсеніш. талдау, қолданба. Математика, 3 семестр Дәрежелік қатардың жинақтылық радиусын д'Аламбер критерийі арқылы табыңыз: (89 () n n (n!)) p (n +)! n= Тейлор қатары f(x)
РЕСЕЙ ФЕДЕРАЦИЯСЫНЫҢ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ
ЖОЛДАР. Сандық сызықтар. Негізгі анықтамалар Сандардың шексіз тізбегі берілсін Өрнегі (шексіз қосынды) a, a 2,..., a n,... a i = a + a 2 + + a n +... () i= a деп аталады. сандар қатары. Сандар
ҚАЗАН МЕМЛЕКЕТТІК УНИВЕРСИТЕТІ Математикалық статистика кафедрасы
Ресей Федерациясының Білім және ғылым министрлігі В.А.Волков ФУРЬЕР ИНТЕГРАЛЫНЫҢ СЕРИЯСЫ Оқу электронды мәтіндік басылымы 4865 Электроника және физикалық қондырғыларды автоматтандыру мамандықтарының студенттеріне арналған;
џ. Сандар қатары туралы түсінік. a, a 2,..., a,... сандар тізбегі берілсін.Сандар қатары a = a + a 2 +... + a +... (.) a, сандары, a 2,.. ., a,... қатар мүшелері деп аталады, а
Әдістемелік жұмыс TFKP бойынша есептер шығару Күрделі сандар Комплекс сандарға амалдар Күрделі жазықтық Комплекс санды алгебралық және тригонометриялық экспоненциалды түрде беруге болады.
Siberian Mathematical Journal Шілде тамыз, 2005. том 46, 4 УДК 517.53 ФУНКЦИЯЛАРДАН БӨЛІНГЕН ТҮЙІНДЕРДЕГІ ИНТЕРПОЛЯЦИЯЛЫҚ БӨЛШЕКТЕР ҮШІН ЖЫНЫНДАУ ШАРТТАРЫ АГ Липчинский Аннотация:
МӘСКЕУ МЕМЛЕКЕТТІК АВТОМОБИЛЬ ЖӘНЕ ЖОЛ ТЕХНИКАЛЫҚ УНИВЕРСИТЕТІ (МАДИ)
Стандартты әдістер, бірақ басқа мысалмен тұйыққа жетті.
Қандай қиындық бар және қай жерде кедергі болуы мүмкін? Сабынды арқанды бір жаққа қойып, себептерін байсалды түрде талдап, шешудің практикалық әдістерімен танысайық.
Бірінші және ең маңызды: жағдайлардың басым көпшілігінде қатардың конвергенциясын зерттеу үшін белгілі бір әдісті қолдану қажет, бірақ қатардың жалпы термині соншалықты күрделі толтыруға толы, онымен не істеу керектігі анық емес. . Ал сіз шеңбер бойымен айналасыз: бірінші белгі жұмыс істемейді, екіншісі жұмыс істемейді, үшінші, төртінші, бесінші әдіс жұмыс істемейді, содан кейін сызбалар бір жаққа тасталады және бәрі жаңадан басталады. Бұл әдетте тәжірибенің болмауына немесе есептеудің басқа бөлімдеріндегі олқылыққа байланысты. Атап айтқанда, егер жүгіру реттілік шектеулеріжәне үстірт бөлшектелген функция шектеулері, онда қиын болады.
Басқаша айтқанда, адам білімінің немесе тәжірибесінің жетіспеушілігінен қажетті шешімді көрмейді.
Кейде «тұтылу» да кінәлі, мысалы, қатардың конвергенциясының қажетті критерийі жай орындалмаса, бірақ білмеушілік, немқұрайлылық немесе немқұрайлылық салдарынан бұл көрінбейді. Математика профессоры жабайы қайталанатын тізбектер мен сандар қатарының көмегімен балалар мәселесін шешкен велосипедтегідей болды =)
Ең жақсы дәстүрлерде бірден өмір сүретін мысалдар: қатарлар ![]() және олардың туыстары - алшақтайды, өйткені бұл теорияда дәлелденді реттілік шектеулері. Сірә, бірінші семестрде 1-2-3 беттік дәлелдеме үшін жаныңыздан ұрып-соғуыңыз мүмкін, бірақ қазір сілтеме жасай отырып, серияның конвергенциясы үшін қажетті шарттың орындалмағанын көрсету жеткілікті. белгілі фактілерге. Атақты? Егер студент n-дәреженің түбірі өте күшті нәрсе екенін білмесе, онда, айталық, қатар
және олардың туыстары - алшақтайды, өйткені бұл теорияда дәлелденді реттілік шектеулері. Сірә, бірінші семестрде 1-2-3 беттік дәлелдеме үшін жаныңыздан ұрып-соғуыңыз мүмкін, бірақ қазір сілтеме жасай отырып, серияның конвергенциясы үшін қажетті шарттың орындалмағанын көрсету жеткілікті. белгілі фактілерге. Атақты? Егер студент n-дәреженің түбірі өте күшті нәрсе екенін білмесе, онда, айталық, қатар ![]() оны тығырыққа тіреді. Шешім екі және екі сияқты болса да: , яғни. анық себептерге байланысты екі қатар да алшақтайды. Қарапайым түсініктеме «бұл шектеулер теория жүзінде дәлелденді» (тіпті оның мүлдем жоқтығы да) өтеуге жеткілікті, өйткені есептеулер өте ауыр және олар сандық қатарлар бөліміне жатпайды.
оны тығырыққа тіреді. Шешім екі және екі сияқты болса да: , яғни. анық себептерге байланысты екі қатар да алшақтайды. Қарапайым түсініктеме «бұл шектеулер теория жүзінде дәлелденді» (тіпті оның мүлдем жоқтығы да) өтеуге жеткілікті, өйткені есептеулер өте ауыр және олар сандық қатарлар бөліміне жатпайды.
Келесі мысалдарды зерттегеннен кейін сіз көптеген шешімдердің қысқалығы мен ашықтығына таң қаласыз:
1-мысал
Қатардың жинақтылығын зерттеңіз
Шешім: ең алдымен орындалуын тексеріңіз конвергенцияның қажетті критерийі. Бұл формальдылық емес, «аз қантөгіс» мысалымен күресудің тамаша мүмкіндігі.
«Оқиғаны тексеру» дивергентті қатарды (жалпыланған гармоникалық қатардың жағдайы) ұсынады, бірақ қайтадан сұрақ туындайды, алымдағы логарифмді қалай ескеру керек?
Сабақтың соңындағы тапсырмалардың шамамен мысалдары.
Екі жақты (тіпті үш жақты) пайымдауды жүргізу қажет болғанда сирек емес:
6-мысал
Қатардың жинақтылығын зерттеңіз ![]()
Шешім: біріншіден, санауыштың бос сөзімен мұқият айналысыңыз. Кезектілік шектеулі: . Содан кейін: ![]()
Сериалдарымызды сериалдармен салыстырайық. Жаңа ғана алынған қос теңсіздіктің арқасында, барлық «en» үшін бұл дұрыс болады: ![]()
Енді қатарды дивергентті гармоникалық қатармен салыстырайық.
Бөлшек бөлгіш Аздаубөлшектің бөлімі, сондықтан бөлшектің өзі – Көбірекбөлшек (анық болмаса, алғашқы бірнеше мүшелерді жазыңыз). Осылайша, кез келген «en» үшін: ![]()
Сонымен, салыстыру үшін серия ![]() алшақтайдыгармоникалық қатармен бірге.
алшақтайдыгармоникалық қатармен бірге.
Егер бөлгішті аздап өзгертсек: ![]() , онда пайымдаудың бірінші бөлігі ұқсас болады:
, онда пайымдаудың бірінші бөлігі ұқсас болады: ![]() . Бірақ қатардың дивергенциясын дәлелдеу үшін салыстырудың шекті сынағы ғана қолданылады, өйткені теңсіздік жалған.
. Бірақ қатардың дивергенциясын дәлелдеу үшін салыстырудың шекті сынағы ғана қолданылады, өйткені теңсіздік жалған.
Жинақтаушы қатарларға қатысты жағдай «айна», яғни, мысалы, қатар үшін салыстыру критерийлерінің екеуі де (теңсіздік ақиқат), қатар үшін тек шектеу критерийі (теңсіздік жалған) қолданылуы мүмкін.
Біз саяхатымызды жабайы табиғат арқылы жалғастырамыз, онда әдемі және шырынды бөкендер көкжиекте көрінді:
7-мысал
Қатардың жинақтылығын зерттеңіз
Шешім: қажетті конвергенция критерийі қанағаттандырылды және біз қайтадан классикалық сұрақ қоямыз: не істеу керек? Біздің алдымызда конвергентті қатарға ұқсайтын нәрсе бар, дегенмен мұнда нақты ереже жоқ - мұндай ассоциациялар жиі алдамшы.
Жиі, бірақ бұл жолы емес. Көмегімен Шекті салыстыру критерийіҚатарымызды жинақты қатармен салыстырайық. Лимитті есептеу кезінде біз пайдаланамыз тамаша шек ![]() , қайда ретінде шексіз азстендтер:
, қайда ретінде шексіз азстендтер: 
жинақталадыжанында бірге.
«Үшке» көбейту мен бөлудің стандартты жасанды техникасын қолданудың орнына бастапқыда жинақты қатармен салыстыруға болады.
Бірақ бұл жерде жалпы терминнің тұрақты көбейткіші қатардың жинақтылығына әсер етпейтінін ескерген жөн. Дәл осы стильде келесі мысалдың шешімі жобаланған:
8-мысал
Қатардың жинақтылығын зерттеңіз
Сабақ соңында үлгі.
9-мысал
Қатардың жинақтылығын зерттеңіз
Шешім: алдыңғы мысалдарда біз синустың шектелгендігін пайдаландық, бірақ қазір бұл қасиет ойыннан тыс. Жоғары бөлшектің бөлгіші өсу ретіалымға қарағанда, сондықтан синус аргументі және бүкіл жалпы термин шексіз кішкентай. Конвергенцияның қажетті шарты, сіз түсінгеніңіздей, қанағаттандырылды, бұл бізге жұмыстан бас тартуға мүмкіндік бермейді.
Біз барлау жүргіземіз: сәйкес тамаша эквиваленттілік ![]() , ойша синусты тастап, сериясын алыңыз. Ал, осындай нәрсе ....
, ойша синусты тастап, сериясын алыңыз. Ал, осындай нәрсе ....
Шешім қабылдау:
Зерттелетін қатарды дивергентті қатармен салыстырайық . Біз шекті салыстыру критерийін қолданамыз: 
Шексіз азды баламасымен ауыстырайық: үшін ![]() .
.

Нөлден басқа шекті сан алынады, бұл зерттелетін қатарды білдіреді алшақтайдыгармоникалық қатармен бірге.
10-мысал
Қатардың жинақтылығын зерттеңіз
Бұл өз қолыңызбен жасалатын мысал.
Мұндай мысалдардағы келесі әрекеттерді жоспарлау үшін синусты, арксинусты, тангенсті, арктангенсті ойша қабылдамау көп көмектеседі. Бірақ есіңізде болсын, бұл мүмкіндік тек қашан болады шексіз азАргумент, жақында мен арандатушылық серияға тап болдым:
11-мысал
Қатардың жинақтылығын зерттеңіз ![]() .
.
Шешім: мұнда доғаның жанамасының шектеулілігін пайдалану пайдасыз, ал эквиваленттілік те жұмыс істемейді. Шығару таңқаларлық қарапайым: 
Оқу сериясы алшақтайды, өйткені қатардың жинақтылығының қажетті критерийі қанағаттандырылмаған.
Екінші себеп«Жұмыстағы гаг» техникалық сипаттағы қиындықтарды тудыратын қарапайым мүшенің лайықты талғампаздығынан тұрады. Дөрекі айтқанда, жоғарыда талқыланған сериялар «сіз болжаған сандар» санатына жататын болса, онда олар «сіз шешесіз» санатына жатады. Шын мәнінде, бұл «әдеттегі» мағынада күрделілік деп аталады. Саваннаның бірнеше факторларын, дәрежесін, тамырын және басқа тұрғындарын әркім дұрыс шеше алмайды. Әрине, факториалдар ең көп проблемаларды тудырады:
12-мысал
Қатардың жинақтылығын зерттеңіз
Факториалды қуатқа қалай көтеруге болады? Оңай. Өкілеттіктермен операциялар ережесіне сәйкес өнімнің әрбір факторын қуатқа дейін көтеру қажет:
Және, әрине, назар аудару және тағы бір рет назар аудару, д'Аламбер белгісінің өзі дәстүрлі түрде жұмыс істейді: 
Осылайша, зерттелетін сериялар жинақталады.
Мен сізге белгісіздікті жоюдың ұтымды техникасын еске саламын: ол түсінікті болған кезде өсу ретіалым және бөлгіш - бұл жақшаларды ашуға және азапқа салудың қажеті жоқ.
13-мысал
Қатардың жинақтылығын зерттеңіз
Жыртқыш өте сирек кездеседі, бірақ ол табылды және оны камера объективімен айналып өту әділетсіздік болар еді.
Қос леп белгісі факториалды деген не? Факториал оң жұп сандардың көбейтіндісін «желдейді»: 
Сол сияқты факториал оң тақ сандардың көбейтіндісін «орнатады»: 
Арасындағы айырмашылық неде екенін талдаңыз
14-мысал
Қатардың жинақтылығын зерттеңіз
Бұл тапсырмада дәрежелермен шатастырмауға тырысыңыз, тамаша эквиваленттерЖәне тамаша шектер.
Сабақтың соңындағы шешімдер мен жауаптардың үлгісі.
Бірақ студент тек жолбарыстарды ғана емес, қу барыстарды да тамақтандырады:
15-мысал
Қатардың жинақтылығын зерттеңіз ![]()
Шешім: конвергенцияның қажетті критерийі, шектеу критерийі, д'Аламбер және Коши критерийлері бірден жоғалады. Бірақ ең сорақысы, бізді қайта-қайта құтқарған теңсіздіктері бар ерекшелік дәрменсіз. Шынында да, дивергентті қатармен салыстыру мүмкін емес, өйткені теңсіздік ![]() дұрыс емес - көбейткіш-логарифм бөлшектің өзін азайтып, бөлгішті ғана арттырады
дұрыс емес - көбейткіш-логарифм бөлшектің өзін азайтып, бөлгішті ғана арттырады ![]() бөлшекке қатысты. Және тағы бір жаһандық сұрақ: неге біз бастапқыда біздің сериалымызға сенімдіміз?
бөлшекке қатысты. Және тағы бір жаһандық сұрақ: неге біз бастапқыда біздің сериалымызға сенімдіміз? ![]() дивергентті қатарлармен салыстыру керек пе? Ол мүлдем сәйкес келе ме?
дивергентті қатарлармен салыстыру керек пе? Ол мүлдем сәйкес келе ме?
Интегралдық қасиеті? Дұрыс емес интеграл ![]() мұңды көңіл-күйді тудырады. Енді, егер бізде қатар болса
мұңды көңіл-күйді тудырады. Енді, егер бізде қатар болса ![]() ... сосын иә. Тоқта! Идеялар осылай туады. Біз екі қадамда шешім қабылдаймыз:
... сосын иә. Тоқта! Идеялар осылай туады. Біз екі қадамда шешім қабылдаймыз:
1) Алдымен қатарлардың жинақтылығын зерттейміз ![]() . Біз қолданамыз интегралдық қасиеті:
. Біз қолданамыз интегралдық қасиеті:![]()
Интеграл үздіксізқосулы

Осылайша, сан ![]() сәйкес бұрыс интегралмен бірге ажырайды.
сәйкес бұрыс интегралмен бірге ажырайды.
2) Біздің қатарымызды дивергентті қатармен салыстырыңыз ![]() . Біз шекті салыстыру критерийін қолданамыз:
. Біз шекті салыстыру критерийін қолданамыз:
Нөлден басқа шекті сан алынады, бұл зерттелетін қатарды білдіреді алшақтайдықатарлас ![]() .
.
Және мұндай шешімде ерекше немесе шығармашылық ештеңе жоқ - осылайша шешім қабылдау керек!
Мен келесі екі қозғалысты өз бетінше жасауды ұсынамын:
16-мысал
Қатардың жинақтылығын зерттеңіз ![]()
Тәжірибесі бар студент көп жағдайда серияның жақындайтынын немесе ажырайтынын бірден көреді, бірақ жыртқыш бұталарда ептілікпен жасырынып қалады:
17-мысал
Қатардың жинақтылығын зерттеңіз ![]()
Шешім: бір қарағанда, бұл серияның өзін қалай ұстайтыны мүлдем анық емес. Ал егер алдымызда тұман болса, онда қатардың жинақталуына қажетті шартты өрескел тексеруден бастау қисынды. Белгісіздікті жою үшін біз батпайтынды қолданамыз Қосалқы өрнек арқылы көбейту және бөлу әдісі:
Қажетті конвергенция белгісі жұмыс істемеді, бірақ біздің тамбовтық жолдасымызды жарыққа шығарды. Орындалған түрлендірулер нәтижесінде эквивалентті қатар алынды ![]() , бұл өз кезегінде конвергентті қатарға қатты ұқсайды.
, бұл өз кезегінде конвергентті қатарға қатты ұқсайды.
Біз таза шешім жазамыз:
Осы қатарды жинақты қатармен салыстырыңыз. Біз шекті салыстыру критерийін қолданамыз:
Қосалқы өрнекке көбейту және бөлу:

Нөлден басқа шекті сан алынады, бұл зерттелетін қатарды білдіреді жинақталадыжанында бірге.
Мүмкін кейбіреулер біздің африкалық сафариде қасқырлар қайдан келді деген сұрақ туындауы мүмкін. Білмеймін. Олар әкелген шығар. Сіз келесі трофей терісін аласыз:
18-мысал
Қатардың жинақтылығын зерттеңіз ![]()
Сабақтың соңындағы шешімнің мысалы
Ақырында, көптеген студенттерді үмітсіздендіретін тағы бір ой: қатардың жинақтылығының сирек критерийін қолданудың орнына? Раабе белгісі, Абел белгісі, Гаусс белгісі, Дирихле белгісі және басқа да белгісіз жануарлар. Идея жұмыс істейді, бірақ нақты мысалдарда ол өте сирек жүзеге асырылады. Өз басым практиканың барлық жылдарында 2-3 рет қана жүгіндім Раабенің белгісістандартты арсеналдан ештеңе көмектеспеген кезде. Мен өзімнің экстремалды квестімнің барысын толығымен жаңғыртып отырмын:
19-мысал
Қатардың жинақтылығын зерттеңіз
Шешім: Сөзсіз д'Аламбердің белгісі. Есептеулер барысында мен дәрежелердің қасиеттерін белсенді түрде қолданамын, сонымен қатар екінші керемет шек:
Міне, сізге бір. Д'Аламбер белгісі жауап бермеді, бірақ мұндай нәтижені ештеңе алдын ала көрсетпесе де.
Нұсқаулықты қарап шыққаннан кейін мен теорияда дәлелденген аз белгілі шекті таптым және күштірек Коши критерийін қолдандым:
Міне, сізге екі. Және, ең бастысы, серияның жақындайтыны немесе ажырайтыны мүлдем анық емес (мен үшін өте сирек жағдай). Қажетті салыстыру белгісі? Көп үмітсіз - мен санаусыз жолмен алым мен бөлгіштің өсу ретін анықтасам да, бұл бәрібір сыйлыққа кепілдік бермейді.
Толық д'Аламбер, бірақ ең сорақысы, серияны шешу керек. Керек. Өйткені, бұл бірінші рет бас тартуым болады. Сосын бұдан да күшті белгілер бар сияқты екені есіме түсті. Менің алдымда енді қасқыр да, барыс та, жолбарыс та емес еді. Бұл үлкен діңін бұлғап тұрған үлкен піл болды. Маған гранатомет алуға тура келді:
Раабенің белгісі
Оң сандар қатарын қарастырайық.
Егер шектеу болса  , Бұл:
, Бұл:
а) қатарда алшақтайды. Сонымен қатар, алынған мән нөл немесе теріс болуы мүмкін.
б) қатарда жинақталады. Атап айтқанда, қатарлар үшін жинақталады.
в) Қашан Раабенің белгісі жауап бермейді.
Біз шекті құрастырамыз және бөлшекті мұқият жеңілдетеміз: 
Иә, сурет, жұмсақ айтқанда, жағымсыз, бірақ мен енді таң қалдым. жергілікті ережелер, ал бірінші ой, кейінірек белгілі болғандай, дұрыс болып шықты. Бірақ алдымен, шамамен бір сағат бойы мен «әдеттегі» әдістерді қолдана отырып, шегін бұрап, бұрдым, бірақ белгісіздік жойылғысы келмеді. Ал шеңберде жүру, тәжірибе көрсеткендей, шешімнің дұрыс таңдалмағанының әдеттегі белгісі.
Мен орыс халық даналығына жүгінуге тура келді: «Егер ештеңе көмектеспесе, нұсқауларды оқыңыз». Мен Фихтенгольцтың 2-ші томын ашқанда, үлкен қуанышқа орай, мен бірдей серияның зерттеуін таптым. Содан кейін шешім үлгіге сәйкес жүрді.