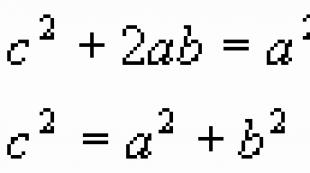Պյութագորասի թեորեմն ապացուցելու տարբեր եղանակներ՝ օրինակներ, նկարագրություն և ակնարկներ։ Անկախ խնդիրների լուծում

Դասարան: 8

Դասի նպատակները.

• Ուսումնական:հասնել Պյութագորասի թեորեմի յուրացմանը, ուղղանկյուն եռանկյունի անհայտ կողմի հաշվարկման հմտությունները սերմանել՝ օգտագործելով երկու հայտնիները, սովորեցնել, թե ինչպես կիրառել Պյութագորասի թեորեմը պարզ խնդիրներ լուծելու համար։
• Զարգացող:նպաստել համեմատելու, դիտարկելու, ուշադրության, վերլուծական և սինթետիկ մտածողության ունակության զարգացմանը, հորիզոնների ընդլայնմանը.
• Ուսումնական:գիտելիքների անհրաժեշտության ձևավորում, մաթեմատիկայի նկատմամբ հետաքրքրություն

Դասի տեսակը:նոր նյութի ներկայացման դաս

Սարքավորումներ:համակարգիչ, մուլտիմեդիա պրոյեկտոր, պրեզենտացիա դասի համար ( Հավելված 1)

Դասի պլան:

1. Կազմակերպման ժամանակ
2. բանավոր վարժություններ
3. Հետազոտական ​​աշխատանք՝ առաջ քաշելով վարկած և փորձարկել այն առանձին դեպքերում
4. Նոր նյութի բացատրություն
   ա) Պյութագորասի մասին
   բ) թեորեմի հայտարարություն և ապացույց
5. Վերոնշյալի համախմբում խնդրի լուծման միջոցով
6. Տնային աշխատանք, դասի ամփոփում.

Դասերի ժամանակ

Սլայդ 2: Կատարեք վարժությունները

1. Ընդարձակեք փակագծերը՝ (3 + x) 2
2. Հաշվեք 3 2 + x 2 x = 1, 2, 3, 4 համար
   – Կա՞ բնական թիվ, որի քառակուսին 10, 13, 18, 25 է:
3. Գտե՛ք 11 սմ, 50 սմ, 7 դմ կողմերով քառակուսու մակերեսը։
   Ո՞րն է քառակուսու մակերեսի բանաձևը:
   Ինչպե՞ս գտնել ուղղանկյուն եռանկյան մակերեսը:

Սլայդ 3: Հարցի պատասխան

– Անկյուն, որի չափը 90° է: (Ուղիղ)

Եռանկյան ուղիղ անկյան հակառակ կողմը: (Հիպոթենուզ)

- Եռանկյուն, քառակուսի, տրապեզիա, շրջան - սրանք երկրաչափական ... (ձևեր)

- Ուղղանկյուն եռանկյան փոքր կողմը: (Քաթեթ)

- Մի կետից բխող երկու ճառագայթներից կազմված գործիչ: (ներարկում)

- Եռանկյան գագաթից դեպի հակառակ կողմը պարունակող ուղիղը գծված ուղղահայաց հատված: (բարձրություն)

- Երկու հավասար կողմերով եռանկյուն . (Isosceles)

Սլայդ 4: Առաջադրանք

Կառուցեք 3 սմ, 4 սմ և 6 սմ կողմերով ուղղանկյուն եռանկյուն:

Առաջադրանքը բաժանված է տողերի.

	1 շարք	2 շարք	3 շարք
ոտքը ա	3	3
ոտքը բ	4		4
Հիպոթենուզա հետ		6	6

Հարցեր.

- Ինչ-որ մեկը ստացե՞լ է տրված կողմերով եռանկյունի:

- Ի՞նչ եզրակացություն կարող է լինել։ (Ուղղանկյուն եռանկյունը չի կարող կամայականորեն սահմանվել: Նրա կողմերի միջև կախվածություն կա):

- Չափեք ստացված կողմերը: ( Յուրաքանչյուր տողից մոտավոր միջին արդյունքը մուտքագրվում է աղյուսակում)

	1 շարք	2 շարք	3 շարք
ոտքը ա	3	3	~4,5
ոտքը բ	4	~5,2	4
Հիպոթենուզա հետ	~5	6	6

- Փորձեք հարաբերություններ հաստատել ոտքերի և հիպոթենուսի միջև յուրաքանչյուր դեպքում:

(Առաջարկվում է վերհիշել բանավոր վարժությունները և ստուգել նույն հարաբերությունները այլ թվերի միջև):

-Ուշադրություն է հրավիրվում այն ​​փաստի վրա, որ ստույգ արդյունքը չի ստացվի, քանի որ. չափումները չեն կարող ճշգրիտ համարվել:

Ուսուցիչը գուշակություններ է խնդրում (վարկածներ)Ուսանողները ձևակերպում են.

-Այո, իսկապես, հիպոթենուսի և ոտքերի միջև կապ կա, և առաջինը դա ապացուցեց գիտնականը, ում անունը դուք ինքներդ կնշեք։ Այս թեորեմը կոչվում է նրա անունով։

Սլայդ 5: Վերծանել

Սլայդ 6: Պյութագորաս Սամոսից

Ո՞վ կանվանի այսօրվա դասի թեման:

Ուսանողները նոթատետրերում գրում են դասի թեման՝ «Պյութագորասի թեորեմ»

Պյութագորասի թեորեմը երկրաչափության հիմնական թեորեմներից է։ Նրա օգնությամբ ապացուցվում են բազմաթիվ այլ թեորեմներ և լուծվում խնդիրներ տարբեր ոլորտներից՝ ֆիզիկա, աստղագիտություն, շինարարություն և այլն։ Դա հայտնի էր Պյութագորասի ապացուցումից շատ առաջ։ Հին եգիպտացիներն այն օգտագործում էին 3, 4 և 5 միավորների կողերով ուղղանկյուն եռանկյունի կառուցելիս՝ օգտագործելով պարան՝ շենքեր, բուրգեր դնելիս ուղիղ անկյուններ կառուցելու համար: Հետեւաբար, նման եռանկյունը կոչվում է Եգիպտական ​​եռանկյուն.

Այս թեորեմն ապացուցելու ավելի քան երեք հարյուր եղանակ կա: Մենք այսօր կանդրադառնանք դրանցից մեկին:

Սլայդ 7: Պյութագորասի թեորեմ

Թեորեմ. Ուղղանկյուն եռանկյունում հիպոթենուսի քառակուսին հավասար է ոտքերի քառակուսիների գումարին:

Տրված է.

Ուղղանկյուն եռանկյուն,

a, b - ոտքեր, հետ- հիպոթենուզա

Ապացուցել.

Ապացույց.

1. Շարունակում ենք ուղղանկյուն եռանկյան ոտքերը՝ ոտք ա- երկարության համար բ, ոտք բ- երկարության համար ա.

Ի՞նչ ձևով կարելի է կառուցել եռանկյունին: Ինչու մինչև քառակուսի: Ո՞րն է լինելու հրապարակի կողմը:

2. Եռանկյունը լրացնում ենք մի կողմ ունեցող քառակուսի ա + բ.

Ինչպե՞ս կարող եք գտնել այս հրապարակի տարածքը:

3. Հրապարակի մակերեսը կազմում է

- Քառակուսին բաժանենք մասերի` 4 եռանկյունի և գ կողմով քառակուսի:

Այլապես ինչպե՞ս կարող եք գտնել բնօրինակ հրապարակի տարածքը:

Ինչու՞ են ստացված ուղղանկյուն եռանկյունները համահունչ:

4. Մյուս կողմից,

5. Ստացված հավասարությունները հավասարեցրե՛ք.

Թեորեմն ապացուցված է.

Այս թեորեմի կատակերգական ձևակերպում կա. «Պյութագորասյան շալվարները բոլոր ուղղություններով հավասար են»: Հավանաբար, նման ձևակերպումը պայմանավորված է նրանով, որ այս թեորեմն ի սկզբանե հաստատվել է հավասարաչափ ուղղանկյուն եռանկյունու համար։ Ավելին, այն հնչում էր մի փոքր այլ կերպ. «Ուղղանկյուն եռանկյան հիպոթենուսի վրա կառուցված քառակուսու մակերեսը հավասար է նրա ոտքերի վրա կառուցված քառակուսիների տարածքների գումարին»:

Սլայդ 8: Պյութագորասի թեորեմի մեկ այլ ձևակերպում

Եվ ես ձեզ կտամ այս թեորեմի մեկ այլ ձևակերպում հատվածում.

Եթե ​​մեզ տրվի եռանկյուն
Եվ ավելին, ուղիղ անկյան տակ,
Դա հիպոթենուսի քառակուսին է
Մենք միշտ կարող ենք հեշտությամբ գտնել.
Մենք ոտքերը կառուցում ենք քառակուսու մեջ,
Մենք գտնում ենք աստիճանների գումարը
Եվ այսպես պարզ ձևով
Մենք կգանք արդյունքի։

-Այսպես, այսօր դուք ծանոթացաք պլանաչափության ամենահայտնի թեորեմին՝ Պյութագորասի թեորեմին։ Ինչպե՞ս է ձևակերպվում Պյութագորասի թեորեմը: Ուրիշ ինչպե՞ս կարելի է այն ձևակերպել։

Նյութի առաջնային ամրացում

Սլայդ 9: Խնդիրների լուծում ըստ պատրաստի գծագրերի.

Սլայդ 10: Խնդիրների լուծում նոթատետրում

Խնդիրները լուծելու համար խորհրդի մոտ միաժամանակ կանչվում են երեք աշակերտ:

Սլայդ 11: 12-րդ դարի հնդիկ մաթեմատիկոս Բհասկարայի խնդիրը

Ամփոփելով դասը.

Ի՞նչ նոր սովորեցիք այսօրվա դասին:

- Ձևակերպե՛ք Պյութագորասի թեորեմը.

-Ի՞նչ սովորեցիր անել դասին:

Տնային աշխատանք:

- Իմացեք Պյութագորասի թեորեմը ապացույցներով

- առաջադրանքներ թիվ 483 դասագրքից գ, դ; Թիվ 484 քաղ

– Ավելի առաջադեմ ուսանողների համար՝ գտե՛ք Պյութագորասի թեորեմի այլ ապացույցներ, սովորե՛ք դրանցից մեկը:

Գնահատվում է ամբողջ դասարանի աշխատանքը՝ առանձնացնելով առանձին սովորողներին:

Դաս «Պյութագորասի թեորեմ» թեմայով.

Դասի տեսակը՝ դաս սովորելու նոր նյութ։ (ըստ «Երկրաչափություն, 7–9» դասագրքի, ուսումնական հաստատությունների դասագիրք; Լ.Ս. Աթանասյան և այլք - 12-րդ հրատ. - Մ .: Կրթություն, 2009 թ.):

Թիրախ:

ուսանողներին ծանոթացնել Պյութագորասի թեորեմին և այս թեորեմի հետ կապված պատմական տեղեկատվությանը. զարգացնել հետաքրքրությունը մաթեմատիկայի ուսումնասիրության, տրամաբանական մտածողության նկատմամբ. Ուշադրություն.

Դասերի ընթացքում.

1. Կազմակերպչական պահ.

ՍԼԱՅԴ 2 Հեքիաթ «Տուն».

Մեր դասի թեման է «Պյութագորասի թեորեմը»։ Այսօր դասի ընթացքում կծանոթանանք Պյութագորասի կենսագրությանը, կուսումնասիրենք հնության ամենահայտնի երկրաչափական թեորեմներից մեկը, որը կոչվում է Պյութագորասի թեորեմ՝ պլանաչափության հիմնական թեորեմներից մեկը։

2. Գիտելիքների ակտուալացում.(Նոր նյութի ուսումնասիրության նախապատրաստումը, թեորեմի ապացուցման համար անհրաժեշտ նյութը կրկնվում է)

1) Հարցեր.

Ո՞ր քառանկյունն է կոչվում քառակուսի:

Ինչպե՞ս գտնել քառակուսու մակերեսը:

Ո՞ր եռանկյունն է կոչվում ուղղանկյուն եռանկյուն:

Ինչպե՞ս են կոչվում ուղղանկյուն եռանկյան կողմերը:

Ինչպե՞ս գտնել ուղղանկյուն եռանկյան մակերեսը:

3. Նոր նյութի ուսուցում.

1) Պատմության տեղեկանք.

ՍԼԱՅԴ 3 և 4.

Մեծ գիտնական Պյութագորասը ծնվել է մոտ 570 մ.թ.ա. Սամոս կղզում. Պյութագորասի հայրը Մնեսարքոսն էր՝ գոհար քանդակող։ Պյութագորասի մոր անունը անհայտ է։ Բազմաթիվ հին վկայությունների համաձայն՝ ծնված տղան առասպելական գեղեցիկ էր և շուտով ցույց տվեց իր ակնառու կարողությունները: Ինչպես ցանկացած հայր, Մնեսարկոսը երազում էր, որ որդին շարունակի իր գործը՝ ոսկեգործի արհեստը։ Կյանքն այլ կերպ էր դատում. Ապագա մեծ մաթեմատիկոսն ու փիլիսոփան արդեն մանկության տարիներին մեծ կարողություններ է ցուցաբերել գիտությունների համար։

Պյութագորասին վերագրվում է ամբողջ թվերի և համամասնությունների հատկությունների ուսումնասիրությունը, Պյութագորասի թեորեմն ապացուցելը և այլն: Պյութագորասը անուն չէ, այլ մականուն, որը փիլիսոփան ստացել է այն բանի համար, որ միշտ ճիշտ և համոզիչ է խոսում, ինչպես հունական օրակուլը: (Պյութագորաս - «համոզիչ խոսք»):

Իր ելույթներով նա ձեռք բերեց 2000 աշակերտ, որոնք ընտանիքներով կազմեցին դպրոց-պետություն, որտեղ գործում էին Պյութագորասի օրենքներն ու կանոնները։ Պյութագորասի դպրոցը կամ, ինչպես կոչվում է նաև Պյութագորաս միություն, միաժամանակ եղել է փիլիսոփայական դպրոց, քաղաքական կուսակցություն և կրոնական եղբայրություն։

Պյութագորասի սիրելի երկրաչափական պատկերը հնգագրամն էր, որը նաև կոչվում է Պյութագորաս աստղ։ Պյութագորասցիներն օգտագործում էին այս պատկերը՝ նկարելով այն ավազի մեջ՝ միմյանց ողջունելու և ճանաչելու համար: Պենտագրամը ծառայել է որպես նրանց գաղտնաբառ և եղել է առողջության և երջանկության խորհրդանիշ։

Ավանդույթն ասում է, որ երբ Պյութագորասը եկավ իր անունը կրող թեորեմին, աստվածներին բերեց 100 ցուլ: Ք.ա. 500 թվականին Պյութագորասը սպանվեց փողոցային կռվի ժամանակ ժողովրդական ապստամբության ժամանակ։ Ներկայումս Պյութագորասի թեորեմի շուրջ 200 ապացույց կա։

Թեորեմի հայտարարություն

2) Թեորեմի ապացույց.

Կառուցենք a + b կողմ ունեցող քառակուսու ուղղանկյուն:

Երեխաները ուսուցչի օգնությամբ ապացուցում են թեորեմը ըստ գծագրի, ապա ապացույցը գրում տետրում։

Ապացույց:

քառակուսի տարածք

- թեորեմն ապացուցված է.

4. Գիտելիքների առաջնային համախմբում.

Դասագրքային աշխատանք (Պյութագորասի թեորեմի կիրառումը խնդրի լուծման գործում).

Խնդիրները լուծվում են գրատախտակում և նոթատետրում:

Եզրակացություն. օգտագործելով Պյութագորասի թեորեմը, կարող եք լուծել երկու տեսակի խնդիր.

1. Գտե՛ք ուղղանկյուն եռանկյան հիպոթենուսը, եթե ոտքերը հայտնի են:

2. Գտեք ոտքը, եթե հիպոթենուսը և մյուս ոտքը հայտնի են:

.

5. Խնդիրների ինքնուրույն լուծում.

Թիվ 483 (բ), 484 (բ)

6. Տնային առաջադրանք. P 54, No 483 (d), 484 (d).

7. Դասի արդյունքը.

Ի՞նչ նոր սովորեցիք այսօրվա դասին:

Ո՞ր եռանկյունների համար է կիրառվում Պյութագորասի թեորեմը:

Ավարտեք դասը բանաստեղծությամբ.

Շատերը գիտեն Շամիսոյի սոնետը.

Ճշմարտությունը հավերժ կմնա, որքան շուտ

Թույլ մարդը դա կիմանա:

Իսկ հիմա Պյութագորասի թեորեմը

Վերնան, ինչպես իր հեռավոր տարիքում։

Զոհը առատ էր

Աստվածներ Պյութագորասից. Հարյուր ցուլ

Տվեց մորթին ու այրմանը

Լույսի հետևում մի ճառագայթ է, որը եկել է ամպերից:

Հետեւաբար, այն ժամանակվանից

Մի փոքր ճշմարտություն է ծնվում աշխարհում,

Ցուլերը մռնչում են՝ զգալով նրան, հետևելով նրան։

Նրանք չեն կարող կանգնեցնել լույսը

Եվ կարող են միայն փակել իրենց աչքերը դողալու համար

Վախից, որ Պյութագորասը սերմանել է նրանց մեջ։

Հարց - պատասխան Անկյուն, որի չափը 90 ° է ՈՒՂԻՂ Եռանկյան ուղիղ անկյան դիմաց գտնվող կողմը ՀԻՊՈՏԵՆՈՒՍ Եռանկյունը, քառակուսին, տրապեզոիդը, շրջանը երկրաչափական են ... ՆԿԱՐՆԵՐ Ուղղանկյուն եռանկյան փոքր կողմը ԿԱՏԵԹ Երկու ճառագայթներով կազմված պատկերը: մեկ կետ ԱՆԿՅՈՒՆ Եռանկյան գագաթից գծված ուղղահայաց հատված դեպի հակառակ կողմը պարունակող ուղիղը ԲԱՐՁՐՈՒԹՅՈՒՆ Եռանկյուն, որի երկու կողմերը հավասար են հավասարաչափ.

Պյութագորաս Սամոսացին (մոտ 580 - մոտ 500 մ.թ.ա.) Հին հույն մաթեմատիկոս և փիլիսոփա։ Ծնվել է Սամոս կղզում։ Նա կազմակերպեց իր սեփական դպրոցը՝ Պյութագորասի դպրոցը (Պյութագորասի միություն), որը միաժամանակ փիլիսոփայական դպրոց էր, քաղաքական կուսակցություն և կրոնական եղբայրություն։ Նա առաջինն էր, ով ապացուցեց հիպոթենուսի և ուղղանկյուն եռանկյունու ոտքերի կապը։

XII դարի հնդիկ մաթեմատիկոսի Բհասկարայի խնդիրը Գետի ափին միայնակ բարդի է աճել։ Հանկարծ քամու պոռթկումը կոտրեց նրա բեռնախցիկը։ Խեղճ բարդին ընկել է. Իսկ ուղիղ գծի անկյունը Գետի ընթացքի հետ նրա բունն էր։ Հիշեք հիմա, որ այս վայրում Բ գետը ընդամենը չորս ոտնաչափ լայնություն ուներ։ Գլուխը թեքվել էր գետի եզրին։ Բունից ընդամենը երեք ոտք է մնացել, աղաչում եմ, հիմա շուտ ասա՝ բարդին ինչքա՞ն բարձր է։

1

Շապովալովա Լ.Ա. (կայարան Եգորլիկսկայա, MBOU ESOSH No. 11)

1. Գլեյզեր Գ.Ի. Մաթեմատիկայի պատմություն դպրոցում VII - VIII դասարաններ, ուղեցույց ուսուցիչների համար, - Մ: Կրթություն, 1982 թ.

2. Դեմպան Ի.Յա., Վիլենկին Ն.Յա. «Մաթեմատիկայի դասագրքի էջերի հետևում» Ձեռնարկ 5-6-րդ դասարանների աշակերտների համար. - Մ.: Լուսավորություն, 1989:

3. Զենկևիչ Ի.Գ. «Մաթեմատիկայի գեղագիտության դաս». - Մ.: Լուսավորություն, 1981:

4. Լիցման Վ. Պյութագորասի թեորեմը. - Մ., 1960։

5. Վոլոշինով Ա.Վ. «Պյութագորաս». - Մ., 1993:

6. Պիչուրին Լ.Ֆ. «Հանրահաշվի դասագրքի էջերից այն կողմ». - Մ., 1990:

7. Զեմլյակով Ա.Ն. «Երկրաչափությունը 10-րդ դասարանում». - Մ., 1986:

8. Թերթ «Մաթեմատիկա» 17/1996 թ.

9. Թերթ «Մաթեմատիկա» 3/1997 թ.

10. Անտոնով Ն.Պ., Վիգոդսկի Մ.Յա., Նիկիտին Վ.Վ., Սանկին Ա.Ի. «Տարրական մաթեմատիկայի խնդիրների ժողովածու». - Մ., 1963։

11. Դորոֆեև Գ.Վ., Պոտապով Մ.Կ., Ռոզով Ն.Խ. «Մաթեմատիկական ձեռնարկ». - Մ., 1973:

12. Շչետնիկով Ա.Ի. «Պյութագորասի ուսմունքը թվի և մեծության մասին». - Նովոսիբիրսկ, 1997 թ.

13. «Իրական թվեր. Իռացիոնալ արտահայտություններ» 8-րդ դասարան. Տոմսկի համալսարանի հրատարակչություն. - Տոմսկ, 1997 թ.

14. Աթանասյան Մ.Ս. «Երկրաչափություն» 7-9 դասարան. - Մ.: Լուսավորություն, 1991:

15. URL՝ www.moypifagor.narod.ru/

16. URL՝ http://www.zaitseva-irina.ru/html/f1103454849.html:

Այս ուսումնական տարում ես ծանոթացա մի հետաքրքիր թեորեմի, որը հայտնի էր, ինչպես պարզվեց, հնագույն ժամանակներից.

«Ուղղանկյուն եռանկյան հիպոթենուսի վրա կառուցված քառակուսին հավասար է ոտքերի վրա կառուցված քառակուսիների գումարին»։

Սովորաբար այս հայտարարության հայտնաբերումը վերագրվում է հին հույն փիլիսոփա և մաթեմատիկոս Պյութագորասին (մ.թ.ա. VI դար): Բայց հին ձեռագրերի ուսումնասիրությունը ցույց տվեց, որ այս հայտարարությունը հայտնի էր Պյութագորասի ծնունդից շատ առաջ։

Հետաքրքրվեցի, թե այս դեպքում ինչու է դա կապված Պյութագորասի անվան հետ։

Թեմայի արդիականությունը. Պյութագորասի թեորեմը մեծ նշանակություն ունի. այն օգտագործվում է երկրաչափության մեջ բառացիորեն ամեն քայլափոխի։ Կարծում եմ, որ Պյութագորասի գործերը դեռևս արդիական են, քանի որ ուր էլ նայենք, ամենուր կարող ենք տեսնել նրա մեծ գաղափարների պտուղները՝ մարմնավորված ժամանակակից կյանքի տարբեր ճյուղերում։

Իմ հետազոտության նպատակն էր պարզել, թե ով է Պյութագորասը և ինչ առնչություն ունի այս թեորեմի հետ:

Ուսումնասիրելով թեորեմի պատմությունը՝ ես որոշեցի պարզել.

Կա՞ն այս թեորեմի այլ ապացույցներ:

Ի՞նչ նշանակություն ունի այս թեորեմը մարդկանց կյանքում։

Ի՞նչ դեր է խաղացել Պյութագորասը մաթեմատիկայի զարգացման գործում:

Պյութագորասի կենսագրությունից

Պյութագորաս Սամոսացին հույն մեծ գիտնական է: Նրա համբավը կապված է Պյութագորասի թեորեմի անվան հետ։ Թեև հիմա մենք արդեն գիտենք, որ այս թեորեմը հայտնի էր Հին Բաբելոնում Պյութագորասից 1200 տարի առաջ, իսկ Եգիպտոսում նրանից 2000 տարի առաջ հայտնի էր ուղղանկյուն եռանկյունի 3, 4, 5 կողմերով, մենք դեռ այն անվանում ենք այս հնագույնի անունով: գիտնական.

Պյութագորասի կյանքի մասին գրեթե ոչինչ հաստատապես հայտնի չէ, սակայն նրա անվան հետ կապված են մեծ թվով լեգենդներ։

Պյութագորասը ծնվել է մ.թ.ա. 570 թվականին Սամոս կղզում։

Պյութագորասը գեղեցիկ տեսք ուներ, երկար մորուք ուներ, իսկ գլխին՝ ոսկեգույն դիադեմ։ Պյութագորասը ոչ թե անուն է, այլ մականուն, որը ստացել է փիլիսոփան՝ միշտ ճիշտ ու համոզիչ խոսելու համար, ինչպես հունական օրակուլը։ (Պյութագորաս - «համոզիչ խոսք»):

550 թվականին Պյութագորասը որոշում է կայացնում և գնում Եգիպտոս։ Այսպիսով, Պյութագորասի առաջ բացվում է անհայտ երկիր և անհայտ մշակույթ։ Շատ զարմացած և զարմացած Պյութագորասին այս երկրում, և եգիպտացիների կյանքի որոշ դիտարկումներից հետո Պյութագորասը հասկացավ, որ գիտելիքի ճանապարհը, որը պաշտպանված է քահանաների կաստայի կողմից, անցնում է կրոնով:

Եգիպտոսում տասնմեկ տարի սովորելուց հետո Պյութագորասը գնում է հայրենիք, որտեղ ճանապարհին ընկնում է բաբելոնյան գերության մեջ։ Այնտեղ նա ծանոթանում է բաբելոնական գիտությանը, որն ավելի զարգացած էր, քան եգիպտականը։ Բաբելոնացիները գիտեին, թե ինչպես լուծել գծային, քառակուսի և որոշ տեսակի խորանարդ հավասարումներ: Գերությունից փախած՝ նա չկարողացավ երկար մնալ հայրենիքում՝ այնտեղ տիրող բռնության ու բռնակալության մթնոլորտի պատճառով։ Նա որոշեց տեղափոխվել Կրոտոն (հունական գաղութ Հյուսիսային Իտալիայում)։

Հենց Կրոտոնում է սկսվում Պյութագորասի կյանքի ամենափառահեղ շրջանը։ Այնտեղ նա հիմնեց կրոնա-էթիկական եղբայրության կամ գաղտնի վանական միության նման մի բան, որի անդամները պարտավոր էին վարել այսպես կոչված Պյութագորասյան կենսակերպը։

Պյութագորասը և Պյութագորասը

Պյութագորասը Ապենինյան թերակղզու հարավում գտնվող հունական գաղութում կազմակերպեց կրոնական և բարոյական եղբայրություն, ինչպիսին է վանական միաբանությունը, որը հետագայում կոչվելու էր Պյութագորասի միություն: Միության անդամները պետք է հավատարիմ մնան որոշակի սկզբունքներին՝ նախ ձգտել դեպի գեղեցիկն ու փառավորը, երկրորդ՝ օգտակար լինել, երրորդը՝ ձգտել բարձր հաճույքի։

Բարոյական և էթիկական կանոնների համակարգը, որը Պյութագորասը կտակել է իր ուսանողներին, կազմվել է Պյութագորասի «Ոսկե հատվածների» բարոյական կոդի մեջ, որոնք շատ տարածված էին Հնության, Միջնադարի և Վերածննդի դարաշրջանում:

Պյութագորասի ուսումնասիրությունների համակարգը բաղկացած էր երեք բաժիններից.

Ուսուցումներ թվերի մասին՝ թվաբանություն,

Ուսուցումներ գործիչների մասին՝ երկրաչափություն,

Ուսուցումներ տիեզերքի կառուցվածքի մասին՝ աստղագիտություն.

Պյութագորասի կողմից հաստատված կրթական համակարգը տևեց շատ դարեր։

Պյութագորասի դպրոցը շատ բան արեց երկրաչափությանը գիտության բնույթ հաղորդելու համար։ Պյութագորասի մեթոդի հիմնական առանձնահատկությունը երկրաչափության համադրությունն էր թվաբանության հետ։

Պյութագորասը շատ է առնչվել համամասնություններին և առաջընթացներին և, հավանաբար, թվերի նմանությանը, քանի որ նրան է վերագրվում խնդրի լուծումը. տրված է երկու ցուցանիշ»:

Պյութագորասը և իր աշակերտները ներկայացրեցին բազմանկյուն, ընկերական, կատարյալ թվեր հասկացությունը և ուսումնասիրեցին դրանց հատկությունները: Թվաբանությունը, որպես հաշվարկի պրակտիկա, չէր հետաքրքրում Պյութագորասին, և նա հպարտորեն հայտարարեց, որ «թվաբանությունը վեր է դասում վաճառականի շահերից»։

Պյութագորաս միության անդամները Հունաստանի շատ քաղաքների բնակիչներ էին։

Պյութագորացիներն իրենց հասարակություն էին ընդունում նաև կանանց: Միությունը ծաղկեց ավելի քան քսան տարի, իսկ հետո սկսվեցին նրա անդամների հալածանքները, ուսանողներից շատերը սպանվեցին։

Շատ տարբեր լեգենդներ կային հենց Պյութագորասի մահվան մասին: Բայց Պյութագորասի և նրա աշակերտների ուսմունքները շարունակեցին ապրել:

Պյութագորասի թեորեմի ստեղծման պատմությունից

Ներկայումս հայտնի է, որ այս թեորեմը չի հայտնաբերվել Պյութագորասի կողմից։ Այնուամենայնիվ, ոմանք կարծում են, որ հենց Պյութագորասն է առաջինը տվել դրա ամբողջական ապացույցը, իսկ մյուսները հերքում են նրան այս արժանիքը: Ոմանք Պյութագորասին են վերագրում այն ​​ապացույցը, որը Էվկլիդեսը տալիս է իր Elements-ի առաջին գրքում։ Մյուս կողմից, Պրոկլոսը պնդում է, որ տարրերի ապացույցը պայմանավորված է հենց Էվկլիդեսով: Ինչպես տեսնում ենք, մաթեմատիկայի պատմությունը գրեթե հուսալի կոնկրետ տվյալներ չունի Պյութագորասի կյանքի և նրա մաթեմատիկական գործունեության վերաբերյալ։

Պյութագորասի թեորեմի մեր պատմական ակնարկը սկսենք հին Չինաստանից: Այստեղ հատուկ ուշադրություն է գրավում Չու-պեյի մաթեմատիկական գիրքը։ Այս շարադրանքը սա ասում է Պյութագորասի եռանկյունու մասին 3, 4 և 5 կողմերով.

«Եթե ուղիղ անկյունը քայքայվում է իր բաղկացուցիչ մասերի, ապա նրա կողմերի ծայրերը միացնող գիծը կլինի 5, երբ հիմքը 3 է, իսկ բարձրությունը՝ 4»։

Շատ հեշտ է վերարտադրել դրանց կառուցման մեթոդը։ Վերցրեք 12 մ երկարությամբ պարան և 3 մ հեռավորության վրա գունավոր շերտով կապեք: մի ծայրից, իսկ մյուսից 4 մետր: 3 և 4 մետր երկարությամբ կողմերի միջև կփակվի ուղիղ անկյուն:

Հինդուիստների մոտ երկրաչափությունը սերտորեն կապված էր պաշտամունքի հետ։ Շատ հավանական է, որ հիպոթենուսի քառակուսի թեորեմն արդեն հայտնի է եղել Հնդկաստանում մ.թ.ա. 8-րդ դարում: Զուտ ծիսական դեղատոմսերի հետ մեկտեղ կան երկրաչափական աստվածաբանական բնույթի գործեր։ Այս գրվածքներում, որոնք թվագրվում են մ.թ.ա. 4-րդ կամ 5-րդ դարով, մենք հանդիպում ենք 15, 36, 39 կողմերով եռանկյունի կառուցման հետ:

Միջնադարում Պյութագորասի թեորեմը սահմանում էր եթե ոչ առավելագույն հնարավոր, ապա գոնե լավ մաթեմատիկական գիտելիքների սահմանը: Պյութագորասի թեորեմի բնորոշ գծագիրը, որն այժմ երբեմն դպրոցականները վերածում են, օրինակ, պրոֆեսորի կամ տղամարդու խալաթ հագած գլխարկի, այն ժամանակ հաճախ օգտագործվում էր որպես մաթեմատիկայի խորհրդանիշ։

Եզրափակելով՝ ներկայացնում ենք Պյութագորասի թեորեմի տարբեր ձևակերպումներ՝ թարգմանված հունարենից, լատիներենից և գերմաներենից։

Էվկլիդեսի թեորեմը կարդում է (բառացի թարգմանություն).

«Ուղղանկյուն եռանկյան մեջ ուղիղ անկյունը ընդգրկող կողմի քառակուսին հավասար է այն կողմերի քառակուսիներին, որոնք պարփակում են ուղիղ անկյունը»։

Ինչպես տեսնում եք, տարբեր երկրներում և տարբեր լեզուներում կան ծանոթ թեորեմի ձևակերպման տարբեր տարբերակներ: Ստեղծված տարբեր ժամանակներում և տարբեր լեզուներով՝ դրանք արտացոլում են մեկ մաթեմատիկական օրինաչափության էությունը, որի ապացույցը նույնպես ունի մի քանի տարբերակներ։

Պյութագորասի թեորեմն ապացուցելու հինգ եղանակ

հին չինական ապացույցներ

Հին չինական գծագրում չորս հավասար ուղղանկյուն եռանկյուններ՝ a, b և c ոտքերով, դրված են այնպես, որ դրանց արտաքին ուրվագիծը կազմում է քառակուսի a + b կողմով, իսկ ներքինը կազմում է քառակուսի c կողմով, որը կառուցված է գծի վրա: հիպոթենուզա

a2 + 2ab + b2 = c2 + 2ab

Ապացույց Ջ. Գարդֆիլդի կողմից (1882)

Եկեք դասավորենք երկու հավասար ուղղանկյուն եռանկյուններ այնպես, որ դրանցից մեկի ոտքը մյուսի շարունակությունն է։

Քննարկվող տրապեզոիդի մակերեսը համարվում է հիմքերի գումարի և բարձրության կեսի արտադրյալը.

Մյուս կողմից, տրապեզոիդի մակերեսը հավասար է ստացված եռանկյունների տարածքների գումարին.

Հավասարեցնելով այս արտահայտությունները՝ ստանում ենք.

Ապացույցը պարզ է

Այս ապացույցը ստացվում է հավասարաչափ ուղղանկյուն եռանկյունու ամենապարզ դեպքում։

Հավանաբար թեորեմը նրանից է սկսվել։

Իրոք, անհրաժեշտ է միայն նայել հավասարաչափ ուղղանկյուն եռանկյունների սալիկապատմանը, որպեսզի տեսնեք, որ թեորեմը ճշմարիտ է:

Օրինակ, ABC եռանկյան համար. AC հիպոթենուսի վրա կառուցված քառակուսին պարունակում է 4 սկզբնական եռանկյուն, իսկ ոտքերի վրա կառուցված քառակուսիները պարունակում են երկու: Թեորեմն ապացուցված է.

Հին հինդուների ապացույցը

Կողք ունեցող քառակուսին (a + b), կարելի է բաժանել մասերի կամ ինչպես նկ. 12. ա, կամ ինչպես նկ. 12բ. Պարզ է, որ 1-ին, 2-րդ, 3-րդ, 4-րդ մասերը երկու նկարներում էլ նույնն են: Իսկ եթե հավասարներից (տարածքներից) հանվեն հավասարները, ապա հավասարները կմնան, այսինքն. c2 = a2 + b2.

Էվկլիդեսի ապացույցը

Երկու հազարամյակների ընթացքում ամենատարածվածը Էվկլիդեսի կողմից հորինված Պյութագորասի թեորեմի ապացույցն էր։ Այն զետեղված է նրա հայտնի «Սկիզբներ» գրքում։

Էվկլիդեսը իջեցրեց BH բարձրությունը աջ անկյան գագաթից մինչև հիպոթենուս և ապացուցեց, որ դրա երկարացումը հիպոթենուսի վրա ավարտված քառակուսին բաժանում է երկու ուղղանկյունների, որոնց մակերեսները հավասար են ոտքերի վրա կառուցված համապատասխան քառակուսիների մակերեսներին։

Այս թեորեմի ապացուցման մեջ օգտագործված գծանկարը կատակով կոչվում է «Պյութագորասյան շալվար»։ Երկար ժամանակ նա համարվում էր մաթեմատիկական գիտության խորհրդանիշներից մեկը։

Պյութագորասի թեորեմի կիրառում

Պյութագորասի թեորեմի նշանակությունը կայանում է նրանում, որ երկրաչափության թեորեմների մեծ մասը կարելի է բխել դրանից կամ նրա օգնությամբ և լուծել բազմաթիվ խնդիրներ։ Բացի այդ, Պյութագորասի թեորեմի և դրա հակադարձ թեորեմի գործնական նշանակությունն այն է, որ դրանք կարող են օգտագործվել հատվածների երկարությունները գտնելու համար՝ առանց այդ հատվածները չափելու։ Սա, այսպես ասած, ճանապարհ է բացում ուղիղ գծից դեպի հարթություն, հարթությունից դեպի ծավալային տարածություն և դրանից դուրս։ Հենց այս պատճառով է, որ Պյութագորասի թեորեմն այդքան կարևոր է մարդկության համար, որը ձգտում է բացահայտել ավելի շատ չափումներ և ստեղծել տեխնոլոգիաներ այդ հարթություններում:

Եզրակացություն

Պյութագորասի թեորեմն այնքան հայտնի է, որ դժվար է պատկերացնել մի մարդու, ով չի լսել դրա մասին։ Ես իմացա, որ Պյութագորասի թեորեմն ապացուցելու մի քանի եղանակ կա։ Ես ուսումնասիրեցի մի շարք պատմական և մաթեմատիկական աղբյուրներ, այդ թվում նաև ինտերնետի տեղեկատվությունը, և հասկացա, որ Պյութագորասի թեորեմը հետաքրքիր է ոչ միայն իր պատմությամբ, այլև այն պատճառով, որ այն կարևոր տեղ է զբաղեցնում կյանքում և գիտության մեջ: Այդ են վկայում այս աշխատության մեջ իմ կողմից տրված այս թեորեմի տեքստի տարբեր մեկնաբանությունները և դրա ապացուցման ուղիները։

Այսպիսով, Պյութագորասի թեորեմը երկրաչափության հիմնական և, կարելի է ասել, ամենակարևոր թեորեմներից մեկն է։ Դրա նշանակությունը կայանում է նրանում, որ երկրաչափության թեորեմների մեծ մասը կարելի է դուրս բերել դրանից կամ նրա օգնությամբ։ Պյութագորասի թեորեմը ուշագրավ է նաև նրանով, որ ինքնին բոլորովին ակնհայտ չէ։ Օրինակ, հավասարաչափ եռանկյունու հատկությունները կարելի է տեսնել անմիջապես գծագրում: Բայց որքան էլ նայեք ուղղանկյուն եռանկյունին, դուք երբեք չեք տեսնի, որ նրա կողմերի միջև կա պարզ հարաբերություն՝ c2 = a2 + b2: Հետեւաբար, վիզուալիզացիան հաճախ օգտագործվում է դա ապացուցելու համար: Պյութագորասի արժանիքն այն էր, որ նա տվեց այս թեորեմի գիտական ​​ամբողջական ապացույցը։ Հետաքրքիր է հենց ինքը՝ գիտնականի անձը, որի հիշողությունը պատահաբար չի պահպանվում այս թեորեմով։ Պյութագորասը հրաշալի բանախոս է, ուսուցիչ և դաստիարակ, իր դպրոցի կազմակերպիչը՝ կենտրոնացած երաժշտության և թվերի ներդաշնակության, բարության և արդարության, գիտելիքի և առողջ ապրելակերպի վրա։ Նա կարող է օրինակ ծառայել մեզ՝ հեռավոր հետնորդներիս։

Մատենագիտական ​​հղում

Թումանովա Ս.Վ. ՊՅՈՒԹԱԳՈՐԱՍԻ ԹԵՈՐԵՄԸ ԱՊԱՑՈՒՑՄԱՆ ՄԻ ՄԻ ՄԻ ՈՒՂԻ // Սկսեք գիտությունից. - 2016. - No 2. - P. 91-95;
URL՝ http://science-start.ru/ru/article/view?id=44 (մուտքի ամսաթիվ՝ 01/10/2020):

Պյութագորասի թեորեմ- Էվկլիդեսյան երկրաչափության հիմնարար թեորեմներից մեկը, որը հաստատում է հարաբերությունը

ուղղանկյուն եռանկյան կողմերի միջև:

Ենթադրվում է, որ դա ապացուցել է հույն մաթեմատիկոս Պյութագորասը, ում անունով էլ այն կոչվել է։

Պյութագորասի թեորեմի երկրաչափական ձևակերպումը.

Թեորեմն ի սկզբանե ձևակերպված էր հետևյալ կերպ.

Ուղղանկյուն եռանկյունում հիպոթենուսի վրա կառուցված քառակուսու մակերեսը հավասար է քառակուսիների մակերեսների գումարին,

կառուցված կաթետերի վրա:

Պյութագորասի թեորեմի հանրահաշվական ձևակերպումը.

Ուղղանկյուն եռանկյունում հիպոթենուսի երկարության քառակուսին հավասար է ոտքերի երկարությունների քառակուսիների գումարին:

Այսինքն, նշանակում է միջանցիկ եռանկյան հիպոթենուսի երկարությունը գ, և ոտքերի երկարությունները միջով աև բ:

Երկու ձևակերպումներն էլ Պյութագորասի թեորեմներհամարժեք են, բայց երկրորդ ձևակերպումն ավելի տարրական է՝ ոչ

պահանջում է տարածք հասկացությունը: Այսինքն՝ երկրորդ հայտարարությունը կարելի է ճշտել՝ տարածքի մասին ոչինչ չիմանալով և

ուղղանկյուն եռանկյան միայն կողմերի երկարությունները չափելով:

Հակադարձ Պյութագորասի թեորեմը.

Եթե ​​եռանկյան մի կողմի քառակուսին հավասար է մյուս երկու կողմերի քառակուսիների գումարին, ապա

եռանկյունը ուղղանկյուն է.

Կամ, այլ կերպ ասած.

Դրական թվերի ցանկացած եռակի համար ա, բև գ, այնպիսին է, որ

կա ոտքերով ուղղանկյուն եռանկյուն աև բև հիպոթենուզա գ.

Պյութագորասի թեորեմը հավասարաչափ եռանկյունու համար.

Պյութագորասի թեորեմ հավասարակողմ եռանկյան համար.

Պյութագորասի թեորեմի ապացույցները.

Այս պահին գիտական ​​գրականության մեջ գրանցվել է այս թեորեմի 367 ապացույց։ Հավանաբար թեորեմը

Պյութագորասը միակ թեորեմն է, որն ունի նման տպավորիչ թվով ապացույցներ։ Նման բազմազանություն

կարելի է բացատրել միայն թեորեմի հիմնարար նշանակությամբ երկրաչափության համար։

Իհարկե, կոնցեպտուալ առումով բոլորը կարելի է բաժանել փոքր թվով դասարանների։ Դրանցից ամենահայտնին.

ապացույցը տարածքի մեթոդ, աքսիոմատիկև էկզոտիկ ապացույցներ(Օրինակ,

միջոցով դիֆերենցիալ հավասարումներ).

1. Պյութագորասի թեորեմի ապացույցը նմանատիպ եռանկյունների առումով:

Հանրահաշվական ձևակերպման հետևյալ ապացույցը կառուցված ապացույցներից ամենապարզն է

անմիջապես աքսիոմներից: Մասնավորապես, այն չի օգտագործում գործչի տարածքի հայեցակարգը:

Թող լինի ABCկա ուղղանկյուն եռանկյուն Գ. Եկեք մի բարձրություն քաշենք Գև նշել

դրա հիմքի միջոցով Հ.

Եռանկյուն ACHնման է եռանկյունին ԱԲ C երկու անկյուններում: Նմանապես, եռանկյունին CBHհամանման ABC.

Ներկայացնելով նշումը.

մենք ստանում ենք.

,

որը համապատասխանում է -

Ծալվելով ա 2 և բ 2, մենք ստանում ենք.

կամ , որը պետք է ապացուցվեր։

2. Պյութագորասի թեորեմի ապացուցումը տարածքի մեթոդով։

Հետևյալ ապացույցները, չնայած իրենց թվացյալ պարզությանը, ամենևին էլ այնքան էլ պարզ չեն. Բոլոր նրանց

օգտագործել տարածքի հատկությունները, որոնց ապացույցն ավելի բարդ է, քան բուն Պյութագորասի թեորեմի ապացույցը։

• Ապացուցում էքվիլրացման միջոցով:

Դասավորեք չորս հավասար ուղղանկյուն

եռանկյուն, ինչպես ցույց է տրված նկարում

աջ կողմում։

Կողքերով քառանկյուն գ- քառակուսի,

քանի որ երկու սուր անկյունների գումարը 90° է, և

մշակված անկյունը 180° է։

Ամբողջ գործչի մակերեսը, մի կողմից,

քառակուսու մակերեսը կողմով ( ա+բ), իսկ մյուս կողմից՝ չորս եռանկյունների մակերեսների գումարը և

Ք.Ե.Դ.

3. Պյութագորասի թեորեմի ապացույցը անվերջ փոքր մեթոդով.

​

Հաշվի առնելով նկարում ներկայացված գծագիրը և

դիտելով կողմի փոփոխությունըա, մենք կարող ենք

անսահմանի համար գրի՛ր հետևյալ կապը

փոքր կողային հավելումներհետև ա(օգտագործելով նմանություն

եռանկյուններ):

Օգտագործելով փոփոխականների տարանջատման մեթոդը, մենք գտնում ենք.

Երկու ոտքերի ավելացման դեպքում հիպոթենուսը փոխելու ավելի ընդհանուր արտահայտություն.

Ինտեգրելով այս հավասարումը և օգտագործելով նախնական պայմանները, մենք ստանում ենք.

Այսպիսով, մենք հասնում ենք ցանկալի պատասխանին.

Ինչպես հեշտ է տեսնել, վերջնական բանաձևում քառակուսի կախվածությունը հայտնվում է գծայինի շնորհիվ

եռանկյան կողմերի և աճի համաչափությունը, մինչդեռ գումարը կապված է անկախի հետ

ներդրումներ տարբեր ոտքերի աճից:

Ավելի պարզ ապացույց կարելի է ձեռք բերել, եթե ենթադրենք, որ ոտքերից մեկը աճ չի զգում

(այս դեպքում՝ ոտքը բ): Այնուհետև ինտեգրման հաստատունի համար մենք ստանում ենք.