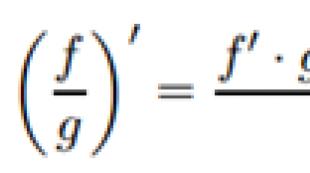արհեստներ

Առաջին և երկրորդ ածանցյալ սահմանումը. Դումմիների ածանցյալի լուծում. սահմանում, ինչպես գտնել, լուծումների օրինակներ: Հիպերբոլիկ ֆունկցիաների ածանցյալներ

ԱՌԱՋԻՆ ածանցյալ

(առաջին ածանցյալ)Ֆունկցիայի արժեքի աճի տեմպը, երբ նրա արգումենտն ինչ-որ պահի աճում է, եթե ֆունկցիան ինքնին սահմանված է այս կետում: Գրաֆիկի վրա ֆունկցիայի առաջին ածանցյալը ցույց է տալիս նրա թեքության անկյունը։ Եթե y=f(x),դրա առաջին ածանցյալը մի կետում x0այն սահմանն է, որին f(x0+а)–f(x0)/аինչպես Աձգտում է անսահման փոքր արժեքի: Առաջին ածանցյալը կարելի է նշել dy/dxկամ y (x).Գործառույթ y(x)կետում ունի հաստատուն արժեք x0,Եթե dy/dxկետում x0հավասար է զրոյի: Առաջին ածանցյալը, որը հավասար է զրոյի, անհրաժեշտ, բայց ոչ բավարար պայման է, որպեսզի ֆունկցիան հասնի իր առավելագույնին կամ նվազագույնին տվյալ կետում:

Տնտեսություն. Բառարան. - Մ.՝ «ԻՆՖՐԱ-Մ», «Վես Միր» հրատարակչություն։ Ջ. Բլեք. Գլխավոր խմբագրություն՝ տնտեսագիտության դոկտոր Օսադչայա Ի.Մ.. 2000 .

Տնտեսական բառարան. 2000 .

Տեսեք, թե ինչ է «FIRST DERIVATIV»-ը այլ բառարաններում.

- (ածանցյալ) Այն արագությունը, որով ֆունկցիայի արժեքը մեծանում է, երբ նրա արգումենտն ինչ-որ կետում ավելանում է, եթե ֆունկցիան ինքնին սահմանված է այդ կետում: Գրաֆիկի վրա ֆունկցիայի առաջին ածանցյալը ցույց է տալիս նրա թեքության անկյունը։ Եթե y \u003d f (x), դրա առաջին ածանցյալը կետում ... ... Տնտեսական բառարան

Այս տերմինն այլ իմաստներ ունի, տես Ածանցյալ։ Ածանցյալ ածանցյալ հասկացության նկարազարդում ... Վիքիպեդիա

Ածանցյալը դիֆերենցիալ հաշվարկի հիմնական հասկացությունն է, որը բնութագրում է ֆունկցիայի փոփոխության արագությունը։ Այն սահմանվում է որպես ֆունկցիայի աճի հարաբերակցության սահմանը նրա արգումենտի աճին, երբ արգումենտի աճը ձգտում է զրոյի, եթե այդպիսի սահմանը ... ... Վիքիպեդիա

Հատուկ տեսակի սահմանային արժեքի խնդիր; բաղկացած է D տիրույթում x=(x1,..., x n) փոփոխականներ գտնելուց: Դիֆերենցիալ հավասարման (1) լուծումները հավասար կարգի 2m-ի բոլոր կարգի ածանցյալների տրված արժեքների համար՝ m-ից ոչ բարձր սահմանի վրա: D տիրույթի S (կամ դրա մի մասը) ... Մաթեմատիկական հանրագիտարան

- (երկրորդ ածանցյալ) Ֆունկցիայի առաջին ածանցյալի առաջին ածանցյալը: Առաջին ածանցյալը չափում է ֆունկցիայի թեքությունը. երկրորդ ածանցյալը չափում է, թե ինչպես է թեքությունը փոխվում աճող փաստարկով: y-ի երկրորդ ածանցյալը = f(x)…… Տնտեսական բառարան

Այս հոդվածը կամ բաժինը վերանայման կարիք ունի: Խնդրում ենք բարելավել հոդվածը հոդվածներ գրելու կանոններին համապատասխան։ Fractional pro ... Վիքիպեդիա

- (խաչ մասնակի ածանցյալ) Ֆունկցիայի մեկ արգումենտի երկու կամ ավելի փոփոխականներից փոխելու ազդեցությունը այս ֆունկցիայի ածանցյալի վրա՝ վերցված մեկ այլ արգումենտի նկատմամբ: Եթե y \u003d f (x, z), ապա դրա ածանցյալը կամ y ֆունկցիայի առաջին ածանցյալը x արգումենտի նկատմամբ կազմում է ... ... Տնտեսական բառարան

կետային արագության անալոգային- Մեխանիզմի ընդհանրացված կոորդինատի երկայնքով կետի շարժման առաջին ածանցյալը ...

կապի անկյունային արագության անալոգը- Կապի պտտման անկյան առաջին ածանցյալը մեխանիզմի ընդհանրացված կոորդինատի նկատմամբ ... Պոլիտեխնիկական տերմինաբանական բացատրական բառարան

մեխանիզմի ընդհանրացված արագություն- Մեխանիզմի ընդհանրացված կոորդինատի առաջին ածանցյալը ժամանակի նկատմամբ ... Պոլիտեխնիկական տերմինաբանական բացատրական բառարան

Գրքեր

Դիֆերենցիալ երկրաչափության և տոպոլոգիայի խնդիրների ժողովածու, Միշչենկո Ա.Ս.
Իմ գիտական հոդվածները Գիրք 3. Խտության մատրիցային մեթոդ լազերի քվանտային տեսություններում, կամայական ատոմ, Բոնդարև Բորիս Վլադիմիրովիչ. Այս գիրքը դիտարկում է հրապարակված գիտական հոդվածները, որոնցում լազերի, կամայական ատոմի և խամրված քվանտային տատանվող նոր քվանտային տեսությունները ներկայացված են խտության մատրիցների մեթոդով։

Ահա թեման ուսումնասիրելիս հարմարության և պարզության համար ամփոփ աղյուսակ:

Մշտականy=C

Հզորության ֆունկցիա y = x p

(x p)" = p x p - 1

Էքսպոնենցիալ ֆունկցիաy = x

(a x)" = a x ln a

Մասնավորապես, երբa = eմենք ունենք y = e x

(e x)" = e x

լոգարիթմական ֆունկցիա

(log a x) " = 1 x ln a

Մասնավորապես, երբa = eմենք ունենք y = log x

(ln x)" = 1 x

Եռանկյունաչափական ֆունկցիաներ

(sin x) "= cos x (cos x)" = - sin x (t g x) " = 1 cos 2 x (c t g x)" = - 1 sin 2 x.

Հակադարձ եռանկյունաչափական ֆունկցիաներ

(a r c sin x) " = 1 1 - x 2 (a r c cos x) " = - 1 1 - x 2 (a r c t g x) " = 1 1 + x 2 (a r c c t g x) " = - 1 1 + x 2.

Հիպերբոլիկ գործառույթներ

(s h x) " = c h x (c h x) " = s h x (t h x) " = 1 c h 2 x (c t h x) " = - 1 s h 2 x

Եկեք վերլուծենք, թե ինչպես են ստացվել նշված աղյուսակի բանաձևերը, կամ, այլ կերպ ասած, կապացուցենք ֆունկցիայի յուրաքանչյուր տեսակի համար ածանցյալների բանաձևերի ստացումը։

հաստատունի ածանցյալ

Ապացույց 1

Այս բանաձևը ստանալու համար հիմք ենք ընդունում ֆունկցիայի ածանցյալի սահմանումը մի կետում: Մենք օգտագործում ենք x 0 = x, որտեղ xընդունում է ցանկացած իրական թվի արժեքը, կամ, այլ կերպ ասած, xցանկացած թիվ է f (x) = C ֆունկցիայի տիրույթից: Ֆունկցիայի աճի հարաբերակցության սահմանը արգումենտի աճին գրենք ∆ x → 0:

lim ∆ x → 0 ∆ f (x) ∆ x = lim ∆ x → 0 C - C ∆ x = lim ∆ x → 0 0 ∆ x = 0

Խնդրում ենք նկատի ունենալ, որ 0 ∆ x արտահայտությունն ընկնում է սահմանային նշանի տակ: Դա «զրոյի բաժանված զրոյի» անորոշությունը չէ, քանի որ համարիչը պարունակում է ոչ թե անվերջ փոքր արժեք, այլ զրո: Այլ կերպ ասած, հաստատուն ֆունկցիայի աճը միշտ զրո է։

Այսպիսով, f (x) = C հաստատուն ֆունկցիայի ածանցյալը հավասար է զրոյի ամբողջ սահմանման տիրույթում։

Օրինակ 1

Հաշվի առնելով մշտական գործառույթները.

f 1 (x) = 3, f 2 (x) = a, a ∈ R, f 3 (x) = 4: 13 7 22, f 4 (x) = 0, f 5 (x) = - 8 7

Լուծում

Եկեք նկարագրենք տրված պայմանները. Առաջին ֆունկցիայում տեսնում ենք 3 բնական թվի ածանցյալը։ Հետևյալ օրինակում դուք պետք է վերցնեք ածանցյալը Ա, Որտեղ Ա- ցանկացած իրական թիվ: Երրորդ օրինակը մեզ տալիս է 4 իռացիոնալ թվի ածանցյալը: 13 7 22 , չորրորդը՝ զրոյի ածանցյալը (զրոն ամբողջ թիվ է)։ Վերջապես, հինգերորդ դեպքում ունենք ռացիոնալ կոտորակի ածանցյալը՝ 8 7:

Պատասխան.Տրված ֆունկցիաների ածանցյալները զրո են ցանկացած իրականի համար x(սահմանման ողջ տիրույթում)

f 1 "(x) = (3) " = 0, f 2" (x) = (a) " = 0, a ∈ R, f 3" (x) = 4. 13 7 22" = 0, f 4 "(x) = 0" = 0, f 5" (x) = - 8 7" = 0

Հզորության ֆունկցիայի ածանցյալ

Մենք դիմում ենք հզորության ֆունկցիային և դրա ածանցյալի բանաձևին, որն ունի ձև՝ (x p) " = p x p - 1, որտեղ ցուցիչը էջցանկացած իրական թիվ է:

Ապացույց 2

Ահա այն բանաձևի ապացույցը, երբ ցուցիչը բնական թիվ է. p = 1, 2, 3,…

Կրկին մենք հիմնվում ենք ածանցյալի սահմանման վրա: Գրենք ուժային ֆունկցիայի աճի հարաբերակցության սահմանը փաստարկի աճին.

(x p) " = lim ∆ x → 0 = ∆ (x p) ∆ x = lim ∆ x → 0 (x + ∆ x) p - x p ∆ x

Համարիչի արտահայտությունը պարզեցնելու համար մենք օգտագործում ենք Նյուտոնի երկանդամ բանաձևը.

(x + ∆ x) p - x p = C p 0 + x p + C p 1 x p - 1 ∆ x + C p 2 x p - 2 (∆ x) 2 + . . . + + C p p - 1 x (∆ x) p - 1 + C p p (∆ x) p - x p = = C p 1 x p - 1 ∆ x + C p 2 x p - 2 (∆ x) 2 + . . . + C p p - 1 x (∆ x) p - 1 + C p p (∆ x) p

Այսպիսով.

(x p) " = lim ∆ x → 0 ∆ (x p) ∆ x = lim ∆ x → 0 (x + ∆ x) p - x p ∆ x = = lim ∆ x → 0 (C p 1 x p - 1 ∆ x + C p 2 x p - 2 (∆ x) 2 + . . . + C p p - 1 x (∆ x) p - 1 + C p p (∆ x) p) ∆ x = = lim ∆ x → 0 (C p 1 x p - 1 + C p 2 x p - 2 ∆ x + . . . + C p p - 1 x (∆ x) p - 2 + C p p (∆ x) p - 1) = = C p 1 x p - 1 + 0 + 0 + ... + 0 = p! 1! (p - 1) x p - 1 = p x p - 1

Այսպիսով, մենք ապացուցեցինք ուժային ֆունկցիայի ածանցյալի բանաձևը, երբ ցուցիչը բնական թիվ է:

Ապացույց 3

Տալ ապացույց այն դեպքի համար, երբ p-ցանկացած իրական թիվ, բացի զրոյից, մենք օգտագործում ենք լոգարիթմական ածանցյալը (այստեղ մենք պետք է հասկանանք տարբերությունը լոգարիթմական ֆունկցիայի ածանցյալից): Ավելի ամբողջական պատկերացում ունենալու համար ցանկալի է ուսումնասիրել լոգարիթմական ֆունկցիայի ածանցյալը և լրացուցիչ զբաղվել անուղղակիորեն տրված ֆունկցիայի ածանցյալով և բարդ ֆունկցիայի ածանցյալով։

Դիտարկենք երկու դեպք՝ երբ xդրական և երբ xբացասական են.

Այսպիսով, x > 0: Այնուհետև՝ x p > 0: Մենք վերցնում ենք y \u003d x p հավասարության լոգարիթմը e հիմքի վրա և կիրառում ենք լոգարիթմի հատկությունը.

y = x p ln y = ln x p ln y = p ln x

Այս փուլում ստացվել է անուղղակիորեն սահմանված ֆունկցիա։ Սահմանենք դրա ածանցյալը.

(ln y) " = (p ln x) 1 y y " = p 1 x ⇒ y " = p y x = p x p x = p x p - 1

Այժմ մենք դիտարկում ենք այն դեպքը, երբ x-բացասական թիվ.

Եթե ցուցանիշը էջզույգ թիվ է, ապա x-ի համար սահմանվում է նաև հզորության ֆունկցիան< 0 , причем является четной: y (x) = - y ((- x) p) " = - p · (- x) p - 1 · (- x) " = = p · (- x) p - 1 = p · x p - 1

Հետո xp< 0 и возможно составить доказательство, используя логарифмическую производную.

Եթե էջկենտ թիվ է, ապա x-ի համար սահմանվում է հզորության ֆունկցիան< 0 , причем является нечетной: y (x) = - y (- x) = - (- x) p . Тогда x p < 0 , а значит логарифмическую производную задействовать нельзя. В такой ситуации возможно взять за основу доказательства правила дифференцирования и правило нахождения производной сложной функции:

y "(x) \u003d (- (- x) p) " \u003d - ((- x) p) " \u003d - p (- x) p - 1 (- x) " = \u003d p (- x ) p - 1 = p x p - 1

Վերջին անցումը հնարավոր է, քանի որ եթե էջկենտ թիվ է, ուրեմն p - 1կա՛մ զույգ թիվ, կա՛մ զրո (p = 1-ի համար), հետևաբար՝ բացասականի համար xհավասարությունը (- x) p - 1 = x p - 1 ճիշտ է:

Այսպիսով, մենք ապացուցեցինք ցանկացած իրական p-ի համար հզորության ֆունկցիայի ածանցյալի բանաձևը:

Օրինակ 2

Տրված գործառույթներ.

f 1 (x) = 1 x 2 3, f 2 (x) = x 2 - 1 4, f 3 (x) = 1 x log 7 12

Որոշեք դրանց ածանցյալները:

Լուծում

Տրված ֆունկցիաների մի մասը վերափոխում ենք աղյուսակային ձևի y = x p , հիմնվելով աստիճանի հատկությունների վրա, այնուհետև օգտագործում ենք բանաձևը.

f 1 (x) \u003d 1 x 2 3 \u003d x - 2 3 ⇒ f 1 "(x) \u003d - 2 3 x - 2 3 - 1 \u003d - 2 3 x - 5 3 f 2" (x) \u003d x 2 - 1 4 = 2 - 1 4 x 2 - 1 4 - 1 = 2 - 1 4 x 2 - 5 4 f 3 (x) = 1 x log 7 12 = x - log 7 12 ⇒ f 3 " ( x) = - log 7 12 x - log 7 12 - 1 = - log 7 12 x - log 7 12 - log 7 7 = - log 7 12 x - log 7 84

Էքսպոնենցիալ ֆունկցիայի ածանցյալ

Ապացույց 4

Մենք բխում ենք ածանցյալի բանաձևից՝ հիմնվելով սահմանման վրա.

(a x) " = lim ∆ x → 0 a x + ∆ x - a x ∆ x = lim ∆ x → 0 a x (a ∆ x - 1) ∆ x = a x lim ∆ x → 0 a ∆ x - 1 ∆ x = 0 0

Մենք ստացանք անորոշություն. Այն ընդլայնելու համար մենք գրում ենք նոր փոփոխական z = a ∆ x - 1 (z → 0 որպես ∆ x → 0): Այս դեպքում a ∆ x = z + 1 ⇒ ∆ x = log a (z + 1) = ln (z + 1) ln a . Վերջին անցման համար օգտագործվում է լոգարիթմի նոր հիմքի անցման բանաձևը։

Եկեք փոխարինում կատարենք սկզբնական սահմանաչափով.

(a x) " = a x lim ∆ x → 0 a ∆ x - 1 ∆ x = a x ln a lim ∆ x → 0 1 1 z ln (z + 1) = = a x ln a lim ∆ x → 0 1 ln (z + 1) 1 z = a x ln a 1 ln lim ∆ x → 0 (z + 1) 1 z

Հիշեք երկրորդ հրաշալի սահմանը և այնուհետև մենք ստանում ենք էքսպոնենցիալ ֆունկցիայի ածանցյալի բանաձևը.

(a x) " = a x ln a 1 ln lim z → 0 (z + 1) 1 z = a x ln a 1 ln e = a x ln a

Օրինակ 3

Էքսպոնենցիալ ֆունկցիաները տրված են.

f 1 (x) = 2 3 x, f 2 (x) = 5 3 x, f 3 (x) = 1 (e) x

Պետք է գտնել դրանց ածանցյալները։

Լուծում

Մենք օգտագործում ենք էքսպոնենցիալ ֆունկցիայի ածանցյալի և լոգարիթմի հատկությունների բանաձևը.

f 1 "(x) = 2 3 x" = 2 3 x ln 2 3 = 2 3 x (ln 2 - ln 3) f 2 "(x) = 5 3 x" = 5 3 x ln 5 1 3 = 1 3 5 3 x ln 5 f 3 "(x) = 1 (e) x" = 1 e x " = 1 e x ln 1 e = 1 e x ln e - 1 = - 1 e x

Լոգարիթմական ֆունկցիայի ածանցյալ

Ապացույց 5

Ներկայացնում ենք ցանկացածի համար լոգարիթմական ֆունկցիայի ածանցյալի բանաձևի ապացույցը xսահմանման տիրույթում և լոգարիթմի a հիմքի ցանկացած վավեր արժեք: Ելնելով ածանցյալի սահմանումից՝ ստանում ենք.

(log a x) " = lim ∆ x → 0 log a (x + ∆ x) - log a x ∆ x = lim ∆ x → 0 log a x + ∆ x x ∆ x = = lim ∆ x → 0 1 ∆ x log a 1 + ∆ x x = lim ∆ x → 0 log a 1 + ∆ x x 1 ∆ x = = lim ∆ x → 0 log a 1 + ∆ x x 1 ∆ x x x = lim ∆ x → 0 1 x log a 1 + ∆ x x ∆ x = = 1 x log a lim ∆ x → 0 1 + ∆ x x x ∆ x = 1 x log a e = 1 x ln e ln a = 1 x ln a

Հավասարությունների նշված շղթայից երևում է, որ փոխակերպումները կառուցվել են լոգարիթմի հատկության հիման վրա։ Հավասարությունը lim ∆ x → 0 1 + ∆ x x ∆ x = e ճշմարիտ է երկրորդ ուշագրավ սահմանին համապատասխան:

Օրինակ 4

Տրված են լոգարիթմական ֆունկցիաները.

f 1 (x) = log log 3 x, f 2 (x) = log x

Անհրաժեշտ է հաշվարկել դրանց ածանցյալները:

Լուծում

Եկեք կիրառենք ստացված բանաձևը.

f 1 "(x) = (log ln 3 x)" = 1 x ln (ln 3); f 2 "(x) \u003d (ln x)" \u003d 1 x ln e \u003d 1 x

Այսպիսով, բնական լոգարիթմի ածանցյալը բաժանվում է մեկով x.

Եռանկյունաչափական ֆունկցիաների ածանցյալներ

Ապացույց 6

Մենք օգտագործում ենք մի քանի եռանկյունաչափական բանաձևեր և առաջին հրաշալի սահմանը՝ եռանկյունաչափական ֆունկցիայի ածանցյալի բանաձևը հանելու համար։

Ըստ սինուսի ֆունկցիայի ածանցյալի սահմանման՝ ստանում ենք.

(sin x) " = lim ∆ x → 0 sin (x + ∆ x) - sin x ∆ x

Սինուսների տարբերության բանաձևը թույլ կտա մեզ կատարել հետևյալ գործողությունները.

(sin x) " = lim ∆ x → 0 sin (x + ∆ x) - sin x ∆ x = = lim ∆ x → 0 2 sin x + ∆ x - x 2 cos x + ∆ x + x 2 ∆ x = = lim ∆ x → 0 sin ∆ x 2 cos x + ∆ x 2 ∆ x 2 = = cos x + 0 2 lim ∆ x → 0 sin ∆ x 2 ∆ x 2

Ի վերջո, մենք օգտագործում ենք առաջին հրաշալի սահմանը.

sin "x = cos x + 0 2 lim ∆ x → 0 sin ∆ x 2 ∆ x 2 = cos x

Այսպիսով, ֆունկցիայի ածանցյալը մեղք xկամք cos x.

Նույն կերպ կապացուցենք նաև կոսինուսի ածանցյալի բանաձևը.

cos "x = lim ∆ x → 0 cos (x + ∆ x) - cos x ∆ x = = lim ∆ x → 0 - 2 sin x + ∆ x - x 2 sin x + ∆ x + x 2 ∆ x = = - lim ∆ x → 0 sin ∆ x 2 sin x + ∆ x 2 ∆ x 2 = = - sin x + 0 2 lim ∆ x → 0 sin ∆ x 2 ∆ x 2 = - sin x

Նրանք. cos x ֆունկցիայի ածանցյալը կլինի – մեղք x.

Տարբերակման կանոնների հիման վրա մենք բխում ենք շոշափողի և կոտանգենսի ածանցյալների բանաձևերը.

t g «x = sin x cos x» = մեղք «x cos x - sin x cos «x cos 2 x = = cos x cos x - sin x (- sin x) cos 2 x = մեղք 2 x + cos 2 x cos. 2 x = 1 cos 2 x c t g "x = cos x sin x" = cos "x sin x - cos x sin "x sin 2 x = = - sin x sin x - cos x cos x sin 2 x = - մեղք 2 x. + cos 2 x sin 2 x = - 1 sin 2 x

Հակադարձ եռանկյունաչափական ֆունկցիաների ածանցյալներ

Հակադարձ ֆունկցիաների ածանցյալի մասին բաժինը տրամադրում է համապարփակ տեղեկատվություն արկսինի, արկկոսինի, արկտանգենսի և արկոտանգենսի ածանցյալների բանաձևերի ապացույցների վերաբերյալ, ուստի մենք այստեղ նյութը չենք կրկնօրինակի:

Հիպերբոլիկ ֆունկցիաների ածանցյալներ

Ապացույց 7

Հիպերբոլիկ սինուսի, կոսինուսի, տանգենսի և կոտանգենսի ածանցյալների բանաձևերը կարող ենք ստանալ՝ օգտագործելով տարբերակման կանոնը և էքսպոնենցիալ ֆունկցիայի ածանցյալի բանաձևը.

s h "x = e x - e - x 2" = 1 2 e x "- e - x" == 1 2 e x - - e - x = e x + e - x 2 = c h x c h "x = e x + e - x 2" = 1 2 e x "+ e - x" == 1 2 e x + - e - x = e x - e - x 2 = s h x t h "x = s h x c h x" = s h "x c h x - s h x c h "x c h 2 x = c h 2 x - s. 2 x c h 2 x = 1 c h 2 x c t h "x = c h x s h x" = c h "x s h x - c h x s h "x s h 2 x = s h 2 x - c h 2 x s h 2 x = - 1 s h 2

Եթե տեքստում սխալ եք նկատել, ընդգծեք այն և սեղմեք Ctrl+Enter

Շատ հեշտ է հիշել:

Դե, մենք հեռու չենք գնա, անմիջապես կդիտարկենք հակադարձ ֆունկցիան։ Որքա՞ն է էքսպոնենցիալ ֆունկցիայի հակառակը: Լոգարիթմ:

Մեր դեպքում հիմքը մի թիվ է.

Նման լոգարիթմը (այսինքն՝ հիմք ունեցող լոգարիթմը) կոչվում է «բնական», և դրա համար մենք օգտագործում ենք հատուկ նշում՝ փոխարենը գրում ենք։

Ինչի՞ն է հավասար. Իհարկե, .

Բնական լոգարիթմի ածանցյալը նույնպես շատ պարզ է.

Օրինակներ.

Գտե՛ք ֆունկցիայի ածանցյալը:
Ո՞րն է ֆունկցիայի ածանցյալը:

Պատասխանները: Ցուցանիշը և բնական լոգարիթմը ֆունկցիաներ են, որոնք ածանցյալի առումով եզակի պարզ են: Ցանկացած այլ հիմքի հետ էքսպոնենցիալ և լոգարիթմական ֆունկցիաները կունենան այլ ածանցյալ, որը մենք կվերլուծենք ավելի ուշ՝ տարբերակման կանոնները անցնելուց հետո։

Տարբերակման կանոններ

Ի՞նչ կանոններ: Եվս մեկ նոր տերմին, էլի՞...

Տարբերակումածանցյալը գտնելու գործընթացն է։

Միայն և ամեն ինչ: Ի՞նչ այլ բառ է այս գործընթացի համար: Ոչ proizvodnovanie... Մաթեմատիկայի դիֆերենցիալը կոչվում է ֆունկցիայի բուն աճ: Այս տերմինը գալիս է լատիներեն տարբերակից՝ տարբերություն։ Այստեղ.

Այս բոլոր կանոնները բխեցնելիս մենք կօգտագործենք երկու գործառույթ, օրինակ և. Մեզ անհրաժեշտ կլինեն նաև դրանց ավելացման բանաձևեր.

Ընդհանուր առմամբ կա 5 կանոն.

հաստատունը հանվում է ածանցյալի նշանից։

Եթե - ինչ-որ հաստատուն թիվ (հաստատուն), ապա.

Ակնհայտ է, որ այս կանոնը նույնպես գործում է տարբերության համար.

Եկեք ապացուցենք դա։ Թողեք, կամ ավելի հեշտ:

Օրինակներ.

Գտեք ֆունկցիաների ածանցյալները.

կետում;
կետում;
կետում;
կետում։

Լուծումներ:

(ածանցյալը բոլոր կետերում նույնն է, քանի որ գծային ֆունկցիա է, հիշու՞մ եք):

Արտադրանքի ածանցյալ

Այստեղ ամեն ինչ նման է. մենք ներկայացնում ենք նոր գործառույթ և գտնում ենք դրա աճը.

Ածանցյալ:

Օրինակներ.

Գտնել ֆունկցիաների ածանցյալները և;
Գտե՛ք ֆունկցիայի ածանցյալը մի կետում:

Լուծումներ:

Էքսպոնենցիալ ֆունկցիայի ածանցյալ

Այժմ ձեր գիտելիքները բավարար են, որպեսզի սովորեք, թե ինչպես գտնել ցանկացած էքսպոնենցիոնալ ֆունկցիայի ածանցյալը, և ոչ միայն ցուցիչը (դուք դեռ մոռացե՞լ եք, թե դա ինչ է):

Այսպիսով, որտեղ է որոշ թվեր:

Մենք արդեն գիտենք ֆունկցիայի ածանցյալը, ուստի եկեք փորձենք մեր ֆունկցիան բերել նոր հիմքի.

Դա անելու համար մենք օգտագործում ենք մի պարզ կանոն. Ապա.

Դե, ստացվեց: Այժմ փորձեք գտնել ածանցյալը և մի մոռացեք, որ այս ֆունկցիան բարդ է:

Տեղի է ունեցել?

Ահա, ստուգեք ինքներդ.

Բանաձևը շատ նման է ցուցիչի ածանցյալին. ինչպես եղել է, այնպես էլ մնացել է, հայտնվել է միայն գործոնը, որն ընդամենը թիվ է, բայց ոչ փոփոխական։

Օրինակներ.
Գտեք ֆունկցիաների ածանցյալները.

Պատասխանները:

Սա ընդամենը մի թիվ է, որը հնարավոր չէ հաշվարկել առանց հաշվիչի, այսինքն՝ չի կարելի գրել ավելի պարզ ձևով։ Հետեւաբար, պատասխանում այն մնացել է այս տեսքով.

Նկատի ունեցեք, որ այստեղ երկու ֆունկցիաների գործակիցն է, ուստի մենք կիրառում ենք համապատասխան տարբերակման կանոնը.

Այս օրինակում երկու ֆունկցիաների արտադրյալը.

Լոգարիթմական ֆունկցիայի ածանցյալ

Այստեղ դա նման է. դուք արդեն գիտեք բնական լոգարիթմի ածանցյալը.

Հետևաբար, լոգարիթմից կամայական գտնել այլ հիմքով, օրինակ.

Մենք պետք է այս լոգարիթմը բերենք հիմք: Ինչպե՞ս փոխել լոգարիթմի հիմքը: Հուսով եմ հիշում եք այս բանաձևը.

Միայն հիմա փոխարեն մենք կգրենք.

Հայտարարը պարզվեց, որ պարզապես հաստատուն է (հաստատուն թիվ, առանց փոփոխականի): Ածանցյալը շատ պարզ է.

Էքսպոնենցիալ և լոգարիթմական ֆունկցիաների ածանցյալները գրեթե երբեք չեն գտնում քննության ժամանակ, բայց դրանց իմացությունը ավելորդ չի լինի։

Բարդ ֆունկցիայի ածանցյալ։

Ի՞նչ է «բարդ ֆունկցիան»: Ոչ, սա լոգարիթմ չէ և աղեղային շոշափող չէ: Այս ֆունկցիաները կարող են դժվար հասկանալի լինել (չնայած եթե լոգարիթմը ձեզ դժվար է թվում, կարդացեք «Լոգարիթմներ» թեման և ամեն ինչ կստացվի), բայց մաթեմատիկայի առումով «բարդ» բառը չի նշանակում «դժվար»։

Պատկերացրեք մի փոքրիկ փոխակրիչ. երկու հոգի նստած և ինչ-որ գործողություններ են անում ինչ-որ առարկաներով: Օրինակ՝ առաջինը շոկոլադե սալիկը փաթաթում է փաթաթանով, իսկ երկրորդը կապում է ժապավենով։ Ստացվում է այսպիսի կոմպոզիտային առարկա՝ ժապավենով փաթաթված և կապած շոկոլադե սալիկ։ Շոկոլադե սալիկ ուտելու համար հարկավոր է հակառակ քայլերն անել հակառակ հերթականությամբ։

Եկեք ստեղծենք նմանատիպ մաթեմատիկական խողովակաշար՝ նախ կգտնենք թվի կոսինուսը, իսկ հետո ստացված թիվը կկտրենք։ Այսպիսով, նրանք մեզ տալիս են մի թիվ (շոկոլադ), ես գտնում եմ դրա կոսինուսը (փաթաթան), և հետո դուք քառակուսի եք կազմում իմ ստացածը (կապում եք ժապավենով): Ինչ է պատահել? Գործառույթ. Սա բարդ ֆունկցիայի օրինակ է. երբ դրա արժեքը գտնելու համար մենք կատարում ենք առաջին գործողությունը ուղղակիորեն փոփոխականի հետ, իսկ հետո ևս մեկ երկրորդ գործողություն՝ առաջինի արդյունքում տեղի ունեցածի հետ:

Այլ կերպ ասած, Կոմպլեքս ֆունկցիան այն ֆունկցիան է, որի արգումենտը մեկ այլ ֆունկցիա է: .

Մեր օրինակի համար.

Մենք կարող ենք նույն գործողությունները կատարել հակառակ հերթականությամբ. սկզբում դուք քառակուսի եք դնում, իսկ հետո ես փնտրում եմ ստացված թվի կոսինուսը. Հեշտ է կռահել, որ արդյունքը գրեթե միշտ տարբեր է լինելու։ Բարդ ֆունկցիաների կարևոր հատկանիշ. երբ փոխվում է գործողությունների հերթականությունը, ֆունկցիան փոխվում է։

Երկրորդ օրինակը (նույնը): .

Վերջին գործողությունը, որը մենք անում ենք, կկոչվի «արտաքին» գործառույթը, և առաջինը կատարված գործողությունը, համապատասխանաբար «ներքին» գործառույթը(սրանք ոչ պաշտոնական անուններ են, ես դրանք օգտագործում եմ միայն նյութը պարզ լեզվով բացատրելու համար):

Փորձեք ինքներդ որոշել, թե որ գործառույթն է արտաքին և որը ներքին.

Պատասխանները:Ներքին և արտաքին ֆունկցիաների տարանջատումը շատ նման է փոփոխվող փոփոխականներին. օրինակ՝ ֆունկցիայի մեջ

Ի՞նչ քայլեր ենք ձեռնարկելու առաջին հերթին: Սկզբում մենք հաշվարկում ենք սինուսը, և միայն դրանից հետո այն բարձրացնում ենք խորանարդի: Այսպիսով, դա ներքին գործառույթ է, ոչ թե արտաքին:
Իսկ սկզբնական գործառույթը նրանց կազմն է.
Ներքին: ; արտաքին:
Փորձաքննություն.
Ներքին: ; արտաքին:
Փորձաքննություն.
Ներքին: ; արտաքին:
Փորձաքննություն.
Ներքին: ; արտաքին:
Փորձաքննություն.

փոխում ենք փոփոխականները և ստանում ֆունկցիա։

Դե, հիմա մենք կքաղենք մեր շոկոլադը - փնտրեք ածանցյալը: Գործընթացը միշտ հակադարձվում է՝ սկզբում փնտրում ենք արտաքին ֆունկցիայի ածանցյալը, այնուհետև արդյունքը բազմապատկում ենք ներքին ֆունկցիայի ածանցյալով։ Բնօրինակի օրինակի համար այն ունի հետևյալ տեսքը.

Մեկ այլ օրինակ.

Այսպիսով, վերջապես ձևակերպենք պաշտոնական կանոնը.

Բարդ ֆունկցիայի ածանցյալը գտնելու ալգորիթմ.

Թվում է, թե պարզ է, չէ՞:

Եկեք ստուգենք օրինակներով.

Լուծումներ:

1) Ներքին՝ ;

Արտաքին:

2) ներքին՝ ;

(ուղղակի մի փորձեք նվազեցնել մինչ այժմ: Կոսինուսի տակից ոչինչ չի հանվում, հիշո՞ւմ եք):

3) ներքին՝ ;

Արտաքին:

Միանգամից պարզ է դառնում, որ այստեղ եռաստիճան բարդ ֆունկցիա կա. ի վերջո, սա արդեն ինքնին բարդ ֆունկցիա է, և մենք դեռ արմատը հանում ենք դրանից, այսինքն՝ կատարում ենք երրորդ գործողությունը (շոկոլադը դնում ենք փաթաթայի մեջ։ և ժապավենով պայուսակի մեջ): Բայց վախենալու պատճառ չկա. ամեն դեպքում, մենք այս գործառույթը «կբացենք» սովորական հերթականությամբ՝ վերջից։

Այսինքն՝ սկզբում տարբերակում ենք արմատը, հետո կոսինուսը, հետո միայն փակագծերում արտահայտությունը։ Եվ հետո մենք բազմապատկում ենք այդ ամենը:

Նման դեպքերում հարմար է համարակալել գործողությունները։ Այսինքն՝ պատկերացնենք, թե ինչ գիտենք։ Ի՞նչ հերթականությամբ ենք մենք կատարելու գործողություններ այս արտահայտության արժեքը հաշվարկելու համար: Դիտարկենք օրինակ.

Որքան ուշ կատարվի գործողությունը, այնքան «արտաքին» կլինի համապատասխան գործառույթը։ Գործողությունների հաջորդականությունը - ինչպես նախկինում.

Այստեղ բնադրումը հիմնականում 4 մակարդակ է։ Եկեք որոշենք գործողությունների ընթացքը.

1. Արմատական արտահայտություն. .

2. Արմատ. .

3. Սինուս. .

4. Քառակուսի. .

5. Բոլորը միասին դնելով.

ածանցյալ. ՀԱՄԱՌՈՏ ՀԻՄՆԱԿԱՆ ՄԱՍԻՆ

Ֆունկցիայի ածանցյալ- ֆունկցիայի աճի հարաբերակցությունը փաստարկի ավելացմանը՝ փաստարկի անվերջ փոքր աճով.

Հիմնական ածանցյալներ.

Տարբերակման կանոններ.

հաստատունը հանվում է ածանցյալի նշանից.

Գումարի ածանցյալը:

Ածանցյալ արտադրանք.

Գործակիցի ածանցյալ.

Բարդ ֆունկցիայի ածանցյալ.

Բարդ ֆունկցիայի ածանցյալը գտնելու ալգորիթմ.

Սահմանում ենք «ներքին» ֆունկցիան, գտնում դրա ածանցյալը։
Սահմանում ենք «արտաքին» ֆունկցիան, գտնում դրա ածանցյալը։
Մենք բազմապատկում ենք առաջին և երկրորդ կետերի արդյունքները:

Կարելի է հանել ցուցանակից ածանցյալ:

(af(x)"=af" (x).

Օրինակ:

Հանրահաշվական գումարի ածանցյալմի քանի ֆունկցիա (վերցված հաստատուն թվով) հավասար է դրանց հանրահաշվական գումարին ածանցյալներ:

(f 1 (x) + f 2 (x) - f 3 (x))" = f 1 "(x) + f 2 "(x) - f 3 "(x):

Օրինակ:

(0.3 x 2 - 2 x + 0.8) «= (0.3 x 2)» - (2 x) «+ (0.8)» = 0.6 x - 2 ( ածանցյալվերջին ժամկետըհավասարումը զրո է):

Եթե ֆունկցիայի ածանցյալ g-ն ոչ զրոյական է, ապա ունի նաև f/g հարաբերակցությունը վերջնական ածանցյալ. Այս հատկությունը կարելի է գրել այսպես.

Թող գործառույթները y = f(x) և y = g(x) ունեն վերջավոր ածանցյալներ x 0 կետում: Հետո գործառույթները f ± g և f g ունեն նաև վերջնական ածանցյալներըսա կետ. Այնուհետև մենք ստանում ենք.

(f ± g) ′ = f ′ ± g ′,

(f g) ′ = f ′ g + f g ′:

Բարդ ֆունկցիայի ածանցյալ։

Թող ֆունկցիան y = f(x) ունի վերջնական ածանցյալ մի կետում x 0, z = s(y) ֆունկցիան ունի վերջավոր ածանցյալ y կետում 0 = f(x 0):

Հետո բարդ գործառույթ z = s (f(x)) այս կետում ունի նաև վերջավոր ածանցյալ: Սա կարելի է գրել ձևով.

Հակադարձ ֆունկցիայի ածանցյալ.

Թող y = f(x) ֆունկցիան ունենա հակադարձ ֆունկցիա x = g(y) որոշների վրա ընդմիջում(a, b) և գոյություն ունի ոչ զրոյական վերջնական ածանցյալայս ֆունկցիան x 0 կետում, որը պատկանում է տիրույթներ, այսինքն. x 0 ∈ (a, b).

Հետո հակադարձ ֆունկցիաԱյն ունի ածանցյալկետում y 0 = f(x 0):

Իմպլիցիտ ֆունկցիայի ածանցյալ:

Եթե ֆունկցիան y = f(x) անուղղակիորեն սահմանված է հավասարումը F(x, y(x)) = 0, ապա դրա ածանցյալհայտնաբերվում է պայմանից.

Նրանք դա ասում են ֆունկցիան y = f(x) սահմանել անուղղակիորեն, Եթե նա նույնությամբբավարարում է հարաբերությունը.

որտեղ F(x, y) երկու արգումենտների ինչ-որ ֆունկցիա է:

Պարամետրականորեն տրված ֆունկցիայի ածանցյալ:

Եթե ֆունկցիան y = f(x) տրված է պարամետրականորեն՝ օգտագործելով դիտարկվածը

Բացարձակապես անհնար է լուծել մաթեմատիկայի ֆիզիկական խնդիրներ կամ օրինակներ՝ առանց դրա ածանցյալի և դրա հաշվարկման մեթոդների իմացության։ Ածանցյալը մաթեմատիկական վերլուծության ամենակարևոր հասկացություններից է։ Մենք որոշեցինք այսօրվա հոդվածը նվիրել այս հիմնարար թեմային: Ի՞նչ է ածանցյալը, ի՞նչ ֆիզիկական և երկրաչափական նշանակություն ունի, ինչպե՞ս հաշվարկել ֆունկցիայի ածանցյալը։ Այս բոլոր հարցերը կարելի է միավորել մեկի մեջ՝ ինչպե՞ս հասկանալ ածանցյալը:

Ածանցյալի երկրաչափական և ֆիզիկական նշանակությունը

Թող ֆունկցիա լինի f(x) , տրված որոշակի ընդմիջումով (ա, բ) . Այս միջակայքին են պատկանում x և x0 կետերը։ Երբ x-ը փոխվում է, ֆունկցիան ինքնին փոխվում է: Փաստարկի փոփոխություն - դրա արժեքների տարբերություն x-x0 . Այս տարբերությունը գրված է այսպես դելտա x և կոչվում է արգումենտի ավելացում։ Ֆունկցիայի փոփոխությունը կամ ավելացումը երկու կետում ֆունկցիայի արժեքների տարբերությունն է: Ածանցյալ սահմանում.

Մի կետում ֆունկցիայի ածանցյալը տվյալ կետում ֆունկցիայի աճի հարաբերակցության սահմանն է փաստարկի աճին, երբ վերջինս հակված է զրոյի:

Հակառակ դեպքում կարելի է գրել այսպես.

Ի՞նչ իմաստ ունի նման սահման գտնելը։ Բայց ո՞րը.

Կետում ֆունկցիայի ածանցյալը հավասար է OX առանցքի անկյան շոշափմանը և տվյալ կետում ֆունկցիայի գրաֆիկին շոշափողին:

Ածանցյալի ֆիզիկական նշանակությունը. ճանապարհի ժամանակային ածանցյալը հավասար է ուղղագիծ շարժման արագությանը։

Իսկապես, դպրոցական օրերից բոլորը գիտեն, որ արագությունը մասնավոր ճանապարհ է։ x=f(t) և ժամանակ տ . Միջին արագությունը որոշակի ժամանակահատվածում.

Միանգամից շարժման արագությունը պարզելու համար t0 դուք պետք է հաշվարկեք սահմանը.

Կանոն առաջին. հանել հաստատունը

Հաստատունը կարելի է հանել ածանցյալի նշանից։ Ավելին, դա պետք է արվի. Մաթեմատիկայի օրինակներ լուծելիս, որպես կանոն, վերցրեք. եթե դուք կարող եք պարզեցնել արտահայտությունը, անպայման պարզեցրեք .

Օրինակ. Եկեք հաշվարկենք ածանցյալը.

Կանոն երկրորդ՝ ֆունկցիաների գումարի ածանցյալ

Երկու ֆունկցիաների գումարի ածանցյալը հավասար է այս ֆունկցիաների ածանցյալների գումարին։ Նույնը վերաբերում է ֆունկցիաների տարբերության ածանցյալին։

Մենք չենք տա այս թեորեմի ապացույցը, այլ ավելի շուտ կդիտարկենք գործնական օրինակ:

Գտե՛ք ֆունկցիայի ածանցյալը.

Երրորդ կանոն՝ ֆունկցիաների արտադրյալի ածանցյալ

Երկու տարբերակելի ֆունկցիաների արտադրյալի ածանցյալը հաշվարկվում է բանաձևով.

Օրինակ՝ գտե՛ք ֆունկցիայի ածանցյալը.

Լուծում:

Այստեղ կարևոր է ասել բարդ ֆունկցիաների ածանցյալների հաշվարկի մասին։ Կոմպլեքս ֆունկցիայի ածանցյալը հավասար է այս ֆունկցիայի ածանցյալի արտադրյալին միջանկյալ փաստարկի նկատմամբ միջանկյալ փաստարկի ածանցյալին անկախ փոփոխականի նկատմամբ։

Վերոնշյալ օրինակում մենք հանդիպում ենք արտահայտության.

Այս դեպքում միջանկյալ արգումենտը 8x է հինգերորդ ուժին: Նման արտահայտության ածանցյալը հաշվարկելու համար մենք նախ դիտարկում ենք արտաքին ֆունկցիայի ածանցյալը միջանկյալ արգումենտի նկատմամբ, այնուհետև բազմապատկում ենք հենց միջանկյալ փաստարկի ածանցյալով՝ անկախ փոփոխականի նկատմամբ։

Չորրորդ կանոն. Երկու ֆունկցիաների քանորդի ածանցյալ

Երկու ֆունկցիաների քանորդի ածանցյալի որոշման բանաձև.

Մենք փորձեցինք խոսել զրոյից ածանցյալների մասին: Այս թեման այնքան էլ պարզ չէ, որքան թվում է, այնպես որ զգուշացե՛ք. օրինակներում հաճախ են որոգայթներ, ուստի զգույշ եղեք ածանցյալները հաշվարկելիս:

Այս և այլ թեմաների վերաբերյալ ցանկացած հարցով կարող եք դիմել ուսանողական ծառայությանը: Կարճ ժամանակում մենք կօգնենք ձեզ լուծել ամենադժվար վերահսկողությունը և զբաղվել առաջադրանքներով, նույնիսկ եթե նախկինում երբեք չեք զբաղվել ածանցյալների հաշվարկով: