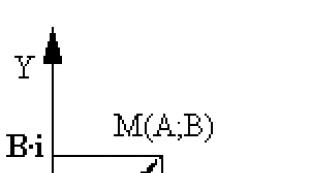ՊԱՏՄԱԿԱՆ ԱՌԱՋՆՈՐԴԵՑ

Կոմպլեքս թվերը ներմուծվեցին մաթեմատիկա, որպեսզի հնարավոր լինի վերցնել ցանկացած իրական թվի քառակուսի արմատը։ Սա, սակայն, բավարար պատճառ չէ մաթեմատիկայի մեջ նոր թվեր ներմուծելու համար։ Պարզվեց, որ եթե դուք հաշվարկներ կատարեք սովորական կանոնների համաձայն այն արտահայտությունների վրա, որոնցում առաջանում է բացասական թվի քառակուսի արմատ, ապա կարող եք գալ մի արդյունքի, որն այլևս չի պարունակում բացասական թվի քառակուսի արմատը: XVI դ. Կարդանոն գտել է խորանարդ հավասարման լուծման բանաձեւը. Պարզվեց, որ երբ խորանարդ հավասարումն ունի երեք իրական արմատ, բացասական թվի քառակուսի արմատը տեղի է ունենում Կարդանոյի բանաձևում: Հետևաբար, բացասական թվերի քառակուսի արմատները սկսեցին օգտագործվել մաթեմատիկայի մեջ և դրանք անվանեցին երևակայական թվեր, դրանով իսկ, այսպես ասած, նրանք ձեռք բերեցին անօրինական գոյության իրավունք: Գաուսը լիարժեք քաղաքացիական իրավունքներ տվեց երևակայական թվերին, ով դրանք անվանեց բարդ թվեր, տվեց երկրաչափական մեկնաբանություն և ապացուցեց հանրահաշվի հիմնարար թեորեմը, որն ասում է, որ յուրաքանչյուր բազմանդամ ունի առնվազն մեկ իրական արմատ:

1. ՀԱՄԱԼԻՐ ԹՎԻ ՀԱՍԿԱՑՈՒԹՅՈՒՆԸ

Մաթեմատիկայի և ֆիզիկայի բազմաթիվ խնդիրների լուծումը կրճատվում է հանրահաշվական հավասարումների լուծման վրա։ Ուստի հանրահաշվական հավասարումների ուսումնասիրությունը մաթեմատիկայի ամենակարեւոր հարցերից է։ Հավասարումները լուծելի դարձնելու ցանկությունը թիվ հասկացության ընդլայնման հիմնական պատճառներից մեկն է։

Այսպիսով, X+A=B ձևի հավասարումների լուծելիության համար դրական թվերը բավարար չեն։ Օրինակ, X+5=2 հավասարումը չունի դրական արմատներ։ Հետեւաբար, դուք պետք է մուտքագրեք բացասական թվեր և զրո:

Ռացիոնալ թվերի բազմության վրա լուծելի են առաջին աստիճանի հանրահաշվական հավասարումները, այսինքն. A · X+B=0 (A0) ձևի հավասարումներ. Այնուամենայնիվ, մեկից բարձր աստիճանի հանրահաշվական հավասարումները կարող են ռացիոնալ արմատներ չունենալ: Օրինակ, այդպիսիք են X 2 =2, X 3 =5 հավասարումները: Նման հավասարումների լուծման անհրաժեշտությունը իռացիոնալ թվերի ներդրման պատճառներից մեկն էր։ Ռացիոնալ և իռացիոնալ թվերը կազմում են իրական թվերի բազմությունը:

Սակայն իրական թվերը բավարար չեն հանրահաշվական որևէ հավասարում լուծելու համար։ Օրինակ՝ իրական գործակիցներով և բացասական դիսկրիմինանտով քառակուսի հավասարումը իրական արմատներ չունի: Դրանցից ամենապարզը X 2 +1=0 հավասարումն է։ Ուստի անհրաժեշտ է ընդլայնել իրական թվերի բազմությունը՝ դրան ավելացնելով նոր թվեր։ Այս նոր թվերը իրական թվերի հետ միասին կազմում են մի բազմություն, որը կոչվում է բազմություն բարդ թվեր.

Նախ պարզենք, թե ինչ ձև պետք է ունենան կոմպլեքս թվերը։ Ենթադրում ենք, որ բարդ թվերի բազմության վրա X 2 +1=0 հավասարումն ունի արմատ։ Այս արմատը նշում ենք տառով ես Այսպիսով, ես այնպիսի բարդ թիվ է, որ ես 2 = –1.

Ինչ վերաբերում է իրական թվերին, ապա պետք է ներկայացնել բարդ թվերի գումարման և բազմապատկման գործողությունները, որպեսզի դրանց գումարը և արտադրյալը լինեն կոմպլեքս թվեր։ Այնուհետև, մասնավորապես, ցանկացած իրական թվերի համար A + B արտահայտությունը ես կարելի է դիտարկել որպես բարդ թվի ընդհանուր ներկայացում: «Բարդ» անվանումը առաջացել է «կոմպոզիտ» բառից՝ A + B արտահայտության ձևով ես .

Կոմպլեքս թվեր կոչվում են A+B ձևի արտահայտություններ ես , որտեղ A-ն և B-ն իրական թվեր են, և ես ինչ-որ կերպար այնպիսին է, որ ես 2 = –1, և նշվում է Z տառով:

A թիվը կոչվում է A+B բարդ թվի իրական մասը ես, իսկ B թիվը նրա երևակայական մասն է։ Թիվ ես կոչվում է երևակայական միավոր:

Օրինակ՝ 2+3 համարի համալիրի իրական մասը ես 2 է, իսկ երևակայականը՝ 3։

Կոմպլեքս թվի խիստ սահմանման համար անհրաժեշտ է ներմուծել այդ թվերի հավասարության հայեցակարգը:

Երկու կոմպլեքս թվեր A+B ես և C+D ես կանչեց հավասարեթե և միայն եթե A=C և B=D, այսինքն. երբ նրանց իրական և երևակայական մասերը հավասար են:

2. ՀԱՄԱԼԻՐ ԹՎԻ ԵՐԿՐԱՉԱՓԱԿԱՆ ՄԵԿՆԱԲԱՆՈՒԹՅՈՒՆԸ

Իրական թվերը երկրաչափորեն ներկայացված են թվային տողի կետերով: Համալիր թիվ A+B ես կարելի է դիտել որպես իրական թվերի զույգ (A;B): Հետևաբար, բնական է բարդ թիվը ներկայացնել հարթության կետերի տեսքով: Ուղղանկյուն կոորդինատային համակարգում կոմպլեքս թիվը Z=A+B· ես ներկայացված է հարթ կետով՝ կոորդինատներով (A;B), և այս կետը նշվում է նույն Z տառով (Նկար 1): Ակնհայտ է, որ այս դեպքում ձեռք բերված նամակագրությունը մեկ առ մեկ է։ Այն հնարավորություն է տալիս կոմպլեքս թվերը մեկնաբանել որպես հարթության կետեր, որոնց վրա ընտրված է կոորդինատային համակարգը: Այս կոորդինատային հարթությունը կոչվում է բարդ հարթություն . The abscissa կոչվում է իրական առանցք , որովհետեւ դրա վրա կան իրական թվերին համապատասխանող կետեր: y առանցքը կոչվում է երևակայական առանցք – այն պարունակում է երևակայական բարդ թվերին համապատասխան կետեր:

Ոչ պակաս կարևոր և հարմար է A+B բարդ թվի մեկնաբանությունը ես որպես վեկտոր, այսինքն. վեկտորներ, որոնք ծագում են մի կետում

O(0;0) և ավարտվում է M(A;B) կետով (Նկար 2):

Կոմպլեքս թվերի բազմության միջև հաստատված համապատասխանությունը, մի կողմից, և հարթության կետերի կամ վեկտորների բազմությունների միջև, մյուս կողմից, թույլ է տալիս բարդ թվերին լինել կետեր կամ վեկտորներ։

3.ՀԱՄԱԼԻՐ ԹԻՎԻ ՄՈԴՈՒԼ

Թող կոմպլեքս թիվ Z=A+B· ես . Խոնարհված Հետ Զկոչվում է կոմպլեքս A – B թիվը ես , որը նշանակվում է , այսինքն.

Ա-Բ ես .

Նկատի ունեցեք, որ = A + B ես , ուրեմն ցանկացած Z թվի համար ունենք =Z հավասարություն։

մոդուլ կոմպլեքս թիվ Z=A+B ես կանչեց թիվև նշվում է , այսինքն.

Բանաձևից (1) հետևում է, որ Z ցանկացած բարդ թվի համար և =0, եթե և միայն Z=0, այսինքն. երբ A=0 և B=0: Եկեք ապացուցենք, որ ցանկացած բարդ թվի համար Z բանաձևերը վավեր են.

4. ՀԱՄԱԼԻՐ ԹՎԵՐԻ ՀԱՎԵԼՈՒՄ ԵՎ ԲԱԶՄԱՑՆՈՒՄ

գումար երկու կոմպլեքս թվեր A+B ես և C+D ես կոչվում է կոմպլեքս թիվ (A+C ) + ( B+D)· ես , այսինքն. ( A+B ես) + ( C+D ես)=( A+C) + (B+D) ես

աշխատանք երկու կոմպլեքս թվեր A+B ես և C+D ես կոչվում է կոմպլեքս թիվ (A C – B D)+(A D+B C) ես , այսինքն.

(A + B ես ) (C + D ես )=(A C – B D) + (A D + B C) ես

Բանաձևերից բխում է, որ գումարումը և բազմապատկումը կարելի է կատարել բազմանդամների հետ գործողությունների կանոններով՝ ենթադրելով. ես 2 = -1: Կոմպլեքս թվերի գումարման և բազմապատկման գործողություններն ունեն իրական թվերի հատկություններ: Հիմնական հատկություններ.

Գույքի փոխանցում.

Z 1 + Z 2 \u003d Z 2 + Z 1, Z 1 Z 2 \u003d Z 2 Z 1

Ասոցիատիվ հատկություն.

(Z 1 + Z 2) + Z 3 \u003d Z 1 + (Z 2 + Z 3), (Z 1 Z 2) Z 3 \u003d Z 1 (Z 2 Z 3)

Բաշխման սեփականություն.

Z 1 (Z 2 + Z 3) \u003d Z 1 Z 2 + Z 1 Z 3

Կոմպլեքս թվերի գումարի երկրաչափական պատկերը

Երկու բարդ թվերի գումարման սահմանման համաձայն՝ գումարի իրական մասը հավասար է անդամների իրական մասերի գումարին, գումարի երևակայական մասը հավասար է անդամների երևակայական մասերի գումարին։ Վեկտորների գումարի կոորդինատները որոշվում են նույն կերպ.

Կոորդինատներով երկու վեկտորների գումարը (A 1 ;B 1) և (A 2 ;B 2) կոորդինատներով վեկտոր է (A 1 +A 2 ;B 1 +B 2): Հետևաբար, Z 1 և Z 2 կոմպլեքս թվերի գումարին համապատասխան վեկտորը գտնելու համար անհրաժեշտ է գումարել Z 1 և Z 2 կոմպլեքս թվերին համապատասխան վեկտորները։

Օրինակ 1: Գտե՛ք Z 1 =2 - 3× կոմպլեքս թվերի գումարը և արտադրյալը ես Եվ

Z 2 \u003d -7 + 8 × ես .

Z 1 + Z 2 \u003d 2 - 7 + (-3 + 8) × ես = - 5 + 5× ես

Z 1× Z 2 = (2 – 3× ես )× (–7 + 8× ես ) = –14 + 16× ես + 21× ես + 24 = 10 + 37× ես

5. ԲԱԺԻՆ ԹՎԵՐԻ ՀԱՆՑՈՒՄ ԵՎ ԲԱԺԱՆՈՒՄ

Կոմպլեքս թվերի հանումը գումարման հակադարձ գործողությունն է. Z 1 և Z 2 ցանկացած բարդ թվերի համար գոյություն ունի, և ավելին, միայն մեկը՝ Z թիվը, այնպիսին, որ.

Եթե ​​հավասարության երկու մասերին (–Z 2) գումարենք Z 2 թվի հակադիրը.

Z + Z 2 + (-Z 2) \u003d Z 1 + (-Z 2), որտեղից

Z \u003d Z 1 + Z 2 թիվը կոչվում է թվերի տարբերություն Z 1 և Z 2.

Բաժանումը ներկայացվում է որպես բազմապատկման հակադարձ.

Z × Z 2 \u003d Z 1

Երկու մասերը բաժանելով Z 2-ի վրա՝ ստանում ենք.

Այս հավասարումը ցույց է տալիս, որ Z 2 0

Կոմպլեքս թվերի տարբերության երկրաչափական պատկերը

Z 1 և Z 2 կոմպլեքս թվերի Z 2 - Z 1 տարբերությունը համապատասխանում է Z 1 և Z 2 թվերին համապատասխանող վեկտորների տարբերությանը։ Երկու կոմպլեքս թվերի Z 2 և Z 1 տարբերության մոդուլը ըստ մոդուլի սահմանման Z 2 - Z 1 վեկտորի երկարությունն է: Մենք կառուցում ենք այս վեկտորը որպես Z 2 և (–Z 1) վեկտորների գումար (Նկար 4): Այսպիսով, երկու կոմպլեքս թվերի տարբերության մոդուլը բարդ հարթության այն կետերի հեռավորությունն է, որոնք համապատասխանում են այդ թվերին։

Երկու բարդ թվերի տարբերության մոդուլի այս կարևոր երկրաչափական մեկնաբանությունը հնարավորություն է տալիս հաջողությամբ օգտագործել պարզ երկրաչափական փաստեր։

Օրինակ 2: Տրված են կոմպլեքս թվեր Z 1 = 4 + 5 ես և Z 2 = 3 + 4 ես . Գտե՛ք Z 2 - Z 1 տարբերությունը և գործակիցը

Z 2 - Z 1 \u003d (3 + 4) ես) – (4 + 5 ես) = –1 – ես

==

6. ՀԱՄԱԼԻՐ ԹՎԻ ԵՌԱԳՈՆՈՄԵՏՐԻԱԿԱՆ ՁԵՎԸ

Z կոմպլեքս թիվը A+B ձևով գրելը ես կանչեց հանրահաշվական ձև համալիր համարը. Բացի հանրահաշվական ձևից, օգտագործվում են նաև բարդ թվեր գրելու այլ ձևեր։

Հաշվի առեք եռանկյունաչափական ձև բարդ թվի նշում. Z=A+B կոմպլեքս թվի իրական և երևակայական մասեր ես արտահայտվում են իր մոդուլով = r և j արգումենտով հետևյալ կերպ.

A= r cosj; Բ= ր սինջ .

Z թիվը կարելի է գրել այսպես.

Z= r cosj + ես sinj = r (cosj + ես սինջ)

Z = r (cosj + ես սինջ ) (2)

Այս մուտքը կոչվում է բարդ թվի եռանկյունաչափական ձև .

r = կոմպլեքս թվի մոդուլն է:

j թիվը կոչվում է բարդ թվի արգումենտ.

Z0 կոմպլեքս թվի արգումենտը իրական առանցքի դրական ուղղության և Z վեկտորի միջև անկյան արժեքն է, իսկ անկյան արժեքը համարվում է դրական, եթե հաշվարկը ժամացույցի սլաքի ուղղությամբ է, իսկ բացասական, եթե այն ժամացույցի սլաքի ուղղությամբ է:

Z=0 թվի համար արգումենտը սահմանված չէ, և միայն այս դեպքում է թիվը տրվում միայն իր մոդուլով։

Ինչպես նշվեց վերևում = r =, հավասարությունը (2) կարող է գրվել որպես

A+B ես =· cosj + ես · սինջ,որտեղից, հավասարեցնելով իրական և երևակայական մասերը, ստանում ենք.

կոսժ =, սինջ = (3)

Եթե սինջբաժանել ըստ կոսժմենք ստանում ենք.

տգյ= (4)

Այս բանաձեւը ավելի հարմար է օգտագործել j փաստարկը գտնելու համար, քան բանաձեւերը (3): Այնուամենայնիվ, j-ի ոչ բոլոր արժեքները, որոնք բավարարում են հավասարությունը (4) A + B թվի արգումենտներ են: ես . Ուստի փաստարկը գտնելիս պետք է հաշվի առնել, թե որ քառորդում է գտնվում A + B կետը ես .

7. ՄՈԴՈՒԼԻ ԵՎ ՀԱՄԱԼԻՐ ԹԻՎԻ փաստարկի հատկությունները.

Օգտագործելով եռանկյունաչափական ձևը՝ հարմար է գտնել կոմպլեքս թվերի արտադրյալը և գործակիցը։

Թող Z 1 = r 1 ( cosj 1 +եսսինջ 1), Z 2 = r 2 ( cosj 2 +եսսինջ 2).Ապա.

Z 1 Z 2 = r 1 r 2 =

= r 1 r 2 .

Այսպիսով, եռանկյունաչափական ձևով գրված բարդ թվերի արտադրյալը կարելի է գտնել բանաձևով.

Z 1 Z 2 = r 1 r 2 (5)

Բանաձևից (5) հետևում է, որ երբ կոմպլեքս թվերը բազմապատկվում են, դրանց մոդուլները բազմապատկվում են և արգումենտները գումարվում են:

Եթե ​​Z 1 \u003d Z 2, ապա մենք ստանում ենք.

Z2=2= r 2 (cos2j +ես sin2j)

Z 3 \u003d Z 2 Z \u003d r 2 ( cos2j +ես sin2j ) r (cosj + եսսինջ )=

= r 3 ( cos3j +ես sin3j)

Ընդհանուր առմամբ, ցանկացած բարդ թվի համար Զ=r (cosj + եսսինջ) 0և ցանկացած բնական թիվ n, բանաձևը վավեր է.

Zn=[ r (cosj + ես sinj )] n = r n (cosnj + եսսինջ),(6)

որը կոչվում է De Moivre-ի բանաձեւ.

Եռանկյունաչափական ձևով գրված երկու բարդ թվերի գործակիցը կարելի է գտնել բանաձևով.

[cos(j 1 – j 2) + եսմեղք (j 1 - j 2)]:(7)

= = cos(–j 2) + եսմեղք (–j 2)

Օգտագործելով բանաձև 5

(cosj 1 + ես sinj 1)× (cos(–j 2) + ես sin(–j 2)) =

cos(j 1 – j 2) + եսմեղք (j 1 - j 2):

Օրինակ 3:

-8 թիվը գրում ենք եռանկյունաչափական տեսքով

8 = 8 (cos(p + 2p k) + ես sin(p + 2p k )), k О Z

Թող Z = r× (cosj + i×

r 3× (cos3j + i× sin3j ) = 8 (cos(p + 2p k ) + ես sin(p + 2p k )), k О Z

Ապա 3j =p + 2p k , k О Z

ժ= , k О Զ

Հետևաբար.

Z = 2 (cos() + ես sin()), k О Z

k = 0,1,2...

k = 0

Z 1 = 2 (cos + եսմեղք) = 2 ( ես) = 1+× ես

k = 1

Z 2 = 2 (cos( ​​+ ) + ես sin( + )) = 2 (cosp + ես sinp) = –2

k = 2

Z 3 = 2 (cos( ​​+ ) + ես sin( + )) = 2 (cos + եսմեղք) = 1–× ես

Պատասխան՝ Z 13 =; Z 2 \u003d -2

Օրինակ 4:

1 թիվը գրում ենք եռանկյունաչափական ձևով

1 = 1 (cos(2p k) + ես sin(2p k )), k О Z

Թող Z = r× (cosj + i× sinj ), ապա այս հավասարումը կգրվի այսպես.

r 4× (cos4j + i× sin4j ) = cos(2p k) + ես sin(2p k )), k О Z

4j = 2p k , k О Z

j = , k О Z

Z = cos+ i× մեղք

k = 0,1,2,3...

k = 0

Z1 = cos0+ i× sin0 = 1 + 0 = 1

k = 1

Z2 = cos+ i× մեղք=0+ ես = ես

k = 2

Z 3 \u003d cosp + ես sinp = -1 + 0 = -1

k = 3

Z4 = cos+ i× մեղք

Պատասխան՝ Z 13 = 1

Z 24 = ես

8. Արմատի հզորացում և արդյունահանում

Բանաձև 6-ը ցույց է տալիս, որ r համալիր թիվը բարձրացնելը (cosj + ես sinj ) բնական ցուցիչով դրական ամբողջ թվին, նրա մոդուլը բարձրացվում է նույն ցուցիչով հզորության, իսկ արգումենտը բազմապատկվում է ցուցիչով:

[ r (cosj + ես sinj )] n = r n (cos nj + ես sin nj )

Թիվ Զկանչեց աստիճանի արմատ n w թվից (նշվում է ), եթե Z n =w .

Այս սահմանումից հետևում է, որ հավասարման յուրաքանչյուր լուծում Z n = wաստիճանի արմատն է n w թվից։ Այսինքն՝ աստիճանի արմատը հանելու համար n w թվից բավական է լուծել հավասարումը Z n =w.Եթե ​​w =0, ապա ցանկացած n-ի համար հավասարումը Z n = wունի միայն մեկ լուծում Զ= 0. Եթե ​​w 0, ապա Զ0 , և, հետևաբար, Z և w-ը կարող են ներկայացվել եռանկյունաչափական ձևով

Z = r (cosj + ես sinj ), w = p (հարմարավետ + ես մեղսավոր)

Z n = w հավասարումը կունենա հետևյալ ձևը.

r n (cos nj + ես sin nj ) = p (հարմարավետ + ես մեղսավոր)

Երկու կոմպլեքս թվեր հավասար են, եթե և միայն այն դեպքում, եթե դրանց մոդուլները հավասար են, և դրանց արգումենտները տարբերվում են 2p-ի բազմապատիկ թվերով: Հետևաբար, r n = p և nj = y + 2p k , որտեղ kн Z կամ r = և ժ= , որտեղ kн Z .

Այսպիսով, բոլոր լուծումները կարելի է գրել հետևյալ կերպ.

Z K =, kn Z (8)

Formula 8-ը կոչվում է De Moivre-ի երկրորդ բանաձեւը.

Այսպիսով, եթե w 0, ապա w թվից կա n աստիճանի ճիշտ n արմատ. բոլորն էլ պարունակվում են 8-րդ բանաձևում: Աստիճանի բոլոր արմատները n w թվից ունեն նույն մոդուլը, բայց տարբեր արգումենտներ, որոնք տարբերվում են գումարի չափով, որը թվի բազմապատիկն է: Հետևում է, որ բարդ թվերը, որոնք n աստիճանի արմատներ են w կոմպլեքս թվից, համապատասխանում են բարդ հարթության կետերին, որոնք գտնվում են կետում կենտրոնացված շառավղով շրջանագծի գագաթներում գտնվող կանոնավոր n-անկյունի գագաթներում։ Z = 0:

Խորհրդանիշը միանշանակ նշանակություն չունի։ Հետեւաբար, այն օգտագործելիս պետք է հստակ հասկանալ, թե ինչ է նշանակում այս խորհրդանիշը: Օրինակ, օգտագործելով նշումը, դուք պետք է մտածեք պարզ դարձնելու մասին, որ այս նշանը նշանակում է զույգ բարդ թվեր ես Եվ -ի , կամ մեկը, հետո ո՞րը։

Բարձրագույն ուժերի հավասարումներ

Բանաձև 8-ը սահմանում է n աստիճանի երկակի հավասարման բոլոր արմատները: Իրավիճակն անչափ ավելի բարդ է n աստիճանի ընդհանուր հանրահաշվական հավասարման դեպքում.

a n × Z n+ a n–1× Z n–1 +...+ a 1× Z 1 + a 0 = 0(9)

Որտեղ a n,..., a 0 տրված են կոմպլեքս թվեր:

Բարձրագույն մաթեմատիկայի ընթացքում ապացուցվում է Գաուսի թեորեմը. յուրաքանչյուր հանրահաշվական հավասարում ունի առնվազն մեկ արմատ բարդ թվերի բազմության մեջ։ Այս թեորեմն ապացուցել է գերմանացի մաթեմատիկոս Կարլ Գաուսը 1779 թվականին։

Գաուսի թեորեմի հիման վրա մենք կարող ենք ապացուցել, որ 9-րդ հավասարման ձախ կողմը միշտ կարող է ներկայացվել որպես արտադրյալ.

,

Որտեղ Z 1, Z 2,..., Z K որոշ տարբեր բարդ թվեր են,

իսկ a 1 ,a 2 ,...,a k-ը բնական թվեր են, և.

a 1 + a 2 + ... + a k = n

Սա ենթադրում է, որ Z 1, Z 2,..., Z K թվերը 9-րդ հավասարման արմատներն են: Այս դեպքում ասում են, որ Z 1-ը a 1-ի բազմակի արմատն է, Z 2-ը a 2-ի բազմակի արմատն է և այսպես շարունակ։

Գաուսի թեորեմը և հենց նոր ձևակերպված թեորեմը լուծումներ են տալիս արմատների գոյության մասին, բայց ոչինչ չեն ասում, թե ինչպես գտնել այդ արմատները։ Եթե ​​առաջին և երկրորդ աստիճանների արմատները հեշտությամբ կարելի է գտնել, ապա երրորդ և չորրորդ ուժերի հավասարումների համար բանաձևերը ծանր են, իսկ չորրորդից բարձր աստիճանի հավասարումների համար նման բանաձևեր ընդհանրապես գոյություն չունեն։ Ընդհանուր մեթոդի բացակայությունը չի խանգարում գտնել հավասարման բոլոր արմատները: Ամբողջ թվային գործակիցներով հավասարումը լուծելու համար հաճախ օգտակար է հետևյալ թեորեմը. ամբողջ թվային գործակիցներով ցանկացած հանրահաշվական հավասարման ամբողջ արմատները հաստատուն անդամի բաժանարարներ են։

Եկեք ապացուցենք այս թեորեմը.

Թող Z = k հավասարման ամբողջ արմատը լինի

a n× Z n + a n–1× Z n–1 +...+ a 1× Z 1 + a 0 = 0

ամբողջ թվային գործակիցներով։ Հետո

a n× k n + a n–1× k n–1 +...+ a 1× k 1 + a 0 = 0

a 0 = – k(a n× k n–1 + a n–1× k n–2 +...+ a 1)

Փակագծերում գտնվող թիվը, ըստ արված ենթադրությունների, ակնհայտորեն ամբողջ թիվ է, ինչը նշանակում է, որ k-ն a 0 թվի բաժանարարն է:

9.ՔՈՎԱԴՐԱՏԻԿ ՀԱՎԱՍԱՐՈՒՄ ԱՆՀԱՅՏԻ ԲԱՐԴԻ ՀԵՏ

Դիտարկենք Z 2 = a հավասարումը, որտեղ a-ն տրված իրական թիվ է, Z-ն անհայտ է:

Սա հավասարումն է.

Ա թիվը գրում ենք a = (– 1)× (– ա) = ձևով ես 2× = ես 2× () 2. Այնուհետև Z 2 = a հավասարումը կգրվի Z 2 - ձևով. ես 2×() 2 = 0

դրանք. (Z- i× ) (Z + i× ) = 0

Հետևաբար, հավասարումն ունի երկու արմատ՝ Z 1.2 = i×

Բացասական թվից արմատի ներդրված հասկացությունը թույլ է տալիս իրական գործակիցներով գրել ցանկացած քառակուսի հավասարման արմատները

a× Z 2 + b× Z + c = 0

Հայտնի ընդհանուր բանաձեւի համաձայն

Z 1,2 = (10)

Այսպիսով, ցանկացած իրական a(a0), b, c-ի համար հավասարման արմատները կարելի է գտնել 10-րդ բանաձևով: Ավելին, եթե դիսկրիմինանտը, այսինքն. արմատական ​​արտահայտություն 10-րդ բանաձևում

D \u003d b 2 - 4 × a × c

դրական է, ապա a× Z 2 + b× Z + c = 0 հավասարումը ունի երկու իրական տարբեր արմատներ: Եթե ​​D = 0, ապա a × Z 2 + b × Z + c = 0 հավասարումը ունի մեկ արմատ: Եթե ​​Դ< 0, то уравнение a× Z 2 + b× Z + c = 0 имеет два различных комплексных корня.

Քառակուսային հավասարման բարդ արմատներն ունեն նույն հատկությունները, ինչ իրական արմատների հայտնի հատկությունները:

Եկեք ձևակերպենք հիմնականները.

Թող Z 1 ,Z 2 լինի a× Z 2 + b× Z + c = 0, a0 քառակուսային հավասարման արմատները: Այնուհետև հատկությունները ճշմարիտ են.

Z 1× Z 2 =

1. Բոլոր բարդ Z-ի համար բանաձեւը

a × Z 2 + b × Z + c \u003d a × (Z - Z 1) × (Z - Z 2)

Օրինակ 5:

Z 2 - 6 Z + 10 \u003d 0

D \u003d b 2 - 4 a c

D \u003d 6 2 - 4 10 \u003d - 4

– 4 = ես 2 · 4

Z 1,2 =

Պատասխան՝ Z 1 \u003d Z 2 \u003d 3 + ես

Օրինակ 6:

3 Z 2 +2 Z + 1 = 0

D \u003d b 2 - 4 a c

D \u003d 4 - 12 \u003d - 8

D \u003d -1 8 \u003d 8 ես 2

Z 1,2 = =

Պատասխան՝ Z 1 \u003d Z 2 \u003d -

Օրինակ 7:

Z 4 - 8 Z 2 - 9 = 0

t 2 - 8 t - 9 = 0

D \u003d b 2 - 4 a c \u003d 64 + 36 \u003d 100

t 1 \u003d 9 t 2 \u003d - 1

Z 2 \u003d 9 Z 2 \u003d - 1

Z 3.4 = ես

Պատասխան՝ Z 1.2 \u003d 3, Z 3.4 \u003d ես

Օրինակ 8:

Z 4 + 2 Z 2 - 15 \u003d 0

t 2 + 2 t - 15 \u003d 0

D \u003d b 2 - 4 a c \u003d 4 + 60 \u003d 64

t 1,2 = = = –14

t 1 \u003d - 5 t 2 \u003d 3

Z 2 \u003d - 5 Z 2 \u003d 3

Z 2 \u003d - 1 5 Z 3.4 \u003d

Z2 = ես 2 · 5

Z 1,2 = ես

Պատասխան՝ Z 1,2 = ես , Z 3,4 =

Օրինակ 9:

Z 2 = 24 10 ես

Թող Z = X + Y ես

(X + Y ես ) 2 = X 2 + 2 X Y ես – Y2

X 2 + 2 X Y Y ես – Y 2 = 24 10 ես

(X 2 Y 2) + 2 X Y ես = 24 10 ես

բազմապատկել X 2 0-ով

X 4 - 24 X 2 - 25 = 0

t 2 - 24 t - 25 = 0

t 1 t 2 \u003d - 25

t 1 \u003d 25 t 2 \u003d - 1

X 2 \u003d 25 X 2 \u003d - 1 - լուծումներ չկան

X 1 \u003d 5 X 2 \u003d - 5

Y 1 = - Y 2 =

Y 1 = - 1 Y 2 = 1

Z 1,2 \u003d (5 - ես )

Պատասխան՝ Z 1,2 \u003d (5 - ես )

ԱՌԱՋԱԴՐԱՆՔՆԵՐ:

(2 - Y) 2 + 3 (2 - Y) Y + Y 2 = 6

4 - 4 Y + Y 2 + 6 Y - 3 Y 2 + Y 2 = 6

-Y 2 + 2Y - 2 \u003d 0 / -1

Y 2 - 2Y + 2 = 0

D \u003d b 2 - 4 a c \u003d 4 - 8 \u003d - 4

– 4 = – 1 4 = 4 ես 2

Y 1,2 = = = 1 ես

Y 1 = 1– ես Y 2 \u003d 1 + ես

X 1 = 1 + ես X 2 \u003d 1– ես

Պատասխան՝ (1+ ես ; 1–ես }

{1–ես ; 1 + ես }

Եկեք հրապարակենք այն

Եթե ​​Ձեզ անհրաժեշտ է անվանել երկու քաղաքների միջև եղած հեռավորությունը, ապա կարող եք մեկ թիվ տալ մղոններով, կիլոմետրերով կամ գծային հեռավորության այլ միավորներով: Այնուամենայնիվ, եթե դուք պետք է նկարագրեք, թե ինչպես հասնել մի քաղաքից մյուսը, ապա ձեզ հարկավոր է ավելի շատ տեղեկատվություն տրամադրել, քան քարտեզի երկու կետերի միջև եղած հեռավորությունը: Այս դեպքում արժե ասել այն ուղղությամբ, որով դուք պետք է շարժվեք և շուրջը:

Տեղեկատվության այն տեսակը, որն արտահայտում է միաչափ չափում, գիտության մեջ կոչվում է սկալյար մեծություն: Սկալյարները թվեր են, որոնք օգտագործվում են մաթեմատիկական հաշվարկների մեծ մասում: Օրինակ, զանգվածը և արագությունը, որն ունի օբյեկտը, սկալյար մեծություններ են:

Բնական երևույթները հաջողությամբ վերլուծելու համար մենք պետք է աշխատենք վերացական առարկաների և մեթոդների հետ, որոնք կարող են ներկայացնել բազմաչափ մեծություններ։ Այստեղ անհրաժեշտ է հրաժարվել սկալյար թվերից՝ հօգուտ բարդերի։ Դրանք հնարավորություն են տալիս միաժամանակ արտահայտել երկու չափսեր։

Կոմպլեքս թվերը ավելի հեշտ է հասկանալ, երբ դրանք ներկայացված են գրաֆիկական տեսքով: Եթե ​​տողը ունի որոշակի երկարություն և ուղղություն, ապա սա կլինի գրաֆիկական ներկայացում: Այն նաև հայտնի է որպես վեկտոր:

Տարբերությունները բարդ և սկալյար մեծությունների միջև

Թվերի այնպիսի տեսակներ, ինչպիսիք են ամբողջ թվերը, ռացիոնալները և իրականները, երեխաներին ծանոթ են դպրոցից: Նրանք բոլորն ունեն միաչափություն: Թվային գծի ուղիղությունը դա ցույց է տալիս գրաֆիկորեն: Դուք կարող եք շարժվել վեր կամ վար դրա վրա, բայց այս գծի երկայնքով բոլոր «շարժումները» կսահմանափակվեն հորիզոնական առանցքով: Միաչափ, սկալյար թվերը բավարար են տարրերի քանակը հաշվելու, քաշն արտահայտելու կամ մարտկոցի հաստատուն լարումը չափելու համար: Բայց դրանք ավելի բարդ բան չեն կարող նշանակել։ Սկալյարները չեն կարող միաժամանակ արտահայտել հեռավորությունը և ուղղությունը երկու քաղաքների միջև կամ ամպլիտուդը փուլով: Անհրաժեշտ է այս տեսակի թվերը ներկայացնել արդեն արժեքների բազմաչափ միջակայքի տեսքով։ Այսինքն՝ մեզ պետք են վեկտորային մեծություններ, որոնք կարող են ունենալ ոչ միայն մեծություն, այլեւ տարածման ուղղություն։

Եզրակացություն

Սկալյար թիվը մաթեմատիկական օբյեկտի տեսակ է, որը մարդիկ սովոր են օգտագործել առօրյա կյանքում՝ դա ջերմաստիճան, երկարություն, քաշ և այլն: Կոմպլեքս թիվը մի արժեք է, որը ներառում է երկու տեսակի տվյալներ:

Վեկտորը բարդ թվի գրաֆիկական ներկայացում է: Այն կարծես սլաքի է մեկնարկային կետով և սահմանված երկարությամբ և ուղղությամբ: Երբեմն «վեկտոր» բառը օգտագործվում է ռադիոտեխնիկայում, որտեղ այն արտահայտում է ազդանշանների միջև փուլային տեղաշարժը:

Քառակուսային հավասարման հատկությունները ուսումնասիրելիս սահմանվել է սահմանափակում՝ զրոյից փոքր դիսկրիմինանտի համար լուծում չկա։ Անմիջապես սահմանվեց, որ խոսքը իրական թվերի բազմության մասին է։ Մաթեմատիկոսի հետաքրքրասեր միտքը կհետաքրքրի` ո՞րն է իրական արժեքների վերապահման մեջ պարունակվող գաղտնիքը:

Ժամանակի ընթացքում մաթեմատիկոսները ներմուծեցին կոմպլեքս թվեր հասկացությունը, որտեղ որպես միավոր ընդունվում է մինուս մեկի երկրորդ արմատի պայմանական արժեքը։

Պատմական անդրադարձ

Մաթեմատիկական տեսությունը զարգանում է հաջորդաբար՝ պարզից մինչև բարդ։ Եկեք պարզենք, թե ինչպես է առաջացել «բարդ թիվ» կոչվող հասկացությունը և ինչու է դա անհրաժեշտ:

Հին ժամանակներից մաթեմատիկայի հիմքը եղել է սովորական հաշիվը։ Հետազոտողները գիտեին միայն բնական արժեքների շարքը: Գումարը և հանումը պարզ էին. Քանի որ տնտեսական հարաբերությունները բարդացան, նույն արժեքները ավելացնելու փոխարեն սկսեցին օգտագործել բազմապատկումը։ Կային բազմապատկման հակադարձ գործողություն՝ բաժանում:

Բնական թվի հայեցակարգը սահմանափակում էր թվաբանական գործողությունների կիրառումը։ Անհնար է լուծել բոլոր բաժանման խնդիրները ամբողջ թվային արժեքների բազմության վրա: հանգեցրել է նախ ռացիոնալ իմաստների, իսկ հետո՝ իռացիոնալ իմաստների հասկացությանը։ Եթե ​​ռացիոնալի համար հնարավոր է նշել կետի ճշգրիտ տեղը գծի վրա, ապա իռացիոնալների համար անհնար է նման կետ նշել: Դուք կարող եք միայն մոտավոր հաշվարկել միջակայքը: Ռացիոնալ և իռացիոնալ թվերի միավորումը կազմել է իրական բազմություն, որը կարող է ներկայացվել որպես որոշակի գիծ՝ տրված սանդղակով։ Գծի երկայնքով յուրաքանչյուր քայլ բնական թիվ է, և դրանց միջև կան ռացիոնալ և իռացիոնալ արժեքներ:

Սկսվեց տեսական մաթեմատիկայի դարաշրջանը։ Աստղագիտության, մեխանիկայի, ֆիզիկայի զարգացումը պահանջում էր ավելի ու ավելի բարդ հավասարումների լուծում։ Ընդհանուր առմամբ, գտնվել են քառակուսի հավասարման արմատները։ Ավելի բարդ խորանարդ բազմանդամ լուծելիս գիտնականները բախվեցին հակասության: Բացասականից խորանարդի արմատ հասկացությունն իմաստ ունի, բայց քառակուսի արմատի համար ստացվում է անորոշություն։ Ընդ որում, քառակուսի հավասարումը միայն խորանարդի հատուկ դեպքն է։

1545 թվականին իտալացի Ջ.Կարդանոն առաջարկեց ներդնել երևակայական թվի հասկացությունը։

Այս թիվը մինուս մեկի երկրորդ արմատն էր։ Կոմպլեքս թիվ տերմինը վերջնականապես ձևավորվեց միայն երեք հարյուր տարի անց հայտնի մաթեմատիկոս Գաուսի աշխատություններում։ Նա առաջարկեց պաշտոնապես տարածել հանրահաշվի բոլոր օրենքները մինչև երևակայական թիվը։ Իրական գիծը ընդլայնվել է դեպի հարթություն: Աշխարհը մեծացել է.

Հիմնական հասկացություններ

Հիշեք մի շարք գործառույթներ, որոնք սահմանափակումներ ունեն իրական հավաքածուի վրա.

• y = arcsin(x), որը սահմանվում է բացասական և դրական արժեքների միջակայքում:
• y = ln(x), իմաստ ունի դրական փաստարկների համար:
• քառակուսի արմատ y = √x, հաշվարկված է միայն x ≥ 0-ի համար:

Նշանակելով i = √(-1), մենք ներկայացնում ենք այնպիսի հասկացություն, որպես երևակայական թիվ, որը կվերացնի բոլոր սահմանափակումները վերը նշված գործառույթների սահմանման տիրույթից: Նման արտահայտությունները, ինչպիսիք են y = arcsin(2), y = ln(-4), y = √(-5) իմաստ ունեն բարդ թվերի որոշ տարածության մեջ:

Հանրահաշվական ձևը կարելի է գրել որպես z = x + i×y արտահայտություն իրական x և y արժեքների բազմության վրա, իսկ i 2 = -1:

Նոր հայեցակարգը վերացնում է ցանկացած հանրահաշվական ֆունկցիայի օգտագործման բոլոր սահմանափակումները և իր տեսքով հիշեցնում է ուղիղ գծի գրաֆիկ՝ իրական և երևակայական արժեքների կոորդինատներում:

Կոմպլեքս ինքնաթիռ

Կոմպլեքս թվերի երկրաչափական ձևը տեսողականորեն թույլ է տալիս մեզ ներկայացնել դրանց շատ հատկություններ: Re(z) առանցքի վրա մենք նշում ենք x-ի իրական արժեքները, Im(z)-ի վրա՝ y-ի երևակայական արժեքները, այնուհետև հարթության վրա z կետը ցույց կտա պահանջվող բարդ արժեքը:

Սահմանումներ:

• Re(z) - իրական առանցք:
• Im(z) - նշանակում է երևակայական առանցք:
• z-ը բարդ թվի պայմանական կետ է:
• Վեկտորի երկարության թվային արժեքը զրոյական կետից մինչև z կոչվում է մոդուլ։
• Իրական և երևակայական առանցքները հարթությունը բաժանում են քառորդների։ Կոորդինատների դրական արժեքով - I քառորդ: Երբ իրական առանցքի արգումենտը փոքր է 0-ից, իսկ երևակայական առանցքը մեծ է 0 - II քառորդից: Երբ կոորդինատները բացասական են՝ III եռամսյակ: Վերջին, չորրորդ եռամսյակը պարունակում է բազմաթիվ դրական իրական արժեքներ և բացասական երևակայական արժեքներ:

Այսպիսով, x և y կոորդինատների արժեքներով հարթության վրա միշտ կարելի է պատկերացնել բարդ թվի կետ: i խորհրդանիշը ներմուծվում է իրական մասը երևակայականից առանձնացնելու համար։

Հատկություններ

1. Երբ երևակայական արգումենտի արժեքը զրո է, մենք ստանում ենք ընդամենը մի թիվ (z = x), որը գտնվում է իրական առանցքի վրա և պատկանում է իրական բազմությանը։
2. Հատուկ դեպքում, երբ իրական արգումենտի արժեքը դառնում է զրո, z = i×y արտահայտությունը համապատասխանում է երևակայական առանցքի վրա գտնվող կետի դիրքին։
3. z = x + i×y ընդհանուր ձևը կլինի արգումենտների ոչ զրոյական արժեքների համար: Նշանակում է կոմպլեքս թիվը բնութագրող կետի գտնվելու վայրը քառորդներից մեկում։

եռանկյունաչափական նշում

Հիշեք բևեռային կոորդինատների համակարգը և մեղքի և cos-ի սահմանումը: Ակնհայտ է, որ այս ֆունկցիաների օգնությամբ հնարավոր է նկարագրել ինքնաթիռի ցանկացած կետի գտնվելու վայրը։ Դա անելու համար բավական է իմանալ բևեռային ճառագայթի երկարությունը և իրական առանցքի թեքության անկյունը:

Սահմանում. ∣z ∣ ձևի մուտքը, որը բազմապատկվում է cos(ϴ) եռանկյունաչափական ֆունկցիաների և i ×sin(ϴ) երևակայական մասի գումարով կոչվում է եռանկյունաչափական բարդ թիվ։ Այստեղ նշանակումը իրական առանցքի նկատմամբ թեքության անկյունն է

ϴ = arg(z), և r = ∣z∣, ճառագայթի երկարությունը:

Եռանկյունաչափական ֆունկցիաների սահմանումից և հատկություններից հետևում է De Moivre-ի շատ կարևոր բանաձևը.

z n = r n × (cos(n × ϴ) + i × sin (n × ϴ)):

Օգտագործելով այս բանաձեւը՝ հարմար է լուծել եռանկյունաչափական ֆունկցիաներ պարունակող հավասարումների բազմաթիվ համակարգեր։ Հատկապես, երբ առաջանում է հզորացման խնդիր։

Մոդուլ և փուլ

Բարդ հավաքածուի նկարագրությունը լրացնելու համար մենք առաջարկում ենք երկու կարևոր սահմանումներ.

Իմանալով Պյութագորասի թեորեմը՝ հեշտ է հաշվարկել ճառագայթի երկարությունը բևեռային կոորդինատային համակարգում։

r = ∣z∣ = √(x 2 + y 2), բարդ տարածության վրա նման նշումը կոչվում է «մոդուլ» և բնութագրում է 0-ից մինչև հարթության մի կետ հեռավորությունը:

Կոմպլեքս ճառագայթի թեքության անկյունը դեպի իրական ուղիղ ϴ սովորաբար կոչվում է փուլ:

Սահմանումից երևում է, որ իրական և երևակայական մասերը նկարագրվում են ցիկլային ֆունկցիաներով։ Այսինքն:

• x = r × cos(ϴ);
• y = r × sin(ϴ);

Ընդհակառակը, փուլը կապված է հանրահաշվական արժեքների հետ բանաձևի միջոցով.

ϴ = արկտան (x / y) + μ, ուղղումը մ ներմուծվում է երկրաչափական ֆունկցիաների պարբերականությունը հաշվի առնելու համար:

Էյլերի բանաձեւ

Մաթեմատիկոսները հաճախ օգտագործում են էքսպոնենցիալ ձևը։ Բարդ հարթության թվերը գրվում են որպես արտահայտություն

z = r × e i × ϴ , որը բխում է Էյլերի բանաձեւից։

Նման ռեկորդը լայն տարածում է գտել ֆիզիկական մեծությունների գործնական հաշվարկի համար։ Էքսպոնենցիալ կոմպլեքս թվերի տեսքով ներկայացման ձևը հատկապես հարմար է ինժեներական հաշվարկների համար, որտեղ անհրաժեշտ է դառնում հաշվարկել սինուսոիդային հոսանքներով սխեմաներ և անհրաժեշտ է իմանալ տվյալ ժամանակահատվածով ֆունկցիաների ինտեգրալների արժեքը։ Հաշվարկներն իրենք են ծառայում որպես գործիք տարբեր մեքենաների և մեխանիզմների նախագծման մեջ:

Գործողությունների սահմանում

Ինչպես արդեն նշվեց, հիմնական մաթեմատիկական ֆունկցիաների հետ աշխատելու հանրահաշվական օրենքները կիրառվում են բարդ թվերի վրա։

գումարային գործողություն

Բարդ արժեքներ ավելացնելիս ավելացվում են նաև դրանց իրական և երևակայական մասերը։

z = z 1 + z 2, որտեղ z 1 և z 2 ընդհանուր բարդ թվեր են: Արտահայտությունը փոխակերպելով՝ փակագծերը բացելուց և նշումը պարզեցնելուց հետո մենք ստանում ենք իրական փաստարկը x \u003d (x 1 + x 2), երևակայական արգումենտը y \u003d (y 1 + y 2):

Գրաֆիկի վրա սա կարծես երկու վեկտորի գումարում լինի՝ ըստ հայտնի զուգահեռագծի կանոնի։

հանման գործողություն

Այն համարվում է գումարման հատուկ դեպք, երբ մի թիվը դրական է, մյուսը՝ բացասական, այսինքն՝ գտնվում է հայելային քառորդում։ Հանրահաշվական նշումը նման է իրական և երևակայական մասերի տարբերությունին:

z \u003d z 1 - z 2, կամ, հաշվի առնելով արգումենտների արժեքները, գումարման գործողության նման, մենք ստանում ենք իրական արժեքներ x \u003d (x 1 - x 2) և երևակայական y \u003d (y 1 - y 2):

Բազմապատկում բարդ հարթությունում

Օգտագործելով բազմանդամների հետ աշխատելու կանոնները՝ դուրս ենք բերում բարդ թվեր լուծելու բանաձև։

Հետևելով z=z 1 ×z 2 ընդհանուր հանրահաշվական կանոններին՝ մենք նկարագրում ենք յուրաքանչյուր փաստարկ և տալիս նմանատիպեր։ Իրական և երևակայական մասերը կարելի է գրել հետևյալ կերպ.

• x \u003d x 1 × x 2 - y 1 × y 2,
• y = x 1 × y 2 + x 2 × y 1.

Ավելի գեղեցիկ է թվում, եթե օգտագործենք էքսպոնենցիալ բարդ թվեր։

Արտահայտությունն ունի հետևյալ տեսքը.

Բաժանում

Բաժանման գործողությունը որպես բազմապատկման գործողության հակադարձ դիտարկելիս մենք ստանում ենք պարզ արտահայտություն էքսպոնենցիալ տեսքով։ Z 1-ի արժեքը z 2-ի վրա բաժանելը դրանց մոդուլների և փուլային տարբերության բաժանման արդյունքն է: Ձևականորեն, կոմպլեքս թվերի էքսպոնենցիալ ձևն օգտագործելիս այն ունի հետևյալ տեսքը.

z \u003d z 1 / z 2 \u003d r 1 × e i ϴ 1 / r 2 × e i ϴ 2 \u003d r 1 / r 2 × e i (ϴ 1- ϴ 2) :

Հանրահաշվական նշումների տեսքով բարդ հարթության թվերի բաժանման գործողությունը մի փոքր ավելի բարդ է գրված.

Փաստարկները գրելով և բազմանդամ փոխակերպումներ կատարելով՝ հեշտ է ստանալ համապատասխանաբար x \u003d x 1 × x 2 + y 1 × y 2 արժեքները, y \u003d x 2 × y 1 - x 1 × y 2, Այնուամենայնիվ, նկարագրված տարածության մեջ այս արտահայտությունը իմաստ ունի, եթե z 2 ≠ 0:

Մենք արդյունահանում ենք արմատը

Վերոհիշյալ բոլորը կարող են կիրառվել ավելի բարդ հանրահաշվական ֆունկցիաների սահմանման մեջ՝ բարձրացնելով մինչև ցանկացած ուժ և հակադարձ դրան՝ հանելով արմատը:

Օգտագործելով n հզորության բարձրացման ընդհանուր հայեցակարգը, մենք ստանում ենք սահմանումը.

z n = (r × e i ϴ) n .

Օգտագործելով ընդհանուր հատկությունները, մենք կարող ենք այն վերաշարադրել հետևյալ ձևով.

z n = r n × e i ϴ n.

Մենք ստացանք բարդ թիվը մինչև հզորության հասցնելու պարզ բանաձև:

Գիտական ​​աստիճանի սահմանումից մենք ստանում ենք մի շատ կարևոր հետևանք. Երևակայական միավորի զույգ հզորությունը միշտ 1 է: Երևակայական միավորի ցանկացած կենտ հզորությունը միշտ -1 է:

Այժմ ուսումնասիրենք հակադարձ ֆունկցիան՝ արմատից հանելը։

Նշման պարզության համար մենք վերցնում ենք n = 2: C բարդ հարթության վրա z համալիր արժեքի քառակուսի արմատը սովորաբար համարվում է z = ± արտահայտությունը, որը վավեր է զրոյից մեծ կամ հավասար ցանկացած իրական փաստարկի համար: w ≤ 0-ի համար լուծում չկա:

Դիտարկենք ամենապարզ քառակուսի հավասարումը z 2 = 1: Օգտագործելով բարդ թվերի բանաձևերը, մենք վերագրում ենք r 2 × e i 2ϴ = r 2 × e i 2ϴ = e i 0: Արձանագրությունից երևում է, որ r 2 = 1 և ϴ = 0, հետևաբար, մենք ունենք եզակի լուծում, որը հավասար է 1-ի: Բայց դա հակասում է այն հասկացությանը, որ z = -1, նույնպես համապատասխանում է քառակուսի արմատի սահմանմանը:

Եկեք պարզենք, թե ինչն ենք մենք հաշվի չենք առնում: Եթե ​​հիշենք եռանկյունաչափական նշումը, ապա մենք վերականգնում ենք հայտարարությունը՝ ϴ փուլի պարբերական փոփոխությամբ, կոմպլեքս թիվը չի փոխվում: Թող p-ն նշանակի ժամանակաշրջանի արժեքը, ապա մենք ունենք r 2 × e i 2ϴ = e i (0+ p) , որտեղից 2ϴ = 0 + p, կամ ϴ = p / 2: Հետևաբար, մենք ունենք e i 0 = 1 և e i p /: 2 = -1. Ստացանք երկրորդ լուծումը, որը համապատասխանում է քառակուսի արմատի ընդհանուր ըմբռնմանը։

Այսպիսով, բարդ թվի կամայական արմատ գտնելու համար մենք կհետևենք ընթացակարգին.

• Գրում ենք w= ∣w∣ × e i (arg (w) + pk) էքսպոնենցիալ ձևը, k-ն կամայական ամբողջ թիվ է։
• Ցանկալի թիվը կարող է ներկայացվել նաև էյլերի ձևով z = r × e i ϴ:
• Եկեք օգտագործենք արմատի հանման ֆունկցիայի ընդհանուր սահմանումը r n *e i n ϴ = ∣w∣ × e i (arg (w) + pk) .
• Մոդուլների և արգումենտների հավասարության ընդհանուր հատկություններից գրում ենք r n = ∣w∣ և nϴ = arg (w) + p×k:
• Կոմպլեքս թվի արմատի վերջնական գրառումը նկարագրվում է z = √∣w∣ × e i (arg (w) + pk) / n բանաձևով:
• Մեկնաբանություն. ∣w∣ արժեքը, ըստ սահմանման, դրական իրական թիվ է, ուստի ցանկացած հզորության արմատ իմաստ ունի:

Դաշտ և խոնարհում

Եզրափակելով՝ մենք տալիս ենք երկու կարևոր սահմանումներ, որոնք քիչ նշանակություն ունեն կոմպլեքս թվերով կիրառական խնդիրների լուծման համար, բայց էական նշանակություն ունեն մաթեմատիկական տեսության հետագա զարգացման համար։

Ասում են, որ գումարման և բազմապատկման արտահայտությունները դաշտ են կազմում, եթե դրանք բավարարում են z բարդ հարթության որևէ տարրի աքսիոմներին.

1. Բարդ տերմինների տեղերի փոփոխությունից բարդ գումարը չի փոխվում։
2. Հայտարարությունը ճշմարիտ է. բարդ արտահայտության մեջ երկու թվերի ցանկացած գումար կարող է փոխարինվել դրանց արժեքով:
3. Կա չեզոք արժեք 0, որի համար z + 0 = 0 + z = z ճշմարիտ է:
4. Ցանկացած z-ի համար կա հակադիր՝ z, որի գումարումը տալիս է զրո:
5. Երբ փոխվում են բարդ գործոնների տեղերը, բարդ արտադրանքը չի փոխվում։
6. Ցանկացած երկու թվի բազմապատկումը կարող է փոխարինվել դրանց արժեքով։
7. Գոյություն ունի չեզոք 1 արժեք, որով բազմապատկումը չի փոխում կոմպլեքս թիվը։
8. Յուրաքանչյուր z ≠ 0-ի համար կա z -1-ի փոխադարձություն, որը բազմապատկելուց ստացվում է 1:
9. Երկու թվերի գումարը երրորդով բազմապատկելը համարժեք է դրանցից յուրաքանչյուրը այդ թվով բազմապատկելուն և արդյունքները գումարելուն։
10. 0 ≠ 1.

z 1 = x + i×y և z 2 = x - i×y թվերը կոչվում են խոնարհված:

Թեորեմ.Խոնարհման համար հայտարարությունը ճշմարիտ է.

• Գումարի խոնարհումը հավասար է խոնարհվող տարրերի գումարին։
• Արտադրանքի խոնարհումը հավասար է խոնարհումների արտադրյալին։
• հավասար է թվին:

Ընդհանուր հանրահաշիվում նման հատկությունները կոչվում են դաշտային ավտոմորֆիզմներ։

Օրինակներ

Հետևելով բարդ թվերի վերը նշված կանոններին և բանաձևերին, դուք կարող եք հեշտությամբ գործել դրանք:

Դիտարկենք ամենապարզ օրինակները.

Առաջադրանք 1.Օգտագործելով 3y +5 x i= 15 - 7i հավասարումը, որոշե՛ք x և y։

Լուծում. Հիշեք բարդ հավասարումների սահմանումը, ապա 3y = 15, 5x = -7: Հետեւաբար, x = -7 / 5, y = 5:

Առաջադրանք 2.Հաշվեք 2 + i 28 և 1 + i 135 արժեքները:

Լուծում. Ակնհայտ է, որ 28-ը զույգ թիվ է, հզորության մեջ կոմպլեքս թվի սահմանման հետևանքից մենք ունենք i 28 = 1, ինչը նշանակում է, որ արտահայտությունը 2 + i 28 = 3 է: Երկրորդ արժեքը, i 135 = - 1, ապա 1 + i 135 = 0:

Առաջադրանք 3.Հաշվեք 2 + 5i և 4 + 3i արժեքների արտադրյալը:

Լուծում. Կոմպլեքս թվերի բազմապատկման ընդհանուր հատկություններից ստանում ենք (2 + 5i)X(4 + 3i) = 8 - 15 + i(6 + 20): Նոր արժեքը կլինի -7 + 26i:

Առաջադրանք 4.Հաշվե՛ք z 3 = -i հավասարման արմատները։

Լուծում. Բարդ թվեր գտնելու մի քանի եղանակ կա: Դիտարկենք հնարավորներից մեկը. Ըստ սահմանման, ∣ - i∣ = 1, -i-ի փուլը -p / 4 է: Բնօրինակ հավասարումը կարելի է վերաշարադրել որպես r 3 *e i 3ϴ = e - p/4+ pk , որտեղից z = e - p / 12 + pk /3, ցանկացած ամբողջ թվի համար:

Լուծումների բազմությունն ունի ձև (e - ip/12, e ip /4, e i 2 p/3):

Ինչու են անհրաժեշտ բարդ թվեր

Պատմությունը գիտի բազմաթիվ օրինակներ, երբ գիտնականները, աշխատելով տեսության վրա, չեն էլ մտածում դրանց արդյունքների գործնական կիրառման մասին։ Մաթեմատիկան առաջին հերթին մտքի խաղ է, պատճառահետևանքային հարաբերությունների խստիվ պահպանում։ Գրեթե բոլոր մաթեմատիկական կոնստրուկցիաները վերածվում են ինտեգրալ և դիֆերենցիալ հավասարումների լուծմանը, իսկ դրանք, իրենց հերթին, որոշ մոտավորությամբ լուծվում են բազմանդամների արմատները գտնելու միջոցով։ Այստեղ մենք առաջին հերթին հանդիպում ենք երևակայական թվերի պարադոքսին։

Բնագետները, լուծելով լիովին գործնական խնդիրներ, դիմելով տարբեր հավասարումների լուծումների, հայտնաբերում են մաթեմատիկական պարադոքսներ։ Այս պարադոքսների մեկնաբանումը հանգեցնում է բացարձակապես զարմանալի բացահայտումների։ Էլեկտրամագնիսական ալիքների երկակի բնույթը նման օրինակ է: Կոմպլեքս թվերը վճռորոշ դեր են խաղում դրանց հատկությունները հասկանալու համար:

Սա իր հերթին գործնական կիրառություն է գտել օպտիկայի, ռադիոէլեկտրոնիկայի, էներգետիկայի և շատ այլ տեխնոլոգիական ոլորտներում։ Մեկ այլ օրինակ, շատ ավելի դժվար է հասկանալ ֆիզիկական երեւույթները. Հակամատերը գուշակվում էր գրչի ծայրին: Եվ միայն երկար տարիներ անց սկսվում են այն ֆիզիկապես սինթեզելու փորձերը։

Չի կարելի մտածել, որ նման իրավիճակներ կան միայն ֆիզիկայում։ Ոչ պակաս հետաքրքիր բացահայտումներ են արվում վայրի բնության մեջ, մակրոմոլեկուլների սինթեզում, արհեստական ​​ինտելեկտի ուսումնասիրության ժամանակ։ Եվ այս ամենը պայմանավորված է մեր գիտակցության ընդլայնմամբ՝ խուսափելով բնական արժեքների պարզ գումարում-հանումից։

ԱռարկաԲարդ թվեր և բազմանդամներ

Դասախոսություն 22

§1. Բարդ թվեր. հիմնական սահմանումներ

Խորհրդանիշ մուտքագրեք հարաբերակցությունը
և կոչվում է երևակայական միավոր: Այլ կերպ ասած,
.

Սահմանում. Ձևի արտահայտություն
, Որտեղ
, կոչվում է կոմպլեքս թիվ, իսկ թիվը կոչվում է բարդ թվի իրական մասը և նշել
, թիվ - երևակայական մաս և նշել
.

Այս սահմանումից բխում է, որ իրական թվերն այն բարդ թվերն են, որոնց երևակայական մասը հավասար է զրոյի։

Հարմար է կոմպլեքս թվերը ներկայացնել որպես հարթության կետեր, որոնց վրա տրված է դեկարտյան ուղղանկյուն կոորդինատային համակարգ, այն է՝ բարդ թիվ.
համընկնումի կետ
և հակառակը։ առանցքի վրա
ցուցադրվում են իրական թվեր, և այն կոչվում է իրական առանցք: Ձևի բարդ թվեր

կոչվում են զուտ երևակայական։ Դրանք ցուցադրվում են առանցքի վրա կետերի տեսքով:
, որը կոչվում է երևակայական առանցք։ Այս հարթությունը, որը ծառայում է կոմպլեքս թվերի ներկայացմանը, կոչվում է բարդ հարթություն։ Կոմպլեքս թիվ, որը իրական չէ, այսինքն. այնպիսին է, որ
, երբեմն կոչվում է երեւակայական։

Երկու կոմպլեքս թվերը հավասար են, եթե և միայն այն դեպքում, եթե դրանք ունեն նույն իրական և երևակայական մասերը:

Կոմպլեքս թվերի գումարումը, հանումը և բազմապատկումը կատարվում են բազմանդամ հանրահաշվի սովորական կանոններով՝ հաշվի առնելով այն հանգամանքը, որ.

. Բաժանման գործողությունը կարող է սահմանվել որպես բազմապատկման գործողության հակադարձ և կարելի է ապացուցել արդյունքի եզակիությունը (եթե բաժանարարը տարբերվում է զրոյից): Այնուամենայնիվ, գործնականում օգտագործվում է այլ մոտեցում.

Կոմպլեքս թվեր
Եվ
կոչվում են խոնարհված, բարդ հարթության վրա դրանք ներկայացված են իրական առանցքի նկատմամբ սիմետրիկ կետերով։ Ակնհայտ է, որ.

1)

;

2)
;

3)
.

Այժմ բաժանեք վրա կարելի է անել հետևյալ կերպ.

.

Դժվար չէ դա ցույց տալ

,

որտեղ խորհրդանիշ նշանակում է ցանկացած թվաբանական գործողություն:

Թող
որոշ երևակայական թիվ և իրական փոփոխական է: Երկու երկանդամների արտադրյալը

իրական գործակիցներով քառակուսի եռանկյուն է:

Այժմ, մեր տրամադրության տակ ունենալով բարդ թվեր, մենք կարող ենք լուծել ցանկացած քառակուսի հավասարում
.Եթե, ապա

և հավասարումն ունի երկու բարդ խոնարհված արմատներ

.

Եթե
, ապա հավասարումն ունի երկու տարբեր իրական արմատներ։ Եթե
, ապա հավասարումն ունի երկու նույնական արմատներ։

§2. Բարդ թվի եռանկյունաչափական ձև

Ինչպես նշվեց վերևում, համալիր համարը
հարմար է կետով ներկայացնել
. Նման թիվը կարելի է նույնացնել նաև այս կետի շառավիղի վեկտորի հետ
. Այս մեկնաբանությամբ կոմպլեքս թվերի գումարումն ու հանումը կատարվում է ըստ վեկտորների գումարման և հանման կանոնների։ Բարդ թվերի բազմապատկման և բաժանման համար ավելի հարմար է մեկ այլ ձև.

Ներկայացնում ենք համալիր հարթության վրա
բևեռային կոորդինատային համակարգ. Հետո որտեղ
,
և կոմպլեքս թիվը
կարելի է գրել այսպես.

Նշման այս ձևը կոչվում է եռանկյունաչափական (ի տարբերություն հանրահաշվական ձևի
) Այս ձևով համարը կոչվում է մոդուլ և - բարդ թվի փաստարկ . Դրանք նշված են.
,

. Մոդուլի համար մենք ունենք բանաձև

Թվի արգումենտը սահմանվում է ոչ միանշանակ, բայց մինչև տերմին
,
. Փաստարկի արժեքը, որը բավարարում է անհավասարությունները
, կոչվում է հիմնական և նշվում
. Հետո,
. Փաստարկի հիմնական արժեքի համար կարող եք ստանալ հետևյալ արտահայտությունները.

,

թվային փաստարկ
համարվում է չսահմանված:

Եռանկյունաչափական ձևով երկու բարդ թվերի հավասարության պայմանն ունի ձև՝ թվերի մոդուլները հավասար են, իսկ արգումենտները տարբերվում են բազմապատիկով։
.

Գտե՛ք երկու բարդ թվերի արտադրյալը եռանկյունաչափական տեսքով.

Այսպիսով, թվերը բազմապատկելիս դրանց մոդուլները բազմապատկվում են, իսկ արգումենտները գումարվում են։

Նմանապես, կարելի է հաստատել, որ բաժանելիս թվերի մոդուլները բաժանվում են, իսկ արգումենտները հանվում։

Հասկանալով աստիճանավորումը որպես բազմապատկման՝ մենք կարող ենք ստանալ կոմպլեքս թիվը մինչև հզորության հասցնելու բանաձևը.

Մենք բխում ենք բանաձևից
- արմատ Կոմպլեքս թվի րդ հզորությունը (չշփոթել իրական թվի թվաբանական արմատի հետ): Արմատների արդյունահանման գործողությունը հզորացման գործողության հակառակն է: Ահա թե ինչու
կոմպլեքս թիվ է այնպիսին է, որ
.

Թող
հայտնի, և
պահանջվում է գտնել. Հետո

Եռանկյունաչափական ձևով երկու բարդ թվերի հավասարությունից հետևում է, որ

,
,
.

Այստեղից
(դա թվաբանական արմատ է):

,
.

Հեշտ է դա հաստատել կարող է միայն ընդունել էապես տարբեր արժեքներ, օրինակ, երբ
. Վերջապես մենք ունենք բանաձև.

,
.

Այսպիսով, արմատը բարդ թվից ունի րդ աստիճան տարբեր արժեքներ. Համալիր հարթության վրա այս արժեքները ճիշտ տեղակայված են գագաթներում. -գոն մակագրված է շառավղով շրջանագծի մեջ
կենտրոնացած է ծագման վրա: «Առաջին» արմատը փաստարկ ունի
, երկու «հարեւան» արմատների փաստարկները տարբերվում են ըստ
.

Օրինակ. Վերցնենք երևակայական միավորի խորանարդային արմատը.
,
,
. Ապա.

,

§1. Կոմպլեքս թվեր

1°. Սահմանում. Հանրահաշվական նշում.

Սահմանում 1. Կոմպլեքս թվերկոչվում են իրական թվերի դասավորված զույգեր Եվ , եթե նրանց համար սահմանված է հավասարություն հասկացությունը, գումարման և բազմապատկման գործողությունները, որոնք բավարարում են հետևյալ աքսիոմներին.

1) երկու թիվ
Եվ
հավասար, եթե և միայն, եթե
,
, այսինքն.

 , .

2) կոմպլեքս թվերի գումարը
Եվ

և հավասար
, այսինքն.

+ = .

3) կոմպլեքս թվերի արտադրյալը
Եվ
համարը կոչվում է
և հավասար է, այսինքն.

∙=.

Նշվում է կոմպլեքս թվերի բազմությունը Գ.

Բանաձևեր (2), (3) ձևի թվերի համար
վերցնել ձևը

որտեղից հետևում է, որ ձևի թվերի գումարման և բազմապատկման գործողությունները
համընկնում է իրական թվերի գումարման և բազմապատկման հետ  ձևի կոմպլեքս թիվը
նույնացվում է իրական թվով .

Համալիր համարը
կանչեց երևակայական միավորև նշվում է , այսինքն.
Այնուհետև (3)-ից 

(2), (3)-ից  ինչը նշանակում է

(4) արտահայտությունը կոչվում է հանրահաշվական նշումհամալիր համարը.

Հանրահաշվական ձևով գումարման և բազմապատկման գործողությունները ստանում են հետևյալ ձևը.

Նշվում է կոմպլեքս թիվը
, - իրական մասը, երևակայական մասն է, զուտ երևակայական թիվ է։ Նշանակում:
,
.

Սահմանում 2. Համալիր համարը
կանչեց զուգորդելկոմպլեքս թվով
.

Բարդ խոնարհման հատկությունները.

1)

2)
.

3) Եթե
, Դա
.

4)
.

5)
իրական թիվ է։

Ապացուցումն իրականացվում է ուղղակի հաշվարկով։

Սահմանում 3. Թիվ
կանչեց մոդուլհամալիր համարը
և նշվում է
.

Ակնհայտ է, որ
, և


. Բանաձևերը նույնպես ակնհայտ են.
Եվ
.

2°. Գումարման և բազմապատկման գործողությունների հատկությունները.

1) Փոխադարձություն.
,
.

2) ասոցիատիվություն.
.

3) բաշխվածություն.

1) - 3) ապացույցն իրականացվում է իրական թվերի համանման հատկությունների հիման վրա ուղղակի հաշվարկներով։

4)
,
.

5) , Գ ! , բավարարելով հավասարումը
. Այդպիսին

6) ,Գ, 0, ! :
. Այդպիսին Գտնվում է հավասարումը բազմապատկելով



.

Օրինակ. Պատկերացրեք բարդ թիվ
հանրահաշվական ձևով։ Դա անելու համար կոտորակի համարիչն ու հայտարարը բազմապատկեք հայտարարի խոնարհումով: Մենք ունենք:

3°. Կոմպլեքս թվերի երկրաչափական մեկնաբանություն. Բարդ թվեր գրելու եռանկյունաչափական և էքսպոնենցիալ ձև:

Թող հարթության վրա տրվի ուղղանկյուն կոորդինատային համակարգ: Հետո
Գկարելի է հարթության վրա մի կետ կապել կոորդինատների հետ
.(տես նկ. 1): Ակնհայտ է, որ նման նամակագրությունը մեկ առ մեկ է։ Այս դեպքում իրական թվերը գտնվում են աբսցիսայի առանցքի վրա, իսկ զուտ երևակայական թվերը՝ օրդինատների առանցքի վրա։ Հետեւաբար, abscissa առանցքը կոչվում է իրական առանցք, և y առանցքը − երևակայական առանցք. Այն հարթությունը, որի վրա գտնվում են բարդ թվերը, կոչվում է բարդ հարթություն.

Նշենք, որ Եվ
ծագման նկատմամբ համաչափ են և Եվ սիմետրիկ են Օքսի նկատմամբ։

Յուրաքանչյուր կոմպլեքս թիվ (այսինքն՝ հարթության յուրաքանչյուր կետ) կարող է կապված լինել վեկտորի հետ, որի սկիզբը O կետում է, իսկ վերջը՝ կետում:
. Վեկտորների և կոմպլեքս թվերի համապատասխանությունը մեկ առ մեկ է: Ուստի կոմպլեքս թվին համապատասխան վեկտորը , որը նշվում է նույն տառով

Դ վեկտորային գիծ
համալիր թվին համապատասխան
, հավասար է
, և
,
.

Օգտագործելով վեկտորի մեկնաբանությունը, կարելի է տեսնել, որ վեկտորը
− վեկտորների գումարը Եվ , Ա
− վեկտորների գումարը Եվ
.(տես նկ. 2): Հետևաբար, հետևյալ անհավասարությունները ճշմարիտ են.

Երկարության հետ մեկտեղ վեկտոր ներկայացնում ենք անկյունը վեկտորի միջև իսկ Ox առանցքը՝ հաշվված Ox առանցքի դրական ուղղությամբ. եթե հաշվարկը հակառակ է, ապա անկյան նշանը համարվում է դրական, եթե ժամացույցի սլաքի ուղղությամբ՝ բացասական։ Այս անկյունը կոչվում է բարդ թվի արգումենտև նշվում է
. Անկյուն սահմանվում է ոչ թե եզակի, այլ ճշգրտությամբ
…. Համար
փաստարկը սահմանված չէ.

Բանաձևերը (6) սահմանում են այսպես կոչված եռանկյունաչափական նշումհամալիր համարը.

(5)-ից հետևում է, որ եթե
Եվ
Դա

, .

Սկսած (5)
ինչով Եվ Կոմպլեքս թիվը եզակիորեն սահմանված է: Հակառակը ճիշտ չէ, այն է՝ կոմպլեքս թվով դրա մոդուլը եզակի է, իսկ փաստարկը , շնորհիվ (7), − ճշգրտությամբ
. (7)-ից հետևում է նաև, որ փաստարկը կարելի է գտնել որպես հավասարման լուծում

Այնուամենայնիվ, այս հավասարման ոչ բոլոր լուծումներն են (7-ի) լուծումները:

Կոմպլեքս թվի արգումենտի բոլոր արժեքների մեջ ընտրվում է մեկը, որը կոչվում է փաստարկի հիմնական արժեք և նշվում է.
. Սովորաբար փաստարկի հիմնական արժեքը ընտրվում է կամ միջակայքում
, կամ միջակայքում

Եռանկյունաչափական ձևով հարմար է կատարել բազմապատկման և բաժանման գործողություններ։

Թեորեմ 1.Կոմպլեքս թվերի արտադրյալի մոդուլ Եվ հավասար է մոդուլների արտադրյալին, իսկ արգումենտը հավասար է արգումենտների գումարին, այսինքն.

, Ա .

Նմանապես

,

Ապացույց.Թող ,. Այնուհետև ուղիղ բազմապատկմամբ ստանում ենք.

Նմանապես

.■

Հետևանք(De Moivre-ի բանաձեւը). Համար
Moivre-ի բանաձևը վավեր է

Պ օրինակ. Գտեք կետի երկրաչափական դիրքը
. Թեորեմ 1-ից հետևում է, որ.

Հետևաբար, այն կառուցելու համար նախ պետք է կառուցեք կետ , որը հակադարձ է միավոր շրջանագծի մասին, այնուհետև գտե՛ք դրան համաչափ կետ x առանցքի շուրջ:

Թող
, այսինքն.
Կոմպլեքս համարը
նշվում է
, այսինքն. ՌԷյլերի բանաձևը վավեր է

Որովհետեւ
, Դա
,
. Թեորեմ 1-ից
ինչ վերաբերում է գործառույթին
հնարավոր է աշխատել այնպես, ինչպես սովորական էքսպոնենցիալ ֆունկցիայի հետ, այսինքն. հավասարությունները ճշմարիտ են

,
,
.

Սկսած (8)
էքսպոնենցիալ նշումհամալիր համարը

, Որտեղ
,

Օրինակ. .

4°. Արմատներ Կոմպլեքս թվի հզորությունը:

Դիտարկենք հավասարումը

, ՀԵՏ , Ն .

Թող
, և (9) հավասարման լուծումը փնտրվում է ձևով
. Այնուհետև (9) ձևը վերցնում է
, որտեղից մենք գտնում ենք, որ
,
, այսինքն.

,
,
.

Այսպիսով, հավասարումը (9) ունի արմատներ

, .

Ցույց տանք, որ (10)-ի մեջ կան հենց տարբեր արմատներ. Իսկապես,

տարբեր են, քանի որ նրանց փաստարկները տարբեր են և ավելի քիչ են տարբերվում
. Հետագայում,
, որովհետեւ
. Նմանապես
.

Այսպիսով, հավասարումը (9) համար
ունի հենց արմատները
գտնվում է կանոնավորի գագաթներում -գոն մակագրված է շառավղով շրջանագծի մեջ կենտրոնացած է T. O.

Այսպիսով, ապացուցվել է

Թեորեմ 2.արմատների արդյունահանում Կոմպլեքս թվի հզորությունը
միշտ հնարավոր է. Բոլոր արմատային արժեքները -րդ աստիճանի գտնվում է ճիշտի վերևում -գոն ներգծված շրջանագծի մեջ, որի կենտրոնը զրոյական է և շառավղով
. Որտեղ,

Հետևանք.Արմատներ 1-րդ աստիճանը արտահայտվում են բանաձևով

.

1-ի երկու արմատների արտադրյալը արմատ է, 1-ը՝ արմատ - միասնության աստիճանից, արմատ
:
.