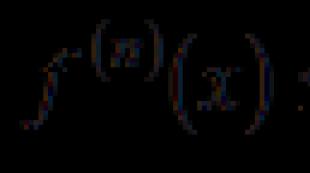दूसरे क्रम के समीकरण की जड़ें। रैखिक सजातीय अंतर समीकरण. एक रैखिक सजातीय के लिए एक सामान्य समाधान का निर्माण

स्थिर गुणांक वाले दूसरे क्रम के सजातीय रैखिक अंतर समीकरणों का रूप होता है

जहाँ p और q वास्तविक संख्याएँ हैं। आइए उदाहरण देखें कि स्थिर गुणांक वाले सजातीय दूसरे क्रम के अंतर समीकरण कैसे हल किए जाते हैं।

दूसरे क्रम के रैखिक सजातीय अंतर समीकरण का समाधान विशेषता समीकरण की जड़ों पर निर्भर करता है। अभिलक्षणिक समीकरण समीकरण k²+pk+q=0 है।

1) यदि अभिलक्षणिक समीकरण के मूल भिन्न-भिन्न वास्तविक संख्याएँ हैं:

तब स्थिर गुणांक वाले रैखिक सजातीय दूसरे क्रम के अंतर समीकरण के सामान्य समाधान का रूप होता है

2) यदि अभिलक्षणिक समीकरण के मूल वास्तविक संख्याओं के बराबर हों

(उदाहरण के लिए, शून्य के बराबर विवेचक के साथ), तो एक सजातीय दूसरे क्रम के अंतर समीकरण का सामान्य समाधान है

3) यदि अभिलक्षणिक समीकरण के मूल सम्मिश्र संख्याएँ हैं

(उदाहरण के लिए, एक ऋणात्मक संख्या के बराबर विवेचक के साथ), तो एक सजातीय दूसरे क्रम के अंतर समीकरण का सामान्य समाधान फॉर्म में लिखा जाता है

स्थिर गुणांक वाले रैखिक सजातीय दूसरे क्रम के अंतर समीकरणों को हल करने के उदाहरण

सजातीय दूसरे क्रम के अंतर समीकरणों के सामान्य समाधान खोजें:

हम विशिष्ट समीकरण बनाते हैं: k²-7k+12=0. इसका विभेदक D=b²-4ac=1>0 है, इसलिए मूल भिन्न वास्तविक संख्याएँ हैं।

इसलिए, इस सजातीय दूसरे क्रम DE का सामान्य समाधान है

आइए विशेषता समीकरण बनाएं और हल करें:

जड़ें वास्तविक और विशिष्ट हैं। इसलिए हमारे पास इस सजातीय अंतर समीकरण का एक सामान्य समाधान है:

इस मामले में, विशेषता समीकरण

जड़ें अलग और वैध हैं. इसलिए, दूसरे क्रम के सजातीय अंतर समीकरण का सामान्य समाधान यहां है

विशेषता समीकरण

चूँकि मूल वास्तविक और समान हैं, इस अवकल समीकरण के लिए हम सामान्य समाधान इस प्रकार लिखते हैं

विशेषता समीकरण यहाँ है

चूँकि विवेचक एक ऋणात्मक संख्या है, अभिलक्षणिक समीकरण के मूल सम्मिश्र संख्याएँ हैं।

इस सजातीय दूसरे क्रम के अंतर समीकरण का सामान्य समाधान इस प्रकार है

विशेषता समीकरण

यहां से हमें इस अंतर का सामान्य समाधान मिलता है। समीकरण:

स्व-परीक्षण के उदाहरण.

§ 9. स्थिर गुणांकों के साथ दूसरे क्रम के रैखिक सजातीय अंतर समीकरण

स्थिर गुणांकों के साथ दूसरे क्रम के LODE की परिभाषा

विशेषता समीकरण:

मामला एक। शून्य से भी बड़ा विवेचक

केस 2. विभेदक शून्य है

केस 3. शून्य से भी कम विभेदक

स्थिर गुणांक वाले दूसरे क्रम के LODE का सामान्य समाधान खोजने के लिए एल्गोरिदम

§ 10. स्थिर गुणांकों के साथ दूसरे क्रम के रैखिक अमानवीय अंतर समीकरण

स्थिर गुणांकों के साथ दूसरे क्रम एलपीडीई का निर्धारण

स्थिरांकों के परिवर्तन की विधि

एलएनडीडीई को एक विशेष दाहिनी ओर से हल करने की विधि

एलएनडीई के सामान्य समाधान की संरचना पर प्रमेय

1. कार्य आर (एक्स) - डिग्री का बहुपद टी

2. कार्य आर (एक्स) - एक संख्या और एक घातीय फलन का गुणनफल

3. कार्य आर (एक्स) - त्रिकोणमितीय कार्यों का योग

एक विशेष दाहिनी ओर के साथ एलपीडीई का सामान्य समाधान खोजने के लिए एल्गोरिदम

आवेदन

§ 9. स्थिर गुणांकों के साथ दूसरे क्रम के रैखिक सजातीय अंतर समीकरण

दूसरे क्रम का अवकल समीकरण कहलाता है स्थिर गुणांकों के साथ रैखिक सजातीय विभेदक समीकरण (LODE)।, अगर ऐसा दिखता है:

कहाँ पीऔर क्यू

किसी LODE का सामान्य समाधान खोजने के लिए, इसके दो अलग-अलग आंशिक समाधान ढूंढना पर्याप्त है। तब LODE के सामान्य समाधान का रूप होगा

कहाँ साथ 1 और साथ

लियोनार्ड यूलर ने फॉर्म में एलडीई के विशेष समाधान देखने का प्रस्ताव रखा

कहाँ क- एक निश्चित संख्या.

इस फ़ंक्शन को दो बार विभेदित करना और इसके लिए व्यंजकों को प्रतिस्थापित करना पर, य"और य"समीकरण में, हमें मिलता है:

परिणामी समीकरण कहलाता है विशेषता समीकरणलोडू. इसे संकलित करने के लिए, इसे मूल समीकरण में प्रतिस्थापित करना पर्याप्त है य", य"और परकेअनुसार क 2 , कऔर 1:

विशेषता समीकरण को हल करने के बाद, अर्थात्। जड़ें मिल गयीं क 1 और क 2, हम मूल LODE के लिए विशेष समाधान भी ढूंढेंगे।

अभिलक्षणिक समीकरण एक द्विघात समीकरण है, इसके मूल विवेचक के माध्यम से ज्ञात किये जाते हैं

इस स्थिति में, निम्नलिखित तीन स्थितियाँ संभव हैं।

मामला एक. शून्य से भी बड़ा विवेचक , इसलिए, जड़ें क 1 और क 2 वैध और विशिष्ट:

क 1¹ क 2

कहाँ साथ 1 और साथ 2 - मनमाना स्वतंत्र स्थिरांक।

केस 2. विभेदक शून्य है , इसलिए, जड़ें क 1 और क 2 वास्तविक और बराबर:

क 1 = क 2 = क

इस मामले में, LODE के सामान्य समाधान का रूप है

कहाँ साथ 1 और साथ 2 - मनमाना स्वतंत्र स्थिरांक।

केस 3. शून्य से भी कम विभेदक . इस मामले में, समीकरण की कोई वास्तविक जड़ें नहीं हैं:

कोई जड़ें नहीं हैं.

इस मामले में, LODE के सामान्य समाधान का रूप है

कहाँ साथ 1 और साथ 2 - मनमाना स्वतंत्र स्थिरांक,

इस प्रकार, स्थिर गुणांक वाले दूसरे क्रम के LODE का एक सामान्य समाधान ढूंढना, विशेषता समीकरण की जड़ों को खोजने और समीकरण के सामान्य समाधान के लिए सूत्रों का उपयोग करने (इंटीग्रल की गणना का सहारा लिए बिना) के लिए नीचे आता है।

स्थिर गुणांक वाले दूसरे क्रम के LODE का सामान्य समाधान खोजने के लिए एल्गोरिदम:

1. समीकरण को उस रूप में घटाएँ जहाँ पीऔर क्यू- कुछ वास्तविक संख्याएँ।

2. एक विशेषता समीकरण बनाएँ.

3. अभिलक्षणिक समीकरण का विवेचक ज्ञात कीजिए।

4. सूत्रों का उपयोग करते हुए (तालिका 1 देखें), विवेचक के संकेत के आधार पर, सामान्य समाधान लिखें।

तालिका नंबर एक

संभावित सामान्य समाधानों की तालिका

इस लेख में हम स्थिर गुणांक वाले रैखिक सजातीय दूसरे क्रम के अंतर समीकरणों को हल करने के सिद्धांतों की जांच करेंगे, जहां पी और क्यू मनमानी वास्तविक संख्याएं हैं। पहले, आइए सिद्धांत पर ध्यान केंद्रित करें, फिर प्राप्त परिणामों को उदाहरणों और समस्याओं को हल करने में लागू करें।

यदि आपके सामने अपरिचित शब्द आते हैं, तो अंतर समीकरणों के सिद्धांत की परिभाषाओं और अवधारणाओं पर अनुभाग देखें।

आइए हम एक प्रमेय तैयार करें जो इंगित करता है कि एलओडी का सामान्य समाधान किस रूप में खोजा जाए।

प्रमेय.

एकीकरण अंतराल X पर निरंतर गुणांक वाले एक रैखिक सजातीय अंतर समीकरण का सामान्य समाधान एक रैखिक संयोजन द्वारा निर्धारित किया जाता है , कहाँ X पर LDE के रैखिक रूप से स्वतंत्र आंशिक समाधान हैं, और मनमाना स्थिरांक हैं।

इस प्रकार, स्थिर गुणांक वाले रैखिक सजातीय दूसरे क्रम के अंतर समीकरण के सामान्य समाधान का रूप y 0 =C 1 ⋅y 1 +C 2 ⋅y 2 है, जहां y 1 और y 2 आंशिक रैखिक रूप से स्वतंत्र समाधान हैं, और C 1 और C2 मनमाना स्थिरांक हैं। यह सीखना बाकी है कि y 1 और y 2 का आंशिक समाधान कैसे खोजा जाए।

यूलर ने फॉर्म में विशेष समाधान खोजने का सुझाव दिया।

यदि हम स्थिर गुणांक वाले दूसरे क्रम के LODE का आंशिक समाधान लेते हैं, तो इस समाधान को समीकरण में प्रतिस्थापित करते समय हमें पहचान प्राप्त करनी चाहिए:

तो हमें तथाकथित मिला विशेषता समीकरणस्थिर गुणांकों के साथ दूसरे क्रम का रैखिक सजातीय अंतर समीकरण। इस विशेषता समीकरण के समाधान k 1 और k 2 निरंतर गुणांक के साथ हमारे दूसरे क्रम के LODE के आंशिक समाधान निर्धारित करते हैं।

गुणांक पी और क्यू के आधार पर, विशेषता समीकरण की जड़ें हो सकती हैं:

पहले मामले मेंमूल अंतर समीकरण के रैखिक रूप से स्वतंत्र आंशिक समाधान हैं और, स्थिर गुणांक वाले दूसरे क्रम के LODE का सामान्य समाधान है।

फ़ंक्शन और वास्तव में रैखिक रूप से स्वतंत्र हैं, क्योंकि व्रोनस्की निर्धारक किसी भी वास्तविक x के लिए गैर-शून्य है।

दूसरे मामले मेंएक विशेष समाधान फ़ंक्शन है। दूसरे विशेष समाधान के रूप में हम लेते हैं। आइए हम दिखाएं कि स्थिर गुणांक वाले दूसरे क्रम के LODE का वास्तव में एक विशेष समाधान क्या है और y 1 और y 2 की रैखिक स्वतंत्रता साबित करें।

चूँकि k 1 = k 0 और k 2 = k 0 अभिलक्षणिक समीकरण के समान मूल हैं, इसका रूप है। इसलिए, मूल रैखिक सजातीय अंतर समीकरण है। आइए इसे इसमें प्रतिस्थापित करें और सुनिश्चित करें कि समीकरण एक पहचान बन जाए:

इस प्रकार, यह मूल समीकरण का आंशिक समाधान है।

आइए हम कार्यों की रैखिक स्वतंत्रता दिखाएं और। ऐसा करने के लिए, आइए व्रोनस्की निर्धारक की गणना करें और सुनिश्चित करें कि यह शून्य से भिन्न है।

निष्कर्ष: स्थिर गुणांक वाले दूसरे क्रम के LODE के रैखिक रूप से स्वतंत्र आंशिक समाधान हैं और, और सामान्य समाधान मौजूद है।

तीसरे मामले मेंहमारे पास एलडीई और के जटिल आंशिक समाधानों की एक जोड़ी है। सामान्य समाधान इस प्रकार लिखा जाएगा . इन विशेष समाधानों को दो वास्तविक कार्यों द्वारा प्रतिस्थापित किया जा सकता है और, वास्तविक और काल्पनिक भागों के अनुरूप। यदि हम सामान्य समाधान को रूपांतरित करें तो इसे स्पष्ट रूप से देखा जा सकता है , से सूत्रों का उपयोग करना एक जटिल चर के कार्य का सिद्धांतप्रकार:


जहाँ C 3 और C 4 स्वेच्छ स्थिरांक हैं।

तो, आइए सिद्धांत को संक्षेप में प्रस्तुत करें।

स्थिर गुणांक वाले दूसरे क्रम के रैखिक सजातीय अंतर समीकरण का सामान्य समाधान खोजने के लिए एल्गोरिदम।

आइए प्रत्येक मामले के लिए उदाहरण देखें।

उदाहरण।

स्थिर गुणांक वाले दूसरे क्रम के रैखिक सजातीय अंतर समीकरण का सामान्य समाधान खोजें .

दूसरे क्रम के रैखिक अंतर समीकरण (एलडीई) का निम्नलिखित रूप है:

जहां , , और ऐसे कार्य दिए गए हैं जो उस अंतराल पर निरंतर हैं जिस पर समाधान मांगा गया है। यह मानते हुए कि a 0 (x) ≠ 0, हम (2.1) को विभाजित करते हैं और, गुणांकों के लिए नए नोटेशन पेश करने के बाद, हम समीकरण को इस रूप में लिखते हैं:

आइए बिना सबूत के स्वीकार करें कि (2.2) में कुछ अंतराल पर एक अद्वितीय समाधान है जो किसी भी प्रारंभिक शर्तों को संतुष्ट करता है, यदि विचाराधीन अंतराल पर कार्य होते हैं, और निरंतर होते हैं। यदि, तो समीकरण (2.2) को सजातीय कहा जाता है, और समीकरण (2.2) को अन्यथा अमानवीय कहा जाता है।

आइए दूसरे क्रम के समाधान के गुणों पर विचार करें।

परिभाषा।कार्यों का एक रैखिक संयोजन अभिव्यक्ति है, जहां मनमानी संख्याएं हैं।

प्रमेय.यदि और - समाधान

तो उनका रैखिक संयोजन भी इस समीकरण का हल होगा।

सबूत।

आइए अभिव्यक्ति को (2.3) में रखें और दिखाएं कि परिणाम पहचान है:

आइए शर्तों को पुनर्व्यवस्थित करें:

चूँकि फलन समीकरण (2.3) के समाधान हैं, तो अंतिम समीकरण में प्रत्येक कोष्ठक शून्य के बराबर है, जिसे सिद्ध करने की आवश्यकता है।

परिणाम 1.सिद्ध प्रमेय से यह निष्कर्ष निकलता है कि यदि समीकरण (2.3) का एक हल है, तो इस समीकरण का भी एक हल है।

परिणाम 2.यह मानते हुए, हम देखते हैं कि लॉड के दो समाधानों का योग भी इस समीकरण का एक समाधान है।

टिप्पणी।प्रमेय में सिद्ध समाधानों का गुण किसी भी क्रम की समस्याओं के लिए मान्य रहता है।

§3. व्रोन्स्की का निर्धारक.

परिभाषा।कार्यों की एक प्रणाली को एक निश्चित अंतराल पर रैखिक रूप से स्वतंत्र कहा जाता है यदि इनमें से किसी भी कार्य को अन्य सभी के रैखिक संयोजन के रूप में प्रस्तुत नहीं किया जा सकता है।

दो कार्यों के मामले में इसका मतलब यह है , अर्थात। . अंतिम शर्त को या के रूप में फिर से लिखा जा सकता है . इस अभिव्यक्ति के अंश में निर्धारक है कार्यों के लिए व्रोनस्की निर्धारक कहा जाता है और। इस प्रकार, दो रैखिक रूप से स्वतंत्र कार्यों के लिए व्रोनस्की निर्धारक शून्य के बराबर नहीं हो सकता है।

होने देना रैखिक रूप से स्वतंत्र समाधान और समीकरण (2.3) के लिए व्रोन्स्की निर्धारक है। आइए प्रतिस्थापन द्वारा यह सुनिश्चित करें कि फलन समीकरण को संतुष्ट करता है। (3.1)

वास्तव में, । चूँकि फलन और समीकरण (2.3) को संतुष्ट करते हैं, तो, अर्थात्। – समीकरण का समाधान (3.1). आइए यह समाधान खोजें: ; . कहाँ , . , , .

इस सूत्र के दाईं ओर आपको धन चिह्न लेने की आवश्यकता है, क्योंकि केवल इस मामले में ही पहचान प्राप्त होती है। इस प्रकार,

(3.2)

इस सूत्र को लिउविले सूत्र कहा जाता है। यह ऊपर दिखाया गया था कि रैखिक रूप से स्वतंत्र कार्यों के लिए व्रोनस्की निर्धारक शून्य के बराबर नहीं हो सकता है। नतीजतन, एक ऐसा बिंदु है जिस पर समीकरण (2.3) के रैखिक रूप से स्वतंत्र समाधान के लिए निर्धारक शून्य से भिन्न है। फिर लिउविले के सूत्र से यह पता चलता है कि विचाराधीन अंतराल में सभी मानों के लिए फ़ंक्शन गैर-शून्य होगा, क्योंकि किसी भी मूल्य के लिए सूत्र (3.2) के दाईं ओर दोनों कारक गैर-शून्य हैं।

§4. दूसरे क्रम के लोड के सामान्य समाधान की संरचना।

प्रमेय.यदि और समीकरण (2.3) के रैखिक रूप से स्वतंत्र समाधान हैं, तो उनका रैखिक संयोजन , जहां और मनमाना स्थिरांक हैं, इस समीकरण का सामान्य समाधान होगा।

सबूत।

क्या समीकरण (2.3) का एक समाधान है, जो दूसरे क्रम के लोदो के समाधान के गुणों पर प्रमेय से अनुसरण करता है। हमें बस वह समाधान दिखाना है इच्छा सामान्य, अर्थात। यह दिखाना आवश्यक है कि किसी भी प्रारंभिक स्थिति के लिए, कोई इन शर्तों को पूरा करने के लिए मनमाने ढंग से स्थिरांक चुन सकता है। आइए प्रारंभिक शर्तों को इस रूप में लिखें:

रैखिक बीजगणितीय समीकरणों की इस प्रणाली से स्थिरांक विशिष्ट रूप से निर्धारित होते हैं, क्योंकि इस प्रणाली का निर्धारक लोडु के रैखिक रूप से स्वतंत्र समाधान के लिए व्रोन्स्की निर्धारक का मान है:

,

और ऐसा निर्धारक, जैसा कि हमने पिछले पैराग्राफ में देखा, शून्येतर है। प्रमेय सिद्ध हो चुका है।

उदाहरण।सिद्ध कीजिए कि फलन , जहां और मनमाना स्थिरांक हैं, लॉड का एक सामान्य समाधान है।

समाधान।

प्रतिस्थापन द्वारा यह सत्यापित करना आसान है कि यह समीकरण कार्य करता है और संतुष्ट करता है। चूंकि, ये फ़ंक्शन रैखिक रूप से स्वतंत्र हैं . इसलिए, सामान्य समाधान की संरचना पर प्रमेय के अनुसार, दूसरा क्रम लोड इस समीकरण का एक सामान्य समाधान है.

दूसरे क्रम के विभेदक समीकरण

§1. समीकरण के क्रम को कम करने की विधियाँ।

दूसरे क्रम के अंतर समीकरण का रूप है:

https://pandia.ru/text/78/516/images/image002_107.gif" width=”19” ऊंचाई=”25 src=”>.gif” width=”119” ऊंचाई=”25 src=”> ( या डिफरेंशियल" href='/text/category/differentcial/' rel='bookmark'>2रे ऑर्डर डिफरेंशियल इक्वेशन)। दूसरे ऑर्डर डिफरेंशियल इक्वेशन के लिए कॉची समस्या (1..gif' width='85' ऊंचाई= '25 src = ">.gif" चौड़ाई = "85" ऊंचाई = "25 src = ">.gif" ऊंचाई = "25 src = ">।

मान लें कि दूसरे क्रम के अंतर समीकरण का रूप इस प्रकार है: https://pandia.ru/text/78/516/images/image009_41.gif" ऊँचाई = "25 src = ">..gif" चौड़ाई = "39" ऊँचाई = " 25 src='>.gif' चौड़ाई='265' ऊंचाई='28 src='>.

इस प्रकार, दूसरे क्रम का समीकरण https://pandia.ru/text/78/516/images/image015_28.gif" width=”34″ ऊंचाई=”25 src=”>.gif” width=”118” ऊंचाई= 25 src='>.gif' चौड़ाई='117' ऊंचाई='25 src='>.gif' चौड़ाई='34' ऊंचाई='25 src='>. इसे हल करने पर, हम दो मनमाने स्थिरांकों के आधार पर मूल अंतर समीकरण का सामान्य अभिन्न अंग प्राप्त करते हैं: DIV_ADBLOCK219">

उदाहरण 1।अवकल समीकरण को हल करें https://pandia.ru/text/78/516/images/image021_18.gif" width=”70″ ऊंचाई=”25 src=”>.gif” ऊंचाई=”25 src=”>.gif " width = "39" ऊँचाई = "25 src = ">.gif" चौड़ाई = "157" ऊँचाई = "25 src = ">.gif" चौड़ाई = "112" ऊँचाई = "25 src = ">।

यह वियोज्य चर के साथ एक विभेदक समीकरण है: https://pandia.ru/text/78/516/images/image026_19.gif" width="99" ऊंचाई="41 src=">, यानी..gif" width= " 96" ऊँचाई = "25 src = ">.gif" चौड़ाई = "53" ऊँचाई = "25 src = ">.gif" चौड़ाई = "48" ऊँचाई = "38 src = ">..gif" चौड़ाई = = 99 " ऊँचाई = "38 src = ">..gif" चौड़ाई = "95" ऊँचाई = "25 src = ">।

2..gif' width='117' ऊंचाई='25 src='>, यानी..gif' width='102' ऊंचाई='25 src='>..gif' width='117' ऊंचाई= '25 src = ">.gif" चौड़ाई = "106" ऊंचाई = "25 src = ">.gif" चौड़ाई = "34" ऊंचाई = "25 src = ">.gif" चौड़ाई = "117" ऊंचाई = "25 src = " >.gif" चौड़ाई = "111" ऊंचाई = "27 src = ">

समाधान।

इस दूसरे क्रम के समीकरण में स्पष्ट रूप से वांछित फ़ंक्शन शामिल नहीं है https://pandia.ru/text/78/516/images/image043_16.gif" width='98' ऊंचाई='25 src='>.gif' width= " 33" ऊँचाई = "25 src = ">.gif" चौड़ाई = "105" ऊँचाई = "36 src = ">, जो एक रैखिक समीकरण है..gif" चौड़ाई = "109" ऊँचाई = "36 src = ">। . gif" width=”144” ऊंचाई=”36 src=”>.gif” ऊंचाई=”25 src=”> कुछ कार्यों से..gif” width=”25” ऊंचाई=”25 src=>.gif “ width='127' ऊँचाई='25 src='>.gif' width='60' ऊँचाई='25 src='> - समीकरण का क्रम कम कर दिया गया है।

§2. दूसरे क्रम का रैखिक अवकल समीकरण।

दूसरे क्रम के रैखिक अंतर समीकरण (एलडीई) का निम्नलिखित रूप है:

https://pandia.ru/text/78/516/images/image059_12.gif" width=”42” ऊंचाई=”25 src=”>.gif” width=”42” ऊंचाई=”25 src=”>. gif" width=”42” ऊंचाई=”25 src=”> और, गुणांकों के लिए नए नोटेशन पेश करने के बाद, हम समीकरण को इस रूप में लिखते हैं:

https://pandia.ru/text/78/516/images/image064_12.gif" width=”76″ ऊंचाई=”25 src=”>.gif” width=”35” ऊंचाई=”25 src=”>. gif" width = "30" ऊंचाई = "25 src = "> निरंतर..gif" चौड़ाई = "165" ऊंचाई = "25 src = ">.gif" चौड़ाई = "95" ऊंचाई = "25 src = "> - मनमानी संख्या.

प्रमेय.यदि https://pandia.ru/text/78/516/images/image074_11.gif' width='42' ऊंचाई='25 src='> - समाधान है

https://pandia.ru/text/78/516/images/image076_10.gif' width='182' ऊंचाई='25 src='> भी इस समीकरण का एक समाधान होगा.

सबूत।

आइए अभिव्यक्ति https://pandia.ru/text/78/516/images/image077_11.gif" width='420' ऊंचाई='25 src='> रखें।

आइए शर्तों को पुनर्व्यवस्थित करें:

https://pandia.ru/text/78/516/images/image073_10.gif" width=”42” ऊंचाई=”25 src=”>.gif” width=”54” ऊंचाई=”25 src=”>. gif' width='94' ऊंचाई='25 src='> भी इस समीकरण का एक समाधान है।

परिणाम 2.यह मानते हुए कि https://pandia.ru/text/78/516/images/image083_11.gif' width='58' ऊंचाई='25 src='> भी इस समीकरण का एक समाधान है।

टिप्पणी।प्रमेय में सिद्ध समाधानों का गुण किसी भी क्रम की समस्याओं के लिए मान्य रहता है।

§3. व्रोन्स्की का निर्धारक.

परिभाषा।कार्यों की प्रणाली https://pandia.ru/text/78/516/images/image084_10.gif" width=”61” ऊंचाई=”25 src=”>.gif” width=”110” ऊंचाई=”47 src= " >..gif" width=”106” ऊंचाई=”42 src=”>..gif” width=”42” ऊंचाई=”25 src=”>.gif” width=”181” ऊंचाई=”47 src= " >.gif" width=”42″ ऊंचाई=”25 src=”> समीकरण (2.3)..gif” width=”182” ऊंचाई=”25 src=”>. (3.1)

वास्तव में, ..gif' width='18' ऊँचाई='25 src='> समीकरण को संतुष्ट करता है (2..gif' width='42' ऊँचाई='25 src='> समीकरण (3.1) का एक समाधान है। .gif" चौड़ाई = "87" ऊंचाई = "28 src = ">..gif" चौड़ाई = "182" ऊंचाई = "34 src = ">..gif" चौड़ाई = "162" ऊंचाई = "42 src = "> .gif" width=”51″ ऊँचाई=”25 src=”> पहचान प्राप्त होती है। इस प्रकार,

https://pandia.ru/text/78/516/images/image107_7.gif" width=”18” ऊंचाई=”25 src=”>, जिसमें समीकरण के रैखिक रूप से स्वतंत्र समाधान के लिए निर्धारक (2..gif) " width= "42" ऊंचाई='25 src='>.gif' ऊंचाई='25 src='> सूत्र (3.2) के दाईं ओर दोनों कारक गैर-शून्य हैं।

§4. दूसरे क्रम के लोड के सामान्य समाधान की संरचना।

प्रमेय.यदि https://pandia.ru/text/78/516/images/image074_11.gif' width='42' ऊंचाई='25 src='> समीकरण के रैखिक रूप से स्वतंत्र समाधान हैं (2..gif' width=' 19" ऊँचाई = "25 src = ">.gif" width = "129" ऊँचाई = "25 src = "> समीकरण (2.3) का एक समाधान है, जो दूसरे क्रम के समाधान के गुणों पर प्रमेय से अनुसरण करता है। gif" चौड़ाई = "85" ऊंचाई = "25 src = ">.gif" चौड़ाई = "19" ऊंचाई = "25 src = ">.gif" चौड़ाई = "220" ऊंचाई = "47">

रैखिक बीजगणितीय समीकरणों की इस प्रणाली से स्थिरांक https://pandia.ru/text/78/516/images/image003_79.gif" width='19' ऊँचाई='25 src='> विशिष्ट रूप से निर्धारित किए जाते हैं, क्योंकि के निर्धारक यह सिस्टम है https://pandia.ru/text/78/516/images/image006_56.gif" width=”51” ऊंचाई=”25 src=”>:

https://pandia.ru/text/78/516/images/image116_7.gif" width=”138″ ऊंचाई=”25 src=”>.gif” width=”19” ऊंचाई=”25 src=”>. gif" width = "69" ऊंचाई = "25 src = ">.gif" चौड़ाई = "235" ऊंचाई = "48 src = ">..gif" चौड़ाई = "143" ऊंचाई = "25 src = "> (5 ..gif' width='77' ऊंचाई='25 src='>. पिछले पैराग्राफ के अनुसार, यदि इस समीकरण के दो रैखिक रूप से स्वतंत्र आंशिक समाधान ज्ञात हैं, तो दूसरे क्रम के Lod का सामान्य समाधान आसानी से निर्धारित किया जा सकता है। एक सरल विधि एल. यूलर द्वारा प्रस्तावित स्थिर गुणांक वाले समीकरण का आंशिक समाधान खोजने के लिए..gif" width='25' ऊंचाई='26 src='>, हमें एक बीजगणितीय समीकरण प्राप्त होता है, जिसे विशेषता कहा जाता है:

https://pandia.ru/text/78/516/images/image124_5.gif" width=”59″ ऊंचाई=”26 src=”> केवल k के उन मानों के लिए समीकरण (5.1) का समाधान होगा यह विशेषता समीकरण (5.2) के मूल हैं..gif" width=”49″ ऊँचाई=”25 src=”>..gif” width=”76” ऊँचाई=”28 src=”>.gif” width= "205" ऊँचाई = "47 src = "> और सामान्य समाधान (5..gif" width = "45" ऊँचाई = "25 src = ">..gif" width = "74" ऊँचाई = "26 src = " >..gif' width='83 ' ऊंचाई='26 src='>. आइए जांचें कि यह फ़ंक्शन समीकरण (5.1)..gif' width='190' ऊंचाई='26 src='> को संतुष्ट करता है। इन भावों को प्रतिस्थापित करते हुए समीकरण (5.1) में, हम पाते हैं

https://pandia.ru/text/78/516/images/image141_6.gif" width=”328″ ऊंचाई=”26 src=”>, क्योंकि..gif” width=”137” ऊंचाई=”26 src= ">.

विशेष समाधान https://pandia.ru/text/78/516/images/image145_6.gif' width='86' ऊंचाई='28 src='> रैखिक रूप से स्वतंत्र हैं, क्योंकि..gif' width='166' ऊंचाई = "26 src = ">.gif" चौड़ाई = "45" ऊँचाई = "25 src = ">..gif" चौड़ाई = "65" ऊँचाई = "33 src = ">.gif" चौड़ाई = "134" ऊँचाई = "25 src='>.gif' width='267' ऊंचाई='25 src='>.gif' चौड़ाई='474' ऊंचाई=25 src='>.

इस समानता के बायीं ओर के दोनों कोष्ठक समान रूप से शून्य के बराबर हैं..gif" width=”174” ऊँचाई=”25 src=”>..gif” width=”132” ऊँचाई=”25 src=”> है समीकरण (5.1) का हल ..gif' width='129' ऊँचाई='25 src='> इस तरह दिखेगा:

https://pandia.ru/text/78/516/images/image162_6.gif" width=”179” ऊंचाई=”25 src=”> f(x) (6.1)

सामान्य समाधान के योग के रूप में प्रस्तुत किया गया है https://pandia.ru/text/78/516/images/image164_6.gif" width=”195” ऊंचाई=”25 src=”> (6.2)

और कोई विशेष समाधान https://pandia.ru/text/78/516/images/image166_6.gif" width='87' ऊंचाई='25 src='> समीकरण (6.1)..gif' का समाधान होगा चौड़ाई='272' ऊंचाई='25 src='> f(x). यह समानता एक पहचान है, क्योंकि..gif' width='128' ऊंचाई='25 src='> f(x. अतः.gif' width='85' ऊंचाई='25 src='>.gif' चौड़ाई =='138' ऊंचाई='25 src='>.gif' चौड़ाई='18' ऊंचाई='25 src='> इस समीकरण के रैखिक रूप से स्वतंत्र समाधान हैं। इस प्रकार:

https://pandia.ru/text/78/516/images/image173_5.gif" width=”289″ ऊंचाई=”48 src=”>

https://pandia.ru/text/78/516/images/image002_107.gif" width=”19” ऊंचाई=”25 src=”>.gif” width=”11” ऊंचाई=”25 src=”>. gif" width='51' ऊंचाई='25 src='>, और ऐसा निर्धारक, जैसा कि हमने ऊपर देखा, सिस्टम से गैर-शून्य है..gif' width='19' ऊंचाई='25 src='> समीकरणों का (6 ..gif" width=”76″ ऊँचाई=”25 src=”>.gif” width=”76″ ऊँचाई=”25 src=”>.gif” width=”140” ऊँचाई=”25 src ==> समीकरण हल करेगा

https://pandia.ru/text/78/516/images/image179_5.gif" width='91' ऊंचाई='25 src='> समीकरण (6.5) में, हम पाते हैं

https://pandia.ru/text/78/516/images/image181_5.gif" width=”140” ऊंचाई=”25 src=”>.gif” width=”128” ऊंचाई=”25 src=”> f (एक्स) (7.1)

जहां https://pandia.ru/text/78/516/images/image185_5.gif" width=”34” ऊंचाई=”25 src=”> समीकरण (7.1) उस स्थिति में जब दाईं ओर f(x) ) का एक विशेष रूप है। इस विधि को अनिश्चित गुणांकों की विधि कहा जाता है और इसमें दाहिनी ओर f(x) के प्रकार के आधार पर एक विशेष समाधान का चयन करना शामिल है। निम्नलिखित रूप के दाहिनी ओर पर विचार करें:

1..gif' width='282' ऊँचाई='25 src='>.gif' width='53' ऊँचाई='25 src='>, शून्य हो सकता है। आइए हम उस रूप को इंगित करें जिसमें इस मामले में एक विशेष समाधान लिया जाना चाहिए।

a) यदि संख्या https://pandia.ru/text/78/516/images/image191_5.gif" width=”393″ऊंचाई=”25 src=”>.gif” width=”157” ऊंचाई=”25 स्रोत=>.

समाधान।

समीकरण के लिए https://pandia.ru/text/78/516/images/image195_4.gif" width=”86” ऊंचाई=”25 src=”>..gif” width=”62” ऊंचाई=”25 src = ">..gif" चौड़ाई = "101" ऊंचाई = "25 src = ">.gif" चौड़ाई = "153" ऊंचाई = "25 src = ">.gif" चौड़ाई = "383" ऊंचाई = "25 src = " >.

हम समानता के बाएँ और दाएँ पक्षों पर दोनों भागों को https://pandia.ru/text/78/516/images/image009_41.gif" ऊँचाई = "25 src = "> तक कम करते हैं

https://pandia.ru/text/78/516/images/image206_5.gif" width=”111” ऊंचाई=”40 src=”>

समीकरणों की परिणामी प्रणाली से हम पाते हैं: https://pandia.ru/text/78/516/images/image208_5.gif" width='189' ऊंचाई='25 src='>, और दिए गए का सामान्य समाधान समीकरण है:

https://pandia.ru/text/78/516/images/image190_5.gif" width=”11” ऊंचाई=”25 src=”>.gif” width=”423” ऊंचाई=”25 src=”>,

जहां https://pandia.ru/text/78/516/images/image212_5.gif' width='158' ऊंचाई='25 src='>.

समाधान।

संबंधित विशेषता समीकरण का रूप है:

https://pandia.ru/text/78/516/images/image214_6.gif" width=”53″ ऊंचाई=”25 src=”>.gif” width=”85” ऊंचाई=”25 src=”>. gif" width = "45" ऊंचाई = "25 src = ">.gif" चौड़ाई = "219" ऊंचाई = "25 src = ">..gif" चौड़ाई = "184" ऊंचाई = "35 src = ">। अंतिम सामान्य समाधान के लिए हमारे पास निम्नलिखित अभिव्यक्ति है:

https://pandia.ru/text/78/516/images/image223_4.gif" width=”170” ऊंचाई=”25 src=”>.gif” width=”13” ऊंचाई=”25 src=”> उत्कृष्ट शून्य से. आइए हम इस मामले में विशेष समाधान के प्रकार को इंगित करें।

ए) यदि संख्या https://pandia.ru/text/78/516/images/image227_5.gif" width='204' ऊंचाई='25 src='>,

जहां https://pandia.ru/text/78/516/images/image226_5.gif" width=”16” ऊंचाई=”25 src=”> समीकरण के लिए विशेषता समीकरण का मूल है (5..gif” चौड़ाई='229' ऊंचाई='25 स्रोत=>,

जहां https://pandia.ru/text/78/516/images/image229_5.gif' width='147' ऊंचाई='25 src='>.

समाधान।

समीकरण के लिए विशेषता समीकरण की जड़ें https://pandia.ru/text/78/516/images/image231_4.gif" width=”58″ ऊंचाई=”25 src=”>.gif” width=”203” ऊंचाई = "25 स्रोत = ">.

उदाहरण 3 में दिए गए समीकरण के दाएँ पक्ष का एक विशेष रूप है: f(x) https://pandia.ru/text/78/516/images/image235_3.gif" width="50" ऊँचाई="25 src= ">.gif " width='55' ऊंचाई='25 src='>.gif' चौड़ाई='229' ऊंचाई='25 src='>.

निर्धारित करने के लिए https://pandia.ru/text/78/516/images/image240_2.gif" width=”11” ऊंचाई=”25 src=”>.gif” width=”43” ऊंचाई=”25 src=” > और इसे दिए गए समीकरण में प्रतिस्थापित करें:

समान पदों का हवाला देते हुए, गुणांकों को https://pandia.ru/text/78/516/images/image245_2.gif" width='46' ऊंचाई='25 src='>.gif' width='100' ऊंचाई पर बराबर करते हुए = "25 स्रोत = ">.

दिए गए समीकरण का अंतिम सामान्य समाधान है: https://pandia.ru/text/78/516/images/image249_2.gif" width=”281″ ऊंचाई=”25 src=”>.gif” width=”47 " ऊँचाई = "25 src = ">.gif" चौड़ाई = "10" ऊँचाई = "25 src = "> क्रमशः, और इनमें से एक बहुपद शून्य के बराबर हो सकता है। आइए हम इस सामान्य मामले में विशेष समाधान के प्रकार को इंगित करें .

a) यदि संख्या https://pandia.ru/text/78/516/images/image255_2.gif" width="605" ऊंचाई="51">, (7.2)

जहां https://pandia.ru/text/78/516/images/image257_2.gif' width='121' ऊंचाई='25 src='>.

बी) यदि संख्या https://pandia.ru/text/78/516/images/image210_5.gif' width='80' ऊंचाई='25 src='> है, तो lndu का विशेष समाधान इस तरह दिखेगा:

https://pandia.ru/text/78/516/images/image259_2.gif" width=”17” ऊंचाई=”25 src=”>. अभिव्यक्ति में (7..gif” width=”121” ऊंचाई= "25 स्रोत='>.

उदाहरण 4.समीकरण के विशेष समाधान के प्रकार को इंगित करें

https://pandia.ru/text/78/516/images/image262_2.gif" width=”129” ऊंचाई=”25 src=”>..gif” width=”95” ऊंचाई=”25 src=”> . Lodu का सामान्य समाधान इस प्रकार है:

https://pandia.ru/text/78/516/images/image266_2.gif" width=”183″ ऊंचाई=”25 src=”>..gif” width=”42” ऊंचाई=”25 src=”> ..gif" चौड़ाई = "36" ऊँचाई = "25 src = ">.gif" चौड़ाई = "351" ऊँचाई = "25 src = ">।

आगे के गुणांक https://pandia.ru/text/78/516/images/image273_2.gif" width=”34” ऊंचाई=”25 src=”>.gif” width=”42” ऊंचाई=”28 src=” > दाईं ओर f1(x) वाले समीकरण के लिए एक विशेष समाधान है, और भिन्नता" href='/text/category/variatciya/' rel='bookmark'> मनमाने स्थिरांक की भिन्नता (लैग्रेंज विधि)।

स्थिर गुणांकों और विशेष मुक्त पदों वाले समीकरण के मामले को छोड़कर, किसी समीकरण का सीधे तौर पर कोई विशेष समाधान ढूंढना बहुत मुश्किल है। इसलिए, समीकरण का एक सामान्य समाधान खोजने के लिए, मनमाना स्थिरांक की भिन्नता की विधि का आमतौर पर उपयोग किया जाता है, जो हमेशा चतुर्भुज में समीकरण का सामान्य समाधान ढूंढना संभव बनाता है यदि संबंधित सजातीय समीकरण के समाधान की मौलिक प्रणाली ज्ञात हो . यह विधि इस प्रकार है.

उपरोक्त के अनुसार, एक रैखिक सजातीय समीकरण का सामान्य समाधान है:

https://pandia.ru/text/78/516/images/image278_2.gif" width=”46” ऊंचाई=”25 src=”>.gif” width=”51” ऊंचाई=”25 src=”> – स्थिरांक नहीं, लेकिन f(x) के कुछ, अभी तक अज्ञात फलन। . अंतराल से लिया जाना चाहिए। वास्तव में, इस मामले में, व्रोन्स्की निर्धारक अंतराल के सभी बिंदुओं पर गैर-शून्य है, यानी, पूरे स्थान पर - विशेषता समीकरण की जटिल जड़..gif" width='20' ऊंचाई='25 src='> प्रपत्र के रैखिक रूप से स्वतंत्र आंशिक समाधान :

सामान्य समाधान सूत्र में, यह मूल रूप की अभिव्यक्ति से मेल खाता है।