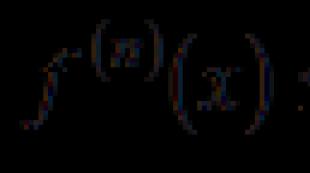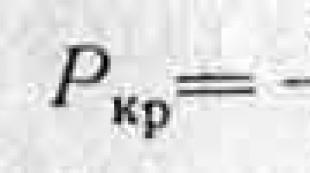किसी कठोर पिंड का एक निश्चित अक्ष के चारों ओर घूमना। किसी कठोर पिंड की एक निश्चित अक्ष के चारों ओर घूर्णी गति। कोणीय वेग और कोणीय त्वरण एक निश्चित अक्ष के चारों ओर त्वरित घूर्णी गति

और सेवलीवा।

किसी पिंड की आगे की गति के दौरान (ई. एम. निकितिन द्वारा पाठ्यपुस्तक में § 60), इसके सभी बिंदु समान प्रक्षेप पथ के साथ चलते हैं और प्रत्येक दिए गए क्षण में उनकी समान गति और समान त्वरण होता है।

इसलिए, किसी पिंड की अनुवादात्मक गति किसी एक बिंदु की गति, आमतौर पर गुरुत्वाकर्षण के केंद्र की गति से निर्धारित होती है।

किसी भी समस्या में कार (समस्या 147) या डीजल लोकोमोटिव (समस्या 141) की गति पर विचार करते समय, हम वास्तव में उनके गुरुत्वाकर्षण के केंद्रों की गति पर विचार करते हैं।

किसी पिंड की घूर्णी गति (ई.एम. निकितिन, § 61) को उसके किसी एक बिंदु की गति से नहीं पहचाना जा सकता है। गति के दौरान किसी भी घूमने वाले पिंड (डीजल फ्लाईव्हील, इलेक्ट्रिक मोटर रोटर, मशीन स्पिंडल, पंखे के ब्लेड, आदि) की धुरी आसपास के स्थिर पिंडों के सापेक्ष अंतरिक्ष में एक ही स्थान पर रहती है।

किसी भौतिक बिंदु की गति या आगे बढ़नासमय के आधार पर शरीरों की विशेषता बताई जाती है रैखिक मात्राएँ s (पथ, दूरी), v (गति) और a (त्वरण) इसके घटकों a t और a n के साथ।

घूर्णी गतिसमय के आधार पर शरीर की विशेषताएँ बताई जाती हैं कोणीय मान: φ (रोटेशन का कोण रेडियन में), ω (कोणीय वेग रेडियन/सेकंड में) और ε (कोणीय त्वरण रेडियन/सेकंड 2 में)।

किसी पिंड की घूर्णी गति का नियम समीकरण द्वारा व्यक्त किया जाता है
φ = एफ(टी).

कोणीय वेग- किसी पिंड के घूर्णन की गति को दर्शाने वाली मात्रा को सामान्य स्थिति में समय के संबंध में घूर्णन के कोण के व्युत्पन्न के रूप में परिभाषित किया जाता है
ω = dφ/dt = f" (t).

कोणीय त्वरण- कोणीय वेग के परिवर्तन की दर को दर्शाने वाली मात्रा को कोणीय वेग के व्युत्पन्न के रूप में परिभाषित किया गया है
ε = dω/dt = f"" (t).

किसी पिंड की घूर्णी गति पर समस्याओं को हल करना शुरू करते समय, यह ध्यान रखना आवश्यक है कि तकनीकी गणना और समस्याओं में, एक नियम के रूप में, कोणीय विस्थापन रेडियंस φ में नहीं, बल्कि क्रांतियों φ में व्यक्त किया जाता है।

इसलिए, क्रांतियों की संख्या से कोणीय विस्थापन के रेडियन माप तक जाने में सक्षम होना आवश्यक है और इसके विपरीत।

चूँकि एक पूर्ण क्रांति 2π रेड से मेल खाती है
φ = 2πφ के बारे में और φ के बारे में = φ/(2π).

तकनीकी गणना में कोणीय गति को अक्सर प्रति मिनट उत्पन्न क्रांतियों (आरपीएम) में मापा जाता है, इसलिए यह स्पष्ट रूप से समझना आवश्यक है कि ω रेड/सेकंड और एन आरपीएम एक ही अवधारणा को व्यक्त करते हैं - किसी पिंड के घूमने की गति (कोणीय गति), लेकिन विभिन्न इकाइयों में - रेड/सेकंड में या आरपीएम में।

कोणीय वेग की एक इकाई से दूसरी इकाई में संक्रमण सूत्रों के अनुसार किया जाता है
ω = πn/30 और n = 30ω/π.

किसी पिंड की घूर्णी गति के दौरान, उसके सभी बिंदु वृत्तों में घूमते हैं, जिनके केंद्र एक निश्चित सीधी रेखा (घूर्णन पिंड की धुरी) पर स्थित होते हैं। इस अध्याय में दी गई समस्याओं को हल करते समय, कोणीय मात्राओं φ, ω और ε के बीच संबंध को स्पष्ट रूप से समझना बहुत महत्वपूर्ण है, जो शरीर की घूर्णी गति की विशेषता है, और रैखिक मात्रा s, v, a t और an, विशेषता है। इस शरीर के विभिन्न बिंदुओं की गति (चित्र 205)।

यदि R किसी घूमते हुए पिंड के ज्यामितीय अक्ष से किसी बिंदु A (चित्र 205 R = OA) की दूरी है, तो φ - पिंड के घूर्णन का कोण और s - के एक बिंदु द्वारा तय की गई दूरी के बीच संबंध है उसी समय के दौरान शरीर को इस प्रकार व्यक्त किया जाता है:
एस = φआर.

प्रत्येक दिए गए क्षण में किसी पिंड के कोणीय वेग और एक बिंदु के वेग के बीच संबंध समानता द्वारा व्यक्त किया जाता है
वी = ωआर.

किसी बिंदु का स्पर्शरेखीय त्वरण कोणीय त्वरण पर निर्भर करता है और सूत्र द्वारा निर्धारित किया जाता है
ए टी = εR.

किसी बिंदु का सामान्य त्वरण पिंड के कोणीय वेग पर निर्भर करता है और संबंध द्वारा निर्धारित होता है
ए एन = ω 2 आर.

इस अध्याय में दी गई समस्या को हल करते समय यह स्पष्ट रूप से समझना आवश्यक है कि घूर्णन एक कठोर पिंड की गति है, किसी बिंदु की नहीं। एक भी भौतिक बिंदु घूमता नहीं है, बल्कि एक वृत्त में घूमता है - यह एक वक्रीय गति करता है।

§ 33. एकसमान घूर्णी गति

यदि कोणीय वेग ω=const है, तो घूर्णी गति को एकसमान गति कहा जाता है।

एकसमान घूर्णन समीकरण का रूप है
φ = φ 0 + ωt.

विशेष मामले में जब घूर्णन का प्रारंभिक कोण φ 0 =0,
φ = ωt.

एक समान रूप से घूमने वाले पिंड का कोणीय वेग
ω = φ/t
इस प्रकार व्यक्त किया जा सकता है:
ω = 2π/टी,
जहां टी शरीर के घूमने की अवधि है; φ=2π - एक अवधि के लिए घूर्णन का कोण।

§ 34. एकसमान घूर्णी गति

परिवर्तनशील कोणीय वेग के साथ घूर्णी गति को असमान कहा जाता है (नीचे § 35 देखें)। यदि कोणीय त्वरण ε=स्थिरांक हो, तो घूर्णन गति कहलाती है समान रूप से परिवर्तनशील. इस प्रकार, किसी पिंड का एकसमान घूमना गैर-समान घूर्णी गति का एक विशेष मामला है।

एकसमान घूर्णन का समीकरण
(1) φ = φ 0 + ω 0 t + εt 2/2
और किसी भी समय किसी पिंड के कोणीय वेग को व्यक्त करने वाला समीकरण,
(2) ω = ω 0 + εt
किसी पिंड की घूर्णी एकसमान गति के लिए बुनियादी सूत्रों के एक सेट का प्रतिनिधित्व करते हैं।

इन सूत्रों में केवल छह मात्राएँ शामिल हैं: किसी दी गई समस्या के लिए तीन स्थिरांक φ 0, ω 0 और ε और तीन चर φ, ω और t। नतीजतन, एक समान रोटेशन के लिए प्रत्येक समस्या की स्थिति में कम से कम चार निर्दिष्ट मात्राएँ होनी चाहिए।

कुछ समस्याओं को हल करने की सुविधा के लिए समीकरण (1) और (2) से दो और सहायक सूत्र प्राप्त किए जा सकते हैं।

आइए हम (1) और (2) से कोणीय त्वरण ε को बाहर करें:
(3) φ = φ 0 + (ω + ω 0)t/2.

आइए हम समय t को (1) और (2) से हटा दें:
(4) φ = φ 0 + (ω 2 - ω 0 2)/(2ε).

आराम की स्थिति से शुरू होने वाले समान रूप से त्वरित घूर्णन के विशेष मामले में, φ 0 = 0 और ω 0 = 0। इसलिए, उपरोक्त मूल और सहायक सूत्र निम्नलिखित रूप लेते हैं:
(5) φ = εt 2/2;
(6) ω = εt;
(7) φ = ωt/2;
(8) φ = ω 2 /(2ε).

§ 35. असमान घूर्णी गति

आइए एक समस्या को हल करने के एक उदाहरण पर विचार करें जिसमें किसी पिंड की गैर-समान घूर्णी गति निर्दिष्ट है।

बिल्कुल कठोर शरीर -एक शरीर में गति के दौरान उसके भागों की सापेक्ष स्थिति नहीं बदलती है।

एक कठोर पिंड की अनुवादात्मक गति - यह इसकी गति है जिसमें शरीर से मजबूती से जुड़ी कोई भी सीधी रेखा अपनी मूल दिशा के समानांतर रहते हुए चलती है।

किसी कठोर पिंड की स्थानांतरीय गति के दौरान, उसके सभी बिंदु कम समय dt में समान रूप से चलते हैं, इन बिंदुओं का त्रिज्या वेक्टर समान मात्रा में बदलता है। तदनुसार, समय के प्रत्येक क्षण में इसके सभी बिंदुओं का वेग समान और बराबर होता है। इसलिए, किसी कठोर पिंड की सुविचारित अनुवादात्मक गति की गतिकी उसके किसी भी बिंदु की गति के अध्ययन के लिए आती है। आमतौर पर हम अंतरिक्ष में स्वतंत्र रूप से घूम रहे एक कठोर पिंड के जड़त्व केंद्र की गति पर विचार करते हैं।

किसी कठोर पिंड की घूर्णी गति - यह एक ऐसी गति है जिसमें इसके सभी बिंदु वृत्तों में घूमते हैं, जिनके केंद्र शरीर के बाहर स्थित होते हैं . सीधी रेखा को पिंड के घूर्णन की धुरी कहा जाता है।

कोणीय वेग- शरीर के घूमने की गति को दर्शाने वाली वेक्टर मात्रा; घूर्णन के कोण का उस समय से अनुपात जिसके दौरान यह घूर्णन हुआ; समय के संबंध में किसी पिंड के घूर्णन कोण के पहले व्युत्पन्न द्वारा निर्धारित एक वेक्टर। कोणीय वेग वेक्टर को दाएँ पेंच नियम के अनुसार घूर्णन अक्ष के अनुदिश निर्देशित किया जाता है। ω=φ/t=2π/T=2πn, जहां T घूर्णन अवधि है, n घूर्णन आवृत्ति है। ω=lim Δt → 0 Δφ/Δt=dφ/dt.

कोणीय त्वरण- समय के संबंध में कोणीय वेग के पहले व्युत्पन्न द्वारा निर्धारित वेक्टर। जब कोई पिंड एक निश्चित अक्ष के चारों ओर घूमता है, तो कोणीय त्वरण वेक्टर को घूर्णन अक्ष के साथ कोणीय वेग के प्रारंभिक वृद्धि के वेक्टर की ओर निर्देशित किया जाता है। समय के संबंध में घूर्णन कोण का दूसरा व्युत्पन्न। जब कोई पिंड एक निश्चित अक्ष के चारों ओर घूमता है, तो कोणीय त्वरण वेक्टर को घूर्णन अक्ष के साथ कोणीय वेग के प्रारंभिक वृद्धि के वेक्टर की ओर निर्देशित किया जाता है। जब गति त्वरित होती है, तो वेक्टर ε, वेक्टर φ के सह-दिशात्मक होता है, और जब यह धीमी होती है, तो यह इसके विपरीत होता है। ε=dω/dt.

यदि dω/dt> 0, तो εω

यदि dω/dt< 0, то ε ↓ω

4. जड़त्व का सिद्धांत (न्यूटन का प्रथम नियम)। जड़त्वीय संदर्भ प्रणाली. सापेक्षता का सिद्धांत.

न्यूटन का प्रथम नियम (जड़त्व का नियम): प्रत्येक भौतिक बिंदु (शरीर) आराम की स्थिति या एक समान रैखिक गति बनाए रखता है जब तक कि अन्य निकायों का प्रभाव उसे इस स्थिति को बदलने के लिए मजबूर नहीं करता

किसी पिंड की आराम की स्थिति या एकसमान सीधी गति बनाए रखने की इच्छा कहलाती है जड़ता. इसलिए न्यूटन के प्रथम नियम को जड़त्व का नियम कहा जाता है।

न्यूटन का पहला नियम जड़त्वीय संदर्भ तंत्र के अस्तित्व को बताता है।

जड़त्वीय संदर्भ फ्रेम- यह एक संदर्भ प्रणाली है जिसके सापेक्ष एक मुक्त भौतिक बिंदु, अन्य निकायों से अप्रभावित, एक सीधी रेखा में समान रूप से चलता है; यह एक ऐसी प्रणाली है जो या तो आराम की स्थिति में है या किसी अन्य जड़त्वीय प्रणाली के सापेक्ष समान रूप से और सीधी रेखा में घूम रही है।

सापेक्षता का सिद्धांत- एक मौलिक भौतिक नियम, जिसके अनुसार कोई भी प्रक्रिया आराम की स्थिति में एक पृथक सामग्री प्रणाली में समान रूप से आगे बढ़ती है, और एक ही प्रणाली में एक समान सीधी गति की स्थिति में आगे बढ़ती है। गति या विश्राम की अवस्थाओं को मनमाने ढंग से चुने गए जड़त्वीय संदर्भ फ्रेम के संबंध में परिभाषित किया जाता है। सापेक्षता का सिद्धांत आइंस्टीन के सापेक्षता के विशेष सिद्धांत का आधार है।

5. गैलीलियन परिवर्तन।

सापेक्षता का सिद्धांत (गैलीली): किसी दिए गए जड़त्वीय संदर्भ प्रणाली के अंदर किए गए कोई भी प्रयोग (मैकेनिकल, इलेक्ट्रिकल, ऑप्टिकल) यह पता लगाना संभव नहीं बनाते हैं कि यह प्रणाली आराम पर है या समान रूप से और सीधा चल रही है; एक जड़त्वीय संदर्भ तंत्र से दूसरे जड़त्वीय संदर्भ तंत्र में संक्रमण के संबंध में प्रकृति के सभी नियम अपरिवर्तनीय हैं।

आइए दो संदर्भ प्रणालियों पर विचार करें: जड़त्वीय फ्रेम K (निर्देशांक x, y, z के साथ), जिसे हम पारंपरिक रूप से स्थिर मानेंगे, और प्रणाली K' (निर्देशांक x', y', z' के साथ), K के सापेक्ष समान रूप से चलती है और गति U ( U = const) के साथ सीधा। आइए दोनों प्रणालियों में एक मनमाना बिंदु A के निर्देशांक के बीच संबंध खोजें। आर = आर'+आर0=आर'+यूटी. (1.)

समीकरण (1.) को निर्देशांक अक्षों पर प्रक्षेपणों में लिखा जा सकता है:

y=y'+Uyt; (2.)

z=z'+Uzt; समीकरण (1.) और (2.) को गैलीलियन समन्वय परिवर्तन कहा जाता है।

संभावित ऊर्जा और बल के बीच संबंध

संभावित क्षेत्र का प्रत्येक बिंदु, एक ओर, शरीर पर कार्य करने वाले बल वेक्टर के एक निश्चित मूल्य से मेल खाता है, और दूसरी ओर, संभावित ऊर्जा के एक निश्चित मूल्य से मेल खाता है। इसलिए, बल और स्थितिज ऊर्जा के बीच एक निश्चित संबंध होना चाहिए।

इस संबंध को स्थापित करने के लिए, आइए हम अंतरिक्ष में एक मनमाने ढंग से चुनी गई दिशा के साथ होने वाले शरीर के एक छोटे से विस्थापन के दौरान क्षेत्र बलों द्वारा किए गए प्राथमिक कार्य की गणना करें, जिसे हम पत्र द्वारा निरूपित करते हैं। ये काम बराबर है

दिशा पर बल का प्रक्षेपण कहां है.

चूँकि इस मामले में कार्य संभावित ऊर्जा के भंडार के कारण किया जाता है, यह अक्ष खंड पर संभावित ऊर्जा के नुकसान के बराबर है:

अंतिम दो भावों से हमें प्राप्त होता है

यह सूत्र समन्वय अक्षों पर बल वेक्टर के प्रक्षेपण को निर्धारित करता है। यदि ये अनुमान ज्ञात हैं, तो बल वेक्टर स्वयं निर्धारित हो जाता है:

गणित वेक्टर में ,

जहां a, x, y, z का एक अदिश फलन है, जिसे इस अदिश का ग्रेडिएंट कहा जाता है और इसे प्रतीक द्वारा दर्शाया जाता है . इसलिए, बल विपरीत चिह्न के साथ ली गई संभावित ऊर्जा प्रवणता के बराबर है

घुमानेवालावे ऐसी गति कहते हैं जिसमें शरीर से जुड़े दो बिंदु होते हैं, इसलिए, इन बिंदुओं से गुजरने वाली सीधी रेखा गति के दौरान गतिहीन रहती है (चित्र 2.16)। निश्चित सीधी रेखा ए बीबुलाया अक्ष।

चावल। 2.1 वी. किसी पिंड की घूर्णी गति की परिभाषा की ओर

घूर्णी गति के दौरान पिंड की स्थिति घूर्णन के कोण φ, रेड को निर्धारित करती है (चित्र 2.16 देखें)। चलते समय, घूर्णन का कोण समय के साथ बदलता है, अर्थात। किसी पिंड की घूर्णी गति के नियम को एक निश्चित अर्ध-तल के बीच डायहेड्रल कोण Ф = Ф(/) के मान के समय में परिवर्तन के नियम के रूप में परिभाषित किया गया है। को () ,घूर्णन की धुरी से गुज़रने वाला, और गतिशील एन 1शरीर से जुड़ा एक आधा तल और घूर्णन की धुरी से भी गुजर रहा है।

घूर्णी गति के दौरान शरीर के सभी बिंदुओं के प्रक्षेप पथ घूर्णन की धुरी पर केंद्रों के साथ समानांतर विमानों में स्थित संकेंद्रित वृत्त होते हैं।

शरीर की घूर्णी गति की गतिज विशेषताएँ। जिस तरह एक बिंदु के लिए गतिज विशेषताओं को पेश किया गया था, उसी तरह एक गतिज अवधारणा पेश की गई है जो फ़ंक्शन φ(c) के परिवर्तन की दर को दर्शाती है, जो घूर्णी गति के दौरान शरीर की स्थिति निर्धारित करती है, अर्थात। कोणीय वेग सह = एफ = एस/एफ/एस //, कोणीय वेग आयाम [सीओ] = रेड /साथ।

तकनीकी गणना में, विभिन्न आयामों के साथ कोणीय वेग की अभिव्यक्ति का अक्सर उपयोग किया जाता है - प्रति मिनट क्रांतियों की संख्या के संदर्भ में: [i] = आरपीएम, और के बीच संबंध पीऔर सह को इस प्रकार दर्शाया जा सकता है: सह = 27w/60 = 7w/30।

सामान्य तौर पर, कोणीय वेग समय के साथ बदलता रहता है। कोणीय वेग में परिवर्तन की दर का माप कोणीय त्वरण e = c/co/c//= co = f है, कोणीय त्वरण का आयाम [e] = rad/s 2 है।

प्रस्तुत कोणीय गतिक विशेषताएँ पूरी तरह से एक फ़ंक्शन को निर्दिष्ट करके निर्धारित की जाती हैं - घूर्णन का कोण बनाम समय।

घूर्णी गति के दौरान शरीर के बिंदुओं की गतिज विशेषताएँ। मुद्दे पर गौर करें एमपिंड घूर्णन अक्ष से दूरी p पर स्थित है। यह बिंदु त्रिज्या p के एक वृत्त के अनुदिश गति करता है (चित्र 2.17)।

चावल। 2.17.

घूर्णन के दौरान शरीर के बिंदु

वक्राकार लंबाई एम क्यू एमत्रिज्या p के वृत्त को इस प्रकार परिभाषित किया गया है एस= पीटीपी, जहां एफ घूर्णन का कोण है, रेड। यदि किसी पिंड की गति का नियम φ = φ(g) के रूप में दिया गया है, तो एक बिंदु की गति का नियम एमप्रक्षेपवक्र के साथ सूत्र द्वारा निर्धारित किया जाता है एस= рф(7).

किसी बिंदु की गति को निर्दिष्ट करने की प्राकृतिक विधि के साथ गतिज विशेषताओं की अभिव्यक्तियों का उपयोग करते हुए, हम एक घूमते हुए पिंड के बिंदुओं के लिए गतिज विशेषताएँ प्राप्त करते हैं: सूत्र के अनुसार गति (2.6)

वी= 5 = आरएफ = आरएसओ; (2.22)

अभिव्यक्ति के अनुसार स्पर्शरेखीय त्वरण (2.12)

i t = K = sor = er; (2.23)

सूत्र के अनुसार सामान्य त्वरण (2.13)

ए„=और 2 /р = с 2 р 2 /р = ogr; (2.24)

अभिव्यक्ति का उपयोग करके कुल त्वरण (2.15)

ए = -]ए + ए] =पीएक्स/ई 2 + सीओ 4। (2.25)

कुल त्वरण की दिशा की विशेषता को p माना जाता है - बिंदु द्वारा वर्णित वृत्त की त्रिज्या से कुल त्वरण के वेक्टर के विचलन का कोण (चित्र 2.18)।

चित्र से. 2.18 हमें मिलता है

tgjLi = अजा एन=रे/पीसीओ 2 =जी/(ओ 2. (2.26)

चावल। 2.18.

ध्यान दें कि घूमते हुए पिंड के बिंदुओं की सभी गतिक विशेषताएँ घूर्णन अक्ष की दूरियों के समानुपाती होती हैं। वे-

उनकी पहचान एक ही फ़ंक्शन के व्युत्पन्न - घूर्णन के कोण के माध्यम से निर्धारित की जाती है।

कोणीय और रैखिक गतिज विशेषताओं के लिए वेक्टर अभिव्यक्तियाँ। घूर्णन की धुरी के साथ, एक घूर्णन पिंड की कोणीय गतिक विशेषताओं के विश्लेषणात्मक विवरण के लिए, अवधारणा घूर्णन कोण वेक्टर(चित्र 2.19): φ = φ(/)ए:, जहां को- खाओ

घूर्णन अक्ष वेक्टर

1; को=sop51 .

वेक्टर f को इस अक्ष के अनुदिश निर्देशित किया गया है ताकि इसे "अंत" से देखा जा सके

घूर्णन वामावर्त हो रहा है।

चावल। 2.19.

सदिश रूप में विशेषताएँ

यदि वेक्टर φ(/) ज्ञात है, तो घूर्णी गति की अन्य सभी कोणीय विशेषताओं को वेक्टर रूप में दर्शाया जा सकता है:

• कोणीय वेग वेक्टर सह = एफ = एफ को।कोणीय वेग वेक्टर की दिशा घूर्णन कोण के व्युत्पन्न का संकेत निर्धारित करती है;
• कोणीय त्वरण वेक्टर є = сo = Ф को।इस वेक्टर की दिशा कोणीय वेग के व्युत्पन्न का संकेत निर्धारित करती है।

प्रस्तुत वैक्टर с और є हमें बिंदुओं की गतिज विशेषताओं के लिए वेक्टर अभिव्यक्ति प्राप्त करने की अनुमति देते हैं (चित्र 2.19 देखें)।

ध्यान दें कि बिंदु के वेग वेक्टर का मापांक कोणीय वेग वेक्टर और त्रिज्या वेक्टर के वेक्टर उत्पाद के मापांक के साथ मेल खाता है: |cox जी= सोग्विपा = बकवास। सदिश с और r की दिशाओं और सदिश उत्पाद की दिशा के नियम को ध्यान में रखते हुए, हम वेग सदिश के लिए एक अभिव्यक्ति लिख सकते हैं:

वी= सह xg.

वैसे ही ये दिखाना भी आसान है

• ? एक्स
• - उदाहरण के लिएBіpa= єр = परऔर

सोसर = सीओ पी = आई.

(इसके अलावा, इन गतिज विशेषताओं के सदिश संबंधित सदिश उत्पादों के साथ दिशा में मेल खाते हैं।

इसलिए, स्पर्शरेखा और सामान्य त्वरण वैक्टर को वेक्टर उत्पादों के रूप में दर्शाया जा सकता है:

• (2.28)
• (2.29)

ए एक्स = जीएक्स जी

ए= सह एक्स वी

घूर्णन का कोण, कोणीय वेग और कोणीय त्वरण

किसी कठोर पिंड का एक निश्चित अक्ष के चारों ओर घूमनायह ऐसी गति कहलाती है जिसमें गति के पूरे समय शरीर के दो बिंदु गतिहीन रहते हैं। इस स्थिति में, अपने निश्चित बिंदुओं से गुजरने वाली सीधी रेखा पर स्थित शरीर के सभी बिंदु भी गतिहीन रहते हैं। इस लाइन को कहा जाता है शरीर के घूर्णन की धुरी.

अगर एऔर में- शरीर के निश्चित बिंदु (चित्र 15)। ), तो घूर्णन की धुरी ही धुरी है आस्ट्रेलिया,जिसकी अंतरिक्ष में कोई भी दिशा हो सकती है, जरूरी नहीं कि लंबवत हो। एक अक्ष दिशा आउंससकारात्मक रूप में लिया जाता है।

हम घूर्णन अक्ष के माध्यम से एक निश्चित तल खींचते हैं द्वाराऔर मोबाइल पी,एक घूमते हुए शरीर से जुड़ा हुआ। माना कि समय के आरंभिक क्षण में दोनों तल संपाती होते हैं। फिर समय के एक क्षण में टीगतिमान विमान और घूमते पिंड की स्थिति को विमानों और संबंधित रैखिक कोण के बीच के डायहेड्रल कोण द्वारा निर्धारित किया जा सकता है φ इन तलों में स्थित सीधी रेखाओं और घूर्णन अक्ष के लंबवत के बीच। कोना φ बुलाया शरीर के घूमने का कोण.

चयनित संदर्भ प्रणाली के सापेक्ष शरीर की स्थिति किसी में भी पूरी तरह से निर्धारित होती है

समय में क्षण, यदि समीकरण दिया जाए φ =एफ(टी) (5)

कहाँ एफ(टी)- समय का कोई दो बार अवकलनीय फलन। इस समीकरण को कहा जाता है एक निश्चित अक्ष के चारों ओर एक कठोर पिंड के घूमने के लिए समीकरण।

एक निश्चित अक्ष के चारों ओर घूमने वाले शरीर में स्वतंत्रता की एक डिग्री होती है, क्योंकि इसकी स्थिति केवल एक पैरामीटर - कोण को निर्दिष्ट करके निर्धारित की जाती है φ .

कोना φ यदि इसे वामावर्त दिशा में प्लॉट किया जाता है तो इसे सकारात्मक माना जाता है, और अक्ष की सकारात्मक दिशा से देखने पर इसे विपरीत दिशा में नकारात्मक माना जाता है। आस्ट्रेलिया.एक निश्चित अक्ष के चारों ओर घूमने के दौरान किसी पिंड के बिंदुओं के प्रक्षेप पथ, घूर्णन अक्ष के लंबवत विमानों में स्थित वृत्त होते हैं।

एक निश्चित अक्ष के चारों ओर एक कठोर पिंड की घूर्णी गति को चिह्नित करने के लिए, हम कोणीय वेग और कोणीय त्वरण की अवधारणाओं का परिचय देते हैं। शरीर का बीजगणितीय कोणीय वेगसमय के किसी भी क्षण को इस क्षण के घूर्णन कोण के समय के संबंध में पहला व्युत्पन्न कहा जाता है, अर्थात। dφ/dt = φ.यह एक सकारात्मक मात्रा है जब शरीर वामावर्त घूमता है, क्योंकि समय के साथ घूर्णन का कोण बढ़ता है, और जब शरीर दक्षिणावर्त घूमता है तो यह नकारात्मक होता है, क्योंकि घूर्णन का कोण कम हो जाता है।

कोणीय वेग मॉड्यूल द्वारा निरूपित किया जाता है ω. तब ω= ׀dφ/dt׀= ׀φ ׀ (6)

कोणीय वेग का आयाम (6) के अनुसार निर्धारित किया गया है

[ω] = कोण/समय = रेड/एस = एस -1.

इंजीनियरिंग में, कोणीय वेग घूर्णी गति है जिसे प्रति मिनट क्रांतियों में व्यक्त किया जाता है। 1 मिनट में शरीर एक कोण में घूम जाएगा 2πп,अगर पी- प्रति मिनट क्रांतियों की संख्या. इस कोण को एक मिनट में सेकंड की संख्या से विभाजित करने पर, हमें मिलता है: (7)

शरीर का बीजगणितीय कोणीय त्वरणबीजगणितीय गति के समय के संबंध में पहला व्युत्पन्न कहा जाता है, अर्थात। घूर्णन कोण का दूसरा व्युत्पन्न d 2 φ/dt 2 = ω. आइए हम कोणीय त्वरण मॉड्यूल को निरूपित करें ε , तब ε=|φ| (8)

कोणीय त्वरण का आयाम (8) से प्राप्त होता है:

[ε ] = कोणीय वेग/समय = रेड/एस 2 = एस -2

अगर φ’’>0 पर φ’>0 , तो बीजगणितीय कोणीय वेग समय के साथ बढ़ता है और इसलिए, शरीर उस समय सकारात्मक दिशा (वामावर्त) में त्वरित गति से घूमता है। पर φ’’<0 और φ’<0 शरीर तेजी से नकारात्मक दिशा में घूमता है। अगर φ’’<0 पर φ’>0 , तो हमारे पास सकारात्मक दिशा में धीमी गति से घूर्णन होता है। पर φ’’>0 और φ’<0 , अर्थात। नकारात्मक दिशा में धीमी गति से घूर्णन होता है। आकृतियों में कोणीय वेग और कोणीय त्वरण को घूर्णन अक्ष के चारों ओर चाप तीरों द्वारा दर्शाया गया है। कोणीय वेग के लिए चाप तीर पिंडों के घूमने की दिशा को इंगित करता है;

त्वरित घूर्णन के लिए, कोणीय वेग और कोणीय त्वरण के लिए चाप तीरों की दिशाएँ समान होती हैं; धीमी गति से घूमने के लिए, उनकी दिशाएँ विपरीत होती हैं।

किसी कठोर पिंड के घूमने के विशेष मामले

घूर्णन को एक समान कहा जाता है यदि ω=const, φ= φ't

यदि घूर्णन एकसमान होगा ε= स्थिरांक. φ'= φ' 0 + φ't और

सामान्य तौर पर, यदि φ’’ हमेशा नहीं,

शरीर के बिंदुओं का वेग और त्वरण

एक निश्चित अक्ष के चारों ओर एक कठोर पिंड के घूमने का समीकरण ज्ञात है φ= एफ(टी)(चित्र 16)। दूरी एसअंक एमएक चलते हुए विमान में पीएक गोलाकार चाप (बिंदु प्रक्षेपवक्र) के साथ, बिंदु से मापा जाता है एम ओ,एक निश्चित तल में स्थित, कोण के माध्यम से व्यक्त किया गया φ लत s=hφ, कहाँ एच-वृत्त की त्रिज्या जिसके अनुदिश बिंदु गति करता है। यह एक बिंदु से सबसे कम दूरी है एमघूर्णन की धुरी पर. इसे कभी-कभी किसी बिंदु के घूर्णन की त्रिज्या भी कहा जाता है। जब पिंड एक निश्चित अक्ष के चारों ओर घूमता है तो शरीर के प्रत्येक बिंदु पर घूर्णन की त्रिज्या अपरिवर्तित रहती है।

एक बिंदु की बीजगणितीय गति एमसूत्र द्वारा निर्धारित किया गया है v τ =s'=hφप्वाइंट स्पीड मॉड्यूल: v=hω(9)

एक निश्चित अक्ष के चारों ओर घूमते समय शरीर के बिंदुओं का वेग इस अक्ष से उनकी न्यूनतम दूरी के समानुपाती होता है।आनुपातिकता गुणांक कोणीय वेग है। बिंदुओं के वेग प्रक्षेप पथ के स्पर्शरेखा के अनुदिश निर्देशित होते हैं और इसलिए, घूर्णन की त्रिज्या के लंबवत होते हैं। एक सीधी रेखा खंड पर स्थित शरीर बिंदुओं का वेग ओम,(9) के अनुसार एक रेखीय कानून के अनुसार वितरित किया जाता है। वे परस्पर समानांतर हैं, और उनके सिरे घूर्णन अक्ष से गुजरने वाली एक ही सीधी रेखा पर स्थित हैं। हम एक बिंदु के त्वरण को स्पर्शरेखा और सामान्य घटकों में विघटित करते हैं, अर्थात। a=a τ +a nτस्पर्शरेखा और सामान्य त्वरण की गणना सूत्र (10) का उपयोग करके की जाती है

चूँकि एक वृत्त के लिए वक्रता त्रिज्या है पी=एच(चित्र 17 ). इस प्रकार,

बिंदुओं की स्पर्शरेखा, सामान्य और कुल त्वरण, साथ ही वेग भी एक रैखिक कानून के अनुसार वितरित किए जाते हैं। वे घूर्णन अक्ष के बिंदुओं की दूरी पर रैखिक रूप से निर्भर करते हैं। सामान्य त्वरण वृत्त की त्रिज्या के अनुदिश घूर्णन अक्ष की ओर निर्देशित होता है। स्पर्शरेखीय त्वरण की दिशा बीजगणितीय कोणीय त्वरण के चिह्न पर निर्भर करती है। पर φ’>0 और φ’’>0 या φ’<0 और φ’<0 हमने पिंड के घूर्णन और सदिशों की दिशाओं को त्वरित किया है एक τऔर वीमेल खाना। अगर φ’ और φ’" फिर अलग-अलग संकेत (धीमी गति से घूमना) हैं एक τऔर वीएक दूसरे के विपरीत निर्देशित।

नामित होना α एक बिंदु के कुल त्वरण और उसके घूर्णन की त्रिज्या के बीच का कोण, हमारे पास है

tgα = | ए τ |/ए एन = ε/ω 2 (11)

सामान्य त्वरण के बाद से एक पीहमेशा ही सकारात्मक। कोना एशरीर के सभी बिंदुओं के लिए समान। इसे कठोर पिंड के घूर्णन की दिशा की परवाह किए बिना, कोणीय त्वरण के चाप तीर की दिशा में त्वरण से घूर्णन की त्रिज्या तक स्थगित किया जाना चाहिए।

कोणीय वेग और कोणीय त्वरण के सदिश

आइए हम किसी पिंड के कोणीय वेग और कोणीय त्वरण के सदिशों की अवधारणाओं का परिचय दें। अगर कोइसकी सकारात्मक दिशा में निर्देशित घूर्णन अक्ष का इकाई वेक्टर है, फिर कोणीय वेग वेक्टर ώ और कोणीय त्वरण ε भावों द्वारा निर्धारित (12)

क्योंकि कपरिमाण और दिशा में एक सदिश स्थिरांक है, तो (12) से यह अनुसरण करता है

ε=dώ/dt(13)

पर φ’>0 और φ’’>0 वेक्टर दिशाएँ ώ और ε मेल खाना। वे दोनों घूर्णन अक्ष के सकारात्मक पक्ष की ओर निर्देशित हैं आउंस(चित्र 18.ए)यदि φ’>0 और φ’’<0 , फिर उन्हें विपरीत दिशाओं में निर्देशित किया जाता है (चित्र 18.बी)। ). त्वरित घूर्णन के दौरान कोणीय त्वरण वेक्टर कोणीय वेग वेक्टर के साथ दिशा में मेल खाता है और धीमी गति से घूर्णन के दौरान इसके विपरीत होता है। वैक्टर ώ और ε घूर्णन अक्ष पर किसी भी बिंदु पर दर्शाया जा सकता है। वे गतिमान सदिश हैं। यह गुण शरीर के बिंदुओं के वेग और त्वरण के लिए वेक्टर सूत्रों से अनुसरण करता है।

जटिल बिंदु आंदोलन

बुनियादी अवधारणाओं

किसी कठोर पिंड की कुछ अधिक जटिल प्रकार की गति का अध्ययन करने के लिए, किसी बिंदु की सबसे सरल जटिल गति पर विचार करना उचित है। कई समस्याओं में, एक बिंदु की गति को एक दूसरे के सापेक्ष चलने वाली दो (या अधिक) संदर्भ प्रणालियों के सापेक्ष माना जाना चाहिए। इस प्रकार, चंद्रमा की ओर बढ़ने वाले अंतरिक्ष यान की गति को पृथ्वी के सापेक्ष और चंद्रमा के सापेक्ष, जो पृथ्वी के सापेक्ष घूम रहा है, दोनों पर एक साथ विचार किया जाना चाहिए। किसी बिंदु के किसी भी आंदोलन को जटिल माना जा सकता है, जिसमें कई आंदोलन शामिल हैं। उदाहरण के लिए, पृथ्वी के सापेक्ष एक नदी के किनारे एक जहाज की आवाजाही को जटिल माना जा सकता है, जिसमें पानी के माध्यम से और साथ में बहते पानी की आवाजाही शामिल है।

सबसे सरल मामले में, किसी बिंदु की जटिल गति में सापेक्ष और अनुवाद संबंधी गतियाँ शामिल होती हैं। आइए इन आंदोलनों को परिभाषित करें। आइए हमारे पास दो संदर्भ प्रणालियाँ एक दूसरे के सापेक्ष गतिमान हैं। यदि इनमें से कोई एक सिस्टम ओ एल एक्स 1 वाई 1 जेड 1(चित्र 19 ) मुख्य या स्थिर के रूप में लिया जाता है (अन्य संदर्भ प्रणालियों के सापेक्ष इसकी गति पर विचार नहीं किया जाता है), फिर दूसरी संदर्भ प्रणाली ऑक्सीज़पहले वाले के सापेक्ष गति करेगा। एक गतिशील संदर्भ फ्रेम के सापेक्ष एक बिंदु की गति ऑक्सीज़बुलाया रिश्तेदार।इस गति की विशेषताएं, जैसे प्रक्षेप पथ, गति और त्वरण कहलाती हैं रिश्तेदार।वे सूचकांक आर द्वारा निर्दिष्ट हैं; गति और त्वरण के लिए वी आर , ए आर .मुख्य या निश्चित सिस्टम संदर्भ फ्रेम के सापेक्ष एक बिंदु की गति ओ 1 एक्स 1 वाई 1 जेड 1बुलाया निरपेक्ष(या जटिल ). इसे कभी-कभी भी कहा जाता है कम्पोजिटआंदोलन। इस गति के प्रक्षेप पथ, गति और त्वरण को निरपेक्ष कहा जाता है। निरपेक्ष गति की गति और त्वरण को अक्षरों द्वारा दर्शाया जाता है वी, एकोई अनुक्रमणिका नहीं.

किसी बिंदु की पोर्टेबल गति वह गति है जो वह संदर्भ के एक गतिशील फ्रेम के साथ मिलकर बनाता है, एक बिंदु के रूप में विचाराधीन समय में इस प्रणाली से कठोरता से जुड़ा हुआ है। सापेक्ष गति के कारण, अलग-अलग समय पर एक गतिमान बिंदु शरीर के विभिन्न बिंदुओं के साथ मेल खाता है एस,जिससे गतिशील संदर्भ प्रणाली जुड़ी हुई है। पोर्टेबल गति और पोर्टेबल त्वरण शरीर के उस बिंदु की गति और त्वरण हैं एस,जिसके साथ गतिमान बिंदु वर्तमान में मेल खाता है। पोर्टेबल गति और त्वरण को दर्शाता है वी इ , ए इ.

यदि शरीर के सभी बिंदुओं का प्रक्षेप पथ एस,चलती संदर्भ प्रणाली से जुड़ा हुआ, चित्र (चित्र 20) में दर्शाया गया है, फिर हमें रेखाओं का एक परिवार मिलता है - एक बिंदु के पोर्टेबल आंदोलन के प्रक्षेपवक्र का एक परिवार एम।बिंदु की सापेक्ष गति के कारण एमसमय के प्रत्येक क्षण में यह पोर्टेबल गति के प्रक्षेप पथों में से एक पर होता है। डॉट एमपोर्टेबल प्रक्षेप पथों के इस परिवार के प्रत्येक प्रक्षेप पथ पर केवल एक बिंदु के साथ मेल खा सकता है। इस संबंध में, कभी-कभी यह माना जाता है कि पोर्टेबल गति के कोई प्रक्षेप पथ नहीं होते हैं, क्योंकि रेखाओं को पोर्टेबल गति के प्रक्षेप पथ के रूप में मानना ​​आवश्यक है, जिसके लिए केवल एक बिंदु वास्तव में प्रक्षेप पथ का एक बिंदु है।

किसी बिंदु की गतिकी में, किसी संदर्भ प्रणाली के सापेक्ष एक बिंदु की गति का अध्ययन किया जाता था, भले ही यह संदर्भ प्रणाली अन्य प्रणालियों के सापेक्ष चलती हो या नहीं। आइए हम सापेक्ष और आलंकारिक गति से युक्त सबसे सरल मामले में जटिल गति पर विचार करके इस अध्ययन को पूरक करें। एक ही निरपेक्ष गति, संदर्भ के विभिन्न गतिमान फ़्रेमों को चुनते हुए, अलग-अलग पोर्टेबल और, तदनुसार, सापेक्ष गतियों से युक्त मानी जा सकती है।

गति जोड़

आइए हम किसी बिंदु की पूर्ण गति की गति निर्धारित करें यदि इस बिंदु की सापेक्ष और पोर्टेबल गति की गति ज्ञात हो। मान लीजिए कि बिंदु ऑक्सीज़ के गतिशील संदर्भ फ्रेम के संबंध में केवल एक सापेक्ष गति करता है और समय के समय टी सापेक्ष गति के प्रक्षेपवक्र पर स्थिति एम पर कब्जा कर लेता है (चित्र 20)। समय t+ t पर, सापेक्ष गति के कारण, बिंदु M 1 स्थिति में होगा, सापेक्ष गति के प्रक्षेपवक्र के साथ MM 1 चला गया है। चलिए मान लेते हैं कि मुद्दा इसमें शामिल है ऑक्सीज़और एक सापेक्ष प्रक्षेपवक्र के साथ यह किसी वक्र पर आगे बढ़ेगा एमएम 2.यदि कोई बिंदु सापेक्ष और पोर्टेबल दोनों आंदोलनों में एक साथ भाग लेता है, तो समय ए में; वह आगे बढ़ेगी एमएम"निरपेक्ष गति के प्रक्षेप पथ पर और समय के क्षण में टी+एटपद ग्रहण करेंगे एम"।यदि समय परथोड़ा और फिर सीमा पर जाएँ पर,शून्य की ओर रुझान होने पर, वक्रों के अनुदिश छोटे-छोटे विस्थापनों को जीवाओं के खंडों द्वारा प्रतिस्थापित किया जा सकता है और विस्थापन सदिशों के रूप में लिया जा सकता है। सदिश विस्थापनों को जोड़ने पर, हमें प्राप्त होता है

इस संबंध में, उच्च क्रम की छोटी मात्रा को शून्य पर छोड़ दिया जाता है पर,शून्य की ओर रुझान. सीमा से गुजरते हुए, हमारे पास (14) है

इसलिए, (14) का रूप (15) होगा

तथाकथित वेग जोड़ प्रमेय प्राप्त होता है: किसी बिंदु की पूर्ण गति की गति इस बिंदु की पोर्टेबल और सापेक्ष गति की गति के वेक्टर योग के बराबर होती है।चूँकि सामान्य स्थिति में पोर्टेबल और सापेक्ष गतियों के वेग लंबवत नहीं होते हैं, तो (15')

सम्बंधित जानकारी।

चावल। 6.4

किसी पिंड की ऐसी गति जिसमें उसके कोई दो बिंदु हों (एऔर मेंचित्र में 6.4) गतिहीन रहना, जिसे एक निश्चित अक्ष के चारों ओर घूमना कहा जाता है।

यह दिखाया जा सकता है कि इस स्थिति में बिंदुओं को जोड़ने वाली सीधी रेखा पर पड़ा शरीर का कोई भी बिंदु गतिहीन रहता है अरे वी.

इन बिन्दुओं से गुजरने वाली धुरी कहलाती है अक्षशव; इसकी सकारात्मक दिशा मनमाने ढंग से चुनी जाती है (चित्र 6.4)।

कोई बात एमएक पिंड जो घूर्णन अक्ष पर नहीं है, एक वृत्त का वर्णन करता है, जिसका केंद्र घूर्णन अक्ष पर स्थित है (चित्र 6.4)।

घूर्णन की एक निश्चित धुरी के साथ शरीर की स्थिति जेड(चित्र 6.5) को केवल एक अदिश पैरामीटर का उपयोग करके वर्णित किया जा सकता है - घूर्णन कोण (आर. यह घूर्णन अक्ष के माध्यम से खींचे गए दो विमानों के बीच का कोण है: एक निश्चित विमान एनऔर चल - आर,शरीर से मजबूती से जुड़ा हुआ (चित्र 6.5)। हम कोण संदर्भ दिशा को सकारात्मक मानते हैं अक्ष के अंत से देखने पर दक्षिणावर्त गति के विपरीत जेड(चित्र 6.5 में एक चाप तीर द्वारा दर्शाया गया है)। कोण के माप की SI इकाई 1 रेडियन 57.3° है। समय पर घूर्णन कोण की कार्यात्मक निर्भरता

एक निश्चित अक्ष के चारों ओर किसी पिंड की घूर्णी गति को पूरी तरह से निर्धारित करता है। इसलिए, समानता (6.3) को एक निश्चित अक्ष के चारों ओर एक कठोर शरीर के घूर्णन का समीकरण कहा जाता है।

किसी पिंड के घूमने की गति को कोणीय वेग से जाना जाता है साथपिंड, जिसे समय के संबंध में घूर्णन कोण के व्युत्पन्न के रूप में परिभाषित किया गया है

और इसका आयाम rad/s (या s"") है।

घूर्णी गति की दूसरी गतिकी विशेषता कोणीय त्वरण है - शरीर के कोणीय वेग का व्युत्पन्न:

कोणीय त्वरण का आयाम rad/s 2 (या) है साथ~ 2).

टिप्पणी।प्रतीक और साथ? वीइस व्याख्यान के निर्दिष्ट हैं बीजगणितीयकोणीय वेग और कोणीय त्वरण का मान। उनके संकेत घूर्णन की दिशा और उसकी प्रकृति (त्वरित या धीमा) का संकेत देते हैं। उदाहरण के लिए, यदि साथ = एफ> 0, फिर कोण (आरसमय के साथ बढ़ता है और इसलिए, पिंड संदर्भ की दिशा में घूमता है (आर।

किसी घूमते हुए पिंड के प्रत्येक बिंदु की गति और त्वरण को उसके कोणीय वेग और कोणीय त्वरण से आसानी से संबंधित किया जा सकता है। एक मनमाने बिंदु की गति पर विचार करें एमनिकाय (चित्र 6.6)।

चूँकि इसका प्रक्षेप पथ एक वृत्त है, तो चाप निर्देशांक.9 बिंदु का है एमशरीर को एक कोण से मोड़ने के बाद इच्छा

कहाँ एच-बिंदु से दूरी एमघूर्णन के अक्ष पर (चित्र 6.6)।

समय के संबंध में इस समानता के दोनों पक्षों को अलग करने पर, हम (5.14) और (6.4) को ध्यान में रखते हुए प्राप्त करते हैं:

जहाँ g g स्पर्शरेखा g पर बिंदु की गति का प्रक्षेपण है, जो चाप के संदर्भ बिंदु और कोण की ओर निर्देशित है

किसी बिंदु के सामान्य त्वरण का परिमाण एम(5.20) और (6.6) के अनुसार यह होगा

और (5.19) और (6.5) के अनुसार स्पर्शरेखा r पर इसके स्पर्शरेखीय त्वरण का प्रक्षेपण

पूर्ण बिंदु त्वरण मॉड्यूल एम

सदिशों की दिशाएँ v, ए, ए„, ए,मामले के लिए जब च> 0 और च > 0 को चित्र में दिखाया गया है। 6.7.

उदाहरण 1. ट्रांसमिशन तंत्र में पहिए / और 2 होते हैं, जो एक बिंदु पर जुड़े होते हैं कोताकि जब वे घूमें तो आपसी फिसलन न हो। पहिया घूर्णन समीकरण 1:

सकारात्मक कोण संदर्भ दिशा (आरचित्र में एक चाप तीर द्वारा दर्शाया गया है। 6.8.

तंत्र के आयाम ज्ञात हैं: जी= 4 सेमी, आर2= 6 सेमी, जी 2 = 2 सेमी.

किसी बिंदु की गति और त्वरण ज्ञात कीजिए एमसमय में क्षण भर के लिए पहिए 2 /| = 2 एस.

समाधान।जब पहिया तंत्र चलता है 1 और 2 बिंदुओं से गुजरने वाली निश्चित अक्षों के चारों ओर घूमते हैं 0 और 0 2 चित्र के तल के लंबवत। 6.8. पहिये का कोणीय वेग और कोणीय त्वरण ज्ञात करना मैंसमय पर / = 2 एस, इन मात्राओं की उपरोक्त परिभाषाओं (6.4) और (6.5) का उपयोग करते हुए:

उनके नकारात्मक संकेत समय की इस बात का संकेत देते हैं टी- 2 एस पहिया / दक्षिणावर्त घूमता है (कोण पढ़ने की दिशा के विपरीत)। (आर) और यह घूर्णन त्वरित हो जाता है। पारस्परिक पहिया फिसलन की अनुपस्थिति के कारण मैंऔर संपर्क बिंदु पर उनके बिंदुओं के 2 वेग सदिश कोबराबर होना चाहिए. आइए हम इस गति के परिमाण को (6.6) का उपयोग करके पहियों के कोणीय वेग के रूप में व्यक्त करें:

अंतिम समानता से हम पहिया 2 के कोणीय वेग के मॉड्यूल को व्यक्त करते हैं और समय 6 = 2 एस के निर्दिष्ट क्षण के लिए इसका मान पाते हैं:

गति दिशा को(चित्र 6.9) इंगित करता है कि पहिया 2 वामावर्त घूमता है और, इसलिए, ओह> 0. (6.10) और अंतिम असमानता से यह स्पष्ट है कि पहियों के कोणीय वेग एक निरंतर नकारात्मक कारक से भिन्न होते हैं (- जी1जी 2): 2 = के साथजी (/जी 2). लेकिन फिर इन गतियों के व्युत्पन्न - पहियों के कोणीय त्वरण - एक ही कारक से भिन्न होने चाहिए: ई 2 =? ] (-जी ] /जी 1)=-2-(-4/2) = 4एस~2।

किसी बिंदु का वेग और त्वरण ज्ञात करना एमसूत्र (6.6) - (6.9) का उपयोग करते हुए चरणबद्ध पहिया 2:

वैक्टर v और, a, और d/ की दिशाएँ चित्र में दिखाई गई हैं। 6.9.