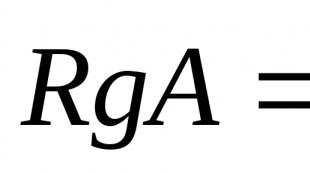Oglašavanje na portalu

Cool work04/02/12. Pogledajmo * Koja se jednačina naziva kvadratnom? * Koje jednačine se nazivaju nepotpune kvadratne jednačine? * Koji. Koncept jednačine linija. Definiranje prave pomoću jednačine Sl.6. Jednadžba vektorske linije

Jednakost oblika F (x, y) = 0 naziva se jednadžba u dvije varijable x, y, ako nije tačno za sve parove brojeva x, y. Kažu dva broja x = x 0 , y=y 0, zadovoljiti neku jednačinu oblika F(x, y)=0, ako prilikom zamjene ovih brojeva umjesto varijabli X I at u jednačini njena lijeva strana nestaje.

Jednačina date prave (u određenom koordinatnom sistemu) je jednačina sa dvije varijable koju zadovoljavaju koordinate svake tačke koja leži na ovoj pravoj, a ne zadovoljavaju je koordinate svake tačke koja ne leži na njoj.

U nastavku, umjesto izraza „daje se jednačina prave F(x, y) = 0" često ćemo reći ukratko: data linija F (x, y) = 0.

Ako su date jednačine dvije prave F(x, y) = 0 I F(x, y) = Q, zatim zajedničko rješenje sistema

daje sve njihove presečne tačke. Tačnije, svaki par brojeva koji je zajedničko rješenje ovog sistema određuje jednu od tačaka presjeka.

*) U slučajevima kada koordinatni sistem nije imenovan, pretpostavlja se da je kartezijanski pravougaoni.

157. Bodovi se daju *) M 1 (2; - 2), M 2 (2; 2), M 3 (2; - 1), M 4 (3; -3), M 5 (5; -5), M 6 (3; -2). Odredite koje objavljene tačke leže na pravoj definisanoj jednadžbom X+ y = 0, a koje ne leže na njemu. Koja je prava definisana ovom jednačinom? (Nacrtajte ga na crtežu.)

158. Na pravoj definisanoj jednačinom X 2 +y 2 =25, naći tačke čije su apscise jednake sledećim brojevima: a) 0, b) - 3, c) 5, d) 7; na istoj pravoj naći tačke čije su ordinate jednake sledećim brojevima: e) 3, f) - 5, g) - 8. Koja prava je određena ovom jednačinom? (Nacrtajte ga na crtežu.)

159. Odredi koje su prave određene sljedećim jednačinama (konstruiraj ih na crtežu):

1) x - y = 0; 2) x + y = 0; 3) x- 2 = 0; 4) x+ 3 = 0;

5) y - 5 = 0; 6) y+ 2 = 0; 7) x = 0; 8) y = 0;

9) x 2 - xy = 0; 10) xy+ y 2 = 0; jedanaest) x 2 - y 2 = 0; 12) xy= 0;

13) y 2 - 9 = 0; 14) xy 2 - 8xy+15 = 0; 15) y 2 +5y+4 = 0;

16) X 2 y - 7xy + 10y = 0; 17) y =|x|; 18) x =|at|; 19)y + |x|=0;

20) x +|at|= 0; 21)y =|X- 1|; 22) y = |x+ 2|; 23) X 2 + at 2 = 16;

24) (x-2) 2 +(y-1) 2 =16; 25) (x+ 5) 2 +(y- 1) 2 = 9;

26) (X - 1) 2 + y 2 = 4; 27) x 2 +(y + 3) 2 = 1; 28) (x -3) 2 + y 2 = 0;

29) X 2 + 2y 2 = 0; 30) 2X 2 + 3y 2 + 5 = 0

31) (x- 2) 2 + (y + 3) 2 + 1=0.

160. Zadati redovi:

1)X+ y = 0; 2)x - y = 0; 3) x 2 + y 2 - 36 = 0;

4) x 2 +y 2 -2x==0; 5) x 2 +y 2 + 4x-6y-1 =0.

Odredi koji od njih prolazi kroz ishodište.

161. Dati redovi:

1) x 2 + y 2 = 49; 2) (x- 3) 2 + (y+ 4) 2 = 25;

3) (x+ 6) 2 + (y - 3) 2 = 25; 4) ( x + 5) 2 + (y - 4) 2 = 9;

5) x 2 +y 2 - 12x + 16y = 0; 6) x 2 +y 2 - 2x + 8at+ 7 = 0;

7) x 2 +y 2 - 6x + 4y + 12 = 0.

Nađite njihove tačke preseka: a) sa osom Oh; b) sa osom OU.

162.Nađi tačke preseka dve prave;

1)X 2 +y 2 = 8, x-y = 0;

2) X 2 +y 2 -16x+4at+18 = 0, x + y= 0;

3) X 2 +y 2 -2x+4at -3 = 0, X 2 + y 2 = 25;

4) X 2 +y 2 -8x+10u+40 = 0, X 2 + y 2 = 4.

163. Tačke su date u polarnom koordinatnom sistemu

M 1 (1; ), M 2 (2; 0), M 3 (2; )

M 4 (
;) I M 5 (1; )

Odredite koje od ovih tačaka leže na pravoj definisanoj jednačinom u polarnim koordinatama  = 2 cos , a koje ne leže na njoj. Koja je prava određena ovom jednačinom? (Nacrtaj na crtežu :)

164. Na pravoj definisanoj jednačinom  = , pronađite tačke čiji su polarni uglovi jednaki sljedećim brojevima: a) ,b) - , c) 0, d) . Koja je prava definisana ovom jednačinom?

(Izgradite ga na crtežu.)

165.Na pravoj definisanoj jednačinom  = , pronađite tačke čiji su polarni radijusi jednaki sljedećim brojevima: a) 1, b) 2, c)
. Koja je prava definisana ovom jednačinom? (Izgradite ga na crtežu.)

166. Utvrdi koje su prave određene u polarnim koordinatama sljedećim jednačinama (konstruiraj ih na crtežu):

1)  = 5; 2)  = ; 3)  = ; 4)  cos  = 2; 5)  sin  = 1;

6)  = 6 cos ; 7)  = 10 sin ; 8) sin  = 9) sin  =

167. Konstruirajte sljedeće Arhimedove spirale na crtežu:

1)  = 5, 2)  = 5; 3)  = ; 4)r = -1.

168. Na crtežu konstruirajte sljedeće hiperboličke spirale:

1)  = ; 2) = ; 3) = ; 4) = - .

169. Na crtežu konstruirajte sljedeće logaritamske spirale:

,
.

170. Odredi dužine segmenata u koje seče Arhimedova spirala

zraka koja izlazi iz pola i nagnuta je prema polarnoj osi pod uglom
. Napravite crtež.

171. O Arhimedovoj spirali
tačka uzeta SA,čiji je polarni radijus 47. Odredi koliko dijelova ova spirala seče polarni polumjer tačke SA, Napravite crtež.

172. Na hiperboličnoj spirali
nađi tačku R,čiji je polarni radijus 12. Napravi crtež.

173. Na logaritamskoj spirali
nađi tačku Q čiji je polarni radijus 81. Nacrtaj.

Pogledajmo * Koja se jednačina naziva kvadratnom? * Koje jednačine se nazivaju nepotpune kvadratne jednačine? * Koja se kvadratna jednačina naziva redukovanom? * Šta se naziva korenom kvadratne jednačine? * Šta znači riješiti kvadratnu jednačinu? Koja se jednačina naziva kvadratnom? Koje se jednadžbe nazivaju nepotpunim kvadratnim jednadžbama? Koja se kvadratna jednačina naziva redukovana? Šta je korijen kvadratne jednačine? Šta znači riješiti kvadratnu jednačinu? Koja se jednačina naziva kvadratnom? Koje se jednadžbe nazivaju nepotpunim kvadratnim jednadžbama? Koja se kvadratna jednačina naziva redukovana? Šta je korijen kvadratne jednačine? Šta znači riješiti kvadratnu jednačinu?
















Algoritam za rješavanje kvadratne jednadžbe: 1. Odrediti najracionalniji način rješavanja kvadratne jednadžbe 2. Odaberite najracionalniji način rješavanja 3. Određivanje broja korijena kvadratne jednačine 4. Pronalaženje korijena kvadratne jednadžbe Radi boljeg pamćenje popuni tabelu... Za bolje pamćenje popuni tabelu... Za bolje pamćenje popuni tabelu...






Dodatni uvjet Korijeni jednadžbe Primjeri 1. c = c = 0, a 0 ax 2 = 0 x 1 = 0 2. c = 0, a 0, b 0 ax 2 + bx = 0 x 1 = 0, x 2 = -b /a 3. c = 0, a 0, c 0 ax 2 + c = 0 a) x 1.2 = ±(c/a), gdje je c/a 0. b) ako je c/a 0, onda nema rješenja 4. a 0 ax 2 + bx + c = 0 x 1,2 =(-b±D)/2 a, gdje je D = b 2 – 4 ac, D0 5. c – paran broj (b = 2k), a 0, u 0, c 0 h 2 + 2kx + c = 0 x 1.2 =(-b±D)/a, D 1 = k 2 – ac, gdje je k = 6. Inverzna teorema Vietinoj teoremi x 2 + px + q = 0x 1 + x 2 = - p x 1 x 2 = q


II. Posebne metode 7. Metoda izolacije kvadrata binoma. Cilj: Svesti opštu jednačinu na nepotpunu kvadratnu jednačinu. Napomena: metoda je primjenjiva na sve kvadratne jednadžbe, ali nije uvijek zgodna za korištenje. Koristi se za dokazivanje formule za korijene kvadratne jednadžbe. Primjer: riješiti jednačinu x 2 -6 x+8=0 8. Metoda “prenošenja” najvećeg koeficijenta. Korijeni kvadratnih jednadžbi ax 2 + bx + c = 0 i y 2 +by+ac=0 povezani su relacijama: i Napomena: metoda je dobra za kvadratne jednačine sa “pogodnim” koeficijentima. U nekim slučajevima vam omogućava da usmeno riješite kvadratnu jednačinu. Primjer: riješiti jednačinu 2 x 2 -9 x-5=0 Na osnovu teorema: Primjer: riješiti jednačinu 157 x x-177=0 9. Ako je u kvadratnoj jednadžbi a+b+c=0, onda je jedan od korijeni su 1, a drugi, prema Vietinoj teoremi, jednak je c / a 10. Ako je u kvadratnoj jednadžbi a + c = b, tada je jedan od korijena jednak -1, a drugi, prema Vietinoj teorema, jednaka je -c / a Primjer: riješimo jednačinu 203 x x + 17 = 0 x 1 =y 1 /a, x 2 =y 2 /a


III. Opće metode rješavanja jednačina 11. Metoda faktorizacije. Cilj: Reducirati opštu kvadratnu jednačinu na oblik A(x)·B(x)=0, gdje su A(x) i B(x) polinomi u odnosu na x. Metode: Izuzimanje zajedničkog faktora iz zagrada; Korištenje skraćenih formula za množenje; Metoda grupisanja. Primjer: riješiti jednačinu 3 x 2 +2 x-1=0 12. Metoda uvođenja nove varijable. Dobar izbor nove varijable čini strukturu jednačine transparentnijom. Primjer: riješite jednačinu (x 2 +3 x-25) 2 -6(x 2 +3 x-25) = - 8









Prava linija na ravni iu prostoru.

Proučavanje svojstava geometrijskih figura pomoću algebre naziva se analitička geometrija , a mi ćemo koristiti tzv koordinatni metod .

Prava na ravni se obično definira kao skup tačaka koje imaju svojstva jedinstvena za njih. Činjenica da su x i y koordinate (brojevi) tačke koja leži na ovoj pravoj zapisane analitički u obliku neke jednačine.

Def.1 Jednadžba linije (jednačina krive) na Oxy ravni naziva se jednadžba (*), koju zadovoljavaju koordinate x i y svake tačke na datoj pravoj, a ne zadovoljavaju je koordinate bilo koje druge tačke koja ne leži na ovoj pravoj.

Iz definicije 1 slijedi da svaka linija na ravni odgovara nekoj jednadžbi između trenutnih koordinata ( x,y ) tačke ove prave i obrnuto, svaka jednačina odgovara, uopšteno govoreći, određenoj pravoj.

Ovo dovodi do dva glavna problema analitičke geometrije na ravni.

1. Prava je data u obliku skupa tačaka. Moramo napraviti jednačinu za ovu liniju.

2. Zadata je jednačina prave. Potrebno je proučiti njegova geometrijska svojstva (oblik i položaj).

Primjer. Da li tačke lažu A(-2;1) I IN (1;1) na liniji 2 X +at +3=0?

Problem nalaženja presečnih tačaka dve prave date jednačinama i svodi se na pronalaženje koordinata koje zadovoljavaju jednačinu obe prave, tj. na rješavanje sistema od dvije jednačine sa dvije nepoznate.

Ako ovaj sistem nema pravih rješenja, tada se prave ne sijeku.

Koncept linije je uveden u UCS na sličan način.

Prava na ravni se može definisati sa dve jednačine

Gdje X I at – proizvoljne koordinate tačke M(x;y), leži na ovoj liniji, i t - varijabla pod nazivom parametar , parametar određuje položaj tačke na ravni.

Na primjer, ako je , tada vrijednost parametra t=2 odgovara tački (3;4) na ravni.

Ako se parametar promijeni, tačka na ravni se pomiče, opisujući ovu liniju. Ova metoda definiranja linije se zove parametarska, a jednačina (5.1) je parametarska jednačina prave.

Da bi se prešlo sa parametarskih jednačina na opštu jednačinu (*), mora se nekako eliminisati parametar iz dve jednačine. Međutim, napominjemo da takva tranzicija nije uvijek preporučljiva i nije uvijek moguća.

Prava na ravni se može specificirati vektorska jednadžba , gdje je t parametar skalarne varijable. Svaka vrijednost parametra odgovara određenom vektoru ravnine. Prilikom promjene parametra, kraj vektora će opisivati ​​određenu liniju.

Vektorska jednadžba u DSC odgovaraju dvije skalarne jednadžbe

(5.1), tj. jednadžba projekcija na koordinatne ose vektorske jednadžbe prave je njegova



parametarska jednačina.

Vektorska jednačina i jednadžbe parametarskih linija imaju mehaničko značenje. Ako se tačka kreće u ravni, tada se navedene jednačine nazivaju jednačine kretanja , a linija je putanja tačke, parametar t je vrijeme.

Zaključak: svaka linija na ravni odgovara jednačini oblika.

U opštem slučaju, BILO KOJA JEDNAČINA POGLEDA odgovara određenoj liniji čija su svojstva određena datom jednačinom (s tim da nijedna geometrijska slika ne odgovara jednačini na ravni).

Neka je odabran koordinatni sistem na ravni.

Def. 5.1. Jednačina linije ova vrsta jednačine se zoveF(x;y) =0, koje zadovoljavaju koordinate svake tačke koje leži na ovoj pravoj, a ne zadovoljavaju koordinate bilo koje tačke koja ne leži na njoj.

Jednačina oblikaF(x;y )=0 – naziva se opšta jednačina prave ili jednačina u implicitnom obliku.

Dakle, linija G je geometrijsko mjesto tačaka koje zadovoljavaju ovu jednačinu G=((x, y): F(x;y)=0).

Linija se također zove krivo.

Rješavanje jednačine

Ilustracija grafičke metode za pronalaženje korijena jednadžbe

Rješavanje jednadžbe je zadatak pronalaženja takvih vrijednosti argumenata pri kojima se ova jednakost postiže. Mogućim vrijednostima argumenata se mogu nametnuti dodatni uvjeti (cijeli, realni, itd.).

Zamjena drugog korijena proizvodi netačnu izjavu:

.

Dakle, drugi korijen mora biti odbačen kao strani.

Vrste jednadžbi

Postoje algebarske, parametarske, transcendentalne, funkcionalne, diferencijalne i druge vrste jednadžbi.

Neke klase jednadžbi imaju analitička rješenja, koja su zgodna jer ne samo da daju tačnu vrijednost korijena, već vam također omogućavaju da rješenje napišete u obliku formule, koja može uključivati ​​parametre. Analitički izrazi omogućavaju ne samo izračunavanje korijena, već i analizu njihovog postojanja i njihove količine ovisno o vrijednostima parametara, što je često čak i važnije za praktičnu upotrebu od specifičnih vrijednosti korijena.

Jednačine za koje su poznata analitička rješenja uključuju algebarske jednačine ne veće od četvrtog stepena: linearne jednačine, kvadratne jednačine, kubne jednačine i jednačine četvrtog stepena. Algebarske jednadžbe viših stupnjeva u opštem slučaju nemaju analitičko rješenje, iako se neke od njih mogu svesti na jednačine nižih stupnjeva.

Jednačina koja uključuje transcendentalne funkcije naziva se transcendentalna. Među njima su poznata analitička rješenja za neke trigonometrijske jednadžbe, jer su nule trigonometrijskih funkcija dobro poznate.

U opštem slučaju, kada se analitičko rešenje ne može naći, koriste se numeričke metode. Numeričke metode ne daju tačno rješenje, već samo omogućavaju da se interval u kojem leži korijen suzi na određenu unaprijed određenu vrijednost.

Primjeri jednadžbi

vidi takođe

Književnost

  • Bekarevich, A. B. Jednačine u školskom kursu matematike / A. B. Bekarevich. - M., 1968.
  • Markushevich, L. A. Jednačine i nejednakosti u završnom ponavljanju srednjoškolskog kursa algebre / L. A. Markushevich, R. S. Cherkasov. / Matematika u školi. - 2004. - br. 1.
  • Kaplan Y. V. Rivnyannya. - Kijev: Radjanska škola, 1968.
  • Jednačina- članak iz Velike sovjetske enciklopedije
  • Jednačine// Collier's Encyclopedia. - Otvoreno društvo. 2000.
  • Jednačina// Enciklopedija oko svijeta
  • Jednačina// Matematička enciklopedija. - M.: Sovjetska enciklopedija. I. M. Vinogradov. 1977-1985.

Linkovi

  • EqWorld - Svijet matematičkih jednačina - sadrži opsežne informacije o matematičkim jednačinama i sistemima jednačina.

Wikimedia fondacija. 2010.

Sinonimi:

Antonimi:

  • Khadzhimba, Raul Dzhumkovich
  • ES COMPUTER

Pogledajte šta je "jednačina" u drugim rječnicima:

    JEDNAČINA- (1) matematički prikaz problema pronalaženja takvih vrijednosti argumenata (vidi (2)), za koje su vrijednosti dva podatka (vidi) jednake. Argumenti od kojih ovise ove funkcije nazivaju se nepoznate, a vrijednosti nepoznanica na kojima se vrijednosti ... ... Velika politehnička enciklopedija

    JEDNAČINA- JEDNAČINA, jednačine, up. 1. Radnja pod Ch. izjednačiti izjednačiti i stanje prema pogl. izjednačiti izjednačiti. Jednaka prava. Jednadžba vremena (prevođenje pravog solarnog vremena u srednje solarno vrijeme, prihvaćeno u društvu i nauci; ... ... Ushakov's Explantatory Dictionary

    JEDNAČINA- (jednačina) Zahtjev da matematički izraz poprimi određenu vrijednost. Na primjer, kvadratna jednadžba se piše kao: ax2+bx+c=0. Rješenje je vrijednost x pri kojoj data jednačina postaje identitet. U… … Ekonomski rječnik

    JEDNAČINA- matematički prikaz problema pronalaženja vrijednosti argumenata za koje su vrijednosti dvije date funkcije jednake. Argumenti od kojih zavise ove funkcije nazivaju se nepoznanicama, a vrijednosti nepoznanica kod kojih su vrijednosti funkcije jednake ... ... Veliki enciklopedijski rječnik

    JEDNAČINA- JEDNAČINA, dva izraza povezana znakom jednakosti; ovi izrazi uključuju jednu ili više varijabli koje se nazivaju nepoznate. Riješiti jednačinu znači pronaći sve vrijednosti nepoznanica po kojima ona postaje identitet, ili ustanoviti... Moderna enciklopedija

Prava na ravni je skup tačaka na ovoj ravni koje imaju određena svojstva, dok tačke koje ne leže na datoj ravni nemaju ta svojstva. Jednačina prave definira analitički izražen odnos između koordinata tačaka koje leže na ovoj pravoj. Neka je ovaj odnos zadan jednadžbom

F( x,y)=0. (2.1)

Par brojeva koji zadovoljava (2.1) nije proizvoljan: if X dato, onda at ne može biti ništa, značenje at povezano sa X. Kada se promeni X promjene at, i tačka sa koordinatama ( x,y) opisuje ovu liniju. Ako su koordinate tačke M 0 ( X 0 ,at 0) zadovoljavaju jednačinu (2.1), tj. F( X 0 ,at 0)=0 je tačna jednakost, tada tačka M 0 leži na ovoj pravoj. I obrnuto je tačno.

Definicija. Jednačina prave na ravni je jednačina koju zadovoljavaju koordinate bilo koje tačke koja leži na ovoj pravoj, a ne zadovoljavaju je koordinate tačaka koje ne leže na ovoj pravoj.

Ako je jednadžba određene linije poznata, onda se proučavanje geometrijskih svojstava ove linije može svesti na proučavanje njene jednadžbe - to je jedna od glavnih ideja analitičke geometrije. Za proučavanje jednačina postoje dobro razvijene metode matematičke analize koje pojednostavljuju proučavanje svojstava linija.

Kada se razmatraju linije koristi se termin trenutna tačka linija – varijabilna tačka M( x,y), krećući se duž ove linije. Koordinate X I at trenutna tačka se pozivaju trenutne koordinate linijske tačke.

Ako iz jednačine (2.1) možemo eksplicitno izraziti at
kroz X, odnosno zapisati jednačinu (2.1) u obliku , tada se kriva definisana takvom jednačinom naziva raspored funkcije f(x).

1. Jednačina je data: , ili . Ako X onda uzima proizvoljne vrijednosti at uzima vrijednosti jednake X. Prema tome, prava definisana ovom jednačinom sastoji se od tačaka jednako udaljenih od koordinatnih osa Ox i Oy - to je simetrala I–III koordinatnih uglova (prava na slici 2.1).

Jednačina, ili, određuje simetralu II–IV koordinatnih uglova (prava na slici 2.1).

0 x 0 x C 0 x

pirinač. 2.1 sl. 2.2 sl. 2.3

2. Jednačina je data: , gdje je C neka konstanta. Ova jednačina se može napisati drugačije: . Ovu jednačinu zadovoljavaju te i samo te tačke, ordinate at koji su jednaki C za bilo koju vrijednost apscise X. Ove tačke leže na pravoj liniji paralelnoj sa Ox osom (slika 2.2). Slično, jednačina definira pravu liniju paralelnu sa Oy osi (slika 2.3).

Nije svaka jednadžba oblika F( x,y)=0 definiše pravu na ravni: jednačinu zadovoljava jedna tačka – O(0,0), a jednačinu ne zadovoljava nijedna tačka na ravni.

U navedenim primjerima koristili smo datu jednačinu da konstruišemo liniju koja je određena ovom jednačinom. Razmotrimo inverzni problem: konstruirajte njegovu jednačinu koristeći datu liniju.


3. Napravite jednačinu za kružnicu sa centrom u tački P( a,b) I
radijus R .

○ Krug sa centrom u tački P i poluprečnikom R je skup tačaka koje se nalaze na udaljenosti R od tačke P. To znači da je za bilo koju tačku M koja leži na kružnici, MP = R, ali ako tačka M ne leži na krug, zatim MP ≠ R.. ●