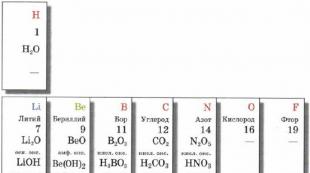
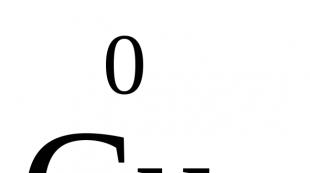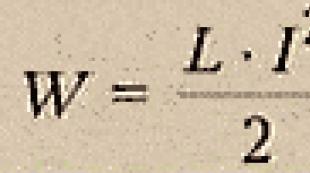игри

Как да решаваме уравнения с естествен логаритъм. Логаритмично уравнение: основни формули и техники. Логаритъм от двете страни на уравнението

Логаритмични уравнения и неравенствавъв версиите на изпита по математика е посветен на задача C3 ... Всеки ученик трябва да се научи да решава задачи C3 от изпита по математика, ако иска да издържи предстоящия изпит за „добър“ или „отличен“. Тази статия предоставя кратък преглед на обичайните логаритмични уравнения и неравенства, както и основните методи за тяхното решаване.

И така, нека разгледаме няколко примера днес. логаритмични уравнения и неравенства, които бяха предложени на студентите във вариантите на изпита по математика от минали години. Но започва с обобщениеосновните теоретични точки, които ни трябват, за да ги решим.

Логаритмична функция

Определение

Функция за преглед

0, \, a \ ne 1 \] "title =" (! LANG: Изобразено от QuickLaTeX.com">!}

са наречени логаритмична функция.

Основни свойства

Основни свойства на логаритмичната функция г= дневник а х:

Графиката на логаритмичната функция е логаритмична крива:

Свойства на логаритмите

Логаритъм на произведениетодве положителни числа са равни на сумата от логаритмите на тези числа:

Заглавие = "(! LANG: Изобразено от QuickLaTeX.com">!}

Логаритъм на частнотодве положителни числа са равни на разликата от логаритмите на тези числа:

Заглавие = "(! LANG: Изобразено от QuickLaTeX.com">!}

Ако аи б а≠ 1, след това за произволно число r справедливо равенство:

Заглавие = "(! LANG: Изобразено от QuickLaTeX.com">!}

Равенстводневник а T= дневник а с, където а > 0, а ≠ 1, T > 0, с> 0, е вярно, ако и само ако T = с.

Ако а, б, ° ССа положителни числа и аи ° Сса различни от единството, то равенството ( формулата за преход към новата основа на логаритъма):

Заглавие = "(! LANG: Изобразено от QuickLaTeX.com">!}

Теорема 1.Ако е(х)> 0 и ж(х)> 0, след това логаритмичното уравнение log а е(х) = дневник a g(х) (където а > 0, а≠ 1) е еквивалентно на уравнението е(х) = ж(х).

Решаване на логаритмични уравнения и неравенства

Пример 1.Решете уравнението:

Решение.Обхватът на валидни стойности включва само тези хза които изразът под знака на логаритъма е по-голям от нула. Тези стойности се определят от следната система от неравенства:

Заглавие = "(! LANG: Изобразено от QuickLaTeX.com">!}

Имайки предвид това

Заглавие = "(! LANG: Изобразено от QuickLaTeX.com">!}

получаваме интервал, който определя диапазона на допустимите стойности на това логаритмично уравнение:

Въз основа на теорема 1, всички условия на която тук са изпълнени, преминаваме към следното еквивалентно квадратно уравнение:

Само първият корен е в обхвата на валидните стойности.

Отговор:х = 7.

Пример 2.Решете уравнението:

Решение.Обхватът на допустимите стойности на уравнението се определя от системата от неравенства:

ql-right-eqno ">

Решение.Обхватът на допустимите стойности на уравнението се определя тук лесно: х > 0.

Използваме заместване:

Уравнението приема формата:

Обратно заместване:

И двете Отговорътса включени в диапазона на допустимите стойности на уравнението, тъй като са положителни числа.

Пример 4.Решете уравнението:

Решение.Нека започнем отново решението, като определим диапазона на допустимите стойности на уравнението. Определя се от следната система от неравенства:

ql-right-eqno ">

Основите на логаритмите са еднакви, така че в диапазона на допустимите стойности можете да отидете на следното квадратно уравнение:

Първият корен не е включен в диапазона на допустимите стойности на уравнението, вторият е включен.

Отговор: х = -1.

Пример 5.Решете уравнението:

Решение.Ще търсим решения в интервала х > 0, х≠ 1. Преобразуваме уравнението в еквивалента:

И двете Отговорътса включени в диапазона на допустимите стойности на уравнението.

Пример 6.Решете уравнението:

Решение.Системата от неравенства, определяща диапазона на допустимите стойности на уравнението, този път има формата:

Заглавие = "(! LANG: Изобразено от QuickLaTeX.com">!}

Използвайки свойствата на логаритъма, трансформираме уравнението в уравнение, еквивалентно в диапазона от допустими стойности:

Използвайки формулата за преход към нова основа на логаритъма, получаваме:

Диапазонът от валидни стойности включва само една отговор: х = 4.

Да отидем сега на логаритмични неравенства ... Точно с това ще трябва да се справите на изпита по математика. За да разрешим допълнителни примери, се нуждаем от следната теорема:

Теорема 2.Ако е(х)> 0 и ж(х)> 0, тогава:
в а> 1 логаритмично неравенство log a е(х)> дневник а ж(х) е еквивалентно на неравенството със същото значение: е(х) > ж(х);
на 0< а < 1 логарифмическое неравенство log a е(х)> дневник а ж(х) е еквивалентно на неравенството на противоположното значение: е(х) < ж(х).

Пример 7.Решете неравенството:

Решение.Нека започнем с определяне на диапазона от валидни стойности за неравенство. Изразът под знака на логаритмичната функция трябва да приема само положителни стойности. Това означава, че търсеният диапазон от допустими стойности се определя от следната система от неравенства:

Заглавие = "(! LANG: Изобразено от QuickLaTeX.com">!}

Тъй като основата на логаритъма е число по-малко от едно, съответната логаритмична функция ще бъде намаляваща и следователно преходът към следното квадратно неравенство ще бъде еквивалентен по теорема 2:

И накрая, като вземем предвид диапазона от допустими стойности, получаваме отговор:

Пример 8.Решете неравенството:

Решение.Нека започнем отново, като дефинираме диапазона от валидни стойности:

Заглавие = "(! LANG: Изобразено от QuickLaTeX.com">!}

На множеството от допустимите стойности на неравенството извършваме еквивалентни трансформации:

След като премахнем и преминем към еквивалентното неравенство по теорема 2, получаваме:

Като се вземе предвид диапазонът на допустимите стойности, получаваме окончателното отговор:

Пример 9.Решете логаритмичното неравенство:

Решение.Обхватът на валидните стойности на неравенството се определя от следната система:

Заглавие = "(! LANG: Изобразено от QuickLaTeX.com">!}

Вижда се, че в диапазона на допустимите стойности изразът в основата на логаритъма винаги е по-голям от единица и следователно преходът към следното неравенство ще бъде еквивалентен по теорема 2:

Като се вземе предвид диапазонът на допустимите стойности, получаваме окончателния отговор:

Пример 10.Решете неравенството:

Решение.

Обхватът на допустимите стойности на неравенството се определя от системата от неравенства:

Заглавие = "(! LANG: Изобразено от QuickLaTeX.com">!}

Метод I.Нека използваме формулата за преход към нова основа на логаритъма и да преминем към неравенство, еквивалентно в диапазона от допустими стойности.

С това видео започвам дълга серия от уроци по логаритмични уравнения. Сега имате три примера наведнъж, въз основа на които ще се научим да решаваме най-простите задачи, които се наричат така - протозои.

log 0,5 (3x - 1) = −3

lg (x + 3) = 3 + 2 lg 5

Нека ви напомня, че най-простото логаритмично уравнение е следното:

log a f (x) = b

В този случай е важно променливата x да присъства само вътре в аргумента, тоест само във функцията f (x). А числата a и b са просто числа и в никакъв случай не са функции, съдържащи променливата x.

Основни методи за решение

Има много начини за решаване на такива конструкции. Например повечето учители в училището предлагат следния начин: Незабавно изразете функцията f (x) с формулата е ( х) = а б. Тоест, когато срещнете най-простата конструкция, можете да преминете направо към решението без допълнителни действия и конструкции.

Да, разбира се, решението ще се окаже правилно. Проблемът с тази формула обаче е, че повечето студенти не разбирам, откъде идва и защо издигаме буквата а на буквата b.

В резултат на това често виждам много обидни грешки, когато например тези букви са обърнати. Тази формула трябва или да бъде разбрана, или натъпкана, а вторият метод води до грешки в най-неподходящите и най-критични моменти: на изпити, тестове и т.н.

Ето защо предлагам на всички мои ученици да се откажат от стандартната училищна формула и да използват втория подход за решаване на логаритмични уравнения, който, както вероятно вече се досещате от името, се нарича канонична форма.

Идеята зад каноничната форма е проста. Нека да разгледаме отново нашия проблем: отляво имаме log a, докато буквата a означава точно число и в никакъв случай функция, съдържаща променлива x. Следователно тази буква подлежи на всички ограничения, които са наложени върху основата на логаритъма. а именно:

1 ≠ a> 0

От друга страна, от същото уравнение виждаме, че логаритъмът трябва да е равен на числото b и не се налагат ограничения върху тази буква, тъй като тя може да приема всякакви стойности - както положителни, така и отрицателни. Всичко зависи от това какви стойности приема функцията f (x).

И тук си спомняме нашето прекрасно правило, че всяко число b може да бъде представено като логаритъм на основата a от a до степен на b:

b = log a a b

Как си спомняте тази формула? Много е просто. Нека напишем следната конструкция:

b = b 1 = b log a a

Разбира се, възникват всички ограничения, които написахме в началото. Сега нека използваме основното свойство на логаритъма и въведем фактора b като степента на a. Получаваме:

b = b 1 = b log a a = log a a b

В резултат на това оригиналното уравнение ще бъде пренаписано, както следва:

log a f (x) = log a a b → f (x) = a b

Това е всичко. Новата функция вече не съдържа логаритъм и се решава с помощта на стандартни алгебрични техники.

Разбира се, сега някой ще възрази: защо да си правите труда да измисляте някаква канонична формула, защо да извършвате две допълнителни ненужни стъпки, ако можете веднага да преминете от първоначалната конструкция към крайната формула? Да, дори и тогава, че по-голямата част от учениците не разбират откъде идва тази формула и в резултат на това редовно правят грешки, когато я прилагат.

Но тази последователност от действия, състояща се от три стъпки, ви позволява да решите оригиналното логаритмично уравнение, дори ако не разбирате откъде идва окончателната формула. Между другото, точно този запис се нарича канонична формула:

log a f (x) = log a a b

Удобството на каноничната форма се крие и във факта, че тя може да се използва за решаване на много широк клас логаритмични уравнения, а не само най-простите, които разглеждаме днес.

Примери за решение

Сега нека разгледаме примери от реалния живот. И така, ние решаваме:

log 0,5 (3x - 1) = −3

Нека го пренапишем така:

log 0,5 (3x - 1) = log 0,5 0,5 −3

Много ученици бързат и се опитват незабавно да повишат числото 0,5 до степента, която ни дойде от първоначалния проблем. Всъщност, когато вече сте добре обучени в решаването на подобни проблеми, можете веднага да следвате тази стъпка.

Въпреки това, ако сега едва започвате да изучавате тази тема, по-добре е да не бързате никъде, за да не правите обидни грешки. И така, пред нас е каноничната форма. Ние имаме:

3x - 1 = 0,5 −3

Това вече не е логаритмично уравнение, а линейно по отношение на променливата x. За да решим това, нека първо се справим с числото 0,5 на степен −3. Имайте предвид, че 0,5 е 1/2.

(1/2) −3 = (2/1) 3 = 8

Преобразувайте всички десетични дроби в правилни дроби, когато решавате логаритмичното уравнение.

Пренаписваме и получаваме:

3x - 1 = 8
3x = 9
х = 3

Това е, имаме отговор. Първата задача е решена.

Втора задача

Да преминем към втората задача:

Както можете да видите, това уравнение вече не е най-простото. Дори само защото разликата е отляво, а не един единствен логаритъм в една основа.

Следователно, трябва по някакъв начин да се отървете от тази разлика. В този случай всичко е много просто. Нека разгледаме отблизо основите: вляво е числото под корена:

Обща препоръка: във всички логаритмични уравнения, опитайте се да се отървете от радикали, тоест от записи с корени и отидете на степенни функции, просто защото експонентите на тези степени лесно се изваждат от знака на логаритъма и в крайна сметка , такава нотация значително опростява и ускорява изчисленията. Нека го запишем така:

Сега си припомняме забележителното свойство на логаритъма: от аргумента, както и от основата, можете да извлечете степени. В случай на основания се случва следното:

log a k b = 1 / k loga b

С други думи, числото, което е застанало в степента на основата, се пренася напред и в същото време се обръща, тоест става обратното число. В нашия случай имаше степен на основаване с степен 1/2. Следователно можем да го изобразим като 2/1. Получаваме:

5 2 log 5 x - log 5 x = 18
10 log 5 x - log 5 x = 18

Моля, обърнете внимание: в никакъв случай не трябва да се отървавате от логаритмите на тази стъпка. Помнете математиката от 4-5 клас и процедурата: първо се извършва умножение и едва след това събиране и изваждане. В този случай изваждаме един от същия от 10 елемента:

9 log 5 x = 18
log 5 x = 2

Сега нашето уравнение изглежда така, както трябва. Това е най-простата конструкция и ние я решаваме с каноничната форма:

log 5 x = log 5 5 2
х = 5 2
х = 25

Това е всичко. Втората задача е решена.

Трети пример

Да преминем към третата задача:

lg (x + 3) = 3 + 2 lg 5

Нека ви напомня следната формула:

lg b = log 10 b

Ако по някаква причина сте объркани от log b, тогава когато извършвате всички изчисления, можете просто да регистрирате 10 b. Можете да работите с десетични логаритми по същия начин, както с други: извадете градуси, съберете и представите произволни числа във формата lg 10.

Именно тези свойства сега ще използваме, за да решим проблема, тъй като той не е най-простият, който записахме в самото начало на нашия урок.

Като начало отбележете, че факторът 2 преди lg 5 може да бъде въведен и се превръща в степен на основата 5. Освен това свободният член 3 може да бъде представен и като логаритъм - това е много лесно да се наблюдава от нашата нотация.

Преценете сами: всяко число може да бъде представено като логаритмична основа 10:

3 = log 10 10 3 = log 10 3

Нека пренапишем оригиналния проблем, като вземем предвид получените промени:

lg (x - 3) = lg 1000 + lg 25
log (x - 3) = log 1000 25
lg (x - 3) = lg 25 000

Пред нас отново е каноничната форма и я получихме, заобикаляйки етапа на трансформации, тоест най-простото логаритмично уравнение никога не се е появявало у нас.

Точно за това говорих в самото начало на урока. Каноничната форма позволява решаването на по-широк клас проблеми от стандартната училищна формула, дадена от повечето училищни учители.

Е, това е всичко, отърваваме се от знака на десетичния логаритъм и получаваме проста линейна конструкция:

х + 3 = 25 000
х = 24,997

Всичко! Проблемът е решен.

Бележка за обхвата

Тук бих искал да направя една важна забележка относно обхвата на определението. Със сигурност сега има ученици и учители, които ще кажат: "Когато решаваме изрази с логаритми, е задължително да запомним, че аргументът f (x) трябва да е по-голям от нула!" В тази връзка възниква логичният въпрос: защо в нито един от разглежданите проблеми не сме изисквали това неравенство да бъде изпълнено?

Не се безпокой. В тези случаи няма да възникнат допълнителни корени. И това е още един страхотен трик, който ви позволява да ускорите решението. Просто знайте, че ако в даден проблем променливата x се среща само на едно място (или по-скоро в един аргумент от единичен логаритъм) и никъде другаде в нашия случай няма променлива x, тогава напишете домейна не е задължителнозащото ще работи автоматично.

Преценете сами: в първото уравнение получихме, че 3x - 1, тоест аргументът трябва да е равен на 8. Това автоматично означава, че 3x - 1 ще бъде по-голямо от нула.

Със същия успех можем да запишем, че във втория случай x трябва да е равно на 5 2, тоест със сигурност е по-голямо от нула. И в третия случай, където х + 3 = 25 000, тоест отново очевидно по-голямо от нула. С други думи, домейнът се удовлетворява автоматично, но само ако x се среща само в аргумента само на един логаритъм.

Това е всичко, което трябва да знаете за основните задачи. Само това правило, заедно с правилата за трансформация, ще ви позволи да решите много широк клас проблеми.

Но нека бъдем честни: за да разберете най-накрая тази техника, за да научите как да прилагате каноничната форма на логаритмичното уравнение, не е достатъчно само да гледате един видео урок. Ето защо, точно сега, изтеглете опциите за независимо решение, които са приложени към този видео урок и започнете да решавате поне една от тези две независими произведения.

Ще ви отнеме само няколко минути. Но ефектът от такова обучение ще бъде много по-висок в сравнение с това, ако току-що гледахте този видео урок.

Надявам се този урок да ви помогне да разберете логаритмичните уравнения. Използвайте каноничната форма, опростете изразите, използвайки правила за работа с логаритми - и никой проблем няма да е плашещ за вас. И имам всичко за днес.

Отчитане на обхвата

Сега нека поговорим за областта на логаритмичната функция, както и как тя влияе върху решението на логаритмичните уравнения. Помислете за конструкция на формата

log a f (x) = b

Такъв израз се нарича най-прост - в него има само една функция, а числата a и b са точно числа и в никакъв случай не е функция, която зависи от променливата x. Може да се реши много просто. Просто трябва да използвате формулата:

b = log a a b

Тази формула е едно от ключовите свойства на логаритъма и когато се замести в нашия оригинален израз, получаваме следното:

log a f (x) = log a a b

f (x) = a b

Това е позната формула от училищните учебници. Много студенти вероятно ще имат въпрос: тъй като в оригиналния израз функцията f (x) е под знака на log, върху нея са наложени следните ограничения:

f (x)> 0

Това ограничение е в сила, тъй като логаритъмът на отрицателните числа не съществува. Така че, може би поради това ограничение трябва да въведете проверка за отговори? Може би те трябва да бъдат заменени в източника?

Не, в най-простите логаритмични уравнения допълнителна проверка не е необходима. И ето защо. Разгледайте нашата окончателна формула:

f (x) = a b

Факт е, че числото a във всеки случай е по-голямо от 0 - това изискване се налага и от логаритъма. Числото а е основата. В този случай не се налагат ограничения върху числото b. Но това няма значение, защото без значение в каква степен повдигаме положително число, на изхода все пак ще получим положително число. По този начин изискването f (x)> 0 се изпълнява автоматично.

Това, което наистина си струва да проверите, е обхватът на функцията под знака на дневника. Може да има доста сложни структури и в процеса на решаването им определено трябва да ги следвате. Да видим.

Първа задача:

Първа стъпка: трансформирайте дроба вдясно. Получаваме:

Отърваваме се от знака на логаритъма и получаваме обичайното ирационално уравнение:

От получените корени ни подхожда само първият, тъй като вторият корен е по-малък от нула. Единственият отговор ще бъде числото 9. Това е всичко, проблемът е решен. Не се изискват допълнителни проверки, че изразът под знака на логаритъма е по-голям от 0, тъй като той не просто е по-голям от 0, но според условието на уравнението е равен на 2. Следователно изискването „по-голямо от нула “ се удовлетворява автоматично.

Да преминем към втората задача:

Тук всичко е същото. Пренаписваме конструкцията, заменяйки трите:

Отърваваме се от знаците на логаритъма и получаваме ирационално уравнение:

Квадратираме двете страни, като вземем предвид ограниченията, и получаваме:

4 - 6x - x 2 = (x - 4) 2

4 - 6x - x 2 = x 2 + 8x + 16

x 2 + 8x + 16 −4 + 6x + x 2 = 0

2x 2 + 14x + 12 = 0 |: 2

x 2 + 7x + 6 = 0

Решаваме полученото уравнение чрез дискриминанта:

D = 49 - 24 = 25

x 1 = −1

x 2 = −6

Но x = −6 не ни подхожда, защото ако заместим това число в нашето неравенство, получаваме:

−6 + 4 = −2 < 0

В нашия случай се изисква то да е по-голямо от 0 или, в краен случай, равно. Но x = −1 ни подхожда:

−1 + 4 = 3 > 0

Единственият отговор в нашия случай е x = −1. Това е цялото решение. Нека се върнем към самото начало на нашите изчисления.

Основният извод от този урок е, че не е необходимо да проверявате ограниченията за функция в най-простите логаритмични уравнения. Защото в процеса на решаване всички ограничения се изпълняват автоматично.

Това обаче по никакъв начин не означава, че можете да забравите за проверката напълно. В процеса на работа върху логаритмично уравнение, то може да се превърне в ирационално, което ще има свои собствени ограничения и изисквания за дясната страна, както видяхме днес на два различни примера.

Чувствайте се свободни да решавате подобни проблеми и бъдете особено внимателни, ако има корен в спора.

Логаритмични уравнения с различни основи

Продължаваме да изучаваме логаритмичните уравнения и анализираме още два доста интересни трика, с помощта на които е модерно да се решават по-сложни конструкции. Но първо, нека си спомним как се решават най-простите задачи:

log a f (x) = b

В тази нотация a и b са точно числа, а във функцията f (x) трябва да присъства променливата x и само там, тоест x трябва да бъде само в аргумента. Ще преобразуваме такива логаритмични уравнения, използвайки каноничната форма. За да направите това, обърнете внимание на това

b = log a a b

Освен това a b е точно аргументът. Нека пренапишем този израз, както следва:

log a f (x) = log a a b

Точно това се опитваме да постигнем, така че и лявото, и дясното да са логаритъмът на основата а. В този случай можем, образно казано, да зачеркнем знаците на log, а от гледна точка на математиката можем да кажем, че просто приравняваме аргументите:

f (x) = a b

В резултат на това ще получим нов израз, който ще бъде много по-лесен за решаване. Нека приложим това правило към днешните си задачи.

И така, първата конструкция:

На първо място, отбелязвам, че вдясно има дроб с логаритм в знаменателя. Когато видите такъв израз, няма да е излишно да си спомните прекрасното свойство на логаритмите:

Преведено на руски, това означава, че всеки логаритъм може да бъде представен като частно от два логаритма с произволна основа s. Разбира се, 0< с ≠ 1.

Така че: тази формула има един чудесен специален случай, когато променливата c е равна на променливата б. В този случай получаваме конструкция от формата:

Именно тази конструкция наблюдаваме от знака вдясно в нашето уравнение. Нека заменим тази конструкция с log a b, получаваме:

С други думи, в сравнение с първоначалния проблем сме разменили аргумента и основата на логаритъма. Вместо това трябваше да обърнем дроба.

Припомняме, че всяка степен може да бъде получена от основата според следното правило:

С други думи, коефициентът k, който е степента на основата, се изважда като обърната дроб. Нека го представим като обърната дроб:

Дробният множител не може да бъде оставен отпред, тъй като в този случай няма да можем да представим този запис като канонична форма (все пак в каноничната форма няма допълнителен множител пред втория логаритъм). Следователно, нека поставим дроб 1/4 в аргумента като степен:

Сега приравняваме аргументите, чиито основи са едни и същи (и нашите бази наистина са еднакви) и пишем:

х + 5 = 1

x = −4

Това е всичко. Получихме отговора на първото логаритмично уравнение. Моля, обърнете внимание: в оригиналния проблем променливата x се среща само в един журнал и е в нейния аргумент. Следователно няма нужда да проверяваме домейна и нашето число x = −4 наистина е отговорът.

Сега да преминем към втория израз:

lg 56 = lg 2 log 2 7 - 3lg (x + 4)

Тук, в допълнение към обичайните логаритми, ще трябва да работим с lg f (x). Как да се реши такова уравнение? На необучен ученик може да изглежда, че това е някаква твърдост, но всъщност всичко се решава по елементарен начин.

Разгледайте отблизо термина lg 2 log 2 7. Какво можем да кажем за него? Причините и аргументите за log и lg са едни и същи и това трябва да е подсказващо. Нека си припомним отново как се изваждат градусите под знака на логаритъма:

log a b n = nlog a b

С други думи, каква е била силата на числото b в аргумента, става фактор пред самия log. Нека използваме тази формула, за да изразим lg 2 log 2 7. Не се страхувайте от lg 2 – това е най-често срещаният израз. Можете да го пренапишете така:

Всички правила, които важат за всеки друг логаритъм, са верни за него. По-специално, факторът отпред може да се добави към силата на аргумента. Нека напишем:

Много често учениците не виждат това действие направо, защото не е добре да влизате в единия дневник под знака на другия. Всъщност в това няма нищо престъпно. Освен това получаваме формула, която може лесно да се изчисли, ако запомните важно правило:

Тази формула може да се разглежда както като дефиниция, така и като едно от нейните свойства. Във всеки случай, ако преобразувате логаритмично уравнение, трябва да знаете тази формула по същия начин като логаритмичното представяне на произволно число.

Връщаме се към нашата задача. Пренаписваме го, като вземем предвид факта, че първият член вдясно от знака за равенство просто ще бъде равен на lg 7. Имаме:

lg 56 = lg 7 - 3lg (x + 4)

Нека преместим lg 7 наляво, получаваме:

lg 56 - lg 7 = −3lg (x + 4)

Извадете изразите отляво, защото имат еднаква основа:

lg (56/7) = −3lg (x + 4)

Сега нека разгледаме отблизо полученото уравнение. Това е практически каноничната форма, но вдясно има коефициент -3. Нека го поставим в правилния аргумент lg:

log 8 = log (x + 4) −3

Пред нас е каноничната форма на логаритмичното уравнение, така че зачеркваме знаците на lg и приравняваме аргументите:

(x + 4) −3 = 8

х + 4 = 0,5

Това е всичко! Решихме второто логаритмично уравнение. В този случай не са необходими допълнителни проверки, тъй като в оригиналния проблем x присъства само в един аргумент.

Позволете ми да повторя ключовите точки на този урок.

Основната формула, която се изучава във всички уроци на тази страница, посветени на решаването на логаритмични уравнения, е каноничната форма. И не се плашете от факта, че повечето училищни учебници ви учат да решавате подобни проблеми по различен начин. Този инструмент работи много ефективно и ви позволява да решавате много по-широк клас проблеми от най-простите, които изучавахме в самото начало на нашия урок.

Освен това ще бъде полезно да знаете основните свойства за решаване на логаритмични уравнения. а именно:

Формулата за преход към една основа и специалния случай, когато обръщаме лога (това ни беше много полезно в първия проблем);
Формулата за добавяне и премахване на градуси от знака на логаритъма. Тук много студенти замръзват и не виждат от близко разстояние, че самата експоненциална и вмъкната степен може да съдържа log f (x). Няма нищо лошо в това. Можем да въведем една лога по знака на другата и в същото време значително да опростим решението на задачата, което наблюдаваме във втория случай.

В заключение бих искал да добавя, че не е необходимо да проверявате обхвата във всеки един от тези случаи, тъй като навсякъде променливата x присъства само в един знак на log и в същото време е в нейния аргумент. В резултат на това всички изисквания на обхвата се изпълняват автоматично.

Проблеми с променлив корен

Днес ще разгледаме логаритмичните уравнения, които за много ученици изглеждат нестандартни, ако не и напълно нерешими. Говорим за изрази, базирани не на числа, а на променливи и дори функции. Ще решаваме такива конструкции, използвайки нашата стандартна техника, а именно чрез каноничната форма.

Като начало нека си припомним как се решават най-простите задачи, които се основават на обикновени числа. И така, най-простата е конструкция на формата

log a f (x) = b

За да разрешим такива проблеми, можем да използваме следната формула:

b = log a a b

Пренаписваме оригиналния си израз и получаваме:

log a f (x) = log a a b

След това приравняваме аргументите, тоест пишем:

f (x) = a b

Така се отърваваме от знака на дневника и решаваме вече често срещания проблем. В този случай корените, получени по време на решението, ще бъдат корените на оригиналното логаритмично уравнение. Освен това записът, когато и лявото, и дясното стоят на един и същ логаритъм с една и съща основа, се нарича канонична форма. До такъв рекорд ще се опитаме да сведем днешните конструкции. Така че да тръгваме.

Първа задача:

log x - 2 (2x 2 - 13x + 18) = 1

Заменете 1 с log x - 2 (x - 2) 1. Степента, която наблюдаваме в аргумента, всъщност е числото b, което стои вдясно от знака за равенство. Така ще пренапишем израза си. Получаваме:

log x - 2 (2x 2 - 13x + 18) = log x - 2 (x - 2)

Какво виждаме? Пред нас е каноничната форма на логаритмичното уравнение, така че можем спокойно да приравним аргументите. Получаваме:

2x 2 - 13x + 18 = x - 2

Но решението не свършва дотук, защото това уравнение не е еквивалентно на първоначалното. В крайна сметка, получената конструкция се състои от функции, които са дефинирани на цялата числова права, а нашите първоначални логаритми не са дефинирани навсякъде и не винаги.

Следователно трябва да запишем обхвата отделно. Нека не бъдем умни и първо запишем всички изисквания:

Първо, аргументът на всеки от логаритмите трябва да е по-голям от 0:

2x 2 - 13x + 18> 0

х - 2> 0

Второ, основата трябва не само да е по-голяма от 0, но и да е различна от 1:

х - 2 ≠ 1

В резултат на това получаваме системата:

Но не се тревожете: когато обработвате логаритмични уравнения, такава система може да бъде значително опростена.

Преценете сами: от една страна, от нас се изисква квадратичната функция да е по-голяма от нула, а от друга страна, тази квадратична функция е приравнена на определен линеен израз, който също трябва да бъде по-голям от нула.

В този случай, ако изискваме x - 2> 0, то автоматично ще бъде изпълнено изискването 2x 2 - 13x + 18> 0. Следователно можем спокойно да зачеркнем неравенството, съдържащо квадратичната функция. По този начин броят на изразите, съдържащи се в нашата система, ще бъде намален до три.

Разбира се, можем също да зачеркнем линейното неравенство, тоест да зачеркнем x - 2> 0 и да изискваме 2x 2 - 13x + 18> 0. Но трябва да признаете, че решаването на най-простото линейно неравенство е много по-бързо и по-лесно, отколкото квадратно, дори при условие, че в резултат на решаването на цялата тази система получаваме едни и същи корени.

Като цяло, опитайте се да оптимизирате изчисленията си, когато е възможно. И в случай на логаритмични уравнения, зачеркнете най-трудните неравенства.

Нека пренапишем нашата система:

Ето такава система от три израза, с два от които всъщност вече разбрахме. Нека запишем квадратното уравнение отделно и го решим:

2x 2 - 14x + 20 = 0

x 2 - 7x + 10 = 0

Пред нас е даден квадратен трином и следователно можем да използваме формулите на Виета. Получаваме:

(x - 5) (x - 2) = 0

х 1 = 5

х 2 = 2

И сега се връщаме към нашата система и откриваме, че x = 2 не ни подхожда, защото се изисква x да бъде строго по-голямо от 2.

Но x = 5 ни подхожда идеално: числото 5 е по-голямо от 2 и в същото време 5 не е равно на 3. Следователно единственото решение на тази система ще бъде x = 5.

Това е всичко, проблемът е решен, включително и като се вземе предвид ОДЗ. Нека да преминем към второто уравнение. Тук ще намерим още интересни и информативни изчисления:

Първата стъпка: както миналия път, ние привеждаме цялото нещо в канонична форма. За това можем да напишем числото 9, както следва:

Не е нужно да докосвате корена с корена, но е по-добре да трансформирате аргумента. Нека преминем от корен към рационален показател. Нека запишем:

Нека не пренаписвам цялото ни голямо логаритмично уравнение, а просто приравнявам аргументите веднага:

x 3 + 10x 2 + 31x + 30 = x 3 + 9x 2 + 27x + 27

x 2 + 4x + 3 = 0

Пред нас е новозададеният квадратен трином, използваме формулите на Виета и пишем:

(x + 3) (x + 1) = 0

x 1 = −3

x 2 = −1

И така, получихме корените, но никой не ни гарантира, че те ще отговарят на оригиналното логаритмично уравнение. В края на краищата знаците на регистрационните файлове налагат допълнителни ограничения (тук трябваше да напишем системата, но поради тромавостта на цялата структура реших да изчисля домейна отделно).

Първо, не забравяйте, че аргументите трябва да са по-големи от 0, а именно:

Това са изискванията, наложени от областта на дефиниция.

Веднага отбелязваме, че тъй като приравняваме първите два израза на системата един към друг, тогава можем да изтрием всеки от тях. Нека изтрием първия, защото изглежда по-заплашителен от втория.

В допълнение, имайте предвид, че решението на второто и третото неравенство ще бъде едни и същи набори (кубът на някакво число е по-голям от нула, ако самото това число е по-голямо от нула; подобно на корен от трета степен - тези неравенства са напълно аналогичен, така че един от тях можем да го зачеркнем).

Но това няма да работи с третото неравенство. Нека се отървем от радикалния знак вляво, за който ще изградим и двете части в куб. Получаваме:

И така, получаваме следните изисквания:

- 2 ≠ x> −3

Кой от нашите корени: x 1 = −3 или x 2 = −1 отговаря на тези изисквания? Очевидно само x = −1, тъй като x = −3 не удовлетворява първото неравенство (тъй като нашето неравенство е строго). И така, връщайки се към нашия проблем, получаваме един корен: x = −1. Това е всичко, проблемът е решен.

Още веднъж ключовите точки на тази задача:

Чувствайте се свободни да прилагате и решавате логаритмични уравнения, като използвате каноничната форма. Учениците, които правят такъв запис и не преминават директно от първоначалния проблем към конструкция като log a f (x) = b, правят много по-малко грешки от тези, които бързат нанякъде, пропускайки междинните стъпки на изчисленията;
Веднага след като в логаритъма се появи променлива основа, проблемът престава да бъде най-простият. Следователно при решаването му е необходимо да се вземе предвид областта на дефиницията: аргументите трябва да са по-големи от нула, а основите не само трябва да са по-големи от 0, но и не трябва да са равни на 1.

Има различни начини за налагане на крайните изисквания към крайните отговори. Например, можете да решите цялата система, съдържаща всички изисквания за домейна. От друга страна, можете първо да решите самия проблем и след това да си спомните за областта на дефиницията, да я разработите отделно под формата на система и да насложите върху получените корени.

Кой начин да изберете при решаване на конкретно логаритмично уравнение зависи от вас. Във всеки случай отговорът ще бъде същият.

Както знаете, когато умножавате изрази със степени, техните експоненти винаги се сумират (a b * a c = a b + c). Този математически закон е изведен от Архимед, а по-късно, през 8-ми век, математикът Вирасен създава таблица с цели показатели. Именно те послужиха за по-нататъшното откриване на логаритмите. Примери за използване на тази функция могат да бъдат намерени почти навсякъде, където трябва да опростите тромаво умножение чрез просто събиране. Ако отделите 10 минути, четейки тази статия, ще ви обясним какво представляват логаритмите и как да работите с тях. Прост и достъпен език.

Определение в математиката

Логаритъмът е израз в следната форма: log ab = c, тоест логаритъмът на всяко неотрицателно число (тоест всяко положително) "b" на базата на неговата основа "a" се счита за степен " c", до който трябва да се повдигне основата "a", така че накрая да се получи стойността "b". Нека анализираме логаритъма с помощта на примери, например има израз log 2 8. Как да намерим отговора? Много е просто, трябва да намерите такава степен, така че от 2 до желаната степен да получите 8. След като направихме някои изчисления в ума си, получаваме числото 3! И правилно, защото 2 на степен на 3 дава числото 8 в отговора.

Разновидности на логаритмите

За много ученици и студенти тази тема изглежда сложна и неразбираема, но всъщност логаритмите не са толкова страшни, основното е да разберете общото им значение и да запомните техните свойства и някои правила. Има три различни типа логаритмични изрази:

Естествен логаритъм ln a, където основата е числото на Ойлер (e = 2.7).
Десетична а, основа 10.
Логаритъм на произволно число b към основа a> 1.

Всеки от тях се решава по стандартен начин, включващ опростяване, редукция и последващо свеждане до един логаритъм с помощта на логаритмични теореми. За да получите правилните стойности на логаритмите, трябва да запомните техните свойства и последователността на действията при решаването им.

Правила и някои ограничения

В математиката има няколко правила-ограничения, които се приемат като аксиома, тоест не подлежат на обсъждане и са верни. Например, не можете да разделите числата на нула и все още не можете да извлечете четен корен от отрицателни числа. Логаритмите също имат свои собствени правила, следвайки които лесно можете да се научите да работите дори с дълги и обемни логаритмични изрази:

основата "a" винаги трябва да е по-голяма от нула и в същото време да не е равна на 1, в противен случай изразът ще загуби смисъла си, тъй като "1" и "0" във всяка степен винаги са равни на техните стойности;
ако a> 0, тогава a b> 0, се оказва, че "c" също трябва да бъде по-голямо от нула.

Как решавате логаритми?

Например, като се има предвид задачата да се намери отговора на уравнението 10 x = 100. Много е лесно, трябва да изберете такава степен, като повишите числото десет, до което получаваме 100. Това, разбира се, 10 2 = 100 .

Сега нека представим този израз като логаритмичен. Получаваме log 10 100 = 2. При решаване на логаритми всички действия почти се сближават, за да се намери степента, към която е необходимо да се въведе основата на логаритъма, за да се получи даденото число.

За да определите точно стойността на неизвестна степен, е необходимо да се научите как да работите с таблицата на градусите. Изглежда така:

Както можете да видите, някои експоненти могат да бъдат отгатнати интуитивно, ако имате технически начин на мислене и познания за таблицата за умножение. По-големите стойности обаче ще изискват таблица за мощност. Може да се използва дори от тези, които не знаят нищо за сложни математически теми. Лявата колона съдържа числа (база а), горният ред числа е степента c, до която се повдига числото a. На пресечната точка в клетките се определят стойностите на числата, които са отговорът (a c = b). Вземете, например, първата клетка с числото 10 и я квадратирайте, получаваме стойността 100, която е посочена в пресечната точка на нашите две клетки. Всичко е толкова просто и лесно, че дори най-истинският хуманист ще разбере!

Уравнения и неравенства

Оказва се, че при определени условия степента е логаритъмът. Следователно всеки математически числов израз може да бъде записан като логаритмично равенство. Например, 3 4 = 81 може да се запише като логаритъм от 81 към основа 3, равен на четири (log 3 81 = 4). За отрицателните степени правилата са едни и същи: 2 -5 = 1/32, записваме го като логаритъм, получаваме log 2 (1/32) = -5. Една от най-увлекателните области на математиката е темата за "логаритмите". Ще разгледаме примери и решения на уравнения малко по-долу, веднага след изучаване на техните свойства. Сега нека разгледаме как изглеждат неравенствата и как да ги разграничим от уравненията.

Даден е израз от следния вид: log 2 (x-1)> 3 - това е логаритмично неравенство, тъй като неизвестната стойност "x" е под знака на логаритъма. И също така в израза се сравняват две стойности: логаритъмът на необходимото число към основа две е по-голям от числото три.

Най-важната разлика между логаритмичните уравнения и неравенствата е, че уравненията с логаритми (например логаритъм 2 x = √9) предполагат една или повече конкретни числови стойности в отговора, докато решаването на неравенството определя и диапазона на допустимите стойности. и точките, нарушаващи тази функция. В резултат на това отговорът не е прост набор от отделни числа, както в отговора на уравнението, а непрекъсната серия или набор от числа.

Основни теореми за логаритмите

При решаване на примитивни задачи за намиране на стойностите на логаритъма, неговите свойства може да не са известни. Когато обаче става дума за логаритмични уравнения или неравенства, на първо място е необходимо ясно да се разберат и приложат на практика всички основни свойства на логаритмите. По-късно ще се запознаем с примери за уравнения, нека първо анализираме всяко свойство по-подробно.

Основната идентичност изглежда така: a logaB = B. Прилага се само ако a е по-голямо от 0, не е равно на единица и B е по-голямо от нула.
Логаритъмът на произведението може да се представи в следната формула: log d (s 1 * s 2) = log d s 1 + log d s 2. В този случай предпоставка е: d, s 1 и s 2> 0; а ≠ 1. Можете да дадете доказателство за тази формула от логаритми, с примери и решение. Нека log като 1 = f 1 и log като 2 = f 2, тогава a f1 = s 1, a f2 = s 2. Получаваме, че s 1 * s 2 = a f1 * a f2 = a f1 + f2 (свойства на мощности ), и по-нататък по дефиниция: log a (s 1 * s 2) = f 1 + f 2 = log a s1 + log като 2, което е необходимо да се докаже.
Логаритъмът на частното изглежда така: log a (s 1 / s 2) = log a s 1 - log a s 2.
Теоремата под формата на формула приема следната форма: log a q b n = n / q log a b.

Тази формула се нарича "свойство на степента на логаритъма". Наподобява свойствата на обикновените степени и не е изненадващо, защото цялата математика се основава на естествени постулати. Нека да разгледаме доказателството.

Нека log a b = t, оказва се a t = b. Ако повдигнем и двете части на степен на m: a tn = b n;

но тъй като a tn = (a q) nt / q = b n, следователно log a q b n = (n * t) / t, тогава log a q b n = n / q log a b. Теоремата е доказана.

Примери за проблеми и неравенства

Най-често срещаните типове логаритмни задачи са примери за уравнения и неравенства. Те се намират в почти всички задачници, а също така са включени в задължителната част от изпитите по математика. За прием в университет или доставка приемни изпитипо математика трябва да знаете как правилно да решавате такива задачи.

За съжаление няма единен план или схема за решаване и определяне на неизвестната стойност на логаритъма, но към всяко математическо неравенство или логаритмично уравнение могат да се прилагат определени правила. На първо място е необходимо да се разбере дали изразът може да бъде опростен или приведен в общ вид. Опростете дълго логаритмични изразиможете, ако използвате правилно техните свойства. Да ги опознаем скоро.

При решаване на логаритмични уравнения е необходимо да се определи какъв вид логаритъм е пред нас: пример за израз може да съдържа естествен логаритъм или десетичен знак.

Ето примери ln100, ln1026. Тяхното решение се свежда до факта, че трябва да определите степента, до която основата 10 ще бъде равна съответно на 100 и 1026. За решения на естествени логаритми трябва да приложите логаритмични идентичности или техните свойства. Нека разгледаме примерите за решаване на логаритмични задачи от различен тип.

Как да използваме логаритмни формули: с примери и решения

И така, нека разгледаме примери за използване на основните теореми за логаритмите.

Свойството на логаритъма на продукта може да се използва в задачи, където е необходимо да се разшири голямо значение b в по-прости фактори. Например log 2 4 + log 2 128 = log 2 (4 * 128) = log 2 512. Отговорът е 9.
log 4 8 = log 2 2 2 3 = 3/2 log 2 2 = 1,5 - както можете да видите, използвайки четвъртото свойство на степента на логаритъма, беше възможно да се реши един привидно сложен и неразрешим израз. Просто трябва да разложите основата и след това да извадите стойностите на мощността от знака на логаритъма.

Задачи от изпита

Логаритмите често се срещат на приемните изпити, особено много логаритмични проблеми на изпита (държавен изпит за всички завършили училище). Обикновено тези задачи присъстват не само в част A (най-лесната тестова част от изпита), но и в част C (най-трудните и обемни задачи). Изпитът предполага точно и перфектно познаване на темата "Естествени логаритми".

Примери и решения на проблемите са взети от длъжностното лице опции за изпита... Нека видим как се решават подобни задачи.

Даден е log 2 (2x-1) = 4. Решение:
пренапишем израза, като го опростим малко log 2 (2x-1) = 2 2, чрез дефиницията на логаритъма получаваме, че 2x-1 = 2 4, следователно 2x = 17; х = 8,5.

Най-добре е всички логаритми да се преобразуват в една основа, така че решението да не е тромаво и объркващо.
Всички изрази под знака на логаритъма са посочени като положителни, следователно, когато степента на степента се изважда от фактора, който е под знака на логаритъма и като негова основа, изразът, оставащ под логаритъма, трябва да бъде положителен .

Подготовката за финалния тест по математика включва важен раздел – „Логаритми“. Задачите от тази тема задължително се съдържат в изпита. Опитът от последните години показва, че логаритмичните уравнения създават трудности за много ученици. Следователно учениците с различни нива на обучение трябва да разберат как да намерят правилния отговор и бързо да се справят с тях.

Минете успешно сертификационния тест с помощта на образователния портал "Школково"!

В подготовка за сингъл държавен изпитзрелостниците се нуждаят от надежден източник, който предоставя най-пълна и точна информация за успешното решаване на тестови задачи. Учебникът обаче не винаги е под ръка, а намирането на необходимите правила и формули в интернет често отнема време.

Образователен портал "Школково" ви позволява да се подготвите за Единния държавен изпит навсякъде по всяко време. Нашият сайт предлага най-удобния подход за повторение и усвояване на голямо количество информация за логаритми, както и за едно и няколко неизвестни. Започнете с лесни уравнения. Ако сте се справили с тях лесно, преминете към по-сложни. Ако имате проблеми с решаването на определено неравенство, можете да го добавите към любимите си, за да можете да се върнете към него по-късно.

Можете да намерите необходимите формули за изпълнение на задачата, повторение на специални случаи и методи за изчисляване на корена на стандартното логаритмично уравнение, като погледнете секцията "Теоретична справка". Учителите в Школково са събрали, систематизирали и представили всички необходими материали за успешно преподаване в най-проста и разбираема форма.

За да се справите лесно със задачи от всякаква сложност, на нашия портал можете да се запознаете с решението на някои типични логаритмични уравнения. За да направите това, отидете в секцията "Директории". Представихме голям брой примери, включително уравненията на профилното ниво на изпита по математика.

Ученици от училища в цяла Русия могат да използват нашия портал. За да започнете, просто се регистрирайте в системата и започнете да решавате уравненията. За да консолидирате резултатите, ви съветваме да се връщате към уебсайта на Школково всеки ден.

Преди да решим логаритмичните уравнения, нека повторим още веднъж определението на логаритъма и основните формули.

Логаритъмположително число бпо разум ае индикатор за степента, в която е необходимо да се изгради а, Придобивам б.

Освен това, class = "tex" alt = "(! LANG: b> 0, \; a> 0, \; a \ neq 1">.!}

Нека обърнем внимание на диапазона от приемливи стойности на логаритъма:

class = "tex" alt = "(! LANG: b> 0, \; a> 0, \; a \ neq 1">. !}

Основна логаритмична идентичност:

Основни формули за логаритми:

(Логаритъмът на произведението е равен на сбора от логаритмите)

(Логаритъмът на частното е равен на разликата между логаритмите)
(Формула за логаритъм на степента)

Формулата за преход към нова база:

Знаем как изглежда графиката на логаритмична функция. Тази функция е монотонна. Ако основата на логаритъма е по-голяма от единица, логаритмичната функция нараства монотонно. Ако основата е по-голяма от нула и по-малка от единица, логаритмичната функция намалява монотонно. И във всеки случай той приема всяка от стойностите си само веднъж. Това означава, че ако логаритмите на две числа в която и да е основа са равни, тогава самите числа са равни.

Всичко това ще ни бъде полезно при решаването на логаритмични уравнения.

Най-прости логаритмични уравнения

1. Решете уравнението:

Основите на логаритмите са равни, равни са и самите логаритми, което означава, че числата, от които са взети, също са равни.
Обикновено учениците запомнят това правило в кратка жаргонна формулировка: „Изхвърлете логаритмите!“ Разбира се, ние ги „изхвърляме“ не просто така, а използвайки свойството монотонност на логаритмичната функция.

Получаваме:

Когато решавате логаритмични уравнения, не забравяйте за диапазон от валидни стойностилогаритъм. Не забравяйте, че изразът е дефиниран с class = "tex" alt = "(! LANG: b> 0, \; a> 0, \; a \ neq 1">.!}

Много е добре, ако след като намерите корена на уравнението, просто го включите в уравнението. Ако след такова заместване лявата или дясната страна на уравнението няма смисъл, тогава намереното число не е корен на уравнението и не може да бъде отговорът на проблема. Това е добър начин за тестване за изпита.

2. Решете уравнението:

От лявата страна на уравнението - логаритъмът, отдясно - числото 7. Прилагайки основното логаритмично тъждество, ние представяме числото 7 като. Тогава всичко е просто.

Отговор: -124

3. Решете уравнението:

Виждате ли числото 2 пред логаритъма от дясната страна на уравнението? Сега ви пречи да "изхвърляте логаритми". Какво да правим с него, така че лявата и дясната страна да са само 5 логаритма по основата? Разбира се, формулата за логаритъма на степента ще помогне.

4. Решете уравнението:

Валиден диапазон: class = "tex" alt = "(! LANG: 4-x> 0."> Значит, class="tex" alt="x> -4.">!}

Нека представим 2 от дясната страна на уравнението като - така че лявото и дясното в уравнението да са логаритми на база 5.

Функцията нараства монотонно и взема стойността си точно веднъж. Логаритмите са равни, техните основи са равни. Нека "изхвърлим" логаритмите! Разбира се, class = "tex" alt = "(! LANG: x> -4">.!}

5. Решете уравнението:

Нека запишем решението като верига от еквивалентни преходи. Записваме ODZ и "премахваме" логаритмите:

Клас = "tex" alt = "(! LANG: \ log _ (8) \ left (x ^ (2) + x \ right) = \ log _ (8) \ left (x ^ (2) -4 \ right ) \ Стрелка наляво \ наляво \ (\ начало (матрица) x ^ (2) + x> 0 \\ x ^ (2) -4> 0 \\ x ^ (2) + x = x ^ (2) -4 \ край (матрица) \ надясно \ Лява дясна стрелка \ ляво \ (\ начало (матрица) x ^ (2) + x> 0 \\ x ^ (2) -4> 0 \\ x = -4 \ край (матрица) \ надясно \ Стрелка наляво надясно x = -4">!}
Отговор: –4.

Имайте предвид, че решенията на логаритмични уравнения се записват най-добре като верига от еквивалентни преходи. Това ще ни помогне да не забравяме за диапазона от валидни стойности.

6. Решете уравнението:.

Нека преминем от логаритъмната основа 4 (в степен) към логаритъмната основа 2. Правим това с помощта на формулата за преместване към друга основа:

Нека запишем решението като верига от еквивалентни преходи.

Клас = "tex" alt = "(! LANG: 2 ^ (\ log _ (4) \ наляво (4x + 5 \ надясно)) = 9 \ Стрелка надясно наляво \ наляво \ (\ начало (матрица) 2 ^ \ frac (( \ log _ (2) \ ляво (4x + 5 \ надясно))) (2) = 9 \\ 4x + 5> 0 \ край (матрица) \ дясно \ Стрелка вляво \ наляво \ (\ начало (матрица) \ наляво (2 ^ (\ log _ (2) \ вляво (4x + 5 \ надясно)) \ вдясно) ^ (\ frac (1) (2)) = 9 \\ x> -1 \ frac (1) (4) \ край (матрица) \ надясно \ Лява стрелка надясно \ ляво \ (\ начало (матрица) \ ляво (4x + 5 \ надясно) ^ (\ frac (1) (2)) = 9 \\ x> -1 \ frac ( 1) (4) \ край (матрица) \ надясно \ ляво стрелка надясно \ ляво \ (\ начало (матрица) \ sqrt (4x + 5) = 9 \\ x> -1 \ frac (1) (4) \ край ( матрица) \ надясно \ Стрелка надясно \ наляво \ (\ начало (матрица) 4x + 5 = 81 \\ x> -1 \ frac (1) (4) \ край (матрица) \ надясно. \ Стрелка надясно наляво \ наляво \ (\ начало (матрица) x = 19 \\ x> -1 \ frac (1) (4) \ край (матрица) \ вдясно.">!}

7. Решете уравнението:.

Моля, обърнете внимание: променливата NSи под логаритъма, и в основата на логаритъма. Не забравяйте, че основата на логаритъма трябва да е положителна и да не е равна на 1.

ODZ:
class = "tex" alt = "(! LANG: \ ляв \ (\ начало (матрица) 12-x> 0 \\ x> 0 \\ x \ neq 1 \ край (матрица) \ дясно.">!}

Сега можете да "премахнете" логаритмите.

Външен корен, защото class = "tex" alt = "(! LANG: x> 0">.!}

8. Решете уравнението.

ODZ уравнения: class = "tex" alt = "(! LANG: x> 0">!}

Нека направим замяна. Както при алгебричните уравнения, ние правим променливи промени, когато е възможно.

Да се върнем към променливата NS:

9. Решете уравнението:

Изразът под логаритъма винаги е положителен - тъй като към неотрицателната стойност добавяме 25. Изразът под корена вдясно също е положителен. означава, NSможе да бъде всяко реално число.

Нека представим сбора от логаритмите от лявата страна като логаритъм на произведението. От дясната страна - да отидем на логаритъм основа 3. И използвайте формулата за логаритъм на степента.

"Изхвърляме" логаритмите.

Такова уравнение се нарича биквадратично. Тя включва изрази и. Нека направим замяна

Да се върнем към променливата NS... Получаваме:

Намерихме всички корени на оригиналното уравнение.

Логаритмичните уравнения могат да се срещнат в задача номер 5 на профил USE по математика и в задача номер 13. И ако в задача номер 5 трябва да решите най-простото уравнение, то в задача 13 решението се състои от две точки. Втората точка е изборът на корени в даден сегмент или интервал.