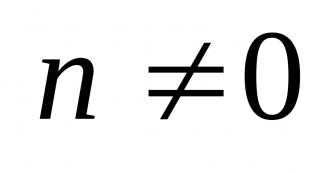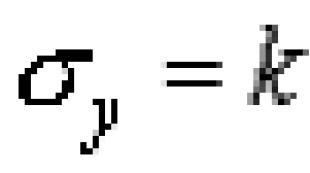Mat analiz funksiyası. Riyazi analiz. Baxın, digər lüğətlərdə “riyazi analiz” nədir
Yu.V.Obrubov tərəfindən tərtib edilmişdir
Kaluqa - 2012
Riyazi analizə giriş.
Həqiqi rəqəmlər. Dəyişənlər və sabitlər.
Riyaziyyatın əsas anlayışlarından biri də budur nömrə.
Saymaqla alınan müsbət ədədlər 1,2,3, ... deyilir təbii.
... -3, -2, -1,0,1,2,3, ... ədədlərinə tam ədədlər deyilir. İki tam ədədin sonlu nisbəti kimi təqdim edilə bilən ədədlər ( 
) adlandırılır rasional.
Bunlara tam və kəsr, müsbət və mənfi ədədlər daxildir. Sonsuz təkrar olunmayan kəsrlər kimi göstərilə bilən ədədlər deyilir irrasional.
İrrasional ədədlərə misal ola bilər 
,
. İrrasional ədədlər çoxluğunda onlar fərqləndirirlər transsendental
nömrələri. Bunlar cəbri olmayan əməliyyatların nəticəsi olan ədədlərdir. Bunlardan ən məşhuru rəqəmdir 
və həmyaşıd olmayan nömrə 
. Rasional və irrasional ədədlər deyilir etibarlıdır
. Həqiqi ədədlər nömrə xəttində nöqtələrlə təmsil olunur. Say oxundakı hər bir nöqtə tək bir həqiqi ədədə uyğun gəlir və əksinə, hər bir həqiqi ədədə ədəd oxunda bir nöqtə uyğun gəlir. Beləliklə, həqiqi ədədlər ilə ədəd xəttinin nöqtələri arasında tək-tək uyğunluq qurulmuşdur. Bu, “a rəqəmi” və “a nöqtəsi” terminlərini bir-birinin əvəzində istifadə etməyə imkan verir.
Müxtəlif fiziki, iqtisadi, sosial proseslərin öyrənilməsi prosesində çox vaxt tədqiq olunan hadisələrin parametrlərinin ədədi dəyərlərini təmsil edən kəmiyyətlərlə məşğul olmaq lazımdır. Eyni zamanda onların bəziləri dəyişir, bəziləri isə öz dəyərlərini saxlayır.
dəyişən
Müxtəlif ədədi qiymətlər alan kəmiyyət deyilir. Verilmiş məsələdə və ya təcrübədə ədədi qiyməti dəyişməyən kəmiyyət deyilir Sabit.
Dəyişənlər adətən Latın hərfləri ilə işarələnir 
və daimi 
.
dəyişən 
qəbul edə biləcəyi dəyərlər toplusu məlum olduqda verilmiş sayılır. Bu çoxluğa dəyişənin diapazonu deyilir.
Ədədi dəyişənin müxtəlif növ dəyər dəstləri var.
interval
a və b ədədlərinin arasına daxil edilmiş x qiymətləri çoxluğudur, a və b ədədləri isə nəzərdən keçirilən çoxluğa aid deyil. Aralıq aşağıdakılarla işarələnir: (a,b);a seqment
a və b ədədlərinin arasına daxil edilmiş x dəyərlərinin çoxluğu adlanır, a və b ədədləri isə nəzərdən keçirilən çoxluğa aiddir. Seqment ,a≤x≤b ilə işarələnir. Bütün həqiqi ədədlərin çoxluğu açıq intervaldır. İşarə olunur: (- ∞,+ ∞), -∞<х <+∞, R. X nöqtəsinin qonşuluğu
0
x 0 nöqtəsi olan ixtiyari interval (а, b) adlanır, bu intervalın bütün nöqtələri a bərabərsizliyini təmin edir. ε
- a nöqtəsinin qonşuluğu
a-ε bərabərsizliyini təmin edən a nöqtəsində mərkəzləşmiş intervaldır Funksiya riyazi analizin əsas anlayışlarından biridir. X və Y həqiqi ədədlərin ixtiyari çoxluğu olsun. Əgər hər bir x X rəqəminə hansısa qaydaya və ya qanuna görə unikal dəqiq müəyyən edilmiş yY həqiqi ədədi verilirsə, onda onlar deyirlər ki, funksiyası
X tərif sahəsi və Y dəyərlər dəsti ilə y \u003d f (x) təyin edin. x dəyişəni adlanır arqument
funksiyaları. Bir funksiyanın tərifində iki məqam vacibdir: tərif sahəsinin göstəricisi və uyğunluq qanununun qurulması. Tərifin əhatə dairəsi
və ya mövcudluq sahəsi
Funksiya, funksiyanın mövcud olduğu, yəni məna kəsb etdiyi arqument dəyərlərinin məcmusudur. Ərazini dəyişdirin
Funksiya x-in icazə verilən dəyərləri üçün qəbul etdiyi y dəyərlər toplusu adlanır. Funksiya təyin etmə yolları.
Funksiyanı təyin etməyin analitik üsulu. Funksiyanı təyin etməyin bu üsulu ilə uyğunluq qanunu hansı riyazi çevrilmələrlə x arqumentinin məlum dəyərindən istifadə edərək y-nin uyğun qiymətini tapa biləcəyinizi göstərən bir düstur (analitik ifadə) kimi yazılır. Funksiya onun bütün tərif sahəsi üzərində tək analitik ifadə ilə müəyyən edilə bilər və ya bir neçə analitik ifadənin toplusunu təmsil edə bilər. Məsələn: y \u003d günah (x 2 + 1) 2. Funksiyanı təyin etməyin cədvəl üsulu Bir hadisənin və ya prosesin birbaşa müşahidəsi və ya eksperimental tədqiqi nəticəsində x arqumentinin dəyərləri və y-nin müvafiq dəyərləri müəyyən bir ardıcıllıqla yazılır. Bu cədvəl x-in y funksiyasını təyin edir. Bir funksiyanın təyin edilməsinin cədvəl üsuluna misal olaraq triqonometrik funksiyalar cədvəlləri, loqarifmlər cədvəlləri, tarixlər və valyuta məzənnələri, temperatur və rütubət və s. ola bilər. 3. Funksiyanı təyin etməyin qrafik üsulu. Funksiyanı təyin etməyin qrafik üsulu texniki qurğular vasitəsilə koordinat müstəvisində nöqtələrin (x, y) göstərilməsidir. Riyazi analizdə funksiyanın təyin edilməsinin qrafik üsulundan istifadə edilmir, lakin həmişə analitik olaraq verilmiş funksiyaların qrafik təsvirinə müraciət edilir. Hər şey mümkün qədər sadə ifadə edilməlidir, lakin daha sadə deyil. Səyahətimiz John Doe adlandıracağımız uydurma bir personajla başlayır. Dünyanın istənilən şəhərində asanlıqla tapıla bilən orta səviyyəli işçidir. Demək olar ki, hər gün Con yüksək həyəcan siqnallarına oyanır və öz maşını ilə işə gedir. Liftlə ofisinə qədər qalxır, orada kompüteri işə salır və istifadəçi adı və şifrəsini daxil edir. Con bütün bunları onların necə işlədiyini zərrə qədər təsəvvür etmədən edir. Ola bilsin ki, o, gündəlik istifadə etdiyi cihazların və cihazların necə düzüldüyünü və necə işlədiyini öyrənməkdə maraqlı olardı, lakin bunun üçün nə vaxtı, nə də gücü var. O, avtomobilləri, liftləri, kompüterləri və zəngli saatları tamamilə fərqli və ortaq heç nəyi olmayan mürəkkəb mexanizmlər hesab edir. Conun sözlərinə görə, onların hər birinin necə işlədiyini başa düşmək üçün illərlə araşdırma tələb olunur. Bəzi insanlar şeylərə bizim John Doe-dan bir az fərqli baxırlar. Onlar bilirlər ki, lift qurğularında elektrik mühərrikləri avtomobil alternatorlarına çox oxşardır. Onlar bilirlər ki, liftin hərəkətinə cavabdeh olan elektrik mühərrikini idarə edən proqramlaşdırıla bilən məntiq nəzarətçisi John Doe iş kompüterinə çox bənzəyir. Onlar bilirlər ki, fundamental səviyyədə PLC, zəngli saat və kompüter nisbətən sadə tranzistor nəzəriyyəsinə əsaslanır. John Doe və adi bir insanın inanılmaz dərəcədə mürəkkəb hesab etdiyi şey, hakerin sadə mexaniki və elektrik prinsiplərindən ən çox istifadə etməsidir. Problem bu prinsiplərin necə tətbiq olunmasındadır. Mürəkkəb ideyalardan fundamental prinsipləri mücərrəd etmək bizə onları Albert Eynşteynin yuxarıda sitat gətirdiyi qeyri-müəyyən məsləhətinə haqq qazandıracaq şəkildə başa düşməyə və sadələşdirməyə imkan verir. Bir çoxumuz hesablamaya mürəkkəb bir şey kimi baxırıq. (Con Doe cihazın prinsipini və müxtəlif mexanizmlərin işləməsini eyni hesab edir.) Siz mürəkkəb, mürəkkəb şeylər yığınını görürsünüz. Onları başa düşmək üçün çox vaxt və səy lazımdır. Bəs sizə riyazi analizin (hesablamanın) əksər mexanizmlər kimi ilk baxışdan göründüyü qədər mürəkkəb olmadığını desək necə olar? Hər kəsin başa düşməsi üçün verilən bir neçə əsas prinsip var və bunu edən kimi dünyaya və onun necə işlədiyinə dair yeni bir baxışınız olacaq? Tipik hesablama dərsliyi təxminən min səhifədən ibarətdir. Tipik John Doe onda başa düşmək və öyrənmək üçün min çətin şey görəcək və haker iki əsas prinsipi (törəmə və inteqral) və bu prinsiplərin 998 nümunəsini görəcək. Biz birlikdə bu prinsiplərin nə olduğunu anlamağa çalışacağıq. Ostindəki Texas Universitetinin professoru Michael Starbird tərəfindən görülən işlərə əsaslanaraq, hər kəsin anlaya biləcəyi gündəlik nümunələrdən istifadə edəcəyik. Riyazi analiz dünyamızın xüsusi gözəlliyini - onu statik yox, dinamik şəkildə müşahidə edə bildiyiniz zaman yaranan gözəlliyi ortaya qoyur. Ümid edirik ki, hər şey sizin üçün uğurlu olacaq. Başlamazdan əvvəl, kökləri dəyişmə və hərəkətin çox diqqətlə təhlilinə dayanan hesablamanın yaranma tarixinə qısaca nəzər salmaq istərdim. Zenon paradoksu Eleyalı Zenon eramızdan əvvəl 4-cü əsrdə yaşamış bir filosofdur. O, bir neçə incə, lakin dərin paradokslar qaldırdı, onlardan ikisi nəticədə hesablamanın yaranmasına səbəb oldu. Zenon paradokslarını həll etmək üçün bəşəriyyət iki min ildən çox vaxt apardı. Təsəvvür edə bildiyiniz kimi, asan deyildi. Çətinliklər əsasən sonsuzluq ideyası ilə bağlı idi. Riyazi baxımdan sonsuzluq problemi nədir? 17-ci əsrdə İsaak Nyuton və Qotfrid Leybniz Zenon paradokslarını həll etməyə və riyazi analiz yaratmağa nail oldular. Gəlin bu paradokslara daha yaxından nəzər salaq ki, onların ətrafında niyə bu qədər hay-küy yaranıb. Ox Havada uçan bir ox təsəvvür edin. Çox əminliklə deyə bilərik ki, oxu hərəkətdədir. İndi müəyyən bir zamanda oxu nəzərdən keçirin. O, artıq hərəkət etmir, ancaq istirahətdədir. Amma biz dəqiq bilirik ki, ox hərəkətdədir, o zaman o, necə sakitləşə bilər?! Bu paradoksun mahiyyəti budur. Bu, axmaq görünə bilər, amma əslində bu, riyazi baxımdan nəzərə alınmalı olan çox mürəkkəb bir anlayışdır. Daha sonra öyrənəcəyik ki, biz riyazi analizin iki prinsipindən biri (hesablama) - törəmə ideyası ilə əlaqələndirəcəyimiz ani dəyişmə sürəti anlayışı ilə məşğul oluruq. Bu, bizə müəyyən bir zamanda oxun sürətini hesablamağa imkan verəcək - bəşəriyyətin iki minillikdən çox müddət ərzində edə bilmədiyi bir şey. Dixotomiya Gəlin həmin oxa yenidən baxaq. Bu dəfə təsəvvür edin ki, o, bizim istiqamətdə uçur. Zenon iddia edirdi ki, biz tərpənməməliyik, çünki ox bizə heç vaxt dəyə bilməz. Təsəvvür edin ki, ox havada olduqdan sonra o, yay ilə hədəf arasındakı məsafənin yarısını qət etməlidir. Müəyyən bir nöqtəyə yarı yolda çatdıqdan sonra, o, yenidən yarı məsafəni qət etməli olacaq - bu dəfə bu nöqtə ilə hədəf arasında. Təsəvvür edin ki, biz bunu davam etdirəcəyik. Beləliklə, ox daim istinad nöqtəsi ilə hədəf arasındakı məsafənin yarısını qət edir. Bunu nəzərə alsaq, ox bizə heç vaxt dəyə bilməyəcəyi qənaətinə gələ bilərik! Real həyatda ox sonunda hədəfinə dəyəcək və bizdə paradoksun nə demək olduğunu düşünməyə vadar edəcək. Birinci paradoksda olduğu kimi, riyazi analizin prinsiplərindən biri - inteqraldan istifadə etməklə bu problemi necə həll edəcəyimizi daha sonra nəzərdən keçirəcəyik. İnteqral sonsuzluq anlayışına riyazi funksiya kimi baxmağa imkan verir. Alim və mühəndislərin fikrincə, bu, son dərəcə güclü bir vasitədir. Hesablamanın iki əsas prinsipi Riyazi təhlilin iki fundamental prinsipinin mahiyyətini Zenon paradokslarının həllində tətbiq etməklə nümayiş etdirmək olar. törəmə. Törəmə Ox paradoksundakı oxun sürətini hesablamağa imkan verəcək bir üsuldur. Bunu ardıcıl azalan zaman intervallarında oxun mövqeyini təhlil etməklə edirik. Okun dəqiq sürəti ölçmələr arasındakı vaxtın sonsuz kiçik olduğu ortaya çıxanda məlum olacaq. İnteqral.İnteqral, Dixotomiya paradoksundakı oxun mövqeyini hesablamağa imkan verəcək bir üsuldur. Bunu, oxun sürətini ardıcıl azalan zaman intervalları vasitəsilə təhlil edərək edəcəyik. Ölçmələr arasındakı vaxt sonsuz kiçik olduqda oxun dəqiq mövqeyini biləcəyik. Törəmə və inteqral arasında bəzi oxşarlıqları görmək asandır. Hər iki dəyər tədricən azalan vaxt intervallarında bumun mövqeyinin və ya sürətinin təhlili zamanı hesablanır. Daha sonra öyrənəcəyik ki, inteqral və törəmə, əslində, eyni keramika kondansatörün iki tərəfidir. Niyə hesablamanın əsaslarını öyrənməliyik? Cərəyanı, gərginliyi və müqaviməti sadə bir tənliklə birləşdirən Ohm Qanununu hamımız bilirik. İndi bir kondansatör nümunəsindən istifadə edərək Ohm Qanununa baxaq. Kondansatörün cari gücü gərginlikdən və vaxtdan asılıdır. Bu halda vaxt kritik dəyişəndir və istənilən dinamik hadisədə nəzərə alınmalıdır. Riyazi analiz bizə şeylərin zamanla necə dəyişdiyini anlamağa və qiymətləndirməyə imkan verir. Bir kondansatör vəziyyətində, cərəyan tutumun saniyədə volta bərabərdir və ya i = C(dv/dt), burada: i - cari güc (ani); Bu dövrədə kondansatördə elektrik cərəyanı yoxdur. Voltmetr batareyanın gərginliyini göstərəcək, lakin ampermetr heç nə göstərməyəcək. Potensiometr toxunulmaz qaldıqca gərginlik dəyişməyəcək. Bu halda i = C(0/dt) = 0 amer. Bəs potensiometri tənzimləməyə başlasaq nə olacaq? Tənliyə əsasən, yaranan cərəyan gücü kondansatördə görünəcəkdir. Bu cərəyan potensiometrin nə qədər sürətlə hərəkət etməsi ilə əlaqəli olan gərginliyin dəyişməsindən asılı olacaq. Bu qrafiklər kondansatördəki gərginlik, cərəyan və potensiometri çevirdiyimiz sürət arasındakı əlaqəni göstərir. Əvvəlcə yavaş-yavaş edirik. Sürətin artması gərginliyin dəyişməsinə səbəb olur ki, bu da öz növbəsində cərəyanın kəskin artmasına səbəb olur. Bütün mərhələlərdə kondansatördəki cərəyan onun içindəki gərginliyin dəyişmə sürəti ilə mütənasibdir. Riyazi analiz, daha dəqiq desək, törəmə bizə dəyişmə sürətini təyin etmək imkanı verir, beləliklə, müəyyən bir zamanda kondansatördəki cərəyanın dəyərini dəqiq bilək. Eynilə, Zenon oxunun ani sürətini hesablaya bilərik. Bu, arsenalınızda olması lazım olan inanılmaz dərəcədə güclü bir vasitədir. Material xüsusi olaraq sayt üçün hazırlanmışdır - hackaday.com saytının məqaləsinə əsasən P.S. Mənim adım Aleksandrdır. Bu mənim şəxsi, müstəqil layihəmdir. Məqaləni bəyəndinizsə çox şadam. Sayta kömək etmək istəyirsiniz? Sadəcə olaraq, bu yaxınlarda axtardığınız reklam üçün aşağıya baxın. Müəllif hüquqları saytı © - Bu xəbər sayta məxsusdur və blogun əqli mülkiyyətidir, müəllif hüquqları qanunu ilə qorunur və mənbəyə aktiv keçid olmadan heç bir yerdə istifadə edilə bilməz. Daha ətraflı - "Müəlliflik haqqında" Bunu axtarırsınız? Bəlkə bu qədər uzun müddət tapa bilmədiyin şey budur? RİYASİ TƏHLİL riyaziyyatın bir hissəsidir funksiyaları və onların ümumiləşdirilməsi metodu ilə öyrənilir məhdudiyyətlər. Həd anlayışı sonsuz kiçik kəmiyyət anlayışı ilə sıx bağlıdır, ona görə də demək olar ki, M. a. funksiyaları və onların ümumiləşdirilməsini sonsuz kiçik metodla öyrənir. Adı "M. a." - riyaziyyatın bu hissəsinin köhnə adının qısaldılmış modifikasiyası - "Sonsuz kiçik analiz"; sonuncu məzmunu daha dolğun açır, lakin o, həm də qısaldılır (“Sonsuz kiçiklər vasitəsi ilə təhlil” başlığı mövzunu daha dəqiq səciyyələndirərdi). Klassik M. və. tədqiq (təhlil) obyektləri ilk növbədə funksiyalardır. “İlk növbədə” ona görə ki, M. a.-nin inkişafı. onun metodları ilə funksionallardan, operatorlardan və s.-dən daha mürəkkəb birləşmələrin öyrənilməsinin mümkünlüyünə gətirib çıxardı. Təbiətdə və texnologiyada hər yerdə hərəkət və proseslərə rast gəlinir, to-çovdar funksiyaları ilə təsvir olunur; təbiət hadisələrinin qanunları da adətən funksiyalarla təsvir olunur. M. a.-nın obyektiv əhəmiyyəti də bundan irəli gəlir. funksiyaların öyrənilməsi vasitəsi kimi. M. a. terminin geniş mənasında riyaziyyatın çox böyük bir hissəsini əhatə edir. O daxildir diferensial, inteqral hesablamalar, kompleks dəyişənlər nəzəriyyəsinin funksiyaları, nəzəriyyə adi diferensial tənliklər, nəzəriyyə qismən diferensial tənliklər, nəzəriyyə inteqral tənliklər, variasiya hesablamaları, funksional analiz və digər riyazi fənlər. Müasir ədəd nəzəriyyəsi Və ehtimal nəzəriyyəsiüsulları tətbiq etmək və inkişaf etdirmək M. və. Buna baxmayaraq, termin M. a. tez-tez yalnız nəzəriyyəni birləşdirən riyazi analizin əsaslarını adlandırmaq üçün istifadə olunur real rəqəm, limitlər nəzəriyyəsi, nəzəriyyə sıralar, diferensial və inteqral hesablamalar və onların bilavasitə tətbiqləri, məsələn, maksimal və minimumlar nəzəriyyəsi, nəzəriyyə gizli funksiyalar, Furye sıraları, Furye inteqralları. Funksiya. M.-də a. Lobaçevski və Dirixleyə görə funksiyanın tərifindən çıxış. Əgər hər bir ədəd üçün xz müəyyən Fnömrələr dəstinin k.-l-ə görə. qanunlar arasında yer alır y, onda bu funksiyanı müəyyən edir bir dəyişəndən X. Funksiya oxşar şəkildə müəyyən edilir dəyişənlərdən, harada x=(x 1 , ..., x n) -
n ölçülü fəzanın nöqtəsi; funksiyalarını da nəzərə alın nöqtələrdən x=(x 1 , X 2 ,
...) bəzi sonsuz ölçülü fəzanın, lakin daha çox funksionallar adlanır. elementar funksiyalar. M.-də əsas dəyər və. oynamaq elementar funksiyalar. Praktikada onlar əsasən elementar funksiyalarla işləyirlər, daha mürəkkəb xarakterli funksiyaları təxmin edirlər. Elementar funksiyaları təkcə real deyil, həm də kompleks x üçün hesab etmək olar, onda bu funksiyalar haqqında təsəvvürlər müəyyən mənada tamamlanır. Bu baxımdan M. a.-nın mühüm bir qolu, adlanır. mürəkkəb dəyişənin funksiyaları nəzəriyyəsi və ya nəzəriyyə analitik funksiyalar. Həqiqi nömrə. Funksiya anlayışı mahiyyətcə həqiqi (rasional və irrasional) ədəd anlayışına əsaslanır. Nəhayət, yalnız 19-cu əsrin sonlarında formalaşdı. Xüsusilə, rəqəmlərlə həndəsi nöqtələr arasında məntiqi cəhətdən qüsursuz bir əlaqə qurulmuşdur. düzbucaqlı koordinat sistemlərini riyaziyyata gətirən R.Dekartın (R.Dekart, 17-ci əsrin ortaları) ideyalarının formal əsaslandırılmasına və onlarda funksiyaların qrafiklərlə təsvirinə səbəb olan düz xətt. Limit. M.-də a. funksiyaların öyrənilməsi üsuludur. Ardıcıllığın həddi ilə funksiyanın həddini fərqləndirin. Bu anlayışlar nəhayət yalnız 19-cu əsrdə formalaşdı, baxmayaraq ki, digər yunanların onlar haqqında təsəvvürləri var idi. alimlər. Təkcə onu demək kifayətdir ki, Arximed (e.ə. 3-cü əsr) parabolanın seqmentini limitə keçid adlandıracağımız bir proseslə hesablaya bildi (müq. tükənmə üsulu). Davamlı funksiyalar. M. a.-da öyrənilən mühüm funksiya, forma davamlı funksiyalar. Bu konsepsiyanın mümkün təriflərindən biri: funksiya y=f(x).bir dəyişəndən X, interval üzrə verilmişdir ( a, b),
çağırdı bir nöqtədə davamlıdır X,Əgər Funksiya fasiləsizdir ( a, b),
bütün nöqtələrində davamlıdırsa; onda bu, sözün gündəlik mənasında davamlı olan əyridir. Törəmə və . Davamlı funksiyalar arasında malik olan funksiyaları ayırmaq lazımdır törəmə. Funksiya törəməsi bir nöqtədə bu nöqtədə dəyişmə sürətinə, yəni limitə malikdir Zamanla y oxu boyunca hərəkət edən nöqtənin koordinatına sahib olsaq X, onda f "(x). nöqtənin bir anda ani sürətidir X. f "(x) törəməsinin işarəsi ilə .
f (x)-dəki dəyişikliyin xarakterini mühakimə edin: əgər f "(z)> 0 ( f"(x) <0
).
interval üzrə ( c, d), onda funksiya / bu intervalda artır (azalır). Əgər x nöqtəsindəki / funksiyası yerli ekstremuma (maksimum və ya minimum) çatırsa və bu nöqtədə törəməsi varsa, sonuncu f "(x 0) \u003d 0 nöqtəsində sıfıra bərabərdir. Bərabərlik (1) ekvivalent bərabərliklə əvəz edilə bilər burada sonsuz kiçikdir, yəni f funksiyasının nöqtədə törəməsi varsa X, onda onun bu nöqtədəki artımı iki şərtə parçalanır. Bunlardan birincisi dəndir (mütənasibdir), ikincisi - daha sürətli sıfıra meyl edir Qiymət (2) ref. diferensial kiçik artıma uyğun funksiyalar təxminən bərabər hesab edilə bilər dy: Diferensialla bağlı yuxarıdakı mülahizə M. a üçün xarakterikdir. Onlar bir çox dəyişənlərin funksiyalarına və funksionallara genişlənir. Məsələn, əgər funksiya dəyişənlərdən davamlıdır qismən törəmələr nöqtədə x=(x 1 , ... , x n), sonra onun artımı
müstəqil dəyişənlərin artımlarına uyğun gələn kimi yazıla bilər harda, yəni hamısı varsa Burada (3)-ün sağ tərəfindəki birinci termin diferensialdır dz funksiyaları f. Xətti olaraq asılıdır və ikinci müddət daha sürətli sıfıra meyl edir verilsin (bax Art. Variasiyaların hesablanması) x(t) funksiya siniflərinə uzadılıb ,
intervalında davamlı törəmə olan və sərhəd şərtlərini ödəyən x( t0)\u003d x 0, x( t1)=x l, Harada x 0, x 1 - verilmiş nömrələr; h(t) funksiyasının sinfi olsun. ,
üzərində davamlı törəmə olan və h( t0)=h(t1)=0. Aydındır ki, əgər Dəyişikliklər hesablamasında sübut edilmişdir ki, L-də müəyyən şərtlər altında funksional J(x) artımını aşağıdakı kimi yazmaq olar. harada və beləliklə, (4)-ün sağ tərəfindəki ikinci hədd ||h||-dən daha sürətli sıfıra meyl edir və birinci hədd xətti asılı olaraq (4)-ün birinci termini adlanır. funksionalın dəyişməsi və dJ( ilə işarələnir) x, h). İnteqral. Törəmə ilə yanaşı, M. a.-da fundamental əhəmiyyət kəsb edir. Qeyri-müəyyən və müəyyən inteqrallar var. Qeyri-müəyyən inteqral antitörəmə funksiyası ilə sıx bağlıdır. F(x) funksiyası. intervalında f funksiyasının əks törəməsi ( a, b) bu intervalda olarsa F"(x) =f(x). Funksiyanın müəyyən inteqralı (Riemann) / intervalında [ a, b] həddi var Əgər f funksiyası [ intervalında müsbət və davamlıdırsa a, b],
onda onun bu seqmentdəki inteqralı əyri ilə məhdudlaşan fiqurun sahəsinə bərabərdir y=f(x), ox Oh və birbaşa x=a, x=b. Riemann-inteqrasiya edilə bilən funksiyalar sinfi [ üzərindəki bütün davamlı funksiyaları ehtiva edir. a, b]funksiyalar və bəzi kəsikli funksiyalar. Lakin onların hamısı mütləq məhduddur. Çox tez böyüməyən qeyri-məhdud funksiyalar üçün, həmçinin sonsuz intervallarda verilən müəyyən funksiyalar üçün sözdə yanlış inteqrallar, onların müəyyən edilməsi üçün limitə ikiqat keçid tələb olunur. Bir dəyişənin funksiyası üçün Riemann inteqralı anlayışı bir çox dəyişənli funksiyaları əhatə edir (bax. Çoxsaylı inteqral). Digər tərəfdən, M.-nin ehtiyacları və. inteqralın tamam başqa istiqamətdə, mənada ümumiləşdirilməsinə gətirib çıxardı Lebeq inteqralı və ya daha ümumi Lebesgue-Stieltjes inteqralı. Bu inteqralların tərifində vacib olan, ölçülə bilənlər adlanan müəyyən çoxluqlar üçün onların ölçü anlayışının və bu əsasda ölçülə bilən funksiya anlayışının təqdim edilməsidir. Ölçülə bilən funksiyalar və Lebesgue-Stieltjes inteqralı üçün təqdim olunur. Bu halda, müxtəlif ölçülərin geniş spektri və ölçülə bilən çoxluq və funksiyaların müvafiq sinifləri nəzərdən keçirilir. Bu, bu və ya digər inteqralı müəyyən konkret problemə uyğunlaşdırmağa imkan verir. Nyuton-Leybnits düsturu. Törəmə ilə inteqral arasında Nyuton - Leybniz düsturu (teorem) ilə ifadə olunan əlaqə var. Burada f(x) [ üzərində davamlıdır. a, b] funksiyası, F(x) -
onun prototipi. Formula və Taylor. Törəmə və inteqralla yanaşı, riyazi analizdə ən mühüm anlayış (tədqiqat vasitəsi). var Taylor p Taylor seriyası.Əgər f(x) funksiyası , a çağırdı onun Taylor polinomu (n dərəcələri). x-x 0: (Teylor düsturu); yaxınlaşma xətası olarkən da sıfıra meyl edir -dən daha sürətli Beləliklə, x 0 nöqtəsinin yaxınlığındakı f (x) funksiyası onun hesablanması üçün yalnız arifmetika tələb edən çox sadə funksiya (polinom) ilə istənilən dəqiqlik dərəcəsi ilə yaxınlaşdırıla bilər. əməliyyatlar - toplama, çıxma və vurma. Xüsusi əhəmiyyət kəsb edənlərdir müəyyən bir x 0 məhəlləsində analitik olan və sonsuz sayda törəmələri olan funksiyalar, belə ki, onlar üçün bu qonşuluqda sonsuz Taylor güc seriyası kimi təmsil oluna bilər: Müəyyən şərtlər altında Taylor genişlənməsi bir çox dəyişənlərin funksiyaları, həmçinin funksionallar və operatorlar üçün də mümkündür. Tarixi istinad. 17-ci əsrə qədər M. a. ayrı-ayrı problemlərin həlli toplusu idi; məsələn, inteqral hesablamada bunlar fiqurların sahələrini, əyri sərhədləri olan cisimlərin həcmlərini, dəyişən qüvvənin işi və s. hesablamaq üçün tapşırıqlardır. Hər bir tapşırıq və ya konkret məsələ öz üsulu ilə həll edilirdi, bəzən mürəkkəb və çətin olur. (M. a. tarixdən əvvəlki məqalə üçün bax Sonsuz kiçik hesablama),
M. a. vahid və sistemli olaraq. bütövlükdə İ.Nyuton (İ.Nyuton), Q.Leybnits (Q.Leybnits), L.Euler (L.Eyler), C.Laqranj (C.Laqranj) və 17-ci əsrin başqa alimlərinin əsərlərində formalaşmışdır. 18-ci əsrlər və onun - sərhədlər nəzəriyyəsi - başlanğıcda O. Komi (A. Koşi) tərəfindən hazırlanmışdır. 19-cu əsr M. a.-nın ilkin konsepsiyalarının dərin təhlili. 19-20-ci əsrlərdəki inkişafı ilə bağlı olmuşdur. çoxluq nəzəriyyəsi, ölçü nəzəriyyəsi, real dəyişənin funksiyaları nəzəriyyəsi və müxtəlif ümumiləşdirmələrə səbəb olmuşdur. yanan.: La V a l l e - P u s s e n S.-J. e, Sonsuz kiçiklərin təhlili kursu, tərcümə. fransız dilindən, cild 1-2, Moskva, 1933; İlyin V. A., Poznyak E. G., Riyazi analizin əsasları, 3-cü nəşr, 1-ci hissə, M., 1971; 2-ci nəşr, 2-ci hissə, M., 1980; And l and N V. A., Sadovnichiy V. A., Seidov B. X., Riyazi analiz, M., 1979; K u d r i v e in L. D., Riyazi analiz, 2-ci nəşr, cild 1-2, M., 1973; Nikolski S. M., Riyazi analiz kursu, 2-ci nəşr, cild 1-2, M., 1975; Uitteker E. T., W a t s o n J. N., Müasir təhlil kursu, trans. ingilis dilindən, hissə 1-2, 2-ci nəşr, M., 1962-63; F və kht n o l ts G. M., Diferensial və inteqral hesablama kursu, 7-ci nəşr, cild 1-2, M., 1970; 5-ci nəşr, 3-cü cild, M., 1970. S. M. Nikolski. Riyazi ensiklopediya. - M.: Sovet Ensiklopediyası. I. M. Vinoqradov. 1977-1985. RİYASİ TƏHLİL, diferensial hesablama və inteqral hesablama üsulları ilə funksiyaların öyrənilməsinə həsr olunmuş riyaziyyatın bir sıra sahələri ... Müasir ensiklopediya Diferensial və inteqral hesablama metodları ilə funksiyaların öyrənilməsinə həsr olunmuş riyaziyyat sahələrinin məcmusudur. Termin elmidən daha çox pedaqojidir: riyazi analiz kursları universitetlərdə və texniki məktəblərdə tədris olunur ... Böyük ensiklopedik lüğət İngilis dili riyazi analiz; alman riyazi analiz. Riyaziyyatın diferensial və inteqral hesablama metodları ilə funksiyaların öyrənilməsinə həsr olunmuş bölməsi. Antinazi. Sosiologiya Ensiklopediyası, 2009 ... Sosiologiya ensiklopediyası Mövcuddur., sinonimlərin sayı: 2 matan (2) riyazi analiz (2) ASIS sinonim lüğəti. V.N. Trishin. 2013... Sinonim lüğət RİYASİ TƏHLİL- RİYASİ TƏHLİL. Riyaziyyatın diferensial və inteqral hesablama metodları ilə riyazi funksiyaların öyrənilməsinə həsr olunmuş sahələri toplusu. Metodların istifadəsi M. və. ən mühüm ...... həlli üçün təsirli vasitədir. Metodoloji termin və anlayışların yeni lüğəti (dillərin tədrisi nəzəriyyəsi və təcrübəsi) riyazi analiz- — EN riyazi təhlil Limit prosesi və ya yaxınlaşma anlayışı ilə ən açıq şəkildə əlaqəli olan riyaziyyat sahəsi; diferensiasiya nəzəriyyələrini ehtiva edir, ...... Texniki Tərcüməçinin Təlimatı Riyazi analiz- RİYASİ TƏHLİL, diferensial hesablama və inteqral hesablama üsulları ilə funksiyaların öyrənilməsinə həsr olunmuş riyaziyyat bölmələrinin məcmusudur. … İllüstrasiyalı Ensiklopedik Lüğət “... uşağın təbii marağı və modelləşdirməyə olan sevgisini məhv etmək üçün yeganə mexanizm yaratmalı olsaydım, çətin ki, artıq həyata keçirildiyindən daha yaxşısını edərdim - sadəcə olaraq kifayət qədər təsəvvürüm olmazdı. riyaziyyatı öyrənməyin müasir metodlarında təcəssüm tapmış belə həssas, sönük fikirlərlə rəqabət aparır. Təsviri sənəti belə öyrənməyi düşünün: Uşaqlar, uşaq bağçasında rəsm yoxdur. Bunun əvəzinə boya məhsullarının kimyasını, işığın fizikasını və gözün anatomiyasını öyrənək. 12 il bu aspektləri öyrəndikdən sonra, əgər uşaqlar (daha doğrusu, artıq yeniyetmələr) hələ də sənətə nifrət etmirlərsə, özbaşına rəsm çəkməyə başlaya bilərlər. Nəhayət, indi sənətə hörmət etməyə başlamaq üçün möhkəm təmələ sahibdirlər. Düzdür? Həm də şeirlə. Təsəvvür edin ki, bu sitatı (formula) öyrənirsiniz: “Ancaq əsas odur ki, özünə sadiq ol; O zaman gecənin gündüzün ardınca gəldiyi kimi, Sən də başqalarına xəyanət etməzsən”. -Uilyam Şekspir, Hamlet Bu, "özün ol" deməyin zərif bir yoludur (və bu, riyaziyyat haqqında hörmətsiz yazmaq deməkdirsə, belə də olsun). Amma riyaziyyat dərsində şeiri nəzərdən keçirsəydik, məna axtarmaq əvəzinə hecaların sayını hesablayar, iambik pentametri təhlil edər, isim, fel və sifətləri qeyd edərdik. Riyaziyyat və poeziya eyni şeyi izah etmək, xarakterizə etmək üçün müxtəlif yollar kimidir. Düsturlar məqsədə çatmaq üçün vasitədir, riyazi həqiqəti ifadə etmək üsuludur. Biz unudmuşuq ki, riyaziyyat fikirlərlə işləyir, bu fikirləri ifadə edən düsturların mexaniki manipulyasiyası deyil. Etməyəcəyim şey budur: artıq yazdığım dərslikləri təkrar danışmayacağam. Burada və indi cavablara ehtiyacınız varsa, tonlarla veb saytlar, video dərslər və 20 dəqiqə kömək etmək. Bunun əvəzinə hesablamanın əsaslarına yiyələnək. Tənliklər kifayət deyil - mən fikir anları istəyirəm ki, həqiqətən onların mənasını görəsiniz və riyaziyyatın dilini başa düşəsiniz. Formal riyazi dil sadəcə ünsiyyət vasitəsidir. Qrafiklər, informativ animasiyalar və sadə dil bir səhifə mücərrəd sübutdan daha çox fikir verə bilər. Hesab edirəm ki, hər kəs hesablamanın əsas prinsiplərini başa düşə bilər. Şekspirin əsərlərindən həzz almaq üçün şair olmaq məcburiyyətində deyilik. Əgər cəbri bilirsinizsə və riyaziyyatla maraqlanırsınızsa, bu sizin üçün çox asan olacaq. Bir müddət əvvəl oxumaq və yazmaq xüsusi təlim keçmiş katiblərin işi idi. Və bu gün istənilən 10 yaşlı uşaq bunu edə bilər. Niyə? Çünki biz bunu gözləyirik. İmkanların inkişafında gözləntilər böyük rol oynayır. Beləliklə, hesablamanın başqa bir mövzu olmasını gözləyin. Bəzi insanlar ən xırda təfərrüatlara (yazıçılar/riyaziyyatçılar) düşürlər. Ancaq qalanlarımız baş verənlərə heyran ola və onu anlamağa çalışa bilərik. İstərdim ki, hamı riyazi analizin əsas anlayışlarını mənimsəsin və “Vay!” desin. Bu sadə bir nümunə idi, amma əsas fikri anladın? Diski götürdük, böldük və parçaları bir az fərqli şəkildə birləşdirdik. Riyazi analiz göstərdi ki, disk və üzük bir-biri ilə sıx bağlıdır: disk həqiqətən də üzüklər toplusudur. Bu hesablamada çox məşhur bir mövzudur: Böyük şeylər daha kiçik şeylərdən ibarətdir. Və bəzən bu kiçik obyektlərlə işləmək daha asan və aydın olur. Hesablamada bir çox nümunə fizikaya əsaslanır. Bu, əlbəttə ki, gözəldir, lakin onları dərk etmək çətin ola bilər: düzünü desəm, müxtəlif fiziki düsturları, məsələn, cismin sürətinin düsturu kimi yadda saxlamaq həmişə mümkün deyil. Sadə vizual nümunələrlə başlamağı xoşlayıram, çünki beynimiz belə işləyir. Araşdırdığımız halqa/dairə - siz eyni şeyi müxtəlif diametrli bir neçə boru parçası ilə modelləşdirə bilərsiniz: riyaziyyatın həqiqətən işlədiyinə əmin olmaq üçün onları ayırın, hizalayın və kobud üçbucaq şəklində qoyun. Sadə fiziki düsturla bunu etmək mümkün deyil. Pedantik riyaziyyatçıların klaviaturalarını yandırdıqlarını hiss edirəm. Ona görə də “sərtlik” haqqında bir neçə kəlmə əlavə edəcəyəm. Biz hesablamanı Nyuton və ya Leybnisin kəşf etdiyi kimi öyrətmədiyimizi bilirsinizmi? Onlar intuitiv “flux” və “sonsuz kiçik” ideyalarından istifadə edirdilər. Amma nəzəri cəhətdən işləyirmi? Biz hesablamaları "dəqiq" sübut etmək üçün mürəkkəb mexaniki modellər yaratmışıq, lakin bu cür sübutlar prosesində intuisiyamızı itirmişik. Biz şəkərin şirinliyinə elm dili ilə izah etmək əvəzinə, beyin kimyası baxımından baxırıq “Şəkərin enerjisi çoxdur. Yeyin." Mən tələbələrə hesablama öyrətmək və ya elm adamları yetişdirmək istəmirəm (və edə də bilmirəm). Ancaq hər kəs hesablamanı Nyutonun başa düşdüyü "qeyri-dəqiq" səviyyədə başa düşsəydi, pis olardımı? Bir vaxtlar onun üçün etdiyi kimi, dünyanı sizin üçün də dəyişmək üçün? Dəqiqliyə vaxtından əvvəl diqqət yetirmək tələbələri dağıtır və riyaziyyatı öyrənməyi çətinləşdirir. Budur yaxşı bir nümunə: e rəqəmi texniki olaraq bir limitlə müəyyən edilir, lakin o, artım haqqında intuitiv təxminlərin köməyi ilə dəqiq kəşf edilmişdir. Təbii loqarifm inteqral və ya böyümə vaxtı kimi görünə bilər. Yeni başlayanlar üçün hansı izahatlar daha yaxşıdır? Gəlin əllə bir az çəkək və yol boyu kimyaya qərq edək. Xoşbəxt hesablama. (P.S: Bir mehriban oxucu bu ideyanı daha əyani şəkildə təqdim etməyə kömək edən animasiyalı powerpoint slayd şousu yaratdı (onu PowerPoint-də izləmək daha yaxşıdır, animasiyalar orada görünəcək). Təşəkkür edirəm!) Rus dili lüğətinə görə təhlil- bu, bir şeyin ayrı-ayrı tərəflərini, xassələrini, komponentlərini nəzərə alaraq elmi araşdırma üsuludur. Riyaziyyatın ən mühüm sahələrindən biri adlanır riyazi analiz və tez-tez hətta sadəcə təhlil. Dərhal sual yaranır: riyazi analizlə dəqiq nə təhlil edilir? Cavab aydındır - funksiyaları təhlil edilir. Funksiya(latınca "funksiya" - həyata keçirmək) dəyişən ədədi qiymətlər arasındakı əlaqəni təmsil edir. Təhlil tədqiqat üsulu olduğundan ikinci sual yaranır: bu üsul nədir? Cavab riyazi analizin ikinci adını verir - diferensial və inteqral hesablamalar. Hesablama hesablama qaydalarını təyin edən riyaziyyatın bir sahəsidir. söz " diferensial" latın "diferensiasiya" sözündən gəlir, yəni. fərq. söz " inteqral” belə aydın mənşəyə malik deyil (“inteqrator” - bütöv; “inteqro” - bərpa), lakin hissələri bütövlükdə birləşdirmək, fərqliliklərə bölünmüş bərpa etmək mənasını daşıyır. Bu bərpa ilə əldə edilir ümumiləşdirmə. İlk nəticələri ümumiləşdirək: · əsas obyektlər oxudu riyazi analizdə funksiyalardır. · Funksiyalar dəyişən ədədi dəyərlər arasında müxtəlif növ asılılıqlardır. · Riyazi analizin metodu diferensiasiyadır– funksiya qiymətlərinin fərqləri ilə işləmək və inteqrasiya- məbləğlərin hesablanması. Beləliklə, riyazi analizi mənimsəmək üçün ilk növbədə funksiya anlayışını başa düşmək lazımdır. Funksiya vacib riyazi anlayışdır, çünki funksiyalar hərəkəti və dəyişikliyi təsvir etməyin riyazi yoludur. Funksiya bir prosesdir. Hərəkətin ən mühüm növü düz xətt üzrə mexaniki hərəkətdir. Hərəkət edərkən obyektin qət etdiyi məsafələr ölçülür, lakin bu, hərəkəti tam təsvir etmək üçün açıq şəkildə kifayət deyil. Həm Axilles, həm də tısbağa başlanğıc nöqtədən eyni məsafədə hərəkət edə bilər, lakin onların hərəkəti sürət baxımından fərqlənir və sürəti vaxtı ölçmədən ölçmək mümkün deyil. Artıq bu nümunənin nəzərdən keçirilməsindən aydın olur ki, bir dəyişən hərəkəti və dəyişikliyi təsvir etmək üçün kifayət deyil. Intuitiv olaraq aydındır ki, zaman eyni şəkildə dəyişir, məsafə isə daha sürətli və ya daha yavaş dəyişə bilər. Zamanın hər anında cismin başlanğıc nöqtəsindən nə qədər uzaqlaşdığı məlum olarsa, hərəkət tam təsvir edilir. Beləliklə, mexaniki hərəkət zamanı iki dəyişənin - hər şeydən asılı olmayaraq dəyişən vaxt və zamandan asılı olan məsafə arasında uyğunluq var. Bu fakt funksiyanın tərifi üçün əsasdır. Bu iki dəyişən artıq vaxt və məsafə adlandırılmır. Funksiya tərifi: funksiyası – qaydadır yoxsa qanun, müstəqil dəyişənin hər bir qiymətinin qoyulması X
asılı dəyişənin müəyyən dəyəri saat
. Müstəqil dəyişən X
arqument və asılı adlanır saat
- funksiyası. Bəzən deyirlər ki, funksiya iki dəyişən arasındakı əlaqədir. Bir dəyişənin nə olduğunu necə təsəvvür etmək olar? Dəyişən bir nöqtənin (termometr və ya muncuqlu iynə) hərəkət etdiyi nömrə xəttidir (hökmdar və ya miqyas). Funksiya iki pəncərəli x və y dişli mexanizmdir. Bu mexanizm pəncərədə quraşdırmaq imkanı verir X
hər hansı bir dəyər, ancaq qutuda saat
funksiyanın dəyəri dişli çarxların köməyi ilə avtomatik olaraq görünəcəkdir. Tapşırıq 1. Xəstənin temperaturu hər saat ölçülür. Bir funksiya var - temperaturun vaxtından asılılığı. Bu xüsusiyyəti necə təqdim etmək olar? Cavab verin: cədvəl və qrafik. Hərəkət davamlı olduğu kimi funksiya da davamlıdır, lakin praktikada bu davamlılığı düzəltmək mümkün deyil. Siz yalnız tək arqument və funksiya dəyərlərini tuta bilərsiniz. Bununla belə, davamlılığı nəzəri cəhətdən təsvir etmək hələ də mümkündür. Tapşırıq 2. Qalileo Qaliley sərbəst düşən cismin birinci saniyədə bir məsafə vahidi, ikincidə 3 vahid, üçüncüdə 5 vahid və s. qət etdiyini kəşf etdi. Zamanın məsafədən asılılığını müəyyən edin. göstərici: Qatılan məsafə ilə məsafənin sayı arasındakı əlaqənin ümumi düsturunu çıxarın. Funksiyaların təyin edilməsi yolları. Riyazi təhlilin problemləri. Funksiyanın bir təsvirindən digərinə keçid (funksiya qiymətlərinin hesablanması, eksperimental ədədi və qrafik məlumatlardan təqribi analitik funksiyaların qurulması, funksiyaların tədqiqi və planlarının qurulması). Bir proses kimi funksiyanın xassələrinin riyazi tədqiqi. Nümunə 1: zamanın məlum yol funksiyasından sürəti axtarın (fərqləndirmə). Nümunə 2: Sürətlə zamanın məlum funksiyasından istifadə edərək yolun tapılması (inteqrasiya).Funksiya. Əsas təriflər və anlayışlar.
Albert Eynşteyn
C - faradlarla ölçülən tutum;
dv - gərginliyin dəyişməsi;
dt zamanın dəyişməsidir. 
Digər lüğətlərdə "RİYASİ TƏHLİL"in nə olduğuna baxın:
Yaxşı, hər şey aydındır, bəs sizin böyük ideyanız nədir?
Amma riyaziyyat çətindir!
Beləliklə, riyazi analiz nədən ibarətdir?
Bir neçə nümunə
Riyazi ciddilik haqqında bir az (bu elmin fanatikləri üçün)
|
növbəti mühazirə ==>
Yaradıcılıq: Dəftərləri x (kim?) müəllim yoxlayır |
