Kompleks nömrələri olan seriyalar. Mürəkkəb terminləri olan seriyalar. Güc kompleksi seriyası
1. Kompleks ədədlər. Kompleks ədədlər formanın nömrələri deyilir x+iy, Harada X Və y - real ədədlər, i-xəyali vahid, bərabərliklə müəyyən edilir i 2 =-1. Həqiqi rəqəmlər X Və saat müvafiq olaraq adlanır etibarlıdır Və xəyali hissələr kompleks ədəd z. Onlar üçün qeyd təqdim olunur: x=Rez; y=imz.
Həndəsi olaraq hər bir kompleks ədəd z=x+iy nöqtə ilə təmsil olunur M (x; y) koordinat müstəvisi xOy(Şəkil 26). Bu vəziyyətdə təyyarə hoy kompleks say müstəvisi adlanır və ya z kompleks dəyişəninin müstəvisi.
Qütb koordinatları r Və φ xal M, z mürəkkəb ədədinin şəkli olanlar adlanır modul Və arqument kompleks ədəd z; onlar üçün qeydlər təqdim olunur: r=|z|, φ=Argz.
Təyyarənin hər bir nöqtəsi bir-birindən 2kπ (k müsbət və ya mənfi tam ədəddir) ilə fərqlənən qütb bucağının sonsuz sayda qiymətlərinə uyğun gəldiyi üçün Arg z-nin sonsuz qiymətli funksiyasıdır.
Qütb bucağının dəyərləri φ , -π bərabərsizliyini ödəyir< φ ≤ π çağırılır əsas əhəmiyyəti arqument z və arg z işarəsi verin.
Aşağıda, təyinat φ yalnız z arqumentinin əsas dəyərinə qənaət edin , olanlar. qoyaq φ =argz, arqumentin bütün digər dəyərləri üçün z bərabərliyi əldə edirik
Arg z = arg z + 2kπ =φ + 2kπ.
z kompleks ədədinin modulu və arqumenti ilə onun həqiqi və xəyali hissələri arasındakı əlaqələr düsturlarla qurulur.
x = r cos φ; y = r sin φ.
Arqument z düsturla da müəyyən edilə bilər
arg z = arctg (y / x) + C,
Harada İLƏ= 0 at x > 0, İLƏ x üçün = +π<0, saat> 0; C \u003d - π at x < 0, saat< 0.
Əvəz olunur x Və saat kompleks ədədlərin qeydində z = x+iy vasitəsilə ifadə edirlər r Və φ , biz sözdə almaq Kompleks ədədin triqonometrik forması:
Kompleks ədədlər z 1 \u003d x 1 + iy 1 Və z 2 \u003d x 2 + iy 2 hesab olunur bərabərdir yalnız və yalnız onların həqiqi və xəyali hissələri ayrı-ayrılıqda bərabər olduqda:
z1 = z2, Əgər x 1 = x 2, y 1 = y 2 .
Triqonometrik formada verilmiş ədədlər üçün bərabərlik bu ədədlərin modulları bərabər olduqda və arqumentlər 2π-nin tam qatı ilə fərqləndikdə baş verir:
z 1 = z 2,Əgər |z 1 | = |z 2 | Və Arg z 1 = Arg z 2 +2kπ.
İki mürəkkəb ədəd z = x+iy və z = x -iy bərabər həqiqi və əks xəyali hissələrə deyilir birləşmiş. Birləşən mürəkkəb ədədlər üçün münasibətlər
|z 1 | = |z 2 |; arg z 1 = -arg z 2,
(son bərabərlik forması verilə bilər Arg z 1 + Arg z 2 = 2kπ).
Kompleks ədədlər üzərində əməliyyatlar aşağıdakı qaydalarla müəyyən edilir.

Əlavə. Əgər z 1 \u003d x 1 + iy 1, z 2 \u003d x 2 + iy 2, Bu
Kompleks ədədlərin toplanması kommutativ və assosiativ qanunlara tabedir:
![]()
Çıxarma. Əgər , Bu
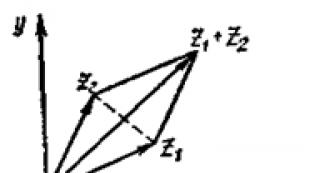
Mürəkkəb ədədlərin toplanması və çıxılmasının həndəsi izahı üçün onları müstəvidə nöqtələr kimi deyil, təsvir etmək faydalıdır. z, və vektorlar: z ədədi = x + iy vektorla təmsil olunur başlanğıcı O nöqtəsində (müstəvinin "sıfır" nöqtəsi - koordinatların başlanğıcı) və son nöqtədə olan M(x; y). Sonra kompleks ədədlərin toplanması və çıxması vektorların toplanması və çıxılması qaydasına uyğun olaraq yerinə yetirilir (şək. 27).
Vektorların toplama və çıxma əməliyyatlarının belə həndəsi şərhi bərabərsizliklərlə ifadə olunan iki və bir neçə kompleks ədədin cəminin və fərqinin modulu haqqında teoremlərin qurulmasını asanlaşdırır:
| |z 1 |-|z 2 | | ≤ |z 1 ±z 2 | ≤ |z 1 | + |z 2 | ,
Bundan əlavə, bunu xatırlamaqda fayda var iki kompleks ədədin fərqinin modulu z1 Və z2 z müstəvisində onların təsvirləri olan nöqtələr arasındakı məsafəyə bərabərdir:| |z 1 -z 2 |=d(z 1 ,z 2) .
Vurma. Əgər z 1 \u003d x 1 + iy 1, z 2 \u003d x 2 + iy 2. Bu
z 1 z 2 \u003d (x 1 x 2 -y 1 y 2) + i (x 1 y 2 + x 2 y 1).
Beləliklə, kompleks ədədlər binom kimi vurulur, i 2 -1 ilə əvəz olunur.
ƏGƏR, onda
Beləliklə, məhsulun modulu somnoektellərin modullarının hasilinə və məhsulun arqumentinə bərabərdir-amillərin arqumentlərinin cəmi. Mürəkkəb ədədlərin vurulması kommutativ, assosiativ və paylayıcı (toplama ilə bağlı) qanunlara tabedir:
Bölmə. Cəbri formada verilmiş iki mürəkkəb ədədin hissəsini tapmaq üçün dividend və bölən bölücü ilə birləşdirilən ədədə vurulmalıdır:

" Əgər triqonometrik formada verilir, onda
Beləliklə, bölmənin modulu dividend və bölən modulun əmsalına bərabərdir, A arqumentözəl divident və bölən arqumentləri arasındakı fərqə bərabərdir.
Ekponentasiya. Əgər z= , onda Nyuton binom düsturu ilə əldə edirik
(S müsbət tam ədəddir); yaranan ifadədə dərəcələri əvəz etmək lazımdır i onların mənaları:
i 2 \u003d -1; i 3 =i; i 4 =1; i 5 =1,…
və ümumiyyətlə,
i 4k = 1; i 4k+1 =i; i 4k+2 = -1; i 4k+3 = -i .
Əgər, onda
(Burada P müsbət tam və ya mənfi tam ədəd ola bilər).
Xüsusilə,
(De Moivre düsturu).
Kök çıxarılması. Əgər P müsbət tam ədəddir, onda kompleks ədədin n-ci kökü z düsturla tapılan n fərqli qiymətə malikdir

burada k=0, 1, 2, ..., n-1.
437.
Əgər (z 1 z 2)/z 3 tapın z1 = 3 + 5i, z 2 = 2 + 3i, z 3 = 1+2i.
∆
438.
nömrə z= 2 + 5i.
∆ Kompleks ədədin modulunu tapın: . Arqumentin əsas qiymətini tapın: . Buna görə də, ▲
439.
Kompleksi triqonometrik formada təmsil edin
nömrə ![]()
∆ Tap ![]() , ; , , yəni.
, ; , , yəni.
440.
Triqonometrik forma kompleksində təmsil olunur
rəqəmlər 1, i, -1, -i.
441.
Nömrələri təmsil edir ,
,
triqonometrik formada və sonra kompleks ədədi tapın
z 1 /(z 2 z 3).
∆ Tap
Beləliklə,
442. Bütün dəyərləri tapın.
∆ Kompleks ədədi triqonometrik formada yazırıq. Bizdə , , . Beləliklə,

Beləliklə, , ,
443. İkili tənliyi həll edin ω 5 + 32i = 0.
∆ Tənliyi yenidən formada yazaq ω 5 + 32i = 0. Nömrə -32i triqonometrik formada təmsil edir:
Əgər k = 0 sonra (A).
k=1,(B).
k=2,(C).
k=3,(D).
k=4,(E).
İki müddətli tənliyin kökləri radius dairəsinə yazılmış düzgün beşbucaqlının təpələrinə uyğundur. R=2 mənşəyində mərkəzləşmişdir (şək. 28).
Ümumiyyətlə, iki müddətli tənliyin kökləri ω n \u003d a, Harada A-mürəkkəb ədəd, nizamlının təpələrinə uyğundur n-qon, mərkəzi başlanğıcda və radiusu ▲-ə bərabər olan dairəyə yazılmışdır

444. De Moivre düsturundan istifadə edərək ifadə edin cos5φ Və sin5 φ vasitəsilə cosφ Və sinφ.
∆ Bərabərliyin sol tərəfini Nyuton binom düsturuna görə çeviririk:
Bərabərliyin real və xəyali hissələrini bərabərləşdirmək qalır:
445. Kompleks ədəd verilmişdir z=2-2i. Tapın Rez, İmz, |z|, argz.
446. z = -12 + 5i.
447 . Moivre düsturundan istifadə edərək ifadəni hesablayın (cos 2° + isin 2°) 45 .
448. De Moivre düsturundan istifadə edərək hesablayın.
449. Kompleks ədədi triqonometrik formada ifadə edin
z = 1 + cos 20° + isin 20°.
450. İfadəsini qiymətləndirin (2 + 3i) 3 .
451.
İfadəsini qiymətləndirin 
452. İfadəsini qiymətləndirin
453. Kompleks ədədi triqonometrik formada ifadə edin 5-3i.
454. Kompleks ədədi triqonometrik formada ifadə edin -1 + i.
455.
İfadəsini qiymətləndirin 
456.
İfadəsini qiymətləndirin  əvvəllər pay və məxrəcdə olan amilləri triqonometrik formada təqdim etdikdən sonra.
əvvəllər pay və məxrəcdə olan amilləri triqonometrik formada təqdim etdikdən sonra.
457. Bütün dəyərləri tapın
458.
İkili tənliyi həll edin ![]()
459. ifadə cos4φ Və sin4φ vasitəsilə cosφ Və sinφ.
460. Nöqtələr arasındakı məsafəni göstərin z1 Və z2 bərabərdir | z2-z1|.
∆ Bizdə var z 1 \u003d x 1 + iy 1, z 2 \u003d x 2 + iy 2, z 2 -z 1 \u003d (x 2 -x 1) + i (y 2 -y 1), harada
olanlar. | z2-z1| verilmiş nöqtələr arasındakı məsafəyə bərabərdir. ▲
461. Hansı xətt nöqtə ilə təsvir olunur z, burada tənliyi ödəyir ilə-sabit kompleks ədəd və R>0?
462.
Bərabərsizliklərin həndəsi mənası nədir: 1) | z-c|
463. Bərabərsizliklərin həndəsi mənası nədir: 1) Rez > 0; 2) mən z< 0 ?
2. Mürəkkəb terminləri olan silsilələr. Kompleks ədədlərin ardıcıllığını nəzərdən keçirək z 1 , z 2 , z 3 , ..., harada z p \u003d x p + iy p (n \u003d 1, 2, 3, ...). sabit nömrə c = a + biçağırdı limit ardıcıllıqlar z 1 , z 2 , z 3 , ..., əgər hər hansı bir ixtiyari kiçik ədəd üçün δ>0 nömrə var N, mənası nədir z səh rəqəmlərlə n > N bərabərsizliyini təmin edin \z n-ilə\< δ . Bu vəziyyətdə yazın .
Mürəkkəb ədədlər ardıcıllığının limitinin mövcudluğu üçün zəruri və kafi şərt aşağıdakı kimidir: ədəd c=a+bi kompleks ədədlərin ardıcıllığının həddidir x 1 + iy 1, x 2 + iy 2, x 3 + iy 3, ... yalnız və yalnız əgər ,.
![]() (1)
(1)
üzvləri kompleks ədədlər adlanır birləşən,Əgər nthüçün S n seriyasının qismən cəmi n → ∞ müəyyən son həddə meyl edir. Əks halda (1) seriyası çağırılır fərqli.
Seriya (1) yalnız və yalnız həqiqi şərtləri olan seriyalar yaxınlaşdıqda birləşir
(2) Silsilənin yaxınlaşmasını tədqiq edin Hədləri sonsuz azalan həndəsi proqressiya təşkil edən bu sıra yaxınlaşır; ona görə də mürəkkəb terminli verilmiş sıra mütləq yaxınlaşır. ^

474. Sıranın yaxınlaşma sahəsini tapın
19.4.1. Mürəkkəb terminlərlə ədədi sıra. Konvergensiyanın bütün əsas tərifləri, yaxınlaşan sıraların xassələri, mürəkkəb sıralar üçün yaxınlaşma meyarları real vəziyyətdən heç bir şəkildə fərqlənmir.
19.4.1.1. Əsas təriflər. Kompleks ədədlərin sonsuz ardıcıllığı verilsin z 1 , z 2 , z 3 , …, z n , … .Nömrənin həqiqi hissəsi z n işarə edəcəyik a n , xəyali - b n
(bunlar. z n = a n + i b n , n = 1, 2, 3, …).
Nömrə seriyası- qeyd yazın.
Qismənməbləğlərsıra: S 1 = z 1 , S 2 = z 1 + z 2 , S 3 = z 1 + z 2 + z 3 , S 4 = z 1 + z 2 + z 3 + z 4 , …,
S n = z 1 + z 2 + z 3 + … + z n , …
Tərif. Limit varsa S
üçün seriyanın qismən cəminin ardıcıllığı  , düzgün kompleks ədəddirsə, seriyanın yaxınlaşdığı deyilir; nömrə S
silsilənin cəmini çağırıb yazın S
= z
1
+ z
2
+ z
3
+ … +
z
n
+ ... və ya
, düzgün kompleks ədəddirsə, seriyanın yaxınlaşdığı deyilir; nömrə S
silsilənin cəmini çağırıb yazın S
= z
1
+ z
2
+ z
3
+ … +
z
n
+ ... və ya  .
.
Qismən cəmlərin həqiqi və xəyali hissələrini tapın:
S n = z 1 + z 2 + z 3 + … + z n = (a 1 + i b 1) + (a 2 + i b 2) + (a 3 + i b 3) + … + (a n + i b n ) = (a 1 + a 2 + a 3 +…+ a n ) +
Harada simvollar  Və
Və  qismən cəminin həqiqi və xəyali hissələri göstərilir. Ədədi ardıcıllıq o halda birləşir ki, onun həqiqi və xəyali hissələrindən ibarət ardıcıllıqlar birləşsin. Beləliklə, mürəkkəb terminləri olan sıra yalnız və yalnız onun həqiqi və xəyal hissələrinin əmələ gətirdiyi sıralar yaxınlaşdıqda yaxınlaşır. Mürəkkəb terminlərlə sıraların yaxınlaşmasını öyrənmək üsullarından biri də bu müddəaya əsaslanır.
qismən cəminin həqiqi və xəyali hissələri göstərilir. Ədədi ardıcıllıq o halda birləşir ki, onun həqiqi və xəyali hissələrindən ibarət ardıcıllıqlar birləşsin. Beləliklə, mürəkkəb terminləri olan sıra yalnız və yalnız onun həqiqi və xəyal hissələrinin əmələ gətirdiyi sıralar yaxınlaşdıqda yaxınlaşır. Mürəkkəb terminlərlə sıraların yaxınlaşmasını öyrənmək üsullarından biri də bu müddəaya əsaslanır.
Misal. Konvergensiya seriyalarını araşdırın  .
.
İfadənin bir neçə dəyərini yazaq  : Əlavə dəyərlər vaxtaşırı təkrarlanır. Bir sıra real hissələr: ; xəyali hissələr silsiləsi; hər iki sıra yaxınlaşır (şərti), belə ki, orijinal seriya birləşir.
: Əlavə dəyərlər vaxtaşırı təkrarlanır. Bir sıra real hissələr: ; xəyali hissələr silsiləsi; hər iki sıra yaxınlaşır (şərti), belə ki, orijinal seriya birləşir.
19.4.1.2. Mütləq yaxınlaşma.
Tərif. Sıra  çağırdı tamamilə konvergent silsilələr yaxınlaşarsa
çağırdı tamamilə konvergent silsilələr yaxınlaşarsa  , üzvlərinin mütləq dəyərlərindən ibarətdir.
, üzvlərinin mütləq dəyərlərindən ibarətdir.
İxtiyari şərtləri olan ədədi həqiqi sıralarda olduğu kimi, əgər seriyalar yaxınlaşsa, sübut etmək asandır.  , onda sıra mütləq birləşir
, onda sıra mütləq birləşir  (
( , beləliklə serialın real və xəyali hissələrinin meydana gətirdiyi serialdır
, beləliklə serialın real və xəyali hissələrinin meydana gətirdiyi serialdır  , tamamilə birləşir). Əgər sıra
, tamamilə birləşir). Əgər sıra  birləşir və sıra
birləşir və sıra  ayrılır, sonra sıra
ayrılır, sonra sıra  şərti konvergent adlanır.
şərti konvergent adlanır.
Sıra  qeyri-mənfi şərtləri olan seriyadır, ona görə də onun yaxınlaşmasını öyrənmək üçün bütün məlum işarələrdən (müqayisə teoremlərindən tutmuş Koşi inteqral meyarına qədər) istifadə edilə bilər.
qeyri-mənfi şərtləri olan seriyadır, ona görə də onun yaxınlaşmasını öyrənmək üçün bütün məlum işarələrdən (müqayisə teoremlərindən tutmuş Koşi inteqral meyarına qədər) istifadə edilə bilər.
Misal. Konvergensiya seriyalarını araşdırın  .
.
Bir sıra modullar yaradaq ():  . Bu seriya birləşir (Cauchy testi
. Bu seriya birləşir (Cauchy testi  ), beləliklə, orijinal seriya tamamilə birləşir.
), beləliklə, orijinal seriya tamamilə birləşir.
19.4. 1 . 3 . Konvergent sıraların xassələri. Mürəkkəb şərtləri olan konvergent sıralar üçün həqiqi şərtləri olan seriyaların bütün xassələri doğrudur:
Seriyanın yaxınlaşması üçün zəruri meyar.
Konvergent seriyanın ümumi termini sıfıra meyllidir
 .
.
Əgər seriya birləşirsə  , onda onun qalıqlarından hər hansı biri yaxınlaşır.Əksinə, seriyanın hər hansı qalığı yaxınlaşırsa, o zaman silsilənin özü yaxınlaşır.
, onda onun qalıqlarından hər hansı biri yaxınlaşır.Əksinə, seriyanın hər hansı qalığı yaxınlaşırsa, o zaman silsilənin özü yaxınlaşır.
Əgər sıra yaxınlaşırsa, ondan sonrakı qalığının cəmin
-ci termin sıfıra meyl edir
 .
.
Konvergent seriyanın bütün şərtləri eyni ədədə vurularsailə , onda silsilənin yaxınlaşması qorunur və cəmi vurulurilə .
Konvergent sıralar (A
) Və (IN
) müddətə görə əlavə və çıxıla bilər; yaranan sıra da yaxınlaşacaq və onun cəmi bərabərdir
 .
.
Konvergent sıranın şərtləri ixtiyari olaraq qruplaşdırılarsa və hər bir mötərizə cütündəki hədlərin cəmindən yeni sıra təşkil edilərsə, onda bu yeni sıra da yaxınlaşacaq və onun cəmi ilkin sıraların cəminə bərabər olacaqdır. .
Əgər seriya mütləq yaxınlaşırsa, onda onun şərtlərinin hər hansı bir dəyişməsi üçün yaxınlaşma qorunur və cəmi dəyişmir.
Əgər sıralar (A
) Və (IN
) onların cəminə mütləq yaxınlaşır
 Və
Və
 , onda onların ixtiyari şərtlər sırası üçün hasili də mütləq yaxınlaşır və onun cəmi bərabərdir
, onda onların ixtiyari şərtlər sırası üçün hasili də mütləq yaxınlaşır və onun cəmi bərabərdir
 .
.
Simvol bax W 1 + W 2 +…+ W n +…= (1), Harada W n = u n + i· v n (n = 1, 2, …) mürəkkəb ədədlər (mürəkkəb ədədlərin ardıcıllığı) adlanır kompleks ədədlərə yaxındır.
Nömrələri W n (n = 1, 2, …) çağırdı bir sıra üzvləri, üzv W nçağırdı seriyanın ümumi üzvü.
Nömrələri yazın S n = W 1 + W 2 +…+ W n (2) (n = 1, 2, …) , adlandırılır seriyanın qismən məbləğləri (1).
Sonlu və ya sonsuz hədd S ardıcıllıqlar S nçağırdı bu seriyanın cəmi.
Əgər limit S sonludur, onda sıra deyilir yaxınlaşma, limit sonsuzdursa və ya ümumiyyətlə mövcud deyilsə, o zaman sıra fərqli.
Əgər S seriyaların cəmi (1), sonra yazın  .
.
Qoy  , A
, A  . Aydındır ki σ
n =
u 1
+
u 2
+…+
u n ,
τ
n =
v 1
+
v 2
+…+
v n. Bərabərliyi hardan bilək
. Aydındır ki σ
n =
u 1
+
u 2
+…+
u n ,
τ
n =
v 1
+
v 2
+…+
v n. Bərabərliyi hardan bilək
 (Səlbəttə) iki bərabərliyə bərabərdir
(Səlbəttə) iki bərabərliyə bərabərdir
 Və
Və
 . Buna görə də (1) seriyasının yaxınlaşması iki həqiqi seriyanın yaxınlaşmasına bərabərdir:
. Buna görə də (1) seriyasının yaxınlaşması iki həqiqi seriyanın yaxınlaşmasına bərabərdir:  Və
Və  . Buna görə də yaxınlaşan ədədi sıraların əsas xassələri yaxınlaşan kompleks sıralara da şamil edilir.
. Buna görə də yaxınlaşan ədədi sıraların əsas xassələri yaxınlaşan kompleks sıralara da şamil edilir.
Məsələn, mürəkkəb seriyalar üçün Koşi meyarı etibarlıdır: (1) seriyası yalnız və yalnız varsa birləşir 
 , bu hamı üçünn
>
Nvə hər hansısəh= 1, 2, … bərabərsizlik.
, bu hamı üçünn
>
Nvə hər hansısəh= 1, 2, … bərabərsizlik.
Bu meyar birbaşa seriyaların yaxınlaşması üçün zəruri meyarları nəzərdə tutur: (1) seriyasının yaxınlaşması üçün onun ümumi termini zəruri və kifayətdirW n → 0 .
Konvergent sıraların aşağıdakı xüsusiyyətləri etibarlıdır: sıralar varsa
 Və
Və
 onların cəminə yaxınlaşırSVəd, sonra sıralar
onların cəminə yaxınlaşırSVəd, sonra sıralar
 Və
Və
 müvafiq olaraq məbləğlərə yaxınlaşırS
±
dvə λS
.
müvafiq olaraq məbləğlərə yaxınlaşırS
±
dvə λS
.
Kompleks ədədlərin mütləq yaxınlaşan seriyası.
Kompleks ədədlər seriyası  (1) çağırdı tamamilə konvergent silsilələr yaxınlaşarsa
(1) çağırdı tamamilə konvergent silsilələr yaxınlaşarsa  (2).
(2).
Teorem.
Kompleks ədədlərin hər bir mütləq yaxınlaşan seriyası (1) yaxınlaşır.
Sübut.
Aydındır ki, bizim üçün müəyyən etmək kifayətdir ki, sıra (1) üçün sıraların yaxınlaşması üçün Koşi kriteriyasının şərtləri ödənilir. İstənilən götür  . (1) sıralarının mütləq yaxınlaşmasına görə (2) sıra yaxınlaşır. Buna görə də seçilmişlər üçün
. (1) sıralarının mütləq yaxınlaşmasına görə (2) sıra yaxınlaşır. Buna görə də seçilmişlər üçün 
 , hər hansı bir üçün n
>
N Və p=1,2,… bərabərsizlik təmin ediləcək
, hər hansı bir üçün n
>
N Və p=1,2,… bərabərsizlik təmin ediləcək  , Amma
, Amma 
 , və daha çox, bərabərsizlik
, və daha çox, bərabərsizlik  hər hansı üçün n
>
N Və səh=1,2,…
Nəticə etibarilə, (1) seriyası üçün kompleks sıraların yaxınlaşması üçün Koşi kriteriyasının şərtləri ödənilir. Buna görə də (1) seriyası birləşir. Teorem düzgündür.
hər hansı üçün n
>
N Və səh=1,2,…
Nəticə etibarilə, (1) seriyası üçün kompleks sıraların yaxınlaşması üçün Koşi kriteriyasının şərtləri ödənilir. Buna görə də (1) seriyası birləşir. Teorem düzgündür.
Teorem.
Bir sıra kompleks ədədlər üçün
 (1) mütləq yaxınlaşandır, həqiqi sıraların mütləq yaxınlaşması zəruri və kifayətdir
(1) mütləq yaxınlaşandır, həqiqi sıraların mütləq yaxınlaşması zəruri və kifayətdir
 (3) və
(3) və
 (4) , haradaW n
=
u n +
i·
v n
(n
= 1, 2,…).
(4) , haradaW n
=
u n +
i·
v n
(n
= 1, 2,…).
Sübut,
aşağıdakı aşkar bərabərsizliklərə əsaslanır
 (5)
(5)
Zərurət.(1) seriyası mütləq yaxınlaşsın, göstərək ki, (3) və (4) sıraları mütləq yaxınlaşsın, yəni sıralar yaxınlaşsın.  Və
Və  (6). (1) seriyasının mütləq yaxınlaşmasından belə çıxır ki, (2) seriyası
(6). (1) seriyasının mütləq yaxınlaşmasından belə çıxır ki, (2) seriyası  yaxınlaşır, onda (5) bərabərsizliyin sol tərəfi sayəsində (6) sıra yaxınlaşacaq, yəni (3) və (4) seriyaları mütləq yaxınlaşacaq.
yaxınlaşır, onda (5) bərabərsizliyin sol tərəfi sayəsində (6) sıra yaxınlaşacaq, yəni (3) və (4) seriyaları mütləq yaxınlaşacaq.
Adekvatlıq.(3) və (4) sıraları mütləq yaxınlaşsın, göstərək ki, (1) seriyası da mütləq yaxınlaşır, yəni (2) seriyası yaxınlaşır. (3) və (4) sıralarının mütləq yaxınlaşmasından belə nəticə çıxır ki, (6) sıra yaxınlaşır, ona görə də silsilələr də yaxınlaşır.  . Buna görə də (5) bərabərsizliyinin sağ tərəfinə görə (2) sıra yaxınlaşır, yəni. (1) seriyası mütləq birləşir.
. Buna görə də (5) bərabərsizliyinin sağ tərəfinə görə (2) sıra yaxınlaşır, yəni. (1) seriyası mütləq birləşir.
Deməli, (1) kompleks sırasının mütləq yaxınlaşması (3) və (4) həqiqi ədədlər sıralarının mütləq yaxınlaşmasına bərabərdir. Buna görə də mütləq yaxınlaşan kompleks sıralar həqiqi mütləq yaxınlaşan ədədi sıraların bütün əsas xassələrinə tabedir. Xüsusilə, mütləq yaxınlaşan mürəkkəb sıra üçün onun şərtlərinin dəyişdirilməsi haqqında teorem etibarlıdır, yəni. Mütləq yaxınlaşan sıradakı şərtlərin dəyişdirilməsi seriyanın cəminə təsir etmir. Mürəkkəb sıraların mütləq yaxınlaşmasını müəyyən etmək üçün müsbət seriyanın yaxınlaşması üçün istənilən meyardan istifadə etmək olar.
Cauchy işarəsi.
(1) seriyasının limiti olsun
 , onda əgərq
< 1 , то ряд (1) абсолютно сходится, если
q>1, sonra (1) seriyası ayrılır.
, onda əgərq
< 1 , то ряд (1) абсолютно сходится, если
q>1, sonra (1) seriyası ayrılır.
D'Alembert işarəsi.
Kompleks ədədlərin (1) seriyası üçün məhdudiyyət varsa
 , sonra daq
< 1 этот ряд абсолютно сходится, а если
q> 1, sonra sıra ayrılır.
, sonra daq
< 1 этот ряд абсолютно сходится, а если
q> 1, sonra sıra ayrılır.
Misal.
Mütləq yaxınlaşma sıralarını araşdırın  , Burada
, Burada  .
.
tapaq
 . Aydındır ki
. Aydındır ki  =
=
 =
=
 . Buna görə də silsilələr tamamilə konvergentdir.
. Buna görə də silsilələr tamamilə konvergentdir.
Mütləq yaxınlaşan sıralar çoxaldıla bilər. Mütləq yaxınlaşan və yaxınlaşan sıranın hasili yaxınlaşır. İki konvergentin məhsulu ayrıla bilər.
Ölçü: px
Təəssürat səhifədən başlayın:
transkript
1 8 (S) ardıcıllığının mürəkkəb ədədi S seriyası (46) silsilənin cəmi adlanır a k seriyası silsilənin -ci qalığı adlanır (46) Konvergent k seriyası S S r və lm r üçün həmin ε > N, N: r< ε Для сходящегося ряда (46) необходимым и достаточным признаком его сходимости является критерий Коши: ряд (46) сходится тогда и только тогда, если ε >, N, N: a< ε p k k Необходимым условием сходимости ряда (46) является требование lm a Действительно, из сходимости ряда (46) следует, согласно критерию Коши, что ε >, N > ki, p üçün, S S gəlir< ε Если сходится ряд ak k a (47) с действительными положительными членами, то очевидно, сходится и ряд (46), который в этом случае называется абсолютно сходящимся А для ряда (47) уже можно применить признаки Даламбера и Коши: ряд (47) сходится, если, начиная с a некоторого номера N соотношение l < a, N значит, сходится абсолютно ряд (46)), если a q <, N k ; и ряд (47) сходится (а,
2 9 Funksiyalar silsiləsi və onların xassələri Vahid yaxınlaşma Veyerştrass teoremi Birqiymətli funksiyaların sonsuz ardıcıllığı ((Z)) kompleks müstəvisinin G sahəsində müəyyən edilsin ((Z)) U U formasının ifadəsi (48) funksional sıra adlandırılacaq (48) seriyası G oblastında konvergent adlanır, əgər Z G ona uyğun gələn ədəd seriyası yaxınlaşırsa, əgər (48) seriyası G bölgəsində yaxınlaşırsa, onda bu bölgədə bir-birini təyin etmək olar. G bölgəsinin hər bir nöqtəsindəki qiyməti G bölgəsindəki müvafiq ədəd seriyasının (48) cəminə bərabər olan qiymətli funksiyadır. Sonra G, > k () U k()< ε Заметим, что в общем случае N зависит и от ε и от Определение Если ε >, N(ε), N(ε): ε, N (ε,), N(ε,) : G k U k sahəsi< ε G, то ряд (48) называется равномерно сходящимся в k k Если остаток ряда обозначить r U, то тогда условие равномерной сходимости ряда (48) можем записать в виде: r < ε, N(ε), G Достаточным признаком равномерной сходимости ряда (48) является признак Вейерштрасса: Если всюду в области G члены функционального ряда (48) могут быть мажорированы членами некоторого абсолютно сходящегося числового ряда a, те
3 a U, G, (49) sonra (48) silsiləsi vahid şəkildə yaxınlaşır N Həqiqətən, a seriyası yaxınlaşdığından, sonra >< ε, U U a < ε при N, что и доказывает равномерную k k k k k k сходимость ряда (48) в области G Приведем некоторые теоремы о равномерно сходящихся рядах Они доказываются совершенно также, как соответствующие теоремы вещественного анализа и поэтому приведем их без доказательства Теорема 5 Если функции U непрерывны в области G, а ряд U сходится в этой области равномерно к функции, то также непрерывна в G Теорема 6 Если ряд (48) непрерывных функций U сходится равномерно в области G к функции, то интеграл от этой функции по любой кусочногладкой кривой, целиком лежащей в области G, можно вычислить путем почленного интегрирования ряда (48), те Теорема 7 Если члены d U d U сходящегося в области G ряда U имеют непрерывные производные в этой области и ряд U равномерно сходится в G, то данный ряд U можно почленно дифференцировать в области G, причем U U, где U - сумма ряда
4 Kompleks analizdə funksional silsilələr üçün real analizdən məlum olan funksional silsilənin müddət üzrə diferensiallaşdırılmasının mümkünlüyü haqqında teoremi əhəmiyyətli dərəcədə gücləndirməyə imkan verən Veyerştrass teoremi mövcuddur.Bunu bəyan etməzdən və sübut etməzdən əvvəl qeyd edirik. ki, l xətti boyunca bərabər yaxınlaşan U seriyası bütün şərtlərini l ilə məhdudlaşan ϕ funksiyasına vurduqdan sonra bərabər qalır.< M Тогда для остатков ρ и r рядов U и U ϕ справедливо соотношение ϕ U U r < M r ρ ϕ ε и, тк N, >N:r< и одновременно с ним ρ < ε, то этим доказано M высказанное утверждение Если сумма данного ряда есть S, то сумма ряда, полученного после умножения на ϕ, очевидно будет ϕ S Теорема 8 (Вейерштрасса) Если члены ряда - аналитические в некоторой области G функции и этот ряд сходится в области G равномерно, то его сумма также является функцией аналитической в G, ряд можно почленно дифференцировать и полученный ряд F равномерно сходится к () F Выберем любую внутреннюю точку области G и построим круг столь малого радиуса с центром в этой точке, чтобы он целиком лежал внутри G (рис) В силу равномерной сходимости данного ряда в G, G ρ Рис он, в частности, равномерно сходится на окружности этого круга Пусть - любая точка на Умножим ряд () () () () () (5) на величину Полученный ряд
5 eyni zamanda onun cəminə () () () () () yaxınlaşır, çünki (5) funksiyası məhduddur, çünki bu çevrənin nöqtələri üçün ρ çevrənin radiusudur (xatırlayın: - burada sabitdir) Onda , yuxarıda göstərilənlərə əsasən, (5) seriyası termin üzrə inteqrasiya oluna bilər: () d () d () d d π π π π Funksiyaların analitikliyinə görə, Koşi düsturu onlara əsasən tətbiq oluna bilər. ondan () d π, (5) alırıq və (5)-də sağdakı sıraların cəmidir və buna görə də Tk nöqtəsində - G sahəsinin istənilən nöqtəsində π () d bərabərliyini əldə edirik, onda teoremin birinci hissəsi isbat edilir. alırıq ki, silsilələr bərabər yaxınlaşır və onun cəmi (k) (k) -ə bərabərdir.
Formanın 6 seriyası burada Güc seriyası Abel teoremi Ümumi funksional sıraların çox mühüm halı dərəcə seriyaları (), (53) - bəzi kompleks ədədlər və - kompleks müstəvinin sabit nöqtəsidir. seriya, əvvəlkilərin ümumi teoremləri bölmələr tətbiq oluna bilər.Onlarda təsbit olunduğu kimi bir çox xassələr vahid yaxınlaşmanın nəticəsidir.(53) qüvvələr sırasının yaxınlaşma bölgəsini təyin etmək üçün aşağıdakı teorem vacib olur.Teorem 9 (Abel) Əgər güc seriyası (53) müəyyən nöqtədə yaxınlaşır, sonra mütləq və şərti ödəyən istənilən nöqtədə, üstəlik, dairədə birləşir.< ρ, радиусом ρ, меньшим < сходится равномерно, ряд Δ Выберем произвольную точку, удовлетворяющую условию < Обозначим q сходимости ряда следовательно M >, ki M, q< В силу необходимого признака его члены стремятся к нулю при, отсюда () M M q M, Тогда, где q < (54) Ряд справа в (54) бесконечно убывающая геометрическая прогрессия со знаменателем q < Тогда из (54) следует сходимость и рассматриваемого ряда
7p< достаточно в силу признака Вейерштрасса (53) В круге построить сходящийся числовой ряд, можорирующий данный ряд в рассматриваемой области Очевидно, таковым является ряд ρ M, также представляющий собой сумму бесконечной геометрической прогрессии со знаменателем, меньшим единицы Из теоремы Абеля можно вывести ряд следствий, в известной мере аналогичным следствиям из теоремы Абеля в теории степенных рядов вещественного анализа Если степенной ряд (53) расходится в некоторой точке, то он расходится и во всех точках, удовлетворяющих неравенству >(53) sırasının yaxınlaşdığı nöqtədən nöqtəyə qədər olan məsafələrin dəqiq yuxarı həddi güc sıralarının yaxınlaşma radiusu və bölgə adlanır.<, называется кругом сходимости степенного ряда В точках границы ряд может как сходиться так и расходиться Пример Найти область сходимости ряда Δ Находим радиус сходимости по признаку Даламбера lm () и наш ряд сходится в круге < При <, те, исследуется особо В этом случае и, значит, областью абсолютной сходимости является
8p< В круге любого радиуса ρ, меньшего чем радиус сходимости, степенной ряд (53) сходится равномерно 3 Внутри круга сходимости степенной ряд сходится к аналитической функции В самом деле, члены ряда u есть функции, аналитические на всей плоскости Z, ряд сходится в любой замкнутой подобласти круга сходимости Тогда по теореме Вейерштрасса сумма ряда есть аналитическая функция 4 Степенной ряд внутри круга сходимости можно почленно интегрировать и дифференцировать любое число раз, причем радиус сходимости полученных рядов равен радиусу сходимости исходного ряда 5 Коэффициенты степенного ряда (53) находятся по формулам! () () (55) Доказательство этого факта приводится методами, аналогичными методам вещественного анализа Ряд Тейлора Теорема Тейлора Нули аналитических функций Итак степенной ряд внутри круга сходимости определяет некоторую аналитическую функцию Возникает вопрос: можно ли функции, аналитической внутри некоторого круга, сопоставить степенной ряд, сходящийся в этом круге к данной функции? < Теорема 9 (Тейлора) Функция, аналитическая внутри круга, может быть представлена в этом круге сходящимся степенным рядом, причем этот ряд определен однозначно
9 ρ ρ çevrəsində ixtiyari bir nöqtə seçək< и построим окружность ρ точке радиусом < с центром в ρ (рис), содержащую точку внутри Такое построение возможно для любой точки внутри этого круга Так как < ρ, а внутри круга < Рис аналитична, то по формуле Коши имеем π ρ () d (56) Преобразуем подынтегральное выражение: (57) <, то < Так как Поэтому второй сомножитель справа в (57) можно представить как сумму степенного ряда (прогрессии), ту которая первый член есть, а знаменатель прогрессии есть Так как, те () () (58) ρ, то ряд (58) сходится равномерно по, так как он мажорируется сходящимся числовым рядом Подставляя (58) в (56) и интегрируя почленно, получаем ρ (< ρ)
10 () d () ρ π () d () π ρ () qeydini təqdim edək və (59) seçilmiş nöqtədə yaxınlaşan dərəcə sırası kimi yenidən yazaq: (59) (6) () (6) Düsturda (6) ρ məhəlləsi Koşi teoreminə əsasən bölgədə yerləşən istənilən qapalı konturla əvəz edilə bilər.< и содержащим точку внутри Так как - произвольная точка данной области, то отсюда следует, что ряд (6) сходится к круге ρ < этот ряд сходится равномерно Итак, функция всюду внутри круга < аналитическая внутри круга <, причем в разлагается в этом круге в сходящийся степенной ряд Коэффициенты разложения (6) на основании формулы Коши для производных аналитической функции имеет вид () d () π ρ () ()! (6) Для доказательства единственности разложения (6) допустим, что имеет еще место формула разложения (), (6)
11 burada da bir əmsal olacaqdır<, поэтому на основании формулы (55) Ряд (6) сходящимся в круге () () (6) Тем самым единственность определения коэффициентов доказана Разложение функции, аналитической в круге! <, что совпадает с, в сходящийся степенной ряд (6), часто называется разложением Тейлора, а сам ряд (6) Рядом Тейлора Доказанная теорема устанавливает взаимнооднозначное соответствие между функцией, аналитической в окрестности некоторой точки и степенным рядом с центром в этой точке, это означает эквивалентность конкретной аналитической функции, как функции бесконечное число раз дифференцируемой и функцией, представимой в виде суммы степенного ряда G и Заметим, наконец, что, если функция является аналитической в области G - внутренняя точка, то радиус сходимости ряда Тейлора () () () этой функции не меньше расстояния от точки до! границы области G (имеется в виду ближайшее расстояние) Пример Разложить в ряд Тейлора по степеням Δ Эта функция является аналитической на всей комплексной плоскости за исключением точек, Поэтому в круге < функция может быть ± разложена в ряд Тейлора При условии < выражение рассматриваться как сумма бесконечно убывающей прогрессии может q, q < Поэтому
12 , < Пример 3 Найти разложение в ряд Тейлора в круге < Определение по формуле (6) здесь довольно затруднительно Поэтому, представим π Так как < и <, то, используя геометрическую, получаем q q, Используя показательную форму чисел и находим окончательно 4 s π (63) Тк расстояние от центра разложения до ближайших особых точек (те до границы аналитичности) есть, то радиус сходимости ряда (63) есть Рис X Y
13 4 4 3 Nümunə<, 4 3 < Ближайшей к центру разложения особой точкой является точка, до которой расстояние равно, поэтому В заключение приведем основные разложения: e (<)!! 3! cos! 4 3 4! ; (<)! ; s () m 3 3! 5 5! m m m!! (<) ()! ; m(m)(m)! ; l 3 3 () 4 (<) Если для аналитической функции (), то точка называется нулем аналитической функции В этом случае разложение функции в ряд Тейлора в окрестности точки имеет вид () () тк () Если в разложении функции окрестности точки и, следовательно, разложение имеет вид, в ряд Тейлора в,
14 onda () (), (64) nöqtəsi funksiyanın sıfırı adlanır Əgər, onda sıfır düzülüş və ya çoxluq adi adlanırsa Teylor seriyasının əmsalları üçün düsturlardan görürük ki, əgər nöqtə ardıcıllığın sıfırı, onda () () şəklində yenidən yazmaq olar, lakin () () () [ () ] () ϕ, ϕ () (), () ϕ və yaxınlaşma dairəsi Bu seriya açıq şəkildə (64) seriyası ilə eynidir, burada formanın hər hansı funksiyası tam ədəddir, ϕ () və nizamın sıfırı sıfırdır və (±) Misal 6 Funksiya üçün sıfırın sırasını tapın. 8 s Məxrəci güclərdə genişləndirin: 3 3! 8 5 5! ! 5! 3! 5 5! ϕ
15 5 ϕ, burada ϕ, və ϕ və 3! funksiyasının nöqtəsi, belə ki, 5 nöqtəsi! ϕ analitikdir orijinal Laurent seriyası və onun yaxınlaşma bölgəsi üçün 5-ci dərəcəli sıfırdır. Laurent seriyasında analitik funksiyanın parçalanması. Formanın bir sırasını nəzərdən keçirək () burada kompleks müstəvinin sabit nöqtəsi, (65) bəzi mürəkkəb ədədlərdir.Gəlin onun yaxınlaşma sahəsini təyin edək.Bunun üçün (65) hansısa radiuslu bir nöqtədə mərkəzləşdirilmiş formada təmsil edirik və xüsusilə, o, sıfıra və ya sonsuzluğa bərabər ola bilər. yaxınlaşma, bu sıra mürəkkəb dəyişənin bəzi analitik funksiyasına yaxınlaşır, bunlar (),< (67)
16 Dəyişənlər silsiləsinin yaxınlaşma bölgəsini müəyyən etmək üçün () () təyin olunarsa, onda bu sıra əvəz edək formasını alacaq - kompleksi olan bəzi analitik funksiya ϕ () yaxınlaşma dairəsi daxilində adi güc seriyası. dəyişən Nəticə qüvvələr sırasının yaxınlaşma radiusu r olsun Onda ϕ,< r Возвращаясь к старой переменной и полагая ϕ () () (68), >r Buradan belə çıxır ki, silsilənin yaxınlaşma bölgəsi, r çevrəsindən kənar bölgə, (69) () alırıq.<, то существует общая область сходимости этих рядов круговое кольцо r < <, в которой ряд (65) сходится к аналитической функции (), r < < (7) Так как ряды (67) и (68) являются обычными степенными рядами, то в указанной области функция обладает всеми свойствами суммы степенного ряда Это означает, что ряд Лорана сходится внутри своего кольца сходимости к некоторой функции, аналитической в данном кольце
17 Əgər r > olarsa, onda (67) və (68) sıralarının ümumi yaxınlaşma bölgəsi yoxdur, beləliklə, bu halda (65) seriyası heç bir yerdə heç bir funksiyaya yaxınlaşmır Qeyd edək ki, silsilənin nizamlı hissəsidir. seriya (7) və Nümunə 7 Genişləndirin - seriyanın əsas hissəsi (65) () a)< < ; б) >; V)< < называется правильной частью или в ряд Лорана в кольцах: Во всех кольцах функция регулярна (аналитична) и поэтому может быть представлена рядом Лорана (доказательство этого факта в следующем пункте) Перепишем функцию в виде а) Так как <, то второе слагаемое есть сумма убывающей геометрической прогрессии Поэтому () Здесь главная часть состоит из одного слагаемого < б) в этом случае, поэтому () 3
18 Bu genişlənmənin müntəzəm hissəsi yoxdur< в) Для случая < функцию также надо привести к сходящейся геометрической прогрессии, но со знаменателем Это даст: 3 Заметим, что в главной части этого разложения присутствует одно слагаемое Возникает вопрос: можно ли функции аналитической в некотором круговом кольце, сопоставить ряд Лорана, сходящийся к этой функции в данном кольце? На этот вопрос отвечает Теорема Функция, аналитическая в круговом кольце < <, однозначно представляется в этом кольце сходящимся рядом Лорана дробь На Рис 3 Δ Зафиксируем произвольную точку внутри данного кольца и контурами окружности и с центром в, радиусы которых удовлетворяют условиям < < < < < (рис 3) Согласно формуле Коши для многосвязной области имеем π () d () выполняется неравенство q, можно представить в виде d (7) Поэтому
19 (7) -dəki sıraların vahid yaxınlaşması sayəsində mümkün olan müddət üzrə inteqrasiya aparırıq, d π, (7) alırıq, burada d π, (73) (7) π olar. π d d, (d üçün), (74) burada d π (75) (75) inteqrasiya istiqamətini dəyişdirərək, alırıq
20 π () () d ()() d π, > (76) Dairəvi halqada (73) və (76) inteqranlarının analitikliyinə görə< < в соответствии с теоремой Коши значения интегралов не изменятся при произвольной деформации контуров интегрирования в области аналитичности Это позволяет объединить формулы (73) и (76): π () d (), ±, ±, (77) где - произвольный замкнутый контур, лежащий в указанном кольце и содержащий точку внутри Возвратимся теперь к формуле (7), получим где коэффициенты () (), (78) () для всех определяются однообразной формулой (77) Так как - люба точка кольца < <, то отсюда следует, что ряд (78) сходится к внутри данного кольца причем в замкнутом кольце < < ряд сходится к равномерно Доказательство единственности разложения (78) опускаем Из полученных результатов следует, что областью сходимости ряда (78) Лорана является круговое кольцо < <, на границах которого имеется хотя бы по одной особой точке аналитической функции ряд (78), к которой сходится Замечание Формула (77) для определения коэффициентов разложения в ряд Лорана (78) не всегда практически удобна Поэтому часто прибегают к разложению рациональной дроби на простейшие с использованием геометрической прогрессии, а также используют разложение в ряд Тейлора элементарные функции Приведем примеры
21 Nümunə 8 Δ-da ()() nöqtəsinin yaxınlığında Laurent seriyasını (güc sahibi olanlar) Y genişləndirin. mərkəzsiz”< < ; Рис 4 X б) внешность круга >Bu halqaların hər birində analitikdir və sərhədlərdə tək nöqtələrə malikdir. Gəlin bu bölgələrin hər birində səlahiyyətlərdə funksiyanı genişləndirək)< < ; ; [ () () () ] () < Этот ряд сходится, так как Так что ()() () () () (), ; >) Burada bizdə 3 var, () () () () () konvergent sıradır, çünki<
22 s Nəticə olaraq ()() () () olanlar, 3, 3 Nümunə 9 Laurent sırasında Δ funksiyasını nöqtənin yaxınlığında genişləndirin Bizdə:, s s s cos cos s s! cos 4 () () 3 4! 3! () 5! () (scos)!! 5
Mövzu Mürəkkəb ədədlər seriyası A formalı kompleks ədədləri olan k ak ədəd sırasını nəzərdən keçirək, əgər onun qismən cəmlərinin S a k k ardıcıllığı yaxınlaşırsa, sıra konvergent adlanır. Üstəlik, ardıcıllığın limiti S
Mövzu Funksional komplekslər seriyası Tərif. Əgər G. sahəsində yaxınlaşan k, N, N U k G eyni vaxtda ödənilirsə, o zaman sıra vahid adlanır.Serialın vahid yaxınlaşması üçün kafi meyar kriteriyadır.
MÜHAZİrə N37. Analitik funksiyalar seriyası. Qüvvət seriyasında analitik funksiyanın parçalanması. Taylor seriyası. Laurent seriyası..Qüvvət seriyasında analitik funksiyanın genişləndirilməsi.....Taylor seriyası.... 3.Analitikin genişləndirilməsi.
Modul Mövzu Funksiya ardıcıllıqları və seriyaları Ardıcıllıqların və silsilənin vahid yaxınlaşmasının xassələri Güc seriyaları Mühazirə Funksiya ardıcıllıqlarının və sıralarının tərifləri Vahid
Mühazirə 7 Taylor və Laurent seriyası 7. Taylor seriyası Bu hissədə biz görəcəyik ki, güc seriyası və analitik funksiya anlayışları eyni obyekti təyin edir: müsbət yaxınlaşma radiusuna malik istənilən güc seriyası.
Riyazi analiz Bölmə: Mürəkkəb dəyişənin funksiyaları nəzəriyyəsi Mövzu: Kompleks müstəvidə silsilələr Müəllim Yanuşçik O.V. 217 9. Mürəkkəb müstəvidə sıra 1. Ədədi sıra Ardıcıllıq olsun
5 Qüvvət seriyası 5 Qədər seriyası: tərifi, yaxınlaşma oblastı (a + a) + a () + K + a () + K a) (, (5) ədədlərinin dərəcə sıraları adlanır.
Federal Təhsil Agentliyi Moskva Dövlət Geodeziya və Kartoqrafiya Universiteti (MIIGAiK) ALİ RİYAZİYYAT kursu üzrə MÜSTƏQİL İŞ ÜÇÜN METODOLOJİ TƏLİMATLAR VƏ TAPŞIQLAR
Funksiyalar seriyası Mühazirələr 7-8 1 Konvergensiya sahəsi 1 Funksiyaların müəyyən intervalda təyin olunduğu u () u () u () u (), 1 2 u () formalı sıra funksional sıra adlanır. Bütün nöqtələrin dəsti
MÜHAZİrə N38. Sonsuzluqda analitik funksiyanın davranışı. xüsusi nöqtələr. Funksiya qalıqları..sonsuzluqda nöqtənin qonşuluğu.....Sonsuzluqda nöqtənin qonşuluğunda Laurent genişlənməsi.... 3. Davranış
RUSİYA FEDERASİYASININ TƏHSİL VƏ ELM NAZİRLİYİ Milli Tədqiqat Nijni Novqorod Dövlət Universiteti N.İ.Lobaçevski adına N.P.Semerikova A.A.Dubkov AA Xarçeva ANALİTİK FUNKSİYALAR SERİSİ
Belarus Respublikası Təhsil Nazirliyi Vitebsk Dövlət Texnoloji Universiteti Mövzu. Nəzəri və tətbiqi riyaziyyat kafedrası “Sətirlər”. Dos tərəfindən hazırlanmışdır. E.B. Dunina. Əsas
V.V. Juk, A.M. Kamachkin 1 güc seriyası. Konvergensiya radiusu və yaxınlaşma intervalı. Konvergensiyanın təbiəti. İnteqrasiya və fərqləndirmə. 1.1 Konvergensiya radiusu və yaxınlaşma intervalı. Funksional diapazon
Mövzu Laurent seriyası və onun yaxınlaşma sahəsi. n C n n C n n n n C n n formasının bir sırasını nəzərdən keçirək, burada kompleks müstəvinin sabit nöqtəsi, bəzi kompleks ədədlərdir. C n Bu seriya Laurent seriyası adlanır.
MÜHAZİrə N 7 .Güc
Riyazi analiz Bölmə: Ədədi və funksional silsilələr Mövzu: Güc seriyası. Güc seriyasında funksiyanın genişləndirilməsi Müəllim Rozhkova S.V. 3 g 34. Güc seriyası
4 Analitik funksiyalar silsiləsi 4. Funksional ardıcıllıqlar Ω C və f n olsun: Ω C. Funksiyalar ardıcıllığı (f n) nöqtə istiqamətində f funksiyasına yaxınlaşır: Ω C, əgər hər bir z Ω lim n f n(z) = f(z) olarsa.
Funksional silsilələr Funksional sıralar onun cəmi və funksional sahəsi o Həqiqi və ya kompleks ədədlərin Δ bölgəsində k (k 1) funksiyalarının ardıcıllığı verilsin.
Dosent Musina MV tərəfindən hazırlanmış mühazirələr Tərif Formanın ifadəsi Ədədi və funksional sıra Ədədi sıralar: əsas anlayışlar (), burada nömrələr seriyası (və ya sadəcə seriya) adlanır.
Ədədi sıra Ədədi ardıcıllıq Opr Ədədi ardıcıllıq x natural ədədlər çoxluğunda müəyyən edilmiş ədədi funksiyadır - ardıcıllığın ümumi üzvü x =, x =, x =, x =,
Ch Güc seriyası a a a a a a a a () formasında olan sıra dərəcə sırası adlanır, burada, a, sabitlərdir, seriyanın əmsalları adlanır.Bəzən daha ümumi formalı qüdrət silsiləsi hesab olunur: a a (a) a () a) a (a) (), harada
Mühazirə 8 Seriyalar və tək nöqtələr. Laurent seriyası. İzolyasiya edilmiş tək nöqtələr. 6. Sıralar və tək nöqtələr 6.7. Laurent seriyası teoremi (P. Laurent): Əgər f() funksiyası r halqasında analitikdirsə< a < R r R то она может быть разложена
Federal Təhsil Agentliyi Ali Peşəkar Təhsil Federal Dövlət Təhsil Müəssisəsi Cənub FEDERAL UNİVERSİTETİ R. M. Gavrilova, G. S. Kostetskaya Metodik
Mövzu 9 Güc seriyası Qüvvət seriyası formanın funksional sırasıdır, ədədlər isə ... seriyanın əmsalları və seriyanın genişlənmə nöqtəsidir., ..., ... R ... adlanır. mərkəz Güc seriyası Güc seriyasının ümumi termini
4 Funksiya seriyası 4 Əsas təriflər Ümumi oblast X u), u (), K, u (),K (TƏDİQİ İfadə u) + u () + K + u () + olan sonsuz funksiyalar ardıcıllığı olsun.
Mühazirə 3 Taylor və Maclaurin seriyası Güc seriyalarının tətbiqi Funksiyaların güc seriyalarına genişləndirilməsi Taylor və Maclaurin seriyası Tətbiqlər üçün verilmiş funksiyanı güc seriyasına, həmin funksiyalara genişləndirə bilmək vacibdir.
Mühazirə 6 Qüdrət silsiləsində funksiyanın genişləndirilməsi Genişlənmənin unikallığı Teylor və Maklaurin silsiləsi Bəzi elementar funksiyaların dərəcə seriyasında genişlənmə Qüdrət seriyalarının tətbiqi Əvvəlki mühazirələrdə
Metallurgiya Fakültəsi Ali Riyaziyyat Bölümü
Laurent Seriyası Daha ümumi güc seriyaları z z 0-ın həm müsbət, həm də mənfi səlahiyyətlərini ehtiva edən sıralardır. Teylor seriyası kimi onlar da analitik funksiyalar nəzəriyyəsində mühüm rol oynayırlar.
Seriya Ədədi sıra Ümumi anlayışlar Def Hər bir natural ədədə müəyyən qanuna uyğun olaraq müəyyən ədəd verilirsə, nömrələnmiş ədədlər çoxluğuna ədədi ardıcıllıq deyilir,
S A Lavrenchenko wwwlwrecekoru Mühazirə Funksional silsilələr Funksional silsilənin anlayışı Əvvəllər biz ədəd seriyalarını öyrənirdik, yəni sıra üzvləri ədədlər idi.İndi isə funksional sıraların öyrənilməsinə müraciət edirik, yəni.
Mövzu Laurent seriyası və onun yaxınlaşma sahəsi. Müstəvinin C (z z) n = C (z z) n + n n n= n= z-nin C n kompleksinin sabit nöqtəsi olduğu formalı sıra Laurent seriyası adlanır. C n (z z) n= - bəzi komplekslər
Mühazirə. funksional sıralar. Funksiya sıralarının tərifi Üzvləri x-in funksiyaları olan sıra funksional sıra adlanır: u = u (x) + u + K+ u + K = x x-in müəyyən qiymətini verərək, biz
SERİYA NƏZƏRİYYƏSİ Sıralar nəzəriyyəsi riyazi analizin ən mühüm komponentidir və həm nəzəri, həm də çoxsaylı praktik tətbiqlər tapır. Ədədi və funksional sıraları fərqləndirin.
Konvergensiya radiusu Tərif. Qüdrət seriyası c 0 + c (t a) + c 2 (t a) 2 + + c (t a) + = c (t a), () şəklində olan funksional sıradır, burada c 0, c, c 2,.. ., c, ... C gücün əmsalları adlanır
MOSKVA DÖVLƏT TEXNIKİ UNİVERSİTETİ V.M. Lyubimov, E.A. Jukova, V.A. Uxova, Yu.A. Şurinov
82 4. Bölmə 4. Funksional və güc seriyası 4.2. Dərs 3 4.2. Dərs 3 4.2.. Funksiyanın Taylor genişləndirilməsi TƏSVİR 4.2.. y = f(x) funksiyası bəzi qonşuluqda sonsuz diferensiallana bilsin.
Mühazirə. Güc seriyası. Harmonik analiz; seriyası və Furye çevrilməsi. Ortoqonallıq xassəsi.8. Ümumi funksional sıra.8.. Funksiyalardan yayınma U + U + U seriyası funksional sıra adlanır, əgər onun
Starkov V.N. Giriş mühazirəsi üçün materiallar Sual 9. Qüvvət sıralarında analitik funksiyaların parçalanması Tərif. Formanın funksional seriyası (((... (..., burada kompleks sabitlər (seriyanın əmsalları
Sgups Ali Riyaziyyat Departamenti tipik bir hesablamanın həyata keçirilməsi üçün təlimatlar "Satırlar" Novosibirsk 006 Bəzi nəzəri məlumatlar Rəqəmsal seriyası Let u ; u ; u ; ; u ; sonsuz sayda var
E işğalı. Taylor sıraları. Mat güc seriyasının yekunu. təhlil, proqram. Riyaziyyat, 3-cü semestr Funksiyanın dərəcələrdə dərəcə sırasına genişlənməsini tapın, dərəcələrin yaxınlaşma radiusunu hesablayın: A f()
Fəsil seriyası Müəyyən ədədi ardıcıllığın üzvlərinin cəminin formal qeydi Ədədi sıra ədədi sıra adlanır Cəmlər S seriyanın qismən cəmi adlanır Limit S, S limiti varsa, o zaman sıra
Təcrübə 8 Qalıq 8 Qalığın müəyyən edilməsi 8 Qalığın hesablanması 8 Loqarifmik qalığın 8 Qalığın təyin edilməsi
~ ~ FCF Kompleks dəyişən funksiyasının törəməsi Koşi-Riman şərtinin FCF FCF qanunauyğunluğu anlayışı Kompleks ədədin təsviri və forması FCF forması: burada iki dəyişənin real funksiyası realdır.
ALİ RİYAZİYYAT KURSU ÜZRƏ HESABLAMA TƏLİMATLARI ÜÇÜN METODOLOJİ TƏLİMATLAR “ADİ DİFFERENTİAL TƏNLİKLƏR SERISI QOŞ İNTEQRALLAR” III HİSSƏ MÖVZU SERİYA Mündəricat Seriya Ədədi silsilələr Konvergensiya və fərqlilik.
Federal Təhsil Agentliyi Arxangelsk Dövlət Texniki Universiteti İnşaat Mühəndisliyi Fakültəsi SERIES Müstəqil iş üçün tapşırıqları yerinə yetirmək üçün təlimatlar Arxangelsk
MÜRƏKKƏB DƏYİŞƏNƏN ƏMƏLİYYAT HESABININ FUNKSİYALARI NƏZƏRİYYƏSİNİN Elementləri.
Riyazi analiz Hissə 3. Ədədi və funksional sıra. Çoxsaylı inteqrallar. Sahə nəzəriyyəsi. dərslik N.D.Vysk MATI-RGTU im. K.E. Tsiolkovski Ali riyaziyyat kafedrası RİYASİ TƏHLİL
Mühazirə 3. Deduksiyalar. Əsas qalıq teoremi f () funksiyasının təcrid olunmuş a a nöqtəsində qalığı dairə boyu i müsbət istiqamətdə alınan f () 2 inteqralının qiymətinə bərabər kompleks ədəddir.
Rəqəm və güc seriyası Dərs. Nömrə xətləri. Sıra cəmi. Konvergensiya meyarları.Serialların cəmini hesablayın. 6 Qərar. Sonsuz həndəsi irəliləyişin hədlərinin cəmi q-dir, burada q irəliləyişin məxrəcidir.
S A Lavrenchenko wwwlawreceoru Mühazirə Funksiyaların Taylor seriyası ilə təmsil olunması Bir faydalı hədd Son mühazirədə aşağıdakı strategiya hazırlanmışdır: funksiyanın təmsil oluna bilməsi üçün kifayət qədər şərtlə,
M.V.Deykalova KOMPLEKS TƏHLİL İmtahan üçün suallar (qrup МХ-21, 215) Birinci kollokviumun sualları 1 1. Kompleks dəyişənli funksiyanın nöqtədə diferensiallaşması. Cauchy Riemann (D'Alembert Euler) şərtləri.
Variant Tapşırığı funksiyanın qiymətini hesablayın və cavabı cəbri formada verin: a sh ; b l Həlli a Triqonometrik sinus ilə hiperbolik sinus arasındakı əlaqə düsturundan istifadə edək: ; sh -s alın
Mühazirə Ədədi sıralar yaxınlaşma əlamətləri Ədədlər sırası yaxınlaşma əlamətləri Sonsuz birliyin üzvlərindən ibarət + + + + ədədi ardıcıllığın sonsuz ifadəsinə ədədi sıra deyilir.
4. Funksional silsilələr, yaxınlaşma sahəsi Funksional silsilənin yaxınlaşma sahəsi () bu seriyanın yaxınlaşdığı arqumentin dəyərlərinin çoxluğudur. (2) funksiyası sıranın qismən cəmi adlanır;
Mühazirə 3 Skayar tənliyin həlli üçün mövcudluq və təklik teoremi Problemin ifadəsi Əsas nəticə Koşi məsələsini nəzərdən keçirək d f () d =, () =
RUSİYA FEDERASİYASI TƏHSİL VƏ ELM NAZİRLİYİ KAZAN DÖVLƏT MEMARLIK VƏ İNŞAAT UNİVERSİTETİ Ali riyaziyyat fakültəsi ƏDƏDİ VƏ FONKSİYONEL SERİYALAR üçün Təlimatlar
(funksional silsilələr güc seriyalarının yaxınlaşma bölgəsi yaxınlaşma intervalının tapılması qaydası - misal yaxınlaşma intervalı radiusunun nümunələri) Funksiyaların sonsuz ardıcıllığı verilsin, Funksional
S A Lavrenchenko wwwlawrecekoru Mühazirə Funksiyaların dərəcə seriyaları ilə təmsil olunması Giriş Funksiyaların dərəcə seriyaları ilə təmsil olunması aşağıdakı məsələlərin həllində faydalıdır: - funksiyaların inteqrasiyası.
E işğalı. Güc seriyası. Taylor Series Mat. təhlil, proqram. Riyaziyyat, 3-cü semestr D'Alember kriteriyasından istifadə edərək dərəcə sırasının yaxınlaşma radiusunu tapın: (89 () n n (n!)) p (n +)! n= Teylor seriyası f(x)
RUSİYA FEDERASİYASI TƏHSİL VƏ ELM NAZİRLİYİ
SƏRƏLƏR. Nömrə xətləri. Əsas təriflər Sonsuz ədədlər ardıcıllığı verilsin (sonsuz cəm) a, a 2,..., a n,... a i = a + a 2 + + a n +... () i= ifadəsi a adlanır. nömrə seriyası. Nömrələri
KAZAN DÖVLƏT UNİVERSİTETİ Riyazi Statistika Kafedrası
Rusiya Federasiyasının Təhsil və Elm Nazirliyi V.A.Volkov FURİER İNTEQRALININ SERİSİ Tədris elektron mətn nəşri 4865 Fiziki qurğuların elektronikası və avtomatlaşdırılması ixtisaslarının tələbələri üçün;
џ. Nömrə seriyası anlayışı. a, a 2,..., a,... ədədlərinin ardıcıllığı verilsin Ədədlər seriyası a = a + a 2 +... + a +... (.) a, ədədləri ifadəsidir. a 2,.. ., a,... sıranın şərtləri adlanır, a
Metodik işlənmə TFKP üzrə məsələlərin həlli Kompleks ədədlər Kompleks ədədlər üzərində əməliyyatlar Mürəkkəb müstəvi Kompleks ədəd cəbri və triqonometrik eksponensialda göstərilə bilər.
Siberian Mathematical Journal İyul Avqust, 2005. Cild 46, 4 UDC 517.53 FUNKSİYALARDAN AYRILAN DÜZÜNLƏRDƏ İNTERPOLASİYON FRAKSİYALARININ YÖNÜŞMƏ ŞƏRTLƏRİ AG Lipchinsky Considered:
MOSKVA AVTOMOBİL VƏ YOL DÖVLƏT TEXNİKİ UNİVERSİTETİ (MADI)
Standart üsullar, lakin başqa bir nümunə ilə dalana çatdı.
Çətinlik nədir və harada tıxac ola bilər? Gəlin sabunlu ipi bir kənara qoyub, səbəbləri sakitcə təhlil edək və həllin praktiki üsulları ilə tanış olaq.
Birinci və ən vacib: halların böyük əksəriyyətində seriyanın yaxınlaşmasını öyrənmək üçün hansısa tanış metodu tətbiq etmək lazımdır, lakin seriyanın ümumi termini o qədər çətin doldurma ilə doludur ki, onunla nə edəcəyiniz heç də aydın deyil. . Və siz dairələrdə gəzirsiniz: birinci işarə işləmir, ikinci işləmir, üçüncü, dördüncü, beşinci üsul işləmir, sonra qaralamalar kənara atılır və hər şey yenidən başlayır. Bu, adətən hesablamanın digər bölmələrində təcrübənin olmaması və ya boşluqlarla bağlıdır. Xüsusilə, qaçarsanız ardıcıllıq məhdudiyyətləri və səthi şəkildə sökülüb funksiya məhdudiyyətləri, onda çətin olacaq.
Başqa sözlə, insan sadəcə olaraq bilik və təcrübə çatışmazlığı səbəbindən lazımi həll yolunu görmür.
Bəzən "tutulma" da günahkardır, məsələn, seriyanın yaxınlaşması üçün lazımi meyar sadəcə yerinə yetirilmədikdə, lakin məlumatsızlıq, diqqətsizlik və ya səhlənkarlıq səbəbindən bu gözdən qaçır. Və belə çıxır ki, riyaziyyat professoru vəhşi təkrarlanan ardıcıllıqlar və nömrələr seriyalarının köməyi ilə uşaq problemini həll etdiyi velosipeddəki kimi =)
Ən yaxşı ənənələrdə, dərhal canlı nümunələr: sıralar ![]() və onların qohumları - bir-birindən ayrılırlar, çünki nəzəri cəhətdən sübut edilmişdir ardıcıllıq məhdudiyyətləri. Çox güman ki, birinci semestrdə 1-2-3 səhifəlik bir sübuta görə ruhunuzdan döyüləcəksiniz, amma indi silsilələrin yaxınlaşması üçün lazımi şərtin yerinə yetirilmədiyini göstərmək kifayətdir. məlum faktlara. Məşhur? Tələbə n-ci dərəcənin kökünün son dərəcə güclü bir şey olduğunu bilmirsə, deməli, seriya
və onların qohumları - bir-birindən ayrılırlar, çünki nəzəri cəhətdən sübut edilmişdir ardıcıllıq məhdudiyyətləri. Çox güman ki, birinci semestrdə 1-2-3 səhifəlik bir sübuta görə ruhunuzdan döyüləcəksiniz, amma indi silsilələrin yaxınlaşması üçün lazımi şərtin yerinə yetirilmədiyini göstərmək kifayətdir. məlum faktlara. Məşhur? Tələbə n-ci dərəcənin kökünün son dərəcə güclü bir şey olduğunu bilmirsə, deməli, seriya ![]() onu darmadağın et. Həll iki və iki kimi olsa da: , yəni. məlum səbəblərə görə hər iki seriya bir-birindən ayrılır. "Bu məhdudiyyətlər nəzəri cəhətdən sübut edilmişdir" (və ya ümumiyyətlə olmaması) təvazökar bir şərh kompensasiya üçün kifayətdir, axırda hesablamalar olduqca ağırdır və onlar mütləq ədədi seriyalar bölməsinə aid deyillər.
onu darmadağın et. Həll iki və iki kimi olsa da: , yəni. məlum səbəblərə görə hər iki seriya bir-birindən ayrılır. "Bu məhdudiyyətlər nəzəri cəhətdən sübut edilmişdir" (və ya ümumiyyətlə olmaması) təvazökar bir şərh kompensasiya üçün kifayətdir, axırda hesablamalar olduqca ağırdır və onlar mütləq ədədi seriyalar bölməsinə aid deyillər.
Növbəti nümunələri öyrəndikdən sonra bir çox həllərin qısalığına və şəffaflığına təəccüblənəcəksiniz:
Misal 1
Seriyanın yaxınlaşmasını araşdırın
Həll: ilk növbədə icranı yoxlayın konvergensiya üçün zəruri meyardır. Bu, formallıq deyil, “kiçik qan tökülməsi” misalı ilə məşğul olmaq üçün böyük şansdır.
“Səhnənin yoxlanılması” divergent sıra təklif edir (ümumiləşmiş harmonik silsilənin işi), lakin yenə sual yaranır ki, paylayıcıda loqarifmi necə nəzərə almaq olar?
Dərsin sonunda tapşırıqların təxmini nümunələri.
İki tərəfli (və ya hətta üç tərəfli) əsaslandırma aparmaq lazım olduqda nadir deyil:
Misal 6
Seriyanın yaxınlaşmasını araşdırın ![]()
Həll: birincisi, hesablayıcının mənasız sözləri ilə diqqətlə məşğul olun. Ardıcıllıq məhduddur: . Sonra: ![]()
Gəlin seriallarımızı seriallarla müqayisə edək. Yenicə əldə edilən ikiqat bərabərsizlik sayəsində bütün "en" üçün doğru olacaq: ![]()
İndi gəlin seriyanı divergent harmonik sıra ilə müqayisə edək.
Kəsrin məxrəci az kəsrin məxrəci, yəni fraksiyanın özü – daha çox fraksiyalar (əgər aydın deyilsə, ilk bir neçə şərti yazın). Beləliklə, hər hansı bir "en" üçün: ![]()
Beləliklə, müqayisə üçün serial ![]() ayrılır harmonik sıra ilə birlikdə.
ayrılır harmonik sıra ilə birlikdə.
Məxrəci bir az dəyişsək: ![]() , onda əsaslandırmanın birinci hissəsi oxşar olacaq:
, onda əsaslandırmanın birinci hissəsi oxşar olacaq: ![]() . Lakin seriyanın fərqliliyini sübut etmək üçün, bərabərsizlik yanlış olduğundan, yalnız müqayisənin limit testi artıq tətbiq olunur.
. Lakin seriyanın fərqliliyini sübut etmək üçün, bərabərsizlik yanlış olduğundan, yalnız müqayisənin limit testi artıq tətbiq olunur.
Yaxınlaşan sıralarla bağlı vəziyyət "güzgü"dür, yəni məsələn, sıra üçün həm müqayisə meyarından (bərabərsizlik doğrudur), həm də seriya üçün yalnız məhdudlaşdırıcı meyardan (bərabərsizlik yanlışdır) istifadə edilə bilər.
Zərif və şirəli antilopların üfüqdə göründüyü vəhşi təbiətdə safarimizə davam edirik:
Misal 7
Seriyanın yaxınlaşmasını araşdırın
Həll: zəruri yaxınlaşma meyarı təmin edilir və biz yenə klassik sualı veririk: nə etməli? Qarşımızda konvergent seriyaya bənzəyən bir şey var, lakin burada aydın bir qayda yoxdur - bu cür birləşmələr çox vaxt aldadıcı olur.
Tez-tez, amma bu dəfə deyil. İstifadə etməklə Limit müqayisə meyarı Gəlin seriyalarımızı konvergent sıra ilə müqayisə edək. Limiti hesablayarkən istifadə edirik gözəl hədd ![]() , Halbuki sonsuz kiçik dayanır:
, Halbuki sonsuz kiçik dayanır: 
birləşir yanında ilə birlikdə.
Standart süni “üç”ə vurma və bölmə texnikasından istifadə etmək əvəzinə, əvvəlcə yaxınlaşan sıra ilə müqayisə etmək mümkün idi.
Ancaq burada ümumi terminin sabit çarpanının seriyanın yaxınlaşmasına təsir etmədiyinə dair bir xəbərdarlıq arzu edilir. Və məhz bu üslubda aşağıdakı nümunənin həlli nəzərdə tutulmuşdur:
Misal 8
Seriyanın yaxınlaşmasını araşdırın
Dərsin sonunda nümunə.
Misal 9
Seriyanın yaxınlaşmasını araşdırın
Həll: əvvəlki misallarda biz sinusun məhdudluğundan istifadə etdik, lakin indi bu xüsusiyyət oyundan kənardır. Daha yüksək olan kəsrin məxrəci böyümə qaydası saydan çox, buna görə də sinus arqumenti və bütün ümumi müddət sonsuz kiçik. Konvergensiya üçün zəruri şərt, başa düşdüyünüz kimi, təmin edilir, bu da bizə işdən yayınmağa imkan vermir.
Kəşfiyyat aparacağıq: uyğun olaraq əlamətdar ekvivalentlik ![]() , zehni olaraq sinüs atmaq və bir sıra almaq. Yaxşı, belə bir şey ....
, zehni olaraq sinüs atmaq və bir sıra almaq. Yaxşı, belə bir şey ....
Qərar qəbul etmək:
Gəlin tədqiq olunan seriyaları fərqli seriyalarla müqayisə edək. Limit müqayisə meyarından istifadə edirik: 
Sonsuz kiçiki ekvivalentlə əvəz edək: üçün ![]() .
.

Sıfırdan başqa sonlu ədəd alınır, bu o deməkdir ki, tədqiq olunan sıra ayrılır harmonik sıra ilə birlikdə.
Misal 10
Seriyanın yaxınlaşmasını araşdırın
Bu, özünüz etməyin bir nümunəsidir.
Bu cür nümunələrdə sonrakı hərəkətləri planlaşdırmaq üçün sinus, arksinus, tangens, arktangensin zehni rədd edilməsi çox kömək edir. Ancaq unutmayın ki, bu imkan yalnız o zaman mövcuddur sonsuz kiçik arqument, çox keçməmiş təxribatçı bir seriala rast gəldim:
Misal 11
Seriyanın yaxınlaşmasını araşdırın ![]() .
.
Həll: burada qövs tangensinin məhdudluğundan istifadə etmək faydasızdır və ekvivalentlik də işləmir. Çıxış təəccüblü dərəcədə sadədir: 
Tədqiqat seriyası ayrılır, çünki silsilənin yaxınlaşması üçün lazımi meyar təmin olunmur.
İkinci səbəb"İşdə tıxac" texniki xarakterli çətinliklərə səbəb olan ümumi üzvün layiqli mürəkkəbliyindən ibarətdir. Kobud desək, yuxarıda müzakirə olunan silsilələr “təxmin etdiyiniz rəqəmlər” kateqoriyasına aiddirsə, bu, “sən qərar verərsən” kateqoriyasına aiddir. Əslində buna "adi" mənada mürəkkəblik deyilir. Hər kəs savannanın bir neçə faktorialını, dərəcələrini, köklərini və digər sakinlərini düzgün həll etməyəcək. Əlbəttə ki, faktorlar ən çox problem yaradır:
Misal 12
Seriyanın yaxınlaşmasını araşdırın
Faktorialı gücə necə qaldırmaq olar? Asanlıqla. Güclərlə əməliyyatlar qaydasına görə, məhsulun hər bir amilini bir gücə yüksəltmək lazımdır:
Və, əlbəttə ki, diqqət və diqqət, d'Alembert işarəsi özü ənənəvi olaraq işləyir: 
Beləliklə, öyrənilən seriya birləşir.
Mən sizə qeyri-müəyyənliyi aradan qaldırmaq üçün rasional texnikanı xatırladıram: aydın olduqda böyümə qaydası say və məxrəc - əziyyət çəkmək və mötərizələri açmaq heç də lazım deyil.
Misal 13
Seriyanın yaxınlaşmasını araşdırın
Heyvan çox nadirdir, amma tapılır və onu kamera obyektivi ilə yan keçmək ədalətsizlik olardı.
İkiqat nida faktorial nədir? Faktorial müsbət cüt ədədlərin hasilini "küləklər": 
Eynilə, faktorial müsbət tək ədədlərin hasilini “qurur”: 
Aralarındakı fərqin nə olduğunu təhlil edin
Misal 14
Seriyanın yaxınlaşmasını araşdırın
Və bu vəzifədə dərəcələrlə qarışmamağa çalışın, gözəl ekvivalentlər Və gözəl məhdudiyyətlər.
Dərsin sonunda nümunə həllər və cavablar.
Lakin tələbə təkcə pələngləri deyil, hiyləgər bəbirlər də ovlarını izləyir:
Misal 15
Seriyanın yaxınlaşmasını araşdırın ![]()
Həll: zəruri yaxınlaşma meyarı, məhdudlaşdırıcı kriteriya, d'Alembert və Koşi meyarları, demək olar ki, dərhal yox olur. Amma ən pisi odur ki, bizi dəfələrlə xilas edən bərabərsizliklərlə bağlı xüsusiyyət gücsüzdür. Həqiqətən, divergent sıra ilə müqayisə qeyri-mümkündür, çünki bərabərsizlik ![]() səhv - çarpan-loqarifm yalnız məxrəci artırır, fraksiyanın özünü azaldır
səhv - çarpan-loqarifm yalnız məxrəci artırır, fraksiyanın özünü azaldır ![]() kəsrə münasibətdə. Və başqa bir qlobal sual: niyə biz əvvəlcə serialımızın olduğuna əminik
kəsrə münasibətdə. Və başqa bir qlobal sual: niyə biz əvvəlcə serialımızın olduğuna əminik ![]() ayrılmağa məcburdur və bəzi divergent seriyalarla müqayisə edilməlidir? O, ümumiyyətlə uyğun gəlirmi?
ayrılmağa məcburdur və bəzi divergent seriyalarla müqayisə edilməlidir? O, ümumiyyətlə uyğun gəlirmi?
İnteqral xüsusiyyət? Yanlış inteqral ![]() qəmli əhval-ruhiyyə oyadır. İndi bir sıra olsaydı
qəmli əhval-ruhiyyə oyadır. İndi bir sıra olsaydı ![]() ... onda bəli. Dayan! İdeyalar belə yaranır. İki mərhələdə qərar veririk:
... onda bəli. Dayan! İdeyalar belə yaranır. İki mərhələdə qərar veririk:
1) Əvvəlcə sıraların yaxınlaşmasını öyrənirik ![]() . istifadə edirik ayrılmaz xüsusiyyət:
. istifadə edirik ayrılmaz xüsusiyyət:![]()
İnteqral davamlı haqqında

Beləliklə, bir nömrə ![]() uyğun olmayan inteqralla birlikdə ayrılır.
uyğun olmayan inteqralla birlikdə ayrılır.
2) Seriyalarımızı fərqli seriyalarla müqayisə edin ![]() . Limit müqayisə meyarından istifadə edirik:
. Limit müqayisə meyarından istifadə edirik:
Sıfırdan başqa sonlu ədəd alınır, bu o deməkdir ki, tədqiq olunan sıra ayrılır ilə yanaşı ![]() .
.
Və belə bir qərarda qeyri-adi və yaradıcı bir şey yoxdur - belə qərar verilməlidir!
Aşağıdakı iki hərəkəti müstəqil şəkildə tərtib etməyi təklif edirəm:
Misal 16
Seriyanın yaxınlaşmasını araşdırın ![]()
Təcrübəsi olan bir tələbə əksər hallarda seriyanın birləşdiyini və ya ayrıldığını dərhal görür, lakin bir yırtıcı kolluqda məharətlə gizlənir:
Misal 17
Seriyanın yaxınlaşmasını araşdırın ![]()
Həll: ilk baxışda bu serialın necə davrandığı heç də aydın deyil. Və əgər qarşımızda duman varsa, o zaman silsilənin yaxınlaşması üçün zəruri şərtin kobud yoxlamasından başlamaq məntiqlidir. Qeyri-müəyyənliyi aradan qaldırmaq üçün batmazdan istifadə edirik qoşma ifadə ilə vurma və bölmə üsulu:
Zəruri yaxınlaşma əlaməti işə yaramadı, amma Tambov yoldaşımızı üzə çıxardı. Görülən çevrilmələr nəticəsində ekvivalent sıra əldə edilmişdir ![]() , bu da öz növbəsində konvergent seriyaya çox bənzəyir.
, bu da öz növbəsində konvergent seriyaya çox bənzəyir.
Təmiz bir həll yazırıq:
Bu seriyanı konvergent sıra ilə müqayisə edin. Limit müqayisə meyarından istifadə edirik:
Əlavə ifadə ilə çarpın və bölün:

Sıfırdan başqa sonlu ədəd alınır, bu o deməkdir ki, tədqiq olunan sıra birləşir yanında ilə birlikdə.
Bəlkə bəzilərinin sualı var, qurdlar bizim Afrika safarimizdə haradan gəldi? bilmirəm. Yəqin ki, gətiriblər. Aşağıdakı kubok dərisini əldə edəcəksiniz:
Misal 18
Seriyanın yaxınlaşmasını araşdırın ![]()
Dərsin sonunda həll nümunəsi
Və nəhayət, ümidsizlik içində bir çox tələbəni ziyarət edən daha bir fikir: sıraların yaxınlaşması üçün daha nadir meyardan istifadə edib-etməmək əvəzinə? Raabe əlaməti, Abel əlaməti, Qauss əlaməti, Dirixlet əlaməti və digər naməlum heyvanlar. İdeya işləyir, amma real nümunələrdə çox nadir hallarda həyata keçirilir. Şəxsən mən bütün təcrübə illərində cəmi 2-3 dəfə müraciət etmişəm Raabe işarəsi standart arsenaldan heç bir şey həqiqətən kömək etmədikdə. Ekstremal axtarışımın gedişatını tam şəkildə təkrarlayıram:
Misal 19
Seriyanın yaxınlaşmasını araşdırın
Həll: Şübhəsiz ki, d'Alemberin əlaməti. Hesablamalar zamanı dərəcələrin xassələrindən də fəal şəkildə istifadə edirəm ikinci gözəl hədd:
Budur sizin üçün bir. D'Alemberin işarəsi cavab vermədi, baxmayaraq ki, belə bir nəticəni heç bir şey qabaqcadan göstərmədi.
Təlimatdan keçdikdən sonra mən nəzəri cəhətdən sübut edilmiş az tanınan bir limit tapdım və daha güclü radikal Koşi meyarını tətbiq etdim:
Budur sizin üçün iki. Və ən əsası, serialın yaxınlaşması və ya ayrılması heç də aydın deyil (mənim üçün olduqca nadir vəziyyətdir). Lazımi müqayisə əlaməti? Çox ümid etmədən - ağlasığmaz bir şəkildə say və məxrəcin böyümə qaydasını başa düşsəm də, bu yenə də mükafata zəmanət vermir.
Tam bir d'Alembert, amma ən pisi odur ki, serialın həlli lazımdır. Lazımdır. Axı bu, ilk dəfə imtina edəcək. Və sonra xatırladım ki, görünür, daha güclü əlamətlər var. Məndən əvvəl artıq canavar, bəbir və pələng yox idi. Bu, böyük gövdəsini yelləyən nəhəng bir fil idi. Mən qumbaraatan götürməli oldum:
Raabe işarəsi
Müsbət ədədlər seriyasını nəzərdən keçirək.
Limit varsa  , Bu:
, Bu:
a) Bir sıra ayrılır. Üstəlik, nəticədə alınan dəyər sıfır və ya mənfi ola bilər.
b) Bir sıra birləşir. Xüsusilə, seriyalar üçün birləşir.
c) Nə vaxt Raabenin işarəsi cavab vermir.
Həddini tərtib edirik və kəsri diqqətlə sadələşdiririk: 
Bəli, şəkil, yumşaq desək, xoşagəlməzdir, amma daha təəccüblənmədim. lopital qaydalar, və ilk fikir, sonradan göründüyü kimi, doğru çıxdı. Ancaq əvvəlcə, təxminən bir saat ərzində "adi" üsullardan istifadə edərək limiti bükdüm və çevirdim, lakin qeyri-müəyyənlik aradan qalxmaq istəmədi. Təcrübənin dediyi kimi, dairələrdə gəzmək səhv həll yolunun seçildiyinin tipik bir əlamətidir.
Mən rus xalq müdrikliyinə müraciət etməli oldum: "Heç bir şey kömək etmirsə, təlimatları oxuyun". Və Fichtenholtzun 2-ci cildini açanda böyük sevinclə eyni seriyanın tədqiqatını tapdım. Və sonra həll modelə uyğun olaraq getdi.