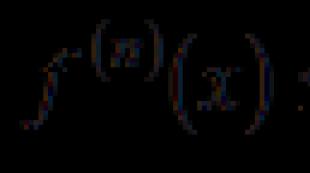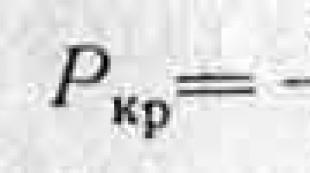الحرف

معادلة المستوى هي المسافة من نقطة إلى مستوى. المسافة من نقطة إلى الطائرة. طريق. طريقة المتجهات

الحفاظ على خصوصيتك مهم بالنسبة لنا. لهذا السبب، قمنا بتطوير سياسة الخصوصية التي تصف كيفية استخدامنا لمعلوماتك وتخزينها. يرجى مراجعة ممارسات الخصوصية الخاصة بنا وإعلامنا إذا كانت لديك أي أسئلة.

جمع واستخدام المعلومات الشخصية

تشير المعلومات الشخصية إلى البيانات التي يمكن استخدامها لتحديد هوية شخص معين أو الاتصال به.

قد يُطلب منك تقديم معلوماتك الشخصية في أي وقت عند الاتصال بنا.

فيما يلي بعض الأمثلة على أنواع المعلومات الشخصية التي قد نجمعها وكيف يمكننا استخدام هذه المعلومات.

ما هي المعلومات الشخصية التي نجمعها:

عند تقديم طلب على الموقع، قد نقوم بجمع معلومات مختلفة، بما في ذلك اسمك ورقم هاتفك وعنوان بريدك الإلكتروني وما إلى ذلك.

كيف نستخدم المعلومات الشخصية الخاصة بك:

تتيح لنا المعلومات الشخصية التي نجمعها الاتصال بك بشأن العروض الفريدة والعروض الترويجية وغيرها من الأحداث والأحداث القادمة.
من وقت لآخر، قد نستخدم معلوماتك الشخصية لإرسال إشعارات ومراسلات مهمة.
قد نستخدم أيضًا المعلومات الشخصية لأغراض داخلية، مثل إجراء عمليات التدقيق وتحليل البيانات والأبحاث المختلفة من أجل تحسين الخدمات التي نقدمها وتزويدك بالتوصيات المتعلقة بخدماتنا.
إذا شاركت في سحب جائزة أو مسابقة أو عرض ترويجي مماثل، فقد نستخدم المعلومات التي تقدمها لإدارة مثل هذه البرامج.

الكشف عن المعلومات لأطراف ثالثة

نحن لا نكشف عن المعلومات الواردة منك إلى أطراف ثالثة.

الاستثناءات:

إذا لزم الأمر - وفقًا للقانون، والإجراءات القضائية، وفي الإجراءات القانونية و/أو بناءً على الطلبات العامة أو الطلبات المقدمة من السلطات الحكومية في أراضي الاتحاد الروسي - للكشف عن معلوماتك الشخصية. يجوز لنا أيضًا الكشف عن معلومات عنك إذا قررنا أن هذا الكشف ضروري أو مناسب للأغراض الأمنية أو إنفاذ القانون أو أي أغراض أخرى ذات أهمية عامة.
في حالة إعادة التنظيم أو الدمج أو البيع، يجوز لنا نقل المعلومات الشخصية التي نجمعها إلى الطرف الثالث الذي يخلفه.

حماية المعلومات الشخصية

نحن نتخذ الاحتياطات - بما في ذلك الإدارية والفنية والمادية - لحماية معلوماتك الشخصية من الضياع والسرقة وسوء الاستخدام، بالإضافة إلى الوصول غير المصرح به والكشف والتغيير والتدمير.

احترام خصوصيتك على مستوى الشركة

للتأكد من أن معلوماتك الشخصية آمنة، نقوم بتوصيل معايير الخصوصية والأمان لموظفينا وننفذ ممارسات الخصوصية بشكل صارم.

تحديد المسافة بين: 1 - النقطة والمستوى؛ 2 - مستقيم ومسطح. 3 - الطائرات. 4 - يتم اعتبار عبور الخطوط المستقيمة معًا، نظرًا لأن خوارزمية الحل لجميع هذه المشكلات هي نفسها في الأساس وتتكون من إنشاءات هندسية يجب تنفيذها لتحديد المسافة بين نقطة معينة A والمستوى α. إذا كان هناك أي فرق، فهو يتكون فقط من حقيقة أنه في الحالتين 2 و 3، قبل البدء في حل المشكلة، يجب تحديد نقطة تعسفية A على الخط المستقيم m (الحالة 2) أو المستوى β (الحالة 3). المسافات بين الخطوط المتقاطعة، نحصرها أولاً في مستويين متوازيين α و β ثم نحدد المسافة بين هذه المستويات.

دعونا نفكر في كل حالة من الحالات المذكورة لحل المشكلات.

1. تحديد المسافة بين النقطة والمستوى.

يتم تحديد المسافة من نقطة إلى مستوى من خلال طول القطعة العمودية المرسومة من نقطة إلى المستوى.

ولذلك، فإن حل هذه المشكلة يتمثل في تنفيذ العمليات الرسومية التالية بشكل تسلسلي:

1) من النقطة A نخفض الخط العمودي على المستوى α (الشكل 269)؛

2) أوجد نقطة M تقاطع هذا العمودي مع المستوى M = a ∩ α؛

3) تحديد طول الجزء.

إذا كان المستوى α في وضع عام، فمن أجل خفض خط عمودي على هذا المستوى، فمن الضروري أولاً تحديد اتجاه الإسقاطات الأفقية والأمامية لهذا المستوى. يتطلب العثور على نقطة التقاء هذا العمودي مع المستوى أيضًا إنشاءات هندسية إضافية.

يتم تبسيط حل المشكلة إذا كانت الطائرة α تشغل موقعًا معينًا بالنسبة لمستويات الإسقاط. في هذه الحالة، يتم تنفيذ كل من إسقاط العمودي وإيجاد نقطة التقاءه بالمستوى دون أي إنشاءات مساعدة إضافية.

مثال 1. حدد المسافة من النقطة A إلى مستوى الإسقاط الأمامي α (الشكل 270).

حل. من خلال A" نرسم الإسقاط الأفقي للخط العمودي l" ⊥ h 0α، ومن خلال A" - إسقاطه الأمامي l" ⊥ f 0α. نحدد النقطة M" = l" ∩ f 0α . منذ صباحا || π 2، ثم [A" M"] == |AM| = د.

يتضح من المثال قيد النظر مدى بساطة حل المشكلة عندما تحتل الطائرة موضعًا بارزًا. لذلك، إذا تم تحديد مستوى موضع عام في البيانات المصدر، فقبل متابعة الحل، يجب نقل المستوى إلى موضع عمودي على أي مستوى إسقاط.

مثال 2. حدد المسافة من النقطة K إلى المستوى المحدد بواسطة ΔАВС (الشكل 271).

1. نقوم بنقل الطائرة ΔАВС إلى موضع الإسقاط *. للقيام بذلك، ننتقل من النظام xπ 2 /π 1 إلى x 1 π 3 /π 1: يتم اختيار اتجاه المحور x 1 الجديد بشكل عمودي على الإسقاط الأفقي للمستوى الأفقي للمثلث.

2. أسقط ΔABC على مستوى جديد π 3 (يتم إسقاط المستوى ΔABC على π 3، في [ C " 1 B " 1 ]).

3. قم بإسقاط النقطة K على نفس المستوى (K" → K" 1).

4. من خلال النقطة K" 1 نرسم (K" 1 M" 1) ⊥ القطعة [C" 1 B" 1]. المسافة المطلوبة d = |K" 1 M" 1 |

يتم تبسيط حل المشكلة إذا تم تحديد المستوى بواسطة آثار، حيث ليست هناك حاجة لرسم إسقاطات لخطوط المستوى.

مثال 3. حدد المسافة من النقطة K إلى المستوى α، المحددة بواسطة المسارات (الشكل 272).

* الطريقة الأكثر عقلانية لنقل مستوى المثلث إلى موضع الإسقاط هي استبدال مستويات الإسقاط، لأنه في هذه الحالة يكفي إنشاء إسقاط مساعد واحد فقط.

حل. نستبدل المستوى π 1 بالمستوى π 3، ولهذا نرسم محورًا جديدًا x 1 ⊥ f 0α. على h 0α نحدد نقطة عشوائية 1" ونحدد إسقاطها الأفقي الجديد على المستوى π 3 (1" 1). من خلال النقطتين X α 1 (X α 1 = h 0α 1 ∩ x 1) و 1" 1 نرسم h 0α 1. نحدد الإسقاط الأفقي الجديد للنقطة K → K" 1. من النقطة K" 1 نخفض العمودي على h 0α 1 ونحدد نقطة تقاطعه مع h 0α 1 - M" 1. سيشير طول المقطع K" 1 M" 1 إلى المسافة المطلوبة.

2. تحديد المسافة بين الخط المستقيم والمستوى.

يتم تحديد المسافة بين الخط والمستوى بطول القطعة المتعامدة التي تسقط من نقطة عشوائية على الخط إلى المستوى (انظر الشكل 248).

ولذلك فإن حل مشكلة تحديد المسافة بين الخط المستقيم m والمستوى α لا يختلف عن الأمثلة التي تمت مناقشتها في الفقرة 1 لتحديد المسافة بين نقطة ومستوى (انظر الشكل 270 ... 272). كنقطة، يمكنك أن تأخذ أي نقطة تنتمي إلى الخط م.

3. تحديد المسافة بين الطائرات.

يتم تحديد المسافة بين المستويات من خلال حجم القطعة المتعامدة التي تسقط من نقطة مأخوذة على مستوى ما إلى مستوى آخر.

ويترتب على هذا التعريف أن خوارزمية حل مشكلة إيجاد المسافة بين المستويين α و β تختلف عن خوارزمية مماثلة لحل مشكلة تحديد المسافة بين الخط m والمستوى α فقط في ذلك الخط m يجب أن ينتمي إلى المستوى α ، أي لتحديد المسافة بين المستويين α و β ما يلي:

1) خذ خطًا مستقيمًا m في المستوى α؛

2) حدد نقطة تعسفية أ على السطر م؛

3) من النقطة A، قم بخفض الخط العمودي l إلى المستوى β؛

4) تحديد النقطة M - نقطة التقاء الخط العمودي l بالمستوى β؛

5) تحديد حجم القطعة.

من الناحية العملية، يُنصح باستخدام خوارزمية حل مختلفة، والتي ستختلف عن تلك المقدمة فقط في أنه قبل الشروع في الخطوة الأولى، يجب نقل المستويات إلى موضع الإسقاط.

يؤدي تضمين هذه العملية الإضافية في الخوارزمية إلى تبسيط تنفيذ جميع النقاط الأخرى دون استثناء، مما يؤدي في النهاية إلى حل أبسط.

مثال 1. حدد المسافة بين المستويين α و β (الشكل 273).

حل. ننتقل من النظام xπ 2 /π 1 إلى x 1 π 1 /π 3. فيما يتعلق بالمستوى الجديد π 3، فإن المستويين α و β يشغلان موقع إسقاط، وبالتالي فإن المسافة بين الآثار الأمامية الجديدة f 0α 1 و f 0β 1 هي المسافة المطلوبة.

في الممارسة الهندسية، غالبًا ما يكون من الضروري حل مشكلة بناء مستوى موازٍ لمستوى معين وإزالته منه على مسافة معينة. يوضح المثال 2 أدناه الحل لمثل هذه المشكلة.

مثال 2. مطلوب بناء إسقاطات لمستوى β موازية لمستوى معين α (m || n)، إذا كان من المعروف أن المسافة بينهما هي d (الشكل 274).

1. في المستوى α، ارسم خطوطًا أفقية عشوائية h (1، 3) وخطوطًا أمامية f (1،2).

2. من النقطة 1 نستعيد l المتعامد على المستوى α(l" ⊥ h, l" ⊥ f").

3. على الخط العمودي l نحدد نقطة عشوائية A.

4. حدد طول المقطع - (يشير الموضع على الرسم البياني إلى الاتجاه غير المشوه متريًا للخط المستقيم l).

5. ضع القطعة = d على الخط المستقيم (1"A 0) من النقطة 1".

6. ضع علامة على الإسقاطات l" و l" النقطتين B" و B"، المقابلة للنقطة B 0.

7. من خلال النقطة B نرسم المستوى β (h 1 ∩ f 1). إلى β || α، فمن الضروري الامتثال للشرط ح 1 || ح و و 1 || F.

4. تحديد المسافة بين الخطوط المتقاطعة.

يتم تحديد المسافة بين الخطوط المتقاطعة بطول العمودي الموجود بين المستويات المتوازية التي تنتمي إليها الخطوط المتقاطعة.

من أجل رسم مستويين متوازيين بشكل متبادل α و β من خلال تقاطع الخطين المستقيمين m و f، يكفي رسم خط مستقيم عبر النقطة A (A ∈ m) p موازيًا للخط المستقيم f، ومن خلال النقطة B (B ∈ f) خط مستقيم k موازي للمستقيم م . الخطوط المتقاطعة m و p و f و k تحدد المستويين المتوازيين α و β (انظر الشكل 248، e). المسافة بين المستويين α و β تساوي المسافة المطلوبة بين خطي التقاطع m و f.

يمكن اقتراح طريقة أخرى لتحديد المسافة بين الخطوط المتقاطعة، وهي أنه باستخدام بعض طرق تحويل الإسقاطات المتعامدة، يتم نقل أحد الخطوط المتقاطعة إلى موضع الإسقاط. في هذه الحالة، يتدهور أحد إسقاطات الخط إلى نقطة. المسافة بين الإسقاطات الجديدة لخطوط العبور (النقطة أ" 2 والقطعة ج" 2 د" 2) هي المسافة المطلوبة.

في التين. 275 يوضح حلاً لمشكلة تحديد المسافة بين الخطين المتقاطعين a وb، مع إعطاء المقطعين [AB] و[CD]. يتم تنفيذ الحل بالتسلسل التالي:

1. انقل أحد خطوط التقاطع (أ) إلى موضع موازٍ للمستوى π 3؛ للقيام بذلك، انتقل من نظام مستويات الإسقاط xπ 2 /π 1 إلى x 1 π 1 /π 3 الجديد، حيث يكون المحور x 1 موازيًا للإسقاط الأفقي للخط المستقيم a. حدد أ" 1 [أ" 1 ب" 1] و ب" 1.

2. عن طريق استبدال المستوى π 1 بالمستوى π 4، نترجم الخط المستقيم

ولوضع a" 2، عموديًا على المستوى π 4 (يتم رسم المحور x 2 الجديد بشكل عمودي على a" 1).

3. إنشاء إسقاط أفقي جديد للخط المستقيم ب" 2 - [ C" 2 D" 2 ].

4. المسافة من النقطة أ" 2 إلى الخط المستقيم ج" 2 د" 2 (القطعة (أ" 2 م" 2 ] (هي المسافة المطلوبة.

يجب أن يؤخذ في الاعتبار أن نقل أحد خطوط التقاطع إلى موضع الإسقاط ليس أكثر من نقل مستويات التوازي، التي يمكن فيها إحاطة الخطين a و b، أيضًا بموضع الإسقاط.

في الواقع، من خلال نقل الخط a إلى موضع عمودي على المستوى π 4، فإننا نضمن أن أي مستوى يحتوي على خط a يكون عموديًا على المستوى π 4، بما في ذلك المستوى α المحدد بالخطين a و m (a ∩ m، m | | ب). إذا رسمنا الآن خطًا n، موازيًا للخط a ومتقاطعًا ب، فسنحصل على المستوى β، وهو المستوى الثاني من التوازي، والذي يحتوي على الخطين المتقاطعين a وb. منذ β || α, ثم β ⊥ π 4 .

إيجاد المسافة من نقطة إلى مستوى هي مشكلة شائعة تنشأ عند حل مسائل الهندسة التحليلية المختلفة، على سبيل المثال يمكن اختزال هذه المشكلة في إيجاد المسافة بين خطين مستقيمين متقاطعين أو بين خط مستقيم ومستوى موازي لجسم ما. هو - هي.

خذ بعين الاعتبار المستوى $β$ والنقطة $M_0$ ذات الإحداثيات $(x_0;y_0; z_0)$ التي لا تنتمي إلى المستوى $β$.

التعريف 1

أقصر مسافة بين نقطة ومستوى ستكون العمودية المرسومة من النقطة $M_0$ إلى المستوى $β$.

الشكل 1. المسافة من نقطة إلى مستوى. Author24 - تبادل أعمال الطلاب عبر الإنترنت

نناقش أدناه كيفية العثور على المسافة من نقطة إلى مستوى باستخدام طريقة الإحداثيات.

اشتقاق صيغة الطريقة الإحداثية لإيجاد المسافة من نقطة إلى مستوى في الفضاء

العمودي من النقطة $M_0$ الذي يتقاطع مع المستوى $β$ عند النقطة $M_1$ والإحداثيات $(x_1;y_1; z_1)$ يقع على خط مستقيم متجه اتجاهه هو المتجه الطبيعي للمستوى $β$. في هذه الحالة، طول متجه الوحدة $n$ يساوي واحدًا. وبناء على ذلك، فإن المسافة من $β$ إلى النقطة $M_0$ ستكون:

$ρ= |\vec(n) \cdot \vec(M_1M_0)|\left(1\right)$، حيث $\vec(M_1M_0)$ هو المتجه العادي للمستوى $β$، و $\vec( n)$ هي وحدة المتجه الطبيعي للمستوى قيد النظر.

في الحالة التي تكون فيها معادلة المستوى بالشكل العام $Ax+ By + Cz + D=0$، فإن إحداثيات المتجه الطبيعي للمستوى هي معاملات المعادلة $\(A;B;C\ )$، والمتجه العادي للوحدة في هذه الحالة له الإحداثيات، محسوبة باستخدام المعادلة التالية:

$\vec(n)= \frac($A;B;C$)(\sqrt(A^2 + B^2 + C^2))\left(2\right)$.

يمكننا الآن إيجاد إحداثيات المتجه العادي $\vec(M_1M_0)$:

$\vec(M_0M_1)= $x_0 – x_1;y_0-y_1;z_0-z_1$\left(3\right)$.

نعبر أيضًا عن المعامل $D$ باستخدام إحداثيات نقطة تقع في المستوى $β$:

$D= Ax_1+By_1+Cz_1$

يمكن تعويض إحداثيات وحدة المتجه الطبيعي من المساواة $(2)$ في معادلة المستوى $β$، فيصبح لدينا:

$ρ= \frac(|A(x_0 -x_1) + B(y_0-y_1)+C(z_0-z_1)|)(\sqrt(A^2+B^2+C^2))= \frac( |Ax_0+ By_0 + Cz_0-(Ax_1+By_1+Cz_1)|)(\sqrt(A^2+B^2+C^2)) = \frac(Ax_0+ By_0 + Cz_0 + D)(\sqrt(A^2) +B^2+C^2))\left(4\right)$

المساواة $(4)$ هي صيغة لإيجاد المسافة من نقطة إلى مستوى في الفضاء.

خوارزمية عامة لإيجاد المسافة من النقطة $M_0$ إلى المستوى

إذا لم يتم إعطاء معادلة المستوى في الصورة العامة، فأنت بحاجة أولاً إلى تحويلها إلى الصورة العامة.
بعد ذلك، من الضروري التعبير من المعادلة العامة للمستوى عن المتجه الطبيعي لمستوى معين من خلال النقطة $M_0$ ونقطة تنتمي إلى مستوى معين، ولهذا نحتاج إلى استخدام المساواة $(3)$ .
المرحلة التالية هي البحث عن إحداثيات وحدة المتجه الطبيعي للمستوى باستخدام الصيغة $(2)$.
أخيرًا، يمكنك البدء في إيجاد المسافة من النقطة إلى المستوى، ويتم ذلك عن طريق حساب المنتج القياسي للمتجهين $\vec(n)$ و$\vec(M_1M_0)$.

شروط التوازي والتعامد

1°. شرط المستوى المشترك لطائرتين

دع طائرتين تعطى:

أ 1 س + ب 1 ذ + ج 1 ض + د 1 = 0, ن 1 = {أ 1 ; ب 1 ; ج 1 } ≠ 0 ;(1)

أ 2 س + ب 2 ذ + ج 2 ض + د 2 = 0, ن 2 = {أ 2 ; ب 2 ; ج 2 } ≠ 0 .(2)

متى تكون مستوية (أي متوازية أو متزامنة)؟ من الواضح أن هذا سيكون هو الحال فقط إذا كانت متجهاتها العادية على خط مستقيم. وبتطبيق معيار المستوى المشترك نحصل على

الجملة 1.يكون المستويان متحدين المستوى إذا وفقط إذا كان حاصل الضرب الاتجاهي لمتجهيهما الطبيعيين يساوي المتجه الصفري:

[ن 1 , ن 2 ] = 0 .

2°. شرط مصادفة طائرتين

الاقتراح 2.يتطابق المستويان (1) و (2) إذا وفقط إذا كانت معاملاتها الأربعة متناسبة، أي أن هناك رقمًا مثل ذلك

أ 2 = أ 1 , ب 2 = ب 1 , ج 2 = ج 1 , د 2 = د 1 . (3)

دليل.لتتحقق الشروط (3). ومن ثم يمكن كتابة معادلة المستوى الثاني على النحو التالي:

λ أ 1 س + λ ب 1 ذ + λ ج 1 ض + λ د 1 = 0.

lect ≠ 0، وإلا لكان كذلك أ 2 = ب 2 = ج 2 = د 2 = 0، وهو ما يتعارض مع الشرط ن 2 ≠ 0 . ولذلك فإن المعادلة الأخيرة تعادل المعادلة (1)، مما يعني أن المستويين متطابقان.

فلنعلم الآن، على العكس من ذلك، أن هذه المستويات متطابقة. إذن فإن متجهاتها الطبيعية تكون على خط واحد، أي أن هناك رقمًا مثل ذلك

أ 2 = أ 1 , ب 2 = ب 1 , ج 2 = ج 1 .

يمكن الآن إعادة كتابة المعادلة (2) على النحو التالي:

λ أ 1 س + λ ب 1 ذ + λ ج 1 ض + د 2 = 0.

بضرب المعادلة (1) بـ lect، نحصل على معادلة مكافئة للمستوى الأول (منذ lect ≠ 0):

λ أ 1 س + λ ب 1 ذ + λ ج 1 ض + λ د 1 = 0.

لنأخذ نقطة ما ( س 0 , ذ 0 , ض 0) من المستوى الأول (وبالتالي المستوى الثاني) واستبدال إحداثياته في المعادلتين الأخيرتين؛ نحصل على المساواة الصحيحة:

λ أ 1 س 0 + λ ب 1 ذ 0 + λ ج 1 ض 0 + د 2 = 0 ;

λ أ 1 س 0 + λ ب 1 ذ 0 + λ ج 1 ض 0 + λ د 1 = 0.

بطرح الجزء السفلي من الجزء العلوي نحصل على د 2 - α د 1 = 0، أي د 2 = د 1, ريال.

3°. شرط عمودي طائرتين

من الواضح أنه من الضروري والكافي لهذا أن تكون المتجهات العمودية متعامدة.

الاقتراح 3.يكون المستويان متعامدين إذا وفقط إذا كان المنتج القياسي للمتجهات العادية يساوي صفرًا:

(ن 1 , ن 2) = 0 .

دع المعادلة الطائرة تعطى

فأس + بواسطة + تشيكوسلوفاكيا + د = 0, ن = {أ; ب; ج} ≠ 0 ,

والفترة م 0 = (س 0 , ذ 0 , ض 0). دعونا نستنتج صيغة المسافة من نقطة إلى مستوى:

دعونا نأخذ نقطة تعسفية س = (س 1 , ذ 1 , ض 1) الكذب في هذه الطائرة. إحداثياتها تلبي معادلة المستوى:

فأس 1 + بواسطة 1 + تشيكوسلوفاكيا 1 + د = 0.

ولنلاحظ الآن أن المسافة المطلوبة ديساوي القيمة المطلقة لإسقاط المتجهات إلى اتجاه المتجه ن (هنا نأخذ الإسقاط ككمية عددية وليس كمتجه). بعد ذلك، نطبق الصيغة لحساب الإسقاط:

صيغة مماثلة صالحة للمسافة دمن النقطة م 0 = (س 0 , ذ 0) مستوى إلى خط مستقيم تعطى بالمعادلة العامة فأس + بواسطة + ج = 0.

يجب أن تكون هناك طائرة . دعونا نرسم عادي
من خلال أصل الإحداثيات O. واسمحوا معين
- الزوايا المتكونة من العمودي مع محاور الإحداثيات.
. يترك – طول الجزء العادي
حتى يتقاطع مع المستوى . بافتراض أن اتجاه جيب التمام للوضع الطبيعي معروف ، نشتق معادلة المستوى .

يترك
) هي نقطة تعسفية على المستوى. وحدة المتجه العادي لها إحداثيات. دعونا نجد إسقاط المتجه
إلى وضعها الطبيعي.

منذ هذه النقطة مينتمي إلى الطائرة، ثم

هذه هي معادلة مستوى معين، تسمى طبيعي .

المسافة من النقطة إلى المستوى

دع الطائرة تعطى ,م*
- نقطة في الفضاء، د – بعدها عن الطائرة .

تعريف. انحراف نقاط م*من الطائرة يسمى الرقم ( + د), لو م* وتقع على الجانب الآخر من المستوى حيث يكون الاتجاه الموجب للنقاط العادية والرقم (- د)، إذا كانت النقطة تقع على الجانب الآخر من المستوى:

نظرية. دع الطائرة مع الوحدة عادي يتم إعطاؤه بالمعادلة العادية:

يترك م*
– نقطة في الفضاء الانحراف ر. م* من الطائرة يعطى بالتعبير

دليل.الإسقاط ر.
* نشير بالعادة س. انحراف النقطة م*من الطائرة متساوية

قاعدة.لايجاد انحراف ت. م* من المستوى، تحتاج إلى استبدال الإحداثيات t في المعادلة العادية للمستوى. م* . المسافة من نقطة إلى مستوى هي .

تخفيض معادلة المستوى العام إلى الشكل الطبيعي

دع نفس المستوى يتم تعريفه بمعادلتين:

المعادلة العامة

معادلة عادية.

بما أن المعادلتين تحددان نفس المستوى، فإن معاملاتهما متناسبة:

لنقم بتربيع المساواة الثلاثة الأولى ونجمعها:

من هنا سنجد – عامل التطبيع:

. (10)

وبضرب المعادلة العامة للمستوى بعامل التطبيع نحصل على المعادلة العادية للمستوى:

أمثلة على المشاكل حول موضوع "الطائرة".

مثال 1.إنشاء معادلة الطائرة المرور بنقطة معينة
(2,1,-1) وموازى للمستوى.

حل. عادي للطائرة :
. بما أن المستويين متوازيين، فالعمودي ومن الطبيعي أيضا أن الطائرة المطلوبة . باستخدام معادلة المستوى الذي يمر عبر نقطة معينة (3)، نحصل على المستوى المعادلة:

إجابة:

مثال 2.قاعدة العمودي الذي سقط من نقطة الأصل إلى المستوى ، هي النقطة
. أوجد معادلة المستوى .

حل. المتجه
أمر طبيعي للطائرة . نقطة م 0 ينتمي إلى الطائرة. يمكنك استخدام معادلة المستوى الذي يمر عبر نقطة معينة (3):

إجابة:

مثال 3.بناء الطائرة ، مرورا بالنقاط

وعمودي على المستوى :.

لذلك، إلى حد ما م (س, ذ, ض) تابعة للطائرة ، فمن الضروري أن ثلاثة ناقلات
كانت مستوية:

=0.

يبقى الكشف عن المحدد وإحضار التعبير الناتج إلى شكل معادلة عامة (1).

مثال 4.طائرة يتم الحصول عليها بواسطة المعادلة العامة:

العثور على انحراف النقطة
من طائرة معينة.

حل. دعونا نعيد معادلة المستوى إلى الصورة العادية.

دعونا نعوض بإحداثيات النقطة في المعادلة العادية الناتجة م*.

إجابة:
.

مثال 5.هل الطائرة تتقاطع مع الجزء؟

حل. لقطع أ.بعبرت الطائرة والانحرافات و من الطائرة يجب أن يكون لها علامات مختلفة:

مثال 6.تقاطع ثلاث طائرات عند نقطة واحدة.

النظام لديه حل فريد، وبالتالي فإن المستويات الثلاثة لها نقطة مشتركة واحدة.

مثال 7.إيجاد منصفات زاوية ثنائية السطوح مكونة من طائرتين معلومتين.

يترك و - انحراف نقطة ما
من الطائرتين الأولى والثانية.

على أحد المستويين المنصفين (المقابلة للزاوية التي يقع فيها أصل الإحداثيات) تكون هذه الانحرافات متساوية في المقدار والإشارة، وعلى الجانب الآخر تكون متساوية في المقدار ومعاكسة في الإشارة.

هذه هي معادلة المستوى المنصف الأول.

هذه هي معادلة المستوى المنصف الثاني.

مثال 8.تحديد موقع نقطتين معينتين و نسبة إلى الزوايا ثنائية السطوح التي تشكلها هذه الطائرات.