Limit va davomiylik

bitta o'zgaruvchining funktsiyalari

3.1.1. Ta'rif. Raqam A x uchun intilish x har qanday raqam uchun 0
raqam bor
(
), va shart bajariladi:

Agar
, Bu
.

(Ramzi:
).

Agar grafik ishora qilsa G funktsiyalari

, Qachon nuqtaga cheksiz yaqinlashadi (bular.
), (3.1-rasmga qarang), u holda bu holat funktsiyaning geometrik ekvivalentidir.
da
chegaraviy qiymatga ega (chegara) A(ramzlik:
).

Funktsiya grafigi,

Guruch. 3.1

Shuni ta'kidlash kerakki, funktsiyaning chegara qiymatini (chegarasini) aniqlashda at x uchun intilish x 0 nuqtada funktsiyaning harakati haqida hech narsa aytmaydi x 0 . Aynan shu nuqtada x 0 funktsiyasi aniqlanmagan bo'lishi mumkin
, balki
.

Agar
, u holda funksiya uchun cheksiz kichik deb ataladi
.

Interval deyiladi  - nuqta qo'shnisi x 0 markazi chipli. Ushbu nomdan foydalanib, biz buni aytishimiz mumkin: agar biron bir raqam uchun raqam mavjud bo'lsa va shart bajariladi: agar
, Bu
.

3.1.2. Ta'rif. , har qanday konvergent uchun bo'lsa x 0 ketma-ketlik
keyingi ketma-ketlik
ga yaqinlashadi A.

3.1.3. 3.1.1 va 3.1.2 bo'limlari ta'riflarining ekvivalentligini isbotlaylik.

Birinchi ta'rif ma'nosida birinchi bo'lsin va ruxsat
(
), keyin hammasi , ularning cheklangan sonidan tashqari tengsizlikni qanoatlantiradi
, Qayerda  tomonidan tanlangan  birinchi ta'rif ma'nosida, ya'ni.
, ya'ni. birinchi ta'rif ikkinchisini nazarda tutadi. Hozir ruxsat bering
ikkinchi ta'rif ma'nosida va ikkinchi ta'rif ma'nosida deb faraz qilaylik
, ya'ni. ba'zilar uchun o'zboshimchalik bilan kichik uchun (masalan, uchun
) ketma-ketligi topildi
, lekin ayni paytda
. Biz qarama-qarshilikka keldik, shuning uchun birinchisi ikkinchi ta'rifdan kelib chiqadi.

3.1.4. Ushbu ta'riflarning ekvivalentligi ayniqsa qulaydir, chunki ketma-ketliklar chegaralarining xususiyatlari bo'yicha ilgari tasdiqlangan barcha teoremalar deyarli avtomatik ravishda yangi holatga o'tkaziladi. Faqat cheklash tushunchasini aniqlashtirish kerak. Tegishli teorema quyidagi formulaga ega:

Agar
, u holda u nuqtaning ba'zi  - qo'shnisi bilan chegaralanadi x 0 markazi chipli.

3.2.1.Teorema. Mayli
,
,

Keyin,
,

,

.

3.2.2. Mayli

- ixtiyoriy, yaqinlashuvchi x 0 funktsiya argument qiymatlari ketma-ketligi va
. Moslashuvchi ketma-ketliklar
Va
bu funksiyalarning qiymatlari chegaralarga ega A Va B. Ammo keyin, 2.13.2-bo'lim teoremasi tufayli, ketma-ketliklar
,
Va
mos ravishda teng chegaralarga ega A +B,
Va
. Funktsiyaning nuqtadagi chegarasining ta'rifiga ko'ra (2.5.2-bo'limga qarang), bu shuni anglatadi

,
,

.

3.2.3. Teorema. Agar
,
, va ba'zi yaqin joylarda

yuzaga keladi

.

3.2.4. Funksiyaning nuqtadagi chegarasining ta'rifi bo'yicha x Har qanday ketma-ketlik uchun 0
shu kabi

funktsiya qiymatlari ketma-ketligi teng chegaraga ega A. Bu har kim uchun shuni anglatadi
raqam bor
amalga oshirildi. Xuddi shunday, ketma-ketlik uchun
raqam bor
har qanday raqam uchun shunday
amalga oshirildi. Tanlash
, biz buni hamma uchun topamiz
amalga oshirildi. Ushbu tengsizliklar zanjiridan biz har qanday ga egamiz, bu shuni anglatadiki
.

3.2.5. Ta'rif. Raqam A da funksiyaning chegara qiymati (chegara) deyiladi x uchun intilish x 0 o'ngda (ramz:
), agar biron-bir son uchun raqam () mavjud va shart bajariladi: agar
, Bu
.

To'plam o'ng  - nuqta qo'shnisi deb ataladi x 0 . Chapdagi chegara qiymati (chegara) tushunchasi xuddi shunday ta'riflangan (
).

3.2.6. Teorema. at funksiyasi ga teng chegara qiymatiga (chegara) ega A keyin va faqat qachon

,

3.3.1. Ta'rif. Raqam A da funksiyaning chegara qiymati (chegara) deyiladi x cheksizlikka moyillik, agar biron bir son uchun raqam mavjud bo'lsa
(
) va quyidagi shart bajariladi:

Agar
, Bu.

(Ramzi:
.)

Bir guruh
chaqirdi D- cheksizlik mahallasi.

3.3.2. Ta'rif. Raqam A da funksiyaning chegara qiymati (chegara) deyiladi x plyus cheksizlikka moyillik, agar har qanday son uchun raqam mavjud bo'lsa D() va shart bajariladi:

Agar
, Bu.

(Ramzi:
).

Agar grafik ishora qilsa G funktsiyalari
cheksiz o'sish bilan
yagona gorizontal chiziqqa cheksiz yaqinlashish
(3.2-rasmga qarang), u holda bu holat funktsiyaning geometrik ekvivalentidir.
da
soniga teng chegaraviy qiymatga (chegara) ega A(ramzlik:
).

Funksiya grafigi
,

Bir guruh
chaqirdi D- mahalla va cheksizlik.

Limit tushunchasi
.

Mashqlar.

Limitlar haqidagi barcha teoremalarni holatlarga tatbiq eting:

1)
, 2)
, 3)
, 4)
, 5)
.

3.4.1. Ta'rif. Funktsiya cheksiz katta funktsiya (yoki oddiygina cheksiz katta) deb ataladi, agar har qanday son uchun

, tengsizlikni qanoatlantirsa, tengsizlik qanoatlantiriladi
.

(Ramzi:
.)

Agar bajarilgan bo'lsa
, keyin ular yozadilar
.

Agar bajarilgan bo'lsa
, keyin ular yozadilar
.

3.4.2. Teorema. Mayli
Va
da
.

Keyin
uchun cheksiz katta funksiya hisoblanadi.

3.4.3. Bu ixtiyoriy raqam bo'lsin. Chunki , u holda son uchun cheksiz kichik funksiya
hamma uchun shunday raqam bor x tengsizlik shunday bo'ladi
, lekin keyin xuddi shu uchun x tengsizlik qanoatlantiriladi
. Bular. uchun cheksiz katta funksiya hisoblanadi.

3.4.4.Teorema. uchun va uchun cheksiz katta funksiya bo'lsin.

Keyin uchun cheksiz kichik funktsiya.

(Ushbu teorema 3.8.2-bo'limdagi teoremaga o'xshash tarzda isbotlangan.)

3.4.5. Funktsiya
qachon chegaralanmagan deb ataladi
, agar biron bir raqam uchun
va nuqtaning istalgan d-mahallasi nuqtani belgilashingiz mumkin x bu mahalladan shunday
.

3.5.1. TA'RIF. Funktsiya chaqiriladi davomiy nuqtada , Agar
.

Oxirgi shartni quyidagicha yozish mumkin:

.

Bu belgi uzluksiz funksiyalar uchun chegara belgisi va funksiya belgisini almashtirish mumkinligini bildiradi

Yoki shunday: . Yoki yana, boshida bo'lgani kabi.

belgilaylik
. Keyin
va =
va oxirgi ro'yxatga olish shakli shaklni oladi

.

Chegara belgisi ostidagi ifoda funktsiya nuqtasining o'sish natijasida hosil bo'lgan o'sishini ifodalaydi
dalil x nuqtada, odatda sifatida belgilanadi
. Natijada nuqtada funksiyaning uzluksizligi shartini yozishning quyidagi shaklini olamiz

,

nuqtadagi funksiyaning uzluksizligining "ishchi ta'rifi" deb ataladi.

Funktsiya chaqiriladi davomiy nuqtada chap, Agar
.

Funktsiya chaqiriladi davomiy nuqtada o'ngda, Agar
.

3.5.2. Misol.
. Bu funksiya har qanday uchun uzluksizdir. Limitlarning xossalari haqidagi teoremalardan foydalanib, biz darhol qo'lga kiritamiz: har qanday ratsional funktsiya u aniqlangan har bir nuqtada uzluksizdir, ya'ni. shakl funktsiyasi
.

MASHQLAR.

3.6.1. Maktab darsligi buni (yuqori darajada qat'iylik bilan) isbotlaydi
(birinchi ajoyib chegara). Vizual geometrik mulohazalardan darhol shundan kelib chiqadi
. E'tibor bering, chap tengsizlikdan bu ham kelib chiqadi
, ya'ni. funktsiyasi nima
nolda uzluksiz. Bu yerdan barcha trigonometrik funktsiyalarning ular aniqlangan barcha nuqtalarda uzluksizligini isbotlash unchalik qiyin emas. Aslida, qachon
cheksiz kichik funktsiyaning mahsuloti sifatida
cheklangan funksiya uchun
.

3.6.2. (2-ajoyib chegara). Biz allaqachon bilganimizdek

,

Qayerda natural sonlar orqali ishlaydi. Buni ko'rsatish mumkin
. Bundan tashqari
.

MASHQLAR.

3.7.1. TEOREMA (murakkab funksiyaning uzluksizligi haqida).

Agar funktsiya
nuqtada uzluksiz va
, va funksiya
bir nuqtada uzluksiz , keyin murakkab funksiya
nuqtada uzluksizdir.

3.7.2. Ushbu bayonotning to'g'riligi quyidagi tarzda yozilgan davomiylik ta'rifidan darhol kelib chiqadi:

3.8.1. TEOREMA. Funktsiya har bir nuqtada uzluksiz (
).

3.8.2. Agar funktsiyani oqilona deb hisoblasak
har qanday uchun belgilangan va qat'iy monotonik (uchun qat'iy kamayadi
, bilan qat'iy ortib bormoqda
), unda isbot qilish qiyin emas.

Da
bizda ... bor:

bular. bizda bo'lganda
, bu funktsiyani bildiradi da uzluksizdir.

Da
hammasi avvalgisiga tushadi:

Da
.

Da
funktsiyasi
hamma uchun doimiy, shuning uchun doimiy.

3.9.1. TEOREMA (teskari funktsiyaning birgalikda mavjudligi va uzluksizligi haqida).

Uzluksiz funktsiya nuqtaning ba'zi d - qo'shnilarida qat'iy kamaysin (qat'iy ortib borsin),
. Keyin ba'zi e - nuqtaning mahallasida teskari funksiya mavjud
, bu qat'iy kamayadi (qat'iy ortadi) va nuqtaning e - qo'shnisida uzluksizdir.

3.9.2. Bu yerda faqat teskari funksiyaning nuqtadagi uzluksizligini isbotlaymiz.

Keling, qabul qilaylik, davr y nuqtalar orasida joylashgan
Va
, shuning uchun, agar
, Bu
, Qayerda.

3.10.1. Shunday qilib, uzluksiz funktsiyalar ustidagi har qanday ruxsat etilgan arifmetik amallar yana uzluksiz funktsiyalarga olib keladi. Ulardan murakkab va teskari funksiyalarning hosil bo`lishi uzluksizlikni buzmaydi. Shuning uchun, ma'lum darajada mas'uliyat bilan, barcha elementar funktsiyalar argumentning barcha ruxsat etilgan qiymatlari uchun uzluksiz ekanligini ta'kidlashimiz mumkin.

MASHQ.

Buni isbotlang
da
(ikkinchi ajoyib chegaraning yana bir shakli).

3.11.1. Ekvivalent cheksiz kichiklar tushunchasidan foydalansak, chegaralarni hisoblash juda soddalashtirilgan. Ekvivalentlik tushunchasini ixtiyoriy funksiyalar holiga umumlashtirish qulay.

Ta'rif. va funksiyalari if uchun ekvivalent deyiladi
(o'rniga yozishingiz mumkin
,
,
,
,
).

Ishlatilgan belgi f ~ g.

Ekvivalentlik quyidagi xususiyatlarga ega

Quyidagi ekvivalent cheksiz kichiklar ro'yxatini yodda tutish kerak:

~
da
; (1)

~ da ; (2)

~
da ; (3)

~ da ; (4)

~ da ; (5)

~ da ; (6)

~ da ; (7)

~ p da ; (8)

~ da
; (9)

~
da . (10)

Bu erda va mustaqil o'zgaruvchilar emas, balki funktsiyalar bo'lishi mumkin
Va
ba'zi xatti-harakatlar uchun mos ravishda nolga va bittaga moyil x. Masalan,

~
da
,

~
da
.

Ekvivalentlik (1) - birinchi ajoyib chegarani yozishning yana bir shakli. Ekvivalentlar (2), (3), (6) va (7) to'g'ridan-to'g'ri isbotlanishi mumkin. Ekvivalentlik (4) ekvivalentliklarning 2) xususiyatini hisobga olgan holda (1) dan olinadi:

~
.

Xuddi shunday, (5) va (7) (2) va (6) dan olinadi. Haqiqatdan ham

~
,

~
.

(8) ning ekvivalentligi (7) va (6) ning ketma-ket qo'llanilishi bilan isbotlanadi:

va (9) va (10) o'rniga (6) va (8) dan olinadi
.

3.11.2. Teorema. Mahsulot va nisbatda chegaralarni hisoblashda siz funktsiyalarni ekvivalentlarga o'zgartirishingiz mumkin. Ya'ni, agar ~
, keyin yoki ikkala chegara bir vaqtning o'zida mavjud emas, va
, yoki bu chegaralarning ikkalasi bir vaqtning o'zida mavjud emas.

Birinchi tenglikni isbotlaylik. Chegaralardan biri aytaylik:
mavjud. Keyin

.

3.11.3. (raqam yoki belgi bo'lsin,
yoki
). Turli b.m.larning xatti-harakatlarini ko'rib chiqamiz. funktsiyalar (infinitesimal atamasini shunday qisqartiramiz).

TA'RIFLAR.
va ekvivalent b.m deb ataladi. uchun funktsiyalar, agar
(da ).

biz uni b.m deb nomlaymiz. b.m dan yuqori buyurtma funktsiyasi
, Agar
(da ).

3.11.4. Agar va ekvivalenti b.m. keyin funktsiyalar
b.m bor. dan yuqori tartibli funktsiya
va nima. - b.m. at funksiyasi, bunda barcha x uchun va agar bu nuqtada funksiya olinadigan uzilish nuqtasi deb ataladi. ikkinchi turdagi uzilishlarga ega. Gapning o'zi Nazorat ishi

Kollokviumga. Bo'limlar: " Cheklash Va davomiylikfunktsiyalari yaroqli o'zgaruvchan" funktsiyalaribittao'zgaruvchan", “Differensial hisoblash funktsiyalari bir nechta o'zgaruvchilar"

Test va savollar mavzulari va misollari (testlar individual standart hisob-kitoblar kollokvium) 1-semestr testi 1-bo'lim «Haqiqiy o'zgaruvchining funksiyasining chegarasi va uzluksizligi»

Nazorat ishi

Kollokviumga. Bo'limlar: " Cheklash Va davomiylikfunktsiyalari yaroqli o'zgaruvchan", “Differensial hisoblash funktsiyalaribittao'zgaruvchan", “Differensial hisoblash funktsiyalari bir nechta o'zgaruvchilar". Raqamlar ketma-ketligi...

Nazorat ishi

Kollokviumga. Bo'limlar: " Cheklash Va davomiylikfunktsiyalari yaroqli o'zgaruvchan", “Differensial hisoblash funktsiyalaribittao'zgaruvchan", “Differensial hisoblash funktsiyalari bir nechta o'zgaruvchilar". Raqamlar ketma-ketligi...

Test topshiriqlari va savollariga mavzular va misollar (test ishi individual standart hisob-kitoblar kollokviumlari) 1-semestr test ishi “haqiqiy o‘zgaruvchining chegarasi va uzluksizligi” bo‘limi

Nazorat ishi

Kollokviumga. Bo'limlar: " Cheklash Va davomiylikfunktsiyalari yaroqli o'zgaruvchan", “Differensial hisoblash funktsiyalaribittao'zgaruvchan", “Differensial hisoblash funktsiyalari bir nechta o'zgaruvchilar". Raqamlar ketma-ketligi...

19-ma'ruza Bir necha o'zgaruvchili funksiyaning chegarasi va uzluksizligi

Leksiya

... Cheklash Va davomiylikfunktsiyalari bir nechta o'zgaruvchilar. 19.1. Kontseptsiya funktsiyalari bir nechta o'zgaruvchilar. Qayta ko'rib chiqish orqali funktsiyalari bir nechta o'zgaruvchilar... xususiyatlari funktsiyalaribittao'zgaruvchan, davomiy segmentida. Xususiyatlarga qarang funktsiyalari, davomiy ustida...

Funktsiyaning uzluksizligi. Buzilish nuqtalari.

Buqa yuradi, chayqaladi, xo'rsinib ketadi:
- Oh, doska tugayapti, endi men yiqilib tushaman!

Ushbu darsda biz funktsiyaning uzluksizligi tushunchasini, uzilish nuqtalarining tasnifini va umumiy amaliy masalani ko'rib chiqamiz. funktsiyalarning uzluksizligini o'rganish. Mavzuning nomidan ko'pchilik intuitiv ravishda nima muhokama qilinishini taxmin qiladi va material juda oddiy deb o'ylaydi. Bu to'g'ri. Ammo bu oddiy vazifalar, ko'pincha e'tiborsizlik va ularni hal qilishda yuzaki yondashuv uchun jazolanadi. Shuning uchun, men sizga maqolani juda diqqat bilan o'rganishingizni va barcha nozikliklar va texnikani qo'lga kiritishingizni maslahat beraman.

Nimani bilishingiz va nimaga qodir bo'lishingiz kerak? Juda ham emas. Darsni yaxshi o'rganish uchun siz nima ekanligini tushunishingiz kerak funktsiya chegarasi. Tayyorgarlik darajasi past bo'lgan o'quvchilar uchun maqolani tushunish kifoya Funktsiya chegaralari. Yechimlarga misollar va qo'llanmadagi chegaraning geometrik ma'nosiga qarang Elementar funksiyalarning grafiklari va xossalari. Bundan tashqari, o'zingiz bilan tanishish tavsiya etiladi grafiklarni geometrik o'zgartirishlar, chunki amaliyot ko'p hollarda rasm chizishni o'z ichiga oladi. Istiqbollar hamma uchun optimistikdir, hatto to'liq choynak ham keyingi yoki ikki soat ichida o'z-o'zidan vazifani uddalay oladi!

Funktsiyaning uzluksizligi. To'xtash nuqtalari va ularning tasnifi

Funksiyaning uzluksizligi tushunchasi

Butun son chizig‘ida uzluksiz bo‘lgan ba’zi funksiyalarni ko‘rib chiqamiz:

Yoki qisqacha aytganda, bizning funktsiyamiz uzluksiz (haqiqiy sonlar to'plami) ustida.

Davomiylikning "filist" mezoni nima? Shubhasiz, uzluksiz funksiya grafigini qalamni qog‘ozdan ko‘tarmasdan chizish mumkin.

Bunday holda, ikkita oddiy tushunchani aniq ajratib ko'rsatish kerak: funktsiya sohasi Va funksiyaning uzluksizligi. Umuman bu bir xil narsa emas. Masalan:

Bu funktsiya butun son satrida aniqlanadi, ya'ni uchun hamma"X" ning ma'nosi "y" ning o'ziga xos ma'nosiga ega. Xususan, agar , keyin . E'tibor bering, boshqa nuqtada tinish belgilari mavjud, chunki funktsiya ta'rifiga ko'ra, argumentning qiymati mos kelishi kerak. yagona narsa funktsiya qiymati. Shunday qilib, domen bizning vazifamiz: .

Biroq bu funksiya uzluksiz ishlamaydi! Ayni paytda u azob chekayotgani aniq bo'shliq. Bu atama ham juda tushunarli va ingl; haqiqatan ham bu erda qalamni qog'ozdan yirtib tashlash kerak bo'ladi. Birozdan keyin biz to'xtash nuqtalarining tasnifini ko'rib chiqamiz.

Funksiyaning nuqta va intervaldagi uzluksizligi

Muayyan matematik masalada funksiyaning nuqtadagi uzluksizligi, oraliqdagi funksiyaning uzluksizligi, yarim interval yoki segmentdagi funksiyaning uzluksizligi haqida gapirish mumkin. Ya'ni, "shunchaki uzluksizlik" yo'q– funktsiya QAYoRDA uzluksiz bo‘lishi mumkin. Va hamma narsaning asosiy "qurilish bloki" funksiyaning uzluksizligi nuqtada .

Matematik tahlil nazariyasi nuqtadagi funktsiyaning uzluksizligi ta'rifini "delta" va "epsilon" mahallalari yordamida beradi, ammo amalda foydalanishda boshqa ta'rif mavjud bo'lib, biz unga diqqat bilan qaraymiz.

Avval eslaylik bir tomonlama chegaralar birinchi darsda hayotimizga kirib kelgan Funktsiya grafiklari haqida. Kundalik vaziyatni ko'rib chiqing:

Agar biz o'qni nuqtaga yaqinlashtirsak chap(qizil o'q), keyin "o'yinlar" ning tegishli qiymatlari o'q bo'ylab nuqtaga o'tadi (qizil o'q). Matematik jihatdan bu fakt yordamida aniqlanadi chap qo'l chegarasi:

Kirishga e'tibor bering ("x chapda ka to'g'ri keladi" deb o'qiladi). "Qo'shimcha" "minus nol" ramziy ma'noni anglatadi , mohiyatan bu raqamga chap tomondan yaqinlashayotganimizni anglatadi.

Xuddi shunday, agar siz "ka" nuqtasiga yaqinlashsangiz o'ngda(ko'k o'q), keyin "o'yinlar" bir xil qiymatga keladi, lekin yashil o'q bo'ylab va o'ng qo'l chegarasi quyidagicha formatlanadi:

"Qo'shimcha" ramziy ma'noni anglatadi , va yozuv: "x o'ngda ka ga moyil" deb o'qiydi.

Agar bir tomonlama chegaralar chekli va teng bo'lsa(bizning holatimizda bo'lgani kabi): , keyin UMUMIY chegara borligini aytamiz. Bu oddiy, umumiy chegara bizning "odatiy" funktsiya chegarasi, chekli songa teng.

E'tibor bering, agar funktsiya belgilanmagan bo'lsa (grafik novdasidagi qora nuqta chiqarib tashlang), yuqoridagi hisob-kitoblar o'z kuchida qoladi. Bir necha bor ta'kidlanganidek, xususan maqolada cheksiz kichik funktsiyalar haqida, iboralar "x" degan ma'noni anglatadi cheksiz yaqin nuqtaga yaqinlashadi, esa AHAMIYATI YO'Q, funktsiyaning o'zi berilgan nuqtada aniqlanganmi yoki yo'qmi. Yaxshi misol keyingi paragrafda funksiya tahlil qilinganda topiladi.

Ta'rif: funksiya nuqtada uzluksiz bo‘ladi, agar funksiyaning berilgan nuqtadagi chegarasi shu nuqtadagi funksiya qiymatiga teng bo‘lsa: .

Ta'rif quyidagi atamalarda batafsil bayon etilgan:

1) Funktsiya nuqtada aniqlanishi kerak, ya'ni qiymat mavjud bo'lishi kerak.

2) Funktsiyaning umumiy chegarasi bo'lishi kerak. Yuqorida ta'kidlab o'tilganidek, bu bir tomonlama chegaralarning mavjudligi va tengligini anglatadi: .

3) Funksiyaning berilgan nuqtadagi chegarasi funksiyaning shu nuqtadagi qiymatiga teng bo lishi kerak: .

Agar buzilgan bo'lsa kamida bitta uchta shartdan, keyin funksiya nuqtada uzluksizlik xususiyatini yo'qotadi.

Funksiyaning oraliqdagi uzluksizligi zukkolik bilan va juda sodda tarzda tuzilgan: funktsiya berilgan intervalning har bir nuqtasida uzluksiz bo'lsa, intervalda uzluksizdir.

Xususan, ko'pgina funktsiyalar cheksiz oraliqda, ya'ni haqiqiy sonlar to'plamida uzluksizdir. Bu chiziqli funktsiya, polinomlar, ko'rsatkichlar, sinuslar, kosinuslar va boshqalar. Va umuman olganda, har qanday elementar funktsiya uning ustida doimiy ta'rif sohasi, masalan, logarifmik funktsiya oraliqda uzluksizdir. Umid qilamanki, hozir siz asosiy funktsiyalarning grafiklari qanday ko'rinishi haqida juda yaxshi tasavvurga egasiz. Ularning uzluksizligi haqida batafsil ma'lumotni Fichtenholtz ismli mehribon odamdan olish mumkin.

Segment va yarim oraliqdagi funktsiyaning uzluksizligi bilan hamma narsa ham qiyin emas, lekin bu haqda sinfda gapirish to'g'riroq. segmentdagi funksiyaning minimal va maksimal qiymatlarini topish haqida, lekin hozircha bu haqda tashvishlanmaylik.

Tanaffus nuqtalarining tasnifi

Funksiyalarning qiziqarli hayoti har xil maxsus nuqtalarga boy va tanaffus nuqtalari ularning tarjimai holidagi sahifalardan faqat bittasi.

Eslatma : har holda, men bir elementar nuqtaga to'xtalib o'taman: uzilish nuqtasi har doim yagona nuqta- "ketma-ket bir nechta tanaffus nuqtalari" yo'q, ya'ni "uzilish oralig'i" degan narsa yo'q.

Bu nuqtalar, o'z navbatida, ikkita katta guruhga bo'lingan: birinchi turdagi yorilishlar Va ikkinchi turdagi yorilishlar. Bo'shliqning har bir turi o'ziga xos xususiyatlarga ega, biz ularni hozir ko'rib chiqamiz:

Birinchi turdagi uzilish nuqtasi

Agar bir nuqtada uzluksizlik sharti buzilgan bo'lsa va bir tomonlama chegaralar cheklangan , keyin chaqiriladi birinchi turdagi uzilish nuqtasi.

Keling, eng optimistik holatdan boshlaylik. Darsning asl g'oyasiga ko'ra, men nazariyani "umumiy ma'noda" aytmoqchi edim, ammo materialning haqiqatini namoyish qilish uchun men aniq belgilar bilan variantga qaror qildim.

Bu abadiy alanga fonida yangi turmush qurganlarning fotosurati kabi qayg'uli, ammo quyidagi surat odatda qabul qilinadi. Funksiya grafigini chizmada tasvirlaymiz:


Bu funktsiya nuqtadan tashqari butun son chizig'ida uzluksizdir. Va aslida, maxraj nolga teng bo'lishi mumkin emas. Biroq, chegaraning ma'nosiga muvofiq, biz mumkin cheksiz yaqin"nol" ga chapdan ham, o'ngdan ham yaqinlashing, ya'ni bir tomonlama chegaralar mavjud va aniqki, mos keladi:
(Uzluksizlikning 2-sharti qanoatlantirilgan).

Lekin funksiya nuqtada aniqlanmagan, shuning uchun uzluksizlikning 1-sharti buziladi va funktsiya bu nuqtada uzilishga duchor bo'ladi.

Ushbu turdagi tanaffus (mavjud umumiy chegara) deyiladi ta'mirlanadigan bo'shliq. Nima uchun olinadigan? Chunki funktsiya mumkin qayta belgilang buzilish nuqtasida:

Bu g'alati ko'rinadimi? Balki. Ammo bunday funktsiya belgisi hech narsaga zid emas! Endi bo'shliq yopildi va hamma xursand:


Rasmiy tekshirishni amalga oshiramiz:

2) - umumiy chegara mavjud;
3)

Shunday qilib, har uch shart ham qondiriladi va funktsiyaning nuqtadagi uzluksizligi ta'rifi bilan nuqtada uzluksiz bo'ladi.

Biroq, matan nafratlanuvchilari, masalan, funktsiyani yomon tarzda belgilashlari mumkin :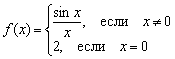


Qizig'i shundaki, birinchi ikkita uzluksizlik sharti bu erda qondiriladi:
1) – funksiya berilgan nuqtada aniqlangan;
2) - umumiy chegara mavjud.

Lekin uchinchi chegaradan o'tmagan: , ya'ni nuqtadagi funksiya chegarasi teng emas berilgan funktsiyaning berilgan nuqtadagi qiymati.

Shunday qilib, bir nuqtada funktsiya uzilishga duchor bo'ladi.

Ikkinchi, qayg'uli holat deyiladi birinchi turdagi yorilish sakrash bilan. Va qayg'u bir tomonlama chegaralardan kelib chiqadi cheklangan va har xil. Misol darsning ikkinchi chizmasida ko'rsatilgan. Bunday bo'shliq odatda qachon sodir bo'ladi qismlarga bo'lingan funktsiyalar, ular allaqachon maqolada aytib o'tilgan Grafik o'zgarishlar haqida.

Bo'laklarga bo'linish funktsiyasini ko'rib chiqing va biz uning chizmasini tugatamiz. Grafikni qanday qurish mumkin? Juda oddiy. Yarim oraliqda biz parabola (yashil) bo'lagini, oraliqda - to'g'ri chiziq segmentini (qizil) va yarim intervalda - to'g'ri chiziqni (ko'k) chizamiz.

Bundan tashqari, tengsizlik tufayli kvadratik funktsiya (yashil nuqta) uchun qiymat aniqlanadi va tengsizlik tufayli chiziqli funktsiya (ko'k nuqta) uchun qiymat aniqlanadi:

Eng qiyin holatda, siz grafikning har bir qismini nuqta-nuqta qurishga murojaat qilishingiz kerak (birinchi qismga qarang). funksiyalar grafiklari haqida dars).

Endi biz faqat mavzu bilan qiziqamiz. Keling, buni davomiylik uchun tekshiramiz:

2) Bir tomonlama chegaralarni hisoblaymiz.

Chap tomonda bizda qizil chiziq segmenti bor, shuning uchun chap tomon chegarasi:

O'ng tomonda ko'k to'g'ri chiziq va o'ng tomonda chegara mavjud:

Natijada biz oldik chekli sonlar, va ular teng emas. Chunki bir tomonlama chegaralar cheklangan va har xil: , keyin bizning funktsiyamiz toqat qiladi sakrash bilan birinchi turdagi uzilish.

Bo'shliqni bartaraf etishning iloji yo'qligi mantiqan to'g'ri - funktsiyani oldingi misolda bo'lgani kabi aniqlab bo'lmaydi va "bir-biriga yopishtirish" mumkin emas.

Ikkinchi turdagi uzilish nuqtalari

Odatda, yorilishning barcha boshqa holatlari aqlli ravishda ushbu toifaga tasniflanadi. Men hamma narsani sanab o'tmayman, chunki amalda 99% muammolarga duch kelasiz cheksiz bo'shliq- chap yoki o'ng qo'lda va ko'pincha ikkala chegara cheksizdir.

Va, albatta, eng aniq rasm - nol nuqtadagi giperbola. Bu erda ikkala bir tomonlama chegaralar cheksizdir: , shuning uchun funksiya nuqtada ikkinchi turdagi uzilishga duchor bo'ladi.

Men maqolalarimni iloji boricha xilma-xil tarkib bilan to'ldirishga harakat qilaman, shuning uchun keling, hali duch kelmagan funksiya grafigini ko'rib chiqaylik:

standart sxema bo'yicha:

1) Funktsiya bu nuqtada aniqlanmagan, chunki maxraj nolga tushadi.

Albatta, biz darhol funktsiya nuqtada uzilishga duchor bo'ladi degan xulosaga kelishimiz mumkin, lekin ko'pincha shart tomonidan talab qilinadigan uzilishning tabiatini tasniflash yaxshi bo'lar edi. Buning uchun:

Shuni eslatib o'tamanki, biz ro'yxatga olishni nazarda tutamiz cheksiz kichik manfiy son, va yozuv ostida - cheksiz kichik musbat son.

Bir tomonlama chegaralar cheksizdir, ya'ni funksiya nuqtada 2-turdagi uzilishlarga duchor bo'ladi. Y o'qi vertikal asimptota grafik uchun.

Ikkala bir tomonlama chegaralarning mavjudligi odatiy hol emas, lekin ulardan faqat bittasi cheksizdir, masalan:

Bu funksiyaning grafigi.

Biz uzluksizlik nuqtasini ko'rib chiqamiz:

1) Funktsiya bu nuqtada aniqlanmagan.

2) Bir tomonlama chegaralarni hisoblaymiz:

Bunday bir tomonlama chegaralarni hisoblash usuli haqida ma'ruzaning so'nggi ikki misolida gaplashamiz, garchi ko'plab o'quvchilar allaqachon hamma narsani ko'rgan va taxmin qilgan.

Chap chegara chekli va nolga teng (biz "nuqtaning o'ziga bormaymiz"), lekin o'ng chegara cheksizdir va grafikning to'q sariq novdasi unga cheksiz yaqinlashadi. vertikal asimptota, tenglama bilan berilgan (qora nuqta chiziq).

Shunday qilib, funktsiya buziladi ikkinchi turdagi uzilishlar nuqtada.

1-turdagi uzilishga kelsak, funktsiya uzilish nuqtasining o'zida aniqlanishi mumkin. Masalan, qismli funksiya uchun Koordinatalarning boshiga qora qalin nuqta qo'ying. O'ng tomonda giperbolaning novdasi, o'ng tomon esa cheksizdir. O'ylaymanki, deyarli hamma bu grafik qanday ko'rinishi haqida tasavvurga ega.

Hamma intiqlik bilan kutgan narsa:

Funktsiyani uzluksizligi uchun qanday tekshirish mumkin?

Bir nuqtada uzluksizlik uchun funktsiyani o'rganish allaqachon o'rnatilgan muntazam sxema bo'yicha amalga oshiriladi, bu doimiylikning uchta shartini tekshirishdan iborat:

1-misol

Funktsiyani o'rganish

Yechim:

1) Qo'llash doirasidagi yagona nuqta - bu funktsiya aniqlanmagan.

2) Bir tomonlama chegaralarni hisoblaymiz:

Bir tomonlama chegaralar chekli va tengdir.

Shunday qilib, ushbu nuqtada funktsiya olinadigan uzilishga duchor bo'ladi.

Ushbu funktsiyaning grafigi qanday ko'rinishga ega?

Men soddalashtirmoqchiman , va oddiy parabola olinganga o'xshaydi. LEKIN asl funktsiya nuqtasida aniqlanmagan, shuning uchun quyidagi band talab qilinadi:

Keling, rasm chizamiz:

Javob: funktsiya butun son chizig'ida uzluksiz bo'lib, u olinadigan uzilishga duchor bo'lgan nuqtadan tashqari.

Funktsiya yaxshi yoki unchalik yaxshi bo'lmagan tarzda aniqlanishi mumkin, ammo shartga ko'ra, bu shart emas.

Bu juda uzoq misol deysizmi? Arzimaydi. Amalda bu o'nlab marta sodir bo'lgan. Saytning deyarli barcha vazifalari haqiqiy mustaqil ishlar va testlardan kelib chiqadi.

Keling, sevimli modullarimizdan xalos bo'laylik:

2-misol

Funktsiyani o'rganish davomiylik uchun. Funktsiya uzilishlarining tabiatini aniqlang, agar ular mavjud bo'lsa. Chizmani bajaring.

Yechim: Ba'zi sabablarga ko'ra, talabalar qo'rqishadi va modulli funktsiyalarni yoqtirmaydilar, garchi ularda hech qanday murakkab narsa yo'q. Biz allaqachon darsda bunday narsalarga biroz to'xtalib o'tdik. Grafiklarning geometrik o'zgarishlari. Modul salbiy bo'lmagani uchun u quyidagicha kengaytiriladi: , bu erda "alfa" qandaydir ifodadir. Bu holda va bizning funktsiyamiz qisman yozilishi kerak:

Lekin ikkala bo'lakning kasrlari ga kamaytirilishi kerak. Oldingi misoldagi kabi qisqartirish oqibatlarsiz amalga oshmaydi. Asl funktsiya nuqtada aniqlanmagan, chunki maxraj nolga tushadi. Shuning uchun tizim qo'shimcha shartni ko'rsatishi va birinchi tengsizlikni qat'iy qilishi kerak:

Endi JUDA FOYDALI qaror qilish texnikasi haqida: qoralama bo'yicha topshiriqni yakunlashdan oldin, rasm chizish foydalidir (shartlar talab qiladimi yoki yo'qmi). Bu, birinchidan, uzluksizlik va uzilish nuqtalarini darhol ko'rishga yordam beradi, ikkinchidan, bir tomonlama chegaralarni topishda sizni xatolardan 100% himoya qiladi.

Keling, rasm chizamiz. Bizning hisob-kitoblarimizga ko'ra, nuqtaning chap tomoniga parabolaning bo'lagini (ko'k rang) va o'ngga - parabolaning bo'lagini (qizil rang) chizish kerak, bunda funktsiya aniqlanmagan. o'ziga ishora:

Agar shubhangiz bo'lsa, bir nechta x qiymatlarini oling va ularni funktsiyaga ulang (modul mumkin bo'lgan minus belgisini yo'q qilishini eslab) va grafikni tekshiring.

Keling, uzluksizlik funksiyasini analitik jihatdan ko‘rib chiqamiz:

1) Funktsiya nuqtada aniqlanmagan, shuning uchun biz darhol uning uzluksiz emasligini aytishimiz mumkin.

2) Uzluksizlik xarakterini aniqlaymiz, buning uchun biz bir tomonlama chegaralarni hisoblaymiz:

Bir tomonlama chegaralar chekli va har xil bo'lib, bu funksiya nuqtada sakrash bilan 1-turdagi uzilishga duchor bo'lishini anglatadi. Yana bir bor e'tibor bering, chegaralarni topishda, tanaffus nuqtasidagi funksiya aniqlangan yoki aniqlanmaganligi muhim emas.

Endi qolgan narsa chizmani qoralamadan o'tkazish (u xuddi tadqiqot yordamida qilingan ;-)) va vazifani bajarishdir:

Javob: funktsiya butun son chizig'ida uzluksiz bo'lib, u sakrash bilan birinchi turdagi uzilishga duchor bo'lgan nuqtadan tashqari.

Ba'zan ular uzluksiz sakrashning qo'shimcha belgisini talab qiladi. Bu oddiygina hisoblanadi - o'ng chegaradan chap chegarani ayirish kerak: , ya'ni tanaffus nuqtasida bizning funktsiyamiz 2 birlik pastga sakrab chiqdi (minus belgisi bizga aytadi).

3-misol

Funktsiyani o'rganish davomiylik uchun. Funktsiya uzilishlarining tabiatini aniqlang, agar ular mavjud bo'lsa. Chizma qiling.

Bu siz o'zingiz hal qilishingiz mumkin bo'lgan misol, dars oxirida namunali yechim.

Funktsiya uch qismdan iborat bo'lganda, vazifaning eng mashhur va keng tarqalgan versiyasiga o'tamiz:

4-misol

Funksiyaning uzluksizligini tekshirib, funksiya grafigini tuzing .

Yechim: funktsiyaning barcha uch qismi mos keladigan intervallarda uzluksiz ekanligi aniq, shuning uchun bo'laklar orasidagi "birikma" ning faqat ikkita nuqtasini tekshirish qoladi. Birinchidan, chizma chizmasini tuzamiz; Men maqolaning birinchi qismida qurilish texnikasini etarlicha batafsil izohladim. Bitta narsa shundaki, biz alohida nuqtalarimizni diqqat bilan kuzatib borishimiz kerak: tengsizlik tufayli qiymat to'g'ri chiziqqa (yashil nuqta) tegishli va tengsizlik tufayli qiymat parabolaga (qizil nuqta) tegishli:


Xo'sh, printsipial jihatdan, hamma narsa aniq =) Faqat qarorni rasmiylashtirish qoladi. Ikki "qo'shilish" nuqtasining har biri uchun biz odatda 3 ta uzluksizlik shartini tekshiramiz:

men) Biz nuqtani davomiylik uchun tekshiramiz

1)

Bir tomonlama chegaralar chekli va har xil bo'lib, bu funksiya nuqtada sakrash bilan 1-turdagi uzilishga duchor bo'lishini anglatadi.

Uzluksiz sakrashni o'ng va chap chegaralar orasidagi farq sifatida hisoblaylik:
, ya'ni grafik bir birlikni silkitdi.

II) Biz nuqtani davomiylik uchun tekshiramiz

1) – funksiya berilgan nuqtada aniqlanadi.

2) Bir tomonlama chegaralarni toping:

– bir tomonlama chegaralar chekli va tengdir, demak, umumiy chegara bor.

3) – funksiyaning nuqtadagi chegarasi ushbu funksiyaning berilgan nuqtadagi qiymatiga teng.

Yakuniy bosqichda biz rasmni yakuniy versiyaga o'tkazamiz, shundan so'ng biz oxirgi akkordni qo'yamiz:

Javob: funktsiya butun son chizig'ida uzluksiz bo'lib, sakrash bilan birinchi turdagi uzilishga duchor bo'lgan nuqtadan tashqari.

5-misol

Funksiyaning uzluksizligini tekshirib, uning grafigini tuzing .

Bu mustaqil yechish uchun misol, qisqacha yechim va dars oxirida muammoning taxminiy namunasi.

Bir nuqtada funksiya uzluksiz bo'lishi kerak, ikkinchisida esa uzilish bo'lishi kerak degan taassurot paydo bo'lishi mumkin. Amalda, bu har doim ham shunday emas. Qolgan misollarni e'tiborsiz qoldirmaslikka harakat qiling - bir nechta qiziqarli va muhim xususiyatlar bo'ladi:

6-misol

Funktsiya berilgan . Nuqtalardagi uzluksizlik funksiyasini o‘rganing. Grafik tuzing.

Yechim: va yana darhol qoralama ustidagi rasmni bajaring:

Ushbu grafikning o'ziga xos xususiyati shundaki, bo'laklar funktsiyasi abscissa o'qi tenglamasi bilan berilgan. Bu erda bu maydon yashil rangda chizilgan, lekin daftarda u odatda oddiy qalam bilan qalin rangda ta'kidlangan. Va, albatta, bizning qo'chqorlarimiz haqida unutmang: qiymat tangent filialiga (qizil nuqta) tegishli va qiymat to'g'ri chiziqqa tegishli.

Chizmadan hamma narsa aniq - funktsiya butun son chizig'i bo'ylab uzluksizdir, faqat 3-4 o'xshash misollardan so'ng to'liq avtomatlashtirishga olib keladigan yechimni rasmiylashtirish qoladi:

men) Biz nuqtani davomiylik uchun tekshiramiz

1) – funksiya berilgan nuqtada aniqlangan.

2) Bir tomonlama chegaralarni hisoblaymiz:

, bu umumiy chegara borligini anglatadi.

Har holda, sizga arzimas bir haqiqatni eslatib o'taman: doimiyning chegarasi doimiyning o'ziga teng. Bunday holda, nol chegarasi nolga teng bo'ladi (chap qo'l chegarasi).

3) – funksiyaning nuqtadagi chegarasi ushbu funksiyaning berilgan nuqtadagi qiymatiga teng.

Shunday qilib, funktsiyaning nuqtadagi uzluksizligi ta'rifi bilan funksiya nuqtada uzluksizdir.

II) Biz nuqtani davomiylik uchun tekshiramiz

1) – funksiya berilgan nuqtada aniqlangan.

2) Bir tomonlama chegaralarni toping:

Va bu erda - birining chegarasi birlikning o'ziga teng.

- umumiy chegara mavjud.

3) – funksiyaning nuqtadagi chegarasi ushbu funksiyaning berilgan nuqtadagi qiymatiga teng.

Shunday qilib, funktsiyaning nuqtadagi uzluksizligi ta'rifi bilan funksiya nuqtada uzluksizdir.

Odatdagidek, tadqiqotdan so'ng biz rasmimizni yakuniy versiyaga o'tkazamiz.

Javob: funksiya nuqtalarda uzluksiz.

E'tibor bering, bu holatda bizdan uzluksizlik uchun butun funktsiyani o'rganish haqida hech narsa so'ralmagan va formulani shakllantirish yaxshi matematik shakl hisoblanadi. aniq va aniq berilgan savolga javob. Aytgancha, agar shartlar sizga grafik yaratishni talab qilmasa, unda siz uni tuzmaslikka to'liq huquqingiz bor (garchi keyinchalik o'qituvchi sizni buni qilishga majbur qilishi mumkin).

O'zingiz hal qilish uchun kichik matematik "tilni burish":

7-misol

Funktsiya berilgan 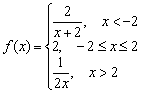. Nuqtalardagi uzluksizlik funksiyasini o‘rganing. Agar mavjud bo'lsa, to'xtash nuqtalarini tasniflang. Chizmani bajaring.

Barcha "so'zlarni" to'g'ri "talaffuz qilishga" harakat qiling =) Va grafikni aniqroq chizing, aniqlik, hamma joyda ortiqcha bo'lmaydi;-)

Esingizda bo'lsa, men darhol chizma sifatida chizishni to'ldirishni tavsiya qildim, lekin vaqti-vaqti bilan siz grafikning qanday ko'rinishini darhol aniqlay olmaydigan misollarga duch kelasiz. Shuning uchun, ba'zi hollarda, birinchi navbatda, bir tomonlama chegaralarni topish foydali bo'ladi va shundan keyingina o'rganishga asoslanib, filiallarni tasvirlaydi. Oxirgi ikkita misolda biz bir tomonlama chegaralarni hisoblash texnikasini ham o'rganamiz:

8-misol

Funksiyaning uzluksizligini tekshirib, uning sxematik grafigini tuzing.

Yechim: yomon nuqtalar aniq: (ko'rsatkichning maxrajini nolga tushiradi) va (butun kasrning maxrajini nolga tushiradi). Ushbu funktsiyaning grafigi qanday ko'rinishi aniq emas, ya'ni birinchi navbatda biroz tadqiqot qilish yaxshiroqdir.

Topologiya– funksiyalarning chegaralari va uzluksizligini o‘rganish bilan shug‘ullanuvchi matematikaning bir bo‘limi. Topologiya algebra bilan birgalikda matematikaning umumiy asosini tashkil qiladi.

Topologik bo'shliq yoki raqam - nuqtalari o'rtasida ma'lum bir yaqinlik munosabati berilgan bir hil Evklid fazomizning kichik to'plami. Bu erda raqamlar qattiq jismlar sifatida emas, balki ularning sifat xususiyatlarini saqlab qolgan doimiy deformatsiyaga imkon beruvchi juda elastik kauchukdan yasalgan narsalar sifatida qaraladi.

Shakllarni birma-bir uzluksiz xaritalash deyiladi gomeomorfizm. Boshqacha aytganda, raqamlar gomeomorf, agar birining uzluksiz deformatsiya bilan boshqasiga o'tkazilishi mumkin bo'lsa.

Misollar. Quyidagi raqamlar gomeomorf (turli guruhlardagi raqamlar gomeomorf emas), rasmda ko'rsatilgan. 2.

1. O'z-o'zidan kesishmagan segment va egri chiziq.

2. Doira, kvadratning ichki qismi, lenta.

3. Sfera, kub va tetraedr yuzasi.

4. Doira, ellips va tugunli aylana.

5. Tekislikdagi halqa (teshikli doira), fazoda halqa, ikki marta buralgan halqa, silindrning yon yuzasi.

6. Möbius chizig'i, ya'ni. bir marta o'ralgan halqa va uch marta o'ralgan halqa.

7. Torus (donut) yuzasi, tutqichli shar va tugunli torus.

8. Ikkita tutqichli shar va ikkita teshikli simit.

Matematik analizda funksiyalar chegaralar usuli bilan o‘rganiladi. O'zgaruvchi va chegara asosiy tushunchalardir.

Turli hodisalarda ba'zi miqdorlar o'zlarining son qiymatini saqlab qoladilar, boshqalari o'zgaradi. O'zgaruvchining barcha raqamli qiymatlari to'plami deyiladi ushbu o'zgaruvchining o'zgarish sohasi.

O'zgaruvchining harakat qilish usullaridan eng muhimi o'zgaruvchining ma'lum chegaraga intilishidir.

Doimiy raqam a chaqirdi o'zgaruvchan chegara, orasidagi farqning mutlaq qiymati bo'lsa x Va a() o'zgaruvchan qiymatni o'zgartirish jarayonida bo'ladi x xohlagancha kichik:

"Siz xohlagancha kichik" nimani anglatadi? O'zgaruvchan qiymat X chegaraga intiladi A, agar har qanday ixtiyoriy kichik (ixtiyoriy kichik) son uchun o'zgaruvchining o'zgarishida shunday moment mavjud bo'lsa X, undan boshlab tengsizlik amal qiladi .

Chegaraning ta'rifi oddiy geometrik ma'noga ega: tengsizlik shuni anglatadiki X nuqtaning qo'shnisida joylashgan a, bular. oraliqda .

Shunday qilib, chegaraning ta'rifi geometrik shaklda berilishi mumkin:

Raqam A o'zgaruvchining chegarasi hisoblanadi X, agar har qanday o'zboshimchalik bilan kichik (o'zboshimchalik bilan kichik) uchun - sonning qo'shnisi A o'zgaruvchini o'zgartirishda bunday momentni belgilashingiz mumkin X, shundan boshlab uning barcha qiymatlari nuqtaning ko'rsatilgan qo'shnisiga to'g'ri keladi A.

Izoh. O'zgaruvchan qiymat X uning chegarasiga turli yo'llar bilan yaqinlasha oladi: bu chegaradan kamroq (chapda), ko'proq (o'ngda), chegara qiymati atrofida o'zgarib turadi.

Ketma-ketlik chegarasi

Funktsiya har bir elementga ko'ra qonun (qoida) deb ataladi x ba'zi to'plam X bitta elementga mos keladi y to'plamlar Y.

Funktsiya barcha natural sonlar to'plamida aniqlanishi mumkin: . Bu funksiya deyiladi tabiiy argument funktsiyasi yoki raqamli ketma-ketlik.

Ketma-ketlikni, har qanday cheksiz to'plam kabi, sanab o'tish orqali aniqlab bo'lmagani uchun, u umumiy atama bilan belgilanadi: , bu yerda ketma-ketlikning umumiy atamasi.

Diskret o'zgaruvchi - ketma-ketlikning umumiy atamasi.

Muvofiqlik uchun "bir nuqtadan boshlab" so'zlari "bir qatordan boshlanadigan" so'zlarini anglatadi.

Raqam A ketma-ketlikning chegarasi deb ataladi , agar har qanday o'zboshimchalik bilan kichik (o'zboshimchalik bilan kichik) son uchun bunday raqam mavjud bo'lsa N, bu raqam bilan ketma-ketlikning barcha a'zolari uchun n>N tengsizlik mavjud .

yoki da .

Geometrik jihatdan ketma-ketlik chegarasining ta'rifi quyidagilarni anglatadi: har qanday o'zboshimchalik bilan kichik (o'zboshimchalik bilan kichik) - sonning qo'shnisi uchun A shunday raqam borki, ketma-ketlikning barcha shartlari dan katta N, raqamlar, bu yaqinlikka tushadi. Ketma-ketlikning boshlang'ich shartlarining faqat cheklangan soni qo'shnidan tashqarida paydo bo'ladi. Natural son N ga bog'liq : .