Kūno impulsas iš jėgos. Impulsų išsaugojimo įstatymas. Iš kur kilo terminas „impulsas“?
Kūno impulsas
Kūno impulsas yra dydis, lygus kūno masės sandaugai pagal jo greitį.
Reikia atsiminti, kad kalbame apie kūną, kurį galima pavaizduoti kaip materialų tašką. Kūno impulsas ($ p $) dar vadinamas judesio kiekiu. Impulso sąvoką į fiziką įvedė René Descartes (1596-1650). Terminas „impulsas“ atsirado vėliau (impulsus lotyniškai reiškia „stumti“). Impulsas yra vektorinis dydis (kaip greitis) ir išreiškiamas formule:
$ p↖ (→) = mυ↖ (→) $
Impulso vektoriaus kryptis visada sutampa su greičio kryptimi.
Impulso vienetas SI yra kūno, kurio masė yra $ 1 $ kg, impulsas, judantis 1 $ m / s greičiu, todėl impulso vienetas yra $ 1 $ kg $ · $ m / s.
Jei per laiko intervalą $ ∆t $ kūną (medžiagos tašką) veikia pastovi jėga, tada pagreitis taip pat bus pastovus:
$ a↖ (→) = ((υ_2) ↖ (→) - (υ_1) ↖ (→)) / (∆t) $
kur $ (υ_1) ↖ (→) $ ir $ (υ_2) ↖ (→) $ yra kūno pradinis ir galutinis greičiai. Pakeitę šią reikšmę į antrojo Niutono dėsnio išraišką, gauname:
$ (m ((υ_2) ↖ (→) - (υ_1) ↖ (→))) / (∆t) = F↖ (→) $
Atidarę skliaustus ir naudodami kūno impulso išraišką, gauname:
$ (p_2) ↖ (→) - (p_1) ↖ (→) = F↖ (→) ∆t $
Čia $ (p_2) ↖ (→) - (p_1) ↖ (→) = ∆p↖ (→) $ yra impulso pokytis per laiką $ ∆t $. Tada ankstesnė lygtis bus tokia:
$ ∆p↖ (→) = F↖ (→) ∆t $
Išraiška $ ∆p↖ (→) = F↖ (→) ∆t $ yra matematinis antrojo Niutono dėsnio atvaizdas.
Jėgos sandauga pagal jos veikimo laiką vadinama jėgos impulsas... Štai kodėl taško impulso pokytis lygus jį veikiančios jėgos impulso pokyčiui.
Išraiška $ ∆p↖ (→) = F↖ (→) ∆t $ vadinama kūno judėjimo lygtis... Pažymėtina, kad vieną ir tą patį veiksmą – taško impulso pokytį – galima gauti su maža jėga per ilgą laiką, o su didele jėga – per trumpą laiką.
Impulsas tel. Impulsų kaitos įstatymas
Mechaninės sistemos impulsas (impulsas) yra vektorius, lygus visų šios sistemos materialių taškų impulsų sumai:
$ (p_ (sistema)) ↖ (→) = (p_1) ↖ (→) + (p_2) ↖ (→) + ... $
Pokyčio ir impulso išsaugojimo dėsniai yra antrojo ir trečiojo Niutono dėsnių pasekmė.
Apsvarstykite sistemą, susidedančią iš dviejų kūnų. Jėgos ($ F_ (12) $ ir $ F_ (21) $ paveiksle, kuriomis sistemos kūnai sąveikauja tarpusavyje, vadinamos vidinėmis.
Tegul, be vidinių jėgų, sistemą veikia išorinės jėgos $ (F_1) ↖ (→) $ ir $ (F_2) ↖ (→) $. Kiekvienam kūnui galime parašyti lygtį $ ∆p↖ (→) = F↖ (→) ∆t $. Sudėjus kairę ir dešinę šių lygčių puses, gauname:
$ (∆p_1) ↖ (→) + (∆p_2) ↖ (→) = ((F_ (12)) ↖ (→) + (F_ (21)) ↖ (→) + (F_1) ↖ (→) + (F_2) ↖ (→)) ∆t $
Pagal trečiąjį Niutono dėsnį $ (F_ (12)) ↖ (→) = - (F_ (21)) ↖ (→) $.
Vadinasi,
$ (∆p_1) ↖ (→) + (∆p_2) ↖ (→) = ((F_1) ↖ (→) + (F_2) ↖ (→)) ∆t $
Kairėje pusėje yra geometrinė visų sistemos kūnų impulsų pokyčių suma, lygi pačios sistemos impulso pokyčiui - $ (∆p_ (sistema)) ↖ (→) $. sąskaitoje lygybę $ (∆p_1) ↖ (→) + (∆p_2) ↖ (→) = ((F_1) ↖ (→) + (F_2) ↖ (→)) ∆t $ galima parašyti:
$ (∆p_ (sistema)) ↖ (→) = F↖ (→) ∆t $
čia $ F↖ (→) $ – visų kūną veikiančių išorinių jėgų suma. Gautas rezultatas reiškia, kad sistemos impulsą gali keisti tik išorinės jėgos, o sistemos impulso pokytis nukreipiamas taip pat, kaip ir visa išorinė jėga. Tai yra mechaninės sistemos impulso kitimo dėsnio esmė.
Vidinės jėgos negali pakeisti viso sistemos impulso. Jie keičia tik atskirų sistemos kūnų impulsus.
Impulso išsaugojimo įstatymas
Impulso išsaugojimo dėsnis išplaukia iš lygties $ (∆p_ (sist)) ↖ (→) = F↖ (→) ∆t $. Jei sistemos neveikia jokios išorinės jėgos, tai lygties $ (∆p_ (sistema)) ↖ (→) = F↖ (→) ∆t $ dešinioji pusė išnyksta, o tai reiškia, kad bendras sistemos impulsas lieka nepakitęs:
$ (∆p_ (sistema)) ↖ (→) = m_1 (υ_1) ↖ (→) + m_2 (υ_2) ↖ (→) = pastovus $
Vadinama sistema, kurios neveikia jokios išorinės jėgos arba atsirandančios išorinės jėgos yra nulis uždaryta.
Impulso išsaugojimo įstatymas sako:
Bendras uždaros kūnų sistemos impulsas išlieka pastovus bet kokiai sistemos kūnų sąveikai tarpusavyje.
Gautas rezultatas galioja sistemai, kurioje yra savavališkas skaičius kūnų. Jei išorinių jėgų suma nėra lygi nuliui, bet jų projekcijų į kurią nors kryptį suma lygi nuliui, tai sistemos impulso projekcija šia kryptimi nekinta. Taigi, pavyzdžiui, kūnų sistema Žemės paviršiuje negali būti laikoma uždara dėl visus kūnus veikiančios gravitacijos jėgos, tačiau impulsų projekcijų suma horizontalia kryptimi gali likti nepakitusi (jei nėra trinties), nes šia kryptimi gravitacijos jėga neveikia.
Reaktyvinis varymas
Panagrinėkime pavyzdžius, patvirtinančius impulso tvermės dėsnio pagrįstumą.
Paimkite vaikišką guminį balioną, pripūskite ir atleiskite. Pamatysime, kad kai oras pradės iš jo išeiti viena kryptimi, pats kamuolys skris kita. Rutulio judėjimas yra reaktyvinio judėjimo pavyzdys. Tai paaiškinama impulso tvermės dėsniu: bendras „rutulio plius oras jame“ sistemos impulsas prieš oro ištekėjimą lygus nuliui; judėjimo metu jis turi išlikti lygus nuliui; todėl rutulys juda priešinga čiurkšlės ištekėjimo krypčiai ir tokiu greičiu, kad jo impulsas būtų lygus oro srovės impulsui.
Reaktyvus judėjimas vadinamas kūno judėjimu, kuris atsiranda, kai kuri nors jo dalis atsiskiria nuo jo bet kokiu greičiu. Dėl impulso tvermės dėsnio kūno judėjimo kryptis yra priešinga atskirtos dalies judėjimo krypčiai.
Raketų skrydžiai yra pagrįsti reaktyvinio judėjimo principu. Šiuolaikinė kosminė raketa yra labai sudėtingas orlaivis. Raketos masę sudaro raketinio kuro masė (tai yra kaitinamosios dujos, susidarančios deginant kurą ir išmetamos reaktyvinės srovės pavidalu) ir galutinė, arba, kaip sakoma, „sausoji“ raketos masė, likusi po raketos išmetimo iš raketos.
Kai iš raketos dideliu greičiu išmetama reaktyvinė dujų srovė, pati raketa veržiasi priešinga kryptimi. Pagal impulso išsaugojimo dėsnį, raketos impulsas $ m_ (p) υ_p $ turi būti lygus išmetamų dujų impulsui $ m_ (dujos) υ_ (dujos) $:
$ m_ (p) υ_p = m_ (dujos) υ_ (dujos) $
Iš to išplaukia, kad raketos greitis
$ υ_p = ((m_ (dujos)) / (m_p)) υ_ (dujos) $
Iš šios formulės matyti, kad kuo didesnis raketos greitis, tuo didesnis išmetamų dujų greitis ir darbinio kūno masės (ty kuro masės) ir galutinio („sauso“) santykis. “) raketos masė.
Formulė $ υ_p = ((m_ (dujos)) / (m_p)) υ_ (dujos) $ yra apytikslė. Neatsižvelgiama į tai, kad degant kurui raketos masė skrendant tampa vis mažesnė. Tikslią raketos greičio formulę 1897 m. gavo K. E. Ciolkovskis ir vadinasi jo vardu.
Jėgos darbas
Terminą „darbas“ į fiziką 1826 metais įvedė prancūzų mokslininkas J. Poncelet. Jei kasdieniame gyvenime darbu vadinamas tik žmogaus darbas, tai fizikoje ir ypač mechanikoje visuotinai priimta, kad darbas atliekamas jėga. Fizinis darbo kiekis paprastai žymimas raide $ A $.
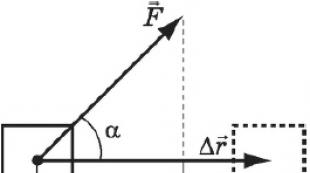
Jėgos darbas Tai jėgos veikimo matas, priklausantis nuo jos modulio ir krypties, taip pat nuo jėgos taikymo taško judėjimo. Esant pastoviai jėgai ir linijiniam judėjimui, darbas nustatomas pagal lygybę:
$ A = F | ∆r↖ (→) | cosα $
kur $ F $ – kūną veikianti jėga, $ ∆r↖ (→) $ – poslinkis, $ α $ – kampas tarp jėgos ir poslinkio.

Jėgos darbas yra lygus jėgos ir poslinkio modulių sandaugai ir kampo tarp jų kosinusui, ty vektorių $ F↖ (→) $ ir $ ∆r↖ (→) $ skaliarinei sandaugai. .
Darbas yra skaliarinis dydis. Jei $ α 0 $, o jei $ 90 °
Kai kūną veikia kelios jėgos, bendras darbas (visų jėgų darbo suma) yra lygus susidariusios jėgos darbui.
Darbo vienetas SI yra džaulis(1 USD J). $ 1 $ J yra darbas, kurį 1 $ N vertės jėga atlieka pakeliui į $ 1 $ m šios jėgos veikimo kryptimi. Šis vienetas pavadintas anglų mokslininko J. Joule (1818-1889) vardu: $ 1 $ J = $ 1 $ N $ · $ m. Taip pat dažnai naudojami kilodžauliai ir milidžauliai: $ 1 $ kJ $ = 1 000 $ J, $ 1 $ mJ $ = 0,001 $ J.
Gravitacijos darbas
Apsvarstykite kūną, slenkantį išilgai pasvirusios plokštumos, kurios polinkio kampas $ α $ ir aukštis $ H $.

Išreikškime $ ∆x $ kaip $ H $ ir $ α $:
$ ∆x = (H) / (sinα) $
Atsižvelgiant į tai, kad gravitacijos jėga $ F_t = mg $ sudaro kampą ($ 90 ° - α $) su judėjimo kryptimi, naudojant formulę $ ∆x = (H) / (sin) α $, gauname išraišką gravitacijos jėgos darbui $ A_g $:
$ A_g = mg · cos (90 ° -α) · (H) / (sinα) = mgH $
Iš šios formulės matyti, kad gravitacijos darbas priklauso nuo aukščio ir nepriklauso nuo plokštumos pasvirimo kampo.
Tai seka:
- gravitacijos darbas priklauso ne nuo trajektorijos, kuria juda kūnas, formos, o tik nuo pradinės ir galutinės kūno padėties;
- kai kūnas juda uždara trajektorija, gravitacijos darbas yra lygus nuliui, tai yra, gravitacija yra konservatyvi jėga (jėgos, turinčios šią savybę, vadinamos konservatyviosiomis).
Veikia reakcijos jėgos, yra lygus nuliui, nes reakcijos jėga ($ N $) nukreipta statmenai $ ∆x $ poslinkiui.
Trinties jėgos darbas
Trinties jėga nukreipta priešingai $ ∆x $ poslinkiui ir sudaro su ja $ 180 ° $ kampą, todėl trinties jėgos darbas yra neigiamas:
$ A_ (tr) = F_ (tr) ∆x cos180 ° = -F_ (tr) ∆x $
Kadangi $ F_ (tr) = μN, N = mgcosα, ∆x = l = (H) / (sinα), $ tada
$ A_ (tr) = μmgHctgα $
Elastinės jėgos darbas
Tegul išorinė jėga $ F↖ (→) $ veikia neįtemptą $ l_0 $ ilgio spyruoklę, ištempdama ją $ ∆l_0 = x_0 $. Padėtyje $ x = x_0F_ (kontrolė) = kx_0 $. Nutraukus jėgos $ F↖ (→) $ veikimą taške $ х_0 $, spyruoklė suspaudžiama veikiant jėgai $ F_ (kontrolė) $.

Nustatykime tamprumo jėgos darbą, kai spyruoklės dešiniojo galo koordinatė pasikeičia nuo $ x_0 $ iki $ x $. Kadangi tamprumo jėga šioje sekcijoje kinta tiesiškai, Huko dėsnyje galite naudoti jos vidutinę vertę šiame skyriuje:
$ F_ (ctrl.) = (Kx_0 + kx) / (2) = (k) / (2) (x_0 + x) $
Tada darbas (atsižvelgiant į tai, kad kryptys $ (F_ (plg. lyginti)) ↖ (→) $ ir $ (∆x) ↖ (→) $ sutampa) yra lygus:
$ A_ (kontrolė) = (k) / (2) (x_0 + x) (x_0-x) = (kx_0 ^ 2) / (2) - (kx ^ 2) / (2) $
Galima parodyti, kad paskutinės formulės forma nepriklauso nuo kampo tarp $ (F_ (plg. lyginti)) ↖ (→) $ ir $ (∆x) ↖ (→) $. Tampriųjų jėgų darbas priklauso tik nuo spyruoklės deformacijų pradinėje ir galutinėje būsenose.
Taigi elastinė jėga, kaip ir gravitacija, yra konservatyvi jėga.
Jėgos galia
Galia yra fizinis dydis, matuojamas darbo ir laiko, per kurį jis pagaminamas, santykiu.
Kitaip tariant, galia parodo, kiek darbo atliekama per laiko vienetą (SI - už 1 USD s).
Galia nustatoma pagal formulę:
kur $ N $ yra galia, $ A $ yra darbas, atliktas per laiką $ ∆t $.
Pakeitę į formulę $ N = (A) / (∆t) $ vietoj darbo $ A $ jos išraišką $ A = F | (∆r) ↖ (→) | cosα $, gauname:
$ N = (F | (∆r) ↖ (→) | cosα) / (∆t) = Fυcosα $
Galia lygi jėgos ir greičio vektorių modulių sandaugai iš kampo tarp šių vektorių kosinuso.
SI galia matuojama vatais (W). Vienas vatas ($ 1 $ W) yra tokia galia, kuriai esant $ 1 $ J darbas atliekamas už $ 1 $ s: $ 1 $ W $ = 1 $ J / s.
Šis agregatas pavadintas anglų išradėjo J. Watt (Watt), kuris sukonstravo pirmąjį garo variklį, vardu. Pats J. Wattas (1736-1819) panaudojo kitą galios vienetą – arklio galias (AG), kurį pristatė tam, kad būtų galima palyginti garo mašinos ir arklio našumą: $ 1 AG. $ = 735,5 $ W.
Technologijoje dažnai naudojami didesni galios vienetai - kilovatai ir megavatai: $ 1 $ kW $ = $ 1000 W, $ 1 $ MW $ = $ 1 000 000 W.
Kinetinė energija. Kinetinės energijos kitimo dėsnis
Jei kūnas ar keli tarpusavyje sąveikaujantys kūnai (kūnų sistema) gali dirbti, tada jie sako, kad turi energijos.
Kasdieniniame gyvenime dažnai vartojamas žodis „energija“ (iš graikų kalbos „energia“ – veiksmas, veikla). Taigi, pavyzdžiui, žmonės, kurie gali greitai atlikti darbą, vadinami energingais, turinčiais didelę energiją.
Energija, kurią kūnas turi dėl judėjimo, vadinama kinetine energija.
Kaip ir apskritai energijos apibrėžimo atveju, apie kinetinę energiją galime pasakyti, kad kinetinė energija yra judančio kūno gebėjimas atlikti darbą.
Raskime kūno, kurio masė $ m $, judančio greičiu $ υ $, kinetinę energiją. Kadangi kinetinė energija yra energija, atsirandanti dėl judėjimo, nulinė jos būsena yra būsena, kurioje kūnas yra ramybės būsenoje. Radę darbą, reikalingą kūnui suteikti tam tikrą greitį, rasime jo kinetinę energiją.
Tam apskaičiuojame darbą poslinkio $ ∆r↖ (→) $ atkarpoje, kai jėgos vektorių $ F↖ (→) $ ir poslinkio $ ∆r↖ (→) $ kryptys sutampa. Šiuo atveju darbas lygus
kur $ ∆x = ∆r $

Taško judėjimui su pagreičiu $ α = const $ judesio išraiška yra tokia:
$ ∆x = υ_1t + (prie ^ 2) / (2), $
kur $ υ_1 $ yra pradinis greitis.
Lygtyje $ A = F ∆x $ pakeitę $ ∆x $ išraišką iš $ ∆x = υ_1t + (es ^ 2) / (2) $ ir naudodami antrąjį Niutono dėsnį $ F = ma $, gauname:
$ A = ma (υ_1t + (at ^ 2) / (2)) = (mat) / (2) (2υ_1 + at) $
Pagreičio išreiškimas pradiniais $ υ_1 $ ir galutiniais $ υ_2 $ greičiais $ a = (υ_2-υ_1) / (t) $ ir pakeitimas $ A = ma (υ_1t + (es ^ 2) / (2)) = (mat) / (2) (2υ_1 + at) $ turime:
$ A = (m (υ_2-υ_1)) / (2) (2υ_1 + υ_2-υ_1) $
$ A = (mυ_2 ^ 2) / (2) - (mυ_1 ^ 2) / (2) $
Dabar pradinį greitį prilyginę nuliui: $ υ_1 = 0 $, gauname išraišką kinetinė energija:
$ E_K = (mυ) / (2) = (p ^ 2) / (2m) $
Taigi, judantis kūnas turi kinetinę energiją. Ši energija yra lygi darbui, kurį reikia atlikti norint padidinti kūno greitį nuo nulio iki $ υ $ vertės.
Iš $ E_K = (mυ) / (2) = (p ^ 2) / (2m) $ išplaukia, kad jėgos, perkeliančios kūną iš vienos padėties į kitą, darbas yra lygus kinetinės energijos pokyčiui:
$ A = E_ (K_2) -E_ (K_1) = ∆E_K $
Lygybė $ A = E_ (K_2) -E_ (K_1) = ∆E_K $ išreiškia kinetinės energijos kitimo teorema.
Kūno kinetinės energijos pasikeitimas(materialusis taškas) tam tikrą laiką yra lygus per šį laiką kūną veikiančios jėgos atliktam darbui.
Potencinė energija
Potenciali energija yra energija, kurią lemia sąveikaujančių kūnų arba to paties kūno dalių tarpusavio išsidėstymas.
Kadangi energija apibrėžiama kaip kūno gebėjimas atlikti darbą, tai potenciali energija natūraliai apibrėžiama kaip jėgos darbas, kuris priklauso tik nuo santykinės kūnų padėties. Tai yra gravitacijos $ A = mgh_1-mgh_2 = mgH $ ir tamprumo jėgos darbas:
$ A = (kx_0 ^ 2) / (2) - (kx ^ 2) / (2) $
Potenciali kūno energija, Sąveikaujant su Žeme, vadinamas dydis, lygus šio kūno masės $ m $ sandaugai pagal gravitacijos pagreitį $ g $ ir kūno aukštį $ h $ virš Žemės paviršiaus:
Tampriai deformuoto kūno potencinė energija yra vertė, lygi pusei kūno elastingumo (standumo) koeficiento $ k $ ir deformacijos kvadrato $ ∆l $ sandaugos:
$ E_p = (1) / (2) k∆l ^ 2 $
Konservatyvių jėgų (gravitacijos ir elastingumo) darbas, atsižvelgiant į $ E_p = mgh $ ir $ E_p = (1) / (2) k∆l ^ 2 $, išreiškiamas taip:
$ A = E_ (p_1) -E_ (p_2) = - (E_ (p_2) -E_ (p_1)) = - ∆E_p $
Ši formulė leidžia pateikti bendrą potencialios energijos apibrėžimą.
Sistemos potencinė energija yra dydis, priklausantis nuo kūnų padėties, kurio pokytis pereinant sistemai iš pradinės būsenos į galutinę būseną yra lygus sistemos vidinių konservatyviųjų jėgų darbui, paimtam su priešingas ženklas.
Minuso ženklas dešinėje lygties pusėje $ A = E_ (p_1) -E_ (p_2) = - (E_ (p_2) -E_ (p_1)) = - ∆E_p $ reiškia, kad atliekant darbą vidinėmis jėgomis (pavyzdžiui, krentant kūnui ant žemės veikiant gravitacijai sistemoje „akmuo – Žemė“), sistemos energija mažėja. Darbas ir potencialios energijos pokyčiai sistemoje visada turi priešingų ženklų.
Kadangi darbas lemia tik potencialios energijos pokytį, tai mechanikoje fizinę reikšmę turi tik energijos pokytis. Todėl nulinės energijos lygio pasirinkimas yra savavališkas ir nulemtas tik patogumo sumetimais, pavyzdžiui, atitinkamų lygčių rašymo paprastumu.
Mechaninės energijos kitimo ir tvermės dėsnis
Visa mechaninė sistemos energija jo kinetinės ir potencialinės energijos suma vadinama:
Jį lemia kūnų padėtis (potencinė energija) ir jų greitis (kinetinė energija).
Pagal kinetinės energijos teoremą,
$ E_k-E_ (k_1) = A_p + A_ (pr), $
kur $ A_p $ yra potencialių jėgų darbas, $ A_ (pr) $ yra nepotencinių jėgų darbas.
Savo ruožtu potencialių jėgų darbas yra lygus kūno potencinės energijos skirtumui pradinėje $ E_ (p_1) $ ir galutinėje $ E_p $ būsenose. Turėdami tai omenyje, gauname išraišką mechaninės energijos kitimo dėsnis:
$ (E_k + E_p) - (E_ (k_1) + E_ (p_1)) = A_ (pr) $
kur kairioji lygybės pusė yra visos mechaninės energijos pokytis, o dešinioji – nepotencinių jėgų darbas.
Taigi, mechaninės energijos kitimo dėsnis skaito:
Sistemos mechaninės energijos pokytis lygus visų nepotencinių jėgų darbui.
Mechaninė sistema, kurioje veikia tik potencialios jėgos, vadinama konservatyvia.
Konservatyvioje sistemoje $ A_ (pr) = 0 $. tai reiškia mechaninis energijos tvermės dėsnis:
Uždaroje konservatyvioje sistemoje bendra mechaninė energija išsaugoma (laikui bėgant nekinta):
$ E_k + E_p = E_ (k_1) + E_ (p_1) $
Mechaninės energijos tvermės dėsnis kildinamas iš Niutono mechanikos dėsnių, kurie taikomi materialių taškų (arba makrodalelių) sistemai.
Tačiau mechaninės energijos tvermės dėsnis galioja ir mikrodalelių sistemai, kur patys Niutono dėsniai nebegalioja.
Mechaninės energijos tvermės dėsnis yra laiko homogeniškumo pasekmė.
Laiko vienodumas susideda iš to, kad tomis pačiomis pradinėmis sąlygomis fizinių procesų eiga nepriklauso nuo momento, kada šios sąlygos susidaro.
Suminės mechaninės energijos tvermės dėsnis reiškia, kad konservatyvioje sistemoje pasikeitus kinetinei energijai, turėtų keistis ir jos potenciali energija, kad jų suma liktų pastovi. Tai reiškia galimybę vienos rūšies energiją paversti kita.
Atsižvelgiant į įvairias materijos judėjimo formas, nagrinėjamos įvairios energijos rūšys: mechaninė, vidinė (lygi molekulių chaotiško judėjimo kinetinės energijos kūno masės centro atžvilgiu ir potencialios sąveikos energijos sumai). molekulių tarpusavyje), elektromagnetinė, cheminė (kuri susideda iš elektronų judėjimo kinetinės energijos ir elektrinės jų sąveikos tarpusavyje ir su atominiais branduoliais energijos), branduolinė ir kt. Iš to, kas pasakyta, aišku. kad energijos skirstymas į skirtingus tipus yra gana savavališkas.
Gamtos reiškinius dažniausiai lydi vienos energijos rūšies transformacija į kitą. Taigi, pavyzdžiui, įvairių mechanizmų dalių trintis veda prie mechaninės energijos pavertimo šiluma, tai yra vidinė energija.Šilumos varikliuose, atvirkščiai, vidinė energija virsta mechanine energija; galvaniniuose elementuose cheminė energija paverčiama elektros energija ir kt.
Šiuo metu energijos sąvoka yra viena iš pagrindinių fizikos sąvokų. Ši koncepcija yra neatsiejamai susijusi su vienos judėjimo formos pavertimo kita idėja.
Šiuolaikinėje fizikoje energijos sąvoka suformuluota taip:
Energija yra bendras kiekybinis visų rūšių medžiagų judėjimo ir sąveikos matas. Energija neatsiranda iš nieko ir neišnyksta, ji gali tik pereiti iš vienos formos į kitą. Energijos sąvoka sujungia visus gamtos reiškinius.
Paprasti mechanizmai. Mechanizmų efektyvumas
Paprasti mechanizmai vadinami įtaisais, kurie keičia kūną veikiančių jėgų dydį arba kryptį.
Jie naudojami dideliems kroviniams perkelti arba kelti su nedidelėmis pastangomis. Tai yra svirtis ir jos atmainos - blokai (judantys ir fiksuoti), vartai, pasvirusi plokštuma ir jos atmainos - pleištas, varžtas ir kt.
Svirties rankena. Sverto taisyklė
Ranka yra tvirtas kūnas, kuris gali suktis aplink fiksuotą atramą.

Sverto taisyklė sako:
Svirtis yra subalansuota, jei jai taikomos jėgos yra atvirkščiai proporcingos jų pečiams:
$ (F_2) / (F_1) = (l_1) / (l_2) $
Iš formulės $ (F_2) / (F_1) = (l_1) / (l_2) $, taikydami jai proporcingumo savybę (kraštinių proporcijos narių sandauga yra lygi jos vidurinių narių sandaugai), gali gauti tokią formulę:
Tačiau $ F_1l_1 = M_1 $ yra jėgos, linkusios pasukti svirtį pagal laikrodžio rodyklę, momentas, o $ F_2l_2 = M_2 $ yra jėgos, linkusios pasukti svirtį prieš laikrodžio rodyklę, momentas. Taigi, $ M_1 = M_2 $, kaip reikia.
Svirtį žmonės pradėjo naudoti senovėje. Su jo pagalba buvo galima pakelti sunkias akmens plokštes statant piramides Senovės Egipte. Be svertų tai nebūtų buvę įmanoma. Iš tiesų, pavyzdžiui, Cheopso piramidės, kurios aukštis siekia 147 m, statybai buvo panaudota daugiau nei du milijonai riedulių, iš kurių mažiausio masė siekė 2,5 USD tonų!
Šiais laikais svirtys plačiai naudojamos tiek gamyboje (pavyzdžiui, kranai), tiek kasdieniame gyvenime (žirklės, vielos pjaustytuvai, svarstyklės).
Fiksuotas blokas
Fiksuoto bloko veikimas panašus į vienodų rankų svirties veikimą: $ l_1 = l_2 = r $. Taikoma jėga $ F_1 $ yra lygi apkrovai $ F_2 $, o pusiausvyros sąlyga yra:
Fiksuotas blokas naudojamas, kai reikia keisti jėgos kryptį nekeičiant jos dydžio.
Kilnojamas blokas
Judamas blokas veikia kaip svirtis, kurios petys yra: $ l_2 = (l_1) / (2) = r $. Šiuo atveju pusiausvyros sąlyga yra tokia:
kur $ F_1 $ yra taikoma jėga, $ F_2 $ yra apkrova. Naudojant kilnojamąjį bloką, stiprumas padidėja dvigubai.
„Polyspast“ (blokų sistema)

Įprastą skriemulio bloką sudaro $ n $ kilnojamųjų ir $ n $ fiksuotų blokų. Jo taikymas suteikia stiprumo padidėjimą $ 2n $ kartų:
$ F_1 = (F_2) / (2n) $
Galios skriemulys susideda iš n kilnojamojo ir vieno fiksuoto bloko. Naudojant galios dėsnio skriemulio bloką, stiprumas padidėja $ 2 ^ n $ kartų:
$ F_1 = (F_2) / (2 ^ n) $

Varžtas
Sraigtas yra pasvirusi plokštuma, apvyniota ant ašies.

Propelerį veikiančių jėgų pusiausvyros sąlyga yra tokia:
$ F_1 = (F_2h) / (2πr) = F_2tgα, F_1 = (F_2h) / (2πR) $

kur $ F_1 $ - išorinė jėga, veikianti varžtą ir veikianti atstumu $ R $ nuo jo ašies; $ F_2 $ - jėga, veikianti varžto ašies kryptimi; $ h $ - varžto žingsnis; $ r $ - vidutinis sriegio spindulys; $ α $ - sriegio pasvirimo kampas. $ R $ yra svirties (veržliarakčio), kuri suka varžtą $ F_1 $ jėga, ilgis.
Efektyvumas
Naudingumo koeficientas (COP) – naudingo darbo ir visų panaudotų darbų santykis.
Efektyvumas dažnai išreiškiamas procentais ir žymimas graikiška raide $ η $ ("tai"):
$ η = (A_п) / (A_3) 100 % $
kur $ A_n $ yra naudingas darbas, $ A_3 $ yra visas išleistas darbas.
Naudingas darbas visada yra tik dalis viso darbo, kurį žmogus praleidžia naudodamas tą ar kitą mechanizmą.
Dalis tobulo darbo praleidžiama įveikiant trinties jėgas. Kadangi $ A_3> A_n $, efektyvumas visada yra mažesnis nei $ 1 $ (arba $< 100%$).
Kadangi kiekvienas šios lygybės darbas gali būti išreikštas atitinkamos jėgos ir nuvažiuoto atstumo sandauga, jį galima perrašyti taip: $ F_1s_1≈F_2s_2 $.
Tai seka, laimėdami veikiančio mechanizmo pagalba pakeliui pralaimime tiek pat kartų ir atvirkščiai... Šis dėsnis vadinamas auksine mechanikos taisykle.
Auksinė mechanikos taisyklė yra apytikslis dėsnis, nes joje neatsižvelgiama į darbą siekiant įveikti naudojamų prietaisų dalių trintį ir sunkumą. Nepaisant to, jis gali būti labai naudingas analizuojant bet kurio paprasto mechanizmo veikimą.

Taigi, pavyzdžiui, dėl šios taisyklės galime iš karto pasakyti, kad paveiksle parodytas darbuotojas, dvigubai padidinęs kėlimo galią 10 USD cm, turės nuleisti priešingą svirties galą 20 USD. $ cm.
Kūnų susidūrimas. Elastingas ir neelastingas smūgis
Kūnų judėjimo po susidūrimo problemai išspręsti naudojami impulso ir mechaninės energijos tvermės dėsniai: šių dydžių reikšmės po susidūrimo nustatomos pagal žinomus impulsus ir energiją prieš susidūrimą. Apsvarstykite elastingo ir neelastinio smūgio atvejus.
Smūgis vadinamas absoliučiai neelastingu, po kurio kūnai sudaro vieną kūną, judantį tam tikru greičiu. Pastarojo greičio problema išspręsta naudojant impulso išsaugojimo dėsnį kūnų, kurių masės $ m_1 $ ir $ m_2 $ (jei kalbame apie du kūnus), sistemos prieš ir po smūgio:
$ m_1 (υ_1) ↖ (→) + m_2 (υ_2) ↖ (→) = (m_1 + m_2) υ↖ (→) $
Akivaizdu, kad kūnų kinetinė energija neelastinio smūgio metu neišsaugoma (pavyzdžiui, $ (υ_1) ↖ (→) = - (υ_2) ↖ (→) $ ir $ m_1 = m_2 $ po smūgio ji tampa lygi nuliui) .
Smūgis vadinamas absoliučiai elastingu, kai išsaugoma ne tik impulsų suma, bet ir smūgiuojančių kūnų kinetinės energijos suma.
Kad poveikis būtų absoliučiai elastingas, lygtys
$ m_1 (υ_1) ↖ (→) + m_2 (υ_2) ↖ (→) = m_1 (υ "_1) ↖ (→) + m_2 (υ" _2) ↖ (→); $
$ (m_ (1) υ_1 ^ 2) / (2) + (m_ (2) υ_2 ^ 2) / (2) = (m_1 (υ "_1) ^ 2) / (2) + (m_2 (υ" _2) ) ^ 2) / (2) $
kur $ m_1, m_2 $ yra rutulių masės, $ υ_1, υ_2 $ yra rutulių greičiai prieš susidūrimą, $ υ "_1, υ" _2 $ yra rutulių greičiai po smūgio.
USE kodifikatoriaus temos: kūno impulsas, kūnų sistemos impulsas, judesio tvermės dėsnis.
Pulsas kūnas yra vektorinis dydis, lygus kūno masės sandaugai pagal greitį:
Specialių impulso matavimo vienetų nėra. Impulso matmuo yra tiesiog masės matmens ir greičio matmens sandauga:
Kodėl impulso sąvoka įdomi? Pasirodo, juo galima suteikti antrajam Niutono dėsniui kiek kitokią, taip pat itin naudingą formą.
Antrasis Niutono dėsnis impulsų forma
Leisti būti jėgų, veikiančių masės kūnui, rezultatas. Pradedame nuo įprasto antrojo Niutono dėsnio rašymo:
Atsižvelgiant į tai, kad kūno pagreitis yra lygus greičio vektoriaus išvestinei, antrasis Niutono dėsnis perrašomas taip:
Po išvestiniu ženklu įvedame konstantą:
Kaip matote, impulso išvestinė gaunama kairėje pusėje:
. ( 1 )
Santykis (1) yra nauja antrojo Niutono dėsnio rašymo forma.
Antrasis Niutono dėsnis impulsų forma. Kūno impulso išvestinė yra kūnui veikiančių jėgų rezultatas.
Galima sakyti ir taip: susidaranti kūną veikianti jėga lygi kūno impulso kitimo greičiui.
Išvestinė formulėje (1) gali būti pakeista galutinių prieaugių santykiu:
. ( 2 )
Šiuo atveju per laiko intervalą kūną veikia vidutinė jėga. Kuo mažesnė reikšmė, tuo santykis artimesnis išvestinei, o vidutinė jėga yra artimesnė jos momentinei vertei tam tikru laiko momentu.
Užduotyse, kaip taisyklė, laiko intervalas yra gana trumpas. Pavyzdžiui, tai gali būti laikas, kai kamuolys atsitrenkia į sieną, o tada vidutinė jėga, veikianti kamuolį iš sienos pusės smūgio metu.
Vektorius kairėje santykio (2) pusėje vadinamas impulso pasikeitimas metu . Impulso pokytis yra skirtumas tarp galutinio ir pradinio impulso vektorių. Būtent, jei yra kūno impulsas tam tikru pradiniu laiko momentu, yra kūno impulsas po tam tikro laikotarpio, tada impulso pokytis yra skirtumas:
Dar kartą pabrėžiame, kad impulso pokytis yra vektorių skirtumas (1 pav.):
Pavyzdžiui, leiskite kamuoliukui skristi statmenai sienai (impulsas prieš smūgį lygus) ir atšoka neprarasdamas greičio (impulsas po smūgio lygus). Nepaisant to, kad impulso modulis nepasikeitė (), impulsas keičiasi:
Geometriškai ši situacija parodyta fig. 2:
Impulso kitimo modulis, kaip matome, yra lygus rutulio pradinio impulso dvigubam moduliui:.
Perrašykime formulę (2) taip:
, ( 3 )
arba, aprašant impulso pokytį, kaip nurodyta pirmiau:
Kiekis vadinamas jėgos impulsas. Nėra specialaus jėgos impulso matavimo vieneto; jėgos impulso matmuo yra tiesiog jėgos ir laiko matmenų sandauga:
(Atkreipkite dėmesį, kad tai yra dar vienas galimas kūno impulso matavimo vienetas.)
Žodinė lygybės (3) formuluotė yra tokia: kūno judesio pokytis lygus tam tikrą laiką kūną veikiančios jėgos impulsui. Tai, žinoma, vėlgi yra antrasis Niutono dėsnis impulsų forma.
Jėgos skaičiavimo pavyzdys
Kaip pavyzdį, kaip taikyti antrąjį Niutono dėsnį impulsų forma, panagrinėkime šią problemą.
Užduotis.
G masės rutulys, skrendantis horizontaliai m/s greičiu, atsitrenkia į lygią vertikalią sieną ir neprarasdamas greičio atsimuša į ją. Rutulio kritimo kampas (tai yra kampas tarp rutulio judėjimo krypties ir statmens sienai) lygus. Streikas trunka iki. Raskite vidutinę jėgą,
veikiantis kamuolį smūgio metu.
Sprendimas. Pirmiausia parodykime, kad atspindžio kampas yra lygus kritimo kampui, tai yra, rutulys atsimuš į sieną tokiu pat kampu (3 pav.).
Pagal (3) mes turime:. Iš to išplaukia, kad impulso kitimo vektorius bendrakryptis su vektoriumi, tai yra nukreipta statmenai sienelei kamuoliuko atšokimo kryptimi (5 pav.).
 |
| Ryžiai. 5. Į užduotį |
Vektoriai ir
lygus moduliu
(kadangi kamuoliuko greitis nepasikeitė). Todėl trikampis sudarytas iš vektorių ir yra lygiašonis. Tai reiškia, kad kampas tarp vektorių ir yra lygus, tai yra, atspindžio kampas tikrai lygus kritimo kampui.
Be to, dabar atkreipkite dėmesį, kad mūsų lygiašonis trikampis turi kampą (tai kritimo kampas); todėl šis trikampis yra lygiakraštis. Taigi:
Tada reikiama vidutinė jėga, veikianti rutulį:
Kūnų sistemos impulsas
Pradėkime nuo paprastos dviejų kūnų sistemos situacijos. Būtent, tebūnie kūnas 1 ir kūnas 2 su impulsais ir atitinkamai. Šių kūnų sistemos impulsas yra kiekvieno kūno impulsų vektorinė suma:
Pasirodo, kad kūnų sistemos impulsui yra formulė, panaši į antrąjį Niutono dėsnį formoje (1). Išveskime šią formulę.
Visus kitus objektus, su kuriais sąveikauja mūsų svarstomi kūnai 1 ir 2, vadinsime išoriniai kūnai. Jėgos, kuriomis išoriniai kūnai veikia kūnus 1 ir 2, vadinamos išorinės jėgos. Tegul yra išorinė jėga, veikianti kūną 1. Panašiai ir išorinė jėga, veikianti kūną 2 (6 pav.).
Be to, 1 ir 2 kūnai gali sąveikauti vienas su kitu. Tegul kūnas 2 veikia kūną 1 jėga. Tada kūnas 1 veikia kūną 2 jėga. Pagal trečiąjį Niutono dėsnį, jėgos ir yra lygios pagal dydį ir priešingos kryptimi:. Jėga ir yra vidinės jėgos, veikiantis sistemoje.
Parašykime kiekvienam kūnui 1 ir 2 antrąjį Niutono dėsnį (1):
, ( 4 )
. ( 5 )
Pridėkime lygybes (4) ir (5):
Kairėje gautos lygybės pusėje yra išvestinių suma, lygi vektorių ir sumos išvestinei. Dešinėje pusėje, remiantis trečiuoju Niutono dėsniu:
Bet - tai yra kūnų 1 ir 2 sistemos impulsas. Taip pat pažymėkime - tai yra išorinių jėgų, veikiančių sistemą, rezultatas. Mes gauname:
. ( 6 )
Taigi, kūnų sistemos impulso kitimo greitis yra sistemai veikiančių išorinių jėgų rezultatas. Lygybė (6), kuri atlieka antrojo Niutono dėsnio vaidmenį kūnų sistemai, yra tai, ką norėjome gauti.
Formulė (6) buvo gauta dviejų kūnų atveju. Dabar apibendrinkime savo samprotavimus savavališko skaičiaus kūnų sistemoje atveju.
Kūnų sistemos impulsas kūnai vadinami visų į sistemą įtrauktų kūnų impulsų vektorine suma. Jei sistema susideda iš kūnų, tada šios sistemos impulsas yra:
Tada viskas daroma lygiai taip pat, kaip ir aukščiau (tik techniškai atrodo kiek sudėtingiau). Jei kiekvienam kūnui užrašysime lygybes, panašias į (4) ir (5), o tada pridėsime visas šias lygybes, tada kairėje pusėje vėl gausime sistemos impulso išvestinę, o dešinėje bus tik išorinių jėgų suma (vidinės jėgos, sudėjus poromis, pagal trečiąjį Niutono dėsnį duos nulį). Todėl lygybė (6) lieka galioti bendruoju atveju.
Impulso išsaugojimo įstatymas
Kūnų sistema vadinama uždaryta, jei išorinių kūnų veiksmai tam tikros sistemos kūnams yra arba nežymiai maži, arba vienas kitą panaikina. Taigi, esant uždarai kūnų sistemai, esminė yra tik šių kūnų sąveika tarpusavyje, bet ne su jokiais kitais kūnais.
Išorinių jėgų, veikiančių uždarą sistemą, rezultatas yra lygus nuliui:. Šiuo atveju iš (6) gauname:
Bet jei vektoriaus išvestinė išnyksta (vektoriaus kitimo greitis lygus nuliui), tai pats vektorius laikui bėgant nekinta:
Impulsų išsaugojimo įstatymas. Uždarosios kūnų sistemos impulsas laikui bėgant išlieka pastovus bet kokiai kūnų sąveikai šioje sistemoje.
Paprasčiausios impulso išsaugojimo dėsnio problemos išsprendžiamos pagal standartinę schemą, kurią dabar parodysime.
Užduotis. G masės kūnas lygiu horizontaliu paviršiumi juda m/s greičiu. R masės kūnas juda jo link m/s greičiu. Atsiranda absoliučiai neelastingas smūgis (kūnai sulimpa). Raskite kūnų greitį po smūgio.
Sprendimas. Situacija parodyta fig. 7. Ašis nukreipta į pirmojo kūno judėjimą.
 |
| Ryžiai. 7. Į užduotį |
Kadangi paviršius lygus, nėra trinties. Kadangi paviršius yra horizontalus ir juo vyksta judėjimas, gravitacijos jėga ir atramos reakcija subalansuoja viena kitą:
Taigi šių kūnų sistemą veikiančių jėgų vektorinė suma lygi nuliui. Tai reiškia, kad kūnų sistema yra uždara. Todėl jam įvykdytas impulso išsaugojimo įstatymas:
. ( 7 )
Sistemos impulsas prieš smūgį yra kūnų impulsų suma:
Po neelastinio smūgio buvo gautas vienas masės kūnas, kuris juda reikiamu greičiu:
Iš impulso išsaugojimo dėsnio (7) turime:
Iš čia randame po smūgio susiformavusio kūno greitį:
Pereikime prie ašies projekcijų:
Pagal sąlygą turime: m / s, m / s, todėl
Minuso ženklas rodo, kad sulipę kūnai juda priešinga ašiai kryptimi. Siekimo greitis: m/s.
Impulsų projekcijos išsaugojimo dėsnis
Vykdant užduotis dažnai susiduriama su tokia situacija. Kūnų sistema nėra uždara (sistemą veikiančių išorinių jėgų vektorinė suma nėra lygi nuliui), tačiau yra tokia ašis, išorinių jėgų projekcijų ašyje suma lygi nuliui bet kuriuo metu. Tada galime sakyti, kad išilgai tam tikros ašies mūsų kūnų sistema elgiasi kaip uždara, o sistemos impulso projekcija į ašį išsaugoma.
Parodykime tai griežčiau. Projektuokime lygybę (6) į ašį:
Jei atsirandančių išorinių jėgų projekcija išnyksta, tada
Todėl projekcija yra konstanta:
Impulsų projekcijos išsaugojimo dėsnis. Jei sistemą veikiančių išorinių jėgų sumos projekcija į ašį lygi nuliui, tai sistemos impulso projekcija laikui bėgant nekinta.
Pažvelkime į konkrečios problemos pavyzdį, kaip veikia impulsų projekcijos tvermės dėsnis.
Užduotis. Masinis berniukas, čiuoždamas ant lygaus ledo, meta masinį akmenį kampu į horizontą. Raskite greitį, kuriuo berniukas rieda atgal po to, kai buvo išmestas.
Sprendimas. Situacija schematiškai parodyta fig. aštuoni . Berniukas vaizduojamas kaip tiesmukas.
 |
| Ryžiai. 8. Į užduotį |
Sistemos „berniukas + akmuo“ impulsas nėra saugomas. Tai matyti bent jau iš to, kad po metimo atsiranda vertikalioji sistemos impulso dedamoji (būtent vertikalioji akmens impulso dedamoji), kurios iki metimo nebuvo.
Todėl berniuko ir akmens suformuota sistema nėra uždara. Kodėl? Faktas yra tas, kad metimo metu išorinių jėgų vektorinė suma nėra lygi nuliui. Reikšmė yra didesnė už sumą, ir dėl šio pertekliaus atsiranda vertikalus sistemos impulso komponentas.
Tačiau išorinės jėgos veikia tik vertikaliai (be trinties). Todėl impulso projekcija horizontalioje ašyje išsaugoma. Prieš metimą ši projekcija buvo lygi nuliui. Nukreipdami ašį į metimą (kad berniukas eitų neigiamos pusašios kryptimi), gauname.
Kasdieniame gyvenime, norint apibūdinti žmogų, kuris daro spontaniškus veiksmus, kartais vartojamas epitetas „impulsyvus“. Tuo pačiu metu kai kurie žmonės net neprisimena, o nemaža dalis net nežino, su kokiu fiziniu kiekiu šis žodis asocijuojasi. Kas slepiasi po „kūno impulso“ sąvoka ir kokias savybes jis turi? Tokie puikūs mokslininkai kaip René Descartesas ir Isaacas Newtonas ieškojo atsakymų į šiuos klausimus.
Kaip ir bet kuris mokslas, fizika veikia su aiškiai suformuluotomis sąvokomis. Šiuo metu yra priimtas toks dydžio apibrėžimas, vadinamas kūno impulsu: tai vektorinis dydis, kuris yra kūno mechaninio judėjimo matas (dydis).
Tarkime, kad klausimas nagrinėjamas klasikinės mechanikos rėmuose, ty manoma, kad kūnas juda įprastu, o ne reliatyvistiniu greičiu, o tai reiškia, kad jis yra bent eilės tvarka mažesnis už šviesos greitį vakuume. . Tada pagal 1 formulę apskaičiuojamas kūno pulso modulis (žr. nuotrauką žemiau).
Taigi pagal apibrėžimą ši reikšmė yra lygi kūno masės sandaugai pagal jo greitį, kuriuo kartu nukreipiamas jo vektorius.
SI (Tarptautinė vienetų sistema) impulso matavimo vienetas yra 1 kg / m / s.
Iš kur kilo terminas „impulsas“?
Keletą šimtmečių prieš tai, kai fizikoje atsirado sąvoka apie kūno mechaninio judėjimo dydį, buvo manoma, kad bet kokio judėjimo erdvėje priežastis yra ypatinga jėga – postūmis.
XIV amžiuje Jeanas Buridanas pakoregavo šią koncepciją. Jis siūlė, kad skraidantis trinkelių akmuo turėtų impulsą, tiesiogiai proporcingą jo greičiui, kuris būtų nepakitęs, jei nebūtų oro pasipriešinimo. Tuo pačiu metu, anot šio filosofo, didesnio svorio kūnai turėjo galimybę „sulaikyti“ daugiau tokios varomosios jėgos.
Tolimesnį koncepcijos, vėliau vadinamos impulsu, plėtojimą davė Rene Descartes, pavadinęs ją žodžiais „paspartinimas“. Tačiau jis neatsižvelgė, kad greitis turi kryptį. Štai kodėl jo pateikta teorija kai kuriais atvejais prieštaravo patirčiai ir nesulaukė pripažinimo.

Anglų mokslininkas Johnas Wallisas pirmasis atspėjo, kad impulsas taip pat turėtų turėti kryptį. Tai įvyko 1668 m. Tačiau jam prireikė dar poros metų, kol jis suformulavo gerai žinomą impulso tvermės dėsnį. Teorinį šio fakto įrodymą, nustatytą empiriškai, pateikė Izaokas Niutonas, panaudojęs jo atrastą ir jo vardu pavadintą trečiąjį ir antrąjį klasikinės mechanikos dėsnius.
Materialiųjų taškų sistemos impulsas
Pirmiausia panagrinėkime atvejį, kai kalbame apie greitį, daug mažesnį už šviesos greitį. Tada, pagal klasikinės mechanikos dėsnius, bendras materialių taškų sistemos impulsas yra vektorinis dydis. Ji lygi jų masių sandaugų sumai greičiu (žr. 2 formulę aukščiau esančiame paveikslėlyje).
Šiuo atveju vieno materialaus taško impulsas imamas kaip vektorinis dydis (3 formulė), kuris yra bendrakryptis su dalelės greičiu.
Jei kalbame apie riboto dydžio kūną, tai pirmiausia jis mintyse suskaidomas į mažas dalis. Taigi dar kartą nagrinėjama materialių taškų sistema, tačiau jos impulsas apskaičiuojamas ne įprastiniu sumavimu, o integravimu (žr. 4 formulę).
Kaip matote, priklausomybės nuo laiko nėra, todėl išorinių jėgų neveikiamas (arba jų įtaka abipusiai kompensuojamas) sistemos impulsas laikui bėgant išlieka nepakitęs.

Apsaugos įstatymo įrodymas
Ir toliau laikykime baigtinio dydžio kūną materialių taškų sistema. Kiekvienam iš jų antrasis Niutono dėsnis suformuluotas pagal 5 formulę.
Atkreipkime dėmesį į tai, kad sistema uždaryta. Tada, susumavus visus taškus ir pritaikius trečiąjį Niutono dėsnį, gauname 6 išraišką.
Taigi uždaros sistemos impulsas yra pastovus.
Tautos dėsnis galioja ir tais atvejais, kai bendras iš išorės sistemą veikiančių jėgų kiekis yra lygus nuliui. Iš to išplaukia vienas svarbus konkretus teiginys. Sakoma, kad kūno impulsas yra pastovus, jei nėra išorinės įtakos arba kompensuojama kelių jėgų įtaka. Pavyzdžiui, nesant trinties po smūgio lazda, ritulys turi išlaikyti savo pagreitį. Tokia situacija bus stebima net nepaisant to, kad šį kūną veikia gravitacijos jėga ir atramos (ledo) reakcija, nes, nors ir vienodo dydžio, bet nukreiptos priešingomis kryptimis, yra, jie kompensuoja vienas kitą.
Savybės
Kūno ar materialaus taško impulsas yra adityvus dydis. Ką tai reiškia? Viskas paprasta: mechaninės materialių taškų sistemos impulsas susideda iš visų į sistemą įtrauktų materialių taškų impulsų.
Antroji šio dydžio savybė yra ta, kad jis išlieka nepakitęs sąveikų, keičiančių tik mechanines sistemos charakteristikas, metu.
Be to, impulsas yra nekintamas bet kokio atskaitos sistemos sukimosi atžvilgiu.

Reliatyvistinis atvejis
Tarkime, kad kalbame apie nesąveikaujančius materialius taškus, kurių greitis yra nuo 10 iki 8 laipsnio arba šiek tiek mažesnis SI sistemoje. Trimatis impulsas apskaičiuojamas pagal 7 formulę, kur c suprantamas kaip šviesos greitis vakuume.
Tuo atveju, kai jis uždarytas, galioja impulso išsaugojimo dėsnis. Tuo pačiu metu trimatis impulsas nėra reliatyvistiškai nekintamas dydis, nes yra jo priklausomybė nuo atskaitos sistemos. Taip pat yra 4D parinktis. Vienam materialiam taškui jis nustatomas pagal 8 formulę.
Impulsas ir energija
Šie dydžiai, kaip ir masė, yra glaudžiai susiję vienas su kitu. Praktiniuose uždaviniuose dažniausiai naudojami santykiai (9) ir (10).

Apibrėžimas per de Broglie bangas
1924 m. buvo iškelta hipotezė, kad ne tik fotonai, bet ir bet kurios kitos dalelės (protonai, elektronai, atomai) turi bangų ir dalelių dvilypumą. Jos autorius buvo prancūzų mokslininkas Louisas de Broglie. Jei šią hipotezę išversime į matematikos kalbą, galime teigti, kad su bet kuria dalele, kuri turi energiją ir impulsą, banga yra susieta su dažniu ir ilgiu, išreikštu atitinkamai 11 ir 12 formulėmis (h yra Plancko konstanta).
Iš paskutinio ryšio matome, kad impulso modulis ir bangos ilgis, žymimi raide „lambda“, yra atvirkščiai proporcingi vienas kitam (13).
Jei laikome santykinai mažos energijos dalelę, kuri juda greičiu, neproporcingu šviesos greičiui, tada impulso modulis apskaičiuojamas taip pat, kaip ir klasikinėje mechanikoje (žr. 1 formulę). Todėl bangos ilgis apskaičiuojamas pagal 14 išraišką. Kitaip tariant, jis yra atvirkščiai proporcingas dalelės masės ir greičio sandaugai, ty jos impulsui.

Dabar jūs žinote, kad kūno impulsas yra mechaninio judėjimo matas, ir jūs susipažinote su jo savybėmis. Tarp jų praktiniu požiūriu ypač svarbus išsaugojimo įstatymas. Netgi nuo fizikos nutolę žmonės tai stebi kasdieniame gyvenime. Pavyzdžiui, visi žino, kad šaunamieji ginklai ir artilerijos dalys atšoka iššaudant. Impulso išsaugojimo dėsnį aiškiai parodo biliardo žaidimas. Su jo pagalba galite numatyti kamuoliukų išsiplėtimo kryptį po smūgio.
Įstatymas buvo pritaikytas atliekant skaičiavimus, būtinus tiriant galimų sprogimų pasekmes, kuriant reaktyvinius automobilius, kuriant šaunamuosius ginklus ir daugelyje kitų gyvenimo sričių.
.22 kalibro kulka sveria tik 2g.Jei tokią kulką į ką nors mesti, jis nesunkiai pagaus net ir be pirštinių. Jei bandysite pagauti tokią kulką, kuri išskrido iš snukio 300 m/s greičiu, čia nepadės net pirštinės.
Jei ant jūsų rieda žaislinis vežimėlis, galite jį sustabdyti pirštu. Jei ant jūsų užrieda sunkvežimis, turėtumėte pasitraukti iš kelio.


Apsvarstykite problemą, kuri parodo jėgos impulso ir kūno impulso kitimo ryšį.
Pavyzdys. Rutulio masė yra 400 g, rutulio greitis po smūgio yra 30 m/s. Jėga, kuria koja veikė rutulį, buvo 1500 N, o smūgio laikas – 8 ms. Raskite rutulio jėgos impulsą ir kūno judesio pokytį.

Kūno impulsų pasikeitimas
Pavyzdys.Įvertinkite vidutinę jėgą iš grindų į kamuolį smūgio metu.
1) Smūgio metu kamuolį veikia dvi jėgos: atramos reakcijos jėga, gravitacijos jėga.

Reakcijos jėga keičiasi smūgio metu, todėl galima rasti vidutinę lytinės reakcijos jėgą.
2) Impulso pasikeitimas  korpusas parodytas paveikslėlyje
korpusas parodytas paveikslėlyje

3) Iš antrojo Niutono dėsnio

Svarbiausia prisiminti
1) Kūno impulso, jėgos impulso formulės;
2) Impulso vektoriaus kryptis;
3) Raskite kūno impulso kitimą
Bendras antrojo Niutono dėsnio išvedimas

Grafikas F (t). Kintamo stiprumo
Jėgos impulsas skaitine prasme yra lygus figūros plotui po F (t) grafiku.

Pavyzdžiui, jei jėga nėra pastovi laike, ji didėja tiesiškai F = kt, tada šios jėgos impulsas yra lygus trikampio plotui. Šią jėgą galite pakeisti tokia pastovia jėga, kuri per tą patį laikotarpį pakeis kūno judesį tiek pat.

Vidutinė gaunamoji jėga
IMPULSŲ IŠSAUGOJIMO DĖSNIS
Testavimas internetu
Uždara kūnų sistema
Tai kūnų, kurie sąveikauja tik vienas su kitu, sistema. Nėra išorinių sąveikos jėgų.
Realiame pasaulyje tokia sistema negali egzistuoti; nėra būdo pašalinti bet kokią išorinę sąveiką. Uždara kūnų sistema yra fizinis modelis, kaip ir materialus taškas yra modelis. Tai yra kūnų, neva sąveikaujančių tik tarpusavyje, sistemos modelis, į išorines jėgas neatsižvelgiama, jos apleidžiamos.
Impulso išsaugojimo įstatymas
Uždaroje kūnų sistemoje vektorius kūnų impulsų suma kūnams sąveikaujant nekinta. Jei vieno kūno impulsas padidėjo, tai reiškia, kad kito kūno (ar kelių kūnų) impulsas tuo momentu sumažėjo lygiai tiek pat.
Panagrinėkime pavyzdį. Mergina ir berniukas čiuožia. Uždara kūnų sistema – mergaitė ir berniukas (neatsižvelgiame į trintį ir kitas išorines jėgas). Mergina stovi vietoje, jos impulsas lygus nuliui, nes greitis lygus nuliui (žr. kūno impulso formulę). Po to, kai berniukas, judėdamas tam tikru greičiu, susidurs su mergina, ji taip pat pradės judėti. Dabar jos kūnas turi impulsą. Skaitinė mergaitės impulso reikšmė lygiai tokia pati, kiek sumažėjo berniuko impulsas po susidūrimo.
Vienas 20 kg sveriantis kūnas juda greičiu, antras 4 kg sveriantis kūnas juda ta pačia kryptimi greičiu. Kokie yra kiekvieno kūno impulsai. Koks yra sistemos impulsas?


Kūnų sistemos impulsas yra visų į sistemą įtrauktų kūnų impulsų vektorinė suma. Mūsų pavyzdyje tai yra dviejų vektorių (kadangi mes kalbame apie du kūnus), kurie nukreipti ta pačia kryptimi, suma, todėl

Dabar apskaičiuokime kūnų sistemos impulsą pagal ankstesnį pavyzdį, jei antrasis kūnas juda priešinga kryptimi.

Kadangi kūnai juda priešingomis kryptimis, gauname skirtingų krypčių impulsų vektorinę sumą. Daugiau apie vektorių sumą.

Svarbiausia prisiminti
1) Kas yra uždara kūnų sistema;
2) Impulso tvermės dėsnis ir jo taikymas
Impulsas fizikoje
Išvertus iš lotynų kalbos „impulsas“ reiškia „stumti“. Šis fizinis dydis taip pat vadinamas „judesio kiekiu“. Į mokslą jis buvo įtrauktas maždaug tuo pačiu metu, kai buvo atrasti Niutono dėsniai (XVII a. pabaigoje).
Fizikos šaka, tirianti materialių kūnų judėjimą ir sąveiką, yra mechanika. Impulsas mechanikoje yra vektorinis dydis, lygus kūno masės sandaugai pagal jo greitį: p = mv. Impulso ir greičio vektorių kryptys visada sutampa.
SI sistemoje impulso vienetu laikomas 1 kg sveriančio kūno impulsas, judantis 1 m/s greičiu. Todėl impulso SI vienetas yra 1 kg ∙ m / s.
Skaičiavimo uždaviniuose nagrinėjamos greičio ir impulsų vektorių projekcijos bet kurioje ašyje ir naudojamos šių projekcijų lygtys: pavyzdžiui, jei pasirinkta x ašis, tada nagrinėjamos projekcijos v (x) ir p (x). Pagal impulso apibrėžimą šie dydžiai yra susiję ryšiu: p (x) = mv (x).
Priklausomai nuo to, kuri ašis pasirinkta ir kur ji nukreipta, impulso vektoriaus projekcija į ją gali būti teigiama arba neigiama.
Impulso išsaugojimo įstatymas
Materialių kūnų impulsai jų fizinės sąveikos metu gali keistis. Pavyzdžiui, susidūrus dviem rutuliukams, pakabintiems ant siūlų, jų impulsai tarpusavyje keičiasi: vienas rutulys gali pajudėti iš stacionarios būsenos arba padidinti greitį, o kitas, priešingai, gali sumažinti greitį arba sustoti. Tačiau uždaroje sistemoje, t.y. kai kūnai sąveikauja tik vienas su kitu ir nėra veikiami išorinių jėgų, šių kūnų impulsų vektorinė suma išlieka pastovi bet kuriai jų sąveikai ir judėjimui. Tai yra impulso išsaugojimo dėsnis. Matematiškai tai galima išvesti iš Niutono dėsnių.
Impulso tvermės dėsnis galioja ir tokioms sistemoms, kur kūnus veikia kažkokios išorinės jėgos, tačiau jų vektorių suma lygi nuliui (pavyzdžiui, gravitacijos jėgą atsveria paviršiaus tamprumo jėga). Tradiciškai tokia sistema taip pat gali būti laikoma uždara.
Matematine forma impulso išsaugojimo dėsnis parašytas taip: p1 + p2 +… + p (n) = p1 ’+ p2’ +… + p (n) ’(momentas p yra vektoriai). Dviejų kūnų sistemoje ši lygtis atrodo taip: p1 + p2 = p1 '+ p2' arba m1v1 + m2v2 = m1v1 '+ m2v2'. Pavyzdžiui, nagrinėjamu atveju su kamuoliukais bendras abiejų rutulių impulsas prieš sąveiką bus lygus bendram impulsui po sąveikos.