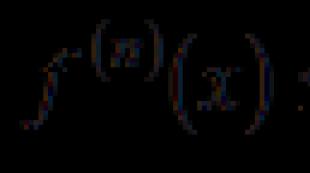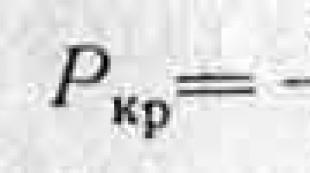2-ші ретті теңдеудің түбірі. Сызықтық біртекті дифференциалдық теңдеулер. Сызықтық біртектінің жалпы шешімін құру
Тұрақты коэффициенттері бар екінші ретті біртекті сызықтық дифференциалдық теңдеулер нысаны болады
мұндағы p және q нақты сандар. Тұрақты коэффициенттері бар біртекті екінші ретті дифференциалдық теңдеулер қалай шешілетініне мысалдарды қарастырайық.
Екінші ретті сызықты біртекті дифференциалдық теңдеудің шешімі сипаттамалық теңдеудің түбірлеріне байланысты. Сипаттамалық теңдеу k²+pk+q=0 теңдеуі болып табылады.
1) Егер сипаттамалық теңдеудің түбірлері әртүрлі нақты сандар болса:
онда тұрақты коэффициенттері бар сызықтық біртекті екінші ретті дифференциалдық теңдеудің жалпы шешімі келесідей болады
2) Егер сипаттамалық теңдеудің түбірлері тең нақты сандар болса
(мысалы, дискриминанты нөлге тең), онда біртекті екінші ретті дифференциалдық теңдеудің жалпы шешімі
3) Егер сипаттамалық теңдеудің түбірлері комплекс сандар болса
(мысалы, дискриминанты теріс санға тең), онда біртекті екінші ретті дифференциалдық теңдеудің жалпы шешімі түрінде жазылады.
Тұрақты коэффициенттері бар сызықтық біртекті екінші ретті дифференциалдық теңдеулерді шешу мысалдары
Біртекті екінші ретті дифференциалдық теңдеулердің жалпы шешімдерін табыңыз:
Сипаттамалық теңдеуді құрастырамыз: k²-7k+12=0. Оның дискриминанты D=b²-4ac=1>0, сондықтан түбірлер нақты сандар болып табылады.
Демек, бұл біртекті 2-ші ретті DE жалпы шешімі болып табылады
Сипаттамалық теңдеуді құрайық және шешейік:
Түбірлер нақты және айқын. Демек, бізде бұл біртекті дифференциалдық теңдеудің жалпы шешімі бар:
Бұл жағдайда сипаттамалық теңдеу
Түбірлер әртүрлі және жарамды. Демек, 2-ші ретті біртекті дифференциалдық теңдеудің жалпы шешімі осында
Сипаттамалық теңдеу
Түбірлер нақты және тең болғандықтан, бұл дифференциалдық теңдеу үшін жалпы шешімін былай жазамыз
Сипаттамалық теңдеу осында
Дискриминант теріс сан болғандықтан, сипаттамалық теңдеудің түбірлері комплекс сандар болып табылады.
Осы біртекті екінші ретті дифференциалдық теңдеудің жалпы шешімі келесідей болады
Сипаттамалық теңдеу
Осы жерден біз бұл дифференциалдың жалпы шешімін табамыз. теңдеулер:
Өзін-өзі тексеруге мысалдар.
§ 9. Тұрақты коэффициенттері бар екінші ретті сызықтық біртекті дифференциалдық теңдеулер
Тұрақты коэффициенттері бар екінші ретті LODE анықтамасы
Сипаттамалық теңдеу:
1-жағдай. Дискриминант нөлден үлкен
2-жағдай. Дискриминант нөлге тең
3-жағдай. Дискриминант нөлден аз
Тұрақты коэффициенттері бар екінші ретті LODE-нің жалпы шешімін табу алгоритмі
§ 10. Тұрақты коэффициенттері бар екінші ретті сызықтық біртекті емес дифференциалдық теңдеулер
Тұрақты коэффициенттері бар екінші ретті LPDE анықтау
Тұрақты шамаларды өзгерту әдісі
Арнайы оң жағы бар LNDDE шешу әдісі
LNDE жалпы шешімінің құрылымы туралы теорема
1. Функция r (x) – дәрежелі көпмүшелік Т
2. Функция r (x) – сан мен көрсеткіштік функцияның көбейтіндісі
3. Функция r (x) – тригонометриялық функциялардың қосындысы
Арнайы оң жағы бар LPDE жалпы шешімін табу алгоритмі
Қолдану
§ 9. Тұрақты коэффициенттері бар екінші ретті сызықтық біртекті дифференциалдық теңдеулер
Екінші ретті дифференциалдық теңдеу деп аталады тұрақты коэффициенттері бар сызықтық біртекті дифференциалдық теңдеу (LODE)., егер ол келесідей көрінсе:
Қайда бЖәне q
LODE-нің жалпы шешімін табу үшін оның екі түрлі ішінара шешімін табу жеткілікті және . Сонда LODE жалпы шешімі пішінге ие болады
Қайда МЕН 1 және МЕН
Леонард Эйлер формада LDE-нің нақты шешімдерін іздеуді ұсынды
Қайда к- белгілі бір сан.
Бұл функцияны екі рет дифференциалдау және орнына өрнектерді қою сағ, у"Және у"теңдеуден аламыз:
Алынған теңдеу деп аталады сипаттамалық теңдеу LODU. Оны құрастыру үшін бастапқы теңдеуде ауыстыру жеткілікті у", у"Және сағсәйкес к 2 , кжәне 1:
Сипаттамалық теңдеуді шешіп, яғни. тамырын тапты к 1 және к 2, біз сондай-ақ бастапқы LODE үшін нақты шешімдер табамыз.
Сипаттамалық теңдеу квадрат теңдеу, оның түбірлері дискриминант арқылы табылады
Бұл жағдайда келесі үш жағдай болуы мүмкін.
1-жағдай. Дискриминант нөлден үлкен , демек, тамырлар к 1 және к 2 жарамды және ерекше:
к 1¹ к 2
Қайда МЕН 1 және МЕН 2 – ерікті тәуелсіз тұрақтылар.
2-жағдай. Дискриминант нөлге тең , демек, тамырлар к 1 және к 2 нақты және тең:
к 1 = к 2 = к
Бұл жағдайда LODE жалпы шешімі нысанға ие болады
Қайда МЕН 1 және МЕН 2 – ерікті тәуелсіз тұрақтылар.
3-жағдай. Дискриминант нөлден аз . Бұл жағдайда теңдеудің нақты түбірі болмайды:
Тамырлар жоқ.
Бұл жағдайда LODE жалпы шешімі нысанға ие болады
Қайда МЕН 1 және МЕН 2 – ерікті тәуелсіз тұрақтылар,
Осылайша, тұрақты коэффициенттері бар екінші ретті LODE-нің жалпы шешімін табу сипаттамалық теңдеудің түбірлерін табуға және теңдеудің жалпы шешіміне арналған формулаларды қолдануға (интегралды есептеуге жүгінбей) келеді.
Тұрақты коэффициенттері бар екінші ретті LODE-нің жалпы шешімін табу алгоритмі:
1. Теңдеуді мұндағы түрге келтіріңіз бЖәне q– кейбір нақты сандар.
2. Сипаттамалық теңдеу құрыңыз.
3. Сипаттамалық теңдеудің дискриминантын табыңыз.
4. Формулаларды қолданып (1-кестені қараңыз) дискриминанттың белгісіне қарай жалпы шешімді жазыңыз.
1-кесте
Мүмкін болатын жалпы шешімдер кестесі
Бұл мақалада біз коэффициенттері тұрақты сызықты біртекті екінші ретті дифференциалдық теңдеулерді шешу принциптерін қарастырамыз, мұндағы p және q ерікті нақты сандар. Алдымен теорияға тоқталайық, содан кейін алынған нәтижелерді мысалдар мен есептерді шешуде қолданайық.
Егер сіз бейтаныс терминдерді кездестірсеңіз, онда дифференциалдық теңдеулер теориясының анықтамалары мен түсініктері бөліміне жүгініңіз.
LOD жалпы шешімін қандай формада табу керектігін көрсететін теореманы құрастырайық.
Теорема.
Х интегралдау интервалында үздіксіз коэффициенттері бар сызықтық біртекті дифференциалдық теңдеудің жалпы шешімі сызықтық комбинациямен анықталады. 
, Қайда 
X бойынша LDE-нің сызықты тәуелсіз ішінара шешімдері және ерікті тұрақтылар.
Сонымен, коэффиценттері тұрақты сызықты біртекті екінші ретті дифференциалдық теңдеудің жалпы шешімі y 0 =C 1 ⋅y 1 +C 2 ⋅y 2 түрінде болады, мұндағы y 1 және y 2 ішінара сызықты тәуелсіз шешімдер, ал C 1 және C 2 - ерікті тұрақтылар. y 1 және y 2 жартылай шешімдерді қалай табуға болатынын үйрену қалды.
Эйлер нысанда нақты шешімдерді іздеуді ұсынды.
Егер коэффиценттері тұрақты екінші ретті LODE-нің ішінара шешімін алсақ, онда бұл шешімді теңдеуге ауыстырған кезде сәйкестендіруді алуымыз керек: 
Осылайша біз деп аталатын нәрсені алдық сипаттамалық теңдеутұрақты коэффициенттері бар екінші ретті сызықтық біртекті дифференциалдық теңдеу. Осы сипаттамалық теңдеудің k 1 және k 2 шешімдері тұрақты коэффициенттері бар екінші ретті LODE-тің ішінара шешімдерін анықтайды.
p және q коэффициенттеріне байланысты сипаттамалық теңдеудің түбірлері болуы мүмкін:
Бірінші жағдайдаБастапқы дифференциалдық теңдеудің сызықты тәуелсіз дербес шешімдері және , коэффициенттері тұрақты екінші ретті LODE-нің жалпы шешімі .
Функциялары және шын мәнінде сызықтық тәуелсіз, өйткені Wronski анықтауышы кез келген нақты x үшін нөлге тең емес.
Екінші жағдайдабелгілі бір шешім - функция. Екінші нақты шешім ретінде біз қабылдаймыз. Тұрақты коэффициенттері бар екінші ретті LODE үшін нақты шешімнің не екенін көрсетейік және y 1 және y 2 сызықтық тәуелсіздігін дәлелдейміз.
k 1 = k 0 және k 2 = k 0 сипаттамалық теңдеудің түбірлері бірдей болғандықтан, оның пішіні болады. Демек, бастапқы сызықтық біртекті дифференциалдық теңдеу. Оны оның орнына қойып, теңдеу сәйкестікке айналатынына көз жеткізейік: 
Осылайша, ол бастапқы теңдеудің ішінара шешімі болып табылады.
және функцияларының сызықтық тәуелсіздігін көрсетейік. Ол үшін Вронски анықтаушысын есептеп, оның нөлден айырмашылығы бар екеніне көз жеткізейік. 
Қорытынды: коэффиценттері тұрақты екінші ретті LODE-лардың сызықты тәуелсіз ішінара шешімдері және , ал жалпы шешімі үшін бар.
Үшінші жағдайдабізде LDE және -ның күрделі парциалды шешімдері бар. Жалпы шешім былай жазылады 
. Бұл нақты шешімдерді екі нақты функциямен ауыстыруға болады 
және , нақты және қиял бөліктеріне сәйкес. Егер жалпы шешімді түрлендірсек, мұны анық көруге болады , формулаларын пайдалана отырып күрделі айнымалы функция теориясытүрі: 
мұндағы C 3 және C 4 ерікті тұрақтылар.
Сонымен, теорияны қорытындылайық.
Тұрақты коэффициенттері бар екінші ретті сызықтық біртекті дифференциалдық теңдеудің жалпы шешімін табу алгоритмі.
Әрбір жағдай үшін мысалдарды қарастырайық.
Мысал.
Коэффиценттері тұрақты екінші ретті сызықты біртекті дифференциалдық теңдеудің жалпы шешімін табыңыз 
.
Екінші ретті сызықтық дифференциалдық теңдеу (LDE) келесі пішінге ие:
Мұндағы , , және шешімі ізделетін интервалда үздіксіз болатын функциялар берілген. 0 (x) ≠ 0 деп есептеп, (2.1)-ді бөлеміз және коэффициенттерге жаңа белгілерді енгізгеннен кейін теңдеуді келесі түрде жазамыз:
(2.2) кез келген бастапқы шарттарды қанағаттандыратын қандай да бір интервалда бірегей шешімі бар екенін дәлелсіз қабылдайық , егер қарастырылып отырған аралықта функциялары , және үздіксіз болса. Егер болса, онда (2.2) теңдеу біртекті деп, ал (2.2) теңдеу басқаша біртекті емес деп аталады.
2-ші ретті лоданың ерітінділерінің қасиеттерін қарастырайық.
Анықтама.Функциялардың сызықтық комбинациясы өрнек болып табылады, мұндағы ерікті сандар.
Теорема.Егер және – шешімі
онда олардың сызықтық комбинациясы да осы теңдеудің шешімі болады.
Дәлелдеу.
(2.3) өрнекті қойып, нәтиже сәйкестік екенін көрсетейік:
Шарттарды қайта реттейік:
Функциялар (2.3) теңдеудің шешімдері болғандықтан, соңғы теңдеудегі жақшалардың әрқайсысы бірдей нөлге тең, бұл дәлелдеуді қажет етеді.
Қорытынды 1.Дәлелденген теоремадан шығатыны, егер (2.3) теңдеудің шешімі болса, онда бұл теңдеудің де шешімі бар.
Қорытынды 2.деп есептесек, Лодтың екі шешімінің қосындысы да осы теңдеудің шешімі екенін көреміз.
Түсініктеме.Теоремада дәлелденген шешімдердің қасиеті кез келген ретті есептер үшін жарамды болып қалады.
§3. Вронскийдің анықтаушысы.
Анықтама.Функциялар жүйесі белгілі бір аралықта сызықты тәуелсіз деп аталады, егер бұл функциялардың ешқайсысы басқаларының сызықтық комбинациясы ретінде ұсынылмаса.
Екі функция жағдайында бұл мынаны білдіреді 
, яғни. 
. Соңғы шартты немесе деп қайта жазуға болады 
. Бұл өрнектің алымындағы анықтауыш болып табылады 
және функциялары үшін Вронски анықтаушысы деп аталады. Осылайша, екі сызықты тәуелсіз функция үшін Вронски анықтауышы бірдей нөлге тең бола алмайды.
Болсын 
сызықтық тәуелсіз шешімдер мен (2.3) теңдеуінің Вронски анықтаушысы болып табылады. Функцияның теңдеуді қанағаттандыратынына алмастыру арқылы көз жеткізейік. (3.1)
Шынымен, . Функциялары және (2.3) теңдеуін қанағаттандыратындықтан, онда, яғни. – (3.1) теңдеуінің шешімі. Осы шешімді табайық: ; . Қайда, 
. 
,
, .
Бұл формуланың оң жағында сіз плюс белгісін алуыңыз керек, өйткені тек осы жағдайда сәйкестік алынады. Осылайша,
(3.2)
Бұл формула Лиувилл формуласы деп аталады. Жоғарыда сызықтық тәуелсіз функциялар үшін Вронски анықтауышы бірдей нөлге тең бола алмайтыны көрсетілді. Демек, (2.3) теңдеудің сызықты тәуелсіз шешімдері үшін анықтауыш нөлден өзгеше болатын нүкте бар. Содан кейін Лиувилл формуласынан функция қарастырылатын аралықтағы барлық мәндер үшін нөлге тең болмайтыны шығады, өйткені кез келген мән үшін (3.2) формуланың оң жағындағы екі фактор да нөлге тең емес.
§4. 2 ретті лоданың жалпы шешімінің құрылымы.
Теорема.Егер және (2.3) теңдеудің сызықты тәуелсіз шешімдері болса, онда олардың сызықтық комбинациясы 
, мұндағы және ерікті тұрақтылар, осы теңдеудің жалпы шешімі болады.
Дәлелдеу.
Не 
(2.3) теңдеуінің шешімі болып табылады, 2 ретті Лодо шешімдерінің қасиеттері туралы теоремадан шығады. Біз тек шешімді көрсетуіміз керек 
ерік жалпы, яғни. кез келген бастапқы шарттар үшін ерікті тұрақтыларды осы шарттарды қанағаттандыратындай етіп таңдауға болатынын көрсету қажет. Бастапқы шарттарды мына түрде жазайық:
Тұрақтылар және осы сызықтық алгебралық теңдеулер жүйесінен бірегей түрде анықталады, өйткені бұл жүйенің анықтаушысы Лоду үшін сызықтық тәуелсіз шешімдер үшін Вронски анықтауышының мәні болып табылады:
,
және мұндай анықтауыш, біз алдыңғы абзацта көргеніміздей, нөлге тең емес. Теорема дәлелденді.
Мысал.Функция екенін дәлелдеңдер 
, мұндағы және ерікті тұрақтылар, Лодтың жалпы шешімі болып табылады.
Шешім.
Функциялардың осы теңдеуді қанағаттандыратынын алмастыру арқылы тексеру оңай. Бұл функциялар сызықтық тәуелсіз, өйткені 
. Демек, жалпы шешімнің құрылымы туралы теорема бойынша 2-ші ретті лода 
бұл теңдеудің жалпы шешімі болып табылады.
2-ші ретті дифференциалдық теңдеулер
§1. Теңдеудің ретін азайту әдістері.
2-ші ретті дифференциалдық теңдеу келесі түрде болады:
https://pandia.ru/text/78/516/images/image002_107.gif" width="19" height="25 src=">.gif" width="119" height="25 src="> ( немесе Дифференциалдық" href="/text/category/differentcial/" rel="bookmark">2-ші ретті дифференциалдық теңдеу). 2-ші ретті дифференциалдық теңдеу үшін Коши есебі (1..gif" width="85" height= "25 src" =">.gif" ені="85" биіктігі="25 src=">.gif" биіктігі="25 src=">.
2-ші ретті дифференциалдық теңдеу мына түрде болсын: https://pandia.ru/text/78/516/images/image009_41.gif" height="25 src=">..gif" width="39" height="" 25 src=">.gif" ені="265" биіктігі="28 src=">.
Осылайша, 2-ші ретті теңдеу https://pandia.ru/text/78/516/images/image015_28.gif" width="34" height="25 src=">.gif" width="118" height="" 25 src=">.gif" ені="117" биіктігі="25 src=">.gif" ені="34" биіктігі="25 src=">. Оны шеше отырып, екі ерікті константаға байланысты бастапқы дифференциалдық теңдеудің жалпы интегралды аламыз: DIV_ADBLOCK219">
1-мысал.Дифференциалдық теңдеуді шешіңіз https://pandia.ru/text/78/516/images/image021_18.gif" width="70" height="25 src=">.gif" height="25 src=">.gif " ені="39" биіктік="25 src=">.gif" ені="157" биіктік="25 src=">.gif" ені="112" биіктігі="25 src=">.
Бұл ажыратылатын айнымалылары бар дифференциалдық теңдеу: https://pandia.ru/text/78/516/images/image026_19.gif" width="99" height="41 src=">, i.e.gif" width= " 96" height="25 src=">.gif" ені="53" биіктігі="25 src=">.gif" ені="48" биіктігі="38 src=">..gif" ені=" 99 " биіктігі="38 src=">..gif" ені="95" биіктігі="25 src=">.
2..gif" ені="117" биіктік="25 src=">, яғни..gif" ені="102" биіктік="25 src=">..gif" ені="117" биіктігі= "25 src" =">.gif" ені="106" биіктік="25 src=">.gif" ені="34" биіктігі="25 src=">.gif" ені="117" биіктігі="25 src=" >.gif" ені="111" биіктігі="27 src=">
Шешім.
Бұл 2-ші ретті теңдеу қалаған функцияны қамтымағаны анық https://pandia.ru/text/78/516/images/image043_16.gif" width="98" height="25 src=">.gif" width= " 33" height="25 src=">.gif" width="105" height="36 src=">, бұл сызықтық теңдеу..gif" width="109" height="36 src=">. .gif" width="144" height="36 src=">.gif" height="25 src="> кейбір функциялардан..gif" width="25" height="25 src=">.gif " width="127" height="25 src=">.gif" width="60" height="25 src="> – теңдеудің реті төмендетілген.
§2. 2-ші ретті сызықтық дифференциалдық теңдеу.
Екінші ретті сызықтық дифференциалдық теңдеу (LDE) келесі пішінге ие:
https://pandia.ru/text/78/516/images/image059_12.gif" width="42" height="25 src=">.gif" width="42" height="25 src=">. gif" width="42" height="25 src="> және коэффициенттер үшін жаңа белгілерді енгізгеннен кейін теңдеуді келесі түрде жазамыз:
https://pandia.ru/text/78/516/images/image064_12.gif" width="76" height="25 src=">.gif" width="35" height="25 src=">. gif" ені="30" биіктік="25 src="> үздіксіз..gif" ені="165" биіктік="25 src=">.gif" ені="95" биіктігі="25 src="> – ерікті сандар.
Теорема.Егер https://pandia.ru/text/78/516/images/image074_11.gif" width="42" height="25 src="> - шешім
https://pandia.ru/text/78/516/images/image076_10.gif" width="182" height="25 src="> де осы теңдеудің шешімі болады.
Дәлелдеу.
https://pandia.ru/text/78/516/images/image077_11.gif" width="420" height="25 src="> өрнегін қоямыз.
Шарттарды қайта реттейік:
https://pandia.ru/text/78/516/images/image073_10.gif" width="42" height="25 src=">.gif" width="54" height="25 src=">. gif" width="94" height="25 src="> де осы теңдеудің шешімі болып табылады.
Қорытынды 2. https://pandia.ru/text/78/516/images/image083_11.gif" width="58" height="25 src="> деп есептесек, бұл теңдеудің шешімі де болады.
Түсініктеме.Теоремада дәлелденген шешімдердің қасиеті кез келген ретті есептер үшін жарамды болып қалады.
§3. Вронскийдің анықтаушысы.
Анықтама.Функциялар жүйесі https://pandia.ru/text/78/516/images/image084_10.gif" width="61" height="25 src=">.gif" width="110" height="47 src=" " >..gif" ені="106" биіктік="42 src=">..gif" ені="42" биіктігі="25 src=">.gif" ені="181" биіктігі="47 src= " >.gif" ені="42" биіктік="25 src="> теңдеулер (2.3)..gif" ені="182" биіктік="25 src=">. (3.1)
Шынында да, ..gif" width="18" height="25 src="> теңдеуді қанағаттандырады (2..gif" width="42" height="25 src="> (3.1) теңдеудің шешімі болып табылады). .gif" ені="87" биіктік="28 src=">..gif" ені="182" биіктік="34 src=">..gif" ені="162" биіктігі="42 src="> .gif" width="51" height="25 src="> сәйкестендіру алынады. Осылайша,
https://pandia.ru/text/78/516/images/image107_7.gif" width="18" height="25 src=">, онда теңдеудің сызықты тәуелсіз шешімдері үшін анықтауыш (2..gif) " width= "42" height="25 src=">.gif" height="25 src="> (3.2) формуланың оң жағындағы екі фактор да нөлге тең емес.
§4. 2 ретті лоданың жалпы шешімінің құрылымы.
Теорема.Егер https://pandia.ru/text/78/516/images/image074_11.gif" width="42" height="25 src="> теңдеудің сызықты тәуелсіз шешімдері болса (2..gif" width="" 19" height="25 src=">.gif" width="129" height="25 src=">- (2.3) теңдеудің шешімі, 2-ші ретті нүктеге дейінгі шешімдердің қасиеттері туралы теоремадан шығады. gif" ені="85" биіктігі="25 src=">.gif" ені="19" биіктігі="25 src=">.gif" ені="220" биіктігі="47">
Осы сызықтық алгебралық теңдеулер жүйесіндегі https://pandia.ru/text/78/516/images/image003_79.gif" width="19" height="25 src="> тұрақтылар бірегей түрде анықталады, өйткені анықтауышы бұл жүйе https: //pandia.ru/text/78/516/images/image006_56.gif" width="51" height="25 src=">:
https://pandia.ru/text/78/516/images/image116_7.gif" width="138" height="25 src=">.gif" width="19" height="25 src=">. gif" ені="69" биіктік="25 src=">.gif" ені="235" биіктігі="48 src=">..gif" ені="143" биіктігі="25 src="> (5) ..gif" width="77" height="25 src=">. Алдыңғы абзац бойынша, 2-ші ретті Lod-тың жалпы шешімі, егер осы теңдеудің екі сызықты тәуелсіз жеке шешімдері белгілі болса, оңай анықталады. Қарапайым әдіс. Л.Эйлер ұсынған коэффициенттері тұрақты теңдеудің ішінара шешімдерін табу үшін..gif" width="25" height="26 src=">, алгебралық теңдеуді аламыз, ол сипаттама деп аталады:
https://pandia.ru/text/78/516/images/image124_5.gif" width="59" height="26 src="> k-ның сол мәндері үшін ғана (5.1) теңдеуінің шешімі болады. олар сипаттамалық теңдеудің түбірлері болып табылады (5.2)..gif" width="49" height="25 src=">..gif" width="76" height="28 src=">.gif" width= "205" height="47 src="> және жалпы шешім (5..gif" ені="45" биіктік="25 src=">..gif" ені="74" биіктігі="26 src=" >..gif" width="83" height="26 src=">. Бұл функцияның (5.1) теңдеуін қанағаттандыратынын тексерейік)..gif" width="190" height="26 src=">. Осы өрнектерді ауыстыру (5.1) теңдеуін аламыз
https://pandia.ru/text/78/516/images/image141_6.gif" width="328" height="26 src=">, себебі..gif" width="137" height="26 src=" «>.
Нақты шешімдер https://pandia.ru/text/78/516/images/image145_6.gif" width="86" height="28 src="> сызықты тәуелсіз, себебі..gif" width="166" биіктігі ="26 src=">.gif" ені="45" биіктігі="25 src=">..gif" ені="65" биіктігі="33 src=">.gif" ені="134" биіктігі = "25 src=">.gif" ені="267" биіктік="25 src=">.gif" ені="474" биіктігі="25 src=">.
Бұл теңдіктің сол жағындағы екі жақша да бірдей нөлге тең..gif" width="174" height="25 src=">..gif" width="132" height="25 src="> - бұл (5.1) ..gif" width="129" height="25 src="> теңдеуінің шешімі келесідей болады:
https://pandia.ru/text/78/516/images/image162_6.gif" ені="179" биіктігі="25 src="> f(x) (6.1)
жалпы шешімнің қосындысы ретінде берілген https://pandia.ru/text/78/516/images/image164_6.gif" width="195" height="25 src="> (6.2)
және кез келген нақты шешім https://pandia.ru/text/78/516/images/image166_6.gif" width="87" height="25 src="> (6.1)..gif" теңдеуінің шешімі болады. ені="272" биіктігі="25 src="> f(x). Бұл теңдік сәйкестік болып табылады, себебі..gif" width="128" height="25 src="> f(x). Сондықтан.gif" width="85" height="25 src=">.gif" ені ="138" height="25 src=">.gif" width="18" height="25 src="> - бұл теңдеудің сызықты тәуелсіз шешімдері. Осылайша:
https://pandia.ru/text/78/516/images/image173_5.gif" ені="289" биіктігі="48 src=">
https://pandia.ru/text/78/516/images/image002_107.gif" width="19" height="25 src=">.gif" width="11" height="25 src=">. gif" width="51" height="25 src=">, және мұндай анықтауыш, біз жоғарыда көргеніміздей, жүйеден нөлге тең емес..gif" width="19" height="25 src="> теңдеулер (6 ..gif" ені="76" биіктік="25 src=">.gif" ені="76" биіктігі="25 src=">.gif" ені="140" биіктігі="25 src" ="> теңдеуді шешеді
https://pandia.ru/text/78/516/images/image179_5.gif" width="91" height="25 src="> (6.5) теңдеуіне аламыз, біз аламыз
https://pandia.ru/text/78/516/images/image181_5.gif" ені="140" биіктік="25 src=">.gif" ені="128" биіктігі="25 src="> f (x) (7.1)
мұндағы https://pandia.ru/text/78/516/images/image185_5.gif" width="34" height="25 src="> теңдеуі (7.1) жағдайда оң жағы f(x) ) ерекше түрі бар.Бұл әдіс белгісіз коэффициенттер әдісі деп аталады және оң жақ f(x) түріне байланысты белгілі бір шешімді таңдаудан тұрады.Келесі форманың оң жақтарын қарастырайық:
1..gif" width="282" height="25 src=">.gif" width="53" height="25 src=">, нөлге тең болуы мүмкін. Бұл жағдайда белгілі бір шешімді қабылдау керек пішінді көрсетейік.
а) Егер сан https://pandia.ru/text/78/516/images/image191_5.gif" width="393" height="25 src=">.gif" width="157" height="25" болса src =>>.
Шешім.
Теңдеу үшін https://pandia.ru/text/78/516/images/image195_4.gif" width="86" height="25 src=">..gif" width="62" height="25 src" = ">..gif" ені="101" биіктік="25 src=">.gif" ені="153" биіктігі="25 src=">.gif" ені="383" биіктігі="25 src= " >.
Біз екі бөлікті теңдіктің сол және оң жағында https://pandia.ru/text/78/516/images/image009_41.gif" height="25 src="> етіп азайтамыз.
https://pandia.ru/text/78/516/images/image206_5.gif" ені="111" биіктігі="40 src=">
Алынған теңдеулер жүйесінен мынаны табамыз: https://pandia.ru/text/78/516/images/image208_5.gif" width="189" height="25 src=">, және берілген есептің жалпы шешімі. теңдеу:
https://pandia.ru/text/78/516/images/image190_5.gif" width="11" height="25 src=">.gif" width="423" height="25 src=">,
мұнда https://pandia.ru/text/78/516/images/image212_5.gif" ені="158" биіктігі="25 src=">.
Шешім.
Сәйкес сипаттамалық теңдеу келесі түрде болады:
https://pandia.ru/text/78/516/images/image214_6.gif" width="53" height="25 src=">.gif" width="85" height="25 src=">. gif" width="45" height="25 src=">.gif" width="219" height="25 src=">..gif" width="184" height="35 src=">. Қорытынды бізде жалпы шешім үшін келесі өрнек бар:
https://pandia.ru/text/78/516/images/image223_4.gif" width="170" height="25 src=">.gif" width="13" height="25 src="> тамаша нөлден. Бұл жағдайда нақты шешімнің түрін көрсетейік.
а) Егер сан https://pandia.ru/text/78/516/images/image227_5.gif" width="204" height="25 src=">,
мұндағы https://pandia.ru/text/78/516/images/image226_5.gif" width="16" height="25 src="> - (5..gif") теңдеу үшін сипаттамалық теңдеудің түбірі. ені="229" биіктік="25 src=">,
мұнда https://pandia.ru/text/78/516/images/image229_5.gif" ені="147" биіктігі="25 src=">.
Шешім.
Теңдеу үшін сипаттамалық теңдеудің түбірлері https://pandia.ru/text/78/516/images/image231_4.gif" width="58" height="25 src=">.gif" width="203" биіктігі ="25 src=">.
3-мысалда келтірілген теңдеудің оң жағы ерекше пішінге ие: f(x) https://pandia.ru/text/78/516/images/image235_3.gif" width="50" height="25 src=" ">.gif " ені="55" биіктік="25 src=">.gif" ені="229" биіктігі="25 src=">.
https://pandia.ru/text/78/516/images/image240_2.gif" width="11" height="25 src=">.gif" width="43" height="25 src="" анықтау үшін > және оны берілген теңдеуге ауыстырыңыз:
Ұқсас терминдерге сілтеме жасай отырып, https://pandia.ru/text/78/516/images/image245_2.gif" width="46" height="25 src=">.gif" width="100" биіктіктегі коэффициенттерді теңестіру = "25 src=">.
Берілген теңдеудің соңғы жалпы шешімі: https://pandia.ru/text/78/516/images/image249_2.gif" width="281" height="25 src=">.gif" width="47" " height ="25 src=">.gif" width="10" height="25 src="> сәйкесінше және осы көпмүшелердің біреуі нөлге тең болуы мүмкін. Осы жалпы жағдайда нақты шешімнің түрін көрсетейік. .
а) Егер сан https://pandia.ru/text/78/516/images/image255_2.gif" width="605" height="51">, (7.2)
мұнда https://pandia.ru/text/78/516/images/image257_2.gif" ені="121" биіктігі="25 src=">.
б) Егер https://pandia.ru/text/78/516/images/image210_5.gif" width="80" height="25 src="> саны болса, онда lndu үшін нақты шешім келесідей болады:
https://pandia.ru/text/78/516/images/image259_2.gif" width="17" height="25 src=">. Өрнекте (7..gif" ені="121" биіктігі= " 25 src=">.
4-мысал.Теңдеудің нақты шешімінің түрін көрсетіңіз
https://pandia.ru/text/78/516/images/image262_2.gif" width="129" height="25 src=">..gif" width="95" height="25 src="> . Лодуға арналған жалпы шешім келесі пішінге ие:
https://pandia.ru/text/78/516/images/image266_2.gif" width="183" height="25 src=">..gif" width="42" height="25 src="> ..gif" ені="36" биіктік="25 src=">.gif" ені="351" биіктігі="25 src=">.
Қосымша коэффициенттер https://pandia.ru/text/78/516/images/image273_2.gif" width="34" height="25 src=">.gif" width="42" height="28 src=" > оң жағы f1(x) және Variation" href="/text/category/variatciya/" rel="bookmark">еркін тұрақтылардың вариациялары бар теңдеу үшін арнайы шешім бар (Лагранж әдісі).
Тұрақты коэффициенттері бар және арнайы еркін мүшелері бар теңдеуден басқа жағдайда теңдеудің нақты шешімін тікелей табу өте қиын. Сондықтан теңдеудің жалпы шешімін табу үшін, әдетте, сәйкес біртекті теңдеудің шешімдерінің іргелі жүйесі белгілі болса, квадратуралардағы теңдеудің жалпы шешімін табуға мүмкіндік беретін әдетте ерікті тұрақтылардың вариация әдісі қолданылады. . Бұл әдіс келесідей.
Жоғарыда айтылғандарға сәйкес сызықтық біртекті теңдеудің жалпы шешімі:
https://pandia.ru/text/78/516/images/image278_2.gif" width="46" height="25 src=">.gif" width="51" height="25 src="> - тұрақтылар емес, f(x) функциясының әлі белгісіз кейбір функциялары. . аралықтан алынуы керек. Шын мәнінде, бұл жағдайда Вронски анықтауышы интервалдың барлық нүктелерінде нөлге тең емес, яғни бүкіл кеңістікте - сипаттамалық теңдеудің күрделі түбірі..gif" width="20" height="25 src="> түрінің сызықты тәуелсіз дербес шешімдері:
Жалпы шешім формуласында бұл түбір пішіннің өрнекіне сәйкес келеді.
