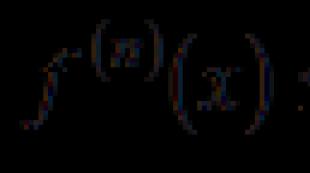Қолөнер

Жазықтық теңдеуі деп нүктеден жазықтыққа дейінгі қашықтықты айтады. Нүктеден жазықтыққа дейінгі қашықтық. жол. Векторлық әдіс

Құпиялықты сақтау біз үшін маңызды. Осы себепті біз сіздің ақпаратыңызды қалай пайдаланатынымызды және сақтайтынымызды сипаттайтын Құпиялылық саясатын әзірледік. Құпиялылық тәжірибелерімізді қарап шығыңыз және сұрақтарыңыз болса, бізге хабарлаңыз.

Жеке ақпаратты жинау және пайдалану

Жеке ақпарат белгілі бір адамды анықтау немесе байланысу үшін пайдаланылуы мүмкін деректерге жатады.

Бізбен байланысқан кез келген уақытта сізден жеке ақпаратыңызды беру сұралуы мүмкін.

Төменде біз жинай алатын жеке ақпарат түрлерінің және мұндай ақпаратты қалай пайдалана алатынымыздың кейбір мысалдары берілген.

Біз қандай жеке ақпаратты жинаймыз:

Сайтта өтініш жіберген кезде біз әртүрлі ақпаратты, соның ішінде атыңызды, телефон нөміріңізді, электрондық пошта мекенжайыңызды және т.б. жинай аламыз.

Жеке ақпаратыңызды қалай қолданамыз:

Біз жинайтын жеке ақпарат бізге бірегей ұсыныстар, жарнамалық акциялар және басқа оқиғалар мен алдағы оқиғалар туралы сізбен байланысуға мүмкіндік береді.
Уақыт өте келе біз сіздің жеке ақпаратыңызды маңызды хабарламалар мен хабарламаларды жіберу үшін пайдалана аламыз.
Сондай-ақ біз жеке ақпаратты біз ұсынатын қызметтерді жақсарту және қызметтерімізге қатысты ұсыныстар беру үшін аудиттер жүргізу, деректерді талдау және әртүрлі зерттеулер сияқты ішкі мақсаттарда пайдалана аламыз.
Егер сіз ұтыс ойынына, конкурсқа немесе ұқсас науқанға қатыссаңыз, біз сіз берген ақпаратты осындай бағдарламаларды басқару үшін пайдалана аламыз.

Ақпаратты үшінші тұлғаларға ашу

Біз сізден алынған ақпаратты үшінші тұлғаларға жария етпейміз.

Ерекшеліктер:

Қажет болған жағдайда - заңға сәйкес, сот тәртібімен, сот ісін жүргізуде және/немесе Ресей Федерациясының аумағындағы мемлекеттік органдардың қоғамдық сұраныстары немесе сұраулары негізінде - жеке мәліметтеріңізді жария етуге. Сондай-ақ, мұндай ашу қауіпсіздік, құқық қорғау немесе басқа да қоғамдық маңызды мақсаттар үшін қажет немесе сәйкес екенін анықтасақ, сіз туралы ақпаратты аша аламыз.
Қайта ұйымдастыру, біріктіру немесе сату жағдайында біз жинаған жеке ақпаратты тиісті мұрагерге үшінші тарапқа бере аламыз.

Жеке ақпаратты қорғау

Біз сіздің жеке ақпаратыңызды жоғалудан, ұрланудан және теріс пайдаланудан, сондай-ақ рұқсатсыз кіруден, жария етуден, өзгертуден және жоюдан қорғау үшін сақтық шараларын, соның ішінде әкімшілік, техникалық және физикалық шараларды қабылдаймыз.

Компания деңгейінде құпиялылығыңызды құрметтеу

Сіздің жеке ақпаратыңыздың қауіпсіз болуын қамтамасыз ету үшін біз қызметкерлерге құпиялылық пен қауіпсіздік стандарттарын хабарлаймыз және құпиялылық тәжірибесін қатаң түрде орындаймыз.

Ара қашықтықты анықтау: 1 - нүкте мен жазықтық; 2 - түзу және тегіс; 3 - ұшақтар; 4 – қиылысатын түзулер бірге қарастырылады, өйткені бұл есептердің барлығының шешу алгоритмі мәні бойынша бірдей және берілген А нүктесі мен α жазықтығы арасындағы қашықтықты анықтау үшін орындалуы қажет геометриялық конструкциялардан тұрады. Егер қандай да бір айырмашылық болса, ол тек 2 және 3 жағдайларда есепті шешуді бастамас бұрын m түзуінде (2-жағдай) немесе β жазықтығында (3-жағдай) ерікті А нүктесін белгілеу керек. қиылысатын түзулер арасындағы қашықтықтарды анықтау үшін алдымен оларды параллель α және β жазықтықтарына қосамыз, содан кейін осы жазықтықтардың арасындағы қашықтықты анықтаймыз.

Мәселені шешудің көрсетілген жағдайларының әрқайсысын қарастырайық.

1. Нүкте мен жазықтықтың арақашықтығын анықтау.

Нүктеден жазықтыққа дейінгі қашықтық нүктеден жазықтыққа жүргізілген перпендикуляр кесіндінің ұзындығымен анықталады.

Сондықтан бұл мәселені шешу келесі графикалық операцияларды ретімен орындаудан тұрады:

1) А нүктесінен α жазықтығына перпендикуляр түсіреміз (269-сурет);

2) осы перпендикулярдың M = a ∩ α жазықтығымен қиылысуының М нүктесін табыңыз;

3) кесіндінің ұзындығын анықтау.

Егер α жазықтығы жалпы жағдайда болса, онда осы жазықтыққа перпендикуляр түсіру үшін алдымен осы жазықтықтың горизонталь және фронталь проекцияларының бағытын анықтау керек. Осы перпендикулярдың жазықтықпен түйісетін нүктесін табу қосымша геометриялық конструкцияларды да қажет етеді.

Егер α жазықтығы проекция жазықтықтарына қатысты белгілі бір орынды алып жатса, есептің шешімі жеңілдетілген. Бұл жағдайда перпендикулярдың проекциясы да, оның жазықтықпен кездесу нүктесін табу да ешқандай қосымша көмекші конструкцияларсыз жүзеге асырылады.

МЫСАЛ 1. А нүктесінен фронталь проекциялық α жазықтығына дейінгі қашықтықты анықтаңыз (270-сурет).

ШЕШІМ. А" арқылы l" ⊥ h 0α перпендикулярының горизонталь проекциясын, ал А" арқылы - оның l" ⊥ f 0α фронталь проекциясын саламыз. М" = l" ∩ f 0α нүктесін белгілейміз. AM || бастап π 2, содан кейін [A" M"] == |AM| = d.

Қарастырылған мысалдан ұшақ проекциялық позицияны алған кезде есептің қаншалықты оңай шешілетіні анық. Сондықтан, егер бастапқы деректерде жалпы позиция жазықтығы көрсетілсе, онда шешімге кіріспес бұрын, жазықтықты кез келген проекция жазықтығына перпендикуляр орынға жылжыту керек.

МЫСАЛ 2. К нүктесінен ΔАВС көрсетілген жазықтыққа дейінгі қашықтықты анықтаңыз (271-сурет).

1. ΔАВС жазықтығын проекциялық жағдайға * ауыстырамыз. Ол үшін xπ 2 /π 1 жүйесінен x 1 π 3 /π 1 жүйесіне көшеміз: жаңа x 1 осінің бағыты үшбұрыштың горизонталь жазықтығының горизонталь проекциясына перпендикуляр таңдалады.

2. ΔABC жаңа π 3 жазықтығына проекциялаңыз (ΔABC жазықтығы [ C " 1 B " 1 ] ішінде π 3-ке проекцияланады).

3. К нүктесін бір жазықтыққа проекциялау (K" → K" 1).

4. K" 1 нүктесі арқылы (K" 1 M" 1)⊥ [C" 1 B" 1] кесіндісін саламыз. Қажетті қашықтық d = |K" 1 M" 1 |

Егер жазықтық іздер арқылы анықталса, есептің шешімі жеңілдетіледі, өйткені деңгей сызықтарының проекцияларын салудың қажеті жоқ.

МЫСАЛ 3. Жолдармен көрсетілген K нүктесінен α жазықтығына дейінгі қашықтықты анықтаңыз (272-сурет).

* Үшбұрыш жазықтығын проекциялау орнына ауыстырудың ең ұтымды жолы проекция жазықтықтарын ауыстыру болып табылады, өйткені бұл жағдайда тек бір ғана көмекші проекцияны тұрғызу жеткілікті.

ШЕШІМ. π 1 жазықтығын π 3 жазықтығымен ауыстырамыз, ол үшін жаңа ось x 1 ⊥ f 0α саламыз. h 0α бойынша ерікті 1" нүктесін белгілеп, оның π 3 (1" 1) жазықтығындағы жаңа горизонталь проекциясын анықтаймыз. X α 1 (X α 1 = h 0α 1 ∩ x 1) және 1" 1 нүктелері арқылы h 0α 1 сызамыз. K → K" 1 нүктесінің жаңа горизонталь проекциясын анықтаймыз. K" 1 нүктесінен h 0α 1 перпендикулярын түсіріп, оның h 0α 1 - M" 1 қиылысу нүктесін белгілейміз. K" 1 M" 1 сегментінің ұзындығы қажетті қашықтықты көрсетеді.

2. Түзу мен жазықтықтың арақашықтығын анықтау.

Түзу мен жазықтық арасындағы қашықтық түзудің еркін нүктесінен жазықтыққа түсірілген перпендикуляр кесіндінің ұзындығымен анықталады (248-суретті қараңыз).

Сондықтан m түзу мен α жазықтығы арасындағы қашықтықты анықтау мәселесінің шешімі нүкте мен жазықтықтың арасындағы қашықтықты анықтауға арналған 1-тармақта қарастырылған мысалдардан еш айырмашылығы жоқ (270 ... 272-суретті қараңыз). Нүкте ретінде m түзуіне жататын кез келген нүктені алуға болады.

3. Жазықтықтар арасындағы қашықтықты анықтау.

Жазықтықтар арасындағы қашықтық бір жазықтықта алынған нүктеден екінші жазықтыққа түсірілген перпендикуляр кесіндінің өлшемімен анықталады.

Бұл анықтамадан α және β жазықтықтарының арақашықтығын табу есебін шешу алгоритмі m түзуі мен α жазықтығы арасындағы қашықтықты анықтау есебін шешуге арналған ұқсас алгоритмнен тек m түзуінің α жазықтығына жатуы керек деген жағдайда ғана ерекшеленетіні шығады. , яғни α және β жазықтықтарының арасындағы қашықтықты анықтау үшін келесідей:

1) α жазықтығында m түзуін алу;

2) m түзуінде еркін А нүктесін таңдау;

3) А нүктесінен β жазықтығына перпендикуляр l түсіреміз;

4) М нүктесін - l перпендикулярының β жазықтығымен түйісетін нүктесін анықтаңыз;

5) кесіндінің өлшемін анықтау.

Тәжірибеде басқа шешім алгоритмін қолданған жөн, оның берілгеннен айырмашылығы тек бірінші қадамға кіріспес бұрын, жазықтықтарды проекциялық позицияға ауыстыру керек.

Бұл қосымша операцияны алгоритмге қосу барлық басқа нүктелердің орындалуын ерекшеліксіз жеңілдетеді, бұл ақыр соңында қарапайым шешімге әкеледі.

МЫСАЛ 1. α және β жазықтықтарының арасындағы қашықтықты анықтаңыз (273-сурет).

ШЕШІМ. xπ 2 /π 1 жүйесінен x 1 π 1 /π 3 жүйесіне көшеміз. Жаңа π 3 жазықтығына қатысты α және β жазықтықтары проекциялық позицияны алады, сондықтан f 0α 1 және f 0β 1 жаңа фронтальды іздер арасындағы қашықтық қалаған болып табылады.

Инженерлік тәжірибеде көбінесе берілген жазықтыққа параллель және одан берілген қашықтықта алынған жазықтықты салу мәселесін шешу қажет. Төмендегі 2-мысал осындай мәселенің шешімін көрсетеді.

МЫСАЛ 2. Берілген α (m || n) жазықтығына параллель β жазықтығының проекцияларын салу қажет, егер олардың арасындағы қашықтық d екені белгілі болса (274-сурет).

1. α жазықтығында ерікті көлденең h (1, 3) және алдыңғы сызықтар f (1,2) сызыңыз.

2. 1 нүктеден α(l" ⊥ h, l" ⊥ f") жазықтығына l перпендикулярын қалпына келтіреміз.

3. l перпендикулярында еркін А нүктесін белгілейміз.

4. Кесіндінің ұзындығын анықтаңыз - (позиция диаграммада l түзуінің метрикалық бұрмаланбаған бағытын көрсетеді).

5. 1 нүктеден бастап түзу сызыққа (1"A 0) = d кесіндісін салыңыз.

6. В 0 нүктесіне сәйкес келетін l" және l" нүктелері В" және В" проекцияларына белгілеңіз.

7. В нүктесі арқылы β (h 1 ∩ f 1) жазықтығын жүргіземіз. β || үшін α, h 1 || шартын орындау қажет h және f 1 || f.

4. Қиылысатын түзулердің арақашықтығын анықтау.

Қиылысатын түзулер арасындағы қашықтық қиылысатын түзулер жататын параллель жазықтықтар арасындағы перпендикуляр ұзындығымен анықталады.

Қиылысатын m және f түзулері арқылы өзара параллель α және β жазықтықтарын жүргізу үшін А нүктесі арқылы (A ∈ m) f түзуіне параллель p түзуін, ал В нүктесі арқылы (В ∈ f) жүргізсек жеткілікті. m түзуіне параллель k түзу. Қиылысатын m және p, f және k түзулері өзара параллель α және β жазықтықтарын анықтайды (248, е-суретті қараңыз). α және β жазықтықтарының арақашықтығы m және f қиылысу сызықтары арасындағы қажетті қашықтыққа тең.

Қиылысатын түзулер арасындағы қашықтықты анықтаудың тағы бір әдісін ұсынуға болады, ол ортогональды проекцияларды түрлендірудің қандай да бір әдісін қолдана отырып, қиылысатын түзулердің бірі проекциялық жағдайға көшірілетіндігінен тұрады. Бұл жағдайда түзудің бір проекциясы нүктеге айналады. Қиылысу сызықтарының жаңа проекциялары арасындағы қашықтық (А" 2 нүктесі және С" 2 D" 2 кесіндісі) талап етілетін қашықтық болып табылады.

Суретте. 275 [AB] және [CD] кесінділері берілген a және b қиылысу сызықтары арасындағы қашықтықты анықтау мәселесінің шешімін көрсетеді. Шешім келесі ретпен орындалады:

1. (а) қиылысу түзулерінің бірін π 3 жазықтығына параллель орынға ауыстырыңыз; Ол үшін xπ 2 /π 1 проекциялық жазықтықтар жүйесінен жаңа x 1 π 1 /π 3, х 1 осі а түзуінің горизонталь проекциясына параллель болады. a" 1 [A" 1 B" 1 ] және b" 1 анықтаңыз.

2. π 1 жазықтығын π 4 жазықтығымен ауыстырып, түзуді аударамыз.

және a" 2, π 4 жазықтығына перпендикуляр орналастыру үшін (жаңа x 2 осі a" 1-ге перпендикуляр жүргізілген).

3. b" 2 - [ C" 2 D" 2 ] түзуінің жаңа горизонталь проекциясын тұрғызыңыз.

4. A" 2 нүктесінен C" 2 D" 2 түзуіне дейінгі қашықтық (сегмент (A" 2 M" 2 ] (қажетті).

Қиылысатын сызықтардың біреуінің проекциялық позицияға ауысуы а және b түзулері қоршауға болатын параллельдік жазықтықтарды проекциялық күйге ауыстырудан басқа ештеңе емес екенін есте ұстаған жөн.

Шындығында, а түзуін π 4 жазықтығына перпендикуляр орынға жылжыту арқылы біз a түзуін қамтитын кез келген жазықтықтың π 4 жазықтығына перпендикуляр болуын қамтамасыз етеміз, оның ішінде a және m түзулерімен анықталған α жазықтығы (a ∩ m, m | | b). Егер енді а түзуіне параллель және b түзуіне қиылысатын n түзуін жүргізсек, онда а және b қиылысатын түзулерін қамтитын параллелизмнің екінші жазықтығы болып табылатын β жазықтығын аламыз. β || бастап α, содан кейін β ⊥ π 4 .

Нүктеден жазықтыққа дейінгі қашықтықты табу аналитикалық геометрияның әртүрлі есептерін шешу кезінде туындайтын кең таралған мәселе; мысалы, бұл есепті қиылысатын екі түзу арасындағы немесе түзу мен жазықтыққа параллель жазықтықтың арасындағы қашықтықты табуға дейін қысқартуға болады. ол.

$β$ жазықтығы мен $β$ жазықтығына жатпайтын $(x_0;y_0; z_0)$ координаталары бар $M_0$ нүктесін қарастырайық.

Анықтама 1

Нүкте мен жазықтық арасындағы ең қысқа қашықтық $M_0$ нүктесінен $β$ жазықтығына жүргізілген перпендикуляр болады.

Сурет 1. Нүктеден жазықтыққа дейінгі қашықтық. Author24 - студенттер жұмысын онлайн алмасу

Төменде біз координат әдісі арқылы нүктеден жазықтыққа дейінгі қашықтықты қалай табуға болатынын қарастырамыз.

Кеңістіктегі нүктеден жазықтыққа дейінгі қашықтықты табудың координаталық әдісінің формуласын шығару

$M_1$ нүктесінде $β$ жазықтығымен $(x_1;y_1; z_1)$ координаталарымен қиылысатын $M_0$ нүктесінен перпендикуляр бағыт векторы $β$ жазықтығының нормаль векторы болатын түзуде жатыр. Бұл жағдайда $n$ бірлік векторының ұзындығы біреуге тең. Сәйкесінше, $β$ нүктесінен $M_0$ нүктесіне дейінгі қашықтық:

$ρ= |\vec(n) \cdot \vec(M_1M_0)|\left(1\right)$, мұнда $\vec(M_1M_0)$ $β$ жазықтығының қалыпты векторы және $\vec( n)$ – қарастырылатын жазықтықтың бірлік нормаль векторы.

Жазықтықтың теңдеуі $Ax+ By + Cz + D=0$ жалпы түрінде берілген жағдайда, жазықтықтың нормаль векторының координаталары $$A;B;C$ теңдеуінің коэффициенттері болып табылады. )$, және бұл жағдайда бірлік қалыпты вектор келесі теңдеу арқылы есептелетін координаттарға ие:

$\vec(n)= \frac($A;B;C$)(\sqrt(A^2 + B^2 + C^2))\left(2\оң)$.

Енді $\vec(M_1M_0)$ қалыпты векторының координаталарын таба аламыз:

$\vec(M_0M_1)= $x_0 – x_1;y_0-y_1;z_0-z_1$\сол(3\оң)$.

Сонымен қатар $β$ жазықтығында жатқан нүктенің координаталары арқылы $D$ коэффициентін өрнектейміз:

$D= Ax_1+By_1+Cz_1$

$(2)$ теңдігінен бірлік нормаль векторының координаталарын $β$ жазықтығының теңдеуіне ауыстыруға болады, сонда бізде:

$ρ= \frac(|A(x_0 -x_1) + B(y_0-y_1)+C(z_0-z_1)|)(\sqrt(A^2+B^2+C^2))= \frac( |Ax_0+ By_0 + Cz_0-(Ax_1+By_1+Cz_1)|)(\sqrt(A^2+B^2+C^2)) = \frac(Ax_0+ By_0 + Cz_0 + D)(\sqrt(A^2) +B^2+C^2))\left(4\оң)$

$(4)$ теңдігі – кеңістіктегі нүктеден жазықтыққа дейінгі қашықтықты табу формуласы.

$M_0$ нүктесінен жазықтыққа дейінгі қашықтықты табудың жалпы алгоритмі

Егер жазықтықтың теңдеуі жалпы түрде берілмесе, алдымен оны жалпы түрге келтіру керек.
Осыдан кейін жазықтықтың жалпы теңдеуінен $M_0$ нүктесі арқылы берілген жазықтықтың нормаль векторын және берілген жазықтыққа жататын нүктені өрнектеу керек, ол үшін $(3)$ теңдігін пайдалану керек. .
Келесі кезең $(2)$ формуласы арқылы жазықтықтың бірлік нормаль векторының координаталарын іздеу.
Соңында нүктеден жазықтыққа дейінгі қашықтықты табуға болады, бұл $\vec(n)$ және $\vec(M_1M_0)$ векторларының скаляр көбейтіндісін есептеу арқылы жүзеге асырылады.

Параллелизм және перпендикулярлық шарттары

1°. Екі жазықтықтың сәйкестік шарты

Екі жазықтық берілсін:

А 1 x + Б 1 ж + C 1 z + D 1 = 0, n 1 = {А 1 ; Б 1 ; C 1 } ≠ 0 ;(1)

А 2 x + Б 2 ж + C 2 z + D 2 = 0, n 2 = {А 2 ; Б 2 ; C 2 } ≠ 0 .(2)

Олар қашан компланар (яғни параллель немесе сәйкес)? Бұл олардың қалыпты векторлары коллинеар болған жағдайда ғана болатыны анық. Салыстырмалылық критерийін қолданып, аламыз

Сөйлем 1.Екі жазықтық компланар болады, егер олардың нормаль векторларының көлденең көбейтіндісі нөлдік векторға тең болса ғана:

[n 1 , n 2 ] = 0 .

2°. Екі жазықтықтың сәйкес келу шарты

Ұсыныс 2.(1) және (2) жазықтықтары сәйкес келеді, егер олардың барлық төрт коэффициенті пропорционал болса, яғни λ саны бар

А 2 = λ А 1 , Б 2 = λ Б 1 , C 2 = λ C 1 , D 2 = λ D 1 . (3)

Дәлелдеу.(3) шарттар орындалсын. Сонда екінші жазықтықтың теңдеуін былай жазуға болады:

λ А 1 x + λ Б 1 ж + λ C 1 z + λ D 1 = 0.

λ ≠ 0, әйтпесе ол болар еді А 2 = Б 2 = C 2 = D 2 = 0, бұл шартқа қайшы келеді n 2 ≠ 0 . Демек, соңғы теңдеу (1) теңдеуіне тең, бұл екі жазықтықтың сәйкес келетінін білдіреді.

Енді, керісінше, бұл ұшақтардың сәйкес келетінін білейік. Сонда олардың нормаль векторлары коллинеар, яғни λ саны бар

А 2 = λ А 1 , Б 2 = λ Б 1 , C 2 = λ C 1 .

Енді (2) теңдеуді келесі түрде қайта жазуға болады:

λ А 1 x + λ Б 1 ж + λ C 1 z + D 2 = 0.

(1) теңдеуді λ-ға көбейтіп, бірінші жазықтықтың эквивалентті теңдеуін аламыз (λ ≠ 0 болғандықтан):

λ А 1 x + λ Б 1 ж + λ C 1 z + λ D 1 = 0.

Бір нүктені алайық ( x 0 , ж 0 , z 0) бірінші (демек, екінші) жазықтықтан және оның координаттарын соңғы екі теңдеуге ауыстырыңыз; дұрыс теңдіктерді аламыз:

λ А 1 x 0 + λ Б 1 ж 0 + λ C 1 z 0 + D 2 = 0 ;

λ А 1 x 0 + λ Б 1 ж 0 + λ C 1 z 0 + λ D 1 = 0.

Жоғарыдан төменгіні алып тастасақ, біз аламыз D 2 − λ D 1 = 0, яғни. D 2 = λ D 1, QED.

3°. Екі жазықтықтың перпендикулярлық шарты

Әлбетте, бұл үшін нормаль векторлардың перпендикуляр болуы қажет және жеткілікті.

Ұсыныс 3.Екі жазықтық перпендикуляр болады, егер қалыпты векторлардың скаляр көбейтіндісі нөлге тең болса ғана:

(n 1 , n 2) = 0 .

Жазық теңдеу берілсін

Балта + Авторы + Cz + D = 0, n = {А; Б; C} ≠ 0 ,

және кезең М 0 = (x 0 , ж 0 , z 0). Нүктеден жазықтыққа дейінгі қашықтық формуласын шығарайық:

Ерікті нүктені алайық Q = (x 1 , ж 1 , z 1) осы жазықтықта жатыр. Оның координаталары жазық теңдеуді қанағаттандырады:

Балта 1 + Авторы 1 + Cz 1 + D = 0.

Енді талап етілетін қашықтыққа назар аударайық гвекторлық проекцияның абсолюттік мәніне тең векторының бағытына n (мұнда проекцияны вектор емес, сандық шама ретінде аламыз). Содан кейін проекцияны есептеу үшін формуланы қолданамыз:

Ұқсас формула қашықтық үшін жарамды гнүктесінен М 0 = (x 0 , ж 0) жалпы теңдеумен берілген түзуге дейінгі жазықтық Балта + Авторы + C = 0.

Ұшақ болсын . Нормалды салайық
координаталар басы арқылы O. Берілсін
– нормальмен құрылған бұрыштар координат осьтерімен.
. Болсын – қалыпты сегменттің ұзындығы
жазықтықпен қиылысқанша. Нормалдың бағыттағы косинустары белгілі деп есептейміз , жазықтықтың теңдеуін шығарамыз .

Болсын
) — жазықтықтағы ерікті нүкте. Бірлік қалыпты вектордың координаттары болады. Вектордың проекциясын табайық
қалыптыға.

Нүктеден бастап Мұшаққа жатады, онда

Бұл берілген жазықтықтың теңдеуі деп аталады қалыпты .

Нүктеден жазықтыққа дейінгі қашықтық

Ұшақ берілсін ,М*
- кеңістіктегі нүкте; г – оның ұшақтан қашықтығы.

Анықтама. Ауытқу ұпай М*жазықтықтан сан деп аталады ( + г), Егер М* қалыпты нүктелердің оң бағыты болатын жазықтықтың екінші жағында жатыр , және саны (- г), егер нүкте жазықтықтың екінші жағында орналасса:

Теорема. Ұшақ жіберіңіз қалыпты бірлікпен қалыпты теңдеумен берілген:

Болсын М*
– кеңістіктегі нүкте Ауытқу t. М* жазықтықтан өрнек арқылы беріледі

Дәлелдеу.Проекция т.
* қалыпты деп белгілейміз Q. Нүктелік ауытқу М*жазықтықтан тең

Ереже.Табу ауытқу Т. М* жазықтықтан t координаталарын жазықтықтың қалыпты теңдеуіне ауыстыру керек. М* . Нүктеден жазықтыққа дейінгі қашықтық .

Жалпы жазық теңдеуді қалыпты түрге келтіру

Бір жазықтық екі теңдеумен анықталсын:

Жалпы теңдеу

Қалыпты теңдеу.

Екі теңдеу де бір жазықтықты анықтайтындықтан, олардың коэффициенттері пропорционал:

Алғашқы үш теңдікті квадраттап, оларды қосайық:

Осы жерден табамыз - нормалаушы фактор:

. (10)

Жазықтықтың жалпы теңдеуін нормалаушы коэффициентке көбейту арқылы жазықтықтың нормаль теңдеуін аламыз:

«Ұшақ» тақырыбына есептер мысалдары.

1-мысал.Жазықтықтың теңдеуін құрыңыз берілген нүктеден өту
(2,1,-1) және жазықтыққа параллель.

Шешім. Жазықтыққа қалыпты :
. Жазықтықтар параллель болғандықтан, нормаль болады қалаған жазықтыққа да қалыпты . Берілген нүктеден (3) өтетін жазықтықтың теңдеуін пайдаланып, жазықтық үшін аламыз теңдеу:

Жауап:

2-мысал.Перпендикулярдың табаны басынан жазықтыққа түскен , мәні болып табылады
. Жазықтықтың теңдеуін табыңыз .

Шешім. Вектор
ұшақ үшін қалыпты жағдай . Нүкте М 0 ұшаққа жатады. Берілген нүкте (3) арқылы өтетін жазықтықтың теңдеуін қолдануға болады:

Жауап:

3-мысал.Ұшақ құрастыру , нүктелер арқылы өту

және жазықтыққа перпендикуляр :.

Сондықтан, белгілі бір уақытта М (x, ж, z) ұшаққа тиесілі болды , үш вектор болуы керек
салыстырмалы болды:

=0.

Анықтауышты ашу және алынған өрнекті жалпы теңдеу (1) түріне келтіру қалды.

4-мысал.Ұшақ жалпы теңдеу арқылы берілген:

Нүктелік ауытқуды табыңыз
берілген жазықтықтан.

Шешім. Жазықтықтың теңдеуін қалыпты түрге келтірейік.

Алынған қалыпты теңдеуге нүктенің координаталарын алайық М*.

Жауап:
.

5-мысал.Жазықтық кесіндіні қиып жатыр ма?

Шешім. Кесу ABұшақты кесіп өтті, ауытқулар Және ұшақтан әртүрлі белгілер болуы керек:

6-мысал.Үш жазықтықтың бір нүктедегі қиылысуы.

Жүйенің бірегей шешімі бар, сондықтан үш жазықтықтың бір ортақ нүктесі бар.

7-мысал.Берілген екі жазықтықпен құрылған екібұрышты бұрыштың биссектрисаларын табу.

Болсын Және - белгілі бір нүктенің ауытқуы
бірінші және екінші жазықтықтардан.

Биссектриса жазықтықтарының бірінде (координаталар басы жататын бұрышқа сәйкес) бұл ауытқулар шамасы мен таңбасы бойынша тең, ал екіншісінде шамасы бойынша тең және таңбасы бойынша қарама-қарсы.

Бұл бірінші биссектриса жазықтығының теңдеуі.

Бұл екінші биссектриса жазықтығының теңдеуі.

8-мысал.Берілген екі нүктенің орнын анықтау Және осы жазықтықтар түзетін екібұрышты бұрыштарға қатысты.