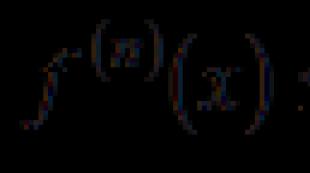Туындыны кім енгізді? Туынды дегеніміз не?Туынды функцияның анықтамасы мен мағынасы. Функцияның нүктедегі туындысының геометриялық мағынасы

В9 есебінде келесі шамалардың бірін анықтау керек болатын функцияның немесе туындының графигі берілген:

1. Қандай да бір нүктедегі туындының мәні x 0,
2. Максималды немесе минималды ұпайлар (экстремум ұпайлары),
3. Функциялардың өсу және кему интервалдары (монтондылық интервалдары).

Бұл есепте берілген функциялар мен туындылар әрқашан үздіксіз болып табылады, бұл шешімді әлдеқайда жеңілдетеді. Тапсырма математикалық талдау бөліміне жататынына қарамастан, оны ең әлсіз оқушылар да орындай алады, өйткені мұнда терең теориялық білім қажет емес.

Туынды, экстремум нүктелері мен монотондылық интервалдарының мәнін табу үшін қарапайым және әмбебап алгоритмдер бар - олардың барлығы төменде талқыланады.

Ақылсыз қателіктер жібермеу үшін B9 мәселесінің шарттарын мұқият оқып шығыңыз: кейде сіз өте ұзақ мәтіндерді кездестіресіз, бірақ шешімнің барысына әсер ететін бірнеше маңызды шарттар бар.

Туынды мәнді есептеу. Екі нүктелік әдіс

Егер мәселеге қандай да бір х 0 нүктесінде осы графикке жанама болатын f(x) функциясының графигі берілсе және осы нүктедегі туындының мәнін табу қажет болса, келесі алгоритм қолданылады:

1. Тангенс графигінен екі «адекватты» нүктені табыңыз: олардың координаттары бүтін болуы керек. Бұл нүктелерді A (x 1 ; y 1) және B (x 2 ; y 2) деп белгілейік. Координаталарды дұрыс жазыңыз - бұл шешімнің негізгі нүктесі және мұнда кез келген қате дұрыс емес жауапқа әкеледі.
2. Координаталарды біле отырып, Δx = x 2 − x 1 аргументінің өсімін және Δy = y 2 − y 1 функциясының өсімшесін есептеу оңай.
3. Соңында D = Δy/Δx туындысының мәнін табамыз. Басқаша айтқанда, функцияның өсімін аргументтің өсіміне бөлу керек - және бұл жауап болады.

Тағы бір рет атап өтейік: А және В нүктелерін жиі болатындай f(x) функциясының графигінен емес, дәл тангенсінен іздеу керек. Тангенс сызығы міндетті түрде кемінде осындай екі нүктеден тұрады - әйтпесе мәселе дұрыс тұжырымдалмайды.

А (−3; 2) және В (−1; 6) нүктелерін қарастырып, өсімшелерді табыңыз:
Δx = x 2 − x 1 = −1 − (−3) = 2; Δy = y 2 − y 1 = 6 − 2 = 4.

Туындының мәнін табайық: D = Δy/Δx = 4/2 = 2.

Тапсырма. Суретте у = f(x) функциясының графигі және абсцисса x 0 нүктесінде оған жанама көрсетілген. f(x) функциясының x 0 нүктесіндегі туындысының мәнін табыңыз.

А (0; 3) және В (3; 0) нүктелерін қарастырыңыз, өсімшелерді табыңыз:
Δx = x 2 − x 1 = 3 − 0 = 3; Δy = y 2 − y 1 = 0 − 3 = −3.

Енді туындының мәнін табамыз: D = Δy/Δx = −3/3 = −1.

Тапсырма. Суретте у = f(x) функциясының графигі және абсцисса x 0 нүктесінде оған жанама көрсетілген. f(x) функциясының x 0 нүктесіндегі туындысының мәнін табыңыз.

А (0; 2) және В (5; 2) нүктелерін қарастырып, өсімдерді табыңыз:
Δx = x 2 − x 1 = 5 − 0 = 5; Δy = y 2 − y 1 = 2 − 2 = 0.

Туындының мәнін табу қалады: D = Δy/Δx = 0/5 = 0.

Соңғы мысалдан біз ережені тұжырымдай аламыз: егер жанама OX осіне параллель болса, функцияның жанама нүктесіндегі туындысы нөлге тең болады. Бұл жағдайда ештеңені санаудың қажеті жоқ - сызбаға қараңыз.

Максималды және минималды ұпайларды есептеу

Кейде функцияның графигінің орнына В9 есебі туындының графигін береді және функцияның ең үлкен немесе ең кіші нүктесін табуды талап етеді. Бұл жағдайда екі нүктелік әдіс пайдасыз, бірақ басқа, одан да қарапайым алгоритм бар. Алдымен терминологияны анықтайық:

1. x 0 нүктесі f(x) функциясының ең үлкен нүктесі деп аталады, егер осы нүктенің кейбір маңайында келесі теңсіздік орындалса: f(x 0) ≥ f(x).
2. x 0 нүктесі f(x) функциясының ең кіші нүктесі деп аталады, егер осы нүктенің кейбір маңайында келесі теңсіздік орындалса: f(x 0) ≤ f(x).

Туынды графиктен максималды және минималды нүктелерді табу үшін мына қадамдарды орындаңыз:

1. Барлық қажет емес ақпаратты алып тастап, туынды графикті қайта сызыңыз. Тәжірибе көрсеткендей, қажетсіз деректер тек шешімге кедергі келтіреді. Сондықтан, біз координат осінде туындының нөлдерін белгілейміз - және солай.
2. Нөлдер арасындағы интервалдардағы туындының таңбаларын табыңыз. Егер қандай да бір x 0 нүктесі үшін f'(x 0) ≠ 0 екені белгілі болса, онда тек екі нұсқа мүмкін: f'(x 0) ≥ 0 немесе f'(x 0) ≤ 0. Туындының таңбасы: бастапқы сызбадан оңай анықтауға болады: егер туынды график OX осінен жоғары жатса, онда f'(x) ≥ 0. Және керісінше, егер туынды график OX осінен төмен болса, онда f'(x) ≤ 0.
3. Туындының нөлдері мен белгілерін қайтадан тексереміз. Таңбаның минустан плюсқа өзгеретін жері - ең төменгі нүкте. Керісінше, егер туындының таңбасы плюстен минусқа өзгерсе, бұл максималды нүкте. Санау әрқашан солдан оңға қарай жүргізіледі.

Бұл схема тек үздіксіз функциялар үшін жұмыс істейді - B9 мәселесінде басқалар жоқ.

Тапсырма. Суретте [−5 аралықта анықталған f(x) функциясының туындысының графигі көрсетілген; 5]. Осы кесіндідегі f(x) функциясының ең кіші нүктесін табыңыз.

Қажетсіз ақпараттан арылып, тек шекараны қалдырайық [−5; 5] және x = −3 және x = 2,5 туындысының нөлдері. Біз сондай-ақ белгілерді атап өтеміз:

Әлбетте, x = −3 нүктесінде туындының таңбасы минустан плюсқа өзгереді. Бұл ең төменгі нүкте.

Тапсырма. Суретте [−3 аралықта анықталған f(x) функциясының туындысының графигі көрсетілген; 7]. Осы кесіндідегі f(x) функциясының ең үлкен нүктесін табыңыз.

Тек шекараларды қалдырып, графикті қайта салайық [−3; 7] және туындының нөлдері x = −1,7 және x = 5. Алынған графиктегі туындының белгілерін белгілейік. Бізде бар:

Әлбетте, x = 5 нүктесінде туындының таңбасы плюстен минусқа өзгереді - бұл максималды нүкте.

Тапсырма. Суретте [−6 аралықта анықталған f(x) функциясының туындысының графигі көрсетілген; 4]. f(x) функциясының [−4 кесіндісіне жататын ең үлкен нүктелерінің санын табыңыз; 3].

Есептің шарттарынан графтың кесіндімен шектелген бөлігін ғана қарастыру жеткілікті екендігі шығады [−4; 3]. Сондықтан біз тек шекараларды белгілейтін жаңа графикті саламыз [−4; 3] және оның ішіндегі туындының нөлдері. Атап айтқанда, x = −3,5 және x = 2 нүктелері. Біз мынаны аламыз:

Бұл графикте бір ғана максималды нүкте x = 2. Дәл осы нүктеде туындының таңбасы плюстен минусқа өзгереді.

Бүтін емес координаталары бар нүктелер туралы шағын ескерту. Мысалы, соңғы есепте x = −3,5 нүктесі қарастырылды, бірақ дәл осындай табыспен х = −3,4 алуға болады. Егер мәселе дұрыс құрастырылған болса, мұндай өзгерістер жауапқа әсер етпеуі керек, өйткені «тұрғылықты жері жоқ» ұпайлары мәселені шешуге тікелей қатыспайды. Әрине, бұл трюк бүтін нүктелермен жұмыс істемейді.

Функциялардың өсу және кему аралықтарын табу

Мұндай есепте максимум және ең кіші нүктелер сияқты функцияның өзі өсетін немесе кемитін аймақтарды табу үшін туынды графикті пайдалану ұсынылады. Алдымен, өсу және кему дегеніміз не екенін анықтайық:

1. Егер осы кесіндінің кез келген екі x 1 және x 2 нүктелері үшін мына тұжырым ақиқат болса, f(x) функциясы кесіндіде өседі деп аталады: x 1 ≤ x 2 ⇒ f(x 1) ≤ f(x 2) . Басқаша айтқанда, аргумент мәні неғұрлым үлкен болса, функция мәні соғұрлым үлкен болады.
2. Егер осы кесіндінің кез келген екі x 1 және x 2 нүктелері үшін мына тұжырым дұрыс болса, f(x) функциясы кесіндіде кемімелі деп аталады: x 1 ≤ x 2 ⇒ f(x 1) ≥ f(x 2) . Анау. Үлкенірек аргумент мәні кішірек функция мәніне сәйкес келеді.

Көбею және азайту үшін жеткілікті шарттарды тұжырымдаймыз:

1. Үздіксіз f(x) функциясының кесіндіде өсуі үшін оның сегмент ішіндегі туындысы оң болуы жеткілікті, яғни. f’(x) ≥ 0.
2. Үздіксіз f(x) функциясының кесіндіде кемуі үшін оның кесінді ішіндегі туындысы теріс болуы жеткілікті, яғни. f’(x) ≤ 0.

Бұл сөздерді дәлелсіз қабылдайық. Осылайша, біз өсу және кему аралықтарын табу схемасын аламыз, ол көптеген жағынан экстремум нүктелерін есептеу алгоритміне ұқсас:

1. Барлық қажет емес ақпаратты алып тастаңыз. Туындының бастапқы графигінде бізді ең алдымен функцияның нөлдері қызықтырады, сондықтан біз тек соларды қалдырамыз.
2. Туындының белгілерін нөлдер арасындағы аралықта белгілеңіз. f’(x) ≥ 0 болған жерінде функция артады, ал f’(x) ≤ 0 болғанда, ол кемиді. Егер мәселе x айнымалысына шектеулер орнатса, біз оларды жаңа графикте қосымша белгілейміз.
3. Енді біз функцияның әрекетін және шектеулерді білеміз, мәселеде қажетті шаманы есептеу қалады.

Тапсырма. Суретте [−3 аралықта анықталған f(x) функциясының туындысының графигі көрсетілген; 7.5]. f(x) функциясының кему аралықтарын табыңыз. Жауабыңызда осы интервалдарға енгізілген бүтін сандардың қосындысын көрсетіңіз.

Әдеттегідей графикті қайта сызып, шекараларды белгілейік [−3; 7.5], сонымен қатар x = −1.5 және x = 5.3 туындысының нөлдері. Содан кейін туындының белгілерін атап өтеміз. Бізде бар:

Туынды (− 1,5) интервалында теріс болғандықтан, бұл функцияның кему интервалы. Осы аралықтағы барлық бүтін сандарды қосу қалады:
−1 + 0 + 1 + 2 + 3 + 4 + 5 = 14.

Тапсырма. Суретте [−10 аралықта анықталған f(x) функциясының туындысының графигі көрсетілген; 4]. f(x) функциясының өсу аралықтарын табыңыз. Жауабыңызда олардың ең үлкенінің ұзындығын көрсетіңіз.

Керек емес ақпараттан арылайық. Тек шекараларды қалдырайық [−10; 4] және туындының нөлдері, олардың осы жолы төртеуі болды: x = −8, x = −6, x = −3 және x = 2. Туындының белгілерін белгілеп, келесі суретті алайық:

Бізді функцияның ұлғаю интервалдары қызықтырады, яғни. онда f’(x) ≥ 0. Графикте мұндай екі интервал бар: (−8; −6) және (−3; 2). Олардың ұзындығын есептейік:
l 1 = − 6 − (−8) = 2;
l 2 = 2 − (−3) = 5.

Интервалдардың ең үлкенінің ұзындығын табу керек болғандықтан, жауап ретінде l 2 = 5 мәнін жазамыз.

Функция нүктеде және оның кейбір маңайында анықталсын. Аргументке нүкте функцияның анықталу облысына түсетіндей өсім берейік. Содан кейін функция ұлғайтылады.

АНЫҚТАУ. Функцияның нүктедегі туындысы осы нүктедегі функция өсімінің аргумент өсіміне қатынасының шегі деп аталады, at (егер бұл шек бар болса және ақырлы болса), яғни.

Белгілеу: ,,,.

Оң жақтағы нүктедегі функцияның туындысы (сол жақта) шақырды

(егер бұл шектеу бар болса және шекті болса).

Белгіленген: , – оң жақтағы нүктедегі туынды,

, сол жақтағы нүктедегі туынды.

Келесі теорема дұрыс екені анық.

ТЕОРЕМА. Функцияның нүктесінде туындысы болады, егер осы нүктеде функцияның оң және сол жағындағы туындылары бар болса және бір-біріне тең болса ғана. Оның үстіне

Төмендегі теорема нүктедегі функцияның туындысының бар болуы мен осы нүктедегі функцияның үздіксіздігі арасындағы байланысты орнатады.

ТЕОРЕМА (нүктедегі функцияның туындысының болуының қажетті шарты). Егер функцияның нүктесінде туындысы болса, онда бұл нүктедегі функция үздіксіз болады.

ДӘЛЕЛ

Бар болсын. Содан кейін

,

Мұнда шексіз аз.

Түсініктеме

функцияның туындысы және белгілеңіз

функцияның дифференциациясы .

ГЕОМЕТРИЯЛЫҚ ЖӘНЕ ФИЗИКАЛЫҚ МӘНІ

1) Туындының физикалық мағынасы. Егер функция және оның аргументі физикалық шамалар болса, онда туынды айнымалының нүктедегі айнымалыға қатысты өзгеру жылдамдығы болып табылады. Мысалы, егер уақыт нүктесінің жүріп өткен жолы болса, оның туындысы уақыт моментіндегі жылдамдық болып табылады. Егер уақыт мезетінде өткізгіштің көлденең қимасы арқылы өтетін электр мөлшері болса, онда уақыт мезетіндегі электр мөлшерінің өзгеру жылдамдығы, яғни. уақыт мезетіндегі ағымдағы күш.

2) Туындының геометриялық мағынасы.

Біраз қисық болсын, қисықтағы нүкте болсын.

Кем дегенде екі нүктені қиылысатын кез келген түзу деп аталады секант .

Бір нүктедегі қисыққа жанама нүкте қисық бойымен қозғалатын болса, секанттың шекті орны деп аталады.

Анықтамадан белгілі болғандай, егер қисыққа жанама нүктеде болса, онда ол жалғыз.

Қисықты қарастырайық (яғни функцияның графигі). Оның нүктесінде тік емес жанама болсын. Оның теңдеуі: (нүкте арқылы өтетін және бұрыштық коэффициенті бар түзудің теңдеуі).

Еңістің анықтамасы бойынша

мұндағы – түзудің оське еңкею бұрышы.

Секанттың оське еңкею бұрышы болсын, мұндағы. Өйткені тангенс, содан кейін қашан

Демек,

Осылайша, біз мұны алдық – нүктедегі функция графигіне жанаманың бұрыштық коэффициенті(функцияның нүктедегі туындысының геометриялық мағынасы). Сондықтан нүктедегі қисыққа жанаманың теңдеуін түрінде жазуға болады

Түсініктеме . Нүктедегі қисыққа жүргізілген жанамаға перпендикуляр нүкте арқылы өтетін түзу деп аталады нүктедегі қисыққа қалыпты . Перпендикуляр түзулердің бұрыштық коэффициенттері қатынас арқылы байланысты болғандықтан, нүктедегі қисыққа нормальдың теңдеуі келесідей болады.

, Егер .

Егер болса, онда нүктедегі қисыққа жанама пішінге ие болады

және қалыпты.

ТАНГЕНТ ЖӘНЕ НОРМАЛДЫ ТЕҢДЕЛЕР

Тангенс теңдеуі

функциясы теңдеу арқылы берілсін ж=f(x), теңдеуді жазу керек жанаманүктесінде x 0. Туынды анықтамасынан:

ж/(x)=limΔ x→0Δ жΔ x

Δ ж=f(x+Δ x)−f(x).

теңдеу жанамафункция графигіне: ж=kx+б (к,б=const). Туындының геометриялық мағынасынан: f/(x 0)=тгα= кӨйткені x 0 және f(x 0)∈ түзу, содан кейін теңдеу жанамабылай жазылады: ж−f(x 0)=f/(x 0)(x−x 0) , немесе

ж=f/(x 0)· x+f(x 0)−f/(x 0)· x 0.

Қалыпты теңдеу

Қалыпты- перпендикуляр жанама(суретті қараңыз). Осының негізінде:

тгβ= тг(2π−α)= ctgα=1 тгα=1 f/(x 0)

Өйткені нормальдың көлбеу бұрышы β1 бұрышы болса, онда бізде:

тгβ1= тг(π−β)=− тгβ=−1 f/(x).

нүкте ( x 0,f(x 0))∈ қалыпты, теңдеу мына түрді алады:

ж−f(x 0)=−1f/(x 0)(x−x 0).

ДӘЛЕЛ

Бар болсын. Содан кейін

,

Мұнда шексіз аз.

Бірақ бұл оның нүктеде үздіксіз екенін білдіреді (үздіксіздіктің геометриялық анықтамасын қараңыз). ∎

Түсініктеме . Функцияның нүктедегі үзіліссіздігі нүктеде осы функцияның туындысының болуы үшін жеткілікті шарт емес. Мысалы, функция үздіксіз, бірақ нүктеде туындысы жоқ. Шынымен,

сондықтан жоқ.

Әлбетте, сәйкестік кейбір жиындарда анықталған функция. Олар оны шақырады функцияның туындысы және белгілеңіз

Функцияның туынды функциясын табу операциясы деп аталады функцияның дифференциациясы .

Қосынды мен айырманың туындысы

Туындылары бізге белгілі f(x) және g(x) функциялары берілсін. Мысалы, жоғарыда қарастырылған қарапайым функцияларды алуға болады. Сонда осы функциялардың қосындысы мен айырмасының туындысын табуға болады:

(f + g)' = f ' + g '

(f - g)’ = f ' - g '

Сонымен, екі функцияның қосындысының (айырымы) туындысы туындылардың қосындысына (айырымы) тең. Қосымша шарттар болуы мүмкін. Мысалы, (f + g + h)' = f' + g' + h'.

Қатаң айтқанда, алгебрада «алу» ұғымы жоқ. «Жағымсыз элемент» деген ұғым бар. Сондықтан f − g айырмасын f + (−1) g қосындысы ретінде қайта жазуға болады, содан кейін бір ғана формула қалады – қосындының туындысы.

Мақаланың мазмұны

ТУЫНДЫ– функцияның туындысы ж = f(x), белгілі бір аралықта берілген ( а, б) нүктесінде xбұл интервал функция өсімінің қатынасы ұмтылатын шек деп аталады fосы нүктеде аргументтің өсімі нөлге ұмтылған кезде аргументтің сәйкес өсіміне дейін.

Туынды әдетте келесідей белгіленеді:

Басқа белгілер де кеңінен қолданылады:

Лезде жылдамдық.

Нүкте болсын Мтүзу сызықта қозғалады. Қашықтық скейбір бастапқы позициядан есептелетін жылжымалы нүкте М 0 , уақытқа байланысты т, яғни. суақыт функциясы бар т: с= f(т). Бір уақытта рұқсат етіңіз тқозғалатын нүкте Мқашықтықта болды сбастапқы позициядан М 0 және келесі сәтте т+D торнын тапты М 1 - қашықтықта с+D сбастапқы позициядан ( суретті қараңыз.).

Осылайша, белгілі бір уақыт аралығында Д тқашықтық ссомасына өзгертілді D с. Бұл жағдайда олар уақыт интервалында D тшамасы с D өсімін алды с.

Орташа жылдамдық барлық жағдайда нүктенің қозғалыс жылдамдығын дәл сипаттай алмайды Мбелгілі бір уақытта т. Егер, мысалы, D интервалының басындағы дене төте тез қозғалады, ал соңында өте баяу, содан кейін орташа жылдамдық нүкте қозғалысының көрсетілген ерекшеліктерін көрсете алмайды және қазіргі уақытта оның қозғалысының шынайы жылдамдығы туралы түсінік бере алмайды т. Орташа жылдамдықты пайдаланып шынайы жылдамдықты дәлірек көрсету үшін D қысқа уақыт кезеңін алу керек т. Нүктенің қазіргі кездегі қозғалыс жылдамдығын толық сипаттайды торташа жылдамдықтың D нүктесіне ұмтылатын шегі т® 0. Бұл шек ағымдағы жылдамдық деп аталады:

Сонымен, берілген мезеттегі қозғалыс жылдамдығы жол өсу қатынасының шегі D деп аталады суақыт ұлғаюына D т, уақыт өсімі нөлге ұмтылғанда. Өйткені

Туындының геометриялық мағынасы. Функция графигіне жанама.

Жанама сызықтарды салу дифференциалдық есептеулердің пайда болуына әкелген мәселелердің бірі болып табылады. Лейбниц жазған дифференциалдық есептеуге қатысты бірінші жарияланған жұмыс деп аталады Бөлшек те, иррационал шамалар да кедергі болып табылмайтын максимумдар мен минимумдардың, сондай-ақ жанамалардың жаңа әдісі және бұл үшін есептеудің ерекше түрі.

Қисық функцияның графигі болсын ж =f(x) тікбұрышты координаталар жүйесінде ( см. күріш.).

Кейбір құндылықта xфункциясы маңызды ж =f(x). Бұл құндылықтар xЖәне жқисықтағы нүкте сәйкес келеді М 0(x, ж). Аргумент болса xберу арттыру D x, содан кейін аргументтің жаңа мәні x+D xжаңа функция мәніне сәйкес келеді y+ D ж = f(x + D x). Қисықтың сәйкес нүктесі нүкте болады М 1(x+D x,ж+D ж). Егер сіз секантты салсаңыз М 0М 1 және j арқылы белгіленеді осьтің оң бағытымен көлденеңінен жасалған бұрыш Өгіз, бұл суреттен бірден байқалады.

Егер қазір Д xнөлге ұмтылады, содан кейін нүкте М 1 нүктеге жақындай отырып, қисық бойымен қозғалады М 0, және бұрыш j D-мен өзгереді x. Сағат Dx® 0 j бұрышы белгілі бір шегіне ұмтылады және нүкте арқылы өтетін түзу М 0 және х осінің оң бағыты, а бұрышы бар құраушы қажетті жанама болады. Оның еңісі:

Демек, f´( x) = tga

анау. туынды мән f´( x) берілген аргумент мәні үшін xфункциясының графигіне жанама арқылы құрылған бұрыштың тангенсіне тең f(x) сәйкес нүктеде М 0(x,ж) оң ось бағытымен Өгіз.

Функциялардың дифференциалдығы.

Анықтама. Егер функция ж = f(x) нүктесінде туындысы бар x = x 0 болса, онда функция осы нүктеде дифференциалданады.

Туындысы бар функцияның үздіксіздігі. Теорема.

Егер функция ж = f(x) белгілі бір уақытта дифференциалданады x = x 0 болса, онда ол осы нүктеде үздіксіз болады.

Осылайша, функцияның үзіліс нүктелерінде туындысы болуы мүмкін емес. Қарама-қарсы тұжырым дұрыс емес, яғни. бір сәтте бұл фактіден x = x 0 функциясы ж = f(x) үзіліссіз болуы оның осы нүктеде дифференциалданатынын білдірмейді. Мысалы, функция ж = |x| барлығы үшін үздіксіз x(–Ґ x x = 0 туындысы жоқ. Бұл кезде графикке жанама жоқ. Оң жақ тангенс пен сол жақ тангенс бар, бірақ олар сәйкес келмейді.

Дифференциалданатын функциялар туралы кейбір теоремалар. Туындының түбірлері туралы теорема (Ролле теоремасы).Егер функция f(x) кесіндіде үздіксіз [а,б], осы сегменттің барлық ішкі нүктелерінде және ұштарында дифференциалданады x = аЖәне x = бнөлге дейін барады ( f(а) = f(б) = 0), содан кейін кесіндінің ішінде [ а,б] кем дегенде бір нүкте бар x= бірге, а c b, онда туынды fў( x) нөлге дейін барады, яғни. fў( в) = 0.

Ақырлы өсу теоремасы (Лагранж теоремасы).Егер функция f(x) [ интервалында үздіксіз а, б] және осы сегменттің барлық ішкі нүктелерінде дифференциалданады, содан кейін кесіндінің ішінде [ а, б] кем дегенде бір нүкте бар бірге, а c b бұл

f(б) – f(а) = fў( в)(б– а).

Екі функцияның өсімшелерінің қатынасы туралы теорема (Коши теоремасы).Егер f(x) Және g(x) – кесіндіде үздіксіз екі функция [а, б] және осы сегменттің барлық ішкі нүктелерінде дифференциалданатын және gў( x) осы сегменттің ішінде еш жерде жоғалмайды, содан кейін сегменттің ішінде [ а, б] мұндай нүкте бар x = бірге, а c b бұл

Әртүрлі ретті туындылар.

Функция болсын ж =f(x) кейбір интервалда дифференциалданады [ а, б]. Туынды мәндер f ў( x), жалпы айтқанда, тәуелді x, яғни. туынды f ў( x) функциясы да болып табылады x. Бұл функцияны дифференциалдау кезінде функцияның екінші туындысы деп аталатынды аламыз f(x), ол белгіленеді f ўў ( x).

Туынды n-функция реті f(x) туындының (бірінші ретті) туындысы деп аталады n- 1- th және белгісімен белгіленеді ж(n) = (ж(n– 1))ў.

Әртүрлі ретті дифференциалдар.

Функция дифференциалы ж = f(x), Қайда x– тәуелсіз айнымалы, иә dy = f ў( x)dx, кейбір функциялардан x, бірақ бастап xбірінші факторға ғана байланысты болуы мүмкін f ў( x), екінші фактор ( dx) тәуелсіз айнымалының өсімі xжәне бұл айнымалының мәніне тәуелді емес. Өйткені dyбастап функциясы бар x, онда бұл функцияның дифференциалын анықтай аламыз. Функцияның дифференциалының дифференциалы осы функцияның екінші дифференциалы немесе екінші ретті дифференциалы деп аталады және белгіленеді. d 2ж:

d(dx) = d 2ж = f ўў( x)(dx) 2 .

Дифференциалды n-бірінші ретті дифференциалдың бірінші дифференциалы деп аталады n- 1- реті:

d n y = d(d n–1ж) = f(n)(x)dx(n).

Жартылай туынды.

Егер функция бір емес, бірнеше аргументке тәуелді болса x i(мен 1-ден өзгереді n,мен= 1, 2,… n),f(x 1,x 2,… x n), содан кейін дифференциалды есептеуде тек бір аргумент өзгерген кезде бірнеше айнымалы функцияның өзгеру жылдамдығын сипаттайтын ішінара туынды ұғымы енгізіледі, мысалы, x i. қатысты 1-ші ретті ішінара туынды x iкәдімгі туынды ретінде анықталады және басқа барлық аргументтер деп болжанады x i, тұрақты мәндерді сақтаңыз. Жартылай туындылар үшін белгілеу енгізіледі

Осылайша анықталған 1-ші ретті жартылай туындылар (бірдей аргументтердің функциялары ретінде) өз кезегінде ішінара туындылары да болуы мүмкін, бұл екінші ретті ішінара туындылар және т.б. Әртүрлі аргументтерден алынған мұндай туындылар аралас деп аталады. Бір ретті үздіксіз аралас туындылар дифференциалдау ретіне тәуелді емес және бір-біріне тең.

Анна Чугайнова

(\large\bf Функцияның туындысы)

Функцияны қарастырыңыз y=f(x), интервалда көрсетілген (а, б). Болсын x- интервалдың кез келген тіркелген нүктесі (а, б), А Δx- мәні болатын ерікті сан x+Δxинтервалына да жатады (а, б). Бұл сан Δxаргумент өсімі деп аталады.

Анықтама. Функция өсімі y=f(x)нүктесінде x, аргумент өсіміне сәйкес Δx, нөмірге хабарласайық

Δy = f(x+Δx) - f(x).

Біз бұған сенеміз Δx ≠ 0. Берілген бекітілген нүктеде қарастырыңыз xосы нүктедегі функция өсімінің сәйкес аргумент өсіміне қатынасы Δx

Бұл қатынасты айырма қатынасы деп атаймыз. Құннан бері xтұрақты деп есептейміз, айырмашылық қатынасы аргументтің функциясы болып табылады Δx. Бұл функция барлық аргумент мәндері үшін анықталған Δx, нүктенің кейбір жеткілікті шағын төңірегіне жатады Δx=0, нүктенің өзін қоспағанда Δx=0. Осылайша, көрсетілген функцияның шегінің болуы туралы мәселені қарауға құқығымыз бар Δx → 0.

Анықтама. Функцияның туындысы y=f(x)берілген бекітілген нүктеде xшегі деп аталады Δx → 0айырмашылық қатынасы, яғни

Бұл шектеу болған жағдайда.

Белгі. y′(x)немесе f′(x).

Туындының геометриялық мағынасы: Функцияның туындысы f(x)бұл кезеңде xосі арасындағы бұрыштың тангенсіне тең Өгізжәне осы функцияның графигіне сәйкес нүктедегі жанама:

f′(x 0) = \tgα.

Туындының механикалық мағынасы: Жолдың уақытқа қатысты туындысы нүктенің түзу сызықты қозғалысының жылдамдығына тең:

Түзуге жанаманың теңдеуі y=f(x)нүктесінде M 0 (x 0 ,y 0)пішінді алады

y-y 0 = f′(x 0) (x-x 0).

Бір нүктедегі қисыққа нормаль сол нүктедегі жанамаға перпендикуляр болады. Егер f′(x 0)≠ 0, содан кейін түзуге нормальдың теңдеуі y=f(x)нүктесінде M 0 (x 0 ,y 0)былай жазылған:

Функцияның дифференциалдығы туралы түсінік

Функция болсын y=f(x)белгілі бір аралықта анықталады (а, б), x- осы аралықтағы кейбір бекітілген аргумент мәні, Δx- аргументтің мәні болатындай аргументтің кез келген өсімі x+Δx ∈ (a, b).

Анықтама. Функция y=f(x)берілген нүктеде дифференциалданатын деп аталады x, егер өсу Δyнүктесінде бұл функция x, аргумент өсіміне сәйкес Δx, түрінде көрсетуге болады

Δy = A Δx +αΔx,

Қайда А- кейбір сан тәуелсіз Δx, А α - аргумент функциясы Δx, ол шексіз аз Δx→ 0.

Екі шексіз аз функцияның туындысы болғандықтан αΔxқарағанда жоғары ретті шексіз аз Δx(3 шексіз аз функцияның қасиеті), онда былай жаза аламыз:

Δy = A Δx +o(Δx).

Теорема. Функция үшін y=f(x)берілген нүктеде дифференциалданатын болды x, бұл нүктеде оның соңғы туындысы болуы қажет және жеткілікті. Бола тұра A=f′(x), яғни

Δy = f′(x) Δx +o(Δx).

Туындыны табу операциясы әдетте дифференциалдау деп аталады.

Теорема. Егер функция y=f(x) x, онда ол осы нүктеде үздіксіз болады.

Түсініктеме. Функцияның үздіксіздігінен y=f(x)бұл кезеңде x, жалпы айтқанда, функцияның дифференциалдығы орындалмайды f(x)бұл кезеңде. Мысалы, функция y=|x|- нүктеде үздіксіз x=0, бірақ туындысы жоқ.

Дифференциалдық функция туралы түсінік

Анықтама. Функция дифференциалы y=f(x)осы функцияның туындысы мен тәуелсіз айнымалының өсімшесінің көбейтіндісі деп аталады x:

dy = y′ Δx, df(x) = f′(x) Δx.

Функция үшін y=xБіз алып жатырмыз dy=dx=x′Δx = 1· Δx= Δx, яғни dx=Δx- тәуелсіз айнымалының дифференциалы осы айнымалының өсімшесіне тең.

Осылайша, біз жаза аламыз

dy = y′ dx, df(x) = f′(x) dx

Дифференциалды dyжәне ұлғайту Δyфункциялары y=f(x)бұл кезеңде x, екеуі де бірдей аргумент өсіміне сәйкес келеді Δx, жалпы айтқанда, бір-біріне тең емес.

Дифференциалдың геометриялық мағынасы: Аргумент өскен кезде функцияның дифференциалы осы функцияның графигіне жанама ординатасының өсіміне тең. Δx.

Дифференциация ережелері

Теорема. Функциялардың әрқайсысы болса u(x)Және v(x)берілген нүктеде дифференциалданады x, содан кейін осы функциялардың қосындысы, айырмасы, көбейтіндісі және бөлімі (бөлінген жағдайда v(x)≠ 0) осы нүктеде де дифференциалданады және формулалар орындалады:

Күрделі функцияны қарастырайық y=f(φ(x))≡ F(x), Қайда y=f(u), u=φ(x). Бұл жағдайда uшақырды аралық аргумент, x - тәуелсіз айнымалы.

Теорема. Егер y=f(u)Және u=φ(x)олардың аргументтерінің дифференциалданатын функциялары, содан кейін күрделі функцияның туындысы y=f(φ(x))бар және аралық аргументке қатысты осы функцияның туындысына және тәуелсіз айнымалыға қатысты аралық аргументтің туындысына тең, яғни.

Түсініктеме. Үш функцияның суперпозициясы болып табылатын күрделі функция үшін y=F(f(φ(x))), дифференциалдау ережесінің пішіні бар

y′ x = y′ u u′ v v′ x,

функциялары қайда v=φ(x), u=f(v)Және y=F(u)- олардың аргументтерінің дифференциалданатын функциялары.

Теорема. Функция болсын y=f(x)артады (немесе азаяды) және нүктенің кейбір маңайында үздіксіз болады x 0. Сонымен қатар, бұл функция көрсетілген нүктеде дифференциалданатын болсын x 0және оның осы кездегі туындысы f′(x 0) ≠ 0. Содан кейін тиісті нүктенің кейбір төңірегінде y 0 =f(x 0)үшін кері анықталады y=f(x)функциясы x=f -1 (y), ал көрсетілген кері функция сәйкес нүктеде дифференциалданады y 0 =f(x 0)және оның осы кездегі туындысы үшін жформула жарамды

Туындылар кестесі

Бірінші дифференциал түрінің инварианттылығы

Күрделі функцияның дифференциалын қарастырайық. Егер y=f(x), x=φ(t)- олардың аргументтерінің функциялары дифференциалданады, содан кейін функцияның туындысы y=f(φ(t))формуласымен өрнектеледі

y′ t = y′ x x′ t.

А- приорит dy=y′ t dt, содан кейін аламыз

dy = y′ t dt = y′ x · x′ t dt = y′ x (x′ t dt) = y′ x dx,

dy = y′ x dx.

Сонымен, біз дәлелдедік

Функцияның бірінші дифференциал түрінің инварианттық қасиеті: аргумент болған жағдайдағыдай xтәуелсіз айнымалы болып табылады және аргумент болған жағдайда xөзі жаңа айнымалының дифференциалданатын функциясы болып табылады dyфункциялары y=f(x)осы функцияның туындысын аргументтің дифференциалына көбейткенге тең dx.

Дифференциалды жуықтап есептеулерде қолдану

дифференциал екенін көрсеттік dyфункциялары y=f(x), жалпы айтқанда, өсімге тең емес Δyбұл функция. Алайда, қарағанда кішіліктің жоғары ретті шексіз аз функциясына дейін Δx, шамамен теңдік жарамды

Δy ≈ dy.

Қатынас осы теңдік теңдігінің салыстырмалы қателігі деп аталады. Өйткені Δy-dy=o(Δx), онда бұл теңдіктің салыстырмалы қателігі азайған сайын қалағандай аз болады |Δх|.

Соны ескере отырып Δy=f(x+δ x)-f(x), dy=f′(x)Δx, Біз алып жатырмыз f(x+δ x)-f(x) ≈ f′(x)Δxнемесе

f(x+δ x) ≈ f(x) + f′(x)Δx.

Бұл шамамен теңдік қателікпен мүмкіндік береді o(Δx)функциясын ауыстырыңыз f(x)нүктенің шағын ауданында x(яғни шағын мәндер үшін Δx) аргументтің сызықтық функциясы Δx, оң жағында тұру.

Жоғары ретті туындылар

Анықтама. Функцияның екінші туындысы (немесе екінші ретті туындысы). y=f(x)оның бірінші туындысының туындысы деп аталады.

Функцияның екінші туындысының белгісі y=f(x):

Екінші туындының механикалық мағынасы. Егер функция y=f(x)түзу бойындағы материалдық нүктенің қозғалыс заңын, содан кейін екінші туындыны сипаттайды f″(x)уақыт моментіндегі қозғалатын нүктенің үдеуіне тең x.

Үшінші және төртінші туындылар да осылай анықталады.

Анықтама. n th туынды (немесе туынды n-ші ретті) функциялары y=f(x)оның туындысы деп аталады n-1ші туынды:

y (n) =(y (n-1))′, f (n) (x)=(f (n-1) (x))′.

Белгілері: y″′, y IV, ж Вжәне т.б.

Туындының геометриялық мағынасы

ҚИСЫСҚА ТАНГЕНТ АНЫҚТАУ Қисық сызыққа жанама y=ƒ(x)нүктесінде Мнүкте арқылы жүргізілген секанттың шекті орны деп аталады Мжәне оған іргелес нүкте М 1нүкте болған жағдайда қисық М 1қисық бойымен нүктеге шексіз жақындайды М. ТУЫНДЫҚТЫҢ ГЕОМЕТРИЯЛЫҚ МӘНІ Функцияның туындысы y=ƒ(x)нүктесінде X 0 сандық жағынан оське көлбеу бұрышының тангенсіне тең Оқисығына жанама y=ƒ(x)нүктесінде M (x 0; ƒ(x 0)).

ҚИСЫСҚА DOTIC VARIATION Қисық сызыққа дейін нүктелі y=ƒ(x)дәл Мнүктесі арқылы жүргізілген түзудің шекаралық орны деп аталады Мжәне онымен келесі нүкте М 1қисық, ақыл-ойдан тыс, қандай нүкте М 1қисық нүктеге еріксіз жақындайды М. ГЕОМЕТРИЯЛЫҚ ЗМИСТ ПОХИДНОЙ Ұқсас функциялар y=ƒ(x)дәл x 0сандық жағынан еңістің оське жанамасына тең Одотикалық, қисыққа дейін орындалады y=ƒ(x)дәл M (x 0; ƒ(x 0)).

Туындының практикалық мағынасы

Белгілі бір функцияның туындысы ретінде тапқан шама іс жүзінде нені білдіретінін қарастырайық.

Ең біріншіден, туынды- бұл функцияның берілген нүктедегі өзгеру жылдамдығын сипаттайтын дифференциалдық есептеудің негізгі түсінігі.

«Өзгеріс жылдамдығы» дегеніміз не? Функцияны елестетіп көрейік f(x) = 5. (x) аргументінің мәніне қарамастан оның мәні ешбір жолмен өзгермейді. Яғни, оның өзгеру жылдамдығы нөлге тең.

Енді функцияны қарастырыңыз f(x) = x. х-тің туындысы бірге тең. Шынында да, (x) аргументіндегі әрбір өзгерген сайын функцияның мәні де бірге өсетінін байқау қиын емес.

Алынған ақпарат тұрғысынан енді жай функциялардың туындылары кестесін қарастырайық. Осының негізінде функцияның туындысын табудың физикалық мәні бірден түсінікті болады. Бұл түсінік практикалық есептерді шешуді жеңілдетуі керек.

Сәйкесінше, туынды функцияның өзгеру жылдамдығын көрсетсе, қос туынды үдеу көрсетеді.

2080.1947