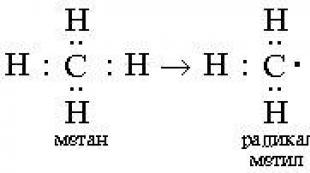მაგარი ნამუშევარი 04/02/12. მიმოვიხილოთ * რომელ განტოლებას ეწოდება კვადრატული? * რომელ განტოლებებს უწოდებენ არასრულ კვადრატულ განტოლებებს? * რომელი. ხაზოვანი განტოლების ცნება. ხაზის განსაზღვრა განტოლების გამოყენებით ნახ.6. ვექტორული ხაზის განტოლება

F ფორმის ტოლობა (x, y) = 0ეწოდება განტოლება ორ ცვლადში x, y,თუ ეს არ არის ჭეშმარიტი ყველა წყვილი რიცხვისთვის x, y.ორ რიცხვს ამბობენ x = x 0 , y=y 0, დააკმაყოფილოს ფორმის გარკვეული განტოლება F(x, y)=0,თუ ცვლადების ნაცვლად ამ რიცხვების ჩანაცვლებისას Xდა ზეგანტოლებაში მისი მარცხენა მხარე ქრება.

მოცემული წრფის განტოლება (განკუთვნილ კოორდინატულ სისტემაში) არის განტოლება ორი ცვლადით, რომელიც კმაყოფილდება ამ წრფეზე მდებარე ყველა წერტილის კოორდინატებით და არ კმაყოფილდება ყოველი წერტილის კოორდინატებით, რომლებიც არ დევს მასზე.

შემდეგში გამოთქმის ნაცვლად მოცემულია „წრფის განტოლება F(x, y) = 0" ჩვენ ხშირად ვიტყვით მოკლედ: მოცემული ხაზი F (x, y) = 0.

თუ მოცემულია ორი წრფის განტოლება F(x, y) = 0და Ф(x, y) = Q,შემდეგ სისტემის ერთობლივი გადაწყვეტა

იძლევა ყველა მათ გადაკვეთის წერტილებს. უფრო ზუსტად, რიცხვების თითოეული წყვილი, რომელიც წარმოადგენს ამ სისტემის ერთობლივ ამოხსნას, განსაზღვრავს ერთ-ერთ გადაკვეთის წერტილს.

*) იმ შემთხვევებში, როდესაც კოორდინატთა სისტემა არ არის დასახელებული, ვარაუდობენ, რომ იგი დეკარტის მართკუთხაა.

157. ქულები მოცემულია *) მ 1 (2; - 2), მ 2 (2; 2), მ 3 (2; - 1), მ 4 (3; -3), მ 5 (5; -5), მ 6 (3; -2). დაადგინეთ, რომელი გამოქვეყნებული წერტილები დევს განტოლებით განსაზღვრულ წრფეზე X+ y = 0,და რომელი არ წევს მასზე. რომელი ხაზი განისაზღვრება ამ განტოლებით? (დახაზეთ იგი ნახატზე.)

158. განტოლებით განსაზღვრულ წრფეზე X 2 +y 2 =25, იპოვეთ წერტილები, რომელთა აბსციები უდრის შემდეგ რიცხვებს: ა) 0, ბ) - 3, გ) 5, დ) 7; იმავე წრფეზე იპოვეთ წერტილები, რომელთა ორდინატები უდრის შემდეგ რიცხვებს: ე) 3, ვ) - 5, გ) - 8. რომელი წრფე განისაზღვრება ამ განტოლებით? (დახაზეთ იგი ნახატზე.)

159. დაადგინეთ რომელი წრფეებია განსაზღვრული შემდეგი განტოლებებით (ააგეთ ისინი ნახაზზე):

1) x - y = 0; 2) x + y = 0; 3) x- 2 = 0; 4) x+ 3 = 0;

5) y - 5 = 0; 6) წ+ 2 = 0; 7) x = 0; 8) წ = 0;

9) x 2 - xy = 0; 10) xy+ y 2 = 0; თერთმეტი) x 2 - წ 2 = 0; 12) xy= 0;

13) y 2 - 9 = 0; 14) xy 2 - 8xy+15 = 0; 15) y 2 +5y+4 = 0;

16) X 2 y - 7xy + 10წ = 0; 17) y =|x|; 18) x =|ზე|; 19)წ + |x|=0;

20) x +|ზე|= 0; 21)y =|X- 1|; 22) წ = |x+ 2|; 23) X 2 + ზე 2 = 16;

24) (x-2) 2 +(წ-1) 2 =16; 25) (x+ 5) 2 +(წ- 1) 2 = 9;

26) (X - 1) 2 + წ 2 = 4; 27) x 2 +(წ + 3) 2 = 1; 28) (x -3) 2 + წ 2 = 0;

29) X 2 + 2წ 2 = 0; 30) 2X 2 + 3წ 2 + 5 = 0

31) (x- 2) 2 + (წ + 3) 2 + 1=0.

160. მოცემული სტრიქონები:

1)X+ y = 0; 2)x - y = 0; 3) x 2 + წ 2 - 36 = 0;

4) x 2 +წ 2 -2x==0; 5) x 2 +წ 2 + 4x-6წ-1 =0.

დაადგინეთ, რომელი მათგანი გადის საწყისზე.

161. მოცემული სტრიქონები:

1) x 2 + წ 2 = 49; 2) (x- 3) 2 + (წ+ 4) 2 = 25;

3) (x+ 6) 2 + (y - 3) 2 = 25; 4) ( x + 5) 2 + (y - 4) 2 = 9;

5) x 2 +წ 2 - 12x + 16y = 0; 6) x 2 +წ 2 - 2x + 8ზე+ 7 = 0;

7) x 2 +წ 2 - 6x + 4y + 12 = 0.

იპოვეთ მათი გადაკვეთის წერტილები: ა) ღერძთან ოჰ;ბ) ღერძით OU.

162.იპოვეთ ორი წრფის გადაკვეთის წერტილები;

1)X 2 +y 2 = 8, x-y = 0;

2) X 2 +y 2 -16x+4ზე+18 = 0, x + y= 0;

3) X 2 +y 2 -2x+4ზე -3 = 0, X 2 + y 2 = 25;

4) X 2 +y 2 -8x+10у+40 = 0, X 2 + y 2 = 4.

163. ქულები მოცემულია პოლარული კოორდინატთა სისტემაში

მ 1 (1; ), მ 2 (2; 0), მ 3 (2; )

მ 4 (
;) და მ 5 (1; )

დაადგინეთ, რომელი წერტილი დევს განტოლებით განსაზღვრულ წრფეზე პოლარულ კოორდინატებში  = 2 cos  და რომელი არ დევს მასზე. რომელი ხაზი განისაზღვრება ამ განტოლებით? (დახატე ნახატზე :)

164.  = განტოლებით განსაზღვრულ წრფეზე , იპოვეთ წერტილები, რომელთა პოლარული კუთხეები უდრის შემდეგ რიცხვებს: ა) ბ) - , გ) 0, დ) . რომელი ხაზი განისაზღვრება ამ განტოლებით?

(აშენეთ იგი ნახატზე.)

165.განტოლებით განსაზღვრულ წრფეზე  = იპოვეთ წერტილები, რომელთა პოლარული რადიუსი უდრის შემდეგ რიცხვებს: ა) 1, ბ) 2, გ)
. რომელი ხაზი განისაზღვრება ამ განტოლებით? (აშენეთ იგი ნახატზე.)

166. დაადგინეთ, რომელი წრფეებია განსაზღვრული პოლარულ კოორდინატებში შემდეგი განტოლებებით (ააგეთ ისინი ნახაზზე):

1)  = 5; 2)  = ; 3)  = ; 4)  cos  = 2; 5)  sin  = 1;

6)  = 6 cos ; 7)  = 10 ცოდვა ; 8) ცოდვა  = 9) ცოდვა  =

167. ააგეთ არქიმედეს შემდეგი სპირალები ნახაზზე:

1)  = 5, 2)  = 5; 3)  = ; 4)р = -1.

168. ააგეთ ნახატზე შემდეგი ჰიპერბოლური სპირალები:

1)  = ; 2) = ; 3) = ; 4) = - .

169. ააგეთ ნახაზზე შემდეგი ლოგარითმული სპირალები:

,
.

170. განსაზღვრეთ იმ მონაკვეთების სიგრძეები, რომლებშიც არქიმედეს სპირალი ჭრის

სხივი, რომელიც გამოდის პოლუსიდან და მიდრეკილია პოლარული ღერძისკენ კუთხით
. გააკეთე ნახატი.

171. არქიმედეს სპირალზე
აღებული წერტილი თან,რომლის პოლარული რადიუსი არის 47. დაადგინეთ რამდენ ნაწილად ჭრის ეს სპირალი წერტილის პოლარულ რადიუსს თან,გააკეთე ნახატი.

172. ჰიპერბოლურ სპირალზე
იპოვე წერტილი R,რომლის პოლარული რადიუსი არის 12. გააკეთე ნახატი.

173. ლოგარითმული სპირალზე
იპოვეთ Q წერტილი, რომლის პოლარული რადიუსია 81. გააკეთეთ ნახატი.

მიმოვიხილოთ * რომელ განტოლებას ეწოდება კვადრატული? * რომელ განტოლებებს უწოდებენ არასრულ კვადრატულ განტოლებებს? * რომელ კვადრატულ განტოლებას ეწოდება შემცირებული? * რას ჰქვია კვადრატული განტოლების ფესვი? * რას ნიშნავს კვადრატული განტოლების ამოხსნა? რომელ განტოლებას ეწოდება კვადრატული? რომელ განტოლებებს უწოდებენ არასრულ კვადრატულ განტოლებებს? რომელ კვადრატულ განტოლებას ეწოდება შემცირებული? რა არის კვადრატული განტოლების ფესვი? რას ნიშნავს კვადრატული განტოლების ამოხსნა? რომელ განტოლებას ეწოდება კვადრატული? რომელ განტოლებებს უწოდებენ არასრულ კვადრატულ განტოლებებს? რომელ კვადრატულ განტოლებას ეწოდება შემცირებული? რა არის კვადრატული განტოლების ფესვი? რას ნიშნავს კვადრატული განტოლების ამოხსნა?

კვადრატული განტოლების ამოხსნის ალგორითმი: 1. კვადრატული განტოლების ამოხსნის ყველაზე რაციონალური ხერხის დადგენა 2. ამოხსნის ყველაზე რაციონალური ხერხის არჩევა 3. კვადრატული განტოლების ფესვების რაოდენობის განსაზღვრა 4. კვადრატული განტოლების ფესვების პოვნა უკეთესისთვის დამახსოვრება, შეავსე ცხრილი... უკეთესი დასამახსოვრებლად შეავსე ცხრილი... უკეთესი დასამახსოვრებლად შეავსე ცხრილი...

დამატებითი პირობა განტოლების ფესვები მაგალითები 1. c = c = 0, a 0 ax 2 = 0 x 1 = 0 2. c = 0, a 0, b 0 ax 2 + bx = 0 x 1 = 0, x 2 = -b /a 3. c = 0, a 0, c 0 ax 2 + c = 0 a) x 1.2 = ±(c/a), სადაც c/a 0. ბ) თუ c/a 0, მაშინ ამონახსნები არ არსებობს 4. a 0 ax 2 + bx + c = 0 x 1.2 =(-b±D)/2 a, სადაც D = b 2 – 4 ac, D0 5. c – ლუწი რიცხვი (b = 2k), a 0, 0-ში, c 0 х 2 + 2kx + c = 0 x 1.2 =(-b±D)/а, D 1 = k 2 – ac, სადაც k = 6. ვიეტას თეორემის შებრუნებული თეორემა x 2 + px + q = 0x 1 + x 2 = - p x 1 x 2 = q

II. სპეციალური მეთოდები 7. ბინომის კვადრატის გამოყოფის მეთოდი. მიზანი: ზოგადი განტოლების შემცირება არასრულ კვადრატულ განტოლებამდე. შენიშვნა: მეთოდი გამოიყენება ნებისმიერი კვადრატული განტოლებისთვის, მაგრამ ყოველთვის არ არის მოსახერხებელი გამოსაყენებლად. გამოიყენება კვადრატული განტოლების ფესვების ფორმულის დასამტკიცებლად. მაგალითი: ამოხსენით განტოლება x 2 -6 x+8=0 8. უმაღლესი კოეფიციენტის „გადაცემის“ მეთოდი. კვადრატული განტოლებების ფესვები ax 2 + bx + c = 0 და y 2 +by+ac=0 დაკავშირებულია მიმართებებით: და შენიშვნა: მეთოდი კარგია კვადრატული განტოლებისთვის „მოხერხებული“ კოეფიციენტებით. ზოგიერთ შემთხვევაში, ის საშუალებას გაძლევთ ამოხსნათ კვადრატული განტოლება ზეპირად. მაგალითი: ამოხსენით განტოლება 2 x 2 -9 x-5=0 თეორემებზე დაყრდნობით: მაგალითი: ამოხსენით განტოლება 157 x x-177=0 9. თუ კვადრატულ განტოლებაში a+b+c=0, მაშინ ერთ-ერთი ფესვები არის 1, ხოლო მეორე, ვიეტას თეორემის მიხედვით, უდრის c/a 10-ს. თუ კვადრატულ განტოლებაში a + c = b, მაშინ ერთ-ერთი ფესვი უდრის -1-ს, ხოლო მეორე, ვიეტას მიხედვით. თეორემა, უდრის -c / a-ს მაგალითი: ამოხსენით განტოლება 203 x x + 17 = 0 x 1 =y 1 /a, x 2 =y 2 /a

III. განტოლებების ამოხსნის ზოგადი მეთოდები 11. ფაქტორიზაციის მეთოდი. მიზანი: შევამციროთ ზოგადი კვადრატული განტოლება ფორმამდე A(x)·B(x)=0, სადაც A(x) და B(x) არის პოლინომები x-ის მიმართ. მეთოდები: საერთო ფაქტორის ფრჩხილებიდან ამოღება; შემოკლებული გამრავლების ფორმულების გამოყენება; დაჯგუფების მეთოდი. მაგალითი: ამოხსენით განტოლება 3 x 2 +2 x-1=0 12. ახალი ცვლადის შემოღების მეთოდი. ახალი ცვლადის კარგი არჩევანი ხდის განტოლების სტრუქტურას უფრო გამჭვირვალე მაგალითი: ამოხსენი განტოლება (x 2 +3 x-25) 2 -6(x 2 +3 x-25) = - 8

სწორი ხაზი თვითმფრინავზე და სივრცეში.

ალგებრის გამოყენებით გეომეტრიული ფიგურების თვისებების შესწავლას ე.წ ანალიტიკური გეომეტრია , და გამოვიყენებთ ე.წ კოორდინატთა მეთოდი .

სიბრტყეზე ხაზი ჩვეულებრივ განისაზღვრება, როგორც წერტილების ერთობლიობა, რომლებსაც აქვთ მათთვის უნიკალური თვისებები. ის, რომ ამ წრფეზე მდებარე წერტილის x და y კოორდინატები (რიცხვები) ანალიტიკურად იწერება რაღაც განტოლების სახით.

დეფ.1 წრფის განტოლება (მრუდის განტოლება) Oxy სიბრტყეზე ეწოდება განტოლება (*), რომელიც კმაყოფილდება მოცემული წრფის თითოეული წერტილის x და y კოორდინატებით და არ კმაყოფილდება ამ წრფეზე არ მდებარე სხვა წერტილის კოორდინატებით.

განმარტება 1-დან გამომდინარეობს, რომ სიბრტყეზე ყველა ხაზი შეესაბამება გარკვეულ განტოლებას მიმდინარე კოორდინატებს შორის ( x, y ) ამ წრფის წერტილები და პირიქით, ყველა განტოლება შეესაბამება, ზოგადად, გარკვეულ წრფეს.

ეს წარმოშობს თვითმფრინავზე ანალიტიკური გეომეტრიის ორ მთავარ პრობლემას.

1. წრფე მოცემულია წერტილთა სიმრავლის სახით. ჩვენ უნდა შევქმნათ განტოლება ამ ხაზისთვის.

2. მოცემულია წრფის განტოლება. აუცილებელია მისი გეომეტრიული თვისებების (ფორმა და მდებარეობა) შესწავლა.

მაგალითი. ნუ ქულები ტყუილი ა(-2;1) და IN (1;1) მე-2 ხაზზე X +ზე +3=0?

განტოლებებით მოცემული ორი წრფის გადაკვეთის წერტილების პოვნის პრობლემა და მოდის კოორდინატების პოვნამდე, რომლებიც აკმაყოფილებენ ორივე წრფის განტოლებას, ე.ი. ორი უცნობი განტოლების სისტემის ამოხსნას.

თუ ამ სისტემას არ აქვს რეალური გადაწყვეტილებები, მაშინ ხაზები არ იკვეთება.

ხაზის კონცეფცია UCS-შიც ანალოგიურად არის დანერგილი.

სიბრტყეზე ხაზი შეიძლება განისაზღვროს ორი განტოლებით

სად X და ზე - თვითნებური წერტილის კოორდინატები M (x;y), ამ ხაზზე წევს და ტ - ცვლადი ე.წ პარამეტრი , პარამეტრი განსაზღვრავს წერტილის პოზიციას სიბრტყეზე.

მაგალითად, თუ , მაშინ t=2 პარამეტრის მნიშვნელობა შეესაბამება სიბრტყეზე (3;4) წერტილს.

თუ პარამეტრი იცვლება, სიბრტყეზე წერტილი მოძრაობს და აღწერს ამ ხაზს. ხაზის განსაზღვრის ამ მეთოდს ე.წ პარამეტრული და განტოლება (5.1) არის წრფის პარამეტრული განტოლება.

პარამეტრული განტოლებიდან ზოგად განტოლებაზე (*) გადასასვლელად, უნდა ამოიღოთ პარამეტრი ორი განტოლებიდან. თუმცა, ჩვენ აღვნიშნავთ, რომ ასეთი გადასვლა ყოველთვის არ არის მიზანშეწონილი და ყოველთვის არ არის შესაძლებელი.

შეიძლება განისაზღვროს ხაზი თვითმფრინავზე ვექტორული განტოლება , სადაც t არის სკალარული ცვლადი პარამეტრი. თითოეული პარამეტრის მნიშვნელობა შეესაბამება კონკრეტულ სიბრტყის ვექტორს. პარამეტრის შეცვლისას ვექტორის ბოლო აღწერს გარკვეულ ხაზს.

ვექტორული განტოლება DSC-ში შეესაბამება ორი სკალარული განტოლება

(5.1), ე.ი. წრფის ვექტორული განტოლების კოორდინატულ ღერძებზე პროგნოზების განტოლება არის მისი

პარამეტრული განტოლება.

ვექტორულ განტოლებას და პარამეტრულ ხაზოვან განტოლებებს მექანიკური მნიშვნელობა აქვს. თუ წერტილი მოძრაობს სიბრტყეზე, მაშინ მითითებული განტოლებები ეწოდება მოძრაობის განტოლებები , და ხაზი არის წერტილის ტრაექტორია, პარამეტრი t არის დრო.

დასკვნა: სიბრტყეზე ყველა ხაზი შეესაბამება ფორმის განტოლებას.

ზოგად შემთხვევაში, ხედის ნებისმიერი განტოლება შეესაბამება გარკვეულ ხაზს, რომლის თვისებები განისაზღვრება მოცემული განტოლებით (გარდა იმისა, რომ არც ერთი გეომეტრიული გამოსახულება არ შეესაბამება განტოლებას სიბრტყეზე).

აირჩიე კოორდინატთა სისტემა სიბრტყეზე.

დეფ. 5.1. ხაზოვანი განტოლება ამ ტიპის განტოლება ეწოდებაF(x;y) =0, რომელიც კმაყოფილდება ამ წრფეზე მდებარე ყველა წერტილის კოორდინატებით და არ კმაყოფილდება არცერთი წერტილის კოორდინატებით, რომელიც არ დევს მასზე.

ფორმის განტოლებაF(x;y )=0 – ეწოდება წრფის ან განტოლების ზოგად განტოლებას იმპლიციტური ფორმით.

ამრიგად, წრფე Г არის ამ განტოლების დამაკმაყოფილებელი წერტილების ლოკუსი Г=((x, y): F(x;y)=0).

ხაზი ასევე ე.წ მრუდე.

განტოლების ამოხსნა

განტოლების ფესვების პოვნის გრაფიკული მეთოდის ილუსტრაცია

განტოლების ამოხსნა არის არგუმენტების ისეთი მნიშვნელობების პოვნა, რომლითაც მიიღწევა ეს თანასწორობა. არგუმენტების შესაძლო მნიშვნელობებზე შეიძლება დაწესდეს დამატებითი პირობები (მთლიანი, რეალური და ა.შ.).

სხვა ფესვის ჩანაცვლება წარმოშობს არასწორ განცხადებას:

.

ამრიგად, მეორე ფესვი უნდა განადგურდეს, როგორც ზედმეტი.

განტოლებების სახეები

არსებობს ალგებრული, პარამეტრული, ტრანსცენდენტული, ფუნქციური, დიფერენციალური და სხვა სახის განტოლებები.

განტოლების ზოგიერთ კლასს აქვს ანალიტიკური გადაწყვეტილებები, რომლებიც მოსახერხებელია, რადგან ისინი არა მხოლოდ აძლევენ ფესვის ზუსტ მნიშვნელობას, არამედ საშუალებას გაძლევთ დაწეროთ ამოხსნა ფორმულის სახით, რომელიც შეიძლება შეიცავდეს პარამეტრებს. ანალიტიკური გამონათქვამები საშუალებას იძლევა არა მხოლოდ გამოთვალოთ ფესვები, არამედ გაანალიზოთ მათი არსებობა და მათი რაოდენობა პარამეტრის მნიშვნელობებზე დაყრდნობით, რაც ხშირად უფრო მნიშვნელოვანია პრაქტიკული გამოყენებისთვის, ვიდრე ფესვების სპეციფიკური მნიშვნელობები.

განტოლებები, რომელთა ანალიტიკური ამონახსნები ცნობილია, მოიცავს ალგებრულ განტოლებებს არაუმეტეს მეოთხე ხარისხის: წრფივი განტოლება, კვადრატული განტოლება, კუბური განტოლება და მეოთხე ხარისხის განტოლება. უფრო მაღალი ხარისხის ალგებრულ განტოლებებს ზოგად შემთხვევაში არ აქვთ ანალიტიკური ამონახსნები, თუმცა ზოგიერთი მათგანი შეიძლება შემცირდეს უფრო დაბალი ხარისხის განტოლებამდე.

განტოლებას, რომელიც მოიცავს ტრანსცენდენტურ ფუნქციებს, ეწოდება ტრანსცენდენტული. მათ შორის ცნობილია ანალიტიკური ამონახსნები ზოგიერთი ტრიგონომეტრიული განტოლებისთვის, ვინაიდან ცნობილია ტრიგონომეტრიული ფუნქციების ნულები.

ზოგად შემთხვევაში, როდესაც ანალიზური ამოხსნა ვერ მოიძებნება, გამოიყენება რიცხვითი მეთოდები. რიცხვითი მეთოდები არ იძლევა ზუსტ გადაწყვეტას, მაგრამ მხოლოდ საშუალებას აძლევს შემცირდეს ინტერვალი, რომელშიც ფესვი დევს გარკვეულ წინასწარ განსაზღვრულ მნიშვნელობამდე.

განტოლებების მაგალითები

იხილეთ ასევე

ლიტერატურა

• ბეკარევიჩი, ა.ბ. განტოლებები სასკოლო მათემატიკის კურსში / ა.ბ.ბეკარევიჩი. - მ., 1968 წ.
• მარკუშევიჩი, ლ. ა. განტოლებები და უტოლობები საშუალო სკოლის ალგებრის კურსის საბოლოო გამეორებაში / ლ. / მათემატიკა სკოლაში. - 2004. - No1.
• Kaplan Y. V. Rivnyannya. - კიევი: რადიანსკის სკოლა, 1968 წ.
• განტოლება- სტატია დიდი საბჭოთა ენციკლოპედიიდან
• განტოლებები// კოლიერის ენციკლოპედია. - ღია საზოგადოება. 2000 წ.
• განტოლება// ენციკლოპედია მსოფლიოს გარშემო
• განტოლება// მათემატიკური ენციკლოპედია. - მ.: საბჭოთა ენციკლოპედია. I. M. ვინოგრადოვი. 1977-1985 წწ.

ბმულები

• EqWorld - მათემატიკური განტოლებების სამყარო - შეიცავს ვრცელ ინფორმაციას მათემატიკური განტოლებებისა და განტოლებათა სისტემების შესახებ.

ფონდი ვიკიმედია. 2010 წელი.

სინონიმები:

ანტონიმები:

• ხაჯიმბა, რაულ ჯუმკოვიჩი
• ES კომპიუტერი

ნახეთ, რა არის „განტოლება“ სხვა ლექსიკონებში:

განტოლება- (1) არგუმენტების ისეთი მნიშვნელობების პოვნის პრობლემის მათემატიკური წარმოდგენა (იხ. (2)), რომლისთვისაც ორი მონაცემის მნიშვნელობები (იხ.) ტოლია. არგუმენტებს, რომლებზეც ეს ფუნქციებია დამოკიდებული, ეწოდება უცნობი, ხოლო უცნობის მნიშვნელობებს, რომლებზეც მნიშვნელობები ... ... დიდი პოლიტექნიკური ენციკლოპედია

განტოლება- განტოლება, განტოლებები, შდრ. 1. ქმედება ჩ. გათანაბრება გათანაბრება და მდგომარეობა ჩ. გათანაბრება გათანაბრება. Თანაბარი უფლებები. დროის განტოლება (ჭეშმარიტი მზის დროის თარგმნა საშუალო მზის დროში, მიღებული საზოგადოებაში და მეცნიერებაში;... ... უშაკოვის განმარტებითი ლექსიკონი

განტოლება- (განტოლება) მოთხოვნა, რომ მათემატიკური გამოხატულება მიიღოს კონკრეტული მნიშვნელობა. მაგალითად, კვადრატული განტოლება იწერება: ax2+bx+c=0. ამონახსნი არის x-ის მნიშვნელობა, რომლის დროსაც მოცემული განტოლება ხდება იდენტურობა. ში…… ეკონომიკური ლექსიკონი

განტოლება- არგუმენტების მნიშვნელობების პოვნის პრობლემის მათემატიკური წარმოდგენა, რომლებისთვისაც ორი მოცემული ფუნქციის მნიშვნელობები ტოლია. არგუმენტებს, რომლებზეც ეს ფუნქციებია დამოკიდებული, ეწოდება უცნობი, ხოლო უცნობის მნიშვნელობებს, რომლებზეც ფუნქციის მნიშვნელობები ტოლია... ... დიდი ენციკლოპედიური ლექსიკონი

განტოლება- EQUATION, ორი გამონათქვამი, რომლებიც დაკავშირებულია ტოლობის ნიშნით; ეს გამონათქვამები მოიცავს ერთ ან მეტ ცვლადს, რომელსაც უცნობები ეწოდება. განტოლების ამოხსნა ნიშნავს უცნობების ყველა მნიშვნელობის პოვნას, რომლითაც ის იდენტურად იქცევა, ან დაადგინო... თანამედროვე ენციკლოპედია

სიბრტყეზე წრფე არის ამ სიბრტყის წერტილების ერთობლიობა, რომლებსაც აქვთ გარკვეული თვისებები, ხოლო წერტილებს, რომლებიც არ დევს მოცემულ წრფეზე, არ გააჩნიათ ეს თვისებები. წრფის განტოლება განსაზღვრავს ანალიტიკურად გამოხატულ ურთიერთობას ამ წრფეზე მდებარე წერტილების კოორდინატებს შორის. დაე, ეს ურთიერთობა იყოს მოცემული განტოლებით

F( x, y)=0. (2.1)

(2.1) დამაკმაყოფილებელი რიცხვების წყვილი არ არის თვითნებური: თუ Xმოცემული, მაშინ ზეარ შეიძლება იყოს არაფერი, მნიშვნელობა ზედაკავშირებული X. როცა იცვლება Xცვლილებები ზედა წერტილი კოორდინატებით ( x, y) აღწერს ამ ხაზს. თუ M 0 წერტილის კოორდინატები ( X 0 ,ზე 0) დააკმაყოფილეთ განტოლება (2.1), ე.ი. F( X 0 ,ზე 0)=0 არის ჭეშმარიტი ტოლობა, მაშინ წერტილი M 0 დევს ამ წრფეზე. პირიქითაც მართალია.

განმარტება. სიბრტყეზე წრფის განტოლება არის განტოლება, რომელიც კმაყოფილდება ამ წრფეზე მდებარე ნებისმიერი წერტილის კოორდინატებით და არ კმაყოფილდება იმ წერტილების კოორდინატებით, რომლებიც არ დევს ამ წრფეზე..

თუ გარკვეული წრფის განტოლება ცნობილია, მაშინ ამ წრფის გეომეტრიული თვისებების შესწავლა შეიძლება მისი განტოლების შესწავლამდე შემცირდეს - ეს არის ანალიტიკური გეომეტრიის ერთ-ერთი მთავარი იდეა. განტოლებების შესასწავლად არის კარგად განვითარებული მათემატიკური ანალიზის მეთოდები, რომლებიც ამარტივებს ხაზების თვისებების შესწავლას.

ხაზების განხილვისას გამოიყენება ტერმინი მიმდინარე წერტილიხაზი – ცვლადი წერტილი M( x, y), მოძრაობს ამ ხაზის გასწვრივ. კოორდინატები Xდა ზემიმდინარე წერტილს უწოდებენ მიმდინარე კოორდინატებიხაზის წერტილები.

თუ (2.1) განტოლებიდან შეგვიძლია გამოვხატოთ ცალსახად ზე
მეშვეობით X, ანუ ჩაწერეთ განტოლება (2.1) სახით, მაშინ ასეთი განტოლებით განსაზღვრული მრუდი ე.წ. განრიგიფუნქციები f(x).

1. განტოლება მოცემულია: , ან . თუ Xიღებს თვითნებურ მნიშვნელობებს, მაშინ ზეიღებს ტოლ ღირებულებებს X. შესაბამისად, ამ განტოლებით განსაზღვრული წრფე შედგება Ox და Oy კოორდინატთა ღერძებისგან თანაბარი მანძილისგან დაშორებული წერტილებისგან - ეს არის I–III კოორდინატთა კუთხეების ბისექტორი (სწორი ხაზი ნახ. 2.1-ზე).

განტოლება, ან, განსაზღვრავს II–IV კოორდინატთა კუთხეების ბისექტრისს (სწორი ხაზი ნახ. 2.1-ზე).

0 x 0 x C 0 x

ბრინჯი. 2.1 ნახ. 2.2 ნახ. 2.3

2. განტოლება მოცემულია: , სადაც C არის რაღაც მუდმივი. ეს განტოლება შეიძლება სხვანაირად დაიწეროს: . ამ განტოლებას აკმაყოფილებენ ის და მხოლოდ ის წერტილები, ორდინატები ზერომლებიც უდრის C-ს ნებისმიერი აბსცისის მნიშვნელობისთვის X. ეს წერტილები დევს სწორ ხაზზე Ox-ის ღერძის პარალელურად (ნახ. 2.2). ანალოგიურად, განტოლება განსაზღვრავს სწორ ხაზს Oy ღერძის პარალელურად (ნახ. 2.3).

არა ყველა განტოლება ფორმის F( x, y)=0 განსაზღვრავს წრფეს სიბრტყეზე: განტოლება კმაყოფილდება ერთი წერტილით – O(0,0), ხოლო განტოლება არ კმაყოფილდება სიბრტყის არც ერთი წერტილით.

მოცემულ მაგალითებში ჩვენ გამოვიყენეთ მოცემული განტოლება ამ განტოლებით განსაზღვრული წრფის ასაგებად. განვიხილოთ შებრუნებული ამოცანა: ააგეთ მისი განტოლება მოცემული წრფის გამოყენებით.

3. შექმენით განტოლება წრეზე, რომლის ცენტრია P წერტილში ა, ბ) და
რადიუსი R .

○ წრე P წერტილში ცენტრით და R რადიუსით არის წერტილების ერთობლიობა, რომელიც მდებარეობს P წერტილიდან R მანძილზე. ეს ნიშნავს, რომ წრეზე მდებარე ნებისმიერი M წერტილისთვის MP = R, მაგრამ თუ წერტილი M არ დევს წრე, შემდეგ დეპუტატი ≠ რ.. ●