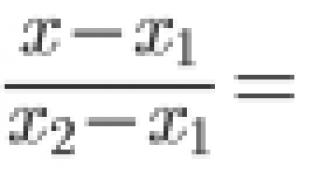
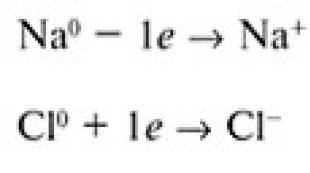განტოლებები x მოდულით. განტოლებები მოდულით. მოდულით განტოლებების ამოხსნის თავისებურებები
MBOU საშუალო სკოლა No. 17, ივანოვო
« განტოლებები მოდულით"
მეთოდოლოგიური განვითარება
შედგენილი
მათემატიკის მასწავლებელი
ლებედევა ნ.ვ.20010 წ
განმარტებითი შენიშვნა
თავი 1. შესავალი
ნაწილი 2. ძირითადი თვისებები ნაწილი 3. რიცხვის მოდულის ცნების გეომეტრიული ინტერპრეტაცია განყოფილება 4. y = |x| ფუნქციის გრაფიკი ნაწილი 5. კონვენციებითავი 2. მოდულის შემცველი განტოლებების ამოხსნა
ნაწილი 1. |F(x)| ფორმის განტოლებები = m (უმარტივესი) ნაწილი 2. F(|x|) = m ფორმის განტოლებები ნაწილი 3. |F(x)| ფორმის განტოლებები = G(x) ნაწილი 4. |F(x)| ფორმის განტოლებები = ± F(x) (ყველაზე ლამაზი) ნაწილი 5. |F(x)| ფორმის განტოლებები = |G(x)| ნაწილი 6. არასტანდარტული განტოლებების ამოხსნის მაგალითები ნაწილი 7. |F(x)| ფორმის განტოლებები + |G(x)| = 0 ნაწილი 8. ფორმის განტოლებები |a 1 x ± b 1 | ± |a 2 x ± 2 | ± …|a n x ± n-ში | = მ ნაწილი 9. განტოლებები, რომლებიც შეიცავს რამდენიმე მოდულსთავი 3. მოდულით სხვადასხვა განტოლების ამოხსნის მაგალითები.
ნაწილი 1. ტრიგონომეტრიული განტოლებები ნაწილი 2. ექსპონენციალური განტოლებები განყოფილება 3. ლოგარითმული განტოლებები ნაწილი 4. ირაციონალური განტოლებები ნაწილი 5. მოწინავე ამოცანები პასუხები ვარჯიშებზე ბიბლიოგრაფიაგანმარტებითი შენიშვნა.
რეალური რიცხვის აბსოლუტური მნიშვნელობის (მოდულის) ცნება მისი ერთ-ერთი არსებითი მახასიათებელია. ეს კონცეფცია ფართოდ არის გავრცელებული ფიზიკური, მათემატიკური და ტექნიკური მეცნიერებების სხვადასხვა განყოფილებაში. მათემატიკის კურსების სწავლების პრაქტიკაში ქ უმაღლესი სკოლარუსეთის ფედერაციის თავდაცვის სამინისტროს პროგრამის შესაბამისად, "რიცხვის აბსოლუტური მნიშვნელობის" კონცეფცია არაერთხელ ჩნდება: მე -6 კლასში შემოდის მოდულის განმარტება, მისი გეომეტრიული მნიშვნელობა; მე-8 კლასში ყალიბდება აბსოლუტური ცდომილების ცნება, განიხილება მოდულის შემცველი უმარტივესი განტოლებებისა და უტოლობების ამოხსნა და არითმეტიკული კვადრატული ფესვის თვისებების შესწავლა; მე-11 კლასში კონცეფცია გვხვდება განყოფილებაში „ფესვი ნ- ხარისხი."სწავლების გამოცდილება გვიჩვენებს, რომ მოსწავლეები ხშირად აწყდებიან სირთულეებს ამოცანების გადაწყვეტისას, რომლებიც საჭიროებენ ამ მასალის ცოდნას და ხშირად გამოტოვებენ მათ შესრულების დაწყების გარეშე. მე-9 და მე-11 კლასის კურსების საგამოცდო დავალებების ტექსტებშიც შედის მსგავსი დავალებები. გარდა ამისა, მოთხოვნები, რომლებსაც უნივერსიტეტები უყენებენ სკოლის კურსდამთავრებულებს, განსხვავებულია, კერძოდ, მეტი მაღალი დონევიდრე სასკოლო სასწავლო გეგმის მოთხოვნები. თანამედროვე საზოგადოებაში ცხოვრებისთვის ძალიან მნიშვნელოვანია აზროვნების მათემატიკური სტილის ჩამოყალიბება, რომელიც გამოიხატება გარკვეულ გონებრივ უნარებში. მოდულებით პრობლემების გადაჭრის პროცესში საჭიროა ისეთი ტექნიკის გამოყენების უნარი, როგორიცაა განზოგადება და დაზუსტება, ანალიზი, კლასიფიკაცია და სისტემატიზაცია და ანალოგია. ასეთი ამოცანების გადაჭრა საშუალებას გაძლევთ შეამოწმოთ თქვენი ცოდნა სასკოლო კურსის ძირითადი სექციების, დონის შესახებ ლოგიკური აზროვნება, საწყისი კვლევის უნარები. ეს ნაშრომი ეძღვნება ერთ-ერთ განყოფილებას - მოდულის შემცველი განტოლებების ამოხსნას. იგი შედგება სამი თავისგან. პირველ თავში მოცემულია ძირითადი ცნებები და ყველაზე მნიშვნელოვანი თეორიული მოსაზრებები. მეორე თავში შემოთავაზებულია მოდულის შემცველი განტოლების ცხრა ძირითადი ტიპი, განიხილება მათი ამოხსნის მეთოდები და განიხილება სხვადასხვა დონის სირთულის მაგალითები. მესამე თავი გთავაზობთ უფრო რთულ და არასტანდარტულ განტოლებებს (ტრიგონომეტრიული, ექსპონენციალური, ლოგარითმული და ირაციონალური). თითოეული ტიპის განტოლებისთვის არის სავარჯიშოები დამოუკიდებელი გადაწყვეტილება(პასუხები და ინსტრუქციები თან ერთვის). ამ სამუშაოს მთავარი მიზანია მასწავლებელთა მეთოდოლოგიური დახმარება გაკვეთილებისთვის მომზადებაში და არჩევითი კურსების ორგანიზებაში. მასალა ასევე შეიძლება გამოყენებულ იქნას როგორც სასწავლო დახმარებასაშუალო სკოლის მოსწავლეებისთვის. ნაშრომში შემოთავაზებული ამოცანები საინტერესოა და ყოველთვის არ არის ადვილი გადასაჭრელი, რაც შესაძლებელს ხდის სტუდენტების საგანმანათლებლო მოტივაციის გააზრებას, მათი შესაძლებლობების გამოცდას და სკოლის კურსდამთავრებულთა მომზადების დონის გაზრდას უნივერსიტეტებში შესასვლელად. შემოთავაზებული სავარჯიშოების დიფერენცირებული შერჩევა გულისხმობს მასალის დაუფლების რეპროდუქციული დონიდან კრეატიულზე გადასვლას, ასევე შესაძლებლობას ასწავლოს როგორ გამოიყენო შენი ცოდნა არასტანდარტული პრობლემების გადაჭრისას.თავი 1. შესავალი.
ნაწილი 1. აბსოლუტური მნიშვნელობის განსაზღვრა .
განმარტება : რეალური რიცხვის აბსოლუტური მნიშვნელობა (მოდული). ადაურეკა არა უარყოფითი რიცხვი: აან -ა. Დანიშნულება: │ ა │ ჩანაწერი შემდეგნაირად იკითხება: „ა რიცხვის მოდული“ ან „ა რიცხვის აბსოლუტური მნიშვნელობა“│ a, თუ a > 0
│a│ = │ 0, თუ a = 0 (1)
│ - და, თუ ამაგალითები: 1) │2,5│ = 2,5 2) │-7│ = 7 3) │1 - √2│ = √2 – 1
- გამოხატვის მოდულის გაფართოება:
ნაწილი 2. ძირითადი თვისებები.
განვიხილოთ აბსოლუტური მნიშვნელობის ძირითადი თვისებები. ქონება #1: საპირისპირო რიცხვებს აქვთ თანაბარი მოდულები, ე.ი. │а│=│- а│მოდით ვაჩვენოთ, რომ თანასწორობა სწორია. ჩამოვწეროთ რიცხვის განმარტება - ა : │- ა│= (2) შევადაროთ სიმრავლეები (1) და (2). ცხადია, რიცხვების აბსოლუტური მნიშვნელობების განმარტებები ადა - ადაწყვილება. აქედან გამომდინარე, │а│=│- а│შემდეგი თვისებების განხილვისას, ჩვენ შემოვიფარგლებით მათი ფორმულირებით, რადგან მათი მტკიცებულება მოცემულია ქონება #2: რეალური რიცხვების სასრული რაოდენობის ჯამის აბსოლუტური მნიშვნელობა არ აღემატება ტერმინების აბსოლუტური მნიშვნელობების ჯამს: │а 1 + а 2 +…+ а n │ ≤│а 1 │+│а 2 │ + … + │а n │ ქონება #3: ორ რეალურ რიცხვს შორის სხვაობის აბსოლუტური მნიშვნელობა არ აღემატება მათი აბსოლუტური სიდიდეების ჯამს: │а - в│ ≤│а│+│в│ ქონება #4: რეალური რიცხვების სასრული რაოდენობის ნამრავლის აბსოლუტური მნიშვნელობა უდრის ფაქტორების აბსოლუტური სიდიდეების ნამრავლს: │а·в│=│а│·│в│ ქონება #5: რეალური რიცხვების კოეფიციენტის აბსოლუტური მნიშვნელობა უდრის მათი აბსოლუტური სიდიდეების კოეფიციენტს:

ნაწილი 3. რიცხვის მოდულის ცნების გეომეტრიული ინტერპრეტაცია.
თითოეული რეალური რიცხვი შეიძლება ასოცირებული იყოს რიცხვით წრფეზე არსებულ წერტილთან, რომელიც იქნება ამ რეალური რიცხვის გეომეტრიული გამოსახულება. რიცხვთა ხაზის თითოეული წერტილი შეესაბამება მის დაშორებას საწყისიდან, ე.ი. სეგმენტის სიგრძე საწყისიდან მოცემულ წერტილამდე. ეს მანძილი ყოველთვის განიხილება, როგორც არაუარყოფითი მნიშვნელობა. შესაბამისად, შესაბამისი სეგმენტის სიგრძე იქნება გეომეტრიული ინტერპრეტაციამოცემული რეალური რიცხვის აბსოლუტური მნიშვნელობა
წარმოდგენილი გეომეტრიული ილუსტრაცია ნათლად ადასტურებს თვისებას No1, ე.ი. საპირისპირო რიცხვების მოდულები ტოლია. აქედან ადვილად გასაგებია ტოლობის მართებულობა: │х – а│= │а – x│. │х│= m განტოლების ამონახსნი, სადაც m ≥ 0, კერძოდ x 1,2 = ± m, ასევე უფრო აშკარა ხდება. მაგალითები: 1) │х│= 4 x 1.2 = ± 4 2) │х - 3│= 1
 x 1.2 = 2; 4
x 1.2 = 2; 4 განყოფილება 4. y = │х│ ფუნქციის გრაფიკი
ამ ფუნქციის დომენი არის ყველა რეალური რიცხვი.ნაწილი 5. კონვენციები.
მომავალში, განტოლებების ამოხსნის მაგალითების განხილვისას გამოყენებული იქნება შემდეგი კონვენციები: ( - სისტემის ნიშანი [ - მთლიანობის ნიშანი განტოლებათა სისტემის ამოხსნისას (უტოლობა) გვხვდება სისტემაში შემავალი განტოლებათა (უტოლობათა) ამონახსნების კვეთა. განტოლებათა სიმრავლის (უტოლობა) ამოხსნისას გვხვდება განტოლებათა სიმრავლეში შემავალი ამონახსნების გაერთიანება (უტოლობა).თავი 2. მოდულის შემცველი განტოლებების ამოხსნა.
ამ თავში განვიხილავთ განტოლებების ამოხსნის ალგებრულ მეთოდებს, რომლებიც შეიცავს ერთ ან მეტ მოდულს.ნაწილი 1. │F (x)│= m ფორმის განტოლებები
ამ ტიპის განტოლებას უმარტივესს უწოდებენ. მას აქვს ამონახსნი, თუ და მხოლოდ იმ შემთხვევაში, თუ m ≥ 0. მოდულის განმარტებით, საწყისი განტოლება უდრის ორი განტოლების სიმრავლეს: │ ფ(x)│=მ
 მაგალითები:
მაგალითები:
№1. ამოხსენით განტოლება: │7х - 2│= 9


 პასუხი: x 1
= - 1; X 2
= 1
4
/
7
№2
პასუხი: x 1
= - 1; X 2
= 1
4
/
7
№2
│x 2 + 3x + 1│ = 1

 x 2 + 3x + 2 = 0 x 2 +3x = 0 x 1 = -1; x 2 = -2 x (x + 3) = 0 x 1 = 0; x 2 = -3 პასუხი: ფესვების ჯამი არის - 2.№3
x 2 + 3x + 2 = 0 x 2 +3x = 0 x 1 = -1; x 2 = -2 x (x + 3) = 0 x 1 = 0; x 2 = -3 პასუხი: ფესვების ჯამი არის - 2.№3
│x 4 -5x 2 + 2│= 2 x 4 – 5x 2 = 0 x 4 – 5x 2 + 4 = 0 x 2 (x 2 – 5) = 0 აღნიშნავს x 2 = m, m ≥ 0 x = 0 ; ±√5 მ 2 – 5მ + 4 = 0 მ = 1; 4 - ორივე მნიშვნელობა აკმაყოფილებს პირობას m ≥ 0 x 2 = 1 x 2 = 4 x = ± 1 x = ± 2 პასუხი: მე-7 განტოლების ფესვების რაოდენობა. Სავარჯიშოები:
№1. ამოხსენით განტოლება და მიუთითეთ ფესვების ჯამი: │х - 5│= 3 №2 . ამოხსენით განტოლება და მიუთითეთ უფრო მცირე ფესვი: │x 2 + x│= 0 №3 . ამოხსენით განტოლება და მიუთითეთ უფრო დიდი ფესვი: │x 2 – 5x + 4│= 4 №4 .ამოხსენით განტოლება და მიუთითეთ მთელი ფესვი: │2x 2 – 7x + 6│= 1 №5 .ამოხსენით განტოლება და მიუთითეთ ფესვების რაოდენობა: │x 4 – 13x 2 + 50│= 14
ნაწილი 2. F(│х│) = m ფორმის განტოლებები
ფუნქციის არგუმენტი მარცხენა მხარეს არის მოდულის ნიშნის ქვეშ, ხოლო მარჯვენა მხარე დამოუკიდებელია ცვლადისგან. განვიხილოთ ამ ტიპის განტოლებების ამოხსნის ორი გზა. 1 გზა:აბსოლუტური მნიშვნელობის განმარტებით, თავდაპირველი განტოლება უდრის ორი სისტემის ერთობლიობას. თითოეულ მათგანში პირობა დაწესებულია სუბმოდულურ გამოხატულებაზე. ფ(│x│) =მ ვინაიდან ფუნქცია F(│x│) ლუწია განსაზღვრების მთელ სფეროზე, F(x) = m და F(- x) = m განტოლებების ფესვები საპირისპირო რიცხვების წყვილია. მაშასადამე, საკმარისია ერთ-ერთი სისტემის ამოხსნა (მაგალითების ამგვარად განხილვისას მოცემულია ერთი სისტემის ამოხსნა). მეთოდი 2:ახალი ცვლადის დანერგვის მეთოდის გამოყენება. ამ შემთხვევაში შემოღებულია აღნიშვნა │x│= a, სადაც a ≥ 0. ეს მეთოდი დიზაინით ნაკლებად მოცულობითია.
ვინაიდან ფუნქცია F(│x│) ლუწია განსაზღვრების მთელ სფეროზე, F(x) = m და F(- x) = m განტოლებების ფესვები საპირისპირო რიცხვების წყვილია. მაშასადამე, საკმარისია ერთ-ერთი სისტემის ამოხსნა (მაგალითების ამგვარად განხილვისას მოცემულია ერთი სისტემის ამოხსნა). მეთოდი 2:ახალი ცვლადის დანერგვის მეთოდის გამოყენება. ამ შემთხვევაში შემოღებულია აღნიშვნა │x│= a, სადაც a ≥ 0. ეს მეთოდი დიზაინით ნაკლებად მოცულობითია. მაგალითები: №1 . ამოხსენით განტოლება: 3x 2 – 4│x│= - 1 გამოვიყენოთ ახალი ცვლადის შესავალი. ავღნიშნოთ │x│= a, სადაც a ≥ 0. ვიღებთ განტოლებას 3a 2 - 4a + 1 = 0 D = 16 – 12 = 4 a 1 = 1 a 2 = 1 / 3 დავუბრუნდეთ საწყის ცვლადს: │ x│=1 და │х│= 1/3. თითოეულ განტოლებას ორი ფესვი აქვს. პასუხი: x 1 = 1; X 2 = - 1; X 3 = 1 / 3 ; X 4 = - 1 / 3 . №2. ამოხსენით განტოლება: 5x 2 + 3│x│- 1 = 1/2 │x│ + 3x 2
 მოდი ვიპოვოთ პოპულაციის პირველი სისტემის ამონახსნი: 4x 2 + 5x – 2 =0 D = 57 x 1 = -5+√57 / 8 x 2 = -5-√57 / 8 გაითვალისწინეთ, რომ x 2 არ აკმაყოფილებს პირობა x ≥ 0. ამოხსნა მეორე სისტემა იქნება x 1 მნიშვნელობის საპირისპირო რიცხვი. პასუხი: x 1
=
-5+√57
/
8
; X 2
=
5-√57
/
8
.№3
.
ამოხსენით განტოლება: x 4 – │х│= 0 ავღნიშნოთ │х│= a, სადაც a ≥ 0. მივიღებთ განტოლებას a 4 – a = 0 a · (a 3 – 1) = 0 a 1 = 0 a 2 = 1 დაუბრუნდით საწყის ცვლადს: │х│=0 და │х│= 1 x = 0; ± 1 პასუხი: x 1
= 0; X 2
= 1; X 3
= - 1.
მოდი ვიპოვოთ პოპულაციის პირველი სისტემის ამონახსნი: 4x 2 + 5x – 2 =0 D = 57 x 1 = -5+√57 / 8 x 2 = -5-√57 / 8 გაითვალისწინეთ, რომ x 2 არ აკმაყოფილებს პირობა x ≥ 0. ამოხსნა მეორე სისტემა იქნება x 1 მნიშვნელობის საპირისპირო რიცხვი. პასუხი: x 1
=
-5+√57
/
8
; X 2
=
5-√57
/
8
.№3
.
ამოხსენით განტოლება: x 4 – │х│= 0 ავღნიშნოთ │х│= a, სადაც a ≥ 0. მივიღებთ განტოლებას a 4 – a = 0 a · (a 3 – 1) = 0 a 1 = 0 a 2 = 1 დაუბრუნდით საწყის ცვლადს: │х│=0 და │х│= 1 x = 0; ± 1 პასუხი: x 1
= 0; X 2
= 1; X 3
= - 1.
Სავარჯიშოები: №6. ამოხსენით განტოლება: 2│х│ - 4.5 = 5 – 3 / 8 │х│ №7 . ამოხსენით განტოლება, მიუთითეთ ფესვების რაოდენობა თქვენს პასუხში: 3x 2 - 7│x│ + 2 = 0 №8 . ამოხსენით განტოლება, თქვენს პასუხში მიუთითეთ მთელი რიცხვები: x 4 + │x│ - 2 = 0
ნაწილი 3. │F(x)│ = G(x) ფორმის განტოლებები
ამ ტიპის განტოლების მარჯვენა მხარე დამოკიდებულია ცვლადზე და, შესაბამისად, აქვს ამონახსნი, თუ და მხოლოდ მაშინ, თუ მარჯვენა მხარე არის ფუნქცია G(x) ≥ 0. თავდაპირველი განტოლება შეიძლება ამოხსნას ორი გზით. : 1 გზა:სტანდარტი, რომელიც ეფუძნება მოდულის გამჟღავნებას მის განმარტებაზე დაფუძნებული და შედგება ექვივალენტური გადასვლისგან ორი სისტემის კომბინაციაზე. │ ფ(x)│ =გ(X)
 ეს მეთოდი რაციონალურად შეიძლება გამოვიყენოთ G(x) ფუნქციის რთული გამოხატვის შემთხვევაში და F(x) ფუნქციისთვის ნაკლებად რთული, რადგან ვარაუდობენ, რომ F(x) ფუნქციის უტოლობა ამოხსნილი იქნება. მეთოდი 2:შედგება ეკვივალენტურ სისტემაზე გადასვლაში, რომელშიც პირობა დაწესებულია მარჯვენა მხარეს. │ ფ(x)│=
გ(x)
ეს მეთოდი რაციონალურად შეიძლება გამოვიყენოთ G(x) ფუნქციის რთული გამოხატვის შემთხვევაში და F(x) ფუნქციისთვის ნაკლებად რთული, რადგან ვარაუდობენ, რომ F(x) ფუნქციის უტოლობა ამოხსნილი იქნება. მეთოდი 2:შედგება ეკვივალენტურ სისტემაზე გადასვლაში, რომელშიც პირობა დაწესებულია მარჯვენა მხარეს. │ ფ(x)│=
გ(x)

 ეს მეთოდი უფრო მოსახერხებელია გამოსაყენებლად, თუ G(x) ფუნქციის გამოხატულება ნაკლებად რთულია, ვიდრე F(x) ფუნქციისთვის, რადგან მიღებულია G(x) ≥ 0 უტოლობის ამოხსნა. გარდა ამისა, იმ შემთხვევაში რამდენიმე მოდულიდან, რეკომენდებულია მეორე ვარიანტის გამოყენება. მაგალითები:
№1.
ამოხსენით განტოლება: │x + 2│= 6 -2x
ეს მეთოდი უფრო მოსახერხებელია გამოსაყენებლად, თუ G(x) ფუნქციის გამოხატულება ნაკლებად რთულია, ვიდრე F(x) ფუნქციისთვის, რადგან მიღებულია G(x) ≥ 0 უტოლობის ამოხსნა. გარდა ამისა, იმ შემთხვევაში რამდენიმე მოდულიდან, რეკომენდებულია მეორე ვარიანტის გამოყენება. მაგალითები:
№1.
ამოხსენით განტოლება: │x + 2│= 6 -2x  (1 გზა) პასუხი: x = 1 1
/
3
№2.
(1 გზა) პასუხი: x = 1 1
/
3
№2.
│х 2 – 2х - 1│= 2·(x + 1)
 (2 გზა) პასუხი: ფესვების ნამრავლია 3.
(2 გზა) პასუხი: ფესვების ნამრავლია 3.№3. ამოხსენით განტოლება და მიუთითეთ ფესვების ჯამი თქვენს პასუხში:
│x - 6│= x 2 - 5x + 9

პასუხი: ფესვების ჯამი არის 4.
Სავარჯიშოები: №9. │x + 4│= - 3x №10. ამოხსენით განტოლება, მიუთითეთ ამონახსნების რაოდენობა თქვენს პასუხში:│x 2 + x - 1│= 2x – 1 №11 . ამოხსენით განტოლება, მიუთითეთ ფესვების ნამრავლი თქვენს პასუხში:│x + 3│= x 2 + x – 6
ნაწილი 4. │F(x)│= F(x) და │F(x)│= - F(x) ფორმის განტოლებები
ამ ტიპის განტოლებებს ზოგჯერ უწოდებენ "ყველაზე ლამაზს". ვინაიდან განტოლებების მარჯვენა მხარე დამოკიდებულია ცვლადზე, ამონახსნები არსებობს, თუ და მხოლოდ მაშინ, თუ მარჯვენა მხარე არაუარყოფითია. მაშასადამე, თავდაპირველი განტოლებები უდრის უტოლობას:│F(x)│= F(x) F(x) ≥ 0 და │F(x)│= - F(x) F(x) მაგალითები: №1 . ამოხსენით განტოლება, თქვენს პასუხში მიუთითეთ უფრო მცირე მთელი ფესვი: │5x - 3│= 5x – 3 5x – 3 ≥ 0 5x ≥ 3 x ≥ 0.6 პასუხი: x = 1№2. ამოხსენით განტოლება, თქვენს პასუხში მიუთითეთ ინტერვალის სიგრძე: │х 2 - 9│= 9 – x 2 x 2 – 9 ≤ 0 (x – 3) (x + 3) ≤ 0 [- 3; 3] პასუხი: ინტერვალის სიგრძეა 6.№3 . ამოხსენით განტოლება და თქვენს პასუხში მიუთითეთ მთელი რიცხვების ამონახსნები: │2 + x – x 2 │= 2 + x – x 2 2 + x – x 2 ≥ 0 x 2 – x – 2 ≤ 0 [- 1; 2] პასუხი: 4 მთლიანი ხსნარი.№4 . ამოხსენით განტოლება და მიუთითეთ ყველაზე დიდი ფესვი თქვენს პასუხში:
│4 – x -
 │= 4 – x –
│= 4 – x –  x 2 – 5x + 5 = 0 D = 5 x 1.2 =
x 2 – 5x + 5 = 0 D = 5 x 1.2 =  ≈ 1,4
≈ 1,4პასუხი: x = 3.
Სავარჯიშოები:
№12.
ამოხსენით განტოლება, თქვენს პასუხში მიუთითეთ მთელი ფესვი: │x 2 + 6x + 8│= x 2 + 6x + 8 №13.
ამოხსენით განტოლება, მიუთითეთ მთელი რიცხვების ამონახსნები თქვენს პასუხში: │13x – x 2 - 36│+ x 2 – 13x + 36 = 0 №14.
ამოხსენით განტოლება; თქვენს პასუხში მიუთითეთ მთელი რიცხვი, რომელიც არ არის განტოლების ფესვი: 
ნაწილი 5. │F(x)│= │G(x)│ ფორმის განტოლებები
ვინაიდან განტოლების ორივე მხარე არაუარყოფითია, გამოსავალი მოიცავს ორი შემთხვევის განხილვას: სუბმოდულური გამონათქვამები ტოლია ან საპირისპირო ნიშნით. მაშასადამე, თავდაპირველი განტოლება უდრის ორი განტოლების კომბინაციას: │ ფ(x)│= │ გ(x)│ მაგალითები:
№1.
ამოხსენით განტოლება, თქვენს პასუხში მიუთითეთ მთელი ფესვი: │x + 3│=│2x - 1│
მაგალითები:
№1.
ამოხსენით განტოლება, თქვენს პასუხში მიუთითეთ მთელი ფესვი: │x + 3│=│2x - 1│  პასუხი: მთელი ფესვი x = 4.№2.
ამოხსენით განტოლება: │
x – x 2 - 1│=│2x – 3 – x 2 │
პასუხი: მთელი ფესვი x = 4.№2.
ამოხსენით განტოლება: │
x – x 2 - 1│=│2x – 3 – x 2 │  პასუხი: x = 2.№3
.
ამოხსენით განტოლება და თქვენს პასუხში მიუთითეთ ფესვების ნამრავლი:
პასუხი: x = 2.№3
.
ამოხსენით განტოლება და თქვენს პასუხში მიუთითეთ ფესვების ნამრავლი: 


 ძირეული განტოლებები 4x 2 + 2x – 1 = 0 x 1.2 = - 1±√5 / 4 პასუხი: ფესვების ნამრავლია – 0,25. Სავარჯიშოები:
№15
. ამოხსენით განტოლება და თქვენს პასუხში მიუთითეთ მთელი ამონახსნი: │x 2 – 3x + 2│= │x 2 + 6x - 1│ №16.
ამოხსენით განტოლება, მიუთითეთ უფრო მცირე ფესვი თქვენს პასუხში:│5x - 3│=│7 - x│ №17
. ამოხსენით განტოლება და მიუთითეთ ფესვების ჯამი თქვენს პასუხში:
ძირეული განტოლებები 4x 2 + 2x – 1 = 0 x 1.2 = - 1±√5 / 4 პასუხი: ფესვების ნამრავლია – 0,25. Სავარჯიშოები:
№15
. ამოხსენით განტოლება და თქვენს პასუხში მიუთითეთ მთელი ამონახსნი: │x 2 – 3x + 2│= │x 2 + 6x - 1│ №16.
ამოხსენით განტოლება, მიუთითეთ უფრო მცირე ფესვი თქვენს პასუხში:│5x - 3│=│7 - x│ №17
. ამოხსენით განტოლება და მიუთითეთ ფესვების ჯამი თქვენს პასუხში: 
ნაწილი 6. არასტანდარტული განტოლებების ამოხსნის მაგალითები
ამ განყოფილებაში განვიხილავთ არასტანდარტული განტოლებების მაგალითებს, რომელთა ამოხსნისას გამოხატვის აბსოლუტური მნიშვნელობა ვლინდება განმარტებით. მაგალითები:№1.
ამოხსენით განტოლება, თქვენს პასუხში მიუთითეთ ფესვების ჯამი: x · │x│- 5x – 6 = 0  პასუხი: ფესვების ჯამი არის 1 №2.
.
ამოხსენით განტოლება, მიუთითეთ უფრო მცირე ფესვი თქვენს პასუხში: x 2 - 4x ·
პასუხი: ფესვების ჯამი არის 1 №2.
.
ამოხსენით განტოლება, მიუთითეთ უფრო მცირე ფესვი თქვენს პასუხში: x 2 - 4x ·  - 5 = 0
- 5 = 0  პასუხი: უფრო პატარა ფესვი x = - 5. №3.
ამოხსენით განტოლება:
პასუხი: უფრო პატარა ფესვი x = - 5. №3.
ამოხსენით განტოლება:  პასუხი: x = -1. Სავარჯიშოები:
№18.
ამოხსენით განტოლება და მიუთითეთ ფესვების ჯამი: x · │3x + 5│= 3x 2 + 4x + 3
პასუხი: x = -1. Სავარჯიშოები:
№18.
ამოხსენით განტოლება და მიუთითეთ ფესვების ჯამი: x · │3x + 5│= 3x 2 + 4x + 3
№19.
ამოხსენით განტოლება: x 2 – 3x = 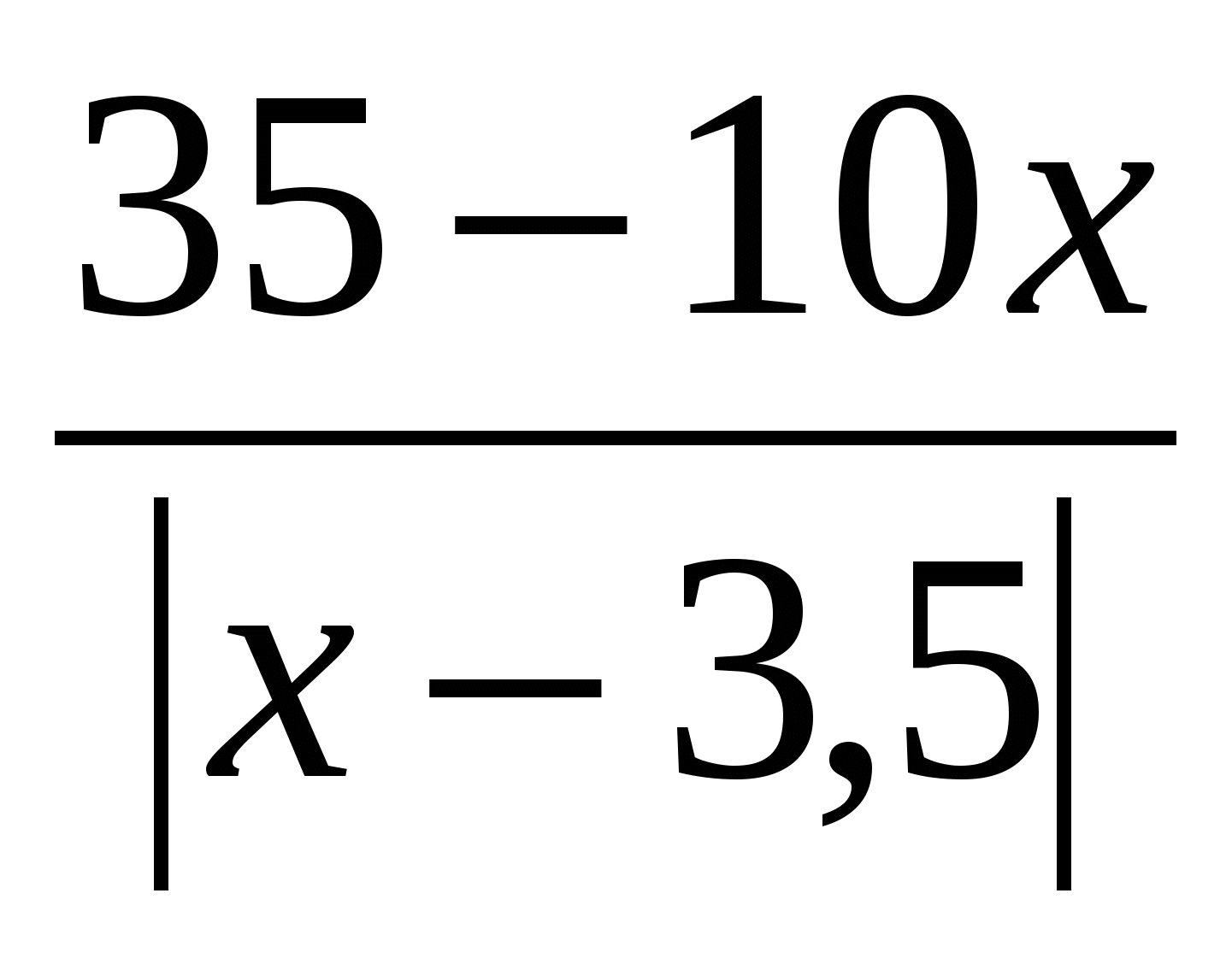
№20.
ამოხსენით განტოლება: 
ნაწილი 7. │F(x)│+│G(x)│=0 ფორმის განტოლებები
ადვილი შესამჩნევია, რომ ამ ტიპის განტოლების მარცხენა მხარეს არის არაუარყოფითი სიდიდეების ჯამი. მაშასადამე, თავდაპირველ განტოლებას აქვს გამოსავალი, თუ და მხოლოდ მაშინ, თუ ორივე წევრი ერთდროულად ნულის ტოლია. განტოლება უდრის განტოლებათა სისტემას: │ ფ(x)│+│ გ(x)│=0 მაგალითები:
№1
. ამოხსენით განტოლება:
მაგალითები:
№1
. ამოხსენით განტოლება:  პასუხი: x = 2. №2.
ამოხსენით განტოლება: პასუხი: x = 1. Სავარჯიშოები:
№21.
ამოხსენით განტოლება: №22
. ამოხსენით განტოლება და მიუთითეთ ფესვების ჯამი თქვენს პასუხში: №23
. ამოხსენით განტოლება და თქვენს პასუხში მიუთითეთ ამონახსნების რაოდენობა:
პასუხი: x = 2. №2.
ამოხსენით განტოლება: პასუხი: x = 1. Სავარჯიშოები:
№21.
ამოხსენით განტოლება: №22
. ამოხსენით განტოლება და მიუთითეთ ფესვების ჯამი თქვენს პასუხში: №23
. ამოხსენით განტოლება და თქვენს პასუხში მიუთითეთ ამონახსნების რაოდენობა: ნაწილი 8. │a 1 x + b 1 │±│a 2 x + b 2 │± … │a n x +b n │= m ფორმის განტოლებები
ამ ტიპის განტოლებების ამოსახსნელად გამოიყენება ინტერვალის მეთოდი. თუ ამას მოვაგვარებთ მოდულების თანმიმდევრული გაფართოებით, მივიღებთ ნსისტემების ნაკრები, რაც ძალიან შრომატევადი და მოუხერხებელია. განვიხილოთ ინტერვალის მეთოდის ალგორითმი: 1). იპოვნეთ ცვლადი მნიშვნელობები X, რომლისთვისაც თითოეული მოდული უდრის ნულს (სუბმოდულარული გამონათქვამების ნულები): 2). მონიშნეთ ნაპოვნი მნიშვნელობები რიცხვით ხაზზე, რომელიც იყოფა ინტერვალებად (ინტერვალების რაოდენობა შესაბამისად უდრის ნ+1
) 3). დაადგინეთ, რა ნიშნით ვლინდება თითოეული მოდული თითოეულ მიღებულ ინტერვალზე (ამოხსნის მიღებისას შეგიძლიათ გამოიყენოთ რიცხვითი წრფე, რომ მონიშნოთ მასზე ნიშნები) 4). თავდაპირველი განტოლება აგრეგატის ტოლფასია ნ+1
სისტემები, რომელთაგან თითოეულში მითითებულია ცვლადის წევრობა Xერთ-ერთი ინტერვალი. მაგალითები:
№1
. ამოხსენით განტოლება და მიუთითეთ ყველაზე დიდი ფესვი თქვენს პასუხში:
2). მონიშნეთ ნაპოვნი მნიშვნელობები რიცხვით ხაზზე, რომელიც იყოფა ინტერვალებად (ინტერვალების რაოდენობა შესაბამისად უდრის ნ+1
) 3). დაადგინეთ, რა ნიშნით ვლინდება თითოეული მოდული თითოეულ მიღებულ ინტერვალზე (ამოხსნის მიღებისას შეგიძლიათ გამოიყენოთ რიცხვითი წრფე, რომ მონიშნოთ მასზე ნიშნები) 4). თავდაპირველი განტოლება აგრეგატის ტოლფასია ნ+1
სისტემები, რომელთაგან თითოეულში მითითებულია ცვლადის წევრობა Xერთ-ერთი ინტერვალი. მაგალითები:
№1
. ამოხსენით განტოლება და მიუთითეთ ყველაზე დიდი ფესვი თქვენს პასუხში:  1). ვიპოვოთ სუბმოდულური გამოსახულებების ნულები: x = 2; x = -3 2). მოდი მოვნიშნოთ ნაპოვნი მნიშვნელობები რიცხვთა ხაზზე და განვსაზღვროთ, რა ნიშნით ვლინდება თითოეული მოდული მიღებულ ინტერვალებზე:
1). ვიპოვოთ სუბმოდულური გამოსახულებების ნულები: x = 2; x = -3 2). მოდი მოვნიშნოთ ნაპოვნი მნიშვნელობები რიცხვთა ხაზზე და განვსაზღვროთ, რა ნიშნით ვლინდება თითოეული მოდული მიღებულ ინტერვალებზე: x – 2 x – 2 x – 2 - - + - 3 2 x 2x + 6 2x + 6 2x + 6 - + + 3)
 - ამონახსნები არ არის განტოლებას ორი ფესვი აქვს. პასუხი: უდიდესი ფესვი x = 2. №2.
ამოხსენით განტოლება და მიუთითეთ მთელი ფესვი თქვენს პასუხში:
- ამონახსნები არ არის განტოლებას ორი ფესვი აქვს. პასუხი: უდიდესი ფესვი x = 2. №2.
ამოხსენით განტოლება და მიუთითეთ მთელი ფესვი თქვენს პასუხში:  1). ვიპოვოთ სუბმოდულური გამოსახულებების ნულები: x = 1,5; x = - 1 2). მოდი მოვნიშნოთ ნაპოვნი მნიშვნელობები რიცხვთა ხაზზე და განვსაზღვროთ რა ნიშნით ვლინდება თითოეული მოდული მიღებულ ინტერვალებზე: x + 1 x + 1 x + 1 - + +
1). ვიპოვოთ სუბმოდულური გამოსახულებების ნულები: x = 1,5; x = - 1 2). მოდი მოვნიშნოთ ნაპოვნი მნიშვნელობები რიცხვთა ხაზზე და განვსაზღვროთ რა ნიშნით ვლინდება თითოეული მოდული მიღებულ ინტერვალებზე: x + 1 x + 1 x + 1 - + + -1 1.5 x 2x – 3 2x – 3 2x – 3 - - +
3).
 ბოლო სისტემას არ აქვს ამონახსნები, ამიტომ განტოლებას ორი ფესვი აქვს. განტოლების ამოხსნისას ყურადღება უნდა მიაქციოთ „-“ ნიშანს მეორე მოდულის წინ. პასუხი: მთელი ფესვი x = 7. №3.
ამოხსენით განტოლება, თქვენს პასუხში მიუთითეთ ფესვების ჯამი: 1). ვიპოვოთ სუბმოდულური გამოსახულებების ნულები: x = 5; x = 1; x = - 2 2). მოდი მოვნიშნოთ ნაპოვნი მნიშვნელობები რიცხვთა ხაზზე და განვსაზღვროთ რა ნიშნით ვლინდება თითოეული მოდული მიღებული ინტერვალებით: x – 5 x – 5 x – 5 x – 5 - - - +
ბოლო სისტემას არ აქვს ამონახსნები, ამიტომ განტოლებას ორი ფესვი აქვს. განტოლების ამოხსნისას ყურადღება უნდა მიაქციოთ „-“ ნიშანს მეორე მოდულის წინ. პასუხი: მთელი ფესვი x = 7. №3.
ამოხსენით განტოლება, თქვენს პასუხში მიუთითეთ ფესვების ჯამი: 1). ვიპოვოთ სუბმოდულური გამოსახულებების ნულები: x = 5; x = 1; x = - 2 2). მოდი მოვნიშნოთ ნაპოვნი მნიშვნელობები რიცხვთა ხაზზე და განვსაზღვროთ რა ნიშნით ვლინდება თითოეული მოდული მიღებული ინტერვალებით: x – 5 x – 5 x – 5 x – 5 - - - + -2 1 5 x x – 1 x – 1 x – 1 x – 1 - - + + x + 2 x + 2 x + 2 x + 2 - + + +
3).
 განტოლებას აქვს ორი ფესვი x = 0 და 2. პასუხი: ფესვების ჯამი არის 2. №4
.
ამოხსენით განტოლება: 1). ვიპოვოთ სუბმოდულური გამოსახულებების ნულები: x = 1; x = 2; x = 3. 2). მოდით განვსაზღვროთ, რა ნიშნით ვლინდება თითოეული მოდული მიღებულ ინტერვალებზე. 3).
განტოლებას აქვს ორი ფესვი x = 0 და 2. პასუხი: ფესვების ჯამი არის 2. №4
.
ამოხსენით განტოლება: 1). ვიპოვოთ სუბმოდულური გამოსახულებების ნულები: x = 1; x = 2; x = 3. 2). მოდით განვსაზღვროთ, რა ნიშნით ვლინდება თითოეული მოდული მიღებულ ინტერვალებზე. 3).  მოდით გავაერთიანოთ პირველი სამი სისტემის გადაწყვეტილებები. პასუხი: ; x = 5.
მოდით გავაერთიანოთ პირველი სამი სისტემის გადაწყვეტილებები. პასუხი: ; x = 5.Სავარჯიშოები: №24. ამოხსენით განტოლება:
 №25.
ამოხსენით განტოლება და მიუთითეთ ფესვების ჯამი თქვენს პასუხში: №26.
ამოხსენით განტოლება და მიუთითეთ უფრო მცირე ფესვი თქვენს პასუხში: №27.
ამოხსენით განტოლება და მიუთითეთ უფრო დიდი ფესვი თქვენს პასუხში:
№25.
ამოხსენით განტოლება და მიუთითეთ ფესვების ჯამი თქვენს პასუხში: №26.
ამოხსენით განტოლება და მიუთითეთ უფრო მცირე ფესვი თქვენს პასუხში: №27.
ამოხსენით განტოლება და მიუთითეთ უფრო დიდი ფესვი თქვენს პასუხში: ნაწილი 9. განტოლებები, რომლებიც შეიცავს რამდენიმე მოდულს
განტოლებები, რომლებიც შეიცავს მრავალ მოდულს, ვარაუდობენ აბსოლუტური მნიშვნელობების არსებობას სუბმოდულურ გამოსახულებებში. ამ ტიპის განტოლებების გადაჭრის ძირითადი პრინციპია მოდულების თანმიმდევრული გამჟღავნება, დაწყებული "გარედან". ამოხსნის დროს გამოიყენება No1, No3 სექციებში განხილული ტექნიკა.მაგალითები:
№1.
ამოხსენით განტოლება:  პასუხი: x = 1; - თერთმეტი. №2.
ამოხსენით განტოლება:
პასუხი: x = 1; - თერთმეტი. №2.
ამოხსენით განტოლება:
პასუხი: x = 0; 4; - 4. №3.
ამოხსენით განტოლება და თქვენს პასუხში მიუთითეთ ფესვების ნამრავლი:  პასუხი: ფესვების ნამრავლია – 8. №4.
ამოხსენით განტოლება:
პასუხი: ფესვების ნამრავლია – 8. №4.
ამოხსენით განტოლება:  ავღნიშნოთ მოსახლეობის განტოლებები (1)
და (2)
და განიხილეთ თითოეული მათგანის გამოსავალი ცალკე დიზაინის სიმარტივისთვის. ვინაიდან ორივე განტოლება შეიცავს ერთზე მეტ მოდულს, უფრო მოსახერხებელია ექვივალენტური გადასვლის განხორციელება სისტემების სიმრავლეზე. (1)
ავღნიშნოთ მოსახლეობის განტოლებები (1)
და (2)
და განიხილეთ თითოეული მათგანის გამოსავალი ცალკე დიზაინის სიმარტივისთვის. ვინაიდან ორივე განტოლება შეიცავს ერთზე მეტ მოდულს, უფრო მოსახერხებელია ექვივალენტური გადასვლის განხორციელება სისტემების სიმრავლეზე. (1)

 (2)
(2)


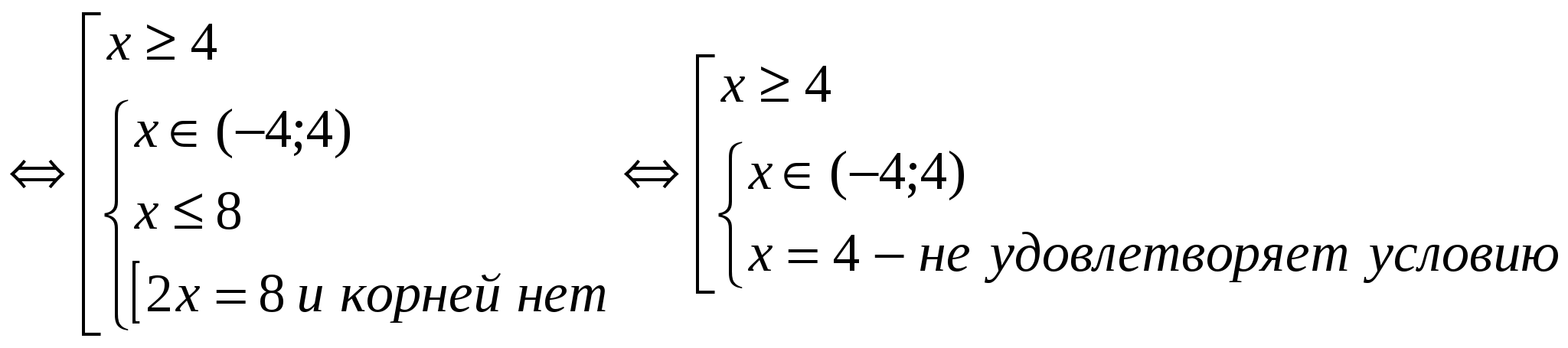 პასუხი:
პასუხი:
Სავარჯიშოები:
№36.
ამოხსენით განტოლება, მიუთითეთ ფესვების ჯამი თქვენს პასუხში: 5 │3x-5│ = 25 x №37.
ამოხსენით განტოლება, თუ ერთზე მეტი ფესვია, თქვენს პასუხში მიუთითეთ ფესვების ჯამი: │x + 2│ x – 3x – 10 = 1 №38.
ამოხსენით განტოლება: 3 │2x -4│ = 9 │x│ №39.
ამოხსენით განტოლება და მიუთითეთ ფესვების რაოდენობა თქვენს პასუხში: 2 │ sin x│ = √2 №40
. ამოხსენით განტოლება და მიუთითეთ ფესვების რაოდენობა თქვენს პასუხში:
ნაწილი 3. ლოგარითმული განტოლებები.
შემდეგი განტოლებების ამოხსნამდე აუცილებელია ლოგარითმების თვისებების მიმოხილვა და ლოგარითმული ფუნქცია. მაგალითები: №1. ამოხსენით განტოლება, მიუთითეთ ფესვების ნამრავლი თქვენს პასუხში: log 2 (x+1) 2 + log 2 │x+1│ = 6 O.D.Z. x+1≠0 x≠ - 1შემთხვევა 1: თუ x ≥ - 1, მაშინ log 2 (x+1) 2 + log 2 (x+1) = 6 log 2 (x+1) 3 = log 2 2 6 (x+1) 3 = 2 6 x+1 = 4 x = 3 – აკმაყოფილებს პირობას x ≥ - 1 2 შემთხვევა: თუ x log 2 (x+1) 2 + log 2 (-x-1) = 6 log 2 (x+1) 2 + log 2 (-(x+1)) = 6 ჟურნალი 2 (-(x+1) 3) = ჟურნალი 2 2 6- (x+1) 3 = 2 6- (x+1) = 4 x = - 5 – აკმაყოფილებს x - 1 მდგომარეობას
პასუხი: ფესვების ნამრავლია – 15.
№2.
ამოხსენით განტოლება, მიუთითეთ ფესვების ჯამი თქვენს პასუხში: lg  ო.დ.ზ.
ო.დ.ზ. 



პასუხი: ფესვების ჯამი არის 0,5.
№3.
ამოხსენით განტოლება: log 5  ო.დ.ზ.
ო.დ.ზ. 
 პასუხი: x = 9. №4.
ამოხსენით განტოლება: │2 + log 0.2 x│+ 3 = │1 + log 5 x│ O.D.Z. x > 0 გამოვიყენოთ ფორმულა სხვა ბაზაზე გადასასვლელად. │2 - ჟურნალი 5 x│+ 3 = │1 + ჟურნალი 5 x│
პასუხი: x = 9. №4.
ამოხსენით განტოლება: │2 + log 0.2 x│+ 3 = │1 + log 5 x│ O.D.Z. x > 0 გამოვიყენოთ ფორმულა სხვა ბაზაზე გადასასვლელად. │2 - ჟურნალი 5 x│+ 3 = │1 + ჟურნალი 5 x│
│2 - log 5 x│- │1 + log 5 x│= - 3 ვიპოვოთ სუბმოდულური გამოსახულებების ნულები: x = 25; x = ეს რიცხვები ყოფს მისაღები მნიშვნელობების დიაპაზონს სამ ინტერვალად, ამიტომ განტოლება ექვივალენტურია სამის კომბინაციასისტემები  პასუხი :)
პასუხი :)