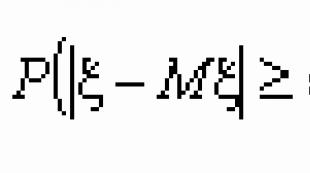შემთხვევითი ფენომენების შესწავლის პრაქტიკა გვიჩვენებს, რომ მიუხედავად იმისა, რომ ინდივიდუალური დაკვირვების შედეგები, თუნდაც ერთსა და იმავე პირობებში ჩატარებული, შეიძლება მნიშვნელოვნად განსხვავდებოდეს, ამავე დროს, დაკვირვებების საკმაოდ დიდი რაოდენობის საშუალო შედეგები სტაბილურია და სუსტად არის დამოკიდებული ინდივიდუალური დაკვირვების შედეგები.

შემთხვევითი ფენომენების ამ შესანიშნავი თვისების თეორიული საფუძველია დიდი რიცხვების კანონი. სახელწოდება „დიდი რიცხვების კანონი“ აერთიანებს თეორემების ჯგუფს, რომელიც ადგენს შემთხვევითი ფენომენების დიდი რაოდენობის საშუალო შედეგების სტაბილურობას და ხსნის ამ სტაბილურობის მიზეზს.

დიდი რიცხვების კანონის უმარტივესი ფორმა და ისტორიულად ამ ნაწილის პირველი თეორემა არის ბერნულის თეორემა, რომელშიც ნათქვამია, რომ თუ მოვლენის ალბათობა ყველა ცდაში ერთნაირია, მაშინ ცდების რაოდენობის მატებასთან ერთად მოვლენის სიხშირე მიდრეკილია მოვლენის ალბათობაზე და წყვეტს შემთხვევითობას.

პუასონის თეორემა ამბობს, რომ მოვლენის სიხშირე დამოუკიდებელი ცდების სერიაში მიდრეკილია მისი ალბათობების საშუალო არითმეტიკისკენ და წყვეტს შემთხვევითობას.

ალბათობის თეორიის ზღვრული თეორემები, თეორემები მოივრ-ლაპლასიახსნას მოვლენის წარმოშობის სიხშირის სტაბილურობის ბუნება. ეს ბუნება მდგომარეობს იმაში, რომ მოვლენის შემთხვევების რაოდენობის შეზღუდვის განაწილება ცდების რაოდენობის შეუზღუდავი ზრდით (თუ მოვლენის ალბათობა ყველა ცდაში ერთნაირია) არის ნორმალური დისტრიბუცია.

ცენტრალური ლიმიტის თეორემა ხსნის ფართოდ გავრცელებულს ნორმალური კანონიდისტრიბუციები. თეორემა ამბობს, რომ როდესაც შემთხვევითი ცვლადი წარმოიქმნება დიდი რაოდენობით დამოუკიდებელი შემთხვევითი ცვლადების დამატების შედეგად სასრული დისპერსიებით, ამ შემთხვევითი ცვლადის განაწილების კანონი პრაქტიკულად გამოდის. ნორმალურიკანონით.

ქვემოთ მოცემული თეორემა სახელწოდებით " დიდი რიცხვების კანონი" აცხადებს, რომ გარკვეულ, საკმაოდ ზოგად პირობებში, შემთხვევითი ცვლადების რაოდენობის მატებასთან ერთად, მათი არითმეტიკული საშუალო მიდრეკილია მათემატიკური მოლოდინების საშუალო არითმეტიკისკენ და წყვეტს შემთხვევითობას.

ლიაპუნოვის თეორემა ხსნის ფართოდ გავრცელებულს ნორმალური კანონიგანაწილება და ხსნის მისი წარმოქმნის მექანიზმს. თეორემა საშუალებას გვაძლევს განვაცხადოთ, რომ როდესაც შემთხვევითი ცვლადი წარმოიქმნება დიდი რაოდენობით დამოუკიდებელი შემთხვევითი ცვლადების დამატების შედეგად, რომელთა ცვალებადობა მცირეა ჯამის ვარიაციასთან შედარებით, ამ შემთხვევითი ცვლადის განაწილების კანონი ბრუნდება. პრაქტიკულად ნორმალურიკანონით. და რადგან შემთხვევითი ცვლადები ყოველთვის წარმოიქმნება უსასრულო რაოდენობის მიზეზებით და ყველაზე ხშირად არცერთ მათგანს არ აქვს დისპერსია შედარებადი შემთხვევითი ცვლადის დისპერსიასთან, პრაქტიკაში შემხვედრი შემთხვევითი ცვლადების უმეტესობა ექვემდებარება ნორმალურ განაწილების კანონს.

დიდი რიცხვების კანონის თვისობრივი და რაოდენობრივი დებულებები ეფუძნება ჩებიშევის უთანასწორობა. ის განსაზღვრავს ზედა ზღვარს ალბათობაზე, რომ შემთხვევითი ცვლადის მნიშვნელობის გადახრა მისი მათემატიკური მოლოდინიდან მეტია გარკვეულ მითითებულ რიცხვზე. აღსანიშნავია, რომ ჩებიშევის უთანასწორობა იძლევა მოვლენის ალბათობის შეფასებას. შემთხვევითი ცვლადისთვის, რომლის განაწილებაც უცნობია, ცნობილია მხოლოდ მისი მათემატიკური მოლოდინი და დისპერსია.

ჩებიშევის უთანასწორობა.თუ შემთხვევით ცვლადს x აქვს ვარიაცია, მაშინ ნებისმიერი e > 0-ისთვის მოქმედებს შემდეგი უტოლობა: , სად მ x და დ x - შემთხვევითი ცვლადის x-ის მათემატიკური მოლოდინი და ვარიაცია.

ბერნულის თეორემა.მოდით m n იყოს წარმატებების რაოდენობა n ბერნულის ცდაში და p წარმატების ალბათობა ინდივიდუალურ ცდაში. მაშინ ნებისმიერი e > 0-ისთვის ეს მართალია .

ცენტრალური ლიმიტის თეორემა.თუ შემთხვევითი ცვლადები x 1 , x 2 , …, x n , … არიან წყვილში დამოუკიდებელი, იდენტურად განაწილებული და აქვთ სასრული დისპერსიები, მაშინ n-სთვის ერთნაირად x (-,)

რა არის წარმატებული გამყიდველების საიდუმლო? თუ რომელიმე კომპანიაში საუკეთესო გამყიდველებს დააკვირდებით, შეამჩნევთ, რომ მათ ერთი რამ აქვთ საერთო. თითოეული მათგანი უფრო მეტ ადამიანს ხვდება და უფრო მეტ პრეზენტაციას აკეთებს, ვიდრე ნაკლებად წარმატებული გამყიდველები. ამ ადამიანებს ესმით, რომ გაყიდვები რიცხვების თამაშია და რაც უფრო მეტ ადამიანს ეტყვიან თავიანთ პროდუქტებსა თუ სერვისებზე, მით უფრო მეტ გარიგებას დახურავენ - ეს ყველაფერია. მათ ესმით, რომ თუ ისინი დაუკავშირდნენ არა მხოლოდ იმ რამდენიმეს, ვინც მათ აუცილებლად იტყვის დიახ, არამედ მათთანაც, ვისი ინტერესი მათი შეთავაზებით არც თუ ისე დიდია, მაშინ საშუალოების კანონი იმუშავებს მათ სასარგებლოდ.

თქვენი შემოსავალი იქნება დამოკიდებული გაყიდვების რაოდენობაზე, მაგრამ, ამავე დროს, პირდაპირპროპორციული იქნება თქვენს მიერ გაკეთებული პრეზენტაციების რაოდენობისა. როგორც კი გაიგებთ და ივარჯიშებთ საშუალოების კანონს, ახალი ბიზნესის დაწყებასთან ან ახალ სფეროში მუშაობასთან დაკავშირებული შფოთვა დაიწყებს კლებას. შედეგად, გაიზრდება კონტროლის გრძნობა და ნდობა თქვენი ფულის გამომუშავების უნარის მიმართ. თუ თქვენ უბრალოდ გააკეთებთ პრეზენტაციებს და აუმჯობესებთ თქვენს უნარებს ამ პროცესში, გარიგებები მოვა.

იმის ნაცვლად, რომ იფიქროთ გარიგებების რაოდენობაზე, უკეთ იფიქრეთ პრეზენტაციების რაოდენობაზე. აზრი არ აქვს დილით გაღვიძებას ან საღამოს სახლში მისვლას და ფიქრს, ვინ იყიდის თქვენს პროდუქტს. ამის ნაცვლად, უმჯობესია დაგეგმოთ რამდენი ზარი გჭირდებათ დღეში. და შემდეგ, რაც არ უნდა მოხდეს - განახორციელეთ ყველა ეს ზარი! ეს მიდგომა გაგიადვილებთ მუშაობას – რადგან ეს მარტივი და კონკრეტული მიზანია. თუ იცით, რომ გაქვთ კონკრეტული და მისაღწევი მიზანი, გაგიადვილდებათ დაგეგმილი ზარების განხორციელება. თუ ამ პროცესის განმავლობაში რამდენჯერმე გაიგონებთ "დიახ", მით უკეთესი!

და თუ "არა", მაშინ საღამოს იგრძნობთ, რომ გულწრფელად გააკეთეთ ყველაფერი, რაც შეგეძლოთ და არ გაწუხებთ ფიქრები იმაზე, თუ რამდენი ფული გამოიმუშავეთ ან რამდენი თანამგზავრი შეიძინეთ დღეში.

ვთქვათ, თქვენს კომპანიაში ან ბიზნესში, საშუალო გამყიდველი ხურავს ერთ გარიგებას ოთხ პრეზენტაციაზე. ახლა წარმოიდგინეთ, რომ თქვენ ხატავთ ბარათებს გემბანიდან. სამი ლუქსის თითოეული ბარათი - ყვავი, ბრილიანტი და კლუბი - არის პრეზენტაცია, რომელშიც პროფესიონალურად წარმოგიდგენთ პროდუქტს, სერვისს ან შესაძლებლობას. თქვენ ამას ისე კარგად აკეთებთ, როგორც შეგიძლიათ, მაგრამ მაინც არ დახურავთ გარიგებას. და თითოეული გულის ბარათი არის გარიგება, რომელიც საშუალებას გაძლევთ მიიღოთ ფული ან შეიძინოთ ახალი კომპანიონი.

ასეთ ვითარებაში არ გინდათ დასტაზე რაც შეიძლება მეტი კარტის გამოღება? ვთქვათ, გთავაზობენ იმდენი კარტის დახატვას, რამდენიც გინდა, თან გადაგიხდით ან გთავაზობენ ახალ კომპანიონს ყოველ ჯერზე, როცა გულის კარტს ათამაშებ. თქვენ ენთუზიაზმით დაიწყებთ ბარათების დახატვას, ძლივს შეამჩნევთ, რა შეესაბამება თქვენს მიერ ახლახან ამოღებულ ბარათს.

თქვენ იცით, რომ ორმოცდათორმეტი კარტის გემბანში არის ცამეტი გული. და ორ გემბანში არის ოცდაექვსი გულის ბარათი და ა.შ. იმედგაცრუებული დარჩებით, როცა ყვავი, ბრილიანტი ან ჯოხები დახატავთ? Რათქმაუნდა არა! თქვენ მხოლოდ იფიქრებთ, რომ ყოველი ასეთი „მისტი“ რასთან მოგაახლოებთ? გულის ბარათამდე!

მაგრამ იცი რა? ასეთი შეთავაზება უკვე მოგცეს. თქვენ იმყოფებით უნიკალურ მდგომარეობაში, რომ მიიღოთ იმდენი, რამდენიც გსურთ და დახატოთ იმდენი გული, რამდენიც გსურთ დახატოთ თქვენს ცხოვრებაში. და თუ უბრალოდ კეთილსინდისიერად „დახატავთ ბარათებს“, გაიუმჯობესებთ უნარებს და გაუძლებთ ცოტა ყვავი, ბრილიანტი და ჯოხები, გახდებით შესანიშნავი გამყიდველი და მიაღწევთ წარმატებას.

ერთ-ერთი რამ, რაც გაყიდვებს ასე სახალისოს ხდის, არის ის, რომ ყოველ ჯერზე, როცა გემბანს არევთ, ბარათები სხვაგვარად ირევა. ზოგჯერ ყველა გული მთავრდება გემბანის დასაწყისში და იღბლიანი სტრიქის შემდეგ (როდესაც გვეჩვენება, რომ არასდროს წავაგებთ!) განსხვავებული სარჩელის ბარათების გრძელი რიგი გველოდება. და სხვა დროს, პირველ გულამდე მისასვლელად, თქვენ უნდა გაიაროთ უსასრულო რაოდენობის ყვავი, ხელკეტები და ბრილიანტები. და ზოგჯერ სხვადასხვა კოსტიუმების ბარათები მკაცრად წესრიგში ჩნდება. მაგრამ ნებისმიერ შემთხვევაში, ორმოცდათორმეტი კარტის თითოეულ გემბანში, გარკვეული თანმიმდევრობით, ყოველთვის არის ცამეტი გული. უბრალოდ ამოიღეთ ბარათები, სანამ არ იპოვით მათ.

მდებარეობა: Leylya,  

სიტყვები დიდი რიცხვების შესახებ ეხება ტესტების რაოდენობას - განიხილება შემთხვევითი ცვლადის მნიშვნელობების დიდი რაოდენობა ან შემთხვევითი ცვლადების დიდი რაოდენობის კუმულაციური ეფექტი. ამ კანონის არსი შემდეგია: თუმცა შეუძლებელია იმის პროგნოზირება, თუ რა მნიშვნელობას მიიღებს ინდივიდუალური შემთხვევითი ცვლადი ერთ ექსპერიმენტში, თუმცა, დიდი რაოდენობით დამოუკიდებელი შემთხვევითი ცვლადის მოქმედების მთლიანი შედეგი კარგავს თავის შემთხვევით ბუნებას და შეუძლია. იწინასწარმეტყველა თითქმის საიმედოდ (ანუ მაღალი ალბათობით). მაგალითად, შეუძლებელია იმის პროგნოზირება, თუ რა მიმართულებით დაეცემა ერთი მონეტა. თუმცა, თუ 2 ტონა მონეტას გადაყრით, მაშინ დიდი დარწმუნებით შეგვიძლია ვთქვათ, რომ გერბთან ერთად ჩამოვარდნილი მონეტების წონა უდრის 1 ტონას.

დიდი რიცხვების კანონი უპირველეს ყოვლისა ეხება ეგრეთ წოდებულ ჩებიშევის უტოლობას, რომელიც აფასებს ერთ ტესტში შემთხვევითი ცვლადის მიღების ალბათობას, რომელიც გადახრის საშუალო მნიშვნელობიდან არაუმეტეს მოცემული მნიშვნელობით.

ჩებიშევის უთანასწორობა. დაე X- თვითნებური შემთხვევითი ცვლადი, a=M(X) , ა დ(X) - მისი განსხვავება. მაშინ

მაგალითი. მანქანაზე ჩართული ყდის დიამეტრის ნომინალური (ანუ საჭირო) მნიშვნელობა უდრის 5 მმდა დისპერსია აღარ არის 0.01 (ეს არის აპარატის სიზუსტის ტოლერანტობა). გამოთვალეთ ალბათობა, რომ ერთი ბუჩქის დამზადებისას მისი დიამეტრის გადახრა ნომინალურიდან ნაკლები იქნება 0.5 მმ .

გამოსავალი. დაე რ.ვ. X- წარმოებული ბუჩქის დიამეტრი. პირობის მიხედვით, მისი მათემატიკური მოლოდინი უდრის ნომინალურ დიამეტრს (თუ არ არის სისტემატური გაუმართაობა მანქანის პარამეტრებში): a=M(X)=5 და დისპერსიას დ(X)≤0.01. ჩებიშევის უტოლობის გამოყენება ზე ε = 0.5, ვიღებთ:

ამრიგად, ასეთი გადახრის ალბათობა საკმაოდ მაღალია და, შესაბამისად, შეგვიძლია დავასკვნათ, რომ ნაწილის ერთჯერადი წარმოებისას, თითქმის დარწმუნებულია, რომ დიამეტრის გადახრა ნომინალურიდან არ აღემატება. 0.5 მმ .

მისი მნიშვნელობით, სტანდარტული გადახრა σ ახასიათებს საშუალოდშემთხვევითი ცვლადის გადახრა მისი ცენტრიდან (ანუ მისი მათემატიკური მოლოდინიდან). რადგან ეს საშუალოდგადახრა, შემდეგ ტესტირების დროს შესაძლებელია დიდი (ხაზგასმით o) გადახრები. რამდენად დიდი გადახრებია პრაქტიკულად შესაძლებელი? ნორმალურად განაწილებული შემთხვევითი ცვლადების შესწავლისას ჩვენ გამოვიყვანეთ „სამი სიგმის“ წესი: ნორმალურად განაწილებული შემთხვევითი ცვლადი. X ერთ ტესტშიპრაქტიკულად არ გადაუხვევს საშუალოდან უფრო მეტად ვიდრე 3σ, სად σ= σ(X)– r.v-ის სტანდარტული გადახრა. X. ეს წესი გამოვიყვანეთ იქიდან, რომ მივიღეთ უტოლობა

.

მოდით ახლა შევაფასოთ ამის ალბათობა თვითნებურიშემთხვევითი ცვლადი Xმიიღეთ მნიშვნელობა, რომელიც განსხვავდება საშუალოდან არაუმეტეს სამჯერ სტანდარტული გადახრით. ჩებიშევის უტოლობის გამოყენება ზე ε = 3σდა იმის გათვალისწინებით, რომ დ(Х)= ს 2 , ვიღებთ:

.

ამრიგად, ზოგადადჩვენ შეგვიძლია შევაფასოთ შემთხვევითი ცვლადის საშუალოდან გადახრის ალბათობა არაუმეტეს სამი სტანდარტული გადახრით რიცხვით 0.89 , ხოლო ნორმალური განაწილებისთვის ეს შეიძლება გარანტირებული იყოს ალბათობით 0.997 .

ჩებიშევის უტოლობა შეიძლება განზოგადდეს დამოუკიდებელი იდენტურად განაწილებული შემთხვევითი ცვლადების სისტემაზე.

განზოგადებული ჩებიშევის უთანასწორობა. თუ დამოუკიდებელი შემთხვევითი ცვლადები X 1 , X 2 , … , X ნ მ(X მე )= ადა განსხვავებები დ(X მე )= დ, ეს

ზე ნ=1 ეს უტოლობა გარდაიქმნება ზემოთ ჩამოყალიბებულ ჩებიშევის უტოლობად.

ჩებიშევის უტოლობა, რომელსაც დამოუკიდებელი მნიშვნელობა აქვს შესაბამისი ამოცანების გადასაჭრელად, გამოიყენება ე.წ. ჩებიშევის თეორემის დასამტკიცებლად. ჯერ ამ თეორემის არსზე ვისაუბრებთ, შემდეგ კი მის ფორმალურ ფორმულირებას მივცემთ.

დაე X 1 , X 2 , … , X ნ– დამოუკიდებელი შემთხვევითი ცვლადების დიდი რაოდენობა მათემატიკური მოლოდინებით M(X 1 )=ა 1 , … , M(X ნ )=ა ნ. მიუხედავად იმისა, რომ თითოეულ მათგანს, ექსპერიმენტის შედეგად, შეუძლია მიიღოს მნიშვნელობა შორს მისი საშუალოდან (ანუ მათემატიკური მოლოდინი), თუმცა, შემთხვევითი ცვლადი.
, მათი საშუალო არითმეტიკულის ტოლი, დიდი ალბათობით მიიღებს მნიშვნელობას ფიქსირებულ რიცხვთან ახლოს
(ეს არის ყველა მათემატიკური მოლოდინის საშუალო). ეს ნიშნავს შემდეგს. მოდით, ტესტის შედეგად დამოუკიდებელი შემთხვევითი ცვლადები X 1 , X 2 , … , X ნ(ბევრია!) შესაბამისად აიღო ღირებულებები X 1 , X 2 , … , X ნშესაბამისად. მაშინ თუ ეს მნიშვნელობები თავად შეიძლება აღმოჩნდეს შორს შესაბამისი შემთხვევითი ცვლადების საშუალო მნიშვნელობებისგან, მათი საშუალო მნიშვნელობა
სავარაუდოდ რიცხვთან ახლოს იქნება
. ამრიგად, შემთხვევითი ცვლადების დიდი რაოდენობის საშუალო არითმეტიკული მაჩვენებელი უკვე კარგავს თავის შემთხვევით ხასიათს და მისი პროგნოზირება შესაძლებელია დიდი სიზუსტით. ეს აიხსნება იმით, რომ მნიშვნელობების შემთხვევითი გადახრები X მესაწყისი ა მეშეიძლება იყოს სხვადასხვა ნიშნის და, შესაბამისად, მთლიანობაში ეს გადახრები, სავარაუდოდ, კომპენსირებულია.

ტერემა ჩებიშევი (დიდი რიცხვების კანონიჩებიშევის სახით). დაე X 1 , X 2 , … , X ნ … – წყვილი დამოუკიდებელი შემთხვევითი ცვლადების თანმიმდევრობა, რომელთა ვარიაციები შემოიფარგლება ერთი და იგივე რაოდენობით. მაშინ, რაც არ უნდა მცირე რიცხვი ავიღოთ ε, უტოლობის ალბათობა

იქნება ერთთან, როგორც სასურველია, თუ ნომერი ნაიღეთ საკმარისად დიდი შემთხვევითი ცვლადები. ფორმალურად ეს ნიშნავს, რომ თეორემის პირობებში

ამ ტიპის კონვერგენციას ეწოდება კონვერგენცია ალბათობით და აღინიშნება:

ამრიგად, ჩებიშევის თეორემა ამბობს, რომ თუ საკმარისად დიდია დამოუკიდებელი შემთხვევითი ცვლადების რაოდენობა, მაშინ მათი საშუალო არითმეტიკული ერთ ტესტში თითქმის საიმედოდ მიიღებს მათემატიკური მოლოდინების საშუალო მნიშვნელობას.

ყველაზე ხშირად, ჩებიშევის თეორემა გამოიყენება სიტუაციებში, სადაც შემთხვევითი ცვლადებია X 1 , X 2 , … , X ნ … აქვთ იგივე განაწილება (ანუ იგივე განაწილების კანონი ან იგივე ალბათობის სიმკვრივე). სინამდვილეში, ეს არის იგივე შემთხვევითი ცვლადის შემთხვევების დიდი რაოდენობა.

შედეგი(განზოგადებული ჩებიშევის უთანასწორობა). თუ დამოუკიდებელი შემთხვევითი ცვლადები X 1 , X 2 , … , X ნ … აქვთ იგივე განაწილება მათემატიკური მოლოდინებით მ(X მე )= ადა განსხვავებები დ(X მე )= დ, ეს

, ე.ი.
.

მტკიცებულება გამომდინარეობს განზოგადებული ჩებიშევის უთანასწორობიდან ზღვარზე გადასვლით ნ→∞ .

კიდევ ერთხელ აღვნიშნოთ, რომ ზემოთ დაწერილი ტოლობები არ იძლევა იმის გარანტიას, რომ რაოდენობრივი მნიშვნელობა აქვს
ისწრაფვის აზე ნ→∞. ეს რაოდენობა კვლავ რჩება შემთხვევით ცვლადად და მისი ინდივიდუალური მნიშვნელობები შეიძლება საკმაოდ შორს იყოს ა. მაგრამ ასეთის ალბათობა (შორს ა) მნიშვნელობები ზრდით ნმიდრეკილია 0-მდე.

კომენტარი. დასკვნა აშკარად მოქმედებს უფრო ზოგად შემთხვევაში, როდესაც დამოუკიდებელი შემთხვევითი ცვლადებია X 1 , X 2 , … , X ნ … აქვთ განსხვავებული განაწილება, მაგრამ იგივე მათემატიკური მოლოდინები (თანაბარი ა) და ერთობლივად შეზღუდული დისპერსიები. ეს საშუალებას გვაძლევს ვიწინასწარმეტყველოთ გარკვეული რაოდენობის გაზომვის სიზუსტე, თუნდაც ეს გაზომვები განხორციელდეს სხვადასხვა ინსტრუმენტებით.

მოდით უფრო დეტალურად განვიხილოთ ამ შედეგის გამოყენება რაოდენობების გაზომვისას. მოდით გამოვიყენოთ რაიმე მოწყობილობა ნერთი და იგივე სიდიდის გაზომვები, რომელთა ნამდვილი მნიშვნელობა უდრის ადა ჩვენ არ ვიცით. ასეთი გაზომვების შედეგები X 1 , X 2 , … , X ნშეიძლება მნიშვნელოვნად განსხვავდებოდეს ერთმანეთისგან (და ნამდვილი მნიშვნელობიდან ა) სხვადასხვა შემთხვევითი ფაქტორების გამო (წნევის ცვლილება, ტემპერატურა, შემთხვევითი ვიბრაცია და ა.შ.). განვიხილოთ რ.ვ. X– ინსტრუმენტის წაკითხვა სიდიდის ერთჯერადი გაზომვისთვის, ასევე r.v. X 1 , X 2 , … , X ნ– ინსტრუმენტის კითხვა პირველ, მეორე, ..., ბოლო გაზომვისას. ამრიგად, თითოეული რაოდენობა X 1 , X 2 , … , X ნ მხოლოდ ერთი შემთხვევაა ს.ვ. Xდა, შესაბამისად, მათ ყველას აქვთ იგივე განაწილება, რაც r.v. X. ვინაიდან გაზომვის შედეგები ერთმანეთზე არ არის დამოკიდებული, მაშინ რ.ვ. X 1 , X 2 , … , X ნშეიძლება ჩაითვალოს დამოუკიდებლად. თუ მოწყობილობა არ წარმოქმნის სისტემურ შეცდომას (მაგალითად, სკალის ნული არ არის "გამორთული", ზამბარა არ არის დაჭიმული და ა.შ.), მაშინ შეგვიძლია ვივარაუდოთ, რომ მათემატიკური მოლოდინი M(X) = a, და, შესაბამისად M(X 1 ) = ... = M(X ნ ) = ა. ამრიგად, დაკმაყოფილებულია ზემოაღნიშნული შედეგის პირობები და შესაბამისად, როგორც რაოდენობის მიახლოებითი მნიშვნელობა აჩვენ შეგვიძლია ავიღოთ შემთხვევითი ცვლადის „რეალიზაცია“.
ჩვენს ექსპერიმენტში (რომელიც შედგება სერიის ჩატარებისგან ნგაზომვები), ე.ი.

.

გაზომვების დიდი რაოდენობით, ამ ფორმულის გამოყენებით გაანგარიშების კარგი სიზუსტე პრაქტიკულად გარკვეულია. ეს არის პრაქტიკული პრინციპის დასაბუთება, რომ გაზომვების დიდი რაოდენობით, მათი არითმეტიკული საშუალო პრაქტიკულად დიდად არ განსხვავდება გაზომილი მნიშვნელობის ნამდვილი მნიშვნელობისაგან.

"შერჩევის" მეთოდი, რომელიც ფართოდ გამოიყენება მათემატიკურ სტატისტიკაში, ემყარება დიდი რიცხვების კანონს, რაც საშუალებას აძლევს ადამიანს მიიღოს მისი ობიექტური მახასიათებლები მისაღები სიზუსტით შემთხვევითი ცვლადის მნიშვნელობების შედარებით მცირე ნიმუშიდან. მაგრამ ეს იქნება განხილული შემდეგ ნაწილში.

მაგალითი. გარკვეული რაოდენობა იზომება საზომ მოწყობილობაზე, რომელიც არ ახდენს სისტემატურ დამახინჯებას აერთხელ (მიღებულია ღირებულება X 1 ), და შემდეგ კიდევ 99 ჯერ (მიღებული მნიშვნელობები X 2 , … , X 100 ). ნამდვილი გაზომვის მნიშვნელობისთვის აპირველი გაზომვის შედეგი მიიღება პირველ რიგში
, შემდეგ კი ყველა გაზომვის საშუალო არითმეტიკული
. მოწყობილობის გაზომვის სიზუსტე ისეთია, რომ σ გაზომვის სტანდარტული გადახრა არ არის 1-ზე მეტი (შესაბამისად, დისპერსიული დ=σ 2 ასევე არ აღემატება 1). თითოეული გაზომვის მეთოდისთვის შეაფასეთ ალბათობა იმისა, რომ გაზომვის შეცდომა არ აღემატებოდეს 2-ს.

გამოსავალი. დაე რ.ვ. X- ინსტრუმენტის კითხვა ერთი გაზომვისთვის. მერე პირობით M(X)=a. დასმულ კითხვებზე პასუხის გასაცემად ვიყენებთ განზოგადებულ ჩებიშევის უტოლობას

ე =2 პირველი ამისთვის ნ=1 და შემდეგ ამისთვის ნ=100 . პირველ შემთხვევაში ვიღებთ
და მეორეში. ამგვარად, მეორე შემთხვევა პრაქტიკულად გარანტირებულია განსაზღვრული გაზომვის სიზუსტით, ხოლო პირველი ამ თვალსაზრისით დიდ ეჭვებს ტოვებს.

მოდით გამოვიყენოთ ზემოაღნიშნული განცხადებები ბერნულის სქემაში წარმოქმნილ შემთხვევით ცვლადებზე. გავიხსენოთ ამ სქემის არსი. დაე, წარმოიქმნას ნ დამოუკიდებელი გამოცდები, რომელთაგან თითოეული შეიცავს გარკვეულ მოვლენას აშეიძლება გამოჩნდეს იგივე ალბათობით რ, ა ქ=1–რ(მნიშვნელობით, ეს არის საპირისპირო მოვლენის ალბათობა - მოვლენა არ მოხდეს ა) . დავხარჯოთ რაღაც რიცხვი ნასეთი ტესტები. განვიხილოთ შემთხვევითი ცვლადები: X 1 - მოვლენის შემთხვევების რაოდენობა ავ 1 - ტესტი, ..., X ნ- მოვლენის შემთხვევების რაოდენობა ავ ნ- ტესტი. ყველა შევიდა ს.ვ. შეუძლია ღირებულებების აღება 0 ან 1 (მოვლენა აშეიძლება გამოჩნდეს ან არ გამოჩნდეს ტესტში) და მნიშვნელობა 1 პირობის მიხედვით მიღებულია ყოველ ცდაში ალბათობით გვ(მოვლენის დადგომის ალბათობა ათითოეულ საცდელში) და ღირებულება 0 ალბათობით ქ= 1 – გვ. ამრიგად, ამ რაოდენობებს აქვთ განაწილების იგივე კანონები:

X 1

X ნ

ამრიგად, ამ რაოდენობების საშუალო მნიშვნელობები და მათი ვარიაციები ასევე იგივეა: M(X 1 )=0 ∙ ქ+1 ∙ p= p, …, M(X ნ )= გვ ; დ(X 1 )=(0 2 ∙ ქ+1 2 ∙ გვ)− გვ 2 = გვ∙(1− გვ)= გვ ∙ q,…, დ(X ნ )= გვ ∙ ქ. ამ მნიშვნელობების ჩანაცვლებით განზოგადებულ ჩებიშევის უტოლობაში, ჩვენ ვიღებთ

.

ცხადია, რომ რ.ვ. X=X 1 +…+X ნარის მოვლენის შემთხვევების რაოდენობა ასულ ნტესტები (როგორც ამბობენ - "წარმატების რაოდენობა" ნტესტები). შეუშვით ჩატარებული ნტესტირების ღონისძიება აგამოჩნდა კ მათგან. მაშინ წინა უტოლობა შეიძლება დაიწეროს როგორც

.

მაგრამ სიდიდე
, მოვლენის შემთხვევების რაოდენობის თანაფარდობის ტოლია ავ ნდამოუკიდებელი ცდები, ცდების მთლიან რაოდენობას, ადრე ეწოდებოდა მოვლენის ფარდობითი სიხშირე ავ ნტესტები. ამიტომ არის უთანასწორობა

.

ახლა გადავდივართ ლიმიტზე ნ→∞, მივიღებთ
, ე.ი.
(ალბათობით). ეს არის ბერნულის ფორმით დიდი რიცხვების კანონის შინაარსი. აქედან გამომდინარეობს, რომ საკმარისად დიდი რაოდენობის ტესტებით ნფარდობითი სიხშირის თვითნებურად მცირე გადახრები
მოვლენები მისი ალბათობიდან რ- თითქმის საიმედო მოვლენები და დიდი გადახრები - თითქმის შეუძლებელია. მიღებული დასკვნა ფარდობითი სიხშირეების ასეთი სტაბილურობის შესახებ (რაზეც ადრე ვისაუბრეთ, როგორც ექსპერიმენტულიფაქტი) ამართლებს მოვლენის ალბათობის ადრე შემოღებულ სტატისტიკურ განმარტებას, როგორც რიცხვს, რომლის გარშემოც იცვლება მოვლენის ფარდობითი სიხშირე.

იმის გათვალისწინებით, რომ გამოხატულება გვ∙ ქ= გვ∙(1− გვ)= გვ− გვ 2 არ აღემატება ცვლილების ინტერვალს
(ამის გადამოწმება ადვილია ამ სეგმენტზე ამ ფუნქციის მინიმუმის მოძიებით), ზემოაღნიშნული უთანასწორობიდან
ამის მიღება ადვილია

,

რომელიც გამოიყენება შესაბამისი პრობლემების გადაჭრისას (ერთ-ერთი მათგანი ქვემოთ იქნება მოცემული).

მაგალითი. მონეტა 1000-ჯერ იყო გადაყრილი. შეაფასეთ ალბათობა იმისა, რომ გერბის გარეგნობის ფარდობითი სიხშირის გადახრა მისი ალბათობიდან იქნება 0,1-ზე ნაკლები.

გამოსავალი. უთანასწორობის გამოყენება
ზე გვ= ქ=1/2 , ნ=1000 , ε=0.1, მივიღებთ .

მაგალითი. შეაფასეთ ალბათობა, რომ წინა მაგალითის პირობებში რიცხვი კჩამოშვებული ემბლემები იქნება დიაპაზონში 400 ადრე 600 .

გამოსავალი. მდგომარეობა 400< კ<600 ნიშნავს რომ 400/1000< კ/ ნ<600/1000 , ე.ი. 0.4< ვ ნ (ა)<0.6 ან
. როგორც წინა მაგალითიდან ვნახეთ, ასეთი მოვლენის ალბათობა არ არის ნაკლები 0.975 .

მაგალითი. რაიმე მოვლენის ალბათობის გამოთვლა აჩატარდა 1000 ექსპერიმენტი, რომელშიც მოვლენა აგამოჩნდა 300-ჯერ. შეაფასეთ ალბათობა იმისა, რომ ფარდობითი სიხშირე (უდრის 300/1000 = 0.3) დაშორებულია ჭეშმარიტ ალბათობას რარაუმეტეს 0.1.

გამოსავალი. ზემოაღნიშნული უტოლობის გამოყენება
n=1000-ისთვის, ε=0.1, მივიღებთ.

დიდ და მრავალფეროვან მასალაზე აღმოჩენილი შემთხვევითი მოვლენების სიხშირეების სტაბილიზაციის ფენომენი თავდაპირველად არ გაამართლა და აღიქმებოდა წმინდა ემპირიულ ფაქტად. პირველი თეორიული შედეგი ამ სფეროში იყო ცნობილი ბერნულის თეორემა, რომელიც გამოქვეყნდა 1713 წელს, რომელმაც საფუძველი ჩაუყარა დიდი რიცხვების კანონებს.

ბერნულის თეორემა თავისი შინაარსით არის ზღვრული თეორემა, ანუ ასიმპტომური მნიშვნელობის დებულება, რომელიც ამბობს, რა მოუვა ალბათურ პარამეტრებს დაკვირვების დიდი რაოდენობით. ამ ტიპის ყველა თანამედროვე მრავალრიცხოვანი განცხადების წინაპარი სწორედ ბერნულის თეორემაა.

დღეს, როგორც ჩანს, დიდი რიცხვების მათემატიკური კანონი არის მრავალი რეალური პროცესის ზოგიერთი ზოგადი თვისების ასახვა.

დიდი რიცხვების კანონის მინიჭების სურვილით, რაც შეესაბამება ამ კანონის გამოყენების შორს ამოწურულ პოტენციურ შესაძლებლობებს, ჩვენი საუკუნის ერთ-ერთმა უდიდესმა მათემატიკოსმა A.N. კოლმოგოროვმა ჩამოაყალიბა მისი არსი შემდეგნაირად: დიდი რიცხვების კანონი არის ”ზოგადი პრინციპი, რომლის ძალითაც დიდი რაოდენობით შემთხვევითი ფაქტორების მთლიანი მოქმედება იწვევს შემთხვევითობისგან თითქმის დამოუკიდებელ შედეგს”.

ამრიგად, დიდი რიცხვების კანონს აქვს ორი ინტერპრეტაცია. ერთი არის მათემატიკური, ასოცირდება კონკრეტულ მათემატიკურ მოდელებთან, ფორმულირებებით, თეორიებით და მეორე უფრო ზოგადია, სცილდება ამ ჩარჩოებს. მეორე ინტერპრეტაცია დაკავშირებულია მეტ-ნაკლებად მიმართული მოქმედების ფორმირების ფენომენთან, რომელიც ხშირად შეინიშნება პრაქტიკაში, დიდი რაოდენობით ფარული ან ხილული მოქმედი ფაქტორების ფონზე, რომლებსაც გარეგნულად არ აქვთ ასეთი უწყვეტობა. მეორე ინტერპრეტაციასთან ასოცირებული მაგალითებია ფასები თავისუფალ ბაზარზე და საზოგადოებრივი აზრის ფორმირება კონკრეტულ საკითხზე.

დიდი რიცხვების კანონის ამ ზოგადი ინტერპრეტაციის შემდეგ, მოდით მივმართოთ ამ კანონის კონკრეტულ მათემატიკურ ფორმულირებებს.

როგორც ზემოთ ვთქვით, პირველი და ფუნდამენტურად ყველაზე მნიშვნელოვანი ალბათობის თეორიისთვის არის ბერნულის თეორემა. ამ მათემატიკური ფაქტის შინაარსი, რომელიც ასახავს მიმდებარე სამყაროს ერთ-ერთ ყველაზე მნიშვნელოვან კანონს, ქვემოთ ჩამოდის.

განვიხილოთ შეუსაბამო (ანუ დამოუკიდებელი) ტესტების თანმიმდევრობა, რომელთა პირობები თანმიმდევრულად მრავლდება ტესტიდან ტესტამდე. ყოველი ტესტის შედეგი არის ჩვენთვის საინტერესო მოვლენის გამოჩენა ან არ დადგომა ა.

ეს პროცედურა (ბერნულის სქემა) აშკარად შეიძლება ჩაითვალოს ტიპიურად მრავალი პრაქტიკული სფეროსთვის: „ბიჭი - გოგო“ ახალშობილთა თანმიმდევრობით, ყოველდღიური მეტეოროლოგიური დაკვირვებები („წვიმდა - არ იყო“), წარმოებული პროდუქციის ნაკადის კონტროლი ( "ნორმალური - დეფექტური") და ა.შ.

მოვლენის დადგომის სიხშირე აზე პტესტები ( t A -

მოვლენის სიხშირე ავ პტესტები) აქვს ზრდასთან ერთად პმისი ღირებულების სტაბილიზაციის ტენდენცია ემპირიული ფაქტია.

ბერნულის თეორემა.ავირჩიოთ ნებისმიერი თვითნებურად მცირე დადებითი რიცხვი e. მაშინ

ჩვენ ხაზს ვუსვამთ, რომ ბერნულის მიერ დადგენილი მათემატიკური ფაქტი გარკვეულ მათემატიკურ მოდელში (ბერნულის სქემაში) არ უნდა აგვერიოს სიხშირის სტაბილურობის ემპირიულად დადგენილ კანონზომიერებაში. ბერნული არ დაკმაყოფილდა მხოლოდ ფორმულით (9.1), არამედ, პრაქტიკის საჭიროებების გათვალისწინებით, მისცა ამ ფორმულაში არსებული უთანასწორობის შეფასება. ამ ინტერპრეტაციას ქვემოთ მივმართავთ.

ბერნულის კანონი დიდი რიცხვების შესახებ იყო დიდი რაოდენობის მათემატიკოსების კვლევის საგანი, რომლებიც მის დახვეწას ცდილობდნენ. ერთ-ერთი ასეთი დახვეწა მოიპოვა ინგლისელმა მათემატიკოსმა მოივრემ და ამჟამად მას მოივრე-ლაპლასის თეორემა ეწოდება. ბერნულის სქემაში განიხილეთ ნორმალიზებული რაოდენობების თანმიმდევრობა:

მოივრის ინტეგრალური თეორემა - ლაპლასი.ავირჩიოთ ნებისმიერი ორი რიცხვი X (და x 2.ამ შემთხვევაში x, x 7, შემდეგ at პ -» °°

თუ (9.3) ფორმულის მარჯვენა მხარეს არის ცვლადი x xუსასრულობისკენ მიდრეკილება, მაშინ მიღებული ლიმიტი, რომელიც დამოკიდებულია მხოლოდ x 2-ზე (ინდექსი 2 შეიძლება მოიხსნას ამ შემთხვევაში), იქნება განაწილების ფუნქცია, მას ე.წ. სტანდარტული ნორმალური განაწილება,ან გაუსის კანონი.

ფორმულის მარჯვენა მხარე (9.3) უდრის y = F(x 2) - F(x x). F(x 2)-> 1 საათზე x 2-> °° და F(x,) -> 0 x-ზე, -> საკმარისად დიდის არჩევის გამო

X] > 0 და X]n საკმარისად დიდია აბსოლუტური სიდიდით, მივიღებთ შემდეგ უტოლობას:

ფორმულის (9.2) გათვალისწინებით, ჩვენ შეგვიძლია გამოვყოთ პრაქტიკულად სანდო შეფასებები:

თუ y = 0.95 ნდობის დონე (ანუ 0.05 შეცდომის ალბათობა) შეიძლება ვინმეს არასაკმარისი მოეჩვენოს, შეგიძლიათ „ითამაშოთ უსაფრთხოდ“ და ააწყოთ ოდნავ უფრო ფართო ნდობის ინტერვალი ზემოთ ნახსენები სამი სიგმის წესის გამოყენებით:

ეს ინტერვალი შეესაბამება ძალიან მაღალ ნდობის დონეს y = 0,997 (იხ. ნორმალური განაწილების ცხრილები).

განვიხილოთ მონეტის სროლის მაგალითი. მოდით გადავყაროთ მონეტა n = 100 ჯერ. შეიძლება მოხდეს, რომ სიხშირე რძალიან განსხვავდება ალბათობისგან რ= 0,5 (თუ ვივარაუდოთ, რომ მონეტა სიმეტრიულია), მაგალითად, იქნება ის ნულის ტოლი? ამისათვის აუცილებელია, რომ გერბი ერთხელაც არ ამოვარდეს. ასეთი მოვლენა თეორიულად შესაძლებელია, მაგრამ ჩვენ უკვე გამოვთვალეთ მსგავსი ალბათობა; ამ მოვლენისთვის ის ტოლი იქნება ეს ღირებულება

ძალიან მცირეა, მისი რიგი არის რიცხვი, რომელსაც აქვს 30 ნული ათობითი წერტილის შემდეგ. ასეთი ალბათობის მქონე მოვლენა უსაფრთხოდ შეიძლება ჩაითვალოს პრაქტიკულად შეუძლებლად. სიხშირის რა გადახრები ალბათობიდან არის პრაქტიკულად შესაძლებელი ექსპერიმენტების დიდი რაოდენობით? მოივრე-ლაპლასის თეორემის გამოყენებით ამ კითხვას შემდეგნაირად ვპასუხობთ: ალბათობით ზე= 0,95 გერბის სიხშირე რჯდება ნდობის ინტერვალში:

თუ შეცდომა 0.05 არ არის პატარა, თქვენ უნდა გაზარდოთ ექსპერიმენტების რაოდენობა (მონეტების გადაყრა). როდესაც იზრდება პნდობის ინტერვალის სიგანე მცირდება (სამწუხაროდ, არა ისე სწრაფად, როგორც ჩვენ გვსურს, მაგრამ უკუპროპორციულია -იოანე).მაგალითად, როდის პ= 10000 ჩვენ ამას მივიღებთ რმდგომარეობს ნდობის ინტერვალში ნდობის ალბათობით ზე= 0,95: 0,5 ± 0,01.

ამრიგად, რაოდენობრივად გავიგეთ სიხშირის ალბათობასთან მიახლოების საკითხი.

ახლა ვიპოვოთ მოვლენის ალბათობა მისი სიხშირის მიხედვით და შევაფასოთ ამ მიახლოების შეცდომა.

მოდით ჩავატაროთ ექსპერიმენტების დიდი რაოდენობა პ(გადააგდე მონეტა), იპოვე ღონისძიების სიხშირე ადა გვინდა შევაფასოთ მისი ალბათობა რ.

დიდი რიცხვების კანონიდან პშემდეგნაირად:

ახლა შევაფასოთ სავარაუდო ტოლობის პრაქტიკულად შესაძლო შეცდომა (9.7). ამისათვის ჩვენ ვიყენებთ უტოლობას (9.5) სახით:

Პოვნა რმიერ რჩვენ უნდა გადავწყვიტოთ უტოლობა (9.8), ამისთვის ჩვენ უნდა გავაფორმოთ ის და ამოხსნათ შესაბამისი კვადრატული განტოლება. შედეგად ვიღებთ:

სად

უხეში შეფასებისთვის რმიერ რშეიძლება იყოს ფორმულაში (9.8) რმარჯვნივ შეცვალეთ რან ფორმულებში (9.10), (9.11) ვივარაუდოთ, რომ

შემდეგ მივიღებთ:

შეუშვით პ= 400 ექსპერიმენტი მიღებულია სიხშირის მნიშვნელობა რ= 0.25, შემდეგ y = 0.95 ნდობის დონით ვპოულობთ:

რა მოხდება, თუ ჩვენ უნდა ვიცოდეთ ალბათობა უფრო ზუსტად, ვთქვათ, არაუმეტეს 0,01 შეცდომით? ამისათვის საჭიროა ექსპერიმენტების რაოდენობის გაზრდა.

ფორმულაში (9.12) ვარაუდით ალბათობა რ= 0.25, ჩვენ ვატოლებთ შეცდომის მნიშვნელობას მოცემულ მნიშვნელობას 0.01 და ვიღებთ განტოლებას P:

ამ განტოლების ამოხსნით, მივიღებთ n~ 7500.

ახლა განვიხილოთ კიდევ ერთი კითხვა: შეიძლება თუ არა ექსპერიმენტებში მიღებული ალბათობიდან სიხშირის გადახრა აიხსნას შემთხვევითი მიზეზებით, თუ ეს გადახრა აჩვენებს, რომ ალბათობა არ არის ისეთი, როგორსაც ველოდით? სხვა სიტყვებით რომ ვთქვათ, გამოცდილება ადასტურებს მიღებულ სტატისტიკურ ჰიპოთეზას ან, პირიქით, მოითხოვს მის უარყოფას?

მოდით, მაგალითად, გადააგდოთ მონეტა პ= 800-ჯერ, ვიღებთ გერბის გარეგნობის სიხშირეს რ= 0.52. ჩვენ ეჭვი გვეპარებოდა, რომ მონეტა ასიმეტრიული იყო. გამართლებულია ეს ეჭვი? ამ კითხვაზე პასუხის გასაცემად, ჩვენ გამოვიყვანთ ვარაუდიდან, რომ მონეტა სიმეტრიულია (p = 0.5). მოდი ვიპოვოთ ნდობის ინტერვალი (დარწმუნების ალბათობით ზე= 0,95) გერბის გარეგნობის სიხშირეზე. თუ ექსპერიმენტში მიღებული მნიშვნელობა რ= 0,52 ჯდება ამ ინტერვალში - ყველაფერი ნორმალურია, მონეტის სიმეტრიის შესახებ მიღებული ჰიპოთეზა არ ეწინააღმდეგება ექსპერიმენტულ მონაცემებს. ფორმულა (9.12) ზე რ= 0,5 იძლევა 0,5 ± 0,035 ინტერვალს; მიღებული ღირებულება p = 0.52 ჯდება ამ ინტერვალში, რაც ნიშნავს, რომ მონეტა უნდა "გაიწმინდოს" ასიმეტრიის ეჭვებისგან.

მსგავსი მეთოდები გამოიყენება იმისთვის, რომ ვიმსჯელოთ, არის თუ არა შემთხვევითი მოვლენებში დაფიქსირებული მათემატიკური მოლოდინებიდან სხვადასხვა გადახრები შემთხვევითი თუ „მნიშვნელოვანი“. მაგალითად, შემთხვევით აღმოჩნდა თუ არა ნაკლებწონიანობა შეფუთული საქონლის რამდენიმე ნიმუშში, თუ ეს მიუთითებს მომხმარებლის სისტემატურ მოტყუებაზე? შემთხვევით გაიზარდა თუ არა გამოჯანმრთელების მაჩვენებელი პაციენტებში, რომლებიც იყენებდნენ ახალ პრეპარატს, თუ ეს გამოწვეულია პრეპარატის ეფექტით?

ნორმალური კანონი განსაკუთრებით მნიშვნელოვან როლს ასრულებს ალბათობის თეორიასა და მის პრაქტიკულ გამოყენებაში. ზემოთ უკვე ვნახეთ, რომ შემთხვევითი ცვლადი - ბერნულის სქემაში რაიმე მოვლენის შემთხვევების რაოდენობა - პ-» °° დაყვანილია ნორმალურ კანონმდე. თუმცა, არსებობს ბევრად უფრო ზოგადი შედეგი.

ცენტრალური ლიმიტის თეორემა.დიდი რაოდენობით დამოუკიდებელი (ან სუსტად დამოკიდებული) შემთხვევითი ცვლადების ჯამი, რომლებიც შედარებულია ერთმანეთთან მათი განსხვავებების თანმიმდევრობით, ნაწილდება ჩვეულებრივი კანონის მიხედვით, მიუხედავად იმისა, თუ როგორი იყო ტერმინების განაწილების კანონები. ზემოაღნიშნული განცხადება არის ცენტრალური ლიმიტის თეორიის უხეში თვისებრივი ფორმულირება. ამ თეორემას მრავალი ფორმა აქვს, ერთმანეთისგან განსხვავდება იმ პირობებით, რომლებსაც შემთხვევითი ცვლადები უნდა აკმაყოფილებდეს, რათა მათი ჯამი იყოს „ნორმალიზებული“ ტერმინების რაოდენობის ზრდით.

ნორმალური განაწილების სიმკვრივე Dx) გამოიხატება ფორმულით:

სად A -შემთხვევითი ცვლადის მათემატიკური მოლოდინი X ს= V7) არის მისი სტანდარტული გადახრა.

x 1? x 2 ინტერვალში მოხვედრის ალბათობის გამოსათვლელად გამოიყენება ინტეგრალი:

ვინაიდან ინტეგრალი (9.14) სიმკვრივით (9.13) არ არის გამოხატული ელემენტარული ფუნქციების მიხედვით („არ არის აღებული“), მაშინ (9.14) გამოსათვლელად იყენებენ სტანდარტული ნორმალური განაწილების ინტეგრალური განაწილების ფუნქციის ცხრილებს, როდესაც a = 0, a = 1 (ასეთი ცხრილები ხელმისაწვდომია ალბათობის თეორიის ნებისმიერ სახელმძღვანელოში):

ალბათობა (9.14) განტოლების (10.15) გამოყენებით გამოიხატება ფორმულით:

მაგალითი. იპოვეთ შემთხვევითი ცვლადის ალბათობა X,აქვს ნორმალური განაწილება პარამეტრებით ა, a, გადაუხვევს მათემატიკური მოლოდინის მოდულს არაუმეტეს 3-ით.

ფორმულის (9.16) და ნორმალური კანონის განაწილების ფუნქციის ცხრილის გამოყენებით ვიღებთ:

მაგალითი. ღონისძიება 700 დამოუკიდებელი ექსპერიმენტიდან თითოეულში ახდება მუდმივი ალბათობით რ= 0.35. იპოვეთ მოვლენის ალბათობა ამოხდება:

• 1) ზუსტად 270-ჯერ;
• 2) 270-ზე ნაკლები და 230-ჯერ მეტი;
• 3) 270-ზე მეტი.

მათემატიკური მოლოდინის პოვნა ა = და ა.შდა სტანდარტული გადახრა:

შემთხვევითი ცვლადი - მოვლენის შემთხვევების რაოდენობა A:

ცენტრირებული და ნორმალიზებული მნიშვნელობის პოვნა X:

ნორმალური განაწილების სიმკვრივის ცხრილებიდან ვხვდებით f(x):

მოდი ვიპოვოთ ახლა R w (x,> 270) = P 700 (270 F(1.98) = = 1 - 0.97615 = 0.02385.

დიდი რაოდენობის პრობლემების კვლევაში სერიოზული ნაბიჯი გადადგა 1867 წელს P.L. Chebyshev-ის მიერ. მან განიხილა ძალიან ზოგადი შემთხვევა, როდესაც არაფერია საჭირო დამოუკიდებელი შემთხვევითი ცვლადებისგან, გარდა მათემატიკური მოლოდინებისა და დისპერსიების არსებობისა.

ჩებიშევის უთანასწორობა.თვითნებურად მცირე დადებითი რიცხვისთვის e, შემდეგი უტოლობა მოქმედებს:

ჩებიშევის თეორემა.თუ x x, x 2, ..., x p -წყვილი დამოუკიდებელი შემთხვევითი ცვლადები, რომელთაგან თითოეულს აქვს მათემატიკური მოლოდინი E(Xj) = ციდა დისპერსიას D(x,) =), და დისპერსიები ერთნაირად შეზღუდულია, ე.ი. 1,2 ..., შემდეგ ნებისმიერი თვითნებურად მცირე დადებითი რიცხვისთვის ეშემდეგი კავშირი მოქმედებს:

შედეგი. თუ a, =აიო, -o 2, მე= 1.2 ..., მაშინ

დავალება. რამდენჯერ უნდა გადააგდოთ მონეტა ისე, რომ ამის ალბათობა არ იყოს ნაკლები y - 0,997, შეიძლება ითქვას, რომ გერბის ამოვარდნის სიხშირე იქნება ინტერვალში (0,499; 0,501)?

დავუშვათ, რომ მონეტა სიმეტრიულია, p - q - 0.5. გამოვიყენოთ ჩებიშევის თეორემა ფორმულაში (9.19) შემთხვევით ცვლადზე. X-გერბის გარეგნობის სიხშირე პმონეტის გადაყრა. ზემოთ უკვე ვაჩვენეთ X = X x + X 2 + ... +X“,სად X t -შემთხვევითი ცვლადი, რომელიც იღებს 1 მნიშვნელობას, თუ მონეტა არის თავი, და მნიშვნელობა 0, თუ ის კუდია. Ისე:

მოდით დავწეროთ უტოლობა (9.19) მოვლენის საპირისპირო მოვლენისთვის, რომელიც მითითებულია ალბათობის ნიშნით:

ჩვენს შემთხვევაში [e = 0.001, cj 2 = /?-p)]t არის გერბის შემთხვევების რაოდენობა პსროლა. ამ სიდიდეების ბოლო უტოლობაში ჩანაცვლებით და იმის გათვალისწინებით, რომ პრობლემის პირობების მიხედვით, უტოლობა უნდა დაკმაყოფილდეს, მივიღებთ:

მოცემული მაგალითი გვიჩვენებს ჩებიშევის უტოლობის გამოყენების შესაძლებლობას შემთხვევითი ცვლადების გარკვეული გადახრების ალბათობის შესაფასებლად (ისევე, როგორც ეს მაგალითი, რომელიც დაკავშირებულია ამ ალბათობების გამოთვლასთან). ჩებიშევის უთანასწორობის უპირატესობა ის არის, რომ ის არ საჭიროებს შემთხვევითი ცვლადების განაწილების კანონების ცოდნას. რა თქმა უნდა, თუ ასეთი კანონი ცნობილია, მაშინ ჩებიშევის უთანასწორობა ძალიან უხეში შეფასებებს იძლევა.

მოდით შევხედოთ იმავე მაგალითს, მაგრამ იმ ფაქტის გამოყენებით, რომ მონეტის სროლა ბერნულის სქემის განსაკუთრებული შემთხვევაა. წარმატებების რაოდენობა (მაგალითში - გერბების რაოდენობა) ემორჩილება ბინომურ კანონს და დიდი პეს კანონი შეიძლება წარმოდგენილი იყოს ნორმალური კანონით მათემატიკური მოლოდინით მოივრის - ლაპლასის ინტეგრალური თეორემის გამო. a = pr = n? 0.5 და სტანდარტული გადახრით ა =yfnpq- 25=0,5ლ/ლ. შემთხვევით ცვლადს - გერბის ჩამოვარდნის სიხშირე - აქვს მათემატიკური მოლოდინი = 0.5 და სტანდარტული გადახრა.

მაშინ გვაქვს:

ბოლო უტოლობიდან ვიღებთ:

ნორმალური განაწილების ცხრილებიდან ვხვდებით:

ჩვენ ვხედავთ, რომ ნორმალური მიახლოება იძლევა მონეტის გადაყრის რაოდენობას, რომელიც იძლევა მოცემულ შეცდომას გერბის ალბათობის შეფასებისას, რაც 37-ჯერ ნაკლებია ჩებიშევის უტოლობის გამოყენებით მიღებულ შეფასებასთან შედარებით (მაგრამ ჩებიშევის უტოლობა შესაძლებელს ხდის მსგავსი გამოთვლები იმ შემთხვევაში, როდესაც არ გვაქვს ინფორმაცია შესასწავლი შემთხვევითი ცვლადის განაწილების კანონის შესახებ).

ახლა განვიხილოთ ფორმულის (9.16) გამოყენებით გადაჭრილი გამოყენებული პრობლემა.

კონკურენციის პრობლემა. ორ კონკურენტ სარკინიგზო კომპანიას აქვს თითო მატარებელი მოსკოვსა და სანკტ-პეტერბურგს შორის. ეს მატარებლები დაახლოებით ერთნაირად არის აღჭურვილი და მიდიან და ჩამოდიან დაახლოებით ერთსა და იმავე დროს. მოდი ვიჩვენოთ, რომ პ= 1000 მგზავრი დამოუკიდებლად და შემთხვევით ირჩევს თავის მატარებელს, ამიტომ, როგორც მგზავრების მიერ მატარებლის არჩევის მათემატიკური მოდელი, ვიყენებთ ბერნულის სქემას. პგამოწვევები და წარმატების ალბათობა რ= 0.5. კომპანიამ უნდა გადაწყვიტოს, რამდენი ადგილი უნდა უზრუნველყოს მატარებელში, ორი ურთიერთსაწინააღმდეგო პირობის გათვალისწინებით: ერთის მხრივ, არ გინდათ, რომ ცარიელი ადგილები გქონდეთ, მეორე მხრივ, არ გსურთ უკმაყოფილო ხალხი. ადგილების ნაკლებობა (შემდეგ ჯერზე უპირატესობას ანიჭებენ კონკურენტ კომპანიებს). რა თქმა უნდა, მისი მიწოდება შესაძლებელია მატარებელში პ= 1000 ადგილი, მაგრამ შემდეგ აშკარად ცარიელი ადგილები იქნება. შემთხვევითი ცვლადი - მატარებელში მგზავრების რაოდენობა - მიღებული მათემატიკური მოდელის ფარგლებში მოივრის ინტეგრალური თეორიის გამოყენებით - ლაპლასი ემორჩილება ნორმალურ კანონს მათემატიკური მოლოდინით. a = pr = n/2 და ვარიაცია a 2 = npq = p/4თანმიმდევრობით. იმის ალბათობა, რომ მეტი სმგზავრები, განისაზღვრება თანაფარდობით:

დააყენეთ რისკის დონე ა, ანუ იმის ალბათობა, რომ მეტი მოვა სმგზავრები:

აქედან:

თუ აარის ბოლო განტოლების რისკის ფესვი, რომელიც ნაპოვნია ნორმალური კანონის განაწილების ფუნქციის ცხრილებიდან, შემდეგ მივიღებთ:

თუ, მაგალითად, პ = 1000, ა= 0.01 (რისკის ეს დონე ნიშნავს ადგილების რაოდენობას სსაკმარისი იქნება 100-დან 99 შემთხვევაში), მაშინ x a ~ 2.33 და s = 537 ადგილი. უფრო მეტიც, თუ ორივე კომპანია მიიღებს რისკის ერთსა და იმავე დონეს ა= 0.01, მაშინ ორ მატარებელს სულ 1074 ადგილი ექნება, აქედან 74 ცარიელი იქნება. ანალოგიურად, შეიძლება გამოითვალოს, რომ 514 ადგილი საკმარისი იქნება ყველა შემთხვევის 80%-ში, ხოლო 549 ადგილი საკმარისი იქნება 1000 შემთხვევიდან 999-ში.

მსგავსი მოსაზრებები ეხება სხვა კონკურენტ სერვისის პრობლემებს. მაგალითად, თუ თკინოთეატრები იგივეს ეჯიბრებიან პმაყურებლები, მაშინ ეს უნდა იქნას მიღებული რ= -. ჩვენ ვიღებთ,

რა არის ადგილების რაოდენობა სკინოთეატრში უნდა განისაზღვროს თანაფარდობა:

ცარიელი ადგილების საერთო რაოდენობა უდრის:

ამისთვის ა = 0,01, პ= 1000 და თ= 2, 3, 4 ამ რიცხვის მნიშვნელობები დაახლოებით უდრის 74, 126, 147, შესაბამისად.

მოდით შევხედოთ სხვა მაგალითს. დაე მატარებელი შედგება P - 100 ვაგონი. თითოეული მანქანის წონა არის შემთხვევითი ცვლადი მათემატიკური მოლოდინით A - 65 ტონა და საშუალო კვადრატული მოლოდინი o = 9 ტონა ლოკომოტივს შეუძლია მატარებლის გადაყვანა, თუ მისი წონა არ აღემატება 6600 ტონას; წინააღმდეგ შემთხვევაში, თქვენ უნდა დააკავშიროთ მეორე ლოკომოტივი. თქვენ უნდა იპოვოთ ალბათობა, რომ ამის გაკეთება არ მოგიწევთ.

ინდივიდუალური მანქანების წონა: , რომელსაც იგივე მათემატიკური მოლოდინი აქვს A - 65 და იგივე განსხვავება დ- o 2 = 81. მათემატიკური მოლოდინების წესის მიხედვით: E(x) - 100 * 65 = 6500. ვარიაციების დამატების წესის მიხედვით: D(x) = 100 x 81 = 8100. ფესვის ამოღებით ვპოულობთ სტანდარტულ გადახრას. იმისათვის, რომ ერთმა ლოკომოტივმა გაიყვანოს მატარებელი, მატარებლის წონა უნდა იყოს Xაღმოჩნდა შემზღუდველი, ანუ ჩავარდა ინტერვალში (0; 6600). შემთხვევითი ცვლადი x - 100 წევრის ჯამი - შეიძლება ჩაითვალოს ნორმალურად განაწილებულად. ფორმულის გამოყენებით (9.16) ვიღებთ:

აქედან გამომდინარეობს, რომ ლოკომოტივი "გაუმკლავდება" მატარებელს დაახლოებით 0,864 ალბათობით. ახლა მატარებელში ვაგონების რაოდენობა ორით შევამციროთ, ე.ი პ= 98. ახლა გამოვთვალოთ ალბათობა იმისა, რომ ლოკომოტივი „გაუმკლავდეს“ მატარებელს, მივიღებთ 0,99 რიგის მნიშვნელობას, ანუ თითქმის გარკვეულ მოვლენას, თუმცა ამისთვის მხოლოდ ორი ვაგონის ამოღება იყო საჭირო.

ასე რომ, თუ საქმე გვაქვს შემთხვევითი ცვლადების დიდი რაოდენობის ჯამებთან, მაშინ შეგვიძლია გამოვიყენოთ ნორმალური კანონი. ბუნებრივია, ეს ბადებს კითხვას: რამდენი შემთხვევითი ცვლადის დამატებაა საჭირო, რათა ჯამის განაწილების კანონი უკვე „ნორმალიზებული“ იყოს? ეს დამოკიდებულია იმაზე, თუ როგორია ტერმინების განაწილების კანონები. არსებობს ისეთი რთული კანონები, რომ ნორმალიზება ხდება მხოლოდ ტერმინების ძალიან დიდი რაოდენობით. მაგრამ ეს კანონები მათემატიკოსების მიერ არის გამოგონილი; ბუნება, როგორც წესი, განზრახ არ ქმნის ასეთ პრობლემებს. ჩვეულებრივ, პრაქტიკაში, იმისთვის, რომ ნორმალური კანონის გამოყენება შესაძლებელი იყოს, საკმარისია ხუთი ან ექვსი ტერმინი.

სიჩქარე, რომლითაც იდენტურად განაწილებული შემთხვევითი ცვლადების ჯამის განაწილების კანონი „ნორმალიზდება“ შეიძლება ილუსტრირებული იყოს შემთხვევითი ცვლადების მაგალითით ერთგვაროვანი განაწილებით ინტერვალზე (0, 1). ასეთი განაწილების მრუდს აქვს მართკუთხედის ფორმა, რომელიც აღარ ჰგავს ნორმალურ კანონს. დავამატოთ ორი ასეთი დამოუკიდებელი ცვლადი – მივიღებთ ეგრეთ წოდებული სიმპსონის კანონის მიხედვით განაწილებულ შემთხვევით ცვლადს, რომლის გრაფიკულ გამოსახულებას აქვს ტოლფერდა სამკუთხედის ფორმა. ის ასევე არ ჰგავს ნორმალურ კანონს, მაგრამ უკეთესია. და თუ დაამატებთ სამ ასეთ თანაბრად განაწილებულ შემთხვევით ცვლადს, მიიღებთ მრუდს, რომელიც შედგება პარაბოლების სამი სეგმენტისგან, ძალიან ჰგავს ნორმალურ მრუდს. თუ თქვენ დაამატებთ ექვს ასეთ შემთხვევით ცვლადს, მიიღებთ მრუდს, რომელიც არ განსხვავდება ნორმალურისგან. ეს არის საფუძველი ფართოდ გავრცელებული მეთოდისთვის ნორმალურად განაწილებული შემთხვევითი ცვლადის მისაღებად და ყველა თანამედროვე კომპიუტერი აღჭურვილია სენსორებით ერთნაირად განაწილებული (0, 1) შემთხვევითი რიცხვებისთვის.

ამის შესამოწმებლად რეკომენდებულია შემდეგი მეთოდი. ჩვენ ვაშენებთ ნდობის ინტერვალს დონის მოვლენის სიხშირისთვის ზე= 0,997 სამი სიგმას წესის მიხედვით:

და თუ მისი ორივე ბოლო არ სცილდება სეგმენტს (0, 1), მაშინ ნორმალური კანონის გამოყენება შეიძლება. თუ ნდობის ინტერვალის რომელიმე საზღვარი არის სეგმენტის მიღმა (0, 1), მაშინ ნორმალური კანონის გამოყენება შეუძლებელია. თუმცა, ზოგიერთ პირობებში, ბინომალური კანონი რაიმე შემთხვევითი მოვლენის სიხშირისთვის, თუ ის არ არის მიდრეკილი ნორმალურზე, მაშინ ის შეიძლება მიდრეკილი იყოს სხვა კანონისკენ.

ბევრ აპლიკაციაში ბერნულის სქემა გამოიყენება, როგორც შემთხვევითი ექსპერიმენტის მათემატიკური მოდელი, რომელშიც ცდების რაოდენობა პდიდია, შემთხვევითი მოვლენა საკმაოდ იშვიათია, ე.ი. რ = და ა.შარა პატარა, მაგრამ არც დიდი (რყევებს O -5-20 დიაპაზონში). ამ შემთხვევაში, შეზღუდვის კავშირი მოქმედებს:

ფორმულას (9.20) ეწოდება პუასონის მიახლოება ბინომიალური კანონისთვის, რადგან მის მარჯვენა მხარეს ალბათობის განაწილებას პუასონის კანონი ეწოდება. ამბობენ, რომ პუასონის განაწილება არის ალბათობის განაწილება იშვიათი მოვლენებისთვის, რადგან ის ხდება მაშინ, როდესაც დაკმაყოფილებულია ლიმიტები: პ -»°°, რ-»0, მაგრამ X = pr oo.

მაგალითი. დაბადების დღეები. რა არის ალბათობა R t (k)რომ 500 კაციან საზოგადოებაში რომხალხი ახალ წელს დაიბადა? თუ ეს 500 ადამიანი შემთხვევით შეირჩევა, მაშინ ბერნულის სქემა შეიძლება გამოყენებულ იქნას წარმატების ალბათობით. P = 1/365. მაშინ

ალბათობის გამოთვლები სხვადასხვა რომმიეცით შემდეგი მნიშვნელობები: RU = 0,3484...; R 2 = 0,2388...; R 3 = 0,1089...; P 4 = 0,0372...; R 5 = 0,0101...; R 6= 0,0023... შესაბამისი მიახლოებები პუასონის ფორმულის გამოყენებით X = 500 1/365 = 1,37

მიეცით შემდეგი მნიშვნელობები: რუ = 0,3481...; R 2 = 0,2385...; P ъ = 0,1089; R 4 = 0,0373...; P 5 = 0,0102...; P 6 = 0.0023... ყველა შეცდომა მხოლოდ მეოთხე ათწილადშია.

აქ მოცემულია სიტუაციების მაგალითები, სადაც შეგიძლიათ გამოიყენოთ პუასონის კანონი იშვიათი მოვლენების შესახებ.

სატელეფონო სადგურზე, არასწორი კავშირი ხდება დაბალი ალბათობით R,ჩვეულებრივ რ~0.005. შემდეგ პუასონის ფორმულა საშუალებას გვაძლევს ვიპოვოთ არასწორი კავშირების ალბათობა კავშირების მოცემული საერთო რაოდენობისთვის n~ 1000 როცა X = pr =1000 0,005 = 5.

ფუნთუშების გამოცხობისას ცომს დაუმატეთ ქიშმიში. მორევის გამო, მოსალოდნელია, რომ ქიშმიშის ფუნთუშების სიხშირე დაახლოებით მიჰყვება პუასონის განაწილებას. R p (k, X),სად X-ქიშმიშის სიმკვრივე ცომში.

რადიოაქტიური ნივთიერება ასხივებს π ნაწილაკებს. მოვლენა, რომელსაც დროთა განმავლობაში აღწევს d-ნაწილაკების რაოდენობა ტმოცემული სივრცის ფართობი, იღებს ფიქსირებულ მნიშვნელობას რომ,ემორჩილება პუასონის კანონს.

ცოცხალი უჯრედების რაოდენობა შეცვლილი ქრომოსომებით რენტგენის სხივების ზემოქმედებისას მიჰყვება პუასონის განაწილებას.

ასე რომ, დიდი რიცხვების კანონები შესაძლებელს ხდის მათემატიკური სტატისტიკის პრობლემის გადაჭრას, რომელიც დაკავშირებულია შემთხვევითი ექსპერიმენტის ელემენტარული შედეგების უცნობი ალბათობების შეფასებასთან. ამ ცოდნის წყალობით ჩვენ ალბათობის თეორიის მეთოდებს პრაქტიკულად მნიშვნელოვანს და გამოსადეგს ვხდით. დიდი რიცხვების კანონები შესაძლებელს ხდის უცნობი ელემენტარული ალბათობების შესახებ ინფორმაციის მოპოვების პრობლემის გადაჭრას სხვა ფორმით - სტატისტიკური ჰიპოთეზების ტესტირების ფორმით.

მოდით უფრო დეტალურად განვიხილოთ სტატისტიკური ჰიპოთეზების ტესტირების ამოცანების გადაჭრის ფორმულირება და სავარაუდო მექანიზმი.

დიდი რიცხვების კანონიალბათობის თეორიაში ნათქვამია, რომ ფიქსირებული განაწილებიდან საკმაოდ დიდი სასრული ნიმუშის ემპირიული საშუალო (საშუალო არითმეტიკული) უახლოვდება ამ განაწილების თეორიულ საშუალოს (მათემატიკურ მოლოდინს). კონვერგენციის ტიპებიდან გამომდინარე, განასხვავებენ დიდი რიცხვების სუსტ კანონს, როდესაც დაახლოება ხდება ალბათობით, და დიდი რიცხვების ძლიერ კანონს შორის, როდესაც კონვერგენცია თითქმის ყველგან ხდება.

ყოველთვის არის საცდელების სასრული რაოდენობა, რომლებშიც, ნებისმიერი წინასწარი ალბათობით, ნაკლებია 1 ზოგიერთი მოვლენის დადგომის ფარდობითი სიხშირე რაც შეიძლება ნაკლებად განსხვავდება მისი ალბათობისგან.

დიდი რიცხვების კანონის ზოგადი მნიშვნელობა: დიდი რაოდენობით იდენტური და დამოუკიდებელი შემთხვევითი ფაქტორების ერთობლივი მოქმედება იწვევს შედეგს, რომელიც, ლიმიტში, შემთხვევითობაზე არ არის დამოკიდებული.

სასრული ნიმუშის ანალიზზე დაფუძნებული ალბათობის შეფასების მეთოდები ეფუძნება ამ თვისებას. ნათელი მაგალითია ამომრჩეველთა შერჩევის საფუძველზე არჩევნების შედეგების პროგნოზირება.

ენციკლოპედიური YouTube

1 / 5

✪ დიდი რიცხვების კანონი

✪ 07 - ალბათობის თეორია. დიდი რიცხვების კანონი

✪ 42 დიდი რიცხვების კანონი

✪ 1 - ჩებიშევის კანონი დიდი რიცხვების შესახებ

✪ მე-11 კლასი, გაკვეთილი 25, გაუსის მრუდი. დიდი რიცხვების კანონი

სუბტიტრები

მოდით გადავხედოთ დიდი რიცხვების კანონს, რომელიც ალბათ ყველაზე ინტუიციური კანონია მათემატიკასა და ალბათობის თეორიაში. და რადგან ის ბევრ რამეს ეხება, ზოგჯერ გამოიყენება და არასწორად ესმით. ნება მომეცით ჯერ განვსაზღვრო სიზუსტისთვის და შემდეგ ვისაუბროთ ინტუიციაზე. ავიღოთ შემთხვევითი ცვლადი, მაგალითად X. ვთქვათ, ვიცით მისი მათემატიკური მოლოდინი ან საშუალო პოპულაციისთვის. დიდი რიცხვების კანონი უბრალოდ ამბობს, რომ თუ ავიღოთ შემთხვევითი ცვლადის დაკვირვების n-ე რიცხვის მაგალითი და ავიღოთ ყველა ამ დაკვირვების საშუალო... ავიღოთ ცვლადი. მოდით ვუწოდოთ მას X, n-ით და ზოლით ზედა. ეს არის ჩვენი შემთხვევითი ცვლადის მე-n რაოდენობის დაკვირვების საშუალო არითმეტიკული. აქ არის ჩემი პირველი დაკვირვება. მე ვაკეთებ ექსპერიმენტს ერთხელ და ვაკეთებ ამ დაკვირვებას, შემდეგ ისევ ვაკეთებ და ვაკეთებ ამ დაკვირვებას, ისევ ვაკეთებ და ვიღებ ამას. მე ვატარებ ამ ექსპერიმენტს მე-n-ჯერ და შემდეგ ვყოფ ჩემი დაკვირვებების რაოდენობაზე. აქ არის ჩემი საშუალო ნიმუში. აქ არის მე ყველა დაკვირვების საშუალო მაჩვენებელი. დიდი რიცხვების კანონი გვეუბნება, რომ ჩემი ნიმუშის საშუალო მიახლოება შემთხვევითი ცვლადის მოსალოდნელ მნიშვნელობას. ან შემიძლია ასევე დავწერო, რომ ჩემი შერჩევის საშუალო მიახლოება პოპულაციის საშუალოს n-ე სიდიდისთვის, რომელიც მიდრეკილია უსასრულობისკენ. მე არ გავაკეთებ მკაფიო განსხვავებას "დაახლოებას" და "კონვერგენციას" შორის, მაგრამ იმედი მაქვს, რომ თქვენ ინტუიციურად გესმით, რომ თუ აქ საკმაოდ დიდ ნიმუშს ავიღებთ, მთლიანი მოსახლეობისთვის მოსალოდნელ მნიშვნელობას მივიღებ. ვფიქრობ, თქვენგან უმეტესობას ინტუიციურად ესმის, რომ თუ საკმარის ტესტებს გავაკეთებ მაგალითების დიდი ნიმუშით, საბოლოოდ ტესტები მომცემს იმ მნიშვნელობებს, რასაც ველოდები, მოსალოდნელი ღირებულებისა და ალბათობის და მთელი ამ ჯაზის გათვალისწინებით. მაგრამ ვფიქრობ, ხშირად გაუგებარია რატომ ხდება ეს. და სანამ დავიწყებ იმის ახსნას, თუ რატომ არის ეს ასე, ნება მომეცით მოვიყვან კონკრეტულ მაგალითს. დიდი რიცხვების კანონი გვეუბნება, რომ... ვთქვათ, გვაქვს შემთხვევითი ცვლადი X. ის უდრის თავების რაოდენობას სამართლიანი მონეტის 100 გადაგდებაში. პირველ რიგში, ჩვენ ვიცით ამ შემთხვევითი ცვლადის მათემატიკური მოლოდინი. ეს არის მონეტების გადაგდების ან ცდების რაოდენობა, გამრავლებული ნებისმიერი ცდის წარმატების შანსზე. ანუ ეს უდრის 50-ს. ანუ დიდი რიცხვების კანონი ამბობს, რომ თუ ავიღებთ ნიმუშს, ან თუ საშუალოდ ამ ცდებს მივიღებ. .. პირველად რომ გავაკეთებ ტესტს, 100-ჯერ გადავაგდებ მონეტას, ან ავიღებ ყუთს ასი მონეტით, შეანჯღრევი და მერე დავთვლი რამდენ თავებს მივიღებ და მივიღებ, ვთქვათ, რიცხვს 55. იქნება X1. შემდეგ ისევ ვაკანკალებ ყუთს და ვიღებ რიცხვს 65. შემდეგ ისევ და მივიღებ 45-ს. და ამას ვაკეთებ n-ჯერ, და შემდეგ ვყოფ ცდების რაოდენობაზე. დიდი რიცხვების კანონი გვეუბნება, რომ ეს საშუალო (ჩემი ყველა დაკვირვების საშუალო) მიუახლოვდება 50-ს, როცა n უახლოვდება უსასრულობას. ახლა მსურს ცოტათი ვისაუბრო იმაზე, თუ რატომ ხდება ეს. ბევრს მიაჩნია, რომ თუ 100 ცდის შემდეგ ჩემი შედეგი საშუალოზე მაღალია, მაშინ ალბათობის კანონების მიხედვით უნდა მივიღო მეტი ან ნაკლები თავი, რათა, ასე ვთქვათ, ანაზღაურდეს განსხვავება. ეს არ არის ზუსტად ის, რაც მოხდება. ამას ხშირად "აზარტული მოთამაშეების შეცდომას" უწოდებენ. ნება მომეცით გაჩვენოთ განსხვავება. შემდეგ მაგალითს გამოვიყენებ. ნება მომეცით დავხატო გრაფიკი. მოდით შევცვალოთ ფერი. ეს არის n, ჩემი x ღერძი არის n. ეს არის ტესტების რაოდენობა, რომელსაც მე გავაკეთებ. და ჩემი Y ღერძი იქნება ნიმუშის საშუალო. ჩვენ ვიცით, რომ ამ თვითნებური ცვლადის მათემატიკური მოლოდინი არის 50. ნება მომეცით დავხატო. ეს არის 50. დავუბრუნდეთ ჩვენს მაგალითს. თუ n არის... ჩემი პირველი ტესტის დროს მივიღე 55, ეს არის ჩემი საშუალო. მონაცემთა შეყვანის მხოლოდ ერთი წერტილი მაქვს. შემდეგ ორი ტესტის შემდეგ ვიღებ 65-ს. ასე რომ, ჩემი საშუალო იქნება 65+55 გაყოფილი 2-ზე. ეს არის 60. და ჩემი საშუალო ოდნავ გაიზარდა. შემდეგ მე მივიღე 45, რამაც ისევ შეამცირა ჩემი არითმეტიკული საშუალო. მე არ ვაპირებ 45-ის შედგენას. ახლა მჭირდება ამ ყველაფრის საშუალო შეფასება. რის ტოლია 45+65? ნება მომეცით გამოვთვალო ეს მნიშვნელობა წერტილის წარმოსადგენად. ეს არის 165 გაყოფილი 3-ზე. ეს არის 53. არა, 55. ასე რომ, საშუალო ბრუნდება 55-მდე. ჩვენ შეგვიძლია გავაგრძელოთ ეს ტესტები. მას შემდეგ, რაც ჩვენ გავაკეთეთ სამი ტესტი და მივიღეთ ეს საშუალო, ბევრი ადამიანი ფიქრობს, რომ ალბათობის ღმერთები დარწმუნდებიან, რომ მომავალში ნაკლები თავები მივიღებთ, რომ მომდევნო რამდენიმე ცდას ექნება დაბალი ქულები საშუალოს შესამცირებლად. მაგრამ ეს ყოველთვის ასე არ არის. მომავალში, ალბათობა ყოველთვის იგივე რჩება. ყოველთვის იქნება 50% შანსი, რომ ხელმძღვანელები მოვიპოვო. ასე არ არის, რომ თავიდან ვიღებ თავების გარკვეულ რაოდენობას, იმაზე მეტს, ვიდრე ველოდები, შემდეგ კი უცებ მომიწევს კუდები. ეს არის აზარტული მოთამაშეების სიცრუე. მხოლოდ იმიტომ, რომ თქვენ მიიღებთ თავების არაპროპორციულად დიდ რაოდენობას, არ ნიშნავს, რომ რაღაც მომენტში დაიწყებთ არაპროპორციულად დიდი რაოდენობის კუდების მიღებას. ეს მთლად სიმართლეს არ შეესაბამება. დიდი რიცხვების კანონი გვეუბნება, რომ არ აქვს მნიშვნელობა. ვთქვათ, გარკვეული სასრული რაოდენობის ტესტების შემდეგ თქვენი საშუალო... ამის ალბათობა საკმაოდ მცირეა, მაგრამ, მიუხედავად ამისა... ვთქვათ, თქვენმა საშუალომ მიაღწია ამ ნიშნულს - 70. თქვენ ფიქრობთ: "ვაუ, ჩვენ დავშორდით მოსალოდნელ ღირებულებას". მაგრამ დიდი რიცხვების კანონი ამბობს, რომ არ აქვს მნიშვნელობა რამდენ ტესტს გავაკეთებთ. წინ ჯერ კიდევ უამრავი გამოწვევა გვაქვს. ამ უსასრულო რაოდენობის გამოცდის მათემატიკური მოლოდინი, განსაკუთრებით მსგავს სიტუაციაში, შემდეგი იქნება. როდესაც თქვენ მიხვალთ სასრულ რიცხვთან, რომელიც გამოხატავს რაიმე დიდ მნიშვნელობას, უსასრულო რიცხვი, რომელიც ემთხვევა მას, კვლავ მიგვიყვანს მოსალოდნელ მნიშვნელობამდე. ეს, რა თქმა უნდა, ძალიან თავისუფალი ინტერპრეტაციაა, მაგრამ ამას დიდი რიცხვების კანონი გვეუბნება. Ეს არის მნიშვნელოვანი. ეს არ გვეუბნება, რომ თუ ჩვენ მივიღებთ ბევრ თავებს, მაშინ რატომღაც გაიზრდება კუდების მიღების ალბათობა კომპენსაციისთვის. ეს კანონი გვეუბნება, რომ არ აქვს მნიშვნელობა რა შედეგს მივიღებთ სასრული რაოდენობის ცდებზე, თუ თქვენ ჯერ კიდევ გაქვთ საცდელების უსასრულო რაოდენობა. და თუ მათ საკმარისად გააკეთებთ, თქვენ კვლავ დაუბრუნდებით მოსალოდნელ მნიშვნელობას. ეს მნიშვნელოვანი პუნქტია. Იფიქრე ამაზე. მაგრამ ლატარიებთან და კაზინოებთან ეს ყოველდღიურად არ გამოიყენება პრაქტიკაში, თუმცა ცნობილია, რომ თუ საკმარის ტესტებს გააკეთებთ... შეგვიძლია გამოვთვალოთ კიდეც... რა არის იმის ალბათობა, რომ სერიოზულად გადავუხვიოთ ნორმას? მაგრამ კაზინოები და ლატარიები ყოველდღიურად მუშაობენ იმ პრინციპით, რომ თუ საკმარის ხალხს მიიღებ, ბუნებრივია, მოკლე დროში, მცირე ნიმუშით, მაშინ რამდენიმე ადამიანი მოხვდება ჯეკპოტში. მაგრამ დიდი ხნის განმავლობაში, კაზინო ყოველთვის გაიმარჯვებს იმ თამაშების პარამეტრების გამო, რომლებსაც ისინი გიწვევთ სათამაშოდ. ეს არის ალბათობის მნიშვნელოვანი პრინციპი, რომელიც ინტუიციურია. მიუხედავად იმისა, რომ ზოგჯერ, როდესაც მას ფორმალურად აგიხსნით შემთხვევითი ცვლადებით, ეს ყველაფერი ცოტა დამაბნეველად გამოიყურება. ყოველივე ეს კანონი ამბობს, რომ რაც უფრო მეტი ნიმუშია, მით მეტია ამ ნიმუშების საშუალო არითმეტიკული მიდრეკილება ჭეშმარიტ საშუალოზე. და უფრო კონკრეტულად რომ ვთქვათ, თქვენი ნიმუშის საშუალო არითმეტიკული თანხვედრა შემთხვევითი ცვლადის მათემატიკურ მოლოდინთან. Სულ ეს არის. შევხვდებით შემდეგ ვიდეოში!

დიდი რიცხვების სუსტი კანონი

დიდი რიცხვების სუსტ კანონს ასევე უწოდებენ ბერნულის თეორემას, იაკობ-ბერნულის სახელით, რომელმაც ეს დაამტკიცა 1713 წელს.

მოდით იყოს უსასრულო თანმიმდევრობა (თანმიმდევრული ჩამოთვლა) იდენტურად განაწილებული და არაკორელირებული შემთხვევითი ცვლადების. ანუ მათი კოვარიანტობა c o v (X i, X j) = 0, ∀ i ≠ j (\displaystyle \mathrm (cov) (X_(i),X_(j))=0,\;\forall i\not =j). დაე . მოდით აღვნიშნოთ პირველის ნიმუშის საშუალოდ n (\displaystyle n)წევრები:

.

მაშინ X ¯ n → P μ (\displaystyle (\bar (X))_(n)\ to ^(\!\!\!\!\!\!\mathbb (P) )\mu).

ანუ ნებისმიერი პოზიტივისთვის ε (\displaystyle \varepsilon)

lim n → ∞ Pr (| X ¯ n − μ |< ε) = 1. {\displaystyle \lim _{n\to \infty }\Pr \!\left(\,|{\bar {X}}_{n}-\mu |<\varepsilon \,\right)=1.}

დიდი რიცხვების გაძლიერებული კანონი

დაე, იყოს დამოუკიდებელი იდენტურად განაწილებული შემთხვევითი ცვლადების უსასრულო თანმიმდევრობა (X i) i = 1 ∞ (\displaystyle \(X_(i)\)_(i=1)^(\infty)), განსაზღვრული ერთი ალბათობის სივრცეზე (Ω , F , P) (\displaystyle (\Omega ,(\mathcal (F)),\mathbb (P))). დაე E X i = μ , ∀ i ∈ N (\displaystyle \mathbb (E) X_(i)=\mu ,\;\forall i\in \mathbb (N) ). მოდით აღვნიშნოთ X ¯ n (\displaystyle (\bar (X))_(n))პირველის საშუალო ნიმუში n (\displaystyle n)წევრები:

X ¯ n = 1 n ∑ i = 1 n X i , n ∈ N (\displaystyle (\bar (X))_(n)=(\frac (1)(n))\sum \limits _(i= 1)^(n)X_(i),\;n\in \mathbb (N)).

მაშინ X ¯ n → μ (\displaystyle (\bar (X))_(n)\ to \mu )თითქმის ყოველთვის.

Pr (lim n → ∞ X ¯ n = μ) = 1. (\displaystyle \Pr \!\left(\lim _(n\to \infty)(\bar (X))_(n)=\mu \ მარჯვენა) = 1.) .

ნებისმიერი მათემატიკური კანონის მსგავსად, დიდი რიცხვების კანონი შეიძლება გამოყენებულ იქნას რეალურ სამყაროში მხოლოდ გარკვეული ვარაუდებით, რომელთა დაკმაყოფილება შესაძლებელია მხოლოდ გარკვეული სიზუსტით. მაგალითად, თანმიმდევრული ტესტის პირობები ხშირად არ შეიძლება შენარჩუნდეს განუსაზღვრელი ვადით და აბსოლუტური სიზუსტით. გარდა ამისა, დიდი რიცხვების კანონი მხოლოდ ამაზე საუბრობს წარმოუდგენლობასაშუალო მნიშვნელობის მნიშვნელოვანი გადახრა მათემატიკური მოლოდინიდან.