अंकगणितीय प्रगति का सूत्र a. अंकगणितीय प्रगति: यह क्या है? नियम और पदनाम

ध्यान!
अतिरिक्त हैं
विशेष धारा 555 में सामग्री।
उन लोगों के लिए जो बहुत "बहुत नहीं ..." हैं
और उन लोगों के लिए जो "बहुत सम ...")

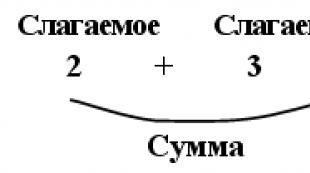
एक अंकगणितीय प्रगति संख्याओं की एक श्रृंखला है जिसमें प्रत्येक संख्या पिछले एक की तुलना में एक ही राशि से अधिक (या कम) होती है।

यह विषय अक्सर कठिन और समझ से बाहर होता है। अक्षरों के लिए सूचकांक, नौवां कार्यकालप्रगति, प्रगति में अंतर - यह सब किसी तरह शर्मनाक है, हाँ ... आइए अंकगणितीय प्रगति का अर्थ समझें और सब कुछ तुरंत काम करेगा।)

अंकगणितीय प्रगति अवधारणा।

अंकगणितीय प्रगति एक बहुत ही सरल और स्पष्ट अवधारणा है। शक? व्यर्थ।) अपने लिए देखें।

मैं संख्याओं की एक अधूरी श्रृंखला लिखूंगा:

1, 2, 3, 4, 5, ...

क्या आप इस पंक्ति को बढ़ा सकते हैं? पाँच के बाद आगे कौन-सी संख्याएँ जाएँगी? हर कोई ... उह-उह ..., संक्षेप में, सभी को एहसास होगा कि संख्या 6, 7, 8, 9, आदि आगे बढ़ेगी।

आइए कार्य को जटिल करें। मैं संख्याओं की एक अधूरी श्रृंखला देता हूं:

2, 5, 8, 11, 14, ...

आप पैटर्न को पकड़ने, श्रृंखला का विस्तार करने और नाम देने में सक्षम होंगे सातवींपंक्ति नंबर?

यदि आपको पता चला कि यह संख्या 20 है - मैं आपको बधाई देता हूं! न केवल आपने महसूस किया अंकगणितीय प्रगति के प्रमुख बिंदु,लेकिन व्यापार में भी उनका सफलतापूर्वक उपयोग किया! यदि आपने इसे नहीं समझा है, तो पढ़ें।

आइए अब मुख्य बिंदुओं को सनसनी से गणित में अनुवाद करें।)

पहला मुख्य बिंदु।

अंकगणितीय प्रगति संख्याओं की श्रृंखला से संबंधित है।यह पहली बार में भ्रमित करने वाला है। हम समीकरणों को हल करने, रेखांकन और वह सब करने के आदी हैं ... और फिर श्रृंखला का विस्तार करें, श्रृंखला की संख्या पाएं ...

कोई खराबी नहीं। यह सिर्फ इतना है कि प्रगति गणित की एक नई शाखा के साथ पहला परिचय है। अनुभाग को "पंक्तियाँ" कहा जाता है और यह संख्याओं और भावों की श्रृंखला के साथ काम करता है। इस्की आद्त डाल लो।)

दूसरा मुख्य बिंदु।

एक समान्तर श्रेणी में, कोई भी संख्या पिछली संख्या से भिन्न होती है उसी राशि से।

पहले उदाहरण में, यह अंतर एक है। आप जो भी संख्या लें, वह पिछले वाले से एक अधिक है। दूसरे में - तीन। कोई भी संख्या जो पिछले एक से तीन से अधिक हो। दरअसल, यह वह क्षण है जो हमें पैटर्न को पकड़ने और बाद की संख्याओं की गणना करने का अवसर देता है।

तीसरा प्रमुख बिंदु।

यह क्षण हड़ताली नहीं है, हाँ ... लेकिन यह बहुत, बहुत महत्वपूर्ण है। यह रहा: प्रगति में प्रत्येक संख्या अपने स्थान पर खड़ी होती है।पहला अंक है, सातवां है, पैंतालीसवां है, आदि। यदि आप उन्हें यादृच्छिक रूप से मिलाते हैं, तो पैटर्न गायब हो जाएगा। गायब हो जाएगा और अंकगणितीय प्रगति... बस नंबरों की एक कतार रहेगी।

यह पूरी बात है।

बेशक, नए विषय में नए नियम और पदनाम दिखाई देते हैं। आपको उन्हें जानने की जरूरत है। अन्यथा, आप कार्य को नहीं समझेंगे। उदाहरण के लिए, आपको कुछ इस तरह तय करना होगा:

समांतर श्रेणी (a n) के पहले छह पद लिखिए यदि a 2 = 5, d = -2.5 है।

क्या यह प्रेरित करता है?) पत्र, कुछ अनुक्रमणिका ... और कार्य, वैसे - आसान नहीं हो सकता। आपको बस शब्दों और पदनामों के अर्थ को समझने की जरूरत है। अब हम इस व्यवसाय में महारत हासिल करेंगे और कार्य पर लौट आएंगे।

शर्तें और पदनाम।

अंकगणितीय प्रगतिसंख्याओं की एक श्रृंखला है जिसमें प्रत्येक संख्या पिछले एक से भिन्न होती है उसी राशि से।

इस मात्रा को कहा जाता है ... आइए इस अवधारणा से अधिक विस्तार से निपटें।

अंकगणितीय प्रगति का अंतर।

अंकगणितीय प्रगति का अंतरवह राशि है जिसके द्वारा प्रगति की कोई भी संख्या अधिकपिछला वाला।

एक महत्वपूर्ण बिंदु। कृपया शब्द पर ध्यान दें "अधिक"।गणितीय रूप से, इसका अर्थ है कि प्रगति में प्रत्येक संख्या प्राप्त होती है जोड़नेपिछली संख्या से अंकगणितीय प्रगति का अंतर।

गणना के लिए, मान लें दूसराश्रृंखला की संख्या, यह आवश्यक है पहलारेखावृत्त जोड़ेंअंकगणितीय प्रगति का यही अंतर। गणना के लिए पांचवां- अंतर आवश्यक है जोड़ेंप्रति चौथा,अच्छा, आदि

अंकगणितीय प्रगति का अंतरशायद सकारात्मक,तब पंक्ति की प्रत्येक संख्या वास्तव में निकलेगी पिछले एक से अधिक।इस प्रगति को कहा जाता है की बढ़ती।उदाहरण के लिए:

8; 13; 18; 23; 28; .....

यहां हर नंबर मिलता है जोड़नेसकारात्मक संख्या, पिछले एक के लिए +5।

अंतर हो सकता है नकारात्मक,तो पंक्ति में प्रत्येक संख्या होगी पिछले वाले से कम।इस तरह की प्रगति को कहा जाता है (आप इस पर विश्वास नहीं करेंगे!) घट रहा है।

उदाहरण के लिए:

8; 3; -2; -7; -12; .....

यहां हर नंबर भी मिलता है जोड़नेपिछले करने के लिए, लेकिन पहले से ही ऋणात्मक संख्या, -5।

वैसे, प्रगति के साथ काम करते समय, इसकी प्रकृति को तुरंत निर्धारित करना बहुत उपयोगी होता है - चाहे वह बढ़ रहा हो या घट रहा हो। यह समाधान को नेविगेट करने, अपनी गलतियों का पता लगाने और बहुत देर होने से पहले उन्हें ठीक करने में बहुत मदद करता है।

अंकगणितीय प्रगति का अंतरनिरूपित, एक नियम के रूप में, पत्र द्वारा डी।

कैसे ढूंढें डी? बहुत सरल। श्रृंखला की किसी भी संख्या में से घटाना आवश्यक है पहले कासंख्या। घटाना। वैसे, घटाव के परिणाम को "अंतर" कहा जाता है।)

आइए परिभाषित करें, उदाहरण के लिए, डीअंकगणितीय प्रगति बढ़ाने के लिए:

2, 5, 8, 11, 14, ...

हम जितनी भी पंक्ति चाहते हैं, उसकी कोई भी संख्या लेते हैं, उदाहरण के लिए, 11. उसमें से घटाना पिछली संख्या,वे। आठ:

यह सही जवाब है। इस अंकगणितीय प्रगति के लिए, अंतर तीन है।

आप बिल्कुल ले सकते हैं प्रगति की कोई भी संख्या,जबसे एक विशिष्ट प्रगति के लिए डी -हमेशा एक ही।कम से कम कहीं पंक्ति की शुरुआत में, कम से कम बीच में, कम से कम कहीं भी। आप केवल पहला नंबर नहीं ले सकते। सिर्फ इसलिए कि सबसे पहले नंबर कोई पिछला नहीं है।)

वैसे, यह जानते हुए कि डी = 3, इस प्रगति की सातवीं संख्या ज्ञात करना बहुत आसान है। पांचवें नंबर में 3 जोड़ें - हमें छठा मिलता है, यह 17 होगा। छठे नंबर में तीन जोड़ें, हमें सातवां नंबर - बीस मिलता है।

हम परिभाषित करते हैं डीघटती हुई अंकगणितीय प्रगति के लिए:

8; 3; -2; -7; -12; .....

मैं आपको याद दिलाता हूं कि, संकेतों की परवाह किए बिना, निर्धारित करने के लिए डीयह किसी भी संख्या से आवश्यक है पिछले एक ले लो।हम प्रगति की कोई भी संख्या चुनते हैं, उदाहरण के लिए -7। पिछला वाला -2 है। फिर:

घ = -7 - (-2) = -7 + 2 = -5

अंकगणितीय प्रगति का अंतर कोई भी संख्या हो सकता है: पूर्ण, भिन्नात्मक, अपरिमेय, जो भी हो।

अन्य शर्तें और पदनाम।

श्रृंखला में प्रत्येक संख्या को कहा जाता है एक अंकगणितीय प्रगति का सदस्य।

प्रगति के प्रत्येक सदस्य का अपना नंबर है।बिना किसी तरकीब के, संख्याएँ सख्ती से क्रम में हैं। पहला, दूसरा, तीसरा, चौथा, आदि। उदाहरण के लिए, प्रगति में 2, 5, 8, 11, 14, ... दो पहला पद है, पांच दूसरा है, ग्यारह चौथा है, ठीक है, आप समझते हैं ...) कृपया स्पष्ट रूप से समझें - नंबर खुदबिल्कुल कोई भी, संपूर्ण, भिन्नात्मक, नकारात्मक, कुछ भी हो सकता है, लेकिन संख्याओं की संख्या- सख्ती से क्रम में!

सामान्य प्रगति कैसे रिकॉर्ड करें? कोई दिक्कत नहीं है! पंक्ति में प्रत्येक संख्या एक अक्षर के रूप में लिखी जाती है। एक नियम के रूप में, अक्षर का उपयोग अंकगणितीय प्रगति को दर्शाने के लिए किया जाता है ए... सदस्य संख्या नीचे दाईं ओर एक इंडेक्स द्वारा इंगित की जाती है। हम सदस्यों को अल्पविराम (या अर्धविराम) से अलग करते हैं, जैसे:

ए 1, ए 2, ए 3, ए 4, ए 5, .....

एक 1पहला नंबर है, एक 3- तीसरा, आदि। कुछ भी पेचीदा नहीं। आप इस श्रंखला को संक्षेप में इस प्रकार लिख सकते हैं: (एक).

प्रगति हैं सीमित और अंतहीन।

अंतिमप्रगति में सदस्यों की सीमित संख्या है। पाँच, अड़तीस, जो भी हो। लेकिन - एक सीमित संख्या।

अनंतप्रगति - में अनंत संख्या में सदस्य हैं, जैसा कि आप अनुमान लगा सकते हैं।)

आप इस तरह की श्रृंखला के माध्यम से अंतिम प्रगति लिख सकते हैं, सभी सदस्य और अंत में एक बिंदु:

ए 1, ए 2, ए 3, ए 4, ए 5.

या तो, यदि कई सदस्य हैं:

ए 1, ए 2, ... ए 14, ए 15.

एक छोटी प्रविष्टि में, आपको सदस्यों की संख्या को अतिरिक्त रूप से इंगित करना होगा। उदाहरण के लिए (बीस सदस्यों के लिए), इस तरह:

(ए एन), एन = 20

पंक्ति के अंत में दीर्घवृत्त द्वारा एक अंतहीन प्रगति को पहचाना जा सकता है, जैसा कि इस पाठ के उदाहरणों में है।

अब आप कार्यों को हल कर सकते हैं। कार्य सरल हैं, विशुद्ध रूप से अंकगणितीय प्रगति के अर्थ को समझने के लिए।

अंकगणितीय प्रगति पर कार्यों के उदाहरण।

आइए कार्य का विस्तार से विश्लेषण करें, जो ऊपर दिया गया है:

1. समांतर श्रेणी (a n) के पहले छह पद लिखिए, यदि a 2 = 5, d = -2.5 हो।

हम कार्य को समझने योग्य भाषा में अनुवाद करते हैं। एक अनंत अंकगणितीय प्रगति दी गई है। इस प्रगति की दूसरी संख्या ज्ञात है: ए 2 = 5.प्रगति में अंतर ज्ञात है: डी = -2.5।इस प्रगति के पहले, तीसरे, चौथे, पांचवें और छठे सदस्यों को खोजना आवश्यक है।

स्पष्टता के लिए, मैं समस्या की स्थिति के अनुसार एक श्रृंखला लिखूंगा। पहले छह पद, जहां दूसरा पद पांच है:

ए 1, 5, ए 3, ए 4, ए 5, ए 6, ....

एक 3 = एक 2 + डी

अभिव्यक्ति में बदलें ए 2 = 5तथा घ = -2.5... माइनस के बारे में मत भूलना!

एक 3=5+(-2,5)=5 - 2,5 = 2,5

तीसरा पद दूसरे से छोटा है। सब कुछ तार्किक है। यदि संख्या पिछले एक से अधिक है नकारात्मकमान, तो संख्या स्वयं पिछले वाले से कम हो जाएगी। प्रगति कम हो रही है। ठीक है, आइए इसे ध्यान में रखते हैं।) हम अपनी श्रृंखला के चौथे सदस्य पर विचार करते हैं:

एक 4 = एक 3 + डी

एक 4=2,5+(-2,5)=2,5 - 2,5 = 0

एक 5 = एक 4 + डी

एक 5=0+(-2,5)= - 2,5

एक 6 = एक 5 + डी

एक 6=-2,5+(-2,5)=-2,5 - 2,5 = -5

तो, तीसरे से छठे तक की शर्तों की गणना की जाती है। परिणाम एक ऐसी श्रृंखला है:

ए 1, 5, 2.5, 0, -2.5, -5, ....

यह पहला पद खोजने के लिए बनी हुई है एक 1प्रसिद्ध दूसरे के अनुसार। यह दूसरी दिशा में एक कदम है, बाईं ओर।) इसलिए, अंकगणितीय प्रगति का अंतर डीमें जोड़ने की आवश्यकता नहीं है एक 2, ए ले जाओ:

एक 1 = एक 2 - डी

एक 1=5-(-2,5)=5 + 2,5=7,5

यही सब है इसके लिए। कार्य उत्तर:

7,5, 5, 2,5, 0, -2,5, -5, ...

रास्ते में, मैं ध्यान दूंगा कि हमने इस कार्य को हल कर लिया है आवर्तकमार्ग। इस डरावना शब्दइसका मतलब है, केवल, प्रगति के सदस्य की तलाश करें पिछली (आसन्न) संख्या से।हम बाद में प्रगति के साथ काम करने के अन्य तरीकों पर विचार करेंगे।

इस सरल कार्य से एक महत्वपूर्ण निष्कर्ष निकाला जा सकता है।

याद रखना:

यदि हम कम से कम एक पद और एक समांतर श्रेणी का अंतर जानते हैं, तो हम इस प्रगति के किसी भी सदस्य को पा सकते हैं।

क्या तुम्हें याद है? यह सरल निष्कर्ष आपको इस विषय पर स्कूल पाठ्यक्रम के अधिकांश कार्यों को हल करने की अनुमति देता है। सभी कार्य तीन मुख्य मापदंडों के इर्द-गिर्द घूमते हैं: अंकगणितीय प्रगति का सदस्य, प्रगति का अंतर, प्रगति के सदस्य की संख्या।हर चीज़।

बेशक, पिछले सभी बीजगणित रद्द नहीं किए गए हैं।) असमानताएं, समीकरण और अन्य चीजें प्रगति से जुड़ी हुई हैं। लेकिन बहुत प्रगति से- सब कुछ तीन मापदंडों के इर्द-गिर्द घूमता है।

आइए एक उदाहरण के रूप में इस विषय पर कुछ लोकप्रिय सत्रीय कार्यों को देखें।

2. अंतिम अंकगणितीय प्रगति को एक श्रृंखला के रूप में लिखिए, यदि n = 5, d = 0.4, और a 1 = 3.6 है।

यहाँ सब कुछ सरल है। सब कुछ पहले ही दिया जा चुका है। आपको यह याद रखने की आवश्यकता है कि अंकगणितीय प्रगति के सदस्यों को कैसे गिना जाता है, गिनें और उन्हें लिखें। यह सलाह दी जाती है कि असाइनमेंट की स्थिति में शब्दों को याद न करें: "अंतिम" और " एन = 5"। चेहरे में पूरी तरह से नीला होने तक गिनती नहीं है।) इस प्रगति में केवल 5 (पांच) सदस्य हैं:

ए 2 = ए 1 + डी = 3.6 + 0.4 = 4

ए 3 = ए 2 + डी = 4 + 0.4 = 4.4

एक 4 = एक 3 + डी = 4.4 + 0.4 = 4.8

एक 5 = एक 4 + डी = 4.8 + 0.4 = 5.2

उत्तर लिखना बाकी है:

3,6; 4; 4,4; 4,8; 5,2.

एक अन्य कार्य:

3. निर्धारित करें कि क्या संख्या 7 अंकगणितीय प्रगति (a n) का सदस्य है, यदि ए 1 = 4.1; घ = 1.2.

हम्म ... कौन जानता है? किसी चीज को कैसे परिभाषित करें?

कैसे-कैसे ... हाँ, एक श्रंखला के रूप में प्रगति लिखिए और देखिए कि वहाँ सात होंगे या नहीं! हम विचार करते हैं:

ए 2 = ए 1 + डी = 4.1 + 1.2 = 5.3

ए 3 = ए 2 + डी = 5.3 + 1.2 = 6.5

एक 4 = एक 3 + डी = 6.5 + 1.2 = 7.7

4,1; 5,3; 6,5; 7,7; ...

अब यह स्पष्ट रूप से देखा गया है कि हम सिर्फ सात हैं के माध्यम से फिसल 6.5 और 7.7 के बीच! सात हमारी संख्याओं की श्रृंखला में शामिल नहीं हुए, और इसलिए, सात दी गई प्रगति के सदस्य नहीं होंगे।

जवाब न है।

और यहाँ GIA के वास्तविक संस्करण पर आधारित एक कार्य है:

4. समांतर श्रेणी के कई क्रमागत सदस्यों को लिखा जाता है:

...; 15; एक्स; 9; 6; ...

यहां एक पंक्ति बिना अंत और शुरुआत के लिखी गई है। कोई सदस्य संख्या नहीं, कोई अंतर नहीं डी... कोई खराबी नहीं। समस्या को हल करने के लिए, अंकगणितीय प्रगति के अर्थ को समझना पर्याप्त है। हम देखते हैं और सोचते हैं कि क्या संभव है डिस्कवरइस श्रृंखला से? तीन मुख्य पैरामीटर क्या हैं?

सदस्य संख्या? यहां एक भी नंबर नहीं है।

लेकिन तीन नंबर हैं और - ध्यान! - शब्द "लगातार"हालत में। इसका मतलब यह है कि संख्या बिना अंतराल के सख्ती से क्रम में है। क्या इस पंक्ति में दो हैं पड़ोसीज्ञात संख्या? हो मेरे पास है! ये 9 और 6 हैं। अतः हम समांतर श्रेणी के अंतर की गणना कर सकते हैं! हम छह . से घटाते हैं पहले कासंख्या, यानी नौ:

केवल छोटी चीजें बची हैं। X के लिए पिछली संख्या क्या है? पंद्रह। इसका मतलब है कि x को सरल जोड़ द्वारा आसानी से पाया जा सकता है। अंकगणितीय प्रगति के अंतर को 15 में जोड़ें:

बस इतना ही। उत्तर: एक्स = 12

हम निम्नलिखित समस्याओं को स्वयं हल करते हैं। नोट: ये समस्याएँ फ़ार्मुलों के बारे में नहीं हैं। विशुद्ध रूप से एक अंकगणितीय प्रगति के अर्थ को समझने के लिए।) हम केवल संख्या-अक्षरों की एक श्रृंखला लिखते हैं, देखते हैं और सोचते हैं।

5. समांतर श्रेणी का पहला धनात्मक पद ज्ञात कीजिए यदि a 5 = -3; डी = 1.1.

6. यह ज्ञात है कि संख्या 5.5 अंकगणितीय प्रगति (ए एन) का सदस्य है, जहां 1 = 1.6; डी = 1.3। इस सदस्य की संख्या n ज्ञात कीजिए।

7. यह ज्ञात है कि समांतर श्रेणी में 2 = 4; एक 5 = 15.1। एक 3 खोजें।

8. अंकगणितीय प्रगति के लगातार कई सदस्यों को लिखा:

...; 15.6; एक्स; 3.4; ...

अक्षर x द्वारा निरूपित प्रगति में पद ज्ञात कीजिए।

9. ट्रेन ने स्टेशन से आगे बढ़ना शुरू किया, अपनी गति में लगातार 30 मीटर प्रति मिनट की वृद्धि की। पांच मिनट में ट्रेन की गति क्या होगी? अपना उत्तर किमी/घंटा में दें।

10. यह ज्ञात है कि समांतर श्रेणी में 2 = 5; एक 6 = -5। 1 . खोजें.

उत्तर (अव्यवस्था में): 7.7; 7.5; 9.5; 9; 0.3; 4.

सब कुछ ठीक हो गया? आश्चर्यजनक! आप अधिक के लिए अंकगणितीय प्रगति में महारत हासिल कर सकते हैं उच्च स्तर, निम्नलिखित पाठों में।

सब कुछ ठीक नहीं हुआ? कोई दिक्कत नहीं है। विशेष धारा 555 में, इन सभी कार्यों को टुकड़ों में हल किया गया है।) और निश्चित रूप से, एक सरल व्यावहारिक तकनीक का वर्णन किया गया है जो ऐसे कार्यों के समाधान को तुरंत स्पष्ट, स्पष्ट रूप से उजागर करती है, जैसे कि आपके हाथ की हथेली में!

वैसे ट्रेन को लेकर पहेली में दो ऐसी समस्याएं हैं जिन पर अक्सर लोग ठोकर खा जाते हैं। एक विशुद्ध रूप से प्रगति पर है, और दूसरा गणित, और भौतिकी में भी किसी भी समस्या के लिए सामान्य है। यह आयामों का एक से दूसरे में अनुवाद है। इसमें दिखाया गया है कि इन समस्याओं को कैसे हल किया जाना चाहिए।

इस पाठ में, हमने अंकगणितीय प्रगति के प्रारंभिक अर्थ और इसके मुख्य मापदंडों की जांच की। यह इस विषय पर लगभग सभी समस्याओं को हल करने के लिए पर्याप्त है। जोड़ें डीसंख्याओं के लिए, एक श्रृंखला लिखें, सब कुछ तय हो जाएगा।

उंगली का घोल एक पंक्ति के बहुत छोटे टुकड़ों के लिए अच्छा काम करता है, जैसा कि इस पाठ के उदाहरणों में है। यदि पंक्ति लंबी है, तो गणना अधिक जटिल हो जाती है। उदाहरण के लिए, यदि प्रश्न में समस्या 9 में, प्रतिस्थापित करें "पांच मिनट"पर "पैंतीस मिनट"समस्या काफी गंभीर हो जाएगी।)

और ऐसे कार्य भी हैं जो संक्षेप में सरल हैं, लेकिन गणना के मामले में अविश्वसनीय हैं, उदाहरण के लिए:

आपको एक समांतर श्रेणी (a n) दी गई है। यदि a 1 = 3 और d = 1/6 हो तो 121 ज्ञात कीजिए।

और क्या, हम 1/6 से कई, कई बार जोड़ेंगे?! आप इसे मार सकते हैं!?

आप कर सकते हैं।) यदि आप सरल सूत्र नहीं जानते हैं जिसके द्वारा ऐसे कार्यों को एक मिनट में हल किया जा सकता है। यह सूत्र अगले पाठ में होगा। और यह समस्या वहीं हल हो जाती है। एक मिनट में।)

अगर आपको यह साइट पसंद है ...

वैसे, मेरे पास आपके लिए कुछ और दिलचस्प साइटें हैं।)

आप उदाहरणों को हल करने का अभ्यास कर सकते हैं और अपने स्तर का पता लगा सकते हैं। त्वरित सत्यापन परीक्षण। सीखना - रुचि के साथ!)

आप कार्यों और डेरिवेटिव से परिचित हो सकते हैं।

पेंटिंग और कविता की तरह ही गणित का अपना सौंदर्य है।

रूसी वैज्ञानिक, मैकेनिक एन.ई. ज़ुकोवस्की

पर बहुत ही सामान्य कार्य प्रवेश परीक्षागणित में अंकगणितीय प्रगति की अवधारणा से संबंधित समस्याएं हैं। ऐसी समस्याओं को सफलतापूर्वक हल करने के लिए, अंकगणितीय प्रगति के गुणों को अच्छी तरह से जानना और उनके आवेदन में कुछ कौशल होना आवश्यक है।

हम पहले अंकगणितीय प्रगति के मुख्य गुणों को याद करते हैं और सबसे महत्वपूर्ण सूत्र प्रस्तुत करते हैं, इस अवधारणा से संबंधित।

परिभाषा। संख्या क्रम, जिसमें प्रत्येक बाद का पद पिछले एक से समान संख्या से भिन्न होता है, अंकगणितीय प्रगति कहा जाता है। इसके अलावा, संख्याप्रगति में अंतर कहा जाता है।

एक अंकगणितीय प्रगति के लिए, निम्नलिखित सूत्र मान्य हैं

, (1)

कहाँ पे । सूत्र (1) को अंकगणितीय प्रगति के सामान्य पद के लिए सूत्र कहा जाता है, और सूत्र (2) अंकगणितीय प्रगति का मुख्य गुण है: प्रगति का प्रत्येक पद इसके पड़ोसी शब्दों के अंकगणितीय माध्य के साथ मेल खाता है और।

ध्यान दें कि इस गुण के कारण ही मानी गई प्रगति को "अंकगणित" कहा जाता है।

उपरोक्त सूत्र (1) और (2) निम्नानुसार सामान्यीकृत हैं:

(3)

राशि की गणना करने के लिएपहला अंकगणितीय प्रगति के सदस्यआमतौर पर सूत्र लागू किया जाता है

(5) जहां और।

सूत्र को ध्यान में रखते हुए (1), तब सूत्र (5) का तात्पर्य है

अगर हम निरूपित करते हैं, तो

कहाँ पे । चूंकि, तब सूत्र (7) और (8) संगत सूत्रों (5) और (6) का एक सामान्यीकरण हैं।

विशेष रूप से , सूत्र (5) से यह इस प्रकार है, क्या

निम्नलिखित प्रमेय के माध्यम से तैयार की गई अंकगणितीय प्रगति की संपत्ति, अधिकांश छात्रों के लिए अल्पज्ञात है।

प्रमेय।तो अगर

सबूत।तो अगर

प्रमेय सिद्ध होता है।

उदाहरण के लिए , प्रमेय का उपयोग करना, यह दिखाया जा सकता है कि

आइए "अंकगणितीय प्रगति" विषय पर समस्याओं को हल करने के विशिष्ट उदाहरणों पर विचार करें।

उदाहरण 1।चलो और। पाना ।

समाधान।सूत्र (6) को लागू करने पर, हम प्राप्त करते हैं। तब से और, तब या।

उदाहरण 2।इसे तीन गुना अधिक होने दें, और भागफल में विभाजित करने पर, हमें 2 और शेषफल 8 प्राप्त होता है। निर्धारित करें और।

समाधान।उदाहरण की स्थिति का तात्पर्य समीकरणों की प्रणाली से है

चूँकि, और, तब समीकरणों के निकाय (10) से हम प्राप्त करते हैं

समीकरणों की इस प्रणाली का हल है और।

उदाहरण 3.खोजें अगर और।

समाधान।सूत्र (5) के अनुसार, हमारे पास या है। हालांकि, संपत्ति (9) का उपयोग करके, हम प्राप्त करते हैं।

तब से और तब से, समानता से समीकरण इस प्रकार हैया ।

उदाहरण 4.खोजें अगर।

समाधान।सूत्र (5) से, हमारे पास है

हालाँकि, प्रमेय का उपयोग करके, कोई लिख सकता है

इससे और सूत्र (11) से हम प्राप्त करते हैं।

उदाहरण 5. दिया गया:। पाना ।

समाधान।तब से। मगर इसलिए।

उदाहरण 6.चलो, और। पाना ।

समाधान।सूत्र (9) का उपयोग करके, हम प्राप्त करते हैं। इसलिए, यदि, तो या।

चूंकि और, तो यहाँ हमारे पास समीकरणों की प्रणाली है

जिसे हल करने पर हमें मिलता है और।

समीकरण की प्राकृतिक जड़एक ।

उदाहरण 7.खोजें अगर और।

समाधान।चूंकि सूत्र (3) के अनुसार हमारे पास वह है, तो समस्या कथन समीकरणों की प्रणाली को दर्शाता है

यदि आप व्यंजक को प्रतिस्थापित करते हैंप्रणाली के दूसरे समीकरण में, तो हम प्राप्त करते हैं या।

द्विघात समीकरण की जड़ें हैंतथा ।

आइए दो मामलों पर विचार करें।

1. चलो, फिर। तब से और तब से।

इस मामले में, सूत्र (6) के अनुसार, हमारे पास है

2. यदि, तब, और

उत्तर: और।

उदाहरण 8.ज्ञात हो कि व. पाना ।

समाधान।सूत्र (5) और उदाहरण की स्थिति को ध्यान में रखते हुए, हम लिखते हैं और।

इसलिए समीकरणों की प्रणाली का अनुसरण करता है

यदि हम निकाय के पहले समीकरण को 2 से गुणा करते हैं, और फिर इसे दूसरे समीकरण में जोड़ते हैं, तो हमें प्राप्त होता है

सूत्र (9) के अनुसार, हमारे पास है... इस संबंध में, (12) से यह निम्नानुसार हैया ।

तब से और तब से।

उत्तर: ।

उदाहरण 9.खोजें अगर और।

समाधान।चूंकि, और शर्त से, तब या।

सूत्र (5) से ज्ञात होता है, क्या । तब से।

इसलिये , यहां हमारे पास रैखिक समीकरणों की एक प्रणाली है

इसलिए हमें मिलता है और। सूत्र (8) को ध्यान में रखते हुए, हम लिखते हैं।

उदाहरण 10.प्रश्न हल करें।

समाधान।से दिया गया समीकरणउसका अनुसरण करता है। मान लीजिए कि,, और। इस मामले में ।

सूत्र (1) के अनुसार आप लिख सकते हैं या।

चूँकि, समीकरण (13) का एक ही उपयुक्त मूल है।

उदाहरण 11.प्रदान किया गया अधिकतम मान ज्ञात कीजिए और।

समाधान।चूंकि, माना जाता है कि अंकगणितीय प्रगति घट रही है। इस संबंध में, व्यंजक अधिकतम मान लेता है जब वह प्रगति के न्यूनतम धनात्मक पद की संख्या होती है।

हम सूत्र (1) और तथ्य का उपयोग करते हैं, जैसा। तब हमें वह मिलता है या।

तब से, या तो ... हालांकि, इस असमानता मेंसबसे बड़ी प्राकृतिक संख्या, इसीलिए ।

यदि मान, और को सूत्र (6) में प्रतिस्थापित किया जाता है, तो हमें प्राप्त होता है।

उत्तर: ।

उदाहरण 12.उन सभी दो अंकों वाली प्राकृत संख्याओं का योग ज्ञात कीजिए जिन्हें 6 से विभाजित करने पर 5 शेषफल प्राप्त होता है।

समाधान।आइए हम सभी दो अंकों वाली प्राकृत संख्याओं के समुच्चय से निरूपित करें, अर्थात्। ... इसके बाद, हम समुच्चय के उन तत्वों (संख्याओं) से मिलकर एक उपसमुच्चय की रचना करते हैं, जिसे 6 से विभाजित करने पर शेषफल 5 प्राप्त होता है।

स्थापित करना मुश्किल नहीं है, क्या । स्पष्टतः , कि सेट के तत्वएक अंकगणितीय प्रगति बनाएँ, जिसमें और।

एक सेट की कार्डिनैलिटी (तत्वों की संख्या) स्थापित करने के लिए, हम यह मानते हैं। चूँकि और, तब सूत्र (1) से यह अनुसरण करता है या। सूत्र (5) को ध्यान में रखते हुए, हम प्राप्त करते हैं।

समस्याओं को हल करने के उपरोक्त उदाहरण किसी भी तरह से संपूर्ण होने का दावा नहीं कर सकते हैं। यह लेख किसी दिए गए विषय पर विशिष्ट समस्याओं को हल करने के लिए आधुनिक तरीकों के विश्लेषण के आधार पर लिखा गया है। अंकगणितीय प्रगति से जुड़ी समस्याओं को हल करने के तरीकों के गहन अध्ययन के लिए, अनुशंसित साहित्य की सूची का उल्लेख करना उचित है।

1. तकनीकी कॉलेजों के आवेदकों के लिए गणित में समस्याओं का संग्रह / एड। एम.आई. स्कैनवी। - एम।: शांति और शिक्षा, 2013 .-- 608 पी।

2. सुप्रुन वी.पी. हाई स्कूल के छात्रों के लिए गणित: अतिरिक्त खंड स्कूल का पाठ्यक्रम... - एम।: लेनांद / उर्स, 2014 .-- 216 पी।

3. मेडिन्स्की एम.एम. प्रश्नों और अभ्यासों में प्रारंभिक गणित का पूरा पाठ्यक्रम। पुस्तक 2: संख्या क्रम और प्रगति। - एम।: एडिथस, 2015 .-- 208 पी।

अभी भी प्रश्न हैं?

ट्यूटर से सहायता प्राप्त करने के लिए - रजिस्टर करें।

साइट, सामग्री की पूर्ण या आंशिक प्रतिलिपि के साथ, स्रोत के लिए एक लिंक आवश्यक है।

उच्च गणित की शाखाओं से एक बहुत ही जटिल शब्द के रूप में कोई "प्रगति" शब्द से सावधान है। इस बीच, सबसे सरल अंकगणितीय प्रगति टैक्सी मीटर (जहां वे अभी भी बनी हुई है) का काम है। और अंकगणितीय अनुक्रम के सार (और गणित में "सार को समझने" से अधिक महत्वपूर्ण कुछ भी नहीं है) को समझना इतना मुश्किल नहीं है, कई प्राथमिक अवधारणाओं का विश्लेषण किया है।

गणित संख्या क्रम

संख्यात्मक अनुक्रम द्वारा संख्याओं की एक श्रृंखला को नाम देने की प्रथा है, जिनमें से प्रत्येक की अपनी संख्या होती है।

ए 1 - अनुक्रम का पहला सदस्य;

और 2 अनुक्रम का दूसरा सदस्य है;

और 7 अनुक्रम का सातवां सदस्य है;

और n अनुक्रम का n-वां सदस्य है;

हालाँकि, हम संख्याओं और संख्याओं के किसी भी मनमाने सेट में रुचि नहीं रखते हैं। हम अपना ध्यान संख्यात्मक अनुक्रम पर केंद्रित करेंगे, जिसमें nवें पद का मान एक निर्भरता द्वारा इसकी क्रमिक संख्या से जुड़ा होता है जिसे गणितीय रूप से स्पष्ट रूप से तैयार किया जा सकता है। दूसरे शब्दों में: n-वें संख्या का संख्यात्मक मान n का कुछ फलन है।

ए - एक संख्यात्मक अनुक्रम के सदस्य का मूल्य;

n इसका क्रमांक है;

f (n) एक ऐसा फलन है जहां संख्यात्मक अनुक्रम n में क्रमसूचक एक तर्क है।

परिभाषा

एक अंकगणितीय प्रगति को आमतौर पर एक संख्यात्मक अनुक्रम कहा जाता है जिसमें प्रत्येक बाद का पद पिछले एक की तुलना में उसी संख्या से अधिक (कम) होता है। अंकगणितीय अनुक्रम के nवें सदस्य का सूत्र इस प्रकार है:

ए एन - अंकगणितीय प्रगति के वर्तमान सदस्य का मूल्य;

a n + 1 - अगली संख्या का सूत्र;

डी - अंतर (एक निश्चित संख्या)।

यह निर्धारित करना आसान है कि यदि अंतर धनात्मक (d> 0) है, तो विचाराधीन श्रृंखला का प्रत्येक बाद का पद पिछले वाले से बड़ा होगा, और इस तरह की अंकगणितीय प्रगति बढ़ रही होगी।

नीचे दिए गए ग्राफ़ में, यह देखना आसान है कि संख्या अनुक्रम को "आरोही" क्यों कहा गया।

ऐसे मामलों में जहां अंतर ऋणात्मक है (डी<0), каждый последующий член по понятным причинам будет меньше предыдущего, график прогрессии станет «уходить» вниз, арифметическая прогрессия, соответственно, будет именоваться убывающей.

निर्दिष्ट सदस्य का मूल्य

कभी-कभी अंकगणितीय प्रगति के किसी भी मनमाने सदस्य का मान निर्धारित करना आवश्यक होता है। आप अंकगणितीय प्रगति के सभी सदस्यों के मूल्यों की क्रमिक रूप से गणना करके ऐसा कर सकते हैं, जो पहले से वांछित तक शुरू होता है। हालाँकि, यह रास्ता हमेशा स्वीकार्य नहीं होता है, उदाहरण के लिए, पाँच-हज़ारवें या आठ-दसवें सदस्य का अर्थ खोजना आवश्यक है। पारंपरिक गणना में लंबा समय लगेगा। हालांकि, विशिष्ट सूत्रों का उपयोग करके एक विशिष्ट अंकगणितीय प्रगति की जांच की जा सकती है। nवें पद के लिए एक सूत्र भी है: अंकगणितीय प्रगति के किसी भी सदस्य के मूल्य को प्रगति के पहले पद के योग के रूप में परिभाषित किया जा सकता है, प्रगति के अंतर के साथ, वांछित शब्द की संख्या से गुणा किया जाता है, घटाया जाता है एक।

वृद्धि और घटती प्रगति दोनों के लिए सूत्र सार्वभौमिक है।

किसी दिए गए सदस्य के मूल्य की गणना करने का एक उदाहरण

आइए एक समान्तर श्रेणी के nवें पद का मान ज्ञात करने की निम्नलिखित समस्या को हल करें।

शर्त: मापदंडों के साथ एक अंकगणितीय प्रगति है:

अनुक्रम में पहला पद 3 है;

संख्या श्रृंखला में अंतर 1.2 है।

असाइनमेंट: आपको 214 सदस्यों का मान ज्ञात करना होगा

हल: किसी दिए गए पद का मान ज्ञात करने के लिए हम सूत्र का प्रयोग करते हैं:

ए (एन) = ए 1 + डी (एन -1)

समस्या कथन से डेटा को व्यंजक में प्रतिस्थापित करते हुए, हमारे पास है:

ए (214) = ए 1 + डी (एन -1)

ए (214) = 3 + 1.2 (214-1) = 258.6

उत्तर: क्रम में 214वाँ पद 258.6 है।

गणना की इस पद्धति के फायदे स्पष्ट हैं - पूरे समाधान में 2 से अधिक लाइनें नहीं लगती हैं।

सदस्यों की दी गई संख्या का योग

बहुत बार, किसी दिए गए अंकगणितीय श्रृंखला में, इसके एक निश्चित खंड के मूल्यों का योग निर्धारित करना आवश्यक होता है। इसके लिए प्रत्येक पद के मूल्यों की गणना और फिर योग की आवश्यकता नहीं होती है। यह विधि तब लागू होती है जब पदों की संख्या, जिसका योग ज्ञात किया जाना चाहिए, छोटा है। अन्य मामलों में, निम्न सूत्र का उपयोग करना अधिक सुविधाजनक है।

1 से n तक की अंकगणितीय प्रगति के सदस्यों का योग पहले और n-वें सदस्यों के योग के बराबर होता है, जिसे सदस्य n की संख्या से गुणा किया जाता है और दो से विभाजित किया जाता है। यदि सूत्र में nवें पद के मान को लेख के पिछले पैराग्राफ से व्यंजक द्वारा प्रतिस्थापित किया जाता है, तो हम प्राप्त करते हैं:

गणना उदाहरण

उदाहरण के लिए, आइए निम्नलिखित शर्तों के साथ किसी समस्या को हल करें:

अनुक्रम में पहला पद शून्य है;

अंतर 0.5 है।

समस्या में, आपको 56 से 101 तक श्रृंखला के सदस्यों का योग निर्धारित करने की आवश्यकता है।

समाधान। आइए प्रगति के योग को निर्धारित करने के लिए सूत्र का उपयोग करें:

एस (एन) = (2 ∙ ए 1 + डी ∙ (एन -1)) एन / 2

सबसे पहले, हम अपनी समस्या की स्थितियों के डेटा को सूत्र में प्रतिस्थापित करते हुए, प्रगति के 101 सदस्यों के मूल्यों का योग निर्धारित करते हैं:

s 101 = (2 0 + 0.5 (101-1)) 101/2 = 2 525

स्पष्ट रूप से, 56वें ​​से 101वें क्रम के सदस्यों का योग ज्ञात करने के लिए, S 55 को S 101 से घटाना आवश्यक है।

एस 55 = (2 0 + 0.5 ∙ (55-1)) ∙ 55/2 = 742.5

इस प्रकार, इस उदाहरण के लिए अंकगणितीय प्रगति का योग:

s 101 - s 55 = 2,525 - 742.5 = 1,782.5

अंकगणितीय प्रगति के व्यावहारिक अनुप्रयोग का एक उदाहरण

लेख के अंत में, आइए पहले पैराग्राफ में दिए गए अंकगणितीय अनुक्रम के उदाहरण पर वापस जाएं - टैक्सीमीटर (टैक्सी कार का काउंटर)। आइए एक उदाहरण पर विचार करें।

एक टैक्सी (जिसमें 3 किमी की दौड़ शामिल है) में सवार होने पर 50 रूबल का खर्च आता है। प्रत्येक बाद के किलोमीटर का भुगतान 22 रूबल / किमी की दर से किया जाता है। यात्रा दूरी 30 किमी। यात्रा की लागत की गणना करें।

1. आइए पहले 3 किमी को छोड़ दें, जिसकी कीमत लैंडिंग मूल्य में शामिल है।

30 - 3 = 27 किमी।

2. आगे की गणना एक अंकगणितीय संख्या श्रृंखला के विश्लेषण से ज्यादा कुछ नहीं है।

सदस्य संख्या - यात्रा किए गए किलोमीटर की संख्या (शून्य से पहले तीन)।

सदस्य मूल्य योग है।

इस समस्या में पहला पद 1 = 50 p के बराबर होगा।

प्रगति में अंतर d = 22 p.

जिस संख्या में हम रुचि रखते हैं वह अंकगणितीय प्रगति के (27 + 1) -वें पद का मान है - 27वें किलोमीटर के अंत में काउंटर रीडिंग 27.999 ... = 28 किमी है।

ए 28 = 50 + 22 (28 - 1) = 644

मनमाने ढंग से लंबी अवधि के लिए कैलेंडर डेटा की गणना कुछ संख्यात्मक अनुक्रमों का वर्णन करने वाले सूत्रों पर आधारित होती है। खगोल विज्ञान में, कक्षा की लंबाई ज्यामितीय रूप से एक खगोलीय पिंड से एक प्रकाशमान की दूरी पर निर्भर करती है। इसके अलावा, सांख्यिकी और गणित की अन्य अनुप्रयुक्त शाखाओं में विभिन्न संख्यात्मक श्रृंखलाओं का सफलतापूर्वक उपयोग किया जाता है।

एक अन्य प्रकार का संख्या अनुक्रम ज्यामितीय है

अंकगणित की तुलना में, परिवर्तन की दरों की तुलना में ज्यामितीय प्रगति की विशेषता बड़ी है। यह कोई संयोग नहीं है कि राजनीति, समाजशास्त्र, चिकित्सा में, वे अक्सर कहते हैं कि इस या उस घटना के प्रसार की उच्च दर को दिखाने के लिए प्रक्रिया तेजी से विकसित होती है, उदाहरण के लिए, एक महामारी के दौरान एक बीमारी।

ज्यामितीय संख्यात्मक श्रृंखला का वां पद पिछले एक से भिन्न होता है जिसमें इसे कुछ स्थिर संख्या से गुणा किया जाता है - हर, उदाहरण के लिए, पहला पद 1 है, हर 2 है, क्रमशः:

एन = 1: 1 ∙ 2 = 2

एन = 2: 2 2 = 4

एन = 3: 4 ∙ 2 = 8

एन = 4: 8 2 = 16

एन = 5: 16 ∙ 2 = 32,

बी एन - ज्यामितीय प्रगति के वर्तमान सदस्य का मूल्य;

बी एन + 1 - ज्यामितीय प्रगति के अगले पद का सूत्र;

q एक ज्यामितीय प्रगति (स्थिर संख्या) का हर है।

यदि अंकगणितीय प्रगति का ग्राफ एक सीधी रेखा है, तो ज्यामितीय एक थोड़ा अलग चित्र चित्रित करता है:

जैसा कि अंकगणित के मामले में, एक ज्यामितीय प्रगति में एक मनमाना पद के मूल्य के लिए एक सूत्र होता है। ज्यामितीय प्रगति का कोई भी n-वाँ पद, n की घात की प्रगति के हर द्वारा पहले पद के गुणनफल के बराबर होता है, जो एक से घटाया जाता है:

उदाहरण। हमारे पास एक ज्यामितीय प्रगति है जिसका पहला पद 3 के बराबर है और प्रगति का हर 1.5 के बराबर है। प्रगति का पाँचवाँ पद ज्ञात कीजिए

बी 5 = बी 1 ∙ क्यू (5-1) = 3 ∙ 1.5 4 = 15.1875

सदस्यों की दी गई संख्या के योग की गणना उसी तरह एक विशेष सूत्र का उपयोग करके की जाती है। एक ज्यामितीय प्रगति के पहले n पदों का योग प्रगति के nवें पद और उसके हर के गुणनफल और प्रगति के पहले पद के बीच के अंतर के बराबर है, जिसे हर से विभाजित करके एक से घटाया जाता है:

यदि ऊपर माने गए सूत्र का उपयोग करके b n को प्रतिस्थापित किया जाता है, तो मानी गई संख्यात्मक श्रृंखला के पहले n पदों के योग का मान रूप लेगा:

उदाहरण। गुणोत्तर श्रेणी 1 के बराबर पहले पद से शुरू होती है। हर को 3 के बराबर सेट किया जाता है। पहले आठ पदों का योग ज्ञात कीजिए।

s8 = 1 (3 8 -1) / (3-1) = 3 280

तो चलिए बैठ जाते हैं और कुछ नंबर लिखना शुरू करते हैं। उदाहरण के लिए:
आप कोई भी संख्या लिख ​​सकते हैं, और जितने चाहें उतने हो सकते हैं (हमारे मामले में, उन्हें)। हम चाहे कितनी भी संख्याएँ लिख लें, हम हमेशा कह सकते हैं कि कौन सा पहला है, कौन सा दूसरा है, और इसी तरह आखिरी तक, यानी हम उन्हें संख्या दे सकते हैं। यह एक संख्या अनुक्रम का एक उदाहरण है:

संख्या क्रम
उदाहरण के लिए, हमारे अनुक्रम के लिए:

निर्दिष्ट संख्या अनुक्रम में केवल एक संख्या के लिए विशिष्ट है। दूसरे शब्दों में, अनुक्रम में तीन सेकंड की संख्या नहीं है। दूसरा नंबर (जैसे -th नंबर) हमेशा एक होता है।
संख्या वाली संख्या को अनुक्रम का वां सदस्य कहा जाता है।

हम आम तौर पर पूरे अनुक्रम को कुछ अक्षर कहते हैं (उदाहरण के लिए,), और इस अनुक्रम का प्रत्येक सदस्य एक ही अक्षर है जिसमें इस सदस्य की संख्या के बराबर सूचकांक होता है:।

हमारे मामले में:

मान लीजिए कि हमारे पास एक संख्यात्मक अनुक्रम है जिसमें आसन्न संख्याओं के बीच का अंतर समान और बराबर है।
उदाहरण के लिए:

आदि।
इस संख्या अनुक्रम को अंकगणितीय प्रगति कहा जाता है।
शब्द "प्रगति" रोमन लेखक बोथियस द्वारा 6 वीं शताब्दी में वापस पेश किया गया था और इसे व्यापक अर्थों में एक अंतहीन संख्या अनुक्रम के रूप में समझा गया था। "अंकगणित" नाम निरंतर अनुपात के सिद्धांत से लिया गया था, जिसमें प्राचीन यूनानी लगे हुए थे।

यह एक संख्यात्मक अनुक्रम है, जिसका प्रत्येक पद पिछले एक के बराबर है, उसी संख्या में जोड़ा जाता है। इस संख्या को अंकगणितीय प्रगति का अंतर कहा जाता है और इसे इसके द्वारा दर्शाया जाता है।

यह निर्धारित करने का प्रयास करें कि कौन से संख्या अनुक्रम अंकगणितीय प्रगति हैं और कौन से नहीं हैं:

ए)
बी)
सी)
डी)

समझा? आइए हमारे उत्तरों की तुलना करें:
एकअंकगणितीय प्रगति - बी, सी।
क्या नहीं हैअंकगणितीय प्रगति - ए, डी।

आइए दी गई प्रगति () पर लौटते हैं और इसके वें सदस्य का मान ज्ञात करने का प्रयास करते हैं। मौजूद दोइसे खोजने का तरीका।

1. विधि

हम प्रगति की संख्या के पिछले मान में तब तक जोड़ सकते हैं जब तक हम प्रगति के वें पद तक नहीं पहुंच जाते। यह अच्छा है कि हमारे पास संक्षेप में बताने के लिए बहुत कुछ नहीं बचा है - केवल तीन मान:

तो, वर्णित अंकगणितीय प्रगति का वां सदस्य बराबर है।

2. विधि

क्या होगा यदि हमें प्रगति के वें पद का मूल्य ज्ञात करना है? सारांश में हमें एक घंटे से अधिक समय लगेगा, और यह एक तथ्य नहीं है कि संख्याओं को जोड़ते समय हमसे गलती नहीं होगी।
बेशक, गणितज्ञ एक ऐसा तरीका लेकर आए हैं जिसमें आपको अंकगणितीय प्रगति के अंतर को पिछले मान से जोड़ने की आवश्यकता नहीं है। आपके द्वारा खींची गई रेखाचित्र को ध्यान से देखें ... निश्चित रूप से आपने पहले ही एक निश्चित पैटर्न पर ध्यान दिया होगा, अर्थात्:

उदाहरण के लिए, आइए देखें कि इस अंकगणितीय प्रगति के वें सदस्य का मान कैसे जोड़ा जाता है:


दूसरे शब्दों में:

स्वतंत्र रूप से किसी दिए गए अंकगणितीय प्रगति के सदस्य के मूल्य को इस तरह से खोजने का प्रयास करें।

परिकलित? अपने नोट्स की तुलना उत्तर से करें:

ध्यान दें कि आपको पिछली पद्धति की तरह ही वही संख्या मिली है, जब हमने अंकगणितीय प्रगति के सदस्यों को पिछले मान में क्रमिक रूप से जोड़ा था।
आइए इस सूत्र को "प्रतिरूपित" करने का प्रयास करें - हम इसे एक सामान्य रूप में लाएंगे और प्राप्त करेंगे:

अंकगणितीय प्रगति समीकरण।

अंकगणितीय प्रगति आरोही और कभी-कभी घट रही है।

आरोही- प्रगति जिसमें सदस्यों का प्रत्येक बाद का मूल्य पिछले एक से अधिक होता है।
उदाहरण के लिए:

घटाना- प्रगति जिसमें सदस्यों का प्रत्येक बाद का मूल्य पिछले एक से कम है।
उदाहरण के लिए:

व्युत्पन्न सूत्र का उपयोग अंकगणितीय प्रगति के बढ़ते और घटते दोनों पदों में पदों की गणना में किया जाता है।
आइए इसे व्यवहार में जांचें।
हमें निम्नलिखित संख्याओं से मिलकर एक अंकगणितीय प्रगति दी गई है: आइए देखें कि इस अंकगणितीय प्रगति की संख्या क्या होगी यदि हम इसकी गणना करने के लिए अपने सूत्र का उपयोग करते हैं:

तब से:

इस प्रकार, हमने सुनिश्चित किया कि सूत्र अंकगणितीय प्रगति को कम करने और बढ़ाने दोनों में काम करता है।
इस अंकगणितीय प्रगति के वें और वें पदों को स्वयं खोजने का प्रयास करें।

आइए प्राप्त परिणामों की तुलना करें:

अंकगणितीय प्रगति संपत्ति

आइए कार्य को जटिल करें - हम अंकगणितीय प्रगति की संपत्ति प्राप्त करेंगे।
मान लीजिए कि हमें निम्नलिखित शर्त दी गई है:
- अंकगणितीय प्रगति, मान ज्ञात कीजिए।
आसान, आप कहते हैं और उस सूत्र के अनुसार गिनना शुरू करें जिसे आप पहले से जानते हैं:

चलो, ए, फिर:

बिल्कुल सही। यह पता चला है कि हम पहले पाते हैं, फिर इसे पहले नंबर में जोड़ते हैं और हम जो खोज रहे हैं उसे प्राप्त करते हैं। यदि प्रगति को छोटे मूल्यों द्वारा दर्शाया जाता है, तो इसमें कुछ भी जटिल नहीं है, लेकिन यदि हमें इस स्थिति में संख्याएँ दी जाती हैं? इसे स्वीकार करें, गणना में गलती होने की संभावना है।
अब विचार करें कि क्या किसी सूत्र का उपयोग करके इस समस्या को एक क्रिया में हल करना संभव है? बेशक, हाँ, और यह वह है जिसे हम अब वापस लेने का प्रयास करेंगे।

आइए अंकगणितीय प्रगति के आवश्यक पद को निरूपित करें, जैसा कि हम इसे खोजने के लिए सूत्र जानते हैं - यह वही सूत्र है जो हमने शुरुआत में प्राप्त किया था:
, फिर:

• प्रगति का पिछला सदस्य है:
• प्रगति का अगला सदस्य है:

आइए प्रगति के पिछले और बाद के सदस्यों को संक्षेप में प्रस्तुत करें:

यह पता चला है कि प्रगति के पिछले और बाद के सदस्यों का योग उनके बीच स्थित प्रगति के सदस्य का दोगुना मूल्य है। दूसरे शब्दों में, ज्ञात पिछले और लगातार मूल्यों के साथ प्रगति के सदस्य के मूल्य को खोजने के लिए, उन्हें जोड़ना और विभाजित करना आवश्यक है।

यह सही है, हमें वही नंबर मिला है। आइए सामग्री को ठीक करें। प्रगति के लिए मूल्य की गणना स्वयं करें, क्योंकि यह बिल्कुल भी कठिन नहीं है।

बहुत बढ़िया! आप प्रगति के बारे में लगभग सब कुछ जानते हैं! सीखने के लिए केवल एक ही सूत्र बचा है, जो कि किंवदंती के अनुसार, सभी समय के महानतम गणितज्ञों में से एक, "गणितज्ञों के राजा" - कार्ल गॉस ...

जब कार्ल गॉस 9 वर्ष का था, एक शिक्षक, अन्य ग्रेड में छात्रों के काम की जांच में व्यस्त, पाठ में निम्नलिखित कार्य निर्धारित करता है: "सभी प्राकृतिक संख्याओं के योग की गणना करें (अन्य स्रोतों के अनुसार) समावेशी। " शिक्षक के आश्चर्य की कल्पना करें जब उनके एक छात्र (वह कार्ल गॉस थे) ने एक मिनट में समस्या का सही उत्तर दिया, जबकि डेयरडेविल के अधिकांश सहपाठियों ने लंबी गणना के बाद गलत परिणाम प्राप्त किया ...

यंग कार्ल गॉस ने एक निश्चित पैटर्न देखा जिसे आप आसानी से देख सकते हैं।
मान लीजिए कि हमारे पास -वें सदस्यों से मिलकर एक अंकगणितीय प्रगति है: हमें अंकगणितीय प्रगति के दिए गए सदस्यों का योग ज्ञात करना है। बेशक, हम सभी मूल्यों को मैन्युअल रूप से जोड़ सकते हैं, लेकिन क्या होगा यदि कार्य में इसके सदस्यों का योग खोजना आवश्यक है, जैसा कि गॉस ढूंढ रहा था?

आइए एक दी गई प्रगति बनाएं। हाइलाइट की गई संख्याओं को ध्यान से देखें और उनके साथ विभिन्न गणितीय संक्रियाओं को करने का प्रयास करें।


या तुमने कोशिश की? आपने क्या गौर किया? सही! उनकी राशि बराबर है

अब मुझे बताओ, दी गई प्रगति में ऐसे कितने जोड़े हैं? बेशक, सभी संख्याओं का ठीक आधा, यानी।
इस तथ्य के आधार पर कि एक समान्तर श्रेणी के दो सदस्यों का योग समान है, और समान समान युग्म हैं, हम पाते हैं कि कुल योग है:
.
इस प्रकार, किसी समांतर श्रेणी के प्रथम पदों के योग का सूत्र इस प्रकार होगा:

कुछ समस्याओं में, हम वें पद को नहीं जानते हैं, लेकिन हम प्रगति में अंतर जानते हैं। योग के सूत्र में, वें पद के सूत्र को प्रतिस्थापित करने का प्रयास करें।
तुमने क्या किया?

बहुत बढ़िया! अब आइए उस समस्या पर लौटते हैं जो कार्ल गॉस को दी गई थी: स्वयं की गणना करें कि -वें से शुरू होने वाली संख्याओं का योग क्या है, और -वें से शुरू होने वाली संख्याओं का योग क्या है।

आपको यह कितना मिला?
गॉस ने पाया कि सदस्यों का योग बराबर होता है और सदस्यों का योग। क्या आपने ऐसा फैसला किया है?

वास्तव में, अंकगणितीय प्रगति के सदस्यों के योग का सूत्र प्राचीन यूनानी वैज्ञानिक डायोफैंटस द्वारा तीसरी शताब्दी में सिद्ध किया गया था, और इस पूरे समय में, मजाकिया लोग अंकगणितीय प्रगति के गुणों का अधिकतम उपयोग कर रहे थे।
उदाहरण के लिए, प्राचीन मिस्र और उस समय के सबसे बड़े निर्माण स्थल की कल्पना करें - पिरामिड का निर्माण ... आकृति इसका एक पक्ष दिखाती है।

आप कहते हैं कि यहां प्रगति कहां है? बारीकी से देखें और पिरामिड की दीवार की प्रत्येक पंक्ति में रेत के ब्लॉकों की संख्या में एक पैटर्न खोजें।


क्या यह एक अंकगणितीय प्रगति नहीं है? गणना करें कि एक दीवार बनाने के लिए कितने ब्लॉकों की आवश्यकता है यदि ब्लॉक ईंटों को आधार में रखा गया है। मुझे आशा है कि आप मॉनिटर पर अपनी उंगली चलाकर गिनती नहीं करेंगे, क्या आपको अंतिम सूत्र और अंकगणितीय प्रगति के बारे में हमने जो कुछ कहा है वह सब कुछ याद है?

इस मामले में, प्रगति इस तरह दिखती है:।
अंकगणितीय प्रगति का अंतर।
अंकगणितीय प्रगति के सदस्यों की संख्या।
आइए अपने डेटा को अंतिम फ़ार्मुलों में बदलें (हम 2 तरीकों से ब्लॉक की संख्या की गणना करेंगे)।

विधि 1।

विधि 2।

और अब आप मॉनिटर पर गणना कर सकते हैं: प्राप्त मूल्यों की तुलना हमारे पिरामिड में मौजूद ब्लॉकों की संख्या से करें। क्या यह एक साथ आया? अच्छा किया, आपने अंकगणितीय प्रगति की शर्तों के योग में महारत हासिल कर ली है।
बेशक, आप आधार पर ब्लॉक से पिरामिड नहीं बना सकते हैं, लेकिन कहां से? इस स्थिति के साथ दीवार बनाने के लिए कितनी रेत ईंटों की आवश्यकता है, इसकी गणना करने का प्रयास करें।
क्या आप संभाल पाओगे?
सही उत्तर ब्लॉक है:

व्यायाम

कार्य:

1. गर्मियों तक माशा आकार में आ रहा है। वह हर दिन स्क्वैट्स की संख्या में वृद्धि करती है। माशा हफ्तों में कितनी बार स्क्वाट करेगी, अगर पहली कसरत में उसने स्क्वाट किया।
2. में निहित सभी विषम संख्याओं का योग क्या है?
3. लॉग को स्टोर करते समय, लंबरजैक उन्हें इस तरह से स्टैक करते हैं कि प्रत्येक शीर्ष परत में पिछले वाले की तुलना में एक लॉग कम होता है। एक चिनाई में कितने लॉग होते हैं, यदि लॉग चिनाई के आधार के रूप में कार्य करते हैं।

उत्तर:

1. आइए अंकगणितीय प्रगति के मापदंडों को परिभाषित करें। इस मामले में
   (सप्ताह = दिन)।

   उत्तर:दो सप्ताह के बाद, माशा को दिन में एक बार बैठना चाहिए।

2. पहली विषम संख्या, अंतिम संख्या।
   अंकगणितीय प्रगति का अंतर।
   में विषम संख्याओं की संख्या आधी है, तथापि, हम एक अंकगणितीय प्रगति का -वाँ पद ज्ञात करने के लिए सूत्र का उपयोग करके इस तथ्य की जाँच करेंगे:

   संख्याओं में विषम संख्याएँ होती हैं।
   उपलब्ध डेटा को सूत्र में बदलें:

   उत्तर:इसमें निहित सभी विषम संख्याओं का योग बराबर होता है।

3. आइए पिरामिड समस्या को याद करें। हमारे मामले के लिए, ए, चूंकि प्रत्येक शीर्ष परत एक लॉग से कम हो जाती है, फिर केवल परतों के एक समूह में, यानी।
   आइए डेटा को सूत्र में बदलें:

   उत्तर:चिनाई में लॉग हैं।

आइए संक्षेप करें

1. - एक संख्यात्मक अनुक्रम जिसमें आसन्न संख्याओं के बीच का अंतर समान और बराबर होता है। यह बढ़ भी सकता है और घट भी सकता है।
2. सूत्र ढूँढनाअंकगणितीय प्रगति का वां सदस्य सूत्र द्वारा लिखा जाता है - प्रगति में संख्याओं की संख्या कहाँ है।
3. एक समान्तर श्रेणी के सदस्यों की संपत्ति- - प्रगति में संख्याओं की संख्या कहाँ है।
4. एक समान्तर श्रेणी के सदस्यों का योगदो तरह से पाया जा सकता है:
   
   , जहां मूल्यों की संख्या है।

अंकगणितीय प्रगति। औसत स्तर

संख्या क्रम

आइए बैठें और कुछ संख्याएँ लिखना शुरू करें। उदाहरण के लिए:

आप कोई भी संख्या लिख ​​सकते हैं, और जितने चाहें उतने हो सकते हैं। लेकिन आप हमेशा कह सकते हैं कि कौन सा पहला है, कौन सा दूसरा है, और इसी तरह, हम उन्हें नंबर दे सकते हैं। यह एक संख्या अनुक्रम का एक उदाहरण है।

संख्या क्रमसंख्याओं का एक समूह है, जिनमें से प्रत्येक को एक अद्वितीय संख्या सौंपी जा सकती है।

दूसरे शब्दों में, प्रत्येक संख्या को एक निश्चित प्राकृतिक संख्या से जोड़ा जा सकता है, और केवल एक ही। और हम इस नंबर को इस सेट से किसी अन्य नंबर को असाइन नहीं करेंगे।

संख्या वाली संख्या को अनुक्रम का वां सदस्य कहा जाता है।

हम आम तौर पर पूरे अनुक्रम को कुछ अक्षर कहते हैं (उदाहरण के लिए,), और इस अनुक्रम का प्रत्येक सदस्य एक ही अक्षर है जिसमें इस सदस्य की संख्या के बराबर सूचकांक होता है:।

यह बहुत सुविधाजनक है यदि अनुक्रम का वां पद किसी सूत्र द्वारा दिया जा सकता है। उदाहरण के लिए, सूत्र

अनुक्रम निर्दिष्ट करता है:

और सूत्र निम्नलिखित अनुक्रम है:

उदाहरण के लिए, एक अंकगणितीय प्रगति एक अनुक्रम है (यहां पहला शब्द बराबर है, और अंतर)। या (, अंतर)।

वां टर्म फॉर्मूला

हम आवर्तक को एक सूत्र कहते हैं जिसमें वें सदस्य का पता लगाने के लिए, आपको पिछले या कई पिछले वाले को जानना होगा:

उदाहरण के लिए, इस तरह के सूत्र का उपयोग करके प्रगति का वां पद खोजने के लिए, हमें पिछले नौ की गणना करनी होगी। उदाहरण के लिए, चलो। फिर:

अच्छा, अब सूत्र क्या है?

प्रत्येक पंक्ति में हम जोड़ते हैं, किसी संख्या से गुणा करते हैं। किसलिए? बहुत आसान: यह वर्तमान सदस्य माइनस की संख्या है:

अब बहुत अधिक सुविधाजनक है, है ना? हम जाँच:

अपने लिए तय करें:

एक समान्तर श्रेणी में, nवें पद का सूत्र ज्ञात कीजिए और सौवाँ पद ज्ञात कीजिए।

समाधान:

पहला पद बराबर है। क्या अंतर है? और यहाँ क्या है:

(ऐसा इसलिए है क्योंकि इसे अंतर कहा जाता है, जो प्रगति के लगातार सदस्यों के अंतर के बराबर है)।

तो सूत्र है:

तो सौवाँ पद है:

से सभी प्राकृत संख्याओं का योग क्या है?

किंवदंती के अनुसार, महान गणितज्ञ कार्ल गॉस ने 9 साल का लड़का होने के कारण कुछ ही मिनटों में इस राशि की गणना की। उसने देखा कि पहली और आखिरी संख्याओं का योग बराबर है, दूसरी और आखिरी का योग लेकिन एक समान है, अंत से तीसरे और तीसरे का योग समान है, और इसी तरह आगे भी। ऐसे कितने जोड़े होंगे? यह सही है, सभी संख्याओं की आधी संख्या, यानी। इसलिए,

किसी भी अंकगणितीय प्रगति के पहले पदों के योग का सामान्य सूत्र होगा:

उदाहरण:
सभी दो अंकों के गुणजों का योग ज्ञात कीजिए।

समाधान:

ऐसी पहली संख्या है। प्रत्येक अगला पिछली संख्या में जोड़कर प्राप्त किया जाता है। इस प्रकार, हमारे लिए ब्याज की संख्या पहले पद और अंतर के साथ एक अंकगणितीय प्रगति बनाती है।

इस प्रगति का वां पद सूत्र है:

कितने सदस्य प्रगति में हैं यदि उन सभी को दोहरे अंक में होना है?

बहुत आसान: ।

प्रगति में अंतिम पद बराबर होगा। फिर योग:

उत्तर: ।

अब आप स्वयं निर्णय लें:

1. हर दिन, एथलीट पिछले दिन की तुलना में अधिक मीटर दौड़ता है। यदि वह पहले दिन किमी मी दौड़ता है तो वह सप्ताहों में कितने किलोमीटर दौड़ेगा?
2. एक साइकिल चालक हर दिन पिछले वाले की तुलना में अधिक किलोमीटर ड्राइव करता है। पहले दिन उन्होंने किमी. किमी की दूरी तय करने के लिए उसे कितने दिनों की यात्रा करने की आवश्यकता है? यात्रा के अंतिम दिन में वह कितने किलोमीटर की यात्रा करेगा?
3. एक स्टोर में एक रेफ्रिजरेटर की कीमत हर साल उतनी ही कम हो जाती है। निर्धारित करें कि हर साल रेफ्रिजरेटर की कीमत कितनी कम हो गई है, अगर, रूबल के लिए बिक्री के लिए रखा गया है, तो छह साल बाद इसे रूबल के लिए बेचा गया था।

उत्तर:

1. यहां सबसे महत्वपूर्ण बात यह है कि अंकगणितीय प्रगति को पहचानना और उसके मापदंडों को निर्धारित करना है। इस मामले में, (सप्ताह = दिन)। आपको इस प्रगति के पहले सदस्यों का योग निर्धारित करने की आवश्यकता है:
   .
   उत्तर:
2. यह यहाँ दिया गया है: इसे खोजना आवश्यक है।
   जाहिर है, आपको पिछली समस्या के समान योग सूत्र का उपयोग करने की आवश्यकता है:
   .
   मानों को प्रतिस्थापित करें:

   जड़ स्पष्ट रूप से फिट नहीं है, तो जवाब है।
   आइए th टर्म फॉर्मूला का उपयोग करके अंतिम दिन के लिए तय की गई दूरी की गणना करें:
   (किमी)।
   उत्तर:

3. दिया गया:। पाना: ।
   यह आसान नहीं हो सकता:
   (रगड़)।
   उत्तर:

अंकगणितीय प्रगति। संक्षेप में मुख्य के बारे में

यह एक संख्यात्मक अनुक्रम है जिसमें आसन्न संख्याओं के बीच का अंतर समान और बराबर होता है।

अंकगणितीय प्रगति आरोही () और घटती () हो सकती है।

उदाहरण के लिए:

समांतर श्रेणी का n-वाँ पद ज्ञात करने का सूत्र

सूत्र द्वारा लिखा गया है, जहाँ प्रगति में संख्याओं की संख्या है।

एक समान्तर श्रेणी के सदस्यों की संपत्ति

यह आपको प्रगति के सदस्य को आसानी से खोजने की अनुमति देता है यदि उसके पड़ोसी सदस्य ज्ञात हों - प्रगति में संख्याओं की संख्या कहां है।

एक समान्तर श्रेणी के सदस्यों का योग

राशि खोजने के दो तरीके हैं:

मूल्यों की संख्या कहां है।

मूल्यों की संख्या कहां है।

शेष 2/3 लेख केवल आपके छात्रों के लिए उपलब्ध हैं!

YouClever के छात्र बनें,

"प्रति माह एक कप कॉफी" की कीमत पर गणित में OGE या USE की तैयारी करें।

और "YouClever" पाठ्यपुस्तक, "100gia" प्रशिक्षण कार्यक्रम (reshebnik), असीमित परीक्षण USE और OGE, समाधानों के विश्लेषण के साथ 6000 समस्याओं और अन्य YouClever और 100gia सेवाओं तक असीमित पहुंच प्राप्त करें।

एक अंकगणितीय प्रगति का योग।

एक अंकगणितीय प्रगति का योग एक साधारण बात है। अर्थ और सूत्र दोनों में। लेकिन इस विषय पर सभी प्रकार के कार्य हैं। प्राथमिक से लेकर काफी ठोस तक।

सबसे पहले, आइए योग के अर्थ और सूत्र को समझें। और फिर हम इसे ठीक कर देंगे। आपकी खुशी के लिए।) योग का अर्थ सरल है, एक हम की तरह। एक अंकगणितीय प्रगति का योग ज्ञात करने के लिए, आपको बस इसके सभी सदस्यों को सावधानीपूर्वक जोड़ने की आवश्यकता है। यदि ये शब्द कम हैं, तो आप बिना किसी सूत्र के जोड़ सकते हैं। लेकिन अगर बहुत कुछ है, या बहुत कुछ है ... जोड़ कष्टप्रद है।) इस मामले में, सूत्र बचाता है।

योग सूत्र सरल दिखता है:

आइए जानें कि सूत्र में कौन से अक्षर शामिल हैं। यह बहुत कुछ स्पष्ट करेगा।

एस नहीं - अंकगणितीय प्रगति का योग। जोड़ परिणाम के सभीसदस्यों के साथ पहलापर अंतिम।क्या यह महत्वपूर्ण है। बिल्कुल जोड़ें सबएक पंक्ति में सदस्य, बिना अंतराल और छलांग के। और, अर्थात्, से शुरू हो रहा है प्रथम।तीसरे और आठवें पदों का योग ज्ञात करने या पाँचवें से बीसवें पदों का योग ज्ञात करने जैसे कार्यों में सूत्र का सीधा प्रयोग निराशाजनक होगा।)

एक 1 - प्रथमप्रगति के सदस्य। यहाँ सब कुछ स्पष्ट है, यह सरल है प्रथमपंक्ति नंबर।

एक- अंतिमप्रगति के सदस्य। पंक्ति की अंतिम संख्या। बहुत परिचित नाम नहीं है, लेकिन, जब राशि पर लागू किया जाता है, तो यह बहुत उपयुक्त होता है। तब आप खुद देख लेंगे।

एन - अंतिम सदस्य की संख्या। यह समझना महत्वपूर्ण है कि सूत्र में यह संख्या जोड़े गए सदस्यों की संख्या के साथ मेल खाता है।

आइए अवधारणा को परिभाषित करें अंतिमसदस्य एक... बैकफिल प्रश्न: कौन सा सदस्य होगा अंतिम एकअगर दिया गया अनंतअंकगणितीय प्रगति?)

एक आश्वस्त उत्तर के लिए, आपको अंकगणितीय प्रगति के प्रारंभिक अर्थ को समझने की आवश्यकता है और ... असाइनमेंट को ध्यान से पढ़ें!)

एक अंकगणितीय प्रगति का योग ज्ञात करने के कार्य में, अंतिम पद हमेशा प्रकट होता है (प्रत्यक्ष या परोक्ष रूप से), जो सीमित होना चाहिए।अन्यथा, अंतिम, विशिष्ट राशि बस मौजूद नहीं है।समाधान के लिए, यह महत्वपूर्ण नहीं है कि कौन सी प्रगति दी गई है: परिमित या अनंत। इससे कोई फर्क नहीं पड़ता कि इसे कैसे सेट किया जाता है: कई संख्याओं द्वारा, या n-वें पद के सूत्र द्वारा।

सबसे महत्वपूर्ण बात यह समझना है कि सूत्र प्रगति के पहले पद से संख्या c तक काम करता है। एन।दरअसल, सूत्र का पूरा नाम इस तरह दिखता है: अंकगणितीय प्रगति के पहले n पदों का योग।इन बहुत पहले सदस्यों की संख्या, अर्थात्। एन, कार्य द्वारा विशेष रूप से निर्धारित किया जाता है। कार्य में, यह सभी मूल्यवान जानकारी अक्सर एन्क्रिप्ट की जाती है, हां ... लेकिन कुछ भी नहीं, नीचे दिए गए उदाहरणों में हम इन रहस्यों को प्रकट करेंगे।)

अंकगणितीय प्रगति के योग के लिए कार्यों के उदाहरण।

सबसे पहले, कुछ उपयोगी जानकारी:

एक अंकगणितीय प्रगति के योग के लिए कार्यों में मुख्य कठिनाई सूत्र के तत्वों के सही निर्धारण में निहित है।

कार्यों के लेखक इन तत्वों को असीमित कल्पना के साथ एन्क्रिप्ट करते हैं।) यहां मुख्य बात डरना नहीं है। तत्त्वों के सार को समझ लेना ही उन्हें समझने के लिए पर्याप्त है। आइए कुछ उदाहरणों पर करीब से नज़र डालें। आइए वास्तविक जीआईए पर आधारित एक सत्रीय कार्य से शुरुआत करें।

1. एक अंकगणितीय प्रगति इस शर्त द्वारा निर्दिष्ट की जाती है: a n = 2n-3.5। इसके पहले 10 सदस्यों का योग ज्ञात कीजिए।

अच्छा असाइनमेंट। आसान।) सूत्र द्वारा राशि निर्धारित करने के लिए हमें क्या जानने की आवश्यकता है? पहले कार्यकाल एक 1, अंतिम अवधि एक, हाँ अंतिम सदस्य की संख्या एन।

अंतिम सदस्य का नंबर कहां से लाएं एन? हाँ वहाँ, हालत में! यह कहता है: राशि का पता लगाएं पहले 10 सदस्य।खैर, कौन सी संख्या होगी अंतिम,दसवां कार्यकाल?) आपको विश्वास नहीं होगा, इसकी संख्या दसवीं है!) तो, के बजाय एकसूत्र में हम स्थानापन्न करेंगे एक 10, और इसके बजाय एन- दस। फिर से, अंतिम सदस्य की संख्या सदस्यों की संख्या के समान होती है।

यह परिभाषित करना बाकी है एक 1तथा एक 10... nवें पद के सूत्र द्वारा गणना करना आसान है, जो समस्या कथन में दिया गया है। सुनिश्चित नहीं है कि यह कैसे करें? पिछले पाठ पर जाएँ, इसके बिना - कुछ भी नहीं।

एक 1= 2 1 - 3.5 = -1.5

एक 10= 210 - 3.5 = 16.5

एस नहीं = एस 10.

हमने एक अंकगणितीय प्रगति के योग के लिए सूत्र के सभी तत्वों का अर्थ पाया। यह उन्हें स्थानापन्न करने और गिनने के लिए बनी हुई है:

यही सब है इसके लिए। उत्तर : 75.

GIA पर आधारित एक अन्य कार्य। थोड़ा और जटिल:

2. आपको एक समांतर श्रेणी (a n) दी गई है, जिसका अंतर 3.7 है; ए 1 = 2.3। इसके प्रथम 15 सदस्यों का योग ज्ञात कीजिए।

हम तुरंत राशि का सूत्र लिखते हैं:

यह सूत्र हमें किसी भी सदस्य का मूल्य उसकी संख्या से ज्ञात करने की अनुमति देता है। हम एक साधारण प्रतिस्थापन की तलाश में हैं:

एक 15 = 2.3 + (15-1) 3.7 = 54.1

यह अंकगणितीय प्रगति के योग के लिए सूत्र में सभी तत्वों को प्रतिस्थापित करने और उत्तर की गणना करने के लिए बनी हुई है:

उत्तर: 423.

वैसे, यदि सूत्र में योग के बजाय एककेवल nवें पद के लिए सूत्र को प्रतिस्थापित करें, हम प्राप्त करते हैं:

हम समान देते हैं, हमें अंकगणितीय प्रगति के सदस्यों के योग के लिए एक नया सूत्र मिलता है:

जैसा कि आप देख सकते हैं, यहां nवें पद की आवश्यकता नहीं है। एक... कुछ कार्यों में यह सूत्र बहुत मदद करता है, हाँ... आप इस सूत्र को याद रख सकते हैं। या आप इसे यहाँ की तरह सही समय पर प्रदर्शित कर सकते हैं। आखिरकार, योग का सूत्र और nवें पद का सूत्र हर तरह से याद रखना चाहिए।)

अब कार्य एक संक्षिप्त एन्क्रिप्शन के रूप में है):

3. तीन से विभाज्य दो अंकों की सभी धनात्मक संख्याओं का योग ज्ञात कीजिए।

कैसे! न पहला सदस्य, न आखिरी, न ही तरक्की... कैसे जिएं!?

आपको अपने दिमाग से सोचना होगा और अंकगणितीय प्रगति के योग के सभी तत्वों को स्थिति से बाहर निकालना होगा। हम जानते हैं कि दो अंकों की संख्या क्या होती है। इनमें दो अंक होते हैं।) दो अंकों की संख्या क्या होगी पहला? 10, मुझे लगता है।) आखिरी बातदो अंकों की संख्या? 99, बिल्कुल! तीन अंकों वाले उसका अनुसरण करेंगे ...

तीन का गुणज ... हम्म ... ये वो संख्याएँ हैं जो तीन से भी विभाज्य हैं, यहाँ! दस तीन से विभाज्य नहीं है, 11 विभाज्य नहीं है ... 12 ... विभाज्य है! तो, कुछ बजता है। समस्या की स्थिति के आधार पर एक श्रृंखला लिखना पहले से ही संभव है:

12, 15, 18, 21, ... 96, 99.

क्या यह श्रृंखला एक अंकगणितीय प्रगति होगी? निश्चित रूप से! प्रत्येक सदस्य पिछले एक से सख्ती से तीन से भिन्न होता है। यदि हम पद में 2 या 4 जोड़ दें, मान लीजिए, परिणाम, अर्थात्। नई संख्या अब पूरी तरह से 3 से विभाजित नहीं होगी। ढेर के लिए, आप तुरंत अंकगणितीय प्रगति के अंतर को निर्धारित कर सकते हैं: डी = 3.यह सुविधाजनक होगा!)

तो, आप प्रगति के कुछ मापदंडों को सुरक्षित रूप से लिख सकते हैं:

संख्या क्या होगी एनअंतिम सदस्य? जो कोई भी यह सोचता है कि 99 घातक रूप से गलत है ... संख्या - वे हमेशा एक पंक्ति में जाते हैं, और हमारे सदस्य शीर्ष तीन पर कूद जाते हैं। वे मेल नहीं खाते।

दो उपाय हैं। सुपर मेहनती के लिए एक तरीका है। आप प्रगति, संख्याओं की पूरी श्रृंखला को चित्रित कर सकते हैं, और सदस्यों की संख्या को अपनी उंगली से गिन सकते हैं।) दूसरा तरीका विचारशील के लिए है। हमें nवें पद का सूत्र याद रखना होगा। यदि हम अपनी समस्या के सूत्र को लागू करते हैं, तो हम पाते हैं कि 99 प्रगति का तीसवां पद है। वे। एन = 30।

हम एक अंकगणितीय प्रगति के योग के सूत्र को देखते हैं:

हम देखते हैं, और हम खुश हैं।) हमने समस्या विवरण से राशि की गणना करने के लिए आवश्यक सभी चीजें निकालीं:

एक 1= 12.

एक 30= 99.

एस नहीं = एस 30.

प्रारंभिक अंकगणित बनी हुई है। हम सूत्र में संख्याओं को स्थानापन्न करते हैं और गिनते हैं:

उत्तर: 1665

एक अन्य प्रकार की लोकप्रिय पहेलियाँ:

4. एक समांतर श्रेढ़ी दी गई है:

-21,5; -20; -18,5; -17; ...

बीसवें से चौंतीसवें तक सदस्यों का योग ज्ञात कीजिए।

हम योग सूत्र को देखते हैं और ... हम परेशान हो जाते हैं।) सूत्र, मैं आपको याद दिला दूं, योग की गणना करता है पहले सेसदस्य। और समस्या में आपको योग की गणना करने की आवश्यकता है बीसवीं से...सूत्र काम नहीं करेगा।

बेशक, आप पूरी प्रगति को एक पंक्ति में चित्रित कर सकते हैं, और सदस्यों को 20 से 34 तक जोड़ सकते हैं। लेकिन ... यह किसी भी तरह बेवकूफी है और इसमें लंबा समय लगता है, है ना?)

एक और अधिक सुरुचिपूर्ण समाधान है। आइए अपनी पंक्ति को दो भागों में विभाजित करें। पहला भाग होगा पहले सदस्य से उन्नीसवीं तक।दूसरे भाग - बीसवीं से चौंतीसवीं तक।यह स्पष्ट है कि यदि हम पहले भाग के सदस्यों के योग की गणना करें एस 1-19, हाँ हम दूसरे भाग की शर्तों के योग के साथ जोड़ते हैं एस 20-34, हमें पहले पद से चौंतीस तक की प्रगति का योग मिलता है एस 1-34... ऐशे ही:

एस 1-19 + एस 20-34 = एस 1-34

इससे पता चलता है कि योग खोजने के लिए एस 20-34सरल घटाव हो सकता है

एस 20-34 = एस 1-34 - एस 1-19

दाहिनी ओर दोनों राशियों को माना जाता है पहले सेसदस्य, यानी मानक योग सूत्र उन पर काफी लागू होता है। शुरू करना?

हम समस्या कथन से प्रगति के मापदंडों को निकालते हैं:

डी = 1.5।

एक 1= -21,5.

पहले 19 और पहले 34 सदस्यों के योग की गणना करने के लिए, हमें 19वें और 34वें सदस्यों की आवश्यकता होगी। हम उन्हें nवें पद के सूत्र के अनुसार गिनते हैं, जैसा कि समस्या 2 में है:

एक 19= -21.5 + (19-1) 1.5 = 5.5

एक 34= -21.5 + (34-1) 1.5 = 28

वहाँ कुछ नहीं बचा है। कुल 34 सदस्यों में से 19 सदस्यों को घटाएं:

एस 20-34 = एस 1-34 - एस 1-19 = 110.5 - (-152) = 262.5

उत्तर: 262.5

एक महत्वपूर्ण नोट! इस समस्या को हल करने के लिए एक बहुत ही उपयोगी ट्रिक है। सीधे निपटान के बजाय आपको क्या चाहिए (एस 20-34),हमने गिना क्या, ऐसा प्रतीत होता है, इसकी आवश्यकता नहीं है - एस 1-19।और तभी उन्होंने ठान लिया और एस 20-34, पूरे परिणाम से अनावश्यक को हटाना। यह "कान से चाल" अक्सर बुरे कार्यों में बचाता है।)

इस पाठ में, हमने उन समस्याओं की जांच की, जिनके समाधान के लिए एक अंकगणितीय प्रगति के योग का अर्थ समझना पर्याप्त है। ठीक है, आपको कुछ सूत्रों को जानना होगा।)

प्रायोगिक उपकरण:

अंकगणितीय प्रगति के योग के लिए किसी भी समस्या को हल करते समय, मैं इस विषय से तुरंत दो मुख्य सूत्र लिखने की सलाह देता हूं।

nवें पद का सूत्र है:

ये सूत्र आपको तुरंत बताएंगे कि समस्या को हल करने के लिए क्या देखना है, किस दिशा में सोचना है। यह मदद करता है।

और अब स्वतंत्र समाधान के लिए कार्य।

5. उन सभी दो अंकों वाली संख्याओं का योग ज्ञात कीजिए जो तीन से विभाज्य नहीं हैं।

कूल?) टिप नोट टू टास्क 4 में छिपी हुई है। खैर, टास्क 3 मदद करेगा।

6. अंकगणितीय प्रगति शर्त द्वारा निर्दिष्ट की जाती है: a 1 = -5.5; एक एन + 1 = एक एन +0.5। पहले 24 सदस्यों का योग ज्ञात कीजिए।

असामान्य?) यह एक पुनरावर्ती सूत्र है। आप इसके बारे में पिछले पाठ में पढ़ सकते हैं। लिंक को नजरअंदाज न करें, ऐसे कार्य अक्सर जीआईए में पाए जाते हैं।

7. वास्या ने छुट्टी के लिए पैसे बचाए। 4550 रूबल जितना! और मैंने अपने सबसे प्यारे व्यक्ति (खुद को) को कुछ दिन की खुशी देने का फैसला किया)। खूबसूरती से जीने के लिए, खुद को कुछ भी नकारे बिना। पहले दिन 500 रूबल खर्च करें, और पिछले एक की तुलना में प्रत्येक बाद के दिन 50 रूबल अधिक खर्च करें! जब तक पैसे की आपूर्ति खत्म नहीं हो जाती। वास्या को कितने दिन की खुशी मिली?

मुश्किल?) समस्या 2 से एक अतिरिक्त सूत्र मदद करेगा।

उत्तर (अव्यवस्था में): 7, 3240, 6.

अगर आपको यह साइट पसंद है ...

वैसे, मेरे पास आपके लिए कुछ और दिलचस्प साइटें हैं।)

आप उदाहरणों को हल करने का अभ्यास कर सकते हैं और अपने स्तर का पता लगा सकते हैं। त्वरित सत्यापन परीक्षण। सीखना - रुचि के साथ!)

आप कार्यों और डेरिवेटिव से परिचित हो सकते हैं।