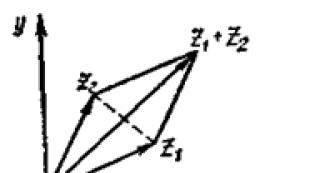
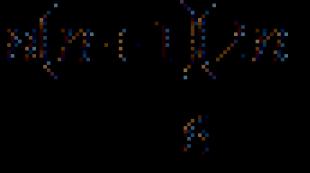Straight line. Basic concepts. Parallel lines. Visual guide (2020) What are parallel lines

This article is about parallel lines and about parallel lines. First, the definition of parallel lines in the plane and in space is given, notation is introduced, examples and graphic illustrations of parallel lines are given. Further, the signs and conditions of parallelism of straight lines are analyzed. In conclusion, solutions are shown for typical problems of proving the parallelism of straight lines, which are given by some equations of a straight line in a rectangular coordinate system on a plane and in three-dimensional space.

Page navigation.

Parallel lines - basic information.

Definition.

Two lines in a plane are called parallel if they do not have common points.

Definition.

Two lines in three dimensions are called parallel if they lie in the same plane and have no common points.

Note that the "if they lie in the same plane" clause in the definition of parallel lines in space is very important. Let's clarify this point: two straight lines in three-dimensional space that do not have common points and do not lie in the same plane are not parallel, but are skew.

Here are some examples of parallel lines. The opposite edges of the notebook sheet lie on parallel lines. The straight lines along which the plane of the wall of the house intersects the planes of the ceiling and floor are parallel. Railroad tracks on level ground can also be thought of as parallel lines.

The symbol "" is used to denote parallel lines. That is, if the lines a and b are parallel, then you can briefly write a b.

Note that if lines a and b are parallel, then we can say that line a is parallel to line b, and also that line b is parallel to line a.

Let us voice a statement that plays an important role in the study of parallel lines in the plane: through a point not lying on a given line, there passes the only line parallel to the given one. This statement is accepted as a fact (it cannot be proved on the basis of the known axioms of planimetry), and it is called the axiom of parallel lines.

For the case in space, the theorem is true: through any point in space that does not lie on a given line, there passes a single line parallel to the given one. This theorem can be easily proved using the axiom of parallel lines given above (you can find its proof in the geometry textbook for grades 10-11, which is listed at the end of the article in the bibliography).

For the case in space, the theorem is true: through any point in space that does not lie on a given line, there passes a single line parallel to the given one. This theorem is easily proved using the axiom of parallel lines given above.

Parallelism of lines - signs and conditions of parallelism.

A sign of parallel lines is a sufficient condition for parallel lines, that is, such a condition, the fulfillment of which guarantees parallel lines. In other words, the fulfillment of this condition is sufficient to state the fact that the lines are parallel.

There are also necessary and sufficient conditions for parallel lines in the plane and in three-dimensional space.

Let us explain the meaning of the phrase "necessary and sufficient condition for parallel lines".

We have already dealt with the sufficient condition for parallel lines. And what is the "necessary condition for parallel lines"? By the name "necessary" it is clear that the fulfillment of this condition is necessary for the lines to be parallel. In other words, if the necessary condition for parallel lines is not satisfied, then the lines are not parallel. Thus, necessary and sufficient condition for lines to be parallel is a condition, the fulfillment of which is both necessary and sufficient for parallel lines. That is, on the one hand, this is a sign of parallel lines, and on the other hand, this is a property that parallel lines have.

Before stating the necessary and sufficient condition for lines to be parallel, it is useful to recall a few auxiliary definitions.

secant line is a line that intersects each of the two given non-coincident lines.

At the intersection of two lines of a secant, eight non-deployed ones are formed. The so-called lying crosswise, corresponding And one-sided corners. Let's show them on the drawing.

Theorem.

If two straight lines on a plane are crossed by a secant, then for their parallelism it is necessary and sufficient that the crosswise lying angles are equal, or the corresponding angles are equal, or the sum of one-sided angles is equal to 180 degrees.

Let us show a graphical illustration of this necessary and sufficient condition for parallel lines in the plane.

You can find proofs of these conditions for parallel lines in geometry textbooks for grades 7-9.

Note that these conditions can also be used in three-dimensional space - the main thing is that the two lines and the secant lie in the same plane.

Here are a few more theorems that are often used in proving the parallelism of lines.

Theorem.

If two lines in a plane are parallel to a third line, then they are parallel. The proof of this feature follows from the axiom of parallel lines.

There is a similar condition for parallel lines in three-dimensional space.

Theorem.

If two lines in space are parallel to a third line, then they are parallel. The proof of this feature is considered in the geometry lessons in grade 10.

Let us illustrate the voiced theorems.

Let us give one more theorem that allows us to prove the parallelism of lines in the plane.

Theorem.

If two lines in a plane are perpendicular to a third line, then they are parallel.

There is a similar theorem for lines in space.

Theorem.

If two lines in three-dimensional space are perpendicular to the same plane, then they are parallel.

Let us draw pictures corresponding to these theorems.

All the theorems formulated above, signs and necessary and sufficient conditions are perfectly suitable for proving the parallelism of straight lines by methods of geometry. That is, to prove the parallelism of two given lines, it is necessary to show that they are parallel to the third line, or to show the equality of cross-lying angles, etc. Many of these problems are solved in geometry lessons in high school. However, it should be noted that in many cases it is convenient to use the method of coordinates to prove the parallelism of lines in a plane or in three-dimensional space. Let us formulate the necessary and sufficient conditions for the parallelism of lines that are given in a rectangular coordinate system.

Parallelism of lines in a rectangular coordinate system.

In this section of the article, we will formulate necessary and sufficient conditions for parallel lines in a rectangular coordinate system, depending on the type of equations that determine these lines, and we will also give detailed solutions to typical problems.

Let's start with the condition of parallelism of two lines on the plane in the rectangular coordinate system Oxy . His proof is based on the definition of the directing vector of the line and the definition of the normal vector of the line on the plane.

Theorem.

For two non-coincident lines to be parallel in a plane, it is necessary and sufficient that the direction vectors of these lines are collinear, or the normal vectors of these lines are collinear, or the direction vector of one line is perpendicular to the normal vector of the second line.

Obviously, the condition of parallelism of two lines in the plane reduces to (direction vectors of lines or normal vectors of lines) or to (direction vector of one line and normal vector of the second line). Thus, if and are the direction vectors of the lines a and b, and And are the normal vectors of lines a and b, respectively, then the necessary and sufficient condition for parallel lines a and b can be written as , or , or , where t is some real number. In turn, the coordinates of the directing and (or) normal vectors of the straight lines a and b are found from the known equations of the straight lines.

In particular, if the line a in the rectangular coordinate system Oxy on the plane defines the general equation of the line of the form , and the straight line b - , then the normal vectors of these lines have coordinates and respectively, and the condition of parallelism of lines a and b will be written as .

If the straight line a corresponds to the equation of the straight line with the slope coefficient of the form . Therefore, if straight lines on a plane in a rectangular coordinate system are parallel and can be given by equations of straight lines with slope coefficients, then the slope coefficients of the lines will be equal. And vice versa: if non-coinciding straight lines on a plane in a rectangular coordinate system can be given by the equations of a straight line with equal slope coefficients, then such straight lines are parallel.

If the line a and the line b in a rectangular coordinate system define the canonical equations of the line on the plane of the form And , or parametric equations of a straight line on a plane of the form And respectively, then the direction vectors of these lines have coordinates and , and the parallelism condition for lines a and b is written as .

Let's take a look at a few examples.

Example.

Are the lines parallel? And ?

Solution.

We rewrite the equation of a straight line in segments in the form of a general equation of a straight line: . Now it is clear that is the normal vector of the straight line , and is the normal vector of the straight line. These vectors are not collinear, since there is no real number t for which the equality ( ). Consequently, the necessary and sufficient condition for the parallelism of lines on the plane is not satisfied, therefore, the given lines are not parallel.

Answer:

No, the lines are not parallel.

Example.

Are lines and parallels?

Solution.

We bring the canonical equation of a straight line to the equation of a straight line with a slope: . Obviously, the equations of the lines and are not the same (in this case, the given lines would be the same) and the slopes of the lines are equal, therefore, the original lines are parallel.

In a plane, lines are called parallel if they have no common points, that is, they do not intersect. To indicate parallelism use a special icon || (parallel lines a || b).

For lines lying in space, the requirement that there are no common points is not enough - for them to be parallel in space, they must belong to the same plane (otherwise they will be skew).

You don’t have to go far for examples of parallel lines, they accompany us everywhere, in the room they are the lines of intersection of the wall with the ceiling and floor, on the notebook sheet there are opposite edges, etc.

It is quite obvious that, having two lines parallel and a third line parallel to one of the first two, it will be parallel to the second.

Parallel lines in the plane are connected by a statement that cannot be proved using the axioms of planimetry. It is accepted as a fact, as an axiom: for any point on a plane that does not lie on a straight line, there is a single straight line that passes through it parallel to the given one. Every sixth grader knows this axiom.

Its spatial generalization, that is, the assertion that for any point in space that does not lie on a line, there is a unique line that passes through it parallel to the given one, is easily proved using the already known axiom of parallelism in the plane.

Properties of parallel lines

• If any of two parallel lines is parallel to the third, then they are mutually parallel.

Parallel lines have this property both in the plane and in space.
As an example, consider its justification in stereometry.

Let the lines b be parallel with the line a.

The case when all the lines lie in the same plane will be left to planimetry.

Suppose a and b belong to the betta plane, and gamma is the plane to which a and c belong (by the definition of parallelism in space, lines must belong to the same plane).

If we assume that the betta and gamma planes are different and mark a certain point B on the line b from the betta plane, then the plane drawn through the point B and the line c must intersect the betta plane in a straight line (we denote it b1).

If the resulting line b1 intersected the gamma plane, then, on the one hand, the intersection point would have to lie on a, since b1 belongs to the betta plane, and on the other hand, it must also belong to c, since b1 belongs to the third plane.
But the parallel lines a and c must not intersect.

Thus, the line b1 must belong to the betta plane and, at the same time, have no common points with a, therefore, according to the axiom of parallelism, it coincides with b.
We have obtained a line b1 coinciding with the line b, which belongs to the same plane with the line c and does not intersect it, that is, b and c are parallel

• Through a point that does not lie on a given line parallel to the given line, only one single line can pass.

• Two straight lines lying on a plane perpendicular to the third are parallel.

• If one of the two parallel lines intersects the plane, the second line intersects the same plane.

• Corresponding and cross-lying internal angles formed by the intersection of parallel two lines of the third are equal, the sum of the internal one-sided ones formed in this case is 180 °.

The converse statements are also true, which can be taken as signs of parallelism of two straight lines.

Condition of parallel lines

The properties and signs formulated above are the conditions for the parallelism of lines, and they can be proved by the methods of geometry. In other words, to prove the parallelism of two existing lines, it suffices to prove their parallelism to the third line or the equality of angles, whether they are corresponding or lying across, etc.

For the proof, they mainly use the method "by contradiction", that is, with the assumption that the lines are not parallel. Based on this assumption, it can be easily shown that in this case the given conditions are violated, for example, the cross-lying internal angles turn out to be unequal, which proves the incorrectness of the assumption made.

1. If two lines are parallel to the third line, then they are parallel:

If a||c And b||c, That a||b.

2. If two lines are perpendicular to the third line, then they are parallel:

If a⊥c And b⊥c, That a||b.

The remaining signs of parallelism of lines are based on the angles formed at the intersection of two lines by a third.

3. If the sum of internal one-sided angles is 180°, then the lines are parallel:

If ∠1 + ∠2 = 180°, then a||b.

4. If the corresponding angles are equal, then the lines are parallel:

If ∠2 = ∠4, then a||b.

5. If the internal cross-lying angles are equal, then the lines are parallel:

If ∠1 = ∠3, then a||b.

Properties of parallel lines

Statements that are inverse to the signs of parallelism of lines are their properties. They are based on the properties of the angles formed by the intersection of two parallel lines by a third line.

1. When two parallel lines intersect with a third line, the sum of the interior one-sided angles formed by them is 180°:

If a||b, then ∠1 + ∠2 = 180°.

2. When two parallel lines intersect with a third line, the corresponding angles formed by them are equal:

If a||b, then ∠2 = ∠4.

3. At the intersection of two parallel lines by a third line, the lying angles formed by them across are equal:

If a||b, then ∠1 = ∠3.

The following property is a special case of each previous one:

4. If a line on a plane is perpendicular to one of the two parallel lines, then it is also perpendicular to the other:

If a||b And c⊥a, That c⊥b.

The fifth property is the axiom of parallel lines:

5. Through a point not lying on a given line, only one line can be drawn parallel to the given line.

Instruction

Before starting the proof, make sure that the lines lie in the same plane and can be drawn on it. The simplest method of proof is the method of measuring with a ruler. To do this, use a ruler to measure the distance between the straight lines in several places as far apart as possible. If the distance remains the same, the given lines are parallel. But this method is not accurate enough, so it is better to use other methods.

Draw a third line so that it intersects both parallel lines. It forms four outer and four inner corners with them. Consider interior corners. Those that lie through the secant line are called cross-lying. Those that lie on one side are called one-sided. Using a protractor, measure the two inner diagonal corners. If they are equal, then the lines will be parallel. If in doubt, measure one-sided interior angles and add up the resulting values. Lines will be parallel if the sum of one-sided interior angles is equal to 180º.

If you don't have a protractor, use a 90º square. Use it to construct a perpendicular to one of the lines. After that, continue this perpendicular in such a way that it intersects another line. Using the same square, check at what angle this perpendicular intersects it. If this angle is also equal to 90º, then the lines are parallel to each other.

In the event that the lines are given in the Cartesian coordinate system, find their guides or normal vectors. If these vectors are, respectively, collinear with each other, then the lines are parallel. Bring the equation of lines to a general form and find the coordinates of the normal vector of each of the lines. Its coordinates are equal to the coefficients A and B. In the event that the ratio of the corresponding coordinates of the normal vectors is the same, they are collinear, and the lines are parallel.

For example, straight lines are given by the equations 4x-2y+1=0 and x/1=(y-4)/2. The first equation is of general form, the second is canonical. Bring the second equation to a general form. Use the proportion conversion rule for this, and you'll end up with 2x=y-4. After reduction to a general form, get 2x-y + 4 = 0. Since the general equation for any straight line is written Ax+By+C=0, then for the first straight line: A=4, B=2, and for the second straight line A=2, B=1. For the first direct coordinate of the normal vector (4;2), and for the second - (2;1). Find the ratio of the corresponding coordinates of the normal vectors 4/2=2 and 2/1=2. These numbers are equal, which means the vectors are collinear. Since the vectors are collinear, the lines are parallel.

They do not intersect, no matter how long they continue. The parallelism of lines in writing is indicated as follows: AB|| WITHE

The possibility of the existence of such lines is proved by a theorem.

Theorem.

Through any point taken outside a given line, one can draw a parallel to this line..

Let AB this line and WITH some point taken outside of it. It is required to prove that WITH you can draw a straight line parallelAB. Let's drop on AB from a point WITH perpendicularWITHD and then we will WITHE^ WITHD, what is possible. Straight CE parallel AB.

For the proof, we assume the opposite, i.e., that CE intersects AB at some point M. Then from the point M to a straight line WITHD we would have two different perpendiculars MD And MS, which is impossible. Means, CE cannot intersect with AB, i.e. WITHE parallel AB.

Consequence.

Two perpendiculars (CEAndD.B.) to one straight line (СD) are parallel.

Axiom of parallel lines.

Through the same point it is impossible to draw two different lines parallel to the same line.

So if a straight line WITHD, drawn through the point WITH parallel to a straight line AB, then any other line WITHE through the same point WITH, cannot be parallel AB, i.e. she continues intersect With AB.

The proof of this not quite obvious truth turns out to be impossible. It is accepted without proof as a necessary assumption (postulatum).

Consequences.

1. If straight(WITHE) intersects with one of parallel(SW), then it intersects with the other ( AB), because otherwise through the same point WITH two different straight lines, parallel AB, which is impossible.

2. If each of the two direct (AAndB) are parallel to the same third line ( WITH) , then they are parallel between themselves.

Indeed, if we assume that A And B intersect at some point M, then two different straight lines, parallel to each other, would pass through this point. WITH, which is impossible.

Theorem.

If straight line is perpendicular to one of the parallel lines, then it is perpendicular to the other parallel.

Let AB || WITHD And EF ^ AB.It is required to prove that EF ^ WITHD.

PerpendicularEF, intersecting with AB, will certainly intersect and WITHD. Let the point of intersection be H.

Suppose now that WITHD not perpendicular to EH. Then some other line, for example HK, will be perpendicular to EH and hence through the same point H two straight parallel AB: one WITHD, by condition, and the other HK as proven before. Since this is impossible, it cannot be assumed that SW was not perpendicular to EH.