Series with complex numbers. Series with complex terms. Power complex series
1. Complex numbers. Complex numbers called numbers of the form x+iy, Where X And y - real numbers, i-imaginary unit, defined by equality i 2 =-1. Real numbers X And at are called respectively valid And imaginary parts complex number z. For them, the notation is introduced: x=Rez; y=imz.
Geometrically, every complex number z=x+iy represented by a dot M (x; y) coordinate plane xOy(Fig. 26). In this case the plane hoy called the complex number plane, or the plane of the complex variable z.
Polar coordinates r And φ points M, which is the image of a complex number z, are called module And argument complex number z; the notation is introduced for them: r=|z|, φ=Argz.
Since each point of the plane corresponds to an infinite number of values of the polar angle, which differ from each other by 2kπ (k is a positive or negative integer), Arg is a z-infinite-valued function of z.
That of the values of the polar angle φ , which satisfies the inequality –π< φ ≤ π are called main importance argument z and denote arg z.
In the following, the designation φ save only for the main value of the argument z , those. let's put φ =argz, whereby for all other values of the argument z we get the equality
Arg z = arg z + 2kπ =φ + 2kπ.
The relations between the modulus and argument of the complex number z and its real and imaginary parts are established by the formulas
x = r cos φ; y = r sin φ.
Argument z can also be determined by the formula
arg z = arctg (y / x) + C,
Where WITH= 0 at x > 0, WITH= +π for x<0, at> 0; C \u003d - π at x < 0, at< 0.
Replacing x And at in complex number notation z = x+iy their expressions through r And φ , we get the so-called trigonometric form of a complex number:
Complex numbers z 1 \u003d x 1 + iy 1 And z 2 \u003d x 2 + iy 2 considered equal if and only if their real and imaginary parts are equal separately:
z1 = z2, If x 1 = x 2, y 1 = y 2 .
For numbers given in trigonometric form, equality takes place if the modules of these numbers are equal, and the arguments differ by an integer multiple of 2π:
z 1 = z 2, If |z 1 | = |z 2 | And Arg z 1 = Arg z 2 +2kπ.
Two complex numbers z = x+iy and z = x -iy with equal real and opposite imaginary parts are called conjugated. For conjugate complex numbers, the relations
|z 1 | = |z 2 |; arg z 1 = -arg z 2,
(the last equality can be given the form Arg z 1 + Arg z 2 = 2kπ).
Operations on complex numbers are defined by the following rules.

Addition. If z 1 \u003d x 1 + iy 1, z 2 \u003d x 2 + iy 2, That
The addition of complex numbers obeys the commutative and associative laws:
![]()
Subtraction. If , That
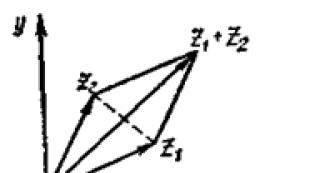
For a geometric explanation of the addition and subtraction of complex numbers, it is useful to represent them not as points on the plane z, and vectors: the number z = x + iy represented by vector having the beginning at the point O ("zero" point of the plane - the origin of coordinates) and the end at the point M(x; y). Then the addition and subtraction of complex numbers is performed according to the rule of addition and subtraction of vectors (Fig. 27).
Such a geometric interpretation of the operations of addition and subtraction of vectors makes it easy to establish theorems on the modulus of the sum and difference of two and the sum of several complex numbers, expressed by the inequalities:
| |z 1 |-|z 2 | | ≤ |z 1 ±z 2 | ≤ |z 1 | + |z 2 | ,
In addition, it is useful to remember that modulus of the difference of two complex numbers z1 And z2 is equal to the distance between the points that are their images on the z plane:| |z 1 -z 2 |=d(z 1 ,z 2) .
Multiplication. If z 1 \u003d x 1 + iy 1, z 2 \u003d x 2 + iy 2. That
z 1 z 2 \u003d (x 1 x 2 -y 1 y 2) + i (x 1 y 2 + x 2 y 1).
Thus, complex numbers are multiplied as binomials, with i 2 replaced by -1.
IF , then
Thus, the modulus of the product is equal to the product of the modules of the somnoektels, and the argument of the product-the sum of the arguments of the factors. The multiplication of complex numbers obeys the commutative, associative and distributive (with respect to addition) laws:
Division. To find the quotient of two complex numbers given in algebraic form, the dividend and the divisor should be multiplied by the number conjugate to the divisor:

" If given in trigonometric form, then
Thus, the modulus of the quotient is equal to the quotient of the modulus of the dividend and divisor, A argument private is equal to the difference between the arguments of the dividend and the divisor.
Exponentiation. If z= , then by the Newton binomial formula we have
(P is a positive integer); in the resulting expression, it is necessary to replace the degrees i their meanings:
i 2 \u003d -1; i 3 =i; i 4 =1; i 5 =1,…
and, in general,
i 4k = 1; i 4k+1 =i; i 4k+2 = -1; i 4k+3 = -i .
If , then
(Here P can be either a positive integer or a negative integer).
In particular,
(De Moivre's formula).
Root extraction. If P is a positive integer, then the nth root of the complex number z has n different values, which are found by the formula

where k=0, 1, 2, ..., n-1.
437.
Find (z 1 z 2)/z 3 if z1 = 3 + 5i, z 2 = 2 + 3i, z 3 = 1+2i.
∆
438.
number z= 2 + 5i.
∆ Find the modulus of the complex number: . Find the main value of the argument: . Therefore, ▲
439.
Represent in trigonometric form the complex
number ![]()
∆ Find ![]() , ; , , i.e.
, ; , , i.e.
440.
Represent in trigonometric form complex
numbers 1, i, -1, -i.
441.
Represent Numbers ,
,
in trigonometric form and then find the complex number
z 1 /(z 2 z 3).
∆ Find
Hence,
442. Find all values.
∆ We write the complex number in trigonometric form. We have , , . Hence,

Hence, , ,
443. Solve a binary equation ω 5 + 32i = 0.
∆ Let us rewrite the equation in the form ω 5 + 32i = 0. Number -32i represent in trigonometric form:
If k = 0 then (A).
k=1,(B).
k=2,(C).
k=3,(D).
k=4,(E).
The roots of the two-term equation correspond to the vertices of a regular pentagon inscribed in a circle of radius R=2 centered at the origin (Fig. 28).
In general, the roots of a two-term equation ω n \u003d a, Where A-complex number, correspond to the vertices of the regular n-gon inscribed in a circle with center at the origin and radius equal to ▲

444. Using De Moivre's formula, express cos5φ And sin5 φ through cosφ And sinφ.
∆ We transform the left side of the equality according to the Newton binomial formula:
It remains to equate the real and imaginary parts of the equality:
445. Given a complex number z=2-2i. Find Rez, Imz, |z|, argz.
446. z = -12 + 5i.
447 . Calculate the expression using the Moivre formula (cos 2° + isin 2°) 45 .
448. Calculate using De Moivre's formula.
449. Express a complex number in trigonometric form
z = 1 + cos 20° + isin 20°.
450. Evaluate expression (2 + 3i) 3 .
451.
Evaluate expression 
452. Evaluate expression
453. Express a complex number in trigonometric form 5-3i.
454. Express a complex number in trigonometric form -1 + i.
455.
Evaluate expression 
456.
Evaluate expression  having previously presented the factors in the numerator and denominator in trigonometric form.
having previously presented the factors in the numerator and denominator in trigonometric form.
457. Find all values
458.
Solve a binary equation ![]()
459. express cos4φ And sin4φ through cosφ And sinφ.
460. Show that the distance between points z1 And z2 equals | z2-z1|.
∆ We have z 1 \u003d x 1 + iy 1, z 2 \u003d x 2 + iy 2, z 2 -z 1 \u003d (x 2 -x 1) + i (y 2 -y 1), where
those. | z2-z1| is equal to the distance between the given points. ▲
461. Which line is described by the point z, satisfying the equation where With-constant complex number, and R>0?
462.
What is the geometric meaning of the inequalities: 1) | z-c|
463. What is the geometric meaning of the inequalities: 1) Rez > 0; 2) im z< 0 ?
2. Series with complex terms. Consider the sequence of complex numbers z 1 , z 2 , z 3 , ..., where z p \u003d x p + iy p (n \u003d 1, 2, 3, ...). constant number c = a + bi called limit sequences z 1 , z 2 , z 3 , ..., if for any arbitrarily small number δ>0 there is a number N, what is the meaning z p with numbers n > N satisfy the inequality \z n-With\< δ . In this case, write .
A necessary and sufficient condition for the existence of a limit of a sequence of complex numbers is as follows: the number c=a+bi is the limit of the sequence of complex numbers x 1 + iy 1, x 2 + iy 2, x 3 + iy 3, ... if and only if , .
![]() (1)
(1)
whose members are complex numbers is called converging, If nth partial sum of the series S n for n → ∞ tends to a certain end limit. Otherwise, series (1) is called divergent.
Series (1) converges if and only if series with real terms converge
(2) Investigate the convergence of the series This series, whose terms form an infinitely decreasing geometric progression, converges; therefore, the given series with complex terms converges absolutely. ^

474. Find the area of convergence of a series
19.4.1. Numerical series with complex terms. All basic definitions of convergence, properties of convergent series, convergence criteria for complex series do not differ in any way from the real case.
19.4.1.1. Basic definitions. Let an infinite sequence of complex numbers be given z 1 , z 2 , z 3 , …, z n , … .The real part of the number z n we will denote a n , imaginary - b n
(those. z n = a n + i b n , n = 1, 2, 3, …).
Number series- type record.
Partialamountsrow: S 1 = z 1 , S 2 = z 1 + z 2 , S 3 = z 1 + z 2 + z 3 , S 4 = z 1 + z 2 + z 3 + z 4 , …,
S n = z 1 + z 2 + z 3 + … + z n , …
Definition. If there is a limit S
sequences of partial sums of the series for  , which is a proper complex number, then the series is said to converge; number S
called the sum of the series and write S
= z
1
+ z
2
+ z
3
+ … +
z
n
+ ... or
, which is a proper complex number, then the series is said to converge; number S
called the sum of the series and write S
= z
1
+ z
2
+ z
3
+ … +
z
n
+ ... or  .
.
Find the real and imaginary parts of the partial sums:
S n = z 1 + z 2 + z 3 + … + z n = (a 1 + i b 1) + (a 2 + i b 2) + (a 3 + i b 3) + … + (a n + i b n ) = (a 1 + a 2 + a 3 +…+ a n ) +
Where symbols  And
And  the real and imaginary parts of the partial sum are indicated. A numerical sequence converges if and only if the sequences composed of its real and imaginary parts converge. Thus, a series with complex terms converges if and only if the series formed by its real and imaginary parts converge. One of the methods for studying the convergence of series with complex terms is based on this assertion.
the real and imaginary parts of the partial sum are indicated. A numerical sequence converges if and only if the sequences composed of its real and imaginary parts converge. Thus, a series with complex terms converges if and only if the series formed by its real and imaginary parts converge. One of the methods for studying the convergence of series with complex terms is based on this assertion.
Example. Investigate for convergence series  .
.
Let's write out several values of the expression  : further values are periodically repeated. A number of real parts: ; series of imaginary parts ; both series converge (conditionally), so the original series converges.
: further values are periodically repeated. A number of real parts: ; series of imaginary parts ; both series converge (conditionally), so the original series converges.
19.4.1.2. Absolute convergence.
Definition. Row  called absolutely convergent if the series converges
called absolutely convergent if the series converges  , composed of the absolute values of its members.
, composed of the absolute values of its members.
Just as for numerical real series with arbitrary terms, it is easy to prove that if the series converges  , then the series necessarily converges
, then the series necessarily converges  (
( , so the series formed by the real and imaginary parts of the series
, so the series formed by the real and imaginary parts of the series  , converge absolutely). If the row
, converge absolutely). If the row  converges, and the series
converges, and the series  diverges, then the series
diverges, then the series  is called conditionally convergent.
is called conditionally convergent.
Row  is a series with non-negative terms, therefore, to study its convergence, all known signs (from comparison theorems to the Cauchy integral criterion) can be used.
is a series with non-negative terms, therefore, to study its convergence, all known signs (from comparison theorems to the Cauchy integral criterion) can be used.
Example. Investigate for convergence series  .
.
Let's make a series of modules ():  . This series converges (the Cauchy test
. This series converges (the Cauchy test  ), so the original series converges absolutely.
), so the original series converges absolutely.
19.4. 1 . 3 . Properties of convergent series. For convergent series with complex terms, all properties of series with real terms are true:
A necessary criterion for the convergence of a series.
The common term of the convergent series tends to zero as
 .
.
If the series converges  , then any of its remainder converges. Conversely, if any remainder of the series converges, then the series itself converges.
, then any of its remainder converges. Conversely, if any remainder of the series converges, then the series itself converges.
If the series converges, then the sum of its remainder aftern
-th term tends to zero at
 .
.
If all terms of a convergent series are multiplied by the same numberWith , then the convergence of the series is preserved, and the sum is multiplied byWith .
Convergent rows (A
) And (IN
) can be added and subtracted term by term; the resulting series will also converge, and its sum is equal to
 .
.
If the terms of the convergent series are grouped arbitrarily and a new series is made up of the sums of the terms in each pair of parentheses, then this new series will also converge, and its sum will be equal to the sum of the original series.
If a series converges absolutely, then for any permutation of its terms, the convergence is preserved and the sum does not change.
If the rows (A
) And (IN
) converge absolutely to their sums
 And
And
 , then their product for an arbitrary order of terms also converges absolutely, and its sum is equal to
, then their product for an arbitrary order of terms also converges absolutely, and its sum is equal to
 .
.
View Symbol W 1 + W 2 +…+ W n +…= (1), Where W n = u n + i· v n (n = 1, 2, …) complex numbers (sequences of complex numbers) are called near complex numbers.
Numbers W n (n = 1, 2, …) called members of a number, member W n called common member of the series.
Type numbers S n = W 1 + W 2 +…+ W n (2) (n = 1, 2, …) , are called partial sums of the series (1).
Finite or infinite limit S sequences S n called the sum of this series.
If limit S is finite, then the series is called converging, if the limit is infinite, or does not exist at all, then the series divergent.
If S the sum of series (1), then we write  .
.
Let  , A
, A  . Obviously σ
n =
u 1
+
u 2
+…+
u n ,
τ
n =
v 1
+
v 2
+…+
v n. How do we know equality
. Obviously σ
n =
u 1
+
u 2
+…+
u n ,
τ
n =
v 1
+
v 2
+…+
v n. How do we know equality
 (S of course) is equivalent to two equalities
(S of course) is equivalent to two equalities
 And
And
 . Therefore, the convergence of series (1) is equivalent to the convergence of two real series:
. Therefore, the convergence of series (1) is equivalent to the convergence of two real series:  And
And  . Therefore, the basic properties of convergent numerical series extend to convergent complex series.
. Therefore, the basic properties of convergent numerical series extend to convergent complex series.
For example, for complex series, the Cauchy criterion is valid: series (1) converges if and only if for any 
 , that for alln
>
Nand anyp= 1, 2, … the inequality.
, that for alln
>
Nand anyp= 1, 2, … the inequality.
This criterion directly implies the necessary criterion for the convergence of the series: for series (1) to converge it is necessary and sufficient that its common termW n → 0 .
The following properties of convergent series are valid: if the rows
 And
And
 converge to their sumsSAndd, then the rows
converge to their sumsSAndd, then the rows
 And
And
 converge respectively to the sumsS
±
dand λS
.
converge respectively to the sumsS
±
dand λS
.
Absolutely convergent series of complex numbers.
Series of complex numbers  (1) called absolutely convergent if the series converges
(1) called absolutely convergent if the series converges  (2).
(2).
Theorem.
Every absolutely convergent series (1) of complex numbers converges.
Proof.
Obviously, it suffices for us to establish that for the series (1) the conditions of the Cauchy criterion for the convergence of the series are satisfied. Take any  . Due to the absolute convergence of series (1), series (2) converges. Therefore, for the chosen
. Due to the absolute convergence of series (1), series (2) converges. Therefore, for the chosen 
 , that for any n
>
N And p=1.2,… the inequality will be satisfied
, that for any n
>
N And p=1.2,… the inequality will be satisfied  , But
, But 
 , and even more so, the inequality
, and even more so, the inequality  for any n
>
N And p=1,2,…
Consequently, for the series (1), the conditions of the Cauchy criterion for the convergence of the complex series are satisfied. Therefore, series (1) converges. The theorem is correct.
for any n
>
N And p=1,2,…
Consequently, for the series (1), the conditions of the Cauchy criterion for the convergence of the complex series are satisfied. Therefore, series (1) converges. The theorem is correct.
Theorem.
In order for a series of complex numbers
 (1) is absolutely convergent, it is necessary and sufficient that the real series converge absolutely
(1) is absolutely convergent, it is necessary and sufficient that the real series converge absolutely
 (3) and
(3) and
 (4) , whereW n
=
u n +
i·
v n
(n
= 1, 2,…).
(4) , whereW n
=
u n +
i·
v n
(n
= 1, 2,…).
Proof,
relies on the following obvious inequalities
 (5)
(5)
Necessity. Let the series (1) converge absolutely, let us show that the series (3) and (4) absolutely converge, i.e., the series converge  And
And  (6). From the absolute convergence of series (1) it follows that series (2)
(6). From the absolute convergence of series (1) it follows that series (2)  converges, then, by virtue of the left side of inequality (5), series (6) will converge, i.e., series (3) and (4) converge absolutely.
converges, then, by virtue of the left side of inequality (5), series (6) will converge, i.e., series (3) and (4) converge absolutely.
Adequacy. Let series (3) and (4) converge absolutely, let us show that series (1) also converges absolutely, i.e., that series (2) converges. It follows from the absolute convergence of series (3) and (4) that series (6) converge, so the series also converges  . Therefore, due to the right side of inequality (5), series (2) converges, i.e., series (1) converges absolutely.
. Therefore, due to the right side of inequality (5), series (2) converges, i.e., series (1) converges absolutely.
So, the absolute convergence of the complex series (1) is equivalent to the absolute convergence of the real number series (3) and (4). Therefore, absolutely convergent complex series are subject to all the basic properties of real absolutely convergent numerical series. In particular, for an absolutely convergent complex series, the theorem on the permutation of its terms is valid, i.e., swapping terms in an absolutely convergent series does not affect the sum of the series. To establish the absolute convergence of a complex series, any criterion for the convergence of a positive series can be used.
Cauchy sign.
Let series (1) have a limit
 , then ifq
< 1 , то ряд (1) абсолютно сходится, если
q>1, then series (1) diverges.
, then ifq
< 1 , то ряд (1) абсолютно сходится, если
q>1, then series (1) diverges.
Sign of d'Alembert.
If for the series (1) of complex numbers there is a limit
 , then atq
< 1 этот ряд абсолютно сходится, а если
q> 1, then the series diverges.
, then atq
< 1 этот ряд абсолютно сходится, а если
q> 1, then the series diverges.
Example.
Investigate for absolute convergence series  , Here
, Here  .
.
Let's find
 . Obviously
. Obviously  =
=
 =
=
 . Therefore, the series is absolutely convergent.
. Therefore, the series is absolutely convergent.
Absolutely convergent series can be multiplied. The product of an absolutely convergent and a convergent series converges. The product of two convergents can diverge.
Size: px
Start impression from page:
transcript
1 8 Complex number series S of the sequence (S) is called the sum of the series (46) The series a k is called the -th remainder of the series (46) For a convergent k series S S r and lm r, those ε > N, N: r< ε Для сходящегося ряда (46) необходимым и достаточным признаком его сходимости является критерий Коши: ряд (46) сходится тогда и только тогда, если ε >, N, N: a< ε p k k Необходимым условием сходимости ряда (46) является требование lm a Действительно, из сходимости ряда (46) следует, согласно критерию Коши, что ε >, N > that for p, it follows that S S< ε Если сходится ряд ak k a (47) с действительными положительными членами, то очевидно, сходится и ряд (46), который в этом случае называется абсолютно сходящимся А для ряда (47) уже можно применить признаки Даламбера и Коши: ряд (47) сходится, если, начиная с a некоторого номера N соотношение l < a, N значит, сходится абсолютно ряд (46)), если a q <, N k ; и ряд (47) сходится (а,
2 9 Function series and their properties Uniform convergence Weierstrass theorem Let an infinite sequence of single-valued functions ((Z)) be defined in a domain G of the complex plane Z ((Z)) An expression of the form U U (48) will be called a functional series Series (48) is called convergent in the domain G if Z G the number series corresponding to it converges If the series (48) converges in the region G, then in this region it is possible to define a single-valued function, the value of which at each point of the region G is equal to the sum of the corresponding number series (48) in the region G Then G, > k () U k()< ε Заметим, что в общем случае N зависит и от ε и от Определение Если ε >, N(ε), N(ε): ε, N (ε,), N(ε,) : the domain G k U k< ε G, то ряд (48) называется равномерно сходящимся в k k Если остаток ряда обозначить r U, то тогда условие равномерной сходимости ряда (48) можем записать в виде: r < ε, N(ε), G Достаточным признаком равномерной сходимости ряда (48) является признак Вейерштрасса: Если всюду в области G члены функционального ряда (48) могут быть мажорированы членами некоторого абсолютно сходящегося числового ряда a, те
3 a U, G, (49) then the series (48) converges uniformly N Indeed, since the series a converges, then >< ε, U U a < ε при N, что и доказывает равномерную k k k k k k сходимость ряда (48) в области G Приведем некоторые теоремы о равномерно сходящихся рядах Они доказываются совершенно также, как соответствующие теоремы вещественного анализа и поэтому приведем их без доказательства Теорема 5 Если функции U непрерывны в области G, а ряд U сходится в этой области равномерно к функции, то также непрерывна в G Теорема 6 Если ряд (48) непрерывных функций U сходится равномерно в области G к функции, то интеграл от этой функции по любой кусочногладкой кривой, целиком лежащей в области G, можно вычислить путем почленного интегрирования ряда (48), те Теорема 7 Если члены d U d U сходящегося в области G ряда U имеют непрерывные производные в этой области и ряд U равномерно сходится в G, то данный ряд U можно почленно дифференцировать в области G, причем U U, где U - сумма ряда
4 For functional series in complex analysis, there is the Weierstrass theorem, which allows us to significantly strengthen the theorem on the possibility of term-by-term differentiation of a functional series, known from real analysis. Before stating and proving it, we note that the series U, which converges uniformly along the line l, remains uniformly after multiplying all its terms by the function ϕ bounded on l Indeed, let the inequality ϕ () be satisfied on the line l< M Тогда для остатков ρ и r рядов U и U ϕ справедливо соотношение ϕ U U r < M r ρ ϕ ε и, тк N, >N:r< и одновременно с ним ρ < ε, то этим доказано M высказанное утверждение Если сумма данного ряда есть S, то сумма ряда, полученного после умножения на ϕ, очевидно будет ϕ S Теорема 8 (Вейерштрасса) Если члены ряда - аналитические в некоторой области G функции и этот ряд сходится в области G равномерно, то его сумма также является функцией аналитической в G, ряд можно почленно дифференцировать и полученный ряд F равномерно сходится к () F Выберем любую внутреннюю точку области G и построим круг столь малого радиуса с центром в этой точке, чтобы он целиком лежал внутри G (рис) В силу равномерной сходимости данного ряда в G, G ρ Рис он, в частности, равномерно сходится на окружности этого круга Пусть - любая точка на Умножим ряд () () () () () (5) на величину Полученный ряд
5 also converges uniformly to its sum () () () () (), since function (5) is limited to, because for points of this circle ρ is the radius of the circle (recall: - here is a constant) Then, according to the above, series (5) can be integrated term by term: () d () d () d d π π π π Due to the analyticity of the functions, the Cauchy formula can be applied to them, on the basis of which we obtain () d π, (5) and the sum of the series on the right in (5) is and, therefore, we obtain the equality π () d at the point Tk - any point of the domain G, then the first part of the theorem is proved. we obtain that the series converges uniformly, and its sum is equal to (k) (k)
6 series of the form where Power series Abel's theorem A very important case of general functional series are power series (), (53) - some complex numbers, and - a fixed point of the complex plane. series, the general theorems of the previous sections can be applied. As it was established in them, many properties are a consequence of uniform convergence. To determine the region of convergence of the power series (53), the following theorem turns out to be essential. Theorem 9 (Abel) If the power series (53) converges at some point, then it converges absolutely and at any point that satisfies the condition, moreover, in the circle< ρ, радиусом ρ, меньшим < сходится равномерно, ряд Δ Выберем произвольную точку, удовлетворяющую условию < Обозначим q сходимости ряда следовательно M >, that M, q< В силу необходимого признака его члены стремятся к нулю при, отсюда () M M q M, Тогда, где q < (54) Ряд справа в (54) бесконечно убывающая геометрическая прогрессия со знаменателем q < Тогда из (54) следует сходимость и рассматриваемого ряда
7p< достаточно в силу признака Вейерштрасса (53) В круге построить сходящийся числовой ряд, можорирующий данный ряд в рассматриваемой области Очевидно, таковым является ряд ρ M, также представляющий собой сумму бесконечной геометрической прогрессии со знаменателем, меньшим единицы Из теоремы Абеля можно вывести ряд следствий, в известной мере аналогичным следствиям из теоремы Абеля в теории степенных рядов вещественного анализа Если степенной ряд (53) расходится в некоторой точке, то он расходится и во всех точках, удовлетворяющих неравенству >The exact upper limit of the distances from the point to the point at which the series (53) converges is called the radius of convergence of the power series, and the region<, называется кругом сходимости степенного ряда В точках границы ряд может как сходиться так и расходиться Пример Найти область сходимости ряда Δ Находим радиус сходимости по признаку Даламбера lm () и наш ряд сходится в круге < При <, те, исследуется особо В этом случае и, значит, областью абсолютной сходимости является
8p< В круге любого радиуса ρ, меньшего чем радиус сходимости, степенной ряд (53) сходится равномерно 3 Внутри круга сходимости степенной ряд сходится к аналитической функции В самом деле, члены ряда u есть функции, аналитические на всей плоскости Z, ряд сходится в любой замкнутой подобласти круга сходимости Тогда по теореме Вейерштрасса сумма ряда есть аналитическая функция 4 Степенной ряд внутри круга сходимости можно почленно интегрировать и дифференцировать любое число раз, причем радиус сходимости полученных рядов равен радиусу сходимости исходного ряда 5 Коэффициенты степенного ряда (53) находятся по формулам! () () (55) Доказательство этого факта приводится методами, аналогичными методам вещественного анализа Ряд Тейлора Теорема Тейлора Нули аналитических функций Итак степенной ряд внутри круга сходимости определяет некоторую аналитическую функцию Возникает вопрос: можно ли функции, аналитической внутри некоторого круга, сопоставить степенной ряд, сходящийся в этом круге к данной функции? < Теорема 9 (Тейлора) Функция, аналитическая внутри круга, может быть представлена в этом круге сходящимся степенным рядом, причем этот ряд определен однозначно
9 Let us choose an arbitrary point inside the circle ρ ρ< и построим окружность ρ точке радиусом < с центром в ρ (рис), содержащую точку внутри Такое построение возможно для любой точки внутри этого круга Так как < ρ, а внутри круга < Рис аналитична, то по формуле Коши имеем π ρ () d (56) Преобразуем подынтегральное выражение: (57) <, то < Так как Поэтому второй сомножитель справа в (57) можно представить как сумму степенного ряда (прогрессии), ту которая первый член есть, а знаменатель прогрессии есть Так как, те () () (58) ρ, то ряд (58) сходится равномерно по, так как он мажорируется сходящимся числовым рядом Подставляя (58) в (56) и интегрируя почленно, получаем ρ (< ρ)
10 Let us introduce the notation () d () ρ π () d () π ρ () and rewrite (59) as a power series converging at the chosen point: (59) (6) () (6) In formula (6), the neighborhood ρ can be replaced, by virtue of the Cauchy theorem, by any closed contour lying in the region< и содержащим точку внутри Так как - произвольная точка данной области, то отсюда следует, что ряд (6) сходится к круге ρ < этот ряд сходится равномерно Итак, функция всюду внутри круга < аналитическая внутри круга <, причем в разлагается в этом круге в сходящийся степенной ряд Коэффициенты разложения (6) на основании формулы Коши для производных аналитической функции имеет вид () d () π ρ () ()! (6) Для доказательства единственности разложения (6) допустим, что имеет еще место формула разложения (), (6)
11 where there would also be one coefficient<, поэтому на основании формулы (55) Ряд (6) сходящимся в круге () () (6) Тем самым единственность определения коэффициентов доказана Разложение функции, аналитической в круге! <, что совпадает с, в сходящийся степенной ряд (6), часто называется разложением Тейлора, а сам ряд (6) Рядом Тейлора Доказанная теорема устанавливает взаимнооднозначное соответствие между функцией, аналитической в окрестности некоторой точки и степенным рядом с центром в этой точке, это означает эквивалентность конкретной аналитической функции, как функции бесконечное число раз дифференцируемой и функцией, представимой в виде суммы степенного ряда G и Заметим, наконец, что, если функция является аналитической в области G - внутренняя точка, то радиус сходимости ряда Тейлора () () () этой функции не меньше расстояния от точки до! границы области G (имеется в виду ближайшее расстояние) Пример Разложить в ряд Тейлора по степеням Δ Эта функция является аналитической на всей комплексной плоскости за исключением точек, Поэтому в круге < функция может быть ± разложена в ряд Тейлора При условии < выражение рассматриваться как сумма бесконечно убывающей прогрессии может q, q < Поэтому
12 , < Пример 3 Найти разложение в ряд Тейлора в круге < Определение по формуле (6) здесь довольно затруднительно Поэтому, представим π Так как < и <, то, используя геометрическую, получаем q q, Используя показательную форму чисел и находим окончательно 4 s π (63) Тк расстояние от центра разложения до ближайших особых точек (те до границы аналитичности) есть, то радиус сходимости ряда (63) есть Рис X Y
13 4 4 3 Example<, 4 3 < Ближайшей к центру разложения особой точкой является точка, до которой расстояние равно, поэтому В заключение приведем основные разложения: e (<)!! 3! cos! 4 3 4! ; (<)! ; s () m 3 3! 5 5! m m m!! (<) ()! ; m(m)(m)! ; l 3 3 () 4 (<) Если для аналитической функции (), то точка называется нулем аналитической функции В этом случае разложение функции в ряд Тейлора в окрестности точки имеет вид () () тк () Если в разложении функции окрестности точки и, следовательно, разложение имеет вид, в ряд Тейлора в,
14 then the point () (), (64) is called the zero of the function If, then the zero is called a prime of order or multiplicity From the formulas for the coefficients of the Taylor series, we see that if the point is a zero of the order, then where () () can be rewritten in the form, but () () () [ () ] () ϕ, ϕ () (), () ϕ, and the circle of convergence of this series is obviously the same as that of the series (64) converse statement where Any function of the form is an integer, ϕ () and zero of order are zeros, and (±) Example 6 Find the order of zero for the function 8 s Expand the denominator in powers: 3 3! 8 5 5! ! 5! 3! 5 5! ϕ
15 5 ϕ, where ϕ, and ϕ and a point of the function 3!, so that the point 5! ϕ is analytic in is the zero of the 5th order for the original Laurent series and its convergence region Decomposition of an analytic function in a Laurent series Consider a series of the form () where is a fixed point of the complex plane, (65) are some complex numbers. Let us establish its area of convergence To do this, we represent (65) in the form centered at a point of some radius, and in particular, it can be equal to zero or infinity Inside the circle of convergence, this series converges to some analytic function of a complex variable, those (),< (67)
16 To determine the region of convergence of a series of variables, setting () () Then this series will take the form let's make a replacement - an ordinary power series converging inside its circle of convergence to some analytical function ϕ () with a complex variable Let the radius of convergence of the resulting power series be r Then ϕ,< r Возвращаясь к старой переменной и полагая ϕ () () (68), >r It follows that the region of convergence of the series, the region external to the circle r, we obtain (69) () is<, то существует общая область сходимости этих рядов круговое кольцо r < <, в которой ряд (65) сходится к аналитической функции (), r < < (7) Так как ряды (67) и (68) являются обычными степенными рядами, то в указанной области функция обладает всеми свойствами суммы степенного ряда Это означает, что ряд Лорана сходится внутри своего кольца сходимости к некоторой функции, аналитической в данном кольце
17 If r >, then the series (67) and (68) do not have a common region of convergence, thus in this case the series (65) does not converge anywhere to any function Note that the series is a regular part of the series (7), and Example 7 Expand - the main part of the row (65) () a)< < ; б) >; V)< < называется правильной частью или в ряд Лорана в кольцах: Во всех кольцах функция регулярна (аналитична) и поэтому может быть представлена рядом Лорана (доказательство этого факта в следующем пункте) Перепишем функцию в виде а) Так как <, то второе слагаемое есть сумма убывающей геометрической прогрессии Поэтому () Здесь главная часть состоит из одного слагаемого < б) в этом случае, поэтому () 3
18 This expansion lacks a regular part< в) Для случая < функцию также надо привести к сходящейся геометрической прогрессии, но со знаменателем Это даст: 3 Заметим, что в главной части этого разложения присутствует одно слагаемое Возникает вопрос: можно ли функции аналитической в некотором круговом кольце, сопоставить ряд Лорана, сходящийся к этой функции в данном кольце? На этот вопрос отвечает Теорема Функция, аналитическая в круговом кольце < <, однозначно представляется в этом кольце сходящимся рядом Лорана дробь На Рис 3 Δ Зафиксируем произвольную точку внутри данного кольца и контурами окружности и с центром в, радиусы которых удовлетворяют условиям < < < < < (рис 3) Согласно формуле Коши для многосвязной области имеем π () d () выполняется неравенство q, можно представить в виде d (7) Поэтому
19 Let us carry out term-by-term integration in (7), which is possible due to the uniform convergence of the series in, we obtain d π, (7) where d π, (73) (7) we will have π π d d, (for d), (74) where d π (75) Changing the direction of integration in (75), we obtain
20 π () () d ()() d π, > (76) Due to the analyticity of the integrands in (73) and (76) in the circular ring< < в соответствии с теоремой Коши значения интегралов не изменятся при произвольной деформации контуров интегрирования в области аналитичности Это позволяет объединить формулы (73) и (76): π () d (), ±, ±, (77) где - произвольный замкнутый контур, лежащий в указанном кольце и содержащий точку внутри Возвратимся теперь к формуле (7), получим где коэффициенты () (), (78) () для всех определяются однообразной формулой (77) Так как - люба точка кольца < <, то отсюда следует, что ряд (78) сходится к внутри данного кольца причем в замкнутом кольце < < ряд сходится к равномерно Доказательство единственности разложения (78) опускаем Из полученных результатов следует, что областью сходимости ряда (78) Лорана является круговое кольцо < <, на границах которого имеется хотя бы по одной особой точке аналитической функции ряд (78), к которой сходится Замечание Формула (77) для определения коэффициентов разложения в ряд Лорана (78) не всегда практически удобна Поэтому часто прибегают к разложению рациональной дроби на простейшие с использованием геометрической прогрессии, а также используют разложение в ряд Тейлора элементарные функции Приведем примеры
21 Example 8 Expand the Laurent series (those in powers) Y in the vicinity of the point ()() in Δ In this case, we will construct two circular rings centered at the point (Fig. 4): a) a circle “without a center”< < ; Рис 4 X б) внешность круга >It is analytic in each of these rings, and has singular points on the boundaries. Let us expand the function in powers in each of these regions)< < ; ; [ () () () ] () < Этот ряд сходится, так как Так что ()() () () () (), ; >) Here we have 3, () () () () () is a convergent series, since<
22 s As a result ()() () () those, 3, 3 Example 9 Expand the function Δ in a Laurent series in the vicinity of the point We have:, s s s cos cos s s! cos 4 () () 3 4! 3! () 5! () (scos)!! 5
Topic Complex number series Consider a number series k ak with complex numbers of the form A series is called convergent if the sequence S of its partial sums S a k k converges. Moreover, the limit S of the sequence
Topic Functional complex series Definition. If k, N, N U k G are satisfied at once, converging in the domain G., then the series is called uniformly. A sufficient criterion for the uniform convergence of a series is the criterion
LECTURE N37. Series of analytic functions. Decomposition of an analytic function in a power series. Taylor series. Laurent series..Expansion of an analytic function in a power series.....Taylor series.... 3.Expansion of an analytic
Module Topic Function sequences and series Properties of uniform convergence of sequences and series Power series Lecture Definitions of function sequences and series Uniformly
Lecture 7 Taylor and Laurent series 7. Taylor series In this part, we will see that the concepts of a power series and an analytic function define the same object: any power series with a positive radius of convergence
Mathematical analysis Section: Theory of functions of a complex variable Topic: Series in the complex plane Lecturer Yanushchik O.V. 217 9. Series in the complex plane 1. Numerical series Let the sequence
5 Power series 5 Power series: definition, domain of convergence Function series of the form (a + a) + a () + K + a () + K a) (, (5) numbers are called power series Numbers
Federal Agency for Education Moscow State University of Geodesy and Cartography (MIIGAiK) METHODOLOGICAL INSTRUCTIONS AND TASKS FOR INDEPENDENT WORK on the course HIGHER MATHEMATICS
Function series Lectures 7-8 1 Convergence area 1 A series of the form u () u () u () u (), 1 2 u () where the functions are defined on a certain interval, is called a functional series. The set of all points
LECTURE N38. Behavior of an analytic function at infinity. special points. Function residues..neighborhood of a point at infinity.....Laurent expansion in a neighborhood of a point at infinity.... 3. Behavior
MINISTRY OF EDUCATION AND SCIENCE OF THE RUSSIAN FEDERATION National Research Nizhny Novgorod State University named after NI Lobachevsky NP Semerikova AA Dubkov AA Kharcheva SERIES OF ANALYTICAL FUNCTIONS
Ministry of Education of the Republic of Belarus Vitebsk State Technological University Topic. "Rows" Department of Theoretical and Applied Mathematics. developed by Assoc. E.B. Dunina. Main
V.V. Zhuk, A.M. Kamachkin 1 Power series. Convergence radius and convergence interval. The nature of the convergence. Integration and differentiation. 1.1 Convergence radius and convergence interval. Functional range
Topic Laurent series and its domain of convergence. Consider a series of the form n C n n C n n n n C n n where is a fixed point of the complex plane, are some complex numbers. C n This series is called the Laurent series.
LECTURE N 7 .Power
Mathematical analysis Section: Numerical and functional series Topic: Power series. Expansion of a function in a power series Lecturer Rozhkova S.V. 3 g. 34. Power series
4 Series of Analytic Functions 4. Functional Sequences Let Ω C and f n: Ω C. A sequence of functions (f n ) converges pointwise to a function f: Ω C if for each z Ω lim n f n(z) = f(z).
Functional series Functional series its sum and area of functional o Let a sequence of functions k (k 1) be given in the region Δ of real or complex numbers
Lectures prepared by Associate Professor Musina MV Definition Expression of the form Numerical and functional series Numerical series: basic concepts (), where it is called a number series (or just a series) Numbers, members of a series (depend on
Numerical series Numerical sequence Opr A numerical sequence is a numerical function defined on the set of natural numbers x - a common member of the sequence x =, x =, x =, x =,
Ch Power series a a a A series of the form a a a a a () is called a power series, where, a, are constants, called the coefficients of the series. Sometimes a power series of a more general form is considered: a a (a) a (a) a (a) (), where
Lecture 8 Series and singular points. Laurent series. Isolated singular points. 6. Series and singular points 6.7. Laurent Series Theorem (P. Laurent): If the function f() is analytic in the ring r< a < R r R то она может быть разложена
Federal Agency for Education Federal State Educational Institution of Higher Professional Education SOUTHERN FEDERAL UNIVERSITY R. M. Gavrilova, G. S. Kostetskaya Methodical
Topic 9 Power series A power series is a functional series of the form, while the numbers ... are the coefficients of the series, and the expansion point of the series., ..., ... R ... is called the center Power series The general term of the power series
4 Function series 4 Basic definitions Let an infinite sequence of functions with a common domain X u), u (), K, u (),K (DEFINITION Expression u) + u () + K + u () +
Lecture 3 Taylor and Maclaurin series Application of power series Expansion of functions into power series Taylor and Maclaurin series For applications, it is important to be able to expand a given function into a power series, those functions
Lecture 6 Expansion of a function in a power series Uniqueness of the expansion Taylor and Maclaurin series Expansion in a power series of some elementary functions Application of power series In previous lectures
Faculty of Metallurgy Department of Higher Mathematics
Laurent Series A more general type of power series are series containing both positive and negative powers of z z 0. Like Taylor series, they play an important role in the theory of analytic functions.
Series Numerical series General concepts Def If each natural number is assigned a certain number according to a certain law, then the set of numbered numbers is called a numerical sequence,
S A Lavrenchenko wwwlwrecekoru Lecture Functional series The concept of a functional series Previously, we studied number series, that is, the members of the series were numbers. Now we turn to the study of functional series, i.e.
Topic Laurent series and its domain of convergence. A series of the form where C (z z) n = C (z z) n + n n n= n= z of the plane, is a fixed point of the complex C n is called the Laurent series. C n (z z) n= - some complex
Lecture. functional rows. Function series definition A series whose members are functions of x is called a functional series: u = u (x) + u + K+ u + K = Giving x a certain value of x, we
THEORY OF SERIES The theory of series is the most important component of mathematical analysis and finds both theoretical and numerous practical applications. Distinguish between numerical and functional series.
Convergence radius Definition. A power series is a functional series of the form c 0 + c (t a) + c 2 (t a) 2 + + c (t a) + = c (t a), () where c 0, c, c 2,..., c, ... C are called the coefficients of the power
MOSCOW STATE TECHNICAL UNIVERSITY OF CIVIL AVIATION V.M. Lyubimov, E.A. Zhukova, V.A. Ukhova, Yu.A. Shurinov
82 4. Section 4. Functional and power series 4.2. Lesson 3 4.2. Lesson 3 4.2.. Taylor expansion of a function DEFINITION 4.2.. Let the function y = f(x) be infinitely differentiable in some neighborhood
Lecture. Power series. Harmonic analysis; series and Fourier transform. Orthogonality property.8. General functional series.8.. Evasion of functions A series U + U + U is called a functional series if its
Starkov V.N. Materials for the introductory lecture Question 9. Decomposition of analytic functions in power series Definition. A functional series of the form (((... (..., where the complex constants (coefficients of the series
Sgups Department of Higher Mathematics Guidelines for the implementation of a typical calculation "Rows" Novosibirsk 006 Some theoretical information Numerical series Let u ; u ; u ; ; u ; there is an infinite number
E occupation. Taylor rows. Summation of power series Mat. analysis, app. Mathematics, 3rd semester Find the expansion of a function into a power series in powers, calculate the radius of convergence of the power series: A f()
Chapter Series The formal notation of the sum of members of a certain numerical sequence Numerical series is called a numerical series Sums S are called partial sums of a series If there is a limit lim S, S then the series
Practice 8 Residue 8 Defining a Residue 8 Calculating Residue 8 Logarithmic Residue 8 Defining a Residue Let an isolated singular point of a function in an isolated singular Residue analytical
~ ~ FCF Derivative of a function of a complex variable FCF of the Cauchy-Riemann condition Concept of regularity of the FCF Depiction and form of a complex number Form of the FCF: where the real function of two variables is real
METHODOLOGICAL INSTRUCTIONS FOR CALCULATION TASKS ON THE COURSE OF HIGHER MATHEMATICS "ORDINARY DIFFERENTIAL EQUATIONS SERIES DOUBLE INTEGRALS" PART III THEME SERIES Contents Series Numerical series Convergence and divergence
Federal Agency for Education Arkhangelsk State Technical University Faculty of Civil Engineering SERIES Guidelines for completing assignments for independent work Arkhangelsk
ELEMENTS OF THE THEORY OF FUNCTIONS OF A COMPLEX VARIABLE OPERATIONAL CALCULUS
Mathematical analysis Part 3. Numerical and functional series. Multiple integrals. Field theory. textbook N.D.Vysk MATI-RGTU im. K.E. Tsiolkovsky Department of Higher Mathematics MATHEMATICAL ANALYSIS
Lecture 3. Deductions. The main residue theorem The residue of the function f () at an isolated singular point a is a complex number equal to the value of the integral f () 2 taken in the positive direction i along the circle
Numerical and power series Lesson. Number lines. Row sum. Convergence criteria. Calculate the sum of the series. 6 Decision. The sum of the terms of an infinite geometric progression q is, where q is the denominator of the progression.
S A Lavrenchenko wwwlawreceoru Lecture Representing functions by Taylor series One useful limit At the last lecture, the following strategy was developed: by a sufficient condition for the representability of a function,
MV Deikalova COMPLEX ANALYSIS Questions for the exam (group МХ-21, 215) Questions of the first colloquium 1 1. Differentiability of a function of a complex variable at a point. Conditions of Cauchy Riemann (D'Alembert Euler).
Option Task Calculate the value of the function and give the answer in algebraic form: a sh ; b l Solution a Let's use the relation formula between the trigonometric sine and the hyperbolic sine: ; sh -s Get
Lecture Numerical series Signs of convergence Number series Signs of convergence An infinite expression of a numerical sequence + + + +, composed of members of an infinite one, is called a numerical series
4. Functional series, area of convergence The area of convergence of a functional series () is the set of values of the argument for which this series converges. Function (2) is called the partial sum of the series;
Lecture 3 Existence and uniqueness theorem for a solution to a scalar equation Statement of the problem Main result Consider the Cauchy problem d f () d =, () =
MINISTRY OF EDUCATION AND SCIENCE OF THE RUSSIAN FEDERATION KAZAN STATE UNIVERSITY OF ARCHITECTURE AND CONSTRUCTION Department of Higher Mathematics NUMERICAL AND FUNCTIONAL SERIES Guidelines for
(functional series power series convergence region order of finding the convergence interval - example convergence interval radius examples) Let an infinite sequence of functions be given, Functional
S A Lavrenchenko wwwlawrecekoru Lecture Representation of functions by power series Introduction Representation of functions by power series is useful in solving the following problems: - integration of functions
E occupation. Power series. Taylor Series Mat. analysis, app. Mathematics, 3rd semester Find the radius of convergence of a power series using the d'Alembert criterion: (89 () n n (n!)) p (n +)! n= Taylor series f(x)
MINISTRY OF EDUCATION AND SCIENCE OF THE RUSSIAN FEDERATION
ROWS. Number lines. Basic definitions Let an infinite sequence of numbers be given The expression (infinite sum) a, a 2,..., a n,... a i = a + a 2 + + a n +... () i= is called a number series. Numbers
KAZAN STATE UNIVERSITY Department of Mathematical Statistics
Ministry of Education and Science of the Russian Federation VA Volkov SERIES OF THE FOURIER INTEGRAL Educational electronic text edition For students of specialties 4865 Electronics and automation of physical installations;
џ. The concept of a number series. Let a sequence of numbers a, a 2,..., a,... be given. A number series is an expression a = a + a 2 +... + a +... (.) Numbers a, a 2,.. ., a,... are called terms of the series, a
Methodical development Solving problems on TFKP Complex numbers Operations on complex numbers Complex plane A complex number can be represented in algebraic and trigonometric exponential
Siberian Mathematical Journal July August, 2005. Volume 46, 4 UDC 517.53 CONVERGENCE CONDITIONS FOR INTERPOLATION FRACTIONS AT KNOTS SEPARATED FROM FUNCTION SINGULAR POINTS AG Lipchinsky Abstract: Considered
MOSCOW AUTOMOBILE AND ROAD STATE TECHNICAL UNIVERSITY (MADI)
Standard methods, but reached a dead end with another example.
What is the difficulty and where can there be a snag? Let's put aside the soapy rope, calmly analyze the reasons and get acquainted with the practical methods of solution.
First and most important: in the vast majority of cases, to study the convergence of a series, it is necessary to apply some familiar method, but the common term of the series is filled with such tricky stuffing that it is not at all obvious what to do with it. And you go around in circles: the first sign does not work, the second does not work, the third, fourth, fifth method does not work, then the drafts are thrown aside and everything starts anew. This is usually due to a lack of experience or gaps in other sections of calculus. In particular, if running sequence limits and superficially disassembled function limits, then it will be difficult.
In other words, a person simply does not see the necessary solution due to a lack of knowledge or experience.
Sometimes “eclipse” is also to blame, when, for example, the necessary criterion for the convergence of the series is simply not fulfilled, but due to ignorance, inattention or negligence, this falls out of sight. And it turns out like in that bike where the professor of mathematics solved a children's problem with the help of wild recurrent sequences and number series =)
In the best traditions, immediately living examples: rows ![]() and their relatives - diverge, since in theory it is proved sequence limits. Most likely, in the first semester, you will be beaten out of your soul for a proof of 1-2-3 pages, but now it is quite enough to show that the necessary condition for the convergence of the series is not met, referring to known facts. Famous? If the student does not know that the root of the nth degree is an extremely powerful thing, then, say, the series
and their relatives - diverge, since in theory it is proved sequence limits. Most likely, in the first semester, you will be beaten out of your soul for a proof of 1-2-3 pages, but now it is quite enough to show that the necessary condition for the convergence of the series is not met, referring to known facts. Famous? If the student does not know that the root of the nth degree is an extremely powerful thing, then, say, the series ![]() put him in a rut. Although the solution is like two and two: , i.e. for obvious reasons, both series diverge. A modest comment “these limits have been proven in theory” (or even its absence at all) is quite enough for offset, after all, the calculations are quite heavy and they definitely do not belong to the section of numerical series.
put him in a rut. Although the solution is like two and two: , i.e. for obvious reasons, both series diverge. A modest comment “these limits have been proven in theory” (or even its absence at all) is quite enough for offset, after all, the calculations are quite heavy and they definitely do not belong to the section of numerical series.
And after studying the next examples, you will only be surprised at the brevity and transparency of many solutions:
Example 1
Investigate the convergence of a series
Solution: first of all, check the execution necessary criterion for convergence. This is not a formality, but a great chance to deal with the example of "little bloodshed".
"Inspection of the scene" suggests a divergent series (the case of a generalized harmonic series), but again the question arises, how to take into account the logarithm in the numerator?
Approximate examples of tasks at the end of the lesson.
It is not uncommon when you have to carry out a two-way (or even three-way) reasoning:
Example 6
Investigate the convergence of a series ![]()
Solution: first, carefully deal with the gibberish of the numerator. The sequence is limited: . Then: ![]()
Let's compare our series with the series . By virtue of the double inequality just obtained, for all "en" it will be true: ![]()
Now let's compare the series with the divergent harmonic series.
Fraction denominator less the denominator of the fraction, so the fraction itself – more fractions (write down the first few terms, if not clear). Thus, for any "en": ![]()
So, by comparison, the series ![]() diverges along with the harmonic series.
diverges along with the harmonic series.
If we change the denominator a little: ![]() , then the first part of the reasoning will be similar:
, then the first part of the reasoning will be similar: ![]() . But to prove the divergence of the series, only the limit test of comparison is already applicable, since the inequality is false.
. But to prove the divergence of the series, only the limit test of comparison is already applicable, since the inequality is false.
The situation with converging series is “mirror”, that is, for example, for a series, both comparison criteria can be used (the inequality is true), and for a series, only the limiting criterion (the inequality is false).
We continue our safari through the wild, where a herd of graceful and succulent antelopes loomed on the horizon:
Example 7
Investigate the convergence of a series
Solution: the necessary convergence criterion is satisfied, and we again ask the classic question: what to do? Before us is something resembling a convergent series, however, there is no clear rule here - such associations are often deceptive.
Often, but not this time. By using Limit comparison criterion Let's compare our series with the convergent series . When calculating the limit, we use wonderful limit ![]() , where as infinitesimal stands:
, where as infinitesimal stands: 
converges together with next to .
Instead of using the standard artificial technique of multiplication and division by a "three", it was possible to initially compare with a convergent series.
But here a caveat is desirable that the constant-multiplier of the general term does not affect the convergence of the series. And just in this style the solution of the following example is designed:
Example 8
Investigate the convergence of a series
Sample at the end of the lesson.
Example 9
Investigate the convergence of a series
Solution: in the previous examples, we used the boundedness of the sine, but now this property is out of play. The denominator of a fraction of a higher order of growth than the numerator, so when the sine argument and the entire common term infinitely small. The necessary condition for convergence, as you understand, is satisfied, which does not allow us to shirk from work.
We will conduct reconnaissance: in accordance with remarkable equivalence ![]() , mentally discard the sine and get a series. Well, something like that….
, mentally discard the sine and get a series. Well, something like that….
Making a decision:
Let us compare the series under study with the divergent series . We use the limit comparison criterion: 
Let us replace the infinitesimal with the equivalent one: for ![]() .
.

A finite number other than zero is obtained, which means that the series under study diverges along with the harmonic series.
Example 10
Investigate the convergence of a series
This is a do-it-yourself example.
For planning further actions in such examples, the mental rejection of the sine, arcsine, tangent, arctangent helps a lot. But remember, this possibility exists only when infinitesimal argument, not so long ago I came across a provocative series:
Example 11
Investigate the convergence of a series ![]() .
.
Solution: it is useless to use the limitedness of the arc tangent here, and the equivalence does not work either. The output is surprisingly simple: 
Study Series diverges, since the necessary criterion for the convergence of the series is not satisfied.
The second reason"Gag on the job" consists in a decent sophistication of the common member, which causes difficulties of a technical nature. Roughly speaking, if the series discussed above belong to the category of “figures you guess”, then these ones belong to the category of “you decide”. Actually, this is called complexity in the "usual" sense. Not everyone will correctly resolve several factorials, degrees, roots and other inhabitants of the savannah. Of course, factorials cause the most problems:
Example 12
Investigate the convergence of a series
How to raise a factorial to a power? Easily. According to the rule of operations with powers, it is necessary to raise each factor of the product to a power:
And, of course, attention and attention again, the d'Alembert sign itself works traditionally: 
Thus, the series under study converges.
I remind you of a rational technique for eliminating uncertainty: when it is clear order of growth numerator and denominator - it is not at all necessary to suffer and open the brackets.
Example 13
Investigate the convergence of a series
The beast is very rare, but it is found, and it would be unfair to bypass it with a camera lens.
What is double exclamation point factorial? The factorial "winds" the product of positive even numbers: 
Similarly, the factorial “winds up” the product of positive odd numbers: 
Analyze what is the difference between
Example 14
Investigate the convergence of a series
And in this task, try not to get confused with the degrees, wonderful equivalences And wonderful limits.
Sample solutions and answers at the end of the lesson.
But the student gets to feed not only tigers - cunning leopards also track down their prey:
Example 15
Investigate the convergence of a series ![]()
Solution: the necessary criterion of convergence, the limiting criterion, the d'Alembert and Cauchy criteria disappear almost instantly. But worst of all, the feature with inequalities, which has repeatedly rescued us, is powerless. Indeed, comparison with a divergent series is impossible, since the inequality ![]() incorrect - the multiplier-logarithm only increases the denominator, reducing the fraction itself
incorrect - the multiplier-logarithm only increases the denominator, reducing the fraction itself ![]() in relation to the fraction. And another global question: why are we initially sure that our series
in relation to the fraction. And another global question: why are we initially sure that our series ![]() is bound to diverge and must be compared with some divergent series? Does he fit in at all?
is bound to diverge and must be compared with some divergent series? Does he fit in at all?
Integral feature? Improper integral ![]() evokes a mournful mood. Now, if we had a row
evokes a mournful mood. Now, if we had a row ![]() … then yes. Stop! This is how ideas are born. We make a decision in two steps:
… then yes. Stop! This is how ideas are born. We make a decision in two steps:
1) First, we study the convergence of the series ![]() . We use integral feature:
. We use integral feature:![]()
Integrand continuous on

Thus, a number ![]() diverges together with the corresponding improper integral.
diverges together with the corresponding improper integral.
2) Compare our series with the divergent series ![]() . We use the limit comparison criterion:
. We use the limit comparison criterion:
A finite number other than zero is obtained, which means that the series under study diverges along with side by side ![]() .
.
And there is nothing unusual or creative in such a decision - that's how it should be decided!
I propose to independently draw up the following two-move:
Example 16
Investigate the convergence of a series ![]()
A student with some experience in most cases immediately sees whether the series converges or diverges, but it happens that a predator deftly disguises itself in the bushes:
Example 17
Investigate the convergence of a series ![]()
Solution: at first glance, it is not at all clear how this series behaves. And if we have fog in front of us, then it is logical to start with a rough check of the necessary condition for the convergence of the series. In order to eliminate uncertainty, we use an unsinkable multiplication and division method by adjoint expression:
The necessary sign of convergence did not work, but brought our Tambov comrade to light. As a result of the performed transformations, an equivalent series was obtained ![]() , which in turn strongly resembles a convergent series .
, which in turn strongly resembles a convergent series .
We write a clean solution:
Compare this series with the convergent series . We use the limit comparison criterion:
Multiply and divide by the adjoint expression:

A finite number other than zero is obtained, which means that the series under study converges together with next to .
Perhaps some have a question, where did the wolves come from on our African safari? Don't know. They probably brought it. You will get the following trophy skin:
Example 18
Investigate the convergence of a series ![]()
An example solution at the end of the lesson
And, finally, one more thought that visits many students in despair: instead of whether to use a rarer criterion for the convergence of the series? Sign of Raabe, sign of Abel, sign of Gauss, sign of Dirichlet and other unknown animals. The idea is working, but in real examples it is implemented very rarely. Personally, in all the years of practice, I have resorted to only 2-3 times sign of Raabe when nothing really helped from the standard arsenal. I reproduce the course of my extreme quest in full:
Example 19
Investigate the convergence of a series
Solution: Without any doubt a sign of d'Alembert. In the course of calculations, I actively use the properties of degrees, as well as second wonderful limit:
Here's one for you. D'Alembert's sign did not give an answer, although nothing foreshadowed such an outcome.
After going through the manual, I found a little-known limit proven in theory and applied a stronger radical Cauchy criterion:
Here's two for you. And, most importantly, it is not at all clear whether the series converges or diverges (an extremely rare situation for me). Necessary sign of comparison? Without much hope - even if in an unthinkable way I figure out the order of growth of the numerator and denominator, this still does not guarantee a reward.
A complete d'Alembert, but the worst thing is that the series needs to be solved. Need to. After all, this will be the first time that I give up. And then I remembered that there seemed to be some more powerful signs. Before me was no longer a wolf, not a leopard and not a tiger. It was a huge elephant waving a big trunk. I had to pick up a grenade launcher:
Sign of Raabe
Consider a positive number series.
If there is a limit  , That:
, That:
a) At a row diverges. Moreover, the resulting value can be zero or negative.
b) At a row converges. In particular, the series converges for .
c) When Raabe's sign does not give an answer.
We compose the limit and carefully simplify the fraction: 
Yes, the picture is, to put it mildly, unpleasant, but I was no longer surprised. lopital rules, and the first thought, as it turned out later, turned out to be correct. But first, for about an hour, I twisted and turned the limit using “usual” methods, but the uncertainty did not want to be eliminated. And walking in circles, as experience suggests, is a typical sign that the wrong way of solving has been chosen.
I had to turn to Russian folk wisdom: "If nothing helps, read the instructions." And when I opened the 2nd volume of Fichtenholtz, to my great joy I found a study of an identical series. And then the solution went according to the model.