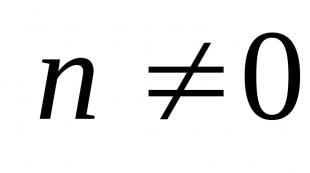Mat analysis function. Mathematical analysis. See what "mathematical analysis" is in other dictionaries
Compiled by Yu.V.Obrubov
Kaluga - 2012
Introduction to mathematical analysis.
Real numbers. Variables and constants.
One of the basic concepts of mathematics is number.
Positive numbers 1,2,3, ..., which are obtained by counting, are called natural.
The numbers ... -3, -2, -1,0,1,2,3, ... are called integers. Numbers that can be represented as a finite ratio of two integers ( 
) are called rational.
These include whole and fractional, positive and negative numbers. Numbers that can be represented as infinite non-repeating fractions are called irrational.
Examples of irrational numbers are 
,
. In the set of irrational numbers, they distinguish transcendental
numbers. These are numbers that are the result of non-algebraic operations. The most famous of these are the number 
and non-peer number 
. Rational and irrational numbers are called valid
. Real numbers are represented by dots on the number line. Each point on the number axis corresponds to one single real number and, conversely, to each real number there corresponds a single point on the number axis. Thus, a one-to-one correspondence has been established between the real numbers and the points of the number line. This makes it possible to use the terms “number a” and “point a” interchangeably.
In the process of studying various physical, economic, social processes, one often has to deal with quantities representing the numerical values of the parameters of the phenomena under study. At the same time, some of them change, while others retain their values.
variable
A quantity that takes on various numerical values is called. A quantity whose numerical value does not change in a given problem or experiment is called constant.
Variables are usually denoted by Latin letters 
and permanent 
.
variable 
is considered given if the set of values that it can take is known. This set is called the range of the variable.
There are various kinds of sets of values of a numerical variable.
interval
is the set of x values enclosed between the numbers a and b, while the numbers a and b do not belong to the set under consideration. The interval is denoted by: (a,b);a segment
is called the set of x values enclosed between the numbers a and b, while the numbers a and b belong to the set under consideration. The segment is denoted by ,a≤x≤b. The set of all real numbers is an open interval. Denoted: (- ∞,+ ∞), -∞<х <+∞, R. Neighborhood of point x
0
an arbitrary interval (а, b) containing a point x 0 is called, all points of this interval satisfy the inequality a ε
- neighborhood of point a
is an interval centered at the point a satisfying the inequality a–ε Function is one of the basic concepts of mathematical analysis. Let X and Y be arbitrary sets of real numbers. If each number x X, according to some rule or law, is assigned a unique well-defined real number yY, then they say that function
with the domain of definition X and the set of values Y. Designate y \u003d f (x). The variable x is called argument
functions. In the definition of a function, two points are essential: an indication of the domain of definition and the establishment of a correspondence law. Scope of definition
or area of existence
A function is a set of argument values for which the function exists, that is, it makes sense. Change area
The function is called the set of values y that it takes for the admissible values of x. Ways to set a function.
Analytical way of defining a function. With this method of setting the function, the correspondence law is written as a formula (analytical expression) indicating by what mathematical transformations, using the known value of the argument x, you can find the corresponding value of y. A function can be defined by a single analytic expression over its entire domain of definition or represent a collection of several analytic expressions. For example: y \u003d sin (x 2 + 1) 2. Tabular way of setting a function As a result of direct observation or experimental study of a phenomenon or process, the values of the argument x and the corresponding values of y are written out in a certain order. This table defines the function y of x. An example of a tabular way of specifying a function can be tables of trigonometric functions, tables of logarithms, dates and exchange rates, temperature and humidity, etc. 3. Graphical way of setting the function. The graphical way to set the function is to display points (x, y) on the coordinate plane by means of technical devices. The graphical method of specifying a function in mathematical analysis is not used, but a graphical illustration of analytically given functions is always resorted to. Everything should be stated as simply as possible, but not simpler. Our journey begins with a fictional character we will call John Doe. He is an average worker who can be easily found in any city in the world. Almost every day, John wakes up to loud alarms and drives to work in his car. He takes the elevator up to his office, where he boots up the computer and enters his username and password. John does all these things without the slightest idea how they work. Perhaps he would be interested to learn about how the devices and devices that he uses daily are arranged and function, however, he has neither the time nor the strength to do this. He considers cars, elevators, computers and alarm clocks to be completely different and complex mechanisms that have nothing in common. According to John, it takes years of study to understand how each of them works. Some people see things a little differently than our John Doe. They know that electric motors in elevator installations are very similar to car alternators. They know that the programmable logic controller that controls the electric motor that is responsible for moving the elevator is very similar to a John Doe work computer. They know that at a fundamental level, the PLC, alarm clock, and computer are based on relatively simple transistor theory. What John Doe and the average person find incredibly complex is the most common use of simple mechanical and electrical principles by a hacker. The problem is how these principles are applied. Abstracting fundamental principles from complex ideas allows us to understand and simplify them in a way that does justice to Albert Einstein's impromptu advice quoted above. Many of us view calculus as something complex. (John Doe considers the principle of the device and functioning of various mechanisms to be the same.) You see a heap of complex, intricate things. In order to understand them, you need a lot of time and effort. But what if we told you that mathematical analysis (calculus) is not as complicated as it seems at first glance, as well as most mechanisms? That there are a few basic principles that everyone is given to understand, and as soon as you do this, you will have a new perspective on the world and how it works? A typical calculus textbook contains about one thousand pages. A typical John Doe will see in it a thousand difficult things to understand and study, and a hacker will see two basic principles (derivative and integral) and 998 examples of these principles. Together we will try to figure out what these principles are. Based on the work done by Michael Starbird, a professor at the University of Texas at Austin, we will use everyday examples that anyone can understand. Mathematical analysis reveals the special beauty of our world - the beauty that occurs when you are able to observe it dynamically, not statically. We hope that everything will work out for you. Before we begin, I would like to briefly go through the history of the emergence of calculus, the roots of which lie in a very careful analysis of change and movement. Zeno's paradox Zeno of Elea is a philosopher who lived in the 4th century BC. He raised several subtle but profound paradoxes, two of which eventually led to the birth of calculus. In order to solve the paradoxes of Zeno, mankind took more than two thousand years. As you can imagine, it was not easy. The difficulties were largely related to the idea of infinity. What is the problem of infinity from a mathematical point of view? In the 17th century, Isaac Newton and Gottfried Leibniz managed to solve Zeno's paradoxes and create mathematical analysis. Let's take a closer look at these paradoxes to understand why there has been so much hype around them. Arrow Imagine an arrow flying through the air. We can say with great certainty that the arrow is in motion. Now consider the arrow at a certain point in time. She no longer moves, but is at rest. But we know for sure that the arrow is in motion, then how can it be at rest?! This is the essence of this paradox. It may seem silly, but in reality it is a very complex concept that should be considered from a mathematical point of view. Later we will find out that we are dealing with the concept of an instantaneous rate of change, which we will associate with the idea of one of the two principles of mathematical analysis (calculus) - the derivative. This will allow us to calculate the speed of the arrow at a certain point in time - something that mankind has not been able to do for more than two millennia. Dichotomy Let's look at that same arrow again. This time, imagine that it flies in our direction. Zeno argued that we should not move, since the arrow could never hit us. Imagine that after the arrow is in the air, it needs to cover half the distance between the bow and the target. Once she reaches a certain point halfway, she will again need to cover half the distance - this time between this point and the target. Imagine if we continue to do so. The arrow thus constantly travels half the distance between the reference point and the target. Given this, we can conclude that the arrow will never be able to hit us! In real life, the arrow will eventually hit its target, leaving us wondering what the paradox means. As in the case of the first paradox, we will later consider how to solve this problem using one of the principles of mathematical analysis - the integral. The integral allows us to view the concept of infinity as a mathematical function. It is an extremely powerful tool, according to scientists and engineers. Two basic principles of calculus The essence of the two fundamental principles of mathematical analysis can be demonstrated by applying them to solve Zeno's paradoxes. Derivative. The derivative is a method that will allow us to calculate the speed of the arrow in the Arrow paradox. We do this by analyzing the position of the arrow at successively decreasing time intervals. The exact speed of the arrow will become known when the time between measurements turns out to be infinitely small. Integral. The integral is a method that will allow us to calculate the position of the arrow in the Dichotomy paradox. We will do this by analyzing the speed of the arrow through successively decreasing intervals of time. We will know the exact position of the arrow when the time between measurements turns out to be infinitely small. It is easy to see some similarities between the derivative and the integral. Both values are calculated during the analysis of the position or speed of the boom at gradually decreasing time intervals. Later we will find out that the integral and the derivative are, in fact, two sides of the same ceramic capacitor. Why should we study the basics of calculus? We all know Ohm's Law, which links current, voltage, and resistance into one simple equation. Now let's look at Ohm's Law using the example of a capacitor. The current strength of a capacitor depends on voltage and time. Time in this case is a critical variable and must be taken into account in any dynamic event. Mathematical analysis allows us to understand and appreciate how things change over time. In the case of a capacitor, the current is equal to the capacitance times volts per second, or i = C(dv/dt), where: i - current strength (instantaneous); In this circuit, there is no electric current in the capacitor. The voltmeter will show battery voltage, but the ammeter will show nothing. The voltage will not change as long as the potentiometer remains intact. In this case, i = C(0/dt) = 0 amer. But what happens if we start adjusting the potentiometer? Judging by the equation, the resulting current strength will appear in the capacitor. This current will depend on the change in voltage, which is related to how fast the potentiometer is moved. These graphs show the relationship between the voltage in the capacitor, the current and the speed at which we turn the potentiometer. We do it slowly at first. An increase in speed leads to a change in voltage, which, in turn, provokes a sharp increase in current. At all stages, the current in the capacitor is proportional to the rate of change of voltage in it. Mathematical analysis, or more precisely, the derivative, gives us the ability to determine the rate of change, so that we know exactly the value of the current in the capacitor at a certain point in time. Similarly, we can calculate the instantaneous speed of Zeno's arrow. This is an incredibly powerful tool that should be in your arsenal. The material was prepared specifically for the site - according to the article of the site hackaday.com P.S. My name is Alexander. This is my personal, independent project. I am very glad if you liked the article. Want to help the site? Just look below for an ad for what you've recently been looking for. Copyright site © - This news belongs to the site, and are the intellectual property of the blog, protected by copyright law and cannot be used anywhere without an active link to the source. Read more - "About Authorship" Are you looking for this? Perhaps this is what you could not find for so long? MATHEMATICAL ANALYSIS part of mathematics, in which functions and their generalizations are studied by the method limits. The concept of a limit is closely connected with the concept of an infinitesimal quantity; therefore, one can also say that M. a. studies functions and their generalizations by the infinitesimal method. Name "M. a." - an abbreviated modification of the old name of this part of mathematics - "Infinitesimal analysis"; the latter reveals the content more fully, but it is also abbreviated (the title "Analysis by means of infinitesimals" would characterize the subject more accurately). In classical M. and. the objects of study (analysis) are primarily functions. "First of all" because the development of M. a. led to the possibility of studying by its methods more complex formations than - functionals, operators, etc. In nature and technology, movements and processes are found everywhere, to-rye are described by functions; the laws of natural phenomena are also usually described by functions. Hence the objective importance of M. a. as a means of learning functions. M. a. in the broad sense of the term, covers a very large part of mathematics. It includes differential, integral calculus, functions of a complex variable theory, theory ordinary differential equations, theory partial differential equations, theory integral equations, calculus of variations, functional analysis and some other mathematical disciplines. Modern number theory And probability theory apply and develop methods M. and. Nevertheless, the term M. a. often used to name only the foundations of mathematical analysis that combine the theory real number, theory of limits, theory rows, differential and integral calculus and their immediate applications, such as the theory of maxima and minima, the theory implicit functions, Fourier series, Fourier integrals. Function. In M. a. proceed from the definition of a function according to Lobachevsky and Dirichlet. If for each number xz of a certain set of Fnumbers, by virtue of the k.-l. law is listed among y, then this defines the function from one variable X. The function is defined similarly from variables, where x=(x 1 , ..., x n) -
point of n-dimensional space; consider also the functions from points x=(x 1 , X 2 ,
...) of some infinite-dimensional space, which, however, are more often called functionals. elementary functions. Fundamental value in M. and. play elementary functions. In practice, they mainly operate with elementary functions, they approximate functions of a more complex nature. Elementary functions can be considered not only for real, but also for complex x; then the ideas about these functions become complete in a certain sense. In this regard, an important branch of M. a., called. the theory of functions of a complex variable, or the theory analytical functions. Real number. The concept of a function is essentially based on the concept of a real (rational and irrational) number. It finally took shape only at the end of the 19th century. In particular, a logically flawless connection has been established between numbers and geometric points. straight line, which led to the formal substantiation of the ideas of R. Descartes (R. Descartes, mid-17th century), who introduced rectangular coordinate systems into mathematics and the representation of functions in them by graphs. Limit. In M. a. the method of studying functions is . Distinguish between the limit of a sequence and the limit of a function. These concepts were finally formed only in the 19th century, although other Greeks had an idea of them. scientists. Suffice it to say that Archimedes (3rd century BC) was able to calculate the segment of a parabola by a process we would call the passage to the limit (cf. exhaustion method). Continuous functions. An important function studied in M. a., form continuous functions. One of the possible definitions of this concept: function y=f(x).from one variable X, given on the interval ( a, b),
called continuous at a point X, If The function is continuous on the interval ( a, b),
if it is continuous at all its points; then it is a curve, continuous in the everyday sense of the word. Derivative and . Among continuous functions, one should single out functions that have derivative. Function derivative at a point has the rate of its change at this point, i.e., the limit If we have the coordinate of a point moving along the y-axis in time X, then f "(x). is the instantaneous speed of a point at a time X. By the sign of the derivative f "(x) .
judge the nature of the change in f (x): if f "(z)> 0 ( f"(x) <0
).
on the interval ( c, d), then the function / increases (decreases) on this interval. If the function / at the point x reaches a local extremum (maximum or minimum) and has a derivative at this point, then the latter is equal to zero at this point f "(x 0) \u003d 0. Equality (1) can be replaced by the equivalent equality where is an infinitesimal when, i.e., if the function f has a derivative at the point X, then its increment at this point is decomposed into two terms. Of these, the first is from (proportional), the second - tends to zero faster than Value (2) ref. differential functions corresponding to the increment At small can be considered approximately equal to dy: The above reasoning about the differential is characteristic of M. a. They extend to functions of many variables and to functionals. For example, if the function from variables has continuous partial derivatives at the point x=(x 1 , ... , x n), then its increment
corresponding to increments of independent variables can be written as where at i.e. if all Here the first term on the right side of (3) is the differential dz functions f. It depends linearly on and the second term tends to zero at faster than Let it be given (see art. Calculus of variations) extended to function classes x(t) ,
having a continuous derivative on the interval and satisfying the boundary conditions x( t0)\u003d x 0, x( t1)=x l , Where x 0, x 1 - given numbers; let, further, be the class of the function h(t) ,
having a continuous derivative on and such that h( t0)=h(t1)=0. Obviously if In the calculus of variations, it is proved that, under certain conditions on L, the increment of the functional J(x) can be written as at where and thus the second term on the right side of (4) tends to zero faster than ||h||, and the first term depends linearly on The first term in (4) is called. variation of the functional and is denoted by dJ( x, h). Integral. Along with the derivative, it is of fundamental importance in M. a. There are indefinite and definite integrals. The indefinite integral is closely related to the antiderivative function. The function F(x). antiderivative of the function f on the interval ( a, b) if on this interval F"(x) =f(x). The definite integral (Riemann) of the function / on the interval [ a, b] there is a limit If the function f is positive and continuous on the segment [ a, b],
then the integral of it on this segment is equal to the area of the figure bounded by the curve y=f(x), axis Oh and direct x=a, x=b. The class of Riemann-integrable functions contains all continuous on [ a, b]functions and some discontinuous functions. But they are all necessarily limited. For unbounded functions that do not grow very quickly, and also for certain functions given on infinite intervals, one introduces the so-called improper integrals, requiring a double passage to the limit for their definition. The concept of the Riemann integral for a function of one variable extends to functions of many variables (see Multiple integral). On the other hand, M.'s needs and. led to a generalization of the integral in a completely different direction, meaning Lebesgue integral or more general Lebesgue-Stieltjes integral. Essential in the definition of these integrals is the introduction for certain sets, called measurable ones, of the concept of their measure and, on this basis, of the concept of a measurable function. For measurable functions and the Lebesgue-Stieltjes integral is introduced. In this case, a wide range of different measures and the corresponding classes of measurable sets and functions are considered. This makes it possible to adapt this or that integral to a certain specific problem. Newton-Leibniz formula. There is a connection between the derivative and the integral, expressed by the formula (theorem) of Newton - Leibniz Here f(x) is continuous on [ a, b] function, a F(x) -
her prototype. Formula and Taylor. Along with the derivative and the integral, the most important concept (research tool) in mathematical analysis. are Taylor p Taylor series. If the function f(x) , a called its Taylor polynomial (degrees n). x-x 0: (Taylor formula); while the approximation error tends to zero at faster than Thus, the function f (x). in the vicinity of the point x 0 can be approximated with any degree of accuracy by a very simple function (polynomial), requiring only arithmetic for its calculation. operations - addition, subtraction and multiplication. Of particular importance are the so-called functions that are analytic in a certain neighborhood x 0 and have an infinite number of derivatives, such that for them in this neighborhood at they can be represented as an infinite Taylor power series: Taylor expansions under certain conditions are also possible for functions of many variables, as well as for functionals and operators. Historical reference. Until the 17th century M. a. was a set of solutions to disparate particular problems; for example, in integral calculus, these are tasks for calculating the areas of figures, the volumes of bodies with curved boundaries, the work of a variable force, etc. Each task or particular problem was solved by its own method, sometimes complex and cumbersome (for the prehistory of M. a. see. article Infinitesimal calculus),
M. a. as a single and systematic. the whole was formed in the works of I. Newton (I. Newton), G. Leibniz (G. Leibniz), L. Euler (L. Euler), J. Lagrange (J. Lagrange) and other scientists of the 17th-18th centuries, and his - the theory of limits - was developed by O. Komi (A. Cauchy) in the beginning. 19th century Deep analysis of the initial concepts of M. a. was associated with development in the 19th and 20th centuries. set theory, measure theory, theory of functions of a real variable and led to various generalizations. Lit.: La V a l l e - P u s s e n S.-J. e, A course in the analysis of infinitesimals, trans. from French, vol. 1-2, Moscow, 1933; Ilyin V. A., Poznyak E. G., Fundamentals of Mathematical Analysis, 3rd ed., Part 1, M., 1971; 2nd ed., part 2, M., 1980; And l and N V. A., Sadovnichiy V. A., Seidov B. Kh., Mathematical analysis, M., 1979; K u d r i v e in L. D., Mathematical analysis, 2nd ed., vol. 1-2, M., 1973; Nikolsky S. M., Course of mathematical analysis, 2nd ed., vol. 1-2, M., 1975; Uitteker E. T., W a t s o n J. N., Course of modern analysis, trans. from English, part 1-2, 2nd ed., M., 1962-63; F and kht n o l ts G. M., Course of differential and integral calculus, 7th ed., vol. 1-2, M., 1970; 5th ed., vol. 3, M., 1970. S. M. Nikolsky. Mathematical encyclopedia. - M.: Soviet Encyclopedia. I. M. Vinogradov. 1977-1985. MATHEMATICAL ANALYSIS, a set of branches of mathematics devoted to the study of functions by methods of differential calculus and integral calculus ... Modern Encyclopedia A set of branches of mathematics devoted to the study of functions by methods of differential and integral calculus. The term is more pedagogical than scientific: courses in mathematical analysis are taught in universities and technical schools ... Big Encyclopedic Dictionary English mathematical analysis; German mathematical analysis. Branch of mathematics devoted to the study of functions by methods of differential and integral calculus. Antinazi. Encyclopedia of Sociology, 2009 ... Encyclopedia of Sociology Exist., number of synonyms: 2 matan (2) mathematical analysis (2) ASIS synonym dictionary. V.N. Trishin. 2013 ... Synonym dictionary MATHEMATICAL ANALYSIS- MATHEMATICAL ANALYSIS. A set of branches of mathematics devoted to the study of mathematical functions by methods of differential and integral calculus. Use of methods M. and. is an effective means of solving the most important ... ... A new dictionary of methodological terms and concepts (theory and practice of teaching languages) mathematical analysis- — EN mathematical analysis The branch of mathematics most explicitly concerned with the limit process or the concept of convergence; includes the theories of differentiation,… … Technical Translator's Handbook Mathematical analysis- MATHEMATICAL ANALYSIS, a set of sections of mathematics devoted to the study of functions by methods of differential calculus and integral calculus. … Illustrated Encyclopedic Dictionary “... if I had to create a mechanism for the sole purpose of destroying the natural curiosity of the child and his love of modeling, I would hardly have done better than it has already been implemented - I simply would not have enough imagination to compete with such insensitive, dull ideas which are embodied in modern methods of studying mathematics. Think of studying fine art like this: Kids, no drawing in kindergarten. Instead, let's study the chemistry of paint products, the physics of light, and the anatomy of the eye. After 12 years of studying these aspects, if children (more precisely already teenagers) still do not hate art, they can start drawing on their own. Ultimately, they now have a solid foundation in order to begin to respect the art. Right? Also with poetry. Imagine studying this quote (formula): “But the main thing: be true to yourself; Then, just as night follows day, You will not betray others.” -William Shakespeare, Hamlet It's an elegant way of saying "be yourself" (and if that means writing about math disrespectfully, so be it). But if we were considering poetry in a math class, instead of looking for meaning, we would be counting the number of syllables, analyzing iambic pentameter, marking nouns, verbs and adjectives. Mathematics and poetry are like different ways to explain, to characterize the same thing. Formulas are a means to an end, a way of expressing mathematical truth. We have forgotten that mathematics operates with ideas, it is not the mechanical manipulation of the formulas that express these ideas. Here's what I won't do: I won't retell textbooks that I've already written. If you need answers here and now, there are tons of websites, video tutorials and 20 minutes to help. Instead, let's master the basics of calculus. Equations are not enough - I want moments of insight so that you really see their meaning and understand the language of mathematics. Formal mathematical language is simply a way of communicating. Graphs, informative animations, and plain language can provide more insight than a page of abstruse evidence. I think that anyone can understand the basic principles of calculus. We don't have to be poets to enjoy the works of Shakespeare. It will be much easier for you if you know algebra and are interested in mathematics. Not so long ago, reading and writing were the work of specially trained scribes. And today any 10-year-old child can do it. Why? Because we expect it. Expectations play a huge role in developing opportunities. So expect calculus to be just another subject. Some people get down to the smallest details (writers/mathematicians). But the rest of us can just admire what is happening and try to understand it. I would like everyone to master the basic concepts of mathematical analysis and say “Wow!”. This was a simple example, but did you get the main idea? We took the disc, divided it, and put the pieces together in a slightly different way. Mathematical analysis showed that the disk and the ring are closely related to each other: the disk is really a set of rings. This is a very popular topic in calculus: Big things are made up of smaller things. And sometimes it is with these small objects that it is easier and clearer to work. Many examples in calculus are based on physics. This, of course, is wonderful, but it can be difficult to perceive them: honestly, it is far from always possible to keep in mind various physical formulas, such as the formula for the speed of an object. I like to start with simple visual examples because that's how our brains work. The ring/circle we've been investigating - you could model the same thing with several pieces of tubes of different diameters: split them up, align them, and lay them in a rough triangle to make sure the math really works. With a simple physical formula, this is unlikely to be done. I feel pedantic mathematicians burning their keyboards. Therefore, I will insert just a few words about "strictness". Do you know that we don't teach calculus the way Newton or Leibniz discovered it? They used the intuitive ideas of "flux" and "infinitely small" which were replaced by limits because "Of course it works in practice. But does it work in theory? We have created complex mechanical models to "exactly" prove calculus, but we have lost our intuition in the process of such proofs. We look at the sweetness of sugar in terms of brain chemistry, instead of explaining it in the language of science “Sugar has a lot of energy. Eat it." I don't want (and can't) teach calculus to students or train scientists. But would it be bad if everyone could understand calculus at the "imprecise" level at which Newton understood it? For it to also change the world for you, as it once did for him? Premature focus on precision disperses students and makes math difficult to learn. Here's a good example: the number e is technically defined by a limit, but it was discovered precisely with the help of an intuitive guess about growth. The natural logarithm can look like an integral, or a time to grow. Which explanations are best for beginners? Let's draw a little by hand, and immerse ourselves in chemistry along the way. Happy computing. (P.S: One kind reader created an animated powerpoint slideshow that helps to present this idea more visually (it is better to watch it in PowerPoint, animations will be visible there). Thank you!) According to the dictionary of the Russian language analysis- this is a method of scientific research by considering individual aspects, properties, components of something. One of the most important branches of mathematics is called mathematical analysis and often even just analysis. The question immediately arises: what exactly is analyzed by mathematical analysis? The answer is clear - functions are analyzed. Function(from the Latin "function" - implementation) represents the relationship between variable numerical values. Since analysis is a research method, a second question arises: what is this method? The answer gives the second name of mathematical analysis - differential and integral calculus. Calculus is a branch of mathematics that lays down the rules for computing. Word " differential" comes from the Latin word "differentiation", i.e. difference. Word " integral” does not have such a clear origin (“integrator” - whole; “integro” - restore), but it has the meaning of combining parts into a whole, restoring broken into differences. This recovery is achieved with summation. Let's sum up the first results: · main objects studied in mathematical analysis are the functions. · Functions are dependencies of various types between variable numerical values. · The method of mathematical analysis is differentiation– work with differences of function values, and integration- calculation of sums. Thus, to master mathematical analysis, first of all, you need to understand the concept of a function. Function is the most important mathematical concept because functions are a mathematical way of describing movement and change. Function is a process. The most important type of movement is mechanical movement in a straight line. When moving, the distances traveled by the object are measured, but this is clearly not enough to fully describe the movement. Both Achilles and the tortoise can move the same distance from the starting point, but their movement differs in speed, and speed cannot be measured without measuring time. Already from the consideration of this example, it becomes clear that one variable is not enough to describe movement and change. It is intuitively clear that time changes uniformly, while distance can change either faster or slower. The movement is completely described if at each moment of time it is known how far the object has moved away from the starting point. So, during mechanical movement, there is a correspondence between the values of two variables - time, which changes independently of anything, and distance, which depends on time. This fact is the basis for the definition of the function. The two variables are no longer called time and distance. Function definition: function – is it a rule or a law, putting each value of the independent variable X
a certain value of the dependent variable at
. Independent variable X
is called an argument, and the dependent at
- function. It is sometimes said that a function is a relationship between two variables. How to visualize what a variable is? A variable is a number line (ruler or scale) along which a point (a thermometer or a needle with a bead) moves. A function is a mechanism of gears with two windows x and y. This mechanism allows you to install in the window X
any value, but in the box at
the value of the function will automatically appear with the help of gears. Task 1. The patient's temperature is measured every hour. There is a function - the dependence of temperature on time. How to present this feature? Answer: table and graph. The function is continuous, like motion is continuous, but in practice it is impossible to fix this continuity. You can only catch single argument and function values. However, it is still possible to describe continuity theoretically. Task 2. Galileo Galilei discovered that a freely falling body travels a distance unit in the first second, 3 units in the second, 5 units in the third, etc. Determine the dependence of time on distance. indication: Derive the general formula for the relationship between the distance traveled and the distance number. Ways to set functions. Problems of mathematical analysis. Transition from one representation of a function to another (calculation of function values, construction of approximate analytical functions from experimental numerical and graphical data, research of functions and plotting). Mathematical study of the properties of a function as a process. Example 1: search for speed from a known path function of time (differentiation). Example 2: Finding a path using a known function of speed versus time (integration).Function. Basic definitions and concepts.
Albert Einstein
C - capacitance, which is measured in farads;
dv - voltage change;
dt is the change in time. 
See what "MATHEMATICAL ANALYSIS" is in other dictionaries:
Well, this is all clear, so what is your great idea?
But math is hard!
So what is math analysis about?
A few examples
A bit about mathematical rigor (for fanatics of this science)
|
next lecture ==>
Creativity: Notebooks are checked by x (who?) teacher |
