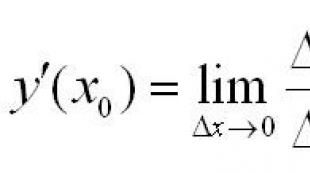Рассмотрим операционный метод решения дифференциальных уравнений на примере уравнения третьего порядка.

Пусть требуется найти частное решение линейного дифференциального уравнения третьего порядка с постоянными коэффициентами

удовлетворяющее начальным условиям:

с 0, с 1 , с 2 - заданные числа.

Пользуясь свойством дифференцирования оригинала, запишем:

В уравнении (6.4.1) перейдем от оригиналов к изображениям

Полученное уравнение называют операторным или уравнением в изображениях. Разрешают его относительно Y.

Алгебраические многочлены от переменной р.

Равенство называют операторным решением дифференциального уравнения (6.4.1).

Находя оригинал y(t) , соответствующий найденному изображению получаем частное решение дифференциального уравнения.

Пример: методом операционного исчисления найти частное решение дифференциального уравнения, удовлетворяющее заданным начальным условиям

Перейдем от оригиналов к изображениям

Запишем исходное уравнение в изображениях и решим его относительно Y

Чтобы найти оригинал полученного изображения, знаменатель дроби разложим на множители и запишем полученную дробь в виде суммы простейших дробей.

Найдем коэффициенты А, В, и С .

Пользуясь таблицей запишем оригинал полученного изображения

Частное решение исходного уравнения.

Аналогично применяется операционный метод для решения систем линейных дифференциальных уравнений с постоянными коэффициентами

Неизвестные функции.

Переходим к изображениям

Получаем систему изображающих уравнений

Решаем систему методом Крамера. Находим определители:

Находим решение изображающей системы X(p), Y(p) , Z(p).

Получили искомое решение системы

С помощью операционного исчисления можно находить решения линейных дифференциальных уравнений с переменными коэффициентами, уравнений в частных производных; вычислять интегралы. При этом решение задач значительно упрощается. Применяется при решении задач уравнений математической физики.

Вопросы для самоконтроля.

1. Какая функция называется оригиналом?

2. Какая функция называется изображением оригинала?

3. Функция Хевисайда и ее изображение.

4. Получить изображение для функций оригиналов, пользуясь определением изображения: f(t) =t , .

5. Получить изображения для функций , пользуясь свойствами преобразований Лапласа.

6. Найти функции оригиналы, пользуясь таблицей изображений: ;

7. Найти частное решение линейного дифференциального уравнения методами операционного исчисления.

Литература: стр. 411-439, стр. 572-594.

Примеры: стр. 305-316.

ЛИТЕРАТУРА

1. Данко П.Е. Высшая математика в упражнениях и задачах. В 2 –х ч. Ч. I: Учеб. пособие для втузов./П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова – М.: Высш. шк., 1997.– 304с.

2. Данко П.Е. Высшая математика в упражнениях и задачах. В 2 –х ч. Ч. II: Учеб. пособие для втузов./ П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова – М.: Высш. шк., 1997.– 416с.

3. Каплан И.А. Практические занятия по высшей математике. Часть 4./ И.А. Каплан - Издательство Харьковского государственного университета, 1966 г., 236 с.

4. Пискунов Н.С. Дифференциальное и интегральное исчисления. В 2-х томах, том 1: учеб. пособие для втузов./ Н.С. Пискунов – М.: изд. «Наука», 1972 .– 456 с.

5. Пискунов Н.С. Дифференциальное и интегральное исчисления для втузов. В 2-х томах, том 2: учеб. Пособие для втузов../ Н.С. Пискунов –М.: изд. «Наука»,1972 .– 456 с.

6. Письменный Д.Т. Конспект лекций по высшей математике: полный курс.–4-е изд./ Д.Т. Письменный –М.: Айрис-пресс, 2006.–608 с. – (Высшее образование).

7. Слободская В.А. Краткий курс высшей математики. Изд. 2-е, переработ. и доп. Учеб. пособие для втузов./ В.А. Слободская – М.: Высш. шк., 1969.– 544с.

© Ирина Александровна Драчева

Конспект лекций Высшая математика

для студентов направления 6.070104 «Морской и речной транспорт»

специальности «Эксплуатация судовых энергетических установок»

дневной и заочной формы обучения 2 курс

Тираж______экз. Подписано к печати ______________

Заказ №__________. Объем__2,78__п.л.

Изд-во «Керченский государственный морской технологический университет»

98309 г. Керчь, Орджоникидзе, 82

На дворе знойная пора, летает тополиный пух, и такая погода располагает к отдыху. За учебный год у всех накопилась усталость, но ожидание летних отпусков/каникул должно воодушевлять на успешную сдачу экзаменов и зачетов. По сезону тупят, кстати, и преподаватели, поэтому скоро тоже возьму тайм-аут для разгрузки мозга. А сейчас кофе, мерный гул системного блока, несколько дохлых комаров на подоконнике и вполне рабочее состояние… …эх, блин,… поэт хренов.

К делу. У кого как, а у меня сегодня 1 июня, и мы рассмотрим ещё одну типовую задачу комплексного анализа – нахождение частного решения системы дифференциальных уравнений методом операционного исчисления . Что необходимо знать и уметь, чтобы научиться её решать? Прежде всего, настоятельно рекомендую обратиться к уроку. Пожалуйста, прочитайте вводную часть, разберитесь с общей постановкой темы, терминологией, обозначениями и хотя бы с двумя-тремя примерами. Дело в том, что с системами диффуров всё будет почти так же и даже проще!

Само собой, вы должны понимать, что такое система дифференциальных уравнений , что значит найти общее решение системы и частное решение системы.

Напоминаю, что систему дифференциальных уравнений можно решить «традиционным» путём: методом исключения или с помощью характеристического уравнения . Способ же операционного исчисления, о котором пойдет речь, применим к системе ДУ, когда задание сформулировано следующим образом:

Найти частное решение однородной системы дифференциальных уравнений , соответствующее начальным условиям .

Как вариант, система может быть и неоднородной – с «довесками» в виде функций и в правых частях:

Но, и в том, и в другом случае нужно обратить внимание на два принципиальных момента условия:

1) Речь идёт только о частном решении .
2) В скобочках начальных условий находятся строго нули , и ничто другое.

Общий ход и алгоритм будет очень похож на решение дифференциального уравнения операционным методом . Из справочных материалов потребуется та же таблица оригиналов и изображений .

Пример 1

, ,

Решение: Начало тривиально: с помощью таблицы преобразования Лапласа перейдем от оригиналов к соответствующим изображениям. В задаче с системами ДУ данный переход обычно прост:

Используя табличные формулы №№1,2, учитывая начальное условие , получаем:

Что делать с «игреками»? Мысленно меняем в таблице «иксы» на «игреки». Используя те же преобразования №№1,2, учитывая начальное условие , находим:

Подставим найденные изображения в исходное уравнение :

Теперь в левых частях уравнений нужно собрать все слагаемые, в которых присутствует или . В правые части уравнений необходимо «оформить» все остальные слагаемые:

Далее в левой части каждого уравнения проводим вынесение за скобки:

При этом на первых позициях следует разместить , а на вторых позициях :

Полученную систему уравнений с двумя неизвестными обычно решают по формулам Крамера . Вычислим главный определитель системы:

В результате расчёта определителя получен многочлен .

Важный технический приём! Данный многочлен лучше сразу же попытаться разложить на множители. В этих целях следовало бы попробовать решить квадратное уравнение , но, у многих читателей намётанный ко второму курсу глаз заметит, что .

Таким образом, наш главный определитель системы:

Дальнейшая разборка с системой, слава Крамеру, стандартна:

В итоге получаем операторное решение системы :

Преимуществом рассматриваемого задания является та особенность, что дроби обычно получаются несложными, и разбираться с ними значительно проще, нежели с дробями в задачах нахождения частного решения ДУ операционным методом . Предчувствие вас не обмануло – в дело вступает старый добрый метод неопределённых коэффициентов , с помощью которого раскладываем каждую дробь на элементарные дроби:

1) Разбираемся с первой дробью:

Таким образом:

2) Вторую дробь разваливаем по аналогичной схеме, при этом корректнее использовать другие константы (неопределенные коэффициенты):

Таким образом:

Чайникам советую записывать разложенное операторное решение в следующем виде:
– так будет понятней завершающий этап – обратное преобразование Лапласа.

Используя правый столбец таблицы, перейдем от изображений к соответствующим оригиналам:

Согласно правилам хорошего математического тона, результат немного причешем:

Ответ:

Проверка ответа осуществляется по стандартной схеме, которая детально разобрана на уроке Как решить систему дифференциальных уравнений? Всегда старайтесь её выполнять, чтобы забить большой плюс в задание.

Пример 2

С помощью операционного исчисления найти частное решение системы дифференциальных уравнений, соответствующее заданным начальным условиям.
, ,

Это пример для самостоятельного решения. Примерный образец чистового оформления задачи и ответ в конце урока.

Решение неоднородной системы дифференциальных уравнений алгоритмически ничем не отличается, разве что технически будет чуть сложнее:

Пример 3

С помощью операционного исчисления найти частное решение системы дифференциальных уравнений, соответствующее заданным начальным условиям.
, ,

Решение: С помощью таблицы преобразования Лапласа, учитывая начальные условия , перейдем от оригиналов к соответствующим изображениям:

Но это ещё не всё, в правых частях уравнений есть одинокие константы. Что делать в тех случаях, когда константа находится сама по себе в полном одиночестве? Об этом уже шла речь на уроке Как решить ДУ операционным методом . Повторим: одиночные константы следует мысленно домножить на единицу , и к единицам применить следующее преобразование Лапласа:

Подставим найденные изображения в исходную систему:

Налево перенесём слагаемые, в которых присутствуют , в правых частях разместим остальные слагаемые:

В левых частях проведём вынесение за скобки, кроме того, приведём к общему знаменателю правую часть второго уравнения:

Вычислим главный определитель системы, не забывая, что результат целесообразно сразу же попытаться разложить на множители:
, значит, система имеет единственное решение.

Едем дальше:



Таким образом, операторное решение системы:

Иногда одну или даже обе дроби можно сократить, причём, бывает, так удачно, что и раскладывать практически ничего не нужно! А в ряде случаев сразу получается халява, к слову, следующий пример урока будет показательным образцом.

Методом неопределенных коэффициентов получим суммы элементарных дробей.

Сокрушаем первую дробь:

И добиваем вторую:

В результате операторное решение принимает нужный нам вид:

С помощью правого столбца таблицы оригиналов и изображений осуществляем обратное преобразование Лапласа:

Подставим полученные изображения в операторное решение системы:

Ответ: частное решение:

Как видите, в неоднородной системе приходится проводить более трудоёмкие вычисления по сравнению с однородной системой. Разберём еще пару примеров с синусами, косинусами, и хватит, поскольку будут рассмотрены практически все разновидности задачи и большинство нюансов решения.

Пример 4

Методом операционного исчисления найти частное решение системы дифференциальных уравнений с заданными начальными условиями ,

Решение: Данный пример я тоже разберу сам, но комментарии будут касаться только особенных моментов. Предполагаю, вы уже хорошо ориентируетесь в алгоритме решения.

Перейдем от оригиналов к соответствующим изображениям:

Подставим найденные изображения в исходную систему ДУ:

Систему решим по формулам Крамера:
, значит, система имеет единственное решение.

Полученный многочлен не раскладывается на множители. Что делать в таких случаях? Ровным счётом ничего. Сойдёт и такой.

В результате операторное решение системы:

А вот и счастливый билет! Метод неопределённых коэффициентов использовать не нужно вообще! Единственное, в целях применения табличных преобразований перепишем решение в следующем виде:

Перейдем от изображений к соответствующим оригиналам:

Подставим полученные изображения в операторное решение системы:

Формула разложения Хевисайда

Пусть изображение функции представляет собой дробно-рациональную функцию.

Теорема. Пусть, где и - дифференцируемые функции. Введем как полюсы функции, т.е. корни (нули) ее знаменателя. Тогда, если, получим формулу Хевисайда:

Доказательство проведем для случая, когда и - многочлены степеней т и п соответственно, при этом т п . Тогда - правильная рациональная дробь. Представим в виде суммы простейших дробей:

Отсюда Коэффициенты найдем из тождества (17.2), переписав его в виде

Умножим обе части последнего равенства на и перейдем к пределу при. Учитывая, что и, получим

откуда и следует (17.1). Теорема доказана.

Замечание 1. Если коэффициенты многочленов и вещественны, то комплексные корни многочлена попарно сопряжены. Следовательно, в формуле (17.1) комплексно сопряженными величинами будут слагаемые, соответствующие комплексно сопряженным корням многочлена, и формула Хевисайда примет вид

где первая сумма распространена на все вещественные корни многочлена, вторая - на все его комплексные корни с положительными мнимыми частями.

Замечание 2. Каждый член формулы (17.1) представляет собой записанное в комплексной форме колебание, где. Таким образом, вещественным корням () соответствуют апериодические колебания, комплексным корням с отрицательными вещественными частями - затухающие колебания, чисто мнимым корням - незатухающие гармонические колебания.

Если знаменатель не имеет корней с положительными вещественными частями, то при достаточно больших значениях получим установившийся режим:

Чисто мнимые корни многочлена с положительными мнимыми частями.

Колебания, соответствующие корням с отрицательными вещественными частями, экспоненциально затухают при и поэтому не входят в установившийся режим.

Пример 1. Найти оригинал изображения

Решение. Имеем. Выпишем корни многочлена: .

По формуле (17.1)

Здесь, так как числа - корни уравнения. Следовательно,

Пример 2. Найти оригинал изображения

где а 0; .

Решение. Здесь функция, помимо очевидного корня, имеет бесконечно много корней, являющихся нулями функции. Решая уравнение, получим, откуда

Таким образом, корни знаменателя имеют вид и, где

По формуле (17.3) находим оригинал

Операторный метод решения дифференциальных уравнений

Дифференциальные уравнения. Рассмотрим задачу Коши для линейного дифференциального уравнения

(здесь) с начальными условиями

Переходя в (18.1) к изображениям, в силу линейности преобразования Лапласа будем иметь

Изображения производных, используя теорему 3 § 16 и начальные условия (18.2), запишем в виде

Подставив (18.4) в (18.3), после несложных преобразований получим операторное уравнение

где (характеристический многочлен); .

Из уравнения (18.5) найдем операторное решение

Решением задачи Коши (18.1), (18.2) является оригинал операторного решения (18.6):

Для задачи Коши в принятых обозначениях можно записать

Операторное уравнение имеет вид

разложим операторное решение на простейшие дроби:

С помощью формул, полученных в § 15, получим оригиналы:

Таким образом, решение задачи Коши будет иметь вид

Пример 1. Решить задачу Коши для дифференциального уравнения с начальными условиями, где.

Решение.

Его решение имеет вид

Используя теорему 2 § 16, последовательно найдем:

Пример 2. Решить задачу Коши для дифференциального уравнения с нулевыми начальными условиями, где - ступенчатая импульсная функция.

Решение. Запишем операторное уравнение

и его решение

Из теоремы 2 § 16 следует

в соответствии с теоремой запаздывания (§ 15)

Окончательно,

Пример 3. На точку массой т , прикрепленную к пружине жесткостью с и находящуюся на гладкой горизонтальной плоскости, действует периодически меняющаяся сила. В момент времени точка подверглась удару, несущему импульс. Пренебрегая сопротивлением, найти закон движения точки, если в начальный момент времени она покоилась в начале координат.

Решение. Уравнение движения запишем в виде

где - упругая сила; - функция Дирака. Решим операторное уравнение

Если (случай резонанса), то

По теореме запаздывания

Окончательно,

Интеграл (формула) Дюамеля. Рассмотрим задачу Коши для уравнения (18.1) при начальных условиях. Операторное решение в этом случае имеет вид

Пусть весовая функция - оригинал для. тогда по теореме 1 § 16 получим

Соотношение (18.7) называется интегралом (формулой) Дюамеля.

Замечание. При ненулевых начальных условиях формула Дюамеля непосредственно неприменима. В этом случае необходимо предварительно преобразовать исходную задачу к задаче с однородными (нулевыми) начальными условиями. Для этого введем новую функцию, полагая

где - начальные значения искомого решения.

Как легко видеть, и следовательно, .

Таким образом, функция - решение уравнения (18.1) с правой частью, полученной в результате подстановки (18.8) в (18.1), при нулевых начальных данных.

Используя (18.7), найдем и.

Пример 4. С помощью интеграла Дюамеля найти решение задачи Коши

с начальными условиями.

Решение. Начальные данные ненулевые. Полагаем, в соответствии с (18.8), . Тогда, и для определения получим уравнение с однородными начальными условиями.

Для рассматриваемой задачи характеристический многочлен, весовая функция. По формуле Дюамеля

Окончательно,

Системы линейных дифференциальных уравнений с постоянными коэффициентами. Задача Коши для системы линейных дифференциальных уравнений в матричной записи имеет вид

где - вектор искомых функций; - вектор правых частей; - матрица коэффициентов; - вектор начальных данных.

На дворе знойная пора, летает тополиный пух, и такая погода располагает к отдыху. За учебный год у всех накопилась усталость, но ожидание летних отпусков/каникул должно воодушевлять на успешную сдачу экзаменов и зачетов. По сезону тупят, кстати, и преподаватели, поэтому скоро тоже возьму тайм-аут для разгрузки мозга. А сейчас кофе, мерный гул системного блока, несколько дохлых комаров на подоконнике и вполне рабочее состояние… …эх, блин,… поэт хренов.

К делу. У кого как, а у меня сегодня 1 июня, и мы рассмотрим ещё одну типовую задачу комплексного анализа – нахождение частного решения системы дифференциальных уравнений методом операционного исчисления . Что необходимо знать и уметь, чтобы научиться её решать? Прежде всего, настоятельно рекомендую обратиться к уроку. Пожалуйста, прочитайте вводную часть, разберитесь с общей постановкой темы, терминологией, обозначениями и хотя бы с двумя-тремя примерами. Дело в том, что с системами диффуров всё будет почти так же и даже проще!

Само собой, вы должны понимать, что такое система дифференциальных уравнений , что значит найти общее решение системы и частное решение системы.

Напоминаю, что систему дифференциальных уравнений можно решить «традиционным» путём: методом исключения или с помощью характеристического уравнения . Способ же операционного исчисления, о котором пойдет речь, применим к системе ДУ, когда задание сформулировано следующим образом:

Найти частное решение однородной системы дифференциальных уравнений , соответствующее начальным условиям .

Как вариант, система может быть и неоднородной – с «довесками» в виде функций и в правых частях:

Но, и в том, и в другом случае нужно обратить внимание на два принципиальных момента условия:

1) Речь идёт только о частном решении .
2) В скобочках начальных условий находятся строго нули , и ничто другое.

Общий ход и алгоритм будет очень похож на решение дифференциального уравнения операционным методом . Из справочных материалов потребуется та же таблица оригиналов и изображений .

Пример 1

, ,

Решение: Начало тривиально: с помощью таблицы преобразования Лапласа перейдем от оригиналов к соответствующим изображениям. В задаче с системами ДУ данный переход обычно прост:

Используя табличные формулы №№1,2, учитывая начальное условие , получаем:

Что делать с «игреками»? Мысленно меняем в таблице «иксы» на «игреки». Используя те же преобразования №№1,2, учитывая начальное условие , находим:

Подставим найденные изображения в исходное уравнение :

Теперь в левых частях уравнений нужно собрать все слагаемые, в которых присутствует или . В правые части уравнений необходимо «оформить» все остальные слагаемые:

Далее в левой части каждого уравнения проводим вынесение за скобки:

При этом на первых позициях следует разместить , а на вторых позициях :

Полученную систему уравнений с двумя неизвестными обычно решают по формулам Крамера . Вычислим главный определитель системы:

В результате расчёта определителя получен многочлен .

Важный технический приём! Данный многочлен лучше сразу же попытаться разложить на множители. В этих целях следовало бы попробовать решить квадратное уравнение , но, у многих читателей намётанный ко второму курсу глаз заметит, что .

Таким образом, наш главный определитель системы:

Дальнейшая разборка с системой, слава Крамеру, стандартна:

В итоге получаем операторное решение системы :

Преимуществом рассматриваемого задания является та особенность, что дроби обычно получаются несложными, и разбираться с ними значительно проще, нежели с дробями в задачах нахождения частного решения ДУ операционным методом . Предчувствие вас не обмануло – в дело вступает старый добрый метод неопределённых коэффициентов , с помощью которого раскладываем каждую дробь на элементарные дроби:

1) Разбираемся с первой дробью:

Таким образом:

2) Вторую дробь разваливаем по аналогичной схеме, при этом корректнее использовать другие константы (неопределенные коэффициенты):

Таким образом:

Чайникам советую записывать разложенное операторное решение в следующем виде:
– так будет понятней завершающий этап – обратное преобразование Лапласа.

Используя правый столбец таблицы, перейдем от изображений к соответствующим оригиналам:

Согласно правилам хорошего математического тона, результат немного причешем:

Ответ:

Проверка ответа осуществляется по стандартной схеме, которая детально разобрана на уроке Как решить систему дифференциальных уравнений? Всегда старайтесь её выполнять, чтобы забить большой плюс в задание.

Пример 2

С помощью операционного исчисления найти частное решение системы дифференциальных уравнений, соответствующее заданным начальным условиям.
, ,

Это пример для самостоятельного решения. Примерный образец чистового оформления задачи и ответ в конце урока.

Решение неоднородной системы дифференциальных уравнений алгоритмически ничем не отличается, разве что технически будет чуть сложнее:

Пример 3

С помощью операционного исчисления найти частное решение системы дифференциальных уравнений, соответствующее заданным начальным условиям.
, ,

Решение: С помощью таблицы преобразования Лапласа, учитывая начальные условия , перейдем от оригиналов к соответствующим изображениям:

Но это ещё не всё, в правых частях уравнений есть одинокие константы. Что делать в тех случаях, когда константа находится сама по себе в полном одиночестве? Об этом уже шла речь на уроке Как решить ДУ операционным методом . Повторим: одиночные константы следует мысленно домножить на единицу , и к единицам применить следующее преобразование Лапласа:

Подставим найденные изображения в исходную систему:

Налево перенесём слагаемые, в которых присутствуют , в правых частях разместим остальные слагаемые:

В левых частях проведём вынесение за скобки, кроме того, приведём к общему знаменателю правую часть второго уравнения:

Вычислим главный определитель системы, не забывая, что результат целесообразно сразу же попытаться разложить на множители:
, значит, система имеет единственное решение.

Едем дальше:



Таким образом, операторное решение системы:

Иногда одну или даже обе дроби можно сократить, причём, бывает, так удачно, что и раскладывать практически ничего не нужно! А в ряде случаев сразу получается халява, к слову, следующий пример урока будет показательным образцом.

Методом неопределенных коэффициентов получим суммы элементарных дробей.

Сокрушаем первую дробь:

И добиваем вторую:

В результате операторное решение принимает нужный нам вид:

С помощью правого столбца таблицы оригиналов и изображений осуществляем обратное преобразование Лапласа:

Подставим полученные изображения в операторное решение системы:

Ответ: частное решение:

Как видите, в неоднородной системе приходится проводить более трудоёмкие вычисления по сравнению с однородной системой. Разберём еще пару примеров с синусами, косинусами, и хватит, поскольку будут рассмотрены практически все разновидности задачи и большинство нюансов решения.

Пример 4

Методом операционного исчисления найти частное решение системы дифференциальных уравнений с заданными начальными условиями ,

Решение: Данный пример я тоже разберу сам, но комментарии будут касаться только особенных моментов. Предполагаю, вы уже хорошо ориентируетесь в алгоритме решения.

Перейдем от оригиналов к соответствующим изображениям:

Подставим найденные изображения в исходную систему ДУ:

Систему решим по формулам Крамера:
, значит, система имеет единственное решение.

Полученный многочлен не раскладывается на множители. Что делать в таких случаях? Ровным счётом ничего. Сойдёт и такой.

В результате операторное решение системы:

А вот и счастливый билет! Метод неопределённых коэффициентов использовать не нужно вообще! Единственное, в целях применения табличных преобразований перепишем решение в следующем виде:

Перейдем от изображений к соответствующим оригиналам:

Подставим полученные изображения в операторное решение системы:

Как решить дифференциальное уравнение
методом операционного исчисления?

На данном уроке будет подробно разобрана типовая и широко распространенная задача комплексного анализа – нахождение частного решения ДУ 2-го порядка с постоянными коэффициентами методом операционного исчисления . Снова и снова избавляю вас от предубеждения, что материал немыслимо сложный и недоступный. Забавно, но для освоения примеров можно вообще не уметь дифференцировать, интегрировать и даже не знать, что такое комплексные числа . Потребуется навык применения метода неопределённых коэффициентов , который детально разобран в статье Интегрирование дробно-рациональных функций . Фактически краеугольным камнем задания являются обычные алгебраические действия, и я уверен, что материал доступен даже для школьника.

Сначала сжатые теоретические сведения о рассматриваемом разделе математического анализа. Основная суть операционного исчисления состоит в следующем: функция действительной переменной с помощью так называемого преобразования Лапласа отображается в функцию комплексной переменной :

Терминология и обозначения:
функция называется оригиналом ;
функция называется изображением ;
заглавной буквой обозначается преобразование Лапласа .

Говоря простым языком, действительную функцию (оригинал) по определённым правилам нужно превратить в комплексную функцию (изображение). Стрелочка обозначает именно это превращение. А сами «определенные правила» и являются преобразованием Лапласа , которое мы рассмотрим лишь формально, чего для решения задач будет вполне достаточно.

Осуществимо и обратное преобразование Лапласа, когда изображение превращается в оригинал:

Зачем всё это нужно? В ряде задач высшей математики бывает очень выгодно перейти от оригиналов к изображениям , поскольку в этом случае решение задания значительно упрощается (шутка). И как раз одну из таких задач мы и рассмотрим. Если вы дожили до операционного исчисления, то формулировка должна быть вам хорошо знакома:

Найти частное решение неоднородного уравнения второго порядка с постоянными коэффициентами при заданных начальных условиях .

Примечание: иногда дифференциальное уравнение может быть и однородным: , для него в вышеизложенной формулировке также применим метод операционного исчисления. Однако в практических примерах однородное ДУ 2-го порядка встречается крайне редко, и далее речь пойдёт о неоднородных уравнениях.

И сейчас будет разобран третий способ – решение ДУ с помощью операционного исчисления. Ещё раз подчеркиваю то обстоятельство, что речь идёт о нахождении частного решения , кроме того, начальные условия строго имеют вид («иксы» равны нулям).

К слову, об «иксах». Уравнение можно переписать в следующем виде:
, где «икс» – независимая переменная, а «игрек» – функция. Я не случайно об этом говорю, поскольку в рассматриваемой задаче чаще всего используются другие буквы:

То есть роль независимой переменной играет переменная «тэ» (вместо «икса»), а роль функции играет переменная «икс» (вместо «игрека»)

Понимаю, неудобно конечно, но лучше придерживаться обозначений, которые встречаются в большинстве задачников и методичек.

Итак, наша задача с другими буквами записывается следующим образом:

Найти частное решение неоднородного уравнения второго порядка с постоянными коэффициентами при заданных начальных условиях .

Смысл задания нисколько не изменился, изменились только буквы.

Как решить данную задачу методом операционного исчисления?

Прежде всего, потребуется таблица оригиналов и изображений . Это ключевой инструмент решения, и без неё не обойтись. Поэтому, по возможности, постарайтесь распечатать указанный справочный материал. Сразу же поясню, что обозначает буква «пэ»: комплексную переменную (вместо привычного «зет»). Хотя для решения задач этот факт не имеет особого значения, «пэ» так «пэ».

С помощью таблицы оригиналы и необходимо превратить в некоторые изображения. Далее следует ряд типовых действий, и используется обратное преобразование Лапласа (тоже есть в таблице). Таким образом, будет найдено искомое частное решение.

Все задачи, что приятно, решаются по достаточно жесткому алгоритму.

Пример 1

, ,

Решение: На первом шаге перейдем от оригиналов к соответствующим изображениям. Используем левую сторону .

Сначала разбираемся с левой частью исходного уравнения. Для преобразования Лапласа справедливы правила линейности , поэтому все константы игнорируем и по отдельности работаем с функцией и её производными.

По табличной формуле №1 превращаем функцию:

По формуле №2 , учитывая начальное условие , превращаем производную:

По формуле №3 , учитывая начальные условия , превращаем вторую производную:

Не путаемся в знаках!

Признаюсь, правильнее говорить не «формулы», а «преобразования», но для простоты время от времени буду называть начинку таблицы формулами.

Теперь разбираемся с правой частью, в которой находится многочлен . В силу того же правила линейности преобразования Лапласа, с каждым слагаемым работаем отдельно.

Смотрим на первое слагаемое: – это независимая переменная «тэ», умноженная на константу. Константу игнорируем и, используя пункт №4 таблицы, выполняем преобразование:

Смотрим на второе слагаемое: –5. Когда константа находится одна-одинёшенька, то пропускать её уже нельзя. С одиночной константой поступают так: для наглядности её можно представить в виде произведения: , а к единице применить преобразование:

Таким образом, для всех элементов (оригиналов) дифференциального уравнения с помощью таблицы найдены соответствующие изображения:

Подставим найденные изображения в исходное уравнение :

Дальнейшая задача состоит в том, чтобы выразить операторное решение через всё остальное, а именно – через одну дробь. При этом целесообразно придерживаться следующего порядка действий:

Для начала раскрываем скобки в левой части:

Приводим подобные слагаемые в левой части (если они есть). В данном случае складываем числа –2 и –3. Чайникам настоятельно рекомендую не пропускать данный этап:

Слева оставляем слагаемые, в которых присутствует , остальные слагаемые переносим направо со сменой знака:

В левой части выносим за скобки операторное решение , в правой части приводим выражение к общему знаменателю:

Многочлен слева следует разложить на множители (если это возможно). Решаем квадратное уравнение:

Таким образом:

Сбрасываем в знаменатель правой части:

Цель достигнута – операторное решение выражено через одну дробь.

Действие второе. Используя метод неопределенных коэффициентов , операторное решение уравнения следует разложить в сумму элементарных дробей:

Приравняем коэффициенты при соответствующих степенях и решим систему:

Если возникли затруднения с , пожалуйста, наверстайте упущенное в статьях Интегрирование дробно-рациональной функции и Как решить систему уравнений? Это очень важно, поскольку разложение на дроби, по существу, самая важная часть задачи.

Итак, коэффициенты найдены: , и операторное решение предстаёт перед нами в разобранном виде:

Обратите внимание, что константы записаны не в числителях дробей. Такая форма записи выгоднее, чем . А выгоднее, потому что финальное действие пройдёт без путаницы и ошибок:

Заключительный этап задачи состоит в том, чтобы с помощью обратного преобразования Лапласа перейти от изображений к соответствующим оригиналам. Используем правый столбец таблицы оригиналов и изображений .

Возможно, не всем понятно преобразование . Здесь использована формула пункта №5 таблицы: . Если подробнее: . Собственно, для похожих случаев формулу можно модифицировать: . Да и все табличные формулы пункта №5 очень легко переписать аналогичным образом.

После обратного перехода искомое частное решение ДУ получается на блюдечке с голубой каёмочкой:

Было:

Стало:

Ответ: частное решение:

При наличии времени всегда желательно выполнять проверку. Проверка выполняется по стандартной схеме, которая уже рассматривалась на уроке Неоднородные дифференциальные уравнения 2-го порядка . Повторим:

Проверим выполнение начального условия :
– выполнено.

Найдём первую производную:

Проверим выполнение второго начального условия :
– выполнено.

Найдём вторую производную:

Подставим , и в левую часть исходного уравнения :

Получена правая часть исходного уравнения.

Вывод: задание выполнено правильно.

Небольшой пример для самостоятельного решения:

Пример 2

С помощью операционного исчисления найти частное решение дифференциального уравнения при заданных начальных условиях.

Примерный образец чистового оформления задания в конце урока.

Наиболее частный гость в дифференциальных уравнениях, как многие давно заметили, экспоненты, поэтому рассмотрим несколько примеров с ними, родными:

Пример 3

, ,

Решение: С помощью таблицы преобразований Лапласа (левая часть таблицы) перейдем от оригиналов к соответствующим изображениям.

Сначала рассмотрим левую часть уравнения. Там отсутствует первая производная. Ну и что из того? Отлично. Работы поменьше. Учитывая начальные условия , по табличным формулам №№1,3 находим изображения:

Теперь смотрим на правую часть: – произведение двух функций. Для того чтобы воспользоваться свойствами линейности преобразования Лапласа, нужно раскрыть скобки: . Так как константы находятся в произведениях, то на них забиваем, и, используя группу №5 табличных формул, находим изображения:

Подставим найденные изображения в исходное уравнение:

Напоминаю, что дальнейшая задача состоит в том, чтобы выразить операторное решение через единственную дробь.

В левой части оставляем слагаемые, в которых присутствует , остальные слагаемые переносим в правую часть. Заодно в правой части начинаем потихоньку приводить дроби к общему знаменателю:

Слева выносим за скобки, справа приводим выражение к общему знаменателю:

В левой части получен неразложимый на множители многочлен . Если многочлен не раскладывается на множители, то его, бедолагу, сразу нужно сбросить на дно правой части, забетонировав ноги в тазике. А в числителе раскрываем скобки и приводим подобные слагаемые:

Наступил самый кропотливый этап: методом неопределенных коэффициентов разложим операторное решение уравнения в сумму элементарных дробей:


Таким образом:

Обратите внимание, как разложена дробь: , скоро поясню, почему именно так.

Финиш: перейдем от изображений к соответствующим оригиналам, используем правый столбец таблицы:

В двух нижних преобразованиях использованы формулы №№6,7 таблицы, и дробь предварительно раскладывалась как раз для «подгонки» под табличные преобразования.

В результате, частное решение:

Ответ: искомое частное решение:

Похожий пример для самостоятельного решения:

Пример 4

Найти частное решение дифференциального уравнения методом операционного исчисления.

Краткое решение и ответ в конце урока.

В Примере 4 одно из начальных условий равно нулю. Это, безусловно, упрощает решение, и самый идеальный вариант, когда оба начальных условия нулевые: . В этом случае производные преобразуются в изображения без хвостов:

Как уже отмечалось, наиболее сложным техническим моментом задачи является разложение дроби методом неопределенных коэффициентов , и в моём распоряжении есть достаточно трудоёмкие примеры. Тем не менее, монстрами запугивать никого не буду, рассмотрим ещё пару типовых разновидностей уравнения:

Пример 5

Методом операционного исчисления найти частное решение дифференциального уравнения, удовлетворяющее заданным начальным условиям.
, ,

Решение: С помощью таблицы преобразований Лапласа перейдем от оригиналов к соответствующим изображениям. Учитывая начальные условия :

С правой частью тоже никаких проблем:

(Напоминаю, что константы-множители игнорируются)

Подставим полученные изображения в исходное уравнение и выполняем стандартные действия, которые, я надеюсь, вы уже хорошо отработали:

Константу в знаменателе выносим за пределы дроби, главное, потом про неё не забыть:

Думал, выносить ли ещё дополнительно двойку из числителя, однако, прикинув, пришел к выводу, что данный шаг практически не упростит дальнейшего решения.

Особенностью задания является полученная дробь. Кажется, что её разложение будет долгим и трудным, но впечатление обманчиво. Естественно, бывают сложные вещи, но в любом случае – вперёд, без страха и сомнений:

То, что некоторые коэффициенты получились дробными, смущать не должно, такая ситуация не редкость. Лишь бы техника вычислений не подвела. К тому же, всегда есть возможность выполнить проверку ответа.

В результате, операторное решение:

Перейдем от изображений к соответствующим оригиналам:

Таким образом, частное решение: