МБОУ СОУ №17 Иванов

« Модулни уравнения»
Методическа разработка

Компилиран

учител по математика

Лебедева Н.В.

20010 г

Обяснителна бележка

Глава 1 Въведение

Раздел 2. Основни характеристики Раздел 3. Геометрична интерпретация на понятието модул на число Раздел 4. Графика на функцията y = |x| Раздел 5 Конвенции

Глава 2

Раздел 1. Уравнения от вида |F(х)| = m (протозои) Раздел 2. Уравнения от вида F(|х|) = m Раздел 3. Уравнения от вида |F(х)| = G(x) Раздел 4. Уравнения от вида |F(х)| = ± F(x) (красиво) Раздел 5. Уравнения от вида |F(х)| = |G(x)| Раздел 6. Примери за решаване на нестандартни уравнения Раздел 7. Уравнения от вида |F(х)| + |G(x)| = 0 Раздел 8. Уравнения от вида |а 1 x ± в 1 | ± |a 2 x ± в 2 | ± …|a n x ± в n | = m Раздел 9. Уравнения, съдържащи множество модули

Глава 3. Примери за решаване на различни уравнения с модул.

Раздел 1. Тригонометрични уравнения Раздел 2. Експоненциални уравнения Раздел 3 Логаритмични уравнения Раздел 4. Ирационални уравнения Раздел 5. Задачи с повишена сложност Отговори на упражненията Библиография

Обяснителна бележка.

Концепцията за абсолютната стойност (модул) на реално число е една от основните му характеристики. Тази концепция се използва широко в различни клонове на физическите, математическите и техническите науки. В практиката на преподаване на курс по математика в гимназияв съответствие с Програмата на Министерството на отбраната на Руската федерация понятието „абсолютна стойност на число“ се среща многократно: в 6-ти клас се въвежда определението на модула, неговото геометрично значение; в 8. клас се формира понятието абсолютна грешка, разглежда се решаването на най-простите уравнения и неравенства, съдържащи модула, изучават се свойствата на аритметичния корен квадратен; в 11. клас понятието се намира в раздела „Корен нта степен“.Преподавателският опит показва, че учениците често срещат трудности при решаването на задачи, които изискват познаване на този материал, и често пропускат, без да започнат да изпълняват. В текстовете на изпитните задачи за курса на 9. и 11. клас също са включени подобни задачи. Освен това изискванията, които университетите налагат на завършилите училище, са различни, а именно повече високо нивоотколкото изискванията на училищната програма. За живота в съвременното общество е много важно формирането на математически стил на мислене, който се проявява в определени умствени умения. В процеса на решаване на проблеми с модули е необходима способност за прилагане на техники като обобщение и конкретизация, анализ, класификация и систематизация, аналогия. Решаването на такива задачи ви позволява да проверите знанията по основните раздели на училищния курс, нивото логично мислене, първоначални изследователски умения. Тази работа е посветена на един от разделите - решението на уравнения, съдържащи модула. Състои се от три глави. Първата глава въвежда основните понятия и най-важните теоретични изчисления. Втората глава предлага девет основни типа уравнения, съдържащи модула, разглежда методите за решаването им и анализира примери с различни нива на сложност. Третата глава предлага по-сложни и нестандартни уравнения (тригонометрични, експоненциални, логаритмични и ирационални). За всеки тип уравнения има упражнения за независимо решение(отговорите и инструкциите са приложени). Основната цел на тази работа е да предостави методическа помощ на учителите при подготовката за уроци и при организирането на факултативни курсове. Материалът може да се използва и като учебно ръководствоза гимназисти. Задачите, предложени в работата, са интересни и не винаги лесни за решаване, което позволява да се направи мотивацията за учене на учениците по-съзнателна, да се тестват техните способности и да се подобри нивото на подготовка на завършилите училище за постъпване в университети. Диференцираният подбор на предложените упражнения предполага преход от репродуктивното ниво на усвояване на материала към творческото, както и възможността да се научи как да прилага знанията си при решаване на нестандартни проблеми.

Глава 1 Въведение.

Раздел 1. Определяне на абсолютната стойност .

Определение : Абсолютната стойност (модул) на реално число Анаречен не отрицателно число: Аили -А. Обозначаване: │ А │ Записът гласи следното: „модул на числото a“ или „абсолютна стойност на числото a“

│ a, ако a > 0

│a│ = │ 0 ако a = 0 (1)

│ - а, ако а
Примери: 1) │2,5│ = 2,5 2) │-7│ = 7 3) │1 - √2│ = √2 – 1

Разширяване на изразния модул:

a) │x - 8│, ако x > 12 b) │2x + 3│, ако x ≤ -2 │x - 8│= x - 8 │ 2x + 3│= - 2x - 3

Раздел 2. Основни свойства.

Помислете за основните свойства на абсолютната стойност. Свойство №1: Противоположните числа имат равни модули, т.е. │а│=│-а│Нека покажем правилността на равенството. Нека запишем определението на числото - А : │- а│= (2) Нека сравним комплекти (1) и (2). Очевидно е, че дефинициите на абсолютните стойности на числата АИ - Асъвпада. следователно │а│=│-а│
Когато разглеждаме следните свойства, ние се ограничаваме до тяхната формулировка, тъй като тяхното доказателство е дадено в Свойство №2: Абсолютната стойност на сумата от краен брой реални числа не надвишава сумата от абсолютните стойности на термините: Свойство #3: Абсолютната стойност на разликата между две реални числа не надвишава сумата от техните абсолютни стойности: │а - в│ ≤│а│+│в│ Имот #4: Абсолютната стойност на произведението на краен брой реални числа е равна на произведението на абсолютните стойности на факторите: │а · в│=│а│·│в│ Имот #5: Абсолютната стойност на частното на реалните числа е равна на частното на техните абсолютни стойности:

Раздел 3. Геометрична интерпретация на понятието модул на число.

Всяко реално число може да бъде свързано с точка от числовата ос, която ще бъде геометрично представяне на това реално число. Всяка точка от числовата ос отговаря на разстоянието си от началото, т.е. дължината на отсечката от началото до дадената точка. Това разстояние винаги се счита за неотрицателна стойност. Следователно дължината на съответния сегмент ще бъде геометрична интерпретацияабсолютната стойност на дадено реално число

Представената геометрична илюстрация ясно потвърждава свойство No1, т.е. модулите на противоположните числа са равни. От тук лесно се разбира валидността на равенството: │x - a│= │a - x│. Също така става по-очевидно да се реши уравнението │х│= m, където m ≥ 0, а именно x 1,2 = ± m. Примери: 1) │х│= 4 x 1,2 = ± 4 2) │х - 3│= 1
х 1,2 = 2; 4

Раздел 4. Графика на функцията y \u003d │х│

Домейнът на тази функция е всички реални числа.

Раздел 5. Символи.

В бъдеще, когато се разглеждат примери за решаване на уравнения, ще се използват следните конвенции: ( - системен знак [ - зададен знак При решаване на система от уравнения (неравенства) се намира пресечната точка на решенията на уравненията (неравенствата), включени в системата. При решаване на набор от уравнения (неравенства) се намира обединение на решения на уравненията (неравенствата), включени в набора.

Глава 2

В тази глава ще разгледаме алгебрични начини за решаване на уравнения, съдържащи един или повече модули.

Раздел 1. Уравнения от вида │F (х) │= m

Уравнение от този тип се нарича най-просто. То има решение тогава и само ако m ≥ 0. По дефиницията на модула първоначалното уравнение е еквивалентно на комбинацията от две уравнения: │ Е(x)│=м
Примери:
№1. Решете уравнението: │7x - 2│= 9


Отговор: x 1 = - 1; х 2 = 1 4 / 7 №2
│x 2 + 3x + 1│= 1

x 2 + 3x + 2 = 0 x 2 + 3x = 0 x 1 = -1; x 2 \u003d -2 x (x + 3) \u003d 0 x 1 \u003d 0; х 2 = -3 Отговор: сумата от корените е - 2.№3
│x 4 -5x 2 + 2│= 2 x 4 - 5x 2 = 0 x 4 - 5x 2 + 4 = 0 x 2 (x 2 - 5) = 0 обозначават x 2 = m, m ≥ 0 x = 0; ±√5 m 2 – 5m + 4 = 0 m = 1; 4 – и двете стойности отговарят на условието m ≥ 0 x 2 = 1 x 2 = 4 x = ± 1 x = ± 2 Отговор: броят на корените на уравнение 7. Упражнения:
№1. Решете уравнението и посочете сумата от корените: │x - 5│= 3 №2 . Решете уравнението и посочете по-малкия корен: │x 2 + x │ \u003d 0 №3 . Решете уравнението и посочете по-големия корен: │x 2 - 5x + 4 │ \u003d 4 №4 .Решете уравнението и посочете целия корен: │2x 2 - 7x + 6│ \u003d 1 №5 .Решете уравнението и посочете броя на корените: │x 4 - 13x 2 + 50 │ = 14

Раздел 2. Уравнения от вида F(│х│) = m

Аргументът на функцията от лявата страна е под знака модул, докато дясната страна е независима от променливата. Нека разгледаме два начина за решаване на уравнения от този тип. 1 начин:По дефиниция на абсолютната стойност първоначалното уравнение е еквивалентно на съвкупността от две системи. Във всяка от които е наложено условие върху израза на подмодула. Е(│х│) =м
Тъй като функцията F(│х│) е четна в цялата област на дефиниране, корените на уравненията F(х) = m и F(-х) = m са двойки противоположни числа. Следователно е достатъчно да се реши една от системите (при разглеждане на примерите по този начин ще бъде дадено решението на една система). 2 начина:Приложение на метода за въвеждане на нова променлива. В този случай се въвежда обозначението │х│= a, където a ≥ 0. Този метод е по-малко обемен като дизайн.
Примери: №1 . Решете уравнението: 3x 2 - 4│x│ = - 1 Нека използваме въвеждането на нова променлива. Означаваме │х│= a, където a ≥ 0. Получаваме уравнението 3a 2 - 4a + 1 = 0 D = 16 - 12 = 4 a 1 = 1 a 2 = 1 / 3 Връщаме се към първоначалната променлива: │х │ = 1 и │х│= 1/3. Всяко уравнение има два корена. Отговор: x 1 = 1; х 2 = - 1; х 3 = 1 / 3 ; х 4 = - 1 / 3 . №2. Решете уравнението: 5x 2 + 3│x│- 1 \u003d 1 / 2 │x│ + 3x 2
Нека намерим решението на първата наборна система: 4x 2 + 5x - 2 \u003d 0 D = 57 x 1 \u003d -5 + √57 / 8 x 2 \u003d -5-√57 / 8 Обърнете внимание, че x 2 прави не отговарят на условието x ≥ 0. Според решението втората система ще бъде противоположното число x 1 . Отговор: x 1 = -5+√57 / 8 ; х 2 = 5-√57 / 8 .№3 . Решете уравнението: x 4 - │х│= 0 Означаваме │х│= a, където a ≥ 0. Получаваме уравнението a 4 - a \u003d 0 a (a 3 - 1) \u003d 0 a 1 \u003d 0 a 2 \u003d 1 Връщаме се към първоначалната променлива: │х│=0 и │х│= 1 x = 0; ± 1 Отговор: x 1 = 0; х 2 = 1; х 3 = - 1.
Упражнения: №6. Решете уравнението: 2│х│ - 4,5 = 5 - 3/8 │х│ №7 . Решете уравнението, като в отговора посочете броя на корените: 3x 2 - 7│x│ + 2 = 0 №8 . Решете уравнението, като в отговора посочете целите решения: x 4 + │х│ - 2 = 0

Раздел 3. Уравнения от вида │F(х)│ = G(х)

Дясната страна на уравнение от този тип зависи от променлива и следователно има решение тогава и само ако дясната страна е функция G(x) ≥ 0. Оригиналното уравнение може да бъде решено по два начина: 1 начин:Стандарт, базиран на разкриването на модула въз основа на неговата дефиниция и се състои в еквивалентен преход към комбинация от две системи. │ Е(x)│ =Ж(Х)

Рационално е този метод да се използва в случай на сложен израз за функцията G(x) и по-малко сложен израз за функцията F(x), тъй като се предполага, че се решават неравенства с функцията F(x). 2 начина:Състои се в прехода към еквивалентна система, в която се налага условие от дясната страна. │ Е(х)│= Ж(х)

Този метод е по-удобен за използване, ако изразът за функцията G(x) е по-малко сложен, отколкото за функцията F(x), тъй като се приема решението на неравенството G(x) ≥ 0. Освен това в случая от няколко модула, този метод се препоръчва да се използва втората опция. Примери: №1. Решете уравнението: │x + 2│= 6 -2x
(1 начин) Отговор: x = 1 1 / 3 №2.
│x 2 - 2x - 1 │ \u003d 2 (x + 1)
(2 начина) Отговор: Произведението на корените е 3.
№3. Решете уравнението, като в отговора запишете сумата от корените:
│x - 6 │ \u003d x 2 - 5x + 9

Отговор: сборът на корените е 4.
Упражнения: №9. │x + 4│= - 3x №10. Решете уравнението, в отговора посочете броя на решенията: │x 2 + x - 1 │ \u003d 2x - 1 №11 . Решете уравнението, в отговора посочете произведението на корените: │x + 3 │ \u003d x 2 + x - 6

Раздел 4. Уравнения от формата │F(x)│= F(x) и │F(x)│= - F(x)

Уравнения от този тип понякога се наричат ​​"красиви". Тъй като дясната страна на уравненията зависи от променливата, решения съществуват тогава и само ако дясната страна е неотрицателна. Следователно оригиналните уравнения са еквивалентни на неравенствата:
│F(x)│= F(x) F(x) ≥ 0 и │F(x)│= - F(x) F(x) Примери: №1 . Решете уравнението, като в отговора посочете по-малкия корен от цяло число: │5x - 3│ \u003d 5x - 3 5x - 3 ≥ 0 5x ≥ 3 x ≥ 0,6 Отговор: x = 1№2. Решете уравнението, като в отговора посочете дължината на празнината: │x 2 - 9 │ \u003d 9 - x 2 x 2 - 9 ≤ 0 (x - 3) (x + 3) ≤ 0 [- 3; 3] Отговор: дължината на празнината е 6.№3 . Решете уравнението, като в отговора посочете броя на целочислените решения: │2 + x - x 2 │ = 2 + x - x 2 2 + x - x 2 ≥ 0 x 2 - x - 2 ≤ 0 [- 1; 2] Отговор: 4 цели решения.№4 . Решете уравнението, в отговора посочете най-големия корен:
│4 - x -
│= 4 – x –
x 2 - 5x + 5 \u003d 0 D \u003d 5 x 1,2 \u003d
≈ 1,4

Отговор: x = 3.

Упражнения: №12. Решете уравнението, като в отговора посочете целия корен: │x 2 + 6x + 8 │= x 2 + 6x + 8 №13. Решете уравнението, като в отговора посочете броя на целочислените решения: │13x - x 2 - 36│+ x 2 - 13x + 36 = 0 №14. Решете уравнението, в отговора посочете цяло число, което не е коренът на уравнението:

Раздел 5. Уравнения от вида │F(x)│= │G(x)│

Тъй като и двете страни на уравнението са неотрицателни, решението включва разглеждане на два случая: изразите на подмодула са равни или противоположни по знак. Следователно първоначалното уравнение е еквивалентно на комбинацията от две уравнения: │ Е(х)│= │ Ж(х)│
Примери: №1. Решете уравнението, в отговора посочете целия корен: │x + 3│ \u003d │2x - 1│
Отговор: цяло число x = 4.№2. Решете уравнението: │ x - x 2 - 1│ \u003d │2x - 3 - x 2 │
Отговор: x = 2.№3 . Решете уравнението, в отговора посочете произведението на корените:




Корените на уравнението 4x 2 + 2x - 1 \u003d 0 x 1,2 \u003d - 1±√5 / 4 Отговор: произведението на корените е 0,25. Упражнения: №15 . Решете уравнението, като в отговора посочете цялото решение: │x 2 - 3x + 2│ \u003d │x 2 + 6x - 1│ №16. Решете уравнението, като в отговора посочете по-малкия корен: │5x - 3│=│7 - x│ №17 . Решете уравнението, като в отговора запишете сумата от корените:

Раздел 6. Примери за решаване на нестандартни уравнения

В този раздел разглеждаме примери за нестандартни уравнения, при решението на които абсолютната стойност на израза се разкрива по дефиниция. Примери:

№1. Решете уравнението, в отговора посочете сумата от корените: x │x│- 5x - 6 \u003d 0
Отговор: сборът на корените е 1 №2. . Решете уравнението, като в отговора посочете по-малкия корен: x 2 - 4x
- 5 = 0
Отговор: по-малък корен x = - 5. №3. Решете уравнението:

Отговор: x = -1. Упражнения: №18. Решете уравнението и напишете сумата от корените: x │3x + 5│= 3x 2 + 4x + 3
№19. Решете уравнението: x 2 - 3x \u003d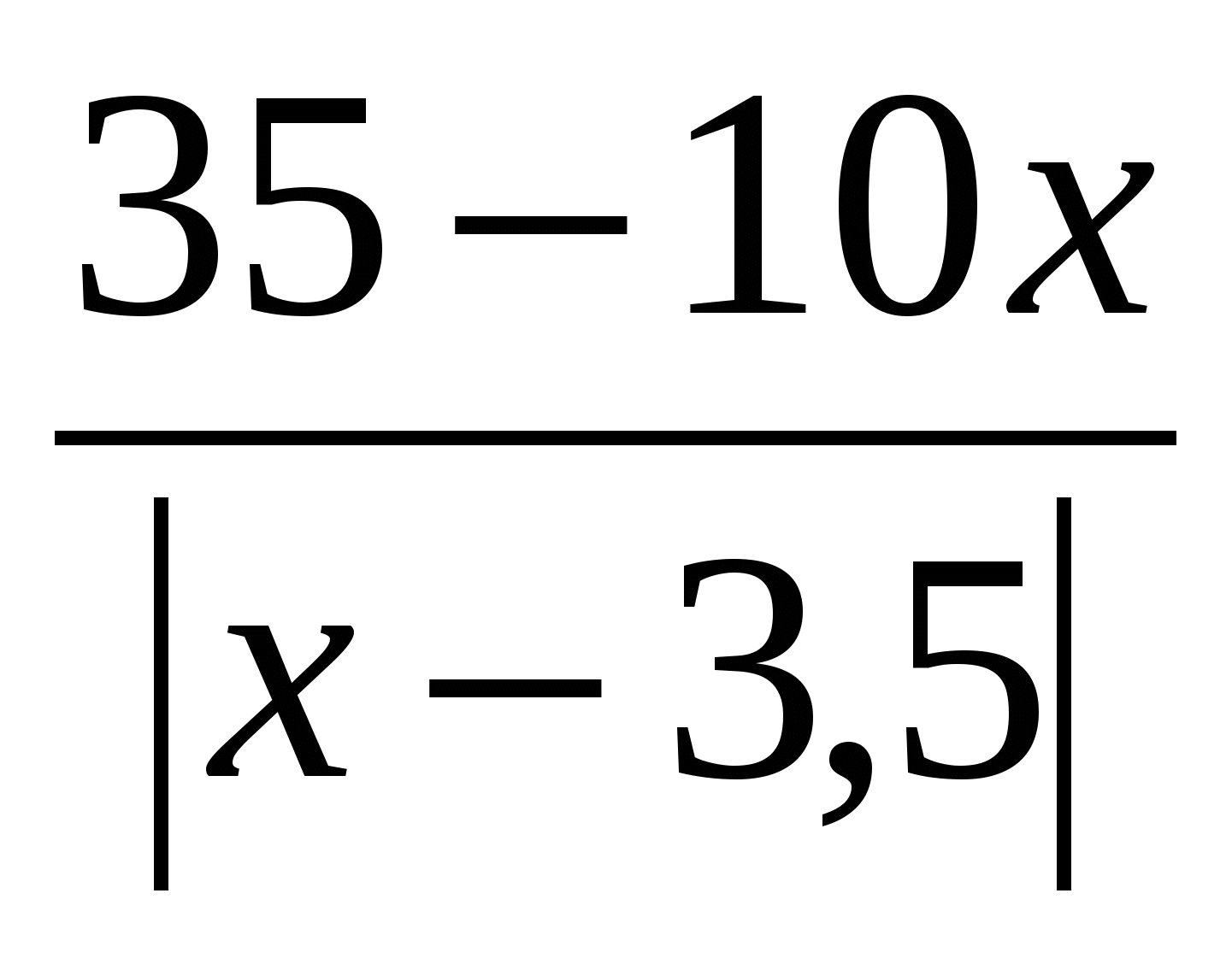

№20. Решете уравнението:

Раздел 7. Уравнения от вида │F(x)│+│G(x)│=0

Лесно е да се види, че в лявата страна на уравнение от този тип, сумата от неотрицателни количества. Следователно първоначалното уравнение има решение тогава и само ако и двата члена едновременно са равни на нула. Уравнението е еквивалентно на системата от уравнения: │ Е(х)│+│ Ж(х)│=0
Примери: №1 . Решете уравнението:
Отговор: x = 2. №2. Решете уравнението: Отговор: x = 1. Упражнения: №21. Решете уравнението: №22 . Решете уравнението, като в отговора запишете сумата от корените: №23 . Решете уравнението, в отговора посочете броя на решенията:

Раздел 8. Уравнения на формата

За решаване на уравнения от този тип се използва методът на интервалите. Ако се реши чрез последователно разширяване на модули, тогава получаваме ннабори от системи, което е много тромаво и неудобно. Помислете за алгоритъма на интервалния метод: 1). Намерете променливи стойности х, за които всеки модул е ​​равен на нула (нули на подмодулни изрази):
2). Намерените стойности са маркирани на числова линия, която е разделена на интервали (броят на интервалите, съответно, е равен на н+1 ) 3). Определете с какъв знак се разкрива всеки модул на всеки от получените интервали (когато правите решение, можете да използвате числова линия, като маркирате знаците върху нея) 4). Първоначалното уравнение е еквивалентно на множеството н+1 системи, във всяка от които е посочена принадлежността на променливата хедин от интервалите. Примери: №1 . Решете уравнението, в отговора посочете най-големия корен:
1). Да намерим нулите на подмодулни изрази: x = 2; x = -3 2). Маркираме намерените стойности на числовата линия и определяме с какъв знак се разкрива всеки модул на получените интервали:
x – 2 x – 2 x – 2 - - + - 3 2 x 2x + 6 2x + 6 2x + 6 - + + 3)
- няма решения Уравнението има два корена. Отговор: най-големият корен е x = 2. №2. Решете уравнението, запишете целия корен в отговора:
1). Да намерим нулите на подмодулни изрази: x = 1.5; x = - 1 2). Маркираме намерените стойности на числовата линия и определяме с какъв знак се разкрива всеки модул на получените интервали: x + 1 x + 1 x + 1 - + +
-1 1,5 х 2х – 3 2х – 3 2х – 3 - - +
3).
Последната система няма решения, следователно уравнението има два корена. Когато решавате уравнението, трябва да обърнете внимание на знака „-“ пред втория модул. Отговор: цяло число x = 7. №3. Решете уравнението, като в отговора посочете сумата от корените: 1). Да намерим нулите на подмодулни изрази: x = 5; х = 1; x = - 2 2). Маркираме намерените стойности на числовата линия и определяме с какъв знак се разкрива всеки модул на получените интервали: x - 5 x - 5 x - 5 x - 5 - - - +
-2 1 5 x x – 1 x – 1 x – 1 x – 1 - - + + x + 2 x + 2 x + 2 x + 2 - + + +
3).
Уравнението има два корена x = 0 и 2. Отговор: сборът на корените е 2. №4 . Решете уравнението: 1). Да намерим нулите на подмодулни изрази: x = 1; х = 2; х = 3. 2). Нека определим знака, с който се разширява всеки модул върху получените интервали. 3).
Ние комбинираме решенията на първите три системи. Отговор: ; х = 5.
Упражнения: №24. Решете уравнението:
№25. Решете уравнението, като в отговора запишете сумата от корените: №26. Решете уравнението, в отговора посочете по-малкия корен: №27. Решете уравнението, дайте по-големия корен в отговора си:

Раздел 9. Уравнения, съдържащи множество модули

Уравненията, съдържащи множество модули, предполагат наличието на абсолютни стойности в изразите на подмодула. Основният принцип за решаване на уравнения от този тип е последователното разкриване на модули, като се започне от "външния". В хода на решението се използват техниките, разгледани в раздели № 1, № 3.

Примери: №1. Решете уравнението:
Отговор: x = 1; - единадесет. №2. Решете уравнението:
Отговор: x = 0; 4; - 4. №3. Решете уравнението, в отговора посочете произведението на корените:
Отговор: Произведението на корените е 8. №4. Решете уравнението:
Означете уравненията на населението (1) И (2) и разгледайте решението на всеки от тях поотделно за удобство на дизайна. Тъй като и двете уравнения съдържат повече от един модул, по-удобно е да се извърши еквивалентен преход към набори от системи. (1)

(2)


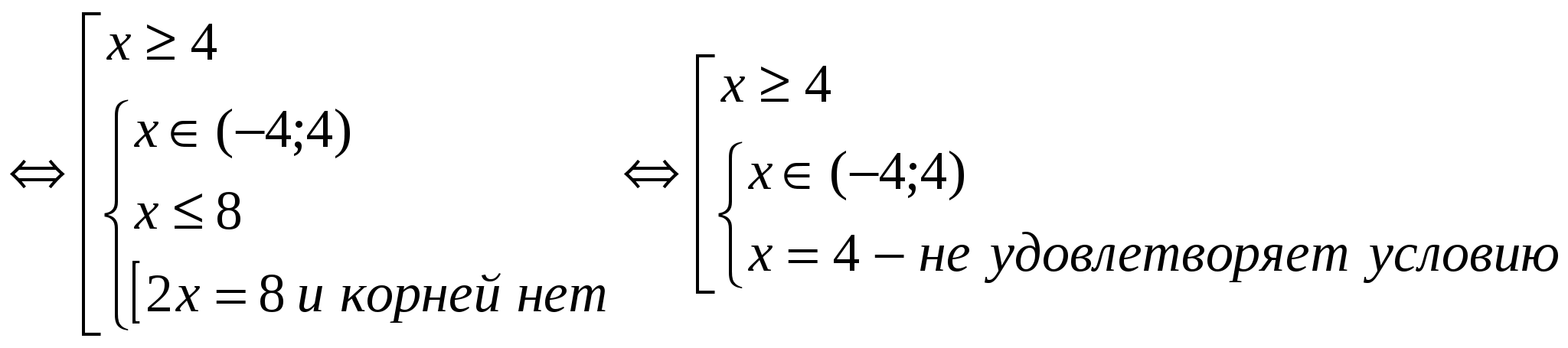Отговор:
Упражнения: №36. Решете уравнението, в отговора посочете сумата от корените: 5 │3x-5│ \u003d 25 x №37. Решете уравнението, ако има повече от един корен, в отговора посочете сумата от корените: │x + 2│ x - 3x - 10 = 1 №38. Решете уравнението: 3 │2x -4│ \u003d 9 │x│ №39. Решете уравнението, като в отговора посочете броя на корените за: 2 │ sin x │ = √2 №40 . Решете уравнението, в отговора посочете броя на корените:

Раздел 3. Логаритмични уравнения.

Преди да решите следните уравнения, е необходимо да прегледате свойствата на логаритмите и логаритмичната функция. Примери: №1. Решете уравнението, в отговора посочете произведението на корените: log 2 (x + 1) 2 + log 2 │x + 1 │ \u003d 6 O.D.Z. x+1≠0 x≠ - 1

Случай 1: ако x ≥ - 1, тогава log 2 (x+1) 2 + log 2 (x+1) = 6 log 2 (x+1) 3 = log 2 2 6 (x+1) 3 = 2 6 x+1 = 4 x = 3 – удовлетворява условието x ≥ - 1 2 случай: ако x log 2 (x+1) 2 + log 2 (-x-1) = 6 log 2 (x+1) 2 + log 2 (-(x+1)) = 6 log 2 (-(x+1) 3) = log 2 2 6- (x+1) 3 = 2 6- (x+1) = 4 x = - 5 – удовлетворява условието x - 1
Отговор: Произведението на корените е 15.
№2. Решете уравнението, в отговора посочете сумата от корените: lg
О.Д.З.

Отговор: сумата от корените е 0,5.
№3. Решете уравнението: log 5
О.Д.З.

Отговор: x = 9. №4. Решете уравнението: │2 + log 0,2 x│+ 3 = │1 + log 5 x│ O.D.Z. x > 0 Нека използваме формулата за преместване към друга база. │2 - log 5 x│+ 3 = │1 + log 5 x│
│2 - log 5 x│- │1 + log 5 x│= - 3 Да намерим нулите на подмодулни изрази: x = 25; x \u003d Тези числа разделят областта на допустимите стойности на три интервала, така че уравнението е еквивалентно на съвкупността от три системи.
Отговор: )