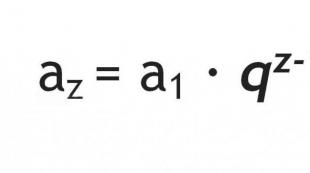Комплексни числа

Въображаеми И комплексни числа. Абсциса и ордината

комплексно число. Конюгирани комплексни числа.

Операции с комплексни числа. Геометричен

представяне на комплексни числа. Сложна равнина.

Модул и аргумент на комплексно число. Тригонометричен

сложна числова форма. Операции със сложен

числа в тригонометрична форма. Формулата на Моавър.

Основна информация за въображаем И комплексни числа са дадени в раздел “Въображаеми и комплексни числа”. Необходимостта от тези числа от нов тип възникна при решаването на квадратни уравнения за случаяд< 0 (здесь д- дискриминанта квадратно уравнение). Дълго време тези числа не намериха физическо приложение, поради което бяха наречени „въображаеми“ числа. Сега обаче те се използват много широко в различни области на физиката.

и технологии: електротехника, хидро- и аеродинамика, теория на еластичността и др.

Комплексни числа се записват във вида:а+би. Тук аИ b – реални числа , А аз – въображаема единица, т.е.д. аз 2 = –1. Номер аНаречен абсцисата,а b – ординатакомплексно числоa + bi.Две комплексни числаа+биИ а–би са наречени конюгаткомплексни числа.

Основни споразумения:

1. Реално числоАможе да се напише и във форматакомплексно число:а+ 0 азили а – 0 аз. Например записи 5 + 0ази 5 – 0 азозначава едно и също число 5 .

2. Комплексно число 0 + биНаречен чисто въображаемо номер. Записвайтебиозначава същото като 0 + би.

3. Две комплексни числаа+би Иc + diсе считат за равни, акоa = cИ b = d. В противен случай комплексните числа не са равни.

Допълнение. Сума от комплексни числаа+биИ c + diсе нарича комплексно число (a+c ) + (b+d ) азПо този начин, при добавяне комплексните числа, техните абциси и ординати се събират отделно.

Това определение съответства на правилата за операции с обикновени полиноми.

Изваждане. Разликата на две комплексни числаа+би(намалено) и c + di(субтрахенд) се нарича комплексно число (a–c ) + (б–г ) аз

По този начин, При изваждане на две комплексни числа техните абсциси и ординати се изваждат отделно.

Умножение. Произведение на комплексни числаа+биИ c + di се нарича комплексно число:

(ac–bd ) + (ad+bc ) азТова определение следва от две изисквания:

1) числа а+биИ c + diтрябва да се умножи като алгебриченбиноми,

2) номер азима основно свойство:аз 2 = – 1.

ПРИМЕР ( а+ би )(а–би) =а 2 +б 2 . следователно работа

две спрегнати комплексни числа е равно на реалното

положително число.

дивизия. Разделете комплексно числоа+би (делим) от другc + di(разделител) - означава да намерите третото числоe + f i(чат), което при умножение с делителc + di, води до дивидентаa + bi.

Ако делителят не е нула, делението винаги е възможно.

ПРИМЕР Намерете (8 +аз ) : (2 – 3 аз) .

Решение Нека пренапишем това отношение като дроб:

Умножаване на неговия числител и знаменател по 2 + 3аз

И След като извършихме всички трансформации, получаваме:

Геометрично представяне на комплексни числа. Реалните числа са представени с точки на числовата ос:

Тук е смисълът Аозначава числото –3, точкаб– номер 2, и О- нула. За разлика от тях комплексните числа са представени от точки в координатната равнина. За целта избираме правоъгълни (декартови) координати с еднакви мащаби по двете оси. След това комплексното числоа+би ще бъдат представени с точка P с абсцисата a и ордината b (виж снимката). Тази координатна система се нарича сложна равнина .

Модул комплексното число е дължината на вектораOP, представляващо комплексно число по координатата ( изчерпателен) самолет. Модул на комплексно числоа+биозначен | а+би| или писмо r

Да разгледаме квадратно уравнение.

Да определим корените му.

Няма реално число, чийто квадрат е -1. Но ако дефинираме оператора с формула азкато въображаема единица, тогава решението на това уравнение може да бъде записано като . При което И - комплексни числа, в които -1 е реалната част, 2 или във втория случай -2 е имагинерната част. Въображаемата част също е реално число. Имагинерната част, умножена по имагинерната единица, означава вече имагинерно число.

Като цяло комплексното число има формата

z = х + iy ,

Където x, y– реални числа, – имагинерна единица. В редица приложни науки, например в електротехниката, електрониката, теорията на сигнала, имагинерната единица се обозначава с й. Реални числа x = Re(z)И y =Аз съм(з)са наречени реални и въображаеми частичисла z.Изразът се нарича алгебрична формаписане на комплексно число.

Всяко реално число е специален случайкомплексно число във формата . Имагинерното число също е частен случай на комплексно число .

Определение на множеството от комплексни числа C

Този израз се чете по следния начин: набор СЪС, състоящ се от такива елементи, че хИ гпринадлежат на множеството от реални числа Ри е имагинерна единица. Имайте предвид, че и т.н.

Две комплексни числа И са равни тогава и само тогава, когато техните реални и имагинерни части са равни, т.е. И .

Комплексните числа и функции се използват широко в науката и технологиите, особено в механиката, анализа на вериги и дизайна. променлив ток, аналогова електроника, теория и обработка на сигнали, теория на автоматичното управление и други приложни науки.

1. Аритметика на комплексни числа

Събирането на две комплексни числа се състои в събиране на техните реални и имагинерни части, т.е.

Съответно разликата на две комплексни числа

Комплексно число Наречен изчерпателно конюгатномер z =x+iy.

Комплексно спрегнатите числа z и z * се различават по знаците на имагинерната част. Очевидно е, че

.

Всяко равенство между сложни изрази остава валидно, ако навсякъде в това равенство аззаменен от - аз, т.е. отидете до равенството на спрегнатите числа. Числа азИ – азса алгебрично неразличими, тъй като .

Произведението (умножението) на две комплексни числа може да се изчисли по следния начин:

Деление на две комплексни числа:

Пример:

1. Сложна равнина

Комплексното число може да бъде представено графично в правоъгълна координатна система. Нека дефинираме правоъгълна координатна система в равнината (x, y).

На ос волние ще поставим реалните части х, нарича се реална (реална) ос, по оста Ой– въображаеми части гкомплексни числа. Нарича се въображаема ос. В този случай всяко комплексно число съответства на определена точка от равнината и такава равнина се нарича сложна равнина. Точка Акомплексната равнина ще съответства на вектора ОА.

Номер хНаречен абсцисатакомплексно число, число г – ордината.

Двойка комплексно спрегнати числа се представя от точки, разположени симетрично спрямо реалната ос.

Ако в самолета, който поставихме полярна координатна система, след това всяко комплексно число zопределен полярни координати. При което модулчисла е полярният радиус на точката и ъгълът - неговия полярен ъгъл или аргумент на комплексно число z.

Модул на комплексно число винаги неотрицателен. Аргументът на комплексно число не е еднозначно определен. Основната стойност на аргумента трябва да отговаря на условието . Всяка точка от комплексната равнина също съответства на общата стойност на аргумента. Аргументи, които се различават с кратно на 2π, се считат за равни. Аргументът номер нула е недефиниран.

Основната стойност на аргумента се определя от изразите:

Очевидно е, че

При което
, .

Представяне на комплексни числа zкато

Наречен тригонометрична формакомплексно число.

Пример.

1. Демонстративна формакомплексни числа

Разграждане в Серия Maclaurinза реални аргументни функции има формата:

За експоненциална функция с комплексен аргумент zразграждането е подобно

.

Разширението на реда на Maclaurin за експоненциалната функция на въображаемия аргумент може да бъде представено като

Получената идентичност се нарича Формула на Ойлер.

За отрицателен аргумент има формата

Като комбинирате тези изрази, можете да дефинирате следните изрази за синус и косинус

.

Използвайки формулата на Ойлер, от тригонометричната форма за представяне на комплексни числа

на разположение показателен(експоненциална, полярна) форма на комплексно число, т.е. представянето му във формата

,

Където - полярни координати на точката с правоъгълни координати (х,г).

Конюгатът на комплексно число се записва в експоненциална форма, както следва.

За експоненциална форма е лесно да се определят следните формули за умножение и деление на комплексни числа

Тоест в експоненциална форма произведението и делението на комплексни числа е по-просто, отколкото в алгебрична форма. При умножението модулите на факторите се умножават, а аргументите се събират. Това правило се прилага за произволен брой фактори. По-специално, когато умножавате комплексно число zНа азвектор zвърти се обратно на часовниковата стрелка на 90

При деление модулът на числителя се разделя на модула на знаменателя и аргументът на знаменателя се изважда от аргумента на числителя.

Използвайки експоненциалната форма на комплексни числа, можем да получим изрази за добре познатите тригонометрични идентичности. Например от самоличността

използвайки формулата на Ойлер, можем да напишем

Приравнявайки реалните и въображаемите части в този израз, получаваме изрази за косинуса и синуса на сбора от ъгли

1. Степени, корени и логаритми на комплексни числа

Повдигане на комплексно число на естествена степен нпроизведени по формулата

Пример. Нека изчислим .

Нека си представим число в тригонометрична форма

’

Прилагайки формулата за степенуване, получаваме

Като поставим стойността в израза r= 1, получаваме т.нар Формулата на Моавър, с който можете да определите изрази за синусите и косинусите на множество ъгли.

корен н-та степен на комплексно число zТо има нразлични стойности, определени от израза

Пример. Нека го намерим.

За да направим това, изразяваме комплексното число () в тригонометрична форма

.

Използвайки формулата за изчисляване на корена на комплексно число, получаваме

Логаритъм на комплексно число z- това е числото w, за което . Натурален логаритъмкомплексното число има безкраен брой стойности и се изчислява по формулата

Състои се от реална (косинус) и имагинерна (синус) част. Това напрежение може да бъде представено като вектор на дължината U m, начална фаза (ъгъл), въртяща се с ъглова скорост ω .

Освен това, ако се добавят сложни функции, тогава се добавят техните реални и имагинерни части. Ако една сложна функция се умножи по постоянна или реална функция, тогава нейните реални и въображаеми части се умножават по един и същ коефициент. Диференцирането/интегрирането на такава сложна функция се свежда до диференциране/интегриране на реалната и въображаемата част.

Например диференциране на сложния израз на стрес

е да го умножите по iω е реалната част на функцията f(z), и – имагинерна част от функцията. Примери: .

Значение zе представена от точка в комплексната равнина z и съответната стойност w- точка в комплексната равнина w. Когато се покаже w = f(z)равнинни линии zтрансформират в равнинни линии w, фигури от една равнина във фигури от друга, но формите на линиите или фигурите могат да се променят значително.

		Алгебрична форма на запис на комплексно число.................................. ......... ...................
		Равнината на комплексните числа............................................. ...................... ............................ ............................ ...
		Комплексно спрегнати числа............................................. .................... .............................. ..........................
	Операции с комплексни числа в алгебрична форма.................................................. ......... ....
		Събиране на комплексни числа.............................................. ......................................................... .................
		Изваждане на комплексни числа..................................................... .................... .............................. .....................
		Умножение на комплексни числа.............................................. ............................ ............................. ..................
		Деление на комплексни числа..................................................... .......... ............................................ ................ ...
	Тригонометрична форма на запис на комплексно число.................................. ......... ..........
	Действия с комплексни числа в тригонометрична форма.................................................. .........
		Умножение на комплексни числа в тригонометрична форма..................................... ........
		Деление на комплексни числа в тригонометрична форма..................................... ........ ...
		Повдигане на комплексно число на степен положително цяло число..................................... ...........
		Извличане на корен от положително цяло число от комплексно число..................................
		Повдигане на комплексно число на рационална степен..................................... .................. .....
		Сложна серия................................................. ... ................................................ ......... ....................
		Комплексни числови редове..................................... .................... .............................. ..........................
		Степенен ред в комплексната равнина..................................... ......... ............................
		Двустранен степенни редовев комплексната равнина.................................................. .....
		Функции на комплексна променлива............................................. .........................................................
		Основни елементарни функции ............................................. .......... ............................................ .
		Формули на Ойлер................................................. ... ................................................ ......... ....................
		Експоненциална форма на представяне на комплексно число.................................. ...................... .
		Връзка между тригонометрични и хиперболични функции..................................
		Логаритмична функция..................................................... ... ................................................ ......... ...
		Обща експоненциална и обща степенна функция..................................... ........ ...............
	Диференциране на функции на комплексна променлива..................................... ......... ...
		Условия на Коши-Риман ............................................. ..................................................... ........... ............
		Формули за изчисляване на производната............................................. ....... ...................................
		Свойства на операцията диференциране................................................. ...................... ............................ ...
		Свойства на реалните и имагинерните части на аналитична функция..................................

	Възстановяване на функция на комплексна променлива от нейната реална или имагинерна
		Метод номер 1. Използване на интеграл на кривата ............................................. .........
		Метод номер 2. Директно приложение на условията на Коши-Риман.....................................
		Метод No3. Чрез производната на търсената функция............................................. ......... .........
	Интегриране на функции на комплексна променлива............................................. ......... ..........
	Интегрална формула на Коши................................................. ..................................................... ........... ...
	Разширяване на функциите в сериите Тейлър и Лоран.................................................. .......... ........................
	Нули и особени точки на функция на комплексна променлива.................................................. ............. .....
		Нули на функция на комплексна променлива..................................... .......... .......................
		Изолирани особени точки на функция на комплексна променлива..................................

14.3 Точка в безкрайност като особена точка на функция на комплексна променлива

	Удръжки................................................. ......................................................... ............. ..................................... ...
		Приспадане в крайната точка............................................. ...... ............................................ ............ ......
		Остатък на функция в безкрайна точка..................................... ........... ...............
	Изчисляване на интеграли с помощта на остатъци............................................. ....... ............................
	Въпроси за самопроверка ............................................. ............................ ............................. ............................. ........
	Литература................................................. ................................................. ...... ...................................
	Предметен индекс................................................. ................................................. ...... ..............

Предговор

Правилното разпределяне на времето и усилията при подготовката за теоретичната и практическата част на изпит или сертифициране на модул е ​​доста трудно, особено след като винаги няма достатъчно време по време на сесията. И както показва практиката, не всеки може да се справи с това. В резултат на това по време на изпита някои студенти решават задачи правилно, но се затрудняват да отговорят на най-простите теоретични въпроси, докато други могат да формулират теорема, но не могат да я приложат.

Настоящите указания за подготовка за изпита по дисциплината „Теория на функциите на комплексната променлива” (ТФКП) са опит да се разреши това противоречие и да се осигури едновременно повторение на теоретичния и практическия материал от дисциплината. Водени от принципа „Теорията без практика е мъртва, практиката без теория е сляпа“, те съдържат както теоретичните положения на курса на ниво дефиниции и формулировки, така и примери, илюстриращи приложението на всяка дадена теоретична позиция и по този начин улесняващи неговото запаметяване и разбиране.

Целта на предл методически препоръки– помогнете на ученика да се подготви за изпита начално ниво. С други думи, съставен е разширен работен справочник, съдържащ основните точки, използвани в часовете по курса TFKP и необходими при изпълнение домашна работаи подготовка за контролни събития. Освен това самостоятелна работаученици, това електронно учебно издание може да се използва при провеждане на занятия в интерактивна форма с помощта на електронна дъска или за поставяне в система за дистанционно обучение.

Моля, имайте предвид, че тази работа не замества нито учебници, нито бележки за лекции. За по-задълбочено проучване на материала се препоръчва да се обърнете към съответните раздели, публикувани от MSTU. Н.Е. Бауман основен учебник.

В края на помагалото има списък с препоръчителна литература и предметен указател, който включва всичко подчертано в текста удебелен курсивусловия. Индексът се състои от хипервръзки към раздели, в които тези термини са строго дефинирани или описани и където са дадени примери за илюстриране на тяхното използване.

Ръководството е предназначено за студенти от 2-ра година на всички факултети на MSTU. Н.Е. Бауман.

1. Алгебрична форма на запис на комплексно число

Запис на формата z = x + iy, където x, y са реални числа, i е имагинерна единица (т.е. i 2 = − 1)

се нарича алгебрична форма на запис на комплексното число z. В този случай x се нарича реална част от комплексното число и се означава Re z (x = Re z), y се нарича имагинерна част от комплексното число и се означава Im z (y = Im z).

Пример. Комплексното число z = 4 − 3i има реална част Re z = 4 и имагинерна част Im z = − 3 .

2. Комплексна числова равнина

IN разглеждат се теории на функциите на комплексна променливакомплексна числова равнина, което се обозначава с или с помощта на букви, обозначаващи комплексни числа z, w и т.н.

Хоризонталната ос на комплексната равнина се нарича реална ос, върху него са поставени реални числа z = x + 0 i = x.

Вертикалната ос на комплексната равнина се нарича въображаема ос;

3. Комплексно спрегнати числа

Наричат ​​се числата z = x + iy и z = x − iy комплексно спрегнат. В комплексната равнина те съответстват на точки, които са симетрични спрямо реалната ос.

4. Операции с комплексни числа в алгебрична форма

4.1 Събиране на комплексни числа

Сумата от две комплексни числа

z 1 = x 1 + iy 1

и z 2 = x 2 + iy 2 се нарича комплексно число

z 1 + z 2

= (x 1 + iy 1 ) + (x 2 + iy 2 ) = (x 1 + x 2 ) + i (y 1 + y 2 ) .

операция

допълнение

комплексни числа е подобна на операцията за добавяне на алгебрични биноми.

Пример. Сумата от две комплексни числа z 1 = 3 + 7i и z 2

= −1 +2 i

ще бъде комплексно число

z 1 + z 2 = (3 +7 i ) +(−1 +2 i ) = (3 −1 ) +(7 +2 ) i = 2 +9 i .

очевидно,

обща сума

конюгат

е

истински

z + z = (x + iy) + (x − iy) = 2 x = 2 Re z .

4.2 Изваждане на комплексни числа

Разликата на две комплексни числа z 1 = x 1 + iy 1

X 2 +iy 2

Наречен

изчерпателен

число z 1 − z 2 = (x 1 + iy 1 ) − (x 2 + iy 2 ) = (x 1 − x 2 ) + i (y 1 − y 2 ) .

Пример. Разликата на две комплексни числа

z 1 = 3 −4 i

и z 2

= −1 +2 i

ще има цялостна

число z 1 − z 2 = (3 − 4i ) − (− 1+ 2i ) = (3 − (− 1) ) + (− 4 − 2) i = 4 − 6i .

По разлика

комплексно спрегнат

е

z − z = (x + iy) − (x − iy) = 2 iy = 2 i Im z .

4.3 Умножение на комплексни числа

Произведение на две комплексни числа

z 1 = x 1 + iy 1

и z 2 = x 2 + iy 2

наречен комплекс

z 1z 2 = (x 1 + iy 1 )(x 2 + iy 2 ) = x 1x 2 + iy 1x 2 + iy 2 x 1 + i 2 y 1 y 2

= (x 1x 2 − y 1 y 2 ) + i (y 1x 2 + y 2 x ) .

По този начин операцията за умножаване на комплексни числа е подобна на операцията за умножение на алгебрични биноми, като се вземе предвид фактът, че i 2 = − 1.

ОПРЕДЕЛЕНИЕ

Алгебричната форма на комплексно число е да напишете комплексното число \(\z\) във формата \(\z=x+i y\), където \(\x\) и \(\y\) са реални числа , \(\i\ ) - имагинерна единица, удовлетворяваща отношението \(\i^(2)=-1\)

Числото \(\ x \) се нарича реална част от комплексното число \(\ z \) и се означава с \(\ x=\име на оператор(Re) z \)

Числото \(\y\) се нарича имагинерна част от комплексното число \(\z\) и се означава с \(\y=\operatorname(Im) z\)

Например:

Комплексното число \(\ z=3-2 i \) и неговото присъединено число \(\ \overline(z)=3+2 i \) са записани в алгебрична форма.

Имагинерната величина \(\ z=5 i \) е записана в алгебрична форма.

Освен това, в зависимост от проблема, който решавате, можете да преобразувате комплексно число в тригонометрично или експоненциално число.

Задача

Запишете числото \(\z=\frac(7-i)(4)+13\) в алгебрична форма, намерете неговите реални и имагинерни части, както и спрегнатото му число.

Решение.

Използвайки термина деление на дроби и правилото за събиране на дроби, получаваме:

\(\z=\frac(7-i)(4)+13=\frac(7)(4)+13-\frac(i)(4)=\frac(59)(4)-\frac( 1)(4)i\)

Следователно реалната част на комплексното число \(\ z=\frac(5 g)(4)-\frac(1)(4) i \) е числото \(\ x=\име на оператор(Re) z= \frac(59) (4) \) , имагинерната част е числото \(\ y=\operatorname(Im) z=-\frac(1)(4) \)

Конюгирано число: \(\ \overline(z)=\frac(59)(4)+\frac(1)(4) i \)

Отговор

\(\ z=\frac(59)(4)-\frac(1)(4) i \), \(\ \operatorname(Re) z=\frac(59)(4) \), \(\ \operatorname(Im) z=-\frac(1)(4) \), \(\ \overline(z)=\frac(59)(4)+\frac(1)(4) i \)

Действия на комплексни числа при сравнение на алгебрична форма

Две комплексни числа \(\ z_(1)=x_(1)+i y_(1) \) се казва, че са равни, ако \(\ x_(1)=x_(2) \), \(\ y_(1 )= y_(2) \) т.е. Техните реални и имагинерни части са равни.

Задача

Определете за кои x и y двете комплексни числа \(\ z_(1)=13+y i \) и \(\ z_(2)=x+5 i \) са равни.

Решение

По дефиниция две комплексни числа са равни, ако техните реална и имагинерна част са равни, т.е. \(\x=13\), \(\y=5\).

Отговор \(\x=13\), \(\y=5\)

допълнение

Добавянето на комплексни числа \(\z_(1)=x_(1)+i y_(1)\) се извършва чрез директно сумиране на реалната и имагинерната част:

\(\ z_(1)+z_(2)=x_(1)+i y_(1)+x_(2)+i y_(2)=\ляво(x_(1)+x_(2)\дясно) +i\наляво(y_(1)+y_(2)\вдясно) \)

Задача

Намерете сумата от комплексни числа \(\ z_(1)=-7+5 i \), \(\ z_(2)=13-4 i \)

Решение.

Реалната част на комплексно число \(\ z_(1)=-7+5 i \) е числото \(\ x_(1)=\operatorname(Re) z_(1)=-7 \) , имагинерната част е числото \( \ y_(1)=\mathrm(Im) \), \(\ z_(1)=5 \) . Реалните и имагинерните части на комплексното число \(\ z_(2)=13-4 i \) са равни на \(\ x_(2)=\име на оператор(Re) z_(2)=13 \) и \( \ y_(2) съответно )=\име на оператор(Im) z_(2)=-4 \) .

Следователно сборът на комплексните числа е:

\(\ z_(1)+z_(2)=\наляво(x_(1)+x_(2)\вдясно)+i\наляво(y_(1)+y_(2)\вдясно)=(-7+ 13)+i(5-4)=6+i \)

Отговор

\(\ z_(1)+z_(2)=6+i \)

Прочетете повече за добавянето на комплексни числа в отделна статия: Събиране на комплексни числа.

Изваждане

Изваждането на комплексни числа \(\z_(1)=x_(1)+i y_(1)\) и \(\z_(2)=x_(2)+i y_(2)\) се извършва чрез директно изваждане реалните и въображаемите части:

\(\ z_(1)-z_(2)=x_(1)+i y_(1)-\left(x_(2)+i y_(2)\right)=x_(1)-x_(2) +\left(i y_(1)-i y_(2)\right)=\left(x_(1)-x_(2)\right)+i\left(y_(1)-y_(2)\right ) \)

Задача

намерете разликата на комплексните числа \(\ z_(1)=17-35 i \), \(\ z_(2)=15+5 i \)

Решение.

Намерете реалните и въображаемите части на комплексни числа \(\ z_(1)=17-35 i \), \(\ z_(2)=15+5 i \) :

\(\ x_(1)=\име на оператор(Re) z_(1)=17, x_(2)=\име на оператор(Re) z_(2)=15 \)

\(\ y_(1)=\име на оператор(Im) z_(1)=-35, y_(2)=\име на оператор(Im) z_(2)=5 \)

Следователно разликата на комплексните числа е:

\(\ z_(1)-z_(2)=\наляво(x_(1)-x_(2)\вдясно)+i\наляво(y_(1)-y_(2)\вдясно)=(17-15 )+i(-35-5)=2-40 i \)

Отговор

\(\ z_(1)-z_(2)=2-40 i \) умножение

Умножението на комплексни числа \(\ z_(1)=x_(1)+i y_(1) \) и \(\ z_(2)=x_(2)+i y_(2) \) се извършва чрез директно създаване числа в алгебрична форма, като се вземе предвид свойството на имагинерната единица \(\i^(2)=-1\) :

\(\ z_(1) \cdot z_(2)=\наляво(x_(1)+i y_(1)\вдясно) \cdot\наляво(x_(2)+i y_(2)\вдясно)=x_ (1) \cdot x_(2)+i^(2) \cdot y_(1) \cdot y_(2)+\left(x_(1) \cdot i y_(2)+x_(2) \cdot i y_(1)\надясно)=\)

\(\ =\наляво(x_(1) \cdot x_(2)-y_(1) \cdot y_(2)\вдясно)+i\наляво(x_(1) \cdot y_(2)+x_(2 ) \cdot y_(1)\right) \)

Задача

Намерете произведението на комплексни числа \(\ z_(1)=1-5 i \)

Решение.

Комплекс от комплексни числа:

\(\ z_(1) \cdot z_(2)=\наляво(x_(1) \cdot x_(2)-y_(1) \cdot y_(2)\вдясно)+i\наляво(x_(1) \cdot y_(2)+x_(2) \cdot y_(1)\right)=(1 \cdot 5-(-5) \cdot 2)+i(1 \cdot 2+(-5) \cdot 5 )=15-23 i\)

Отговор

\(\ z_(1) \cdot z_(2)=15-23 i \) деление

Факторът на комплексните числа \(\z_(1)=x_(1)+i y_(1)\) и \(\z_(2)=x_(2)+i y_(2)\) се определя чрез умножаване числителя и знаменателя към спрегнатото число със знаменателя:

\(\ \frac(z_(1))(z_(2))=\frac(x_(1)+i y_(1))(x_(2)+i y_(2))=\frac(\left (x_(1)+i y_(1)\вдясно)\наляво(x_(2)-i y_(2)\вдясно))(\наляво(x_(2)+i y_(2)\вдясно)\наляво (x_(2)-i y_(2)\right))=\frac(x_(1) \cdot x_(2)+y_(1) \cdot y_(2))(x_(2)^(2) +y_(2)^(2))+i \frac(x_(2) \cdot y_(1)-x_(1) \cdot y_(2))(x_(2)^(2)+y_(2 )^(2)) \)

Задача

Да разделим числото 1 на комплексното число \(\z=1+2i\).

Решение.

Тъй като имагинерната част от реалното число 1 е нула, факторът е:

\(\ \frac(1)(1+2 i)=\frac(1 \cdot 1)(1^(2)+2^(2))-i \frac(1 \cdot 2)(1^( 2)+2^(2))=\frac(1)(5)-i \frac(2)(5)\)

Отговор

\(\ \frac(1)(1+2 i)=\frac(1)(5)-i \frac(2)(5) \)

План на урока.

1. Организационен момент.

2. Представяне на материала.

3. Домашна работа.

4. Обобщаване на урока.

По време на часовете

I. Организационен момент.

II. Представяне на материала.

Мотивация.

Разширяването на набора от реални числа се състои в добавяне на нови числа (въображаеми) към реалните числа. Въвеждането на тези числа се дължи на невъзможността да се извлече корен от отрицателно число в множеството от реални числа.

Запознаване с понятието комплексно число.

Във формуляра са записани въображаеми числа, с които допълваме реални числа би, Където азе въображаема единица и i 2 = - 1.

Въз основа на това получаваме следната дефиниция на комплексно число.

Определение. Комплексното число е израз на формата а+би, Където аИ b- реални числа. В този случай са изпълнени следните условия:

а) Две комплексни числа a 1 + b 1 iИ a 2 + b 2 iравно тогава и само ако a 1 = a 2, b 1 = b 2.

б) Събирането на комплексни числа се определя от правилото:

(a 1 + b 1 i) + (a 2 + b 2 i) = (a 1 + a 2) + (b 1 + b 2) i.

в) Умножението на комплексни числа се определя от правилото:

(a 1 + b 1 i) (a 2 + b 2 i) = (a 1 a 2 - b 1 b 2) + (a 1 b 2 - a 2 b 1) i.

Алгебрична форма на комплексно число.

Записване на комплексно число във формата а+бисе нарича алгебрична форма на комплексно число, където А– реална част, бие въображаемата част и b- реално число.

Комплексно число а+бисе счита за равно на нула, ако неговите реална и имагинерна част са равни на нула: a = b = 0

Комплексно число а+бипри b = 0се счита за същото като реално число а: a + 0i = a.

Комплексно число а+бипри а = 0се нарича чисто въображаема и се обозначава би: 0 + bi = bi.

Две комплексни числа z = a + biИ = a – bi, различаващи се само по знака на въображаемата част, се наричат ​​спрегнати.

Операции с комплексни числа в алгебрична форма.

Можете да извършвате следните операции върху комплексни числа в алгебрична форма.

1) Добавяне.

Определение. Сума от комплексни числа z 1 = a 1 + b 1 iИ z 2 = a 2 + b 2 iсе нарича комплексно число z, чиято реална част е равна на сумата от реалните части z 1И z 2, а имагинерната част е сумата от имагинерните части на числата z 1И z 2, това е z = (a 1 + a 2) + (b 1 + b 2)i.

Числа z 1И z 2се наричат ​​термини.

Събирането на комплексни числа има следните свойства:

1º. Комутативност: z 1 + z 2 = z 2 + z 1.

2º. Асоциативност: (z 1 + z 2) + z 3 = z 1 + (z 2 + z 3).

3º. Комплексно число –а –бинарича обратното на комплексно число z = a + bi. Комплексно число, противоположно на комплексно число z, означено -z. Сума от комплексни числа zИ -zравно на нула: z + (-z) = 0

Пример 1: Извършете събиране (3 – i) + (-1 + 2i).

(3 – i) + (-1 + 2i) = (3 + (-1)) + (-1 + 2) i = 2 + 1i.

2) Изваждане.

Определение.Извадете от комплексно число z 1комплексно число z 2 z,Какво z + z 2 = z 1.

Теорема. Разликата между комплексните числа съществува и е уникална.

Пример 2: Извършете изваждане (4 – 2i) - (-3 + 2i).

(4 – 2i) - (-3 + 2i) = (4 - (-3)) + (-2 - 2) i = 7 – 4i.

3) Умножение.

Определение. Произведение на комплексни числа z 1 =a 1 +b 1 iИ z 2 =a 2 +b 2 iсе нарича комплексно число z, определени от равенството: z = (a 1 a 2 – b 1 b 2) + (a 1 b 2 + a 2 b 1)i.

Числа z 1И z 2се наричат ​​фактори.

Умножението на комплексни числа има следните свойства:

1º. Комутативност: z 1 z 2 = z 2 z 1.

2º. Асоциативност: (z 1 z 2)z 3 = z 1 (z 2 z 3)

3º. Разпределимост на умножението спрямо събирането:

(z 1 + z 2) z 3 = z 1 z 3 + z 2 z 3.

4º. z = (a + bi)(a – bi) = a 2 + b 2- реално число.

На практика умножението на комплексни числа се извършва съгласно правилото за умножаване на сбор по сбор и разделяне на реалната и имагинерната част.

В следващия пример ще разгледаме умножаването на комплексни числа по два начина: по правило и чрез умножаване на сбор по сбор.

Пример 3: Направете умножението (2 + 3i) (5 – 7i).

1 начин. (2 + 3i) (5 – 7i) = (2× 5 – 3× (- 7)) + (2× (- 7) + 3× 5)i = = (10 + 21) + (- 14 + 15 )i = 31 + i.

Метод 2. (2 + 3i) (5 – 7i) = 2 × 5 + 2 × (- 7i) + 3i × 5 + 3i × (- 7i) = = 10 – 14i + 15i + 21 = 31 + i.

4) Разделяне.

Определение. Разделете комплексно число z 1към комплексно число z 2, означава да се намери такова комплексно число z, Какво z · z 2 = z 1.

Теорема.Коефициентът на комплексните числа съществува и е уникален, ако z 2 ≠ 0 + 0i.

На практика частното на комплексните числа се намира чрез умножаване на числителя и знаменателя по конюгата на знаменателя.

Позволявам z 1 = a 1 + b 1 i, z 2 = a 2 + b 2 i, Тогава

.

В следващия пример ще извършим деление, като използваме формулата и правилото за умножение по числото, спрегнато към знаменателя.

Пример 4. Намерете частното .

5) Повишаване на положителна цяла степен.

а) Степени на имагинерната единица.

Възползвайки се от равенството i 2 = -1, лесно е да се дефинира всяка положителна степен на цяло число на имагинерната единица. Ние имаме:

i 3 = i 2 i = -i,

i 4 = i 2 i 2 = 1,

i 5 = i 4 i = i,

i 6 = i 4 i 2 = -1,

i 7 = i 5 i 2 = -i,

i 8 = i 6 i 2 = 1и т.н.

Това показва, че градусните стойности аз н, Където н– цяло положително число, се повтаря периодично, докато индикаторът нараства с 4 .

Затова да се вдигне бройката азна положителна цяла степен, трябва да разделим показателя на 4 и изградете азна степен, чийто показател е равен на остатъка от делението.

Пример 5: Изчислете: (i 36 + i 17) i 23.

i 36 = (i 4) 9 = 1 9 = 1,

i 17 = i 4 × 4+1 = (i 4) 4 × i = 1 · i = i.

i 23 = i 4 × 5+3 = (i 4) 5 × i 3 = 1 · i 3 = - i.

(i 36 + i 17) · i 23 = (1 + i) (- i) = - i + 1= 1 – i.

б) Повишаването на комплексно число на цяло положително число се извършва съгласно правилото за повдигане на бином на съответната степен, тъй като това е частен случай на умножение на еднакви комплексни множители.

Пример 6: Изчислете: (4 + 2i) 3

(4 + 2i) 3 = 4 3 + 3× 4 2 × 2i + 3× 4× (2i) 2 + (2i) 3 = 64 + 96i – 48 – 8i = 16 + 88i.