كلمات معقدةالنطق

مكعب رباعي الأبعاد. المكعب السيبراني - الخطوة الأولى نحو البعد الرابع ما اسم المكعب ذو الجوانب المختلفة

Tesseract عبارة عن مكعب فائق رباعي الأبعاد - مكعب في الفضاء رباعي الأبعاد.
وفقا لقاموس أكسفورد، فإن كلمة tesseract تم صياغتها واستخدامها في عام 1888 من قبل تشارلز هوارد هينتون (1853-1907) في كتابه "عصر جديد من الفكر". في وقت لاحق، أطلق بعض الناس على نفس الشكل اسم رباعي المكعب (اليونانية τετρα - أربعة) - مكعب رباعي الأبعاد.
يتم تعريف التسراكت العادي في الفضاء الإقليدي رباعي الأبعاد على أنه بدن محدب من النقاط (±1، ±1، ±1، ±1). بمعنى آخر يمكن تمثيلها بالمجموعة التالية:
[-1, 1]^4 = ((x_1,x_2,x_3,x_4) : -1 = يقتصر tesseract على ثمانية مستويات زائدة x_i= +- 1, i=1,2,3,4 ، تقاطعها مع التسراكت نفسه يحدده وجوه ثلاثية الأبعاد (وهي عبارة عن مكعبات عادية) يتقاطع كل زوج من الوجوه ثلاثية الأبعاد غير المتوازية لتشكل وجوهًا ثنائية الأبعاد (مربعات) وما إلى ذلك. أخيرًا، يحتوي التسراكت على 8 وجوه ثلاثية الأبعاد و24 وجهًا ثنائي الأبعاد و32 حرفًا و16 الرؤوس.
وصف شعبي
دعونا نحاول أن نتخيل كيف سيبدو المكعب الفائق دون ترك مساحة ثلاثية الأبعاد.
في "مساحة" أحادية البعد - على الخط - نختار قطعة AB بطول L. على مستوى ثنائي الأبعاد على مسافة L من AB، نرسم قطعة DC موازية لها ونربط طرفيها. والنتيجة هي CDBA مربع. وبتكرار هذه العملية مع المستوى، نحصل على مكعب ثلاثي الأبعاد CDBAGHFE. وبإزاحة المكعب في البعد الرابع (عموديًا على الأبعاد الثلاثة الأولى) مسافة L، نحصل على المكعب الفائق CDBAGHFEKLJIOPNM.
يعمل الجزء أحادي البعد AB كجانب للمربع CDBA ثنائي الأبعاد، والمربع - كجانب للمكعب CDBAGHFE، والذي، بدوره، سيكون جانب المكعب الفائق رباعي الأبعاد. القطعة المستقيمة لها نقطتان حدوديتان، والمربع له أربعة رؤوس، والمكعب له ثمانية. في المكعب الفائق رباعي الأبعاد، سيكون هناك 16 رأسًا: 8 رؤوس من المكعب الأصلي و8 رؤوس منزاحة في البعد الرابع. يحتوي على 32 حرفًا - 12 منها تعطي الموضع الأولي والنهائي للمكعب الأصلي، و8 حواف أخرى "ترسم" رؤوسه الثمانية، التي انتقلت إلى البعد الرابع. يمكن تطبيق نفس المنطق على وجوه المكعب الزائد. في الفضاء ثنائي الأبعاد يوجد واحد فقط (المربع نفسه)، والمكعب به 6 وجوه (وجهان من المربع المتحرك وأربعة أخرى تصف جوانبه). يحتوي المكعب الفائق رباعي الأبعاد على 24 وجهًا مربعًا - 12 مربعًا من المكعب الأصلي في موضعين و12 مربعًا من حوافه الاثني عشر.
مثلما أن أضلاع المربع عبارة عن 4 أجزاء أحادية البعد، وأضلاع (أوجه) المكعب عبارة عن 6 مربعات ثنائية الأبعاد، كذلك بالنسبة لـ "المكعب رباعي الأبعاد" (تيسراكت) تكون أضلاعه 8 مكعبات ثلاثية الأبعاد . تكون مساحات الأزواج المتقابلة من مكعبات التسراكت (أي المساحات ثلاثية الأبعاد التي تنتمي إليها هذه المكعبات) متوازية. في الشكل، هذه هي المكعبات: CDBAGHFE وKLJIOPNM وCDBAKLJI وGHFEOPNM وEFBAMNJI وGHDCOPLK وCKIAGOME وDLJBHPNF.
وبالمثل، يمكننا مواصلة التفكير في المكعبات الزائدة أكثرالأبعاد، ولكن من المثير للاهتمام أن نرى كيف سيبدو المكعب الفائق رباعي الأبعاد بالنسبة لنا، نحن سكان الفضاء ثلاثي الأبعاد. لهذا سوف نستخدم طريقة القياس المألوفة بالفعل.
لنأخذ المكعب السلكي ABCDHEFG وننظر إليه بعين واحدة من جانب الحافة. سوف نرى ويمكننا رسم مربعين على المستوى (حافتيه القريبة والبعيدة)، متصلتين بأربعة خطوط - حواف جانبية. وبالمثل، فإن المكعب الفائق رباعي الأبعاد في الفضاء ثلاثي الأبعاد سيبدو وكأنه "صندوقين" مكعبين مدرجين في بعضهما البعض ومتصلين بثمانية حواف. في هذه الحالة، سيتم إسقاط "الصناديق" نفسها - الوجوه ثلاثية الأبعاد - على مساحتنا "، وسوف تمتد الخطوط التي تربطها في اتجاه المحور الرابع. يمكنك أيضًا محاولة تخيل المكعب ليس في الإسقاط، ولكن في صورة مكانية.
تمامًا كما يتكون المكعب ثلاثي الأبعاد من مربع مُزاح بطول وجهه، فإن المكعب المُزاح إلى البعد الرابع سيشكل مكعبًا زائدًا. إنه محدود بثمانية مكعبات، والتي ستبدو في المستقبل وكأنها نوع من الجمال شخصية معقدة. يتكون المكعب الفائق رباعي الأبعاد في حد ذاته من عدد لا حصر له من المكعبات، تمامًا كما يمكن "تقطيع" المكعب ثلاثي الأبعاد إلى عدد لا حصر له من المربعات المسطحة.
من خلال قطع الوجوه الستة لمكعب ثلاثي الأبعاد، يمكنك تحليله إلى شكل مسطح - وهو تطور. سيكون له مربع على كل جانب من الوجه الأصلي بالإضافة إلى وجه آخر - الوجه المقابل له. وسيتألف التطوير ثلاثي الأبعاد للمكعب الفائق رباعي الأبعاد من المكعب الأصلي، وستة مكعبات "تنمو" منه، بالإضافة إلى واحد آخر - "الوجه الفائق" النهائي.
خصائص tesseract هي امتداد للخصائص الأشكال الهندسيةالبعد الأصغر إلى الفضاء رباعي الأبعاد.

النقاط (±1، ±1، ±1، ±1). بمعنى آخر يمكن تمثيلها بالمجموعة التالية:

يقتصر التسراكت على ثمانية مستويات مفرطة، يحدد تقاطعها مع التسراكت نفسه وجوهه ثلاثية الأبعاد (وهي مكعبات عادية). يتقاطع كل زوج من الوجوه غير المتوازية ثلاثية الأبعاد لتشكل وجوهًا ثنائية الأبعاد (مربعات)، وهكذا. أخيرًا، يحتوي التسراكت على 8 وجوه ثلاثية الأبعاد، و24 وجهًا ثنائي الأبعاد، و32 حرفًا، و16 رأسًا.

وصف شعبي

دعونا نحاول أن نتخيل كيف سيبدو المكعب الفائق دون ترك مساحة ثلاثية الأبعاد.

في "مساحة" أحادية البعد - على الخط - نختار قطعة AB بطول L. على مستوى ثنائي الأبعاد على مسافة L من AB، نرسم قطعة DC موازية لها ونربط طرفيها. والنتيجة هي CDBA مربع. وبتكرار هذه العملية مع المستوى، نحصل على مكعب ثلاثي الأبعاد CDBAGHFE. وبإزاحة المكعب في البعد الرابع (عموديًا على الأبعاد الثلاثة الأولى) مسافة L، نحصل على المكعب الفائق CDBAGHFEKLJIOPNM.

بناء tesseract على متن الطائرة

يعمل الجزء أحادي البعد AB كجانب للمربع CDBA ثنائي الأبعاد، والمربع - كجانب للمكعب CDBAGHFE، والذي، بدوره، سيكون جانب المكعب الفائق رباعي الأبعاد. القطعة المستقيمة لها نقطتان حدوديتان، والمربع له أربعة رؤوس، والمكعب له ثمانية. في المكعب الفائق رباعي الأبعاد، سيكون هناك 16 رأسًا: 8 رؤوس من المكعب الأصلي و8 رؤوس منزاحة في البعد الرابع. يحتوي على 32 حرفًا - 12 منها تعطي الموضع الأولي والنهائي للمكعب الأصلي، و8 حواف أخرى "ترسم" رؤوسه الثمانية، التي انتقلت إلى البعد الرابع. يمكن تطبيق نفس المنطق على وجوه المكعب الزائد. في الفضاء ثنائي الأبعاد يوجد واحد فقط (المربع نفسه)، والمكعب به 6 وجوه (وجهان من المربع المتحرك وأربعة أخرى تصف جوانبه). يحتوي المكعب الفائق رباعي الأبعاد على 24 وجهًا مربعًا - 12 مربعًا من المكعب الأصلي في موضعين و12 مربعًا من حوافه الاثني عشر.

مثلما أن أضلاع المربع عبارة عن 4 أجزاء أحادية البعد، وأضلاع (أوجه) المكعب عبارة عن 6 مربعات ثنائية الأبعاد، كذلك بالنسبة لـ "المكعب رباعي الأبعاد" (تيسراكت) تكون أضلاعه 8 مكعبات ثلاثية الأبعاد . تكون مساحات الأزواج المتقابلة من مكعبات التسراكت (أي المساحات ثلاثية الأبعاد التي تنتمي إليها هذه المكعبات) متوازية. في الشكل، هذه هي المكعبات: CDBAGHFE وKLJIOPNM وCDBAKLJI وGHFEOPNM وEFBAMNJI وGHDCOPLK وCKIAGOME وDLJBHPNF.

بطريقة مماثلة، يمكننا مواصلة التفكير في المكعبات الفائقة ذات عدد أكبر من الأبعاد، ولكن من المثير للاهتمام أن نرى كيف سيبدو المكعب الفائق رباعي الأبعاد بالنسبة لنا، نحن سكان الفضاء ثلاثي الأبعاد. لهذا سوف نستخدم طريقة القياس المألوفة بالفعل.

لنأخذ المكعب السلكي ABCDHEFG وننظر إليه بعين واحدة من جانب الحافة. سوف نرى ويمكننا رسم مربعين على المستوى (حافتيه القريبة والبعيدة)، متصلتين بأربعة خطوط - حواف جانبية. وبالمثل، فإن المكعب الفائق رباعي الأبعاد في الفضاء ثلاثي الأبعاد سيبدو وكأنه "صندوقين" مكعبين مدرجين في بعضهما البعض ومتصلين بثمانية حواف. في هذه الحالة، سيتم إسقاط "الصناديق" نفسها - الوجوه ثلاثية الأبعاد - على مساحتنا "، وسوف تمتد الخطوط التي تربطها في اتجاه المحور الرابع. يمكنك أيضًا محاولة تخيل المكعب ليس في الإسقاط، ولكن في صورة مكانية.

تمامًا كما يتكون المكعب ثلاثي الأبعاد من مربع مُزاح بطول وجهه، فإن المكعب المُزاح إلى البعد الرابع سيشكل مكعبًا زائدًا. إنه محدود بثمانية مكعبات، والتي ستبدو في المنظور وكأنها شخصية معقدة إلى حد ما. يتكون المكعب الفائق رباعي الأبعاد في حد ذاته من عدد لا حصر له من المكعبات، تمامًا كما يمكن "تقطيع" المكعب ثلاثي الأبعاد إلى عدد لا حصر له من المربعات المسطحة.

من خلال قطع الوجوه الستة لمكعب ثلاثي الأبعاد، يمكنك تحليله إلى شكل مسطح - وهو تطور. سيكون له مربع على كل جانب من الوجه الأصلي بالإضافة إلى وجه آخر - الوجه المقابل له. وسيتألف التطوير ثلاثي الأبعاد للمكعب الفائق رباعي الأبعاد من المكعب الأصلي، وستة مكعبات "تنمو" منه، بالإضافة إلى واحد آخر - "الوجه الفائق" النهائي.

تمثل خصائص التسراكت استمرارًا لخصائص الأشكال الهندسية ذات البعد الأدنى في الفضاء رباعي الأبعاد.

التوقعات

إلى الفضاء ثنائي الأبعاد

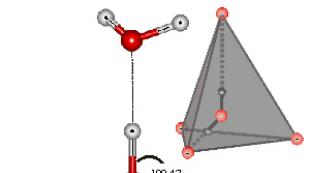
من الصعب تخيل هذا الهيكل، ولكن من الممكن عرض tesseract في مساحات ثنائية أو ثلاثية الأبعاد. بالإضافة إلى ذلك، فإن الإسقاط على المستوى يجعل من السهل فهم موقع رؤوس المكعب الزائد. بهذه الطريقة، من الممكن الحصول على صور لم تعد تعكس العلاقات المكانية داخل التسراكت، ولكنها توضح بنية اتصال قمة الرأس، كما في الأمثلة التالية:

الصورة الثالثة توضح التسراكت في القياس المتساوي بالنسبة لنقطة البناء. يعد هذا التمثيل مهمًا عند استخدام tesseract كأساس لشبكة طوبولوجية لربط معالجات متعددة في الحوسبة المتوازية.

إلى الفضاء ثلاثي الأبعاد

يمثل أحد إسقاطات tesseract على مساحة ثلاثية الأبعاد مكعبين متداخلين ثلاثي الأبعاد، وترتبط القمم المقابلة لهما بقطاعات. المكعبات الداخلية والخارجية لها أحجام مختلفة في الفضاء ثلاثي الأبعاد، ولكنها في الفضاء رباعي الأبعاد تكون مكعبات متساوية. لفهم المساواة بين جميع مكعبات التسراكت، تم إنشاء نموذج التسراكت الدوار.

الأهرامات الستة المقطوعة على طول حواف التسراكت هي صور لستة مكعبات متساوية. ومع ذلك، فإن هذه المكعبات عبارة عن tesseract مثل المربعات (الوجوه) بالنسبة للمكعب. لكن في الحقيقة، يمكن تقسيم التسراكت إلى عدد لا نهائي من المكعبات، كما يمكن تقسيم المكعب إلى عدد لا نهائي من المربعات، أو المربع إلى عدد لا نهائي من الأجزاء.

إسقاط آخر مثير للاهتمام للتسراكت على مساحة ثلاثية الأبعاد هو الاثني عشر وجهًا معينيًا بأقطاره الأربعة التي تربط أزواجًا من القمم المتقابلة في زوايا كبيرة من المعينات. في هذه الحالة، يتم إسقاط 14 من أصل 16 رأسًا من التسراكت في 14 رأسًا من الاثني عشر وجهًا معينيًا، وتتزامن إسقاطات القممتين المتبقيتين في مركزها. في مثل هذا الإسقاط على الفضاء ثلاثي الأبعاد، يتم الحفاظ على المساواة والتوازي لجميع الجوانب أحادية البعد وثنائية الأبعاد وثلاثية الأبعاد.

زوج ستيريو

يتم تصوير زوج استريو من tesseract على شكل إسقاطين على مساحة ثلاثية الأبعاد. تم تصميم صورة التسراكت هذه لتمثيل العمق باعتباره البعد الرابع. يتم عرض زوج الاستريو بحيث ترى كل عين واحدة فقط من هذه الصور، وتظهر صورة مجسمة تعيد إنتاج عمق التسراكت.

تفريغ Tesseract

يمكن طي سطح التسراكت إلى ثمانية مكعبات (على غرار الطريقة التي يمكن بها طي سطح المكعب إلى ستة مربعات). هناك 261 تصميمًا مختلفًا من tesseract. يمكن حساب كشف tesseract عن طريق رسم الزوايا المتصلة على الرسم البياني.

Tesseract في الفن

في فيلم "New Abbott Plain" للمخرجة Edwina A، يعمل المكعب الزائد بمثابة الراوي.
في إحدى حلقات مغامرات جيمي نيوترون، اخترع "الصبي العبقري" جيمي مكعبًا فائقًا رباعي الأبعاد مطابقًا لصندوق الطي من رواية طريق المجد (1963) لروبرت هاينلين.
لقد ذكر روبرت إي هينلين المكعبات الزائدة في ثلاث قصص خيال علمي على الأقل. في "المنزل ذو الأبعاد الأربعة" ("المنزل الذي بناه تيل")، وصف منزلًا تم بناؤه على أنه قطعة أرض غير ملفوفة، وبعد ذلك، بسبب الزلزال، "انطوى" في البعد الرابع وأصبح قطعة أرض "حقيقية" .
تصف رواية Heinlein Glory Road صندوقًا كبيرًا الحجم كان أكبر من الداخل منه من الخارج.
تصف قصة هنري كوتنر "All Tenali Borogov" لعبة تعليمية للأطفال من المستقبل البعيد، تشبه في هيكلها التسراكت.
في رواية أليكس جارلاند ()، يُستخدم مصطلح "تيسراكت" للإشارة إلى المكعب الفائق ثلاثي الأبعاد، بدلاً من المكعب الفائق نفسه. هذه استعارة تهدف إلى إظهار أن النظام المعرفي يجب أن يكون أوسع من ما يمكن معرفته.
مؤامرة المكعب 2: Hypercube تتمحور حول ثمانية غرباء محاصرين في "hypercube" أو شبكة من المكعبات المتصلة.
يستخدم المسلسل التلفزيوني أندروميدا مولدات tesseract كجهاز رسم. وهي مصممة في المقام الأول للتعامل مع المكان والزمان.
لوحة "الصلب" (Corpus Hypercubus) لسلفادور دالي ().
يصور الكتاب الهزلي Nextwave مركبة تتضمن 5 مناطق tesseract.
في الألبوم Voivod Nothingface، إحدى المقطوعات الموسيقية تسمى "In my Hypercube".
في رواية أنتوني بيرس الطريق المكعب، أحد الأقمار المدارية الرابطة الدوليةيُطلق على التطوير اسم tesseract، والذي تم ضغطه إلى 3 أبعاد.
في مسلسل “مدرسة بلاك هول” بالموسم الثالث هناك حلقة “تيسراكت”. يضغط لوكاس على زر سري وتبدأ المدرسة في "التشكل مثل قطعة رياضية".
تم العثور على مصطلح "tesseract" ومشتقه "tesseract" في قصة Madeleine L'Engle "A Wrinkle in Time".
TesseracT هو اسم فرقة djent البريطانية.
في سلسلة أفلام Marvel Cinematic Universe، يعد Tesseract عنصرًا رئيسيًا في الحبكة، وهو قطعة أثرية كونية على شكل مكعب فائق.
في قصة روبرت شيكلي "الآنسة الفأر والبعد الرابع"، يحاول كاتب مقصور على فئة معينة، أحد معارف المؤلف، رؤية القطع من خلال التحديق لساعات في الجهاز الذي صممه: كرة على ساق مع قضبان ملتصقة بها، على التي يتم تركيب المكعبات عليها، ولصقها بجميع أنواع الرموز الباطنية. تذكر القصة عمل هينتون.
في أفلام المنتقم الأول، المنتقمون. Tesseract - طاقة الكون بأكمله

اسماء اخرى

هيكساديكاتورون هيكساديكاتورون)
أوكتوكورون (الإنجليزية) المثمن)
رباعي المكعب
4-مكعب
Hypercube (إذا لم يتم تحديد عدد الأبعاد)

ملحوظات

الأدب

تشارلز هـ. هينتون. البعد الرابع، 1904. ISBN 0-405-07953-2
مارتن جاردنر، الكرنفال الرياضي، 1977. ISBN 0-394-72349-X
إيان ستيوارت، مفاهيم الرياضيات الحديثة، 1995. ISBN 0-486-28424-7

روابط

بالروسية

برنامج ترانسفورماتور 4D تكوين نماذج الإسقاطات ثلاثية الأبعاد للأجسام رباعية الأبعاد (بما في ذلك المكعب الفائق).
برنامج ينفذ بناء tesseract وجميع تحويلاته المتجانسة، مع كود المصدر في C++.

باللغة الإنجليزية

Mushware Limited - برنامج إخراج tesseract ( مدرب تيسركت، ترخيص متوافق مع GPLv2) ولعبة إطلاق النار من منظور الشخص الأول في الفضاء رباعي الأبعاد ( اداناكسيس; الرسومات هي في الأساس ثلاثية الأبعاد؛ يوجد إصدار GPL في مستودعات نظام التشغيل).

متعددات الوجوه

صحيح
(المواد الصلبة الأفلاطونية)

نجمي ثنائي السطوح نجمي ثنائي السطوح نجمي عشروني وجوه نجمي متعدد الوجوه نجمي ثماني السطوح

محدب

المواد الصلبة الارخميدية	مكعب ثماني المسطحات ثنائي المسطحات رباعي الوجوه مقطوع مجسم ثمانيني مقطوع مجسم عشروني مقطوع مكعب مقطوع ثنائي المسطحات معيني مجسم ثنائي المسطحات مجسمات معينية مقطوعة مجسمات عشرونية مقطوعة مكعب أفطس ثنائي المسطحات مقطوع مربعات جذع ated وCosidodecahedron المنشور العادي Antiprism
الهيئات الكاتالونية	معيني ديكاهيدرون معيني كونتاهدرون ترياكيستاهيدرون رباعي السطوح سداسي خماسي دوديكاهدرون ترياكيس ثماني السطوح ترياكيسيسيكوساهدرون إيكوسيتيداليتيتراهيدرون سداسي دالي ثنائي السطوح إيكوسيتي خماسي رباعي السطوح سداسي خماسي ديسداكيهدرون ديسداكستريا كونتاهيدرون
بدون التماثل المكاني الكامل	الهرم المنشور الهرم المزدوج مضاد المنشور Zonohedron متوازي السطوح المعين المنشوري الهرم المقطوع
خماسي السطوح متوازي السطوح

الصيغ،
نظريات,
نظريات

آخر

وبمجرد أن تمكنت من إلقاء المحاضرات بعد العملية، كان السؤال الأول الذي طرحه الطلاب هو:

متى سترسم لنا مكعبًا رباعي الأبعاد؟ لقد وعدنا إلياس عبد الخايفيتش!

أتذكر أن أصدقائي الأعزاء يحبون أحيانًا لحظة من الأنشطة التعليمية الرياضية. ولذلك سأكتب جزء من محاضرتي لعلماء الرياضيات هنا. وسأحاول دون أن أكون مملاً. في بعض النقاط قرأت المحاضرة بشكل أكثر دقة بالطبع.

دعونا نتفق أولا. 4 الأبعاد، وحتى أكثر من 5-6-7- وبشكل عام، لا تُمنح لنا المساحة ذات الأبعاد k في الأحاسيس الحسية.
"نحن بائسون لأننا مجرد ثلاثي الأبعاد"، كما قال معلمي في مدرسة الأحد، الذي أخبرني لأول مرة ما هو المكعب رباعي الأبعاد. كانت مدرسة الأحد، بطبيعة الحال، دينية للغاية - رياضية. في ذلك الوقت كنا ندرس المكعبات المفرطة. قبل أسبوع من ذلك، الحث الرياضي، بعد أسبوع من دورات هاميلتون في الرسوم البيانية - على التوالي، هذا هو الصف السابع.

لا يمكننا لمس أو شم أو سماع أو رؤية مكعب رباعي الأبعاد. ماذا يمكننا أن نفعل حيال ذلك؟ يمكننا أن نتخيل ذلك! لأن دماغنا أكثر تعقيدًا من أعيننا وأيدينا.

لذا، لكي نفهم ما هو المكعب رباعي الأبعاد، دعونا أولاً نفهم ما هو متاح لنا. ما هو المكعب ثلاثي الأبعاد؟

حسنا حسنا! أنا لا أطلب منك تعريفًا رياضيًا واضحًا. فقط تخيل المكعب ثلاثي الأبعاد الأبسط والأكثر عادية. قدَّم؟

بخير.
لكي نفهم كيفية تعميم مكعب ثلاثي الأبعاد في مساحة رباعية الأبعاد، دعونا نتعرف على ماهية المكعب ثنائي الأبعاد. الأمر بسيط جدًا - إنه مربع!

المربع له إحداثيان. المكعب لديه ثلاثة. النقاط المربعة هي نقاط ذات إحداثيتين. الأول من 0 إلى 1. والثاني من 0 إلى 1. نقاط المكعب لها ثلاثة إحداثيات. وكل منها هو أي رقم من 0 إلى 1.

من المنطقي أن نتخيل أن المكعب رباعي الأبعاد هو شيء له 4 إحداثيات وكل شيء من 0 إلى 1.

/* من المنطقي أن نتخيل مكعبًا أحادي البعد، وهو ليس أكثر من قطعة بسيطة من 0 إلى 1. */

إذًا، انتظر، كيف ترسم مكعبًا رباعي الأبعاد؟ ففي نهاية المطاف، لا يمكننا رسم مساحة رباعية الأبعاد على مستوى!
لكننا لا نرسم مساحة ثلاثية الأبعاد على المستوى أيضًا، بل نرسمها تنبؤعلى مستوى رسم ثنائي الأبعاد. نضع الإحداثي الثالث (ض) بزاوية، متخيلين أن المحور من مستوى الرسم يتجه "نحونا".

الآن أصبح من الواضح تمامًا كيفية رسم مكعب رباعي الأبعاد. بنفس الطريقة التي وضعنا بها المحور الثالث بزاوية معينة، لنأخذ المحور الرابع ونضعه أيضًا بزاوية معينة.
و- فويلا! - إسقاط مكعب رباعي الأبعاد على مستوى.

ماذا؟ ما هذا على أي حال؟ أسمع دائمًا همسات من المكاتب الخلفية. اسمحوا لي أن أشرح بمزيد من التفصيل ما هو هذا الخليط من الخطوط.
انظر أولاً إلى المكعب ثلاثي الأبعاد. ماذا فعلنا؟ أخذنا المربع وسحبناه على طول المحور الثالث (ض). إنه مثل العديد والعديد من المربعات الورقية الملتصقة ببعضها البعض في كومة.
إنه نفس الشيء مع المكعب رباعي الأبعاد. دعونا نسمي المحور الرابع، من أجل الراحة والخيال العلمي، "محور الوقت". نحن بحاجة إلى أخذ مكعب عادي ثلاثي الأبعاد وسحبه عبر الزمن من الوقت "الآن" إلى الوقت "بعد ساعة".

لدينا مكعب "الآن". في الصورة هو الوردي.

والآن نسحبه على طول المحور الرابع - على طول محور الوقت (أظهرته باللون الأخضر). ونحصل على مكعب المستقبل - الأزرق.

كل قمة من "المكعب الآن" تترك أثراً في الوقت المناسب - قطعة. ربط حاضرها بمستقبلها.

باختصار، بدون أي كلمات: قمنا برسم مكعبين متطابقين ثلاثي الأبعاد وقمنا بتوصيل القمم المقابلة.
تمامًا كما فعلوا مع مكعب ثلاثي الأبعاد (ارسم مكعبين متماثلين ثنائي الأبعاد وقم بتوصيل القمم).

لرسم مكعب خماسي الأبعاد، سيتعين عليك رسم نسختين من مكعب رباعي الأبعاد (مكعب رباعي الأبعاد بإحداثي خامس 0 ومكعب رباعي الأبعاد بإحداثي خامس 1) وتوصيل القمم المقابلة بالحواف. صحيح أنه سيكون هناك خليط من الحواف على المستوى بحيث سيكون من المستحيل تقريبًا فهم أي شيء.

بمجرد أن نتخيل مكعبًا رباعي الأبعاد ونتمكن من رسمه، يمكننا استكشافه بطرق مختلفة. تذكر أن تستكشفه في عقلك ومن الصورة.
على سبيل المثال. المكعب ثنائي الأبعاد محاط من أربعة جوانب بمكعبات ذات بعد واحد. هذا أمر منطقي: لكل من الإحداثيين بداية ونهاية.
مكعب ثلاثي الأبعاد محاط من ستة جوانب بمكعبات ثنائية الأبعاد. ولكل من الإحداثيات الثلاثة بداية ونهاية.
وهذا يعني أن المكعب رباعي الأبعاد يجب أن يقتصر على ثمانية مكعبات ثلاثية الأبعاد. لكل من الإحداثيات الأربعة - على كلا الجانبين. في الشكل أعلاه نرى بوضوح وجهين يحدانه على طول إحداثي "الزمن".

هنا مكعبان (هما مائلان قليلًا لأن لهما بعدين مسقطين على المستوى بزاوية)، مما يحد من المكعب الزائد الموجود على اليسار واليمين.

من السهل أيضًا ملاحظة "العلوي" و "السفلي".

أصعب شيء هو أن نفهم بصريًا مكان وجود "الأمامي" و "الخلفي". تبدأ الواجهة الأمامية من الحافة الأمامية لـ "مكعب الآن" وإلى الحافة الأمامية لـ "مكعب المستقبل" - وهي حمراء. الجزء الخلفي أرجواني.

من الصعب ملاحظتها لأن المكعبات الأخرى متشابكة تحت الأقدام، مما يحد من المكعب الزائد عند إحداثيات مسقطة مختلفة. لكن لاحظ أن المكعبات لا تزال مختلفة! وها هي الصورة مرة أخرى، حيث يتم تسليط الضوء على "مكعب الحاضر" و"مكعب المستقبل".

بالطبع، من الممكن إسقاط مكعب رباعي الأبعاد في مساحة ثلاثية الأبعاد.
النموذج المكاني الأول المحتمل واضح كما يبدو: تحتاج إلى أخذ إطارين مكعبين وربط رؤوسهما المقابلة بحافة جديدة.
ليس لدي هذا النموذج في المخزون الآن. في المحاضرة، أظهر للطلاب نموذجًا ثلاثي الأبعاد مختلفًا قليلاً لمكعب رباعي الأبعاد.

أنت تعرف كيف يتم إسقاط المكعب على مستوى كهذا.
يبدو الأمر كما لو أننا ننظر إلى مكعب من الأعلى.

الحافة القريبة كبيرة بالطبع. والحافة البعيدة تبدو أصغر، نراها من خلال القريبة.

هذه هي الطريقة التي يمكنك بها عرض مكعب رباعي الأبعاد. المكعب أصبح أكبر الآن، نرى مكعب المستقبل من بعيد، لذلك يبدو أصغر.

على الجانب الآخر. من الجانب العلوي.

مباشرة من جانب الحافة:

من جهة الضلع:

والزاوية الأخيرة غير متناظرة. من باب «أخبرني أني نظرت بين أضلاعه».

حسنا، ثم يمكنك التوصل إلى أي شيء. على سبيل المثال، تمامًا كما يتم تطوير مكعب ثلاثي الأبعاد على مستوى (يشبه قطع ورقة بحيث تحصل على مكعب عند طيها)، يحدث الشيء نفسه مع تطوير مكعب رباعي الأبعاد إلى فضاء. إنه مثل قطع قطعة من الخشب بحيث أنه من خلال طيها في مساحة رباعية الأبعاد نحصل على تسراكت.

لا يمكنك دراسة المكعب رباعي الأبعاد فحسب، بل المكعبات ذات الأبعاد n بشكل عام. على سبيل المثال، هل صحيح أن نصف قطر الكرة المحصورة حول مكعب عدده n أقل من طول حافة هذا المكعب؟ أو هناك سؤال أبسط: ما عدد رؤوس المكعب ذي الأبعاد n؟ كم عدد الحواف (الوجوه ذات البعد الواحد)؟

Tesseract (من اليونانية القديمة τέσσερες ἀκτῖνες - أربعة أشعة) هو مكعب فائق رباعي الأبعاد - وهو نظير للمكعب في الفضاء رباعي الأبعاد.

الصورة عبارة عن إسقاط (منظور) لمكعب رباعي الأبعاد على مساحة ثلاثية الأبعاد.

وفقًا لقاموس أكسفورد، تمت صياغة كلمة "tesseract" واستخدامها في عام 1888 من قبل تشارلز هوارد هينتون (1853-1907) في كتابه "عصر جديد من الفكر". وفي وقت لاحق، أطلق بعض الناس على نفس الشكل اسم "المكعب الرباعي".

الهندسة

يتم تعريف التسراكت العادي في الفضاء الإقليدي رباعي الأبعاد على أنه بدن محدب من النقاط (±1، ±1، ±1، ±1). بمعنى آخر يمكن تمثيلها بالمجموعة التالية:

يقتصر التسراكت على ثمانية مستويات مفرطة، يحدد تقاطعها مع التسراكت نفسه وجوهه ثلاثية الأبعاد (وهي مكعبات عادية). يتقاطع كل زوج من الوجوه غير المتوازية ثلاثية الأبعاد لتشكل وجوهًا ثنائية الأبعاد (مربعات)، وهكذا. أخيرًا، يحتوي التسراكت على 8 وجوه ثلاثية الأبعاد، و24 وجهًا ثنائي الأبعاد، و32 حرفًا، و16 رأسًا.

وصف شعبي

دعونا نحاول أن نتخيل كيف سيبدو المكعب الفائق دون ترك مساحة ثلاثية الأبعاد.

في "مساحة" أحادية البعد - على الخط - نختار قطعة AB بطول L. على مستوى ثنائي الأبعاد على مسافة L من AB، نرسم قطعة DC موازية لها ونربط طرفيها. والنتيجة هي ABCD مربع. وبتكرار هذه العملية مع المستوى، نحصل على مكعب ثلاثي الأبعاد ABCDHEFG. وبإزاحة المكعب في البعد الرابع (عمودي على الأبعاد الثلاثة الأولى) مسافة L، نحصل على المكعب الزائدي ABCDEFGHIJKLMNOP.
http://upload.wikimedia.org/wikipedia/ru/1/13/Construction_tesseract.PNG

يعمل الجزء أحادي البعد AB كجانب للمربع ثنائي الأبعاد ABCD، والمربع - كجانب للمكعب ABCDHEFG، والذي، بدوره، سيكون جانب المكعب الفائق رباعي الأبعاد. يحتوي الخط المستقيم على نقطتين حدوديتين، والمربع له أربعة رؤوس، والمكعب له ثمانية. في المكعب الفائق رباعي الأبعاد، سيكون هناك 16 رأسًا: 8 رؤوس من المكعب الأصلي و8 رؤوس منزاحة في البعد الرابع. يحتوي على 32 حرفًا - 12 منها تعطي الموضع الأولي والنهائي للمكعب الأصلي، و8 حواف أخرى "ترسم" رؤوسه الثمانية، التي انتقلت إلى البعد الرابع. يمكن تطبيق نفس المنطق على وجوه المكعب الزائد. في الفضاء ثنائي الأبعاد يوجد واحد فقط (المربع نفسه)، والمكعب به 6 وجوه (وجهان من المربع المتحرك وأربعة أخرى تصف جوانبه). يحتوي المكعب الفائق رباعي الأبعاد على 24 وجهًا مربعًا - 12 مربعًا من المكعب الأصلي في موضعين و12 مربعًا من حوافه الاثني عشر.

تفريغ Tesseract

لنأخذ المكعب السلكي ABCDHEFG وننظر إليه بعين واحدة من جانب الحافة. سوف نرى ويمكننا رسم مربعين على المستوى (حافتيه القريبة والبعيدة)، متصلتين بأربعة خطوط - حواف جانبية. وبالمثل، فإن المكعب الفائق رباعي الأبعاد في الفضاء ثلاثي الأبعاد سيبدو وكأنه "صندوقين" مكعبين مدرجين في بعضهما البعض ومتصلين بثمانية حواف. في هذه الحالة، سيتم إسقاط "الصناديق" نفسها - الوجوه ثلاثية الأبعاد - على مساحتنا "، وسوف تمتد الخطوط التي تربطها في البعد الرابع. يمكنك أيضًا محاولة تخيل المكعب ليس في الإسقاط، ولكن في صورة مكانية.

تمامًا كما يتكون المكعب ثلاثي الأبعاد من مربع مُزاح بطول وجهه، فإن المكعب المُزاح إلى البعد الرابع سيشكل مكعبًا زائدًا. إنه محدود بثمانية مكعبات، والتي ستبدو في المنظور وكأنها شخصية معقدة إلى حد ما. يتم رسم الجزء الذي بقي في الفضاء "الخاص بنا" بخطوط صلبة، والجزء الذي ذهب إلى الفضاء الفائق - يتم رسمه بخطوط منقطة. يتكون المكعب الفائق رباعي الأبعاد في حد ذاته من عدد لا حصر له من المكعبات، تمامًا كما يمكن "تقطيع" المكعب ثلاثي الأبعاد إلى عدد لا حصر له من المربعات المسطحة.

من خلال قطع الوجوه الستة لمكعب ثلاثي الأبعاد، يمكنك تحليله إلى شكل مسطح - وهو تطور. سيكون له مربع على كل جانب من الوجه الأصلي، بالإضافة إلى واحد آخر - الوجه المقابل له. وسيتألف التطوير ثلاثي الأبعاد للمكعب الفائق رباعي الأبعاد من المكعب الأصلي، وستة مكعبات "تنمو" منه، بالإضافة إلى واحد آخر - "الوجه الفائق" النهائي.

تمثل خصائص التسراكت استمرارًا لخصائص الأشكال الهندسية ذات البعد الأدنى في الفضاء رباعي الأبعاد.

التوقعات

إلى الفضاء ثنائي الأبعاد

يمثل إسقاط tesseract على مساحة ثلاثية الأبعاد مكعبين متداخلين ثلاثي الأبعاد، ترتبط القمم المقابلة لهما بقطاعات. المكعبات الداخلية والخارجية لها أحجام مختلفة في الفضاء ثلاثي الأبعاد، ولكنها في الفضاء رباعي الأبعاد تكون مكعبات متساوية. لفهم المساواة بين جميع مكعبات التسراكت، تم إنشاء نموذج التسراكت الدوار.

الأهرامات الستة المقطوعة على طول حواف التسراكت هي صور لستة مكعبات متساوية.
زوج ستيريو

Tesseract في الفن

في فيلم "New Abbott Plain" للمخرجة Edwina A، يعمل المكعب الزائد بمثابة الراوي.
في إحدى حلقات مغامرات جيمي نيوترون: "الصبي العبقري"، اخترع جيمي مكعبًا فائقًا رباعي الأبعاد مطابقًا لصندوق الطي من رواية Heinlein عام 1963 طريق المجد.
لقد ذكر روبرت إي هينلين المكعبات الزائدة في ثلاث قصص خيال علمي على الأقل. في البيت ذي الأبعاد الأربعة (البيت الذي بناه تيل) (1940)، وصف منزلًا مبنيًا مثل قطعة صغيرة غير ملفوفة.
تصف رواية Heinlein Glory Road الأطباق كبيرة الحجم التي كانت أكبر من الداخل مقارنة بالخارج.
تصف قصة هنري كوتنر "Mimsy Were the Borogoves" لعبة تعليمية للأطفال من المستقبل البعيد، تشبه في هيكلها لعبة tesseract.
في رواية أليكس جارلاند (1999)، تم استخدام مصطلح "تيسراكت" للإشارة إلى المكعب الفائق ثلاثي الأبعاد، بدلاً من المكعب الفائق نفسه. هذه استعارة تهدف إلى إظهار أن النظام المعرفي يجب أن يكون أوسع من ما يمكن معرفته.
مؤامرة المكعب 2: Hypercube تتمحور حول ثمانية غرباء محاصرين في "hypercube" أو شبكة من المكعبات المتصلة.
يستخدم المسلسل التلفزيوني أندروميدا مولدات tesseract كجهاز رسم. وهي مصممة في المقام الأول للتعامل مع المكان والزمان.
لوحة “الصلب” (Corpus Hypercubus) لسلفادور دالي (1954)
يصور الكتاب الهزلي Nextwave مركبة تتضمن 5 مناطق tesseract.
في الألبوم Voivod Nothingface، إحدى المقطوعات الموسيقية تسمى "In my Hypercube".
في رواية أنتوني بيرس Route Cube، يُطلق على أحد الأقمار التي تدور حول الجمعية الدولية للتنمية اسم tesseract الذي تم ضغطه إلى 3 أبعاد.
في مسلسل "المدرسة" الثقب الأسود"" في الموسم الثالث هناك حلقة "Tesseract". يضغط لوكاس على الزر السري وتبدأ المدرسة بالتشكل مثل قطعة رياضية.
تم العثور على مصطلح "tesseract" ومصطلحه المشتق "tesserate" في قصة "A Wrinkle in Time" للكاتبة Madeleine L'Engle.

لقد حدث تطور الدماغ البشري في الفضاء ثلاثي الأبعاد. ولذلك يصعب علينا أن نتخيل مساحات ذات أبعاد أكبر من ثلاثة. في الواقع، لا يستطيع العقل البشري أن يتخيل كائنات هندسية ذات أبعاد أكبر من ثلاثة. وفي الوقت نفسه، يمكننا بسهولة أن نتخيل كائنات هندسية ذات أبعاد ليس فقط ثلاثة، ولكن أيضًا ذات أبعاد اثنين وواحد.

إن الاختلاف والقياس بين الفضاءات أحادية البعد وثنائية الأبعاد، وكذلك الفرق والقياس بين الفضاءات ثنائية الأبعاد وثلاثية الأبعاد، يسمح لنا بفتح شاشة الغموض التي تفصلنا قليلاً عن الفضاءات ذات الأبعاد الأعلى. لفهم كيفية استخدام هذا التشبيه، فكر في كائن بسيط للغاية رباعي الأبعاد - مكعب مفرط، أي مكعب رباعي الأبعاد. لنكون محددين، لنفترض أننا نريد حل مسألة محددة، وهي حساب عدد الوجوه المربعة لمكعب رباعي الأبعاد. وكل دراسة أخرى ستكون متساهلة للغاية، دون أي دليل، وذلك عن طريق القياس البحت.

لفهم كيفية بناء المكعب الفائق من مكعب عادي، يجب عليك أولاً أن تنظر إلى كيفية بناء المكعب العادي من مربع عادي. من أجل الأصالة في عرض هذه المادة، سوف نطلق هنا على المربع العادي اسم SubCube (ولن نخلط بينه وبين الشيطانة).

لبناء مكعب من مكعب فرعي، تحتاج إلى تمديد المكعب الفرعي في الاتجاه عمودي على الطائرةمكعب فرعي في اتجاه البعد الثالث. في هذه الحالة، من كل جانب من المكعب الفرعي الأولي سوف ينمو مكعب فرعي، وهو الوجه الجانبي ثنائي الأبعاد للمكعب، مما سيحدد الحجم ثلاثي الأبعاد للمكعب على أربعة جوانب، اثنان متعامدان على كل اتجاه في مستوى المكعب الفرعي. وعلى طول المحور الثالث الجديد يوجد أيضًا مكعبان فرعيان يحدان من حجم المكعب ثلاثي الأبعاد. هذا هو الوجه ثنائي الأبعاد الذي كان يوجد فيه المكعب الجزئي في الأصل، وذلك الوجه ثنائي الأبعاد للمكعب الذي جاء فيه المكعب الجزئي في نهاية بناء المكعب.

ما قرأته للتو معروض بتفاصيل مفرطة ومع الكثير من التوضيحات. ولسبب وجيه. الآن سوف نقوم بمثل هذه الخدعة، حيث سنقوم رسميًا باستبدال بعض الكلمات في النص السابق بهذه الطريقة:
المكعب -> المكعب الزائد
المكعب الفرعي -> المكعب
الطائرة -> الحجم
الثالث -> الرابع
ثنائي الأبعاد -> ثلاثي الأبعاد
أربعة -> ستة
ثلاثي الأبعاد -> رباعي الأبعاد
اثنان -> ثلاثة
الطائرة -> الفضاء

ونتيجة لذلك، نحصل على النص الهادف التالي، والذي لم يعد يبدو مفصلا بشكل مفرط.

لبناء مكعب فائق من مكعب، تحتاج إلى مد المكعب في اتجاه عمودي على حجم المكعب في اتجاه البعد الرابع. في هذه الحالة، سينمو مكعب من كل جانب من جوانب المكعب الأصلي، وهو الوجه الجانبي ثلاثي الأبعاد للمكعب الزائد، مما سيحد الحجم الرباعي الأبعاد للمكعب الزائد من ستة جوانب، ثلاثة متعامدة على كل اتجاه في المكعب الزائد. مساحة المكعب. وعلى طول المحور الرابع الجديد يوجد أيضًا مكعبان يحدان من الحجم الرباعي الأبعاد للمكعب الزائد. هذا هو الوجه ثلاثي الأبعاد الذي كان يوجد فيه المكعب في الأصل، والوجه ثلاثي الأبعاد للمكعب الزائد حيث جاء المكعب في نهاية بناء المكعب الزائد.

لماذا نحن واثقون جدًا من أننا حصلنا على الوصف الصحيح لبناء المكعب الفائق؟ نعم، لأنه من خلال نفس الاستبدال الرسمي للكلمات، نحصل على وصف لبناء المكعب من وصف بناء المربع. (التحقق من ذلك لنفسك.)

أصبح من الواضح الآن أنه إذا كان هناك مكعب ثلاثي الأبعاد آخر ينمو من كل جانب من جوانب المكعب، فيجب أن ينمو وجه من كل حافة من حواف المكعب الأولي. في المجمل، يحتوي المكعب على 12 حافة، مما يعني أنه سيظهر 12 وجهًا جديدًا (مكعبات فرعية) إضافية على تلك المكعبات الستة التي تحد من الحجم رباعي الأبعاد على طول المحاور الثلاثة للفضاء ثلاثي الأبعاد. ويتبقى مكعبان آخران يحدان هذا الحجم الرباعي الأبعاد من الأسفل والأعلى على طول المحور الرابع. ولكل من هذه المكعبات 6 وجوه.

في المجمل، نجد أن المكعب الزائد له 12+6+6=24 وجهًا مربعًا.

الصورة التالية توضح البنية المنطقية للمكعب الفائق. وهذا يشبه إسقاط المكعب الفائق على مساحة ثلاثية الأبعاد. وينتج عن ذلك إطار ثلاثي الأبعاد من الأضلاع. في الشكل، من الطبيعي أن ترى إسقاط هذا الإطار على المستوى.

في هذا الإطار، يشبه المكعب الداخلي المكعب الأولي الذي بدأ منه البناء والذي يحد الحجم الرباعي الأبعاد للمكعب الفائق على طول المحور الرابع من الأسفل. نقوم بتمديد هذا المكعب الأولي لأعلى على طول المحور الرابع للقياس ويدخل في المكعب الخارجي. لذا فإن المكعبات الخارجية والداخلية من هذا الشكل تحد من المكعب الزائد على طول المحور الرابع للقياس.

وبين هذين المكعبين يمكنك رؤية 6 مكعبات جديدة أخرى، والتي تلامس الوجوه المشتركة مع المكعبين الأولين. تربط هذه المكعبات الستة المكعب الفائق على طول المحاور الثلاثة للفضاء ثلاثي الأبعاد. كما ترون، فهما ليسا فقط على اتصال بالمكعبين الأولين، وهما المكعبان الداخلي والخارجي في هذا الإطار ثلاثي الأبعاد، ولكنهما أيضًا على اتصال ببعضهما البعض.

يمكنك العد مباشرة في الشكل والتأكد من أن المكعب الفائق يحتوي بالفعل على 24 وجهًا. ولكن هذا السؤال يطرح نفسه. يمتلئ إطار المكعب الفائق هذا في مساحة ثلاثية الأبعاد بثمانية مكعبات ثلاثية الأبعاد دون أي فجوات. لإنشاء مكعب فائق حقيقي من هذا الإسقاط ثلاثي الأبعاد للمكعب الزائد، تحتاج إلى قلب هذا الإطار من الداخل إلى الخارج بحيث ترتبط جميع المكعبات الثمانية بحجم رباعي الأبعاد.

يتم ذلك على هذا النحو. ندعو أحد سكان الفضاء رباعي الأبعاد لزيارتنا ونطلب منه مساعدتنا. يمسك المكعب الداخلي لهذا الإطار ويحركه في اتجاه البعد الرابع، الذي يتعامد مع مساحتنا ثلاثية الأبعاد. في فضاءنا ثلاثي الأبعاد، ندرك الأمر كما لو أن الإطار الداخلي بأكمله قد اختفى ولم يبق سوى إطار المكعب الخارجي.

علاوة على ذلك، يقدم مساعدنا رباعي الأبعاد مساعدته في مستشفيات الولادة للولادة غير المؤلمة، لكن النساء الحوامل لدينا خائفات من احتمال اختفاء الطفل ببساطة من المعدة وينتهي به الأمر في مساحة ثلاثية الأبعاد متوازية. لذلك يتم رفض الشخص رباعي الأبعاد بأدب.

ونحن في حيرة من مسألة ما إذا كانت بعض المكعبات قد تفككت عندما قلبنا إطار المكعب الفائق من الداخل إلى الخارج. بعد كل شيء، إذا لامست بعض المكعبات ثلاثية الأبعاد المحيطة بالمكعب الفائق جيرانها على الإطار بوجوههم، فهل ستتلامس أيضًا مع نفس الوجوه إذا قلب المكعب رباعي الأبعاد الإطار من الداخل إلى الخارج؟

دعونا ننتقل مرة أخرى إلى القياس مع المساحات ذات الأبعاد الأقل. قارن صورة إطار المكعب الفائق بإسقاط مكعب ثلاثي الأبعاد على المستوى الموضح في الصورة التالية.

قام سكان الفضاء ثنائي الأبعاد ببناء إطار على مستوى لإسقاط مكعب على مستوى ودعونا، نحن المقيمين ثلاثي الأبعاد، إلى قلب هذا الإطار رأسًا على عقب. نأخذ القمم الأربعة للمربع الداخلي ونحركها بشكل عمودي على المستوى. يرى المقيمون ثنائيو الأبعاد الاختفاء الكامل للإطار الداخلي بأكمله، ولم يتبق لهم سوى إطار المربع الخارجي. مع مثل هذه العملية، تستمر جميع المربعات التي كانت على اتصال بحوافها في التلامس مع نفس الحواف.

لذلك، نأمل أيضًا ألا يتم انتهاك المخطط المنطقي للمكعب الفائق عند قلب إطار المكعب الفائق من الداخل إلى الخارج، ولن يزيد عدد الوجوه المربعة للمكعب الفائق وسيظل مساويًا لـ 24. وهذا بالطبع ، ليس دليلاً على الإطلاق، بل هو مجرد تخمين بالقياس.

بعد كل ما قرأته هنا، يمكنك بسهولة رسم الإطار المنطقي لمكعب خماسي الأبعاد وحساب عدد الرؤوس والحواف والأوجه والمكعبات والمكعبات الفائقة الموجودة فيه. انها ليست صعبة على الاطلاق.