Kom på två rimliga slumpmässiga och omöjliga händelser. Kom på två pålitliga, slumpmässiga och omöjliga händelser själv. Att lära sig nytt material
Lektionens ämne: "Oavsiktliga, pålitliga och omöjliga händelser"
Lektionens plats i läroplanen: "Kombinatorik. Slumpmässiga händelser "lektion 5/8
Lektionstyp: Lektion i bildandet av ny kunskap
Lektionens mål:
Pedagogisk:
o införa en definition av slumpmässig, tillförlitlig och omöjlig händelse;
o undervisa i processen för en verklig situation att definiera termerna för sannolikhetsteorin: tillförlitliga, omöjliga, lika sannolika händelser;
Utvecklande:
o främja utvecklingen av logiskt tänkande,
o elevers kognitiva intresse,
o förmågan att jämföra och analysera,
Pedagogisk:
o främja intresset för studier av matematik,
o utveckling av elevernas synsätt.
o besittning av intellektuella färdigheter och mentala operationer;
Lär ut metoder: förklarande och belysande, reproduktiv, matematisk diktering.
UMK: Matematik: lärobok för årskurs 6. under redaktion av, och andra, förlaget "Utbildning", 2008, Matematik, 5-6: bok. för lärare / [, [ ,]. - M.: Utbildning, 2006.
Didaktiskt material: affischer på tavlan.
Litteratur:
1. Matematik: lärobok. för 6 cl. Allmän utbildning. institutioner /, etc.]; ed. ,; Växte upp. acad. Vetenskaper, Ros. acad. utbildning, förlag "Utbildning". - 10:e upplagan. - M.: Utbildning, 2008.-302 s .: ill. - (Akademisk skolbok).
2. Matematik, 5-b: bok. för lärare / [,]. - M.: Utbildning, 2006 .-- 191 sid. : sjuk.
4. Lösa problem inom statistik, kombinatorik och sannolikhetsteori. 7-9 årskurser. / författare - komp. ... Ed. 2:a, rev. - Volgograd: Lärare, 2006.-428 s.
5. Lektioner i matematik med användning av informationsteknologi. 5-10 betyg. Metodisk - en manual med elektronisk ansökan / etc. 2:a uppl., Stereotyp. - M .: Förlaget "Globus", 2010. - 266 sid. (Modern skola).
6. Matematikundervisning i moderna skolor. Riktlinjer... Vladivostok: PIPPKRO Publishing House, 2003.
LEKTIONSPLANERING
I. Organisatoriskt ögonblick.
II. Muntligt arbete.
III. Att lära sig nytt material.
IV. Bildande av färdigheter och förmågor.
V. Lektionssammanfattning.
V. Läxor.
UNDER Lektionerna
1. Organisatoriskt ögonblick
2. Uppdatering av kunskap
15*(-100) |
Muntligt arbete:
3. Förklaring av det nya materialet
Lärare: Vårt liv är mycket slumpmässigt. Det finns en sådan vetenskap "Theory of Probabilities". Med hennes språk kan många fenomen och situationer beskrivas.
Sådana forntida generaler som Alexander den store eller Dmitry Donskoy, som förberedde sig för strid, förlitade sig inte bara på krigarnas tapperhet och skicklighet utan också på slumpen.
Många människor älskar matematik för de eviga sanningarna två gånger två är alltid fyra, summan av jämna tal är jämn, arean av en rektangel är lika med produkten av dess intilliggande sidor, etc. I alla problem som du löst får alla samma svar - du behöver bara inte göra fel i lösningen.
Det verkliga livet är inte så enkelt och okomplicerat. Resultaten av många fenomen kan inte förutsägas i förväg. Det är till exempel omöjligt att säga säkert på vilken sida myntet som slängs upp kommer att falla, när den första snön faller nästa år, eller hur många människor i staden som kommer att vilja ringa ett telefonsamtal den närmaste timmen. Sådana oförutsägbara fenomen kallas slumpmässig .
Men fallet har också sina egna lagar, som börjar manifestera sig med upprepade upprepningar av slumpmässiga fenomen. Om du slår ett mynt 1000 gånger, kommer "huvudena" att falla ut ungefär hälften av tiden, vilket inte kan sägas om två eller ens tio kast. "Ungefär" betyder inte hälften. Detta kan som regel vara så eller inte. Lagen säger inget säkert alls, men ger en viss grad av säkerhet att någon slumpmässig händelse kommer att inträffa.
Sådana mönster studeras av en speciell sektion av matematik - Sannolikhetsteori . Med dess hjälp är det möjligt att med en större grad av tillförsikt (men fortfarande inte säkert) förutsäga både datumet för det första snöfallet och antalet telefonsamtal.
Sannolikhetsteorin är oupplösligt kopplad till vår vardagsliv... Detta ger oss en underbar möjlighet att upprätta många probabilistiska lagar. empiriskt genom att upprepa slumpmässiga experiment många gånger. Materialet för dessa experiment kommer oftast att vara ett vanligt mynt, en tärning, en uppsättning dominobrickor, backgammon, roulette eller till och med en kortlek. Var och en av dessa föremål, på ett eller annat sätt, är förknippade med spel. Faktum är att fallet förekommer här i den vanligaste formen. Och de första probabilistiska problemen var förknippade med att bedöma spelares chanser att vinna.
Modern sannolikhetsteori har gått bort från spel, men dess rekvisita är fortfarande den enklaste och mest pålitliga källan till slumpen. Efter att ha övat med roulettehjulet och tärningarna kommer du att lära dig hur du beräknar sannolikheten för slumpmässiga händelser i verkliga situationer, vilket gör att du kan bedöma dina chanser att lyckas, testa hypoteser och fatta optimala beslut inte bara i spel och lotterier .
När du löser probabilistiska problem, var mycket försiktig, försök att motivera varje steg du tar, för inget annat område av matematik innehåller så många paradoxer. Som sannolikhetsteori. Och kanske är den främsta förklaringen till detta hennes koppling till den verkliga värld vi lever i.
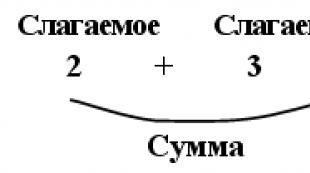
Många spel använder en tärning med olika antal prickar från 1 till 6 på varje ansikte. Spelaren kastar en tärning, tittar på hur många prickar som har fallit ut (på ansiktet som är överst) och gör motsvarande antal drag : 1,2,3 , 4,5 eller 6. Att kasta en tärning kan betraktas som en upplevelse, ett experiment, ett test och resultatet är en händelse. Människor är vanligtvis mycket intresserade av att gissa början av en händelse, förutsäga dess utgång. Vilka förutsägelser kan de göra när de slår tärningen?
Första förutsägelsen: en av siffrorna 1, 2, 3, 4, 5 kommer att hoppa av, eller 6. Tror du att den förutspådda händelsen kommer eller inte? Självklart kommer det definitivt.
En händelse som nödvändigtvis kommer att inträffa i denna upplevelse kallas pålitlig händelse.
Andra förutsägelsen : nummer 7 kommer att hoppa av. Tror du att den förutspådda händelsen kommer eller inte? Det gör det såklart inte, det är bara omöjligt.
En händelse som inte kan inträffa i en given upplevelse kallas omöjlig händelse.
Tredje förutsägelsen : nummer 1 kommer att hoppa av. Tror du att den förutspådda händelsen kommer eller inte? Vi är inte i stånd att besvara denna fråga med full tillförsikt, eftersom den förutsedda händelsen kan inträffa eller inte.
Händelser som under samma förutsättningar kan eller inte kan hända kallas slumpmässig.
Exempel. Boxen innehåller 5 godisar i blått omslag och ett i vitt. Utan att titta i lådan tar de ut en godis på måfå. Kan du berätta i förväg vilken färg det blir?
Träning : Beskriv de händelser som avses i uppgifterna nedan. Hur pålitligt, omöjligt eller oavsiktligt.
1. Slå ett mynt. Vapnet dök upp. (slumpmässig)
2. Jägaren sköt vargen och träffade den. (slumpmässig)
3. Eleven går en promenad varje kväll. När han gick på måndagen träffade han tre bekanta. (slumpmässig)
4. Låt oss mentalt genomföra följande experiment: vänd upp och ner på glaset med vatten. Om detta experiment inte utförs i rymden, utan hemma eller i klassrummet, kommer vattnet att rinna ut. (pålitlig)
5. Tre skott avlossades mot målet." Det blev fem träffar" (omöjlig)
6. Kasta upp stenen. Stenen förblir svävande i luften. (omöjlig)
Exempel Petya tänkte på ett naturligt tal. Evenemanget är som följer:
a) ett jämnt tal är tänkt; (slumpmässig)
b) ett udda tal är tänkt; (slumpmässig)
c) ett tal är tänkt som varken är jämnt eller udda; (omöjlig)
d) ett tal som är udda eller jämnt är tänkt. (pålitlig)
Evenemang som under dessa förhållanden har lika chanser kallas lika sannolikt.
Slumpmässiga händelser som har lika chans kallas lika möjligt eller lika sannolikt .
Placera en affisch på tavlan.
I den muntliga tentamen tar studenten en av biljetterna som lagts ut framför honom. Chanserna att ta någon av examensbiljetterna är lika stora. Det är lika troligt att få valfritt antal poäng från 1 till 6 när man kastar en tärning, liksom "huvuden" eller "svansar" när man kastar ett mynt.
Men det är inte alla händelser lika möjligt... Larmet kanske inte ringer, glödlampan kan brinna ut, bussen kan gå sönder, men under normala förhållanden kan sådana händelser osannolik. Det är mer troligt att larmet ringer, lampan tänds och bussen rör sig.
Vissa händelser chanser mer, det betyder att de är mer sannolika - närmare tillförlitliga. Andra har mindre chanser, de är mindre sannolika – närmare omöjligt.
Omöjliga händelser har inga chanser att hända, och pålitliga händelser har alla chanser att hända, under vissa omständigheter kommer de säkert att hända.
Exempel Petya och Kolya jämför sina födelsedagar. Evenemanget är som följer:
a) deras födelsedagar stämmer inte överens; (slumpmässig)
b) deras födelsedagar är desamma; (slumpmässig)
d) bådas födelsedagar infaller på helgdagar - Nyår(1 januari) och Rysslands självständighetsdag (12 juni). (slumpmässig)
3. Bildande av färdigheter och förmågor
Problem från läroboken nummer 000. Vilka av följande slumpmässiga händelser är tillförlitliga, möjliga:
a) sköldpaddan kommer att lära sig tala;
b) vattnet i vattenkokaren på spisen kommer att koka;
d) du vinner genom att delta i lotteriet;
e) du kommer inte att vinna genom att delta i ett vinn-vinn-lotteri;
f) du kommer att förlora ett parti schack;
g) du kommer att träffa en utomjording imorgon;
h) vädret kommer att försämras nästa vecka; i) du tryckte på samtalet, men det ringde inte; j) idag är det torsdag;
k) efter torsdag är det fredag; m) Blir det torsdag efter fredag?
Lådorna innehåller 2 röda, I gula och 4 gröna bollar. Tre bollar tas ut ur lådan på måfå. Vilka av följande händelser är omöjliga, slumpmässiga, pålitliga:
A: tre gröna bollar kommer att dras;
F: tre röda bollar kommer att dras;
C: bollar i två färger kommer att dras;
D: bollar av samma färg kommer att dras;
E: det är blått bland de långsträckta kulorna;
F: det finns kulor i tre färger bland de långsträckta;
G: Finns det två gula bollar bland de utsträckta?
Testa dig själv. (mattediktat)
1) Ange vilka av följande händelser som är omöjliga, vilka är tillförlitliga, vilka är slumpmässiga:
· Fotbollsmatch "Spartak" - "Dynamo" kommer att sluta oavgjort (slumpmässig)
Du kommer att vinna genom att delta i vinn-vinn-lotteriet ( pålitlig)
Snö kommer att falla vid midnatt och solen kommer att skina efter 24 timmar (omöjlig)
· Imorgon blir det prov i matematik. (slumpmässig)
· Du kommer att väljas till USA:s president. (omöjlig)
· Du kommer att väljas till Rysslands president. (slumpmässig)
2) Du har köpt en TV i en butik som tillverkaren ger två års garanti på. Vilka av följande händelser är omöjliga, vilka är slumpmässiga, vilka är tillförlitliga:
· TV:n går inte sönder inom ett år. (slumpmässig)
TV kommer inte att gå sönder på två år ... (slumpmässig)
· Inom två år behöver du inte betala för TV-reparationer. (pålitlig)
· TV:n kommer att gå sönder under det tredje året. (slumpmässig)
3) Bussen, som tar 15 passagerare, kommer att behöva göra 10 stopp. Vilka av följande händelser är omöjliga, vilka är slumpmässiga, vilka är tillförlitliga:
· Alla passagerare kommer att kliva av bussen vid olika hållplatser. (omöjlig)
· Alla passagerare går av vid en hållplats. (slumpmässig)
· Vid varje stopp kliver åtminstone någon av. (slumpmässig)
· Det blir ett stopp där ingen kliver av. (slumpmässig)
· Ett jämnt antal passagerare kommer att lämna vid alla hållplatser. (omöjlig)
· Ett udda antal passagerare kommer att lämna vid alla hållplatser. (omöjlig)
Lektionssammanfattning
Frågor till studenter:
Vilka händelser kallas slumpmässiga?
Vilka händelser kallas equiprobable?
Vilka händelser kallas trovärdiga? omöjlig?
Vilka händelser kallas mer sannolika? mindre sannolikt?
Läxa : s. 9.3
№ 000. Tänk på tre exempel på tillförlitliga, omöjliga händelser, såväl som händelser om vilka det inte kan sägas att de definitivt kommer att hända.
902. Kartongen innehåller 10 röda, 1 gröna och 2 blå pennor. Två handtag tas ut ur kartongen på måfå. Vilka av följande händelser är omöjliga, tillförlitliga:
A: två röda handtag tas ut; F: två gröna handtag kommer att tas ut; C: två blå handtag tas ut; D: Två handtag i olika färger tas ut;
E: kommer två pennor att tas ut? 03. Egor och Danila kom överens: om nålen på skivspelaren (fig. 205) stannar på det vita fältet, kommer Yegor att måla staketet, och om det är på det blå fältet - Danila. Vilken pojke är mer benägen att måla staketet?
Syftet med lektionen:
- Introducera begreppet pålitliga, omöjliga och slumpmässiga händelser.
- Att bilda kunskap och färdigheter för att bestämma typen av händelser.
- Utveckla: beräkningsskicklighet; Uppmärksamhet; förmågan att analysera, resonera, dra slutsatser; färdigheter i grupparbete.
Under lektionerna
1) Organisatoriskt ögonblick.
Interaktiv övning: barn måste lösa exempel och dechiffrera ord, enligt resultaten delas de in i grupper (pålitliga, omöjliga och slumpmässiga) och bestämma ämnet för lektionen.
1 kort.
| 0,5 | 1,6 | 12,6 | 5,2 | 7,5 | 8 | 5,2 | 2,08 | 0,5 | 9,54 | 1,6 |
2 kort
| 0,5 | 2,1 | 14,5 | 1,9 | 2,1 | 20,4 | 14 | 1,6 | 5,08 | 8,94 | 14 |
3 kort
| 5 | 2,4 | 6,7 | 4,7 | 8,1 | 18 | 40 | 9,54 | 0,78 |
2) Uppdatering av inlärda kunskaper.
Klapplek: jämnt tal - klapp, udda - stå upp.
Uppgift: från en given nummerserie 42, 35, 8, 9, 7, 10, 543, 88, 56, 13, 31, 77, ... bestäm jämna och udda.
3) Att lära sig ett nytt ämne.
Du har kuber på dina bord. Låt oss ta en närmare titt på dem. Vad ser du?
Var används tärningar? Hur?
Grupparbete.
Genomför ett experiment.
Vilka förutsägelser kan du göra när du slår tärningen?
Första förutsägelsen: ett av siffrorna 1,2,3,4,5 eller 6 kommer att tas bort.
En händelse som nödvändigtvis kommer att inträffa i denna upplevelse kallas pålitlig.
Andra förutsägelsen: nummer 7 kommer att tas bort.
Tror du att den förutspådda händelsen kommer eller inte?
Det är omöjligt!
En händelse som inte kan inträffa i en given upplevelse kallas omöjlig.
Tredje förutsägelsen: nummer 1 kommer att tas bort.
Kommer detta evenemang?
En händelse som i en given upplevelse kan eller inte kan inträffa kallas slumpmässig.
4) Konsolidering av det studerade materialet.
I. Bestäm typen av händelse
-Det kommer snörött imorgon.
Kraftig snö imorgon.
Imorgon, trots att det är juli, kommer det att snöa.
Imorgon, trots att det är juli, kommer det ingen snö.
Imorgon kommer det att snöa och det blir snöstorm.
II. Lägg till ett ord i den här meningen så att händelsen blir omöjlig.
Kolya fick ett A i historia.
Sasha slutförde inte en enda uppgift på testet.
Oksana Mikhailovna (historielärare) kommer att förklara det nya ämnet.
III. Ge exempel på omöjliga, oavsiktliga och pålitliga händelser.
IV. Arbeta enligt läroboken (i grupp).
Beskriv händelserna som hänvisas till i uppgifterna nedan som rimliga, omöjliga eller slumpmässiga.
Nr 959. Petya tänkte på ett naturligt tal. Evenemanget är som följer:
a) ett jämnt tal är tänkt;
b) ett udda tal är tänkt;
c) ett tal är tänkt som varken är jämnt eller udda;
d) ett tal som är udda eller jämnt är tänkt.
Nr 960. Du öppnade den här handledningen på vilken sida som helst och valde det första substantivet som kom över. Evenemanget är som följer:
a) det finns en vokal i stavningen av det valda ordet;
b) det finns en bokstav "o" i stavningen av det valda ordet;
c) det finns inga vokaler i stavningen av det valda ordet;
d) det finns ett mjukt tecken i stavningen av det valda ordet.
Lös nr 961, nr 964.
Diskussion av de lösta uppgifterna.
5) Reflektion.
1. Vilka händelser mötte du under lektionen?
2. Ange vilka av följande händelser som är tillförlitliga, vilka som är omöjliga och vilka som är oavsiktliga:
a) det blir inga sommarlov;
b) smörgåsen kommer att falla ner smör;
c) läsåret kommer att sluta någon gång.
6) Läxor:
Kom på två pålitliga, slumpmässiga och omöjliga händelser.
Rita en teckning till en av dem.
Sannolikhetsteori, som alla grenar inom matematiken, arbetar med ett visst antal begrepp. De flesta begrepp inom sannolikhetsteorin ges en definition, men vissa tas som primära, inte definierade, som i geometrin en punkt, en rät linje, ett plan. Det primära begreppet i sannolikhetsteorin är en händelse. En händelse förstås som något om vilket man efter ett visst ögonblick kan säga en och bara en av två saker:
- · Ja, det hände.
- · Nej, det hände inte.
Jag har till exempel en lott. Efter att resultatet av lotteridragningen har publicerats är händelsen som intresserar mig att vinsten på tusen rubel antingen händer eller inte sker. Varje händelse inträffar som ett resultat av ett test (eller erfarenhet). Test (eller erfarenhet) avser de förhållanden som resulterar i en händelse. Att kasta ett mynt är till exempel ett test, och utseendet av ett "vapen" på det är en händelse. Evenemanget betecknas vanligtvis med stora latinska bokstäver: A, B, C,…. Händelser i den materiella världen kan delas in i tre kategorier - pålitliga, omöjliga och oavsiktliga.
En trovärdig händelse är en händelse som man i förväg vet inträffar. Det betecknas med bokstaven W. Så det är tillförlitligt att inte få mer än sex poäng när du kastar en vanlig tärning, utseendet på en vit boll när den tas bort från en urna som bara innehåller vita bollar, etc.
En omöjlig händelse är en händelse som är känt på förhand att den inte kommer att hända. Det betecknas med bokstaven E. Exempel på omöjliga händelser är borttagning av fler än fyra ess från en vanlig kortlek, uppkomsten av en röd boll från en urna som bara innehåller vita och svarta kulor, etc.
En slumpmässig händelse är en händelse som kan eller inte kan inträffa som ett resultat av ett test. Händelser A och B kallas inkompatibla om debuten av en av dem utesluter möjligheten till uppkomsten av den andra. Så uppkomsten av ett eventuellt antal poäng när man kastar en tärning (händelse A) är oförenligt med utseendet på ett annat nummer (händelse B). Ett jämnt antal poäng är oförenligt med ett udda tal. Tvärtom, förlusten av jämna poäng (händelse A) och antalet poäng som är en multipel av tre (händelse B) kommer inte att vara inkonsekventa, eftersom förlusten av sex poäng innebär förekomsten av både händelse A och händelse B, så att förekomsten av en av dem inte utesluter förekomsten av den andra. Du kan utföra operationer med händelser. Unionen av två händelser C = AUB är en händelse C som inträffar om och endast om åtminstone en av dessa händelser A och B inträffar. Skärningen av två händelser D = A ?? B kallas en händelse som inträffar om och endast när händelser av både A och B.
De händelser (fenomen) vi observerar kan delas in i följande tre typer: tillförlitliga, omöjliga och slumpmässiga.
Trovärdig kallas en händelse som nödvändigtvis kommer att inträffa om en viss uppsättning villkor S implementeras. Till exempel, om ett kärl innehåller vatten vid normalt atmosfärstryck och en temperatur på 20 °, då händelsen "vatten i kärlet är i flytande tillstånd ” är pålitlig. I det här exemplet är det inställda atmosfärstrycket och vattentemperaturen uppsättningen villkor S.
Omöjlig kallas en händelse som inte kommer att inträffa om uppsättningen av villkor S är uppfylld. Till exempel kommer händelsen "vatten i kärlet är i fast tillstånd" säkerligen inte att inträffa om uppsättningen av villkor i föregående exempel är uppfyllda.
Slumpmässigär en händelse som, när en uppsättning villkor S är uppfylld, antingen kan inträffa eller inte. Till exempel, om ett mynt kastas, då kan det falla så att det blir antingen ett vapen eller en inskription ovanpå. Därför föll händelsen "när myntet kastades," vapenskölden ut - slumpmässigt. Varje slumpmässig händelse, särskilt fallet av "vapnet", är en konsekvens av verkan av väldigt många slumpmässiga orsaker (i vårt exempel: kraften med vilken myntet kastas, myntets form och många andra ). Det är omöjligt att ta hänsyn till påverkan på resultatet av alla dessa skäl, eftersom deras antal är mycket stort och lagarna för deras agerande är okända. Därför ställer sannolikhetsteorin sig inte till uppgiften att förutsäga om en enskild händelse kommer att inträffa eller inte – den kan helt enkelt inte göra det.
Situationen är annorlunda om slumpmässiga händelser beaktas som kan observeras många gånger under samma förhållanden S, det vill säga om vi talar om masshomogena slumpmässiga händelser. Det visar sig att ett tillräckligt stort antal homogena slumpmässiga händelser, oavsett deras specifika karaktär, lyder vissa lagar, nämligen probabilistiska lagar. Fastställandet av dessa regelbundenheter behandlas av sannolikhetsteorin.
Sålunda är ämnet för sannolikhetsteorin studiet av de sannolikhetslagarna för masshomogena slumpmässiga händelser.
Sannolikhetsteorins metoder används i stor utsträckning inom olika grenar av naturvetenskap och teknologi. Sannolikhetsteori tjänar också till att underbygga matematisk och tillämpad statistik.
Typer av slumpmässiga händelser... Händelser kallas inkonsekvent om förekomsten av en av dem utesluter förekomsten av andra händelser i samma rättegång.
Exempel. Ett mynt kastas. Utseendet på "vapnet" utesluter utseendet på inskriptionen. Händelserna "ett vapen dök upp" och "en inskription dök upp" är oförenliga.
Flera evenemang bildas hela gruppen om minst en av dem dyker upp som ett resultat av testet. I synnerhet om händelserna som bildar en komplett grupp är parvis inkonsekventa, kommer en och endast en av dessa händelser att visas som ett resultat av testet. Detta speciella fall är av största intresse för oss, eftersom det används nedan.
Exempel 2. Två kontantlotter köps. En och bara en av följande händelser kommer säkert att hända: "vinsten föll på den första lotten och föll inte på den andra", "vinsten föll inte på den första lotten och föll på den andra", "vinsten föll på båda lotterna", "på båda lotterna föll inte vinsterna ut." Dessa händelser bildar en komplett grupp av parvis inkompatibla händelser.
Exempel 3. Skytten avlossade ett skott mot målet. En av följande två händelser kommer säkert att hända: hit, miss. Dessa två oförenliga händelser bildar en komplett grupp.
Händelser kallas lika möjligt om det finns anledning att tro att ingen av dem är mer möjlig än den andra.
Exempel 4. Utseendet på "vapnet" och utseendet på en inskription när ett mynt kastas är lika möjliga händelser. Det antas faktiskt att myntet är tillverkat av ett homogent material, har en regelbunden cylindrisk form, och närvaron av myntning påverkar inte nedfallet av den ena sidan av myntet eller den andra.
Egen betecknas med versaler i det latinska alfabetet: A, B, C, .. A 1, A 2 ..
De enda två möjliga enheterna som bildar en komplett grupp kallas motsatta. Om en av de två motsatserna. händelser betecknas med A, sedan andra betecknas med A '.
Exempel 5. Träffar och saknas vid skjutning mot mål - motsatt fält. så jag.
1.1. Lite information från kombinatorik
1.1.1. boende
Tänk på de enklaste koncepten som är förknippade med valet och placeringen av en uppsättning objekt.
Att räkna antalet sätt på vilka dessa åtgärder kan utföras görs ofta när man löser probabilistiska problem.
Definition... Boende fr.o.m n element av k (k ≤n) kallas valfri beställd delmängd från k delar av uppsättningen som består av n olika element.
Exempel. Följande nummersekvenser är placeringar med 2 element från 3 element i uppsättningen (1; 2; 3): 12, 13, 23, 21, 31, 32.
Observera att placeringarna skiljer sig åt i ordningen av deras beståndsdelar och deras sammansättning. Placeringarna 12 och 21 innehåller samma nummer, men deras ordning är annorlunda. Därför anses dessa placeringar vara olika.
Antal olika placeringar från n element av k betecknas och beräknas med formeln:
,
var n! = 1∙2∙...∙(n - 1)∙n(läser" n- faktoriell ").
siffra tvåsiffriga nummer, som kan bestå av siffrorna 1, 2, 3, förutsatt att ingen siffra upprepas är lika med:.
1.1.2. Permutationer
Definition... Permutationer från n element kallas sådana placeringar från n element som skiljer sig endast i arrangemanget av elementen.
Antal permutationer från n element P n beräknas med formeln: P n=n!
Exempel. Hur många sätt kan 5 personer stå i kö? Antalet sätt är lika med antalet permutationer av 5 element, dvs.
P 5 =5!=1∙2∙3∙4∙5=120.
Definition... Om bland n element k identiska, arrangera sedan om dessa n element kallas permutation med upprepningar.
Exempel. Låt det finnas 2 likadana böcker bland 6 böcker. Alla arrangemang av alla böcker på hyllan - permutation med upprepningar.
Antalet olika permutationer med upprepningar (från n element, inklusive k identisk) beräknas med formeln:.
I vårt exempel är antalet sätt som du kan ordna böcker på hyllan:.
1.1.3. Kombinationer
Definition... Kombinationer av n element av k sådana placeringar från n element av k som skiljer sig från varandra med minst ett element.
Antal olika kombinationer av n element av k betecknas och beräknas med formeln:.
Per definition är 0! = 1.
Följande egenskaper är giltiga för kombinationer:
1.
2.
3.
4.
Exempel. Det finns 5 blommor i olika färger. 3 blommor är utvalda till buketten. Antalet olika buketter med 3 blommor av 5 är lika med:.
1.2. Slumpmässiga händelser
1.2.1. evenemang
Insikt om verkligheten inom naturvetenskap sker som ett resultat av tester (experiment, observation, erfarenhet).
Testa
eller erfarenhet är förverkligandet av en viss uppsättning villkor, som kan reproduceras så många gånger som önskas.
Slumpmässig
kallas en händelse som kan eller inte kan inträffa som ett resultat av något test (erfarenhet).
Således betraktas händelsen som ett testresultat.
Exempel. Att kasta ett mynt är en utmaning. Utseendet på en örn när den kastas är en händelse.
De händelser vi observerar skiljer sig åt i graden av möjlighet att de inträffar och i vilken typ av sammankoppling de har.
Evenemanget kallas pålitlig
om det nödvändigtvis kommer att inträffa som ett resultat av detta test.
Exempel. Att erhålla ett positivt eller negativt betyg på tentamen av en student är en tillförlitlig händelse om tentamen fortgår enligt de vanliga reglerna.
Evenemanget kallas omöjlig
om det inte kan inträffa som ett resultat av detta test.
Exempel. Att ta bort en vit kula från en urna, som bara innehåller färgade (icke-vita) kulor, är en omöjlig händelse. Observera att under andra experimentella förhållanden är uppkomsten av en vit boll inte utesluten; sålunda är denna händelse omöjlig endast under villkoren för vår erfarenhet.
I det följande kommer slumpmässiga händelser att betecknas med stort latin bokstäverna A, B, C... En tillförlitlig händelse kommer att betecknas med bokstaven Ω, det omöjliga - med Ø.
Två eller flera evenemang kallas lika möjligt
i detta test, om det finns anledning att tro att ingen av dessa händelser är mer möjlig eller mindre möjlig än andra.
Exempel. Med ett tärningskast, 1, 2, 3, 4, 5 och 6 poäng - alla dessa händelser är lika möjliga. Det förutsätts naturligtvis att tärningarna är gjorda av ett enhetligt material och har rätt form.
Två händelser kallas inkonsekvent
i ett givet test, om utseendet av en av dem utesluter utseendet på den andra, och gemensam
annat.
Exempel. Boxen innehåller standard- och icke-standarddelar. Låt oss ta en detalj för lycka till. Utseendet på en standarddel eliminerar utseendet på en icke-standarddel. Dessa händelser är inkonsekventa.
Flera evenemang bildas komplett grupp av evenemang
i detta test, om som ett resultat av detta test kommer minst en av dem nödvändigtvis att inträffa.
Exempel. Händelserna från exemplet bildar en komplett grupp av lika möjliga och parvis inkompatibla händelser.
Två inkompatibla händelser som bildar en komplett grupp av händelser i en given rättegång kallas motsatta händelser.
Om en av dem betecknas med A, då den andra vanligtvis betecknas med (läs "not A»).
Exempel. Att träffa och missa med ett skott mot ett mål är motsatta händelser.
1.2.2. Klassisk definition av sannolikhet
Sannolikhet för händelse
- ett numeriskt mått på möjligheten av dess offensiv.
Händelse A kallad gynnsam
händelse V om närhelst en händelse inträffar A, händelsen kommer också V.
evenemang A 1 , A 2 , ..., An form falldiagram
, om de:
1) är lika möjliga;
2) parvis inkompatibel;
3) bilda en komplett grupp.
I schemat av fall (och endast i detta schema) finns det en klassisk definition av sannolikheten P(A) evenemang A... Här kallas ett fall för var och en av händelserna som tillhör den valda hela gruppen av lika möjliga och parvis inkompatibla händelser.
Om nÄr antalet av alla fall i schemat, och m- Antalet fall som gynnar evenemanget A, då sannolikhet för händelse
A definieras av jämställdheten:
Följande egenskaper följer av definitionen av sannolikhet:
1. Sannolikheten för en tillförlitlig händelse är lika med en.
Faktum är att om händelsen är säker, så gynnar varje händelse i händelsemönstret händelsen. I detta fall m = n och därför ![]()
2. Sannolikheten för en omöjlig händelse är noll.
Faktum är att om en händelse är omöjlig, så gynnar ingen av händelserna i händelseschemat händelsen. Så m= 0 och därför ![]()
Sannolikheten för en slumpmässig händelse är ett positivt tal mellan noll och ett.
Faktum är att bara en bråkdel av det totala antalet fall i ärendeschemat gynnar en slumpmässig händelse. Därför 0<m<n, och därför 0<m/n<1 и, следовательно, 0 < P (A) < 1.
Så sannolikheten för en händelse uppfyller ojämlikheterna
0 ≤ P (A) ≤ 1.
För närvarande definieras sannolikhetsegenskaperna i form av axiom formulerade av A.N. Kolmogorov.
En av de främsta fördelarna med den klassiska definitionen av sannolikhet är möjligheten att direkt beräkna sannolikheten för en händelse, d.v.s. utan att tillgripa experiment, som ersätts av logiska resonemang.
Problem med direkt beräkning av sannolikheter
Uppgift 1.1... Vad är sannolikheten för att ett jämnt antal poäng (händelse A) inträffar på ett tärningskast?
Lösning... Tänk på händelserna Ai- tappade i poäng, i= 1, 2, ..., 6. Uppenbarligen bildar dessa händelser ett falldiagram. Sedan antalet av alla fall n= 6. Ett jämnt antal poäng gynnas av fall A 2 , A 4 , A 6, dvs. m= 3. Sedan ![]() .
.
Uppgift 1.2... Urnan innehåller 5 vita och 10 svarta kulor. Kulorna blandas noggrant och sedan tas 1 kula ut på måfå. Hur stor är sannolikheten att en boll som tas ut visar sig vara vit?
Lösning... Det finns totalt 15 ärenden som bildar ett ärendediagram. Dessutom den förväntade händelsen A- utseendet på en vit boll, 5 av dem gynnar därför ![]() .
.
Uppgift 1.3... Barnet leker med sex bokstäver i alfabetet: A, A, E, K, P, T. Hitta sannolikheten att han av misstag kan lägga till ordet CARETA (händelse A).
Lösning... Beslutet kompliceras av det faktum att bland bokstäverna finns det samma - två bokstäver "A". Därför är antalet av alla möjliga fall i detta test lika med antalet permutationer med upprepningar av 6 bokstäver:
.
Dessa fall är lika möjliga, parvis oförenliga och utgör en komplett grupp av händelser, d.v.s. bilda ett falldiagram. Endast ett tillfälle gynnar ett evenemang A... Så
.
Uppgift 1.4... Tanya och Vanya kom överens om att fira det nya året i ett sällskap på 10 personer. De båda ville verkligen sitta bredvid varandra. Vad är sannolikheten för att deras önskemål uppfylls, om det är vanligt att fördela platser mellan sina vänner genom lottning?
Lösning... Låt oss beteckna med A evenemanget "uppfyllelse av Tanyas och Vanyas önskemål". 10 personer kan sitta vid 10 bord! olika sätt. Hur många av dessa n= 10! är lika möjliga sätt gynnsamma för Tanya och Vanya? Tanya och Vanya, som sitter bredvid varandra, kan ta 20 olika positioner. Samtidigt kan åtta av deras vänner sitta vid bord 8! på olika sätt alltså m= 20 ∙ 8 !. Därmed, ![]() .
.
Uppgift 1.5... En grupp på 5 kvinnor och 20 män väljer ut tre delegater. Anta att var och en av de närvarande med samma sannolikhet kan väljas, hitta sannolikheten att två kvinnor och en man kommer att väljas.
Lösning... Det totala antalet lika sannolika försöksresultat är lika med antalet sätt på vilka tre delegater kan väljas ut av 25 personer, d.v.s. ... Låt oss nu räkna antalet förmånliga fall, d.v.s. antalet fall där intressehändelsen äger rum. En manlig delegat kan väljas ut på tjugo sätt. I det här fallet måste de andra två delegaterna vara kvinnor, och du kan välja två kvinnor av fem. Därmed, . Så
.
Uppgift 1.6. Fyra bollar är slumpmässigt utspridda över fyra hål, varje boll träffar det ena eller det andra hålet med samma sannolikhet och oberoende av de andra (det finns inga hinder för att slå samma hål för flera bollar). Hitta sannolikheten att det kommer att finnas tre bollar i ett av hålen, en i det andra och inga bollar i de andra två hålen.
Lösning. Totalt antal fall n= 4 4. Antalet sätt du kan välja ett hål med tre bollar,. Antalet sätt som du kan välja ett hål där det kommer att finnas en boll. Antalet sätt du kan välja mellan de fyra bollarna är tre för att placera dem i det första hålet. Det totala antalet gynnsamma fall. Sannolikhet för händelse: ![]()
Uppgift 1.7. Det finns 10 identiska bollar i lådan, märkta med siffrorna 1, 2,..., 10. Sex bollar har dragits för tur. Hitta sannolikheten att det bland de extraherade bollarna kommer att finnas: a) boll # 1; b) bollar #1 och #2.
Lösning... a) Det totala antalet möjliga elementära testresultat är lika med antalet sätt på vilka man kan extrahera sex bollar av tio, dvs.
Låt oss ta reda på antalet utfall som är gynnsamma för händelsen som är intressant för oss: bland de utvalda sex bollarna finns boll #1 och därför har de andra fem bollarna olika nummer. Antalet sådana utfall är uppenbarligen lika med antalet sätt på vilka fem bollar kan väljas från de återstående nio, dvs.
Den önskade sannolikheten är lika med förhållandet mellan antalet utfall som är gynnsamma för den aktuella händelsen och det totala antalet möjliga elementära utfall:
b) Antalet utfall som är gynnsamma för händelsen av intresse för oss (bland de utvalda bollarna finns det bollar #1 och #2, därför har fyra bollar olika nummer) är lika med antalet sätt på vilka fyra bollar kan extraheras från de återstående åtta, dvs Söker sannolikhet ![]()
1.2.3. Statistisk sannolikhet
Den statistiska definitionen av sannolikhet används när resultaten av ett experiment inte är lika möjliga.
Relativ frekvens av händelsen
A definieras av jämställdheten:
,
var m- Antalet försök där evenemanget A kom n- det totala antalet utförda tester.
J. Bernoulli bevisade att med en obegränsad ökning av antalet experiment kommer den relativa frekvensen av inträffandet av en händelse praktiskt taget att skilja sig lite från ett visst konstant antal. Det visade sig att detta konstanta tal är sannolikheten för att en händelse inträffar. Därför kallas naturligtvis den relativa frekvensen av att en händelse inträffar med ett tillräckligt stort antal tester för statistisk sannolikhet, i motsats till den tidigare införda sannolikheten.
Exempel 1.8... Hur uppskattar man det ungefärliga antalet fiskar i sjön?
Släpp in sjön X fisk. Vi kastar nätet och, låt oss säga, vi hittar i det n fisk. Vi markerar var och en av dem och släpper tillbaka dem. Några dagar senare, i samma väder och på samma plats, kastade vi samma nät. Antag att vi finner m fisk i den, bland vilka k märkt. Låt evenemanget A- "den fångade fisken är märkt". Då per definition av den relativa frekvensen.
Men om i sjön X fisk och vi släppte in i den n märkt alltså.
Eftersom R * (A) » R(A), sedan .
1.2.4. Operationer på evenemang. Sannolikhetsadditionssats
Summan, eller förening, av flera händelser kallas en händelse som består i förekomsten av minst en av dessa händelser (i samma test).
Belopp A 1 + A 2 + … + An betecknas enligt följande: ![]() eller
eller ![]() .
.
Exempel... Två tärningar kastas. Låt evenemanget A består i förlust av 4 poäng på 1 tärning, och händelsen V- på hösten 5 poäng på den andra tärningen. evenemang A och Vär gemensamma. Därför händelsen A +V består av att tappa 4 poäng på den första tärningen, eller 5 poäng på den andra tärningen, eller 4 poäng på den första tärningen och 5 poäng på den andra samtidigt.
Exempel. Händelse A- vinster för 1 lån, event V- vinster på det 2:a lånet. Sedan händelsen A + B- vinna minst ett lån (eventuellt två på en gång).
Efter produkt eller skärningspunkten mellan flera händelser är en händelse som består i att alla dessa händelser uppträder gemensamt (i samma test).
Arbete V evenemang A 1 , A 2 , …, An betecknas enligt följande:
.
Exempel. evenemang A och V bestå i ett framgångsrikt slutförande av I- respektive II-omgångarna vid inträde på institutet. Sedan händelsen A× B består i att framgångsrikt genomföra båda omgångarna.
Begreppen summa och produkt av händelser har en tydlig geometrisk tolkning. Låt evenemanget A det finns en träff av en punkt i området A och händelsen V- träffa en punkt i området V... Sedan händelsen A + B det finns en träff av en punkt i föreningen av dessa områden (Fig. 2.1), och händelsen AV det finns en träff av en punkt i skärningspunkten mellan dessa områden (fig. 2.2).
Ris. 2.1 Fig. 2.2
Sats... Om händelser A i(i = 1, 2, …, n) är parvis inkonsekventa, då är sannolikheten för summan av händelser lika med summan av sannolikheterna för dessa händelser: ![]() .
.
Låta A och Ā
- motsatta händelser, dvs. A + Â= Ω, där Ω är en giltig händelse. Av additionssatsen följer att
P (Ω) = R(A) + R(Ā
) = 1 alltså
R(Ā
) = 1 – R(A).
Om händelser A 1 och A 2 är konsekventa, då är sannolikheten för summan av två gemensamma händelser:
R(A 1 + A 2) = R(A 1) + R(A 2) - P ( A 1 × A 2).
Satserna för addition av sannolikheter gör det möjligt att gå från direkt beräkning av sannolikheter till bestämning av sannolikheter för förekomst av komplexa händelser.
Uppgift 1.8... Skytten skjuter ett skott mot målet. Sannolikheten att slå ut 10 poäng (händelse A), 9 poäng (händelse V) och 8 poäng (händelse MED) är lika med 0,11 respektive; 0,23; 0,17. Hitta sannolikheten för att skytten med ett skott kommer att få mindre än 8 poäng (händelse D).
Lösning... Låt oss gå vidare till den motsatta händelsen - med ett skott kommer skytten att slå minst 8 poäng. En händelse inträffar om den inträffar A eller V, eller MED, dvs. ... Sedan händelserna A, B, MEDär parvis inkonsekventa, då, genom additionssatsen,
, var .
Uppgift 1.9... Från brigadens lag, som består av 6 män och 4 kvinnor, väljs två personer ut till den fackliga konferensen. Vad är sannolikheten att bland de utvalda minst en kvinna (händelse A).
Lösning... Om en händelse inträffar A, kommer säkert en av följande inkonsekventa händelser att inträffa: V- "en man och en kvinna valdes ut"; MED- "två kvinnor valdes ut". Därför kan vi skriva: A = B + C... Hitta sannolikheten för händelser V och MED... Två personer av 10 kan väljas på olika sätt. Två kvinnor av 4 kan väljas på olika sätt. En man och en kvinna kan väljas på 6 × 4 sätt. Sedan . Sedan händelserna V och MEDär därför inkonsekventa genom additionssatsen,
P (A) = P (B + C) = P (B) + P (C) = 8/15 + 2/15 = 2/3.
Uppgift 1.10. Femton läroböcker är slumpmässigt placerade på en hylla i biblioteket, varav fem är inbundna. Bibliotekarien tar tre läroböcker på måfå. Hitta sannolikheten för att minst en av de tagna läroböckerna kommer att bindas (händelse A).
Lösning... Det första sättet. Kravet - minst en av de tre inbundna läroböckerna som tagits - kommer att uppfyllas om någon av följande tre inkonsekventa händelser inträffar: V- en inbunden lärobok, MED- två inbundna läroböcker, D- tre inbundna läroböcker.
Händelse av intresse för oss A kan representeras som en summa av händelser: A = B + C + D... Genom additionssatsen,
P (A) = P (B) + P (C) + P (D). (2.1)
Hitta sannolikheten för händelser FÖRE KRISTUS och D(se kombinatoriska scheman): 
Genom att representera dessa sannolikheter i likhet (2.1) får vi slutligen
P (A)= 45/91 + 20/91 + 2/91 = 67/91.
Andra sättet. Händelse A(minst en av de tre läroböckerna är inbunden) och Ā
(ingen av läroböckerna som tas är bundna) är motsatta, alltså P (A) + P (Ā) = 1 (summan av sannolikheterna för två motsatta händelser är 1). Härifrån P (A) = 1 – P (Â). Sannolikhet för händelse Ā
(ingen av de tagna läroböckerna är bundna)
Söker sannolikhet
P (A) = 1 - P (Ā) = 1 – 24/91 = 67/91.
1.2.5. Villkorlig sannolikhet. Sannolikhetsmultiplikationssats
Villkorlig sannolikhet P (B/A) är sannolikheten för händelse B, beräknad under antagandet att händelse A redan har inträffat.
Sats... Sannolikheten för den gemensamma förekomsten av två händelser är lika med produkten av sannolikheterna för en av dem med den villkorliga sannolikheten för den andra, beräknad under antagandet att den första händelsen redan har inträffat:
P (A∙B) = P (A) ∙ Р ( V/A). (2.2)
Två händelser kallas oberoende om förekomsten av någon av dem inte ändrar sannolikheten för att den andra ska inträffa, d.v.s.
P (A) = P (A/B) eller P (B) = P (B/A). (2.3)
Om händelser A och Vär oberoende, då antyder formlerna (2.2) och (2.3).
P (A∙B) = P (A)∙P (B). (2.4)
Det omvända är också sant, d.v.s. om likhet (2.4) gäller för två händelser, är dessa händelser oberoende. Formlerna (2.4) och (2.2) innebär faktiskt
P (A∙B) = P (A)∙P (B) = P (A) × P (B/A), var P (A) = P (B/A).
Formel (2.2) kan generaliseras till fallet med ett ändligt antal händelser A 1 , A 2 ,…,En:
P (A 1 ∙A 2 ∙…∙En)=P (A 1)∙P (A 2 /A 1)∙P (A 3 /A 1 A 2)∙…∙P (A n/A 1 A 2 …En -1).
Uppgift 1.11... Från urnan, i vilken det finns 5 vita och 10 svarta kulor, ta ut två kulor i rad. Hitta sannolikheten att båda bollarna är vita (händelse A).
Lösning... Tänk på händelserna: V- den första bollen som tas ut är vit; MED- den andra kulan som tas bort är vit. Sedan A = BC.
Experimentet kan göras på två sätt:
1) med retur: den borttagna kulan, efter att ha fixerat färgen, återförs till urnan. I det här fallet händelserna V och MED självständig:
P (A) = P (B)∙P (C) = 5/15 x 5/15 = 1/9;
2) ingen retur: den borttagna bollen läggs åt sidan. I det här fallet händelserna V och MED beroende:
P (A) = P (B)∙P (C/V).
För ett evenemang V villkoren är desamma, och för MED situationen har förändrats. Hände V, därför finns det 14 kulor kvar i urnan, varav 4 är vita.
Så, .
Uppgift 1.12... Bland de 50 glödlamporna är 3 icke-standardiserade. Hitta sannolikheten att två glödlampor tagna samtidigt är icke-standardiserade.
Lösning... Tänk på händelserna: A- det första ljuset är icke-standard, V- det andra ljuset är icke-standard, MED- Båda glödlamporna är icke-standardiserade. Det är klart det C = A∙V... Händelse A 3 fall av 50 är gynnsamma, d.v.s. P (A) = 3/50. Om händelsen A har redan anlänt, då händelsen V två fall av 49 är gynnsamma, d.v.s. P (B/A) = 2/49. Därmed,
.
Mål 1.13... Två idrottare skjuter oberoende av varandra på ett mål. Sannolikheten att träffa målet för den första idrottaren är 0,7 och den andra är 0,8. Vad är sannolikheten för att målet kommer att träffas?
Lösning... Målet kommer att träffas om det träffar antingen den första skytten, eller den andra, eller båda tillsammans, d.v.s. en händelse kommer att inträffa A + B var evenemanget är Aär den första idrottaren som träffar målet och tävlingen V- den andra. Sedan
P (A+V)=P (A)+P (B)–P (A∙V)=0, 7+0, 8–0, 7∙0,8=0,94.
Uppgift 1.14. Det finns sex läroböcker om sannolikhetsteori i läsesalen, varav tre är inbundna. Bibliotekarien tog två läroböcker på måfå. Hitta sannolikheten att de två läroböckerna kommer att bindas.
Lösning... Låt oss introducera notationen av händelser : A- den första läroboken som tas är inbunden, V- den andra läroboken är inbunden. Sannolikheten att den första läroboken är bunden är
P (A) = 3/6 = 1/2.
Sannolikheten att den andra läroboken är inbunden, förutsatt att den första läroboken som togs var inbunden, d.v.s. villkorad sannolikhet för en händelse V, är detta: P (B/A) = 2/5.
För att söka sannolikheten för att båda läroböckerna är bundna, är multiplikationssatsen för händelsernas sannolikheter lika med
P (AB) = P (A) ∙ P (B/A)= 1/2 · ∙ 2/5 = 0,2.
Uppgift 1.15. Verkstaden sysselsätter 7 män och 3 kvinnor. Tre personer valdes slumpmässigt ut efter personalnummer. Hitta sannolikheten att alla utvalda individer kommer att vara män.
Lösning... Låt oss introducera notationen av händelser: A- mannen valdes först, V- en man valdes tvåa, MED - den tredje är en man. Sannolikheten att en man kommer att väljas först, P (A) = 7/10.
Sannolikheten att en man väljs tvåa, förutsatt att en man redan har blivit utvald först, d.v.s. villkorad sannolikhet för en händelse V Nästa : P (B/A) = 6/9 = 2/3.
Sannolikheten att en man kommer att väljas trea, förutsatt att två män redan har valts, d.v.s. villkorad sannolikhet för en händelse MEDär detta: P (C/AB) = 5/8.
Söker sannolikheten att alla tre utvalda individerna kommer att vara män, P (ABC) = P (A) P (B/A) P (C/AB) = 7/10 2/3 5/8 = 7/24.
1.2.6. Total sannolikhetsformel och Bayes formel
Låta B 1 , B 2 ,…, B n- parvis inkompatibla händelser (hypoteser) och A- en händelse som endast kan inträffa i samband med en av dem.
Låt oss dessutom veta P (B i) och P (A/B i) (i = 1, 2, …, n).
Under dessa förhållanden är följande formler giltiga: ![]() (2.5)
(2.5) (2.6)
(2.6)
Formel (2.5) kallas formel för total sannolikhet
... Den beräknar sannolikheten för en händelse A(full sannolikhet).
Formel (2.6) kallas Bayes formel
... Det låter dig räkna om sannolikheterna för hypoteser om händelsen A hände.
När man sammanställer exempel är det lämpligt att anta att hypoteserna bildar en komplett grupp.
Mål 1.16... I korgen finns äpplen från fyra träd av samma sort. Från den första - 15% av alla äpplen, från den andra - 35%, från den tredje - 20%, från den fjärde - 30%. Mogna äpplen står för 99%, 97%, 98%, 95% respektive.
a) Vad är sannolikheten för att ett slumpmässigt taget äpple kommer att vara moget (händelse A).
b) Förutsatt att äpplet som tagits på måfå visade sig vara moget, beräkna sannolikheten att det är från det första trädet.
Lösning... a) Vi har fyra hypoteser:
B 1 - ett slumpmässigt äpple tas bort från det första trädet;
B 2 - ett slumpmässigt äpple tas bort från det andra trädet;
B 3 - ett slumpmässigt äpple tas bort från det tredje trädet;
B 4 - äpplet som tas slumpmässigt är taget från det 4:e trädet.
Deras sannolikheter efter tillstånd: P (B 1) = 0,15; P (B 2) = 0,35; P (B 3) = 0,2; P (B 4) = 0,3.
Sannolikheter för villkorad händelse A:
P (A/B 1) = 0,99; P (A/B 2) = 0,97; P (A/B 3) = 0,98; P (A/B 4) = 0,95.
Sannolikheten att ett slumpmässigt äpple visar sig vara moget hittas av formeln för den totala sannolikheten:
P (A)=P (B 1)∙P (A/B 1)+P (B 2)∙P (A/B 2)+P (B 3)∙P (A/B 3)+P (B 4)∙P (A/B 4)=0,969.
b) Bayes formel för vårt fall ser ut så här: ![]() .
.
Uppgift 1.17. En vit boll släpps i en urna som innehåller två bollar, varefter en boll tas slumpmässigt från den. Hitta sannolikheten att den borttagna bollen kommer att visa sig vara vit om alla möjliga antaganden om kulornas initiala sammansättning (efter färg) är lika möjliga.
Lösning... Låt oss beteckna med A händelse - den vita bollen tas bort. Följande antaganden (hypoteser) om den initiala sammansättningen av bollarna är möjliga: B 1- det finns inga vita bollar, I 2- en vit boll, VID 3- två vita bollar.
Eftersom det finns tre hypoteser totalt, och summan av hypotesernas sannolikheter är 1 (eftersom de utgör en komplett grupp av händelser), är sannolikheten för var och en av hypoteserna 1/3, d.v.s.
P (B 1) = P (B 2)= P (B 3) = 1/3.
Den villkorade sannolikheten för att en vit boll kommer att dras, förutsatt att det inte fanns några vita bollar initialt i urnan, P (A/B 1) = 1/3. Den villkorade sannolikheten att en vit boll kommer att dras, givet att det ursprungligen fanns en vit boll i urnan, P (A/B 2) = 2/3. Den villkorade sannolikheten att en vit boll kommer att dras, förutsatt att det fanns två vita bollar i urnan initialt P (A/B 3)=3/ 3=1.
Vi hittar den önskade sannolikheten att den vita bollen kommer att dras med formeln för den totala sannolikheten:
R(A)=P (B 1)∙P (A/B 1)+P (B 2)∙P (A/B 2)+P (B 3)∙P (A/B 3) = 1/3 1/3 + 1/3 2/3 + 1/3 1 = 2/3 .
Mål 1.18... Två maskiner producerar identiska delar som går till en gemensam transportör. Produktiviteten för den första maskinen är dubbelt så stor som den andra. Den första automatiska maskinen producerar i genomsnitt 60% av delarna av utmärkt kvalitet, och den andra - 84%. Den del som togs slumpmässigt från löpande band visade sig vara av utmärkt kvalitet. Hitta sannolikheten att denna del tillverkades av den första maskinen.
Lösning... Låt oss beteckna med A evenemanget är ett föremål av utmärkt kvalitet. Två antaganden kan göras: B 1- detaljen produceras av den första maskinen, dessutom (eftersom den första maskinen producerar dubbelt så många delar som den andra) P (A/B 1) = 2/3; B 2 - delen produceras av den andra maskinen, och P (B 2) = 1/3.
Den villkorade sannolikheten att delen kommer att vara av utmärkt kvalitet om den produceras av den första automatiska maskinen, P (A/B 1)=0,6.
Den villkorade sannolikheten att delen kommer att vara av utmärkt kvalitet om den produceras av den andra automatiska maskinen, P (A/B 1)=0,84.
Sannolikheten att en slumpmässigt tagen deltagare visar sig vara av utmärkt kvalitet, enligt formeln för den totala sannolikheten, är
P (A)=P (B 1) ∙P (A/B 1)+P (B 2) ∙P (A/B 2) = 2/3 0,6 + 1/3 0,84 = 0,68.
Att söka sannolikheten att den tagna utmärkta delen produceras av den första automaten, enligt den Bayesianska formeln är lika med
Mål 1.19... Det finns tre partier med 20 delar vardera. Antalet standarddelar i första, andra och tredje partiet är 20, 15, 10. En del som visade sig vara standard extraherades slumpmässigt från det valda partiet. Delarna återförs till partiet och för andra gången tas en del slumpmässigt bort från samma sats, vilket också visar sig vara standard. Hitta sannolikheten för att delarna återfanns från den tredje satsen.
Lösning... Låt oss beteckna med A händelse - i vart och ett av de två testerna (med retur) togs en standarddel bort. Tre antaganden (hypoteser) kan göras: B 1 - delar tas bort från den första satsen, V 2
- delar tas bort från den andra satsen, V 3 - delar tas bort från den tredje satsen.
Detaljerna togs slumpmässigt från partiet som togs, så sannolikheterna för hypoteserna är desamma: P (B 1) = P (B 2) = P (B 3) = 1/3.
Hitta den betingade sannolikheten P (A/B 1), dvs. sannolikheten att två standarddelar tas bort successivt från den första batchen. Denna händelse är tillförlitlig eftersom i den första satsen är därför alla delar standard P (A/B 1) = 1.
Hitta den betingade sannolikheten P (A/B 2), dvs. sannolikheten att två standarddelar kommer att tas bort sekventiellt (med retur) från den andra batchen: P (A/B 2)= 15/20 ∙ 15/20 = 9/16.
Hitta den betingade sannolikheten P (A/B 3), dvs. sannolikheten att två standarddelar kommer att tas bort sekventiellt (med retur) från den tredje batchen: P (A/B 3) = 10/20 10/20 = 1/4.
Letar efter sannolikheten att båda extraherade standarddelarna är från en tredje sats, använder Bayes formel är 
1.2.7. Upprepade tester
Om flera tester utförs, och sannolikheten för en händelse A i varje försök beror inte på resultatet av andra försök, då kallas sådana försök oberoende av händelsen A. I olika oberoende rättegångar, händelsen A kan ha antingen olika sannolikheter eller samma sannolikhet. Vi kommer vidare att överväga endast sådana oberoende tester där händelsen A har samma sannolikhet.
Låt det produceras P oberoende tester, i var och en av dem en händelse A kan eller kanske inte visas. Låt oss komma överens om att anta att sannolikheten för en händelse A i varje test är densamma, nämligen lika med R. Därför är sannolikheten för utebliven händelse A i varje test är också konstant och lika med 1– R. Ett sådant probabilistiskt schema kallas Bernoullis plan... Låt oss sätta oss i uppgift att beräkna sannolikheten att för P Bernoulli testevenemang A kommer att gå i uppfyllelse exakt k en gång ( kär antalet framgångar) och kommer därför inte att realiseras P- en gång. Det är viktigt att betona att det inte krävs att evenemanget A upprepas exakt k gånger i en specifik sekvens. Den erforderliga sannolikheten betecknas med P n (k).
Till exempel symbolen R 5 (3) betyder sannolikheten att händelsen i fem tester kommer att dyka upp exakt 3 gånger och därför inte inträffar 2 gånger.
Problemet kan lösas med hjälp av den sk Bernoullis formler, som ser ut som: ![]() .
.
Uppgift 1.20. Sannolikheten att förbrukningen av el under en dag inte överstiger den fastställda normen är lika med R= 0,75. Hitta sannolikheten att strömförbrukningen under de kommande 6 dagarna under 4 dagar inte kommer att överstiga normen.
Lösning. Sannolikheten för normal elförbrukning under var och en av 6 dagar är konstant och lika med R= 0,75. Följaktligen är sannolikheten för överdriven förbrukning av el per dag också konstant och lika med q = 1–R=1–0,75=0,25.
Den önskade sannolikheten med Bernoullis formel är
.
Mål 1.21... Två likvärdiga schackspelare spelar schack. Vilket är mer sannolikt: att vinna två matcher av fyra eller tre av sex (oavgjorda matcher beaktas inte)?
Lösning... Motsvarande schackspelare spelar, så sannolikheten att vinna R= 1/2, alltså sannolikheten att förlora qär också 1/2. Eftersom i alla spel är sannolikheten att vinna konstant och det spelar ingen roll i vilken sekvens spelen kommer att vinnas, då är Bernoullis formel tillämplig.
Låt oss ta reda på sannolikheten för att två matcher av fyra kommer att vinnas:
Låt oss ta reda på sannolikheten för att tre matcher av sex kommer att vinnas:
Eftersom P 4 (2) > P 6 (3), är det mer sannolikt att vinna två matcher av fyra än tre av sex.
Däremot kan man se att man använder Bernoullis formel för stora värden n det är ganska svårt, eftersom formeln kräver att man utför åtgärder på enorma antal och därför ackumuleras fel under beräkningsprocessen; som ett resultat kan det slutliga resultatet skilja sig betydligt från det sanna.
För att lösa detta problem finns det flera gränssatser som används för ett stort antal tester.
1. Poissons sats
När du utför ett stort antal tester enligt Bernoulli-schemat (med n=> ∞) och med ett litet antal gynnsamma resultat k(i detta fall antas det att sannolikheten för framgång sidär liten), närmar sig Bernoullis formel Poissons formel ![]() .
.
Exempel 1.22. Sannolikheten för ett äktenskap när en produktionsenhet produceras av ett företag är lika med sid= 0,001. Vad är sannolikheten för att det kommer att finnas färre än 4 defekta när 5000 enheter släpps (händelse A Lösning... Eftersom när stor använder vi den lokala Laplace-satsen: ![]()
Låt oss räkna x:
Fungera ![]() - jämn, därför φ (–1,67) = φ (1,67).
- jämn, därför φ (–1,67) = φ (1,67).
Enligt tabellen i bilaga A.1 finner vi φ (1,67) = 0,0989.
Söker sannolikhet P 2400 (1400) = 0,0989.
3. Laplaces integralsats
Om sannolikheten R inträffande av en händelse A i varje test enligt Bernoulli-schemat är konstant och skiljer sig från noll och ett, sedan med ett stort antal tester n, sannolikhet P n (k 1 , k 2) händelsens inträffande A i dessa tester från k 1 till k 2 gånger är ungefär lika med
R sid(k 1 , k 2) = Φ ( x "") – Φ ( x "), var ![]() - Laplace funktion,
- Laplace funktion,
Den bestämda integralen i Laplace-funktionen beräknas inte i klassen analytiska funktioner, därför används tabell 1 för att beräkna den. A.2, som anges i bilagan.
Exempel 1.24. Sannolikheten för att en händelse inträffar i var och en av hundra oberoende försök är konstant och lika med sid= 0,8. Hitta sannolikheten för att händelsen inträffar: a) minst 75 gånger och inte mer än 90 gånger; b) minst 75 gånger; c) högst 74 gånger.
Lösning... Vi kommer att använda Laplaces integralsats:
R sid(k 1 , k 2) = Φ ( x "") – Φ( x "), där Ф ( x) Är Laplace-funktionen,
a) Enligt villkor, n = 100, sid = 0,8, q = 0,2, k 1 = 75, k 2 = 90. Beräkna x "" och x " :![]()
![]()
Med hänsyn till att Laplace-funktionen är udda, dvs. Ф (- x) = - Ф ( x), vi får
P 100 (75; 90) = Ф (2,5) - Ф (–1,25) = Ф (2,5) + Ф (1,25).
Enligt tabellen. A.2. vi hittar applikationer:
F (2,5) = 0,4938; Ф (1,25) = 0,3944.
Söker sannolikhet
P 100 (75; 90) = 0,4938 + 0,3944 = 0,8882.
b) Kravet på att händelsen förekommer minst 75 gånger innebär att antalet händelser av händelsen kan vara lika med 75, eller 76, ... eller 100. I detta fall bör man alltså acceptera k 1 = 75, k 2 = 100. Sedan ![]()
![]() .
.
Enligt tabellen. A.2. applikationer finner vi Ф (1,25) = 0,3944; Ф (5) = 0,5.
Söker sannolikhet
P 100 (75;100) = (5) – (–1,25) = (5) + (1,25) = 0,5 + 0,3944 = 0,8944.
c) Händelse - " A dök upp minst 75 gånger "och" A dök inte mer än 74 gånger "är motsatta, så summan av sannolikheterna för dessa händelser är 1. Därför är den önskade sannolikheten
P 100 (0;74) = 1 – P 100 (75; 100) = 1 – 0,8944 = 0,1056.