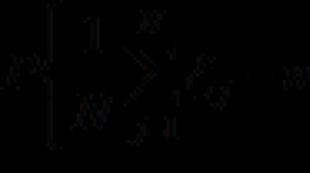Utvecklingsmetoder

Möbius funktion. Möbius inversionsformel. Mobius strip - fantastisk upptäckt "Magic" av Mobius strip

Kommunal budgetläroinrättning gymnasieskola med fördjupning av individ

föremål med. Terbuny

Mobius-remsan

Kompletterad av: Chepurina Anna Vitalievna,

10:e klass elev

Chef: Kirikova M.A.

första matteläraren

kvalifikationskategori

Terbuny by

2015

Introduktion………………………………………………………………………. .................3

Historisk bakgrund………………………………………………………………4

Möbiusremsan – början på en ny topologivetenskap...................................5

Att göra en Mobius-remsa…………………………………………6

Experiment med Mobius-remsa................................................... ................................9

Topologiska egenskaper hos Möbiusremsan………………………..11

Satser om Möbiusremsan………………………………………….12

Knep med Mobius-remsa………………………………………………………………15

Applicering av Möbiusremsan…………………………………………..16

Slutsats................................................. ................................................23

Lista över begagnad litteratur................................................... ........... .25

Ansökan

Introduktion

Nuförtiden är det viktigt att studera de olika egenskaperna och icke-standardiserade tillämpningarna av ovanliga figurer.

Har du någonsin hört talas om en Möbius-remsa? Hur det kan göras, hur det är relaterat till matematik och var det används i livet.

Under arbetets gång kom jag fram till att även om Möbiusremsan upptäcktes redan på 1800-talet, så var den relevant både på 1900- och 1900-talen. Möbiusremsans fantastiska egenskaper har använts och används inom matlagning, teknik, fysik, måleri, arkitektur och i design av smycken och kostymsmycken. Han inspirerade kreativiteten hos många författare och konstnärer.

Intresset för Möbiusremsan har inte bleknat än i dag. I Moskva, i september 2006, ägde festivalen för konstnärlig matematik rum. Talet av en professor från Tokyo mottogs med stor framgång.

Jag var väldigt intresserad och fascinerad av detta ämne. Jag studerade litteraturen, gjorde sedan en Mobius-remsa själv och forskade, genomförde experiment, studerade dess magiska, extraordinära egenskaper.

En Möbiusremsa är en pappersremsa med ena änden vänd ett halvt varv (d.v.s. 180 grader) och limmad i den andra änden. Miljontals människor i alla delar av världen inser inte ens att de använder en Möbiusremsa varje dag.

Mål : berätta och visa dina klasskamrater att ett till synes enkelt band, vände

halvvarv med limmade ändar, kan innehålla mycket

överraskningar.

Studieobjekt: Möbiusremsa.

Uppgifter: identifiera källor och litteratur om detta ämne och analysera dem;

bekanta dig med historien om Mobius-remsan;

lär dig hur man gör en Mobius-remsa;

studera de olika egenskaperna hos Möbiusremsan;

När jag arbetade med ämnet använde jag följande metoder: analys, syntes,

observation, experiment, jämförelse och sociologisk undersökning.

KAPITEL jag

"Möbiusremsan - början på en ny vetenskap"

1. 1. Historisk bakgrund

Den mystiska och berömda Möbiusremsan uppfanns 1858 av en tysk geometerAugust Ferdinand Mobius . De säger att Mobius fick hjälp att öppna sitt "löv" av en piga som sydde ändarna på ett långt band felaktigt. Han väntade sju år på att hans arbete skulle granskas och publicerade utan att vänta resultatet.

Samtidigt som Möbius uppfann en annan elev till K. F. Gauss detta blad -Johann Benedict Listing, Professor vid Högskolan i Göttingen. Han publicerade sitt arbete tre år tidigare än Mobius, 1862. A. F. Mobius föddes i staden Schulpforte. Under en tid, under ledning av K. Gauss, studerade han astronomi. Han började utföra oberoende astronomiska observationer vid Pleisenburg-observatoriet 1818. blev dess direktör. På den tiden stöddes inte matematik, och astronomi gav tillräckligt med pengar för att inte tänka på dem och lämnade tid för ens egna tankar. När Möbius blev professor vid universitetet i Leipzig 1816, introducerade Möbius först projektiv geometri, ett koordinatsystem och analytiska metoder för forskning; fastställt förekomsten av ensidiga ytor (Möbius-remsor), polyedrar, för vilka "kantlagen" inte gäller och som inte har någon volym. Möbius är en av grundarna av teorin om geometriska transformationer, såväl som topologi. Han fick viktiga resultat inom talteorin (Möbius-funktionen) och blev en av sin tids ledande geometrar.

1.2. Möbiusremsan - början på en ny vetenskap om topologi

Från det ögonblick som den tyske matematikern A. F. Möbius upptäckte existensen av ett fantastiskt ensidigt pappersark, började en helt ny gren av matematiken att utvecklas, kallad topologi. Termen "topologi" kan hänföras till två grenar av matematiken. En topologi, vars grundare var Poincaré, kallades under lång tid kombinatorisk. Den andre, vars ursprung var den tyske vetenskapsmannen Georg Cantor, fick namnet general eller set-theoretic.

Kombinatorisk topologi är en gren av geometrin. "Geometri" är ett grekiskt ord, översatt till ryska betyder "landmätning" ("geo" betyder jord på grekiska och "metero" betyder att mäta) studerar figurernas egenskaper. Som all vetenskap är geometri indelad i sektioner.

1. Planimetri (latinskt ord, "planum" - yta + geometri), en sektion av geometri som studerar egenskaperna hos figurer på ett plan (triangel, kvadrat, cirkel, cirkel, etc.)

2. Stereometri (grekiska, "stereos" - rymd + geometri) - en sektion av geometri som studerar egenskaperna hos figurer i rymden (sfär, kub, parallellepiped, etc.)

H. Topologi (grekiska "topos" - plats, terräng + logik) är en av de "yngsta" delarna av modern geometri, som studerar egenskaperna hos sådana figurer som inte förändras om de böjs, sträcks, komprimeras, men inte limmas och inte riva, d.v.s. förändras inte när de deformeras. Exempel på topologiska objekt är: bokstäverna I och H, tunna långa ballonger.

Kombinatorisk topologi studerar egenskaperna hos geometriska figurer som förblir oförändrade under en-till-en och kontinuerliga avbildningar. Under lång tid uppfattades topologi som en vetenskap långt ifrån livet, avsedd endast att "förhärliga det mänskliga sinnet." Men i vår tid har det blivit tydligt att det är direkt relaterat till att förklara universums struktur.

Allmän topologi gränsar till mängdteorin och ligger till grund för matematiken. Detta är en axiomatisk teori utformad för att utforska begrepp som "gräns", "konvergens", "kontinuitet", etc. Grunden till det topologiska rummets axiomatik lades av Felix Hausdorff och kompletterades av den ryske matematikern Pavel Sergeevich Alexandrov.

1.3. Hur man gör en Möbiusremsa

● Möbiusremsan är en av de (matematiska överraskningarna) För att göra en Möbiusremsa, ta en rektangulär remsa ABCD, vrid den 180 grader och limma de motsatta sidorna AB ochCD, dvs. så punkt A och kommer att sammanfallaC och prickar D och V.

Se adj. elva.

● Former och storlekar av pappersremsor för Möbiusremsan.

Remsan ska vara smal och lång, med största möjliga förhållande mellan längd och bredd. Man kan inte göra en Möbiusremsa av ett fyrkantigt pappersark. Det är sant, men det ska inte underskattas att storleksbegränsningar har betydelse när papperet inte får skrynklas. Om det inte är förbjudet att skrynkla papperet kan en Möbius-remsa limmas inte bara från en kvadrat, utan från en rektangel av valfri storlek - de limmade sidorna kan till och med vara hur många gånger som helst än de som inte är limmade.

● Utvecklingsyta.

Eftersom kravet att inte skrynkla papperet är viktigt, låt oss se vad dess matematiska betydelse är.

Det är lätt att förstå att förbudet mot att skrynkla papper avsevärt begränsar

förmågan att manipulera ett pappersark. Till exempel kan ett pappersark rullas till ett rör eller vikas på mitten utan att skrynklas, men det kan inte vikas till fyra. Du kan göra en kon av ett pappersark utan att skrynkla det, men du kan inte göra en sfär eller ens en bit av den: tryck pappersarket mot jordklotet, och veck kommer säkert att dyka upp. Som du kan se kan ett pappersark inte ges någon form. Se adj. 2.

Ytor som kan tillverkas av ett pappersark genom att böja det utan att krossa det kallas framkallningsbara ytor av matematiker. I matematik definieras framkallningsbara ytor på olika sätt: i det metamatematiska språket finns inga ord "papper", "krympla", "gör". Det finns en hel teori om utvecklingsbara ytor, bland vars prestationer finns ett tillfredsställande svar på frågan om vad de kan vara; matematiker kallar detta "klassificering" (svaret tillhör Leonardo Euler). Låt oss bara presentera några egenskaper hos framkallningsbara ytor som experimentella fakta.

Se adj. 3

1. Genom varje punkt A på en framkallningsbar yta som inte ligger på sin gräns passerar ett segment som ligger på ytan som inte slutar vid A. Med andra ord till varje punkt på en framkallningsbar yta (en krökt men inte skrynklig pappersark) kan en sticka fästas så att den gränsar till ytan i viss utsträckning på båda sidor om den tagna punkten. Ett sådant segment kallas en generatrix av ytan (låt oss komma överens om att detta namn endast gäller segment med maximal längd som ligger helt på ytan, det vill säga segment som inte finns i stora segment med denna egenskap).

2. Om två olika generatorer passerar genom en punkt A som inte ligger på gränsen för en yta, och A inte är slutet på någon av dem, så är en tillräckligt liten bit av ytan som omger A platt. I det här fallet kommer vi att kalla punkt A platt.

3. Om punkt A, som inte ligger på ytans gräns, är slutet på någon generator, säg,A , då är grannskapet till punkt A strukturerat så här: genom punkt A passerar den enda generatrisen som inte slutar där, låt oss sägab . Denna generatris delar ytan i två delar. På andra sidan generatrisenb , med vilken generatrisen finnsa , till generatorn b ett platt stycke ligger intill, på andra sidan avb , godtyckligt från punkt A, finns det icke-platta punkter. I denna situation kommer vi att kalla punkt A semi-platt.

Vi betonar att om en punkt på en yta varken är gräns eller platt, så går det genom den en enda generatris som inte slutar vid den, och ändarna av denna generatris ligger på ytans gräns.

●Exempel: Ett pappersark som rullas till en cylinder eller kon har inga platta (eller halvplatta) spetsar. För en cylinder bildar generatorerna en familj av parallella segment, för en kon bildar de en familj av segment som fläktar ut från en punkt. Mer komplexa arrangemang av generatriser är möjliga.

Se adj. 4 .

Till exempel visas generatorerna och de plana punkterna på en framkallningsyta i figuren (där ytan viks ut till ett platt pappersark): tunna linjer är generatorer och de skuggade områdena består av plana spetsar.

Punkter som ligger på gränsen för ett område med plana punkter är antingen gränspunkter för hela ytan eller halvplana. Om en yta är gjord av en papperspolygon (säg en rektangel), så utgör de plana punkterna en eller flera plana polygoner, var och en av dessa polygoner har hörn som ligger på ytans gräns och sidor som antingen ligger på gränsen eller består av av halvplana punkter.

KAPITEL 2

2.1. Experiment med Mobius-remsa

Var och en av oss har en intuitiv uppfattning om vad "yta" är. Ytan på ett pappersark, ytan på väggarna i ett klassrum, ytan på jordklotet är kända för alla. Kan det finnas något mystiskt i ett så vanligt koncept? Ja, kanske ett exempel är Möbiusremsan. För att studera dess egenskaper genomförde jag flera experiment (delade upp dem i två grupper) på egen hand.

jag grupp av experiment

Experiment nr 1. Vi är vana vid att på vilken yta som helst från vilken

vi har att göra (papper, cykel eller volleybolltub) –

två sidor.

Jag började måla Mobius-remsan utan att vända den.

Resultat . Möbiusremsan var helt övermålad.

"Om någon bestämmer sig för att bara färga en sida

ytan på Möbiusremsan, låt honom omedelbart sänka ner det hela i en hink med färg.” - skriver Richard Courant och Herbert Robins på ett utmärkt sätt

bok "Vad är matematik?"

Erfarenhet nr 2. Jag gjorde en spindel och en fluga av papper och skickade runt den "på en promenad".

en vanlig ring, men förbjöd dem att passera gränserna.

Resultat. Spindeln kunde inte ta sig till flugan.

Experiment nr 3. Jag skickade dessa spindlar och flyger bara längs Mobius-remsan. OCH

förbjöd dem att krypa över gränsen.

Resultat.Den stackars flugan blir uppäten om spindeln så klart springer

snabbare!

Erfarenhet nr 4. Jag gjorde en liten man av papper och skickade honom att resa längs Mobius-remsan.

Resultat. Den lilla mannen kommer att återvända till utgångspunkten, där han skulle möta sin spegelbild.

II grupp av experiment

i samband med kapning av Möbius-remsan, visas resultaten i tabellen

erfarenhet

Beskrivning av upplevelsen

Resultat

Jag klippte en enkel ring på längden på mitten.

Jag fick två enkla ringar, lika långa, dubbelt så breda, med två bårder.

Möbiusremsan skars på längden ner i mitten.

Jag fick 1 ring, vars längd är dubbelt så lång, bredden är dubbelt så smal, vriden 1 helt varv, med en bård.

Möbius listbredd

5 cm skär på längden på ett avstånd av 1 cm från kanten.

Jag fick två ringar kopplade till varandra: 1) en Mobius-remsa - längd = längden på den ursprungliga, bredd 3 cm; 2) bredd 1 cm, längd två gånger originalet, vriden två hela varv, med två bårder.

Möbius listbredd

5 cm skär på längden på ett avstånd av 2 cm från kanten.

Jag fick två ringar kopplade till varandra: 1) ringen är en Möbiusremsa 1 cm bred, längd = längden på originalet; 2) ring - 2 cm bred, dubbelt så lång som den ursprungliga, vriden två hela varv, med två bårder.

En Möbiusremsa 5cm bred, skuren på längden med ett avstånd av 3cm från kanten.

Jag fick två ringar kopplade till varandra: 1) ringen är en Möbiusremsa med bredden

1 cm av samma längd; 2) ring – 2 cm bred, dess längd är dubbelt så stor som originalet, vriden två hela varv.

Resultatet av en sociologisk undersökning med elever i 10:e klass.

Frågor

Nej

Har du hört

1. Vet du vad topologi är?

2. Vet du vad en Mobius-remsa är?

3. Visste du egenskaper hos en Mobius-remsa?

Endast 5 % av eleverna i 10:e klass vet vad topologi är. 30 % av eleverna vet vad en Mobius-remsa är, 20 % har hört talas om den. 50% har ingen aning om Mobius-remsan. 25 % av eleverna känner till remsans egenskaper, 10 % har hört talas om dem, 65 % vet ingenting om Möbiusremsans egenskaper.

2.2.Topologiska egenskaper hos Möbiusremsan

Baserat på resultaten av experimenten kan vi formulera följande topologiska egenskaper hos Möbiusremsan relaterade till matematiska överraskningar.

Ensidighet är en topologisk egenskap hos Möbiusremsan, endast karakteristisk för den.

Kontinuitet - på en Möbius-remsa kan vilken punkt som helst anslutas

med någon annan punkt. Det finns inga pauser - fullständig kontinuitet.

Ur topologisk synvinkel är en cirkel omöjlig att skilja från en kvadrat,

eftersom de är lätta att förvandla varandra till varandra utan att gå sönder

kontinuitet.

Anslutning – två snitt kommer att krävas för att halvera ringen. När det gäller Möbius-remsan byts antalet anslutningar ut beroende på förändringen av antalet varv på bandet: om ett varv är dubbelkopplat, om två varv helt enkelt kopplas, om tre varv är dubbelkopplat etc. Men till dela kvadraten i två delar, vi behöver bara ett snitt. Anslutningen bedöms vanligtvis av Betti-numret, eller ibland används Euler-egenskapen.

4. Orientering är en fastighet som saknas i Möbiusremsan. Så om en person kunde resa längs alla krökar av Mobius-remsan, skulle han återvända till startpunkten, men skulle förvandlas till sin spegelbild.

5. "Kromatiskt antal" är det maximala antalet områden som kan ritas på en yta så att var och en av dem har en gemensam gräns med alla andra. Möbiusbandets kromatiska nummer är sex.

6.Satser på Möbiusremsan

Sats 1: λ ≥ π/2

På grund av bevisets komplexitet tar jag inte hänsyn till det i mitt arbete.

Sats 2: λ ≤ √3

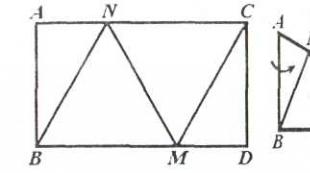
Detta teorem är enklare än det föregående: för att bevisa det räcker det med att förklara hur man limmar en Möbiusremsa från en remsa vars längd är större än √3. Låt oss först anta att dess längd är exakt √3. Sedan kan du placera två vanliga trianglar på denna remsa. Låt oss vika remsan längs sidorna av dessa trianglar, alternerande vikriktningar. Kanterna AB och CD på remsan kommer att riktas in, och punkt A kommer i linje med punkt D och punkt B med punkt C. Resultatet blir en Möbius-remsa, vars kanter är placerade ände mot ände (se bilaga 1.2) )

I denna konstruktion bröts huvudregeln - skrynkla inte papperet. Men det är lätt att förstå att om remsans längd är åtminstone lite mer än √3, kan brytningen längs generatrisen ersättas med böjning utförd i en smal sektion. Kort sagt, vi är inte rädda för en kink längs ett rakt segment: det kan ersättas av en böj nära den. (Irreparabel veckning av papper uppstår när två viklinjer skär varandra, d.v.s. när arket viks som en näsduk - allt detta är känt för oss från vardagliga erfarenheter.) Dess struktur kan föreställas enligt följande: tre identiska regelbundna trianglar ABC, A"B"C", A"B"C" ligger parallellt med varandra, motsvarande hörn är ovanför motsvarande hörn; sidorna AB och A"B", B"C" och B"C", C"A" och CA är förbundna med byglar. Limningslinjen går längs medianen av en av trianglarna.

Varför kan vi inte hitta λ mer exakt?

Innan problemet är löst är det svårt att säga varför det inte är löst. Icke desto mindre är det ibland i olika olösta problem möjligt att spåra vanliga svårigheter, att markera så att säga svåra platser på en matematisk karta, vilket ibland gör det möjligt att förutse framgång eller misslyckande med att lösa ett visst problem

Sats 3. En Möbiusremsa med självkorsningar kan limmas ihop från en remsa av valfri längd större än π/2.

Det är gjort så här. Låt oss ta ett tillräckligt stort udda n och konstruera en regelbunden n-gon inskriven i en cirkel med diameter 1. Betrakta vidare n trianglar som innehåller cirkelns mittpunkt, som var och en begränsas av en sida och två diagonaler av n- gon (n=7). Dessa trianglar täcker vår n-gon, några av dess platser flera gånger. Låt oss nu applicera dessa n trianglar på varandra, varefter vi skär av hälften av triangeln längst till vänster längs den långa medianen och applicerar den på triangeln längst till höger. Resultatet är en rektangulär remsa med ett förhållande mellan längd och bredd som är större än π/2 och som tenderar till π/2 som n, tenderar mot ∞ (remsans bredd tenderar till 1 och längden till π/2). Vik denna remsa konsekvent längs alla linjer som ritas på den, alternerande vikningsriktningarna. Segment AB och CD kommer nästan att sammanfalla - det blir bara några lager av vikt papper mellan dem. I denna "nästan inriktning" kommer punkt A att riktas in med D, och punkt B kommer att riktas in mot C, så om vi kunde "passa igenom tejpen" och limma |AB| med |CD|, så skulle resultatet bli en Möbius-remsa. Tar man tejpen lite längre kan man undvika veck, precis som vi gjorde i beviset på sats 2. Vi har fått fram en Möbiusremsa vars kanter är åtskilda av flera lager papper, se bilaga 1.3. Men låt oss återgå till Möbiusremsan. Sats 1, som vi har sett, gäller faktiskt självkorsande band. Det är osannolikt att villkoret att ingen självskärning inte skulle ha någon effekt på λ; det är dock inte möjligt att ta hänsyn till denna effekt, eftersom matematiken inte har tillräckliga tekniska medel för att studera självkorsningar i tredimensionellt rum. Tvärtom är det ganska troligt att sats 2 inte kan förbättras. När allt kommer omkring innebär att förbättra det att komma med en ny tejpdesign. Erfarenheten visar att optimala konstruktioner är enkla och harmoniska, vilket är vad konstruktionen är från beviset för sats 2. Det är naturligt att anta att om den bästa konstruktionen funnits så hade den hittats – efter så många år!

Det är därför vi kan förvänta oss λ = √3.

Moebius stripptrick

Problem med att knyta knutar

Hur man knyter en knut i en halsduk utan att släppa ändarna? Det kan göras så här. Lägg halsduken på bordet. Korsa armarna över bröstet. Fortsätt att hålla dem i denna position, böj dig över bordet och ta ena änden av halsduken med varje hand i tur och ordning. Efter att armarna har spridits isär bildas en knut automatiskt i mitten av halsduken. Med topologisk terminologi kan vi säga att betraktarens händer, hans kropp och halsduk bildar en sluten kurva i form av en "trebladig" knut. När man sprider armarna rör sig knuten bara från händerna till halsduken.

Knyt en knut i halsduken med ena handen, utan att släppa änden av halsduken från din hand. Svaret på detta pussel finns i boken "Mathematical Wonders and Mysteries" av M. Gardner.

Ur topologisk synvinkel kan västen betraktas som en tvåsidig yta med tre icke sammankopplade kanter, som var och en är en vanlig sluten kurva. Den knäppta västen är en dubbelsidig yta med fyra kanter.

Mystisk slinga.

Åskådaren som bär västen har en ögla placerad på handen och ombeds sedan placera tummen i västens nedre ficka. Nu kan du bjuda in de närvarande att ta bort öglan från din hand utan att ta bort fingret från din västficka. Lösningen är denna: öglan måste dras in i västens hål för ärmen, kastas över betraktarens huvud, dras ut genom det andra hålet för ärmen och flyttas under den andra armen. Som ett resultat av dessa åtgärder kommer öglan att ligga under västen, som omger bröstet. Sänk den tills den dyker upp under västen och låt den sedan falla till golvet.

Vänd västen ut och in utan att ta bort den från personen.

Ägaren till västen måste knäppa fingrarna bakom ryggen. De runt omkring dig bör vända västen ut och in utan att skilja ägarens händer. För att demonstrera denna upplevelse är det nödvändigt att lossa västen och dra den över händerna bakom bärarens rygg. Västen kommer att dingla i luften, men kommer naturligtvis inte av, eftersom händerna är knäppta. Nu måste du ta västens vänstra fåll och, försök att inte rynka västen, trycka den så långt som möjligt in i det högra ärmhålet. Ta sedan höger ärmhål och för in det i samma ärmhål och åt samma håll. Det återstår bara att räta till västen och dra den på ägaren. Västen kommer att vändas ut och in. Vi utförde det här tricket och filmade det med våra klasskamrater. Det finns i presentationen "Mobius Strip".

2.3. Applicering av Möbiusremsan

∞ Vid ingången till Museum of History and Technology i Washington roterar ett stålband vridet ett halvt varv långsamt på en piedestal. 1967, när den internationella matematiska kongressen ägde rum i Brasilien, utfärdade dess arrangörer ett jubileumsstämpel i valörer på fem centavos. Den föreställde en Möbiusremsa. Både monumentet, mer än två meter högt, och den lilla frimärket är unika monument över den tyske matematikern och astronomen August Ferdinand Möbius.

Se bilaga 5.

Patentverket har registrerat många uppfinningar som bygger på samma ensidiga yta.

∞ Möbiusremsan används i många uppfinningar inspirerade av noggranna studier av egenskaperna hos en ensidig yta. Transportbandsremsan, gjord i form av en Möbius-remsa, gör att den kan arbeta dubbelt så lång eftersom hela ytan på plåten slits ut jämnt. 1923 utfärdades ett patent till uppfinnaren Lee de Force, som föreslog att man skulle spela in ljud på film utan att byta rullar på båda sidor samtidigt. Det uppfanns kassetter för bandspelare, där bandet vrids och limmas till en ring, vilket gör det möjligt att spela in eller läsa information från båda sidor samtidigt, vilket fördubblar kassettens kapacitet och därmed speltiden. I matrisskrivare var färgbandet format som en Möbiusremsa för att öka hållbarheten. Detta ger betydande besparingar. Möbiusremsan används i cykel- och volleybolltuber.

∞ På senare tid hittade de en annan användning för den - den började spela rollen som en fjäder, bara en speciell fjäder. En laddad fjäder skjuter som bekant i motsatt riktning. Mobius-remsan, i motsats till alla lagar, ändrar inte driftriktningen, som mekanismer med två stabila positioner. En sådan fjäder kan bli ovärderlig i upprullningsleksaker - den kan inte vridas som en vanlig - en sorts evighetsmaskin.

Se adj. 6.

∞ 1971, uppfinnare från Uralerna P.N. Chesnokov. applicerade ett filter i form av en Mobius-remsa.

∞ Mobius-bladet används i matlagning för att skapa ett intressant och aptitretande utseende för bullar, kex och buskved. Och även vid tillverkning av verktyg för att förbereda och dekorera olika rätter, kraftstrukturer (omrörare).

Se adj. 7.

∞ Med hjälp av en Möbiusremsa skapas hela mästerverk.

Möbiusremsan fungerade som inspiration för skulpturer och grafik. Escher var en av de konstnärer som särskilt älskade det och dedikerade flera av sina litografier till detta matematiska föremål. En känd visar myror som kryper över ytan av en Möbiusremsa.

Se bilaga 9.

∞ Möbiusremsan förekommer också regelbundet i science fiction, som i Arthur C. Clarkes berättelse "Mörkrets mur". Ibland tyder science fiction-historier på att vårt universum kan vara någon form av generaliserad Möbiusremsa. I berättelsen av författaren A.J. Deitch, Bostons tunnelbana bygger en ny linje, vars rutt blir så förvirrande att den förvandlas till en Mobius-remsa, varefter tåg börjar försvinna på denna linje.

∞ Det finns en hypotes om att själva DNA-spiralen också är ett fragment av en Mobius-remsa, och det är den enda anledningen till att den genetiska koden är så svår att tyda och uppfatta. Dessutom förklarar en sådan struktur ganska logiskt orsaken till uppkomsten av biologisk död: spiralen sluter sig själv och självförstörelse inträffar.

Bilaga 10.

∞ Möbiusremsan gillades inte bara av matematiker, utan också av magiker

I över 100 år har Möbiusremsan använts för att utföra olika magiska trick och underhållning. Bladets fantastiska egenskaper demonstrerades även på cirkusen, där ljusa band limmade ihop i form av Möbius-remsor hängdes upp. Magikern tände en cigarett och rörde med den brinnande änden vid mittlinjen på varje band, som var gjort av kaliumnitrat. Den eldiga banan förvandlade det första bandet till ett längre, och det andra till två band, gängade i det andra. (I det här fallet skar magikern Mobius-remsan inte i mitten, utan på ett avstånd av en tredjedel av dess bredd).

∞ Fysiker hävdar att alla optiska lagar är baserade på egenskaperna hos Mobius-remsan, i synnerhet är reflektion i en spegel en slags överföring i tid, kortsiktig, varar hundradelar av en sekund, eftersom vi ser framför oss. ... det stämmer, vår spegel dubbel.

∞Det finns en hypotes om att vårt universum med stor sannolikhet är stängt i samma Mobius-remsa, enligt relativitetsteorin, ju större massa, desto större krökning av rymden. Denna teori bekräftar helt antagandet att ett rymdskepp, som flyger rakt hela tiden, kan återvända till utgångspunkten, detta bekräftar universums obegränsadhet och ändlighet.

Se adj. elva.

∞ Intresset för Möbiusremsan har inte bleknat än i dag. Festivalen för konstnärlig matematik ägde rum i Moskva i september 2006. Talet från professorn från Tokyo Jin Akiyama togs emot med stor framgång. Hans framträdande påminde om en illusionists show, där det fanns en plats för Möbiusremsan (arbete med papper "Möbiusremsan och dess modifieringar").

SPORT

Manuell expander "Robur"

Se adj. 12 .

En avfavoritsaker hos alla skolidrottslärare, som enligt demmed hans egna ord, "tåg intebara musklerna i handen, menoch hjärnmuskel."Carpal expander frånArtemy Lebedev studio upprepar formen av en Möbius-remsa. Ett utmärkt botemedel för att lindra stress, tänka påoändlighet ochbara ett användbart sätt att hålla händerna sysselsatta.

PARFYM

Bugatti parfym

Se adj. 13

FöretagBugattibörjade producera inte bara extremt dyra bilar (modellVeyronkostar 1,3 miljoner euro), men också... parfym. Varje flaska, gjord av kristall och täckt med äkta guld, är designad i form av en ovanlig Möbius-remsa, som bara har en sida. Pris på parfymBugattiär 3500 euro.

Parfym Loewe Quzas, Quizas, Quizas

Se adj. 14 .

Hösten 2011 släpptes en crimson version av doften, vars flaska är insvept i en Mobius-remsa - en symbol för cykeln av passioner i naturen. Kompositionens rikedom består av friskheten hos asiatiska apelsiner, bergamott, röda bär, fortsätter med ett blommigt hjärta av magnolia, fresia och apelsinkronblad, och avslutas med ett sensuellt spår av kashmirträ, gyllene bärnsten och vetiver.

Parfym UFO Limited Edition, Kenzo

Se adj. 15 .

Presentation av doftKenzoägde rum 2009 på en retrospektiv utställning med verk av Ron Arad (RonArad) vid Centre Pompidou i Paris. Det var denna konstnär och arkitekt som kom fram till den kosmiska designen av flaskan i form av en Mobius-remsa. Den är designad för att passa exakt i din handflata.OidentifieradDoftObjekt, eller "Oidentifierat aromatiskt föremål", är begränsat till bara 180 stycken och säljs för $188.

MÖBEL

Mobius bord

Se adj. 16

Ett bord med en yta där du kan stå, sitta och ligga bekvämt.

Bokhylla Infinity

Se adj. 17.

Designern Job Kelevius bröt formen när han designade sin Infinity-bokhylla. Med hjälp av det matematiska konceptet Lemniscate, och något liknande Möbiusremsan, förkroppsligade designern det fysiska konceptet oändlighet i Infinity-hyllan. Det betyder att om du har läst alla böckerna på den här hyllan, tänk på att du har förstått hela litteraturens oändlighet.

Mobius soffa

Se adj. 18.

Född under mottot "Dubbelstol - dubbelt nöje", soffstolenMoebiusDubbelFåtöljskapad av designerGaesolbrännaSkåpbildeWyerfrån Belgien och ger en ny vision av möbler för älskare.

LOGO

Woolmark företagslogotyp

Se adj. 19.

Logotypen skapades 1964 som ett resultat av en designtävling. JurymedlemFrancoGrignanikunde inte motstå och erbjöd sin egen version och gömde sig under en pseudonymFrancescoSeralj. Denna logotyp liknar en Mobius-remsa och är en symbol för företagets evighet och flexibilitet.

Återvinning symbol

Se adj. 20.

Den internationella symbolen för återvinning är Möbiusremsan.Återvinning (andra termer: återvinning, avfallsåtervinning,återvinning och återvinning)- återanvändning eller återgång till cirkulation av industriavfall eller sopor. De vanligaste är sekundära, tertiära och T. e. återvinning i en eller annan skala av material som glas, papper, aluminium, asfalt, järn, tyger och olika typer av plast. Även ekologiskt jordbruks- och hushållsavfall har använts i jordbruket sedan urminnes tider.

Matematik symbol

Se adj. 21.

Möbiusremsan anses vara en symbol för modern matematik, eftersom det var han som gav impulser till ny matematisk forskning.

KLÄDER OCH SKO

Skor

Se adj. 22.

Grundades 2003 av arkitekten Ram Di Koolhaase och skomakaren Galahad ClarkFörenadNakenspecialiserat på tillverkning av innovativa designerskor. En av de mest framgångsrika utvecklingarna av företaget är skorMobius , uppkallad efter geometern August Möbius och hans idé om en ensidig yta. Idén med skorna är denna: läderöverdelen på skorna och sulan är ett enda band, vridet på ett visst sätt.

Mobius halsduk

Se adj. 23.

En intressant sak är Möbius-halsduken som dyker upp i 2000-talets garderober. Du kan själv göra en Möbius-halsduk genom att knyta ändarna på halsduken och vrida den ett varv.

MÅLNING

Graffiti

Se adj. 24.

En modern Möbiusremsa är målad på en vägg i Prag, Tjeckien.   Två typer av fordon rör sig längs bandet: tankar och vägbyggnadsutrustning. En symbol för modern civilisation: förstör-bygg-förstör-bygg..

ARKITEKTUR

Biblioteksbyggnad

Se adj. 25.

Ett projekt för att bygga ett bibliotek i form av en Mobius-remsa i Kazakstan övervägs för närvarande.

Byggnadens kurvor bildar en Möbiusremsa, sålunda flyter det inre utrymmet in i det yttre och vice versa; på liknande sätt förvandlas väggarna till taket, och taket förvandlas tillbaka till väggar. Naturligt ljus kommer in i de inre korridorerna genom geometriska öppningar i det yttre skalet, vilket skapar vackert upplysta utrymmen idealiska för läsning.

Sevärdheter

Se adj. 26.

Berg-och-dalbanan liknar formen av en Mobius-remsa. I Moskva finns världens största inverterade berg-och dalbana, där en person sitter i en upphängd stol och hans ben är i luften. Hastighet - 81 km/h, höjd 30 m. Höjden, jämfört med utländska analoger, är liten, men det mer än lönar sig med överflöd av spiraler, ringar och slingor.

Filmrulle

Se adj. 27.

1923 utfärdades ett patent till uppfinnaren Lee de Force, som föreslog att spela in ljud på film utan att byta rullar, från båda sidor på en gång.

Kassett

Se adj. 28.

Kassetter uppfanns för bandspelare, där bandet vrids och limmas till en ring, vilket gör det möjligt att spela in eller läsa information från båda sidor samtidigt, vilket ökar kassettens kapacitet och därmed speltiden.

Toyota MOB bil

Se adj. 29.

Möbiusremsan är designad av den spanske designern Jorge Marti Vidal och kombinerar skönheten och mystiken hos en Möbiusremsa. Den unika karossformen ger racerbilen bra aerodynamik

Matrix skrivare

Se adj. trettio.

I många matrisskrivare har färgbandet också formen av en Mobius-remsa för att öka dess resurs.

Möbius motstånd

Se adj. 31.

Detta är ett nyuppfunnit elektroniskt element som inte har någon egen induktans.

Slipband

Se adj. 32.

1969 föreslog den sovjetiske uppfinnaren Gubaidullin ett ändlöst slipband i form av ett Möbiusband.

Slutsats

Möbiusremsan är den första ensidiga ytan som en forskare upptäckt. Senare upptäckte matematiker en hel rad ensidiga ytor. Men

den här, den allra första, som lade grunden för en hel riktning inom geometri, fortsätter att dra till sig uppmärksamhet från forskare, uppfinnare, konstnärer och våra studenter. Jag var mycket intresserad av de öppna egenskaperna på Möbiusremsan:

Mobius-remsan har en kant, en sida

En Möbiusremsa är ett topologiskt objekt. Som vilken topologisk figur som helst, ändrar den inte sina egenskaper förrän den skärs, rivs sönder eller dess individuella bitar limmas ihop.

En kant och en sida av Mobius-remsan är inte relaterade till dess position i rymden, och är inte relaterade till begreppen avstånd.

Möbiusremsan hittar många tillämpningar inom matlagning, teknik, fysik, måleri, arkitektur, smyckesdesign och studiet av universums egenskaper. Han inspirerade kreativiteten hos många författare och konstnärer.

μ( n) definieras för alla naturliga tal n och tar värden beroende på typen av expansion av numret n till enkla faktorer:

μ( n) = 1 if n fri från kvadrater (dvs inget primtal är delbart med kvadraten) och nedbrytningen n ett jämnt antal faktorer;
μ( n) = − 1 if n fri från rutor och nedbrytning n i primtalsfaktorer består av ett udda antal faktorer;
μ( n) = 0 if n inte fri från rutor.

Per definition antar vi också μ(1) = 1.

Egenskaper och applikationer

Möbius-funktionen är multiplikativ: för alla samprimtal a Och b jämställdhet gäller μ( ab) = μ( a)μ( b) .

Summan av värdena för Möbius-funktionen över alla delare av ett heltal n, inte lika med ett, är lika med noll

Style="max-width: 98%; höjd: auto; width: auto;" src="/pictures/wiki/files/49/1bee8d0f6bd91176912a8cedc63e174b.png" border="0">

Härifrån följer i synnerhet att för varje icke-tom finit mängd är antalet olika delmängder som består av ett udda antal element lika med antalet olika delmängder som består av ett jämnt antal element - ett faktum som används i bevis.

Möbius-funktionen är relaterad till Mertens-funktionen genom relationen

Mertensfunktionen är i sin tur nära besläktad med problemet med nollor i Riemanns zetafunktion, se artikeln Mertens hypotes.

Mobius inversion

Första Möbius-inversionsformeln

För aritmetiska funktioner f Och g ,

g(n) =	∑	f(d)
	d \| n

då och bara när

Andra Möbius-inversionsformeln

För verkligt värderade funktioner f(x) Och g(x) definieras vid ,

då och bara när

Här tolkas beloppet som .

Wikimedia Foundation. 2010.

Se vad "Mobius-funktionen" är i andra ordböcker:

Möbiusfunktionen μ(n) är en multiplikativ aritmetisk funktion som används inom talteori och kombinatorik, uppkallad efter den tyske matematikern Möbius, som först övervägde den 1831. Innehåll 1 Definition 2 Egenskaper och tillämpningar ... Wikipedia

Typ av transformationer på det komplexa planet (grå) och Riemann-sfären (svart) Innehåll 1 Definition 2 Algebraiska egenskaper ... Wikipedia

En linjär bråkdelfunktion är en funktion av formen där z = (z1,...,zn) är komplexa eller reella variabler, ai,b,ci,d är komplexa eller reella koefficienter. Ofta används termen "fraktionell linjär funktion" för dess speciella fall av transformation... ... Wikipedia

Möbius-serien är en funktionell serie av formen Denna serie studerades av Möbius, som hittade en inversionsformel för denna serie: där μ(s) är Möbius-funktionen ... Wikipedia

MEDICINSK FORSKNINGSMETODER- Jag. Allmänna principer för medicinsk forskning. Tillväxten och fördjupningen av vår kunskap, mer och mer teknisk utrustning på kliniken, baserad på användningen av de senaste landvinningarna inom fysik, kemi och teknik, den tillhörande komplikationen av metoder... ... Stor medicinsk encyklopedi

Ett patologiskt tillstånd som utvecklades under förlossningen och kännetecknas av skador på barnets vävnader och organ, som i regel åtföljs av en störning av deras funktioner. Faktorer som predisponerar för utvecklingen av R. så kallade är felaktiga... ... Medicinsk uppslagsverk

Lemma.

Bevis. Uttalandet är uppenbart. Låt och vara den kanoniska expansionen av numret. Sedan, med hänsyn till att divisorerna har formen , där , ,..., ; , vi får

eftersom den

Sats. (Additiv Möbius inversionsformel.) Låta och vara funktioner av det naturliga argumentet . Sedan om

Bevis. Vi har

Låt . Sedan går den fasta igenom alla värden för talets divisorer. Detta innebär att summeringstecknen i den sista dubbelsumman kan vändas, d.v.s.

Nu med tanke på det

vi får

Det finns en annan form av det beprövade teoremet:

Sats. (Multiplikativ Möbius-inversionsformel.) Låt

där symbolen anger produkten utsträckt till alla delare av talet.

Bevis:

Exempel på användning av Möbius-inversionsformeln:

Problem med antalet ringsekvenser. Se: Hall M. Combinatorics. M.: Mir, , § .

Antalet irreducerbara polynom av en given grad över ett ändligt fält av element. Se: Berlekamp E. Algebraisk kodningsteori. − M.: Mir, 1970, Ch. 3.

Glukhov M. M., Elizarov V. P., Nechaev A. A. Algebra. I t. M.: Helios,. T. , § .

För självstudier:

Möbius inversion på delvis beställda set. Inklusions-exkluderingsprincipen som ett specialfall av Möbius-inversionsformeln. Se: Hall M. Combinatorics. M.: Mir, , § ; Bender E., Goldman J. Om tillämpningar av Möbius-inversion i kombinatorisk analys. I boken: Enumerativa problem med kombinatorisk analys. M.: Mir, 1971. S. - .

Jämförelser för talkombinationer

Låt vara ett primtal.

Lemma.

Bevis. När täljaren i formeln

Följd.

Bevis.

Lemma. Låt , , , vara icke-negativa heltal, och låt , . Sedan

Bevis. Vi har

På andra sidan,

Genom att jämföra koefficienterna vid samma grader får vi det önskade resultatet. ∎

− representationer av icke-negativa heltal och radix. (Här är ett heltal för vilket , ). På uppsättningen av icke-negativa heltal definierar vi den partiella ordningsrelationen (relationen företräde) , antar , om och endast om

Lucas teorem ( ).

Bevis. Enligt föregående lemma,

Var , . Genom att applicera lemma upprepade gånger ett lämpligt antal gånger får vi det önskade resultatet. ∎

Kommentar. Teoremet är inte sant för icke-primära. Till exempel (se Berlekamp, s.),

Följd.

II . Algebraiska strukturer

II. 1. Uppsättningar med binära operationer. Groupoider, semigrupper, monoider

Binär algebraisk operation(eller lag om sammansättning) på en icke-tom uppsättning S kallas kartläggning : , matcha ett par element till ett unikt definierat element. Många operationer kan specificeras på en uppsättning. (Om till exempel såklart är antalet sätt lika med , där är antalet element i .) Om du vill markera ett av dem skriv till exempel , . Ett sådant objekt kallas binär algebra, eller gruppoid. Istället för skriver de ofta , och själva operationen betecknas med någon symbol ( , , , etc.).

Kommentar. Tillsammans med binära operationer övervägs mer generella -ära operationer (unära vid, ternära vid, etc.). De algebraiska strukturerna (systemen) som är förknippade med dem utgör ämnet för forskning av de sk. universella algebror.

En binär operation på en uppsättning kallas associativ, Om

, för alla , , .

En groupoid med en associativ operation kallas halvgrupp.

Ett exempel på en icke-associativ groupoid. På uppsättningen definierar vi operationen som . Operationen är icke-associativ: , men .

Sats. Om en binär operation på en uppsättning är associativ, beror värdet på uttrycket inte på placeringen av parenteser i det.

Bevis. Med , eller uttalandet är uppenbart. För det räcker att med hjälp av induktion visa det

för alla , . Genom induktionshypotesen, placeringen av parentes i

Inte viktigt; särskilt, .

Om då.

Om då

Den högra sidan av den likhet som bevisas (1) reduceras också till samma form. ∎

Elementet kallas neutral angående operationen, om

för vem som helst .

En halvgrupp med ett element kallas monoid(eller semigrupp med identitet) och beteckna , .

En halvgrupp (gruppoid) kan ha högst ett neutralt element: if

, är alltså neutrala element

En groupoid (halvgrupp) kallas subgruppoid (underhalvgrupp) groupoid (halvgrupp), , if

Och för alla , .

I det här fallet säger de att delmängden stängd under drift. Monoid kallas submonoid monoid , , , om och .

Elementet av monoid, kallas reversibel, om det finns ett sådant element (självklart, då vänder vi det). Om elementet har samma egenskap, dvs. , sedan av likheterna följer att elementet faktiskt är unikt (med avseende på ). Detta gör att vi kan prata om omvänd element , till (inverterbart) element , med egenskaper: , .

Om , är inverterbara element av monoiden , , , så är deras produkt också ett inverterbart element, eftersom , . Uppenbarligen är det ett inverterbart element. Därför finns det

Sats. Uppsättningen av alla inverterbara element i monoiden , , stängs under operationen ∗ och bildar en submonoid i , , .

Grupper

Definition av en grupp. En monoid , , , vars alla element är inverterbara kallas grupp.

Med andra ord är en grupp en mängd med en binär operation för vilken följande axiom gäller:

. (Stängd drift.) , .

. (Operationsassociativitet.) ,

. (Förekomsten av ett neutralt element.) ∃ .

. (Förekomsten av ett inverst element.) .

Kommentar. För att återgå till de algebraiska strukturerna som introducerades ovan, observerar vi följande hierarki bland dem: paret , är gruppoid, om axiomet är uppfyllt; halvgrupp, om axiom och ; monoid, om axiom , och ; grupp, om axiomen , , och .

Graderna av element med uppenbara egenskaper bestäms på ett naturligt sätt:

( en gång),

; , ( , , .

Generellt sett är det omöjligt att ordna om element i ett uttryck (dvs. ). Om , då kallas elementen föränderlig, eller pendling. Om två element i en grupp pendlar, anropas gruppen kommutativ, eller Abelian(till ära av den norske matematikern Riehl Henrik Abel ( - )).

En operation i en grupp indikeras oftast med antingen en symbol (addition) eller en symbol (multiplikation). I det här fallet kallas gruppen därefter tillsats eller multiplikativ, dess neutrala element är respektive noll() eller enhet(). I en additiv grupp kallas elementet, inversen av elementet motsatt och är utsedd , men istället skriver de . I en multiplikativ grupp brukar de istället skriva och utelämna operationssymbolen.

Exempel på tillsatsgrupper. 1) , , , , , , , – additivgrupper av ringen och fälten , , . De skriver helt enkelt , , , . 2) Varje ring genom tillägg är en Abelisk grupp. I synnerhet ringen av polynom ,..., ] och ringen av matriser av ordning över ett fält är Abeliska grupper. 3) Varje vektorrum över ett fält med avseende på addition är en abelian grupp. 4) , 1,…, – ett komplett system av minst icke-negativa modulo-rester med modulo-additionsoperationen.

Exempel på multiplikativa grupper. 1) , , är multiplikativa grupper av fält , , . 2) är uppsättningen av inverterbara element i valfri ring med enhet under multiplikation. I synnerhet = ; , är uppsättningen inverterbara matriser från . 3) − alla (verkliga och komplexa) rötter

, , 1,…, , − imaginär enhet,

ekvationen är en multiplikativ Abelsk grupp. 4) - uppsättningen av rotationer av en vanlig -gon i planet och i rymden - en icke-kommutativ grupp (för ).

Vidare används oftare den multiplikativa formen för registrering av operationen. Gruppen betecknas vanligtvis med en enda bokstav utan att specificera operationen. Mängden av alla element i en grupp kallas gruppens huvuduppsättning och betecknas med samma bokstav. Om basmängden är ändlig anropas gruppen slutlig; annars heter det ändlös. Talelementet i en finit grupp kallas dess i ordning. En grupp av ordning 1 kallas enda, eller T rivaliserande. En oändlig grupp sägs ha oändlig ordning. För att indikera gruppens ordning (huvudsetets kardinalitet) används lika symbolerna Card (kardinalnummer) och ().

Om , är delmängder (av huvudmängden) i gruppen, så sätter vi

, , .

Undergrupp av en grupp är en delmängd i vilken själv är en grupp med avseende på samma operation som i . Med andra ord, en delmängd är en undergrupp om och endast om ( en i ) och är sluten under multiplikation och reciprok, d.v.s. , (det finns faktiskt till och med jämlikheter här). Om är en undergrupp i , skriv då ; om på samma gång, då kallas det egen undergrupp och detta betecknas som .

Möbius funktion  (n), Var n– ett naturligt tal, tar följande värden:

Möbius-funktionen låter dig skriva Euler-funktionen som en summa:

Summeringen är över alla divisorer av n (och inte bara över primtalsdelare).

Exempel. Låt oss räkna φ (100) med hjälp av Möbius-funktionen.

Alla delare av 100 är (1, 2, 4, 5, 10, 20, 25, 50, 100).

(2) = (-1) 1 = -1 (två har en primtal divisor – 2)

(4) = 0 (4 divideras med kvadraten av två)

(5) = (-1) 1 = -1 (5 har en primtalsdelare – 5)

(10) = (-1) 2 = 1 (10 har två primtalsfaktorer – 2 och 5)

(20) = 0 (20 dividerat med kvadraten av två)

(25) = 0 (25 dividerat med kvadraten av fem)

(50) = 0 (50 är delbart med både 2 2 och 5 5)

(100) = 0 (100 är delbart med både 2 2 och 5 5)

Således,

Möbius-funktionens egendom:.

Till exempel, n=100, {1, 2, 4, 5, 10, 20, 25, 50, 100}.

16 Ett teorem om antalet sätt att välja k-element, bland vilka det inte finns två intilliggande, från n element ordnade i rad. Bevisa genom att erhålla en återfallsformel.

17 Antal kombinationer med repetitioner

siffra r-kombinationer med upprepningar från n-uppsättningarna är lika

– bevis med hjälp av en återkommande formel.

Metoden bygger på att erhålla en formel som låter dig beräkna värdena för den önskade kvantiteten steg för steg, baserat på de kända initiala värdena och värden som beräknats i tidigare steg.

Formel för återfallr -:e ordningen– formulärets formel

a n = f(n, a n- 1 , a n- 2 , … , a n-r).

Formeln uttrycker kl n>r varje medlem av sekvensen ( a i) genom föregående r medlemmar. Konstruktionen av en återkommande formel består av följande steg.

1. Utveckling av initiala förutsättningar baserat på uppenbara samband.

Låt oss beteckna med f(n,r). Det är uppenbart

2. Logiskt resonemang. Låt oss fixa något element i setet S. Då i förhållande till någon r- kombinationer med upprepningar från n-uppsättningar S vi kan se om den innehåller ett givet fast element eller inte.

Om innehåller, sedan resten ( r-1) objekt kan väljas f(n,r-1) sätt.

Om innehåller inte(det här elementet finns inte i urvalet), då r- en kombination som består av element ( n-1)-set (set S förutom detta fasta element). Antal sådana kombinationer f(n-1,r).

Därför att dessa fall utesluter varandra, då enligt summaregeln

3. Kontrollera formeln på vissa värden och härleda ett allmänt mönster.

1) Låt oss räkna f (n ,0) . Av (2) följer

Sedan f(n,0)=f(n,1)-f(n-1,1). Från (1) f(n,1)=n, f(n-1,1)=n-1.

Därav, f(n,0)=n-(n-1)=1=.

2) f (n ,1) =f(n,0)+f(n-1,1) = 1+n- 1 =n==.

3) f (n ,2) =f(n,1)+f(n-1,2) =n+f(n-1,1)+f(n-2,2) =n+(n-1)+f(n-2,1)+f(n-3,2) = … =

= n+(n-1)+…+2+1 =.

(summan av aritmetisk progression)

4) f (n ,3) =f(n,2)+f(n-1,3) =+f(n-1,2)+f(n-2,3) =++f(n-2,2)+f(n-3,3) = … =

(summan av geometrisk progression)

5) f (n ,4) =

Baserat på särskilda fall kan det antas att

4. Kontrollera de initiala förhållandena med den resulterande formeln.

vilket överensstämmer med (1) #

19, 20) Antalet binära träd med n hörn är lika med C(n), där C(n) är det n:te katalanska talet.

Antalet binära träd med n hörn kallas det katalanska talet, som har många intressanta egenskaper. Det N:te katalanska talet beräknas med formeln (2n)! / (n+1)!n!, som växer exponentiellt. (Wikipedia ger flera bevis på att detta är en form av det katalanska talet.) Antal binära träd av en given storlek 0 1 1 1 2 2 4 14 8 1430 12 208012 16 35357670

Utbyte

Gå till: navigering, Sök

Detta är en artikel om substitution som en syntaktisk operation påtermer . Du kanske är intresserad avomarrangemang .

I matematik Och datavetenskap utbyte- det här är en operation syntaktisk ersättning av underord av en given terma andra villkor, enligt vissa regler. Vanligtvis talar vi om att ersätta en term istället för variabel.

Definitioner och notationer

Det finns ingen universell, överenskommen notation för substitution, och det finns inte heller någon standarddefinition. Begreppet substitution varierar inte bara inom sektioner utan även på nivån för enskilda publikationer. I allmänhet kan vi lyfta fram kontextsubstitution Och substitution "istället för". I det första fallet anges platsen i terminen där bytet sker sammanhang, det vill säga en del av termen som "omger" denna plats. I synnerhet används detta substitutionsbegrepp i omskrivning. Det andra alternativet är vanligare. I det här fallet specificeras substitutionen vanligtvis av någon funktion från en uppsättning variabler till en uppsättning termer. Att indikera ersättningsåtgärder, som regel, använd postfix-notation. Betyder till exempel resultatet av en ersättningsåtgärd på en termin.

I den överväldigande majoriteten av fallen krävs att substitutionen har en ändlig bärare, det vill säga att uppsättningen var ändlig. I det här fallet kan det specificeras genom att helt enkelt lista paren "variabelt värde". Eftersom varje sådan substitution kan reduceras till en sekvens av substitutioner som endast ersätter en variabel var, utan förlust av generalitet kan vi anta att substitutionen ges av ett par "variabelt värde", vilket är vad man brukar göra.

Den sista definitionen av substitution är förmodligen den mest typiska och ofta använda. Det finns dock ingen enskild allmänt accepterad notation för det heller. Används oftast för att indikera substitution a istället för x V t inspelning används t[a/x], t[x:=a] eller t[x←a].

Variabel substitution iλ-kalkyl

I λ-kalkyl bestäms substitution genom strukturell induktion. För godtyckliga objekt och en godtycklig variabel beräknas resultatet av att ersätta en godtycklig fri förekomst utbyte och bestäms av induktion på konstruktionen:

(i) grund:: objekt matchar variabel. Sedan;

(ii) grund:: objekt matchar konstant. Sedan för godtyckliga atomära;

(iii) steg: : objektet är icke-atomärt och ser ut som en applikation. Sedan;

(iv) steg:: objekt är icke-atomiskt och är en abstraktion. Sedan [;

(v) steg:: objektet är icke-atomiskt och är dessutom en abstraktion. Sedan:

för andor;

Variabel substitution i programmering

Utbyte variabel ( engelsk utbyte) V tillämplig programmering tolkas på följande sätt. För att beräkna värdet på en funktion f på argumentet v inträde tillämpas f(v)), Var f bestäms av design f(x) = e. Spela in f(v) betyder i detta fall att i uttrycket e händer utbyte, eller variabel substitution x på v. Bytet utförs i enlighet med semantik av beräkningar.

Utbyte variabel ( engelsk uppdrag) V programmering förstås som uppdrag. Uppdragsoperatören är en manifestation av von Neumanns flaskhalseffekt för traditionella programmeringsspråk . Fri från detta applikativa datorsystem.

http://math.nsc.ru/LBRT/u3/bard/fails/Brenner_Evans.pdf

21 Genererar funktioner.Genereringsfunktion (täljare) och uppräkningsgenererande funktion för kombinationer utan upprepningar.

Genererande funktioner: 1) Z-transformerar 2) generator 3) genererande funktion 4) genererande funktion för sekvensen (a r ) på basis av (g r ) - funktion f, när den expanderas till en serie funktioner med en fast bas (g r ), denna sekvens av koefficienter (a r ) bildas …………*)

Denna serie är formell. Namnet formellt betyder att vi behandlar formeln *) som en bekväm notation för vår sekvens - i det här fallet spelar det ingen roll för vilka (åtgärder och komplexa) värden den konvergerar. Rollen för t reduceras till att särskilja koefficienterna för sekvensen A0, A1,…Ar…. Därför, i teorin om att generera funktioner, beräknas värdena för denna serie aldrig för ett specifikt värde av variabeln t. Endast vissa operationer utförs på sådana serier, och sedan bestäms bara några operationer på sådana serier, och sedan bestäms koefficienterna för individuella potenser av variabeln t.

Vanligtvis som

22 Genererande funktion. Genererande funktion (täljare) och uppräkningsgenererande funktion för kombinationer med upprepningar.

Tillverkningsanläggning för:

Byggregel

1) Om ett element av typ i kan inkluderas i kombinationerna K 1 eller K 2 eller... K i gånger, så har det en motsvarande multiplikator

3) Det återstår att hitta koefficienten. på

exponentiell genererande funktion för placeringskonstruktionsregel

25) Kombinatoriska siffror inkluderar också Stirling siffror av första och andra slaget. Dessa tal definieras som koefficienter i likheterna

och har en enkel kombinatorisk betydelse - lika med antalet element i permutationsgruppen som är produkter av exakt k osammanhängande cykler och lika med antalet partitioner n- element inställt k icke-tomma delmängder. Det är uppenbart. En liknande summa av Stirlingtal av det andra slaget kallas n- Klocknummer och lika med antalet av alla partitioner n-elementuppsättning. Upprepningsformeln är giltig för klocknummer.

När man löser kombinatoriska problem är det ofta användbart formel för inkludering-uteslutning

vilket gör att man kan hitta kardinaliteten för föreningen av uppsättningar om kardinaliteten för deras skärningspunkter är känd. Låt oss använda inkluderings-exkluderingsformeln för att få en explicit formel för Stirlingtalen av det andra slaget.

Stirlingnummer av det första slaget

Material från Wikipedia - den fria encyklopedin

Gå till: navigering, Sök

Stirlingnummer av det första slaget(osignerad) - kvantitet permutationer beställa n Med k cykler.

Definition

Stirlingnummer av det första slaget(med tecken) s(n, k) kallas koefficienter polynom:

Var ( x) n - Pochhammer symbol (minskande faktor):

Som framgår av definitionen har siffror ett alternerande tecken. Deras absoluta värden anger antalet permutationer set bestående av n element med k cykler.

Återkommande förhållande

Stirlingnummer av det första slaget anges återkommande förhållande:

s(n,n) = 1, för n ≥ 0,

s(n,0) = 0, för n > 0,

för 0< k < n.

Bevis.

För n=1 denna likhet kontrolleras direkt. Låt permutationen ( n-1):e ordningen sönderdelas till k cykler. siffra n kan läggas till efter valfritt tal i lämplig loop. Alla resulterande permutationer är olika och innehåller k cykler, deras antal ( n-1)· s(n-1, k). Från vilken permutation som helst ( n-1):e ordningen innehåller k-1 cykel kan en enda permutation bildas n beställning innehållande k cykler genom att lägga till en cykel som bildas av ett singulartal n. Uppenbarligen beskriver denna konstruktion alla permutationer n-th order som innehåller k cykler. Därmed är jämlikhet bevisad.

Exempel

Första raderna:

I kombinatorik Stirlingnummer av det andra slaget från n Förbi k, betecknad med eller, är antalet oordnade partitioner n-elementär set på k icke-tomma delmängder.

Formel för återfall

Stirlingnummer av det andra slaget uppfyller återkommande förhållande:

För n ≥ 0,

För n > 0,

Explicit formel

Exempel

De initiala värdena för Stirlingtalen av det andra slaget anges i tabellen:

Egenskaper

Bijektiv En mappning är en mappning som har egenskaperna att vara injektiv och surjektiv på samma gång.

1. Låt oss först komma ihåg definitionen av den viktiga talteoretiska Möbiu-funktionen

1 om n = 1

µ (n)=0, om det finns ett primtal p, p2 n (-1)k, om n = p1 ... pk är produkten av k olika primtalsfaktorer.

Låt oss bevisa den huvudsakliga egenskapen hos Möbius-funktionen:

Sats 1.

♦ Om n = 1 är den enda divisorn d = 1 och (1) är sant, eftersom µ (1) = 1. Låt nu n > 1. Låt oss representera det i formen

n = p1 s 1 ps 2 2 K ps k k ,

där pi, i 1, k är primtal, si är deras potenser. Om d är en divisor av n, då d = p1 d 1 pd 2 2 K pd k k ,

där 0 ≤ di ≤ si, i 1, k. Om di > 1 för vissa i 1, k, så är µ (d) = 0. Detta betyder att i (1) behöver vi endast beakta de d för vilka di ≤ 1, i 1, k. Varje sådan divisor co-

består av produkten av r olika primtal, där r 1, k, och dess bidrag till summan

(1) är lika med (-1)r och det finns k totalt. Således får vi


	µ (d) = 1 −	K + (− 1) k	0. ♦



	Sats 2. (Mobius inversionsformel). Låt f(n) och g(n) vara funktioner av naturliga
ral argument. Sedan jämställdhet
			∑f(d)

är sant om och endast om jämställdheten är sann
			∑ µ (d)g(
			∑ µ (d)g(

♦ Låt (2) vara sant för vilket n som helst. Sedan

g(d n ) = ∑ f(d′ )

d ′ d n

Om vi ersätter den högra sidan av (3), får vi

∑ µ (d)g(	) = ∑ µ (d) ∑ f(d′ )

		d′

Dubbel summering till höger utförs över alla par d, d′ så att d d′ n. Om du väljer d ′ kommer d att gå igenom alla divisorer d n ′ . Således

∑ µ (d)g(

) = ∑ f(d′ ) ∑ µ (d′ )

d′

n > d′

Men enligt (1) har vi ∑

µ (d′ ) =

n = d′

d′

Detta innebär att jämställdhet (3) upprättas. Låt nu (3) vara sant för vilket n som helst. Sedan

∑ f(d) =

∑ ∑ µ (d′ )g(

) , d′′ = d d ′ - är en divisor av n och dubbelsumman kan

d′

n d'

skrivas om som

∑ µ (d′ )g(d′′ ) =

∑ g(d′′ )

∑ µ(d′)

d′′

n d"

d′′

d′

d′′

Enligt (1) övergår den sista summan till enhet i fallet d′′ = n, i andra fall

Det är i alla fall noll. Detta bevisar (2). ♦ 2. Överväg en tillämpning av Möbius-inversionen.

Låt ett alfabet A av s bokstäver ges. Det finns sn ord med längden n i ett givet alfabet. För varje ord w0 = a1 a2 … kan n - 1 ord definieras

w1 = a2 a3 … an a1, w2 = a3 a4 … a1 a2, …, wk-1 = an a1 … an-1, erhållna från varandra genom cykliska skift. På mängden av alla sn-ord introducerar vi en ekvivalensrelation: vi förklarar två ord ekvivalenta om det ena erhålls från det andra genom ett cykliskt skifte. Vi kommer att vara intresserade av antalet klasser som innehåller exakt n ord. Detta problem uppstår i teorin om synkronisering av koder.

Vi kallar ett ord w degenererat om ekvivalensklassen som innehåller w består av mindre än n ord. Låt oss kalla w periodisk om det finns ett ord u och ett naturligt tal m så att w = u u … u (m gånger).

Sats 3. Ett ord w är periodiskt om och endast om det är degenererat.

som du kan vi ta en 1 a 2 … a p och som m =

♦ Det är klart att om w är periodisk så är den degenererad. Låt w vara degenererad. Låt p vara det minimala heltal så att w = wp. Sedan om

w = a1 a2 … an, sedan wp = a1+p a2+p … an+p (indexerar modulo n). Härifrån får vi det i n p . (Det är lätt att se att p n). ♦ Bakgrund

signifikant genom M(d) - antalet kvadrater som innehåller d ord. Från föregående har vi

d n. Således är formeln giltig∑ dM(d) = sn. d n

Låt oss tillämpa Möbius-inversionsformeln för fallet g(n) = sn , f(d) = dM(d). Då får vi

nM(n) = ∑ µ (d)s n d d n

∑ µ (d)sn d

Således är M(n) talet vi är intresserade av. Om n = p är ett primtal, då

− s)

Det finns en multiplikativ version av Möbius-inversionen. Rättvis

Sats 4. Låt f(n) och g(n) vara funktioner av ett naturligt argument relaterat i enlighet därmed

bär

f(n) = ∏g(d)

µ(n

g(n) = µf(d)

Och omvänt, från (5) följer (4).

Med hjälp av Möbius-inversionsformeln kan man lösa det praktiskt viktiga problemet med antalet irreducerbara polynom av en fast grad över ett ändligt fält. Låt GF(q) vara ett fält av q element och m vara ett naturligt tal. Sedan för numret

Φ m (q) av irreducerbara polynom över fältet GF(q) gäller följande formel:

Låt oss presentera en tabell över de första värdena av funktionen Φ m (2)


Φ m (2)

§ 5. Permanenter och deras tillämpning på uppräknade

1. Permanenter används för att lösa många kombinatoriska problem. Tänk på den numeriska matrisen

A = (ai, j), i = 1, n, j = 1, m, n ≤ m

Den permanenta matrisen A (beteckning - per A) bestäms av jämlikheten

per A = ∑			a 2 j L a nj
(j1 ,K , jn )
(j1 ,K , jn )

där summeringen utförs över alla n-permutationer av m element 1, 2, m. Med andra ord, matrisens permanenta är lika med summan av produkterna av elementen taget en från varje rad och olika kolumner.

Från formel (1) följer några uppenbara egenskaper hos permanenten, liknande egenskaperna hos determinanten för kvadratiska matriser.

1. Om en av raderna(n× m) matris A (n ≤ m) består av nollor, då per A = 0. För n = m gäller samma sak för kolumnerna.

2. När alla element i en av raderna i matris A multipliceras med ett visst tal, multipliceras värdet av permanent A med samma tal.

3. En permanent ändras inte när dess rader och kolumner ordnas om.

Låt oss beteckna med Aij matrisen som erhålls från A genom att ta bort den i:te raden och den j:te kolumnen.

4. Formeln för att sönderdela permanenten i den i:te raden är giltig: per A = ai1 per Ai1 + ai2 per Ai2 + ... + mål per mål (2)

sålunda liknar många egenskaper hos permanenter determinanters.

Huvudegenskapen för determinanter det(A B) = detA detB är dock inte uppfylld för permanenta, och denna omständighet gör deras beräkning mycket svår.


Till exempel,


	2, per


Dock är 4 = per		≠ per

Låt oss överväga en av de viktigaste tillämpningarna av begreppet permanent i kombinatoriska problem.

dachas Låt X = (x1, xm) vara en finit mängd och X1, …, Xn vara ett system av delmängder

I detta fall sägs elementet xi representera mängden Xi. Behovet av att hitta ett system med olika representanter uppstår när man löser många tillämpade problem. Tänk på följande kodningsproblem. Låt det komma något förslag, d.v.s. en ordnad uppsättning ord i något alfabet. Det är nödvändigt att koda denna mening så att varje ord tilldelas en bokstav, och denna bokstav måste vara en del av detta ord, och olika bokstäver måste motsvara olika ord.

Exempel: meningen a bc ab d abe c de cd e kan kodas som abecd. Samtidigt kan meningen ab ab bc abc bcd inte kodas på detta sätt, eftersom de fyra första orden tillsammans bara innehåller tre bokstäver.

För ett system av mängder X1 , … , Xn definierar vi incidensmatris A = (aij), i = 1, n,


	1 om xi
a ij =
	0 annars.
Rättvis
Sats 1. Låt A = (aij), i =		(n ≤ m) incidensmatris
Sats 1. Låt A = (aij), i =		(n ≤ m) incidensmatris

sätter Xl, …, Xn, där Xi X, i = 1, n, X = (x1, …, xm). Sedan för antalet system

personliga företrädare R(X1 , … , Xn ) av uppsättningarna X1 , … , Xn gäller följande likhet:

R(X1, …, Xn) = per A

♦ Faktum är att eftersom elementet aij = 1 i matris A, om xj Xi och aij = 0,

om xj

K, xi

) element X är ett system av olika för-

Xi, sedan uppsättningen (xi

suffix för X1 , … , Xn

om och endast om a1i

K,a ni

poliser a1i

K,a ni

finns i olika kolumner i matris A. Låt oss summera siffrorna

a1i ,K ,a ni

över alla n-permutationer av element 1, 2, …, m. Då får vi från hundra

rons, antalet system för olika representanter för X1, ..., Xn, och å andra sidan värdet av per-

manenta matris A. ♦

a 1i 1 a 2i 2 L a ni n

Följd. Ett system med olika representanter för X1, …, Xn finns om och endast om för motsvarande matris incident A är uppfylld:

Eftersom det i formel (1) finns m(m - 1) ... (m - n +1) termer, är det svårt att beräkna permanent baserat på definitionen. Låt oss presentera en allmän formel för detta ändamål.

2. Låt oss begränsa oss till att betrakta kvadratiska numeriska matriser A = (aij), i, j = 1, n.

Då per A = ∑

(i1,K,in)

där summan sträcker sig över alla permutationer i1 , … , i element

1, 2, … , n. Låt oss tillämpa inklusions-exkluderingsformeln för att beräkna permanenten för matris A. Vi tilldelar varje mängd i1, ..., i en vikt lika med a1i 1,K,a ni n.

Det betyder att det permanenta A är summan av vikterna av de mängder som motsvarar permutationerna. Låt oss introducera n egenskaper P1 , … , Pn på uppsättningen av alla samlingar i1 , i2 , … , i 1, 2, … , n, där egenskapen Pi betyder att det inte finns något element i i samlingen i1 , … , i. Det permanenta A är alltså summan av vikterna av mängderna i1, ..., in, som inte har någon av egenskaperna P1, ..., Pn. Det återstår att bestämma summan av vikterna W(Pi 1 , K , Pi k ) av mängder med k egenskaper

Pi 1, K, Pi k. Vi har för summan av vikterna W(0) för alla mängder i1 , … , ik .
W(0) = ∑		K, ani	= (a 11 + L + a 1n )(a 21 + L + a 2n ) L (a n1 + L + a nn )
i1,K,in
i1,K,in

W(N(Pi)) =		a1i ,K ,a ni		= (a 11 + L + a 1i	L + a1n )L (a n1 + L a ni + L + a nn ) (9)

	≠i

där ^-tecknet ovanför ett element i matris A betyder att detta element ska utelämnas. På samma sätt för sij (dvs< j) имеем


W(N(Pi, Pj)) = (al1 + L + ali	L+a 1j	L + a1n )L (a n1 + L a ni + L + a nj + L + a nn ) (10)

Nu, med hjälp av inkluderings-exkluderingsformeln, får vi Raiser-formeln för permanent A:


per A = ∏ i n = 1 (ai1 + L + ain ) − ∑∏ k n = 1 (a k1 + L + a ki + L + a kn )+ L +

+ (− 1)s	∑∏n
+ (− 1)s	∑∏n	(a k1 + L + a ki1	L+a ki	L +a kn ) +L
	1≤ i1< L < is ≤ k n= 1

Beräkningen av permanenten med hjälp av Raiser-formeln kan organiseras på ett sådant sätt som den kräver

(2n - 1)(n - 4) multiplikationer och (2n - 2)(n + 1) additioner. Även om detta värde växer snabbt när n ökar, ger denna formel det mest effektiva sättet att beräkna permanenta värden.

3. Låt oss nu klargöra frågan om villkoren för att den permanenta (0, 1) matrisen ska vara lika med noll. Låt oss begränsa oss till fallet med en kvadratisk matris.

Sats 2. Låt A = (aij ), i, j = 1, n vara en (0, 1) matris av ordningen n. Sedan

per A= 0 om och endast om A innehåller en submatris med nollor av storleken s × t, där s + t = n + 1.

♦ Låt en sådan nolldelmatris finnas i A. Eftersom permanenten inte ändras på grund av permutationer av rader och kolumner, kan vi anta att denna submatris är placerad i det nedre vänstra hörnet, dvs.

där O - (s × t) är en matris med nollor, har submatris B storlek (n - s) × t. Varje medlem av permanent A måste innehålla ett element från de första t kolumnerna. Därför, om vi letar efter en positiv term av permanenten, måste elementen i dessa kolumner tillhöra parvis olika rader med siffrorna 1, 2, ..., n - s. Men n - s = t - 1< t и поэтому данное условие выполнить нельзя, т.е. per A = 0.

Låt nu per A = 0. Vi bevisar satsen genom induktion på n. För n = 1 är påståendet uppenbart (A = (0)). Låt det vara sant för alla order mindre än n. Om A är en nollmatris av ordningen n, är påståendet uppenbart. Om A inte är en nollmatris, låt aij = 1. Låt oss skriva nedbrytningen av A längs rad i:

per A = ai1 Ai1 + … + ain Ain

Eftersom per A = 0, då per Aij = 0. Men Aij har storlek (n - 1) × (n - 1) och enligt induktionshypotesen finns det en submatris med nollor av storlek

s1 × t1, med s1 + t1 = n - 1 + 1 = n. Låt oss ordna om raderna och kolumnerna så att denna nollsubmatris är i det nedre vänstra hörnet:


A → B =

där O är nollsubmatrisen av storleken s1 × t1, s1 + t1 = n, C - har storleken (n - s1) × t1, D -

har storlek s1 × (n - t) . Det betyder att matriserna C och D är kvadratiska och har ordning (t1 × t1) respektive (s1 × s1). Enligt definitionen av en permanent har vi per B = per A och,

per B = per C per D och därför från per A = 0 följer att antingen per C = 0 eller per D = 0.

Låt per C = 0. Enligt induktionshypotesen finns en noll submatris av storlek

u × v, där u + v = t1 + 1. Låt den placeras i rader med siffrorna i1, …, iu och kolumner med siffrorna j1, …, jv. Betrakta en submatris B som består av rader

i1, …, iu, t1 + 1, …, n och kolumnerna j1, …, jv. Detta är en nollsubmatris med storlek (u + n - t1) × v,

där u + n - t1 + v = n + +1. Så, matris B innehåller en nollsubmatris med storleken s × t, där s + t = n + 1. Eftersom matriserna A och B skiljer sig åt i permutationen av rader och kolumner, är satsen bevisad. ♦

Låt oss nu betrakta ett viktigt specialfall av matrisen A. Låt oss beteckna med A(k, n) en matris med 0,1 element av storleken n × n med k ettor för varje rad och varje kolumn (k > 0).

Sats 3. För valfri matris A(k, n) per A(k, n) > 0.

♦ Låt oss anta motsatsen, att per A(k, n) = 0. Då, enligt sats 2, finns det en noll-

submatris med storleken s × t, där s + t = n + 1. Om vi sedan arrangerar om raderna och kolumnerna i matrisen A(k, n) får vi matrisen

där O är nollmatrisen (s × t).

Låt oss räkna antalet ettor i matriserna B och D. Eftersom A(k, n) har k ettor i varje rad och varje kolumn, så finns det exakt k ettor i varje kolumn i B och varje rad i D

enheter. Det finns n k enheter totalt i A(k, n), så nk ≥ tk + sk = (t + s)n. Den här vägen

som, n ≥ t + s, vilket är omöjligt, eftersom s + t = n + 1 Av denna motsägelse följer att

påståendets giltighet. ♦ Det bevisas på liknande sätt

Sats 3a. Låt A vara en (0,1) matris med storleken n× m (n≤ m). Då är perA = 0 om och endast om den innehåller en nollsubmatris med storleken s×t, där s+t=m+1.

4. Låt oss nu överväga tillämpningen av de frågor som diskuteras på konstruktionen av la-

Tina rutor. latinsk (n × m)-rektangelöver uppsättningen X=(x1 ,…,xm )

kallas en (n× m) -matris av element X, där varje rad är en n-permutation av X, och varje kolumn är en m-permutation av mängden X. För n=m kallas den latinska rektangeln Latinsk torg.

Det är tydligt att för n=1 är antalet latinska 1×m rektanglar lika med m!. När n=2, efter att den första raden har valts, kan valfri permutation tas som den andra raden.

ny produkt som motsäger den valda. Antalet sådana permutationer är Dm, så talet 2× m är

av latinska rektanglar är lika med m! Dm.

En naturlig fråga uppstår i samband med den induktiva konstruktionen av latinska kvadrater. Låt oss konstruera en latinsk (n× m)-rektangel (n< m). Можно ли его расширить до ((n+1)× m) -прямоугольника добавлением (n+1)-й строки?

Rättvis

Sats 4. Varje latinsk (n× m)-rektangel n

♦ Låt X=(x1,…,xm) och en L-latinsk (n×m)-rektangel med element från X. Betrakta en uppsättning mängder A1,...,Am där Ai är elementen i den i:te kolumnen i den latinska rektangeln L. Låt A vara incidensmatris för mängdsystemet A1 ,... ,Am . Den har storleken m×m, och varje rad av matris A innehåller exakt n ettor, eftersom Ai = n, i = 1, m. Varje element xi X kan förekomma i kolumnerna i L högst m gånger, annars skulle det finnas en rad där detta element förekommer två gånger. Totalt antal element

L är lika med m n, så varje element xi X visas exakt n gånger i kolumnerna. Det följer att varje kolumn i matris A innehåller exakt n ettor. Låt oss nu betrakta matrisen A som erhålls genom att ersätta var och en med en nolla och varje nolla med en etta.

Matris A är incidensmatrisen för systemet av mängder X1, …, Xn, där Xi = X\Ai,

i = 1, m. Den innehåller m - n enheter i varje rad och i varje kolumn. Genom teorem

> 0. Låt ai1

…en mil

≠ 0 . Då har vi xi X1 ,K , xi

Xm och alla element

xi,K,xi

parvis olika. Linje

xi,K,xi

kan tas som den (n + 1):e

för en latinsk (n × m)-rektangel L. Fortsätter vi med denna procedur får vi en latinsk

sky square. ♦

Låt oss beteckna l n - antalet latinska kvadrater av ordning n, med element från mängden X = (1, 2, ..., n), där elementen i den första kolumnen och första raden är i naturlig ordning. Här är en tabell över flera kända värden för talet l n:

5. En matris A = (aij) av storleken n × n med reella, icke-negativa element kallas två gånger stokastisk, Om