Lucru grozav04/02/12. Să trecem în revistă * Care ecuație se numește pătratică? * Ce ecuații se numesc ecuații pătratice incomplete? * Care. Conceptul de ecuație de linii. Definirea unei drepte folosind ecuația Fig.6. Ecuația liniei vectoriale

Egalitatea formei F (x, y) = 0 numită ecuație în două variabile X, y, dacă nu este adevărat pentru toate perechile de numere X y. Ei spun două numere X = X 0 , y=y 0, satisface o ecuație a formei F(x, y)=0, dacă la înlocuirea acestor numere în loc de variabile XȘi laîn ecuație, partea stângă dispare.

Ecuația unei linii date (într-un sistem de coordonate desemnat) este o ecuație cu două variabile care este satisfăcută de coordonatele fiecărui punct aflat pe această dreaptă și nu este satisfăcută de coordonatele fiecărui punct care nu se află pe ea.

În cele ce urmează, în locul expresiei „se dă ecuația dreptei F(x, y) = 0" vom spune adesea pe scurt: dată o linie F (x, y) = 0.

Dacă sunt date ecuațiile a două drepte F(x, y) = 0Și Ф(x, y) = Q, apoi soluția comună a sistemului

oferă toate punctele lor de intersecție. Mai precis, fiecare pereche de numere care este o soluție comună a acestui sistem determină unul dintre punctele de intersecție.

*) În cazurile în care sistemul de coordonate nu este numit, se presupune că este dreptunghiular cartezian.

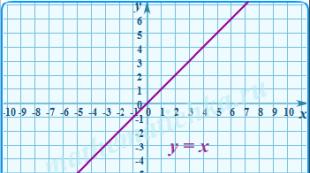
157. Se acordă puncte *) M 1 (2; - 2), M 2 (2; 2), M 3 (2; - 1), M 4 (3; -3), M 5 (5; -5), M 6 (3; -2). Determinați care puncte publicate se află pe linia definită de ecuație X+ y = 0,și care nu se întind pe el. Care linie este definită de această ecuație? (Desenează-l pe desen.)

158. Pe linia definită de ecuație X 2 +y 2 =25, aflați punctele ale căror abscise sunt egale cu următoarele numere: a) 0, b) - 3, c) 5, d) 7; pe aceeași linie găsiți puncte ale căror ordonate sunt egale cu următoarele numere: e) 3, f) - 5, g) - 8. Care dreaptă este determinată de această ecuație? (Desenează-l pe desen.)

159. Stabiliți ce drepte sunt determinate de următoarele ecuații (construiți-le pe desen):

1) x - y = 0; 2) x + y = 0; 3) X- 2 = 0; 4) X+ 3 = 0;

5) y - 5 = 0; 6) y+ 2 = 0; 7) x = 0; 8) y = 0;

9) X 2 - xy = 0; 10) X y+ y 2 = 0; unsprezece) X 2 - y 2 = 0; 12) X y= 0;

13) y 2 - 9 = 0; 14) X y 2 - 8X y+15 = 0; 15) y 2 +5y+4 = 0;

16) X 2 y - 7xy + 10y = 0; 17) y =|X|; 18) x =|la|; 19)y + |X|=0;

20) x +|la|= 0; 21)y =|X- 1|; 22) y = |X+ 2|; 23) X 2 + la 2 = 16;

24) (X-2) 2 +(y-1) 2 =16; 25) (X+ 5) 2 +(y- 1) 2 = 9;

26) (X - 1) 2 + y 2 = 4; 27) X 2 +(y + 3) 2 = 1; 28) (X -3) 2 + y 2 = 0;

29) X 2 + 2y 2 = 0; 30) 2X 2 + 3y 2 + 5 = 0

31) (X- 2) 2 + (y + 3) 2 + 1=0.

160.Linii date:

1)X+ y = 0; 2)x - y = 0; 3) X 2 + y 2 - 36 = 0;

4) X 2 +y 2 -2X==0; 5) X 2 +y 2 + 4X-6y-1 =0.

Determinați care dintre ele trec prin origine.

161.Randurile date:

1) X 2 + y 2 = 49; 2) (X- 3) 2 + (y+ 4) 2 = 25;

3) (X+ 6) 2 + (y - 3) 2 = 25; 4) ( X + 5) 2 + (y - 4) 2 = 9;

5) X 2 +y 2 - 12x + 16y = 0; 6) X 2 +y 2 - 2x + 8la+ 7 = 0;

7) X 2 +y 2 - 6x + 4y + 12 = 0.

Aflați punctele lor de intersecție: a) cu axa Oh; b) cu o axă OU.

162.Aflați punctele de intersecție a două drepte;

1)X 2 +y 2 = 8, x-y = 0;

2) X 2 +y 2 -16X+4la+18 = 0, x + y= 0;

3) X 2 +y 2 -2X+4la -3 = 0, X 2 + y 2 = 25;

4) X 2 +y 2 -8X+10у+40 = 0, X 2 + y 2 = 4.

163. Punctele sunt date în sistemul de coordonate polare

M 1 (1; ), M 2 (2; 0), M 3 (2; )

M 4 (
;) Și M 5 (1; )

Determinați care dintre aceste puncte se află pe dreapta definită de ecuație în coordonatele polare  = 2 cos  și care nu se află pe ea. Care linie este determinată de această ecuație? (Desenează-l pe desen:)

164. Pe dreapta definită de ecuaţia  = , găsiți puncte ale căror unghiuri polare sunt egale cu următoarele numere: a) ,b) - , c) 0, d) . Care linie este definită de această ecuație?

(Construiți-l pe desen.)

165.Pe dreapta definită de ecuaţia  = , găsiți puncte ale căror raze polare sunt egale cu următoarele numere: a) 1, b) 2, c)
. Care linie este definită de această ecuație? (Construiți-l pe desen.)

166. Stabiliți ce drepte sunt determinate în coordonate polare de următoarele ecuații (construiți-le pe desen):

1)  = 5; 2)  = ; 3)  = ; 4)  cos  = 2; 5)  sin  = 1;

6)  = 6 cos ; 7)  = 10 sin ; 8) sin  = 9) sin  =

167. Construiți următoarele spirale lui Arhimede pe desen:

1)  = 5, 2)  = 5; 3)  = ; 4)р = -1.

168. Construiți pe desen următoarele spirale hiperbolice:

1)  = ; 2) = ; 3) = ; 4) = - .

169. Construiți pe desen următoarele spirale logaritmice:

,
.

170. Determinați lungimile segmentelor în care se taie spirala lui Arhimede

rază care iese din pol și înclinată în unghi față de axa polară
. Faceți un desen.

171. Pe spirala lui Arhimede
punct luat CU, a cărui rază polară este 47. Stabiliți câte părți taie această spirală raza polară a punctului CU, Faceți un desen.

172. Pe o spirală hiperbolică
găsi un punct R, a căror rază polară este de 12. Realizați un desen.

173. Pe o spirală logaritmică
găsiți punctul Q a cărui rază polară este 81. Faceți un desen.

Să trecem în revistă * Care ecuație se numește pătratică? * Ce ecuații se numesc ecuații pătratice incomplete? * Care ecuație pătratică se numește redusă? * Ce se numește rădăcina unei ecuații pătratice? * Ce înseamnă să rezolvi o ecuație pătratică? Care ecuație se numește pătratică? Ce ecuații se numesc ecuații pătratice incomplete? Ce ecuație pătratică se numește redusă? Care este rădăcina unei ecuații pătratice? Ce înseamnă să rezolvi o ecuație pătratică? Care ecuație se numește pătratică? Ce ecuații se numesc ecuații pătratice incomplete? Ce ecuație pătratică se numește redusă? Care este rădăcina unei ecuații pătratice? Ce înseamnă să rezolvi o ecuație pătratică?

Algoritm pentru rezolvarea unei ecuații pătratice: 1. Determinați cea mai rațională modalitate de a rezolva o ecuație pătratică 2. Alegeți cea mai rațională modalitate de rezolvare 3. Determinarea numărului de rădăcini ale unei ecuații pătratice 4. Găsirea rădăcinilor unei ecuații pătratice Pentru mai bine memorare, completați tabelul... Pentru o memorare mai bună, completați tabelul... Pentru o memorare mai bună, completați tabelul...

Condiție suplimentară Ecuație Rădăcini Exemple 1. c = c = 0, a 0 ax 2 = 0 x 1 = 0 2. c = 0, a 0, b 0 ax 2 + bx = 0 x 1 = 0, x 2 = -b /a 3. c = 0, a 0, c 0 ax 2 + c = 0 a) x 1.2 = ±(c/a), unde c/a 0. b) dacă c/a 0, atunci nu există soluții 4. a 0 ax 2 + bx + c = 0 x 1.2 =(-b±D)/2 a, unde D = b 2 – 4 ac, D0 5. c – număr par (b = 2k), a 0, în 0, c 0 х 2 + 2kx + c = 0 x 1.2 =(-b±D)/а, D 1 = k 2 – ac, unde k = 6. Teorema inversă teoremei lui Vieta x 2 + px + q = 0x 1 + x 2 = - p x 1 x 2 = q

II. Metode speciale 7. Metoda izolării pătratului unui binom. Scop: Reduceți o ecuație generală la o ecuație pătratică incompletă. Notă: metoda este aplicabilă oricăror ecuații pătratice, dar nu este întotdeauna convenabilă de utilizat. Folosit pentru a demonstra formula pentru rădăcinile unei ecuații pătratice. Exemplu: se rezolvă ecuația x 2 -6 x+8=0 8. Metoda „transferării” celui mai mare coeficient. Rădăcinile ecuațiilor pătratice ax 2 + bx + c = 0 și y 2 +by+ac=0 sunt legate prin relațiile: și Notă: metoda este bună pentru ecuațiile pătratice cu coeficienți „convenienți”. În unele cazuri, vă permite să rezolvați o ecuație pătratică pe cale orală. Exemplu: rezolvați ecuația 2 x 2 -9 x-5=0 Pe baza teoremelor: Exemplu: rezolvați ecuația 157 x x-177=0 9. Dacă într-o ecuație pătratică a+b+c=0, atunci unul dintre rădăcinile este 1, iar a doua, conform teoremei lui Vieta, este egală cu c / a 10. Dacă într-o ecuație pătratică a + c = b, atunci una dintre rădăcini este egală cu -1, iar a doua, conform lui Vieta teorema, este egală cu -c / a Exemplu: rezolvați ecuația 203 x x + 17 = 0 x 1 =y 1 /a, x 2 =y 2 /a

III. Metode generale de rezolvare a ecuaţiilor 11. Metoda factorizării. Scop: Reduceți o ecuație pătratică generală la forma A(x)·B(x)=0, unde A(x) și B(x) sunt polinoame în raport cu x. Metode: Scoaterea factorului comun din paranteze; Utilizarea formulelor de înmulțire prescurtate; Metoda de grupare. Exemplu: se rezolvă ecuația 3 x 2 +2 x-1=0 12. Metoda introducerii unei noi variabile. Alegerea bună a unei noi variabile face ca structura ecuației să fie mai transparentă Exemplu: rezolvați ecuația (x 2 +3 x-25) 2 -6(x 2 +3 x-25) = - 8

Linie dreaptă pe un plan și în spațiu.

Studiul proprietăților figurilor geometrice folosind algebra se numește geometrie analitică , și vom folosi așa-numitul metoda coordonatelor .

O linie pe un plan este de obicei definită ca un set de puncte care au proprietăți unice pentru ele. Faptul că coordonatele x și y (numerele) unui punct situat pe această dreaptă sunt scrise analitic sub forma unei ecuații.

Def.1 Ecuația unei linii (ecuația unei curbe) pe planul Oxy se numește ecuație (*), care este îndeplinită de coordonatele x și y ale fiecărui punct de pe o dreaptă dată și nu este satisfăcută de coordonatele niciunui alt punct care nu se află pe această dreaptă.

Din definiția 1 rezultă că fiecare dreaptă de pe plan corespunde unei ecuații între coordonatele curente ( X y ) puncte ale acestei drepte și invers, fiecărei ecuații îi corespunde, în general, unei anumite drepte.

Acest lucru dă naștere la două probleme principale de geometrie analitică în plan.

1. O linie este dată sub forma unui set de puncte. Trebuie să creăm o ecuație pentru această linie.

2. Este dată ecuația dreptei. Este necesar să se studieze proprietățile sale geometrice (forma și locația).

Exemplu. Nu mint punctele A(-2;1) Și ÎN (1;1) pe linia 2 X +la +3=0?

Problema găsirii punctelor de intersecție a două drepte date de ecuații și se reduce la găsirea coordonatelor care să satisfacă ecuația ambelor drepte, i.e. pentru a rezolva un sistem de două ecuații cu două necunoscute.

Dacă acest sistem nu are soluții reale, atunci liniile nu se intersectează.

Conceptul de linie este introdus în UCS într-un mod similar.

O dreaptă pe un plan poate fi definită prin două ecuații

Unde X Și la – coordonate ale punctelor arbitrare M(x;y), culcat pe această linie și t - o variabilă numită parametru , parametrul determină poziția punctului pe plan.

De exemplu, dacă , atunci valoarea parametrului t=2 corespunde punctului (3;4) din plan.

Dacă parametrul se modifică, punctul din plan se deplasează, descriind această linie. Această metodă de definire a unei linii se numește parametrică, iar ecuația (5.1) este o ecuație parametrică a dreptei.

Pentru a trece de la ecuațiile parametrice la o ecuație generală (*), trebuie să eliminăm cumva parametrul din cele două ecuații. Cu toate acestea, observăm că o astfel de tranziție nu este întotdeauna recomandabilă și nu întotdeauna posibilă.

Se poate specifica o linie pe un plan ecuație vectorială , unde t este un parametru variabil scalar. Fiecare valoare a parametrului corespunde unui vector plan specific. La modificarea parametrului, sfârșitul vectorului va descrie o anumită linie.

Ecuație vectorială în DSC corespund două ecuaţii scalare

(5.1), adică ecuația proiecțiilor pe axele de coordonate ale ecuației vectoriale a unei drepte este ea

ecuație parametrică.

Ecuația vectorială și ecuațiile de linii parametrice au o semnificație mecanică. Dacă un punct se mișcă pe un plan, atunci se numesc ecuațiile indicate ecuațiile de mișcare , iar linia este traiectoria punctului, parametrul t este timpul.

Concluzie: fiecărei drepte de pe plan îi corespunde o ecuație de formă.

În cazul general, ORICE ECUAȚIE A O VEDERE îi corespunde unei anumite linii, ale cărei proprietăți sunt determinate de ecuația dată (cu excepția faptului că nicio imagine geometrică nu corespunde unei ecuații pe un plan).

Să fie ales un sistem de coordonate pe plan.

Def. 5.1. Ecuația liniilor acest tip de ecuație se numeșteF(x;y) =0, care este satisfăcut de coordonatele fiecărui punct situat pe această dreaptă și nu este satisfăcut de coordonatele oricărui punct care nu se află pe acesta.

Ecuația formeiF(x;y )=0 – numită ecuația generală a unei drepte sau a unei ecuații în formă implicită.

Astfel, dreapta Г este locul punctelor care satisfac această ecuație Г=((x, y): F(x;y)=0).

Se mai numește și linia strâmb.

Rezolvarea ecuației

Ilustrarea unei metode grafice pentru găsirea rădăcinilor unei ecuații

Rezolvarea unei ecuații este sarcina de a găsi astfel de valori ale argumentelor la care se realizează această egalitate. Condiții suplimentare (întreg, real etc.) pot fi impuse valorilor posibile ale argumentelor.

Înlocuirea unei alte rădăcini produce o declarație incorectă:

.

Astfel, a doua rădăcină trebuie aruncată ca străină.

Tipuri de ecuații

Există ecuații algebrice, parametrice, transcendentale, funcționale, diferențiale și alte tipuri de ecuații.

Unele clase de ecuații au soluții analitice, care sunt convenabile deoarece nu numai că dau valoarea exactă a rădăcinii, dar vă permit și să scrieți soluția sub forma unei formule, care poate include parametri. Expresiile analitice permit nu numai să se calculeze rădăcinile, ci și să se analizeze existența și cantitatea lor în funcție de valorile parametrilor, ceea ce este adesea chiar mai important pentru utilizare practică decât valorile specifice ale rădăcinilor.

Ecuațiile pentru care sunt cunoscute soluții analitice includ ecuații algebrice nu mai mari de gradul al patrulea: ecuația liniară, ecuația pătratică, ecuația cubică și ecuația de gradul patru. Ecuațiile algebrice de grade superioare în cazul general nu au o soluție analitică, deși unele dintre ele pot fi reduse la ecuații de grade inferioare.

O ecuație care include funcții transcendentale se numește transcendentală. Dintre acestea, soluțiile analitice sunt cunoscute pentru unele ecuații trigonometrice, deoarece zerourile funcțiilor trigonometrice sunt bine cunoscute.

În cazul general, când nu se poate găsi o soluție analitică, se folosesc metode numerice. Metodele numerice nu oferă o soluție exactă, ci permit doar să restrângă intervalul în care se află rădăcina la o anumită valoare predeterminată.

Exemple de ecuații

Vezi si

Literatură

• Bekarevich, A. B. Ecuații într-un curs de matematică școlar / A. B. Bekarevich. - M., 1968.
• Markushevich, L. A. Ecuații și inegalități în repetarea finală a cursului de algebră de liceu / L. A. Markushevich, R. S. Cherkasov. / Matematica la scoala. - 2004. - Nr. 1.
• Kaplan Y. V. Rivnyannya. - Kiev: Şcoala Radyanska, 1968.
• Ecuația- articol din Marea Enciclopedie Sovietică
• Ecuații// Enciclopedia lui Collier. - Societate deschisă. 2000.
• Ecuația// Enciclopedie în jurul lumii
• Ecuația// Enciclopedie matematică. - M.: Enciclopedia Sovietică. I. M. Vinogradov. 1977-1985.

Legături

• EqWorld - World of Mathematical Equations - conține informații extinse despre ecuații matematice și sisteme de ecuații.

Fundația Wikimedia. 2010.

Sinonime:

Antonime:

• Khadzhimba, Raul Dzhumkovich
• ES COMPUTER

Vedeți ce este „Ecuația” în alte dicționare:

ECUAȚIA- (1) o reprezentare matematică a problemei găsirii unor astfel de valori ale argumentelor (a se vedea (2)), pentru care valorile a două date (a se vedea) sunt egale. Argumentele de care depind aceste funcții se numesc necunoscute, iar valorile necunoscutelor la care valorile... ... Marea Enciclopedie Politehnică

ECUAȚIA- ECUAȚIE, ecuații, cf. 1. Acțiune conform cap. egalizare egalizare și condiție conform cap. egalize egalize. Drepturi egale. Ecuația timpului (traducerea timpului solar adevărat în timpul solar mediu, acceptată în societate și în știință;... ... Dicționarul explicativ al lui Ushakov

ECUAȚIA- (ecuație) Cerința ca o expresie matematică să ia o anumită valoare. De exemplu, o ecuație pătratică se scrie ca: ax2+bx+c=0. Soluția este valoarea lui x la care ecuația dată devine o identitate. ÎN… … Dicționar economic

ECUAȚIA- o reprezentare matematică a problemei de a găsi valorile argumentelor pentru care valorile a două funcții date sunt egale. Argumentele de care depind aceste funcții se numesc necunoscute, iar valorile necunoscutelor la care valorile funcției sunt egale... ... Dicţionar enciclopedic mare

ECUAȚIA- ECUAȚIE, două expresii legate printr-un semn egal; aceste expresii implică una sau mai multe variabile numite necunoscute. A rezolva o ecuație înseamnă a găsi toate valorile necunoscutelor la care devine o identitate sau a stabili... Enciclopedie modernă

O linie pe un plan este o colecție de puncte de pe acest plan care au anumite proprietăți, în timp ce punctele care nu se află pe o dreaptă dată nu au aceste proprietăți. Ecuația unei linii definește o relație exprimată analitic între coordonatele punctelor aflate pe această dreaptă. Fie ca aceasta relatie sa fie data de ecuatie

F( X y)=0. (2.1)

O pereche de numere care satisface (2.1) nu este arbitrară: dacă X dat, atunci la nu poate fi nimic, adică la asociat cu X. Când se schimbă X schimbări la, și un punct cu coordonate ( X y) descrie această linie. Dacă coordonatele punctului M 0 ( X 0 ,la 0) satisface ecuația (2.1), i.e. F( X 0 ,la 0)=0 este o egalitate adevărată, atunci punctul M 0 se află pe această dreaptă. Este adevărat și invers.

Definiție. O ecuație a unei drepte pe un plan este o ecuație care este îndeplinită de coordonatele oricărui punct situat pe această dreaptă și nu este satisfăcută de coordonatele punctelor care nu se află pe această dreaptă.

Dacă se cunoaște ecuația unei anumite linii, atunci studiul proprietăților geometrice ale acestei linii poate fi redus la studiul ecuației sale - aceasta este una dintre ideile principale ale geometriei analitice. Pentru a studia ecuațiile, există metode bine dezvoltate de analiză matematică care simplifică studiul proprietăților dreptelor.

Când luăm în considerare liniile, se folosește termenul punctul curent linie – punct variabil M( X y), deplasându-se pe această linie. Coordonatele XȘi la sunt numite punctul curent coordonatele curente puncte de linie.

Dacă din ecuația (2.1) putem exprima explicit la
prin X, adică scrieți ecuația (2.1) sub forma , apoi curba definită de o astfel de ecuație se numește programa funcții f(x).

1. Ecuația este dată: , sau . Dacă X ia valori arbitrare, atunci la ia valori egale cu X. În consecință, linia definită de această ecuație constă din puncte echidistante de axele de coordonate Ox și Oy - aceasta este bisectoarea unghiurilor de coordonate I–III (linia dreaptă în Fig. 2.1).

Ecuația sau determină bisectoarea unghiurilor de coordonate II–IV (dreaptă în Fig. 2.1).

0 x 0 x C 0 x

orez. 2.1 fig. 2.2 fig. 2.3

2. Ecuația este dată: , unde C este o constantă. Această ecuație poate fi scrisă diferit: . Această ecuație este satisfăcută de acele și numai acele puncte, ordonate la care sunt egale cu C pentru orice valoare de abscisă X. Aceste puncte se află pe o linie dreaptă paralelă cu axa Ox (Fig. 2.2). În mod similar, ecuația definește o linie dreaptă paralelă cu axa Oy (Fig. 2.3).

Nu orice ecuație de forma F( X y)=0 definește o dreaptă pe plan: ecuația este satisfăcută de un singur punct – O(0,0), iar ecuația nu este satisfăcută de niciun punct din plan.

În exemplele date, am folosit o ecuație dată pentru a construi o linie determinată de această ecuație. Să luăm în considerare problema inversă: construiește-i ecuația folosind o dreaptă dată.

3. Creați o ecuație pentru un cerc cu centrul în punctul P( a,b) Și
raza R .

○ Un cerc cu centrul în punctul P și raza R este o mulțime de puncte situate la distanța R de punctul P. Aceasta înseamnă că pentru orice punct M situat pe cerc, MP = R, dar dacă punctul M nu se află pe cercul, apoi MP ≠ R.. ●