Mums svarbu išlaikyti jūsų privatumą. Dėl šios priežasties sukūrėme Privatumo politiką, kurioje aprašoma, kaip naudojame ir saugome jūsų informaciją. Peržiūrėkite mūsų privatumo praktiką ir praneškite mums, jei turite klausimų.

Asmeninės informacijos rinkimas ir naudojimas

Asmeninė informacija reiškia duomenis, kurie gali būti naudojami konkretaus asmens tapatybei nustatyti arba susisiekti su juo.

Jūsų gali būti paprašyta pateikti savo asmeninę informaciją bet kuriuo metu, kai susisiekiate su mumis.

Toliau pateikiami keli pavyzdžiai, kokios rūšies asmeninės informacijos galime rinkti ir kaip galime tokią informaciją naudoti.

Kokią asmeninę informaciją renkame:

• Kai pateikiate paraišką svetainėje, galime rinkti įvairią informaciją, įskaitant jūsų vardą, telefono numerį, el. pašto adresą ir kt.

Kaip naudojame jūsų asmeninę informaciją:

• Mūsų renkama asmeninė informacija leidžia mums susisiekti su jumis dėl unikalių pasiūlymų, akcijų ir kitų renginių bei būsimų renginių.
• Retkarčiais galime naudoti jūsų asmeninę informaciją svarbiems pranešimams ir pranešimams siųsti.
• Mes taip pat galime naudoti asmeninę informaciją vidiniais tikslais, pavyzdžiui, atlikti auditą, duomenų analizę ir įvairius tyrimus, siekdami tobulinti teikiamas paslaugas ir teikti rekomendacijas dėl mūsų paslaugų.
• Jei dalyvaujate prizų traukime, konkurse ar panašioje akcijoje, mes galime naudoti jūsų pateiktą informaciją tokioms programoms administruoti.

Informacijos atskleidimas trečiosioms šalims

Mes neatskleidžiame iš jūsų gautos informacijos trečiosioms šalims.

Išimtys:

• Jei reikia – įstatymų nustatyta tvarka, teismine tvarka, teismo procese ir (arba) remiantis viešais prašymais arba Rusijos Federacijos valdžios institucijų prašymais – atskleisti savo asmeninę informaciją. Taip pat galime atskleisti informaciją apie jus, jei nuspręsime, kad toks atskleidimas yra būtinas arba tinkamas saugumo, teisėsaugos ar kitais visuomenei svarbiais tikslais.
• Reorganizavimo, susijungimo ar pardavimo atveju surinktą asmeninę informaciją galime perduoti atitinkamai trečiajai šaliai.

Asmeninės informacijos apsauga

Mes imamės atsargumo priemonių, įskaitant administracines, technines ir fizines, siekdami apsaugoti jūsų asmeninę informaciją nuo praradimo, vagystės ir netinkamo naudojimo, taip pat nuo neteisėtos prieigos, atskleidimo, pakeitimo ir sunaikinimo.

Jūsų privatumo gerbimas įmonės lygiu

Siekdami užtikrinti, kad jūsų asmeninė informacija būtų saugi, savo darbuotojams pranešame apie privatumo ir saugumo standartus ir griežtai vykdome privatumo praktiką.

Šiame straipsnyje rasite trikampio pusiausvyros ir medianos savybes, kurios gali būti naudingos sprendžiant problemas.

Bisektoriai.

1. Trikampio pusiaukampių susikirtimo taškas yra įbrėžto trikampio apskritimo centras.

Įrodymas.

Iš tiesų, taškai, esantys ant kampo pusiausvyros, yra vienodu atstumu nuo kampo kraštų. Vadinasi, bisektorių susikirtimo taškas yra vienodu atstumu nuo visų trikampio kraštinių, tai yra, tai yra įbrėžto apskritimo centras.

2. Trikampio bisektorius dalija priešingą kraštinę į atkarpas, proporcingas gretimoms kraštinėms:

Įrodymas.

Darykime papildomas konstrukcijas. Nubrėžkime taškui lygiagrečią liniją

Tiesės ir tiesės susikirtimo taškas:

∠1=∠2, kadangi - bisektorius ∠

∠2=∠3 guli skersai, kaip pagal konstrukciją.

Todėl ∠1=∠3 ir trikampis yra lygiašonis, ir .

vadinasi,

3. Bisektoriaus ilgis apskaičiuojamas naudojant šias formules:

Įrodykime antrąją formulę.

Įveskime tokį užrašą:

Sulyginkime trikampio ploto išraiškas:

4. Tegul O yra apskritimo centras ir trikampio kampo pusiausvyra:

Tada santykis galioja:

Įrodymas:

Apsvarstykite trikampį:

Taigi kampo pusiausvyra pagal trikampio pusiausvyros savybę

Tebūnie tada

Išreikškime tai. Pagal trikampio pusiausvyros savybę:

Iš čia

Kai kuriose problemose patogu pratęsti trikampio pusiausvyrą iki susikirtimo su apibrėžtuoju apskritimu.

Lemma apie trefoilą.

Duotas trikampis. Taškas – kampo bisektoriaus susikirtimo su trikampio apskritimu taškas. Leisti būti apskritimo, įrašyto į trikampį, centras. Tada

Įrodymas.

Įbrėžti kampai, kurie sudaro vienodus lankus, yra lygūs. Atkreipkite dėmesį į vienodus įrašytus kampus:

Iš čia.

Incircle centras, todėl yra kampo bisector .

Iš trikampio

Tada iš trikampio

Gavau .

Tai yra, trikampis yra lygiašonis.

Iš čia.

Tai įrodė

Įrodykime (1) formulę iš 3 punkto:

Įrodymas:

Tęskime pusiausvyrą, kol ji susikirs su apskritimu. Apsvarstykite trikampius ir . Pažymime vienodus kampus:

Trikampis yra panašus į trikampį dviem kampais. Iš čia:

Pagal susikertančių stygų atkarpų savybę

Pakeiskime (3) į (2) ir naudokime (4):

Atkarpų, į kurias bisektorius dalija trikampio kraštinę, ilgius išreikškime trikampio kraštinių ilgiais. Įveskime tokį užrašą:

Gauname sistemą:

Medianos.

1. Trikampio medianos dalijamos iš susikirtimo taško santykiu 2:1, skaičiuojant nuo viršūnės:

2. Tegul yra taškas trikampio viduje, kad galiotų toks ryšys: , tada yra trikampio medianų susikirtimo taškas.

Įrodymas.

Įrodykime pagalbinę teoremą.

Lemma.

Savavališkam taškui trikampio viduje galioja toks ryšys:

Nukreipkime nuo taškų ir statmenų į :

Iš trikampių panašumo gauname:

Jei laikysime trikampius su bendru pagrindu , tada gauname santykį:

Panašiai gauname

Sudėjus šias lygybes gauname:

Šią lemą naudojame 2 teiginiui įrodyti.

Jei galioja lygybė (1), tada lygybė (2) ir iš lemos išplaukia, kad lygybėje (2) kiekviena trupmena yra lygi .

Įrodykime, kad šiuo atveju segmentai yra medianos.

Jeigu , tada gauname . Nubrėžkime tiesias linijas, lygiagrečias taškui ir per tašką, ir panagrinėkime dvi panašių trikampių poras: ir :

Iš čia gauname

Iš trikampių panašumo gauname, tai yra, taškas yra atkarpos vidurys. Iš čia.

Todėl yra trikampio mediana.

3. Trikampio medianos, susikertančios, padalijame į 6 vienodus trikampius.

Įrodymas.

Įrodykime tai

nes,

nes,

Vadinasi,

Aukštumos.

1. Linijos, kuriose yra trikampio aukščių, susikerta viename taške. Esant ūminiam trikampiui, pačios aukščiai susikerta viename taške.

2. Trikampio aukščių susikirtimo taškas turi tokią savybę: atstumo nuo trikampio viršūnės ir priešingos kraštinės kvadrato suma yra vienoda bet kuriai viršūnei:

Įrodymas.

Įrodykime pirmąją lygybės dalį:

Perrašykime į formą:

Pagal Pitagoro teoremą: (iš trikampių ir)

(iš trikampio)

(iš trikampio)

Pakeitę šias išraiškas į (1), gauname:

Atidarykime skliaustus ir gaukime:

Gavome tapatybę. Panašiai įrodoma ir antroji lygybės dalis.

3. Jei aprašome apskritimą aplink trikampį ir pratęsiame trikampio aukščius tol, kol jie susikerta su šiuo apskritimu,

tada bet kokiam trikampio aukščiui atstumas nuo aukščio pagrindo iki aukščio tęsinio susikirtimo su apskritimu taško yra lygus atstumui nuo aukščio pagrindo iki aukščių susikirtimo taško:

Arba taip: Taškai, simetriški trikampio aukščių sankirtos taškai, palyginti su trikampio kraštinėmis, yra ant trikampio apskritimo.

Įrodymas.

Įrodykime tai.

Norėdami tai padaryti, apsvarstykite trikampius ir , Ir įrodykite, kad :

Naudokime ženklą, kad trikampiai yra lygūs išilgai kraštinės ir dviejų gretimų kampų. - bendroji pusė. Įrodykime dviejų kampų lygybę.

Įrodykime, kad ∠ ∠

Tegu ∠, tada iš trikampio gauname tai

∠. Todėl iš trikampio gauname tai

Bet ∠ ir ∠ remiasi į tą patį lanką, todėl ∠ ∠ ∠

Panašiai matome, kad ∠ ∠

4. Trikampyje taškai ir yra aukščių, nubrėžtų iš viršūnių ir, pagrindai. Įrodyti, kad trikampis yra panašus į trikampį ir panašumo koeficientas yra lygus .

Įrodymas:

Stačiakampio trikampio apibrėžtojo apskritimo centras yra hipotenuzės viduryje . Esmė slypi šiame apskritime, nes - stačiojo trikampio hipotenuzė:

Kaip ir užrašyti kampai, pagrįsti vienu lanku.

iš trikampio:

Iš čia. Kampas yra bendras trikampių kampas ir. Todėl trikampis yra panašus į trikampį. Panašumo koeficientas yra lygus panašių kraštinių, ty kraštinių, esančių priešais vienodus kampus, santykiui:

Cevos teorema

Įleisti į trikampį

Segmentai susikerta viename taške tada ir tik tada

Įrodymas.

Įrodykime, kad jei atkarpos susikerta viename taške, tada santykis (1) yra įvykdytas.

Nesunku patikrinti, ar jei , tada galioja

Taikykime šią proporcijos savybę:

Taip pat:

Cevos teoremą galima parašyti taip:

Jei atkarpos susikerta viename taške, galioja toks ryšys:

Įrodyti Cevos teorema sinusų pavidalu, užtenka antroje lygybės (2) dalyje vietoj trikampių plotų kiekvieno trikampio plotą pakeisti formule .

Iš Nazaro Khangeldjevičiaus Agachanovo ir Vladimiro Viktorovičiaus Truškovo paskaitų, KPK MIPT.

Trikampis yra daugiakampis su trimis kraštinėmis arba uždara laužta linija su trimis grandimis, arba figūra, sudaryta iš trijų atkarpų, jungiančių tris taškus, kurie nėra toje pačioje tiesėje (žr. 1 pav.).

Pagrindiniai trikampio abc elementai

Viršūnės – taškai A, B ir C;

Vakarėliai – viršūnes jungiančios atkarpos a = BC, b = AC ir c = AB;

Kampai – α, β, γ sudarytos iš trijų kraštinių porų. Kampai dažnai žymimi taip pat, kaip ir viršūnės, raidėmis A, B ir C.

Kampas, sudarytas iš trikampio kraštinių ir esantis jo vidinėje srityje, vadinamas vidiniu kampu, o esantis greta jo – gretimu trikampio kampu (2, p. 534).

Trikampio aukščiai, medianos, pusiausvyros ir vidurio linijos

Be pagrindinių trikampio elementų, taip pat atsižvelgiama į kitus segmentus su įdomiomis savybėmis: aukščius, medianas, pusiausvyras ir vidurio linijas.

Aukštis

Trikampio aukščiai- tai statmenai, nuleisti iš trikampio viršūnių į priešingas puses.

Norėdami nubrėžti aukštį, turite atlikti šiuos veiksmus:

1) nubrėžkite tiesią liniją, kurioje yra viena iš trikampio kraštinių (jei aukštis nubrėžtas nuo bukojo trikampio smailiojo kampo viršūnės);

2) iš viršūnės, esančios priešais nubrėžtą liniją, nubrėžkite atkarpą nuo taško iki šios linijos, sudarydami su ja 90 laipsnių kampą.

Taškas, kuriame aukštis kerta trikampio kraštinę, vadinamas aukščio pagrindas (žr. 2 pav.).

Trikampio aukščių savybės

Stačiakampiame trikampyje aukštis, nubrėžtas iš stačiojo kampo viršūnės, padalija jį į du trikampius, panašius į pradinį trikampį.

Smailiame trikampyje jo du aukščiai atskiria panašius trikampius.

Jei trikampis yra smailus, tai visi aukščių pagrindai priklauso trikampio kraštinėms, o bukajame trikampyje du aukščiai patenka į kraštinių tęsinį.

Trys aukštumos smailiame trikampyje susikerta viename taške ir šis taškas vadinamas ortocentras trikampis.

Mediana

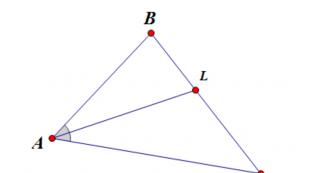
Medianos(iš lot. mediana – „viduris“) – tai atkarpos, jungiančios trikampio viršūnes su priešingų kraštinių vidurio taškais (žr. 3 pav.).

Norėdami sukurti medianą, turite atlikti šiuos veiksmus:

1) rasti šono vidurį;

2) tašką, kuris yra trikampio kraštinės vidurys su priešinga viršūne, sujunkite atkarpa.

Trikampio medianų savybės

Mediana padalija trikampį į du vienodo ploto trikampius.

Trikampio medianos susikerta viename taške, kuris kiekvieną iš jų dalija santykiu 2:1, skaičiuojant nuo viršūnės. Šis taškas vadinamas gravitacijos centras trikampis.

Visas trikampis pagal jo medianas padalintas į šešis vienodus trikampius.

Bisektorius

Bisektoriai(iš lot. bis – du kartus ir seko – pjūvis) yra tiesios linijos atkarpos, uždarytos trikampio viduje, dalijančios jo kampus (žr. 4 pav.).

Norėdami sukurti pusiausvyrą, turite atlikti šiuos veiksmus:

1) sukonstruoti spindulį, išeinantį iš kampo viršūnės ir padalijantį jį į dvi lygias dalis (kampo pusiausvyrą);

2) raskite trikampio kampo su priešinga kraštine susikirtimo tašką;

3) pasirinkite atkarpą, jungiančią trikampio viršūnę su susikirtimo tašku priešingoje pusėje.

Trikampių bisektorių savybės

Trikampio kampo bisektorius dalija priešingą kraštinę santykiu, lygiu dviejų gretimų kraštinių santykiui.

Trikampio vidinių kampų pusiausvyros susikerta viename taške. Šis taškas vadinamas įbrėžto apskritimo centru.

Vidinių ir išorinių kampų pusiausvyros yra statmenos.

Jei trikampio išorinio kampo bisektorius kerta priešingos kraštinės tęsinį, tai ADBD=ACBC.

Trikampio vieno vidinio ir dviejų išorinių kampų pusiausvyros susikerta viename taške. Šis taškas yra vieno iš trijų šio trikampio išorinių apskritimų centras.

Trikampio dviejų vidinių ir vieno išorinio kampo pusiaukampių pagrindai yra toje pačioje tiesėje, jei išorinio kampo pusiausvyra nėra lygiagreti priešingai trikampio kraštinei.

Jei trikampio išorinių kampų pusiausvyros nėra lygiagrečios priešingoms kraštinėms, tada jų pagrindai yra toje pačioje tiesėje.

Studijuodami bet kurią temą mokyklos kurse, galite pasirinkti tam tikrą problemų minimumą, o įvaldę jų sprendimo būdus, studentai galės išspręsti bet kurią problemą programos reikalavimų lygiu studijuojama tema. Siūlau apsvarstyti uždavinius, kurie leistų įžvelgti atskirų temų sąsajas mokykliniame matematikos kurse. Todėl sudaryta užduočių sistema yra efektyvi mokomosios medžiagos kartojimo, apibendrinimo ir sisteminimo priemonė ruošiant mokinius egzaminui.

Norint išlaikyti egzaminą, pravers turėti papildomos informacijos apie kai kuriuos trikampio elementus. Panagrinėkime trikampio medianos savybes ir uždavinius, kuriuos sprendžiant šias savybes galima panaudoti. Siūlomi uždaviniai įgyvendina lygių diferencijavimo principą. Visos užduotys sąlyginai suskirstytos į lygius (lygis nurodomas skliausteliuose po kiekvienos užduoties).

Prisiminkime kai kurias trikampio medianos savybes

1 nuosavybė. Įrodykite, kad trikampio mediana ABC, nubrėžtas iš viršūnės A, mažiau nei pusė šonų sumos AB Ir A.C..

Įrodymas

https://pandia.ru/text/80/187/images/image002_245.gif" alt="$\displaystyle (\frac(AB + AC)(2))$" width="90" height="60">.!}

2 nuosavybė. Mediana supjausto trikampį į dvi lygias sritis.

Įrodymas

Iš trikampio ABC viršūnės B nubrėžkime medianą BD ir aukštį BE..gif" alt="Area" width="82" height="46">!}

Kadangi segmentas BD yra mediana, tada

Q.E.D.

https://pandia.ru/text/80/187/images/image008_96.gif" alt="Mediana" align="left" width="196" height="75 src=">!} 4 nuosavybė. Trikampio medianos padalija trikampį į 6 vienodus trikampius.

Įrodymas

Įrodykime, kad kiekvieno iš šešių trikampių, į kuriuos medianos dalija trikampį ABC, plotas yra lygus trikampio ABC plotui. Norėdami tai padaryti, apsvarstykite, pavyzdžiui, trikampį AOF ir numeskite statmeną AK iš viršūnės A į tiesę BF.

Dėl 2 turto,

https://pandia.ru/text/80/187/images/image013_75.gif" alt="Mediana" align="left" width="105" height="132 src=">!}

6 nuosavybė. Iš stačiojo kampo viršūnės nubrėžto stačiojo trikampio mediana yra lygi pusei hipotenuzės.

Įrodymas

https://pandia.ru/text/80/187/images/image015_62.gif" alt="Mediana" width="273" height="40 src="> что и требовалось доказать.!}

Pasekmės:1. Apskritimo, apriboto apie statųjį trikampį, centras yra hipotenuzės viduryje.

2. Jei trikampyje medianos ilgis lygus pusei kraštinės, į kurią ji nubrėžta, ilgio, tai šis trikampis yra stačiakampis.

UŽDUOTYS

Sprendžiant kiekvieną paskesnę problemą, naudojamos patikrintos savybės.

№1 Temos: medianos padvigubinimas. Sunkumas: 2+

Lygiagretainio ženklai ir savybės Pažymiai: 8,9

Būklė

Tęsiant medianą ESU. trikampis ABC už tašką M segmentas atidėtas M.D., lygus ESU.. Įrodykite, kad keturkampis ABDC- lygiagretainis.

Sprendimas

Panaudokime vieną iš lygiagretainio ženklų. Keturkampio įstrižainės ABDC susikerta taške M ir padalinkite jį per pusę, taigi keturkampis ABDC- lygiagretainis.

Yra tokia teorema Trikampio medianos susikerta viename taške ir šis taškas padalija kiekvieną medianą santykiu 2:1, kur 2 atitinka atkarpą nuo viršūnės, iš kurios brėžiama mediana, iki medianų susikirtimo taško, o 1 – atkarpą nuo medianų susikirtimo taško iki tos pusės, į kurią nubrėžta mediana, vidurio.

Norėdami įrodyti šią teoremą, apsvarstykite trikampį ABC su medianomis AE, BF, CD. Tai yra, taškai D, E, F dalijasi atitinkamai AB, BC, CA kraštinėmis.
Nežinome, ar visos medianos susikerta viename taške (tai dar reikia įrodyti). Tačiau bet kurios dvi medianos susikirs viename taške, nes jos negali būti lygiagrečios. Tegul medianos AE ir BF susikerta taške O.

Vidutinė BF padalija AE medianą į du segmentus AO ir EO. Per tašką E nubrėžkime tiesę, lygiagrečią BF. Ši tiesė kirs kraštinę AC tam tikrame taške L. Taip pat per atkarpos AB vidurį (taškas D) nubrėžsime kitą tiesę, lygiagrečią BF. Jis susikirs AC taške K.

Pagal Thaleso teoremą, jei vienoje kampo pusėje iš jo viršūnės išdėliosime lygias atkarpas ir per šių atkarpų galus brėžiame lygiagrečias linijas, kurios kerta kitą kampo pusę, tai šios lygiagrečios tiesės taip pat nukirs lygias atkarpas. antroje kampo pusėje.

Pažiūrėkime į šio trikampio kampą BCA. Atkarpos BE ir EC yra lygios viena kitai, tiesės BF ir EL lygiagrečios viena kitai. Tada pagal Thaleso teoremą CL = LF.
Jei žiūrėsime į kampą BAC, nes AD = BD ir DK || BF, tada AK = KF.

Kadangi segmentai AF ir CF yra lygūs vienas kitam (kadangi juos sudaro mediana) ir kiekvienas iš jų yra padalintas į du lygius segmentus, tai visi keturi kraštinės AC segmentai yra lygūs vienas kitam: AK = KF = FL = LC.

Apsvarstykite kampą EAC. Lygiagrečios linijos nubrėžtos per trijų vienodų kraštinės AC segmentų galus. Todėl jie nupjauna vienodus segmentus AE pusėje. Segmente AO yra du tokie segmentai, o EO tik vienas. Taigi mes įrodėme, kad bent viena trikampio mediana susikirtimo su kita mediana taške yra padalinta į dvi atkarpas, kurių ilgiai yra susieti 2:1.

Dabar apsvarstykite medianos AE sankirtą su mediana CD. Tegul jie susikerta taške P.

Panašiai kaip ir ankstesnėje, įrodyta, kad lygiagrečios tiesės FM, CD, EN dalija kraštinę AB į lygias atkarpas. Savo ruožtu jie padalija AE į tris vienodus segmentus. Be to, nuo viršūnės A iki medianų susikirtimo yra dvi tokios atkarpos, o po jų – vienas.

Vieno ir to paties segmento negalima padalyti į tris lygias dalis, kad su vienu padalijimo variantu jie būtų vienodo dydžio, o su kitu – kitokio. Todėl taškai O ir P turi sutapti. Tai reiškia, kad visos trys trikampių medianos susikerta viename taške.

Norėdami įrodyti, kad kitos dvi medianos yra padalintos iš susikirtimo taško santykiu 2: 1, galite, kaip ir ankstesniame, nubrėžti lygiagrečias linijas į kraštines AB ir BC.