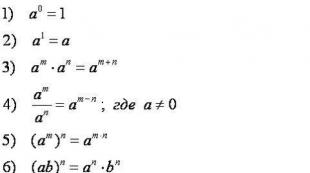B Kuboje. Kubo statyba. Iš kur atsiranda sutrumpintos dauginimo formulės
Pratimai yra operacija, glaudžiai susiję su dauginimu, ši operacija yra daugelio dauginimo apie save. Aš pavaizduosiu formulę: A1 * A2 * ... * AN \u003d AN.
Pavyzdžiui, a \u003d 2, n \u003d 3: 2 * 2 * 2 \u003d 2 ^ 3 \u003d 8.
Apskritai paroda dažnai naudojama įvairiose matematikos ir fizikos formulėse. Ši funkcija turi daugiau mokslo tikslo nei keturi pagrindiniai: papildymas, atimtumas, dauginimas, padalijimas.
Erekcija
Numerio montavimas nėra sudėtingas. Jis yra susijęs su dauginimu, panašiu į dauginimą ir papildymą. Įrašymas yra N-TH, skaičiuojamų "A" skaičiaus santrauka, padauginta viena nuo kitos.
Apsvarstykite pratimą į paprasčiausius pavyzdžius, pereinant prie sudėtingo.
Pavyzdžiui, 42. 42 \u003d 4 * 4 \u003d 16. Keturi kvadratiniai (antrasis laipsnis) yra šešiolika. Jei nesuprantate 4 * 4 dauginimo, tada perskaitykite mūsų tam, kad taptumėte daugybe.
Apsvarstykite kitą pavyzdį: 5^3. 5^3 = 5 * 5 * 5 = 25 * 5 = 125 . Penki Kuboje (trečiame laipsnyje) yra lygi šimtui dvidešimt penki.
Kitas pavyzdys: 9 ^ 3. 9^3 = 9 * 9 * 9 = 81 * 9 = 729 . Devyni Kuboje yra septyni šimtai dvidešimt devynių.
Formulės
Kompetentingai pastatyti tiek, kiek reikia prisiminti ir žinoti toliau išvardytus formules. Nėra nieko daugiau nei natūralus, pagrindinis dalykas yra suprasti esmę ir tada jie bus ne tik prisiminti, bet jie atrodys šviesa.

Erekcija
Kas yra savęs vieni? Tai yra bet kokio kiekio numerių ir kintamųjų produktas. Pavyzdžiui, du - nerocene. Ir tai yra tokių universitetų montavimas šis straipsnis.
Pasinaudojant pratimų skaičiavimu visuotinio laipsnio statybai nebus sunku.
Pavyzdžiui, (3x ^ 2y ^ 3) ^ 2 \u003d 3 ^ 2 * x ^ 2 * 2 * y ^ (3 * 2) \u003d 9x ^ 4Y ^ 6; Jei jis yra neužimtas į laipsnį, kiekvienas kompozitas yra neveiksmingas į laipsnį.
Lengvai iki laipsnio laipsnio kintamasis, laipsnis yra padaugintas. Pavyzdžiui, (x ^ 2) ^ 3 \u003d x ^ (2 * 3) \u003d x ^ 6;
Neigiamas
Neigiamas laipsnis - priešingas skaičius. Kas yra priešingas skaičius? Bet koks numeris x atvirkštinis bus 1 / x. Tai yra x-1 \u003d 1 / x. Tai yra neigiamo laipsnio esmė.
Apsvarstykite pavyzdį (3Y) ^ - 3:
(3Y) ^ - 3 \u003d 1 / (27Y ^ 3).
Kodėl taip? Kadangi yra minus į laipsnį, tai išraiška yra tiesiog perduodama į vardiklį ir tada pastatytas į savo trečiąjį laipsnį. Teisingai?
Kryžminis laipsnis
Pradėkime apsvarstyti klausimą konkrečiu pavyzdžiu. 43/2. Ką daro 3/2 laipsnis? 3 - skaitiklis - numerio montavimas (šiuo atveju 4) kube. Numeris 2 yra vardiklis, tai yra antrojo laipsnio šaknų ekstrahavimas iš tarp (šiuo atveju 4).
Tada mes gauname kvadratinę šaknį 43 \u003d 2 ^ 3 \u003d 8. Atsakymas: 8.
Taigi, dalinio laipsnio denominoras gali būti 3 ir 4, tiek begalybės bet kuriuo skaičiumi ir šis skaičius nustato kvadratinės šaknies, ekstrahuotų iš nurodyto numerio laipsnio. Žinoma, vardiklis negali būti nulis.
Greitas šaknis
Jei šaknis yra pastatytas į laipsnį, lygų pačiam šaknies laipsniui, atsakymas bus šėrimo išraiška. Pavyzdžiui, (√H) 2 \u003d x. Ir taip bet kuriuo atveju lygybės šaknų laipsnį ir šaknies statybos laipsnį.
Jei (√X) ^ 4. Kad (√X) ^ 4 \u003d x ^ 2. Norėdami patikrinti sprendimą perduoti išraišką išraiška su daliniu laipsniu. Kadangi šaknis yra kvadratinis, vardiklis yra 2. ir jei šaknis yra pastatytas į ketvirtąjį laipsnį, tada skaitiklis 4. Mes gauname 4/2 \u003d 2. Atsakymas: x \u003d 2.
Bet kuriuo atveju geriausias variantas yra tiesiog perkeliamas į išraišką su daliniu laipsniu. Jei frakcija nesumažina, šis atsakymas bus ir bus, jei nurodytas numerio šaknis nėra paskirstyta.
Integruoto numerio laipsnis
Kas yra išsamus skaičius? Sudėtingas skaičius yra išraiška, turinti formulę A + B * I; A, B - Galiojantys numeriai. I - numeris, kurį numato -1 suteikia aikštėje.
Apsvarstykite pavyzdį. (2 + 3i) ^ 2.
(2 + 3i) ^ 2 \u003d 22 +2 * 2 * 3i + (3i) ^ 2 \u003d 4 + 12i ^ -9 \u003d -5 + 12i.
Prisiregistruokite kursui "Paspartinti burnos sąskaitą, ne psichikos aritmetika" Norėdami sužinoti, kaip greitai ir teisingai sulenkti, išskaičiuoti, padauginti, padalinti, pastatyti numerius į aikštę ir net išgauti šaknis. 30 dienų išmoksite, kaip naudoti paprastus metodus, kad supaprastintumėte aritmetines operacijas. Kiekvienoje pamokoje, nauji metodai, suprantami pavyzdžiai ir naudingos užduotys.
Prisijungęs
Naudodami mūsų skaičiuoklę, galite apskaičiuoti skaičiaus įrengimą iki laipsnio:
7 klasė
Pratimai pradeda praeiti tik moksleivius tik septintoje klasėje.
Pratimai yra operacija, glaudžiai susiję su dauginimu, ši operacija yra daugelio dauginimo apie save. Aš pavaizduosiu formulę: A1 * A2 * ... * AN \u003d AN.
Pavyzdžiui, a \u003d 2, N \u003d 3: 2 * 2 * 2 \u003d 2 ^ 3 \u003d 8.
Pavyzdžiai sprendžiant:

Pristatymas
Pristatymas dėl pratimo tiek, kiek septintuose greideriuose apskaičiuojamas. Pristatymas gali paaiškinti tam tikras nesuprantamas akimirkas, bet tikriausiai nebus tokių akimirkų dėl mūsų straipsnio.
Rezultatas
Mes peržiūrėjome tik ledkalnio viršų, kad suprastume matematiką geriau - prisiregistruokite prie mūsų kurso: pagreitinti žodinę sąskaitą nėra psichikos aritmetika.
Iš kurso jūs ne tik atpažinsite dešimtys metodų supaprastintam ir greitam dauginimui, papildymui, dauginimui, padaliniams skaičiuoti interesus, bet ir dirbti su specialiomis užduotimis ir švietimo žaidimais! Žodinė sąskaita taip pat reikalauja daug dėmesio ir koncentracijų, kurios aktyviai mokomos sprendžiant įdomias užduotis.
Matematinės išraiškos (formulės) sutrumpintas dauginimas (Kvadratinių sumų ir skirtumų, kubo sumas ir skirtumai, kvadratų skirtumas, kubelių kiekis ir skirtumas) yra labai pakeistos daugelyje tikslių mokslų sričių. Šie 7 simbolių įrašai nėra pakeisti supaprastinant išraiškas, išspręsti lygtis, su daugybe polinomų, mažinant frakcijas, sprendžiant integralų ir daug kitų dalykų. Taigi bus labai naudinga išsiaiškinti, kaip jie yra gauti, už kuriuos jie yra reikalingi, ir svarbiausia, kaip juos prisiminti ir tada taikyti. Tada kreipkitės sutrumpintos dauginimo formulės Praktiškai sunkiausia pamatysite, kas yra H.ir kas yra y. Akivaizdu, kad nėra jokių apribojimų a. ir. \\ T b.ne, o tai reiškia, kad tai gali būti bet kokios skaitmeninės arba raidės išraiškos.
Ir taip čia jie:
Pirmas x 2 - U 2. \u003d (x - y) (x + y) . Suskaičiuoti kvadratinis skirtumas. \\ T Dvi išraiškos turi padauginti skirtumą tarp šių išraiškų jų sumas.
Antra (x + y) 2 \u003d x 2 + 2H + 2 . Rasti kvadratinių sumų Dvi išraiškos turi būti įtrauktos į pirmosios išraiškos kvadratą pridėti dvigubą pirmosios išraiškos produktą antrajame ir antrosios išraiškos aikštėje.
Trečias (x - y) 2 \u003d x 2 - 2H + 2. Suskaičiuoti kvadratinis skirtumas. \\ Tdvi išraiškos reikalingos iš pirmosios išraiškos kvadrato atimti dvigubą pirmosios išraiškos produktą antrajame ir antrosios išraiškos aikštėje.
Ketvirta (x + y) 3 \u003d x 3. + 3x 2 Y + 3H 2 + 3. Suskaičiuoti kubo kiekisdvi išraiškos turi būti įtrauktos į pirmosios išraiškos Kubą, kad pridėtumėte trigubą pirmosios išraiškos aikštės darbą antrajame ir trigauname pirmosios išraiškos produktu ant antrosios išraiškos kvadrato plius kubo.
Penktadalis (x - y) 3 \u003d x 3. - 3x 2 Y + 3H 2 - 3.. Suskaičiuoti kubo skirtumasdvi išraiškos yra būtinos iš pirmosios ekspresijos kubo, kad būtų imtasi trigubos pirmosios išraiškos aikštės darbų antrajame ir trigauname pirmosios išraiškos produkte antrajame minuso kube antroje minoje.
Šeši x 3 + 3. \u003d (x + y) (x 2 - hu + u 2) Suskaičiuoti kubelių kiekisdvi išraiškos turi padauginti pirmosios ir antrosios išraiškos sumas neišsamių šių išraiškų skirtumo aikštėje.
Septintoji dalis x 3 - 3. \u003d (x - y) (x 2 + Hu + u 2) Apskaičiuoti kubiniai skirtumaidvi išraiškos turi padauginti skirtumą tarp pirmojo ir antrojo išraiškos dėl neišsamos šių išraiškų sumos kvadrato.
Sunku nepamiršti, kad visos formulės taikomos skaičiavimų darbui ir priešinga kryptimi (dešinėje į kairę).
Prieš 4 tūkstančius metų dėl šių modelių egzistavimo. Jie buvo plačiai naudojami senovės Babilono ir Egipto gyventojai. Tačiau šiose epochose jie išreiškė žodžiu arba geometriškai ir skaičiavimuose nenaudojo raidžių.
Mes suprasime summa Summa(A + B) 2 \u003d A 2 + 2AB + B 2.
Pirmiausia matematinis modelis Įrodė senovės graikų mokslininką Euklidą, kuris dirbo Aleksandrijoje III a. Pr. Kr. Jie buvo visuotinai naudojami ne "A 2", bet "kvadratas ant segmento", o ne "AB", bet "stačiakampis, sudarytas tarp segmentų A ir B".
Ankstesnėje pamokoje mes susidūrėme su dauginiklių skaidymu. Buvo įvaldyti du būdai: bendras skliaustų ir grupavimo veiksnys. Šioje pamokoje - kitas galingas būdas: sutrumpintos dauginimo formulės. Trumpame įraše - FSU.
Sutrumpinto dauginimo formulės (sumos ir skirtumo kvadratas, sumos kubas ir skirtumas, kvadratų skirtumas, kubelių suma ir skirtumas) yra labai reikalingi visuose matematikos skyriuose. Jie naudojami supaprastinant išraiškas, išspręsti lygtis, polinomanų dauginimą, frakcijų mažinimą, integralų sprendimą ir kt. ir tt Trumpai tariant, yra kiekviena priežastis spręsti su jais. Suprasti, kaip jie yra imtasi, kodėl jie reikalingi, kaip juos prisiminti ir kaip kreiptis.
Mes suprantame?)
Iš kur ateina sutrumpintos dauginimo formulės?
6 ir 7 lygybė nėra labai pažįstami. Kaip ir priešingai. Tai yra specialiai.) Bet kokia lygybė veikia tiek iš kairės į dešinę ir į dešinę į kairę. Tokiu įrašu yra aišku, kur kilęs FSU.
Jie yra paimti iš dauginimo.) Pavyzdžiui:
(A + B) 2 \u003d (A + B) (A + B) \u003d A 2 + AB + BA + B 2 \u003d A 2 + 2AB + B 2
Tai viskas, nėra jokių mokslinių triukų. Tiesiog pakeiskite skliaustelius ir pateikite. Todėl paaiškėja visos sutrumpintos dauginimo formulės. Sutrumpintas Dauginimas yra todėl, kad patys formulėse nėra daugelio skliaustų ir panašių. Sumažintas.) Nedelsiant suteikė rezultatą.
FSU turi žinoti pagal širdį. Be pirmųjų trijų, jūs negalite svajoti apie trejetą, be poilsio - apie ketvirtą su penkiu.)
Kodėl reikia sutrumpintos dauginimo formulės?
Yra dvi priežastys, išmokti netgi gauti šias formules. Pirmasis - baigtas atsakymas ant mašinos smarkiai sumažina klaidų skaičių. Bet tai nėra pagrindinė priežastis. Bet antrasis ...
Jei jums patinka ši svetainė ...
Beje, aš turiu dar vieną įdomių svetainių jums.)
Jis gali būti prieinamas sprendžiant pavyzdžius ir sužinoti jūsų lygį. Bandymai su momentiniu patikrinimu. Sužinokite - su susidomėjimu!)
Galite susipažinti su funkcijomis ir išvestinėmis priemonėmis.
Formulės arba sutrumpintos dauginimo taisyklės yra naudojamos aritmetiniam arba greičiau - Algebra, greičiau apskaičiuoti didelių algebrinių išraiškų skaičiavimo procesą. Patys formulės gaunamos iš algebros egzistuojančių taisyklių dauginti keletą polinomų.
Šių formulių naudojimas suteikia gana veikiančią įvairių matematinių užduočių sprendimą, taip pat padeda supaprastinti išraiškas. Algebrinių transformacijų taisyklės leidžia atlikti tam tikras manipuliacijas su išraiškomis, po kurios galima gauti išraišką dešinėje pusėje kairėje lygybės dalyje arba konvertuoti dešinę lygybės dalį (norint gauti išraiška, kuri stovi kairėje pusėje po lygybės ženklo).
Patogu žinoti formules, naudojamą sutrumpintai dauginimui, taip pat jie dažnai naudojami sprendžiant problemas ir lygtis. Žemiau yra pagrindinės formulės, įtrauktos į šį sąrašą ir jų pavadinimą.
Kvadratinių sumų
Norint apskaičiuoti sumos kvadratą, būtina rasti sumą, sudarytą iš pirmojo termino kvadrato, padvigubėjo pirmojo laikotarpio antrojo ir antrojo lygio produktą. Išraiškos forma, ši taisyklė yra parašyta taip: (A + C) ² \u003d a² + 2AS + c².
Kvadratinis skirtumas. \\ T
Norėdami apskaičiuoti skirtumo kvadratą, būtina apskaičiuoti sumą, susidedančią iš pirmojo skaičiaus kvadrato dvigubo skaičiaus į antrąjį skaičių (paimtas su priešingu ženklu) ir antrojo numerio aikštėje. Išraiškos forma ši taisyklė yra tokia: (a - c) ² \u003d a² - 2As + c².
Kvadratinis skirtumas. \\ T
Dviejų į kvadratą pastatytų skaičių skirtumas yra lygus šių numerių sumos sumai dėl jų skirtumo. Išraiškos forma, ši taisyklė yra tokia: a² - c² \u003d (a + c) · (a - c).
Kubo kiekis
Norint apskaičiuoti dviejų komponentų sumų kubą, būtina apskaičiuoti sumą, sudarytą iš pirmojo termino kubo, trigubo pirmojo termino aikštės darbų ir antrojo, trigubo pirmojo termino produkto ir antrasis kvadratas, taip pat antrojo termino kubas. Išraiškos forma, ši taisyklė yra tokia: (a + c) ³ \u003d a³ + 3A² + 3A² + c³.

Kubelių kiekis
Pagal formulę jis yra lygus komponentų sąlygų sumai apie jų neišsami skirtumo aikštėje. Išraiškos forma, ši taisyklė yra tokia: a³ + c³ \u003d (A + C) · (A² - AC + C²).
Pavyzdys. Būtina apskaičiuoti formos kiekį, kuris yra sudarytas papildant du kubelius. Taip pat žinoma tik savo šalių vertybes.
Jei šalių vertės yra mažos, tiesiog atlikite skaičiavimus.
Jei šalių ilgis išreiškiamas dideliais skaičiais, tada šiuo atveju lengviau taikyti "kubelių" formulės kiekį, kuris žymiai supaprastins skaičiavimus.

Kubo skirtumas
Kubinio skirtumo išraiška yra tokia: kaip pirmojo laikotarpio trečiojo laipsnio suma, antrojo pirmojo nario pirmojo nario kvadrato neigiamas darbas trivariausiu pirmojo nario darbu į antrojo ir neigiamo kvadratą antrojo termino kubas. Matematinės raiškos pavidalu kubo skirtumas atrodo taip: (a - c) ³ \u003d a³ - 3A² + 3AS² - c³.

Kubiniai skirtumai
Kubo skirtumo formulė skiriasi nuo kubelių kiekio tik vieno ženklo. Taigi kubelių skirtumas yra formulė, lygi duomenų skirtumo skaičiui tarp jų neišsamos kvadratinės sumos. Kubelių skirtumas yra toks: A 3 - nuo 3 \u003d (A - C) (ir 2 + AC + C2).
Pavyzdys. Būtina apskaičiuoti figūros tūrį, kuris išliks po atėmimo nuo geltonos spalvos geltonos spalvos ploto, taip pat yra kubas. Žinomas tik mažo ir didelio kubo pusės dydis.
Jei šalių vertybės yra mažos, skaičiavimai yra gana paprasti. Ir jei šalių ilgiai išreiškiami reikšmingais skaičiais, būtina taikyti formulę "kubelių skirtumai" (arba "skirtumo kubas"), kuris žymiai supaprastins skaičiavimus.
Trys gedimai, kurių kiekvienas yra lygus x. ("DisplayStyle X") Šis aritmetinis veikimas vadinamas "erekcija į kubą", nurodomas jo rezultatas x 3 ("DisplayStyle X ^" (3)):
x 3 \u003d x ⋅ x ⋅ x (DisplayStyle x ^ (3) \u003d x cdot x cbot x)Kubo atvirkštinės operacijos statybai yra kubinių šaknų ekstrahavimas. Trečiojo laipsnio geometrinis pavadinimas " kubinis"Yra dėl to, kad antikvariniai matematikai laikomi kubeliais kaip kubiniai numeriai, specialūs suprojektuoti skaičiai (žr. Toliau), nes numerių sąrašas X ("DisplayStyle X") lygus kubo tūrai su briaunos ilgiu lygiu X ("DisplayStyle X").
Kubo seka
, , , , , 125, 216, 343, 512, 729, , 1331, , 2197, 2744, 3375, 4096, 4913, 5832, 6859, 8000, 9261, 10648, 12167, 13824, 15625, 17576, 19683, 21952, 24389, 27000, 29791, 32768, 35937, 39304, 42875, 46656, 50653, 54872, 59319, 64000, 68921, 74088, 79507, 85184, 91125, 97736, 103823, 110592, 117649, 125000, 132651, 140608, 148877, 157464, 166375, 175616, 185193, 195112, 205379, 216000, 226981, 238328…Pirmiausia kubelių kiekis N ("DisplayStyle N") Teigiami natūralūs numeriai apskaičiuojami pagal formulę:
Σ i \u003d 1 ni 3 \u003d 1 3 + 2 3 + 3 3 + ... + N 3 \u003d (n (n + 1) 2) 2 (\\ t fotografavimas į sumą _ (i \u003d 1) ^ (n) i ^ (3) \u003d 1 ^ (3) + 2 ^ (3) + 3 ^ (3) + ldst + n ^ (3) \u003d kairė (((((N (n + 1)) (2)) Teisė) ^ (2))Formulės panaikinimas. \\ T
Kubelių kiekis gali būti rodomas naudojant dauginimo lentelę ir aritmetinio progresavimo sumos sumą. Atsižvelgiant į metodo iliustraciją, dviem dauginimo stalai 5 × 5, Atlikite motyvai N × N lentelėse.
|
|
K-OH (k \u003d 1,2, ...) pasirinktos pirmos lentelės plotas:
k 2 + 2 k σ l \u003d 1 k - 1 l \u003d k 2 + 2 kk (k - 1) 2 \u003d k 3 (desidarstyle k ^ (2) + 2K) (l \u003d 1) ^ (k- 1) l \u003d k ^ (2) + 2K ((k (k (k - 1)) (2) \u003d k ^ (3))Ir numerių suma K-OH (k \u003d 1,2, ...) pasirinkta antrosios lentelės plotas, kuris yra aritmetinis progresavimas:
k σ l \u003d 1 n l \u003d k n (n + 1) 2 (decowstyle k (l \u003d 1) ^ (n) l \u003d k (n (n (n + 1)) (2))))))Apibendrinant per visas pasirinktas pirmosios lentelės sritis, gauname tą patį numerį visose pasirinktos antrosios lentelės srityse:
Σ K \u003d 1 NK 3 \u003d σ K \u003d 1 NKN (n + 1) 2 \u003d N (n + 1) 2 σ k \u003d 1 nk \u003d (n (n + 1) 2) 2 (\\ t \u003d 1) ^ (n) k ^ (3) \u003d (k \u003d 1) ^ (n) k (n (n (n + 1)) (2) \u003d (frac (n (n (n (n +) \\ t 1)) (2)) \\ sumunt _ (k \u003d 1) ^ (n) k \u003d kairė ((((((N (n + 1)) (2)) (2)) \\ tKai kurios savybės
- Dešimtainiame įraše kubas gali baigtis bet kuriuo skaitmeniu (skirtingai nuo kvadrato)
- Dešimtainiame įraše du paskutiniai kubeliai gali būti 00, 01, 03, 04, 07, 08, 09, 11, 19, 21, 29, 29, 21, 23, 29, 31 32, 36, 37, 39, 41, 43, 44, 47, 52, 53, 51, 52, 59, 61, 51, 52, 53, 61, 73, 75, 76, 77, 79, 81, 83, 84, 87, \\ t 88, 89, 91, 92, 93, 96, 97, 99. priešpaskutinio dydžio kubo priklausomybė nuo pastarosios gali būti atstovaujama kaip ši lentelė:
Kuba kaip garbanotieji skaičiai
"Kubinis numeris" Q N \u003d N 3 ("DisplayStyle Q_" (n) \u003d n ^ (3)) Istoriškai buvo laikoma įvairiais erdvinio skaičiaus numeriais. Jis gali būti sudarytas kaip eilinių trikampių skaičių kvadratų skirtumas. T N (DisplayStyle t_ (n)):
Q N \u003d (t n) 2 - (t n - 1) 2, n ⩾ 2 (didorstyle q_ (n) \u003d (t_ (n)) ^ (2) - (t_ (n - 1)) ^ (2), \\ t n geqslant 2) Q 1 + q 2 + q 3 + ⋯ + q N \u003d (T N) 2 ("DisplayStyle Q_" (1) + q_ (2) + q_ (3) + dots + q_ (n) \u003d (t_ (n)) ^ (2))Skirtumas tarp dviejų gretimų kubinių numerių yra centrinis šešiakampis numeris.
Kubinio numerio išraiška per tetraedralinį Π N (3) ("DisplayStyle" \\ PING) ^ ((3))).