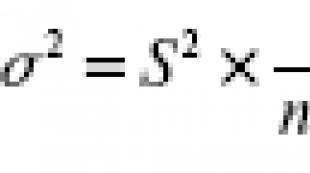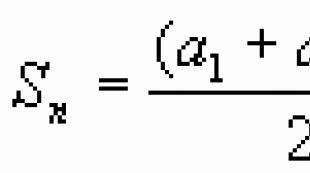កាត

រូបមន្តទាំងអស់ស្ថិតក្នុងវឌ្នភាពនព្វន្ធ។ វឌ្នភាពនព្វន្ធ។ ប្រភេទលេខលំដាប់មួយទៀតគឺធរណីមាត្រ

គណិតវិទ្យាមានភាពស្រស់ស្អាតរៀងៗខ្លួនដូចជាគំនូរនិងកំណាព្យ។

អ្នកវិទ្យាសាស្ត្ររុស្ស៊ីមេកានិច N.E. ហ្សូខូវស្គី

បញ្ហាទាក់ទងនឹងគំនិតនៃការវិវត្តនព្វន្ធគឺជាបញ្ហាទូទៅក្នុងការប្រលងចូលគណិតវិទ្យា។ ដើម្បីដោះស្រាយបញ្ហាទាំងនោះដោយជោគជ័យវាចាំបាច់ត្រូវដឹងឱ្យបានច្បាស់អំពីលក្ខណៈនៃវឌ្នភាពនព្វន្ធនិងមានជំនាញជាក់លាក់ក្នុងការដាក់ពាក្យ។

ដំបូងយើងរំលឹកឡើងវិញនូវលក្ខណៈសំខាន់ៗនៃវឌ្នភាពនព្វន្ធហើយបង្ហាញរូបមន្តសំខាន់បំផុត, ទាក់ទងនឹងគំនិតនេះ។

និយមន័យ។ លំដាប់លេខ, ដែលពាក្យបន្តបន្ទាប់នីមួយៗខុសពីពាក្យមុនដោយលេខដូចគ្នា, ហៅថាការវិវត្តនព្វន្ធ លើសពីនេះទៅទៀតលេខហៅថាភាពខុសគ្នានៃដំណើរការ

ចំពោះការវិវត្តនព្វន្ធរូបមន្តខាងក្រោមមានសុពលភាព

, (1)

កន្លែងណា។ រូបមន្ត (១) ត្រូវបានគេហៅថារូបមន្តសម្រាប់វាក្យស័ព្ទទូទៅនៃវឌ្ithនភាពនព្វន្ធហើយរូបមន្ត (២) គឺជាទ្រព្យសម្បត្តិចម្បងនៃការវិវត្តនព្វន្ធ៖ ពាក្យនីមួយៗនៃការវិវត្តស្របគ្នាជាមួយនឹងមធ្យមនព្វន្តនៃលក្ខខណ្ឌជិតខាងរបស់វានិង។

សូមកត់សម្គាល់ថាវាច្បាស់ណាស់ដោយសារតែលក្ខណៈសម្បត្តិនេះដែលដំណើរការរីកចម្រើនត្រូវបានគេហៅថា“ នព្វន្ធ” ។

រូបមន្តខាងលើ (១) និង (២) មានលក្ខណៈទូទៅដូចខាងក្រោម៖

(3)

ដើម្បីគណនាចំនួនទឹកប្រាក់ដំបូង សមាជិកនៃវឌ្នភាពនព្វន្ធជាធម្មតារូបមន្តត្រូវបានអនុវត្ត

(៥) កន្លែងណានិង។

ដោយគិតគូរពីរូបមន្ត (១), បន្ទាប់មករូបមន្ត (៥) បញ្ជាក់

ប្រសិនបើយើងបញ្ជាក់ដូច្នេះ

កន្លែងណា។ ចាប់តាំងពីពេលនោះមករូបមន្ត (៧) និង (៨) គឺជាការបូកសរុបនៃរូបមន្តដែលត្រូវគ្នា (៥) និង (៦) ។

ជាពិសេស , រូបមន្ត (៥) បញ្ជាក់, អ្វី

ទ្រព្យសម្បត្តិនៃវឌ្នភាពនព្វន្ធដែលបង្កើតឡើងតាមទ្រឹស្តីបទខាងក្រោមស្ថិតក្នុងចំណោមសិស្សដែលមិនសូវស្គាល់

ទ្រឹស្តីបទ។បើអញ្ចឹង

ភស្តុតាង។បើអញ្ចឹង

ទ្រឹស្តីបទត្រូវបានបង្ហាញ។

ឧទាហរណ៍ , ដោយប្រើទ្រឹស្តីបទ, វាអាចត្រូវបានបង្ហាញថា

ចូរយើងបន្តពិចារណាលើឧទាហរណ៍ធម្មតានៃការដោះស្រាយបញ្ហាលើប្រធានបទ "វឌ្ithនភាពនព្វន្ធ" ។

ឧទាហរណ៍ទី ១អនុញ្ញាតឱ្យនិង។ រក។

ដំណោះស្រាយ។អនុវត្តរូបមន្ត (៦) យើងទទួលបាន។ ចាប់តាំងពីនិងបន្ទាប់មកឬ។

ឧទាហរណ៍ទី ២ ។សូមឱ្យវាមានចំនួនបីដងហើយនៅពេលចែកដោយផលបូកយើងទទួលបាន ២ និងនៅសល់ ៨. កំណត់និង។

ដំណោះស្រាយ។លក្ខខណ្ឌនៃឧទាហរណ៍បង្កប់ន័យប្រព័ន្ធសមីការ

ចាប់តាំងពី ,, និងបន្ទាប់មកពីប្រព័ន្ធសមីការ (១០) យើងទទួលបាន

ដំណោះស្រាយចំពោះប្រព័ន្ធសមីការនេះគឺនិង។

ឧទាហរណ៍ទី ៣រកប្រសិនបើនិង។

ដំណោះស្រាយ។យោងតាមរូបមន្ត (៥) យើងមានឬ។ ទោះយ៉ាងណាក៏ដោយដោយប្រើទ្រព្យសម្បត្តិ (៩) យើងទទួលបាន។

ចាប់តាំងពីនិងបន្ទាប់មកពីសមភាព សមីការដូចខាងក្រោមឬ។

ឧទាហរណ៍ទី ៤រកប្រសិនបើ។

ដំណោះស្រាយ។តាមរូបមន្ត (៥) យើងមាន

ទោះយ៉ាងណាក៏ដោយដោយប្រើទ្រឹស្តីបទមនុស្សម្នាក់អាចសរសេរបាន

ពីនេះនិងរូបមន្ត (១១) យើងទទួលបាន។

ឧទាហរណ៍ទី ៥. បានផ្តល់ឱ្យ: រក។

ដំណោះស្រាយ។ចាប់តាំងពីពេលនោះមក។ ទោះយ៉ាងណាក៏ដោយដូច្នេះ។

ឧទាហរណ៍ទី ៦ ។អនុញ្ញាតឱ្យ, និង។ រក។

ដំណោះស្រាយ។ដោយប្រើរូបមន្ត (៩) យើងទទួលបាន។ ដូច្នេះប្រសិនបើ, បន្ទាប់មកឬ។

ចាប់តាំងពីនិង បន្ទាប់មកនៅទីនេះយើងមានប្រព័ន្ធសមីការ

ការដោះស្រាយដែលយើងទទួលបាននិង។

naturalសធម្មជាតិនៃសមីការគឺជា ។

ឧទាហរណ៍ទី ៧ ។រកប្រសិនបើនិង។

ដំណោះស្រាយ។ដោយសាររូបមន្ត (៣) យើងមានដូច្នេះសេចក្តីថ្លែងការណ៍បញ្ហាទាក់ទងនឹងប្រព័ន្ធសមីការ

ប្រសិនបើអ្នកជំនួសកន្សោមនៅក្នុងសមីការទីពីរនៃប្រព័ន្ធបន្ទាប់មកយើងទទួលបានឬ។

rootsសគល់នៃសមីការត្រីកោណគឺនិង។

ចូរយើងពិចារណាករណីពីរ។

1. អនុញ្ញាតឱ្យបន្ទាប់មក។ ចាប់តាំងពីនិងបន្ទាប់មក។

ក្នុងករណីនេះយោងតាមរូបមន្ត (៦) យើងមាន

2. ប្រសិនបើបន្ទាប់មកនិង

ចម្លើយ៖ និង។

ឧទាហរណ៍ទី ៨ ។វាត្រូវបានគេដឹងថានិង។ រក។

ដំណោះស្រាយ។ដោយគិតគូរពីរូបមន្ត (៥) និងលក្ខខណ្ឌនៃឧទាហរណ៍យើងសរសេរចុះនិង។

ដូច្នេះធ្វើតាមប្រព័ន្ធនៃសមីការ

ប្រសិនបើយើងគុណសមីការទីមួយនៃប្រព័ន្ធដោយ ២ ហើយបន្ទាប់មកបន្ថែមវាទៅសមីការទីពីរយើងទទួលបាន

យោងតាមរូបមន្ត (៩) យើងមាន... នៅក្នុងការតភ្ជាប់នេះពី (១២) វាដូចខាងក្រោមឬ។

ចាប់តាំងពីនិងបន្ទាប់មក។

ចម្លើយ៖ ។

ឧទាហរណ៍ទី ៩ ។រកប្រសិនបើនិង។

ដំណោះស្រាយ។ចាប់តាំងពីនិងតាមលក្ខខណ្ឌបន្ទាប់មកឬ។

ពីរូបមន្ត (៥) វាត្រូវបានគេដឹង, អ្វី។ ចាប់តាំងពីពេលនោះមក។

ដូច្នេះ នៅទីនេះយើងមានប្រព័ន្ធសមីការលីនេអ៊ែរ

ដូច្នេះយើងទទួលបាននិង។ ដោយគិតគូរពីរូបមន្ត (៨) យើងសរសេរ។

ឧទាហរណ៍ទី ១០ ។ដោះស្រាយសមីការ។

ដំណោះស្រាយ។ពីសមីការដែលបានផ្តល់ឱ្យវាដូចខាងក្រោម។ ឧបមាថា, និង។ ក្នុងករណីនេះ ។

យោងតាមរូបមន្ត (១) អ្នកអាចសរសេរឬ។

ចាប់តាំងពីពេលនោះមកសមីការ (១៣) មានsuitableសសមរម្យតែមួយ។

ឧទាហរណ៍ទី ១១ ។រកតម្លៃអតិបរមាដែលបានផ្តល់នោះនិង។

ដំណោះស្រាយ។ចាប់តាំងពីការវិវត្តនព្វន្ធដែលបានពិចារណាកំពុងថយចុះ។ ក្នុងន័យនេះកន្សោមយកតម្លៃអតិបរិមានៅពេលវាជាចំនួននៃពាក្យវិជ្ជមានអប្បបរមានៃការវិវត្ត

យើងប្រើរូបមន្ត (១) និងការពិត, ដូច។ បន្ទាប់មកយើងទទួលបានឬ។

ចាប់តាំងពីពេលនោះមកឬ ... ទោះយ៉ាងណាក៏ដោយនៅក្នុងវិសមភាពនេះលេខធម្មជាតិធំបំផុតដូច្នេះ។

ប្រសិនបើតម្លៃនិងត្រូវបានជំនួសនៅក្នុងរូបមន្ត (៦) នោះយើងទទួលបាន។

ចម្លើយ៖ ។

ឧទាហរណ៍ទី ១២ ។កំណត់ផលបូកនៃលេខធម្មជាតិពីរខ្ទង់ទាំងអស់ដែលនៅពេលចែកនឹង ៦ ផ្តល់សល់ ៥ ។

ដំណោះស្រាយ។ចូរយើងកំណត់ដោយសំណុំនៃលេខធម្មជាតិពីរខ្ទង់ទាំងអស់ពោលគឺឧ។ ... បន្ទាប់យើងបង្កើតសំណុំរងដែលមានធាតុទាំងនោះ (លេខ) នៃសំណុំដែលនៅពេលចែកនឹង ៦ ផ្តល់ឱ្យនៅសល់ ៥ ។

វាមិនពិបាកក្នុងការបង្កើតទេ, អ្វី។ ជាក់ស្តែង ថាធាតុនៃសំណុំបង្កើតការវិវត្តនព្វន្ធដែលក្នុងនោះនិង។

ដើម្បីបង្កើតខា (ចំនួនធាតុ) នៃសំណុំយើងសន្មតថា។ ចាប់តាំងពីនិងបន្ទាប់មកពីរូបមន្ត (១) វាដូចខាងក្រោមឬ។ ដោយគិតគូរពីរូបមន្ត (៥) យើងទទួលបាន។

ឧទាហរណ៍ខាងលើនៃការដោះស្រាយបញ្ហាដោយគ្មានមធ្យោបាយអាចអះអាងថាមានភាពពេញលេញ។ អត្ថបទនេះត្រូវបានសរសេរដោយផ្អែកលើការវិភាគវិធីសាស្រ្តទំនើបសម្រាប់ដោះស្រាយបញ្ហាធម្មតាលើប្រធានបទណាមួយ។ ចំពោះការសិក្សាស៊ីជម្រៅអំពីវិធីសាស្រ្តសម្រាប់ដោះស្រាយបញ្ហាដែលជាប់ទាក់ទងនឹងវឌ្ithនភាពនព្វន្ធវាត្រូវបានគេណែនាំឱ្យយោងទៅលើបញ្ជីអក្សរសិល្ប៍ដែលបានណែនាំ។

១. ការប្រមូលបញ្ហាក្នុងគណិតវិទ្យាសម្រាប់បេក្ខជនចូលរៀននៅមហាវិទ្យាល័យបច្ចេកទេស / អេដ។ M.I. ស្គូណាវី។ - អិមៈសន្តិភាពនិងការអប់រំឆ្នាំ ២០១៣- ៦០៨ ទំ។

២. ស៊ូភុន V.P. គណិតវិទ្យាសម្រាប់សិស្សវិទ្យាល័យ៖ ផ្នែកបន្ថែមនៃកម្មវិធីសិក្សារបស់សាលា។ - អិមៈលេនណាន់ / យូអរអេសអេស, 2014 .-- 216 ទំ។

3. មេឌីនស្គីអិម។ បញ្ចប់វគ្គសិក្សាគណិតវិទ្យាបឋមលើបញ្ហានិងលំហាត់។ សៀវភៅទី ២៖ លំដាប់លេខនិងវឌ្នភាព។ - អិមៈអេឌីត, 2015 .-- 208 ទំ។

នៅតែមានសំណួរ?

ដើម្បីទទួលបានជំនួយពីគ្រូ - ចុះឈ្មោះ។

គេហទំព័រដែលមានឯកសារចម្លងពេញលេញឬមួយផ្នែកនៃឯកសារត្រូវការតំណភ្ជាប់ទៅប្រភព។

ប្រភេទមេរៀន៖ការរៀនសម្ភារៈថ្មី។

គោលបំណងមេរៀន៖

ការពង្រីកនិងធ្វើឱ្យគំនិតនិស្សិតកាន់តែស៊ីជម្រៅអំពីបញ្ហាដែលបានដោះស្រាយដោយប្រើវឌ្នភាពនព្វន្ធ ការរៀបចំសកម្មភាពស្វែងរករបស់សិស្សនៅពេលទទួលបានរូបមន្តសម្រាប់ផលបូកនៃសមាជិក n ដំបូងនៃវឌ្នភាពនព្វន្ធ
អភិវឌ្ development ជំនាញដើម្បីទទួលបានចំណេះដឹងថ្មីដោយឯករាជ្យប្រើចំណេះដឹងដែលទទួលបានរួចហើយដើម្បីសម្រេចបាននូវភារកិច្ចដែលបានកំណត់។
ការអភិវឌ្ន៍បំណងប្រាថ្នានិងតំរូវការទូទៅអំពីការពិតដែលទទួលបានការអភិវឌ្ development ឯករាជ្យភាព

ភារកិច្ច:

ធ្វើឱ្យមានលក្ខណៈទូទៅនិងរៀបចំប្រព័ន្ធចំណេះដឹងដែលមានស្រាប់លើប្រធានបទ“ វឌ្នភាពនព្វន្ធ”
ទាញយករូបមន្តសម្រាប់គណនាផលបូកនៃលក្ខខណ្ឌ n ដំបូងនៃការវិវត្តនព្វន្ធ
ដើម្បីបង្រៀនពីរបៀបអនុវត្តរូបមន្តដែលទទួលបានក្នុងការដោះស្រាយបញ្ហាផ្សេងៗ។
ដើម្បីទាក់ទាញការយកចិត្តទុកដាក់របស់សិស្សចំពោះលំដាប់នៃសកម្មភាពនៅពេលរកឃើញតម្លៃនៃកន្សោមលេខ។

ឧបករណ៍:

កាតដែលមានកិច្ចការសម្រាប់ធ្វើការជាក្រុមនិងជាគូ។
ក្រដាសវាយតម្លៃ;
បទបង្ហាញ"វឌ្នភាពនព្វន្ធ" ។

I. ធ្វើបច្ចុប្បន្នភាពចំណេះដឹងជាមូលដ្ឋាន។

1. ការងារឯករាជ្យជាគូ។

ជម្រើសទី ១៖

ផ្តល់និយមន័យនៃវឌ្នភាពនព្វន្ធ។ សរសេររូបមន្តដែលកើតឡើងដដែលៗដែលកំណត់ការវិវត្តនព្វន្ធ។ សួស្តីឧទាហរណ៍នៃវឌ្នភាពនព្វន្ធនិងបង្ហាញពីភាពខុសគ្នារបស់វា។

ជម្រើសទី ២៖

សរសេររូបមន្តសម្រាប់ពាក្យទី ៩ នៃការវិវត្តនព្វន្ធ រកពាក្យទី ១០០ នៃវឌ្នភាពនព្វន្ធ ( មួយ n}: 2, 5, 8 …
នៅពេលនេះសិស្សពីរនាក់នៅខាងក្រោយក្តាររៀបចំចម្លើយចំពោះសំណួរដូចគ្នា។
សិស្សវាយតម្លៃការងាររបស់ដៃគូទល់នឹងក្តារ។ (សន្លឹកចម្លើយត្រូវបានប្រគល់ជូន) ។

2. ពេលហ្គេម។

លំហាត់ទី ១ ។

គ្រូ។ខ្ញុំបានបង្កើតការវិវត្តនព្វន្ធខ្លះ។ គ្រាន់តែសួរខ្ញុំពីរសំនួរដូច្នេះបន្ទាប់ពីចម្លើយអ្នកអាចដាក់ឈ្មោះយ៉ាងឆាប់រហ័សនូវពាក្យទី ៧ នៃវឌ្នភាពនេះ។ (១, ៣, ៥, ៧, ៩, ១១, ១៣, ១៥ ... )

សំណួរនិស្សិត។

តើអ្វីទៅជាអាណត្តិទី ៦ ក្នុងការវិវត្តហើយតើអ្វីជាភាពខុសគ្នា?
តើអ្វីទៅជាការបន្តវេនទី ៨ ហើយតើអ្វីជាភាពខុសគ្នា?

ប្រសិនបើមិនមានសំនួរបន្ថែមទេនោះគ្រូអាចជំរុញពួកគេ -“ ហាមឃាត់” លើឃ (ភាពខុសគ្នា) នោះគឺវាមិនត្រូវបានអនុញ្ញាតឱ្យសួរថាតើអ្វីជាភាពខុសគ្នានោះទេ។ អ្នកអាចសួរសំណួរ៖ តើអ្វីទៅជាការវិវត្តនៃអាណត្តិទី ៦ និងអ្វីដែលជាអាណត្តិទី ៨ នៃការវិវត្ត?

កិច្ចការទី ២ ។

មានលេខចំនួន ២០ សរសេរនៅលើក្តារ៖ 1, 4, 7 10, 13, 16, 19, 22, 25, 28, 31, 34, 37, 40, 43, 46, 49, 52, 55, 58.

គ្រូបង្រៀនឈរនៅពីក្រោយខ្នងរបស់គាត់ទៅក្តារខៀន។ សិស្សហៅលេខតាមលេខហើយគ្រូភ្លាមៗហៅលេខខ្លួនឯង។ ពន្យល់ពីរបៀបដែលខ្ញុំធ្វើវា?

គ្រូចងចាំរូបមន្តសម្រាប់ពាក្យទីប្រាំ a n = 3n - 2ហើយជំនួសតម្លៃដែលបានផ្តល់ឱ្យ n រកឃើញតម្លៃដែលត្រូវគ្នា មួយ n ។

II ។ សេចក្តីថ្លែងការណ៍នៃបញ្ហាអប់រំ។

ខ្ញុំស្នើឱ្យដោះស្រាយបញ្ហាបុរាណមួយដែលមានតាំងពីសហវត្សទី ២ មុនគ។

កិច្ចការ៖សូមឱ្យវាត្រូវបានគេនិយាយទៅអ្នកថា៖ ចែក ១០ បារ៉ែលរវាងមនុស្ស ១០ នាក់ភាពខុសគ្នារវាងមនុស្សម្នាក់ៗនិងអ្នកជិតខាងគឺស្មើនឹង ១/៨ នៃរង្វាស់។

តើកិច្ចការនេះទាក់ទងយ៉ាងដូចម្តេចចំពោះប្រធានបទនៃការវិវត្តនព្វន្ធ? (បន្ទាប់នីមួយៗទទួលបាន ១/៨ នៃរង្វាស់បន្ថែមទៀតដែលមានន័យថាភាពខុសគ្នាឃ = ១/៨ មនុស្ស ១០ នាក់មានន័យថា n = ១០)
តើអ្នកគិតថាលេខ ១០ មានន័យយ៉ាងដូចម្តេច? (ផលបូកនៃសមាជិកទាំងអស់នៃវឌ្នភាព។ )
តើមានអ្វីទៀតដែលអ្នកត្រូវដឹងដើម្បីធ្វើឱ្យងាយស្រួលនិងសាមញ្ញក្នុងការបែងចែកបាឡៃទៅតាមស្ថានភាពភារកិច្ច? (ពាក្យដំបូងកំពុងដំណើរការ។ )

គោលបំណងមេរៀន- ទទួលបានការពឹងផ្អែកនៃផលបូកនៃសមាជិកនៃការវិវត្តនៃចំនួនរបស់ពួកគេពាក្យដំបូងនិងភាពខុសគ្នានិងពិនិត្យមើលថាតើបញ្ហានេះត្រូវបានដោះស្រាយត្រឹមត្រូវនៅសម័យបុរាណដែរឬទេ។

មុននឹងគូរសេចក្តីសន្និដ្ឋាននៃរូបមន្តចូរយើងមើលពីរបៀបដែលជនជាតិអេស៊ីបបុរាណបានដោះស្រាយបញ្ហានេះ។

ហើយពួកគេបានដោះស្រាយវាដូចនេះ៖

១) វិធានការ ១០៖ ១០ = ១ រង្វាស់ - ចំណែកមធ្យម;
២) ១ រង្វាស់∙ = ២ វិធានការ - ទ្វេដង មធ្យមចែករំលែក។
ទ្វេដង មធ្យមចំណែកគឺជាផលបូកនៃភាគហ៊ុនរបស់មនុស្សទី ៥ និងទី ៦ ។
៣) វិធានការ ២ - វិធានការ ១/៨ = ១ ៧/៨ វិធានការ - ពីរដងនៃចំណែករបស់មនុស្សទី ៥ ។
៤) ១ ៧/៨៖ ២ = ៥/១៦ - ចំណែកទី ៥; ដូច្នេះអ្នកអាចស្វែងរកចំណែករបស់មនុស្សមុននិងបន្ទាប់នីមួយៗ។

យើងទទួលបានលំដាប់៖

III ។ ដំណោះស្រាយចំពោះបញ្ហា។

1. ធ្វើការជាក្រុម

ក្រុម I៖រកផលបូកនៃលេខធម្មជាតិ ២០ ជាប់ៗគ្នា៖ ស ២០ = (២០ + ១) ∙ ១០ = ២១០ ។

ជាទូទៅ

ក្រុមទី ២៖រកផលបូកនៃលេខធម្មជាតិពី ១ ដល់ ១០០ (រឿងព្រេងនិទាននៃហ្គូសតូច) ។

ស ១០០ = (១ + ១០០) ∙ ៥០ = ៥០៥០

លទ្ធផល៖

ក្រុមទី ៣៖រកផលបូកនៃលេខធម្មជាតិពី ១ ដល់ ២១ ។

ដំណោះស្រាយ៖ ១ + ២១ = ២ + ២០ = ៣ + ១៩ = ៤ + ១៨ ...

លទ្ធផល៖

ក្រុមទី ៤៖រកផលបូកនៃលេខធម្មជាតិពី ១ ដល់ ១០១ ។

លទ្ធផល៖

វិធីសាស្រ្តសម្រាប់ដោះស្រាយបញ្ហាដែលត្រូវបានគេហៅថា“ វិធីសាស្ត្រហ្គូស” ។

2. ក្រុមនីមួយៗបង្ហាញពីដំណោះស្រាយចំពោះបញ្ហានៅលើក្តារ។

៣. ការបកស្រាយទូទៅនៃដំណោះស្រាយដែលបានស្នើឡើងសម្រាប់ការវិវត្តនព្វន្ធតាមអំពើចិត្ត៖

a ១, ២, ៣, ... , n-២, n-១, n ។
S n = a 1 + a 2 + a 3 + a 4 + … + n-3 + a n-2 + a n-1 + a n ។

ចូរយើងរកផលបូកនេះដោយការវែកញែកតាមរបៀបស្រដៀងគ្នា៖

4. តើយើងបានដោះស្រាយភារកិច្ចនៅនឹងដៃហើយឬនៅ?(បាទ។ )

IV ។ ការយល់ដឹងបឋមនិងការអនុវត្តរូបមន្តដែលទទួលបានក្នុងការដោះស្រាយបញ្ហា។

១. ពិនិត្យមើលដំណោះស្រាយចំពោះបញ្ហាចាស់ដោយប្រើរូបមន្ត។

២. ការអនុវត្តរូបមន្តក្នុងការដោះស្រាយបញ្ហាផ្សេងៗ។

3. លំហាត់ដើម្បីបង្កើតសមត្ថភាពក្នុងការអនុវត្តរូបមន្តនៅពេលដោះស្រាយបញ្ហា។

ក) លេខ ៦១៣

ផ្តល់ឱ្យ :( មួយ n) -វឌ្នភាពនព្វន្ធ;

(a n)៖ ១, ២, ៣, ... , ១៥០០

ស្វែងរក៖ ស ១៥០០

ដំណោះស្រាយ៖ , a ១ = ១, ១៥០០ = ១៥០០,

ខ) ផ្តល់ឱ្យ៖ ( មួយ n) -វឌ្នភាពនព្វន្ធ;
(a n)៖ ១, ២, ៣, ...
S n = 210

ស្វែងរក៖ n
ដំណោះស្រាយ៖

V. ការងារឯករាជ្យជាមួយនឹងការផ្ទៀងផ្ទាត់គ្នា។

ដេនីសបានទៅធ្វើការជាអ្នកនាំសំបុត្រ។ នៅខែដំបូងប្រាក់ខែរបស់គាត់គឺ ២០០ រូប្លិ៍ក្នុងខែបន្ទាប់នីមួយៗកើនឡើង ៣០ រូប្លិ៍។ តើគាត់រកបានប៉ុន្មានក្នុងមួយឆ្នាំ?

ផ្តល់ឱ្យ :( មួយ n) -វឌ្នភាពនព្វន្ធ;
a 1 = 200, d = 30, n = 12
ស្វែងរក៖ ស ១២
ដំណោះស្រាយ៖

ចម្លើយ៖ ដេនីសទទួលបាន ៤៣៨០ រូប្លិ៍ក្នុងមួយឆ្នាំ។

វី។ សង្ខេបកិច្ចការផ្ទះ។

ទំព័រ ៤.៣ - ស្វែងយល់ពីរូបមន្ត។
№№ 585, 623 .
បង្កើតបញ្ហាដែលនឹងត្រូវដោះស្រាយដោយប្រើរូបមន្តសម្រាប់ផលបូកនៃលក្ខខណ្ឌ n ដំបូងនៃការវិវត្តនព្វន្ធ

វី។ ការសង្ខេបមេរៀន។

1. សន្លឹកវាយតម្លៃ

2. បន្តប្រយោគ

ថ្ងៃនេះនៅក្នុងមេរៀនដែលខ្ញុំបានរៀន ...
បានរៀនរូបមន្ត ...
ខ្ញុំគិតថា …

3. តើអ្នកអាចរកផលបូកនៃលេខពី ១ ដល់ ៥០០ បានទេ? តើអ្នកនឹងប្រើវិធីសាស្ត្រអ្វីដើម្បីដោះស្រាយបញ្ហានេះ?

គន្ថនិទ្ទេស។

១. ពិជគណិតថ្នាក់ទី ៩ ។ សៀវភៅសិក្សាសម្រាប់ស្ថាប័នអប់រំ។ អេដ G.V. ដូរ៉ូហ្វៀវ៉ាអិមៈ“ ការអប់រំ” ឆ្នាំ ២០០៩

បាទ / ចាសបាទ៖ ការវិវត្តនព្វន្ធមិនមែនជាប្រដាប់ក្មេងលេងសម្រាប់អ្នកទេ :)

ជាការប្រសើរណាស់, មិត្តភក្តិ, ប្រសិនបើអ្នកកំពុងអានអត្ថបទនេះ, ភាពច្បាស់ខាងក្នុងប្រាប់ខ្ញុំថាអ្នកមិនទាន់ដឹងថាការវិវត្តនព្វន្ធគឺជាអ្វីទេប៉ុន្តែអ្នកពិតជា (ទេដូចនេះ៖ សូអូអូអូ!) ចង់ដឹង។ ដូច្នេះខ្ញុំនឹងមិនធ្វើទុក្ខទោសអ្នកជាមួយនឹងការណែនាំវែងឆ្ងាយហើយឈានដល់ចំនុចត្រង់។

ចូរចាប់ផ្តើមជាមួយឧទាហរណ៍ពីរបី។ ពិចារណាសំណុំលេខជាច្រើន៖

1; 2; 3; 4; ...
15; 20; 25; 30; ...
$ \ sqrt (2); \ 2 \ sqrt (2); \ 3 \ sqrt (2); ... $

តើឈុតទាំងអស់នេះមានអ្វីដូចគ្នា? នៅ glance ដំបូង, គ្មានអ្វី។ ប៉ុន្តែតាមពិតមានអ្វីមួយ។ គឺ៖ ធាតុបន្ទាប់នីមួយៗខុសគ្នាពីធាតុមុនដោយលេខដូចគ្នា.

វិនិច្ឆ័យដោយខ្លួនឯង។ សិតទី ១ គ្រាន់តែជាលេខជាប់ៗគ្នាដែលលេខបន្ទាប់នីមួយៗច្រើនជាងលេខមុន។ ក្នុងករណីទី ២ ភាពខុសគ្នារវាងលេខនៅជាប់គ្នាគឺស្មើនឹង ៥ រួចហើយប៉ុន្តែភាពខុសគ្នានេះនៅតែថេរ។ ក្នុងករណីទីបីrootsសជាទូទៅ។ ទោះយ៉ាងណាក៏ដោយ $ 2 \ sqrt (2) = \ sqrt (2) + \ sqrt (2) $ និង $ 3 \ sqrt (2) = 2 \ sqrt (2) + \ sqrt (2) $, ឧ។ ហើយក្នុងករណីនេះធាតុបន្ទាប់នីមួយៗគ្រាន់តែកើនឡើង $ \ sqrt (2) $ (ហើយកុំខ្លាចថាចំនួននេះមិនសមហេតុផល) ។

ដូច្នេះ៖ លំដាប់ទាំងអស់នេះត្រូវបានគេហៅថាវឌ្ithនភាពនព្វន្ធ។ សូមឱ្យនិយមន័យតឹងរ៉ឹង៖

និយមន័យ។ លំដាប់លេខដែលលេខនីមួយៗខុសពីលេខមុនដោយចំនួនដូចគ្នាត្រូវបានគេហៅថាការវិវត្តនព្វន្ធ។ ចំនួនដែលលេខខុសគ្នាត្រូវបានគេហៅថាភាពខុសគ្នានៃការវិវត្តហើយភាគច្រើនត្រូវបានបង្ហាញដោយអក្សរ $ d $ ។

ការរចនា៖ $ \\ ឆ្វេង (((ក) _ (ន)) ស្តាំ) $ - វឌ្itselfនភាពខ្លួនឯង $ d $ - ភាពខុសគ្នារបស់វា។

ហើយគ្រាន់តែការកត់សម្គាល់សំខាន់ពីរបី។ ដំបូងតែប៉ុណ្ណោះ សណ្តាប់ធ្នាប់លំដាប់លេខ៖ ពួកគេត្រូវបានអនុញ្ញាតឱ្យអានយ៉ាងតឹងរ៉ឹងតាមលំដាប់ដែលពួកគេសរសេរ - ហើយគ្មានអ្វីទៀតទេ។ អ្នកមិនអាចរៀបចំឡើងវិញឬប្តូរលេខបានទេ។

ទីពីរលំដាប់ខ្លួនវាអាចមានកំណត់ឬគ្មានកំណត់។ ឧទាហរណ៍សំណុំ (១; ២; ៣) ច្បាស់ជាវឌ្នភាពនព្វន្ធមានកំណត់។ ប៉ុន្តែប្រសិនបើអ្នកសរសេរអ្វីមួយនៅក្នុងស្មារតី (១; ២; ៣; ៤; ... ) - នេះគឺជាការវិវត្តគ្មានទីបញ្ចប់រួចទៅហើយ។ ពងក្រពើបន្ទាប់ពីលេខបួនដូចដែលបានបង្ហាញថានៅតែមានចំនួនមួយចំនួនកំពុងបន្ត។ ឧទាហរណ៍ច្រើនឥតខ្ចោះ។ :)

ខ្ញុំក៏ចង់កត់សំគាល់ផងដែរថាវឌ្នភាពកំពុងកើនឡើងនិងថយចុះ។ យើងបានឃើញរួចមកហើយនូវការកើនឡើងដែលជាសំណុំដូចគ្នា (១, ២, ៣, ៤; ... ) ហើយនេះគឺជាឧទាហរណ៍នៃការវិវត្តថយចុះ៖

49; 41; 33; 25; 17; ...
17,5; 12; 6,5; 1; −4,5; −10; ...
$ \ sqrt (5); \ \ sqrt (5) -1; \ \ sqrt (5) -2; \ sqrt (5) -3; ... $

មិនអីទេ៖ ឧទាហរណ៍ចុងក្រោយនេះអាចហាក់ដូចជាស្មុគស្មាញពេក។ ប៉ុន្តែអ្វីដែលនៅសល់ខ្ញុំយល់ច្បាស់ចំពោះអ្នក។ ដូច្នេះយើងនឹងណែនាំនិយមន័យថ្មី៖

និយមន័យ។ ការវិវត្តនព្វន្ធត្រូវបានគេហៅថា៖

កើនឡើងប្រសិនបើធាតុបន្ទាប់នីមួយៗធំជាងធាតុមុន។

ថយចុះបើផ្ទុយទៅវិញធាតុបន្តនីមួយៗមានចំនួនតិចជាងធាតុមុន។

លើសពីនេះទៀតមានអ្វីដែលគេហៅថាលំដាប់ស្ថានី - ពួកគេមានលេខដដែលៗដូចគ្នា។ ឧទាហរណ៍ (៣; ៣; ៣; ... ) ។

មានសំណួរតែមួយប៉ុណ្ណោះ៖ តើធ្វើដូចម្តេចដើម្បីសម្គាល់ការវិវត្តដែលកើនឡើងពីការថយចុះ? សំណាងល្អវាទាំងអស់គឺអាស្រ័យលើសញ្ញានៃលេខ $ d $ ពោលគឺឧ។ ការវិវត្តភាពខុសគ្នា៖

ប្រសិនបើ $ d \ gt 0 $, បន្ទាប់មកវឌ្នភាពកំពុងកើនឡើង។
ប្រសិនបើ $ d \ lt 0 $, បន្ទាប់មកការវិវត្តកំពុងធ្លាក់ចុះយ៉ាងច្បាស់។
ទីបំផុតមានករណី $ d = 0 $ - ក្នុងករណីនេះការវិវត្តទាំងមូលត្រូវបានកាត់បន្ថយជាលំដាប់នៃលេខដូចគ្នា៖ (១; ១; ១; ១; ១; ... ) ។

ចូរយើងព្យាយាមគណនាភាពខុសគ្នា $ d $ សម្រាប់ការថយចុះចំនួនបីដែលបានផ្តល់ឱ្យខាងលើ។ ដើម្បីធ្វើដូចនេះវាគ្រប់គ្រាន់ដើម្បីយកធាតុពីរដែលនៅជាប់គ្នា (ឧទាហរណ៍ទីមួយនិងទីពីរ) ហើយដកលេខនៅខាងឆ្វេងពីលេខនៅខាងស្តាំ។ វានឹងមើលទៅដូចនេះ៖

41−49=−8;
12−17,5=−5,5;
$ \ sqrt (5) -1- \ sqrt (5) = - 1 $ ។

ដូចដែលអ្នកអាចឃើញក្នុងករណីទាំងបីនេះភាពខុសគ្នាពិតជាប្រែទៅជាអវិជ្ជមាន។ ហើយឥលូវនេះយើងបានដឹងនិយមន័យតិចឬច្រើនវាដល់ពេលហើយដើម្បីស្វែងយល់ថាតើការវិវត្តត្រូវបានពិពណ៌នានិងលក្ខណៈសម្បត្តិរបស់វាយ៉ាងដូចម្តេច។

សមាជិកវឌ្នភាពនិងរូបមន្តកើតឡើងវិញ

ដោយសារធាតុនៃលំដាប់របស់យើងមិនអាចប្តូរបានគេអាចដាក់លេខបាន៖

\ [\ ឆ្វេង ((ក) _ (ន)) ស្តាំ = \ ខាងឆ្វេង \ ((ក) _ (១)) \ ((ក) _ (២)) ((ក) _ (៣ )), ... \ សិទ្ធិ \) \]

ធាតុបុគ្គលនៃសំណុំនេះត្រូវបានគេហៅថាសមាជិកនៃការវិវត្ត ពួកវាត្រូវបានចង្អុលបង្ហាញដោយលេខ៖ ពាក្យទីមួយអាណត្តិទីពីរ។

លើសពីនេះទៀតដូចដែលយើងបានដឹងរួចមកហើយសមាជិកជិតខាងនៃវឌ្នភាពនេះត្រូវបានទាក់ទងដោយរូបមន្ត៖

\ [((a) _ (n))-((a) _ (n-1)) = d \ Rightarrow ((a) _ (n)) = ((a) _ (n-1)) + ឃ \]

សរុបសេចក្ដីដើម្បីរកពាក្យ $ n $ th ក្នុងដំណើរការអ្នកត្រូវដឹងពីពាក្យ $ n-1 $ th និងភាពខុសគ្នា $ d $ ។ រូបមន្តបែបនេះត្រូវបានគេហៅថាកើតឡើងវិញដោយមានជំនួយរបស់វាអ្នកអាចរកឃើញលេខណាមួយដោយគ្រាន់តែដឹងលេខមុន (ហើយតាមពិត - លេខមុនទាំងអស់) ។ នេះគឺជាការរអាក់រអួលខ្លាំងណាស់ដូច្នេះមានរូបមន្តពិបាកជាងដែលជួយកាត់បន្ថយការគណនាទៅនឹងពាក្យដំបូងនិងភាពខុសគ្នា៖

\ [((ក) _ (n)) = ((ក) _ (១)) + \ ខាងឆ្វេង (n-១ \ ស្តាំ) ឃ \]

ប្រាកដណាស់អ្នកបានជួបរូបមន្តនេះរួចហើយ។ ពួកគេចូលចិត្តផ្តល់ឱ្យវានៅក្នុងគ្រប់ប្រភេទនៃសៀវភៅយោងនិង reshebniks ។ ហើយនៅក្នុងសៀវភៅសិក្សាសមហេតុផលណាមួយលើគណិតវិទ្យានាងបានជាប់ចំណាត់ថ្នាក់លេខ ១ ។

ទោះយ៉ាងណាក៏ដោយខ្ញុំស្នើឱ្យយើងអនុវត្តបន្តិចបន្តួច។

បញ្ហាលេខ ១ ។ សរសេរពាក្យបីដំបូងនៃវឌ្នភាពនព្វន្ធ $ \ left (((a) _ (n)) \ right) $, ប្រសិនបើ $ ((a) _ (1)) = 8, d = -5 $ ។

ដំណោះស្រាយ។ ដូច្នេះយើងដឹងពីពាក្យដំបូង $ ((a) _ (1)) = 8 $ និងភាពខុសគ្នានៃដំណើរការ $ d = -5 $ ។ ចូរយើងប្រើរូបមន្តដែលបានផ្តល់និងជំនួស $ n = 1 $, $ n = 2 $ និង $ n = 3 $៖

\ [\ ចាប់ផ្តើម (តម្រឹម) & ((ក) _ (n)) = ((ក) _ (១)) + \ ខាងឆ្វេង (n-១ \ ស្តាំ) ឃ; \\ & ((ក) _ (១)) = ((ក) _ (១)) + \ ខាងឆ្វេង (១-១ \\ ស្តាំ) ឃ = ((ក) _ (១)) = ៨; \\ & ((ក) _ (២)) = ((ក) _ (១)) + \ ឆ្វេង (២-១ \\ ស្តាំ) ឃ = ((ក) _ (១)) + ឃ = ៨-៥ = ៣; \\ & ((ក) _ (៣)) = ((ក) _ (១)) + \ ខាងឆ្វេង (៣-១ \\ ស្តាំ) ឃ = ((ក) _ (១)) + ២ ឃ = ៨-១០ = -២ ។ \\ \\ បញ្ចប់ (តម្រឹម) \\]

ចម្លើយ៖ (៨; ៣; −២)

អស់ហើយ! សូមកត់សម្គាល់៖ វឌ្នភាពរបស់យើងកំពុងថយចុះ។

ជាការពិត $ n = 1 $ មិនអាចជំនួសបានទេ - ពាក្យដំបូងត្រូវបានគេស្គាល់យើងរួចហើយ។ ទោះយ៉ាងណាក៏ដោយការជំនួសមួយយើងបានធ្វើឱ្យប្រាកដថារូបមន្តរបស់យើងមានប្រសិទ្ធភាពសូម្បីតែសម្រាប់ពាក្យដំបូង។ នៅក្នុងករណីផ្សេងទៀតវាទាំងអស់បានធ្លាក់ចុះទៅជានព្វន្ធតូចតាច។

បញ្ហាលេខ ២ ។ សរសេរពាក្យបីដំបូងនៃវឌ្នភាពនព្វន្ធបើអាណត្តិទី ៧ របស់វាគឺ −៤០ ហើយអាណត្តិទី ១៧ គឺ −៥០ ។

ដំណោះស្រាយ។ ចូរយើងសរសេរអំពីស្ថានភាពនៃបញ្ហានៅក្នុងលក្ខខណ្ឌធម្មតា៖

\ [((ក) _ (៧)) = - ៤០; \ quad ((ក) _ (១៧)) = - ៥០. \]

\ [ឆ្វេង \ (\ ចាប់ផ្តើម (តម្រឹម) & ((ក) _ (៧)) = ((ក) _ (១)) + ៦ ឃ \\ & ((ក) _ (១៧)) = ((ក) _ (១)) + ១៦ ឌី \\ \\ បញ្ចប់ (តម្រឹម) \\ ស្តាំ។ ]

\ [ឆ្វេង \ (\ ចាប់ផ្តើម (តម្រឹម) & ((ក) _ (១)) + ៦ ឃ = -៤០ \\ & ((ក) _ (១)) + ១៦ ឃ = -៥០ \\ បញ្ចប់ (តម្រឹម) ត្រឹមត្រូវហើយ។ ]

ខ្ញុំដាក់សញ្ញានៃប្រព័ន្ធពីព្រោះតម្រូវការទាំងនេះត្រូវតែបំពេញក្នុងពេលដំណាលគ្នា។ ហើយឥឡូវនេះសូមកត់សម្គាល់ថាប្រសិនបើយើងដកទីមួយចេញពីសមីការទីពីរ (យើងមានសិទ្ធិធ្វើដូចនេះដោយសារយើងមានប្រព័ន្ធ) យើងទទួលបាននេះ៖

\ [\ ចាប់ផ្តើម (តម្រឹម) & ((ក) _ (១)) + ១៦ ឌី- \\ ឆ្វេង (((ក) _ (១)) + ៦ ឃ \\ ស្តាំ) =- ៥០- \ ឆ្វេង (-៤០ \\ ស្តាំ); \\ & ((ក) _ (១)) + ១៦ ឃ - ((ក) _ (១)) - ៦ ឃ = -៥០ + ៤០; \\ & 10d = -10; \\ & ឃ = -1 ។ \\ \\ បញ្ចប់ (តម្រឹម) \\]

នោះហើយជារបៀបងាយស្រួលដែលយើងរកឃើញភាពខុសប្លែកគ្នានៅក្នុងដំណើរការនេះ! វានៅសល់ដើម្បីជំនួសលេខដែលរកឃើញទៅក្នុងសមីការណាមួយនៃប្រព័ន្ធ។ ឧទាហរណ៍នៅក្នុងទីមួយ៖

\ [\ ចាប់ផ្តើម (ម៉ាទ្រីស) ((ក) _ (១)) + ៦ ឃ = -៤០; \ quad ឃ = ១ -1 \\ \\ ចុះក្រោម \\ ((ក) _ (១)) -៦ = -៤០; \\ ((ក) _ (១)) = - ៤០ + ៦ = -៣៤ ។ \\ \\ បញ្ចប់ (ម៉ាទ្រីស) \\]

ឥឡូវនេះដោយដឹងពីពាក្យទីមួយនិងភាពខុសគ្នាវានៅតែត្រូវស្វែងរកពាក្យទីពីរនិងទីបី៖

\ [\ ចាប់ផ្តើម (តម្រឹម) & ((ក) _ (២)) = ((ក) _ (១)) + ឃ = -៣៤-១ = -៣៥; \\ & ((ក) _ (៣)) = ((ក) _ (១)) + ២ ឃ = -៣៤-២ = = -៣៦ ។ \\ \\ បញ្ចប់ (តម្រឹម) \\]

រួចរាល់ហើយ! បញ្ហាត្រូវបានដោះស្រាយ។

ចម្លើយ៖ (-៣៤; -៣៥; -៣៦)

យកចិត្តទុកដាក់លើលក្ខណៈគួរឱ្យចាប់អារម្មណ៍នៃវឌ្នភាពដែលយើងបានរកឃើញ៖ ប្រសិនបើយើងយកលក្ខខណ្ឌ $ n $ th និង $ m $ th ហើយដកវាចេញពីគ្នាបន្ទាប់មកយើងទទួលបានភាពខុសគ្នានៃការវិវត្តគុណនឹងលេខ $ n-m $៖

\ [((a) _ (n)) - ((a) _ (m)) = d \ cdot \ ឆ្វេង (n -m \ right) \]

ទ្រព្យសម្បត្តិសាមញ្ញប៉ុន្តែមានប្រយោជន៍ខ្លាំងដែលអ្នកគួរដឹង - ដោយមានជំនួយពីវាអ្នកអាចបង្កើនល្បឿនដំណោះស្រាយបញ្ហាជាច្រើនដែលកំពុងដំណើរការ។ នេះគឺជាឧទាហរណ៍សំខាន់៖

បញ្ហាលេខ ៣ ។ អាណត្តិទី ៥ នៃការវិវត្តនព្វន្ធគឺ ៨.៤ ហើយអាណត្តិទី ១០ គឺ ១៤.៤ ។ រករយៈពេលទីដប់ប្រាំនៃការវិវត្តនេះ។

ដំណោះស្រាយ។ ចាប់តាំងពី $ ((a) _ (5)) = 8.4 $, $ ((a) _ (10)) = 14.4 $ ហើយអ្នកត្រូវរក $ ((a) _ (15)) $ បន្ទាប់មកយើងកត់សំគាល់ដូចខាងក្រោម ៖

\ [\ ចាប់ផ្តើម (តម្រឹម) & ((ក) _ (១៥)) - ((ក) _ (១០)) = ៥ ឃ; \\ & ((ក) _ (១០)) - ((ក) _ (៥)) = ៥ ឃ។ \\ \\ បញ្ចប់ (តម្រឹម) \\]

ប៉ុន្តែតាមលក្ខខណ្ឌ $ ((a) _ (10)) - ((a) _ (5)) = 14.4-8.4 = $ 6 ដូច្នេះ $ 5d = $ 6 មកពីណាយើងមាន៖

\ [\ ចាប់ផ្តើម (តម្រឹម) & ((ក) _ (១៥)) - ១៤.៤ = ៦; \\ & ((ក) _ (១៥)) = ៦ + ១៤.៤ = ២០.៤ ។ \\ \\ បញ្ចប់ (តម្រឹម) \\]

ចម្លើយ៖ ២០.៤

អស់ហើយ! យើងមិនចាំបាច់រៀបចំប្រព័ន្ធសមីការមួយចំនួនហើយគណនាពាក្យដំបូងនិងភាពខុសគ្នានោះទេអ្វីគ្រប់យ៉ាងត្រូវបានដោះស្រាយត្រឹមតែពីរបីបន្ទាត់ប៉ុណ្ណោះ។

ឥឡូវនេះសូមពិចារណាអំពីប្រភេទការងារផ្សេងទៀត - ដើម្បីរកសមាជិកអវិជ្ជមាននិងវិជ្ជមាននៃការវិវត្ត។ វាគ្មានអ្វីជាអាថ៌កំបាំងទេដែលថាប្រសិនបើវឌ្increasesនភាពកើនឡើងខណៈពេលដែលពាក្យទីមួយអវិជ្ជមានបន្ទាប់មកពាក្យវិជ្ជមានមិនយូរមិនឆាប់នឹងលេចចេញមក។ ហើយផ្ទុយទៅវិញ៖ សមាជិកនៃការវិវត្តថយចុះនឹងឆាប់ឬក្រោយមកក្លាយជាអវិជ្ជមាន។

ក្នុងពេលជាមួយគ្នានេះវានៅឆ្ងាយពីការដែលអាចធ្វើទៅបានក្នុងពេលបច្ចុប្បន្ននេះ“ ឆ្ពោះទៅមុខ” តាមលំដាប់លំដោយតាមធាតុ។ ជារឿយៗបញ្ហាត្រូវបានរៀបចំឡើងតាមរបៀបដែលដោយមិនដឹងពីរូបមន្តការគណនានឹងមានសន្លឹកជាច្រើន - យើងនឹងងងុយគេងពេលយើងរកឃើញចម្លើយ។ ដូច្នេះយើងនឹងព្យាយាមដោះស្រាយបញ្ហាទាំងនេះឱ្យបានលឿន។

បញ្ហាលេខ ៤ ។ តើពាក្យអវិជ្ជមានប៉ុន្មាននៅក្នុងវឌ្ithនភាពនព្វន្ធ -៣៨.៥; −35.8; ... ?

ដំណោះស្រាយ។ ដូច្នេះ $ ((a) _ (1)) = - 38.5 $, $ ((a) _ (2)) = - 35.8 $, ពីកន្លែងដែលយើងរកឃើញភាពខុសគ្នាភ្លាមៗ៖

សូមកត់សម្គាល់ថាភាពខុសគ្នាគឺវិជ្ជមានដូច្នេះវឌ្នភាពកើនឡើង។ ពាក្យទីមួយគឺអវិជ្ជមានដូច្នេះនៅចំណុចខ្លះយើងពិតជានឹងជំពប់ដួលលើលេខវិជ្ជមាន។ សំណួរតែមួយគត់គឺថាតើវានឹងកើតឡើងនៅពេលណា។

តោះព្យាយាមស្វែងយល់ថាតើរយៈពេលប៉ុន្មាន (ឧទាហរណ៍រហូតដល់ចំនួនធម្មជាតិណា $ n $) ភាពអវិជ្ជមាននៃលក្ខខណ្ឌត្រូវបានរក្សាទុក៖

\ [\ ចាប់ផ្តើម (តម្រឹម) & ((ក) _ (n)) \ lt ០ \\ ព្រួញស្តាំ ((ក) _ (១)) + \ ខាងឆ្វេង (n-១ \ ស្តាំ) ឃ \ lt ០; \\ & -38.5+ \ ឆ្វេង (n -1 \ right) \ cdot 2.7 \ lt 0; \ quad \ left | \\ ស៊ីឌី ១០ \\ ស្តាំ។ \\ & -385 + 27 \\ cdot \\ ឆ្វេង (n -1 \\ ស្តាំ) \\ lt ០; \\ & -385 + 27n -27 \ lt 0; \\ & 27n \ lt ៤១២; \\ & n \\ lt ១៥ \ frac (៧) (២៧) \ ស្តាំព្រួញ ((n) _ (\ អតិបរមា)) = ១៥ ។ \\ \\ បញ្ចប់ (តម្រឹម) \\]

ខ្សែចុងក្រោយត្រូវការការពន្យល់ខ្លះ។ ដូច្នេះយើងដឹងថា $ n \ lt 15 \ frac (7) (27) $ ។ ម៉្យាងវិញទៀតយើងនឹងពេញចិត្តចំពោះតែចំនួនគត់នៃចំនួន (លើសពីនេះ៖ $ n \ in \ mathbb (N) $) ដូច្នេះចំនួនដែលអនុញ្ញាតធំបំផុតគឺពិតជា $ n = ១៥ $ ហើយដោយគ្មានន័យ ១៦ ។

បញ្ហាលេខ ៥ ។ ក្នុងការវិវត្តនព្វន្ធ $ (() _ (៥)) = - ១៥០, (() _ (៦)) = - ១៤៧ $ ។ រកចំនួនពាក្យវិជ្ជមានដំបូងនៃការវិវត្តនេះ។

វាពិតជាបញ្ហាដូចគ្នានឹងបញ្ហាមុនដែរប៉ុន្តែយើងមិនដឹង $ ((a) _ (1)) $ ទេ។ ប៉ុន្តែលក្ខខណ្ឌជិតខាងត្រូវបានគេដឹង៖ $ ((a) _ (5)) $ និង $ ((a) _ (6)) $ ដូច្នេះយើងអាចរកឃើញភាពខុសគ្នានៃការវិវត្តយ៉ាងងាយស្រួល៖

លើសពីនេះទៀតយើងនឹងព្យាយាមបង្ហាញពីអាណត្តិទី ៥ ទាក់ទងនឹងពាក្យទីមួយនិងភាពខុសគ្នាយោងតាមរូបមន្តស្តង់ដារ៖

\ [\ ចាប់ផ្តើម (តម្រឹម) & ((ក) _ (n)) = ((ក) _ (១)) + \ ខាងឆ្វេង (n-១ \ ស្តាំ) \ cdot ឃ; \\ & ((ក) _ (៥)) = ((ក) _ (១)) + ៤ ឃ; \\ & -150 = ((ក) _ (១)) + ៤ \\ ស៊ីឌី ៣; \\ & ((ក) _ (១)) = -១៥០-១២ = -១៦២ ។ \\ \\ បញ្ចប់ (តម្រឹម) \\]

ឥឡូវនេះយើងបន្តដោយភាពស្រដៀងគ្នាជាមួយភារកិច្ចមុន។ យើងស្វែងយល់ថាតើចំនុចណានៅក្នុងលំដាប់របស់យើងនឹងមានលេខវិជ្ជមាន៖

\ [\ ចាប់ផ្តើម (តម្រឹម) & ((ក) _ (n)) = - ១៦២+ \ ខាងឆ្វេង (n -១ \ ស្តាំ) \ cdot ៣ \ gt ០; \\ & -162 + 3n -3 \ gt 0; \\ & 3n \ gt 165; \\ & n \ gt 55 \ ស្តាំព្រួញ ((n) _ (\ នាទី)) = ៥៦ ។ \\ \\ បញ្ចប់ (តម្រឹម) \\]

ដំណោះស្រាយចំនួនគត់តូចបំផុតចំពោះវិសមភាពនេះគឺ ៥៦ ។

សូមកត់សម្គាល់៖ នៅក្នុងភារកិច្ចចុងក្រោយអ្វីៗទាំងអស់ត្រូវបានកាត់បន្ថយទៅជាវិសមភាពតឹងរ៉ឹងដូច្នេះជម្រើស $ n = ៥៥ $ នឹងមិនសមនឹងយើងទេ។

ឥឡូវនេះយើងបានរៀនពីវិធីដោះស្រាយបញ្ហាងាយៗចូរយើងបន្តទៅបញ្ហាដែលស្មុគស្មាញជាងនេះ។ ប៉ុន្តែជាដំបូងសូមយើងសិក្សាអំពីលក្ខណៈសម្បត្តិដែលមានប្រយោជន៍មួយទៀតនៃវឌ្នភាពនព្វន្ធដែលនាពេលអនាគតនឹងជួយសន្សំសំចៃពេលវេលាច្រើននិងកោសិកាមិនស្មើគ្នា។ :)

មធ្យមនព្វន្ធនិងការចូលបន្ទាត់ស្មើគ្នា

ពិចារណាសមាជិកជាប់គ្នាជាច្រើននៃការវិវត្តនព្វន្ធដែលកំពុងកើនឡើង $ \ left (((a) _ (n)) \ right) $ ។ តោះព្យាយាមសម្គាល់ពួកវានៅលើបន្ទាត់លេខ៖

សមាជិកនៃវឌ្នភាពនព្វន្ធនៅលើបន្ទាត់លេខ

ខ្ញុំបានកត់សម្គាល់ជាពិសេសនូវលក្ខខណ្ឌតាមអំពើចិត្ត $ ((a) _ (n-3)), ... , ((a) _ (n + 3)) $ មិនមែន $ ((a) _ (1)), \ ( (ក) _ (២)), \ ((ក) _ (៣)) $ ។ ល។ ពីព្រោះច្បាប់ដែលខ្ញុំនឹងនិយាយឥឡូវនេះដំណើរការដូចគ្នាចំពោះ“ ផ្នែក” ណាមួយ។

ហើយច្បាប់គឺសាមញ្ញណាស់។ ចូរយើងចងចាំរូបមន្តកើតឡើងដដែលៗហើយសរសេរវាទុកសម្រាប់សមាជិកដែលបានសម្គាល់ទាំងអស់៖

\ [\ ចាប់ផ្តើម (តម្រឹម) & ((ក) _ (n-២)) = ((ក) _ (n-៣)) + ឃ; \\ & ((a) _ (n-1)) = ((a) _ (n-2)) + ឃ; \\ & ((a) _ (n)) = ((a) _ (n-1)) + ឃ; \\ & ((ក) _ (n + ១)) = ((ក) _ (ន)) + ឃ; \\ & ((ក) _ (n + ២)) = ((ក) _ (n + ១)) + ឃ; \\ \\ បញ្ចប់ (តម្រឹម) \\]

ទោះយ៉ាងណាក៏ដោយភាពស្មើគ្នាទាំងនេះអាចត្រូវបានសរសេរខុសគ្នា៖

\ [\ ចាប់ផ្តើម (តម្រឹម) & ((ក) _ (n -១)) = ((ក) _ (n)) - ឃ; \\ & ((a) _ (n -2)) = ((a) _ (n)) - ២ ឃ; \\ & ((a) _ (n -3)) = ((a) _ (n)) - 3d; \\ & ((ក) _ (n + ១)) = ((ក) _ (ន)) + ឃ; \\ & ((ក) _ (n + ២)) = ((ក) _ (ន)) + ២ ឃ; \\ & ((a) _ (n + 3)) = ((a) _ (n)) + 3d; \\ \\ បញ្ចប់ (តម្រឹម) \\]

អញ្ចឹងអី? ហើយការពិតដែលថាពាក្យ $ ((a) _ (n-1)) $ និង $ ((a) _ (n + 1)) $ ស្ថិតនៅចម្ងាយដូចគ្នាពី $ ((a) _ (n)) $ ។ ហើយចម្ងាយនេះស្មើនឹង $ d $ ។ អាចនិយាយដូចគ្នាអំពីសមាជិក $ ((a) _ (n -2)) $ និង $ ((a) _ (n + 2)) $ - ពួកគេក៏ត្រូវបានដកចេញពី $ ((a) _ (n) ) $ ចម្ងាយដូចគ្នាស្មើនឹង ២ ឌី $ អ្នកអាចបន្តដោយគ្មានកំណត់ប៉ុន្តែអត្ថន័យត្រូវបានបង្ហាញយ៉ាងល្អដោយរូបភាព។

សមាជិកនៃវឌ្នភាពស្ថិតនៅចំងាយដូចគ្នាពីមជ្ឈមណ្ឌល

តើនេះមានន័យយ៉ាងណាចំពោះយើង? នេះមានន័យថាអ្នកអាចរកឃើញ $ ((a) _ (n)) $ ប្រសិនបើលេខជិតខាងត្រូវបានគេដឹង៖

\ [((a) _ (n)) = \ frac (((a) _ (n-1)) + ((ក) _ (n + ១))) (២) \]

យើងបានចេញសេចក្តីថ្លែងការណ៍ដ៏ល្អមួយ៖ រាល់សមាជិកនៃវឌ្ithនភាពនព្វន្ធគឺស្មើនឹងមធ្យមនព្វន្តនៃលក្ខខណ្ឌជិតខាង! លើសពីនេះទៅទៀត៖ យើងអាចបង្វែរពី $ ((a) _ (n)) $ ទៅឆ្វេងនិងស្តាំមិនមែនមួយជំហានទេប៉ុន្តែ $ k $ ជំហាន - ហើយរូបមន្តនៅតែត្រឹមត្រូវ៖

\ [((a) _ (n)) = \ frac (((a) _ (n-k)) + ((a) _ (n + k))) (២) \]

ទាំងនោះ។ យើងអាចរកបានយ៉ាងងាយស្រួល $ ((a) _ (150)) $ ប្រសិនបើយើងដឹងថា $ ((a) _ (100)) $ និង $ ((a) _ (200)) $ ព្រោះ $ ((a) _ (១៥០)) = \ frac (((ក) _ (១០០)) + ((ក) _ (២០០))) (២) $ ។ នៅ glance ដំបូងវាអាចហាក់ដូចជាការពិតនេះមិនផ្តល់ឱ្យយើងនូវអ្វីដែលមានប្រយោជន៍។ ទោះយ៉ាងណាក៏ដោយនៅក្នុងការអនុវត្តជាក់ស្តែងបញ្ហាជាច្រើនត្រូវបាន“ ធ្វើឱ្យច្បាស់” ជាពិសេសសម្រាប់ការប្រើប្រាស់មធ្យមនព្វន្ធ។ សូមក្រឡេកមើល៖

បញ្ហាលេខ ៦ ។ រកតម្លៃទាំងអស់នៃ $ x $ ដែលលេខ $ -6 ((x) ^ (២)) $, $ x + ១ $ និង ១៤ $ + ៤ ((x) ^ (២)) $ ជាសមាជិកជាប់គ្នា នៃវឌ្នភាពនព្វន្ធ (តាមលំដាប់លំដោយ)

ដំណោះស្រាយ។ ដោយសារលេខដែលបានចង្អុលបង្ហាញគឺជាសមាជិកនៃវឌ្នភាពលក្ខខណ្ឌនៃមធ្យមនព្វន្ធត្រូវបានគេពេញចិត្តចំពោះពួកគេ៖ ធាតុកណ្តាល $ x + 1 $ អាចត្រូវបានបញ្ជាក់ដោយផ្អែកលើធាតុដែលនៅជាប់គ្នា៖

\ [\ ចាប់ផ្តើម (តម្រឹម) & x + ១ = \ frac (-6 ((x) ^ (២)) + ១៤ + ៤ ((x) ^ (២))) (២); \\ & x + 1 = \ frac (១៤-២ ((x) ^ (២))) (២); \\ & x + 1 = 7 - ((x) ^ (2)); \\ & ((x) ^ (២)) + x-៦ = ០ ។ \\ \\ បញ្ចប់ (តម្រឹម) \\]

លទ្ធផលគឺជាសមីការត្រីកោណមាត្របុរាណ។ rootsសគល់របស់វា៖ $ x = ២ $ និង $ x = -3 $ - ទាំងនេះគឺជាចម្លើយ។

ចម្លើយ៖ −៣; ២ ។

បញ្ហាលេខ ៧ ។ រកតម្លៃ $$ ដែលលេខ $ -1; 4-3; (() ^ (២)) + ១ $ ធ្វើឱ្យមានការវិវត្តនព្វន្ធ (តាមលំដាប់នោះ) ។

ដំណោះស្រាយ។ ជាថ្មីម្តងទៀតយើងបង្ហាញពាក្យកណ្តាលទាក់ទងនឹងមធ្យមនព្វន្ធនៃពាក្យជិតខាង៖

\ [\ ចាប់ផ្តើម (តម្រឹម) & ៤x-៣ = \ frac (x-១ + ((x) ^ (២)) + ១) (២); \\ & 4x-3 = \ frac (((x) ^ (2)) + x) (2); \ quad \\ ឆ្វេង | \ cdot 2 \ ស្តាំ។ \\ & 8x-6 = ((x) ^ (2)) + x; \\ & ((x) ^ (២)) - ៧x + ៦ = ០ ។ \\ \\ បញ្ចប់ (តម្រឹម) \\]

ជាថ្មីម្តងទៀតសមីការត្រីកោណ។ ហើយម្តងទៀតមានrootsសពីរ៖ $ x = ៦ $ និង $ x = ១ $ ។

ចម្លើយ៖ ១; ៦ ។

ប្រសិនបើនៅក្នុងដំណើរការដោះស្រាយបញ្ហាអ្នកទទួលបានលេខឃោរឃៅខ្លះឬអ្នកមិនប្រាកដទាំងស្រុងអំពីភាពត្រឹមត្រូវនៃចម្លើយដែលបានរកឃើញនោះមានបច្ចេកទេសអស្ចារ្យដែលអនុញ្ញាតឱ្យអ្នកពិនិត្យមើល៖ តើយើងដោះស្រាយបញ្ហាបានត្រឹមត្រូវទេ?

ឧទាហរណ៍នៅក្នុងបញ្ហាលេខ ៦ យើងបានទទួលចម្លើយ -៣ និង ២. តើធ្វើដូចម្តេចដើម្បីពិនិត្យមើលថាចម្លើយទាំងនេះត្រឹមត្រូវ? ចូរយើងគ្រាន់តែដោតពួកវាហើយមើលថាមានអ្វីកើតឡើង។ ខ្ញុំសូមរំលឹកអ្នកថាយើងមានលេខបី ($ -6 (() ^ (2)) $, $ + 1 $ និង $ 14 + 4 (() ^ (2)) $) ដែលត្រូវតែបង្កើតការវិវត្តនព្វន្ធ។ ជំនួស $ x = -3 $៖

\ [\ ចាប់ផ្តើម (តម្រឹម) & x = -3 \ ស្តាំព្រួញ \\ & -6 ((x) ^ (២)) = -៥៤; \\ & x + 1 = -2; \\ & ១៤ + ៤ ((x) ^ (២)) = ៥០ ។ \ បញ្ចប់ (តម្រឹម) \]

បានទទួលលេខ -៥៤; −2; ៥០ ដែលខុសគ្នាដោយ ៥២ ច្បាស់ជាការវិវត្តនព្វន្ធ។ រឿងដដែលកើតឡើងចំពោះ $ x = 2 $៖

\ [\ ចាប់ផ្តើម (តម្រឹម) & x = ២ \ ស្តាំព្រួញ \\ & -៦ ((x) ^ (២)) = - ២៤; \\ & x + 1 = 3; \\ & ១៤ + ៤ ((x) ^ (២)) = ៣០ ។ \ បញ្ចប់ (តម្រឹម) \]

ជាថ្មីម្តងទៀតការវិវត្តមួយប៉ុន្តែមានភាពខុសគ្នា ២៧ ។ ដូច្នេះបញ្ហាត្រូវបានដោះស្រាយយ៉ាងត្រឹមត្រូវ។ អ្នកដែលចាប់អារម្មណ៍អាចពិនិត្យមើលបញ្ហាទីពីរដោយខ្លួនឯងប៉ុន្តែខ្ញុំនឹងនិយាយភ្លាមៗថាអ្វីៗក៏ត្រឹមត្រូវនៅទីនោះដែរ។

ជាទូទៅខណៈពេលដែលដោះស្រាយបញ្ហាចុងក្រោយយើងបានឆ្លងកាត់ការពិតគួរឱ្យចាប់អារម្មណ៍មួយទៀតដែលត្រូវចងចាំផងដែរ៖

ប្រសិនបើលេខបីគឺដូចនេះលេខ ២ គឺជាមធ្យមនព្វន្តនៃលេខទីមួយនិងលេខចុងក្រោយបន្ទាប់មកលេខទាំងនេះបង្កើតបានជាការវិវត្តនព្វន្ធ។

នៅពេលអនាគតការយល់ដឹងអំពីសេចក្តីថ្លែងការណ៍នេះនឹងអនុញ្ញាតឱ្យយើងព្យញ្ជនៈ "បង្កើត" វឌ្នភាពចាំបាច់ដោយផ្អែកលើស្ថានភាពនៃបញ្ហា។ ប៉ុន្តែមុននឹងយើងឈានទៅរក“ សំណង់” បែបនេះយើងគួរតែយកចិត្តទុកដាក់លើការពិតមួយបន្ថែមទៀតដែលធ្វើតាមដោយផ្ទាល់ពីអ្វីដែលបានពិចារណារួចហើយ។

ការដាក់ជាក្រុមនិងផលបូកនៃធាតុ

ចូរយើងត្រលប់ទៅអ័ក្សលេខម្តងទៀត។ សូមឱ្យយើងកត់សំគាល់ថាមានសមាជិកជាច្រើននៃការវិវត្តដែលរវាងនោះប្រហែលជា។ មានសមាជិកជាច្រើនទៀត៖

បន្ទាត់លេខមាន ៦ ធាតុសម្គាល់

តោះព្យាយាមបង្ហាញ "កន្ទុយខាងឆ្វេង" ទាក់ទងនឹង $ ((a) _ (n)) $ និង $ d $ និង "កន្ទុយខាងស្តាំ" ទាក់ទងនឹង $ ((a) _ (k)) $ និង $ d $ ។ វាសាមញ្ញណាស់៖

\ [\ ចាប់ផ្តើម (តម្រឹម) & ((ក) _ (n + ១)) = ((ក) _ (n)) + ឃ; \\ & ((ក) _ (n + ២)) = ((ក) _ (ន)) + ២ ឃ; \\ & ((ក) _ (ខេ - ១)) = ((ក) _ (ខេ)) - ឃ; \\ & ((ក) _ (ក -២)) = ((ក) _ (ក)) - ២ ឃ។ \\ \\ បញ្ចប់ (តម្រឹម) \\]

ឥឡូវសូមកត់សំគាល់ថាផលបូកខាងក្រោមនេះស្មើគ្នា៖

\ [\ ចាប់ផ្តើម (តម្រឹម) & ((a) _ (n)) + ((a) _ (k)) = S; \\ & ((a) _ (n + 1)) + ((a) _ (k -1)) = ((a) _ (n)) + d + ((a) _ (k)) - ឃ = ស; \\ & ((a) _ (n + 2)) + ((a) _ (k -2)) = ((a) _ (n)) + 2d + ((a) _ (k)) - 2d = អេស \ បញ្ចប់ (តម្រឹម) \]

និយាយដោយសាមញ្ញប្រសិនបើយើងចាត់ទុកថាជាការចាប់ផ្តើមធាតុពីរនៃការវិវត្តដែលសរុបទាំងអស់គឺស្មើនឹងចំនួន $ S $ ហើយបន្ទាប់មកយើងចាប់ផ្តើមដើរចេញពីធាតុទាំងនេះក្នុងទិសដៅផ្ទុយគ្នា (ឆ្ពោះទៅរកគ្នាឬផ្ទុយទៅវិញដើម្បីរើចេញ) , បន្ទាប់មក ផលបូកនៃធាតុដែលយើងនឹងជំពប់ដួលនឹងស្មើនឹងផងដែរ$ S $ ។ នេះអាចត្រូវបានបង្ហាញយ៉ាងច្បាស់បំផុតតាមក្រាហ្វិក៖

ការចូលបន្ទាត់ស្មើគ្នាផ្តល់នូវចំនួនស្មើគ្នា

ការយល់ដឹងអំពីការពិតនេះនឹងអនុញ្ញាតឱ្យយើងដោះស្រាយបញ្ហាកម្រិតមូលដ្ឋានដែលស្មុគស្មាញជាងអ្វីដែលយើងបានពិចារណាខាងលើ។ ឧទាហរណ៍ដូចជា៖

បញ្ហាលេខ ៨ ។ កំណត់ភាពខុសគ្នានៃវឌ្នភាពនព្វន្ធដែលពាក្យទីមួយមាន ៦៦ ហើយផលនៃពាក្យទី ២ និងទីដប់ពីរគឺតូចបំផុត។

ដំណោះស្រាយ។ តោះសរសេរអ្វីគ្រប់យ៉ាងដែលយើងដឹង៖

\ [\ ចាប់ផ្តើម (តម្រឹម) & ((ក) _ (១)) = ៦៦; \\ & ឃ =? \\ & ((ក) _ (២)) \ cdot ((ក) _ (១២)) = \ នាទី។ \ បញ្ចប់ (តម្រឹម) \]

ដូច្នេះយើងមិនដឹងពីភាពខុសគ្នានៃការវិវត្ត $ d $ ទេ។ តាមពិតដំណោះស្រាយទាំងមូលនឹងត្រូវបានបង្កើតឡើងជុំវិញភាពខុសគ្នាពីព្រោះផលិតផល $ ((a) _ (2)) \ cdot ((a) _ (12)) $ អាចត្រូវបានសរសេរឡើងវិញដូចខាងក្រោម៖

\ [\ ចាប់ផ្តើម (តម្រឹម) & ((ក) _ (២)) = ((ក) _ (១)) + ឃ = ៦៦ + ឃ; \\ & ((ក) _ (១២)) = ((ក) _ (១)) + ១១ ឃ = ៦៦ + ១១ ឃ; \\ & ((ក) _ (២)) \\ ស៊ីឌី ((ក) _ (១២)) = \\ ឆ្វេង (៦៦ + ឃ \\ ស្តាំ) \\ ស៊ីឌី \\ ឆ្វេង (៦៦ + ១១ ឃ \\ ស្តាំ) = \\ & = ១១ \\ ស៊ីឌី \\ ឆ្វេង (ឃ + ៦៦ \\ ស្តាំ) \\ ស៊ីឌី \\ ឆ្វេង (ឃ + ៦ \\ ស្តាំ) ។ \ បញ្ចប់ (តម្រឹម) \]

សម្រាប់អ្នកដែលនៅក្នុងធុង៖ ខ្ញុំបានដកកត្តារួម ១១ ចេញពីវង់ក្រចកទីពីរ។ ដូច្នេះផលិតផលដែលស្វែងរកគឺជាអនុគមន៍ជ្រុងដែលទាក់ទងនឹងអថេរ $ d $ ។ ដូច្នេះសូមពិចារណាមុខងារ $ f \ left (d \ right) = 11 \ left (d + 66 \ right) \ left (d + 6 \ right) $ - ក្រាហ្វរបស់វានឹងជាប៉ារ៉ាបូលដែលមានសាខា ប្រសិនបើយើងពង្រីកតង្កៀបនោះយើងទទួលបាន៖

\ [\ ចាប់ផ្តើម (តម្រឹម) & f \ ឆ្វេង (ឃ \\ ស្តាំ) = ១១ \ ឆ្វេង (((ឃ) ^ (២)) + ៦៦d + ៦d + ៦៦ ស៊ីឌី ៦ \\ ស្តាំ) = \\ & = ១១ (( ឃ) ^ (២)) + ១១ ស៊ីឌី ៧២d + ១១ ស៊ីឌី ៦៦ ស៊ីឌី ៦ បញ្ចប់ (តម្រឹម) \]

ដូចដែលអ្នកបានឃើញហើយមេគុណនៅចំពោះមុខគឺ ១១ - នេះគឺជាចំនួនវិជ្ជមានដូច្នេះយើងពិតជាកំពុងដោះស្រាយជាមួយប៉ារ៉ាបូលដែលមានសាខា៖

ក្រាហ្វមុខងារត្រីកោណ - ប៉ារ៉ាបូល
សូមចំណាំ៖ ប៉ារ៉ាបូលនេះយកតម្លៃអប្បបរមារបស់វានៅចំណុចកំពូលរបស់វាជាមួយអេសស៊ីស៊ីសា $ ((ឃ) _ (០)) $ ។ ជាការពិតយើងអាចគណនាអាក់ស៊ីស៊ីសានេះតាមគ្រោងការណ៍ស្តង់ដារ (ក៏មានរូបមន្ត $ ((ឃ) _ (០)) = (- ខ) / (២ ក) \; $) ប៉ុន្តែវាសមហេតុផលជាង ដើម្បីកត់សម្គាល់ថាចំនុចកំពូលដែលចង់បានស្ថិតនៅលើស៊ីមេទ្រីអ័ក្សនៃប៉ារ៉ាបូលដូច្នេះចំនុច $ ((d) _ (0)) $ គឺស្មើគ្នាពីofសនៃសមីការ $ f \ left (d \ right) = 0 $:

\ [\ ចាប់ផ្តើម (តម្រឹម) & f \ ឆ្វេង (ឃ \\ ស្តាំ) = ០; \\ & ១១ \\ ស៊ីឌី \\ ឆ្វេង (ឃ + ៦៦ \\ ស្តាំ) \\ ស៊ីឌី \\ ឆ្វេង (ឃ + ៦ \\ ស្តាំ) = ០; \\ & ((ឃ) _ (១)) = - ៦៦; \ quad ((ឃ) _ (២)) = - ៦ ។ \\ \\ បញ្ចប់ (តម្រឹម) \\]

នោះហើយជាមូលហេតុដែលខ្ញុំមិនប្រញាប់បើកតង្កៀប៖ តាមទម្រង់ដើមrootsសគឺងាយស្រួលរកណាស់។ ដូច្នេះអេសស៊ីស៊ីស៊ីស្មើនឹងមធ្យមនព្វន្ធនៃលេខ −៦៦ និង −៦៖

\ [((ឃ) _ (០)) = \ frac (-៦៦-៦) (២) =-៣៦ \]

តើលេខដែលរកឃើញផ្តល់ឱ្យយើងអ្វីខ្លះ? ជាមួយវាផលិតផលដែលត្រូវការចំណាយលើតម្លៃតូចបំផុត (ដោយវិធីនេះយើងមិនបានរាប់ $ ((y) _ (\ min)) $ - យើងមិនត្រូវការនេះទេ) ។ ក្នុងពេលជាមួយគ្នានេះលេខនេះគឺជាភាពខុសគ្នារវាងការវិវត្តដំបូងពោលគឺឧ។ យើងបានរកឃើញចម្លើយ។ :)

ចម្លើយ៖ ៣៦

បញ្ហាលេខ ៩ ។ បញ្ចូលលេខបីនៅចន្លោះលេខ $ - \ frac (1) (2) $ និង $ - \ frac (1) (6) $ ដើម្បីឱ្យពួកគេរួមគ្នាជាមួយលេខដែលបានផ្តល់ឱ្យបង្កើតការវិវត្តនព្វន្ធ។

ដំណោះស្រាយ។ ជាទូទៅយើងត្រូវធ្វើលំដាប់លេខប្រាំដោយលេខដំបូងនិងលេខចុងក្រោយបានដឹងរួចមកហើយ។ ចូរបង្ហាញលេខដែលបាត់ដោយអថេរ $ x $, $ y $ និង $ z $៖

\ [\ ឆ្វេង (((ក) _ (ន)) ស្តាំ) = \ ខាងឆ្វេង \ ( - \ frac (១) (២); x; y; z; - \ frac (១) (៦) \\ ស្តាំ ) \]

សូមកត់សម្គាល់ថាលេខ $ y $ គឺជា“ កណ្តាល” នៃលំដាប់របស់យើងវាមានភាពស្មើគ្នាពីលេខទាំងពីរ $ x $ និង $ z $ និងពីលេខ $ - \ frac (១) (២) $ និង $ - \ frac (១) (៦) $ ។ ហើយប្រសិនបើនៅពេលនេះយើងមិនអាចទទួលបាន $ y $ ពីលេខ $ x $ និង $ z $ ទេនោះស្ថានភាពគឺខុសគ្នាជាមួយនឹងការបញ្ចប់នៃដំណើរការ។ ចងចាំមធ្យមនព្វន្ធ៖

ឥឡូវនេះដោយដឹងពី $ y $ យើងនឹងរកឃើញលេខដែលនៅសល់។ សូមកត់សម្គាល់ថា $ x $ ស្ថិតនៅចន្លោះលេខ $ - \ frac (1) (2) $ និង $ y = - \ frac (1) (3) $ ទើបតែរកឃើញ។ នោះហើយជាមូលហេតុដែល

ការវែកញែកស្រដៀងគ្នាយើងរកឃើញចំនួនដែលនៅសល់៖

រួចរាល់ហើយ! យើងរកឃើញលេខទាំងបី។ ចូរយើងសរសេរពួកវានៅក្នុងចម្លើយតាមលំដាប់ដែលពួកគេគួរតែត្រូវបានបញ្ចូលរវាងលេខដើម។

ចម្លើយ៖ $ - \ frac (៥) (១២); \ - \ frac (១) (៣); \ - \ frac (១) (៤) $

បញ្ហាលេខ ១០ ។ បញ្ចូលលេខជាច្រើនរវាងលេខ ២ និង ៤២ ដែលរួមជាមួយលេខទាំងនេះបង្កើតការវិវត្តនព្វន្ធប្រសិនបើអ្នកដឹងថាផលបូកនៃលេខទីមួយទីពីរនិងចុងក្រោយនៃលេខដែលបញ្ចូលគឺ ៥៦ ។

ដំណោះស្រាយ។ កិច្ចការដែលពិបាកជាងនេះទោះយ៉ាងណាត្រូវដោះស្រាយតាមគ្រោងការណ៍ដូចកិច្ចការមុន ៗ - តាមរយៈមធ្យមនព្វន្ធ។ បញ្ហាគឺយើងមិនដឹងច្បាស់ថាត្រូវបញ្ចូលលេខប៉ុន្មាន។ ដូច្នេះដើម្បីភាពជាក់លាក់សូមយើងសន្មត់ថាបន្ទាប់ពីបញ្ចូលអ្វីគ្រប់យ៉ាងនឹងមានលេខ $ n $ ពិតប្រាកដហើយលេខដំបូងគឺ ២ ហើយលេខចុងក្រោយគឺ ៤២ ។ ក្នុងករណីនេះវឌ្ithនភាពនព្វន្ធដែលចង់បានអាចត្រូវបានតំណាងដូចតទៅ៖

\ [\ ឆ្វេង ((ក) _ (ន)) ស្តាំ = \ ខាងឆ្វេង \ (២; (ក) _ (២)); ((ក) _ (៣)) ... ... ក) _ (n-១)) ៤២ ខាងស្តាំ \) \]

\ [((ក) _ (២)) + ((ក) _ (៣)) + ((ក) _ (n-១)) = ៥៦ \]

ទោះយ៉ាងណាក៏ដោយសូមកត់សម្គាល់ថាលេខ $ ((a) _ (2)) $ និង $ ((a) _ (n-1)) $ ត្រូវបានទទួលពីលេខ ២ និង ៤២ នៅគែមដោយមួយជំហានឆ្ពោះទៅរកគ្នា។ ពោលគឺ ... ទៅកណ្តាលនៃលំដាប់។ នេះមានន័យថា

\ [((ក) _ (២)) + ((ក) _ (ន -១)) = ២ + ៤២ = ៤៤ \]

ប៉ុន្តែបន្ទាប់មកកន្សោមដែលបានសរសេរខាងលើអាចត្រូវបានសរសេរឡើងវិញដូចខាងក្រោម៖

\ [\ ចាប់ផ្តើម (តម្រឹម) & ((ក) _ (២)) + ((ក) _ (៣)) + ((ក) _ (n-១)) = ៥៦; \\ & \\ ឆ្វេង (((ក) _ (២)) + ((ក) _ (ន -១)) ស្តាំ) + ((ក) _ (៣)) = ៥៦; \\ & ៤៤ + ((ក) _ (៣)) = ៥៦; \\ & ((ក) _ (៣)) = ៥៦-៤៤ = ១២ ។ \\ \\ បញ្ចប់ (តម្រឹម) \\]

ដោយដឹងពី $ ((a) _ (3)) $ និង $ ((a) _ (1)) $ យើងអាចរកឃើញភាពខុសគ្នានៃការវិវត្តយ៉ាងងាយស្រួល៖

\ [\ ចាប់ផ្តើម (តម្រឹម) & ((ក) _ (៣)) - ((ក) _ (១)) = ១២ - ២ = ១០; \\ & ((ក) _ (៣)) - ((ក) _ (១)) = \ ខាងឆ្វេង (៣-១ \\ ស្តាំ) \\ ស៊ីឌីឃ = ២ ឃ; \\ & ២ ឃ = ១០ \\ ព្រួញស្តាំឃ = ៥ ។ \\ \\ បញ្ចប់ (តម្រឹម) \\]

វានៅសល់តែដើម្បីស្វែងរកសមាជិកដែលនៅសល់៖

\ [\ ចាប់ផ្តើម (តម្រឹម) & ((ក) _ (១)) = ២; \\ & ((ក) _ (២)) = ២ + ៥ = ៧; \\ & ((ក) _ (៣)) = ១២; \\ & ((ក) _ (៤)) = ២ + ៣ \\ ស៊ីឌី ៥ = ១៧; \\ & ((ក) _ (៥)) = ២ + ៤ \\ ស៊ីឌី ៥ = ២២; \\ & ((ក) _ (៦)) = ២ + ៥ \\ ស៊ីឌី ៥ = ២៧; \\ & ((ក) _ (៧)) = ២ + ៦ \\ ស៊ីឌី ៥ = ៣២; \\ & ((ក) _ (៨)) = ២ + ៧ \\ ស៊ីឌី ៥ = ៣៧; \\ & ((ក) _ (៩)) = ២ + ៨ \\ ស៊ីឌី ៥ = ៤២; \\ \\ បញ្ចប់ (តម្រឹម) \\]

ដូច្នេះរួចទៅហើយនៅជំហានទី ៩ យើងនឹងទៅដល់ចុងខាងឆ្វេងនៃលំដាប់ - លេខ ៤២ ។ សរុបមកវាចាំបាច់ត្រូវបញ្ចូលតែ ៧ លេខ៖ ៧; ១២; ១៧; ២២; ២៧; ៣២; ៣៧ ។

ចម្លើយ៖ ៧; ១២; ១៧; ២២; ២៧; ៣២; ៣៧

បញ្ហាពាក្យជាមួយវឌ្នភាព

សរុបសេចក្តីខ្ញុំចង់ពិចារណាអំពីកិច្ចការសាមញ្ញ ៗ មួយចំនួន។ អញ្ចឹងតើសាមញ្ញប៉ុណ្ណា៖ សម្រាប់សិស្សភាគច្រើនដែលសិក្សាគណិតវិទ្យានៅសាលាហើយមិនបានអានអ្វីដែលបានសរសេរខាងលើភារកិច្ចទាំងនេះអាចមើលទៅដូចជាសំណប៉ាហាំង។ ទោះយ៉ាងណាក៏ដោយវាច្បាស់ណាស់ថាមានបញ្ហាបែបនេះដែលកើតមានឡើងនៅក្នុងកម្មវិធី OGE និង USE ក្នុងគណិតវិទ្យាដូច្នេះខ្ញុំសូមណែនាំអ្នកឱ្យស្គាល់ខ្លួនឯងជាមួយពួកគេ។

បញ្ហាលេខ ១១ ។ កងពលតូចបានផលិត ៦២ ផ្នែកនៅក្នុងខែមករាហើយនៅរៀងរាល់ខែបន្ទាប់វាផលិតបាន ១៤ ផ្នែកច្រើនជាងផ្នែកមុន។ តើក្រុមនេះផលិតបានប៉ុន្មានផ្នែកនៅខែវិច្ឆិកា?

ដំណោះស្រាយ។ ជាក់ស្តែងចំនួនផ្នែកដែលបានកំណត់ពេលដោយខែនឹងតំណាងឱ្យការវិវត្តនព្វន្ធកើនឡើង។ លើសពីនេះ៖

\ [\ ចាប់ផ្តើម (តម្រឹម) & ((ក) _ (១)) = ៦២; \ quad ឃ = ១៤; \\ & ((a) _ (n)) = ៦២+ \ ខាងឆ្វេង (n-១ \ ស្តាំ) \\ ស៊ីឌី ១៤. \\ \\ បញ្ចប់ (តម្រឹម) \]

ខែវិច្ឆិកាគឺជាខែទី ១១ នៃឆ្នាំដូច្នេះយើងត្រូវស្វែងរក $ ((a) _ (11)) $៖

\ [((ក) _ (១១)) = ៦២ + ១០ \ ស៊ីឌី ១៤ = ២០២ \]

ដូច្នេះផ្នែកចំនួន ២០២ នឹងត្រូវផលិតនៅខែវិច្ឆិកា។

បញ្ហាលេខ ១២ ។ សិក្ខាសាលាចងភ្ជាប់សៀវភៅបានចងក្រងសៀវភៅចំនួន ២១៦ ក្បាលនៅក្នុងខែមករាហើយនៅខែក្រោយវាចងបានសៀវភៅចំនួន ៤ ក្បាលច្រើនជាងសៀវភៅមុន។ តើសិក្ខាសាលាបានចងសៀវភៅប៉ុន្មាននៅខែធ្នូ?

ដំណោះស្រាយ។ ដូចគ្នាទាំងអស់:

$ \ ចាប់ផ្តើម (តម្រឹម) & ((ក) _ (១)) = ២១៦; \ quad ឃ = ៤; \\ & ((a) _ (n)) = ២១៦+ ខាងឆ្វេង (n-១ \\ ស្តាំ) \\ ស៊ីឌី ៤. \\ \\ បញ្ចប់ (តម្រឹម) $

ខែធ្នូគឺជាខែទី ១២ ចុងក្រោយនៃឆ្នាំដូច្នេះយើងកំពុងស្វែងរក $ ((a) _ (12)) $៖

\ [((ក) _ (១២)) = ២១៦ + ១១ \\ ស៊ីឌី ៤ = ២៦០ \\]

នេះគឺជាចម្លើយ - សៀវភៅចំនួន ២៦០ ក្បាលនឹងត្រូវចងនៅខែធ្នូ។

មែនហើយប្រសិនបើអ្នកបានអានមកដល់ពេលនេះខ្ញុំប្រញាប់ដើម្បីអបអរសាទរអ្នក៖ អ្នកបានឆ្លងកាត់“ វគ្គប្រយុទ្ធវ័យក្មេង” ដោយជោគជ័យក្នុងការវិវត្តនព្វន្ធ។ អ្នកអាចបន្តទៅមេរៀនបន្ទាប់ដោយសុវត្ថិភាពដែលយើងនឹងសិក្សារូបមន្តសម្រាប់ផលបូកនៃការវិវត្តក៏ដូចជាផលវិបាកសំខាន់និងមានប្រយោជន៍ខ្លាំងពីវា។

ឧទាហរណ៍លំដាប់ \ (២ \); \ (៥ \); \ (ប្រាំបី \); \ (ដប់មួយ \); \ (១៤ \) ... គឺជាវឌ្នភាពនព្វន្ធពីព្រោះធាតុបន្ទាប់នីមួយៗខុសគ្នាពីធាតុមុនបី (អាចទទួលបានពីធាតុមុនដោយបន្ថែមទ្រីប)

នៅក្នុងវឌ្នភាពនេះភាពខុសគ្នា \ (ឃ \) គឺវិជ្ជមាន (ស្មើនឹង \ (៣ \)) ហើយដូច្នេះពាក្យបន្ទាប់នីមួយៗធំជាងពាក្យមុន។ ការវិវត្តបែបនេះត្រូវបានគេហៅថា កំពុងកើនឡើង.

ទោះយ៉ាងណាក៏ដោយ \ (ឃ \) ក៏អាចជាអវិជ្ជមានផងដែរ។ ឧទាហរណ៍នៅក្នុងវឌ្ithនភាពនព្វន្ធ \ (១៦ \); \ (ដប់ \); \ (៤ \); \ (- ២ \); \ (- ៨ \) ... ភាពខុសគ្នានៃវឌ្\នភាព \ (ឃ \) គឺស្មើនឹងដក ៦ ។

ហើយក្នុងករណីនេះធាតុបន្ទាប់នីមួយៗនឹងតូចជាងធាតុមុន។ ការវិវត្តទាំងនេះត្រូវបានគេហៅថា ថយចុះ.

កំណត់សំគាល់ការវិវត្តនព្វន្ធ

វឌ្នភាពត្រូវបានបង្ហាញដោយអក្សរឡាតាំងតូចមួយ។

លេខបង្កើតការវិវត្តហៅវា សមាជិកនៃ(ឬធាតុ) ។

ពួកវាត្រូវបានបង្ហាញដោយអក្សរដូចគ្នានឹងការវិវត្តនព្វន្ធដែរប៉ុន្តែមានសន្ទស្សន៍ជាលេខស្មើនឹងចំនួនធាតុតាមលំដាប់លំដោយ។

ឧទាហរណ៍វឌ្នភាពនព្វន្ធ \ (a_n = \ left \ (2; 5; 8; 11; 14 ... \ right \) \) មានធាតុ \ (a_1 = 2 \); \ (a_2 = ៥ \); \ (a_3 = 8 \) និងបន្តទៀត។

និយាយម្យ៉ាងទៀតសម្រាប់វឌ្នភាព \ (a_n = \ ខាងឆ្វេង \ (២; ៥; ៨; ១១; ១៤ ... \ ស្តាំ \\) \)

ការដោះស្រាយបញ្ហាសម្រាប់វឌ្នភាពនព្វន្ធ

ជាគោលការណ៍ព័ត៌មានខាងលើគឺគ្រប់គ្រាន់រួចទៅហើយដើម្បីដោះស្រាយបញ្ហាស្ទើរតែទាំងអស់នៃការវិវត្តនព្វន្ធ (រួមទាំងព័ត៌មានដែលផ្តល់ជូននៅអូជីជី)

ឧទាហរណ៍ (OGE) ។ វឌ្នភាពនព្វន្ធត្រូវបានបញ្ជាក់ដោយលក្ខខណ្ឌ \ (b_1 = 7; d = 4 \) ។ រក \ (b_5 \) ។
ដំណោះស្រាយ៖

ចម្លើយ៖ \ (ខ _៥ = ២៣ \)

ឧទាហរណ៍ (OGE) ។ លក្ខខណ្ឌបីដំបូងនៃវឌ្នភាពនព្វន្ធត្រូវបានផ្តល់ឱ្យ៖ \ (៦២; ៤៩; ៣៦ ... \) រកតម្លៃនៃពាក្យអវិជ្ជមានដំបូងនៃការវិវត្តនេះ។
ដំណោះស្រាយ៖

	យើងត្រូវបានផ្តល់ធាតុដំបូងនៃលំដាប់ហើយយើងដឹងថាវាគឺជាការវិវត្តនព្វន្ធ។ នោះគឺធាតុនីមួយៗខុសគ្នាពីរបស់ជិតខាងដោយលេខដូចគ្នា។ ស្វែងយល់ថាមួយណាដកធាតុមុនចេញពីធាតុបន្ទាប់៖ \ (ឃ = ៤៩-៦២ = -១៣ \) ។
	ឥឡូវនេះយើងអាចស្តារវឌ្នភាពរបស់យើងទៅធាតុ (អវិជ្ជមានដំបូង) ដែលយើងត្រូវការ។
	រួចរាល់។ អ្នកអាចសរសេរចម្លើយ។

ចម្លើយ៖ $-3$

ឧទាហរណ៍ (OGE) ។ ធាតុជាប់ៗគ្នាជាច្រើននៃវឌ្នភាពនព្វន្ធត្រូវបានផ្តល់ឱ្យ៖ \ (… ៥; x; ១០; ១២.៥ ... \\) រកតម្លៃនៃធាតុដែលបង្ហាញដោយអក្សរ \ (x \) ។
ដំណោះស្រាយ៖

	ដើម្បីរក \ (x \) យើងត្រូវដឹងថាតើធាតុបន្ទាប់ខុសគ្នាពីធាតុមុនប៉ុណ្ណានិយាយពីភាពខុសគ្នានៃដំណើរការ។ ចូរយើងរកវាពីធាតុជិតខាងដែលគេស្គាល់ពីរ៖ \ (ឃ = ១២.៥-១០ = ២.៥ \\) ។
	ហើយឥឡូវនេះយើងរកឃើញអ្វីដែលចង់បានដោយគ្មានបញ្ហា៖ \ (x = 5 + 2.5 = 7.5 \) ។
	រួចរាល់។ អ្នកអាចសរសេរចម្លើយ។

ចម្លើយ៖ $7,5$.

ឧទាហរណ៍ (OGE) ។ វឌ្នភាពនព្វន្ធត្រូវបានបញ្ជាក់ដោយលក្ខខណ្ឌដូចខាងក្រោម៖ \ (a_1 = -11 \); \ (a_ (n + 1) = a_n + 5 \) រកផលបូកនៃលក្ខខណ្ឌ ៦ ដំបូងនៃវឌ្នភាពនេះ។
ដំណោះស្រាយ៖

យើងត្រូវស្វែងរកផលបូកនៃលក្ខខណ្ឌ ៦ ដំបូងនៃវឌ្នភាព។ ប៉ុន្តែយើងមិនដឹងពីអត្ថន័យរបស់វាទេយើងត្រូវបានផ្តល់ឱ្យតែធាតុទីមួយប៉ុណ្ណោះ។ ដូច្នេះដំបូងយើងគណនាតម្លៃតាមវេនដោយប្រើដែលបានផ្តល់ឱ្យយើង៖

\ (n = ១ \); \ (a_ (1 + 1) = a_1 + 5 = -11 + 5 = -6 \)
\ (n = ២ \); \ (a_ (2 + 1) = a_2 + 5 = -6 + 5 = -1 \)
\ (n = ៣ \); \ (a_ (3 + 1) = a_3 + 5 = -1 + 5 = 4 \)
ហើយដោយបានគណនាធាតុទាំង ៦ ដែលយើងត្រូវការយើងរកឃើញផលបូករបស់វា។

\ (S_6 = a_1 + a_2 + a_3 + a_4 + a_5 + a_6 = \)
$=(-11)+(-6)+(-1)+4+9+14=9$

ចំនួនដែលអ្នកកំពុងស្វែងរកត្រូវបានរកឃើញ។

ចម្លើយ៖ \ (ស _៦ = ៩ \) ។

ឧទាហរណ៍ (OGE) ។ នៅក្នុងវឌ្នភាពនព្វន្ធ \ (a_ (១២) = ២៣ \); \ (a_ (១៦) = ៥១ \) ។ រកភាពខុសគ្នារវាងវឌ្នភាពនេះ។
ដំណោះស្រាយ៖

ចម្លើយ៖ \ (ឃ = ៧ \) ។

រូបមន្តវឌ្ithនភាពនព្វន្ធសំខាន់

ដូចដែលអ្នកបានឃើញហើយបញ្ហាវិវត្តន៍នព្វន្ធជាច្រើនអាចត្រូវបានដោះស្រាយដោយគ្រាន់តែស្វែងយល់ពីចំណុចសំខាន់ដែលថាការវិវត្តនព្វន្ធគឺជាសង្វាក់នៃលេខហើយធាតុបន្ទាប់នីមួយៗនៅក្នុងខ្សែសង្វាក់នេះទទួលបានដោយបន្ថែមលេខដូចគ្នាទៅលេខមុន (ភាពខុសគ្នា នៃការវិវត្ត) ។

ទោះយ៉ាងណាក៏ដោយពេលខ្លះមានស្ថានភាពនៅពេលដែលវាមានការរអាក់រអួលខ្លាំងក្នុងការសម្រេចចិត្តថា“ ដាក់ក្បាល” ។ ឧទាហរណ៍ស្រមៃថានៅក្នុងឧទាហរណ៍ដំបូងយើងត្រូវរកមិនមែនធាតុទីប្រាំ \ (b_5 \) ទេប៉ុន្តែបីរយប៉ែតសិបប្រាំមួយ \ (b_ (៣៨៦) \) ។ តើវាជាអ្វីយើង \ (៣៨៥ \) គុណនឹង ៤? ឬស្រមៃថានៅក្នុងឧទាហរណ៍ចុងក្រោយអ្នកត្រូវរកផលបូកនៃធាតុចិតសិបបីដំបូង។ អ្នកនឹងត្រូវគេធ្វើទារុណកម្មដើម្បីរាប់ ...

ហេតុដូច្នេះក្នុងករណីបែបនេះពួកគេមិនដោះស្រាយ“ ក្បាលលើ” ទេប៉ុន្តែប្រើរូបមន្តពិសេសដែលទទួលបានសម្រាប់ការវិវត្តនព្វន្ធ។ ហើយរូបមន្តសំខាន់គឺរូបមន្តសម្រាប់រយៈពេលទីប្រាំនៃការវិវត្តនិងរូបមន្តសម្រាប់ផលបូក \ (n \) នៃពាក្យដំបូង។

រូបមន្ត \ (n \) - សមាជិកទី៖ \ (a_n = a_1 + (n -1) d \) ដែល \ (a_1 \) គឺជាពាក្យដំបូងនៃការវិវត្ត
\ (n \) - ចំនួនធាតុដែលកំពុងស្វែងរក
\ (a_n \) គឺជាសមាជិកនៃវឌ្នភាពដែលមានលេខ \ (n \) ។

រូបមន្តនេះអនុញ្ញាតឱ្យយើងស្វែងរកយ៉ាងឆាប់រហ័សយ៉ាងហោចណាស់បីរយសូម្បីតែធាតុទី ១ ដោយដឹងតែដំបូងនិងភាពខុសគ្នានៃការវិវត្ត។

ឧទាហរណ៍។ វឌ្នភាពនព្វន្ធត្រូវបានបញ្ជាក់ដោយលក្ខខណ្ឌ៖ \ (b_1 = -159 \); \ (ឃ = ៨.២ \) ។ រក \ (ខ _ (២៤៦) \) ។
ដំណោះស្រាយ៖

ចម្លើយ៖ \ (ខ _ (២៤៦) = ១៨៥០ \) ។

រូបមន្តសម្រាប់ផលបូកនៃលក្ខខណ្ឌ n ដំបូង៖ \ (S_n = \ frac (a_1 + a_n) (២) \ cdot n \) ដែល

\ (a_n \) - ពាក្យសរុបចុងក្រោយ;

ឧទាហរណ៍ (OGE) ។ វឌ្នភាពនព្វន្ធត្រូវបានបញ្ជាក់ដោយលក្ខខណ្ឌ \ (a_n = 3,4n-0,6 \) ។ រកផលបូកនៃសមាជិក \ (២៥ \) ដំបូងនៃការវិវត្តនេះ។
ដំណោះស្រាយ៖

\ (S_ (២៥) = \) \ (\ frac (a_1 + a_ (២៥)) (២) \) \ (\\ ស៊ីឌី ២៥ \\)		ដើម្បីគណនាផលបូកនៃធាតុម្ភៃប្រាំដំបូងយើងត្រូវដឹងពីតម្លៃនៃពាក្យទីមួយនិងម្ភៃប្រាំ។ វឌ្នភាពរបស់យើងត្រូវបានផ្តល់ដោយរូបមន្តនៃពាក្យទីអាស្រ័យលើចំនួនរបស់វា (សូមមើលព័ត៌មានលំអិត) ។ ចូរគណនាធាតុទីមួយដោយជំនួសមួយសម្រាប់ \ (n \) ។
\ (n = ១; \) \ (a_1 = ៣.៤ ១-០.៦ = ២.៨ \)		ឥឡូវនេះយើងរកឃើញពាក្យទីម្ភៃប្រាំជំនួសដោយម្ភៃប្រាំជំនួសឱ្យ \ (n \) ។
\ (n = ២៥; \) \ (a_ (២៥) = ៣.៤ ២៥-០.៦ = ៨៤.៤ \)		មែនហើយឥឡូវនេះយើងអាចគណនាចំនួនដែលត្រូវការដោយគ្មានបញ្ហា។
\ (S_ (២៥) = \) \ (\ frac (a_1 + a_ (២៥)) (២) \) \ (\\ ស៊ីឌី ២៥ = \) \\ (= \\) \\ (\\ frac (២.៨ + ៨៤.៤) (២) \\) \\ (\\ ស៊ីឌី ២៥ = \\) \\ (១០៩០ \\)		ចម្លើយគឺរួចរាល់។

ចម្លើយ៖ \ (អេស _ (២៥) = ១០៩០ \) ។

សម្រាប់ផលបូក \ (n \) នៃពាក្យដំបូងអ្នកអាចទទួលបានរូបមន្តផ្សេងទៀត៖ អ្នកគ្រាន់តែត្រូវការ \ (S_ (25) = \) \ (\ frac (a_1 + a_ (25)) (2) \) \ (\ cdot ២៥ \) ជំនួសឱ្យ \ (a_n \) ជំនួសរូបមន្តសម្រាប់វា \ (a_n = a_1 + (n-1) d \) ។ យើងទទួលបាន:

រូបមន្តសម្រាប់ផលបូកនៃលក្ខខណ្ឌ n ដំបូង៖ \ (S_n = \) \ (\ frac (2a_1 + (n-1) d) (2) \) \ (\ cdot n \) ដែល

\ (S_n \) - ផលបូកដែលត្រូវការ \ (n \) នៃធាតុទីមួយ;
\ (a_1 \) - ពាក្យសង្ខេបដំបូង;
\ (ឃ \) - ភាពខុសគ្នានៃវឌ្នភាព;
\ (n \) - ចំនួនធាតុនៅក្នុងផលបូក។

ឧទាហរណ៍។ រកផលបូកនៃ \ (៣៣ \) - អតីតសមាជិកនៃវឌ្ithនភាពនព្វន្ធ៖ \ (១៧ \); \ (១៥.៥ \); \ (ដប់បួន \) ...
ដំណោះស្រាយ៖

ចម្លើយ៖ \ (ស _ (៣៣) = - ២៣១ \) ។

បញ្ហាវិវត្តនព្វន្ធដែលស្មុគស្មាញជាង

ឥឡូវនេះអ្នកមានព័ត៌មានទាំងអស់ដែលអ្នកត្រូវការដើម្បីដោះស្រាយបញ្ហាវឌ្ithនភាពនព្វន្ធស្ទើរតែទាំងអស់។ យើងបញ្ចប់ប្រធានបទដោយពិចារណាលើបញ្ហាដែលអ្នកត្រូវការមិនត្រឹមតែអនុវត្តរូបមន្តប៉ុណ្ណោះទេប៉ុន្តែថែមទាំងគិតបន្តិច (ក្នុងគណិតវិទ្យាវាអាចមានប្រយោជន៍☺)

ឧទាហរណ៍ (OGE) ។ រកផលបូកនៃលក្ខខណ្ឌអវិជ្ជមានទាំងអស់នៃវឌ្នភាព៖ \ (- ១៩,៣ \); \ (-១៩ \); \ (- ១៨.៧ \) ...
ដំណោះស្រាយ៖

\ (S_n = \) \ (\ frac (2a_1 + (n-1) d) (2) \) \ (\ cdot n \)		ភារកិច្ចគឺស្រដៀងនឹងកិច្ចការមុន។ យើងចាប់ផ្តើមដោះស្រាយផងដែរ៖ ដំបូងយើងរកឃើញ \\ (ឃ \\) ។
\ (ឃ = a_2 -a_1 = -19 - ( - 19.3) = 0.3 \)		ឥឡូវនេះខ្ញុំនឹងជំនួស \ (ឃ \) នៅក្នុងរូបមន្តសម្រាប់ផលបូក ... ហើយនៅទីនេះមានការបកស្រាយបន្តិចបន្តួចលេចឡើង - យើងមិនដឹង \ (n \) ទេ។ និយាយម្យ៉ាងទៀតយើងមិនដឹងថាតើត្រូវការពាក្យប៉ុន្មានបន្ថែមទេ។ តើធ្វើដូចម្តេចដើម្បីស្វែងយល់? ចូរយើងគិត។ យើងនឹងឈប់បន្ថែមធាតុនៅពេលយើងទៅដល់ធាតុវិជ្ជមានដំបូង។ នោះគឺអ្នកត្រូវស្វែងយល់ពីចំនួនធាតុនេះ។ យ៉ាងម៉េច? ចូរយើងសរសេររូបមន្តសម្រាប់គណនាធាតុណាមួយនៃវឌ្ithនភាពនព្វន្ធៈ \ (a_n = a_1 + (n-1) d \) សម្រាប់ករណីរបស់យើង។
\ (a_n = a_1 + (n-1) ឃ \)
\ (a_n = -19.3 + (n -1) 0.3 \)		យើងត្រូវការ \ (a_n \) ធំជាងសូន្យ។ ចូរយើងស្វែងយល់ថាអ្វីដែល \ (n \) នេះនឹងកើតឡើង។
\ (- ១៩.៣+ (n-១) ០.៣> ០ \)
\ ((n-១) ០.៣> ១៩.៣ \) \ (\|៖ ០៣ \)		យើងបែងចែកផ្នែកទាំងពីរនៃវិសមភាពដោយ \ (០,៣ \) ។
\ (n-១> \) \ (\ frac (១៩,៣) (០,៣) \)		ផ្លាស់ទីដកមួយដោយចងចាំថាត្រូវផ្លាស់ប្តូរសញ្ញា
\ (n> \) \ (\ frac (១៩,៣) (០,៣) \) \ (+ ១ \)		យើងគណនា ...
\ (n> ៦៥.៣៣៣ ... \)		... ហើយវាប្រែថាធាតុវិជ្ជមានដំបូងនឹងមានលេខ \ (៦៦ \) ។ ដូច្នោះហើយអវិជ្ជមានចុងក្រោយមាន \ (n = 65 \) ។ ចូរយើងពិនិត្យមើលវាគ្រាន់តែក្នុងករណី។
\ (n = ៦៥; \) \ (a_ (៦៥) = -១៩.៣+ (៦៥-១) ០.៣ = -០.១ \) \ (n = ៦៦; \) \ (a_ (៦៦) = - ១៩.៣+ (៦៦-១) ០.៣ = ០.២ \)		ដូច្នេះយើងត្រូវបន្ថែមធាតុ \ (៦៥ \) ដំបូង។
\ (ស _ (៦៥) = \) \ (\ frac (២ \ cdot (-១៩.៣) + (៦៥-១) ០.៣) (២) \)\\ (\\ ស៊ីឌី ៦៥ \\) \\ (S_ (៦៥) = \\) \\ (( - ៣៨.៦ + ១៩.២) (២) \\) \\ (\\ ស៊ីឌី ៦៥ = -៦៣០.៥ \\)		ចម្លើយគឺរួចរាល់។

ចម្លើយ៖ \ (អេស _ (៦៥) = - ៦៣០.៥ \) ។

ឧទាហរណ៍ (OGE) ។ វឌ្នភាពនព្វន្ធត្រូវបានបញ្ជាក់ដោយលក្ខខណ្ឌ៖ \ (a_1 = -33 \); \ (a_ (n + 1) = a_n + 4 \) ។ រកផលបូកពីធាតុ \ (២៦ \) ដល់ \ (៤២ \) រួមបញ្ចូល។
ដំណោះស្រាយ៖

\ (a_1 = -33; \) \ (a_ (n + 1) = a_n + 4 \)	នៅក្នុងបញ្ហានេះអ្នកក៏ត្រូវរកផលបូកនៃធាតុដែរប៉ុន្តែមិនចាប់ផ្តើមពីដំបូងទេប៉ុន្តែមកពី \ (២៦ \) - ទី ចំពោះករណីបែបនេះយើងគ្មានរូបមន្តទេ។ តើត្រូវសម្រេចចិត្តយ៉ាងដូចម្តេច? ងាយស្រួល - ដើម្បីទទួលបានផលបូកពី \ (២៦ \) - ទីទៅ \ (៤២ \) - អូដំបូងអ្នកត្រូវរកផលបូកពី \ (១ \) - ទីទៅ \ (៤២ \) - អូហើយបន្ទាប់មកដកលេខចេញ ផលបូកពីវាដំបូងទៅ \ (២៥ \) - ទី (សូមមើលរូបភាព) ។
	ចំពោះវឌ្នភាពរបស់យើង \ (a_1 = -33 \) និងភាពខុសគ្នា \ (ឃ = ៤ \) (បន្ទាប់ពីទាំងអស់វាជាបួនដែលយើងបន្ថែមទៅធាតុមុនដើម្បីរកធាតុបន្ទាប់) ។ ដោយដឹងរឿងនេះយើងរកឃើញផលបូកនៃធាតុ \ (៤២ \) - yh ដំបូង។
\ (S_ (៤២) = \) \ (\ frac (២ \ cdot (-៣៣) + (៤២-១) ៤) (២) \)\ (\\ ស៊ីឌី ៤២ = \\) \ (= \) \ (\ frac (-៦៦ + ១៦៤) (២) \) \ (\ ស៊ីឌី ៤២ = ២០៥៨ \)	ឥឡូវផលបូកនៃធាតុ \ (២៥ \) ដំបូង។
\ (S_ (២៥) = \) \ (\ frac (២ \ cdot (-៣៣) + (២៥-១) ៤) (២) \)\ (\\ ស៊ីឌី ២៥ = \) \\ (= \\) \\ (\\ frac (-66 + 96) (2) \\) \\ (\\ ស៊ីឌី ២៥ = ៣៧៥ \\)	ទីបំផុតយើងគណនាចម្លើយ។
\\ (អេស = អេស (៤២) -អេស (២៥) = ២០៥៨-៣៧៥ = ១៦៨៣ \\)

ចម្លើយ៖ \ (ស = ១៦៨៣ \) ។

ចំពោះវឌ្នភាពនព្វន្ធមានរូបមន្តជាច្រើនទៀតដែលយើងមិនបានពិចារណានៅក្នុងអត្ថបទនេះដោយសារភាពមានប្រយោជន៍ជាក់ស្តែងទាប។ ទោះយ៉ាងណាក៏ដោយអ្នកអាចរកឃើញពួកគេយ៉ាងងាយស្រួល។

មាននរណាម្នាក់ប្រយ័ត្ននឹងពាក្យ“ វឌ្នភាព” ជាពាក្យស្មុគស្មាញពីសាខាគណិតវិទ្យាខ្ពស់។ ទន្ទឹមនឹងនេះការវិវត្តនព្វន្ធសាមញ្ញបំផុតគឺជាការងាររបស់ម៉ែត្រតាក់ស៊ី (ដែលពួកគេនៅតែមាន) ។ ហើយដើម្បីយល់ពីខ្លឹមសារ (ហើយនៅក្នុងគណិតវិទ្យាគ្មានអ្វីសំខាន់ជាង“ ការយល់ដឹងអំពីខ្លឹមសារ”) នៃលំដាប់នព្វន្ធគឺមិនពិបាកនោះទេដោយបានវិភាគគំនិតបឋមមួយចំនួន។

លំដាប់លេខគណិតវិទ្យា

វាជាទម្លាប់ក្នុងការដាក់ឈ្មោះស៊េរីលេខតាមលំដាប់លេខដែលលេខនីមួយៗមានលេខផ្ទាល់ខ្លួន។

ក ១ - សមាជិកដំបូងនៃលំដាប់;

និង ២ គឺជាសមាជិកទីពីរនៃលំដាប់។

និង ៧ គឺជាសមាជិកទី ៧ នៃលំដាប់។

និង n គឺជាសមាជិកទីប្រាំនៃលំដាប់;

ទោះយ៉ាងណាក៏ដោយយើងមិនចាប់អារម្មណ៍លើសំណុំនិងលេខតាមអំពើចិត្តទេ។ យើងនឹងផ្តោតការយកចិត្តទុកដាក់របស់យើងទៅលើលំដាប់លេខដែលតម្លៃនៃពាក្យទីប្រាំត្រូវបានផ្សារភ្ជាប់ជាមួយនឹងលេខធម្មតារបស់វាដោយការពឹងផ្អែកដែលអាចត្រូវបានបង្កើតយ៉ាងច្បាស់គណិតវិទ្យា។ និយាយម្យ៉ាងទៀត៖ តម្លៃលេខនៃលេខ n-th គឺជាមុខងារខ្លះរបស់ n ។

a - តម្លៃនៃសមាជិកនៃលំដាប់លេខមួយ;

n គឺជាលេខស៊េរីរបស់វា;

f (n) គឺជាអនុគមន៍ដែលលំដាប់នៅក្នុងលំដាប់លេខ n គឺជាអាគុយម៉ង់។

និយមន័យ

វាជាទម្លាប់ក្នុងការហៅការវិវត្តនព្វន្ធជាលំដាប់លេខដែលក្នុងនោះពាក្យបន្តបន្ទាប់នីមួយៗធំជាង (តិច) ជាងលេខមុនដោយលេខដូចគ្នា។ រូបមន្តសម្រាប់សមាជិកទី ៩ នៃលំដាប់នព្វន្ធមានដូចខាងក្រោម៖

a n - តម្លៃនៃសមាជិកបច្ចុប្បន្ននៃវឌ្នភាពនព្វន្ធ;

a n + 1 - រូបមន្តសម្រាប់លេខបន្ទាប់;

ឃ - ភាពខុសគ្នា (ចំនួនជាក់លាក់) ។

វាងាយស្រួលកំណត់ថាប្រសិនបើភាពខុសគ្នាជាវិជ្ជមាន (ឃ> ០) នោះពាក្យបន្តបន្ទាប់នីមួយៗនៃស៊េរីដែលកំពុងពិចារណានឹងធំជាងលេខមុនហើយការវិវត្តនព្វន្ធនឹងកើនឡើង។

នៅក្នុងក្រាហ្វខាងក្រោមវាងាយស្រួលមើលថាហេតុអ្វីបានជាលំដាប់លេខត្រូវបានគេហៅថា“ ឡើងលើ” ។

ក្នុងករណីដែលភាពខុសគ្នាគឺអវិជ្ជមាន (ឃ<0), каждый последующий член по понятным причинам будет меньше предыдущего, график прогрессии станет «уходить» вниз, арифметическая прогрессия, соответственно, будет именоваться убывающей.

តម្លៃនៃសមាជិកជាក់លាក់

ពេលខ្លះវាចាំបាច់ដើម្បីកំណត់ពីតម្លៃនៃសមាជិកតាមអំពើចិត្ត n នៃវឌ្ithនភាពនព្វន្ធ។ អ្នកអាចធ្វើដូចនេះដោយការគណនាតាមលំដាប់លំដោយនៃសមាជិកទាំងអស់នៃវឌ្នភាពនព្វន្ធដែលចាប់ផ្តើមពីដំបូងទៅលេខដែលចង់បាន។ ទោះយ៉ាងណាក៏ដោយផ្លូវនេះមិនតែងតែអាចទទួលយកបានទេឧទាហរណ៍វាចាំបាច់ក្នុងការស្វែងរកអត្ថន័យនៃសមាជិកប្រាំពាន់ឬប្រាំបីលាននាក់។ ការគណនាបែបប្រពៃណីនឹងចំណាយពេលយូរ។ ទោះយ៉ាងណាក៏ដោយការវិវត្តនព្វន្ធជាក់លាក់អាចត្រូវបានស៊ើបអង្កេតដោយប្រើរូបមន្តជាក់លាក់។ ក៏មានរូបមន្តសម្រាប់ពាក្យទីប្រាំផងដែរ៖ តម្លៃនៃសមាជិកណាមួយនៃវឌ្ithនភាពនព្វន្ធអាចត្រូវបានកំណត់ថាជាផលបូកនៃពាក្យទី ១ នៃវឌ្នភាពជាមួយនឹងភាពខុសគ្នានៃវឌ្,នភាពគុណនឹងចំនួនពាក្យដែលស្វែងរកបានថយចុះដោយ មួយ។

រូបមន្តគឺជាសកលសម្រាប់ទាំងការកើនឡើងនិងការវិវត្តថយចុះ។

ឧទាហរណ៍នៃការគណនាតម្លៃរបស់សមាជិកដែលបានផ្តល់ឱ្យ

ចូរយើងដោះស្រាយបញ្ហាដូចខាងក្រោមនៃការស្វែងរកតម្លៃនៃពាក្យទីប្រាំនៃវឌ្ithនភាពនព្វន្ធ។

លក្ខខណ្ឌ៖ មានការវិវត្តនព្វន្ធជាមួយប៉ារ៉ាម៉ែត្រ៖

ពាក្យទីមួយនៅក្នុងលំដាប់គឺ ៣;

ភាពខុសគ្នានៃស៊េរីលេខគឺ ១.២ ។

កិច្ចការ៖ អ្នកត្រូវស្វែងរកតម្លៃសមាជិក ២១៤ នាក់

ដំណោះស្រាយ៖ ដើម្បីកំណត់តម្លៃនៃពាក្យដែលបានផ្តល់យើងប្រើរូបមន្ត៖

a (n) = a1 + d (n-1)

ការជំនួសទិន្នន័យពីសេចក្តីថ្លែងការណ៍បញ្ហាទៅក្នុងកន្សោមយើងមាន៖

a (214) = a1 + d (n-1)

a (214) = 3 + 1.2 (214-1) = 258.6

ចម្លើយ៖ ពាក្យទី ២១៤ តាមលំដាប់លំដោយគឺ ២៥៨.៦ ។

គុណសម្បត្តិនៃវិធីសាស្ត្រគណនានេះគឺជាក់ស្តែង - ដំណោះស្រាយទាំងមូលចំណាយពេលមិនលើសពី ២ ជួរ។

ផលបូកនៃចំនួនសមាជិកដែលបានផ្តល់ឱ្យ

ជាញឹកញាប់នៅក្នុងស៊េរីនព្វន្ធដែលបានផ្តល់ឱ្យវាតម្រូវឱ្យកំណត់ផលបូកនៃតម្លៃនៃផ្នែកជាក់លាក់របស់វា។ នេះក៏មិនតម្រូវឱ្យមានការគណនាតម្លៃនៃពាក្យនីមួយៗហើយបន្ទាប់មកបូកសរុប។ វិធីសាស្រ្តនេះអាចអនុវត្តបានប្រសិនបើចំនួនពាក្យដែលត្រូវរកមានតិច។ ក្នុងករណីផ្សេងទៀតវាងាយស្រួលប្រើរូបមន្តខាងក្រោម។

ផលបូកនៃការវិវត្តនព្វន្ធពី ១ ដល់ n គឺស្មើនឹងផលបូកនៃសមាជិកទី ១ និងទី ៩ គុណនឹងចំនួនសមាជិក n និងចែកនឹងពីរ។ ប្រសិនបើនៅក្នុងរូបមន្តតម្លៃនៃពាក្យទី n ត្រូវបានជំនួសដោយកន្សោមពីកថាខណ្ឌមុននៃអត្ថបទយើងទទួលបាន៖

ឧទាហរណ៍នៃការគណនា

ឧទាហរណ៍ចូរយើងដោះស្រាយបញ្ហាមួយដោយមានលក្ខខណ្ឌដូចខាងក្រោម៖

ពាក្យដំបូងនៅក្នុងលំដាប់គឺសូន្យ;

ភាពខុសគ្នាគឺ ០.៥ ។

នៅក្នុងបញ្ហាអ្នកត្រូវកំណត់ផលបូកនៃសមាជិកនៃស៊េរីពីលេខ ៥៦ ដល់ ១០១ ។

ដំណោះស្រាយ។ ចូរប្រើរូបមន្តសម្រាប់កំណត់ផលបូកនៃការវិវត្ត៖

s (n) = (2 ∙ a1 + d ∙ (n-1)) ∙ n / 2

ដំបូងយើងកំណត់ផលបូកនៃតម្លៃនៃសមាជិក ១០១ នៃការវិវត្តដោយជំនួសទិន្នន័យនៃលក្ខខណ្ឌនៃបញ្ហារបស់ពួកគេទៅក្នុងរូបមន្ត៖

s 101 = (2 ∙ 0 + 0.5 ∙ (101-1)) ∙ 101/2 = 2 525

ជាក់ស្តែងដើម្បីស្វែងយល់ពីផលបូកនៃសមាជិកនៃវឌ្fromនភាពពីលេខ ៥៦ ដល់ ១០១ វាចាំបាច់ត្រូវដកអេស ៥៥ ពីអេស ១០១ ។

s 55 = (2 ∙ 0 + 0.5 ∙ (55-1)) ∙ 55/2 = 742.5

ដូច្នេះផលបូកនៃការវិវត្តនព្វន្ធសម្រាប់ឧទាហរណ៍នេះ៖

s 101 - s 55 = 2,525 - 742.5 = 1,782.5

ឧទាហរណ៍នៃការអនុវត្តជាក់ស្តែងនៃវឌ្នភាពនព្វន្ធ

នៅចុងបញ្ចប់នៃអត្ថបទចូរយើងត្រលប់ទៅឧទាហរណ៍នៃលំដាប់នព្វន្ធដែលបានផ្តល់ឱ្យក្នុងកថាខណ្ឌទីមួយ - តាក់ស៊ីម៉ែត្រ (ម៉ែត្រឡានតាក់ស៊ី) ។ សូមពិចារណាឧទាហរណ៍មួយ។

ជិះតាក់ស៊ី (ដែលរួមបញ្ចូលទាំងការរត់ ៣ គីឡូម៉ែត្រ) ត្រូវចំណាយ ៥០ រូប្លិ៍។ រាល់គីឡូម៉ែត្រជាបន្តបន្ទាប់ត្រូវបានបង់ក្នុងអត្រា ២២ រូប្លិ៍ / គីឡូម៉ែត្រ។ ចម្ងាយធ្វើដំណើរ ៣០ គីឡូម៉ែត្រ។ គណនាថ្លៃធ្វើដំណើរ។

1. សូមបោះចោល ៣ គីឡូម៉ែត្រដំបូងដែលតម្លៃនេះត្រូវបានរាប់បញ្ចូលក្នុងតម្លៃចុះចត។

៣០ - ៣ = ២៧ គ។ ម។

2. ការគណនាបន្ថែមគឺគ្មានអ្វីក្រៅពីការវិភាគលើស៊េរីលេខនព្វន្ធ។

លេខសមាជិក - ចំនួនគីឡូម៉ែត្រដែលបានធ្វើដំណើរ (ដកបីដំបូង) ។

តម្លៃសមាជិកគឺជាផលបូក។

ពាក្យទីមួយនៅក្នុងបញ្ហានេះនឹងស្មើនឹង ១ = ៥០ ភី។

ភាពខុសគ្នានៃវឌ្នភាពឃ = ២២ ភី។

លេខដែលយើងចាប់អារម្មណ៍គឺតម្លៃនៃពាក្យ (២៧ + ១) នៃវឌ្ithនភាពនព្វន្ធ - ការរាប់ថយក្រោយនៅចុងគីឡូម៉ែត្រទី ២៧ គឺ ២៧.៩៩៩ ... ... ២៨ គីឡូម៉ែត្រ។

a ២៨ = ៥០ + ២២ (២៨ - ១) = ៦៤៤

ការគណនាទិន្នន័យប្រតិទិនសម្រាប់រយៈពេលវែងតាមអំពើចិត្តគឺផ្អែកលើរូបមន្តពិពណ៌នាអំពីលំដាប់លេខជាក់លាក់។ ក្នុងវិស័យតារាសាស្ត្រប្រវែងនៃគន្លងគោចរគឺអាស្រ័យលើធរណីមាត្រអាស្រ័យលើចំងាយនៃរាងកាយសេឡេស្ទាលទៅពន្លឺ។ លើសពីនេះស៊េរីលេខផ្សេងៗគ្នាត្រូវបានប្រើដោយជោគជ័យនៅក្នុងស្ថិតិនិងផ្នែកគណិតវិទ្យាដែលបានអនុវត្តផ្សេងទៀត។

ប្រភេទលេខលំដាប់មួយទៀតគឺធរណីមាត្រ

ការវិវត្តធរណីមាត្រត្រូវបានកំណត់ដោយទំហំធំបើប្រៀបធៀបជាមួយនព្វន្ធអត្រានៃការផ្លាស់ប្តូរ។ វាមិនមែនជារឿងចៃដន្យទេដែលនៅក្នុងនយោបាយសង្គមវិទ្យាវេជ្ជសាស្ត្រពួកគេតែងតែនិយាយថាដំណើរការនេះមានការវិវឌ្ន៍ជាលំដាប់ដើម្បីបង្ហាញពីអត្រាខ្ពស់នៃការរីករាលដាលនៃបាតុភូតឧទាហរណ៍ជំងឺអំឡុងពេលមានជំងឺរាតត្បាត។

ពាក្យទី N នៃស៊េរីលេខធរណីមាត្រខុសគ្នាពីលេខមុនដែលវាត្រូវបានគុណនឹងចំនួនថេរមួយចំនួន - ភាគបែងឧទាហរណ៍ពាក្យទី ១ គឺ ១ ភាគបែងរៀងគ្នាគឺ ២ បន្ទាប់មក៖

n = 1: 1 ∙ 2 = 2

n = 2: 2 ∙ 2 = 4

n = 3: 4 ∙ 2 = 8

n = 4: 8 ∙ 2 = 16

n = 5: 16 ∙ 2 = 32,

b n - តម្លៃនៃសមាជិកបច្ចុប្បន្ននៃវឌ្នភាពធរណីមាត្រ;

b n + 1 - រូបមន្តនៃពាក្យបន្ទាប់នៃការវិវត្តធរណីមាត្រ;

q គឺជាភាគបែងនៃការវិវត្តធរណីមាត្រ (ចំនួនថេរ) ។

ប្រសិនបើក្រាហ្វនៃការវិវត្តនព្វន្ធគឺជាបន្ទាត់ត្រង់នោះធរណីមាត្រមួយគូររូបភាពខុសគ្នាបន្តិចបន្តួច៖

ដូចក្នុងករណីនព្វន្ធការវិវត្តធរណីមាត្រមានរូបមន្តសម្រាប់តម្លៃនៃពាក្យតាមអំពើចិត្ត។ រាល់ពាក្យ n-th នៃការវិវត្តធរណីមាត្រគឺស្មើនឹងផលបូកនៃពាក្យទីមួយដោយភាគបែងនៃការវិវត្តទៅជាថាមពល n កាត់បន្ថយដោយមួយ៖

ឧទាហរណ៍។ យើងមានវឌ្នភាពធរណីមាត្រដែលពាក្យទីមួយស្មើនឹង ៣ និងភាគបែងនៃការវិវត្តស្មើនឹង ១.៥ ស្វែងរកវឌ្នភាពទី ៥

b 5 = b 1 ∙ q (5-1) = 3 ∙ 1.5 4 = 15.1875

ផលបូកនៃចំនួនសមាជិកដែលបានផ្តល់ត្រូវបានគណនាតាមរបៀបដូចគ្នាដោយប្រើរូបមន្តពិសេស។ ផលបូកនៃលក្ខខណ្ឌ n ដំបូងនៃការវិវត្តធរណីមាត្រគឺស្មើនឹងភាពខុសគ្នារវាងផលបូកនៃពាក្យទីប្រាំនៃការវិវត្តនិងភាគបែងរបស់វានិងពាក្យទី ១ នៃការវិវត្តដែលបែងចែកដោយភាគបែងត្រូវបានកាត់បន្ថយដោយមួយ៖

ប្រសិនបើប៊ី n ត្រូវបានជំនួសដោយរូបមន្តដែលបានពិចារណាខាងលើតម្លៃនៃផលបូកនៃលក្ខខណ្ឌ n ដំបូងនៃស៊េរីលេខដែលបានពិចារណានឹងមានទម្រង់៖

ឧទាហរណ៍។ វឌ្នភាពធរណីមាត្រចាប់ផ្តើមដោយពាក្យទីមួយស្មើនឹង ១. ភាគបែងត្រូវបានកំណត់ស្មើ ៣. រកផលបូកនៃពាក្យ ៨ ដំបូង។

s8 = 1 ∙ (3 8 -1) / (3-1) = 3 280