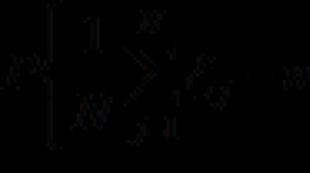თუ მითითებულია წესი, რომლის მიხედვითაც გარკვეული რიცხვი u ასოცირდება სიბრტყის (ან სიბრტყის ზოგიერთ ნაწილთან) ყოველ M წერტილთან, მაშინ ამბობენ, რომ სიბრტყეზე (ან სიბრტყის ნაწილზე) „წერტილის ფუნქცია არის მითითებული“; ფუნქციის სპეციფიკაცია სიმბოლურად გამოიხატება u=f(M) ფორმის ტოლობით. M წერტილთან ასოცირებულ რიცხვს u ეწოდება ამ ფუნქციის მნიშვნელობა M წერტილში. მაგალითად, თუ A არის ფიქსირებული წერტილი სიბრტყეზე, M არის თვითნებური წერტილი, მაშინ მანძილი A-დან M-მდე არის M წერტილის ფუნქცია. ამ შემთხვევაში, f(m)=AM .

მიეცეს რაიმე ფუნქცია u=f(M) და ამავე დროს შემოვიდეს კოორდინატთა სისტემა. მაშინ თვითნებური წერტილი M განისაზღვრება x, y კოორდინატებით. შესაბამისად, ამ ფუნქციის მნიშვნელობა M წერტილში განისაზღვრება x, y კოორდინატებით, ან, როგორც ამბობენ, u=f(M) არის ორი ცვლადის ფუნქცია x და y. ორი ცვლადის x და y ფუნქცია აღინიშნება სიმბოლოთ f(x; y): თუ f(M)=f(x;y), მაშინ ფორმულა u=f(x; y) ეწოდება ამის გამოსახულებას. ფუნქციონირებს შერჩეულ კოორდინატულ სისტემაში. ასე რომ, წინა მაგალითში f(M)=AM; თუ შემოვიყვანთ დეკარტის მართკუთხა კოორდინატთა სისტემას A წერტილის საწყისით, მივიღებთ ამ ფუნქციის გამოსახულებას:

u=sqrt(x^2 + y^2)

პრობლემა 3688 მოცემულია ფუნქცია f (x, y)=x^2–y^2–16.

მოცემულია f (x, y)=x^2–y^2–16 ფუნქცია. დაადგინეთ ამ ფუნქციის გამოხატულება ახალ კოორდინატულ სისტემაში, თუ კოორდინატთა ღერძები ბრუნავს –45 გრადუსიანი კუთხით.

პარამეტრული ხაზის განტოლებები

გარკვეული M წერტილის კოორდინატები ავღნიშნოთ x და y ასოებით; განვიხილოთ t არგუმენტის ორი ფუნქცია:

x=φ(t), y=ψ(t) (1)

როდესაც t იცვლება, x და y მნიშვნელობები, ზოგადად, შეიცვლება, შესაბამისად, წერტილი M გადავა. ტოლობები (1) ეწოდება პარამეტრული ხაზის განტოლებები, რომელიც არის M წერტილის ტრაექტორია; არგუმენტს t ეწოდება პარამეტრი. თუ პარამეტრი t შეიძლება გამოირიცხოს ტოლობებიდან (1), მაშინ ვიღებთ M წერტილის ტრაექტორიის განტოლებას სახით.

F ფორმის ტოლობა (x, y) = 0ეწოდება განტოლება ორ ცვლადში x, y,თუ ეს არ არის ჭეშმარიტი ყველა წყვილი რიცხვისთვის x, y.ორ რიცხვს ამბობენ x = x 0 , y=y 0, დააკმაყოფილოს ფორმის გარკვეული განტოლება F(x, y)=0,თუ ცვლადების ნაცვლად ამ რიცხვების ჩანაცვლებისას Xდა ზეგანტოლებაში მისი მარცხენა მხარე ქრება.

მოცემული წრფის განტოლება (განკუთვნილ კოორდინატულ სისტემაში) არის განტოლება ორი ცვლადით, რომელიც კმაყოფილდება ამ წრფეზე მდებარე ყველა წერტილის კოორდინატებით და არ კმაყოფილდება ყოველი წერტილის კოორდინატებით, რომლებიც არ დევს მასზე.

შემდეგში გამოთქმის ნაცვლად მოცემულია „წრფის განტოლება F(x, y) = 0" ჩვენ ხშირად ვიტყვით მოკლედ: მოცემული ხაზი F (x, y) = 0.

თუ მოცემულია ორი წრფის განტოლება F(x, y) = 0და Ф(x, y) = Q,შემდეგ სისტემის ერთობლივი გადაწყვეტა

იძლევა ყველა მათ გადაკვეთის წერტილებს. უფრო ზუსტად, რიცხვების თითოეული წყვილი, რომელიც წარმოადგენს ამ სისტემის ერთობლივ ამოხსნას, განსაზღვრავს ერთ-ერთ გადაკვეთის წერტილს.

*) იმ შემთხვევებში, როდესაც კოორდინატთა სისტემა არ არის დასახელებული, ვარაუდობენ, რომ იგი დეკარტის მართკუთხაა.

157. ქულები მოცემულია *) მ 1 (2; - 2), მ 2 (2; 2), მ 3 (2; - 1), მ 4 (3; -3), მ 5 (5; -5), მ 6 (3; -2). დაადგინეთ, რომელი გამოქვეყნებული წერტილები დევს განტოლებით განსაზღვრულ წრფეზე X+ y = 0,და რომელი არ წევს მასზე. რომელი ხაზი განისაზღვრება ამ განტოლებით? (დახაზეთ იგი ნახატზე.)

158. განტოლებით განსაზღვრულ წრფეზე X 2 +y 2 =25, იპოვეთ წერტილები, რომელთა აბსციები უდრის შემდეგ რიცხვებს: ა) 0, ბ) - 3, გ) 5, დ) 7; იმავე წრფეზე იპოვეთ წერტილები, რომელთა ორდინატები უდრის შემდეგ რიცხვებს: ე) 3, ვ) - 5, გ) - 8. რომელი წრფე განისაზღვრება ამ განტოლებით? (დახაზეთ იგი ნახატზე.)

159. დაადგინეთ რომელი წრფეებია განსაზღვრული შემდეგი განტოლებებით (ააგეთ ისინი ნახაზზე):

1) x - y = 0; 2) x + y = 0; 3) x- 2 = 0; 4) x+ 3 = 0;

5) y - 5 = 0; 6) წ+ 2 = 0; 7) x = 0; 8) წ = 0;

9) x 2 - xy = 0; 10) xy+ y 2 = 0; თერთმეტი) x 2 - წ 2 = 0; 12) xy= 0;

13) y 2 - 9 = 0; 14) xy 2 - 8xy+15 = 0; 15) y 2 +5y+4 = 0;

16) X 2 y - 7xy + 10წ = 0; 17) y =|x|; 18) x =|ზე|; 19)წ + |x|=0;

20) x +|ზე|= 0; 21)y =|X- 1|; 22) წ = |x+ 2|; 23) X 2 + ზე 2 = 16;

24) (x-2) 2 +(წ-1) 2 =16; 25) (x+ 5) 2 +(წ- 1) 2 = 9;

26) (X - 1) 2 + წ 2 = 4; 27) x 2 +(წ + 3) 2 = 1; 28) (x -3) 2 + წ 2 = 0;

29) X 2 + 2წ 2 = 0; 30) 2X 2 + 3წ 2 + 5 = 0

31) (x- 2) 2 + (წ + 3) 2 + 1=0.

160. მოცემული სტრიქონები:

1)X+ y = 0; 2)x - y = 0; 3) x 2 + წ 2 - 36 = 0;

4) x 2 +წ 2 -2x==0; 5) x 2 +წ 2 + 4x-6წ-1 =0.

დაადგინეთ რომელი მათგანი გადის საწყისზე.

161. მოცემული სტრიქონები:

1) x 2 + წ 2 = 49; 2) (x- 3) 2 + (წ+ 4) 2 = 25;

3) (x+ 6) 2 + (y - 3) 2 = 25; 4) ( x + 5) 2 + (y - 4) 2 = 9;

5) x 2 +წ 2 - 12x + 16y = 0; 6) x 2 +წ 2 - 2x + 8ზე+ 7 = 0;

7) x 2 +წ 2 - 6x + 4y + 12 = 0.

იპოვეთ მათი გადაკვეთის წერტილები: ა) ღერძთან ოჰ;ბ) ღერძით OU.

162.იპოვეთ ორი წრფის გადაკვეთის წერტილები;

1)X 2 +y 2 = 8, x-y = 0;

2) X 2 +y 2 -16x+4ზე+18 = 0, x + y= 0;

3) X 2 +y 2 -2x+4ზე -3 = 0, X 2 + y 2 = 25;

4) X 2 +y 2 -8x+10у+40 = 0, X 2 + y 2 = 4.

163. ქულები მოცემულია პოლარული კოორდინატთა სისტემაში

მ 1 (1; ), მ 2 (2; 0), მ 3 (2; )

მ 4 (
;) და მ 5 (1; )

დაადგინეთ, რომელი წერტილი დევს განტოლებით განსაზღვრულ წრფეზე პოლარულ კოორდინატებში  = 2 cos  და რომელი არ დევს მასზე. რომელი ხაზი განისაზღვრება ამ განტოლებით? (დახატე ნახატზე :)

164.  = განტოლებით განსაზღვრულ წრფეზე , იპოვეთ წერტილები, რომელთა პოლარული კუთხეები უდრის შემდეგ რიცხვებს: ა) ბ) - , გ) 0, დ) . რომელი ხაზი განისაზღვრება ამ განტოლებით?

(აშენეთ იგი ნახატზე.)

165.განტოლებით განსაზღვრულ წრფეზე  = იპოვეთ წერტილები, რომელთა პოლარული რადიუსი უდრის შემდეგ რიცხვებს: ა) 1, ბ) 2, გ)
. რომელი ხაზი განისაზღვრება ამ განტოლებით? (აშენეთ იგი ნახატზე.)

166. დაადგინეთ, რომელი წრფეებია განსაზღვრული პოლარულ კოორდინატებში შემდეგი განტოლებებით (ააგეთ ისინი ნახაზზე):

1)  = 5; 2)  = ; 3)  = ; 4)  cos  = 2; 5)  sin  = 1;

6)  = 6 cos ; 7)  = 10 ცოდვა ; 8) ცოდვა  = 9) ცოდვა  =

167. ააგეთ არქიმედეს შემდეგი სპირალები ნახაზზე:

1)  = 5, 2)  = 5; 3)  = ; 4)р = -1.

168. ააგეთ ნახატზე შემდეგი ჰიპერბოლური სპირალები:

1)  = ; 2) = ; 3) = ; 4) = - .

169. ააგეთ ნახაზზე შემდეგი ლოგარითმული სპირალები:

,
.

170. განსაზღვრეთ იმ მონაკვეთების სიგრძეები, რომლებშიც არქიმედეს სპირალი ჭრის

სხივი, რომელიც გამოდის პოლუსიდან და მიდრეკილია პოლარული ღერძისკენ კუთხით
. გააკეთე ნახატი.

171. არქიმედეს სპირალზე
აღებული წერტილი თან,რომლის პოლარული რადიუსი არის 47. დაადგინეთ რამდენ ნაწილად ჭრის ეს სპირალი წერტილის პოლარულ რადიუსს თან,გააკეთე ნახატი.

172. ჰიპერბოლურ სპირალზე
იპოვე წერტილი R,რომლის პოლარული რადიუსი არის 12. გააკეთე ნახატი.

173. ლოგარითმული სპირალზე
იპოვეთ Q წერტილი, რომლის პოლარული რადიუსია 81. გააკეთეთ ნახატი.

 სიბრტყეზე მოცემულია დეკარტის მართკუთხა კოორდინატთა სისტემა Oxy და გარკვეული წრფე L.

განმარტება. განტოლება F(x;y)=0 (1)დაურეკა წრფის განტოლებალ(მოცემული კოორდინატთა სისტემის მიმართ), თუ ეს განტოლება აკმაყოფილებს L წრფეზე მდებარე რომელიმე წერტილის x და y კოორდინატებს და არა L წრფეზე არ მდებარე რომელიმე წერტილის x და y კოორდინატებს.

რომ. ხაზი თვითმფრინავშიარის წერტილების ლოკუსი (M(x;y)), რომელთა კოორდინატები აკმაყოფილებს განტოლებას (1).

განტოლება (1) განსაზღვრავს L ხაზს.

მაგალითი. წრის განტოლება.

წრე– მოცემული M 0 წერტილიდან თანაბარი მანძილის მქონე წერტილების ერთობლიობა (x 0,y 0).

წერტილი M 0 (x 0,y 0) – წრის ცენტრი.

წრეზე მდებარე ნებისმიერი წერტილისთვის M(x;y), მანძილი MM 0 =R (R=const)

მმ 0 ==რ

(x-x 0 ) 2 + (ოჰ 0 ) 2 =რ 2 –(2) – R რადიუსის წრის განტოლება ცენტრით M 0 წერტილში (x 0,y 0).

წრფის პარამეტრული განტოლება.

მოდით, L წრფეზე წერტილების x და y კოორდინატები გამოვხატოთ t პარამეტრის გამოყენებით:

(3) – წრფის პარამეტრული განტოლება DSC-ში

სადაც (t) და (t) ფუნქციები უწყვეტია t პარამეტრის მიმართ (ამ პარამეტრის ვარიაციის გარკვეულ დიაპაზონში).

(3) განტოლებიდან t პარამეტრის გამოკლებით, ვიღებთ განტოლებას (1).

L წრფე მივიჩნიოთ, როგორც გზა, რომელსაც გადის მატერიალური წერტილი, რომელიც განუწყვეტლივ მოძრაობს გარკვეული კანონის მიხედვით. მოდით, t ​​ცვლადი წარმოადგენდეს დროს, რომელიც დათვლილია გარკვეული საწყისი მომენტიდან. მაშინ მოძრაობის კანონის სპეციფიკაცია წარმოადგენს მოძრავი წერტილის x და y კოორდინატების სპეციფიკაციას, როგორც t დროის x=(t) და y=(t) უწყვეტი ფუნქცია.

მაგალითი. გამოვიყვანოთ პარამეტრული განტოლება r>0 რადიუსის წრეზე, რომლის ცენტრი სათავეშია. მოდით M(x,y) იყოს ამ წრის თვითნებური წერტილი და t იყოს კუთხე რადიუსის ვექტორსა და Ox ღერძს შორის, დათვლილი საათის ისრის საწინააღმდეგოდ.

მაშინ x=r cos x y=r sin t. (4)

განტოლებები (4) არის განხილული წრის პარამეტრული განტოლებები. t პარამეტრს შეუძლია მიიღოს ნებისმიერი მნიშვნელობა, მაგრამ იმისათვის, რომ M(x,y) წერტილი ერთხელ შემოივლოს წრეზე, პარამეტრის ცვლილების დიაპაზონი შემოიფარგლება ნახევარსეგმენტით 0t2.

(4) განტოლებების კვადრატში და მიმატებით ვიღებთ წრის (2) ზოგად განტოლებას.

2. პოლარული კოორდინატთა სისტემა (psc).

მოდით ავირჩიოთ L ღერძი ( პოლარული ღერძი) და განსაზღვრეთ ამ ღერძის წერტილი O ( ბოძი). სიბრტყის ნებისმიერი წერტილი ცალსახად არის განსაზღვრული პოლარული კოორდინატები ρ და φ, სადაც

ρ – პოლარული რადიუსი, უდრის მანძილს M წერტილიდან O პოლუსამდე (ρ≥0);

φ – კუთხევექტორის მიმართულებას შორის OMდა L ღერძი ( პოლარული კუთხე). M(ρ ; φ )

ხაზის განტოლება UCS-შიშეიძლება დაიწეროს:

ρ=f(φ) (5) წრფის აშკარა განტოლება UCS-ში

F=(ρ; φ) (6) იმპლიციტური ხაზის განტოლება UCS-ში

წერტილის დეკარტისა და პოლარული კოორდინატების კავშირი.

(x;y) (ρ ; φ ) სამკუთხედიდან OMA:

tan φ=(კუთხის აღდგენაφ ცნობილის მიხედვითწარმოიქმნება ტანგენსიიმის გათვალისწინებით, რომელ კვადრატში მდებარეობს M წერტილი).(ρ ; φ ) (x;y). x=ρcosφ,y=ρsinφ

მაგალითი . იპოვეთ M(3;4) და P(1;-1) წერტილების პოლარული კოორდინატები.

M-სთვის:=5, φ=arctg (4/3). P-სთვის: ρ=; φ=Π+arctg(-1)=3Π/4.

ბრტყელი ხაზების კლასიფიკაცია.

განმარტება 1.ხაზი ე.წ ალგებრული,თუ რომელიმე დეკარტის მართკუთხა კოორდინატულ სისტემაში, თუ იგი განისაზღვრება F(x;y)=0 (1) განტოლებით, რომელშიც ფუნქცია F(x;y) არის ალგებრული მრავალწევრი.

განმარტება 2.ყოველი არაალგებრული წრფე ეწოდება ტრანსცენდენტული.

განმარტება 3. ალგებრული ხაზი ე.წ შეკვეთის ხაზინ, თუ რომელიმე დეკარტის მართკუთხა კოორდინატულ სისტემაში ეს წრფე განისაზღვრება (1) განტოლებით, რომელშიც ფუნქცია F(x;y) არის n-ე ხარისხის ალგებრული პოლინომი.

ამრიგად, n-ე რიგის წრფე არის ხაზი, რომელიც განსაზღვრულია ზოგიერთ დეკარტის მართკუთხა სისტემაში n ხარისხის ალგებრული განტოლებით ორი უცნობით.

შემდეგი თეორემა ხელს უწყობს განმარტებების სისწორის დადგენას 1,2,3.

თეორემა(დოკუმენტი გვ. 107). თუ რომელიმე დეკარტის მართკუთხა კოორდინატთა სისტემაში წრფე განისაზღვრება n ხარისხის ალგებრული განტოლებით, მაშინ ეს ხაზი ნებისმიერ სხვა დეკარტის მართკუთხა კოორდინატულ სისტემაში განისაზღვრება იმავე n ხარისხის ალგებრული განტოლებით.

სამიზნე:განვიხილოთ ხაზის კონცეფცია თვითმფრინავზე, მიეცით მაგალითები. წრფის განმარტებიდან გამომდინარე, შემოიტანეთ სიბრტყეზე წრფის განტოლების კონცეფცია. განვიხილოთ სწორი ხაზების ტიპები, მიეცით მაგალითები და სწორი ხაზის განსაზღვრის მეთოდები. სწორი ხაზის განტოლების ზოგადი ფორმიდან გადათარგმნის უნარის გაძლიერება სწორი ხაზის განტოლებად „სეგმენტებში“, კუთხოვანი კოეფიციენტით.

1. წრფის განტოლება სიბრტყეზე.
2. სიბრტყეზე სწორი ხაზის განტოლება. განტოლებების სახეები.
3. სწორი ხაზის მითითების მეთოდები.

1. მოდით x და y იყოს ორი თვითნებური ცვლადი.

განმარტება: F(x,y)=0 ფორმის მიმართება ეწოდება განტოლება , თუ ეს არ არის ჭეშმარიტი x და y რიცხვების რომელიმე წყვილისთვის.

მაგალითი: 2x + 7y – 1 = 0, x 2 + y 2 – 25 = 0.

თუ ტოლობა F(x,y)=0 მოქმედებს ნებისმიერი x, y-ისთვის, მაშინ, შესაბამისად, F(x,y) = 0 არის იდენტობა.

მაგალითი: (x + y) 2 - x 2 - 2xy - y 2 = 0

ისინი ამბობენ, რომ x რიცხვები არის 0 და y არის 0 დააკმაყოფილეთ განტოლება , თუ მათი ამ განტოლებაში ჩანაცვლებისას ის გადაიქცევა ნამდვილ ტოლობაში.

ანალიტიკური გეომეტრიის ყველაზე მნიშვნელოვანი კონცეფცია არის ხაზის განტოლების კონცეფცია.

განმარტება: მოცემული წრფის განტოლება არის განტოლება F(x,y)=0, რომელიც აკმაყოფილებს ამ წრფეზე მდებარე ყველა წერტილის კოორდინატებს და არ აკმაყოფილებს ამ წრფეზე არ მდებარე არცერთი წერტილის კოორდინატებს.

y = f(x) განტოლებით განსაზღვრულ წრფეს ეწოდება f(x) გრაფიკი. ცვლადებს x და y ეწოდება მიმდინარე კოორდინატები, რადგან ისინი ცვლადი წერტილის კოორდინატებია.

Ზოგიერთი მაგალითებიხაზის განმარტებები.

1) x – y = 0 => x = y. ეს განტოლება განსაზღვრავს სწორ ხაზს:

2) x 2 - y 2 = 0 => (x-y)(x+y) = 0 => წერტილები უნდა აკმაყოფილებდეს ან განტოლებას x - y = 0, ან განტოლებას x + y = 0, რომელიც შეესაბამება სიბრტყეზე გადამკვეთი სწორი ხაზების წყვილი, რომლებიც კოორდინატთა კუთხეების ბისექტრებია:

3) x 2 + y 2 = 0. ეს განტოლება კმაყოფილდება მხოლოდ ერთი წერტილით O(0,0).

2. განმარტება: სიბრტყეზე ნებისმიერი სწორი ხაზი შეიძლება განისაზღვროს პირველი რიგის განტოლებით

Ax + Wu + C = 0,

უფრო მეტიც, მუდმივები A და B ერთდროულად ნულის ტოლი არ არის, ე.ი. A 2 + B 2 ¹ 0. ეს პირველი რიგის განტოლება ეწოდება სწორი ხაზის ზოგადი განტოლება.

A, B და C მუდმივების მნიშვნელობებიდან გამომდინარე, შესაძლებელია შემდეგი განსაკუთრებული შემთხვევები:

C = 0, A ¹ 0, B ¹ 0 - სწორი ხაზი გადის საწყისზე

A = 0, B ¹ 0, C ¹ 0 (By + C = 0) - სწორი ხაზი Ox ღერძის პარალელურად

B = 0, A ¹ 0, C ¹ 0 (Ax + C = 0) - სწორი ხაზი Oy ღერძის პარალელურად

B = C = 0, A ¹ 0 - სწორი ხაზი ემთხვევა Oy ღერძს

A = C = 0, B ¹ 0 - სწორი ხაზი ემთხვევა Ox ღერძს

სწორი ხაზის განტოლება შეიძლება წარმოდგენილი იყოს სხვადასხვა ფორმით, მოცემული საწყისი პირობებიდან გამომდინარე.

სწორი ხაზის განტოლება კუთხოვანი კოეფიციენტით.

თუ სწორი ხაზის ზოგადი განტოლება Ax + By + C = 0 დაიყვანება ფორმამდე:

და აღვნიშნოთ, მაშინ მიღებული განტოლება ეწოდება სწორი ხაზის განტოლება დახრილობით k.

სწორი ხაზის განტოლება სეგმენტებში.

თუ სწორი ხაზის ზოგად განტოლებაში Ах + Ву + С = 0 С ¹ 0, მაშინ –С-ზე გაყოფით მივიღებთ: ან , სადაც

კოეფიციენტების გეომეტრიული მნიშვნელობა არის ის, რომ კოეფიციენტი აარის წრფის გადაკვეთის წერტილის კოორდინატი Ox ღერძთან და ბ– სწორი ხაზის Oy ღერძთან გადაკვეთის წერტილის კოორდინატი.

წრფის ნორმალური განტოლება.

თუ განტოლების ორივე მხარე Ax + By + C = 0 იყოფა გამოძახებულ რიცხვზე ნორმალიზების ფაქტორი, მაშინ მივიღებთ

xcosj + ysinj - p = 0 – სწორი ხაზის ნორმალური განტოლება.

ნორმალიზების ფაქტორის ნიშანი ± უნდა შეირჩეს ისე, რომ m×С< 0.

p არის საწყისიდან სწორ ხაზზე ჩამოშვებული პერპენდიკულარულის სიგრძე და j არის ამ პერპენდიკულარულის მიერ წარმოქმნილი კუთხე Ox ღერძის დადებითი მიმართულებით.

3. სწორი ხაზის განტოლება წერტილისა და დახრილობის გამოყენებით.

წრფის კუთხური კოეფიციენტი იყოს k-ის ტოლი, წრფე გადის M წერტილში (x 0, y 0). შემდეგ სწორი ხაზის განტოლება იპოვება ფორმულით: y – y 0 = k(x – x 0)

ორ წერტილში გამავალი წრფის განტოლება.

ორი წერტილი M 1 (x 1, y 1, z 1) და M 2 (x 2, y 2, z 2) მოცემულია სივრცეში, მაშინ ამ წერტილებში გამავალი წრფის განტოლება არის:

თუ რომელიმე მნიშვნელი არის ნულის ტოლი, შესაბამისი მრიცხველი უნდა იყოს ნულის ტოლი.

სიბრტყეზე ზემოთ დაწერილი სწორი ხაზის განტოლება გამარტივებულია:

თუ x 1 ¹ x 2 და x = x 1, თუ x 1 = x 2.

წილადი = k ეწოდება ფერდობზესწორი.

F(x, y) = 0 ფორმის ტოლობას ეწოდება განტოლება x, y ორი ცვლადით, თუ ის არ არის ჭეშმარიტი x, y რიცხვების ყველა წყვილისთვის. ისინი ამბობენ, რომ ორი რიცხვი x = x 0, y = y 0 აკმაყოფილებს F(x, y) = 0 ფორმის ზოგიერთ განტოლებას, თუ განტოლებაში x და y ცვლადების ნაცვლად ამ რიცხვების ჩანაცვლებისას მისი მარცხენა მხარე ხდება ნული. .

მოცემული წრფის განტოლება (განკუთვნილ კოორდინატულ სისტემაში) არის განტოლება ორი ცვლადით, რომელიც კმაყოფილდება ამ წრფეზე მდებარე ყველა წერტილის კოორდინატებით და არ კმაყოფილდება ყოველი წერტილის კოორდინატებით, რომლებიც არ დევს მასზე.

შემდეგში გამოთქმის ნაცვლად „F(x, y) = 0 წრფის განტოლების გათვალისწინებით“, ჩვენ ხშირად ვიტყვით უფრო მოკლედ: მოცემული წრფე F(x, y) = 0.

თუ მოცემულია ორი წრფის განტოლება: F(x, y) = 0 და Ф(x, y) = 0, მაშინ სისტემის ერთობლივი ამონახსნი

F(x,y) = 0, Ф(x, y) = 0

იძლევა ყველა მათ გადაკვეთის წერტილებს. უფრო ზუსტად, რიცხვების თითოეული წყვილი, რომელიც წარმოადგენს ამ სისტემის ერთობლივ ამოხსნას, განსაზღვრავს ერთ-ერთ გადაკვეთის წერტილს,

157. მოცემული ქულები *) M 1 (2; -2), M 2 (2; 2), M 3 (2; - 1), M 4 (3; -3), M 5 (5; -5), M 6 (3; -2). დაადგინეთ, მოცემული წერტილებიდან რომელი დევს x + y = 0 განტოლებით განსაზღვრულ წრფეზე და რომელი არ დევს მასზე. რომელი ხაზი განისაზღვრება ამ განტოლებით? (დახაზეთ იგი ნახატზე.)

158. x 2 + y 2 = 25 განტოლებით განსაზღვრულ წრფეზე იპოვეთ წერტილები, რომელთა აბსცისი უდრის შემდეგ რიცხვებს: 1) 0, 2) -3, 3) 5, 4) 7; იმავე წრფეზე იპოვეთ წერტილები, რომელთა ორდინატები უდრის შემდეგ რიცხვებს: 5) 3, 6) -5, 7) -8. რომელი ხაზი განისაზღვრება ამ განტოლებით? (დახაზეთ იგი ნახატზე.)

159. დაადგინეთ რომელი წრფეებია განსაზღვრული შემდეგი განტოლებებით (ააგეთ ნახაზზე): 1)x - y = 0; 2) x + y = 0; 3) x - 2 = 0; 4)x + 3 = 0; 5) y - 5 = 0; 6) y + 2 = 0; 7) x = 0; 8) y = 0; 9) x 2 - xy = 0; 10) xy + y 2 = 0; 11) x 2 - y 2 = 0; 12) xy = 0; 13) y 2 - 9 = 0; 14) x 2 - 8x + 15 = 0; 15) y 2 + by + 4 = 0; 16) x 2 y - 7xy + 10y = 0; 17) y - |x|; 18) x - |y|; 19) y + |x| = 0; 20) x + |y| = 0; 21) y = |x - 1|; 22) y = |x + 2|; 23) x 2 + y 2 = 16; 24) (x - 2) 2 + (y - 1) 2 = 16; 25 (x + 5) 2 + (y-1) 2 = 9; 26) (x - 1) 2 + y 2 = 4; 27) x 2 + (y + 3) 2 = 1; 28) (x - 3) 2 + y 2 = 0; 29) x 2 + 2y 2 = 0; 30) 2x 2 + 3y 2 + 5 = 0; 31) (x - 2) 2 + (y + 3) 2 + 1 = 0.

160. მოცემული ხაზები: l)x + y = 0; 2)x - y = 0; 3)x 2 + y 2 - 36 = 0; 4) x 2 + y 2 - 2x + y = 0; 5) x 2 + y 2 + 4x - 6y - 1 = 0. დაადგინეთ, რომელი მათგანი გადის საწყისზე.

161. მოცემული ხაზები: 1) x 2 + y 2 = 49; 2) (x - 3) 2 + (y + 4) 2 = 25; 3) (x + 6) 2 + (y - Z) 2 = 25; 4) (x + 5) 2 + (y - 4) 2 = 9; 5) x 2 + y 2 - 12x + 16y - 0; 6) x 2 + y 2 - 2x + 8y + 7 = 0; 7) x 2 + y 2 - 6x + 4y + 12 = 0. იპოვეთ მათი გადაკვეთის წერტილები: ა) Ox ღერძით; ბ) Oy ღერძით.

162. იპოვეთ ორი წრფის გადაკვეთის წერტილები:

1) x 2 + y 2 - 8; x - y =0;

2) x 2 + y 2 - 16x + 4y + 18 = 0; x + y = 0;

3) x 2 + y 2 - 2x + 4y - 3 = 0; x 2 + y 2 = 25;

4) x 2 + y 2 - 8y + 10y + 40 = 0; x 2 + y 2 = 4.

163. პოლარულ კოორდინატთა სისტემაში წერტილები M 1 (l; π/3), M 2 (2; 0), M 3 (2; π/4), M 4 (√3; π/6) და M. 5 (1; 2/3π). დაადგინეთ, ამ წერტილებიდან რომელი დევს პოლარული კოორდინატებით განსაზღვრულ წრფეზე p = 2cosΘ განტოლებით და რომელი არ დევს მასზე. რომელი ხაზი განისაზღვრება ამ განტოლებით? (დახაზეთ იგი ნახატზე.)

164. p = 3/cosΘ განტოლებით განსაზღვრულ წრფეზე იპოვეთ წერტილები, რომელთა პოლარული კუთხეები უდრის შემდეგ რიცხვებს: ა) π/3, ბ) - π/3, გ) 0, დ) π/6. რომელი ხაზი განისაზღვრება ამ განტოლებით? (აშენეთ იგი ნახატზე.)

165. p = 1/sinΘ განტოლებით განსაზღვრულ წრფეზე იპოვეთ წერტილები, რომელთა პოლარული რადიუსი უდრის შემდეგ რიცხვებს: ა) 1 6) 2, გ) √2. რომელი ხაზი განისაზღვრება ამ განტოლებით? (აშენეთ იგი ნახატზე.)

166. დაადგინეთ, რომელი წრფეებია განსაზღვრული პოლარულ კოორდინატებში შემდეგი განტოლებებით (ააგეთ ისინი ნახაზზე): 1) p = 5; 2) Θ = π/2; 3) Θ = - π/4; 4) p cosΘ = 2; 5) p sinΘ = 1; 6.) p = 6cosΘ; 7) p = 10 sinΘ; 8) sinΘ = 1/2; 9) სინპი = 1/2.

167. ააგეთ არქიმედეს შემდეგი სპირალები ნახაზზე: 1) p = 20; 2) p = 50; 3) p = Θ/π; 4) p = -Θ/π.

168. ააგეთ ნახატზე შემდეგი ჰიპერბოლური სპირალები: 1) p = 1/Θ; 2) p = 5/Θ; 3) p = π/Θ; 4) р= - π/Θ

169. ააგეთ ნახაზზე შემდეგი ლოგარითმული სპირალები: 1) p = 2 Θ; 2) p = (1/2) Θ.

170. განსაზღვრეთ იმ მონაკვეთების სიგრძეები, რომლებშიც არქიმედეს სპირალი p = 3Θ იჭრება ძელიდან გამომავალი სხივით და პოლარული ღერძისკენ Θ = π/6 კუთხით დახრილი. გააკეთე ნახატი.

171. არქიმედეს სპირალზე p = 5/πΘ აღებულია C წერტილი, რომლის პოლარული რადიუსი არის 47. დაადგინეთ რამდენ ნაწილად ჭრის ეს სპირალი C წერტილის პოლარულ რადიუსს. გააკეთეთ ნახატი.

172. ჰიპერბოლურ სპირალზე P = 6/Θ იპოვეთ P წერტილი, რომლის პოლარული რადიუსი არის 12. გააკეთეთ ნახატი.

173. ლოგარითმულ სპირალზე p = 3 Θ იპოვეთ P წერტილი, რომლის პოლარული რადიუსი არის 81. გააკეთეთ ნახაზი.