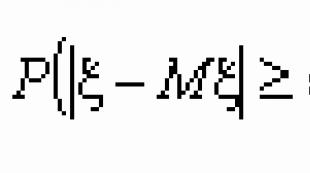Պատահական երևույթների ուսումնասիրության պրակտիկան ցույց է տալիս, որ թեև անհատական ​​դիտարկումների արդյունքները, նույնիսկ նույն պայմաններում կատարվողները, կարող են էապես տարբերվել, միևնույն ժամանակ, բավական մեծ թվով դիտարկումների միջին արդյունքները կայուն են և թույլ կախված են. անհատական ​​դիտարկումների արդյունքները.

Պատահական երևույթների այս ուշագրավ հատկության տեսական հիմքն է մեծ թվերի օրենքը. «Մեծ թվերի օրենքը» անվանումը միավորում է մի խումբ թեորեմներ, որոնք հաստատում են մեծ թվով պատահական երևույթների միջին արդյունքների կայունությունը և բացատրում այս կայունության պատճառը։

Մեծ թվերի օրենքի ամենապարզ ձևը և պատմականորեն այս բաժնի առաջին թեորեմն է Բեռնուլիի թեորեմը, որը նշում է, որ եթե իրադարձության հավանականությունը բոլոր փորձարկումներում նույնն է, ապա փորձությունների քանակի աճի հետ իրադարձության հաճախականությունը հակված է իրադարձության հավանականությանը և դադարում է պատահական լինել։

Պուասոնի թեորեմն ասում է, որ անկախ փորձարկումների շարքում իրադարձության հաճախականությունը հակված է նրա հավանականությունների միջին թվաբանականին և դադարում է պատահական լինելուց։

Հավանականությունների տեսության սահմանային թեորեմներ, թեորեմներ Moivre-Laplaceբացատրել իրադարձության առաջացման հաճախականության կայունության բնույթը. Այս բնույթը կայանում է նրանում, որ իրադարձության դեպքերի քանակի սահմանափակ բաշխումը փորձարկումների քանակի անսահմանափակ աճով (եթե իրադարձության հավանականությունը նույնն է բոլոր փորձարկումներում) նորմալ բաշխում.

Կենտրոնական սահմանային թեորեմը բացատրում է տարածված նորմալ օրենքբաշխումներ. Թեորեմն ասում է, որ երբ պատահական փոփոխականը ձևավորվում է վերջավոր շեղումներ ունեցող մեծ թվով անկախ պատահական փոփոխականների ավելացման արդյունքում, այս պատահական փոփոխականի բաշխման օրենքը գործնականում ստացվում է. նորմալօրենքով։

Ստորև տրված թեորեմը վերնագրված « Մեծ թվերի օրենքը«-ը նշում է, որ որոշակի, բավականին ընդհանուր պայմաններում, պատահական փոփոխականների քանակի աճով, նրանց թվաբանական միջինը հակված է մաթեմատիկական ակնկալիքների միջին թվաբանականին և դադարում է պատահական լինել։

Լյապունովի թեորեմը բացատրում է տարածված նորմալ օրենքբաշխումը և բացատրում է դրա ձևավորման մեխանիզմը: Թեորեմը թույլ է տալիս պնդել, որ երբ պատահական փոփոխականը ձևավորվում է մեծ թվով անկախ պատահական փոփոխականների ավելացման արդյունքում, որոնց շեղումները փոքր են՝ համեմատած գումարի շեղումների հետ, այս պատահական փոփոխականի բաշխման օրենքը շրջվում է. դուրս լինել գործնականում նորմալօրենքով։ Եվ քանի որ պատահական փոփոխականները միշտ ստեղծվում են անսահման թվով պատճառներով, և ամենից հաճախ դրանցից ոչ մեկը չունի ցրվածություն, որը համեմատելի է հենց պատահական փոփոխականի ցրվածության հետ, գործնականում հանդիպող պատահական փոփոխականների մեծ մասը ենթակա է նորմալ բաշխման օրենքի:

Մեծ թվերի օրենքի որակական և քանակական պնդումները հիմնված են Չեբիշևի անհավասարություն. Այն որոշում է այն հավանականության վերին սահմանը, որ պատահական փոփոխականի արժեքի շեղումը նրա մաթեմատիկական ակնկալիքից ավելի մեծ է, քան որոշակի նշված թիվը: Հատկանշական է, որ Չեբիշևի անհավասարությունը գնահատում է իրադարձության հավանականությունը. Պատահական փոփոխականի համար, որի բաշխումն անհայտ է, հայտնի են միայն նրա մաթեմատիկական ակնկալիքը և շեղումը:

Չեբիշևի անհավասարությունը.Եթե ​​x պատահական փոփոխականն ունի շեղում, ապա ցանկացած e > 0-ի համար գործում է հետևյալ անհավասարությունը. , Որտեղ Մ x և Դ x - պատահական x փոփոխականի մաթեմատիկական ակնկալիք և շեղում:

Բեռնուլիի թեորեմը.Թող m n-ն լինի n Բեռնուլիի փորձարկումների հաջողության թիվը և p անհատական ​​փորձարկումներում հաջողության հասնելու հավանականությունը: Այնուհետև ցանկացած e > 0-ի համար դա ճիշտ է .

Կենտրոնական սահմանային թեորեմ.Եթե ​​պատահական փոփոխականները x 1 , x 2 , …, x n , … զույգերով անկախ են, նույնականորեն բաշխված են և ունեն վերջավոր շեղումներ, ապա n-ի համար միատեսակ x (-,)

Ո՞րն է հաջողակ վաճառողների գաղտնիքը: Եթե ​​դիտարկեք ցանկացած ընկերության լավագույն վաճառողներին, ապա կնկատեք, որ նրանք ունեն մեկ ընդհանուր բան. Նրանցից յուրաքանչյուրը հանդիպում է ավելի շատ մարդկանց հետ և ավելի շատ շնորհանդեսներ է անում, քան ոչ այնքան հաջողակ վաճառողները: Այս մարդիկ հասկանում են, որ վաճառքը թվերի խաղ է, և որքան շատ մարդկանց պատմեն իրենց ապրանքների կամ ծառայությունների մասին, այնքան ավելի շատ գործարքներ կփակեն՝ այսքանը: Նրանք հասկանում են, որ եթե շփվեն ոչ միայն այն քչերի հետ, ովքեր իրենց հաստատ այո կասեն, այլ նաև նրանց հետ, ում հետաքրքրությունն իրենց առաջարկի նկատմամբ այնքան էլ մեծ չէ, ապա միջինների օրենքը կգործի իրենց օգտին։

Ձեր եկամուտը կախված կլինի վաճառքների քանակից, բայց միևնույն ժամանակ այն ուղիղ համեմատական ​​կլինի ձեր ներկայացումների քանակին: Հենց որ հասկանաք և կիրառեք միջին ցուցանիշների օրենքը, նոր բիզնես սկսելու կամ նոր ոլորտում աշխատելու հետ կապված անհանգստությունը կսկսի նվազել: Արդյունքում կսկսի աճել վերահսկողության զգացումը և վստահությունը ձեր գումար վաստակելու ունակության նկատմամբ: Եթե ​​դուք պարզապես ներկայացնեք և հղկեք ձեր հմտությունները գործընթացում, գործարքներ կգան:

Գործարքների քանակի մասին մտածելու փոխարեն, ավելի լավ մտածեք շնորհանդեսների քանակի մասին: Իմաստ չկա առավոտյան արթնանալ կամ երեկոյան տուն գալ և մտածել, թե ով կգնի ձեր ապրանքը: Փոխարենը, ավելի լավ է պլանավորել, թե օրական քանի զանգ պետք է կատարեք: Եվ հետո, անկախ ամեն ինչից, կատարեք այդ բոլոր զանգերը: Այս մոտեցումը կհեշտացնի ձեր աշխատանքը, քանի որ դա պարզ և կոնկրետ նպատակ է: Եթե ​​գիտեք, որ ունեք կոնկրետ և հասանելի նպատակ, ապա ձեզ համար ավելի հեշտ կլինի կատարել նախատեսված թվով զանգեր։ Եթե ​​այս գործընթացի ընթացքում մի քանի անգամ լսեք «այո», այնքան ավելի լավ:

Իսկ եթե «ոչ», ապա երեկոյան դուք կզգաք, որ ազնվորեն արել եք այն ամենը, ինչ կարող էիք, և ձեզ չեն տանջի այն մտքերը, թե որքան գումար եք վաստակել կամ քանի ուղեկից եք ձեռք բերել մեկ օրում:

Ենթադրենք, ձեր ընկերությունում կամ բիզնեսում միջին վաճառողը մեկ գործարք է կնքում չորս ներկայացման համար: Հիմա պատկերացրեք, որ դուք քարտեր եք նկարում տախտակամածից: Երեք կոստյումներից յուրաքանչյուր քարտ՝ բահեր, ադամանդներ և մահակներ, ներկայացում է, որտեղ դուք մասնագիտորեն ներկայացնում եք ապրանքը, ծառայությունը կամ հնարավորությունը: Դուք դա անում եք այնքան լավ, որքան կարող եք, բայց դեռ չեք փակում գործարքը։ Եվ յուրաքանչյուր սրտի քարտ գործարք է, որը թույլ է տալիս գումար ստանալ կամ ձեռք բերել նոր ուղեկից:

Նման իրավիճակում չէի՞ք ցանկանա տախտակամածից որքան հնարավոր է շատ խաղաթղթեր հանել: Ենթադրենք, ձեզ առաջարկվում է նկարել այնքան քարտ, որքան ցանկանում եք՝ միաժամանակ վճարելով ձեզ կամ առաջարկելով ձեզ նոր ուղեկից ամեն անգամ, երբ դուք սրտի քարտ եք քաշում: Դուք կսկսեք եռանդով քարտեր նկարել՝ հազիվ նկատելով, թե ինչ կոստյում է այն քարտը, որը հենց նոր հանեցիք:

Դուք գիտեք, որ հիսուներկու քարտերից բաղկացած տախտակամածում կա տասներեք սիրտ: Եվ երկու տախտակամածների մեջ կա քսանվեց սրտի քարտ և այլն: Դուք կհիասթափվե՞ք, երբ նկարեք բահեր, ադամանդներ կամ մահակներ: Իհարկե ոչ! Դուք միայն կմտածեք, որ յուրաքանչյուր նման «միսս» ինչի՞ն է ձեզ ավելի մոտեցնում։ Դեպի սրտի քարտ:

Բայց գիտե՞ք ինչ. Ձեզ արդեն նման առաջարկ է տրվել։ Դուք եզակի վիճակում եք վաստակելու այնքան, որքան ցանկանում եք, և նկարեք այնքան սրտեր, որքան ցանկանում եք նկարել ձեր կյանքում: Եվ եթե դուք պարզապես բարեխղճորեն «քարտեր եք նկարում», կատարելագործում եք ձեր հմտությունները և համբերում եք մի փոքր բահերին, ադամանդներին և մահակներին, դուք կդառնաք հիանալի վաճառող և կհասնեք հաջողության:

Վաճառքներն այնքան զվարճալի բաներից մեկն այն է, որ ամեն անգամ, երբ դուք խառնում եք տախտակամածը, քարտերը խառնվում են այլ կերպ: Երբեմն բոլոր սրտերը հայտնվում են տախտակամածի սկզբում, և հաջողակ շարանից հետո (երբ մեզ թվում է, որ մենք երբեք չենք պարտվի) մեզ սպասում է տարբեր կոստյումի քարտերի երկար շարք: Իսկ մյուս անգամ, առաջին սրտին հասնելու համար, պետք է անցնել անսահման քանակությամբ բահերի, մահակների և ադամանդների միջով: Եվ երբեմն տարբեր կոստյումների քարտերը հայտնվում են խիստ կարգով: Բայց ամեն դեպքում, հիսուներկու քարտերից բաղկացած յուրաքանչյուր տախտակամածում, ինչ-որ հերթականությամբ, միշտ տասներեք սիրտ կա։ Պարզապես հանեք քարտերը, մինչև գտնեք դրանք:

From՝ Leylya,  

Մեծ թվերի մասին բառերը վերաբերում են թեստերի քանակին. դիտարկվում է պատահական փոփոխականի մեծ թվով արժեքներ կամ մեծ թվով պատահական փոփոխականների կուտակային ազդեցություն: Այս օրենքի էությունը հետևյալն է. թեև անհնար է կանխատեսել, թե առանձին պատահական փոփոխականը ինչ արժեք կընդունի մեկ փորձի ժամանակ, այնուամենայնիվ, մեծ թվով անկախ պատահական փոփոխականների գործողության ընդհանուր արդյունքը կորցնում է իր պատահական բնույթը և կարող է. կարելի է կանխատեսել գրեթե հուսալի (այսինքն՝ մեծ հավանականությամբ): Օրինակ, անհնար է գուշակել, թե որ ուղղությամբ կհանդիպի մեկ մետաղադրամը: Սակայն եթե նետեք 2 տոննա մետաղադրամ, ապա մեծ վստահությամբ կարող ենք ասել, որ զինանշանը վեր ընկած մետաղադրամների քաշը հավասար է 1 տոննայի։

Մեծ թվերի օրենքը հիմնականում վերաբերում է այսպես կոչված Չեբիշևի անհավասարությանը, որը մեկ թեստում գնահատում է պատահական փոփոխականի հավանականությունը, որն ընդունի արժեք, որը շեղվում է միջին արժեքից ոչ ավելի, քան տվյալ արժեքով:

Չեբիշևի անհավասարությունը. Թող X- կամայական պատահական փոփոխական, a=M(X) , Ա Դ(X) - դրա տարբերությունը. Հետո

Օրինակ. Մեքենայի միացված թևի տրամագծի անվանական (այսինքն՝ պահանջվող) արժեքը հավասար է. 5 մմ, և ցրվածությունն այլևս չկա 0.01 (սա մեքենայի ճշգրտության հանդուրժողականությունն է): Գնահատեք հավանականությունը, որ մեկ թփի արտադրության ժամանակ նրա տրամագծի շեղումը անվանականից պակաս կլինի, քան 0,5 մմ .

Լուծում. Թող ռ.վ. X- արտադրված թփի տրամագիծը. Ըստ պայմանի, դրա մաթեմատիկական ակնկալիքը հավասար է անվանական տրամագծին (եթե մեքենայի պարամետրերում համակարգված ձախողում չկա). a=M(X)=5 , և ցրվածությունը Դ(X)≤0.01. Չեբիշևի անհավասարության կիրառումը ժամը ε = 0,5, ստանում ենք.

Այսպիսով, նման շեղման հավանականությունը բավականին մեծ է, և, հետևաբար, կարելի է եզրակացնել, որ մասի մեկ արտադրության դեպքում գրեթե վստահ է, որ տրամագծի շեղումը անվանականից չի գերազանցի. 0,5 մմ .

Իր իմաստով ստանդարտ շեղումը σ բնութագրում է միջինպատահական փոփոխականի շեղումն իր կենտրոնից (այսինքն՝ նրա մաթեմատիկական ակնկալիքից): Քանի որ սա միջինշեղում, ապա թեստավորման ժամանակ հնարավոր են մեծ (շեշտը ո) շեղումներ։ Որքա՞ն մեծ շեղումներ են գործնականում հնարավոր: Սովորաբար բաշխված պատահական փոփոխականները ուսումնասիրելիս մենք ստացանք «երեք սիգմա» կանոնը. նորմալ բաշխված պատահական փոփոխական: X մեկ թեստումգործնականում չի շեղվում իր միջինից ավելի քան 3ս, Որտեղ σ= σ(X)– r.v-ի ստանդարտ շեղում. X. Մենք այս կանոնը հանգեցրել ենք այն փաստից, որ մենք ստացել ենք անհավասարությունը

.

Այժմ գնահատենք դրա հավանականությունը կամայականպատահական փոփոխական Xընդունել արժեք, որը միջինից տարբերվում է ստանդարտ շեղումից ոչ ավելի, քան երեք անգամ: Չեբիշևի անհավասարության կիրառումը ժամը ε = 3սև հաշվի առնելով դա Դ(Х)= ս 2 , ստանում ենք.

.

Այսպիսով, ընդհանուր առմամբմենք կարող ենք գնահատել պատահական փոփոխականի՝ իր միջինից շեղվելու հավանականությունը թվով ոչ ավելի, քան երեք ստանդարտ շեղումներով 0.89 , մինչդեռ նորմալ բաշխման դեպքում դա կարելի է երաշխավորել հավանականությամբ 0.997 .

Չեբիշևի անհավասարությունը կարող է ընդհանրացվել անկախ նույնականորեն բաշխված պատահական փոփոխականների համակարգին:

Ընդհանրացված Չեբիշևյան անհավասարություն. Եթե ​​անկախ պատահական փոփոխականներ X 1 , X 2 , …, X n Մ(X ես )= աև շեղումներ Դ(X ես )= Դ, Դա

ժամը n=1 այս անհավասարությունը վերածվում է վերևում ձևակերպված Չեբիշևյան անհավասարության:

Չեբիշևի անհավասարությունը, ունենալով ինքնուրույն նշանակություն համապատասխան խնդիրների լուծման համար, օգտագործվում է այսպես կոչված Չեբիշևի թեորեմի ապացուցման համար։ Մենք նախ կխոսենք այս թեորեմի էության մասին, ապա կտանք դրա պաշտոնական ձևակերպումը։

Թող X 1 , X 2 , …, X n– մեծ թվով անկախ պատահական փոփոխականներ՝ մաթեմատիկական ակնկալիքներով M (X 1 )=ա 1 , … , M (X n )=ա n. Թեև դրանցից յուրաքանչյուրը փորձի արդյունքում կարող է մեծ արժեք վերցնել իր միջինից (այսինքն՝ մաթեմատիկական ակնկալիքից), այնուամենայնիվ, պատահական փոփոխական.
, որը հավասար է նրանց թվաբանական միջինին, ամենայն հավանականությամբ կունենա ֆիքսված թվին մոտ արժեք
(սա բոլոր մաթեմատիկական ակնկալիքների միջինն է): Սա նշանակում է հետեւյալը. Թող թեստի արդյունքում անկախ պատահական փոփոխականներ X 1 , X 2 , …, X n(դրանցից շատերը կան!) համապատասխանաբար վերցրեց արժեքներ X 1 , X 2 , …, X nհամապատասխանաբար. Այնուհետև, եթե այդ արժեքներն իրենք կարող են պարզվել, որ հեռու են համապատասխան պատահական փոփոխականների միջին արժեքներից, ապա դրանց միջին արժեքը.
ամենայն հավանականությամբ թվին մոտ կլինի
. Այսպիսով, մեծ թվով պատահական փոփոխականների թվաբանական միջինն արդեն կորցնում է իր պատահական բնույթը և կարող է կանխատեսվել մեծ ճշգրտությամբ։ Դա կարելի է բացատրել նրանով, որ արժեքների պատահական շեղումները X ես-ից ա եսկարող են լինել տարբեր նշանների, և, հետևաբար, ընդհանուր առմամբ այդ շեղումները, ամենայն հավանականությամբ, փոխհատուցվում են:

Թերեմա Չեբիշև (մեծ թվերի օրենքըՉեբիշևի տեսքով): Թող X 1 , X 2 , …, X n … – զույգ-անկախ պատահական փոփոխականների հաջորդականություն, որոնց շեղումները սահմանափակված են նույն թվով: Այնուհետև, որքան էլ փոքր լինի ε թիվը, անհավասարության հավանականությունը

այնքան մոտ կլինի մեկին, որքան ցանկանաք, եթե համարը nվերցնել բավականաչափ մեծ պատահական փոփոխականներ: Ֆորմալ առումով սա նշանակում է, որ թեորեմի պայմաններում

Կոնվերգենցիայի այս տեսակը կոչվում է կոնվերգենցիա ըստ հավանականության և նշվում է.

Այսպիսով, Չեբիշևի թեորեմն ասում է, որ եթե կա բավականաչափ մեծ թվով անկախ պատահական փոփոխականներ, ապա դրանց միջին թվաբանականը մեկ թեստում գրեթե հուսալիորեն կստանա իրենց մաթեմատիկական ակնկալիքների միջինին մոտ արժեք:

Ամենից հաճախ Չեբիշևի թեորեմը կիրառվում է այն իրավիճակներում, որտեղ պատահական փոփոխականներ են X 1 , X 2 , …, X n … ունեն նույն բաշխումը (այսինքն՝ բաշխման նույն օրենքը կամ հավանականության նույն խտությունը): Փաստորեն, դա պարզապես միևնույն պատահական փոփոխականի մեծ թվով դեպքեր է:

Հետևանք(ընդհանրացված Չեբիշևյան անհավասարություն): Եթե ​​անկախ պատահական փոփոխականներ X 1 , X 2 , …, X n … ունեն նույն բաշխումը մաթեմատիկական ակնկալիքներով Մ(X ես )= աև շեղումներ Դ(X ես )= Դ, Դա

, այսինքն.
.

Ապացույցը բխում է ընդհանրացված Չեբիշևյան անհավասարությունից՝ անցնելով սահմանին ժամը n→∞ .

Եվս մեկ անգամ նկատենք, որ վերը նշված հավասարումները չեն երաշխավորում քանակի արժեքը
ձգտում է Աժամը n→∞. Այս քանակությունը դեռևս մնում է պատահական փոփոխական, և դրա անհատական ​​արժեքները կարող են բավականին հեռու լինել Ա. Բայց այդպիսի հավանականությունը (հեռու Ա) արժեքները՝ աճող nձգտում է 0-ի:

Մեկնաբանություն. Եզրակացության եզրակացությունն ակնհայտորեն վավեր է նաև ավելի ընդհանուր դեպքում, երբ անկախ պատահական փոփոխականներ են X 1 , X 2 , …, X n … ունեն տարբեր բաշխումներ, բայց նույն մաթեմատիկական ակնկալիքները (հավասար Ա) և համատեղ սահմանափակ շեղումներ: Սա թույլ է տալիս կանխատեսել որոշակի մեծության չափման ճշգրտությունը, նույնիսկ եթե այդ չափումները կատարվել են տարբեր գործիքների միջոցով:

Եկեք ավելի մանրամասն քննարկենք այս հետևանքի կիրառումը մեծությունները չափելիս: Եկեք օգտագործենք ինչ-որ սարք nնույն մեծության չափումները, որոնց իրական արժեքը հավասար է Աիսկ մենք չգիտենք. Նման չափումների արդյունքները X 1 , X 2 , …, X nկարող են զգալիորեն տարբերվել միմյանցից (և իրական արժեքից Ա) տարբեր պատահական գործոնների պատճառով (ճնշման փոփոխություններ, ջերմաստիճան, պատահական թրթռում և այլն): Դիտարկենք r.v. X– գործիքի ընթերցում մեծության մեկ չափման համար, ինչպես նաև ռ.վ. X 1 , X 2 , …, X n– գործիքի ընթերցում առաջին, երկրորդ, ..., վերջին չափման ժամանակ: Այսպիսով, քանակներից յուրաքանչյուրը X 1 , X 2 , …, X n կա ս.վ. դեպքերից ընդամենը մեկը. X, և հետևաբար նրանք բոլորն ունեն նույն բաշխումը, ինչ r.v. X. Քանի որ չափումների արդյունքները միմյանցից կախված չեն, ապա ռ.վ. X 1 , X 2 , …, X nկարելի է անկախ համարել։ Եթե ​​սարքը համակարգված սխալ չի առաջացնում (օրինակ՝ սանդղակի զրոն «անջատված չէ», զսպանակը չի ձգվում և այլն), ապա կարելի է ենթադրել, որ մաթեմատիկական ակնկալիքը. M(X) = a, եւ, հետեւաբար M (X 1 ) = ... = M (X n ) = ա. Այսպիսով, վերը նշված հետևանքի պայմանները բավարարված են և հետևաբար, որպես քանակի մոտավոր արժեք. Ամենք կարող ենք վերցնել պատահական փոփոխականի «իրականացում»:
մեր փորձի մեջ (որը բաղկացած է մի շարք nչափումներ), այսինքն.

.

Մեծ թվով չափումների դեպքում այս բանաձևով հաշվարկի լավ ճշգրտությունը գործնականում որոշակի է: Սա այն գործնական սկզբունքի հիմնավորումն է, որ մեծ թվով չափումների դեպքում դրանց միջին թվաբանականը գործնականում շատ չի տարբերվում չափված արժեքի իրական արժեքից:

Մաթեմատիկական վիճակագրության մեջ լայնորեն օգտագործվող «նմուշառման» մեթոդը հիմնված է մեծ թվերի օրենքի վրա, որը թույլ է տալիս ընդունելի ճշգրտությամբ ստանալ դրա օբյեկտիվ բնութագրերը պատահական փոփոխականի արժեքների համեմատաբար փոքր նմուշից: Բայց սա կքննարկվի հաջորդ բաժնում:

Օրինակ. Որոշակի մեծություն չափվում է չափիչ սարքի վրա, որը համակարգված աղավաղումներ չի անում Ամեկ անգամ (ստացված արժեքը X 1 ), իսկ հետո ևս 99 անգամ (ստացված արժեքներ X 2 , …, X 100 ) Ճշմարիտ չափման արժեքի համար Աառաջին չափման արդյունքը վերցվում է
, իսկ հետո բոլոր չափումների միջին թվաբանականը
. Սարքի չափման ճշգրտությունն այնպիսին է, որ չափման σ ստանդարտ շեղումը 1-ից ոչ ավելի է (հետևաբար շեղումը Դ=σ 2 նույնպես չի գերազանցում 1-ը): Յուրաքանչյուր չափման մեթոդի համար գնահատեք հավանականությունը, որ չափման սխալը չի ​​գերազանցի 2-ը:

Լուծում. Թող ռ.վ. X- գործիքի ընթերցում մեկ չափման համար: Հետո պայմանով M(X)=a. Առաջադրված հարցերին պատասխանելու համար մենք կիրառում ենք ընդհանրացված Չեբիշևի անհավասարությունը

ժամը ε =2 առաջին համար n=1 իսկ հետո համար n=100 . Առաջին դեպքում մենք ստանում ենք
, իսկ երկրորդում. Այսպիսով, երկրորդ դեպքը գործնականում երաշխավորում է նշված չափման ճշգրտությունը, մինչդեռ առաջինն այս առումով մեծ կասկածներ է թողնում։

Եկեք կիրառենք վերը նշված պնդումները Բեռնուլիի սխեմայով առաջացող պատահական փոփոխականների վրա: Հիշենք այս սխեմայի էությունը. Թող արտադրվի n անկախ փորձարկումներ, որոնցից յուրաքանչյուրը պարունակում է որոշակի իրադարձություն Ակարող է հայտնվել նույն հավանականությամբ Ռ, Ա ք=1–р(իմաստով սա հակառակ իրադարձության հավանականությունն է՝ իրադարձության չկատարումը Ա) . Եկեք մի քանի թիվ ծախսենք nնման թեստեր. Դիտարկենք պատահական փոփոխականները. X 1 - իրադարձության դեպքերի քանակը ԱՎ 1 -րդ թեստը, ..., X n- իրադարձության դեպքերի քանակը ԱՎ n-րդ թեստը. Բոլորը մտել են ս.վ. կարող է արժեքներ ընդունել 0 կամ 1 (միջոցառում Ակարող է կամ չհայտնվել թեստում), և արժեքը 1 ըստ պայմանի ընդունվում է յուրաքանչյուր դատավարության հավանականությամբ էջ(իրադարձության առաջացման հավանականությունը Այուրաքանչյուր փորձության ժամանակ), և արժեքը 0 հավանականությամբ ք= 1 – էջ. Հետևաբար, այս քանակներն ունեն բաշխման նույն օրենքները.

X 1

X n

Հետևաբար, այս քանակությունների միջին արժեքները և դրանց շեղումները նույնպես նույնն են. M (X 1 )=0 ∙ ք+1 ∙ p= p, …, M (X n )= պ ; Դ(X 1 )=(0 2 ∙ ք+1 2 ∙ էջ)− էջ 2 = էջ∙(1− էջ)= էջ ∙ ք,…, Դ(X n )= էջ ∙ ք. Փոխարինելով այս արժեքները ընդհանրացված Չեբիշևի անհավասարության մեջ՝ մենք ստանում ենք

.

Հասկանալի է, որ ռ.վ. X=X 1 +…+X nիրադարձության դեպքերի թիվն է Աբոլորի մեջ nթեստեր (ինչպես ասում են՝ «հաջողությունների թիվը». nթեստեր): Ներդրեք անցկացվածը nփորձարկման միջոցառում Ահայտնվեց կ նրանցից. Այնուհետև նախորդ անհավասարությունը կարելի է գրել այսպես

.

Բայց մեծությունը
, հավասար է իրադարձության դեպքերի քանակի հարաբերակցությանը ԱՎ nանկախ փորձարկումներ, փորձարկումների ընդհանուր թվին, նախկինում կոչվում էր իրադարձությունների հարաբերական հաճախականություն ԱՎ nթեստեր. Հետևաբար, կա անհավասարություն

.

Անդրադառնալով այժմ սահմանին ժամը n→∞, մենք ստանում ենք
, այսինքն.
(ըստ հավանականության): Սա Բեռնուլիի ձևով մեծ թվերի օրենքի բովանդակությունն է: Այստեղից բխում է, որ բավականաչափ մեծ քանակությամբ թեստերով nհարաբերական հաճախականության կամայական փոքր շեղումներ
իրադարձությունները նրա հավանականությունից Ռ- գրեթե հուսալի իրադարձություններ, իսկ մեծ շեղումները՝ գրեթե անհնարին։ Ստացված եզրակացությունը հարաբերական հաճախականությունների նման կայունության մասին (ինչի մասին մենք նախկինում խոսեցինք որպես փորձարարականփաստ) հիմնավորում է իրադարձության հավանականության նախկինում ներկայացված վիճակագրական սահմանումը որպես մի թիվ, որի շուրջ տատանվում է իրադարձության հարաբերական հաճախականությունը:

Նկատի ունենալով, որ արտահայտությունը էջ∙ ք= էջ∙(1− էջ)= էջ− էջ 2 չի գերազանցում փոփոխության միջակայքը
(սա հեշտ է ստուգել՝ գտնելով այս ֆունկցիայի նվազագույնը այս հատվածում), վերը նշված անհավասարությունից
հեշտ է դա ստանալ

,

որն օգտագործվում է համապատասխան խնդիրների լուծման համար (դրանցից մեկը կներկայացվի ստորև):

Օրինակ. Մետաղադրամը նետվել է 1000 անգամ։ Գնահատեք այն հավանականությունը, որ զինանշանի տեսքի հարաբերական հաճախականության շեղումը դրա հավանականությունից պակաս կլինի 0,1-ից։

Լուծում. Անհավասարության կիրառում
ժամը էջ= ք=1/2 , n=1000 , ε=0.1, մենք կստանանք .

Օրինակ. Գնահատեք հավանականությունը, որ նախորդ օրինակի պայմաններում թիվը կընկած խորհրդանշանները կլինեն սկսած միջակայքում 400 նախքան 600 .

Լուծում. Վիճակ 400< կ<600 նշանակում է, որ 400/1000< կ/ n<600/1000 , այսինքն. 0.4< Վ n (Ա)<0.6 կամ
. Ինչպես հենց նոր տեսանք նախորդ օրինակից, նման իրադարձության հավանականությունը պակաս չէ 0.975 .

Օրինակ. Որոշ իրադարձության հավանականությունը հաշվարկելու համար ԱԻրականացվել է 1000 փորձ, որոնցում տեղի է ունեցել իրադարձություն Ահայտնվել է 300 անգամ։ Գնահատեք հավանականությունը, որ հարաբերական հաճախականությունը (հավասար է 300/1000 = 0,3) հեռու է իրական հավանականությունից Ռոչ ավելի, քան 0.1:

Լուծում. Կիրառելով վերը նշված անհավասարությունը
n=1000, ε=0.1-ի համար ստանում ենք .

Մեծ ու բազմազան նյութի վրա հայտնաբերված պատահական իրադարձությունների առաջացման հաճախականությունների կայունացման ֆենոմենն ի սկզբանե որևէ հիմնավորում չի ունեցել և ընկալվել է որպես զուտ էմպիրիկ փաստ։ Այս ոլորտում առաջին տեսական արդյունքը 1713 թվականին հրատարակված հայտնի Բեռնուլիի թեորեմն էր, որը հիմք դրեց մեծ թվերի օրենքներին։

Բեռնուլիի թեորեմն իր բովանդակությամբ սահմանային թեորեմ է, այսինքն՝ ասիմպտոտիկ նշանակության հայտարարություն, որն ասում է, թե ինչ կլինի հավանականական պարամետրերի հետ մեծ թվով դիտարկումներով։ Այս տեսակի բոլոր ժամանակակից բազմաթիվ պնդումների նախահայրը հենց Բերնուլիի թեորեմն է:

Այսօր թվում է, թե մեծ թվերի մաթեմատիկական օրենքը շատ իրական գործընթացների որոշ ընդհանուր հատկության արտացոլումն է:

Ցանկանալով մեծ թվերի օրենքին տալ հնարավորինս մեծ ծավալ, որը համապատասխանում է այս օրենքը կիրառելու ոչ սպառված պոտենցիալ հնարավորություններին, մեր դարի մեծագույն մաթեմատիկոսներից մեկը Ա.Ն. Կոլմոգորովը ձևակերպեց դրա էությունը հետևյալ կերպ. «Ընդհանուր սկզբունքը, որի ուժով մեծ թվով պատահական գործոնների ընդհանուր գործողությունը հանգեցնում է պատահականությունից գրեթե անկախ արդյունքի»:

Այսպիսով, մեծ թվերի օրենքը երկու մեկնաբանություն ունի. Մեկը մաթեմատիկական է՝ կապված կոնկրետ մաթեմատիկական մոդելների, ձեւակերպումների, տեսությունների հետ, իսկ երկրորդը՝ ավելի ընդհանուր՝ դուրս գալով այս շրջանակից։ Երկրորդ մեկնաբանությունը կապված է քիչ թե շատ ուղղված գործողությունների ձևավորման երևույթի հետ, որը հաճախ նկատվում է գործնականում, մեծ թվով թաքնված կամ տեսանելի գործող գործոնների ֆոնի վրա, որոնք արտաքուստ չունեն այդպիսի շարունակականություն: Երկրորդ մեկնաբանության հետ կապված օրինակներն են ազատ շուկայում գնագոյացումը և որոշակի հարցի վերաբերյալ հասարակական կարծիքի ձևավորումը:

Նկատելով մեծ թվերի օրենքի այս ընդհանուր մեկնաբանությունը՝ անդրադառնանք այս օրենքի հատուկ մաթեմատիկական ձևակերպումներին:

Ինչպես ասացինք վերևում, հավանականությունների տեսության համար առաջին և սկզբունքորեն ամենակարևորը Բեռնուլիի թեորեմն է։ Այս մաթեմատիկական փաստի բովանդակությունը, որն արտացոլում է շրջակա աշխարհի կարևորագույն օրենքներից մեկը, հանգում է հետևյալին.

Դիտարկենք անկապ (այսինքն՝ անկախ) թեստերի հաջորդականությունը, որոնց պայմանները հետևողականորեն վերարտադրվում են թեստից թեստ: Յուրաքանչյուր թեստի արդյունքը մեզ հետաքրքրող իրադարձության հայտնվելն է կամ չկայանալը Ա.

Այս ընթացակարգը (Բեռնուլիի սխեման) ակնհայտորեն կարելի է բնորոշ համարել շատ գործնական ոլորտների համար. «տղա-աղջիկ» նորածինների հաջորդականությամբ, ամենօրյա օդերևութաբանական դիտարկումներ («անձրև եկավ - չեղավ»), արտադրված արտադրանքի հոսքի վերահսկում ( «նորմալ - թերի») և այլն:

Իրադարձությունների առաջացման հաճախականությունը Աժամը Պթեստեր ( t A -

իրադարձությունների հաճախականությունը ԱՎ Պթեստեր) ունի աճի հետ Պդրա արժեքը կայունացնելու միտումը էմպիրիկ փաստ է։

Բեռնուլիի թեորեմը.Եկեք ընտրենք ցանկացած կամայականորեն փոքր դրական թիվ e: Ապա

Մենք շեշտում ենք, որ որոշակի մաթեմատիկական մոդելում (Բեռնուլիի սխեմայում) Բերնուլիի կողմից հաստատված մաթեմատիկական փաստը չպետք է շփոթել հաճախականության կայունության էմպիրիկորեն հաստատված օրինաչափության հետ։ Բեռնուլին չբավարարվեց միայն նշելով (9.1) բանաձևը, այլ, հաշվի առնելով պրակտիկայի կարիքները, տվեց այս բանաձևում առկա անհավասարության գնահատականը: Այս մեկնաբանությանը կանդրադառնանք ստորև։

Բեռնուլիի մեծ թվերի օրենքը եղել է մեծ թվով մաթեմատիկոսների ուսումնասիրության առարկա, ովքեր փորձել են այն կատարելագործել։ Այս ճշգրտումներից մեկը ստացվել է անգլիացի մաթեմատիկոս Մոյվրի կողմից և ներկայումս կոչվում է Moivre-Laplace թեորեմ։ Բեռնուլիի սխեմայում դիտարկեք նորմալացված քանակությունների հաջորդականությունը.

Moivre - Laplace-ի ինտեգրալ թեորեմ.Եկեք ընտրենք ցանկացած երկու թիվ X (Եվ x 2.Այս դեպքում x, x 7, ապա ժամը Պ -» °°

Եթե ​​(9.3) բանաձևի աջ կողմում փոփոխականը x xհակված են դեպի անսահմանություն, ապա արդյունքում ստացվող սահմանը, կախված միայն x 2-ից (այս դեպքում 2 ինդեքսը կարող է հեռացվել), կլինի բաշխման ֆունկցիա, այն կոչվում է. ստանդարտ նորմալ բաշխում,կամ Գաուսի օրենքը.

Բանաձևի աջ կողմը (9.3) հավասար է y = F(x 2) - F(x x): F (x 2)-> 1 ժամը x 2-> °° և F(x,) -> 0 x-ում, -> Բավական մեծի ընտրության շնորհիվ

X] > 0 և X]n-ը բավականաչափ մեծ է բացարձակ արժեքով, մենք ստանում ենք հետևյալ անհավասարությունը.

Հաշվի առնելով բանաձևը (9.2), մենք կարող ենք գործնականում վստահելի գնահատականներ հանել.

Եթե ​​y = 0,95 վստահության մակարդակը (այսինքն՝ 0,05 սխալի հավանականությունը) կարող է ինչ-որ մեկին անբավարար թվալ, դուք կարող եք «անվտանգ խաղալ» և մի փոքր ավելի լայն վստահության միջակայք կառուցել՝ օգտագործելով վերը նշված երեք սիգմա կանոնը.

Այս միջակայքը համապատասխանում է վստահության շատ բարձր մակարդակի y = 0,997 (տես նորմալ բաշխման աղյուսակները):

Դիտարկենք մետաղադրամ նետելու օրինակ: Եկեք մետաղադրամ նետենք n = 100 անգամ։ Կարող է պատահել, որ հաճախականությունը Ռշատ տարբեր կլինի հավանականությունից Ռ= 0,5 (ենթադրենք, որ մետաղադրամը սիմետրիկ է), օրինակ, այն հավասար կլինի՞ զրոյի: Դրա համար անհրաժեշտ է, որ զինանշանը անգամ մեկ անգամ չընկնի։ Նման իրադարձությունը տեսականորեն հնարավոր է, բայց մենք արդեն հաշվարկել ենք նմանատիպ հավանականությունները, այս իրադարձության համար այն հավասար կլինի. Այս արժեքը

չափազանց փոքր է, նրա կարգը տասնորդական կետից հետո 30 զրո ունեցող թիվ է: Նման հավանականություն ունեցող իրադարձությունը կարելի է անվտանգ համարել գործնականում անհնարին։ Հաճախականության ի՞նչ շեղումներ հավանականությունից գործնականում հնարավոր են մեծ թվով փորձերի դեպքում: Օգտագործելով Moivre-Laplace թեորեմը, մենք այս հարցին պատասխանում ենք հետևյալ կերպ՝ հավանականությամբ ժամը= 0,95 զինանշանի հաճախականություն Ռտեղավորվում է վստահության միջակայքում.

Եթե ​​0,05 սխալը քիչ է թվում, դուք պետք է ավելացնեք փորձերի քանակը (մետաղադրամների նետում): Երբ ավելանում է Պվստահության միջակայքի լայնությունը նվազում է (ցավոք, ոչ այնքան արագ, որքան մենք կցանկանայինք, բայց հակադարձ համեմատական ​​է -Հովհ.):Օրինակ, երբ Պ= 10,000 մենք ստանում ենք դա Ռգտնվում է վստահության հավանականության հետ վստահության միջակայքում ժամը= 0,95: 0,5 ± 0,01:

Այսպիսով, մենք քանակապես հասկացանք հաճախականությունը հավանականությանը մոտավորելու հարցը։

Հիմա եկեք գտնենք իրադարձության հավանականությունը՝ հիմնվելով դրա հաճախականության վրա և գնահատենք այս մոտավորության սխալը։

Եկեք կատարենք մեծ թվով փորձեր Պ(նետեք մետաղադրամ), գտեք միջոցառման հաճախականությունը Աև մենք ցանկանում ենք գնահատել դրա հավանականությունը Ռ.

Մեծ թվերի օրենքից Պհետևում է, որ.

Այժմ գնահատենք մոտավոր հավասարության գործնականում հնարավոր սխալը (9.7): Դա անելու համար մենք օգտագործում ենք անհավասարություն (9.5) ձևով.

Գտնել ՌԸստ Ռմենք պետք է լուծենք անհավասարությունը (9.8), դրա համար պետք է այն քառակուսի դնել և լուծել համապատասխան քառակուսի հավասարումը: Արդյունքում մենք ստանում ենք.

Որտեղ

Մոտավոր գնահատականի համար ՌԸստ Ռկարող է լինել բանաձեւով (9.8) Ռաջ կողմում փոխարինել Ռկամ (9.10), (9.11) բանաձեւերում ենթադրել, որ

Այնուհետև մենք ստանում ենք.

Ներս թողնել Պ= 400 փորձ, ստացվել է հաճախականության արժեքը Ռ= 0,25, ապա y = 0,95 վստահության մակարդակով մենք գտնում ենք.

Իսկ եթե մեզ պետք է ավելի ճշգրիտ իմանալ հավանականությունը, ասենք, 0,01-ից ոչ ավելի սխալով: Դրա համար անհրաժեշտ է ավելացնել փորձերի քանակը։

Ենթադրելով (9.12) բանաձևով հավանականությունը Ռ= 0.25, մենք սխալի արժեքը հավասարեցնում ենք տրված արժեքին 0.01 և ստանում ենք հավասարում. P:

Լուծելով այս հավասարումը, մենք ստանում ենք n~ 7500.

Այժմ դիտարկենք մեկ այլ հարց. արդյոք փորձերի արդյունքում ստացված հավանականությունից հաճախականության շեղումը կարելի՞ է բացատրել պատահական պատճառներով, թե՞ այս շեղումը ցույց է տալիս, որ հավանականությունը այն չէ, ինչ մենք ակնկալում էինք: Այսինքն՝ փորձը հաստատո՞ւմ է ընդունված վիճակագրական վարկածը, թե՞ հակառակը պահանջում է այն մերժել։

Եկեք, օրինակ, մետաղադրամ նետենք Պ= 800 անգամ, ստանում ենք զինանշանի տեսքի հաճախականությունը Ռ= 0,52: Մենք կասկածում էինք, որ մետաղադրամն ասիմետրիկ է։ Արդարացվա՞ծ է արդյոք այս կասկածը։ Այս հարցին պատասխանելու համար մենք ելնենք այն ենթադրությունից, որ մետաղադրամը սիմետրիկ է (p = 0.5): Գտնենք վստահության միջակայքը (վստահության հավանականությամբ ժամը= 0,95) զինանշանի տեսքի հաճախականության համար. Եթե ​​փորձի արդյունքում ստացված արժեքը Ռ= 0,52 տեղավորվում է այս միջակայքում - ամեն ինչ նորմալ է, մետաղադրամի համաչափության մասին ընդունված վարկածը չի հակասում փորձարարական տվյալներին: Բանաձև (9.12) ժամը Ռ= 0,5-ը տալիս է 0,5 ± 0,035 ընդմիջում; ստացված արժեք p = 0,52-ը տեղավորվում է այս միջակայքում, ինչը նշանակում է, որ մետաղադրամը պետք է «մաքրվի» ասիմետրիայի կասկածներից։

Նմանատիպ մեթոդներ օգտագործվում են դատելու համար, թե պատահական երևույթներում նկատվող մաթեմատիկական ակնկալիքներից տարբեր շեղումները պատահական են, թե «զգալի»: Օրինակ՝ թերքաշը պատահա՞ն է հայտնաբերվել փաթեթավորված ապրանքների մի քանի նմուշներում, թե՞ դա վկայում է հաճախորդների համակարգված խաբեության մասին։ Արդյո՞ք նոր դեղամիջոցն օգտագործող հիվանդների վերականգնման մակարդակը պատահականորեն աճել է, թե՞ դա պայմանավորված է դեղամիջոցի ազդեցությամբ:

Նորմալ օրենքը հատկապես կարևոր դեր է խաղում հավանականությունների տեսության և դրա գործնական կիրառության մեջ: Վերևում մենք արդեն տեսել ենք, որ պատահական փոփոխականը` Բեռնուլիի սխեմայում ինչ-որ իրադարձության դեպքերի քանակը. Պ-» °°-ն իջեցված է նորմալ օրենքի: Այնուամենայնիվ, կա շատ ավելի ընդհանուր արդյունք.

Կենտրոնական սահմանային թեորեմ.Մեծ թվով անկախ (կամ թույլ կախված) պատահական փոփոխականների գումարը, որոնք համեմատելի են միմյանց հետ իրենց շեղումների հերթականությամբ, բաշխվում է սովորական օրենքի համաձայն՝ անկախ այն բանից, թե ինչպիսին են եղել տերմինների բաշխման օրենքները։ Վերոնշյալ պնդումը կենտրոնական սահմանային տեսության կոպիտ որակական ձևակերպումն է։ Այս թեորեմն ունի բազմաթիվ ձևեր, որոնք միմյանցից տարբերվում են այն պայմաններով, որոնք պետք է բավարարեն պատահական փոփոխականները, որպեսզի դրանց գումարը «նորմալացվի»՝ տերմինների քանակի աճով։

Բաշխման նորմալ խտությունը Dx) արտահայտվում է բանաձևով.

Որտեղ Ա -պատահական փոփոխականի մաթեմատիկական ակնկալիք X ս= V7) նրա ստանդարտ շեղումն է:

X-ի (x 1? x 2) միջակայքում ընկնելու հավանականությունը հաշվարկելու համար օգտագործվում է ինտեգրալը.

Քանի որ ինտեգրալը (9.14) խտությամբ (9.13) չի արտահայտվում տարրական ֆունկցիաներով («չի վերցված»), ապա (9.14) հաշվարկելու համար նրանք օգտագործում են ստանդարտ նորմալ բաշխման ինտեգրալ բաշխման ֆունկցիայի աղյուսակներ, երբ. ա = 0, a = 1 (այդպիսի աղյուսակները հասանելի են հավանականությունների տեսության ցանկացած դասագրքում).

Հավանականությունը (9.14) օգտագործելով (10.15) հավասարումը արտահայտվում է բանաձևով.

Օրինակ. Գտեք պատահական փոփոխականի հավանականությունը X,Պարամետրերով նորմալ բաշխում ունենալը Ա, a-ն իր մաթեմատիկական ակնկալիքների մոդուլից կշեղվի 3-ից ոչ ավելի:

Օգտագործելով բանաձևը (9.16) և նորմալ օրենքի բաշխման ֆունկցիայի աղյուսակը, մենք ստանում ենք.

Օրինակ. 700 անկախ փորձերից յուրաքանչյուրում իրադարձությունը Ատեղի է ունենում մշտական ​​հավանականությամբ Ռ= 0,35: Գտեք իրադարձության հավանականությունը Ակկատարվի:

• 1) ուղիղ 270 անգամ;
• 2) 270-ից պակաս և 230 անգամ ավելի.
• 3) ավելի քան 270 անգամ.

Գտնելով մաթեմատիկական ակնկալիքը Ա = և այլնև ստանդարտ շեղում.

պատահական փոփոխական - իրադարձության դեպքերի քանակը A:

Գտնելով կենտրոնացված և նորմալացված արժեքը X:

Նորմալ բաշխման խտության աղյուսակներից մենք գտնում ենք f(x):

Եկեք հիմա գտնենք R w (x,> 270) = P 700 (270 F (1,98) = = 1 - 0,97615 = 0,02385:

Չեբիշևի կողմից 1867 թվականին լուրջ քայլ կատարվեց մեծ թվով խնդիրների հետազոտության մեջ: Նա համարեց շատ ընդհանուր դեպք, երբ անկախ պատահական փոփոխականներից ոչինչ չի պահանջվում, բացի մաթեմատիկական ակնկալիքների և շեղումների առկայությունից։

Չեբիշևի անհավասարությունը.Կամայական փոքր դրական e թվի համար գործում է հետևյալ անհավասարությունը.

Չեբիշևի թեորեմը.Եթե x x, x 2, ..., x p -զույգերով անկախ պատահական փոփոխականներ, որոնցից յուրաքանչյուրն ունի մաթեմատիկական ակնկալիք E(Xj) = քև շեղում D(x,) =), իսկ շեղումները միատեսակ սահմանափակ են, այսինքն. 1,2 ..., ապա ցանկացած կամայական փոքր դրական թվի համար եգործում է հետևյալ կապը.

Հետևանք. Եթե ա,=նա, -o 2, i= 1.2 ..., ապա

Առաջադրանք. Քանի՞ անգամ պետք է մետաղադրամը նետել, որպեսզի հավանականությունը պակաս չլինի y - 0,997, կարելի՞ է պնդել, որ զինանշանի ընկնելու հաճախականությունը կլինի (0,499; 0,501) միջակայքում։

Ենթադրենք, որ մետաղադրամը սիմետրիկ է, p - q - 0.5. Պատահական փոփոխականին կիրառենք Չեբիշևի թեորեմը (9.19). X-զինանշանի տեսքի հաճախականությունը Պմետաղադրամների նետումներ. Վերևում մենք արդեն ցույց ենք տվել X = X x + X 2 + ... +X",Որտեղ X տ -պատահական փոփոխական, որն ընդունում է 1 արժեքը, եթե մետաղադրամը գլուխ է, և 0 արժեքը, եթե այն պոչ է: Այսպիսով.

Հավանականության նշանի տակ նշված իրադարձությանը հակառակ իրադարձության համար գրենք անհավասարություն (9.19).

Մեր դեպքում [e = 0.001, cj 2 = /?-p)]t-ը զինանշանի երևույթների թիվն է Պնետում. Այս մեծությունները փոխարինելով վերջին անհավասարությամբ և հաշվի առնելով, որ խնդրի պայմանների համաձայն անհավասարությունը պետք է բավարարվի, ստանում ենք.

Տվյալ օրինակը ցույց է տալիս Չեբիշևի անհավասարության օգտագործման հնարավորությունը՝ պատահական փոփոխականների որոշակի շեղումների հավանականությունը գնահատելու համար (ինչպես նաև այնպիսի խնդիրներ, ինչպիսին այս օրինակն է՝ կապված այդ հավանականությունների հաշվարկի հետ): Չեբիշևի անհավասարության առավելությունն այն է, որ այն չի պահանջում պատահական փոփոխականների բաշխման օրենքների իմացություն։ Իհարկե, եթե հայտնի է նման օրենքը, ապա Չեբիշևի անհավասարությունը չափազանց կոպիտ գնահատականներ է տալիս։

Դիտարկենք նույն օրինակը, բայց օգտագործելով այն փաստը, որ մետաղադրամ նետելը Բերնուլիի սխեմայի հատուկ դեպքն է: Հաջողությունների թիվը (օրինակում` զինանշանների թիվը) ենթարկվում է երկանդամ օրենքին, իսկ մեծ Պայս օրենքը կարող է ներկայացվել նորմալ օրենքով՝ մաթեմատիկական ակնկալիքով, որը պայմանավորված է Moivre-Laplace ինտեգրալ թեորեմով: a = pr = n? 0,5 և ստանդարտ շեղումով ա = yfnpq - 25=0,5լ/լ. Պատահական փոփոխականը՝ զինանշանի ընկնելու հաճախականությունը, ունի մաթեմատիկական ակնկալիք=0,5 և ստանդարտ շեղում։

Այնուհետև մենք ունենք.

Վերջին անհավասարությունից ստանում ենք.

Նորմալ բաշխման աղյուսակներից մենք գտնում ենք.

Մենք տեսնում ենք, որ նորմալ մոտարկումը տալիս է մետաղադրամի նետումների թիվը, որը տալիս է զինանշանի հավանականության գնահատման տրված սխալ, որը 37 անգամ փոքր է Չեբիշևի անհավասարության միջոցով ստացված գնահատականի համեմատ (բայց Չեբիշևի անհավասարությունը հնարավորություն է տալիս նմանատիպ հաշվարկներ այն դեպքում, երբ մենք տեղեկություն չունենք ուսումնասիրվող պատահական փոփոխականի բաշխման օրենքի մասին):

Այժմ դիտարկենք մի կիրառական խնդիր, որը լուծված է բանաձևով (9.16):

Մրցակցության խնդիր. Երկու մրցակից երկաթուղային ընկերություններ ունեն մեկական գնացք Մոսկվայի և Սանկտ Պետերբուրգի միջև: Այս գնացքները համալրված են մոտավորապես նույնությամբ և մեկնում և ժամանում են մոտավորապես նույն ժամին։ Եկեք այդպես ձևացնենք Պ= 1000 ուղևոր ինքնուրույն և պատահական ընտրում է իրենց գնացքը, հետևաբար, որպես ուղևորների կողմից գնացքի ընտրության մաթեմատիկական մոդել, մենք օգտագործում ենք Բեռնուլիի սխեման. Պմարտահրավերներ և հաջողության հավանականություն Ռ= 0,5. Ընկերությունը պետք է որոշի, թե քանի տեղ հատկացնի գնացքում՝ հաշվի առնելով երկու իրարամերժ պայմաններ. տեղերի բացակայություն (հաջորդ անգամ կնախընտրեն մրցակից ընկերություններին)։ Իհարկե, դա կարելի է տրամադրել գնացքում Պ= 1000 տեղ, բայց հետո ակնհայտորեն դատարկ տեղեր կլինեն։ Պատահական փոփոխական - գնացքի ուղևորների թիվը - ընդունված մաթեմատիկական մոդելի շրջանակներում, օգտագործելով Moivre-ի ինտեգրալ տեսությունը - Լապլասը ենթարկվում է նորմալ օրենքին մաթեմատիկական ակնկալիքով a = pr = p/2 և շեղում a 2 = npq = p/4հաջորդաբար. Հավանականությունը, որ ավելի քան սուղևորներ, որոշվում է հարաբերակցությամբ.

Սահմանեք ռիսկի մակարդակը Ա, այսինքն հավանականությունը, որ ավելի շատ կգա սուղևորներ:

Այստեղից.

Եթե Ավերջին հավասարման ռիսկի արմատն է, որը հայտնաբերվում է նորմալ օրենքի բաշխման ֆունկցիայի աղյուսակներից, ապա ստանում ենք.

Եթե, օրինակ, Պ = 1000, Ա= 0.01 (ռիսկի այս մակարդակը նշանակում է, որ տեղերի քանակը սբավարար կլինի 100-ից 99 դեպքում), ապա x a ~ 2.33 և s = 537 տեղ. Ավելին, եթե երկու ընկերություններն էլ ընդունեն ռիսկի նույն մակարդակը Ա= 0,01, ապա երկու գնացքները կունենան ընդհանուր 1074 նստատեղ, որից 74-ը դատարկ կլինի։ Նմանապես, կարելի է հաշվարկել, որ 514 մանդատը բավարար կլիներ բոլոր դեպքերի 80%-ի դեպքում, իսկ 549 տեղը 1000-ից 999-ի դեպքում։

Նմանատիպ նկատառումներ կիրառվում են սպասարկման այլ մրցակցային խնդիրների դեպքում: Օրինակ, եթե Տկինոթատրոնները նույնի համար են մրցում Պհանդիսատես, ուրեմն պետք է ընդունել Ռ= -. ստանում ենք,

որքա՞ն է նստատեղերի թիվը սկինոթատրոնում պետք է որոշվի հարաբերակցությամբ.

Դատարկ տարածքների ընդհանուր թիվը հավասար է.

Համար Ա = 0,01, Պ= 1000 և Տ= 2, 3, 4 այս թվի արժեքները մոտավորապես հավասար են համապատասխանաբար 74, 126, 147-ի:

Դիտարկենք մեկ այլ օրինակ։ Թող գնացքը բաղկացած լինի Պ - 100 վագոն։ Յուրաքանչյուր մեքենայի քաշը մաթեմատիկական ակնկալիքով պատահական փոփոխական է Ա - 65 տոննա և միջին քառակուսի սպասման o = 9 տոննա Լոկոմոտիվը կարող է տեղափոխել գնացք, եթե նրա քաշը չի գերազանցում 6600 տոննան; հակառակ դեպքում, դուք պետք է միացնեք երկրորդ լոկոմոտիվը: Դուք պետք է գտնեք հավանականությունը, որ դուք ստիպված չեք լինի դա անել:

առանձին մեքենաների կշիռները. , ունենալով նույն մաթեմատիկական ակնկալիքը Ա - 65 և նույն տարբերությունը դ- o 2 = 81. Ըստ մաթեմատիկական ակնկալիքների կանոնի. E(x) - 100 * 65 = 6500. Տարբերությունները գումարելու կանոնի համաձայն. D(x) = 100 x 81 = 8100. Արմատը հանելով՝ մենք գտնում ենք ստանդարտ շեղումը։ Որպեսզի մեկ լոկոմոտիվը քաշի գնացքը, գնացքի քաշը պետք է լինի Xպարզվեց, որ սահմանափակող է, այսինքն ընկել է միջակայքում (0; 6600): Պատահական x փոփոխականը՝ 100 տերմինների գումարը, կարելի է համարել նորմալ բաշխված։ Օգտագործելով բանաձևը (9.16) մենք ստանում ենք.

Դրանից բխում է, որ լոկոմոտիվը «կդիմի» գնացքին մոտավորապես 0,864 հավանականությամբ։ Այժմ գնացքում մեքենաների թիվը երկուսով կրճատենք, այսինքն Պ= 98. Այժմ հաշվարկելով հավանականությունը, որ լոկոմոտիվը «կհաղթահարի» գնացքը, մենք ստանում ենք 0,99 կարգի արժեք, այսինքն՝ գրեթե որոշակի իրադարձություն, չնայած դրա համար ընդամենը երկու մեքենա պետք է հեռացվեր:

Այսպիսով, եթե գործ ունենք մեծ թվով պատահական փոփոխականների գումարների հետ, ապա կարող ենք օգտագործել նորմալ օրենքը։ Բնականաբար, սա հարց է առաջացնում. քանի՞ պատահական փոփոխական պետք է ավելացնել, որպեսզի գումարի բաշխման օրենքն արդեն «նորմալացված» լինի։ Դա կախված է նրանից, թե որոնք են տերմինների բաշխման օրենքները։ Կան այնպիսի բարդ օրենքներ, որ նորմալացումը տեղի է ունենում միայն շատ մեծ թվով տերմիններով: Բայց այս օրենքները հորինված են մաթեմատիկոսների կողմից, բնությունը, որպես կանոն, միտումնավոր նման անախորժություններ չի ստեղծում։ Սովորաբար գործնականում նորմալ օրենքից օգտվելու համար բավական է հինգ-վեց տերմին։

Նույնական բաշխված պատահական փոփոխականների գումարի բաշխման օրենքը «նորմալացվում» է արագությամբ, կարելի է ցույց տալ պատահական փոփոխականների օրինակով (0, 1) միջակայքում միատեսակ բաշխումով: Նման բաշխման կորը ունի ուղղանկյունի ձև, որն այլևս նման չէ սովորական օրենքին։ Ավելացնենք երկու նման անկախ փոփոխականներ՝ ստանում ենք պատահական փոփոխական՝ բաշխված այսպես կոչված Սիմփսոնի օրենքի համաձայն, որի գրաֆիկական պատկերն ունի հավասարաչափ եռանկյունու ձև։ Դա նույնպես սովորական օրենքի տեսք չունի, բայց ավելի լավ է: Եվ եթե գումարեք երեք նման հավասարաչափ բաշխված պատահական փոփոխականներ, ապա կստանաք պարաբոլների երեք հատվածներից բաղկացած կոր, որը շատ նման է նորմալ կորին: Եթե ​​դուք գումարում եք վեց նման պատահական փոփոխականներ, ապա կստանաք կոր, որը չի տարբերվում սովորականից։ Սա հիմք է հանդիսանում նորմալ բաշխված պատահական փոփոխականի ստացման լայնորեն օգտագործվող մեթոդի համար, և բոլոր ժամանակակից համակարգիչները հագեցված են միատեսակ բաշխված (0, 1) պատահական թվերի սենսորներով:

Հետևյալ մեթոդը առաջարկվում է որպես դա ստուգելու գործնական եղանակներից մեկը: Մենք կառուցում ենք վստահության միջակայք մակարդակով իրադարձությունների հաճախականության համար ժամը= 0,997 ըստ երեք սիգմայի կանոնի.

և եթե դրա երկու ծայրերը չեն անցնում հատվածից այն կողմ (0, 1), ապա կարելի է օգտագործել նորմալ օրենքը։ Եթե ​​վստահության միջակայքի սահմաններից որևէ մեկը գտնվում է հատվածից դուրս (0, 1), ապա նորմալ օրենքը չի կարող օգտագործվել: Այնուամենայնիվ, որոշ պայմաններում, ինչ-որ պատահական իրադարձության հաճախականության երկանդամ օրենքը, եթե այն չի հակված նորմալին, ապա այն կարող է հակված լինել մեկ այլ օրենքի:

Բազմաթիվ կիրառություններում Բեռնուլիի սխեման օգտագործվում է որպես պատահական փորձի մաթեմատիկական մոդել, որում փորձարկումների քանակը Պմեծ է, պատահական իրադարձությունը բավականին հազվադեպ է, այսինքն. Ռ = և այլնոչ փոքր, բայց ոչ մեծ (տատանվում է O -5-20 միջակայքում)։ Այս դեպքում սահմանափակող հարաբերությունը գործում է.

Բանաձևը (9.20) կոչվում է Պուասոնի մոտավորություն երկանդամության օրենքի համար, քանի որ դրա աջ կողմում հավանականությունների բաշխումը կոչվում է Պուասոնի օրենք: Պուասոնի բաշխումը համարվում է հազվագյուտ իրադարձությունների հավանականության բաշխում, քանի որ այն տեղի է ունենում, երբ սահմանները բավարարվում են. Պ -»°°, Ռ-»0, բայց X = pr oo.

Օրինակ. Ծննդյան օրեր. Որքա՞ն է հավանականությունը R t (k)որ 500 հոգանոց հասարակության մեջ Դեպիմարդիկ Ամանորին են ծնվել. Եթե ​​այս 500 հոգին ընտրվեն պատահականության սկզբունքով, ապա Բեռնուլիի սխեման կարող է կիրառվել հաջողության հավանականությամբ. P = 1/365. Հետո

Հավանականության հաշվարկներ տարբեր Դեպիտալ հետևյալ արժեքները. RU = 0,3484...; Ռ 2 = 0,2388...; R 3 = 0,1089...; P 4 = 0,0372...; Ռ 5 = 0,0101...; Ռ 6= 0,0023... Համապատասխան մոտավորություններ՝ օգտագործելով Պուասոնի բանաձևը X = 500 1/365 = 1,37

տալ հետևյալ արժեքները. Ru = 0,3481...; Ռ 2 = 0,2385...; P ъ = 0,1089; Ռ 4 = 0,0373...; P 5 = 0,0102...; P 6 = 0,0023... Բոլոր սխալները միայն չորրորդ տասնորդական տեղում են:

Ահա իրավիճակների օրինակներ, որտեղ դուք կարող եք օգտագործել հազվագյուտ իրադարձությունների մասին Պուասոնի օրենքը:

Հեռախոսակայանում սխալ միացում է տեղի ունենում քիչ հավանականությամբ Ռ,սովորաբար Ռ~0,005. Այնուհետև Պուասոնի բանաձևը թույլ է տալիս մեզ գտնել սխալ միացումների հավանականությունը միացումների ընդհանուր թվի համար n~ 1000 երբ X = պր =1000 0,005 = 5.

Բուլկիներ թխելիս խմորին չամիչ ավելացրեք։ Խառնելու պատճառով չամիչով բլիթների հաճախականությունը պետք է ակնկալվի, որ մոտավորապես համապատասխանի Պուասոնի բաշխմանը R p (k, X),Որտեղ X-չամիչի խտությունը խմորի մեջ.

Ռադիոակտիվ նյութը արտանետում է i-մասնիկներ։ Իրադարձություն, որի ընթացքում d-մասնիկների թիվը հասնում է ժամանակի ընթացքում տտրված տարածքի տարածքը, վերցնում է ֆիքսված արժեք դեպի,հնազանդվում է Պուասոնի օրենքին.

Ռենտգենյան ճառագայթների ազդեցության տակ փոփոխված քրոմոսոմներով կենդանի բջիջների թիվը հետևում է Պուասոնի բաշխմանը:

Այսպիսով, մեծ թվերի օրենքները հնարավորություն են տալիս լուծել մաթեմատիկական վիճակագրության խնդիրը՝ կապված պատահական փորձի տարրական արդյունքների անհայտ հավանականությունների գնահատման հետ։ Այս գիտելիքների շնորհիվ մենք գործնականում իմաստալից և օգտակար ենք դարձնում հավանականությունների տեսության մեթոդները: Մեծ թվերի օրենքները նաև հնարավորություն են տալիս անհայտ տարրական հավանականությունների մասին տեղեկություններ ստանալու խնդիրը լուծել այլ ձևով՝ վիճակագրական վարկածների փորձարկման ձևով։

Եկեք ավելի մանրամասն քննարկենք վիճակագրական վարկածների փորձարկման խնդիրների լուծման ձևակերպումը և հավանական մեխանիզմը:

Մեծ թվերի օրենքըՀավանականությունների տեսության մեջ ասվում է, որ ֆիքսված բաշխումից բավական մեծ վերջավոր նմուշի էմպիրիկ միջինը (թվաբանական միջինը) մոտ է այս բաշխման տեսական միջինին (մաթեմատիկական ակնկալիք): Կախված կոնվերգենցիայի տեսակից՝ տարբերվում են մեծ թվերի թույլ օրենքը, երբ կոնվերգենցիան տեղի է ունենում հավանականության մեջ, և մեծ թվերի ուժեղ օրենքը, երբ կոնվերգենցիան տեղի է ունենում գրեթե ամենուր։

Միշտ կա վերջավոր թվով փորձարկումներ, որոնց դեպքում, ցանկացած կանխավճարային հավանականության դեպքում, ավելի քիչ է 1 ինչ-որ իրադարձության առաջացման հարաբերական հաճախականությունը հնարավորինս քիչ կտարբերվի դրա հավանականությունից:

Մեծ թվերի օրենքի ընդհանուր իմաստը. մեծ թվով միանման և անկախ պատահական գործոնների համատեղ գործողությունը հանգեցնում է մի արդյունքի, որը, ըստ սահմանի, կախված չէ պատահականությունից:

Վերջավոր նմուշի վերլուծության վրա հիմնված հավանականության գնահատման մեթոդները հիմնված են այս հատկության վրա: Վառ օրինակ է ընտրողների ընտրանքային հարցման հիման վրա ընտրությունների արդյունքների կանխատեսումը։

Հանրագիտարան YouTube

1 / 5

✪ Մեծ թվերի օրենքը

✪ 07 - Հավանականության տեսություն: Մեծ թվերի օրենքը

✪ 42 Մեծ թվերի օրենքը

✪ 1 - Չեբիշևի օրենքը մեծ թվերի մասին

✪ 11 դասարան, դաս 25, Գաուսի կոր: Մեծ թվերի օրենքը

սուբտիտրեր

Դիտարկենք մեծ թվերի օրենքը, որը թերևս ամենաինտուիտիվ օրենքն է մաթեմատիկայի և հավանականությունների տեսության մեջ: Եվ քանի որ այն վերաբերում է շատ բաների, երբեմն այն օգտագործվում և սխալ է հասկացվում: Թույլ տվեք նախ սահմանել այն ճշգրտության համար, իսկ հետո կխոսենք ինտուիցիայի մասին: Վերցնենք պատահական փոփոխական, օրինակ X: Ենթադրենք, գիտենք դրա մաթեմատիկական ակնկալիքը կամ միջինը բնակչության համար: Մեծ թվերի օրենքը պարզապես ասում է, որ եթե վերցնենք պատահական փոփոխականի n-րդ թվի դիտարկումների օրինակը և վերցնենք այդ բոլոր դիտարկումների միջինը... Վերցնենք փոփոխական։ Եկեք այն անվանենք X՝ n նիշով և վերևում գտնվող բարով: Սա մեր պատահական փոփոխականի n-րդ թվի դիտարկումների միջին թվաբանականն է: Ահա իմ առաջին դիտարկումը. Ես կատարում եմ փորձը մեկ անգամ և կատարում եմ այս դիտարկումը, այնուհետև նորից եմ անում և անում եմ այս դիտարկումը, և ես դա նորից եմ անում և ստանում եմ սա: Ես այս փորձը կատարում եմ n-րդ անգամ, այնուհետև բաժանում եմ իմ դիտարկումների թվի վրա: Ահա իմ միջին նմուշը: Ահա իմ կատարած բոլոր դիտարկումների միջինը։ Մեծ թվերի օրենքը մեզ ասում է, որ իմ ընտրանքի միջինը կմոտենա պատահական փոփոխականի ակնկալվող արժեքին: Կամ կարող եմ նաև գրել, որ իմ ընտրանքի միջինը կմոտենա պոպուլյացիայի միջինին n-րդ մեծության համար, որը հակված է դեպի անսահմանություն: Ես հստակ տարբերություն չեմ անի «մոտավորության» և «կոնվերգենցիայի» միջև, բայց հուսով եմ, որ դուք ինտուիտիվորեն հասկանում եք, որ եթե ես այստեղ բավականին մեծ նմուշ վերցնեմ, ես կստանամ ակնկալվող արժեքը ընդհանուր բնակչության համար: Կարծում եմ, ձեզանից շատերը ինտուիտիվ հասկանում են, որ եթե ես բավականաչափ թեստեր անեմ օրինակների մեծ նմուշով, ի վերջո թեստերն ինձ կտան այն արժեքները, որոնք ես ակնկալում եմ՝ հաշվի առնելով սպասվող արժեքն ու հավանականությունը և այդ ամբողջ ջազը: Բայց ես կարծում եմ, որ հաճախ անհասկանալի է, թե ինչու է դա տեղի ունենում: Եվ մինչ կսկսեմ բացատրել, թե ինչու է դա այդպես, թույլ տվեք կոնկրետ օրինակ բերել: Մեծ թվերի օրենքը մեզ ասում է, որ... Ենթադրենք, մենք ունենք X պատահական փոփոխական: Այն հավասար է արծաթադրամի 100 նետումի գլուխների թվին: Առաջին հերթին մենք գիտենք այս պատահական փոփոխականի մաթեմատիկական ակնկալիքը: Սա մետաղադրամների նետումների կամ փորձարկումների քանակն է՝ բազմապատկված ցանկացած փորձության հաջողության հավանականությամբ: Այսպիսով, սա հավասար է 50-ի: Այսինքն՝ մեծ թվերի օրենքն ասում է, որ եթե նմուշ վերցնենք, կամ այս փորձարկումները միջինացնեմ, կստանամ։ .. Առաջին անգամ երբ փորձություն անեմ, մետաղադրամը 100 անգամ կնետեմ, կամ կվերցնեմ հարյուր մետաղադրամով տուփը, թափահարեմ այն ​​և հետո կհաշվեմ, թե քանի գլուխ եմ ստանում, և կստանամ, ասենք, 55 թիվը։ կլիներ X1: Այնուհետև ես նորից թափահարում եմ տուփը և ստանում եմ 65 թիվը: Հետո նորից և ստանում եմ 45: Եվ ես դա անում եմ n թվով անգամ, այնուհետև այն բաժանում եմ փորձությունների թվի վրա: Մեծ թվերի օրենքը մեզ ասում է, որ այս միջինը (իմ բոլոր դիտարկումների միջինը) կմոտենա 50-ին, քանի որ n-ը մոտենում է անսահմանությանը: Հիմա ես կցանկանայի մի փոքր խոսել այն մասին, թե ինչու է դա տեղի ունենում: Շատերը կարծում են, որ եթե 100 փորձարկումից հետո իմ արդյունքը միջինից բարձր է, ապա հավանականության օրենքների համաձայն ես պետք է շատ կամ քիչ գլուխներ ստանամ, որպեսզի, այսպես ասած, փոխհատուցեմ տարբերությունը։ Դա հենց այն չէ, ինչ տեղի կունենա: Սա հաճախ անվանում են «խաղամոլների մոլորություն»: Թույլ տվեք ցույց տալ ձեզ տարբերությունը: Ես կօգտագործեմ հետևյալ օրինակը. Թույլ տվեք նկարել գրաֆիկ: Եկեք փոխենք գույնը: Սա n է, իմ x առանցքը n է: Սա այն թեստերի քանակն է, որոնք ես կանեմ: Եվ իմ Y առանցքը կլինի նմուշի միջինը: Մենք գիտենք, որ այս կամայական փոփոխականի մաթեմատիկական ակնկալիքը 50 է: Թույլ տվեք նկարել այն: Սա 50 է։ Վերադառնանք մեր օրինակին։ Եթե ​​n-ն է... Իմ առաջին թեստի ժամանակ ես ստացել եմ 55, դա իմ միջինն է: Ես միայն մեկ տվյալների մուտքագրման կետ ունեմ: Հետո երկու թեստից հետո ես ստանում եմ 65: Այսպիսով, իմ միջինը կլինի 65+55 բաժանված 2-ի: Դա 60 է: Եվ իմ միջինը մի փոքր բարձրացել է: Հետո ստացա 45, որը նորից իջեցրեց իմ թվաբանական միջինը։ Ես չեմ պատրաստվում 45-րդ սյուժեն կազմել: Այժմ ես պետք է միջինը գնահատեմ այս ամենը: Ինչի՞ է հավասար 45+65. Թույլ տվեք հաշվարկել այս արժեքը՝ կետը ներկայացնելու համար: Դա 165-ը բաժանված է 3-ի: Դա 53 է: Ոչ, 55: Այսպիսով, միջինը հետ է գնում մինչև 55: Մենք կարող ենք շարունակել այս թեստերը: Այն բանից հետո, երբ մենք կատարեցինք երեք փորձարկումներ և ստացանք այդ միջինը, շատերը կարծում են, որ հավանականության աստվածները կհամոզվեն, որ մենք ապագայում ավելի քիչ գլուխներ ենք հավաքում, որ հաջորդ մի քանի փորձարկումները կունենան ավելի ցածր միավորներ՝ միջինը նվազեցնելու համար: Բայց միշտ չէ, որ այդպես է։ Հետագայում հավանականությունը միշտ նույնն է մնում։ Միշտ 50% հավանականություն կլինի, որ ես գլուխներ ստանամ։ Այնպես չէ, որ ես սկզբում ստանում եմ որոշակի քանակությամբ գլուխներ, ավելին, քան ես ակնկալում եմ, և հետո հանկարծ ես պետք է պոչեր ստանամ: Սա խաղամոլի մոլորությունն է. Միայն այն պատճառով, որ դուք ստանում եք անհամաչափ մեծ թվով գլուխներ, չի նշանակում, որ ինչ-որ պահի դուք կսկսեք անհամաչափ մեծ քանակությամբ պոչեր ստանալ: Սա լիովին ճիշտ չէ: Մեծ թվերի օրենքը մեզ ասում է, որ դա նշանակություն չունի։ Ասենք, որ որոշակի վերջավոր թվով թեստերից հետո ձեր միջինը... Սրա հավանականությունը բավականին փոքր է, բայց, այնուամենայնիվ... Ասենք ձեր միջինը հասել է այս նշագծին՝ 70։ Մտածում ես՝ «Վա՜յ, մենք հեռացանք սպասված արժեքից»։ Բայց մեծ թվերի օրենքն ասում է, որ կարևոր չէ, թե քանի թեստ ենք մենք անում: Առջևում դեռ անսահման թվով մարտահրավերներ ունենք: Այս անսահման թվով փորձությունների մաթեմատիկական ակնկալիքը, հատկապես նման իրավիճակում, կլինի հետևյալը. Երբ դուք գալիս եք մի վերջավոր թվի, որն արտահայտում է ինչ-որ մեծ արժեք, անսահման թիվը, որը համընկնում է դրա հետ, նորից կհանգեցնի ակնկալվող արժեքին: Սա, իհարկե, շատ ազատ մեկնաբանություն է, բայց ահա թե ինչ է մեզ ասում մեծ թվերի օրենքը: Դա կարեւոր է. Դա մեզ չի ասում, որ եթե մենք շատ գլուխներ ստանանք, ապա ինչ-որ կերպ պոչեր ստանալու հավանականությունը կմեծանա՝ փոխհատուցելու համար։ Այս օրենքը մեզ ասում է, որ նշանակություն չունի, թե ինչ արդյունք կունենա վերջավոր թվով փորձարկումներ, քանի դեռ ձեզ մնացել է անսահման թվով փորձարկումներ: Եվ եթե դրանք բավարար չափով անեք, նորից կվերադառնաք ակնկալվող արժեքին: Սա կարևոր կետ է։ Մտածիր այդ մասին. Բայց սա վիճակախաղերի ու կազինոների դեպքում գործնականում ամեն օր չի կիրառվում, չնայած հայտնի է, որ եթե բավականաչափ թեստեր անես... Կարող ենք նույնիսկ հաշվարկել... ինչքա՞ն է հավանականությունը, որ լրջորեն շեղվենք նորմայից։ Բայց կազինոներն ու վիճակախաղերն ամեն օր աշխատում են այն սկզբունքով, որ եթե բավականաչափ մարդ վերցնես, բնականաբար, կարճ ժամանակում, փոքր նմուշով, ապա մի քանի հոգի կխփեն ջեքփոթը։ Բայց երկար ժամանակով խաղատունը միշտ կհաղթի այն խաղերի պարամետրերի շնորհիվ, որոնք հրավիրում են ձեզ խաղալ: Սա հավանականության կարևոր սկզբունք է, որը ինտուիտիվ է: Թեև երբեմն, երբ դա ձեզ պաշտոնապես բացատրվում է պատահական փոփոխականներով, ամեն ինչ մի փոքր շփոթեցնող է թվում: Այս օրենքն ասում է միայն, որ որքան շատ լինեն նմուշները, այնքան այդ նմուշների միջին թվաբանականը կձգտի իրական միջինին: Իսկ ավելի կոնկրետ լինելու համար, ձեր ընտրանքի միջին թվաբանականը կհամընկնի պատահական փոփոխականի մաթեմատիկական ակնկալիքի հետ: Այսքանը: Կհանդիպենք հաջորդ տեսանյութում:

Մեծ թվերի թույլ օրենքը

Մեծ թվերի թույլ օրենքը կոչվում է նաև Բեռնուլիի թեորեմ՝ ի պատիվ Յակոբ Բեռնուլիի, որն ապացուցել է այն 1713 թ.

Թող լինի նույնական բաշխված և անկապ պատահական փոփոխականների անսահման հաջորդականություն (հաջորդական թվարկում): Այսինքն՝ նրանց կովարիանսը c o v (X i, X j) = 0, ∀ i ≠ j (\displaystyle \mathrm (cov) (X_(i),X_(j))=0,\;\բոլոր i\not =j). Թող . Նշենք առաջինի միջին օրինակով n (\displaystyle n)անդամներ:

.

Հետո X ¯ n → P μ (\ցուցադրման ոճ (\ բար (X))_(n)\ դեպի ^(\!\!\!\!\!\!\mathbb (P) )\mu).

Այսինքն՝ ցանկացած դրականի համար ε (\displaystyle \varepsilon)

lim n → ∞ Pr (| X ¯ n − μ |< ε) = 1. {\displaystyle \lim _{n\to \infty }\Pr \!\left(\,|{\bar {X}}_{n}-\mu |<\varepsilon \,\right)=1.}

Մեծ թվերի ուժեղացված օրենքը

Թող լինի անկախ նույնականորեն բաշխված պատահական փոփոխականների անսահման հաջորդականություն (X i) i = 1 ∞ (\displaystyle \(X_(i)\)_(i=1)^(\infty)), սահմանված մեկ հավանականության տարածության վրա (Ω , F , P) (\displaystyle (\Omega,(\mathcal (F)),\mathbb (P))). Թող E X i = μ , ∀ i ∈ N (\displaystyle \mathbb (E) X_(i)=\mu,\;\բոլոր i\in \mathbb (N)). Նշենք ըստ X ¯ n (\ցուցադրման ոճ (\ բար (X))_(n))առաջինի միջին նմուշը n (\displaystyle n)անդամներ:

X ¯ n = 1 n ∑ i = 1 n X i , n ∈ N (\displaystyle (\bar (X))_(n)=(\frac (1)(n))\sum \սահմանները _(i= 1)^(n)X_(i),\;n\in \mathbb (N)).

Հետո X ¯ n → μ (\ցուցադրման ոճ (\բար (X))_(n)\մինչև \mu)գրեթե միշտ.

Pr (lim n → ∞ X ¯ n = μ) = 1. (\displaystyle \Pr \!\left(\lim _(n\to \infty)(\bar (X))_(n)=\mu \ ճիշտ) = 1.) .

Ինչպես ցանկացած մաթեմատիկական օրենք, մեծ թվերի օրենքը կարող է կիրառվել իրական աշխարհի վրա միայն որոշակի ենթադրությունների ներքո, որոնք կարող են բավարարվել միայն որոշակի աստիճանի ճշգրտությամբ: Օրինակ, փորձարկման հաջորդական պայմանները հաճախ չեն կարող պահպանվել անորոշ ժամանակով և բացարձակ ճշգրտությամբ: Բացի այդ, մեծ թվերի օրենքը միայն խոսում է անհավանականությունմիջին արժեքի զգալի շեղում մաթեմատիկական ակնկալիքից: