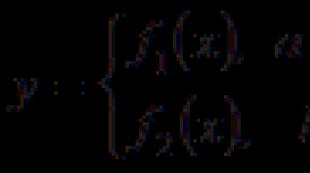Find out which line the equation sets. Determination of the equation of a line, examples of a line on a plane. parallelism condition
The most important concept of analytic geometry is line equation on a plane.
Definition. By the equation of a line (curve) on a plane Oxy is called the equation that the coordinates x and y each point of a given line and the coordinates of any point not lying on this line do not satisfy (Fig. 1).
In the general case, the line equation can be written in the form F (x, y) = 0 or y = f (x).
Example. Find the equation of the set of points equidistant from the points A (-4; 2), B (-2; -6).
Solution. If M (x; y) Is an arbitrary point of the sought line (Fig. 2), then we have AM = BM or
After transformations we get
Obviously, this is the equation of the straight line MD- the perpendicular restored from the middle of the segment AB.
Of all the lines on the plane, straight line... It is a graph of a linear function used in the most commonly used linear economic and mathematical models.
Different types of straight line equation:
1) with slope k and initial ordinate b:
y = kx + b,
where is the angle between the straight line and the positive direction of the axis OH(fig. 3).
Special cases:
- the straight line passes through origin(fig. 4):
– bisector first and third, second and fourth coordinate angles:
y = + x, y = -x;
- straight parallel to the OX axis and myself OX axis(fig. 5):
y = b, y = 0;
- straight parallel to the OY axis and myself axis ОY(fig. 6):
x = a, x = 0;
2) passing in this direction (with slope) k through a given point (fig. 7) :
.
If in the above equation k Is an arbitrary number, then the equation determines bunch of straight lines passing through point , except for a straight line parallel to the axis Oy.
ExampleA (3, -2):
a) at an angle to the axis OH;
b) parallel to the axis OY.
Solution.
a) 
, y - (- 2) = - 1 (x-3) or y = -x + 1;
b) x = 3.
3) passing through two given points (fig. 8) :
.
Example... Equate a straight line through points A (-5.4), B (3, -2).
Solution. 
,
4) the equation of a straight line in segments (fig. 9):
where a, b - the segments to be cut off on the axes, respectively Ox and Oy.
Example... Equate a straight line through a point A (2, -1) if this line cuts off from the positive semiaxis Oy a segment twice as large as from the positive semiaxis Ox(fig. 10).
Solution... By condition b = 2a, then . Substitute the coordinates of the point A (2, -1):
Where a = 1.5.
We finally get:
Or y = -2x + 3.
5) the general equation of the straight line:
Ax + By + C = 0,
where a and b are not equal to zero at the same time.
Some important characteristics of straight lines :
1) distance d from a point to a straight line:
.
2) the angle between straight lines and, respectively:
and 
.
3) the condition for parallelism of lines:
or .
4) the condition of perpendicularity of straight lines:
or 
.
Example 1... Equate two straight lines through a point A (5.1), one of which is parallel to the straight line 3x + 2y-7 = 0 and the other is perpendicular to the same line. Find the distance between parallel lines.
Solution... Figure 11.
1) the equation of a parallel line Ax + By + C = 0:
from the condition of parallelism;
taking the proportionality factor equal to 1, we get A = 3, B = 2;
then. 3x + 2y + C = 0;
meaning WITH find by substituting the coordinates m. A (5.1),
3 * 5 + 2 * 1 + C = 0, where C = -17;
parallel line equation - 3x + 2y-17 = 0.
2) the equation of the perpendicular line from the perpendicularity condition will have the form 2x-3y + C = 0;
substituting the coordinates t. A (5.1), we get 2 * 5-3 * 1 + C = 0, where C = -7;
the equation of the perpendicular line is 2x-3y-7 = 0.
3) the distance between parallel lines can be found as the distance from T. A (5.1) before given straight 3x + 2y-7 = 0:
.
Example 2... The equations of the sides of the triangle are given:
3x-4y + 24 = 0 (AB), 4x + 3y + 32 = 0 (BC), 2x-y-4 = 0 (AC).
Equate the bisector of an angle ABC.
Solution... First, we find the coordinates of the vertex V triangle:
,
where x = -8, y = 0, those. B (-8.0)(fig. 12) .
By the property of the bisector, the distance from each point M (x, y), bisectors BD to the sides AB and Sun are equal, i.e.
,
We get two equations
x + 7y + 8 = 0.7x-y + 56 = 0.
From Figure 12, the slope of the desired straight line is negative (angle with Oh stupid), therefore, the first equation suits us x + 7y + 8 = 0 or y = -1 / 7x-8/7.
Consider a relation of the form F (x, y) = 0 linking variables x and at... Equality (1) will be called an equation with two variables x, y, if this equality is not true for all pairs of numbers X and at... Examples of equations: 2x + 3y = 0, x 2 + y 2 - 25 = 0,
sin x + sin y - 1 = 0.
If (1) is true for all pairs of numbers x and y, then it is called identity... Examples of identities: (x + y) 2 - x 2 - 2xy - y 2 = 0, (x + y) (x - y) - x 2 + y 2 = 0.
Equation (1) will be called the equation of the set of points (x; y), if this equation is satisfied by the coordinates X and at any point of the set and do not satisfy the coordinates of any point that do not belong to this set.
An important concept in analytic geometry is the concept of the equation of a line. Let a rectangular coordinate system and some line be given on the plane α.
Definition. Equation (1) is called the line equation α
(in the created coordinate system) if this equation is satisfied by the coordinates X and at any point on the line α
, and do not satisfy the coordinates of any point that does not lie on this line.
If (1) is the equation of the line α, then we will say that equation (1) defines (sets) line α.
Line α can be determined not only by an equation of the form (1), but also by an equation of the form
F (P, φ) = 0 containing polar coordinates.
- equation of a straight line with a slope;
Let there be given some straight line, not perpendicular to the axis OH... Let's call tilt angle a given straight line to the axis OH injection α to which you want to rotate the axis OH so that the positive direction coincides with one of the directions of the straight line. Tangent of the angle of inclination of the straight line to the axis OH are called slope this straight line and denote by the letter TO.
|
|||
|
|||
Let us derive the equation of this straight line, if we know it TO and the value in the segment OV which she cuts off on the axis OU.
|
|
Equation (2) is called equation of a straight line with slope. If K = 0, then the line is parallel to the axis OH and its equation has the form y = b.
- equation of a straight line passing through two points;
|
|
... This is the equation if y 1 ≠ y 2, can be written as: If y 1 = y 2, then the equation of the sought line has the form y = y 1... In this case, the line is parallel to the axis OH... If x 1 = x 2, then the straight line passing through the points M 1 and M 2 parallel to the axis OU, its equation has the form x = x 1.
- equation of a straight line passing through a given point with a given slope;
|
|
and, conversely, equation (5) with arbitrary coefficients A, B, C (A and B ≠ 0 simultaneously) defines some straight line in a rectangular coordinate system Ooh.
Proof.
First, we prove the first statement. If the line is not perpendicular Oh, then it is determined by an equation of the first degree: y = kx + b, i.e. equation of the form (5), where
A = k, B = -1 and C = b. If the line is perpendicular Oh, then all its points have the same abscissas equal to the value α the segment cut off by a straight line on the axis Oh.
The equation of this line has the form x = α, those. is also an equation of the first degree of the form (5), where A = 1, B = 0, C = - α. This proves the first statement.
Let us prove the converse statement. Let equation (5) be given, and at least one of the coefficients A and B ≠ 0.
If B ≠ 0, then (5) can be written as. Flat 
, we obtain the equation y = kx + b, i.e. equation of the form (2) which determines the straight line.
If B = 0, then A ≠ 0 and (5) takes the form. Denoting through α, we get
x = α, i.e. equation of a straight line perpendicular to Ox.
Lines defined in a rectangular coordinate system by an equation of the first degree are called lines of the first order.
Equation of the form Ax + Wu + C = 0 is incomplete, i.e. any of the coefficients is zero.
1) C = 0; Ah + Wu = 0 and defines a straight line passing through the origin.
2) B = 0 (A ≠ 0); the equation Ax + C = 0 OU.
3) A = 0 (B ≠ 0); Wu + C = 0 and defines a straight parallel Oh.
Equation (6) is called the equation of the straight line "in segments". Numbers a and b are the values of the line segments that the straight line cuts off on the coordinate axes. This form of the equation is convenient for geometric construction of a straight line.
- normal equation of a straight line;
Аx + Вy + С = 0 is the general equation of some straight line, and (5) x cos α + y sin α - p = 0(7)
its normal equation.
Since equation (5) and (7) define the same straight line, then ( A 1x + B 1y + C 1 = 0 and
A 2x + B 2y + C 2 = 0 => 
) the coefficients of these equations are proportional. This means that multiplying all the terms of equation (5) by some factor M, we obtain the equation MA x + MV y + MC = 0 coinciding with equation (7) i.e.
MA = cos α, MB = sin α, MC = - P(8)
To find the factor M, square the first two of these equalities and add:
M 2 (A 2 + B 2) = cos 2 α + sin 2 α = 1
(9)
defines a curve on the plane. A group of terms is called a quadratic form, 
- linear form. If the quadratic form contains only squares of variables, then this form is called canonical, and the vectors of the orthonormal basis, in which the quadratic form has the canonical form, are called the principal axes of the quadratic form.
Matrix 
is called a matrix of quadratic form. Here a 1 2 = a 2 1. To reduce the matrix B to a diagonal form, it is necessary to take the eigenvectors of this matrix as a basis, then 
, where λ 1 and λ 2 are the eigenvalues of the matrix B.
In the basis of the eigenvectors of the matrix B, the quadratic form will have the canonical form: λ 1 x 2 1 + λ 2 y 2 1.
This operation corresponds to the rotation of the coordinate axes. Then the origin of coordinates is shifted, thereby getting rid of the linear shape.
The canonical form of a curve of the second order: λ 1 x 2 2 + λ 2 y 2 2 = a, moreover:
a) if λ 1> 0; λ 2> 0 is an ellipse, in particular, for λ 1 = λ 2 it is a circle;
b) if λ 1> 0, λ 2<0 (λ 1 <0, λ 2 >0) we have a hyperbola;
c) if λ 1 = 0 or λ 2 = 0, then the curve is a parabola and after the rotation of the coordinate axes has the form λ 1 x 2 1 = ax 1 + by 1 + c (here λ 2 = 0). Complementing to a complete square, we will have: λ 1 x 2 2 = b 1 y 2.
An example. The equation of the curve is given 3x 2 + 10xy + 3y 2 -2x-14y-13 = 0 in the coordinate system (0, i, j), where i = (1,0) and j = (0,1).
1. Determine the type of curve.
2. Bring the equation to the canonical form and build a curve in the original coordinate system.
3. Find the appropriate coordinate transformations.
Solution... We bring the quadratic form B = 3x 2 + 10xy + 3y 2 to the principal axes, that is, to the canonical form. The matrix of this quadratic form 
... Find the eigenvalues and eigenvectors of this matrix: 
Characteristic equation: 
; λ 1 = -2, λ 2 = 8. Quadratic form view: 
.
The original equation defines the hyperbola.
Note that the form of the quadratic form is ambiguous. You can write 8x 1 2 -2y 1 2, but the type of the curve remains the same - hyperbola.
Find the principal axes of the quadratic form, that is, the eigenvectors of the matrix B. 
.
The eigenvector corresponding to the number λ = -2 at x 1 = 1: x 1 = (1, -1).
As the unit eigenvector, we take the vector 
, where is the length of the vector x 1.
The coordinates of the second eigenvector corresponding to the second eigenvalue λ = 8 are found from the system 
.
1, j 1).
According to the formulas (5) of paragraph 4.3.3. go to a new basis: 
or
; 
. (*)
We introduce expressions x and y into the original equation and, after transformations, we get:
.
Select complete squares:
.
We carry out a parallel translation of the coordinate axes to a new origin:
, 
.
If we introduce these ratios into (*) and resolve these equalities with respect to x 2 and y 2, then we get:
, 
... In the coordinate system (0 *, i 1, j 1), this equation has the form: 
.
To build a curve, we build a new one in the old coordinate system: the x 2 = 0 axis is set in the old coordinate system by the equation x-y-3 = 0, and the y 2 = 0 axis by the equation x + y-1 = 0. The origin of the new coordinate system 0 * (2, -1) is the intersection point of these lines.
To simplify perception, we will divide the process of plotting into 2 stages:
1. Transition to a coordinate system with axes x 2 = 0, y 2 = 0, specified in the old coordinate system by the equations x-y-3 = 0 and x + y-1 = 0, respectively.
2. Plotting the function graph in the resulting coordinate system.
The final version of the schedule looks like this (see. Solution: Download solution
Exercise... Establish that each of the following equations defines an ellipse, and find the coordinates of its center C, semiaxis, eccentricity, directrix equations. Draw an ellipse in the drawing, specifying the axes of symmetry, foci, and directrix.
Solution.
§ 9. The concept of a line equation.
Specifying a Line Using an Equation
Equality of the form F (x, y) = 0 is called an equation in two variables x, y, if it is not valid for all pairs of numbers x, y. They say that two numbers x = x 0 , y = y 0, satisfy some equation of the form F (x, y) = 0, if, when substituting these numbers instead of variables X and at in the equation, its left-hand side vanishes.
The equation of a given line (in the assigned coordinate system) is an equation with two variables, which is satisfied by the coordinates of each point lying on this line, and the coordinates of every point not lying on it are not satisfied.
In what follows, instead of the expression ", the equation of the line is given F (x, y) = 0 "we will often speak shorter: given a line F (x, y) = 0.
If equations of two lines are given F (x, y) = 0 and Ф (x, y) = Q, then the joint solution of the system
Gives all the points of their intersection. More precisely, each pair of numbers that is a joint solution to this system defines one of the intersection points.
1)X 2 + at 2 = 8, x-y = 0;
2) X 2 + at 2 -16x+4at+18 = 0, x + y= 0;
3) X 2 + at 2 -2x+4at -3 = 0, X 2 + at 2 = 25;
4) X 2 + at 2 -8x+ 10y + 40 = 0, X 2 + at 2 = 4.
163. The points are given in the polar coordinate system
Establish which of these points lie on the line defined by the equation in polar coordinates = 2 cos , and which do not lie on it. Which line is defined by this equation? (Draw it on the drawing :)
164. On the line defined by the equation = 
,
find points whose polar angles are equal to the following numbers: a) 
, b) -, c) 0, d)
... Which line is defined by this equation?
(Build it on the blueprint.)
165. On the line defined by the equation = 
, find points whose polar radii are equal to the following numbers: a) 1, b) 2, c) 
.
Which line is defined by this equation? (Build it on the blueprint.)
166. Establish which lines are determined in polar coordinates by the following equations (build them on the drawing):
1) = 5; 2) =; 3) = 
; 4) cos = 2; 5) sin = 1;
6) = 6 cos ; 7) = 10 sin ; 8) sin =
Consider the function given by the formula (equation)
This function, and hence equation (11), corresponds on the plane to a well-defined line, which is the graph of this function (see Fig. 20). From the definition of the graph of the function it follows that this line consists of those and only those points of the plane whose coordinates satisfy equation (11).
Let now
The line, which is the graph of this function, consists of those and only those points of the plane whose coordinates satisfy equation (12). This means that if a point lies on the specified line, then its coordinates satisfy equation (12). If the point does not lie on this line, then its coordinates do not satisfy equation (12).
Equation (12) is resolved with respect to y. Consider an equation containing x and y and not resolved with respect to y, for example, the equation
Let us show that a line corresponds to this equation in the plane, namely, a circle with a center at the origin and a radius equal to 2. We rewrite the equation in the form
Its left side is the square of the distance of a point from the origin of coordinates (see § 2, item 2, formula 3). It follows from equality (14) that the square of this distance is 4.
This means that any point whose coordinates satisfy equation (14), and hence equation (13), is located at a distance of 2 from the origin of coordinates.
The locus of such points is a circle with a center at the origin and a radius of 2. This circle will be the line corresponding to equation (13). The coordinates of any of its points obviously satisfy Eq. (13). If the point does not lie on the circle we found, then the square of its distance from the origin of coordinates will be either greater or less than 4, which means that the coordinates of such a point do not satisfy Eq. (13).
Suppose now, in the general case, given the equation
on the left side of which there is an expression containing x and y.
Definition. The line defined by equation (15) is the locus of the points of the plane whose coordinates satisfy this equation.
This means that if the line L is determined by the equation, then the coordinates of any point L satisfy this equation, and the coordinates of any point of the plane lying outside L do not satisfy equation (15).
Equation (15) is called the line equation
Comment. Do not think that any equation defines any line. For example, the equation does not define any line. Indeed, for any real values of and y, the left side of this equation is positive, and the right side is equal to zero, and therefore, this equation cannot be satisfied by the coordinates of any point in the plane
A line can be defined on a plane not only by an equation containing Cartesian coordinates, but also by an equation in polar coordinates. The line defined by the equation in polar coordinates is the locus of points on the plane, the polar coordinates of which satisfy this equation.
Example 1. Construct the Archimedes spiral at.
Solution. Let's make a table for some polar angle values and their corresponding polar radius values.
We build a point in the polar coordinate system, which, obviously, coincides with the pole; then, drawing the axis at an angle to the polar axis, we construct a point with a positive coordinate on this axis, after which we similarly construct points with positive values of the polar angle and polar radius (the axes for these points are not indicated in Fig. 30).
Connecting the points together, we get one branch of the curve, indicated in Fig. 30 with a bold line. When changing from 0 to, this branch of the curve consists of an infinite number of turns.
