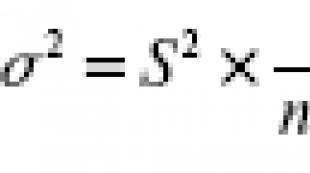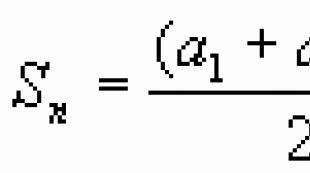Sve formule su u aritmetičkoj progresiji. Aritmetička progresija. Druga vrsta numeričkog niza je geometrijska

Matematika ima svoju ljepotu, baš kao i slikarstvo i poezija.

Ruski naučnik, mehaničar N.E. Zhukovsky

Problemi vezani za pojam aritmetičke progresije vrlo su česti problemi na prijemnim ispitima iz matematike. Za uspješno rješavanje takvih problema potrebno je dobro poznavati svojstva aritmetičke progresije i imati određene vještine u njihovoj primjeni.

Prvo se prisjećamo glavnih svojstava aritmetičke progresije i predstavljamo najvažnije formule, vezano za ovaj koncept.

Definicija. Brojčani niz, u kojem se svaki sljedeći pojam razlikuje od prethodnog za isti broj, naziva aritmetička progresija. Štaviše, brojnaziva se razlika u progresiji.

Za aritmetičku progresiju vrijede sljedeće formule

, (1)

gdje. Formula (1) se naziva formulom za opći pojam aritmetičke progresije, a formula (2) je glavno svojstvo aritmetičke progresije: svaki član progresije poklapa se s aritmetičkom sredinom susjednih članova i.

Imajte na umu da se upravo zbog ovog svojstva razmatrana progresija naziva "aritmetička".

Gore navedene formule (1) i (2) generaliziraju se na sljedeći način:

(3)

Da biste izračunali iznos prvi članovi aritmetičke progresijeobično se primjenjuje formula

(5) gdje i.

Uzimajući u obzir formulu (1), tada formula (5) implicira

Ako označimo, onda

gdje. Budući da su formule (7) i (8) generalizacija odgovarajućih formula (5) i (6).

Posebno, formula (5) implicira, šta

Svojstvo aritmetičke progresije, formulirano pomoću sljedeće teoreme, među učenicima je malo poznato.

Teorema. Ako onda

Dokaz. Ako onda

Teorema je dokazana.

Na primjer , koristeći teoremu, može se pokazati da

Prijeđimo na razmatranje tipičnih primjera rješavanja problema na temu "Aritmetička progresija".

Primjer 1. Neka i. Find.

Rešenje. Primjenjujući formulu (6), dobivamo. Od i, tada ili.

Primjer 2. Neka to bude tri puta više, a dijeljenjem s po količniku dobijemo 2, a ostatak 8. Odredimo i.

Rešenje. Uslov primjera implicira sistem jednačina

Pošto ,, i, tada iz sistema jednačina (10) dobijamo

Rješenje ovog sistema jednadžbi je i.

Primjer 3. Pronađite ako i.

Rešenje. Prema formuli (5) imamo ili. Međutim, korištenjem svojstva (9) dobivamo.

Od i, tada iz jednakosti sledi jednačina ili.

Primjer 4. Pronađi ako.

Rešenje.Po formuli (5) imamo

Međutim, koristeći teoremu, može se pisati

Iz ovoga i formule (11) dobivamo.

Primjer 5. S obzirom :. Find.

Rešenje. Od tada. Međutim, stoga.

Primjer 6. Neka, i. Find.

Rešenje. Koristeći formulu (9), dobivamo. Stoga, ako, tada ili.

Od i, onda ovdje imamo sistem jednadžbi

Rješavajući to, dobivamo i.

Prirodni korijen jednadžbe je .

Primjer 7. Pronađite ako i.

Rešenje. Budući da po formuli (3) to imamo, tada izjava o problemu podrazumijeva sistem jednadžbi

Ako zamijenite izrazu drugu jednačinu sistema, tada dobijamo ili.

Korijeni kvadratne jednadžbe su i.

Razmotrimo dva slučaja.

1. Neka onda. Od i tada.

U ovom slučaju, prema formuli (6), imamo

2. Ako, tada, i

Odgovor: i.

Primjer 8. Poznato je da i. Find.

Rešenje. Uzimajući u obzir formulu (5) i uvjete primjera, zapisujemo i.

Otuda slijedi sistem jednadžbi

Pomnožimo li prvu jednadžbu sistema sa 2, a zatim je dodamo drugoj jednadžbi, dobivamo

Prema formuli (9), imamo... S tim u vezi, iz (12) slijedi ili.

Od i tada.

Odgovor:.

Primjer 9. Pronađite ako i.

Rešenje. Pošto, i prema uvjetu, tada ili.

Iz formule (5) je poznato, šta . Od tada.

Dakle, ovdje imamo sistem linearnih jednadžbi

Otuda dobijamo i. Uzimajući u obzir formulu (8), pišemo.

Primjer 10. Riješite jednadžbu.

Rešenje. Iz date jednadžbe proizlazi da. Pretpostavimo da ,, i. U ovom slučaju .

Prema formuli (1), možete napisati ili.

Budući da tada jednadžba (13) ima jedan odgovarajući korijen.

Primjer 11. Pronađite najveću vrijednost pod uvjetom da i.

Rešenje. Budući da se razmatrana aritmetička progresija smanjuje. S tim u vezi, izraz poprima maksimalnu vrijednost kada je to broj minimalnog pozitivnog člana progresije.

Koristimo formulu (1) i činjenicu, as. Onda dobijemo to ili.

Pošto, tada ili ... Međutim, u ovoj nejednakostinajveći prirodni broj, dakle.

Ako su vrijednosti i zamijenjene formulom (6), tada dobivamo.

Odgovor:.

Primjer 12. Odredite zbir svih dvocifrenih prirodnih brojeva koji, podijeljeni sa 6, daju ostatak 5.

Rešenje. Označimo skupom svih dvocifrenih prirodnih brojeva, tj. ... Zatim konstruiramo podskup koji se sastoji od onih elemenata (brojeva) skupa koji, podijeljeni sa 6, daju ostatak 5.

Nije teško ustanoviti, šta . Očigledno, da su elementi skupaformiraju aritmetičku progresiju, u kojoj i.

Pretpostavljamo da za utvrđivanje kardinalnosti (broja elemenata) skupa. Pošto i, tada iz formule (1) slijedi ili. Uzimajući u obzir formulu (5), dobivamo.

Gore navedeni primjeri rješavanja problema ni na koji način ne mogu tvrditi da su iscrpni. Ovaj članak je napisan na osnovu analize savremenih metoda rješavanja tipičnih problema na zadatu temu. Za dublje proučavanje metoda za rješavanje problema povezanih s aritmetičkom progresijom, preporučljivo je pozvati se na listu preporučene literature.

1. Zbirka matematičkih zadataka za podnosioce zahtjeva za tehničke fakultete / Ur. M.I. Skanavi. - M.: Mir i obrazovanje, 2013.- 608 str.

2. Suprun V.P. Matematika za srednjoškolce: dodatni dijelovi školskog programa. - M.: Lenand / URSS, 2014.- 216 str.

3. Medynsky M.M. Kompletan kurs osnovne matematike u zadacima i vježbama. Knjiga 2: Brojni nizovi i progresije. - M.: Edithus, 2015.- 208 str.

Imate li još pitanja?

Za pomoć od tutora - registrirajte se.

web mjesto, s potpunim ili djelomičnim kopiranjem materijala, potrebna je veza na izvor.

Vrsta lekcije: učenje novog gradiva.

Ciljevi časa:

• proširenje i produbljivanje ideja učenika o problemima riješenim pomoću aritmetičke progresije; organizacija aktivnosti pretraživanja učenika prilikom izvođenja formule za zbir prvih n članova aritmetičke progresije;
• razvoj vještina za samostalno stjecanje novih znanja, korištenje već stečenog znanja za postizanje postavljenog zadatka;
• razvoj želje i potrebe za generalizacijom dobivenih činjenica, razvoj neovisnosti.

Zadaci:

• generalizirati i sistematizirati postojeća znanja na temu „Aritmetička progresija“;
• izvode formule za izračunavanje zbroja prvih n članova aritmetičke progresije;
• naučiti kako primijeniti dobivene formule u rješavanju različitih problema;
• skrenuti pažnju učenika na redoslijed radnji pri pronalaženju vrijednosti numeričkog izraza.

Oprema:

• kartice sa zadacima za rad u grupama i parovima;
• evaluacijski rad;
• prezentacija"Aritmetička progresija".

I. Ažuriranje osnovnih znanja.

1. Samostalan rad u paru.

Prva opcija:

Dajte definiciju aritmetičke progresije. Zapišite ponavljajuću formulu koja definira aritmetičku progresiju. Pozdrav primjer aritmetičke progresije i navedite njenu razliku.

Druga opcija:

Zapišite formulu za n -ti član aritmetičke progresije. Pronađite 100. član aritmetičke progresije ( a n}: 2, 5, 8 …
U ovom trenutku, dva učenika sa zadnje strane ploče pripremaju odgovore na ista pitanja.
Učenici ocjenjuju rad partnera u odnosu na ploču. (Listovi za odgovore se predaju).

2. Trenutak igre.

Vježba 1.

Učitelju. Ja sam zamislio neku aritmetičku progresiju. Samo mi postavite dva pitanja kako biste nakon odgovora mogli brzo nazvati sedmi pojam ove progresije. (1, 3, 5, 7, 9, 11, 13, 15 ...)

Pitanja učenika.

1. Koji je šesti pojam u progresiji i koja je razlika?
2. Koji je osmi pojam u progresiji i koja je razlika?

Ako nema više pitanja, nastavnik ih može stimulirati - „zabraniti“ d (razlika), odnosno nije dopušteno pitati u čemu je razlika. Možete postavljati pitanja: šta je šesti termin progresije, a šta osmi termin progresije?

Zadatak 2.

Na tabli je napisano 20 brojeva: 1, 4, 7 10, 13, 16, 19, 22, 25, 28, 31, 34, 37, 40, 43, 46, 49, 52, 55, 58.

Učitelj stoji okrenut leđima prema tabli. Učenici pozivaju broj broja, a učitelj odmah poziva sam broj. Objasnite kako to radim?

Nastavnik pamti formulu za n -ti termin a n = 3n - 2 i zamjenjujući zadane vrijednosti n, pronalazi odgovarajuće vrijednosti a n.

II. Izjava o obrazovnom problemu.

Predlažem da se riješi drevni problem koji datira iz drugog milenijuma prije nove ere, pronađen u egipatskim papirusima.

Zadatak:„Neka vam se kaže: podijelite 10 mjera ječma na 10 ljudi, razlika između svake osobe i njegovog susjeda jednaka je 1/8 mjere“.

• Kako je ovaj zadatak povezan s temom aritmetičke progresije? (Svaki sljedeći dobije 1/8 mjere više, što znači razlika d = 1/8, 10 ljudi, što znači n = 10.)
• Šta mislite da znači broj 10? (Zbir svih članova progresije.)
• Šta još trebate znati da biste lakše i lakše podijelili ječam prema stanju zadatka? (Prvi termin u progresiji.)

Cilj lekcije- dobijanje ovisnosti zbira članova progresije o njihovom broju, prvom članu i razlici i provjeravanje je li problem ispravno riješen u davna vremena.

Prije nego zaključimo formulu, pogledajmo kako su stari Egipćani riješili problem.

I to su riješili na sljedeći način:

1) 10 mjera: 10 = 1 mjera - prosječno učešće;
2) 1 mjera ∙ = 2 mjere - udvostručena prosek dijeliti.
Udvostručeno prosek udio je zbroj dionica 5. i 6. osobe.
3) 2 mjere - 1/8 mjere = 1 7/8 mjere - dvostruko više od udjela pete osobe.
4) 1 7/8: 2 = 5/16 - udeo petine; i tako dalje, možete pronaći udio svake prethodne i sljedeće osobe.

Dobijamo redosled:

III. Rješenje problema.

1. Rad u grupama

Grupa I: Pronađite zbir 20 uzastopnih prirodnih brojeva: S 20 = (20 + 1) ∙ 10 = 210.

Uglavnom

II grupa: Pronađite zbir prirodnih brojeva od 1 do 100 (Legenda o Malom Gausu).

S 100 = (1 + 100) ∙ 50 = 5050

Izlaz:

III grupa: Pronađite zbir prirodnih brojeva od 1 do 21.

Rešenje: 1 + 21 = 2 + 20 = 3 + 19 = 4 + 18 ...

Izlaz:

IV grupa: Pronađite zbir prirodnih brojeva od 1 do 101.

Izlaz:

Ova metoda za rješavanje razmatranih problema naziva se “Gaussova metoda”.

2. Svaka grupa predstavlja rješenje problema na tabli.

3. Generalizacija predloženih rješenja za proizvoljnu aritmetičku progresiju:

a 1, a 2, a 3, ..., a n-2, a n-1, a n.
S n = a 1 + a 2 + a 3 + a 4 +… + a n-3 + a n-2 + a n-1 + a n.

Pronađimo ovaj iznos zaključivanjem na sličan način:

4. Jesmo li riješili zadatak?(Da.)

IV. Primarno razumijevanje i primjena dobivenih formula u rješavanju problema.

1. Provjera rješenja starog problema pomoću formule.

2. Primjena formule u rješavanju različitih problema.

3. Vježbe za formiranje sposobnosti primjene formule pri rješavanju problema.

A) Ne. 613

S obzirom: ( a n) - aritmetička progresija;

(a n): 1, 2, 3, ..., 1500

Pronađi: S 1500

Rešenje: , a 1 = 1, a 1500 = 1500,

B) S obzirom: ( a n) - aritmetička progresija;
(a n): 1, 2, 3, ...
S n = 210

Pronađi: n
Rešenje:

V. Samostalan rad uz međusobnu provjeru.

Denis je otišao raditi kao kurir. U prvom mjesecu njegova je plaća iznosila 200 rubalja, u svakom sljedećem mjesecu povećavala se za 30 rubalja. Koliko je zaradio za godinu dana?

S obzirom: ( a n) - aritmetička progresija;
a 1 = 200, d = 30, n = 12
Pronađi: S 12
Rešenje:

Odgovor: Denis je za godinu dana primio 4380 rubalja.

Vi. Brifing o domaćim zadacima.

1. str. 4.3 - naučite izvođenje formule.
2. №№ 585, 623 .
3. Napravite problem koji bi se riješio formulom za zbir prvih n članova aritmetičke progresije.

Vii. Rezimirajući lekciju.

1. Evaluacioni list

2. Nastavite rečenice

• Danas sam na lekciji naučio ...
• Naučene formule ...
• Mislim da …

3. Možete li pronaći zbir brojeva od 1 do 500? Kojom metodom ćete riješiti ovaj problem?

Bibliografija.

1. Algebra, 9. razred. Udžbenik za obrazovne institucije. Ed. G.V. Dorofeeva. M.: "Obrazovanje", 2009.

Da, da: napredak aritmetike nije igračka za vas :)

Pa, prijatelji, ako čitate ovaj tekst, onda mi unutrašnja očiglednost kaže da još ne znate šta je aritmetička progresija, ali zaista (ne, ovako: SOOOOO!) Želite znati. Stoga vas neću mučiti dugim uvodima i prijeći na stvar.

Počnimo s nekoliko primjera. Razmotrimo nekoliko skupova brojeva:

• 1; 2; 3; 4; ...
• 15; 20; 25; 30; ...
• $ \ sqrt (2); \ 2 \ sqrt (2); \ 3 \ sqrt (2); ... $

Šta je zajedničko svim ovim skupovima? Na prvi pogled, ništa. Ali u stvari postoji nešto. Naime: svaki sljedeći element razlikuje se od prethodnog istim brojem.

Prosudite sami. Prvi skup su jednostavno uzastopni brojevi, svaki sljedeći više od prethodnog. U drugom slučaju, razlika između susjednih brojeva već je jednaka pet, ali je ta razlika i dalje konstantna. U trećem slučaju, korijeni općenito. Međutim, $ 2 \ sqrt (2) = \ sqrt (2) + \ sqrt (2) $, i $ 3 \ sqrt (2) = 2 \ sqrt (2) + \ sqrt (2) $, tj. iu ovom slučaju, svaki sljedeći element jednostavno se povećava za $ \ sqrt (2) $ (i nemojte se bojati da je ovaj broj iracionalan).

Dakle: sve takve sekvence nazivaju se aritmetičke progresije. Dajmo strogu definiciju:

Definicija. Niz brojeva u kojima se svaki sljedeći razlikuje od prethodnog za potpuno isti iznos naziva se aritmetička progresija. Sam iznos po kojem se brojevi razlikuju naziva se razlika progresije i najčešće se označava slovom $ d $.

Oznaka: $ \ left (((a) _ (n)) \ right) $ - sama progresija, $ d $ - njena razlika.

I samo par važnih napomena. Prvo, samo uredan redosled brojeva: dozvoljeno im je da se čitaju striktno redosledom kojim su napisani - i ništa drugo. Ne možete preurediti ili zamijeniti brojeve.

Drugo, sam niz može biti konačan ili beskonačan. Na primjer, skup (1; 2; 3) je očito konačna aritmetička progresija. Ali ako napišete nešto u duhu (1; 2; 3; 4; ...) - ovo je već beskrajan napredak. Elipsa nakon četiri, takoreći, nagovještava da se još uvijek događa podosta brojeva. Beskonačno mnogo, na primjer. :)

Također želim napomenuti da se progresije povećavaju i smanjuju. Već smo vidjeli sve veće - isti skup (1; 2; 3; 4; ...). I evo primjera smanjenja progresije:

• 49; 41; 33; 25; 17; ...
• 17,5; 12; 6,5; 1; −4,5; −10; ...
• $ \ sqrt (5); \ \ sqrt (5) -1; \ \ sqrt (5) -2; \ \ sqrt (5) -3; ... $

U redu, u redu: ovaj posljednji primjer može izgledati previše komplicirano. Ali ostalo vam je jasno. Stoga ćemo uvesti nove definicije:

Definicija. Aritmetička progresija se naziva:

1. povećava se ako je svaki sljedeći element veći od prethodnog;
2. smanjuje se ako je, naprotiv, svaki sljedeći element manji od prethodnog.

Osim toga, postoje takozvani "stacionarni" nizovi - sastoje se od istog ponavljajućeg broja. Na primjer, (3; 3; 3; ...).

Ostaje samo jedno pitanje: kako razlikovati rastuću progresiju od opadajuće? Srećom, sve ovisi o predznaku broja $ d $, tj. progresija razlike:

1. Ako je $ d \ gt 0 $, progresija se povećava;
2. Ako je $ d \ lt 0 $, onda se progresija očigledno smanjuje;
3. Konačno, postoji slučaj $ d = 0 $ - u ovom slučaju cijela se progresija svodi na stacionarni niz identičnih brojeva: (1; 1; 1; 1; ...) itd.

Pokušajmo izračunati razliku $ d $ za tri gore navedene progresivne progresije. Da biste to učinili, dovoljno je uzeti bilo koja dva susjedna elementa (na primjer, prvi i drugi) i oduzeti broj s lijeve strane od broja s desne strane. To će izgledati ovako:

• 41−49=−8;
• 12−17,5=−5,5;
• $ \ sqrt (5) -1- \ sqrt (5) = - 1 $.

Kao što vidite, u sva tri slučaja razlika se zaista pokazala negativnom. A sada kada smo manje -više shvatili definicije, vrijeme je da shvatimo kako su progresije opisane i koja su njihova svojstva.

Članovi progresije i ponavljajuća formula

Budući da se elementi naših nizova ne mogu zamijeniti, mogu se numerirati:

\ [\ lijevo (((a) _ (n)) \ desno) = \ lijevo \ (((a) _ (1)), \ ((a) _ (2)), ((a) _ (3 )), ... \ udesno \) \]

Pojedinačni elementi ovog skupa nazivaju se članovi progresije. Označeni su brojem: prvi pojam, drugi pojam itd.

Osim toga, kao što već znamo, susjedni članovi progresije povezani su formulom:

\ [((a) _ (n))-((a) _ (n-1)) = d \ Desna strelica ((a) _ (n)) = ((a) _ (n-1)) + d \]

Ukratko, da biste pronašli $ n $ -ti član u progresiji, morate znati $ n-1 $ -ti član i $ d $ razliku. Takva se formula naziva ponavljajućom, jer uz njenu pomoć možete pronaći bilo koji broj, samo znajući prethodni (a zapravo - sve prethodne). Ovo je vrlo nezgodno, pa postoji složenija formula koja sve kalkulacije svodi na prvi član i razliku:

\ [((a) _ (n)) = ((a) _ (1)) + \ lijevo (n-1 \ desno) d \]

Sigurno ste već upoznali ovu formulu. Vole ga davati u svim vrstama priručnika i reshebnika. U svakom razumnom udžbeniku o matematici ona je jedna od prvih.

Međutim, predlažem da malo vježbamo.

Problem broj 1. Ispišite prva tri člana aritmetičke progresije $ \ left (((a) _ (n)) \ right) $, ako je $ ((a) _ (1)) = 8, d = -5 $.

Rešenje. Dakle, znamo da je prvi član $ ((a) _ (1)) = 8 $ i razlika progresije $ d = -5 $. Upotrijebimo formulu koju smo upravo dali i zamijenimo $ n = 1 $, $ n = 2 $ i $ n = 3 $:

\ [\ begin (align) & ((a) _ (n)) = ((a) _ (1)) + \ left (n-1 \ right) d; \\ & ((a) _ (1)) = ((a) _ (1)) + \ lijevo (1-1 \ desno) d = ((a) _ (1)) = 8; \\ & ((a) _ (2)) = ((a) _ (1)) + \ lijevo (2-1 \ desno) d = ((a) _ (1)) + d = 8-5 = 3; \\ & ((a) _ (3)) = ((a) _ (1)) + \ lijevo (3-1 \ desno) d = ((a) _ (1)) + 2d = 8-10 = -2. \\ \ završi (poravnaj) \]

Odgovor: (8; 3; −2)

To je sve! Napomena: naš napredak se smanjuje.

Naravno, $ n = 1 $ nije moglo biti zamijenjeno - prvi izraz nam je već poznat. Međutim, zamijenivši jednu, uvjerili smo se da naša formula funkcionira čak i za prvi termin. U drugim slučajevima, sve se svelo na trivijalnu aritmetiku.

Problem broj 2. Zapišite prva tri člana aritmetičke progresije ako je njen sedmi član −40, a sedamnaesti član −50.

Rešenje. Zapišemo stanje problema uobičajenim izrazima:

\ [((a) _ (7)) = - 40; \ quad ((a) _ (17)) = - 50. \]

\ [\ left \ (\ begin (align) & ((a) _ (7)) = ((a) _ (1)) + 6d \\ & ((a) _ (17)) = ((a) _ (1)) + 16d \\ \ end (poravnaj) \ udesno. \]

\ [\ left \ (\ begin (align) & ((a) _ (1)) + 6d = -40 \\ & ((a) _ (1))) + 16d = -50 \\ \ end (align) \ desno. \]

Stavio sam znak sistema jer se ovi zahtjevi moraju istovremeno ispuniti. I sada primijetite da ako oduzmemo prvu od druge jednadžbe (imamo pravo na to, budući da imamo sistem), dobivamo ovo:

\ [\ begin (align) & ((a) _ (1)) + 16d- \ left (((a) _ (1)) + 6d \ right) =- 50- \ left (-40 \ right); \\ & ((a) _ (1)) + 16d - ((a) _ (1)) - 6d = -50 + 40; \\ & 10d = -10; \\ & d = -1. \\ \ završi (poravnaj) \]

Tako smo lako pronašli razliku u napredovanju! Ostaje zamijeniti pronađeni broj u bilo kojoj jednadžbi sistema. Na primjer, u prvom:

\ [\ begin (matrica) ((a) _ (1)) + 6d = -40; \ quad d = -1 \\ \ Downarrow \\ ((a) _ (1)) -6 = -40; \\ ((a) _ (1)) = - 40 + 6 = -34. \\ \ kraj (matrica) \]

Sada, znajući prvi pojam i razliku, ostaje pronaći drugi i treći član:

\ [\ begin (align) & ((a) _ (2)) = ((a) _ (1)) + d = -34-1 = -35; \\ & ((a) _ (3)) = ((a) _ (1)) + 2d = -34-2 = -36. \\ \ završi (poravnaj) \]

Ready! Problem je riješen.

Odgovor: (-34; -35; -36)

Obratite pažnju na zanimljivo svojstvo progresije koje smo otkrili: ako uzmemo $ n $ th i $ m $ th članove i oduzmemo ih jedan od drugog, tada ćemo dobiti razliku progresije pomnoženu s brojem $ n-m $:

\ [((a) _ (n)) - ((a) _ (m)) = d \ cdot \ lijevo (n -m \ desno) \]

Jednostavno, ali vrlo korisno svojstvo koje biste svakako trebali znati - uz njegovu pomoć možete značajno ubrzati rješavanje mnogih problema koji napreduju. Evo sjajnog primjera:

Problem broj 3. Peti član aritmetičke progresije je 8,4, a deseti 14,4. Pronađi petnaesti član ove progresije.

Rešenje. Budući da je $ ((a) _ (5)) = 8,4 $, $ ((a) _ (10)) = 14,4 $, a vi morate pronaći $ ((a) _ (15)) $, tada primjećujemo sljedeće :

\ [\ begin (align) & ((a) _ (15)) - ((a) _ (10)) = 5d; \\ & ((a) _ (10)) - ((a) _ (5)) = 5d. \\ \ završi (poravnaj) \]

Ali prema uvjetu $ ((a) _ (10)) - ((a) _ (5)) = 14,4-8,4 = 6 USD, dakle 5d = 6 USD, odakle imamo:

\ [\ begin (align) & ((a) _ (15)) - 14.4 = 6; \\ & ((a) _ (15)) = 6 + 14,4 = 20,4. \\ \ završi (poravnaj) \]

Odgovor: 20.4

To je sve! Nismo morali sastaviti neke sustave jednadžbi i izračunati prvi član i razliku - sve je riješeno u samo nekoliko redova.

Razmotrimo sada drugu vrstu zadataka - pronaći negativne i pozitivne članove progresije. Nije tajna da ako se progresija poveća, dok je prvi član negativan, prije ili kasnije u njemu će se pojaviti pozitivni termini. I naprotiv: članovi opadajuće progresije će prije ili kasnije postati negativni.

U isto vrijeme, daleko je od toga da je moguće ovaj trenutak opipati "čelo", uzastopno prolazeći kroz elemente. Često su problemi dizajnirani na takav način da bi bez poznavanja formula proračuni trajali nekoliko listova - samo bismo zaspali dok smo pronašli odgovor. Stoga ćemo te probleme pokušati riješiti na brži način.

Problem broj 4. Koliko negativnih članova ima u aritmetičkoj progresiji -38,5; −35,8; ...?

Rešenje. Dakle, $ ((a) _ (1)) = - 38,5 $, $ ((a) _ (2)) = - 35,8 $, odakle odmah nalazimo razliku:

Imajte na umu da je razlika pozitivna, pa se progresija povećava. Prvi izraz je negativan, pa ćemo u jednom trenutku zaista naići na pozitivne brojeve. Pitanje je samo kada će se to dogoditi.

Pokušajmo saznati: koliko dugo (tj. Do prirodnog broja $ n $) se čuva negativnost pojmova:

\ [\ begin (align) & ((a) _ (n)) \ lt 0 \ Desna strelica ((a) _ (1)) + \ lijevo (n-1 \ desno) d \ lt 0; \\ & -38,5+ \ lijevo (n -1 \ desno) \ cdot 2,7 \ lt 0; \ quad \ lijevo | \ cdot 10 \ udesno. \\ & -385 + 27 \ cdot \ lijevo (n -1 \ desno) \ lt 0; \\ & -385 + 27n -27 \ lt 0; \\ & 27n \ lt 412; \\ & n \ lt 15 \ frac (7) (27) \ Rightarrow ((n) _ (\ max)) = 15. \\ \ završi (poravnaj) \]

Zadnji redak treba neko objašnjenje. Dakle, znamo da je $ n \ lt 15 \ frac (7) (27) $. S druge strane, zadovoljit ćemo se samo cijelim vrijednostima broja (štaviše: $ n \ in \ mathbb (N) $), tako da je najveći dozvoljeni broj točno $ n = 15 $, i nikako 16.

Problem broj 5. U aritmetičkoj progresiji $ (() _ (5)) = - 150, (() _ (6)) = - 147 $. Pronađite broj prvog pozitivnog člana ove progresije.

To bi bio potpuno isti problem kao i prethodni, ali ne znamo $ ((a) _ (1)) $. Ali susjedni pojmovi su poznati: $ ((a) _ (5)) $ i $ ((a) _ (6)) $, tako da možemo lako pronaći razliku progresije:

Osim toga, pokušat ćemo izraziti peti izraz u smislu prvog i razlike prema standardnoj formuli:

\ [\ begin (align) & ((a) _ (n)) = ((a) _ (1)) + \ left (n-1 \ right) \ cdot d; \\ & ((a) _ (5)) = ((a) _ (1)) + 4d; \\ & -150 = ((a) _ (1)) + 4 \ cdot 3; \\ & ((a) _ (1)) = -150-12 = -162. \\ \ završi (poravnaj) \]

Sada nastavljamo analogno s prethodnim zadatkom. Otkrivamo u kojem će trenutku našeg slijeda biti pozitivnih brojeva:

\ [\ begin (align) & ((a) _ (n)) = - 162+ \ left (n -1 \ right) \ cdot 3 \ gt 0; \\ & -162 + 3n -3 \ gt 0; \\ & 3n \ gt 165; \\ & n \ gt 55 \ Desna strelica ((n) _ (\ min)) = 56. \\ \ završi (poravnaj) \]

Najmanje cjelobrojno rješenje ove nejednakosti je 56.

Napomena: u zadnjem zadatku sve se svelo na strogu nejednakost, pa nam opcija $ n = 55 $ neće odgovarati.

Sada kada smo naučili rješavati jednostavne probleme, prijeđimo na složenije. Ali prvo, proučimo još jedno vrlo korisno svojstvo aritmetičkih progresija, koje će nam u budućnosti uštedjeti mnogo vremena i nejednakih ćelija. :)

Aritmetička sredina i jednake alineje

Razmotrimo nekoliko uzastopnih članova rastuće aritmetičke progresije $ \ left (((a) _ (n)) \ right) $. Pokušajmo ih označiti na numeričkoj liniji:

Članovi aritmetičke progresije na brojevnoj pravoj

Posebno sam napomenuo proizvoljne izraze $ ((a) _ (n-3)), ..., ((a) _ (n + 3)) $, a ne bilo koje $ ((a) _ (1)), \ ( (a) _ (2)), \ ((a) _ (3)) $, itd. Jer pravilo, o kojem ću sada govoriti, funkcionira isto za sve "segmente".

A pravilo je vrlo jednostavno. Sjetimo se formule ponavljanja i zapišite je za sve označene članove:

\ [\ begin (align) & ((a) _ (n-2)) = ((a) _ (n-3)) + d; \\ & ((a) _ (n-1)) = ((a) _ (n-2)) + d; \\ & ((a) _ (n)) = ((a) _ (n-1)) + d; \\ & ((a) _ (n + 1)) = ((a) _ (n)) + d; \\ & ((a) _ (n + 2)) = ((a) _ (n + 1)) + d; \\ \ završi (poravnaj) \]

Međutim, ove se jednakosti mogu drugačije prepisati:

\ [\ begin (align) & ((a) _ (n -1)) = ((a) _ (n)) - d; \\ & ((a) _ (n -2)) = ((a) _ (n)) - 2d; \\ & ((a) _ (n -3)) = ((a) _ (n)) - 3d; \\ & ((a) _ (n + 1)) = ((a) _ (n)) + d; \\ & ((a) _ (n + 2)) = ((a) _ (n)) + 2d; \\ & ((a) _ (n + 3)) = ((a) _ (n)) + 3d; \\ \ završi (poravnaj) \]

Pa, pa što? A činjenica da izrazi $ ((a) _ (n-1)) $ i $ ((a) _ (n + 1)) $ leže na istoj udaljenosti od $ ((a) _ (n)) $ . Ova udaljenost je jednaka $ d $. Isto se može reći i za članove $ ((a) _ (n -2)) $ i $ ((a) _ (n + 2)) $ - oni se također uklanjaju iz $ ((a) _ (n) ) $ ista udaljenost jednaka 2d $. Možete nastaviti neograničeno dugo, ali značenje je dobro ilustrirano slikom.

Članovi progresije leže na istoj udaljenosti od središta

Šta ovo znači za nas? To znači da možete pronaći $ ((a) _ (n)) $ ako su poznati susjedni brojevi:

\ [((a) _ (n)) = \ frac (((a) _ (n-1)) + ((a) _ (n + 1))) (2) \]

Došli smo do odlične izjave: svaki član aritmetičke progresije jednak je aritmetičkoj sredini susjednih pojmova! Štaviše: možemo odstupiti od naših $ ((a) _ (n)) $ lijevo i desno ne jedan korak, već $ k $ koraka - i dalje će formula biti točna:

\ [((a) _ (n)) = \ frac (((a) _ (n-k)) + ((a) _ (n + k))) (2) \]

One. lako možemo pronaći neke $ ((a) _ (150)) $ ako znamo $ ((a) _ (100)) $ i $ ((a) _ (200)) $, jer $ ((a) _ (150)) = \ frac (((a) _ (100)) + ((a) _ (200))) (2) $. Na prvi pogled može se činiti da nam ta činjenica ne daje ništa korisno. Međutim, u praksi su mnogi problemi posebno "izoštreni" za upotrebu aritmetičke sredine. Pogledaj:

Problem broj 6. Pronađite sve vrijednosti $ x $ za koje su brojevi $ -6 ((x) ^ (2)) $, $ x + 1 $ i $ 14 + 4 ((x) ^ (2)) $ uzastopni članovi aritmetičke progresije (po redu).

Rešenje. Budući da su navedeni brojevi članovi progresije, za njih je ispunjen uvjet aritmetičke sredine: centralni element $ x + 1 $ može se izraziti u smislu susjednih elemenata:

\ [\ begin (align) & x + 1 = \ frac (-6 ((x) ^ (2)) + 14 + 4 ((x) ^ (2))) (2); \\ & x + 1 = \ frac (14-2 ((x) ^ (2))) (2); \\ & x + 1 = 7 - ((x) ^ (2)); \\ & ((x) ^ (2)) + x-6 = 0. \\ \ završi (poravnaj) \]

Rezultat je klasična kvadratna jednadžba. Njegovi korijeni: $ x = 2 $ i $ x = -3 $ - ovo su odgovori.

Odgovor: −3; 2.

Problem broj 7. Pronađite vrijednosti $$ za koje brojevi $ -1; 4-3; (() ^ (2)) + 1 $ čine aritmetičku progresiju (tim redoslijedom).

Rešenje. Opet, izražavamo srednji pojam u smislu aritmetičke sredine susjednih pojmova:

\ [\ begin (align) & 4x-3 = \ frac (x-1 + ((x) ^ (2)) + 1) (2); \\ & 4x-3 = \ frac (((x) ^ (2)) + x) (2); \ quad \ left | \ cdot 2 \ desno.; \\ & 8x-6 = ((x) ^ (2)) + x; \\ & ((x) ^ (2)) - 7x + 6 = 0. \\ \ završi (poravnaj) \]

Opet kvadratna jednačina. I opet postoje dva korijena: $ x = 6 $ i $ x = 1 $.

Odgovor: 1; 6.

Ako u procesu rješavanja problema dobijete neke brutalne brojeve ili niste potpuno sigurni u točnost pronađenih odgovora, onda postoji prekrasna tehnika koja vam omogućuje da provjerite: jesmo li problem riješili ispravno?

Na primjer, u problemu broj 6 dobili smo odgovore -3 i 2. Kako provjeriti jesu li ovi odgovori tačni? Samo ih uključimo i vidimo šta će se dogoditi. Podsjećam vas da imamo tri broja ($ -6 (() ^ (2)) $, $ + 1 $ i $ 14 + 4 (() ^ (2)) $). Zamjena $ x = -3 $:

\ [\ begin (align) & x = -3 \ Rightarrow \\ & -6 ((x) ^ (2)) = -54; \\ & x + 1 = -2; \\ & 14 + 4 ((x) ^ (2)) = 50. \ end (poravnaj) \]

Primljeni brojevi -54; −2; 50, koji se razlikuju za 52, nesumnjivo je aritmetička progresija. Ista stvar se dešava za $ x = 2 $:

\ [\ begin (align) & x = 2 \ Rightarrow \\ & -6 ((x) ^ (2)) = - 24; \\ & x + 1 = 3; \\ & 14 + 4 ((x) ^ (2)) = 30. \ end (poravnaj) \]

Opet napredovanje, ali s razlikom od 27. Dakle, problem je ispravno riješen. Zainteresovani mogu sami provjeriti drugi problem, ali odmah ću reći: i tu je sve tačno.

Općenito, rješavajući posljednje probleme, naišli smo na još jednu zanimljivu činjenicu, koju također treba zapamtiti:

Ako su tri broja takva da je drugi aritmetička sredina prvog i posljednjeg, tada ti brojevi čine aritmetičku progresiju.

U budućnosti će nam razumijevanje ove izjave doslovno "konstruirati" potrebne progresije, na osnovu stanja problema. No, prije nego što prijeđemo na takvu "izgradnju", trebali bismo obratiti pažnju na još jednu činjenicu, koja direktno proizlazi iz onoga što je već razmatrano.

Grupisanje i zbir elemenata

Vratimo se opet na osi brojeva. Zabilježimo tamo nekoliko članova napredovanja, između kojih je možda. ima mnogo drugih članova:

Brojčana linija ima 6 označenih elemenata

Pokušajmo izraziti "lijevi rep" u smislu $ ((a) _ (n)) $ i $ d $, a "desni rep" u smislu $ ((a) _ (k)) $ i $ d $ . Vrlo je jednostavno:

\ [\ begin (align) & ((a) _ (n + 1)) = ((a) _ (n)) + d; \\ & ((a) _ (n + 2)) = ((a) _ (n)) + 2d; \\ & ((a) _ (k -1)) = ((a) _ (k)) - d; \\ & ((a) _ (k -2)) = ((a) _ (k)) - 2d. \\ \ završi (poravnaj) \]

Sada imajte na umu da su sljedeće sume jednake:

\ [\ begin (align) & ((a) _ (n)) + ((a) _ (k)) = S; \\ & ((a) _ (n + 1)) + ((a) _ (k -1)) = ((a) _ (n)) + d + ((a) _ (k)) - d = S; \\ & ((a) _ (n + 2)) + ((a) _ (k -2)) = ((a) _ (n)) + 2d + ((a) _ (k)) - 2d = S. \ end (poravnaj) \]

Jednostavno rečeno, ako za početak uzmemo u obzir dva elementa progresije, koji su ukupno jednaki nekom broju $ S $, i tada počinjemo hodati od ovih elemenata u suprotnim smjerovima (jedan prema drugom ili obrnuto da se odmaknemo) , onda zbroji elemenata na koje ćemo naići takođe će biti jednaki$ S $. Ovo se najjasnije može grafički prikazati:

Jednako uvlačenje daje jednake količine

Razumijevanje ove činjenice omogućit će nam rješavanje problema fundamentalno višeg stupnja složenosti od onih koje smo gore razmatrali. Na primjer, takve:

Problem broj 8. Odredite razliku aritmetičke progresije u kojoj je prvi član 66, a proizvod drugog i dvanaestog člana najmanji mogući.

Rešenje. Zapišite sve što znamo:

\ [\ begin (align) & ((a) _ (1)) = 66; \\ & d =? \\ & ((a) _ (2)) \ cdot ((a) _ (12)) = \ min. \ end (poravnaj) \]

Dakle, ne znamo razliku u progresiji $ d $. Zapravo, cijelo rješenje bit će izgrađeno oko razlike, budući da se proizvod $ ((a) _ (2)) \ cdot ((a) _ (12)) $ može prepisati na sljedeći način:

\ [\ begin (align) & ((a) _ (2)) = ((a) _ (1)) + d = 66 + d; \\ & ((a) _ (12)) = ((a) _ (1)) + 11d = 66 + 11d; \\ & ((a) _ (2)) \ cdot ((a) _ (12)) = \ lijevo (66 + d \ desno) \ cdot \ lijevo (66 + 11d \ desno) = \\ & = 11 \ cdot \ lijevo (d + 66 \ desno) \ cdot \ lijevo (d + 6 \ desno). \ end (poravnaj) \]

Za one u spremniku: iz druge zagrade sam izvadio zajednički faktor 11. Dakle, traženi proizvod je kvadratna funkcija s obzirom na varijablu $ d $. Stoga, razmotrite funkciju $ f \ left (d \ right) = 11 \ left (d + 66 \ right) \ left (d + 6 \ right) $ - njen graf će biti parabola s granama prema gore, budući da ako proširimo zagrade, dobivamo:

\ [\ begin (align) & f \ left (d \ right) = 11 \ left (((d) ^ (2)) + 66d + 6d + 66 \ cdot 6 \ right) = \\ & = 11 (( d) ^ (2)) + 11 \ cdot 72d + 11 \ cdot 66 \ cdot 6 \ end (poravnaj) \]

Kao što vidite, koeficijent na vodećem terminu je 11 - ovo je pozitivan broj, pa se zaista bavimo parabolom sa granama prema gore:

kvadratni grafikon funkcija - parabola

Napomena: ova parabola uzima svoju minimalnu vrijednost u svom vrhu s apscisom $ ((d) _ (0)) $. Naravno, ovu apscisu možemo izračunati prema standardnoj shemi (postoji i formula $ ((d) _ (0)) = (- b) / (2a) \; $), ali bilo bi razumnije primijetiti da željeni vrh leži na osi simetrije parabole, pa je točka $ ((d) _ (0)) $ jednako udaljena od korijena jednadžbe $ f \ lijevo (d \ desno) = 0 $:

\ [\ begin (align) & f \ left (d \ right) = 0; \\ & 11 \ cdot \ lijevo (d + 66 \ desno) \ cdot \ lijevo (d + 6 \ desno) = 0; \\ & ((d) _ (1)) = - 66; \ quad ((d) _ (2)) = - 6. \\ \ završi (poravnaj) \]

Zato nisam žurio s otvaranjem zagrada: u izvornom obliku korijenje je bilo vrlo, vrlo lako pronaći. Stoga je apscisa jednaka aritmetičkoj sredini brojeva −66 i −6:

\ [((d) _ (0)) = \ frac (-66-6) (2) =-36 \]

Šta nam otkriveni broj daje? Uz to, traženi proizvod poprima najmanju vrijednost (usput, nismo brojali $ ((y) _ (\ min)) $ - ovo nam ne treba). Istovremeno, ovaj broj je razlika između početne progresije, tj. odgovor smo pronašli. :)

Odgovor: −36

Problem broj 9. Umetnite tri broja između brojeva $ - \ frac (1) (2) $ i $ - \ frac (1) (6) $ tako da zajedno s danim brojevima tvore aritmetičku progresiju.

Rešenje. U osnovi, moramo napraviti niz od pet brojeva, s tim da su prvi i zadnji broj već poznati. Označimo nedostajuće brojeve varijablama $ x $, $ y $ i $ z $:

\ [\ lijevo (((a) _ (n)) \ desno) = \ lijevo \ ( - \ frac (1) (2); x; y; z; - \ frac (1) (6) \ right \ ) \]

Imajte na umu da je broj $ y $ "sredina" našeg niza - jednako je udaljen i od brojeva $ x $ i $ z $, i od brojeva $ - \ frac (1) (2) $ i $ - \ frac (1) (6) $. A ako trenutno ne možemo dobiti $ y $ iz brojeva $ x $ i $ z $, onda je situacija drugačija s krajevima progresije. Zapamtite aritmetičku sredinu:

Sada, znajući $ y $, pronaći ćemo preostale brojeve. Imajte na umu da $ x $ leži između brojeva $ - \ frac (1) (2) $ i $ y = - \ frac (1) (3) $ koje smo upravo pronašli. Zbog toga

Slično obrazloženju, nalazimo preostali broj:

Ready! Pronašli smo sva tri broja. Zapišite ih u odgovor redoslijedom kojim ih treba umetnuti između izvornih brojeva.

Odgovor: $ - \ frac (5) (12); \ - \ frac (1) (3); \ - \ frac (1) (4) $

Problem broj 10. Umetnite nekoliko brojeva između brojeva 2 i 42, koji zajedno s tim brojevima tvore aritmetičku progresiju, ako znate da je zbir prvog, drugog i posljednjeg umetnutog broja 56.

Rešenje. Još teži zadatak, koji se, međutim, rješava po istoj shemi kao i prethodni - kroz aritmetičku sredinu. Problem je u tome što ne znamo tačno koliko brojeva treba umetnuti. Stoga, radi definitivnosti, pretpostavimo da će nakon umetanja svega biti tačno $ n $ brojeva, a prvi od njih je 2, a zadnji 42. U ovom slučaju, željena aritmetička progresija može se predstaviti kao:

\ [\ lijevo (((a) _ (n)) \ desno) = \ lijevo \ (2; ((a) _ (2)); ((a) _ (3)); ...; (( a) _ (n-1)); 42 \ udesno \) \]

\ [((a) _ (2)) + ((a) _ (3)) + ((a) _ (n-1)) = 56 \]

Imajte na umu, međutim, da se brojevi $ ((a) _ (2)) $ i $ ((a) _ (n-1)) $ dobivaju iz brojeva 2 i 42 na rubovima za jedan korak jedan prema drugom, tj ... do središta niza. Ovo znači to

\ [((a) _ (2)) + ((a) _ (n-1)) = 2 + 42 = 44 \]

Ali tada se gore napisani izraz može prepisati na sljedeći način:

\ [\ begin (align) & ((a) _ (2)) + ((a) _ (3)) + ((a) _ (n-1)) = 56; \\ & \ lijevo (((a) _ (2)) + ((a) _ (n-1)) \ desno) + ((a) _ (3)) = 56; \\ & 44 + ((a) _ (3)) = 56; \\ & ((a) _ (3)) = 56-44 = 12. \\ \ završi (poravnaj) \]

Poznavajući $ ((a) _ (3)) $ i $ ((a) _ (1)) $, lako možemo pronaći razliku progresije:

\ [\ begin (align) & ((a) _ (3)) - ((a) _ (1)) = 12 - 2 = 10; \\ & ((a) _ (3)) - ((a) _ (1)) = \ lijevo (3-1 \ desno) \ cdot d = 2d; \\ & 2d = 10 \ Desna strelica d = 5. \\ \ završi (poravnaj) \]

Ostaje samo pronaći ostale članove:

\ [\ begin (align) & ((a) _ (1)) = 2; \\ & ((a) _ (2)) = 2 + 5 = 7; \\ & ((a) _ (3)) = 12; \\ & ((a) _ (4)) = 2 + 3 \ cdot 5 = 17; \\ & ((a) _ (5)) = 2 + 4 \ cdot 5 = 22; \\ & ((a) _ (6)) = 2 + 5 \ cdot 5 = 27; \\ & ((a) _ (7)) = 2 + 6 \ cdot 5 = 32; \\ & ((a) _ (8)) = 2 + 7 \ cdot 5 = 37; \\ & ((a) _ (9)) = 2 + 8 \ cdot 5 = 42; \\ \ završi (poravnaj) \]

Tako ćemo već u 9. koraku doći do lijevog kraja niza - broja 42. Ukupno je bilo potrebno umetnuti samo 7 brojeva: 7; 12; 17; 22; 27; 32; 37.

Odgovor: 7; 12; 17; 22; 27; 32; 37

Riječi problemi s progresijama

Zaključno, htio bih razmotriti nekoliko relativno jednostavnih zadataka. Pa, kako jednostavno: većini učenika koji uče matematiku u školi i nisu pročitali gore napisano, ovi zadaci mogu izgledati kao lim. Ipak, upravo se takvi problemi pojavljuju u OGE -u i USE -u u matematici, pa vam preporučujem da se s njima upoznate.

Problem broj 11. Brigada je u januaru proizvela 62 dijela, a svakog narednog mjeseca proizvodila je 14 dijelova više nego u prethodnom. Koliko je dijelova tim napravio u novembru?

Rešenje. Očigledno je da će broj dijelova, raspoređenih po mjesecima, predstavljati sve veću aritmetičku progresiju. Štaviše:

\ [\ begin (align) & ((a) _ (1)) = 62; \ quad d = 14; \\ & ((a) _ (n)) = 62+ \ lijevo (n-1 \ desno) \ cdot 14. \\ \ end (align) \]

Novembar je 11. mjesec u godini, pa moramo pronaći $ ((a) _ (11)) $:

\ [((a) _ (11)) = 62 + 10 \ cdot 14 = 202 \]

Shodno tome, 202 dijela će se proizvoditi u novembru.

Problem broj 12. Radnja za uvezivanje knjiga uvezala je 216 knjiga u januaru, a svakog narednog mjeseca uvezivala je 4 knjige više od prethodnog. Koliko knjiga je radionica uvezala u decembru?

Rešenje. Sve isto:

$ \ begin (align) & ((a) _ (1)) = 216; \ quad d = 4; \\ & ((a) _ (n)) = 216+ \ lijevo (n-1 \ desno) \ cdot 4. \\ \ end (align) $

Decembar je posljednji, 12. mjesec u godini, pa tražimo $ ((a) _ (12)) $:

\ [((a) _ (12)) = 216 + 11 \ cdot 4 = 260 \]

Ovo je odgovor - u decembru će biti uvezano 260 knjiga.

Pa, ako ste do sada čitali, žurim vam čestitati: uspješno ste prošli "kurs mladih boraca" u aritmetičkim progresijama. Možete sigurno preći na sljedeću lekciju, gdje ćemo proučiti formulu za zbir progresije, kao i važne i vrlo korisne posljedice iz nje.

Na primjer, niz \ (2 \); \ (5 \); \ (osam \); \ (jedanaest \); \ (14 \) ... je aritmetička progresija, jer se svaki sljedeći element razlikuje od prethodnog za tri (može se dobiti iz prethodnog dodavanjem trojke):

U ovoj progresiji, razlika \ (d \) je pozitivna (jednaka \ (3 \)), pa je stoga svaki sljedeći član veći od prethodnog. Takve se progresije nazivaju povećava se.

Međutim, \ (d \) može biti i negativno. Na primjer, u aritmetičkoj progresiji \ (16 \); \(deset\); \ (4 \); \ (- 2 \); \ (- 8 \) ... razlika progresije \ (d \) jednaka je minus šest.

I u ovom slučaju svaki sljedeći element bit će manji od prethodnog. Ove progresije se nazivaju opadajući.

Aritmetički zapis progresije

Napredak je označen malim latiničnim slovom.

Brojevi koji tvore progresiju to nazivaju članovi(ili elementi).

Označeni su istim slovom kao aritmetička progresija, ali s numeričkim indeksom jednakim broju elementa po redu.

Na primjer, aritmetička progresija \ (a_n = \ lijevo \ (2; 5; 8; 11; 14 ... \ desno \) \) sastoji se od elemenata \ (a_1 = 2 \); \ (a_2 = 5 \); \ (a_3 = 8 \) i tako dalje.

Drugim riječima, za progresiju \ (a_n = \ lijevo \ (2; 5; 8; 11; 14 ... \ desno \) \)

Rješavanje problema za aritmetičku progresiju

U principu, gornje informacije su već dovoljne za rješavanje gotovo svih problema aritmetičke progresije (uključujući i one ponuđene u OGE -u).

Primjer (OGE). Aritmetička progresija je specificirana uslovima \ (b_1 = 7; d = 4 \). Pronađi \ (b_5 \).
Rešenje:

Odgovor: \ (b_5 = 23 \)

Primjer (OGE). Daju se prva tri člana aritmetičke progresije: \ (62; 49; 36 ... \) Nađite vrijednost prvog negativnog člana ove progresije.
Rešenje:

	Dati su nam prvi elementi niza i znamo da je to aritmetička progresija. To jest, svaki element se razlikuje od susjednog za isti broj. Saznajte koji, oduzimajući prethodni od sljedećeg elementa: \ (d = 49-62 = -13 \).
	Sada možemo vratiti svoj napredak na (prvi negativni) element koji nam je potreban.
	Ready. Možete napisati odgovor.

Odgovor: \(-3\)

Primjer (OGE). Dano je nekoliko uzastopnih elemenata aritmetičke progresije: \ (… 5; x; 10; 12,5 ... \) Nađite vrijednost elementa označenu slovom \ (x \).
Rešenje:

	Da bismo pronašli \ (x \), moramo znati koliko se sljedeći element razlikuje od prethodnog, drugim riječima, razlika progresije. Pronađimo ga iz dva poznata susjedna elementa: \ (d = 12,5-10 = 2,5 \).
	I sada bez problema pronalazimo željenu: \ (x = 5 + 2,5 = 7,5 \).
	Ready. Možete napisati odgovor.

Odgovor: \(7,5\).

Primjer (OGE). Aritmetička progresija je specificirana sljedećim uslovima: \ (a_1 = -11 \); \ (a_ (n + 1) = a_n + 5 \) Nađite zbir prvih šest članova ove progresije.
Rešenje:

Moramo pronaći zbir prvih šest članova progresije. Ali ne znamo njihova značenja, dat nam je samo prvi element. Stoga prvo izračunavamo vrijednosti redom, koristeći sljedeće: \ (n = 1 \); \ (a_ (1 + 1) = a_1 + 5 = -11 + 5 = -6 \) \ (n = 2 \); \ (a_ (2 + 1) = a_2 + 5 = -6 + 5 = -1 \) \ (n = 3 \); \ (a_ (3 + 1) = a_3 + 5 = -1 + 5 = 4 \) Izračunavši šest elemenata koji su nam potrebni, nalazimo njihov zbir.

\ (S_6 = a_1 + a_2 + a_3 + a_4 + a_5 + a_6 = \) \(=(-11)+(-6)+(-1)+4+9+14=9\)

Iznos koji tražite je pronađen.

Odgovor: \ (S_6 = 9 \).

Primjer (OGE). U aritmetičkoj progresiji \ (a_ (12) = 23 \); \ (a_ (16) = 51 \). Pronađite razliku između ove progresije.
Rešenje:

Odgovor: \ (d = 7 \).

Važne formule aritmetičke progresije

Kao što vidite, mnogi problemi aritmetičke progresije mogu se riješiti jednostavnim razumijevanjem glavne stvari - da je aritmetička progresija lanac brojeva, a svaki sljedeći element u ovom lancu dobiva se dodavanjem istog broja prethodnom (razlika progresije).

Međutim, ponekad postoje situacije kada je vrlo nezgodno odlučiti se "frontalno". Na primjer, zamislite da u prvom primjeru moramo pronaći ne peti element \ (b_5 \), već tristo osamdeset šesti \ (b_ (386) \). Šta je to, mi \ (385 \) puta dodamo četiri? Ili zamislite da u pretposljednjem primjeru trebate pronaći zbir prva sedamdeset i tri elementa. Bićete mučeni da brojite ...

Stoga u takvim slučajevima ne rješavaju "čeono", već koriste posebne formule izvedene za aritmetičku progresiju. A glavni su formula za n -ti član progresije i formula za zbir \ (n \) prvih članova.

Formula \ (n \) - th član: \ (a_n = a_1 + (n -1) d \), gdje je \ (a_1 \) prvi član progresije;
\ (n \) - broj elementa koji se traži;
\ (a_n \) je član progresije sa brojem \ (n \).

Ova formula nam omogućava da brzo pronađemo barem tristoti, čak i milioniti element, znajući samo prvi i razliku progresije.

Primjer. Aritmetička progresija je određena uslovima: \ (b_1 = -159 \); \ (d = 8,2 \). Pronađi \ (b_ (246) \).
Rešenje:

Odgovor: \ (b_ (246) = 1850 \).

Formula za zbir prvih n članova: \ (S_n = \ frac (a_1 + a_n) (2) \ cdot n \), gdje

\ (a_n \) - posljednji sažeti pojam;

Primjer (OGE). Aritmetička progresija je određena uslovima \ (a_n = 3,4n-0,6 \). Pronađite zbir prvih \ (25 \) članova ove progresije.
Rešenje:

\ (S_ (25) = \) \ (\ frac (a_1 + a_ (25)) (2) \) \ (\ cdot 25 \)		Da bismo izračunali zbir prvih dvadeset pet elemenata, moramo znati vrijednost prvog i dvadeset petog člana. Naš napredak dat je formulom n -tog člana ovisno o njegovom broju (vidi detalje). Izračunajmo prvi element zamjenom jednog za \ (n \).
\ (n = 1; \) \ (a_1 = 3,4 1-0,6 = 2,8 \)		Sada nalazimo dvadeset peti izraz, zamjenjujući dvadeset pet umjesto \ (n \).
\ (n = 25; \) \ (a_ (25) = 3,4 25-0,6 = 84,4 \)		Pa, sada možemo bez problema izračunati potrebnu količinu.
\ (S_ (25) = \) \ (\ frac (a_1 + a_ (25)) (2) \) \ (\ cdot 25 = \) \ (= \) \ (\ frakcija (2,8 + 84,4) (2) \) \ (\ cdot 25 = \) \ (1090 \)		Odgovor je spreman.

Odgovor: \ (S_ (25) = 1090 \).

Za zbir \ (n \) prvih pojmova možete dobiti drugu formulu: samo trebate \ (S_ (25) = \) \ (\ frac (a_1 + a_ (25)) (2) \) \ (\ cdot 25 \) umjesto \ (a_n \) zamijenite formulu \ (a_n = a_1 + (n-1) d \). Dobijamo:

Formula za zbir prvih n članova: \ (S_n = \) \ (\ frac (2a_1 + (n-1) d) (2) \) \ (\ cdot n \), gdje

\ (S_n \) - potrebna suma \ (n \) prvih elemenata;
\ (a_1 \) - prvi sažeti pojam;
\ (d \) - razlika u progresiji;
\ (n \) - broj stavki u zbiru.

Primjer. Nađi zbroj prvih \ (33 \) - bivših članova aritmetičke progresije: \ (17 \); \ (15,5 \); \ (četrnaest \)…
Rešenje:

Odgovor: \ (S_ (33) = - 231 \).

Složeniji problemi aritmetičke progresije

Sada imate sve potrebne informacije za rješavanje gotovo svakog problema s aritmetičkom progresijom. Temu zaključujemo razmatranjem problema u kojima morate ne samo primijeniti formule, već i malo razmisliti (u matematici ovo može biti korisno ☺)

Primjer (OGE). Pronađite zbir svih negativnih članova progresije: \ (- 19,3 \); \ (-19 \); \ (- 18,7 \) ...
Rešenje:

\ (S_n = \) \ (\ frac (2a_1 + (n-1) d) (2) \) \ (\ cdot n \)		Zadatak je vrlo sličan prethodnom. Počinjemo rješavati i: prvo pronalazimo \ (d \).
\ (d = a_2 -a_1 = -19 - ( - 19,3) = 0,3 \)		Sada bismo zamijenili \ (d \) u formuli za zbir ... i tu se pojavljuje mala nijansa - ne znamo \ (n \). Drugim riječima, ne znamo koliko će termina trebati dodati. Kako to saznati? Hajde da razmislimo. Prestaćemo dodavati elemente kada dođemo do prvog pozitivnog elementa. To jest, morate saznati broj ovog elementa. Kako? Zapišimo formulu za izračunavanje bilo kojeg elementa aritmetičke progresije: \ (a_n = a_1 + (n-1) d \) za naš slučaj.
\ (a_n = a_1 + (n-1) d \)
\ (a_n = -19,3 + (n -1) 0,3 \)		Trebamo da \ (a_n \) bude veće od nule. Hajde da saznamo na čemu će se \ (n \) to dogoditi.
\ (- 19,3+ (n-1) 0,3> 0 \)
\ ((n-1) 0,3> 19,3 \) \ (|: 0,3 \)		Dijelimo obje strane nejednakosti sa \ (0,3 \).
\ (n-1> \) \ (\ frakcija (19,3) (0,3) \)		Krećite se minus jedan, ne zaboravite promijeniti znakove
\ (n> \) \ (\ frakcija (19,3) (0,3) \) \ (+ 1 \)		Računamo ...
\ (n> 65,333 ... \)		... i ispostavlja se da će prvi pozitivni element imati broj \ (66 \). Prema tome, posljednji negativ ima \ (n = 65 \). Hajde da provjerimo za svaki slučaj.
\ (n = 65; \) \ (a_ (65) = -19,3+ (65-1) 0,3 = -0,1 \) \ (n = 66; \) \ (a_ (66) = - 19,3+ (66-1) 0,3 = 0,2 \)		Stoga moramo dodati prve \ (65 \) elemente.
\ (S_ (65) = \) \ (\ frac (2 \ cdot (-19.3) + (65-1) 0.3) (2) \)\ (\ cdot 65 \) \ (S_ (65) = \) \ (( - 38,6 + 19,2) (2) \) \ (\ cdot 65 = -630,5 \)		Odgovor je spreman.

Odgovor: \ (S_ (65) = - 630,5 \).

Primjer (OGE). Aritmetička progresija je specificirana uslovima: \ (a_1 = -33 \); \ (a_ (n + 1) = a_n + 4 \). Pronađite zbir od \ (26 \) th do \ (42 \) elementa uključujući.
Rešenje:

\ (a_1 = -33; \) \ (a_ (n + 1) = a_n + 4 \)	U ovom problemu također morate pronaći zbir elemenata, ali ne počevši od prvog, već od \ (26 \) - th. Za takav slučaj nemamo formulu. Kako se odlučiti? Lako - da biste dobili iznos od \ (26 \) - th do \ (42 \) - oh, prvo morate pronaći zbir od \ (1 \) - th do \ (42 \) - oh, a zatim oduzeti zbroj od toga do \ (25 \) - th (vidi sliku).
	Za našu progresiju \ (a_1 = -33 \), i razliku \ (d = 4 \) (uostalom, to su četiri koje dodajemo prethodnom elementu kako bismo pronašli sljedeći). Znajući to, nalazimo zbir prvih \ (42 \) - yh elemenata.
\ (S_ (42) = \) \ (\ frac (2 \ cdot (-33) + (42-1) 4) (2) \)\ (\ cdot 42 = \) \ (= \) \ (\ frac (-66 + 164) (2) \) \ (\ cdot 42 = 2058 \)	Sada zbir prvih \ (25 \) - elemenata.
\ (S_ (25) = \) \ (\ frac (2 \ cdot (-33) + (25-1) 4) (2) \)\ (\ cdot 25 = \) \ (= \) \ (\ frakcija (-66 + 96) (2) \) \ (\ cdot 25 = 375 \)	Na kraju izračunavamo odgovor.
\ (S = S_ (42) -S_ (25) = 2058-375 = 1683 \)

Odgovor: \ (S = 1683 \).

Za aritmetičku progresiju postoji još nekoliko formula koje nismo razmatrali u ovom članku zbog njihove niske praktične korisnosti. Međutim, lako ih možete pronaći.

Neko je oprezan zbog riječi "progresija", kao vrlo složenog izraza iz grana više matematike. U međuvremenu, najjednostavnija aritmetička progresija je rad taksimetra (gdje i dalje ostaju). A razumjeti suštinu (a u matematici nema ništa važnije od "razumijevanja suštine") aritmetičkog niza nije tako teško, nakon što smo analizirali nekoliko osnovnih pojmova.

Matematički niz brojeva

Uobičajeno je da se niz brojeva imenuje numeričkim nizom, od kojih svaki ima svoj broj.

a 1 - prvi član niza;

i 2 je drugi član niza;

i 7 je sedmi član niza;

i n je n -ti član niza;

Međutim, ne zanima nas bilo koji proizvoljan skup brojeva i brojeva. Pažnju ćemo usmjeriti na numerički niz, u kojem je vrijednost n -tog člana povezana s njegovim rednim brojem zavisnošću koja se može jasno matematički formulirati. Drugim riječima: numerička vrijednost n-tog broja je neka funkcija od n.

a - vrijednost člana numeričkog niza;

n je njegov serijski broj;

f (n) je funkcija u kojoj je red u numeričkom nizu n argument.

Definicija

Uobičajeno je da se aritmetičkom progresijom naziva numerički niz u kojem je svaki sljedeći član veći (manji) od prethodnog za isti broj. Formula za n -ti član aritmetičkog niza je sljedeća:

a n - vrijednost trenutnog člana aritmetičke progresije;

a n + 1 - formula za sljedeći broj;

d - razlika (određeni broj).

Lako je utvrditi da će, ako je razlika pozitivna (d> 0), svaki sljedeći član razmatranog niza biti veći od prethodnog, a takva aritmetička progresija će se povećavati.

Na donjem grafikonu lako je vidjeti zašto se niz brojeva naziva "rastući".

U slučajevima kada je razlika negativna (d<0), каждый последующий член по понятным причинам будет меньше предыдущего, график прогрессии станет «уходить» вниз, арифметическая прогрессия, соответственно, будет именоваться убывающей.

Vrijednost navedenog člana

Ponekad je potrebno odrediti vrijednost bilo kojeg proizvoljnog člana a n aritmetičke progresije. To možete učiniti izračunavanjem uzastopnih vrijednosti svih članova aritmetičke progresije, počevši od prvog do željenog. Međutim, ovaj put nije uvijek prihvatljiv ako je, na primjer, potrebno pronaći značenje pettisućitog ili osmilionitog člana. Tradicionalni izračun trajat će dugo. Međutim, specifična aritmetička progresija može se istražiti pomoću posebnih formula. Postoji i formula za n -ti pojam: vrijednost bilo kojeg člana aritmetičke progresije može se definirati kao zbroj prvog člana progresije s razlikom progresije, pomnožen sa brojem traženog člana, umanjenim za jedan.

Formula je univerzalna i za povećanje i za smanjenje progresije.

Primjer izračunavanja vrijednosti datog člana

Riješimo sljedeći problem pronalaženja vrijednosti n -tog člana aritmetičke progresije.

Stanje: postoji aritmetička progresija sa parametrima:

Prvi član u nizu je 3;

Razlika u nizu brojeva je 1,2.

Zadatak: morate pronaći vrijednost 214 članova

Rješenje: za određivanje vrijednosti datog pojma koristimo formulu:

a (n) = a1 + d (n-1)

Zamjenom podataka iz izraza problema u izraz imamo:

a (214) = a1 + d (n-1)

a (214) = 3 + 1,2 (214-1) = 258,6

Odgovor: 214. član u nizu je 258,6.

Prednosti ove metode izračuna su očite - cijelo rješenje ne traje više od 2 retka.

Zbir datog broja članova

Vrlo često je u danom aritmetičkom nizu potrebno odrediti zbir vrijednosti određenog njegovog segmenta. Ovo također ne zahtijeva izračunavanje vrijednosti svakog pojma, a zatim zbrajanje. Ova metoda je primjenjiva ako je broj pojmova koji se mogu pronaći mali. U drugim slučajevima, prikladnije je koristiti sljedeću formulu.

Zbir članova aritmetičke progresije od 1 do n jednak je zbroju prvog i n -tog člana, pomnožen brojem člana n i podijeljen s dva. Ako se u formuli vrijednost n -tog člana zamijeni izrazom iz prethodnog stavka članka, dobivamo:

Primjer proračuna

Na primjer, riješimo problem sa sljedećim uvjetima:

Prvi član u nizu je nula;

Razlika je 0,5.

U problemu morate odrediti zbir članova serije od 56. do 101.

Rešenje. Upotrijebimo formulu za određivanje zbroja progresije:

s (n) = (2 ∙ a1 + d ∙ (n-1)) ∙ n / 2

Prvo određujemo zbroj vrijednosti 101 člana progresije, zamjenjujući podatke o njihovim uvjetima našeg problema u formulu:

s 101 = (2 ∙ 0 + 0,5 ∙ (101-1)) ∙ 101/2 = 2 525

Očigledno, da bismo saznali zbroj članova progresije od 56. do 101., potrebno je oduzeti S 55 od S 101.

s 55 = (2 ∙ 0 + 0,5 ∙ (55-1)) ∙ 55/2 = 742,5

Dakle, zbroj aritmetičke progresije za ovaj primjer:

s 101 - s 55 = 2.525 - 742.5 = 1.782,5

Primjer praktične primjene aritmetičke progresije

Na kraju članka, vratimo se na primjer aritmetičkog niza navedenog u prvom paragrafu - taksimetar (taksimetar). Razmotrimo primjer.

Ukrcaj u taksi (koji uključuje 3 km trčanja) košta 50 rubalja. Svaki sljedeći kilometar plaća se po cijeni od 22 rubalja / km. Udaljenost putovanja 30 km. Izračunajte cijenu putovanja.

1. Odbacimo prva 3 km čija je cijena uključena u cijenu slijetanja.

30 - 3 = 27 km.

2. Daljnji izračun nije ništa drugo do analiza aritmetičkog niza brojeva.

Broj člana - broj prijeđenih kilometara (minus prva tri).

Vrijednost člana je zbir.

Prvi izraz u ovom problemu bit će jednak 1 = 50 p.

Razlika u progresiji d = 22 str.

broj koji nas zanima je vrijednost (27 + 1) -tog člana aritmetičke progresije - očitanje brojača na kraju 27. kilometra je 27,999 ... = 28 km.

a 28 = 50 + 22 ∙ (28 - 1) = 644

Izračuni kalendarskih podataka za proizvoljno dug period temelje se na formulama koje opisuju određene numeričke sekvence. U astronomiji, dužina orbite geometrijski zavisi od udaljenosti nebeskog tijela do luminara. Osim toga, različiti numerički nizovi uspješno se koriste u statistici i drugim primijenjenim granama matematike.

Druga vrsta numeričkog niza je geometrijska

Geometrijsku progresiju karakteriziraju velike, u usporedbi s aritmetikom, stope promjena. Nije slučajno što u politici, sociologiji, medicini često kažu da se proces razvija eksponencijalno kako bi se pokazala velika stopa širenja neke pojave, na primjer, bolesti tijekom epidemije.

N -ti član geometrijskog numeričkog niza razlikuje se od prethodnog po tome što se množi s nekim konstantnim brojem - nazivnik, na primjer, prvi član je 1, nazivnik 2, zatim:

n = 1: 1 ∙ 2 = 2

n = 2: 2 ∙ 2 = 4

n = 3: 4 ∙ 2 = 8

n = 4: 8 ∙ 2 = 16

n = 5: 16 ∙ 2 = 32,

b n - vrijednost trenutnog člana geometrijske progresije;

b n + 1 - formula sljedećeg člana geometrijske progresije;

q je nazivnik geometrijske progresije (stalan broj).

Ako je grafikon aritmetičke progresije ravna linija, tada geometrijski prikazuje malo drugačiju sliku:

Kao i u slučaju aritmetike, geometrijska progresija ima formulu za vrijednost proizvoljnog člana. Svaki n-ti član geometrijske progresije jednak je proizvodu prvog člana nazivnikom progresije na stepen n, umanjenom za jedan:

Primjer. Imamo geometrijsku progresiju s prvim članom jednakim 3 i nazivnikom progresije jednakim 1,5. Pronađite peti član progresije

b 5 = b 1 ∙ q (5-1) = 3 ∙ 1,5 4 = 15,1875

Zbir datog broja članova izračunava se na isti način pomoću posebne formule. Zbir prvih n članova geometrijske progresije jednak je razlici između proizvoda n -tog člana progresije i njenog nazivnika i prvog člana progresije, podijeljen s nazivnikom umanjenim za jedan:

Ako se b n zamijeni gore navedenom formulom, vrijednost zbroja prvih n članova razmatranog numeričkog niza poprimit će oblik:

Primjer. Geometrijska progresija počinje sa prvim članom jednakim 1. Imenilac je postavljen jednakim 3. Nađite zbir prvih osam članova.

s8 = 1 ∙ (3 8 -1) / (3-1) = 3 280