Намерете онлайн координатите на средата на сегмента. Вектори за манекени. Действия с вектори. Векторни координати. Най-простите задачи с вектори. Изчисляване на разстоянието на точка до линия

Най-накрая се докопах до една обширна и дългоочаквана тема аналитична геометрия. Първо, малко за този раздел на висшата математика... Със сигурност сега си спомнихте училищния курс по геометрия с множество теореми, техните доказателства, чертежи и т.н. Какво да се крие, недолюбвана и често неясна тема за значителна част от учениците. Аналитичната геометрия, колкото и да е странно, може да изглежда по-интересна и достъпна. Какво означава прилагателното "аналитичен"? Веднага се сещат за два щамповани математически оборота: „графичен метод на решение“ и „аналитичен метод на решение“. Графичен метод, разбира се, се свързва с изграждането на графики, чертежи. Аналитиченедин и същ методвключва решаване на проблеми предимночрез алгебрични операции. В тази връзка алгоритъмът за решаване на почти всички проблеми на аналитичната геометрия е прост и прозрачен, често е достатъчно точно да приложите необходимите формули - и отговорът е готов! Не, разбира се, изобщо няма да мине без чертежи, освен това, за по-добро разбиране на материала, ще се опитам да ги доведа над необходимостта.

Отвореният курс на уроци по геометрия не претендира за теоретична пълнота, той е фокусиран върху решаването на практически задачи. Ще включа в лекциите си само това, което от моя гледна точка е важно от практическа гледна точка. Ако имате нужда от по-пълна справка за който и да е подраздел, препоръчвам следната доста достъпна литература:

1) Нещо, което без шега е познато на няколко поколения: Училищен учебник по геометрия, авторите - L.S. Атанасян и компания. Тази закачалка за училищна съблекалня вече издържа 20 (!) преиздания, което, разбира се, не е границата.

2) Геометрия в 2 тома. Авторите L.S. Атанасян, Базилев В.Т.. Това е литература за висше образование, ще ви трябва първи том. Рядко срещаните задачи може да изпаднат от полезрението ми и урокът ще ми бъде от неоценима помощ.

И двете книги са безплатни за изтегляне онлайн. Освен това можете да използвате моя архив с готови решения, които можете да намерите на страницата Изтеглете примери по висша математика.

От инструментите отново предлагам моя собствена разработка - софтуерен пакетвърху аналитична геометрия, което значително ще опрости живота и ще спести много време.

Предполага се, че читателят е запознат с основните геометрични понятия и фигури: точка, права, равнина, триъгълник, успоредник, паралелепипед, куб и др. Препоръчително е да запомните някои теореми, поне теоремата на Питагор, здравейте повторители)

И сега ще разгледаме последователно: концепцията за вектор, действия с вектори, векторни координати. Освен това препоръчвам да прочетете най-важната статия Точково произведение на вектори, както и Вектор и смесен продукт на вектори. Локалната задача няма да е излишна - Разделяне на сегмента в това отношение. Въз основа на горната информация можете уравнение на права линия в равнинаот най-простите примери за решения, което ще позволи научете как да решавате задачи по геометрия. Следните статии също са полезни: Уравнение на равнина в пространството, Уравнения на права линия в пространството, Основни задачи на правата и равнината , други раздели на аналитичната геометрия. Естествено, стандартните задачи ще бъдат разгледани по пътя.

Концепцията за вектор. свободен вектор

Първо, нека повторим училищната дефиниция за вектор. векторНаречен насоченисегмент, за който са посочени неговото начало и край:

В този случай началото на отсечката е точката, краят на отсечката е точката. Самият вектор се означава с . Посокае от съществено значение, ако пренаредите стрелката в другия край на сегмента, ще получите вектор и това вече е напълно различен вектор. Удобно е да се идентифицира концепцията за вектор с движението на физическо тяло: трябва да признаете, че влизането през вратите на институт или излизането от вратите на институт са напълно различни неща.

Удобно е да се разглеждат отделни точки от равнина, пространството като т.нар нулев вектор. Такъв вектор има един и същ край и начало.

!!! Забележка: Тук и по-долу можете да приемете, че векторите лежат в една и съща равнина или можете да предположите, че са разположени в пространството - същността на представения материал е валидна както за равнината, така и за пространството.

Обозначения:Мнозина веднага обърнаха внимание на пръчка без стрелка в обозначението и казаха, че поставят и стрелка отгоре! Точно така, можете да пишете със стрелка: , но допустимо и запис, който ще използвам по-късно. Защо? Очевидно такъв навик се е развил от практически съображения, моите стрелци в училище и университета се оказаха твърде разнообразни и рошави. В образователната литература понякога изобщо не се занимават с клинопис, а подчертават буквите с удебелен шрифт: , като по този начин намекват, че това е вектор.

Това беше стилът, а сега относно начините за писане на вектори:

1) Векторите могат да бъдат написани с две главни латински букви:
и т.н. Докато първата буква задължителнообозначава началната точка на вектора, а втората буква обозначава крайната точка на вектора.

2) Векторите също се пишат с малки латински букви:
По-специално, нашият вектор може да бъде преозначен за краткост с малка латиница.

Дължинаили модулненулев вектор се нарича дължина на отсечката. Дължината на нулевия вектор е нула. Логично.

Дължината на вектора се обозначава със знака по модул: ,

Как да намерим дължината на вектор, ще научим (или повторим, за кого как) малко по-късно.

Това беше елементарна информация за вектора, позната на всички ученици. В аналитичната геометрия т.нар свободен вектор.

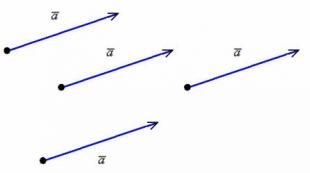
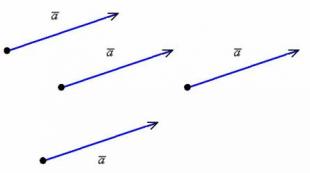
Ако е съвсем просто - вектор може да бъде начертан от всяка точка:

Ние наричахме такива вектори равни (дефиницията за равни вектори ще бъде дадена по-долу), но от чисто математическа гледна точка това е СЪЩИЯ ВЕКТОР или свободен вектор. Защо безплатно? Тъй като в хода на решаването на задачи можете да „прикачите” един или друг „училищен” вектор към ВСЯКА КОЯТА И ДА Е точка от равнината или пространството, от което се нуждаете. Това е много готин имот! Представете си насочен сегмент с произволна дължина и посока - той може да бъде "клониран" безкраен брой пъти и във всяка точка от пространството, всъщност той съществува НАВСЯКЪДЕ. Има такава студентска поговорка: Всеки лектор във f ** u във вектора. В крайна сметка това не е просто остроумна рима, всичко е почти правилно - там може да се прикачи и насочен сегмент. Но не бързайте да се радвате, самите ученици страдат по-често =)

Така, свободен вектор- това Много идентични насочени сегменти. Училищното определение на вектор, дадено в началото на параграфа: „Насочен сегмент се нарича вектор ...“, предполага специфичнинасочен сегмент, взет от дадено множество, който е прикрепен към определена точка в равнината или пространството.

Трябва да се отбележи, че от гледна точка на физиката, концепцията за свободен вектор като цяло е неправилна и точката на приложение има значение. Наистина, директен удар със същата сила по носа или по челото е достатъчен, за да развия глупавия ми пример, води до различни последствия. Въпреки това, не е безплатновектори се намират и в хода на vyshmat (не ходете там :)).

Действия с вектори. Колинеарност на векторите

В училищния курс по геометрия се разглеждат редица действия и правила с вектори: събиране по правилото на триъгълника, събиране по правилото на успоредника, правилото за разликата на векторите, умножение на вектор по число, скаларното произведение на векторите и др.Като семе, ние повтаряме две правила, които са особено подходящи за решаване на задачи от аналитичната геометрия.

Правило за събиране на вектори според правилото на триъгълниците

Помислете за два произволни ненулеви вектора и :

Необходимо е да се намери сумата от тези вектори. Поради факта, че всички вектори се считат за свободни, ние отлагаме вектора от крайвектор:

Сборът от вектори е векторът . За по-добро разбиране на правилото е препоръчително да се вложи физически смисъл в него: нека някое тяло направи път по вектора , а след това по вектора . Тогава сумата от векторите е векторът на получения път, започващ в точката на тръгване и завършващ в точката на пристигане. Подобно правило е формулирано за сумата от произволен брой вектори. Както се казва, тялото може да върви по пътя си силно зигзагообразно, или може би на автопилот - по получения вектор на сумата.

Между другото, ако векторът се отложи от започнетевектор , тогава получаваме еквивалента правило на паралелограмадобавяне на вектори.

Първо, за колинеарността на векторите. Двата вектора се наричат колинеарнаако лежат на една и съща права или на успоредни прави. Грубо казано, говорим за паралелни вектори. Но във връзка с тях винаги се използва прилагателното "колинеарно".

Представете си два колинеарни вектора. Ако стрелките на тези вектори са насочени в една и съща посока, тогава такива вектори се наричат съпосочен. Ако стрелките гледат в различни посоки, тогава векторите ще бъдат противоположно насочени.

Обозначения:колинеарността на векторите се записва с обичайната икона на паралелизъм: , докато детайлизирането е възможно: (векторите са съвместно насочени) или (векторите са насочени противоположно).

работана ненулев вектор от число е вектор, чиято дължина е равна на , а векторите и са съвместно насочени към и противоположно насочени към .

Правилото за умножение на вектор по число е по-лесно за разбиране с картина:

Разбираме по-подробно:

1) Посока. Ако множителят е отрицателен, тогава векторът променя посокатакъм обратното.

2) Дължина. Ако факторът се съдържа в или , тогава дължината на вектора намалява. Така че дължината на вектора е два пъти по-малка от дължината на вектора. Ако модулният множител е по-голям от единица, тогава дължината на вектора се увеличавана време.

3) Моля, имайте предвид това всички вектори са колинеарни, докато един вектор се изразява чрез друг, например, . Обратното също е вярно: ако един вектор може да бъде изразен чрез друг, тогава такива вектори задължително са колинеарни. По този начин: ако умножим вектор по число, получаваме колинеарни(спрямо оригинала) вектор.

4) Векторите са съпосочени. Векторите и също са съпосочени. Всеки вектор от първата група е противоположен на всеки вектор от втората група.

Какви вектори са равни?

Два вектора са равни, ако са съпосочени и имат еднаква дължина. Обърнете внимание, че ко-насочеността предполага, че векторите са колинеарни. Дефиницията ще бъде неточна (излишна), ако кажете: "Два вектора са равни, ако са колинеарни, съвместно насочени и имат еднаква дължина."

От гледна точка на концепцията за свободен вектор, равните вектори са един и същ вектор, който вече беше обсъден в предишния параграф.

Векторни координати в равнината и в пространството

Първата точка е да разгледаме вектори в равнина. Начертайте декартова правоъгълна координатна система и я отделете от началото единиченвектори и :

Вектори и ортогонална. Ортогонална = перпендикулярна. Препоръчвам бавно да свикнете с термините: вместо успоредност и перпендикулярност, използваме съответно думите колинеарностИ ортогоналност.

Обозначаване:ортогоналността на векторите се записва с обичайния перпендикулярен знак, например: .

Разгледаните вектори се наричат координатни векториили orts. Тези вектори се образуват основана повърхността. Какво е основата, мисля, че е интуитивно ясно за много, по-подробна информация може да се намери в статията Линейна (не) зависимост на векторите. Векторна основа.С прости думи основата и произходът на координатите определят цялата система - това е един вид основа, върху която кипи пълен и богат геометричен живот.

Понякога конструираната основа се нарича ортонормалнооснова на равнината: "орто" - тъй като координатните вектори са ортогонални, прилагателното "нормализиран" означава единица, т.е. дължините на базисните вектори са равни на единица.

Обозначаване:основата обикновено се пише в скоби, вътре в които в строг редосновни вектори са изброени, например: . Координатни вектори забранено еразменете местата.

Всякаквиравнинен вектор единствения начинизразено като:
, където - числа, които се наричат векторни координатина тази основа. Но самият израз Наречен векторно разлаганеоснова .

Сервирана вечеря:

Да започнем с първата буква от азбуката: . Чертежът ясно показва, че при декомпозиране на вектора по отношение на основата се използват току-що разгледаните:
1) правилото за умножение на вектор по число: и ;
2) събиране на вектори според правилото на триъгълника: .

Сега мислено отделете вектора от всяка друга точка на равнината. Съвсем очевидно е, че корупцията му „ще го следва безмилостно“. Ето я, свободата на вектора – векторът „носи всичко със себе си“. Това свойство, разбира се, е вярно за всеки вектор. Смешно е, че самите базисни (безплатни) вектори не трябва да се отделят от началото, единият може да се начертае например долу вляво, а другият горе вдясно и нищо няма да се промени от това! Вярно е, че не е нужно да правите това, защото учителят също ще покаже оригиналност и ще ви нарисува „пропуск“ на неочаквано място.

Вектори, илюстрират точно правилото за умножение на вектор по число, векторът е съвместно насочен с основния вектор, векторът е насочен обратно на основния вектор. За тези вектори една от координатите е равна на нула, тя може да бъде внимателно написана, както следва:


А основните вектори, между другото, са така: (всъщност те се изразяват чрез себе си).

И накрая: , . Между другото, какво е векторно изваждане и защо не ви казах за правилото за изваждане? Някъде в линейната алгебра, не помня къде, отбелязах, че изваждането е специален случай на събиране. И така, разширенията на векторите "de" и "e" се записват спокойно като сума: . Следвайте чертежа, за да видите колко добре работи старото добро събиране на вектори според правилото на триъгълника в тези ситуации.

Обмислено разлагане на формата понякога се нарича векторно разлагане в системата орт(т.е. в системата от единични вектори). Но това не е единственият начин да напишете вектор, следната опция е често срещана:

Или със знак за равенство:

Самите базисни вектори се записват, както следва: и

Тоест координатите на вектора са посочени в скоби. В практическите задачи се използват и трите опции за запис.

Съмнявах се дали да говоря, но все пак ще кажа: векторните координати не могат да бъдат пренаредени. Строго на първо мястозапишете координатата, която съответства на единичния вектор, строго на второ мястозапишете координатата, която съответства на единичния вектор. Всъщност и са два различни вектора.

Разбрахме координатите на самолета. Сега помислете за вектори в триизмерно пространство, тук всичко е почти същото! Ще бъде добавена само още една координата. Трудно е да се изпълняват триизмерни чертежи, така че ще се огранича до един вектор, който за простота ще отложа от произхода:

Всякакви 3D космически вектор единствения начинразширяване в ортонормална основа:
, където са координатите на вектора (числото) в дадената основа.

Пример от снимката: . Нека видим как работят векторните правила за действие тук. Първо, умножаване на вектор по число: (червена стрелка), (зелена стрелка) и (пурпурна стрелка). Второ, ето пример за добавяне на няколко, в този случай три вектора: . Векторът на сумата започва в началната точка на тръгване (началото на вектора) и завършва в крайната точка на пристигане (края на вектора).

Всички вектори на триизмерното пространство, разбира се, също са безплатни, опитайте се да отложите мислено вектора от всяка друга точка и ще разберете, че неговото разширяване „остава с него“.

Подобно на корпуса на самолета, в допълнение към писането широко се използват версии със скоби: или .

Ако един (или два) координатни вектора липсват в разширението, вместо това се поставят нули. Примери:
вектор (внимателно ) - записвам ;
вектор (внимателно ) - записвам ;
вектор (внимателно ) - записвам .

Основните вектори се записват, както следва:

Тук, може би, са всички минимални теоретични познания, необходими за решаване на задачи на аналитичната геометрия. Може би има твърде много термини и дефиниции, така че препоръчвам манекените да препрочетат и разберат тази информация отново. И ще бъде полезно за всеки читател от време на време да се позовава на основния урок за по-добро усвояване на материала. Колинеарност, ортогоналност, ортонормална основа, векторна декомпозиция - тези и други понятия ще бъдат често използвани в това, което следва. Отбелязвам, че материалите на сайта не са достатъчни за преминаване на теоретичен тест, колоквиум по геометрия, тъй като внимателно криптирам всички теореми (освен без доказателства) - в ущърб на научния стил на представяне, но плюс за вашето разбиране на субекта. За подробна теоретична информация ви моля да се поклоните на професор Атанасян.

Сега да преминем към практическата част:

Най-простите задачи на аналитичната геометрия.
Действия с вектори в координати

Задачите, които ще бъдат разгледани, е много желателно да се научите как да ги решавате напълно автоматично, а формулите запомни, дори не го помнете нарочно, те сами ще го запомнят =) Това е много важно, тъй като други проблеми на аналитичната геометрия се основават на най-простите елементарни примери и ще бъде досадно да прекарвате допълнително време в ядене на пионки. Не е нужно да закопчавате горните копчета на ризата си, много неща са ви познати от училище.

Представянето на материала ще върви в паралелен ход - както за самолета, така и за космоса. Поради причината, че всички формули ... ще видите сами.

Как да намерим вектор с две точки?

Ако са дадени две точки от равнината и, тогава векторът има следните координати:

Ако са дадени две точки в пространството и, тогава векторът има следните координати:

т.е. от координатите на края на векторатрябва да извадите съответните координати векторно начало.

Задачата:За същите точки запишете формулите за намиране на координатите на вектора. Формули в края на урока.

Пример 1

Като се има предвид две точки в равнината и . Намерете векторни координати

Решение:по съответната формула:

Като алтернатива може да се използва следната нотация:

Естетите ще решат така:

Лично аз съм свикнал с първата версия на записа.

Отговор:

Според условието не се изискваше да се изгради чертеж (което е типично за задачи на аналитичната геометрия), но за да обясня някои точки на манекените, няма да бъда твърде мързелив:

Трябва да се разбере разлика между координатите на точката и векторните координати:

Координати на точкиса обичайните координати в правоъгълна координатна система. Мисля, че всеки знае как да начертава точки в координатната равнина от 5-6 клас. Всяка точка има строго място в равнината и те не могат да бъдат преместени никъде.

Координатите на същия векторе неговото разширяване по отношение на основата , в този случай . Всеки вектор е свободен, следователно, ако желаем или е необходимо, можем лесно да го отделим от друга точка в равнината (за да избегнем объркване, преименувайки го, например, чрез ). Интересното е, че за вектори изобщо не можете да изграждате оси, правоъгълна координатна система, имате нужда само от база, в този случай, ортонормирана основа на равнината.

Записите на координатите на точките и векторните координати изглеждат подобни: , и усещане за координатиабсолютно различно, и трябва да сте наясно с тази разлика. Тази разлика, разбира се, важи и за пространството.

Дами и господа, пълним ръцете си:

Пример 2

а) Дадени точки и . Намерете вектори и .
б) Дават се точки И . Намерете вектори и .
в) Дадени точки и . Намерете вектори и .
г) Дават се точки. Намерете вектори .

Може би достатъчно. Това са примери за самостоятелно решение, опитайте се да не ги пренебрегвате, ще ви се отплати ;-). Чертежи не се изискват. Решения и отговори в края на урока.

Какво е важно при решаването на задачи от аналитичната геометрия?Важно е да бъдете ИЗКЛЮЧИТЕЛНО ВНИМАТЕЛНИ, за да избегнете майсторската грешка „две плюс две е равно на нула“. Предварително се извинявам ако съм допуснал грешка =)

Как да намерим дължината на отсечката?

Дължината, както вече беше отбелязано, се обозначава със знака за модул.

Ако са дадени две точки от равнината и, тогава дължината на отсечката може да се изчисли по формулата

Ако са дадени две точки в пространството и, тогава дължината на сегмента може да се изчисли по формулата

Забележка: Формулите ще останат правилни, ако съответните координати се разменят: и , но първата опция е по-стандартна

Пример 3

Решение:по съответната формула:

Отговор:

За по-голяма яснота ще направя рисунка

Раздел - не е вектор, и не можете да го преместите никъде, разбира се. Освен това, ако завършите чертежа в мащаб: 1 единица. \u003d 1 см (две тетрадни клетки), тогава отговорът може да бъде проверен с обикновена линийка чрез директно измерване на дължината на сегмента.

Да, решението е кратко, но има няколко важни момента в него, които бих искал да изясня:

Първо, в отговора задаваме измерението: „единици“. Условието не казва КАКВО е, милиметри, сантиметри, метри или километри. Следователно общата формулировка ще бъде математически компетентно решение: „единици“ - съкратено като „единици“.

Второ, нека повторим училищния материал, който е полезен не само за разглеждания проблем:

обърни внимание на важен технически трик – изваждането на множителя изпод корена. В резултат на изчисленията получихме резултата и добрият математически стил включва изваждането на фактора изпод корена (ако е възможно). Процесът изглежда така по-подробно: . Разбира се, оставянето на отговора във формата няма да е грешка - но определено е недостатък и тежък аргумент за придирки от страна на учителя.

Ето и други често срещани случаи:

Често под корена се получава например достатъчно голям брой. Как да бъде в такива случаи? На калкулатора проверяваме дали числото се дели на 4:. Да, разделете се напълно, така: . Или може би числото може да се раздели отново на 4? . По този начин: . Последната цифра на числото е нечетна, така че разделянето на 4 за трети път очевидно не е възможно. Опитвам се да разделя на девет: . Като резултат:
Готов.

Изход:ако под корена получим напълно неизвличащо число, тогава се опитваме да извадим фактора под корена - на калкулатора проверяваме дали числото се дели на: 4, 9, 16, 25, 36, 49, и т.н.

В хода на решаването на различни задачи често се намират корени, винаги се опитвайте да извлечете фактори под корена, за да избегнете по-нисък резултат и ненужни проблеми с финализирането на вашите решения според забележка на учителя.

Нека повторим квадратурата на корените и други степени едновременно:

Правилата за действия със степени в общ вид могат да се намерят в училищния учебник по алгебра, но мисля, че всичко или почти всичко вече е ясно от дадените примери.

Задача за самостоятелно решение със сегмент в пространството:

Пример 4

Дадени точки и . Намерете дължината на отсечката.

Решение и отговор в края на урока.

Как да намерим дължината на вектор?

Ако е даден плосък вектор, тогава неговата дължина се изчислява по формулата.

Ако е даден пространствен вектор, тогава неговата дължина се изчислява по формулата .

Тези формули (както и формулите за дължината на отсечка) се извличат лесно с помощта на прословутата питагорова теорема.

Статията по-долу ще обхване въпросите за намиране на координатите на средата на сегмента при наличието на координатите на неговите крайни точки като начални данни. Но преди да пристъпим към изучаването на въпроса, ние въвеждаме редица определения.

Определение 1

Раздел- права линия, свързваща две произволни точки, наречени краища на отсечката. Като пример нека това са точки A и B и съответно отсечката A B .

Ако отсечката A B се продължи в двете посоки от точки A и B, ще получим права линия A B. Тогава отсечката A B е част от получената права линия, ограничена от точки A и B . Отсечката A B обединява точките A и B , които са неговите краища, както и множеството точки, разположени между тях. Ако, например, вземем произволна точка K, лежаща между точки A и B, можем да кажем, че точката K лежи на отсечката A B.

Определение 2

Дължина на рязанее разстоянието между краищата на сегмента в даден мащаб (сегмент от единична дължина). Означаваме дължината на отсечката A B, както следва: A B .

Определение 3

средна точкаТочка на отсечка, която е на еднакво разстояние от краищата му. Ако средата на отсечката A B е обозначена с точка C, тогава равенството ще бъде вярно: A C \u003d C B

Изходни данни: координатна линия O x и несъответстващи точки върху нея: A и B . Тези точки съответстват на реални числа x A и x B . Точка C е средата на сегмент A B: трябва да определите координатата x C .

Тъй като точка C е средата на отсечката A B, равенството ще бъде вярно: | A C | = | C B | . Разстоянието между точките се определя от модула на разликата между техните координати, т.е.

| A C | = | C B | ⇔ x C - x A = x B - x C

Тогава са възможни две равенства: x C - x A = x B - x C и x C - x A = - (x B - x C)

От първото равенство извеждаме формула за координатата на точка C: x C \u003d x A + x B 2 (половината от сумата от координатите на краищата на сегмента).

От второто равенство получаваме: x A = x B , което е невъзможно, т.к в оригиналните данни - несъответстващи точки. По този начин, формула за определяне на координатите на средата на отсечката A B с краища A (x A) и B(xB):

Получената формула ще бъде основа за определяне на координатите на средата на сегмента на равнина или в пространството.

Изходни данни: правоъгълна координатна система на равнината O x y , две произволни несъвпадащи точки с дадени координати A x A , y A и B x B , y B . Точка C е средата на сегмент A B. Необходимо е да се определят координатите x C и y C за точка C .

Да вземем за анализ случая, когато точки A и B не съвпадат и не лежат на една и съща координатна права или права, перпендикулярна на една от осите. A x , A y ; B x , B y и C x , C y - проекции на точки A , B и C върху координатните оси (прави O x и O y).

По конструкция правите A A x , B B x , C C x са успоредни; линиите също са успоредни една на друга. Заедно с това, според теоремата на Талес, от равенството AC \u003d CB следват равенства: A x C x = C x B x и A y C y = C y B y, а те от своя страна, показват, че точката C x - средата на отсечката A x B x, а C y е средата на отсечката A y B y. И тогава, въз основа на формулата, получена по-рано, получаваме:

x C = x A + x B 2 и y C = y A + y B 2

Същите формули могат да се използват в случай, когато точки A и B лежат на една и съща координатна права или права, перпендикулярна на една от осите. Няма да правим подробен анализ на този случай, ще го разгледаме само графично:

Обобщавайки всичко по-горе, координати на средата на отсечката A B на равнината с координатите на краищата A (x A , y A) И B(x B, y B) определена като:

(x A + x B 2 , y A + y B 2)

Изходни данни: координатна система О x y z и две произволни точки с дадени координати A (x A , y A , z A) и B (x B , y B , z B) . Необходимо е да се определят координатите на точка C , която е средата на отсечката A B .

A x , A y , A z ; B x , B y , B z и C x , C y , C z - проекции на всички дадени точки върху осите на координатната система.

Съгласно теоремата на Талес равенствата са верни: A x C x = C x B x , A y C y = C y B y , A z C z = C z B z

Следователно точките C x , C y , C z са средните точки на отсечките A x B x , A y B y , A z B z съответно. Тогава, за определяне на координатите на средата на сегмента в пространството са верни следните формули:

x C = x A + x B 2 , y c = y A + y B 2 , z c = z A + Z B 2

Получените формули са приложими и в случаите, когато точки A и B лежат на една от координатните прави; на права линия, перпендикулярна на една от осите; в една координатна равнина или равнина, перпендикулярна на една от координатните равнини.

Определяне на координатите на средата на сегмент чрез координатите на радиус векторите на неговите краища

Формулата за намиране на координатите на средата на отсечката може да се изведе и според алгебричната интерпретация на векторите.

Изходни данни: правоъгълна декартова координатна система O x y , точки с дадени координати A (x A , y A) и B (x B , x B) . Точка C е средата на сегмент A B.

Според геометричната дефиниция на действията върху вектори ще бъде вярно следното равенство: O C → = 1 2 · O A → + O B → . Точка C в този случай е пресечната точка на диагоналите на паралелограма, построен на базата на векторите O A → и O B → , т.е. точката на средата на диагоналите Координатите на радиус вектора на точката са равни на координатите на точката, тогава равенствата са верни: OA → = (x A , y A) , OB → = (x B , y B) . Нека извършим някои операции с вектори в координати и ще получим:

O C → = 1 2 O A → + O B → = x A + x B 2 , y A + y B 2

Следователно точка C има координати:

x A + x B 2 , y A + y B 2

По аналогия се дефинира формула за намиране на координатите на средната точка на сегмент в пространството:

C (x A + x B 2 , y A + y B 2 , z A + z B 2)

Примери за решаване на задачи за намиране на координатите на средата на отсечка

Сред задачите, включващи използването на формулите, получени по-горе, има както тези, при които въпросът е директно да се изчислят координатите на средата на отсечката, така и тези, които включват привеждане на дадените условия към този въпрос: терминът „медиана“ често се използва, целта е да се намерят координатите на един от краищата на отсечката, както и задачи за симетрия, чието решение като цяло също не трябва да създава затруднения след изучаване на тази тема. Нека разгледаме типични примери.

Пример 1

Първоначални данни:на равнината - точки с дадени координати A (- 7, 3) и B (2, 4) . Необходимо е да се намерят координатите на средата на отсечката A B.

Решение

Нека означим средата на отсечката A B с точка C . Координатите му ще се определят като половината от сбора от координатите на краищата на отсечката, т.е. точки А и Б.

x C = x A + x B 2 = - 7 + 2 2 = - 5 2 y C = y A + y B 2 = 3 + 4 2 = 7 2

Отговор: координати на средата на сегмент A B - 5 2 , 7 2 .

Пример 2

Първоначални данни:координатите на триъгълника A B C са известни: A (- 1 , 0) , B (3 , 2) , C (9 , - 8) . Необходимо е да се намери дължината на медианата A M.

Решение

1. Според условието на задачата A M е медианата, което означава, че M е средата на отсечката B C . На първо място намираме координатите на средата на отсечката B C , т.е. М точки:

x M = x B + x C 2 = 3 + 9 2 = 6 y M = y B + y C 2 = 2 + (- 8) 2 = - 3

1. Тъй като сега знаем координатите на двата края на медианата (точки A и M), можем да използваме формулата, за да определим разстоянието между точките и да изчислим дължината на медианата A M:

A M = (6 - (- 1)) 2 + (- 3 - 0) 2 = 58

Отговор: 58

Пример 3

Първоначални данни:в правоъгълната координатна система на триизмерното пространство е даден паралелепипед A B C D A 1 B 1 C 1 D 1. Дадени са координатите на точка C 1 (1 , 1 , 0), дефинирана е и точката M, която е средата на диагонала B D 1 и има координати M (4 , 2 , - 4) . Необходимо е да се изчислят координатите на точка А.

Решение

Диагоналите на паралелепипед се пресичат в една точка, която е средата на всички диагонали. Въз основа на това твърдение можем да имаме предвид, че познатата от условията на задачата точка M е средата на отсечката А С 1 . Въз основа на формулата за намиране на координатите на средата на отсечката в пространството намираме координатите на точка A: x M = x A + x C 1 2 ⇒ x A = 2 x M - x C 1 = 2 4 - 1 + 7 y M = y A + y C 1 2 ⇒ y A = 2 y M - y C 1 = 2 2 - 1 = 3 z M = z A + z C 1 2 ⇒ z A = 2 z M - z C 1 = 2 (- 4) - 0 = - 8

Отговор:координати на точка А (7, 3, - 8) .

Ако забележите грешка в текста, моля, маркирайте я и натиснете Ctrl+Enter

В тази статия вие и аз ще започнем дискусия за една "магическа пръчка", която ще ви позволи да намалите много проблеми в геометрията до проста аритметика. Тази „пръчка“ може да улесни живота ви много, особено когато се чувствате несигурни в изграждането на пространствени фигури, разрези и т.н. Всичко това изисква известно въображение и практически умения. Методът, който ще започнем да разглеждаме тук, ще ви позволи да се абстрахирате почти напълно от всички видове геометрични конструкции и разсъждения. Методът се нарича "координативен метод". В тази статия ще разгледаме следните въпроси:

1. Координатна равнина
2. Точки и вектори в равнината
3. Изграждане на вектор от две точки
4. Дължина на вектора (разстояние между две точки).
5. Координати на средната точка
6. Точково произведение на вектори
7. Ъгъл между два вектора

Мисля, че вече познахте защо координатният метод се нарича така? Вярно е, че получи такова име, тъй като не оперира с геометрични обекти, а с техните числени характеристики (координати). А самата трансформация, която прави възможно преминаването от геометрия към алгебра, се състои във въвеждане на координатна система. Ако оригиналната фигура е плоска, тогава координатите са двуизмерни, а ако фигурата е триизмерна, тогава координатите са триизмерни. В тази статия ще разгледаме само двуизмерния случай. И основната цел на статията е да ви научи как да използвате някои основни техники на координатния метод (те понякога се оказват полезни при решаване на задачи по планиметрия в част Б на Единния държавен изпит). Следващите два раздела по тази тема са посветени на обсъждането на методите за решаване на задачи C2 (проблема на стереометрията).

Къде би било логично да започнем да обсъждаме координатния метод? Вероятно с концепцията за координатна система. Спомнете си кога я срещнахте за първи път. Струва ми се, че в 7 клас, когато си научил за съществуването на линейна функция напр. Нека ви напомня, че сте го изградили точка по точка. Помниш ли? Избрахте произволно число, поставихте го във формулата и изчислихте по този начин. Например, ако, тогава, ако, тогава и т. н. Какво получихте в резултат? И сте получили точки с координати: и. След това нарисувахте „кръст“ (координатна система), избрахте мащаб върху него (колко клетки ще имате като един сегмент) и отбелязахте точките, които сте получили върху него, които след това свържете с права линия, получената линия е графиката на функцията.

Има няколко неща, които трябва да ви бъдат обяснени малко по-подробно:

1. Избирате един сегмент от съображения за удобство, така че всичко да пасне добре и компактно на снимката

2. Приема се, че оста върви от ляво на дясно, а оста върви отдолу нагоре

3. Те се пресичат под прав ъгъл, а точката на тяхното пресичане се нарича начало. Той е обозначен с буква.

4. В записа на координатата на точка, например, вляво в скоби е координатата на точката по оста, а вдясно по оста. По-специално, просто означава, че точката

5. За да зададете която и да е точка на координатната ос, трябва да посочите нейните координати (2 числа)

6. За всяка точка, лежаща на оста,

7. За всяка точка, лежаща на оста,

8. Оста се нарича ос x

9. Оста се нарича ос y

Сега нека направим следващата стъпка с вас: маркирайте две точки. Свържете тези две точки с линия. И нека поставим стрелката, сякаш чертаем сегмент от точка до точка: тоест ще направим нашия сегмент насочен!

Спомнете си какво е другото име за насочен сегмент? Точно така, това се нарича вектор!

По този начин, ако свържем точка с точка, и началото ще бъде точка А, а краят ще бъде точка Б,тогава получаваме вектор. Ти също си правил тази конструкция в 8 клас, помниш ли?

Оказва се, че векторите, подобно на точките, могат да бъдат обозначени с две числа: тези числа се наричат ​​координати на вектора. Въпрос: мислите ли, че е достатъчно да знаем координатите на началото и края на вектора, за да намерим неговите координати? Оказва се, че да! И е много лесно да се направи:

По този начин, тъй като във вектора точката е началото и края, векторът има следните координати:

Например, ако, тогава координатите на вектора

Сега нека направим обратното, да намерим координатите на вектора. Какво трябва да променим за това? Да, трябва да смените началото и края: сега началото на вектора ще бъде в точка, а краят в точка. Тогава:

Погледнете внимателно, каква е разликата между векторите и? Единствената им разлика са знаците в координатите. Те са противоположни. Този факт е написан така:

Понякога, ако не е изрично посочено коя точка е началото на вектора и коя е краят, тогава векторите се означават не с две главни букви, а с една малка буква, например: и т.н.

Сега малко практикаи намерете координатите на следните вектори:

Преглед:

Сега решете проблема малко по-трудно:

Векторен тор с on-cha-scrap в точка има co-or-di-on-you. Намерете-ди-те абс-цис-су точки.

Все едно е доста прозаично: Нека са координатите на точката. Тогава

Компилирах системата, като определих какви са координатите на вектор. Тогава точката има координати. Интересува ни абсцисата. Тогава

Отговор:

Какво друго можете да правите с вектори? Да, почти всичко е същото като при обикновените числа (освен, че не можете да разделите, но можете да умножите по два начина, единият от които ще обсъдим тук малко по-късно)

1. Векторите могат да бъдат подредени един с друг
2. Векторите могат да се изваждат един от друг
3. Векторите могат да бъдат умножени (или разделени) с произволно число, различно от нула
4. Векторите могат да се умножават един с друг

Всички тези операции имат доста визуално геометрично представяне. Например правилото за триъгълник (или успоредник) за събиране и изваждане:

Векторът се разтяга, свива или променя посоката, когато се умножи или раздели на число:

Тук обаче ще ни интересува въпросът какво се случва с координатите.

1. При събиране (изваждане) на два вектора събираме (изваждаме) техните координати елемент по елемент. т.е.:

2. При умножаване (деляне) на вектор по число, всичките му координати се умножават (дели) на това число:

Например:

· Намерете-ди-сумата от ко-или-ди-нат век-до-ра.

Нека първо намерим координатите на всеки от векторите. И двете имат един и същ произход - началната точка. Краищата им са различни. Тогава, . Сега изчисляваме координатите на вектора. Тогава сумата от координатите на получения вектор е равна на.

Отговор:

Сега сами решете следния проблем:

· Намерете сбора от координатите на вектора

Ние проверяваме:

Нека сега разгледаме следния проблем: имаме две точки в координатната равнина. Как да намеря разстоянието между тях? Нека първата точка бъде, а втората. Нека означим разстоянието между тях като . Нека направим следния чертеж за по-голяма яснота:

Какво съм направил? Първо, свързах точките и, а също и начертах линия, успоредна на оста от точката, и нарисувах линия, успоредна на оста от точката. Дали се пресичат в една точка, образувайки прекрасна фигура? Защо е прекрасна? Да, ти и аз знаем почти всичко за правоъгълния триъгълник. Е, Питагоровата теорема, със сигурност. Желаният сегмент е хипотенузата на този триъгълник, а отсечките са катета. Какви са координатите на точката? Да, те са лесни за намиране от снимката: Тъй като сегментите са успоредни на осите и съответно техните дължини са лесни за намиране: ако обозначим дължините на сегментите, съответно, чрез, тогава

Сега нека използваме питагоровата теорема. Знаем дължините на краката, ще намерим хипотенузата:

По този начин разстоянието между две точки е коренната сума от квадратите на разликите от координатите. Или - разстоянието между две точки е дължината на отсечката, който ги свързва. Лесно е да се види, че разстоянието между точките не зависи от посоката. Тогава:

От това правим три извода:

Нека потренираме малко в изчисляването на разстоянието между две точки:

Например, ако, тогава разстоянието между и е

Или да отидем по друг начин: намерете координатите на вектора

И намерете дължината на вектора:

Както виждате, същото е!

Сега практикувайте малко сами:

Задача: намерете разстоянието между дадените точки:

Ние проверяваме:

Ето още няколко проблема за същата формула, въпреки че звучат малко по-различно:

1. Намерете-ди-те квадрата на дължината на клепача-до-ра.

2. Най-ди-те квадрат на клепача дължина-до-ра

Предполагам, че лесно се справяте с тях? Ние проверяваме:

1. И това е за внимание) Вече намерихме координатите на векторите преди: . Тогава векторът има координати. Квадратът на неговата дължина ще бъде:

2. Намерете координатите на вектора

Тогава квадратът на неговата дължина е

Нищо сложно, нали? Проста аритметика, нищо повече.

Следните пъзели не могат да се класифицират еднозначно, те са по-скоро за обща ерудиция и умение да рисувате прости картини.

1. Намерете-di-тези синус на ъгъла върху-clo-on-from-cut, свържете-една-n-та точка, с оста на абсцисата.

И

Как ще го направим тук? Трябва да намерите синуса на ъгъла между и оста. И къде да търсим синуса? Точно така, в правоъгълен триъгълник. И така, какво трябва да направим? Изградете този триъгълник!

Тъй като координатите на точката и, тогава сегментът е равен, а отсечката. Трябва да намерим синуса на ъгъла. Нека ви напомня, че синусът е съотношението на противоположния катет към хипотенузата

Какво ни остава да правим? Намерете хипотенузата. Можете да го направите по два начина: по теоремата на Питагор (катетата са известни!) или по формулата за разстоянието между две точки (всъщност същото като първия метод!). Ще тръгна по втория път:

Отговор:

Следващата задача ще ви се стори още по-лесна. Тя - на координатите на точката.

Задача 2.От точката per-pen-di-ku-lar се спуска върху оста abs-ciss. Nai-di-te abs-cis-su os-no-va-niya per-pen-di-ku-la-ra.

Нека направим рисунка:

Основата на перпендикуляра е точката, в която той пресича оста x (ос) за мен това е точка. Фигурата показва, че има координати: . Интересува ни абсцисата - тоест компонента "X". Тя е равностойна.

Отговор: .

Задача 3.При условията на предходната задача намерете сбора от разстоянията от точката до координатните оси.

Задачата по принцип е елементарна, ако знаете какво е разстоянието от точка до осите. Ти знаеш? Надявам се, но все пак ви напомням:

И така, в моя чертеж, разположен малко по-високо, вече съм изобразил един такъв перпендикуляр? Каква ос е? към оста. И каква е дължината му тогава? Тя е равностойна. Сега сами начертайте перпендикуляр на оста и намерете нейната дължина. Ще бъде равностойно, нали? Тогава тяхната сума е равна.

Отговор: .

Задача 4.В условията на задача 2 намерете ординатата на точката, симетрична на точката около оста x.

Мисля, че интуитивно разбирате какво е симетрия? Има много предмети: много сгради, маси, самолети, много геометрични фигури: топка, цилиндър, квадрат, ромб и т.н. Грубо казано, симетрията може да се разбере по следния начин: фигура се състои от две (или повече) еднакви половинки. Тази симетрия се нарича аксиална. Тогава какво е ос? Това е точно линията, по която фигурата може, условно казано, да бъде „нарязана“ на еднакви половини (на тази снимка оста на симетрия е права):

Сега да се върнем към нашата задача. Знаем, че търсим точка, която е симетрична спрямо оста. Тогава тази ос е оста на симетрия. И така, трябва да отбележим точка, така че оста да разреже сегмента на две равни части. Опитайте се сами да отбележите такава точка. Сега сравнете с моето решение:

Вие направихте ли същото? Добре! В намерената точка ни интересува ординатата. Тя е равностойна

Отговор:

Сега ми кажете, след като помислих за секунда, каква ще бъде абсцисата на точката, симетрична на точка А около оста y? Какъв е отговора ти? Правилен отговор:.

Най-общо правилото може да се напише така:

Точка, симетрична на точка около оста x, има координатите:

Точка, симетрична на точка около оста y, има координати:

Е, сега е наистина страшно. задача: Намерете координатите на точка, която е симетрична на точка, спрямо началото. Първо се замислете сами, а после вижте моята рисунка!

Отговор:

Сега проблем с паралелограма:

Задача 5: Точките са ver-shi-na-mi-pa-ral-le-lo-gram-ma. Намери точки-ди-те или-ди-он-ту.

Можете да решите този проблем по два начина: логически и координатен метод. Първо ще приложа координатния метод и след това ще ви кажа как можете да решите друго.

Съвсем ясно е, че абсцисата на точката е равна. (той лежи върху перпендикуляра, начертан от точката към оста x). Трябва да намерим ординатата. Нека се възползваме от факта, че нашата фигура е успоредник, което означава, че. Намерете дължината на отсечката, като използвате формулата за разстоянието между две точки:

Спускаме перпендикуляра, свързващ точката с оста. Точката на пресичане се обозначава с буква.

Дължината на сегмента е равна. (намерете сами проблема, където обсъждахме този момент), тогава ще намерим дължината на отсечката, използвайки питагоровата теорема:

Дължината на сегмента е точно същата като неговата ордината.

Отговор: .

Друго решение (ще дам само снимка, която го илюстрира)

Напредък на решението:

1. Похарчете

2. Намерете координатите и дължината на точката

3. Докажете това.

Още едно проблем с дължината на рязане:

Точките са-la-yut-xia top-shi-on-mi tri-angle-no-ka. Намерете дължината на средната му линия, par-ral-lel-noy.

Помните ли каква е средната линия на триъгълник? Тогава за вас тази задача е елементарна. Ако не помните, тогава ще ви напомня: средната линия на триъгълник е линия, която свързва средните точки на противоположните страни. Тя е успоредна на основата и е равна на половината от нея.

Основата е сегмент. Трябваше да търсим дължината му по-рано, тя е равна. Тогава дължината на средната линия е наполовина по-дълга и равна.

Отговор: .

Коментар: Този проблем може да бъде решен по друг начин, към който ще се обърнем малко по-късно.

Междувременно, ето няколко задачи за вас, практикувайте върху тях, те са доста прости, но помагат да „вкарате ръката си“ с помощта на координатния метод!

1. Точките се появяват-la-yut-xia top-shi-on-mi tra-pe-tion. Намерете дължината на средната му линия.

2. Точки и яв-ла-ют-ся вер-ши-на-ми па-рал-ле-ло-грам-ма. Намери точки-ди-те или-ди-он-ту.

3. Намерете дължината от разреза, свържете втората точка и

4. Намерете-ди-те областта за-the-red-shen-noy fi-gu-ry на равнината ko-or-di-nat-noy.

5. Окръжност с център na-cha-le ko-or-di-nat минава през точка. Намерете-де-те нейните ра-ди-мустаци.

6. Nai-di-te ra-di-us circle-no-sti, describe-san-noy близо до десния ъгъл-no-ka, върховете-shi-ny на нещо-ro-go имат co-or - ди-на-ти ко-от-отговор-но

Решения:

1. Известно е, че средната линия на трапец е равна на половината от сбора на неговите основи. Основата е равна, но основата. Тогава

Отговор:

2. Най-лесният начин да решите този проблем е да забележите това (правило на успоредника). Изчислете координатите на векторите и не е трудно: . При добавяне на вектори се добавят координатите. След това има координати. Точката има същите координати, тъй като началото на вектора е точка с координати. Интересуваме се от ординатата. Тя е равностойна.

Отговор:

3. Действаме веднага по формулата за разстоянието между две точки:

Отговор:

4. Погледнете снимката и кажете между кои две фигури е „притисната” защрихованата област? Той е затиснат между два квадрата. Тогава площта на желаната фигура е равна на площта на големия квадрат минус площта на малкия. Страната на малкия квадрат е сегмент, свързващ точките и дължината му е

Тогава площта на малкия квадрат е

Правим същото с голям квадрат: неговата страна е сегмент, свързващ точките и дължината му е равна на

Тогава площта на големия квадрат е

Площта на желаната фигура се намира по формулата:

Отговор:

5. Ако окръжността има начало за център и минава през точка, тогава нейният радиус ще бъде точно равен на дължината на отсечката (направете чертеж и ще разберете защо това е очевидно). Намерете дължината на този сегмент:

Отговор:

6. Известно е, че радиусът на окръжността, описана около правоъгълник, е равен на половината от неговия диагонал. Нека намерим дължината на всеки от двата диагонала (в края на краищата, в правоъгълник те са равни!)

Отговор:

Е, успя ли всичко? Не беше толкова трудно да го разбера, нали? Тук има само едно правило - да можете да направите визуална картина и просто да „четете“ всички данни от нея.

Много малко ни остава. Има буквално още две точки, които бих искал да обсъдя.

Нека се опитаме да решим този прост проблем. Нека две точки и са дадени. Намерете координатите на средата на отсечката. Решението на този проблем е следното: нека точката е желаната среда, тогава тя има координати:

т.е.: координати на средата на отсечката = средноаритметично на съответните координати на краищата на отсечката.

Това правило е много просто и обикновено не създава затруднения за учениците. Нека видим при какви проблеми и как се използва:

1. Find-di-te or-di-na-tu se-re-di-us from-cut, connect-nya-yu-th-th point and

2. Точките са yav-la-yut-xia ver-shi-na-mi-che-you-reh-coal-no-ka. Намерете-ди-те или-ди-на-ту точки на повторно-ре-се-че-ния на неговия dia-go-on-lei.

3. Намерете-ди-те abs-cis-su на центъра на кръга, опишете-сан-ной близо до правоъгълника-но-ка, върховете-ши-имаме нещо-ро-го ко-или-ди- на-ти ко-от-вет-ственно-но.

Решения:

1. Първата задача е просто класика. Действаме незабавно, като определяме средата на сегмента. Тя има координати. Ординатата е равна.

Отговор:

2. Лесно е да се види, че дадения четириъгълник е успоредник (дори ромб!). Можете да го докажете сами, като изчислите дължините на страните и ги сравните една с друга. Какво знам за паралелограма? Неговите диагонали са разделени на две от пресечната точка! Аха! И така, каква е точката на пресичане на диагоналите? Това е средата на всеки от диагоналите! Ще избера по-специално диагонала. Тогава точката има координати.Ординатата на точката е равна на.

Отговор:

3. Какъв е центърът на окръжността, описана около правоъгълника? Той съвпада с пресечната точка на диагоналите му. Какво знаете за диагоналите на правоъгълника? Те са равни и пресечната точка е разделена наполовина. Задачата е сведена до предишната. Вземете, например, диагонала. Тогава, ако е центърът на описаната окръжност, тогава е средата. Търся координати: Абсцисата е равна.

Отговор:

Сега практикувайте малко сами, аз само ще дам отговорите на всеки проблем, за да можете да проверите сами.

1. Nai-di-te ra-di-us circle-no-sti, describe-san-noy близо до триъгълника-но-ка, върховете на някой-ро-го имат ko-or-di -no misters

2. Намерете-ди-те или-ди-на-ту центъра на окръжността, опишете сан-ной близо до триъгълника-но-ка, върховете-ши-имаме нещо-ро-го координати

3. Какъв вид ra-di-y-sa трябва да има окръжност с център в точка, така че да докосва оста abs-ciss?

4. Намерете-di-te or-di-on-tha point of re-re-se-che-ing на оста и from-cut, connect-nya-yu-th-th point and

Отговори:

Всичко ли се получи? Наистина се надявам на това! Сега - последният тласък. Сега бъдете особено внимателни. Материалът, който ще обясня сега, е не само свързан с проблемите с простия координатен метод в част Б, но също така е повсеместен в проблем C2.

Кое от обещанията си още не съм спазил? Спомнете си какви операции с вектори обещах да въведа и кои в крайна сметка въведох? Сигурен ли съм, че не съм забравил нищо? Забравена! Забравих да обясня какво означава умножение на вектори.

Има два начина за умножение на вектор по вектор. В зависимост от избрания метод ще получим обекти от различно естество:

Векторният продукт е доста сложен. Как да го направите и защо е необходимо, ще обсъдим с вас в следващата статия. И в това ще се спрем на скаларното произведение.

Вече има два начина, които ни позволяват да го изчислим:

Както се досещате, резултатът трябва да е същият! Така че нека първо да разгледаме първия начин:

Точков продукт чрез координати

Намерете: - общо обозначение за точков продукт

Формулата за изчисление е както следва:

Тоест точковото произведение = сумата от произведенията на координатите на векторите!

пример:

Find-dee-te

Решение:

Намерете координатите на всеки от векторите:

Изчисляваме скаларното произведение по формулата:

Отговор:

Виждате ли, абсолютно нищо сложно!

Е, сега опитайте сами:

Find-di-te scalar-noe pro-from-ve-de-nie век-до-ров и

Справихте ли се? Може би е забелязал малък трик? Да проверим:

Векторни координати, както в предишната задача! Отговор: .

В допълнение към координатата има и друг начин за изчисляване на скаларния продукт, а именно чрез дължините на векторите и косинуса на ъгъла между тях:

Означава ъгъла между векторите и.

Тоест скаларното произведение е равно на произведението на дължините на векторите и косинуса на ъгъла между тях.

Защо ни е нужна тази втора формула, ако имаме първата, която е много по-проста, поне в нея няма косинуси. И ние имаме нужда от него, за да можем от първата и втората формули да изведем как да намерим ъгъла между векторите!

Нека Тогава запомнете формулата за дължината на вектор!

След това, ако включа тези данни във формулата на точковия продукт, получавам:

Но по друг начин:

И така, какво имаме? Сега имаме формула за изчисляване на ъгъла между два вектора! Понякога за краткост се пише и така:

Тоест алгоритъмът за изчисляване на ъгъла между векторите е както следва:

1. Изчисляваме скаларното произведение чрез координатите
2. Намерете дължините на векторите и ги умножете
3. Разделете резултата от точка 1 на резултата от точка 2

Нека се упражняваме с примери:

1. Намерете ъгъла между клепачите-до-ра-ми и. Дайте отговора си в градуси.

2. При условията на предходната задача намерете косинуса между векторите

Нека направим това: ще ви помогна да решите първия проблем и се опитайте сами да направите втория! Съгласен? Тогава да започваме!

1. Тези вектори са наши стари приятели. Вече разгледахме скаларното им произведение и то беше равно. Техните координати са: , . След това намираме техните дължини:

Тогава търсим косинуса между векторите:

Какъв е косинусът на ъгъла? Това е ъгълът.

Отговор:

Е, сега решете втория проблем сами и след това сравнете! Просто ще дам много кратко решение:

2. има координати, има координати.

Нека е ъгълът между векторите и, тогава

Отговор:

Трябва да се отбележи, че задачите директно върху векторите и метода на координатите в част Б на изпитната работа са доста редки. Въпреки това, по-голямата част от проблемите на C2 могат лесно да бъдат решени чрез въвеждане на координатна система. Така че можете да разглеждате тази статия като основа, въз основа на която ще направим доста сложни конструкции, които ще ни трябват за решаване на сложни проблеми.

КООРДИНАТИ И ВЕКТОРИ. СРЕДНО НИВО

Ние с вас продължаваме да изучаваме метода на координатите. В последната част изведохме редица важни формули, които позволяват:

1. Намерете векторни координати
2. Намерете дължината на вектор (алтернативно: разстоянието между две точки)
3. Добавяне, изваждане на вектори. Умножете ги по реално число
4. Намерете средата на сегмент
5. Изчислете точковото произведение на векторите
6. Намерете ъгъла между векторите

Разбира се, целият координатен метод не се вписва в тези 6 точки. Тя е в основата на такава наука като аналитичната геометрия, с която ще се запознаете в университета. Просто искам да изградя основа, която ще ви позволи да решавате проблеми в една държава. изпит. Разбрахме задачите на част Б в Сега е време да преминем на качествено ново ниво! Тази статия ще бъде посветена на метод за решаване на онези C2 проблеми, при които би било разумно да се премине към координатния метод. Тази разумност се определя от това, което трябва да се намери в проблема и каква цифра е дадена. И така, бих използвал метода на координатите, ако въпросите са:

1. Намерете ъгъла между две равнини
2. Намерете ъгъла между права и равнина
3. Намерете ъгъла между две прави
4. Намерете разстоянието от точка до равнина
5. Намерете разстоянието от точка до права
6. Намерете разстоянието от права линия до равнина
7. Намерете разстоянието между две линии

Ако фигурата, дадена в условието на задачата, е тяло на въртене (топка, цилиндър, конус ...)

Подходящи фигури за координатния метод са:

1. кубоид
2. Пирамида (триъгълна, четириъгълна, шестоъгълна)

Също така според моя опит неуместно е използването на координатния метод за:

1. Намиране на областите на секции
2. Изчисления на обемите на телата

Трябва обаче веднага да се отбележи, че три „неблагоприятни“ ситуации за координатния метод са доста редки на практика. В повечето задачи може да стане ваш спасител, особено ако не сте много силни в триизмерните конструкции (които понякога са доста сложни).

Кои са всички цифри, които изброих по-горе? Те вече не са плоски, като квадрат, триъгълник, кръг, а обемни! Съответно трябва да разгледаме не двуизмерна, а триизмерна координатна система. Изгражда се доста лесно: само в допълнение към абсцисата и ординатите, ще въведем още една ос, апликатната ос. Фигурата показва схематично тяхното относително положение:

Всички те са взаимно перпендикулярни, пресичат се в една точка, която ще наречем начало. Оста на абсцисата, както и преди, ще бъде обозначена, оста на ординатите - , а въведената апликатна ос - .

Ако по-рано всяка точка от равнината се характеризираше с две числа - абсцисата и ординатата, тогава всяка точка в пространството вече се описва с три числа - абсцисата, ординатата, приложението. Например:

Съответно, абсцисата на точката е равна, ординатата е , а приложението е .

Понякога абсцисата на точка се нарича още проекция на точката върху оста на абсцисата, ординатата е проекцията на точката върху оста y, а апликацията е проекцията на точката върху оста на приложението. Съответно, ако е дадена точка, тогава точка с координати:

наречена проекция на точка върху равнина

наречена проекция на точка върху равнина

Възниква естествен въпрос: всички формули, получени за двумерния случай, валидни ли са в пространството? Отговорът е да, те са просто и имат еднакъв вид. За малка подробност. Мисля, че вече познахте коя. Във всички формули ще трябва да добавим още един член, отговорен за оста на приложението. А именно.

1. Ако са дадени две точки: , тогава:

• Координати на вектора:
• Разстояние между две точки (или векторна дължина)
• Средата на сегмента има координати

2. Ако са дадени два вектора: и, тогава:

• Техният точков продукт е:
• Косинусът на ъгъла между векторите е:

Пространството обаче не е толкова просто. Както разбирате, добавянето на още една координата въвежда значително разнообразие в спектъра от фигури, "живеещи" в това пространство. И за по-нататъшно разказване, трябва да представя някакво, грубо казано, "обобщение" на правата линия. Това "обобщение" ще бъде самолет. Какво знаеш за самолета? Опитайте се да отговорите на въпроса какво е самолет? Много е трудно да се каже. Въпреки това, всички ние интуитивно си представяме как изглежда:

Грубо казано, това е един вид безкраен „лист“, хвърлен в космоса. „Безкрайност“ трябва да се разбира, че равнината се простира във всички посоки, тоест нейната площ е равна на безкрайност. Това обяснение "на пръсти" обаче не дава ни най-малка представа за структурата на самолета. И ние ще се интересуваме от него.

Нека си спомним една от основните аксиоми на геометрията:

• Права линия минава през две различни точки на равнина, освен това само една:

Или неговия аналог в космоса:

Разбира се, помните как да извлечете уравнението на права линия от две дадени точки, това изобщо не е трудно: ако първата точка има координати: а втората, тогава уравнението на правата линия ще бъде както следва:

Преминахте през това в 7 клас. В пространството уравнението на права линия изглежда така: нека имаме две точки с координати: , тогава уравнението на права линия, минаваща през тях, има вида:

Например, линия минава през точки:

Как трябва да се разбира това? Това трябва да се разбира по следния начин: точка лежи на права, ако нейните координати удовлетворяват следната система:

Няма да ни интересува много уравнението на права линия, но трябва да обърнем внимание на много важното понятие за насочващия вектор на права линия. - всеки ненулев вектор, лежащ на дадена права или успореден на нея.

Например и двата вектора са вектори на посоката на права линия. Позволявам да бъде точка, лежаща на права линия, и да бъде нейният насочващ вектор. Тогава уравнението на права линия може да се запише в следния вид:

Още веднъж, няма да се интересувам много от уравнението на права линия, но наистина имам нужда да запомните какво е вектор на посоката! Отново: това е ВСЕКИ ненулев вектор, лежащ на права или успореден на нея.

оттегли се триточково уравнение на равнинавече не е толкова тривиален и обикновено не се обхваща в курс за гимназия. Но напразно! Тази техника е жизненоважна, когато прибягваме до координатния метод за решаване на сложни проблеми. Предполагам обаче, че сте изпълнени с желание да научите нещо ново? Освен това ще можете да впечатлите преподавателя си в университета, когато се окаже, че вече знаете как да използвате техниката, която обикновено се изучава в курса на аналитичната геометрия. Така че нека започваме.

Уравнението на равнината не е твърде различно от уравнението на права линия върху равнина, а именно има формата:

някои числа (не всички равни на нула), но променливи, например: и т.н. Както можете да видите, уравнението на равнината не се различава много от уравнението на права линия (линейна функция). Спомняте ли си обаче какво спорихме с вас? Казахме, че ако имаме три точки, които не лежат на една права линия, тогава уравнението на равнината се възстановява еднозначно от тях. Но как? Ще се опитам да ти обясня.

Тъй като уравнението на равнината е:

И точките принадлежат на тази равнина, тогава когато заменим координатите на всяка точка в уравнението на равнината, трябва да получим правилната идентичност:

По този начин има нужда да се решат три уравнения вече с неизвестни! Дилема! Въпреки това, винаги можем да приемем, че (за това трябва да разделим на). Така получаваме три уравнения с три неизвестни:

Ние обаче няма да решаваме такава система, а ще изпишем загадъчния израз, който следва от нея:

Уравнение на равнина, минаваща през три дадени точки

\[\вляво| (\begin(масив)(*(20)(c))(x - (x_0))&((x_1) - (x_0))&((x_2) - (x_0))\\(y - (y_0) )&((y_1) - (y_0))&((y_2) - (y_0))\\(z - (z_0))&((z_1) - (z_0))&((z_2) - (z_0)) \end(масив)) \вдясно| = 0\]

Спри се! Какво друго е това? Много необичаен модул! Обектът, който виждате пред себе си обаче, няма нищо общо с модула. Този обект се нарича детерминанта от трети ред. Оттук нататък, когато се занимавате с метода на координатите в равнина, много често ще се натъквате на същите тези детерминанти. Какво е детерминанта от трети порядък? Колкото и да е странно, това е просто число. Остава да разберем какво конкретно число ще сравним с детерминанта.

Нека първо напишем детерминанта от трети порядък в по-общ вид:

Къде са някои цифри. Освен това под първия индекс имаме предвид номера на реда, а под индекса - номера на колоната. Например, това означава, че даденото число е в пресечната точка на втория ред и третата колона. Нека си зададем следния въпрос: как точно ще изчислим такъв детерминант? Тоест с кое конкретно число ще го сравним? За детерминанта точно от третия ред има евристично (визуално) правило за триъгълник, което изглежда така:

1. Произведението на елементите на главния диагонал (от горния ляв до долния десен) произведението на елементите, които образуват първия триъгълник "перпендикулярно" на главния диагонал, произведението на елементите, които образуват втория триъгълник "перпендикулярно" на главния диагонал
2. Произведението на елементите на вторичния диагонал (от горния десен до долния ляв) произведението на елементите, които образуват първия триъгълник "перпендикулярно" на вторичния диагонал, произведението на елементите, които образуват втория триъгълник "перпендикулярно" на вторичният диагонал
3. Тогава детерминантата е равна на разликата между стойностите, получени на стъпката и

Ако запишем всичко това в числа, тогава получаваме следния израз:

Не е нужно обаче да запомняте метода на изчисление в тази форма, достатъчно е просто да запазите триъгълниците в главата си и самата идея какво се добавя към какво и какво след това се изважда от какво).

Нека илюстрираме метода на триъгълника с пример:

1. Изчислете детерминанта:

Нека разберем какво добавяме и какво изваждаме:

Термини, които идват с "плюс":

Това е основният диагонал: продуктът на елементите е

Първият триъгълник, "перпендикулярен на главния диагонал: произведението на елементите е

Вторият триъгълник, "перпендикулярен на главния диагонал: произведението на елементите е

Събираме три числа:

Термини, които идват с "минус"

Това е страничен диагонал: произведението на елементите е

Първият триъгълник, "перпендикулярен на вторичния диагонал: произведението на елементите е

Вторият триъгълник, "перпендикулярен на вторичния диагонал: произведението на елементите е

Събираме три числа:

Всичко, което остава да се направи, е да се извади от сбора на плюсовете сумата от минусовите:

По този начин,

Както можете да видите, няма нищо сложно и свръхестествено в изчисляването на детерминанти от трети ред. Просто е важно да помните за триъгълниците и да не правите аритметични грешки. Сега се опитайте да изчислите сами:

Ние проверяваме:

1. Първият триъгълник, перпендикулярен на главния диагонал:
2. Вторият триъгълник, перпендикулярен на главния диагонал:
3. Сумата от плюсовите условия:
4. Първи триъгълник, перпендикулярен на страничния диагонал:
5. Вторият триъгълник, перпендикулярен на страничния диагонал:
6. Сборът от членове с минус:
7. Сума от плюс членове минус сума от минус членове:

Ето още няколко детерминанта за вас, изчислете сами стойностите им и сравнете с отговорите:

Отговори:

Е, всичко съвпадна ли? Страхотно, тогава можете да продължите! Ако има трудности, тогава моят съвет е следният: в интернет има куп програми за изчисляване на детерминанта онлайн. Всичко, от което се нуждаете, е да измислите свой собствен детерминант, да го изчислите сами и след това да го сравните с това, което изчислява програмата. И така, докато резултатите не започнат да съвпадат. Сигурен съм, че този момент няма да закъснее!

Сега да се върнем към детерминантата, която написах, когато говорих за уравнението на равнина, преминаваща през три дадени точки:

Всичко, което трябва да направите, е да изчислите стойността му директно (метод на триъгълник) и да зададете резултата на нула. Естествено, тъй като те са променливи, ще получите някакъв израз, който зависи от тях. Именно този израз ще бъде уравнението на равнина, минаваща през три дадени точки, които не лежат на една права линия!

Нека илюстрираме това с прост пример:

1. Построете уравнението на равнината, минаваща през точките

Ние съставяме детерминанта за тези три точки:

опростяване:

Сега го изчисляваме директно според правилото на триъгълниците:

\[(\left| (\begin(array)(*(20)(c))(x + 3)&2&6\\(y - 2)&0&1\\(z + 1)&5&0\end(array)) \ дясно| = \left((x + 3) \right) \cdot 0 \cdot 0 + 2 \cdot 1 \cdot \left((z + 1) \right) + \left((y - 2) \right) \cdot 5 \cdot 6 - )\]

По този начин уравнението на равнината, минаваща през точките, е:

Сега се опитайте сами да решите един проблем и тогава ще го обсъдим:

2. Намерете уравнението на равнината, минаваща през точките

Е, нека обсъдим решението сега:

Правим детерминанта:

И изчислете стойността му:

Тогава уравнението на равнината има вида:

Или, намалявайки с, получаваме:

Сега две задачи за самоконтрол:

1. Постройте уравнението на равнина, минаваща през три точки:

Отговори:

Всичко съвпадна ли? Отново, ако има определени трудности, тогава моят съвет е следният: вземете три точки от главата си (с голяма степен на вероятност те няма да лежат на една права линия), построете самолет върху тях. И след това се проверете онлайн. Например на сайта:

Но с помощта на детерминанти ще построим не само уравнението на равнината. Запомнете, казах ви, че за векторите не е дефиниран само точковият продукт. Има и вектор, както и смесен продукт. И ако скаларното произведение на два вектора ще бъде число, тогава векторното произведение на два вектора ще бъде вектор и този вектор ще бъде перпендикулярен на дадените:

Освен това неговият модул ще бъде равен на площта на паралелограма, изграден върху векторите и. Ще ни трябва този вектор, за да изчислим разстоянието от точка до права. Как можем да изчислим кръстосаното произведение на векторите и дали са дадени техните координати? Определителят от трети порядък отново ни идва на помощ. Преди обаче да премина към алгоритъма за изчисляване на кръстосаното произведение, трябва да направя малко лирично отклонение.

Това отклонение се отнася до базисните вектори.

Схематично те са показани на фигурата:

Защо мислите, че се наричат ​​основни? Факт е, че:

Или на снимката:

Валидността на тази формула е очевидна, защото:

векторен продукт

Сега мога да започна да представям кръстосания продукт:

Векторното произведение на два вектора е вектор, който се изчислява съгласно следното правило:

Сега нека дадем няколко примера за изчисляване на кръстосаното произведение:

Пример 1: Намерете кръстосаното произведение на векторите:

Решение: правя детерминанта:

И аз го изчислявам:

Сега, от писането чрез базисни вектори, ще се върна към обичайната векторна нотация:

По този начин:

Сега опитайте.

Готов? Ние проверяваме:

И по традиция две задачи за контрол:

1. Намерете кръстосаното произведение на следните вектори:
2. Намерете кръстосаното произведение на следните вектори:

Отговори:

Смесен продукт от три вектора

Последната конструкция, от която се нуждая, е смесеното произведение на три вектора. То, като скалар, е число. Има два начина да го изчислите. - чрез детерминанта, - чрез смесеното произведение.

А именно, да кажем, че имаме три вектора:

Тогава смесеното произведение на три вектора, обозначени с, може да се изчисли като:

1. - тоест смесеното произведение е скаларното произведение на вектор и векторното произведение на два други вектора

Например, смесеният продукт на три вектора е:

Опитайте да го изчислите сами, като използвате векторния продукт и се уверете, че резултатите съвпадат!

И отново - два примера за самостоятелно решение:

Отговори:

Избор на координатна система

Е, сега имаме цялата необходима основа от знания за решаване на сложни стереометрични задачи в геометрията. Въпреки това, преди да пристъпим директно към примерите и алгоритмите за тяхното решаване, смятам, че ще бъде полезно да се спрем на следния въпрос: как точно изберете координатна система за определена фигура.В крайна сметка изборът на относителното положение на координатната система и фигурата в пространството в крайна сметка ще определи колко тромави ще бъдат изчисленията.

Напомням ви, че в този раздел разглеждаме следните цифри:

1. кубоид
2. Права призма (триъгълна, шестоъгълна...)
3. пирамида (триъгълна, четириъгълна)
4. Тетраедър (същото като триъгълна пирамида)

За кубоид или куб препоръчвам следната конструкция:

Тоест ще поставя фигурата „в ъгъла“. Кубът и кутията са много добри фигури. За тях винаги можете лесно да намерите координатите на върховете му. Например, ако (както е показано на снимката)

тогава координатите на върха са:

Разбира се, не е нужно да помните това, но е желателно да запомните как най-добре да позиционирате куб или правоъгълна кутия.

права призма

Призмата е по-вредна фигура. Можете да го подредите в пространството по различни начини. Въпреки това мисля, че следното е най-добрият вариант:

Триъгълна призма:

Това означава, че поставяме една от страните на триъгълника изцяло върху оста и един от върховете съвпада с началото.

Шестоъгълна призма:

Това означава, че един от върховете съвпада с началото, а една от страните лежи върху оста.

Четириъгълна и шестоъгълна пирамида:

Ситуация, подобна на куб: комбинираме две страни на основата с координатните оси, комбинираме един от върховете с началото. Единствената малка трудност ще бъде изчисляването на координатите на точката.

За шестоъгълна пирамида - същото като за шестоъгълна призма. Основната задача отново ще бъде намирането на координатите на върха.

Тетраедър (триъгълна пирамида)

Ситуацията е много подобна на тази, която дадох за триъгълната призма: един връх съвпада с началото, едната страна лежи върху координатната ос.

Е, сега ние с вас най-накрая сме близо до започване на решаване на проблеми. От това, което казах в самото начало на статията, можете да направите следния извод: повечето C2 проблеми попадат в 2 категории: проблеми за ъгъла и проблеми за разстоянието. Първо, ще разгледаме проблемите за намиране на ъгъл. Те от своя страна са разделени на следните категории (с увеличаване на сложността):

Проблеми с намирането на ъгли

1. Намиране на ъгъла между две прави
2. Намиране на ъгъла между две равнини

Нека разгледаме тези проблеми последователно: нека започнем с намирането на ъгъла между две прави линии. Хайде, не забравяйте, ние с вас решавахме ли подобни примери преди? Спомняте си, защото вече имахме нещо подобно... Търсихме ъгъл между два вектора. Напомням ви, ако са дадени два вектора: и, тогава ъгълът между тях се намира от отношението:

Сега имаме цел - намиране на ъгъла между две прави линии. Нека се обърнем към "плоската картина":

Колко ъгъла получаваме, когато две прави се пресичат? Вече нещата. Вярно е, че само две от тях не са равни, докато други са вертикални спрямо тях (и следователно съвпадат с тях). И така, какъв ъгъл трябва да вземем предвид ъгълът между две прави линии: или? Тук правилото е: ъгълът между две прави линии винаги е не повече от градуси. Тоест от два ъгъла винаги ще избираме ъгъла с най-малка градусова мярка. Тоест на тази снимка ъгълът между двете линии е равен. За да не се занимават всеки път с намирането на най-малкия от двата ъгъла, хитри математици предложиха да използвате модула. Така ъгълът между две прави линии се определя по формулата:

Вие, като внимателен читател, трябваше да имате въпрос: всъщност откъде да вземем тези числа, които са ни необходими, за да изчислим косинуса на ъгъл? Отговор: ще ги вземем от векторите на посоката на линиите! По този начин алгоритъмът за намиране на ъгъла между две линии е както следва:

1. Прилагаме формула 1.

Или по-подробно:

1. Търсим координатите на вектора на посоката на първата права линия
2. Търсим координатите на вектора на посоката на втория ред
3. Изчислете модула на скаларния им продукт
4. Търсим дължината на първия вектор
5. Търсим дължината на втория вектор
6. Умножете резултатите от точка 4 по резултатите от точка 5
7. Разделяме резултата от точка 3 на резултата от точка 6. Получаваме косинус на ъгъла между правите
8. Ако този резултат ни позволява да изчислим точно ъгъла, ние го търсим
9. В противен случай пишем през арккосинуса

Е, сега е моментът да преминем към задачите: ще демонстрирам подробно решението на първите две, ще представя решението на друга накратко и ще дам отговори само на последните две задачи, вие трябва направете сами всички изчисления за тях.

задачи:

1. В дясната тет-ра-ед-ре намерете-ди-те ъгъла между вас-та-тоя тет-ра-ед-ра и страната на me-di-a-noy bo-ko-how.

2. В дясно-напред шест въглища-пи-ра-ми-де сто-ро-на-ос-но-ва-ния са някак равни, а страничните ребра са равни, намерете ъгъла между правите линии и.

3. Дължините на всички ръбове на десния четири-ти-реч-въглен-ной пи-ра-ми-ди са равни една на друга. Намерете ъгъла между правите линии и ако от-re-zok - you-so-that дадено pi-ra-mi-dy, точката е se-re-di-на нейното bo-ko- th ребро

4. На ръба на куба от-me-che-до точка, така че Намерете-di-te ъгъла между правите и

5. Точка - се-ре-ди-на ръбовете на куба Nai-di-te ъгъла между правите и.

Неслучайно поставих задачите в този ред. Докато все още не сте имали време да започнете да навигирате по метода на координатите, аз самият ще анализирам най-„проблемните“ фигури и ще ви оставя да се справите с най-простия куб! Постепенно трябва да се научите да работите с всички фигури, аз ще увеличавам сложността на задачите от тема на тема.

Нека започнем да решаваме проблеми:

1. Начертайте тетраедър, поставете го в координатната система, както предложих по-рано. Тъй като тетраедърът е правилен, тогава всичките му лица (включително основата) са правилни триъгълници. Тъй като не ни е дадена дължината на страната, мога да я взема равна. Мисля, че разбирате, че ъгълът наистина няма да зависи от това колко ще бъде "разтегнат" нашия тетраедър?. Ще начертая също височината и медианата в тетраедъра. По пътя ще нарисувам основата му (ще ни е от полза и).

Трябва да намеря ъгъла между и. какво знаем ние? Знаем само координатите на точката. И така, трябва да намерим повече координати на точките. Сега мислим: точката е точка на пресичане на височини (или ъглополовящи или медиани) на триъгълник. Точката е издигната точка. Точката е средата на сегмента. След това накрая трябва да намерим: координатите на точките: .

Нека започнем с най-простото: координати на точки. Погледнете фигурата: Ясно е, че приложението на точка е равно на нула (точката лежи върху равнина). Неговата ордината е равна (защото е медиана). По-трудно е да се намери абсцисата му. Това обаче лесно се прави на базата на питагоровата теорема: Да разгледаме триъгълник. Хипотенузата му е равна и един от катетите е равен Тогава:

В крайна сметка имаме:

Сега нека намерим координатите на точката. Ясно е, че неговото приложение отново е равно на нула, а ординатата му е същата като тази на точка, т.е. Да намерим абсцисата му. Това се прави доста тривиално, ако човек го помни височините на равностранен триъгълник се делят на пресечната точка в пропорциятакато се брои отгоре. Тъй като:, тогава желаната абциса на точката, равна на дължината на отсечката, е равна на:. Така координатите на точката са:

Нека намерим координатите на точката. Ясно е, че нейната абсцисса и ордината съвпадат с абсцисата и ординатата на точката. А апликацията е равна на дължината на сегмента. - това е един от краката на триъгълника. Хипотенузата на триъгълник е отсечка - катет. Търси се за причините, които подчертах с удебелен шрифт:

Точката е средата на сегмента. След това трябва да запомним формулата за координатите на средата на сегмента:

Това е всичко, сега можем да търсим координатите на векторите на посоката:

Е, всичко е готово: заместваме всички данни във формулата:

По този начин,

Отговор:

Не бива да се страхувате от такива "ужасни" отговори: за проблеми C2 това е обичайна практика. По-скоро бих се изненадал от "красивия" отговор в тази част. Освен това, както отбелязахте, на практика не прибягнах до нищо друго освен питагоровата теорема и свойството на височините на равностранен триъгълник. Тоест, за да реша стереометричния проблем, използвах самия минимум стереометрия. Печалбата от това е частично "загасена" от доста тромави изчисления. Но те са доста алгоритмични!

2. Начертайте правилна шестоъгълна пирамида заедно с координатната система, както и нейната основа:

Трябва да намерим ъгъла между линиите и. Така нашата задача се свежда до намиране на координатите на точките: . Ще намерим координатите на последните три от малкия чертеж и ще намерим координатата на върха през координатата на точката. Много работа, но трябва да започнете!

а) Координата: ясно е, че нейното приложение и ордината са нула. Да намерим абсцисата. За да направите това, помислете за правоъгълен триъгълник. Уви, в него знаем само хипотенузата, която е равна на. Ще се опитаме да намерим катета (защото е ясно, че удвоената дължина на крака ще ни даде абсцисата на точката). Как да го търсим? Нека си спомним каква фигура имаме в основата на пирамидата? Това е правилен шестоъгълник. Какво означава? Това означава, че всички страни и всички ъгли са равни. Трябва да намерим един такъв ъгъл. Някакви идеи? Има много идеи, но има формула:

Сумата от ъглите на правилния n-ъгълник е .

Така сумата от ъглите на правилния шестоъгълник е градуси. Тогава всеки от ъглите е равен на:

Да погледнем отново снимката. Ясно е, че отсечката е ъглополовяща на ъгъла. Тогава ъгълът е градуси. Тогава:

Тогава къде.

Значи има координати

б) Сега лесно можем да намерим координатата на точката: .

в) Намерете координатите на точката. Тъй като абсцисата му съвпада с дължината на отсечката, тя е равна. Намирането на ординатата също не е много трудно: ако свържем точките и и обозначим пресечната точка на правата, да речем за. (направете сами проста конструкция). Тогава По този начин ординатата на точка B е равна на сумата от дължините на отсечките. Нека отново да разгледаме триъгълника. Тогава

Тогава от Тогава точката има координати

г) Сега намерете координатите на точката. Помислете за правоъгълник и докажете, че По този начин координатите на точката са:

д) Остава да се намерят координатите на върха. Ясно е, че нейната абсцисса и ордината съвпадат с абсцисата и ординатата на точката. Да намерим приложение. От тогава. Помислете за правоъгълен триъгълник. По условие на проблема, страничният ръб. Това е хипотенузата на моя триъгълник. Тогава височината на пирамидата е кракът.

Тогава точката има координати:

Това е всичко, имам координатите на всички точки, които ме интересуват. Търся координатите на насочващите вектори на правите:

Търсим ъгъла между тези вектори:

Отговор:

Отново при решаването на този проблем не използвах никакви сложни трикове, освен формулата за сумата от ъглите на правилен n-ъгъл, както и дефиницията на косинуса и синуса на правоъгълен триъгълник.

3. Тъй като отново не са ни дадени дължините на ръбовете в пирамидата, ще ги считам за равни на единица. По този начин, тъй като ВСИЧКИ ръбове, а не само страничните, са равни едно на друго, тогава в основата на пирамидата и мен лежи квадрат, а страничните лица са правилни триъгълници. Нека изобразим такава пирамида, както и нейната основа върху равнина, маркирайки всички данни, дадени в текста на задачата:

Търсим ъгъла между и. Ще направя много кратки изчисления, когато търся координатите на точките. Ще трябва да ги "дешифрирате":

б) - средата на сегмента. Нейните координати:

в) Ще намеря дължината на отсечката с помощта на Питагоровата теорема в триъгълник. Ще намеря по теоремата на Питагор в триъгълник.

Координати:

г) - средата на сегмента. Координатите му са

д) Векторни координати

е) Векторни координати

ж) Търсене на ъгъл:

Кубът е най-простата фигура. Сигурен съм, че можеш да го разбереш сам. Отговорите на задачи 4 и 5 са ​​както следва:

Намиране на ъгъла между права и равнина

Е, времето за прости пъзели свърши! Сега примерите ще бъдат още по-трудни. За да намерим ъгъла между права и равнина, ще продължим както следва:

1. Използвайки три точки, изграждаме уравнението на равнината
   ,
   използвайки детерминанта от трети порядък.
2. По две точки търсим координатите на насочващия вектор на правата линия:
3. Прилагаме формулата за изчисляване на ъгъла между права линия и равнина:

Както можете да видите, тази формула е много подобна на тази, която използвахме за намиране на ъглите между две прави. Структурата на дясната страна е същата, а отляво сега търсим синус, а не косинус, както преди. Е, беше добавено едно гадно действие - търсенето на уравнението на самолета.

Нека не отлагаме примери за решаване:

1. Os-no-va-ni-em направо-моята награда-ние сме-la-et-xia равни-но-беден-ren-ny триъгълник-nick ти-така-тази награда-ние сме равни. Намерете ъгъла между правата линия и равнината

2. В правоъгълен pa-ral-le-le-pi-pe-de от запад Nai-di-te ъгълът между правата линия и равнината

3. В дясната шествъглена призма всички ръбове са равни. Намерете ъгъла между правата линия и равнината.

4. В десния триъгълен пи-ра-ми-де с ос-бут-ва-ни-ем от запад на реброто Най-ди-те ъгъл, об-ра-зо-ван -на равнина на ос. -но-ва-ния и права-моя, минаваща през се-ре-ди-на на ребрата и

5. Дължините на всички ръбове на дясното четириъгълно пи-ра-ми-ди с върха са равни една на друга. Намерете ъгъла между правата линия и равнината, ако точката е se-re-di-на bo-ko-in-th ръба на pi-ra-mi-dy.

Отново ще реша първите два проблема в детайли, третия - накратко, а последните два оставям да решите сами. Освен това вече трябваше да се справите с триъгълни и четириъгълни пирамиди, но все още не и с призми.

Решения:

1. Начертайте призма, както и нейната основа. Нека го комбинираме с координатната система и маркираме всички данни, които са дадени в формулировката на проблема:

Извинявам се за някакво неспазване на пропорциите, но за решаването на проблема това всъщност не е толкова важно. Самолетът е просто "задната стена" на моята призма. Достатъчно е просто да предположим, че уравнението на такава равнина има формата:

Това обаче може да бъде показано и директно:

Избираме произволни три точки на тази равнина: например, .

Нека направим уравнението на равнината:

Упражнение за вас: изчислете сами тази детерминанта. Успяхте ли? Тогава уравнението на равнината има вида:

Или просто

По този начин,

За да реша примера, трябва да намеря координатите на насочващия вектор на правата линия. Тъй като точката съвпада с началото, координатите на вектора просто ще съвпаднат с координатите на точката.За да направим това, първо намираме координатите на точката.

За да направите това, помислете за триъгълник. Нека начертаем височина (тя също е медиана и ъглополовяща) от върха. Тъй като тогава ординатата на точката е равна. За да намерим абсцисата на тази точка, трябва да изчислим дължината на отсечката. По теоремата на Питагор имаме:

Тогава точката има координати:

Точката е "вдигната" върху точка:

Тогава координатите на вектора:

Отговор:

Както можете да видите, няма нищо фундаментално трудно в решаването на подобни проблеми. Всъщност „правостта“ на фигура като призма опростява процеса малко повече. Сега да преминем към следващия пример:

2. Начертаваме паралелепипед, начертаваме в него равнина и права линия, а също така отделно начертаваме долната му основа:

Първо, намираме уравнението на равнината: Координатите на трите точки, лежащи в нея:

(първите две координати се получават по очевиден начин и лесно можете да намерите последната координата от снимката от точката). След това съставяме уравнението на равнината:

Ние изчисляваме:

Търсим координатите на вектора на посоката: Ясно е, че координатите му съвпадат с координатите на точката, нали? Как да намеря координати? Това са координатите на точката, повдигната по оста на приложението с единица! . След това търсим желания ъгъл:

Отговор:

3. Начертайте правилна шестоъгълна пирамида и след това начертайте равнина и права линия в нея.

Тук дори е проблематично да се начертае равнина, да не говорим за решението на този проблем, но координатният метод не се интересува! Именно в неговата гъвкавост се крие основното му предимство!

Равнината минава през три точки: . Търсим техните координати:

едно). Покажете сами координатите за последните две точки. За това ще трябва да решите проблема с шестоъгълна пирамида!

2) Изграждаме уравнението на равнината:

Търсим координатите на вектора: . (Вижте отново проблема с триъгълната пирамида!)

3) Търсим ъгъл:

Отговор:

Както виждате, в тези задачи няма нищо свръхестествено трудно. Просто трябва да бъдете много внимателни с корените. На последните два проблема ще дам само отговори:

Както можете да видите, техниката за решаване на проблеми е една и съща навсякъде: основната задача е да се намерят координатите на върховете и да се заменят в някои формули. Остава да разгледаме още един клас задачи за изчисляване на ъгли, а именно:

Изчисляване на ъгли между две равнини

Алгоритъмът на решението ще бъде както следва:

1. За три точки търсим уравнението на първата равнина:
2. За останалите три точки търсим уравнението на втората равнина:
3. Прилагаме формулата:

Както виждате, формулата е много подобна на предишните две, с помощта на които търсихме ъгли между прави и между права линия и равнина. Така че запомнянето на този няма да ви е трудно. Нека да преминем направо към проблема:

1. Сто-ро на основата на дясната триъгълна призма е равен, а диагоналът на страничната страна е равен. Намерете ъгъла между равнината и равнината на основата на наградата.

2. В дясно-напред четири-ти-ре-въглищ-ной пи-ра-ми-де всички ръбове на някого са равни, намерете синуса на ъгъла между равнината и равнината Ко-Сту, минаваща през точката на per-pen-di-ku-lyar-но направо-ми.

3. В правилната призма с четири въглища страните на ос-но-ва-ния са равни, а страничните ръбове са равни. На ръба от-ме-че-до точката, така че. Намерете ъгъла между равнините и

4. В дясната четириъгълна призма страните на основите са равни, а страничните ръбове са равни. На ръба от-ме-че-до точка, така че Намерете ъгъла между равнините и.

5. В куба намерете ко-синус на ъгъла между равнините и

Решения на проблеми:

1. Начертавам правилна (в основата - равностранен триъгълник) триъгълна призма и отбелязвам върху нея равнините, които се появяват в условието на задачата:

Трябва да намерим уравненията на две равнини: Основното уравнение се получава тривиално: можете да направите съответния детерминант за три точки, но аз ще направя уравнението веднага:

Сега нека намерим уравнението Точката има координати Точка - Тъй като - медианата и височината на триъгълника, лесно се намира по теоремата на Питагор в триъгълника. Тогава точката има координати: Намерете приложението на точката. За да направите това, разгледайте правоъгълен триъгълник

Тогава получаваме следните координати: Съставяме уравнението на равнината.

Изчисляваме ъгъла между равнините:

Отговор:

2. Изработване на чертеж:

Най-трудното е да се разбере каква мистериозна равнина е, минаваща през точка перпендикулярно. Е, основното е какво е то? Основното нещо е вниманието! Всъщност линията е перпендикулярна. Линията също е перпендикулярна. Тогава равнината, преминаваща през тези две прави, ще бъде перпендикулярна на правата и, между другото, ще премине през точката. Тази равнина също минава през върха на пирамидата. След това желания самолет - И самолетът вече ни е даден. Търсим координати на точки.

Намираме координатата на точката през точката. От малък чертеж е лесно да се заключи, че координатите на точката ще бъдат както следва: Какво остава да намерим сега, за да намерим координатите на върха на пирамидата? Все още трябва да се изчисли височината му. Това се прави с помощта на същата питагорова теорема: първо, докажете това (тривиално от малки триъгълници, образуващи квадрат в основата). Тъй като по условие имаме:

Сега всичко е готово: координати на върха:

Съставяме уравнението на равнината:

Вие вече сте експерт в изчисляването на детерминанти. Лесно ще получите:

Или иначе (ако умножим и двете части по корен от две)

Сега нека намерим уравнението на равнината:

(Не сте забравили как получаваме уравнението на равнината, нали? Ако не разбирате откъде идва това минус единица, тогава се върнете към определението на уравнението на равнината! Просто винаги се оказваше преди това че моят самолет принадлежи на произхода!)

Изчисляваме детерминанта:

(Може да забележите, че уравнението на равнината съвпада с уравнението на правата линия, минаваща през точките и! Помислете защо!)

Сега изчисляваме ъгъла:

Трябва да намерим синуса:

Отговор:

3. Сложен въпрос: какво е правоъгълна призма, какво мислите? Това е просто добре познат паралелепипед за вас! Рисуване веднага! Можете дори да не изобразявате отделно основата, тук има малка полза от нея:

Равнината, както отбелязахме по-рано, се записва като уравнение:

Сега правим самолет

Веднага съставяме уравнението на равнината:

Търси се ъгъл

Сега отговорите на последните два проблема:

Е, сега е моментът да си починете, защото ние с вас сме страхотни и свършихме страхотна работа!

Координати и вектори. Напреднало ниво

В тази статия ще обсъдим с вас друг клас проблеми, които могат да бъдат решени с помощта на координатния метод: проблеми с разстоянието. А именно, ще разгледаме следните случаи:

1. Изчисляване на разстоянието между косите линии.

Поръчал съм дадените задачи с нарастване на сложността им. Най-лесно е да се намери разстояние от точка до равнинаи най-трудната част е намирането разстояние между пресичащите се линии. Въпреки че, разбира се, няма нищо невъзможно! Нека не отлагаме и веднага да преминем към разглеждането на първия клас проблеми:

Изчисляване на разстоянието от точка до равнина

Какво ни е необходимо, за да решим този проблем?

1. Координати на точки

И така, веднага щом получим всички необходими данни, прилагаме формулата:

Вече трябва да знаете как изграждаме уравнението на равнината от предишните задачи, които анализирах в последната част. Да се ​​заемем веднага с работата. Схемата е следната: 1, 2 - помагам ви да решите, и малко подробно, 3, 4 - само отговорът, вие сами взимате решението и сравнявате. Започна!

задачи:

1. Даден е куб. Дължината на ръба на куба е Намерете-ди-те разстояние от се-ре-ди-ни от изрязване до плоско

2. Като се има предвид правото-vil-naya четири-ти-rekh-coal-naya pi-ra-mi-da Bo-ko-voe ръб сто-ро-на os-no-va-nia е равен. Намерете-ди-тези разстояния от точка до равнина, където - се-ре-ди-на ръбовете.

3. В дясно триъгълно пи-ра-ми-де с ос-бут-ва-ни-ем другият ръб е равен, а сто-ро-он ос-но-вания е равен. Намерете-di-тези разстояния от върха до равнината.

4. В дясната шествъглена призма всички ръбове са равни. Намерете-di-тези разстояния от точка до равнина.

Решения:

1. Начертайте куб с единични ръбове, изградете сегмент и равнина, означете средата на сегмента с буквата

.

Първо, нека започнем с един лесен: намерете координатите на точка. Оттогава (запомнете координатите на средата на сегмента!)

Сега съставяме уравнението на равнината върху три точки

\[\вляво| (\begin(array)(*(20)(c))x&0&1\\y&1&0\\z&1&1\end(array)) \right| = 0\]

Сега мога да започна да намирам разстоянието:

2. Отново започваме с чертеж, на който отбелязваме всички данни!

За пирамида би било полезно да начертаете основата й отделно.

Дори фактът, че рисувам като пилешка лапа, няма да ни попречи лесно да решим този проблем!

Сега е лесно да намерите координатите на точка

Тъй като координатите на точката

2. Тъй като координатите на точка а са средата на отсечката, тогава

Лесно можем да намерим координатите на още две точки от равнината. Съставяме уравнението на равнината и го опростяваме:

\[\вляво| (\left| (\begin(array)(*(20)(c))x&1&(\frac(3)(2))\\y&0&(\frac(3)(2))\\z&0&(\frac( (\sqrt 3 ))(2))\end(масив)) \right|) \right| = 0\]

Тъй като точката има координати: , тогава изчисляваме разстоянието:

Отговор (много рядко!):

Е, разбра ли? Струва ми се, че тук всичко е също толкова техническо, колкото и в примерите, които разгледахме с вас в предишната част. Така че съм сигурен, че ако сте усвоили този материал, тогава няма да ви е трудно да решите останалите два проблема. Просто ще ви дам отговорите:

Изчисляване на разстоянието от права до равнина

Всъщност тук няма нищо ново. Как правата и равнината могат да бъдат разположени една спрямо друга? Те имат всички възможности: да се пресичат, или права линия е успоредна на равнината. Какво мислите е разстоянието от правата до равнината, с която се пресича дадената права? Струва ми се, че е ясно, че такова разстояние е равно на нула. Безинтересен случай.

Вторият случай е по-сложен: тук разстоянието вече е различно от нула. Въпреки това, тъй като правата е успоредна на равнината, тогава всяка точка от правата е еднакво отдалечена от тази равнина:

По този начин:

И това означава, че задачата ми е сведена до предишната: търсим координатите на всяка точка от правата, търсим уравнението на равнината, изчисляваме разстоянието от точката до равнината. Всъщност подобни задачи на изпита са изключително редки. Успях да намеря само един проблем, а данните в него бяха такива, че координатният метод не беше много приложим за него!

Сега нека преминем към друг, много по-важен клас проблеми:

Изчисляване на разстоянието на точка до линия

Какво ще ни трябва?

1. Координатите на точката, от която търсим разстоянието:

2. Координати на всяка точка, лежаща на права линия

3. Координати на вектора на посоката на правата линия

Каква формула използваме?

Какво означава за вас знаменателят на тази дроб и така трябва да е ясно: това е дължината на насочващия вектор на правата линия. Ето един много сложен числител! Изразът означава модула (дължината) на векторното произведение на векторите и Как да изчислим векторното произведение, проучихме в предишната част на работата. Освежете знанията си, сега ще ни бъде много полезно!

По този начин алгоритъмът за решаване на проблеми ще бъде както следва:

1. Търсим координатите на точката, от която търсим разстоянието:

2. Търсим координатите на всяка точка от правата, до която търсим разстоянието:

3. Изграждане на вектор

4. Изграждаме вектора на посоката на правата линия

5. Изчислете кръстосаното произведение

6. Търсим дължината на получения вектор:

7. Изчислете разстоянието:

Имаме много работа, а примерите ще са доста сложни! Така че сега съсредоточете цялото си внимание!

1. Дана е десен триъгълен пи-ра-ми-да с връх. Сто-ро-на ос-но-ва-ния пи-ра-ми-ди е равно, ти-со-та е равно. Намерете-di-тези разстояния от se-re-di-ny на bo-ko-th ръба до правата линия, където точките и са se-re-di-ny на ребрата и co-from- vet -ствен-но.

2. Дължините на ребрата и десния ъгъл-no-para-ral-le-le-pi-pe-da са равни, съответно и Find-di-te разстояние от top-shi-ny до pravo-my

3. В дясната призма с шест въглища всички ръбове на рояка са еднакви find-di-тези разстояние от точка до права линия

Решения:

1. Правим чист чертеж, върху който отбелязваме всички данни:

Имаме много работа за вас! Първо бих искал да опиша с думи какво ще търсим и в какъв ред:

1. Координати на точки и

2. Координати на точки

3. Координати на точки и

4. Координати на вектори и

5. Тяхното кръстосано произведение

6. Дължина на вектора

7. Дължината на векторното произведение

8. Разстояние от до

Е, имаме много работа! Да запретнем ръкави!

1. За да намерим координатите на височината на пирамидата, трябва да знаем координатите на точката.Нейното приложение е нула, а ординатата е равна на абсцисата. Най-накрая получихме координатите:

Координати на точки

2. - средата на сегмента

3. - средата на сегмента

средна точка

4. Координати

Векторни координати

5. Изчислете векторния продукт:

6. Дължината на вектора: най-лесният начин е да замените, че сегментът е средната линия на триъгълника, което означава, че е равен на половината от основата. Така.

7. Разглеждаме дължината на векторното произведение:

8. Накрая намерете разстоянието:

Фу, това е всичко! Честно казано, ще ви кажа: решаването на този проблем чрез традиционни методи (чрез конструкции) би било много по-бързо. Но тук намалих всичко до готов алгоритъм! Мисля, че алгоритъмът на решението ви е ясен? Затова ще ви помоля да разрешите сами останалите два проблема. Сравнете отговорите?

Отново повтарям: по-лесно (по-бързо) е тези проблеми да се решават чрез конструкции, вместо да се прибягва до координатния метод. Демонстрирах този начин на решаване само за да ви покажа универсален метод, който ви позволява да „не завършвате нищо“.

И накрая, разгледайте последния клас проблеми:

Изчисляване на разстоянието между косите линии

Тук алгоритъмът за решаване на проблеми ще бъде подобен на предишния. Какво имаме:

3. Всеки вектор, свързващ точките от първия и втория ред:

Как да намерим разстоянието между редовете?

Формулата е:

Числителят е модулът на смесеното произведение (въведехме го в предишната част), а знаменателят - както в предишната формула (модулът на векторното произведение на насочващите вектори на линиите, разстоянието между които търсим за).

ще ви напомня това

тогава формулата за разстояние може да се пренапише като:

Разделете този детерминант на детерминанта! Макар че, честно казано, тук не съм в настроение за шеги! Тази формула всъщност е много тромава и води до доста сложни изчисления. Ако бях на твое място, щях да го използвам само в краен случай!

Нека се опитаме да решим няколко проблема, използвайки горния метод:

1. В дясната триъгълна призма всички ръбове са по някакъв начин равни, намерете разстоянието между правите и.

2. Като се има предвид триъгълна призма с дясна форма, всички ръбове на os-no-va-niya на някого са равни на Se-che-tion, преминавайки през другото ребро и se-re-di-nu ребра са яв-ла-ет-ся квадрат-ра-том. Намерете-ди-те дис-сто-и-ние между направо-ние-ми и

Аз решавам първото, а въз основа на него вие решавате второто!

1. Начертавам призма и маркирам линиите и

Координати на точка C: тогава

Координати на точки

Векторни координати

Координати на точки

Векторни координати

Векторни координати

\[\left((B,\overrightarrow (A(A_1)) \overrightarrow (B(C_1)) ) \right) = \left| (\begin(масив)(*(20)(l))(\begin(array)(*(20)(c))0&1&0\end(array))\\(\begin(array)(*(20) (c))0&0&1\end(масив)\\(\begin(array)(*(20)(c))(\frac((\sqrt 3))(2))&( - \frac(1) (2))&1\край(масив))\край(масив)) \вдясно| = \frac((\sqrt 3 ))(2)\]

Разглеждаме кръстосаното произведение между векторите и

\[\стрелка наддясно (A(A_1)) \cdot \стрелка над права (B(C_1)) = \ляво| \begin(array)(l)\begin(array)(*(20)(c))(\overrightarrow i )&(\overrightarrow j )&(\overrightarrow k )\end(array)\\\begin(array )(*(20)(c))0&0&1\end(масив)\\\begin(array)(*(20)(c))(\frac((\sqrt 3 ))(2))&( - \ frac(1)(2))&1\край(масив)\край(масив) \вдясно| - \frac((\sqrt 3 ))(2)\overrightarrow k + \frac(1)(2)\overrightarrow i \]

Сега разглеждаме неговата дължина:

Отговор:

Сега се опитайте внимателно да изпълните втората задача. Отговорът на него ще бъде:.

Координати и вектори. Кратко описание и основни формули

Векторът е насочен сегмент. - началото на вектора, - края на вектора.
Векторът се означава с или.

Абсолютна стойноствектор - дължината на сегмента, представляващ вектора. Обозначен като.

Координати на вектора:

,
където са краищата на вектора \displaystyle a .

Сума от вектори: .

Продуктът на векторите:

Точково произведение на вектори:

Скаларното произведение на векторите е равно на произведението на техните абсолютни стойности и косинуса на ъгъла между тях:

ОСТАНАЛИТЕ 2/3 СТАТИИ СА ДОСТЪПНИ САМО ЗА YOUCLEVER СТУДЕНТИТЕ!

Станете ученик на YouClever,

Подгответе се за OGE или USE по математика на цената на "чаша кафе на месец",

И също така получете неограничен достъп до учебника "YouClever", програмата за обучение "100gia" (книга с решения), неограничен пробен USE и OGE, 6000 задачи с анализ на решения и други услуги на YouClever и 100gia.