Извънкласен урок – бройен модул. Абсолютната стойност на число. Пълни уроци - Хипермаркет на знанието Модулът на неотрицателно число е неотрицателно число

Цели на урока

Да запознае учениците с такава математическа концепция като модула на числото;
Да научи учениците на умения за намиране на модули на числа;
Затвърдяване на научения материал чрез изпълнение на различни задачи;

Задачи

Затвърдете знанията на децата за модула на числата;
Чрез решаване на тестови задачи проверете как учениците са усвоили изучения материал;
Продължете да внушавате интерес към уроците по математика;
Да култивира логическото мислене, любопитството и постоянството на учениците.

План на урока

1. Общи понятия и определение за модул на число.
2. Геометрично значение на модула.
3. Модулът на числото и неговите свойства.
4. Решаване на уравнения и неравенства, които съдържат модул на число.
5. Исторически сведения за термина „модул на число”.
6. Задание за затвърдяване на знанията по разгледаната тема.
7. Домашна работа.

Общи понятия за модула на числото

Модулът на числото обикновено се нарича самото число, ако няма отрицателна стойност или същото число е отрицателно, но с обратен знак.

Тоест, модулът на неотрицателно реално число a е самото число:

И модулът на отрицателно реално число x е противоположното число:

В запис ще изглежда така:

За по-достъпно разбиране, нека дадем пример. Така, например, модулът на числото 3 е 3, а също и модулът на числото -3 е 3.

От това следва, че модулът на числото означава абсолютна стойност, тоест неговата абсолютна стойност, но без да се взема предвид неговият знак. Казано по-просто, необходимо е да премахнете знака от номера.

Модулът на число може да бъде обозначен и да изглежда така: |3|, |x|, |a| и т.н.

Така, например, модулът на числото 3 се обозначава с |3|.

Също така трябва да се помни, че модулът на числото никога не е отрицателен: |a|≥ 0.

|5| = 5, |-6| = 6, |-12,45| = 12,45 и т.н.

Геометрично значение на модула

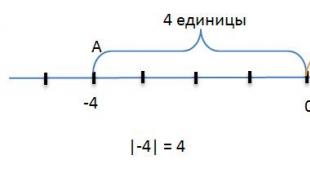
Модулът на числото е разстоянието, което се измерва в единични сегменти от началото до точката. Тази дефиниция разкрива модула от геометрична гледна точка.

Нека вземем координатна права и обозначим две точки върху нея. Нека тези точки съответстват на числа като −4 и 2.

Сега нека обърнем внимание на тази фигура. Виждаме, че точка А, посочена на координатната линия, съответства на числото -4 и ако се вгледате внимателно, ще видите, че тази точка се намира на разстояние 4 единични сегмента от референтната точка 0. От това следва, че дължината на отсечката OA е равна на четири единици. В този случай дължината на сегмента OA, тоест числото 4, ще бъде модулът на числото -4.

В този случай модулът на числото се обозначава и записва по следния начин: |−4| = 4.

Сега нека вземем и обозначим точка B на координатната линия.

Тази точка B ще съответства на числото +2 и, както виждаме, тя се намира на разстояние два единични сегмента от началото. От това следва, че дължината на отсечката OB е равна на две единици. В този случай числото 2 ще бъде модулът на числото +2.

В записа ще изглежда така: |+2| = 2 или |2| = 2.

Сега да обобщим. Ако вземем някакво неизвестно число a и го обозначим на координатната линия като точка A, тогава в този случай разстоянието от точка A до началото, тоест дължината на сегмента OA, е точно модулът на числото „a ”.

Писмено ще изглежда така: |a| = ОА.

Модулът на числото и неговите свойства

Сега нека се опитаме да подчертаем свойствата на модула, да разгледаме всички възможни случаи и да ги напишем с помощта на буквални изрази:

Първо, модулът на числото е неотрицателно число, което означава, че модулът на положително число е равен на самото число: |a| = a, ако a > 0;

Второ, модулите, които се състоят от противоположни числа, са равни: |a| = |–a|. Тоест, това свойство ни казва, че противоположните числа винаги имат еднакви модули, точно както на координатна права, въпреки че имат противоположни числа, те са на същото разстояние от референтната точка. От това следва, че модулите на тези противоположни числа са равни.

Трето, модулът на нула е равен на нула, ако това число е нула: |0| = 0, ако a = 0. Тук можем да кажем с увереност, че модулът на нула е нула по дефиниция, тъй като съответства на началото на координатната права.

Четвъртото свойство на модула е, че модулът на произведението на две числа е равен на произведението на модулите на тези числа. Сега нека разгледаме по-отблизо какво означава това. Ако следваме определението, тогава вие и аз знаем, че модулът на произведението на числата a и b ще бъде равен на a b, или −(a b), ако a b ≥ 0, или – (a b), ако a b е по-голямо от 0. B записът ще изглежда така: |a b| = |a| |b|.

Петото свойство е, че модулът на частното на числата е равен на отношението на модулите на тези числа: |a: b| = |a| : |b|.

И следните свойства на числовия модул:

Решаване на уравнения и неравенства, които включват модула на число

Когато започвате да решавате задачи, които имат числов модул, трябва да запомните, че за да решите такава задача, е необходимо да разкриете знака на модула, като използвате знания за свойствата, на които тази задача съответства.

Упражнение 1

Така например, ако под знака на модула има израз, който зависи от променлива, тогава модулът трябва да бъде разширен в съответствие с дефиницията:

Разбира се, при решаване на задачи има случаи, когато модулът се разкрива еднозначно. Ако например вземем

, тук виждаме, че такъв израз под знака за модул е ​​неотрицателен за всякакви стойности на x и y.

Или, например, да вземем

, виждаме, че този модулен израз не е положителен за никакви стойности на z.

Задача 2

Пред вас се показва координатна линия. На този ред е необходимо да маркирате числата, чийто модул ще бъде равен на 2.

Решение

Първо, трябва да начертаем координатна линия. Вече знаете, че за да направите това, първо на правата трябва да изберете началото, посоката и единичната отсечка. След това трябва да поставим точки от началото, които са равни на разстоянието на два единични сегмента.

Както можете да видите, има две такива точки на координатната линия, едната от които съответства на числото -2, а другата на числото 2.

Исторически сведения за модула на числата

Терминът „модул“ идва от латинското име modulus, което означава „мярка“. Този термин е въведен от английския математик Роджър Коутс. Но знакът за модул е ​​въведен благодарение на немския математик Карл Вайерщрас. Когато е написан, модулът се обозначава със следния символ: | |.

Въпроси за консолидиране на знанията по материала

В днешния урок се запознахме с такова понятие като модула на числото и сега нека проверим как сте усвоили тази тема, като отговорите на зададените въпроси:

1. Как се нарича числото, противоположно на положително число?
2. Как се нарича числото, противоположно на отрицателно число?
3. Назовете числото, противоположно на нулата. Съществува ли такъв номер?
4. Назовете число, което не може да бъде модул на число.
5. Определете модула на число.

Домашна работа

1. Пред вас има числа, които трябва да подредите в низходящ ред на модулите. Ако изпълните задачата правилно, ще разберете името на човека, който пръв въвежда термина „модул“ в математиката.

2. Начертайте координатна права и намерете разстоянието от M (-5) и K (8) до началото.

Предмети > Математика > Математика 6 клас

Днес, приятели, няма да има сополи и сантименталности. Вместо това ще ви изпратя, без въпроси, в битка с един от най-страшните противници в курса по алгебра за 8-9 клас.

Да, разбрахте всичко правилно: говорим за неравенства с модул. Ще разгледаме четири основни техники, с които ще се научите да решавате около 90% от подобни проблеми. Какво ще кажете за останалите 10%? Е, ще говорим за тях в отделен урок. :)

Въпреки това, преди да анализирам някоя от техниките, бих искал да ви напомня два факта, които вече трябва да знаете. В противен случай рискувате изобщо да не разберете материала от днешния урок.

Това, което вече трябва да знаете

Captain Obviousness изглежда намеква, че за да решавате неравенства с модул, трябва да знаете две неща:

1. Как се решават неравенствата;
2. Какво е модул?

Да започнем с втората точка.

Дефиниция на модула

Тук всичко е просто. Има две дефиниции: алгебрична и графична. Като начало - алгебричен:

Определение. Модулът на число $x$ е или самото число, ако е неотрицателно, или противоположното му число, ако оригиналният $x$ все още е отрицателен.

Написано е така:

\[\ляво| x \right|=\left\( \begin(align) & x,\ x\ge 0, \\ & -x,\ x \lt 0. \\\end(align) \right.\]

С прости думи, модулът е „число без минус“. И точно в тази двойственост (на някои места не е нужно да правите нищо с оригиналния номер, но на други ще трябва да премахнете някакъв вид минус) е цялата трудност за начинаещите ученици.

Има и геометрична дефиниция. Също така е полезно да се знае, но ще се обърнем към него само в сложни и някои специални случаи, където геометричният подход е по-удобен от алгебричния (спойлер: не днес).

Определение. Нека точка $a$ е отбелязана на числовата ос. След това модулът $\left| x-a \right|$ е разстоянието от точка $x$ до точка $a$ на тази права.

Ако нарисувате картина, ще получите нещо подобно:

Дефиниране на графичен модул

По един или друг начин, от дефиницията на модул веднага следва неговото ключово свойство: модулът на числото винаги е неотрицателна величина. Този факт ще бъде червена нишка през целия ни разказ днес.

Решаване на неравенства. Интервален метод

Сега нека да разгледаме неравенствата. Има много от тях, но нашата задача сега е да можем да решим поне най-простия от тях. Такива, които се свеждат до линейни неравенства, както и до интервалния метод.

Имам два големи урока по тази тема (между другото, много, МНОГО полезни - препоръчвам да ги изучавате):

1. Интервален метод за неравенства (особено гледайте видеото);
2. Дробните рационални неравенства са много обширен урок, но след него няма да имате абсолютно никакви въпроси.

Ако знаете всичко това, ако фразата „да преминем от неравенство към уравнение“ не ви кара да имате смътно желание да се ударите в стената, значи сте готови: добре дошли в ада в основната тема на урока. :)

1. Неравенства от формата „Модулът е по-малък от функцията“

Това е един от най-честите проблеми с модулите. Необходимо е да се реши неравенство от вида:

\[\ляво| f\надясно| \ltg\]

Функциите $f$ и $g$ могат да бъдат всякакви, но обикновено са полиноми. Примери за такива неравенства:

\[\begin(align) & \left| 2x+3 \надясно| \lt x+7; \\ & \left| ((x)^(2))+2x-3 \right|+3\left(x+1 \right) \lt 0; \\ & \left| ((x)^(2))-2\left| x \right|-3 \right| \lt 2. \\\край (подравняване)\]

Всички те могат да бъдат решени буквално в един ред по следната схема:

\[\ляво| f\надясно| \lt g\Rightarrow -g \lt f \lt g\quad \left(\Rightarrow \left\( \begin(align) & f \lt g, \\ & f \gt -g \\\end(align) \право.\право)\]

Лесно се вижда, че се отърваваме от модула, но в замяна получаваме двойно неравенство (или, което е същото, система от две неравенства). Но този преход отчита абсолютно всички възможни проблеми: ако числото под модула е положително, методът работи; ако е отрицателен, той все още работи; и дори с най-неадекватната функция на мястото на $f$ или $g$, методът пак ще работи.

Естествено възниква въпросът: не може ли да бъде по-просто? За съжаление не е възможно. Това е целият смисъл на модула.

Но стига с философстването. Нека разрешим няколко проблема:

Задача. Решете неравенството:

\[\ляво| 2x+3 \надясно| \lt x+7\]

Решение. И така, пред нас е класическо неравенство под формата „модулът е по-малък“ - дори няма какво да се трансформира. Ние работим по алгоритъма:

\[\begin(align) & \left| f\надясно| \lt g\Стрелка надясно -g \lt f \lt g; \\ & \left| 2x+3 \надясно| \lt x+7\Стрелка надясно -\left(x+7 \right) \lt 2x+3 \lt x+7 \\\end(align)\]

Не бързайте да отваряте скобите, предшествани от „минус“: напълно възможно е поради бързината да направите обидна грешка.

\[-x-7 \lt 2x+3 \lt x+7\]

\[\left\( \begin(align) & -x-7 \lt 2x+3 \\ & 2x+3 \lt x+7 \\ \end(align) \right.\]

\[\left\( \begin(align) & -3x \lt 10 \\ & x \lt 4 \\ \end(align) \right.\]

\[\left\( \begin(align) & x \gt -\frac(10)(3) \\ & x \lt 4 \\ \end(align) \right.\]

Задачата се сведе до две елементарни неравенства. Нека отбележим техните решения на успоредни числови прави:

Пресечна точка на много

Пресечната точка на тези множества ще бъде отговорът.

Отговор: $x\in \left(-\frac(10)(3);4 \right)$

Задача. Решете неравенството:

\[\ляво| ((x)^(2))+2x-3 \right|+3\left(x+1 \right) \lt 0\]

Решение. Тази задача е малко по-трудна. Първо, нека изолираме модула, като преместим втория член надясно:

\[\ляво| ((x)^(2))+2x-3 \right| \lt -3\наляво(x+1 \надясно)\]

Очевидно отново имаме неравенство от формата „модулът е по-малък“, така че се отърваваме от модула, използвайки вече известния алгоритъм:

\[-\left(-3\left(x+1 \right) \right) \lt ((x)^(2))+2x-3 \lt -3\left(x+1 \right)\]

Сега внимание: някой ще каже, че съм малко перверзник с всички тези скоби. Но нека ви напомня още веднъж, че основната ни цел е решете правилно неравенството и получете отговора. По-късно, когато усвоите перфектно всичко, описано в този урок, можете сами да го изопачите, както желаете: отваряйте скоби, добавяйте минуси и т.н.

Като начало, просто ще се отървем от двойното минус вляво:

\[-\left(-3\left(x+1 \right) \right)=\left(-1 \right)\cdot \left(-3 \right)\cdot \left(x+1 \right) =3\ляво(x+1 \дясно)\]

Сега нека отворим всички скоби в двойното неравенство:

Да преминем към двойното неравенство. Този път изчисленията ще бъдат по-сериозни:

\[\left\( \begin(align) & ((x)^(2))+2x-3 \lt -3x-3 \\ & 3x+3 \lt ((x)^(2))+2x -3 \\ \end(align) \right.\]

\[\left\( \begin(align) & ((x)^(2))+5x \lt 0 \\ & ((x)^(2))-x-6 \gt 0 \\ \end( подравняване)\надясно.\]

И двете неравенства са квадратни и могат да бъдат решени чрез интервалния метод (затова казвам: ако не знаете какво е това, по-добре все още да не се заемате с модули). Нека преминем към уравнението в първото неравенство:

\[\begin(align) & ((x)^(2))+5x=0; \\ & x\left(x+5 \right)=0; \\ & ((x)_(1))=0;((x)_(2))=-5. \\\край (подравняване)\]

Както можете да видите, резултатът е непълно квадратно уравнение, което може да бъде решено по елементарен начин. Сега нека разгледаме второто неравенство на системата. Там ще трябва да приложите теоремата на Виета:

\[\begin(align) & ((x)^(2))-x-6=0; \\ & \left(x-3 \right)\left(x+2 \right)=0; \\& ((x)_(1))=3;((x)_(2))=-2. \\\край (подравняване)\]

Отбелязваме получените числа на две успоредни линии (отделно за първото неравенство и отделно за второто):

Отново, тъй като решаваме система от неравенства, ние се интересуваме от пресечната точка на защрихованите множества: $x\in \left(-5;-2 \right)$. Това е отговорът.

Отговор: $x\in \left(-5;-2 \right)$

Мисля, че след тези примери схемата на решение е пределно ясна:

1. Изолирайте модула, като преместите всички други членове в противоположната страна на неравенството. Така получаваме неравенство от вида $\left| f\надясно| \ltg$.
2. Решете това неравенство, като се отървете от модула според описаната по-горе схема. В един момент ще е необходимо да се премине от двойно неравенство към система от два независими израза, всеки от които вече може да бъде решен отделно.
3. И накрая, всичко, което остава, е да пресечем решенията на тези два независими израза - и това е всичко, ще получим окончателния отговор.

Подобен алгоритъм съществува за неравенства от следния тип, когато модулът е по-голям от функцията. Има обаче няколко сериозни „но“. Сега ще говорим за тези „но“.

2. Неравенства от формата „Модулът е по-голям от функцията“

Те изглеждат така:

\[\ляво| f\надясно| \gtg\]

Подобен на предишния? Изглежда. И все пак такива проблеми се решават по съвсем различен начин. Формално схемата е следната:

\[\ляво| f\надясно| \gt g\Rightarrow \left[ \begin(align) & f \gt g, \\ & f \lt -g \\\end(align) \right.\]

С други думи, разглеждаме два случая:

1. Първо, просто игнорираме модула и решаваме обичайното неравенство;
2. След това, по същество, разширяваме модула със знака минус и след това умножаваме двете страни на неравенството по −1, докато имам знака.

В този случай опциите се комбинират с квадратна скоба, т.е. Пред нас е комбинация от две изисквания.

Моля, обърнете внимание отново: следователно това не е система, а цялост в отговора множествата са комбинирани, а не пресичащи се. Това е фундаментална разлика от предишната точка!

Като цяло, много студенти са напълно объркани със съюзите и пресичанията, така че нека разрешим този проблем веднъж завинаги:

• "∪" е знак на съюза. Всъщност това е стилизирана буква „U“, която дойде при нас от английския език и е съкращение за „Union“, т.е. „Асоциации“.
• „∩“ е знакът за пресичане. Тези глупости не идват отникъде, а просто се появяват като контрапункт на „∪“.

За да направите запомнянето още по-лесно, просто нарисувайте крака към тези знаци, за да направите очила (само не ме обвинявайте сега, че насърчавам наркоманиите и алкохолизма: ако сериозно изучавате този урок, значи вече сте наркоман):

Разлика между пресичане и обединение на множества

Преведено на руски това означава следното: съюзът (съвкупността) включва елементи от двете множества, следователно по никакъв начин не е по-малък от всеки от тях; но пресечната точка (системата) включва само тези елементи, които са едновременно както в първото множество, така и във второто. Следователно пресечната точка на множествата никога не е по-голяма от изходните множества.

Значи стана по-ясно? Това е страхотно. Да преминем към практиката.

Задача. Решете неравенството:

\[\ляво| 3x+1 \надясно| \gt 5-4x\]

Решение. Продължаваме по схемата:

\[\ляво| 3x+1 \надясно| \gt 5-4x\дясна стрелка \left[ \begin(align) & 3x+1 \gt 5-4x \\ & 3x+1 \lt -\left(5-4x \right) \\\end(align) \ точно.\]

Решаваме всяко неравенство в популацията:

\[\left[ \begin(align) & 3x+4x \gt 5-1 \\ & 3x-4x \lt -5-1 \\ \end(align) \right.\]

\[\left[ \begin(align) & 7x \gt 4 \\ & -x \lt -6 \\ \end(align) \right.\]

\[\left[ \begin(align) & x \gt 4/7\ \\ & x \gt 6 \\ \end(align) \right.\]

Маркираме всеки получен набор на числовата линия и след това ги комбинираме:

Обединение на комплекти

Съвсем очевидно е, че отговорът ще бъде $x\in \left(\frac(4)(7);+\infty \right)$

Отговор: $x\in \left(\frac(4)(7);+\infty \right)$

Задача. Решете неравенството:

\[\ляво| ((x)^(2))+2x-3 \right| \gt x\]

Решение. Добре? Нищо - всичко е същото. Преминаваме от неравенство с модул към набор от две неравенства:

\[\ляво| ((x)^(2))+2x-3 \right| \gt x\Rightarrow \left[ \begin(align) & ((x)^(2))+2x-3 \gt x \\ & ((x)^(2))+2x-3 \lt -x \\\end(align) \right.\]

Решаваме всяко неравенство. За съжаление, корените там няма да са много добри:

\[\begin(align) & ((x)^(2))+2x-3 \gt x; \\ & ((x)^(2))+x-3 \gt 0; \\&D=1+12=13; \\ & x=\frac(-1\pm \sqrt(13))(2). \\\край (подравняване)\]

Второто неравенство също е малко диво:

\[\begin(align) & ((x)^(2))+2x-3 \lt -x; \\ & ((x)^(2))+3x-3 \lt 0; \\&D=9+12=21; \\ & x=\frac(-3\pm \sqrt(21))(2). \\\край (подравняване)\]

Сега трябва да маркирате тези числа на две оси - по една ос за всяко неравенство. Трябва обаче да маркирате точките в правилния ред: колкото по-голямо е числото, толкова повече точката се премества надясно.

И тук ни очаква настройка. Ако всичко е ясно с числата $\frac(-3-\sqrt(21))(2) \lt \frac(-1-\sqrt(13))(2)$ (членовете в числителя на първия дроб са по-малки от членовете в числителя на втория, така че сумата също е по-малка), с числата $\frac(-3-\sqrt(13))(2) \lt \frac(-1+\sqrt (21))(2)$ също няма да има затруднения (положителното число очевидно е по-отрицателно), тогава с последната двойка всичко не е толкова ясно. Кое е по-голямо: $\frac(-3+\sqrt(21))(2)$ или $\frac(-1+\sqrt(13))(2)$? Разположението на точките върху числовите оси и всъщност отговорът ще зависи от отговора на този въпрос.

Така че нека сравним:

\[\begin(matrix) \frac(-1+\sqrt(13))(2)\vee \frac(-3+\sqrt(21))(2) \\ -1+\sqrt(13)\ vee -3+\sqrt(21) \\ 2+\sqrt(13)\vee \sqrt(21) \\\end(matrix)\]

Изолирахме корена, получихме неотрицателни числа от двете страни на неравенството, така че имаме право да поставим на квадрат и двете страни:

\[\begin(matrix) ((\left(2+\sqrt(13) \right))^(2))\vee ((\left(\sqrt(21) \right))^(2)) \ \ 4+4\sqrt(13)+13\vee 21 \\ 4\sqrt(13)\vee 3 \\\end(matrix)\]

Мисля, че е безсмислено, че $4\sqrt(13) \gt 3$, така че $\frac(-1+\sqrt(13))(2) \gt \frac(-3+\sqrt(21)) ( 2)$, крайните точки на осите ще бъдат поставени така:

Случай на грозни корени

Нека ви напомня, че решаваме множество, така че отговорът ще бъде обединение, а не пресичане на защриховани множества.

Отговор: $x\in \left(-\infty ;\frac(-3+\sqrt(21))(2) \right)\bigcup \left(\frac(-1+\sqrt(13))(2 );+\infty \right)$

Както можете да видите, нашата схема работи чудесно както за прости, така и за много трудни проблеми. Единствената „слаба точка“ в този подход е, че трябва правилно да сравнявате ирационални числа (и повярвайте ми: това не са само корени). Но отделен (и много сериозен) урок ще бъде посветен на проблемите на сравнението. И продължаваме напред.

3. Неравенства с неотрицателни „опашки“

Сега стигаме до най-интересната част. Това са неравенства от вида:

\[\ляво| f\надясно| \gt\наляво| g\надясно|\]

Най-общо казано, алгоритъмът, за който ще говорим сега, е правилен само за модула. Работи във всички неравенства, където има гарантирани неотрицателни изрази отляво и отдясно:

Какво да правим с тези задачи? Просто запомни:

В неравенства с неотрицателни „опашки“ и двете страни могат да бъдат повдигнати на всяка естествена степен. Няма да има допълнителни ограничения.

На първо място, ще се интересуваме от квадратурата - тя изгаря модули и корени:

\[\begin(align) & ((\left(\left| f \right| \right))^(2))=((f)^(2)); \\ & ((\left(\sqrt(f) \right))^(2))=f. \\\край (подравняване)\]

Просто не бъркайте това с вземане на корен от квадрат:

\[\sqrt(((f)^(2)))=\left| f \right|\ne f\]

Безброй грешки бяха направени, когато ученик забрави да инсталира модул! Но това е съвсем различна история (това са, така да се каже, ирационални уравнения), така че няма да навлизаме в това сега. Нека решим по-добре няколко проблема:

Задача. Решете неравенството:

\[\ляво| x+2 \right|\ge \left| 1-2x \right|\]

Решение. Нека веднага да отбележим две неща:

1. Това не е строго неравенство. Точките на числовата ос ще бъдат пробити.
2. И двете страни на неравенството очевидно са неотрицателни (това е свойство на модула: $\left| f\left(x \right) \right|\ge 0$).

Следователно можем да повдигнем на квадрат двете страни на неравенството, за да се отървем от модула и да решим проблема, използвайки обичайния метод на интервала:

\[\begin(align) & ((\left(\left| x+2 \right| \right))^(2))\ge ((\left(\left| 1-2x \right| \right) )^(2)); \\ & ((\left(x+2 \right))^(2))\ge ((\left(2x-1 \right))^(2)). \\\край (подравняване)\]

На последната стъпка измамих малко: промених последователността от членове, като се възползвах от четността на модула (всъщност умножих израза $1-2x$ по −1).

\[\begin(align) & ((\left(2x-1 \right))^(2))-((\left(x+2 \right))^(2))\le 0; \\ & \left(\left(2x-1 \right)-\left(x+2 \right) \right)\cdot \left(\left(2x-1 \right)+\left(x+2 \ дясно)\дясно)\le 0; \\ & \left(2x-1-x-2 \right)\cdot \left(2x-1+x+2 \right)\le 0; \\ & \left(x-3 \right)\cdot \left(3x+1 \right)\le 0. \\\end(align)\]

Решаваме с помощта на интервалния метод. Нека преминем от неравенство към уравнение:

\[\begin(align) & \left(x-3 \right)\left(3x+1 \right)=0; \\ & ((x)_(1))=3;((x)_(2))=-\frac(1)(3). \\\край (подравняване)\]

Отбелязваме намерените корени на числовата ос. Още веднъж: всички точки са защриховани, защото първоначалното неравенство не е строго!

Отървете се от знака за модул

Нека напомня за тези, които са особено упорити: вземаме знаците от последното неравенство, което беше написано преди да преминем към уравнението. И рисуваме върху площите, изисквани в същото неравенство. В нашия случай това е $\left(x-3 \right)\left(3x+1 \right)\le 0$.

Добре, всичко свърши. Проблемът е решен.

Отговор: $x\in \left[ -\frac(1)(3);3 \right]$.

Задача. Решете неравенството:

\[\ляво| ((x)^(2))+x+1 \right|\le \left| ((x)^(2))+3x+4 \right|\]

Решение. Правим всичко по същия начин. Няма да коментирам - просто вижте последователността на действията.

Квадратирайте го:

\[\begin(align) & ((\left(\left| ((x)^(2))+x+1 \right| \right))^(2))\le ((\left(\left | ((x)^(2))+3x+4 \right| \right))^(2)); \\ & ((\left(((x)^(2))+x+1 \right))^(2))\le ((\left(((x)^(2))+3x+4 \десен))^(2)); \\ & ((\left(((x)^(2))+x+1 \right))^(2))-((\left(((x)^(2))+3x+4 \ надясно))^(2))\le 0; \\ & \left(((x)^(2))+x+1-((x)^(2))-3x-4 \right)\times \\ & \times \left(((x) ^(2))+x+1+((x)^(2))+3x+4 \right)\le 0; \\ & \left(-2x-3 \right)\left(2((x)^(2))+4x+5 \right)\le 0. \\\end(align)\]

Интервален метод:

\[\begin(align) & \left(-2x-3 \right)\left(2((x)^(2))+4x+5 \right)=0 \\ & -2x-3=0\ Стрелка надясно x=-1.5; \\ & 2((x)^(2))+4x+5=0\Стрелка надясно D=16-40 \lt 0\Стрелка надясно \varnothing . \\\край (подравняване)\]

На числовата ос има само един корен:

Отговорът е цял интервал

Отговор: $x\in \left[ -1.5;+\infty \right)$.

Малка забележка за последната задача. Както един от моите ученици точно отбеляза, и двата подмодулни израза в това неравенство са очевидно положителни, така че знакът за модул може да бъде пропуснат без вреда за здравето.

Но това е съвсем друго ниво на мислене и друг подход – условно може да се нарече метод на следствията. За това - в отделен урок. Сега нека преминем към последната част от днешния урок и да разгледаме един универсален алгоритъм, който винаги работи. Дори когато всички предишни подходи бяха безсилни. :)

4. Метод на изброяване на опциите

Ами ако всички тези техники не помогнат? Ако неравенството не може да бъде сведено до неотрицателни опашки, ако е невъзможно да се изолира модулът, ако като цяло има болка, тъга, меланхолия?

Тогава на сцената излиза „тежката артилерия“ на цялата математика – методът на грубата сила. Във връзка с неравенства с модул изглежда така:

1. Изпишете всички подмодулни изрази и ги задайте равни на нула;
2. Решете получените уравнения и маркирайте намерените корени на една числова ос;
3. Правата линия ще бъде разделена на няколко секции, в рамките на които всеки модул има фиксиран знак и следователно се разкрива уникално;
4. Решете неравенството на всеки такъв участък (можете отделно да разгледате корените-граници, получени в стъпка 2 - за надеждност). Комбинирайте резултатите - това ще бъде отговорът. :)

И как? слаб? Лесно! Само за дълго време. Да видим на практика:

Задача. Решете неравенството:

\[\ляво| x+2 \надясно| \lt \наляво| x-1 \right|+x-\frac(3)(2)\]

Решение. Тези глупости не се свеждат до неравенства като $\left| f\надясно| \lt g$, $\left| f\надясно| \gt g$ или $\left| f\надясно| \lt \наляво| g \right|$, така че действаме напред.

Изписваме подмодулни изрази, приравняваме ги към нула и намираме корените:

\[\begin(align) & x+2=0\Rightarrow x=-2; \\ & x-1=0\Стрелка надясно x=1. \\\край (подравняване)\]

Общо имаме два корена, които разделят числовата линия на три секции, в които всеки модул се разкрива уникално:

Разделяне на числовата ос с нули на подмодулни функции

Нека разгледаме всеки раздел поотделно.

1. Нека $x \lt -2$. Тогава и двата подмодулни израза са отрицателни и първоначалното неравенство ще бъде пренаписано, както следва:

\[\begin(align) & -\left(x+2 \right) \lt -\left(x-1 \right)+x-1.5 \\ & -x-2 \lt -x+1+ x- 1.5 \\ & x \gt 1.5 \\\end(align)\]

Имаме доста просто ограничение. Нека го пресечем с първоначалното предположение, че $x \lt -2$:

\[\left\( \begin(align) & x \lt -2 \\ & x \gt 1.5 \\\end(align) \right.\Rightarrow x\in \varnothing \]

Очевидно променливата $x$ не може едновременно да бъде по-малка от −2 и по-голяма от 1,5. В тази област няма решения.

1.1. Нека разгледаме отделно граничния случай: $x=-2$. Нека просто заместим това число в първоначалното неравенство и да проверим: вярно ли е?

\[\begin(align) & ((\left. \left| x+2 \right| \lt \left| x-1 \right|+x-1.5 \right|)_(x=-2) ) \ \ & 0 \lt \left| -3\дясно|-2-1,5; \\ & 0 \lt 3-3,5; \\ & 0 \lt -0.5\Стрелка надясно \varnothing . \\\край (подравняване)\]

Очевидно е, че веригата от изчисления ни е довела до неправилно неравенство. Следователно първоначалното неравенство също е невярно и $x=-2$ не е включено в отговора.

2. Нека сега $-2 \lt x \lt 1$. Левият модул вече ще се отвори с „плюс“, но десният все още ще се отвори с „минус“. Ние имаме:

\[\begin(align) & x+2 \lt -\left(x-1 \right)+x-1.5 \\ & x+2 \lt -x+1+x-1.5 \\& x \lt - 2.5 \\\край (подравняване)\]

Отново се пресичаме с първоначалното изискване:

\[\left\( \begin(align) & x \lt -2.5 \\ & -2 \lt x \lt 1 \\\end(align) \right.\Rightarrow x\in \varnothing \]

И отново, множеството от решения е празно, тъй като няма числа, които да са едновременно по-малки от −2,5 и по-големи от −2.

2.1. И отново специален случай: $x=1$. Заменяме в първоначалното неравенство:

\[\begin(align) & ((\left. \left| x+2 \right| \lt \left| x-1 \right|+x-1,5 \right|)_(x=1)) \\ & \ляво| 3\надясно| \lt \наляво| 0 \right|+1-1.5; \\ & 3 \lt -0,5; \\ & 3 \lt -0.5\Стрелка надясно \varnothing . \\\край (подравняване)\]

Подобно на предишния „специален случай“, числото $x=1$ очевидно не е включено в отговора.

3. Последната част от реда: $x \gt 1$. Тук всички модули се отварят със знак плюс:

\[\begin(align) & x+2 \lt x-1+x-1.5 \\ & x+2 \lt x-1+x-1.5 \\ & x \gt 4.5 \\ \end(align)\ ]

И отново пресичаме намереното множество с оригиналното ограничение:

\[\left\( \begin(align) & x \gt 4.5 \\ & x \gt 1 \\\end(align) \right.\Rightarrow x\in \left(4.5;+\infty \right)\ ]

Най-накрая! Намерихме интервал, който ще бъде отговорът.

Отговор: $x\in \left(4,5;+\infty \right)$

И накрая, една забележка, която може да ви спаси от глупави грешки при решаването на реални проблеми:

Решенията на неравенства с модули обикновено представляват непрекъснати множества на числовата ос - интервали и отсечки. Изолираните точки са много по-рядко срещани. И още по-рядко се случва границата на решението (края на сегмента) да съвпада с границата на разглеждания диапазон.

Следователно, ако границите (същите „специални случаи“) не са включени в отговора, тогава областите отляво и отдясно на тези граници почти сигурно няма да бъдат включени в отговора. И обратното: границата, въведена в отговора, което означава, че някои области около нея също ще бъдат отговори.

Имайте това предвид, когато преглеждате вашите решения.

Този урок ще прегледа концепцията за модула на реално число и ще въведе някои от основните му дефиниции, последвани от примери, които демонстрират използването на различни от тези дефиниции.

Предмет:Реални числа

Урок:Модул на реално число

1. Дефиниции на модула

Нека разгледаме такова понятие като модул на реално число, то има няколко дефиниции.

Определение 1. Разстоянието от точка на координатна линия до нула се нарича модулно число, което е координатата на тази точка (фиг. 1).

Пример 1. . Обърнете внимание, че модулите на противоположните числа са равни и неотрицателни, тъй като това е разстояние, но не може да бъде отрицателно, и разстоянието от числата, симетрични около нулата до началото, е равно.

Определение 2. .

Пример 2. Нека разгледаме един от проблемите, поставени в предишния пример, за да демонстрираме еквивалентността на въведените определения. , както виждаме, с отрицателно число под знака на модула, добавянето на още един минус пред него осигурява неотрицателен резултат, както следва от дефиницията на модула.

Последица. Разстоянието между две точки с координати на координатна права може да се намери по следния начин независимо от взаимното разположение на точките (фиг. 2).

2. Основни свойства на модула

1. Модулът на всяко число е неотрицателен

2. Модулът на продукта е произведението на модулите

3. Коефициентният модул е ​​частен модул от модули

3. Разрешаване на проблеми

Пример 3. Решете уравнението.

Решение. Нека използваме дефиницията на втория модул: и напишете нашето уравнение под формата на система от уравнения за различни опции за отваряне на модула.

Пример 4. Решете уравнението.

Решение. Подобно на решението на предишния пример, получаваме това.

Пример 5. Решете уравнението.

Решение. Нека решим чрез следствие от първата дефиниция на модула: . Нека изобразим това на числовата ос, като вземем предвид, че желаният корен ще бъде на разстояние 2 от точка 3 (фиг. 3).

Въз основа на фигурата получаваме корените на уравнението: , тъй като точките с такива координати са на разстояние 2 от точка 3, както се изисква в уравнението.

Отговор. .

Пример 6. Решете уравнението.

Решение. В сравнение с предишния проблем има само едно усложнение - това е, че няма пълно сходство с формулировката на следствието за разстоянието между числата на координатната ос, тъй като под знака за модул има знак плюс, а не минус знак. Но не е трудно да го доведете до необходимата форма, което ще направим:

Нека изобразим това на числовата ос подобно на предишното решение (фиг. 4).

Корени на уравнението .

Отговор. .

Пример 7. Решете уравнението.

Решение. Това уравнение е малко по-сложно от предишното, тъй като неизвестното е на второ място и има знак минус, освен това има и числен множител. За да разрешим първия проблем, използваме едно от свойствата на модула и получаваме:

За да решим втория проблем, нека извършим промяна на променливите: , което ще ни доведе до най-простото уравнение. Чрез втората дефиниция на модул . Заместете тези корени в заместващото уравнение и получете две линейни уравнения:

Отговор. .

4. Корен квадратен и модул

Доста често при решаване на проблеми с корени възникват модули и трябва да обърнете внимание на ситуациите, в които възникват.

При пръв поглед върху тази идентичност може да възникнат въпроси: „защо има модул там?“ и „защо самоличността е фалшива?“ Оказва се, че можем да дадем прост контрапример на втория въпрос: ако това трябва да е вярно, което е еквивалентно, но това е фалшива идентичност.

След това може да възникне въпросът: „такава идентичност не решава ли проблема?“, но има и контрапример за това предложение. Ако това трябва да е вярно, което е еквивалентно, но това е фалшива самоличност.

Съответно, ако си спомним, че квадратният корен от неотрицателно число е неотрицателно число и стойността на модула е неотрицателна, става ясно защо горното твърдение е вярно:

.

Пример 8. Да се ​​изчисли стойността на израза.

Решение. При такива задачи е важно да не се отървете безмислено от корена веднага, а да използвате гореспоменатата идентичност, защото .

Състои се от положителни (естествени) числа, отрицателни числа и нула.

Всички отрицателни числа и само те са по-малки от нула. На числовата ос отрицателните числа са разположени вляво от нулата. За тях, както и за положителните числа, се дефинира връзка на реда, която позволява да се сравни едно цяло число с друго.

За всяко естествено число нима едно и само едно отрицателно число, означено -н, който допълва ндо нула: н + (− н) = 0 . Извикват се и двата номера противоположностедин за друг. Изваждане на цяло число ае еквивалентно на добавянето му с противоположното му: -а.

Свойства на отрицателните числа

Отрицателните числа следват почти същите правила като естествените числа, но имат някои специални характеристики.

Исторически очерк

Литература

• Вигодски М. Я.Наръчник по елементарна математика. - М.: AST, 2003. - ISBN 5-17-009554-6
• Глейзър Г.И.История на математиката в училище. - М.: Образование, 1964. - 376 с.

Връзки

Фондация Уикимедия. 2010 г.

• Безразсъдно причиняване на вреда
• Неотропици

Вижте какво е „неотрицателно число“ в други речници:

Реално число- Реално, или реално число, е математическа абстракция, възникнала от необходимостта да се измерват геометрични и физически величини на околния свят, както и да се извършват такива операции като извличане на корени, изчисляване на логаритми, решаване на... ... Wikipedia

обикновено малко неотрицателно цяло число- Част от кодирането, което представлява стойностите на неограничено неотрицателно цяло число, но където малките стойности е по-вероятно да се срещат по-често (ITU T X.691). Теми... ... Ръководство за технически преводач

РЕАЛНО ЧИСЛО- реално число, положително число, отрицателно число или нула. Концепцията за числово число възниква чрез разширяване на концепцията за рационално число. Необходимостта от това разширение се дължи както на практическото използване на математиката при изразяване на... ... Математическа енциклопедия

просто число- Простото число е естествено число, което има точно два различни естествени делителя: единица и себе си. Всички други естествени числа, с изключение на едно, се наричат ​​съставни. Така всички естествени числа са по-големи от едно... ... Wikipedia

естествено число- ▲ цяло число, изразяващо, реално, число естествено число неотрицателно цяло число; изразява броя на отделните цели обекти в какво л. инертни материали; обозначават броя на реалните цели обекти; изразяване на числа. четири... Идеографски речник на руския език

десетична- Десетичната запетая е вид дроб, който е начин за представяне на реални числа във формата, където знакът на дробта е: или или десетична точка, която служи като разделител между цялото число и дробната част на числото. .. ... Уикипедия Уикипедия

Ръководител на ШМО
учители по математика _______Калашникова Ж.ЮОбщинска бюджетна образователна институция
"СОУ №89"
Тематични тестове по математика за 6. клас
по учебника на I.I. Зубарева и А.Г. Мордкович
Съставител: учители по математика:
Калашникова Жанна Юриевна
Столбова Людмила Антоновна
ЗАТО Северск
2016 г
Съдържание
Тест № 1…………………………………………………………………………………….3-6
Тест № 2………………………………………………………………………………………….7-10
Тест № 3…………………………………………………………………………………………………………….11-14
Отговори……………………………………………………………………………………………………………..15
Тест № 1 „Положителни и отрицателни числа“
Опция 1
Въведете отрицателно дробно число:
-165
38
-7.92
67Опишете събитието „На координатния лъч е отбелязано числото -5,5“
Надежден
Невъзможен
Случаен

Кое от четирите числа е най-голямото?
8,035
80,35
0,8035
803,5
Коя точка се намира на координатната права вдясно от точка O (0)?
М (-4)
Е (-15)
К (15)
D(-1,2)
През нощта температурата на въздуха беше -5°C. През деня термометърът беше вече +3 °C. Как се е променила температурата на въздуха?
Увеличен с 8o
Намален с 2o
Увеличен с 2o
Намалена с 8o
На координатната права е отбелязана точката x(-2) – център на симетрия. Посочете координатите на точките, разположени на тази линия симетрично на точка x.

(-1) и (1)
(-1) и (1)
(3) и (-3)
(0) и (-4)
Кои точки от координатната права не са симетрични спрямо началото - точка O (0).
B(-5) и C(5)
D(0,5) и E(-0,5)
M(-3) и K(13)
A(18) и X(-18)
Какъв е сборът на числата 0,316+0,4?
0,356
0,716
4,316
0,32
Изчислете 25% от числото 0,4.
0,1
0,001
10
100
Изчислете разликата от 9100 и 0,03
0,05
0,6
9,03
350 Вариант 2
Въведете отрицателно дробно число.
8,63
-1045
913-0,2
Опишете събитието „Числото 7 е отбелязано на координатния лъч.“
Случаен
Невъзможен
Надежден
Кое число е най-малкото?
15,49
154,9
1,549
1549
Коя от точките се намира на координатната права вляво от точка O(0).
A (-0,5)
В 6)
M(0,5)
К (38)
През деня термометърът показваше +5°C, а вечерта -2°C. Как се е променила температурата на въздуха?
Увеличен с 3o
Намалена със 7o
Намален с 3o
Увеличен със 7o
На координатната права е отбелязан центърът на симетрия - точка А(-3). Посочете координатите на точките, разположени на тази линия симетрично на точка А.

(-2) и (2)
(0) и (-5)
(-6) и (1)
(-1) и (-5)
Кои точки от координатната права не са симетрични спрямо началото - точка O(0).
A(6) и B(-6)
C(12) и D(-2)
M(-1) и K(1)
X (-9) и Y (9)
Каква е сумата от числата 0,237 и 0,3?
0,24
3,237
0,537
0,267
Изчислете 20% от 0,5
10
0,1
0,2
0,01
Изчислете разликата от 0,07 и 31001250,5
1
425 Тест № 2. Абсолютната стойност на число. Противоположни числа.
Опция 1
Кое от дадените числа има най-малък модул
-11
1013-4,196
-4,2
Посочете неправилно уравнение
85=-85
-1,9=1,9
35= 3558=-58 Модулът на неотрицателно число е неотрицателно число. Вярно ли е това твърдение?
да
Не
Кое от тези числа е противоположно на числото -34?43-43-3434Каква е стойността на израза -(-m), ако m = -15
+15
-15
Изчислете стойността на израза: -2,5∙4--919
-10
1
-1
Решете уравнението: x=40-40
40
40 или -40
Какви цели числа се намират на координатната права между числата 2,75 и 3,9?
-2, -1, 1, 2
-1, 0, 1, 2, 3
-1, 0, 1, 2, 3, 4
-2, -1, 0, 1, 2, 3
Вярно ли е неравенството -30>-50? Да
Не
Избройте всички цели числа x, ако x≤30, 1, 2
0, 1, 2, 3
0, 1, 2, 3, 4
1, 2, 3
Вариант 2
Кое число има най-голям модул?
-0,6
-50,603
493550,530
Посочете неправилно уравнение
-1,5=1,512=12-117=117-325=-325Може ли модулът на отрицателно число да бъде отрицателно число
да
Не

Кое от тези числа е противоположно на 124?
-24
24
-124124 Каква е стойността на израза –(-k), ако k = -9
-9
+9
Изчислете стойността на израза: 2,5:-0,5+1,250
15
-2,5
2,5
Решете уравнението x=100100
-100
100 или -100
Какви цели числа се намират на координатната права между числата 1 и - 4.5
-4, -3, -2, -1, 0
-3, -2, -1
-5, -4, -3, -2, -1
-4, -3, -2, -1, 1
Вярно ли е неравенството -25?<-10?
да
Не
Избройте всички цели числа x, ако x≤44, 3, 2
0, 1, 2, 3
1, 2, 3, 4
0, 1, 2, 3, 4
Тест No3. Сравнение на числата
Опция 1
Кое от неравенствата е невярно?
-20 > 2
0 < -1
-16 > -7
-5 < -3

-320 -920>
<
=
Вярно ли е, че числото 0 е по-голямо от всяко отрицателно число?
да
Не
Числото a е неотрицателно. Как можем да запишем това твърдение като неравенство?
а<0a≤0a≥0a>0Посочете най-голямото от дадените числа.
0,16
-3018-0,4
0,01
За какви естествени стойности на x е вярно неравенството x≤44, 3, 2?
1 , 2, 3, 4
4, 3, 2, 1
0, 1, 2, 3
За какви цели числа на y е вярно неравенството y?<-2?0
-1
0, -1, 1
Няма такива стойности
Числа -6; -3,8; -115; 0.8 разположен:
В низходящ ред
В нарастващ ред
В безпорядък
Прогнозата за времето беше излъчена по радиото: температурата се очаква да падне до -20 °C. Опишете това събитие:
Невъзможен
Надежден
Случаен
Вариант 2
Кое от неравенствата е вярно?
-5 > 0
6 < -17
-34 > -40
-9 < -63
Какъв знак трябва да се постави между тези дроби, за да е вярно неравенството?
-1315 -715<
>
=
Вярно ли е, че числото 0 е по-малко от всяко отрицателно число?
да
Не
Числото x не е по-голямо от нула. Как можем да запишем това твърдение като неравенство?
x≥0x>0x<0x≤0Укажите наименьшее из данных чисел.
-5,92
1,7
-1000
35 За какви естествени стойности на a е вярно неравенството a≤3?1, 2, 3
0, 1, 2, 3
1, 2
0, 1, 2
За какви цели числа на m е вярно неравенството m?<-4?-3, -2, -1
0, -1, -2, -3, 1, 2, 3
0
Няма такива стойности
Числа 1,2; -1,2; -427; -100 разположени:
В безпорядък
В нарастващ ред
В низходящ ред
На координатната права е отбелязана точка A(5). На тази линия произволно е отбелязана друга точка B. Координатата й се оказва противоположна на 5. Опишете това събитие.
Случаен
Надежден
Невъзможен
Отговори
Тест No1 Тест No2
№ Вариант 1 Вариант 2
1 3 4
2 2 3
3 4 3
4 3 1
5 1 2
6 4 4
7 3 2
8 2 3
9 1 2
10 4 1
№ Вариант 1 Вариант 2
1 3 2
2 1 4
3 1 2
4 4 3
5 2 1
6 3 4
7 3 3
8 4 1
9 1 2
10 2 4

Тест No3
№ Вариант 1 Вариант 2
1 4 3
2 1 2
3 1 2
4 3 4
5 1 3
6 2 1
7 4 4
8 2 3