Məktəbə hazırlıq

Riyaziyyat ensiklopediyası. Riyaziyyat Ensiklopediyası Aksiomlar və sübut üsulları

5 cilddə Riyaziyyat Ensiklopediyası kitabını yükləyin tamamilə pulsuz.

Kitabı fayl hostinqindən pulsuz yükləmək üçün pulsuz kitabın təsvirindən dərhal sonra keçidlərə klikləyin.

Hörmətli oxucular, əgər uğur qazana bilməmisinizsə

Riyaziyyat ensiklopediyasını 5 cilddə yükləyin

bu barədə şərhlərdə yazın və biz sizə mütləq kömək edəcəyik.

Ümid edirik ki, siz kitabdan zövq aldınız və oxumaqdan həzz aldınız. Təşəkkür olaraq forum və ya bloqda saytımıza keçid qoya bilərsiniz :) Elektron kitab 5 cilddən ibarət Riyaziyyat Ensiklopediyası yalnız kağız kitab almazdan əvvəl məlumat üçün verilir və çap nəşrlərinə rəqib deyil.

Məqalənin məzmunu

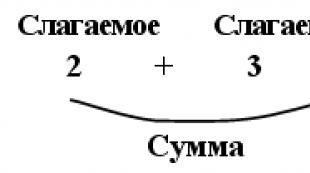
RİYAZİYYAT. Riyaziyyat adətən onun bəzi ənənəvi bölmələrinin adlarını sadalamaqla müəyyən edilir. Əvvəla, bu, ədədlərin, onlar arasındakı əlaqənin və ədədlər üzərində hərəkət qaydalarının öyrənilməsi ilə məşğul olan arifmetikadır. Arifmetika faktları müxtəlif konkret şərhləri qəbul edir; məsələn, 2 + 3 = 4 + 1 nisbəti iki və üç kitabın dörd və bir kitabla eyni sayda kitab təşkil etməsi ifadəsinə uyğundur. 2 + 3 = 4 + 1 tipli hər hansı əlaqə, yəni. sırf riyazi obyektlər arasında fiziki aləmdən heç bir şərhə istinad etmədən əlaqəyə mücərrəd deyilir. Riyaziyyatın mücərrəd təbiəti ondan ən çox həllində istifadə etməyə imkan verir müxtəlif problemlər... Məsələn, ədədlər üzərində əməliyyatlardan bəhs edən cəbr hesabdan kənara çıxan məsələləri həll etməyə imkan verir. Riyaziyyatın daha spesifik sahəsi həndəsədir, onun əsas vəzifəsi cisimlərin ölçülərini və formalarını öyrənməkdir. Cəbri və həndəsi metodların birləşməsi bir tərəfdən triqonometriyaya (əvvəlcə həndəsi üçbucaqların tədqiqinə həsr olunmuş və indi daha geniş məsələləri əhatə edir), digər tərəfdən isə həndəsi cisimlər və fiqurlar cəbri üsullarla tədqiq edilir. Ali cəbr və həndəsənin bir neçə bölməsi vardır ki, onlar daha yüksək abstraksiya dərəcəsinə malikdirlər və adi ədədlərin və adi həndəsi fiqurların öyrənilməsində iştirak etmirlər; həndəsi fənlərin ən mücərrədi topologiya adlanır.

Riyazi təhlil məkanda və ya zamanda dəyişən kəmiyyətlərin tədqiqi ilə məşğul olur və riyaziyyatın daha elementar sahələrində rast gəlinməyən iki əsas anlayışa - funksiya və limitə əsaslanır. Əvvəlcə riyazi analiz diferensial və inteqral hesablamalardan ibarət idisə, indi başqa bölmələri də əhatə edir.

Riyaziyyatın iki əsas sahəsi var - deduktiv əsaslandırmanı vurğulayan xalis riyaziyyat və tətbiqi riyaziyyat. “Tətbiqi riyaziyyat” termini bəzən elmin ehtiyac və tələblərini ödəmək üçün xüsusi olaraq yaradılmış riyaziyyat sahələrinə, bəzən isə riyaziyyatdan vasitə kimi istifadə edən müxtəlif elmlərin (fizika, iqtisadiyyat və s.) sahələrinə aid edilir. vəzifələrini həll etməkdən ibarətdir. Riyaziyyatla bağlı bir çox ümumi yanlış təsəvvürlər "tətbiqi riyaziyyat"ın bu iki şərhinin qarışdırılmasından yaranır. Arifmetika birinci mənada tətbiqi riyaziyyata, ikinci mənada isə mühasibatlığa misaldır.

Məşhur inancın əksinə olaraq, riyaziyyat sürətlə irəliləməyə davam edir. Mathematical Review jurnalı təqribən nəşr edir. Ən son nəticələri özündə əks etdirən 8000 tezis - yeni riyazi faktlar, köhnə faktların yeni sübutları və hətta riyaziyyatın tamamilə yeni sahələri haqqında məlumatlar. Riyaziyyat təhsilində mövcud tendensiya riyaziyyatın tədrisinin daha erkən mərhələsində tələbələri müasir, daha abstrakt riyazi ideyalarla tanış etməkdir. həmçinin bax RİYAZİYYAT TARİXİ. Riyaziyyat sivilizasiyanın təməl daşlarından biridir, lakin çox az adamın bu elmdə mövcud vəziyyət haqqında təsəvvürü var.

Son yüz ildə riyaziyyat həm mövzu, həm də tədqiqat metodları baxımından çox böyük dəyişikliklərə məruz qalmışdır. Bu yazıda biz müasir riyaziyyatın təkamülünün əsas mərhələləri haqqında ümumi fikir verməyə çalışacağıq ki, bunun əsas nəticələrini bir tərəfdən təmiz və tətbiqi riyaziyyat arasındakı fərqin artması hesab etmək olar. və digər tərəfdən, riyaziyyatın ənənəvi sahələrinin tamamilə yenidən nəzərdən keçirilməsi.

RİYASİ METODUN İNKİŞAF EDİLMƏSİ

Riyaziyyatın doğuşu.

Eramızdan əvvəl 2000-ci illərdə tərəfləri 3, 4 və 5 vahid uzunluğunda olan üçbucaqda bucaqlardan birinin 90 ° olduğu (bu müşahidə praktiki ehtiyaclar üçün düzgün bucaq qurmağı asanlaşdırdı). 5 2 = 3 2 + 4 2 nisbətinə diqqət yetirdinizmi? Bununla bağlı bizdə məlumat yoxdur. Bir neçə əsr sonra ümumi bir qayda kəşf edildi: istənilən üçbucaqda ABC zirvədə düz bucaq ilə A və partiyalar b = AS və c = AB, aralarında bu bucağın qapalı olduğu və qarşı tərəf a = e.əəlaqə doğrudur a 2 = b 2 + c 2. Demək olar ki, ayrı-ayrı müşahidələrin kütləsi bir ümumi qanunla izah edildikdə elm başlayır; buna görə də “Pifaqor teoremi”nin kəşfini həqiqi elmi nailiyyətin ilk məlum nümunələrindən biri kimi qiymətləndirmək olar.

Lakin bütövlükdə elm və xüsusilə riyaziyyat üçün daha da vacib olan, formulla yanaşı, odur ümumi qanun sübut etmək cəhdləri var, yəni. onun mütləq başqa həndəsi xassələrdən irəli gəldiyini göstərir. Şərq "sübutlarından" biri sadəliyi ilə xüsusilə diqqəti çəkir: kvadratda buna bərabər olan dörd üçbucaq yazılmışdır. BCDE rəsmdə göstərildiyi kimi. Kvadrat sahə a 2 ümumi sahəsi 2 olan dörd bərabər üçbucağa bölünür e.ə və kvadrat AFGH sahə ( b – c) 2. Bu cür, a 2 = (b – c) 2 + 2e.ə = (b 2 + c 2 – 2e.ə) + 2e.ə = b 2 + c 2. Daha bir addım atmaq və hansı “əvvəlki” xassələrin məlum olduğu fərz edildiyini daha dəqiq öyrənmək ibrətamizdir. Ən bariz həqiqət budur ki, üçbucaqlardan bəri BAC və BEF tam olaraq, boşluqlar və üst-üstə düşmələr olmadan, tərəflər boyunca "uyğundur" BA və Bf, bu o deməkdir ki, iki künc təpəsindədir B və İLƏüçbucaqda ABC birlikdə 90 ° bir açı təşkil edir və buna görə də onun hər üç bucağının cəmi 90 ° + 90 ° = 180 °-dir. Yuxarıdakı "sübut" düsturu da istifadə edir ( e.ə/ 2) üçbucağın sahəsi üçün ABC 90 ° zirvə bucağı A... Əslində, başqa fərziyyələrdən də istifadə olunurdu, lakin deyilənlər kifayətdir ki, biz riyazi sübutun əsas mexanizmini – deduktiv mülahizəni aydın görə bilək ki, bu da bizə nəticə çıxarmağa imkan verir. məlum nəticələr yeni xüsusiyyətlər, bir qayda olaraq, mövcud məlumatlardan birbaşa təqib olunmur.

Aksiomalar və sübut üsulları.

Riyazi metodun əsas xüsusiyyətlərindən biri diqqətlə qurulmuş sırf məntiqi arqumentlərdən istifadə edərək, hər bir sonrakı əlaqənin əvvəlkilərlə əlaqəli olduğu ifadələr zəncirinin yaradılması prosesidir. İlk kifayət qədər aydın mülahizə budur ki, hər hansı bir zəncirdə birinci halqa olmalıdır. Bu vəziyyət yunanlar üçün 7-ci əsrdə riyazi dəlillər toplusunu sistemləşdirməyə başlayanda aydın oldu. e.ə. Bu planı həyata keçirmək üçün yunanlara təqribən lazım idi. 200 ildir və sağ qalan sənədlər yalnız onların necə hərəkət etdikləri barədə təxmini bir fikir verir. Yalnız tədqiqatın son nəticəsi - məşhur haqqında dəqiq məlumatımız var Başlanğıclar Evklid (e.ə. 300-cü il). Evklid bütün qalanların sırf məntiqi vasitələrlə çıxarıldığı başlanğıc nöqtələri sadalamaqla başlayır. Bu müddəalar aksiomlar və ya postulatlar adlanır (terminlər praktiki olaraq bir-birini əvəz edir); onlar istənilən növ obyektlərin ya çox ümumi və bir qədər qeyri-müəyyən xassələrini, məsələn, “bütün hissədən böyükdür” və ya bəzi xüsusi riyazi xassələri, məsələn, hər hansı iki nöqtə üçün onları birləşdirən vahid xəttin olduğunu ifadə edirlər. Yunanların aksiomların “həqiqətinə” daha dərin məna və ya əhəmiyyət verib-verməmələri barədə heç bir məlumatımız yoxdur, baxmayaraq ki, bəzi eyhamlar var ki, müəyyən aksiomları qəbul etməzdən əvvəl yunanlar onları bir müddət müzakirə ediblər. Evklid və onun davamçılarında aksiomalar təbiəti haqqında heç bir şərh edilmədən yalnız riyaziyyatın qurulması üçün başlanğıc nöqtələri kimi təqdim olunur.

Sübut üsullarına gəlincə, onlar, bir qayda olaraq, əvvəllər sübut edilmiş teoremlərin birbaşa istifadəsinə endirilmişdir. Ancaq bəzən düşünmə məntiqinin daha mürəkkəb olduğu ortaya çıxdı. Biz burada riyaziyyatın gündəlik praktikasına daxil olan Evklidin sevimli metodunu - dolayı sübut və ya ziddiyyətlə sübutu qeyd edəcəyik. Ziddiyyətlə sübuta elementar nümunə olaraq göstərəcəyik ki, iki künc kvadratı kəsilmiş, diaqonalın əks uclarında yerləşən şahmat taxtası hər biri iki kvadrata bərabər olan dominolarla örtülə bilməz. (Şahmat taxtasının hər kvadratının yalnız bir dəfə örtülməli olduğu güman edilir.) Tutaq ki, əks (“əks”) ifadə doğrudur, yəni. lövhənin domino sümükləri ilə örtülə biləcəyini. Hər bir kafel bir qara və bir ağ kvadratı əhatə edir, buna görə də dominoların harada yerləşməsindən asılı olmayaraq, onlar bərabər sayda qara və ağ kvadratları əhatə edir. Bununla belə, iki künc kvadratı çıxarıldığına görə, dama taxtasında (əvvəllər ağ kvadratlar qədər qara kvadratlar var idi) digər rəngli kvadratlardan daha çox bir rəngli iki kvadrat var. Bu o deməkdir ki, ilkin fərziyyəmiz doğru ola bilməz, çünki bu, ziddiyyətə gətirib çıxarır. Və ziddiyyətli mühakimələr eyni zamanda yalan ola bilmədiyi üçün (onlardan biri yanlışdırsa, əksi doğrudur), bizim ilkin fərziyyəmiz doğru olmalıdır, çünki ziddiyyətli fərziyyə yanlışdır; buna görə də çapraz şəkildə kəsilmiş iki künc kvadratı olan şahmat taxtası dominolarla örtülə bilməz. Deməli, hansısa mülahizəni isbat etmək üçün onun batil olduğunu fərz edə və bu fərziyyədən həqiqəti məlum olan başqa bir müddəa ilə ziddiyyət çıxara bilərik.

Qədim yunan riyaziyyatının inkişafında mərhələlərdən birinə çevrilmiş ziddiyyətlə sübutun əla nümunəsi rasional ədəd olmayan sübutdur, yəni. kəsr kimi təmsil olunmur səh/q, harada səh və q- tam ədədlər. Əgər, onda 2 = səh 2 /q 2, haradan səh 2 = 2q 2. Tutaq ki, iki tam ədəd var səh və q hansı üçün səh 2 = 2q 2. Başqa sözlə, hesab edirik ki, kvadratı başqa bir tam ədədin kvadratından iki dəfə böyük olan tam ədəd var. Əgər hər hansı tam ədədlər bu şərti ödəyirsə, onda onlardan biri digərlərindən kiçik olmalıdır. Bu rəqəmlərin ən kiçikinə diqqət yetirək. Qoy nömrə olsun səh... 2 ildən q 2 cüt ədəddir və səh 2 = 2q 2, sonra nömrə səh 2 bərabər olmalıdır. Çünki bütün tək ədədlərin kvadratları tək və kvadratdır səh 2 cütdür, rəqəmin özü deməkdir səh bərabər olmalıdır. Başqa sözlə, nömrə səh iki dəfə tam ədəd r... Çünki səh = 2r və səh 2 = 2q 2, bizdə: (2 r) 2 = 4r 2 = 2q 2 və q 2 = 2r 2. Sonuncu bərabərlik bərabərliklə eyni formaya malikdir səh 2 = 2q 2 və biz eyni mülahizəni təkrarlayaraq rəqəmin olduğunu göstərə bilərik q cütdür və belə bir tam ədəd var s, nə q = 2s... Amma sonra q 2 = (2s) 2 = 4s 2 və o vaxtdan bəri q 2 = 2r 2, nəticəyə gəlirik ki, 4 s 2 = 2r 2 və ya r 2 = 2s 2. Bu bizə onun kvadratının digər tam ədədin kvadratından iki dəfə olması şərtini ödəyən ikinci tam ədəd verir. Amma sonra səh belə ən kiçik rəqəm ola bilməz (çünki r = səh/ 2), baxmayaraq ki, əvvəlcə biz bu cür rəqəmlərin ən kiçiyi olduğunu güman etdik. Buna görə də, ilkin fərziyyəmiz yanlışdır, çünki bu, ziddiyyətə gətirib çıxarır və buna görə də belə tam ədədlər yoxdur. səh və q hansı üçün səh 2 = 2q 2 (yəni belə). Bu o deməkdir ki, rəqəm rasional ola bilməz.

Evkliddən 19-cu əsrin əvvəllərinə qədər

Bu dövrdə riyaziyyat üç yenilik nəticəsində əhəmiyyətli dəyişikliklərə məruz qalmışdır.

(1) Cəbrin inkişafı zamanı simvolik qeyd üsulu icad edildi ki, bu da kəmiyyətlər arasında getdikcə daha mürəkkəb əlaqələri qısaldılmış formada təqdim etməyə imkan verdi. Belə bir “kursiv yazı” olmasaydı, yaranacaq narahatçılığa misal olaraq nisbəti sözlə çatdırmağa çalışaq ( a + b) 2 = a 2 + 2ab + b 2: "Bir tərəfi verilmiş iki kvadratın tərəflərinin cəminə bərabər olan kvadratın sahəsi, tərəfləri tərəflərinə bərabər olan düzbucaqlının sahəsinin iki qatı ilə birlikdə onların sahələrinin cəminə bərabərdir. bu kvadratlar."

(2) XVII əsrin birinci yarısında yaradılış. klassik həndəsənin istənilən problemini hansısa cəbri problemə endirməyə imkan verən analitik həndəsə.

(3) 1600-cü ildən 1800-cü ilə qədər olan dövrdə həddi və davamlılıq anlayışları ilə bağlı yüzlərlə problemi asanlıqla və sistemli şəkildə həll etməyə imkan verən sonsuz kiçiklər hesabının yaradılması və inkişafı; qədim yunan riyaziyyatçılarının çətinlikləri. Riyaziyyatın bu qollarından CƏBRİ məqalələrində daha ətraflı bəhs edilir; ANALİTİK HƏNDƏSİ; RİYASİ ANALİZ; HƏNDƏSİYƏ İCLAMA.

17-ci əsrdən bəri. indiyə qədər həll olunmayan sual getdikcə aydınlaşır. Riyaziyyat nədir? 1800-cü ilə qədər cavab kifayət qədər sadə idi. O dövrdə müxtəlif elmlər arasında dəqiq sərhədlər yox idi, riyaziyyat “müxtəlif elmlərin bir hissəsi idi. təbiət fəlsəfəsi"- İntibah dövrünün və 17-ci əsrin əvvəllərinin böyük islahatçıları tərəfindən təklif olunan üsullarla təbiətin sistemli tədqiqi. - Qaliley (1564-1642), F.Bekon (1561-1626) və R.Dekart (1596-1650). Hesab olunurdu ki, riyaziyyatçıların öz tədqiqat sahəsi - ədədlər və həndəsi cisimlər var və riyaziyyatçılar eksperimental üsuldan istifadə etmirlər. Bununla belə, Nyuton və onun ardıcılları Evkliddə həndəsənin təqdim olunduğu kimi aksiomatik metoddan istifadə edərək mexanika və astronomiyanı öyrəndilər. Daha ümumi olaraq, bir təcrübənin nəticələrinin ədədlər və ya ədədlər sistemlərindən istifadə etməklə təqdim olunduğu hər hansı bir elmin riyaziyyatın tətbiq sahəsinə çevrildiyi qəbul edildi (fizikada bu konsepsiya yalnız 19-cu əsrdə quruldu).

Təcrübə elminin riyazi emaldan keçmiş sahələrinə çox vaxt “tətbiqi riyaziyyat” deyilir; bu, çox uğursuz bir addır, çünki bu tətbiqlərdə nə klassik, nə də müasir standartlara görə (ciddi mənada) həqiqətən riyazi arqumentlər yoxdur, çünki onlarda tədqiqatın mövzusu qeyri-riyazi obyektlərdir. Eksperimental məlumatlar ədədlər və ya tənliklər dilinə tərcümə edildikdən sonra (belə “tərcümə” çox vaxt “tətbiqi” riyaziyyatçıdan böyük bacarıq tələb edir) riyazi teoremlərdən geniş istifadə etmək mümkün olur; nəticə sonra geri tərcümə edilir və müşahidələrlə müqayisə edilir. “Riyaziyyat” termininin bu cür prosesə tətbiq edilməsi sonsuz anlaşılmazlıq mənbələrindən biridir. İndi haqqında danışdığımız “klassik” dövrlərdə bu cür anlaşılmazlıq yox idi, çünki eyni insanlar həm “tətbiqi”, həm də “təmiz” riyaziyyatçılar idilər, eyni zamanda riyazi analiz və ya ədədlər nəzəriyyəsi problemləri ilə məşğul olurdular. dinamika və ya optika. Bununla belə, artan ixtisaslaşma və "saf" və "tətbiqi" riyaziyyatçıları təcrid etmək meyli əvvəllər mövcud olan universallıq ənənəsini əhəmiyyətli dərəcədə zəiflətdi və J. von Neumann (1903-1957) kimi elm adamları fəal şəkildə rəhbərlik edə bildilər. elmi fəaliyyət həm tətbiqi, həm də sırf riyaziyyatda qaydadan çox istisna halına gəldi.

Riyazi cisimlərin - ədədlərin, nöqtələrin, xətlərin, bucaqların, səthlərin və s. - onların mövcud olduğunu qəbul etdiyimiz təbiət nədir? Bu cür obyektlərə münasibətdə “həqiqət” anlayışı nə deməkdir? Klassik dövrdə bu suallara kifayət qədər dəqiq cavablar verilirdi. Əlbəttə, o dövrün alimləri aydın başa düşürdülər ki, bizim hisslər aləmində Evklidin “sonsuz uzadılmış düz xətti” və ya “ölçüsü olmayan nöqtəsi” kimi şeylər yoxdur, çünki “saf metallar”, “monoxromatik işıq” yoxdur. Təcrübəçilər öz mülahizələrində işlədikləri "," istilik izolyasiya sistemləri " və s. .d. Bütün bu anlayışlar “Platon ideyaları”, yəni. kökündən fərqli xarakter daşısa da, empirik anlayışların bir növ generativ modelidir. Buna baxmayaraq, üstüörtülü şəkildə güman edilirdi ki, fikirlərin fiziki “təsvirləri” ideyaların özlərinə arzu olunan qədər yaxın ola bilər. Obyektlərin ideyalara yaxınlığı haqqında ümumiyyətlə nəyisə iddia etmək olarsa, deyilir ki, “ideyalar” fiziki obyektlərin belə desək, “məhdud halları”dır. Bu nöqteyi-nəzərdən, Evklidin aksiomları və onlardan alınan teoremlər “ideal” cisimlərin xassələrini ifadə edir ki, bu da proqnozlaşdırıla bilən eksperimental faktlara uyğun olmalıdır. Məsələn, kosmosda üç nöqtənin yaratdığı üçbucağın bucaqlarını optik üsullarla ölçmək, "ideal vəziyyətdə" 180 ° -ə bərabər bir məbləğ verməlidir. Başqa sözlə, aksiomalar fiziki qanunlarla eyni səviyyədə yerləşdirilir və buna görə də onların “həqiqəti” fiziki qanunların həqiqəti kimi qavranılır; olanlar. aksiomalardan gələn məntiqi nəticələr eksperimental məlumatlar ilə müqayisə edilərək yoxlanılır. Əlbəttə ki, razılığa yalnız ölçmə cihazının "qeyri-kamil" təbiəti və ölçülmüş obyektin "qeyri-kamil təbiəti" ilə bağlı səhv daxilində nail olmaq olar. Bununla belə, həmişə nəzərdə tutulur ki, qanunlar "doğrudur"sa, ölçmə proseslərindəki təkmilləşdirmələr, prinsipcə, ölçmə xətasının özbaşına kiçik olmasına imkan verir.

18-ci əsr boyu. Əsas aksiomalardan, xüsusən də astronomiya və mexanikada əldə edilən bütün nəticələrin eksperimental məlumatlara uyğun olduğuna getdikcə daha çox sübut var idi. Və bu nəticələr o dövrdə mövcud olan riyazi aparatdan istifadə olunmaqla əldə edildiyindən, əldə edilən uğurlar Platonun dediyi kimi, “hamıya aydın olan” və tabe olmayan Evklidin aksiomlarının həqiqəti haqqında rəyin möhkəmlənməsinə töhfə verdi. müzakirə.

Şübhələr və yeni ümidlər.

Qeyri-Evklid həndəsəsi.

Evklidin istinad etdiyi postulatlar arasında biri o qədər qeyri-müəyyən idi ki, hətta böyük riyaziyyatçının ilk tələbələri bunu sistemin zəif nöqtəsi hesab edirdilər. başladı... Sözügedən aksiomda deyilir ki, verilmiş düz xəttdən kənarda yerləşən nöqtə vasitəsilə verilmiş düz xəttə paralel yalnız bir düz xətt çəkilə bilər. Əksər həndəsələr paralel aksiomun digər aksiomlardan istifadə etməklə sübut oluna biləcəyinə inanırdılar və Evklid sadəcə belə bir sübut gətirə bilmədiyi üçün paralel təsdiqi postulat kimi formalaşdırmışdır. Amma buna baxmayaraq ən yaxşı riyaziyyatçılar paralel məsələni həll etməyə çalışsa da, onların heç biri Evklidi üstələyə bilmədi. Nəhayət, 18-ci əsrin ikinci yarısında. Evklidin paralel və ziddiyyətli postulatını sübut etməyə cəhdlər edildi. Paralel aksiomun yalan olduğu güman edilirdi. A priori olaraq, Evklidin postulatı iki halda yalan ola bilər: verilmiş düz xəttdən kənar nöqtə ilə tək paralel çəkmək mümkün olmadıqda; yaxud onun vasitəsilə bir neçə paralel çəkmək olarsa. Məlum oldu ki, birinci a priori ehtimal digər aksiomlar tərəfindən istisna edilir. Ənənəvi paralel aksiom əvəzinə yeni aksioma qəbul edərək (verilmiş düz xəttdən kənar nöqtə vasitəsilə verilmiş birinə paralel bir neçə düz xətt çəkilə bilər), riyaziyyatçılar ondan digər aksiomlarla ziddiyyət təşkil edən bir ifadə çıxarmağa çalışdılar, lakin uğursuz oldu: yeni “anti-evklid” və ya “qeyri-evklid” aksiomundan nəticələr çıxarmağa nə qədər cəhd etsələr də, ziddiyyət yaranmadı. Nəhayət, bir-birindən asılı olmayaraq, N.İ.Lobaçevski (1793–1856) və C.Boyai (1802–1860) başa düşdülər ki, Evklidin paralellər postulatı sübuta yetirilməzdir, başqa sözlə, “qeyri-Evklid həndəsəsi”ndə ziddiyyət yaranmayacaq. .

Qeyri-Evklid həndəsəsinin meydana çıxması ilə dərhal bir neçə fəlsəfi problem ortaya çıxdı. Aksiomların aprior zərurətinə dair iddia ortadan qalxdığından, onların “həqiqətini” yoxlamağın yeganə yolu eksperimental olaraq qaldı. Lakin Puankarenin (1854-1912) daha sonra qeyd etdiyi kimi, hər hansı bir hadisənin təsvirində o qədər çox fiziki fərziyyələr gizlənir ki, heç bir təcrübə riyazi aksiomun doğruluğunu və ya yanlışlığını inandırıcı şəkildə sübut edə bilməz. Üstəlik, dünyamızın “qeyri-Evklid” olduğunu fərz etsək belə, bundan bütün Evklid həndəsəsinin yalan olduğu nəticə çıxırmı? Məlum olduğu qədər heç bir riyaziyyatçı belə bir fərziyyəni ciddi qəbul etməyib. İntuisiya diktə etdi ki, həm Evklid, həm də qeyri-Evklid həndəsələri tam hüquqlu riyaziyyatın nümunələridir.

Riyazi "canavarlar".

Birdən onlar tamamilə fərqli tərəfdən eyni nəticələrə gəldilər - 19-cu əsrin riyaziyyatçılarını qərq edən obyektlər kəşf edildi. şoka saldı və "riyazi canavarlar" adlandırıldı. Bu kəşf yalnız 19-cu əsrin ortalarında ortaya çıxan riyazi analizin çox incə sualları ilə birbaşa bağlıdır. Əyrinin eksperimental konsepsiyasının dəqiq riyazi analoqunu tapmağa çalışarkən çətinliklər yarandı. “Fasiləsiz hərəkət” anlayışının mahiyyəti nədən ibarət idi (məsələn, kağız vərəqində hərəkət edən rəsm qələminin ucu) dəqiq riyazi tərifə tabe idi və bu məqsədə davamlılıq anlayışı ciddi riyazi anlayış əldə etdikdə nail olundu. məna ( sm. həmçininƏYRI). İntuitiv olaraq görünürdü ki, onun hər bir nöqtəsindəki "əyri" bir növ istiqamətə malikdir, yəni. ümumi halda, onun hər bir nöqtəsinin yaxınlığında əyri düz xətt kimi, demək olar ki, eyni şəkildə davranır. (Digər tərəfdən, əyrinin çoxbucaqlı kimi sonlu sayda künc nöqtələrinə malik olduğunu təsəvvür etmək asandır, "burulur".) Bu tələbi riyazi şəkildə formalaşdırmaq olar, yəni əyriyə toxunan varlığı fərz edilirdi. , və 19-cu əsrin ortalarına qədər. güman edilirdi ki, “əyri” bəlkə də bəzi “tək” nöqtələr istisna olmaqla, demək olar ki, bütün nöqtələrində tangensə malikdir. Buna görə də heç bir nöqtədə toxunuşu olmayan "əyrilərin" kəşfi əsl qalmaqala səbəb oldu ( sm. həmçinin FUNKSİYALAR NƏZƏRİYYƏSİ). (Triqonometriya və analitik həndəsə ilə tanış olan oxucu asanlıqla yoxlaya bilər ki, tənliklə verilən əyri y = x günah (1 / x), başlanğıcda tangensi yoxdur, lakin heç bir nöqtəsində tangensi olmayan əyrini təyin etmək daha çətindir.)

Bir az sonra daha çox "patoloji" nəticə əldə edildi: kvadratı tamamilə dolduran əyri nümunəsini qura bildik. O vaxtdan bəri "sağlam düşüncə"nin əksinə olaraq yüzlərlə belə "canavarlar" icad edilmişdir. Vurğulamaq lazımdır ki, belə qeyri-adi riyazi obyektlərin mövcudluğu əsas aksiomlardan üçbucağın və ya ellipsin mövcudluğu kimi ciddi və məntiqi qüsursuz irəli gəlir. Riyazi "canavarlar" heç bir eksperimental obyektə uyğun gələ bilməyəcəyindən və yeganə mümkün nəticə ondan ibarətdir ki, riyazi "ideyalar" dünyası gözləniləndən daha zəngin və qeyri-adidir və onlardan yalnız çox azının bizim dünyamızda yazışmaları var. sensasiyalar. Bəs riyazi “canavarlar” məntiqi olaraq aksiomlardan irəli gəlirsə, o zaman aksiomaları yenə də doğru hesab etmək olarmı?

Yeni obyektlər.

Yuxarıdakı nəticələr bir tərəfdən də təsdiqləndi: riyaziyyatda, əsasən cəbrdə ədəd anlayışının ümumiləşdirilməsi olan yeni riyazi obyektlər bir-birinin ardınca meydana çıxmağa başladı. Adi tam ədədlər kifayət qədər “intuitivdir” və kəsrin eksperimental konsepsiyasına gəlmək heç də çətin deyil (baxmayaraq ki, vahidin bir neçə bərabər hissəyə bölünməsi əməliyyatı və onlardan bir neçəsinin seçilməsi əməliyyatı qəbul etmək lazımdır. sayma prosesindən mahiyyətcə fərqlidir). Ədədin kəsr şəklində göstərilə bilmədiyi aydın olduqdan sonra, yunanlar rasional ədədlərlə sonsuz yaxınlaşma ardıcıllığının köməyi ilə düzgün tərifi ən yüksək nailiyyətlərə aid olan irrasional ədədləri nəzərdən keçirməyə məcbur oldular. insan zehni, lakin fiziki dünyamızda real heç bir şeyə demək olar ki, uyğun gəlmir (burada hər hansı ölçmə həmişə səhvə meyllidir). Buna baxmayaraq, irrasional ədədlərin tətbiqi az-çox fiziki anlayışların “ideallaşdırılması” ruhunda baş verdi. Bəs cəbrin inkişafı ilə əlaqədar yavaş-yavaş, böyük müqavimətlə üzləşərək elmi istifadəyə başlayan mənfi ədədlər haqqında nə demək olar? Tam əminliklə iddia etmək olar ki, hazır fiziki obyektlər yox idi, ondan başlayaraq birbaşa abstraksiya prosesindən istifadə edərək mənfi ədəd anlayışını inkişaf etdirə bildik və ibtidai cəbr kursunun tədrisində biz çoxlu sayda obyektlər təqdim etməliyik. mənfi ədədlərin nə olduğunu aydınlaşdırmaq üçün köməkçi və kifayət qədər mürəkkəb nümunələr (yönümlü seqmentlər, temperaturlar, borclar və s.). Platonun riyaziyyatın əsasını təşkil edən ideyalardan tələb etdiyi kimi, belə bir vəziyyət "hamıya aydındır" anlayışından çox uzaqdır və əlamətlər qaydası olan kollec məzunlarına rast gəlmək qeyri-adi deyil (- a)(–b) = ab. həmçinin bax NÖMRƏ.

Vəziyyət "xəyali" və ya "mürəkkəb" nömrələrlə daha pisdir, çünki onlar "rəqəm" daxildir. i, belə i 2 = –1, işarə qaydasının açıq şəkildə pozulmasıdır. Buna baxmayaraq, 16-cı əsrin sonlarından riyaziyyatçılar. 200 il əvvəl onlar bu "obyektləri" müəyyən edə və ya hər hansı köməkçi konstruksiyadan istifadə edərək şərh edə bilməsələr də, mürəkkəb ədədlərlə hesablamalar aparmaqdan çəkinməyin, baxmayaraq ki, sanki "məntiqli idi". . (1800-cü ildən bəri bir neçə şərh təklif edilmişdir mürəkkəb ədədlər, ən məşhuru təyyarədə vektorlardan istifadə etməkdir.)

Müasir aksiomatika.

Çevriliş 19-cu əsrin ikinci yarısında baş verdi. Və bu, rəsmi bəyanatların qəbulu ilə müşayiət olunmasa da, əslində bu, bir növ “müstəqillik bəyannaməsi”nin elan edilməsindən gedirdi. Daha dəqiq desək, riyaziyyatın xarici aləmdən müstəqilliyinin faktiki elan edilməsi haqqında.

Bu nöqteyi-nəzərdən, riyazi “obyektlər”, əgər onların “mövcudluğu” haqqında danışmaq məntiqlidirsə, saf ağlın məhsuludur və onların hər hansı “uyğunluğu” varmı və fiziki cəhətdən hər hansı “təfsir”i qəbul edirlərmi? dünya, riyaziyyat üçün əhəmiyyətsizdir (baxmayaraq ki, bu sualın özü maraqlıdır).

Bu cür "obyektlər" haqqında "doğru" ifadələrin hamısı aksiomalardan eyni məntiqi nəticələrdir. Amma indi aksiomalar tamamilə ixtiyari hesab edilməlidir və buna görə də onların “dəlil”inə və ya “ideallaşdırma” yolu ilə gündəlik təcrübədən çıxarılmasına ehtiyac yoxdur. Praktikada tam azadlıq müxtəlif mülahizələrlə məhdudlaşdırılır. Əlbəttə ki, "klassik" cisimlər və onların aksiomaları dəyişməz olaraq qalır, lakin indi onları riyaziyyatın yeganə obyektləri və aksiomları hesab etmək olmaz və aksiomları atmaq və ya dəyişdirmək vərdişi gündəlik təcrübəyə daxil olub ki, onlardan istifadə etmək mümkün olsun. Evklid həndəsəsindən qeyri-Evklid həndəsəsinə keçiddə olduğu kimi müxtəlif yollarla. (Məhz bu yolla Evklid həndəsəsindən və Lobaçevski-Boyai həndəsəsindən fərqli olaraq “qeyri-Evklid” həndəsələrinin çoxsaylı variantları əldə edilmişdir; məsələn, paralel xətlərin olmadığı qeyri-Evklid həndəsələri var).

Riyazi “obyektlərə” yeni yanaşmadan irəli gələn bir vəziyyəti xüsusilə vurğulamaq istərdim: bütün sübutlar yalnız aksiomalara əsaslanmalıdır. Riyazi sübutun tərifi üzərində düşünsək, belə bir ifadə təkrar kimi görünə bilər. Bununla belə, bu qayda klassik riyaziyyatda onun obyektlərinin və ya aksiomlarının "intuitiv" təbiətinə görə nadir hallarda müşahidə edilmişdir. Hətta Başlanğıclar Evklid, bütün zahiri "sərtliyinə" baxmayaraq, bir çox aksiomlar açıq şəkildə ifadə edilmir və bir çox xüsusiyyətlər ya üstüörtülü şəkildə qəbul edilir, ya da kifayət qədər əsaslandırılmadan təqdim edilir. Evklid həndəsəsini möhkəm bünövrəyə qoymaq üçün onun başlanğıcına tənqidi yenidən baxılması tələb olunurdu. Sübutun ən xırda təfərrüatlarına pedantik nəzarətin müasir riyaziyyatçılara öz qənaətlərində diqqətli olmağı öyrədən "canavarlar"ın meydana çıxmasının nəticəsi olduğunu söyləmək çətin deyil. Klassik obyektlər haqqında ən zərərsiz və “özünə aydın” ifadə, məsələn, düz xəttin əks tərəflərində yerləşən nöqtələri birləşdirən əyrinin bu düz xətti şübhəsiz kəsdiyi ifadəsi müasir riyaziyyatda ciddi formal sübut tələb edir.

Müasir riyaziyyatın məhz aksiomalara sadiqliyinə görə hər hansı bir elmin necə olmasının bariz nümunəsi kimi çıxış etdiyini söyləmək paradoksal görünə bilər. Buna baxmayaraq, bu yanaşma elmi təfəkkürün ən fundamental proseslərindən birinin - natamam bilik şəraitində dəqiq məlumatın əldə edilməsinin xarakterik xüsusiyyətini nümayiş etdirir. Elmi araşdırma obyektlərin müəyyən sinfi, bəzi obyektləri digərlərindən fərqləndirməyə imkan verən xüsusiyyətlərin qəsdən yaddan çıxdığını və yalnız nəzərdən keçirilən obyektlərin ümumi xüsusiyyətlərinin qorunduğunu güman edir. Riyaziyyatı ümumi elmlər dairəsindən fərqləndirən cəhət bu proqrama bütün məqamlarda ciddi riayət olunmasıdır. Hesab edilir ki, riyazi obyektlər bu obyektlərin nəzəriyyəsində istifadə olunan aksiomalarla tam müəyyən edilir; ya da Puankareyə görə, aksiomalar istinad etdikləri obyektlərin “gizli tərifləri” kimi xidmət edir.

MÜASİR RİYAZİYYAT

Hər hansı aksiomların mövcudluğu nəzəri cəhətdən mümkün olsa da, indiyə qədər yalnız az sayda aksioma təklif edilmiş və araşdırılmışdır. Adətən, bir və ya bir neçə nəzəriyyənin inkişafı zamanı bəzi sübut sxemlərinin az və ya çox oxşar şəraitdə təkrarlanması müşahidə olunur. Ümumi sübut sxemlərində istifadə olunan xassələr aşkar edildikdən sonra, onlar aksiomlar şəklində tərtib edilir və onlardan gələn nəticələr aksiomların mücərrəd olduğu xüsusi kontekstlərlə birbaşa əlaqəsi olmayan ümumi nəzəriyyəyə çevrilir. Bu halda əldə edilən ümumi teoremlər müvafiq aksiomaları ödəyən obyektlər sistemlərinin mövcud olduğu istənilən riyazi vəziyyətə şamil edilir. Eyni sübut sxemlərinin müxtəlif riyazi situasiyalarda təkrarlanması eyni ümumi nəzəriyyənin müxtəlif konkretləşdirmələri ilə məşğul olduğumuzu göstərir. Bu o deməkdir ki, uyğun şərhdən sonra hər bir vəziyyətdə bu nəzəriyyənin aksiomları teoremlərə çevrilir. Aksiomalardan çıxarılan istənilən xassə bütün bu vəziyyətlərdə etibarlı olacaq, lakin hər bir hal üçün ayrıca sübuta ehtiyac yoxdur. Belə hallarda riyazi vəziyyətlərin eyni riyazi “struktur”a malik olduğu deyilir.

Quruluş anlayışını hər addımımızda istifadə edirik Gündəlik həyat... Əgər termometr 10°C göstərirsə və proqnozlar bürosu temperaturun 5°C yüksələcəyini proqnozlaşdırırsa, biz heç bir hesablama aparmadan 15°C temperatur gözləyirik.Əgər kitab 10-cu səhifədə açıqdırsa və bizdən 5 səhifəyə daha da baxmaq istənilirsə, ara səhifələri saymadan 15-ci səhifədə açmaqdan çəkinmirik. Hər iki halda hesab edirik ki, rəqəmlərin əlavə edilməsi onların temperatur və ya səhifə nömrələri kimi şərh olunmasından asılı olmayaraq düzgün nəticə verir. Termometrlər üçün bir hesab, səhifə nömrələri üçün başqa bir hesab öyrənmək lazım deyil (baxmayaraq ki, biz saatlarla işləyərkən xüsusi arifmetikadan istifadə edirik, 8 + 5 = 1, çünki saatlar kitabın səhifələrindən fərqli bir quruluşa malikdir). Riyaziyyatçıları maraqlandıran strukturlar, təhlili bu məqalənin növbəti iki bölməsinə həsr olunmuş nümunələrdən asanlıqla göründüyü kimi, bir qədər daha mürəkkəbdir. Onlardan biri qrup nəzəriyyəsi və strukturların və izomorfizmlərin riyazi anlayışlarından bəhs edir.

Qrup nəzəriyyəsi.

Yuxarıda göstərilən prosesi daha yaxşı başa düşmək üçün ümumi kontur, biz müasir riyaziyyatçının laboratoriyasına baxmaq və onun əsas vasitələrindən birini - qrup nəzəriyyəsini ( sm. həmçinin CƏBRƏ XÜLASƏ). Qrup obyektlər toplusudur (və ya "dəst"). G, hər hansı iki obyekti və ya elementi xəritələşdirən əməliyyat müəyyən edilir a, b-dan G, müəyyən edilmiş qaydada qəbul edilir (birinci elementdir a, ikinci - element b), üçüncü element c-dan G ciddi şəkildə müəyyən edilmiş qaydaya əsasən. Qısalıq üçün bu elementi işarə edirik a*b; ulduz (*) iki elementin kompozisiya əməliyyatını bildirir. Qrup vurma adlandıracağımız bu əməliyyat aşağıdakı şərtləri təmin etməlidir:

(1) hər hansı üç element üçün a, b, c-dan G assosiativ mülkiyyət təmin edilir: a* (b*c) = (a*b) *c;

(2) in G belə bir element var e hər hansı bir element üçün a-dan G münasibət saxlayır e*a = a*e = a; bu maddə e qrupun vahid və ya neytral elementi adlanır;

(3) hər hansı element üçün a-dan G belə bir element var aў, tərs və ya simmetrik adlanır elementə a, nə a*aў = aў* a = e.

Əgər bu xassələr aksioma kimi götürülərsə, onda onların məntiqi nəticələri (hər hansı digər aksiom və ya teoremlərdən asılı olmayaraq) birlikdə qruplar nəzəriyyəsi adlanan şeyi təşkil edir. Qruplar riyaziyyatın bütün sahələrində geniş istifadə edildiyi üçün bu nəticələri birdəfəlik çıxarmaq çox faydalı oldu. Minlərlə mümkün qrup nümunələri arasından ən sadələrindən yalnız bir neçəsini seçəcəyik.

(a) Kəsrlər səh/q, harada səh və q- i1 ixtiyari tam ədədlər (üçün q= 1 adi tam ədədlər alırıq). Kəsrlər səh/q qrup vurma ilə əlaqədar qrup yaratmaq ( səh/q) *(r/s) = (pr)/(qs). (1), (2), (3) xassələri hesabın aksiomlarından irəli gəlir. Həqiqətən, [( səh/q) *(r/s)] *(t/u) = (prt)/(qsu) = (səh/q)*[(r/s)*(t/u)]. Vahid 1 = 1/1 rəqəmidir, çünki (1/1) * ( səh/q) = (1H səh) / (1H q) = səh/q... Nəhayət, kəsrin tərsi səh/q, kəsrdir q/səh, çünki ( səh/q)*(q/səh) = (pq)/(pq) = 1.

(b) kimi hesab edin G 0, 1, 2, 3 və kimi dörd tam ədəddən ibarət çoxluq a*b- bölmənin qalan hissəsi a + b tərəfindən 4. Beləliklə tətbiq edilən əməliyyatın nəticələri cədvəldə təqdim olunur. 1 (element a*b xəttin kəsişməsində dayanır a və sütun b). Xassələrin (1) - (3) təmin edildiyini və 0 rəqəminin vahid element olduğunu yoxlamaq asandır.

(c) kimi seçək G 1, 2, 3, 4 və kimi ədədlər toplusu a*b- bölmənin qalan hissəsi ab(adi məhsul) 5 ilə. Nəticədə cədvəl alırıq. 2. (1) - (3) xassələrinin təmin olunduğunu və 1-in vahid element olduğunu yoxlamaq asandır.

(d) Dörd ədəd 1, 2, 3, 4 kimi dörd obyekt 24 şəkildə bir sıra düzülə bilər. Hər bir yer "təbii" yeri verilmiş birinə çevirən transformasiya kimi vizuallaşdırıla bilər; məsələn, 4, 1, 2, 3 yeri çevrilmə nəticəsində yaranır

S: 1 ® 4, 2 ® 1, 3 ® 2, 4 ® 3,

daha rahat formada yazmaq olar

İstənilən iki belə çevrilmə üçün S, T müəyyən edəcəyik S*T ardıcıl icra nəticəsində yaranacaq transformasiya kimi T, daha sonra S... Məsələn, əgər, onda. Bu təriflə 24 mümkün çevrilmənin hamısı bir qrup təşkil edir; onun vahid elementi, elementi isə tərsidir S, tərifdəki oxları əvəz etməklə əldə edilir Səksinə; məsələn, əgər, onda.

Bunu ilk üç nümunədə görmək asandır a*b = b*a; belə hallarda qrup və ya qrup çoxalmasının kommutativ olduğu deyilir. Digər tərəfdən, sonuncu misalda və buna görə də T*S-dən fərqlənir S*T.

(d) misalındakı qrup sözdə xüsusi haldır. simmetrik qrup, əhatə dairəsinə başqa şeylərlə yanaşı, cəbri tənliklərin həlli üsulları və atomların spektrlərində xətlərin davranışı daxildir. (b) və (c) nümunələrindəki qruplar ədədlər nəzəriyyəsində mühüm rol oynayır; misalda (b) 4 rəqəmi istənilən tam ədədlə əvəz edilə bilər n, və 0-dan 3-ə qədər olan ədədlər 0-dan 0-a qədər olan ədədlərdir n- 1 (at n= 12 yuxarıda qeyd etdiyimiz kimi, saatın siferblatlarında dayanan rəqəmlər sistemini alırıq); misalda (c) 5 rəqəmi istənilən sadə ədədlə əvəz edilə bilər R, və 1-dən 4-ə qədər olan ədədlər 1-dən 4-ə qədər olan ədədlərdir səh – 1.

Strukturlar və izomorfizm.

Əvvəlki nümunələr qrupu təşkil edən obyektlərin təbiətinin nə qədər müxtəlif ola biləcəyini göstərir. Amma əslində, hər bir halda, hər şey eyni ssenari üzrə qaynayır: obyektlər toplusunun xassələrindən biz yalnız bu çoxluğu qrupa çevirənləri nəzərdən keçiririk (burada natamam bilik nümunəsi var!). Belə hallarda deyirik ki, seçdiyimiz qrup vurmasının verdiyi qrup quruluşunu nəzərdən keçiririk.

Quruluşun başqa bir nümunəsi sözdə olandır. sifariş strukturu. Bir dəstə E nizam strukturu ilə təchiz edilmiş və ya elementlər arasında sifariş verilmişdir a è b məxsus E, işarə edəcəyimiz bəzi əlaqə verilir R (a,b). (Bu əlaqə hər hansı bir cüt element üçün məna kəsb etməlidir E, lakin ümumiyyətlə bəzi cütlər üçün yanlış, digərləri üçün doğrudur, məsələn, nisbət 7

(1) R (a,a) hamı üçün doğrudur a məxsus E;

(2) dən R (a,b) və R (b,a) bunu izləyir a = b;

(3) dən R (a,b) və R (b,c) izləyir R (a,c).

Burada çoxlu sayda müxtəlif sifarişli dəstlərdən bəzi nümunələr verilmişdir.

(a) E bütün tam ədədlərdən ibarətdir, R (a,b) əlaqədir” a az və ya bərabər b».

(b) E bütün> 1 tam ədədlərdən ibarətdir, R (a,b) əlaqədir” a bölür b və ya bərabərdir b».

Strukturun son nümunəsi olaraq metrik fəzanın strukturunu qeyd edirik; dəstdə belə bir quruluş verilir Eəgər hər bir element cütü a və b aid E, yazışmalara nömrə qoya bilərsiniz d (a,b) і 0, aşağıdakı xüsusiyyətlərə cavab verir:

(1) d (a,b) = 0 yalnız və yalnız əgər a = b;

(2) d (b,a) = d (a,b);

(3) d (a,c) Ј d (a,b) + d (b,c) hər hansı üç verilmiş element üçün a, b, c-dan E.

Burada metrik boşluqların bəzi nümunələri verilmişdir:

(a) adi “üçölçülü” fəza, burada d (a,b) - adi (və ya "Evklid") məsafə;

(b) kürənin səthi, burada d (a,b) - iki nöqtəni birləşdirən dairənin ən kiçik qövsünün uzunluğu a və b kürə üzərində;

Struktur anlayışının dəqiq tərifi olduqca çətindir. Təfərrüatlara varmadan bunu çəkiliş meydançasında deyə bilərik Eçoxluğun elementləri arasında isə müəyyən tipli struktur verilir E(və bəzən digər obyektlər, məsələn, köməkçi rol oynayan ədədlər tərəfindən) nəzərdən keçirilən növün strukturunu xarakterizə edən müəyyən sabit aksiomlar toplusunu təmin edən əlaqələr verilir. Yuxarıda üç növ strukturun aksiomlarını verdik. Təbii ki, nəzəriyyələri tam inkişaf etdirilmiş bir çox başqa struktur növləri var.

Bir çox mücərrəd anlayışlar struktur anlayışı ilə sıx bağlıdır; ən vaciblərindən yalnız birini - izomorfizm anlayışını adlandıracağıq. Əvvəlki bölmədə verilmiş (b) və (c) qruplarının nümunəsini xatırlayın. Bunu cədvəldən yoxlamaq asandır. 1 masaya. 2 uyğunlaşdırılaraq naviqasiya edilə bilər

0 ® 1, 1 ® 2, 2 ® 4, 3 ® 3.

Bu halda biz bu qrupların izomorf olduğunu deyirik. Ümumiyyətlə, iki qrup G və Gμ qrupun elementləri arasındadırsa, izomorfdur G və qrup elementləri Gў belə bir-bir yazışma qura bilərsiniz a « aö nə olarsa c = a*b, sonra cў = aў* bö uyğun maddələr üçün Gў... Qrup nəzəriyyəsindən qrup üçün etibarlı olan hər hansı bir ifadə G, qrup üçün etibarlı olaraq qalır Gў, və əksinə. Cəbri qruplar G və Gμ fərqedilməzdir.

Oxucu asanlıqla görər ki, eyni şəkildə iki izomorf sıralı çoxluq və ya iki izomorf metrik boşluq müəyyən edilə bilər. Göstərilə bilər ki, izomorfizm anlayışı istənilən növ strukturlara şamil edilir.

TƏSNİFAT

Riyaziyyatın köhnə və yeni təsnifatları.

Struktur anlayışı və onunla əlaqəli digər anlayışlar müasir riyaziyyatda həm sırf “texniki”, həm də fəlsəfi və metodoloji baxımdan mərkəzi yer tutmuşdur. Əsas struktur növlərinin ümumi teoremləri riyazi “texnikanın” son dərəcə güclü alətləridir. Riyaziyyatçı hər dəfə öyrəndiyi obyektlərin müəyyən tip strukturun aksiomalarını təmin etdiyini göstərə bilsə, bununla da sübut edir ki, bu tip struktur nəzəriyyəsinin bütün teoremləri onun öyrəndiyi konkret obyektlərə tətbiq olunur (bu ümumi teoremlər olmadan, o, çox güman ki, qaçırılanlar onların xüsusi variantları qarşısında qalacaq və ya əsaslandırmalarını lazımsız fərziyyələrlə yükləmək məcburiyyətində qalacaqlar). Eynilə, əgər iki strukturun izomorf olduğu sübut olunarsa, onda teoremlərin sayı dərhal ikiqat artır: strukturlardan biri üçün sübut edilmiş hər bir teorem dərhal digəri üçün müvafiq teoremi verir. Buna görə də təəccüblü deyil ki, çox mürəkkəb və çətin nəzəriyyələr var, məsələn, ədədlər nəzəriyyəsində “sinfi sahə nəzəriyyəsi” var ki, onların əsas məqsədi strukturların izomorfizmini sübut etməkdir.

Fəlsəfi nöqteyi-nəzərdən strukturların və izomorfizmlərin geniş tətbiqi müasir riyaziyyatın əsas xüsusiyyətini - riyazi “obyektlərin” “təbiətinin” əslində əhəmiyyət kəsb etmədiyini, yalnız obyektlər arasındakı əlaqələrin əhəmiyyətli olduğunu (bir növ biliyin natamamlıq prinsipi).

Nəhayət, struktur anlayışının riyaziyyatın sahələrini yeni şəkildə təsnifləşdirməyə imkan verdiyini qeyd etməmək olmaz. 19-cu əsrin ortalarına qədər. tədqiqatın mövzusuna görə fərqlənirdilər. Arifmetika (və ya ədədlər nəzəriyyəsi) tam ədədlərlə, həndəsə ilə düz xətlər, bucaqlar, çoxbucaqlılar, dairələr, sahələr və s. Cəbr demək olar ki, yalnız ədədi tənliklərin və ya tənliklər sistemlərinin həlli üsulları ilə məşğul olurdu, analitik həndəsə həndəsi məsələlərin ekvivalent cəbri məsələlərə çevrilməsi üçün üsullar işləyib hazırladı. Riyaziyyatın "riyazi analiz" adlanan digər mühüm sahəsinin maraq dairəsinə əsasən diferensial və inteqral hesablamalar və onların həndəsə, cəbr və hətta ədədlər nəzəriyyəsinə müxtəlif tətbiqləri daxildir. Bu tətbiqlərin sayı artdı və onların əhəmiyyəti də artdı ki, bu da riyazi analizin alt bölmələrə bölünməsinə səbəb oldu: funksiyalar nəzəriyyəsi, diferensial tənliklər (adi və qismən törəmələr), diferensial həndəsə, variasiyaların hesablanması və s.

Bir çox müasir riyaziyyatçılar üçün bu yanaşma ilk təbiətşünasların heyvanların təsnifatının tarixinə bənzəyir: bir vaxtlar həm dəniz tısbağası, həm də tuna balıq hesab olunurdu, çünki onlar suda yaşayırdılar və oxşar xüsusiyyətlərə malikdirlər. Müasir yanaşma bizə təkcə səthdə olanı görməyi deyil, həm də daha dərindən baxmağı və riyazi obyektlərin aldadıcı görünüşünün arxasındakı fundamental strukturları tanımağa çalışmağı öyrətdi. Bu baxımdan ən mühüm struktur növlərinin öyrənilməsi vacibdir. Çətin ki, bizim ixtiyarımızda bu növlərin tam və qəti siyahısı var; onların bəziləri son 20 ildə kəşf edilib və gələcəkdə yeni kəşflər gözləmək üçün bütün əsaslar var. Bununla belə, biz artıq bir çox əsas "mücərrəd" struktur növləri haqqında anlayışa sahibik. (Riyaziyyatın "klassik" obyektləri ilə müqayisədə onlar "mücərrəddirlər, baxmayaraq ki, onları "konkret" adlandırmaq çətindir; söhbət daha çox abstraksiya dərəcəsindən gedir).

Məlum strukturları tərkib əlaqələri və ya mürəkkəbliyinə görə təsnif etmək olar. Bir tərəfdən, "cəbri" strukturların geniş bloku var, onun xüsusi bir halı, məsələn, qrup quruluşu; Digər cəbri strukturlar arasında üzüklər və sahələr nəzərdə tutulur ( sm. həmçinin CƏBRƏ XÜLASƏ). Cəbr strukturlarının öyrənilməsi ilə məşğul olan riyaziyyat sahəsi adi və ya klassik cəbrdən fərqli olaraq “müasir cəbr” və ya “mücərrəd cəbr” adlanır. Evklid həndəsəsinin, qeyri-Evklid həndəsəsinin və analitik həndəsənin əhəmiyyətli bir hissəsi də yeni cəbrin bir hissəsi oldu.

Eyni ümumilik səviyyəsində daha iki struktur bloku var. Onlardan biri ümumi topologiya adlanır, struktur növlərinin nəzəriyyələrini əhatə edir, onların xüsusi bir halı metrik fəzanın strukturudur ( sm... TOPOLOGİYA; ABSTRAKT BOŞLAR). Üçüncü blok nizam strukturları və onların uzantıları nəzəriyyələrindən ibarətdir. Strukturun "genişlənməsi" mövcud olanlara yeni aksiomların əlavə edilməsindən ibarətdir. Məsələn, əgər qrup aksiomalarına dördüncü aksioma kimi kommutativlik xassəsini əlavə edirik a*b = b*a, onda biz kommutativ (və ya abelian) qrupun strukturunu alırıq.

Bu üç blokdan sonuncu ikisi son vaxtlara qədər nisbətən sabit vəziyyətdə idi və "müasir cəbr" bloku sürətlə, bəzən gözlənilməz istiqamətlərdə böyüdü (məsələn, "homoloji cəbr" adlı bütöv bir filial inkişaf etdi). Sözdə xaricində. Quruluşların "saf" növlərinin başqa bir səviyyəsi var - "qarışıq" strukturlar, məsələn, cəbri və topoloji, onları birləşdirən yeni aksiomlarla birlikdə. Bir çox belə birləşmələr tədqiq edilmişdir, onların əksəriyyəti iki geniş bloka - "topoloji cəbr" və "cəbr topologiyasına" düşür.

Birlikdə götürdükdə, bu bloklar elmin çox möhkəm "mücərrəd" sahəsini təşkil edir. Bir çox riyaziyyatçılar klassik nəzəriyyələri daha yaxşı başa düşmək və çətin problemləri həll etmək üçün yeni vasitələrlə ümid edirlər. Həqiqətən də, müvafiq abstraksiya və ümumiləşdirmə səviyyəsi ilə qədimlərin vəzifələri yeni işıqda görünə bilər ki, bu da onların həllini tapmağa imkan verəcəkdir. Klassik materialın böyük parçaları yeni riyaziyyatın məngənəsinə düşdü və çevrildi və ya digər nəzəriyyələrlə birləşdirildi. Müasir metodların o qədər də dərindən nüfuz etmədiyi geniş sahələr qalır. Nümunələrə nəzəriyyə daxildir diferensial tənliklər və ədədlər nəzəriyyəsinin çox hissəsi. Çox güman ki, yeni tip strukturlar aşkar edildikdən və hərtərəfli öyrənildikdən sonra bu sahələrdə mühüm irəliləyiş əldə olunacaq.

FƏLSƏFİ ÇƏRƏKLƏR

Hətta qədim yunanlar da aydın başa düşürdülər ki, riyazi nəzəriyyə ziddiyyətlərdən azad olmalıdır. Bu o deməkdir ki, aksiomalardan məntiqi nəticə çıxarmaq mümkün deyil R və onun inkarı belə deyil P... Bununla belə, riyazi obyektlərin real aləmdə uyğunluqları olduğuna, aksiomaların isə təbiət qanunlarının “ideallaşdırılması” olduğuna inanıldığından, riyaziyyatın ardıcıllığına heç kim şübhə etmirdi. Klassik riyaziyyatdan müasir riyaziyyata keçiddə ardıcıllıq problemi başqa məna kəsb etdi. İstənilən riyazi nəzəriyyənin aksiomalarını seçmək azadlığı ardıcıllıq şərti ilə bilərəkdən məhdudlaşdırılmalıdır, lakin bu şərtin yerinə yetiriləcəyinə əmin ola bilərikmi?

Artıq çoxluq anlayışını qeyd etdik. Bu anlayış həmişə riyaziyyatda və məntiqdə az-çox açıq şəkildə istifadə olunub. 19-cu əsrin ikinci yarısında. çoxluq anlayışı ilə məşğul olmaq üçün elementar qaydalar qismən sistemləşdirildi, əlavə olaraq, sözdə məzmunu təşkil edən bəzi mühüm nəticələr əldə edildi. çoxluq nəzəriyyəsi ( sm. həmçinin SET NƏZƏRİYYƏSİ), sanki bütün digər riyazi nəzəriyyələr üçün substrata çevrilmişdir. Antik dövrdən 19-cu əsrə qədər. sonsuz sayda qorxular var idi, məsələn, Elea Zenonunun (e.ə. V əsr) məşhur paradokslarında öz əksini tapmışdır. Bu qorxular qismən metafizik xarakter daşıyırdı və qismən də kəmiyyətlərin ölçülməsi anlayışı ilə bağlı çətinliklər (məsələn, uzunluq və ya zaman) ilə əlaqədar idi. Bu çətinlikləri yalnız 19-cu əsrdən sonra aradan qaldırmaq mümkün olmuşdur. riyazi analizin əsas anlayışları ciddi şəkildə müəyyən edilmişdir. 1895-ci ilə qədər bütün qorxular aradan qalxdı və riyaziyyat çoxluqlar nəzəriyyəsinin sarsılmaz təməlinə söykənirdi. Lakin sonrakı onillikdə çoxluqlar nəzəriyyəsinin (və riyaziyyatın bütün qalan hissələrinin) xas uyğunsuzluğunu göstərən yeni arqumentlər ortaya çıxdı.

Yeni paradokslar çox sadə idi. Bunlardan birincisi, Russell paradoksu, bərbər paradoksu kimi tanınan sadə bir versiyada görünə bilər. Müəyyən bir şəhərdə bərbər özünü təraş etməyən bütün sakinləri təraş edir. Bərbərin özü kim qırxır? Bərbər özünü qırxırsa, o, təkcə özünü qırxmayan sakinləri yox, özünü qırxdıran bir sakini də qırxır; əgər özü təraş etməzsə, o, özünü qırxmayan şəhər sakinlərinin hamısını qırxmaz. “Bütün çoxluqlar çoxluğu” anlayışı nəzərə alındıqda bu tip bir paradoks yaranır. Bu riyazi obyekt çox təbii görünsə də, onun haqqında düşünmək tez bir zamanda ziddiyyətlərə gətirib çıxarır.

Berrinin paradoksu daha açıqdır. On yeddi sözdən çox olmayan bütün rus ifadələrinin dəstini nəzərdən keçirin; rus dilində sözlərin sayı məhduddur, ona görə də belə ifadələrin sayı da məhduddur. Gəlin onların arasında birmənalı şəkildə tam ədəd təyin edənləri seçək, məsələn: "Ən böyük tək ədəd ondan kiçik". Belə ifadələrin sayı da sonludur; deməli, onların təyin etdikləri tam ədədlər çoxluğu sonludur. Bu ədədlərin sonlu çoxluğunu ilə işarə edirik D... Hesabın aksiomlarından belə çıxır ki, aid olmayan tam ədədlər var D, və bu ədədlər arasında ən kiçik rəqəm var n... Bu nömrə n birmənalı şəkildə ifadə ilə müəyyən edilir: "On yeddi rus sözündən çox olmayan bir ifadə ilə müəyyən edilə bilməyən ən kiçik tam ədəd". Amma bu ifadə düz on yeddi sözdən ibarətdir. Buna görə də rəqəmi müəyyənləşdirir n hansı aid olmalıdır D və biz paradoksal bir ziddiyyətə gəlirik.

İntuisiyaçılar və formalistlər.

Çoxluq nəzəriyyəsinin paradokslarının yaratdığı şok müxtəlif reaksiyalar yaratdı. Bəzi riyaziyyatçılar çox qətiyyətli idilər və riyaziyyatın lap əvvəldən yanlış istiqamətdə inkişaf etdiyi və tamam başqa təməl üzərində qurulmalı olduğu fikrini bildirdilər. Bu cür "intuisionistlərin" (özlərini belə adlandırmağa başladığı) baxışlarını heç bir əminliklə təsvir etmək mümkün deyil, çünki onlar öz fikirlərini sırf məntiqi sxemə endirməkdən imtina edirdilər. İntuisionistlərin nöqteyi-nəzərindən məntiqi prosesləri intuitiv olaraq təmsil olunmayan obyektlərə tətbiq etmək düzgün deyil. Yeganə intuitiv şəkildə aydın olan obyektlər 1, 2, 3, ... natural ədədləri və dəqiq müəyyən edilmiş qaydalara uyğun olaraq "tikilmiş" natural ədədlərin sonlu dəstləridir. Lakin belə obyektlərə belə, intuisiyaçılar klassik məntiqin bütün deduksiyalarının tətbiqinə imkan vermirdilər. Məsələn, bunu heç bir açıqlamaya görə etiraf etmədilər R da doğrudur R ya yox R... Belə məhdud vasitələrlə onlar “paradokslardan” asanlıqla qaçırdılar, lakin eyni zamanda təkcə bütün müasir riyaziyyatı deyil, həm də klassik riyaziyyatın nəticələrinin əhəmiyyətli bir hissəsini kənara atdılar və hələ də qalanlar üçün tapmaq lazım idi. yeni, daha mürəkkəb sübutlar.

Müasir riyaziyyatçıların böyük əksəriyyəti intuisiyaçıların arqumentləri ilə razılaşmadı. Qeyri-intuisiyaya malik riyaziyyatçılar paradokslarda istifadə olunan arqumentlərin çoxluqlar nəzəriyyəsi ilə adi riyazi işdə istifadə olunanlardan əhəmiyyətli dərəcədə fərqləndiyini fərq etmişlər və buna görə də bu cür arqumentlər mövcud riyazi nəzəriyyələrə təhlükə yaratmadan qeyri-qanuni hesab edilməlidir. Digər bir müşahidə ondan ibarət idi ki, “paradokslar” meydana çıxmazdan əvvəl mövcud olmuş “sadəlövh” çoxluqlar nəzəriyyəsində “çoxluq”, “xassəli”, “münasibət” terminlərinin mənası şübhə altına alınmırdı - klassik həndəsədə olduğu kimi, “intuitiv” adi həndəsi anlayışların təbiəti. Nəticə etibarı ilə, həndəsədə olduğu kimi hərəkət etmək olar, yəni "intuisiyaya" müraciət etmək üçün bütün cəhdlərdən imtina etmək və çoxluqlar nəzəriyyəsinin başlanğıc nöqtəsi kimi dəqiq tərtib edilmiş aksiomlar sistemini götürmək olar. Bununla belə, “mülk” və ya “münasibət” kimi sözlərin adi mənadan necə məhrum ola biləcəyi bəlli deyil; lakin Berri paradoksu kimi mülahizələri istisna etmək istəyiriksə, bunu etmək lazımdır. Metod aksioma və ya teoremləri tərtib edərkən adi dildən istifadə etməkdən çəkinməkdən ibarətdir; riyaziyyatda “xassələr” və ya “münasibətlər” kimi yalnız sərt qaydaların açıq sisteminə uyğun qurulmuş cümlələrə icazə verilir və aksiomların tərtibinə daxil edilir. Bu proses “formallaşma” adlanır. riyazi dil(adi dilin qeyri-müəyyənliyindən yaranan anlaşılmazlıqların qarşısını almaq üçün daha bir addım atmaq və rəsmiləşdirilmiş cümlələrdə sözlərin özünü xüsusi simvollarla əvəz etmək tövsiyə olunur, məsələn, "və" keçidini & simvolu ilə əvəz etmək, b simvolu ilə "və ya" əlaqəsi, $ simvolu ilə "mövcuddur" və s.). İntuisionistlərin təklif etdiyi üsulları rədd edən riyaziyyatçılara “formalistlər” deyilirdi.

Ancaq orijinal suala heç vaxt cavab verilmədi. “Aksiomatik çoxluq nəzəriyyəsi” ziddiyyətlərdən azaddırmı? 1920-ci illərdə D.Hilbert (1862-1943) və onun məktəbi tərəfindən “rəsmiləşdirilmiş” nəzəriyyələrin ardıcıllığını sübut etmək üçün yeni cəhdlər edilmiş və “metamatematika” adlandırılmışdır. Əsasən, metariyaziyyat "tətbiqi riyaziyyat" bölməsidir, burada riyazi əsaslandırmanın tətbiq olunduğu obyektlər rəsmiləşdirilmiş nəzəriyyənin cümlələri və onların sübutlar içərisində yerləşdiyi yerdir. Bu cümlələr yalnız müəyyən edilmiş qaydalara uyğun olaraq, bu simvolların mümkün "mənası"na (əgər varsa) istinad edilmədən hazırlanmış simvolların maddi birləşmələri kimi qəbul edilməlidir. Yaxşı bir bənzətmə şahmat oyunudur: simvollar fişlərə, cümlələr lövhədə müxtəlif mövqelərə, nəticələr isə fiqurların hərəkət qaydalarına uyğundur. Formallaşdırılmış nəzəriyyənin ardıcıllığını müəyyən etmək üçün bu nəzəriyyədə heç bir sübutun 0 # 0 ifadəsi ilə bitmədiyini göstərmək kifayətdir. Bununla belə, riyazi arqumentlərin ardıcıllığının “metamatematik” sübutunda riyazi arqumentlərin istifadəsinə etiraz etmək olar. nəzəriyyə; riyaziyyat ziddiyyətli olsaydı, o zaman riyazi dəlillər bütün gücünü itirər və biz özümüzü pis bir dairədə tapardıq. Bu etirazlara cavab vermək üçün Hilbert metariyaziyyatda intuisiyaçıların məqbul hesab etdiyi çox məhdud riyazi mülahizələrdən istifadə etdiyini etiraf etdi. Lakin tezliklə K. Gödel (1931) göstərdi ki, arifmetikanın tutarlılığı, həqiqətən də, ardıcıldırsa, bu qədər məhdud vasitələrlə sübut edilə bilməz (bu məqalənin əhatə dairəsi bu əlamətdar nəticənin əldə edildiyi dahiyanə üsulu təqdim etməyə imkan vermir, və metariyaziyyatın sonrakı tarixi).

Mövcud problemli vəziyyəti formalist nöqteyi-nəzərdən ümumiləşdirsək, etiraf etməliyik ki, bu, hələ başa çatmaqdan çox uzaqdır. Çoxluq anlayışının istifadəsi məlum paradoksların qarşısını almaq üçün xüsusi olaraq təqdim edilən qeyd-şərtlərlə məhdudlaşırdı və aksiomatlaşdırılmış çoxluq nəzəriyyəsində yeni paradoksların yaranmayacağına zəmanət yoxdur. Buna baxmayaraq, aksiomatik çoxluq nəzəriyyəsinin məhdudiyyətləri yeni həyat qabiliyyətli nəzəriyyələrin doğulmasına mane olmadı.

RİYAZİYYAT VƏ REAL DÜNYA

Riyaziyyatın müstəqilliyi iddialarına baxmayaraq, heç kim riyaziyyatın və fiziki dünyanın bir-biri ilə əlaqəli olduğunu inkar etməyəcək. Təbii ki, klassik fizikanın problemlərinin həllinə riyazi yanaşma qüvvədə qalır. Bu da bir həqiqətdir ki, riyaziyyatın çox mühüm sahəsində, yəni diferensial tənliklər, adi və qismən törəmələr nəzəriyyəsində fizika və riyaziyyatın qarşılıqlı zənginləşməsi prosesi kifayət qədər məhsuldardır.

Riyaziyyat mikro dünyanın hadisələrini şərh etmək üçün faydalıdır. Bununla belə, riyaziyyatın yeni “tətbiqləri” klassiklərdən xeyli fərqlənir. Fizikanın ən mühüm vasitələrindən biri əvvəllər əsasən qumar və sığorta nəzəriyyəsində istifadə edilən ehtimal nəzəriyyəsi olmuşdur. Fiziklərin "atom halları" və ya "keçidlər" ilə əlaqələndirdiyi riyazi obyektlər təbiətcə çox mücərrəddir və kvant mexanikasının yaranmasından çox əvvəl riyaziyyatçılar tərəfindən təqdim edilmiş və tədqiq edilmişdir. Onu da əlavə edək ki, ilk uğurlardan sonra ciddi çətinliklər yaranıb. Bu, fiziklərin riyazi fikirləri daha incə aspektlərə tətbiq etməyə çalışdıqları bir vaxtda baş verdi. kvant nəzəriyyəsi; buna baxmayaraq, bir çox fiziklər hələ də yeni riyazi nəzəriyyələrə ümidlə baxır və onların yeni problemlərin həllində onlara kömək edəcəyinə inanırlar.

Riyaziyyat - Elm yoxsa İncəsənət?

Ehtimal nəzəriyyəsini və ya riyazi məntiqi “saf” riyaziyyata daxil etsək belə, məlum olur ki, hazırda digər elmlər məlum riyazi nəticələrin 50%-dən azını istifadə edir. Qalan yarım haqqında nə düşünməliyik? Başqa sözlə, riyaziyyatın fiziki məsələlərin həlli ilə bağlı olmayan o sahələrinin arxasında hansı motivlər dayanır?

Biz artıq bu növ teoremin tipik nümayəndəsi kimi ədədin irrasionallığını qeyd etdik. Başqa bir misal J.-L. Laqranjın (1736-1813) sübut etdiyi teoremdir. Onu "vacib" və ya "gözəl" deməsin, çətin ki, riyaziyyatçı tapılmaz. Laqranj teoremi bildirir ki, birdən böyük və ya ona bərabər istənilən tam ədəd dörd ədəddən çox olmayan kvadratların cəmi kimi təqdim edilə bilər; məsələn, 23 = 3 2 + 3 2 + 2 2 + 1 2. Mövcud vəziyyəti nəzərə alsaq, bu nəticənin bəzi eksperimental problemin həllində faydalı ola biləcəyi ağlasığmazdır. Düzdür, fiziklər bu gün tam ədədlərlə keçmişə nisbətən daha tez-tez məşğul olurlar, lakin onların işlədiyi tam ədədlər həmişə məhduddur (nadir hallarda bir neçə yüzdən çox olur); buna görə də, Laqranj teoremi kimi bir teorem yalnız bəzi sərhədləri keçməyən tam ədədlərə tətbiq edildikdə "faydalı" ola bilər. Lakin biz Laqranj teoreminin tərtibini məhdudlaşdıran kimi, o, riyaziyyatçı üçün dərhal maraqlı olmağı dayandırır, çünki bu teoremin bütün cəlbedici qüvvəsi onun bütün tam ədədlərə tətbiq olunmasındadır. (Kompüterlər tərəfindən çox böyük ədədlər üçün yoxlanıla bilən tam ədədlər haqqında çoxlu ifadələr var; lakin heç bir ümumi sübut tapılmadığından, onlar hipotetik olaraq qalır və peşəkar riyaziyyatçılar üçün maraqlı deyil.)

Astronomiya və ya biologiya olsun, hər hansı bir sahədə çalışan elm adamları üçün dərhal tətbiq olunmayan mövzulara diqqət yetirmək qeyri-adi deyil. Bununla belə, eksperimental nəticə dəqiqləşdirilə və təkmilləşdirilə bilsə də, riyazi sübut həmişə yekundur. Məhz buna görə də riyaziyyata və ya heç olmasa onun “reallıqla” heç bir əlaqəsi olmayan hissəsinə sənət kimi baxmaq istəyinə qarşı durmaq çətindir. Riyazi məsələlər kənardan qoyulmur və müasir nöqteyi-nəzərdən qəbul etsək, material seçimində tam sərbəst oluruq. Bəzi riyazi işləri qiymətləndirərkən riyaziyyatçıların heç bir “obyektiv” meyarları yoxdur və onlar öz “zövqlərinə” güvənməli olurlar. Zövqlər zamana, ölkəyə, adət-ənənələrə və fərdlərə görə çox dəyişir. Müasir riyaziyyatda dəb və “məktəblər” var. Hazırda üç belə “məktəb” var ki, onları rahatlıq üçün “klassisizm”, “modernizm” və “abstraksionizm” adlandıracağıq. Aralarındakı fərqləri daha yaxşı başa düşmək üçün riyaziyyatçıların teoremi və ya teoremlər qrupunu qiymətləndirərkən istifadə etdikləri müxtəlif meyarları təhlil edək.

(1) Ümumi rəyə görə, "gözəl" riyazi nəticə qeyri-trivial olmalıdır, yəni. aksiomların və ya əvvəllər sübut edilmiş teoremlərin aşkar nəticəsi olmamalıdır; sübut bəzi istifadə etməlidir yeni fikir ya da köhnə ideyalar dahiyanə şəkildə tətbiq edilir. Başqa sözlə desək, riyaziyyatçı üçün nəticənin özü deyil, onu əldə edərkən qarşılaşdığı çətinlikləri aradan qaldırmaq prosesi önəmlidir.

(2) İstənilən riyazi problemin öz tarixi var, belə desək, “şəcərə” hər hansı elmin tarixinin inkişaf etdiyi eyni ümumi sxem üzrə gedir: ilk uğurlardan sonra sualın cavabına qədər müəyyən vaxt keçə bilər. poza tapılır. Həll yolu əldə edildikdə hekayə bununla bitmir, çünki məlum genişlənmə və ümumiləşdirmə prosesləri başlayır. Məsələn, yuxarıda qeyd olunan Laqranj teoremi istənilən tam ədədin kubların cəmi kimi təqdim edilməsi məsələsinə gətirib çıxarır, dördüncü, beşinci dərəcə və s. Hələ son həllini tapmamış “Müharibə problemi” belə yaranır. Bundan əlavə, qismət olsa, həll etdiyimiz problem bir və ya bir neçə fundamental strukturla bağlı olacaq və bu da öz növbəsində bu strukturlarla bağlı yeni problemlərin yaranmasına səbəb olacaq. Orijinal nəzəriyyə nəhayət "ölsə də" çoxlu canlı tumurcuqlar buraxmağa meyllidir. Müasir riyaziyyatçılar problemlərin o qədər böyük səpələnməsi ilə üzləşirlər ki, hətta eksperimental elmlə bütün əlaqə kəsilsə belə, onların həlli daha bir neçə əsr çəkəcək.

(3) Hər bir riyaziyyatçı razılaşacaq ki, onun qarşısında yeni bir problem yarandıqda, onu istənilən vasitə ilə həll etmək onun vəzifəsidir. Problem klassik riyazi obyektlərə aid olduqda (klassiklər nadir hallarda digər növ obyektlərlə məşğul olurlar), klassiklər onu yalnız klassik vasitələrdən istifadə edərək həll etməyə çalışırlar, digər riyaziyyatçılar isə tapşırıqla bağlı ümumi teoremlərdən istifadə etmək üçün daha çox “mücərrəd” strukturlar təqdim edirlər. Bu yanaşma fərqi yeni deyil. 19-cu əsrdən bəri. riyaziyyatçılar problemin sırf güc yolu ilə həllini tapmağa çalışan “taktiklərə” və düşməni kiçik qüvvələrlə darmadağın etməyə imkan verən dairəvi manevrlərə meylli “strateqlərə” bölünürlər.

(4) Teorem "gözəlliyinin" mühüm elementi onun sadəliyidir. Təbii ki, sadəlik axtarışı bütün elmi düşüncələrə xasdır. Ancaq təcrübəçilər problem həll olunsaydı, "çirkin həllər" ilə barışmağa hazırdırlar. Eynilə, riyaziyyatda klassiklər və abstraksionistlər “patoloji” nəticələrin ortaya çıxmasından çox narahat deyillər. Digər tərəfdən, modernistlər nəzəriyyənin "patologiyalarının" meydana çıxmasını fundamental anlayışların qeyri-kamilliyinin əlaməti kimi görməyə qədər irəliləyirlər.

Riyaziyyat ensiklopediyası

Riyaziyyat ensiklopediyası- Riyaziyyat mövzularına həsr olunmuş beş cildlik sovet ensiklopedik nəşri. -1985-ci ildə "Sovet Ensiklopediyası" nəşriyyatı tərəfindən buraxılmışdır. Baş redaktor: Akademik İ. M. Vinoqradov.

Bu, riyaziyyatın bütün əsas sahələrini əhatə edən fundamental təsvirli nəşrdir. Kitabda mövzu ilə bağlı geniş materiallar, məşhur riyaziyyatçıların tərcümeyi-halı, çertyojlar, qrafiklər, diaqramlar və diaqramlar yer alıb.

Ümumi həcmi: təxminən 3000 səhifə. Məqalələrin həcminə görə bölgüsü:

1-ci cild: Abacus - Huygens prinsipi, 576 s.
2-ci cild: D'Alembert operatoru - Kooperativ oyun, 552 səh.
Cild 3: Koordinatlar - Monomial, 592 s.
Cild 4: Teorem Gözü - Kompleks Funksiya, 608 səh.
5-ci cild: Təsadüfi dəyişən - Cell, 623 s.
5-ci cildə əlavə: mövzu indeksi, qeyd olunan yazı xətalarının siyahısı.

Bağlantılar

Ensiklopediyanı elektron formada yükləyə biləcəyiniz “Riyazi tənliklər dünyası” portalında riyaziyyat üzrə ümumi və xüsusi məlumat kitabçaları və ensiklopediyalar.

Kateqoriyalar:

Kitablar əlifba ilə
Riyaziyyat ədəbiyyatı
Ensiklopediyalar
"Sovet Ensiklopediyası" nəşriyyatının kitabları
SSRİ ensiklopediyaları

Wikimedia Fondu. 2010.

Riyazi kimya
Kvant mexanikasının riyazi əsasları

Digər lüğətlərdə "Riyaziyyat Ensiklopediyası" nın nə olduğuna baxın:

Riyazi məntiq- (nəzəri məntiq, simvolik məntiq) riyaziyyatın əsaslarının sübutlarını və suallarını öyrənən riyaziyyat sahəsi. “Müasir riyazi məntiqin mövzusu çoxşaxəlidir”. P.S.Poretskinin tərifinə görə, “riyazi ... ... Vikipediya

Ensiklopediya- (Novolat ensiklopediyası (XVI əsrdən əvvəl deyil) digər yunan dilindən.

ENSİKLOPEDİYA- (yunan dilindən. enkyklios payeia biliklərin bütün spektrində təlim), elmi. və ya elmi. taksonomiyanı ehtiva edən məşhur istinad nəşri. bilik məcmuəsi. E.-də material əlifba və ya sistematik şəkildə düzülür. prinsipi (bilik sahələri üzrə). ...... Təbiət elmi. ensiklopedik lüğət

RİYASİ MƏNTİQ- ikinciyə gələn müasir məntiqin adlarından biri. mərtəbə. 19 erkən. 20-ci əsr ənənəvi məntiqi əvəz etmək. Simvolik məntiq termini məntiq elminin inkişafında müasir mərhələnin başqa adı kimi də istifadə olunur. Tərif…… Fəlsəfi Ensiklopediya

RİYASİ SONSUZLUK- ümumi ad decomp. riyaziyyatda sonsuzluq ideyasının həyata keçirilməsi. Baxmayaraq ki, M. anlayışının mənaları arasında b. və sonsuzluq termininin istifadə edildiyi digər mənalarda heç bir sərt sərhəd yoxdur (çünki bütün bu anlayışlar son nəticədə çox ... ... Fəlsəfi Ensiklopediya

RİYASİ İNDUKSİYA- tam riyazi induksiya (riyaziyyatda buna çox vaxt tam induksiya deyilir; bu halda bu anlayış qeyri-riyazi formal məntiqdə nəzərdən keçirilən tam induksiya anlayışından fərqləndirilməlidir), - ..-də ümumi cümlələrin sübutu üsulu. ... ... Fəlsəfi Ensiklopediya

RİYASİ FƏRZİYYƏ- tədqiq olunan hadisələr sahəsinin qanununu ifadə edən tənliyin formasında, növündə, təbiətində onun özünəməxsus qanunu kimi onu yeni, hələ də öyrənilməmiş sahəyə genişləndirmək məqsədi ilə ehtimal edilən dəyişiklik. M. müasir dövrdə geniş istifadə olunur. nəzəri ...... Fəlsəfi Ensiklopediya

SİYASİ İQTİSADİYYATDA RİYAZİYYAT MƏKTƏBİ- İngilis dili. siyasi iqtisad üzrə riyazi məktəb; alman Politischen Okonomie-də riyaziyyat Schule. 19-cu əsrin ikinci yarısında yaranan sulu, təsərrüfat istiqaməti, roqo nümayəndələri (L. Valras, V. Pareto, O. Jevons və s.) verdi ... ... Sosiologiya ensiklopediyası

SOSİOLOGİYADA RİYAZİYYAT MƏKTƏBİ- İngilis dili. sosiologiya üzrə riyaziyyat məktəbi; alman Mathematische Schule in der Soziologie. 20-ci əsrin birinci yarısında yaranan sosiologiyada cərəyan, onun qurucuları (A.Zipf, E.Dodd və s.) sosioloqun, nəzəriyyələrin ... ... səviyyəyə çatdığına inanırdılar. Sosiologiya ensiklopediyası

Bina və tikililərin riyazi modeli- Bina və tikililərin riyazi (kompüter) modeli - layihələndirmədə, tikintidə və ... Tikinti materiallarının terminləri, tərifləri və izahları ensiklopediyası

Kitablar

Riyaziyyat Ensiklopediyası (5 kitab dəsti). Riyaziyyat Ensiklopediyası riyaziyyatın bütün sahələri üçün əlverişli istinad kitabıdır. Ensiklopediyanın əsasını riyaziyyatın ən mühüm sahələrinə aid məqalələr təşkil edir. Yerləşdirmə prinsipi ...

Riyaziyyat Ensiklopediyası riyaziyyatın bütün sahələrinə dair məlumat kitabçasıdır. Ensiklopediya riyaziyyatın ən mühüm sahələrinə dair icmal məqalələrə əsaslanır. Bu tip məqalələr üçün əsas tələb, təqdimatın maksimum əlçatanlığı ilə nəzəriyyənin mövcud vəziyyətinin nəzərdən keçirilməsinin mümkün tamlığıdır; bu məqalələr ümumiyyətlə böyük riyaziyyatçılar, aspirantlar və riyaziyyatın əlaqəli sahələrinin mütəxəssisləri, bəzi hallarda isə riyazi metodları öz işlərində tətbiq edən digər bilik sahələrinin mütəxəssisləri, mühəndislər və riyaziyyat müəllimləri üçün açıqdır. Riyaziyyatın fərdi spesifik problemləri və metodları üzrə əlavə, orta həcmli məqalələr təqdim olunur; bu məqalələr daha dar oxucu dairəsi üçün nəzərdə tutulub, ona görə də onlarda təqdimat daha az əlçatan ola bilər. Nəhayət, məqalələrin daha bir növü var - sürətli istinad tərifləri. Ensiklopediyanın sonuncu cildinin sonunda təkcə bütün məqalələrin başlıqlarını deyil, həm də ilk iki növün məqalələrində tərifləri veriləcək bir çox anlayışları özündə əks etdirən mövzu indeksi yerləşdiriləcək. , eləcə də məqalələrdə qeyd olunan ən mühüm nəticələr. Ensiklopediyanın əksər məqalələri hər bir başlıq üçün seriya nömrələri ilə istinadlar siyahısı ilə müşayiət olunur ki, bu da məqalələrin mətnlərində sitat gətirməyə imkan verir. Məqalələrin sonunda (bir qayda olaraq) müəllif və ya mənbə, əgər məqalə əvvəllər dərc olunubsa (əsasən bunlar Böyük Sovet Ensiklopediyasının məqalələridir) göstərilir. Məqalələrdə qeyd olunan xarici (qədim istisna olmaqla) alimlərin adları latın orfoqrafiyası ilə (biblioqrafiyaya istinad yoxdursa) müşayiət olunur.

Riyaziyyat Ensiklopediyasını yükləyin və oxuyun, 3-cü cild, Vinogradov I.M., 1982

Yükləyin və oxuyun Riyaziyyat Ensiklopediyası, 2-ci cild, Vinogradov I.M., 1979

Yükləyin və oxuyun Riyaziyyat Ensiklopediyası, 1-ci cild, Vinogradov I.M., 1977

Cəbr əvvəlcə tənliklərin həlli ilə məşğul olan riyaziyyatın bir qolu idi. Həndəsədən fərqli olaraq, cəbrin aksiomatik konstruksiyası 19-cu əsrin ortalarına qədər, cəbrin mövzusu və təbiəti haqqında prinsipcə yeni baxış meydana çıxana qədər mövcud olmamışdır. Tədqiqatlar getdikcə daha çox sözdə cəbri strukturların öyrənilməsinə yönəlməyə başladı. Bunun iki üstünlüyü var idi. Bir tərəfdən ayrı-ayrı teoremlərin etibarlı olduğu sahələr aydınlaşdırıldı, digər tərəfdən eyni sübutlardan tamamilə fərqli sahələrdə istifadə etmək mümkün oldu. Cəbrin bu bölgüsü 20-ci əsrin ortalarına qədər mövcud olmuş və iki adın meydana çıxmasında öz ifadəsini tapmışdır: “klassik cəbr” və “müasir cəbr”. Sonuncu daha çox başqa bir adla xarakterizə olunur: "mücərrəd cəbr". Fakt budur ki, bu bölmə - riyaziyyatda ilk dəfə - tam abstraksiya ilə xarakterizə olunurdu.

Kiçik Riyaziyyat Ensiklopediyasını yükləyin və oxuyun, Fried E., Pastor I., Reiman I., Reves P., Ruja I., 1976

“Ehtimal və riyazi statistika” ehtimal nəzəriyyəsi, riyazi statistika və onların elm və texnikanın müxtəlif sahələrində tətbiqi haqqında məlumat kitabçasıdır. Ensiklopediya iki hissədən ibarətdir: əsas hissədə sorğu məqalələri, ayrı-ayrı konkret problem və metodlara həsr olunmuş məqalələr, əsas anlayışların təriflərini verən qısa istinadlar, ən mühüm teoremlər və düsturlar yer alır. Tətbiqi məsələlərə - informasiya nəzəriyyəsi, növbə nəzəriyyəsi, etibarlılıq nəzəriyyəsi, eksperimental planlaşdırma və əlaqəli sahələrə - fizika, geofizika, genetika, demoqrafiya və texnologiyanın müəyyən bölmələrinə xeyli yer ayrılmışdır. Məqalələrin əksəriyyəti bu problemə dair ən mühüm əsərlərin biblioqrafiyası ilə müşayiət olunur. Məqalələrin adları da ingilis dilinə tərcümə ilə verilmişdir. İkinci hissə - “Ehtimal nəzəriyyəsi və riyazi statistika üzrə oxucu”da keçmişin rus ensiklopediyaları üçün yazılmış məqalələr, həmçinin başqa əsərlərdə əvvəllər dərc edilmiş ensiklopedik materiallar yer alır. Ensiklopediya ehtimal nəzəriyyəsi və riyazi statistika problemlərini əhatə edən jurnalların, dövri nəşrlərin və davamlı nəşrlərin geniş siyahısı ilə müşayiət olunur.
Ensiklopediyaya daxil edilmiş material riyaziyyat və digər elmlər sahəsində tədqiqat və praktiki işlərində ehtimal metodlarından istifadə edən tələbələr, aspirantlar və tədqiqatçılar üçün zəruridir.

Riyaziyyat Ensiklopediyası riyaziyyatın bütün sahələrinə dair məlumat kitabçasıdır. Ensiklopediya riyaziyyatın ən mühüm sahələrinə dair icmal məqalələrə əsaslanır. Bu tip məqalələr üçün əsas tələb, təqdimatın maksimum əlçatanlığı ilə nəzəriyyənin mövcud vəziyyətinin nəzərdən keçirilməsinin mümkün tamlığıdır; bu məqalələr ümumiyyətlə böyük riyaziyyatçılar, aspirantlar və riyaziyyatın əlaqəli sahələrinin mütəxəssisləri, bəzi hallarda isə riyazi metodları öz işlərində tətbiq edən digər bilik sahələrinin mütəxəssisləri, mühəndislər və riyaziyyat müəllimləri üçün açıqdır. Riyaziyyatın fərdi spesifik problemləri və metodları üzrə əlavə, orta həcmli məqalələr təqdim olunur; bu məqalələr daha dar oxucu dairəsi üçün nəzərdə tutulub, ona görə də onlarda təqdimat daha az əlçatan ola bilər. Nəhayət, məqalələrin daha bir növü var - sürətli istinad tərifləri. Bəzi təriflər ilk iki məqalə növündə verilmişdir. Ensiklopediyanın əksər məqalələri hər bir başlıq üçün seriya nömrələri ilə istinadlar siyahısı ilə müşayiət olunur ki, bu da məqalələrin mətnlərində sitat gətirməyə imkan verir. Məqalələrin sonunda (bir qayda olaraq) müəllif və ya mənbə, əgər məqalə əvvəllər dərc olunubsa (əsasən bunlar Böyük Sovet Ensiklopediyasının məqalələridir) göstərilir. Məqalələrdə qeyd olunan xarici (qədim istisna olmaqla) alimlərin adları latın orfoqrafiyası ilə (biblioqrafiyaya istinad yoxdursa) müşayiət olunur.

Ensiklopediyada məqalələrin düzülüşü prinsipi əlifba sırasıdır. Əgər məqalənin adı sinonimi olan termindirsə, onda sonuncu əsasdan sonra verilir. Bir çox hallarda məqalə başlıqları iki və ya daha çox sözdən ibarətdir. Bu hallarda terminlər ya ən ümumi formada verilir, ya da məna baxımından ən mühüm söz birinci yerə qoyulur. Məqalənin başlığında öz adı varsa, o, birinci yerdə yerləşdirilir (belə məqalələrə istinadlar siyahısında, bir qayda olaraq, terminin adını izah edən ilkin mənbə qeyd olunur). Məqalə başlıqları əsasən təklikdə verilir.

Ensiklopediya digər məqalələrə keçidlər sistemindən geniş istifadə edir, burada oxucu baxılan mövzuya əlavə məlumat tapa bilər. Tərif məqalənin başlığında görünən terminə istinad vermir.

Məqalələrdə yer saxlamaq üçün ensiklopediyalar üçün adi olan bəzi sözlərin abreviaturaları qəbul edilir.

1-ci cild üzərində işləmişdir

“Sovet Ensiklopediyası” nəşriyyatının riyaziyyat redaksiya heyəti - V. İ. BITYUTSKOV (redaksiya müdiri), M. İ. VOYTSEXOVSKİ (elmi redaktor), Yu. A. QORBKOV (elmi redaktor), A. B. İVANOV (elmi redaktor), İVANOVA (böyük elmi redaktor), T. Yu. POPOVA (elmi redaktor), SA RUKOVA (böyük elmi redaktor), E. E. SOBOLEVSKAYA (redaktor), L. V. Sokolova (kiçik redaktor), L. R. XƏBİB (kiçik redaktor).

Nəşriyyatçılar: E. P. RYABOVA (ədəbi nəşr). E. İ. ZHAROVA, A. M. MARTYNOV (biblioqrafiya). A. F. DALKOVSKAYA (transkripsiya). N. A. FEDOROVA (işə qəbul şöbəsi). 3. A. SUXOVA (illüstrasiyaların nəşri). E. I. ALEKSEEVA, N. Yu. Kruzhalova (lüğətin nəşri). M. V. AKIMOVA, A. F. PROŞKO (korrektor). G. V. SMIRNOVA (texniki nəşr).

Rəssam R. İ. MALANİÇEV tərəfindən üz qabığı.

1-ci cild haqqında əlavə məlumat

“Sovet Ensiklopediyası” nəşriyyatı

Ensiklopediyalar lüğətlər, istinad kitabları

Nəşriyyatın elmi və redaksiya heyəti

A. M. PROXOROV (sədr), İ. V. ABAŞİDZE, P. A. AZİMOV, A. P. ALEKSANDROV, V. A. AMBARTZUMYAN, İ. İ. ARTOBOLEVSKİ, A. V. ARTSIXOVSKİ, M. S. ASIMOV, Yu., V. Bərbəyov, Yu., B. Bərbənov, Böyubov, Yu. , B.Ə.Bıxovski, V. X. Vasilenko, L. M. VOLODARSKİ, V. V. VOLSKİ, B. M. VUL, B. G. QAFUROV, S. R. QERŞBERQ, M. S. QİLYAROV, V. P. QLUŞKO, V. M. QLUŞKOV, Q. A. A. Q. A. A. ), VP YELUTIN, VS EMELYANOV, EM ZHUKOV, AA IMSHENETSKY, NN INOZEMTSEV, M. I. KABACHNIK, S. V. KALESNIK, G. A. KARAVAEV, K. K. KARAKEEV, M. K. KARATAEDIRROV, V. I.YALDINKEV, K. KARATAEDİR, V. I. Y. Y. N. KOVALEV (sədrin birinci müavini), FV KONSTANTINOV, VN KUDRYAVTSEV, Mİ KUZNETSOV (sədr müavini), BV KUKARKIN, VG KULIKOV, I. A. KUTUZOV, PP LOBANOV, GM LOZA, Yu. E., MAHEVISAREV, MAKPAİSAREUS Yu.Yu.MATULİS, GI NAAN, GD OBICHKIN, B. E. PATON, V. M. POLEVO Y, M. A. PROKOFIEV, Y. V. PROXOROV, N. F. ROSTOVTSEV, A. M. RUMYANTSEV, B. A. RıBAKOV, V. P. SAMSON, M. İ. SLADKOVSKİ, V. İ. SMIRNOV, DN SOLOVYEV, V. S. Smirnov, D. N. SA TOKAREV, VA TRAPEZNIKOV, E. K. FEDOROV, M. B. XRAPÇENKO, E. İ. ÇAZOV, V. N. ÇERNIQOVSKİ, J. E. ŞMUŞKİS, S. İ. YUTKEVIÇ. L. V. KIRILLOVA, Şuranın katibi.

Moskva 1977

Riyaziyyat ensiklopediyası. Cild 1 (A - D)

Baş redaktor I. M. VİNOQRADOV

Redaksiya heyəti

S. İ. ADYAN, P. S. ALEKSANDROV, N. S. BAXVALOV, V. İ. BITYUTSKOV (baş redaktorun müavini), A. V. BITSADZE, L. N. BOLŞEV, A. A. QONÇAR, N. V EFIMOV, VA KƏLDARİEV, LƏVİTŞİEV, VA İLYDARŞİEV, LƏBMƏLİYEV, M. MİŞÇENKO, SP NOVIKOV, E.Q.POZNYAK, Yu.V.PROXOROV (Baş redaktorun müavini), A.G.SVEŞNIKOV, A.N.TİXONOV, P.L.ULYANOV, A.İ.ŞİRŞOV, S.V.YABLONSK

Riyaziyyat ensiklopediyası. Ed. kollegiya: I. M. Vinoqradov (fəs. red.) [və başqaları] T. 1 - M., " Sovet Ensiklopediyası", 1977

(Ensiklopediyalar. Lüğətlər. İstinad kitabçaları), cild 1. A - G. 1977. 1152 stb. Şəkildən.

Komplektdə icarəyə götürülmüşdür 9. 06. 1976. Çap üçün imzalanmış 18. 02. 1977. Birinci Model mətbəəsində hazırlanmış matrislərdən mətnin çapı. A. A. Jdanova. Qırmızı Əmək Bayrağı ordenli "Sovet Ensiklopediyası" nəşriyyatı. 109817. Moskva, Zh - 28, Pokrovski bulvarı, 8. T - 02616 Tiraj 150.000 nüsxə. Sifariş No 418. Mətbəə kağızı No 1. Kağızın ölçüsü 84xl08 1/14. Cild 36 fiziki. n. l. ; 60, 48 konv. n. l. mətn. 101, 82 s. - red. l. Kitabın qiyməti 7 rubl təşkil edir. 10 r.

Qırmızı Əmək Bayrağı ordeni Moskva SSRİ Nazirlər Sovetinin Nəşriyyat, Poliqrafiya və Kitab Ticarəti üzrə Dövlət Komitəsi yanında “Soyuzpoliqrafprom” №1 mətbəəsi, Moskva, I - 85, Prospekt Mira, 105. Sərəncam No. 865.