Sanoatni kim kiritgan? Hosila nima?Hosila funksiyaning ta'rifi va ma'nosi. Funktsiyaning nuqtadagi hosilasining geometrik ma'nosi
B9 muammosi funksiya yoki hosila grafigini beradi, undan quyidagi miqdorlardan birini aniqlash kerak:
- X 0 nuqtadagi hosilaning qiymati,
- Maksimal yoki minimal ball (ekstremum ball),
- Ortib boruvchi va kamayuvchi funksiyalar intervallari (monotonlik oraliqlari).
Bu masalada keltirilgan funksiyalar va hosilalar doimo uzluksiz bo‘lib, yechimni ancha osonlashtiradi. Topshiriq matematik tahlil bo'limiga tegishli bo'lishiga qaramay, hatto eng zaif talabalar ham buni qila oladilar, chunki bu erda chuqur nazariy bilim talab qilinmaydi.
Losmalar, ekstremum nuqtalar va monotonlik oraliqlarining qiymatini topish uchun oddiy va universal algoritmlar mavjud - ularning barchasi quyida muhokama qilinadi.
Ahmoqona xatolarga yo'l qo'ymaslik uchun B9 muammosining shartlarini diqqat bilan o'qing: ba'zida siz juda uzun matnlarga duch kelasiz, ammo yechim yo'nalishiga ta'sir qiladigan bir nechta muhim shartlar mavjud.
Hosila qiymatini hisoblash. Ikki nuqta usuli
Agar muammoga f(x) funksiyaning grafigi qaysidir x 0 nuqtasida shu grafaga tangens berilgan bo‘lsa va bu nuqtada hosilaning qiymatini topish talab etilsa, quyidagi algoritm qo‘llaniladi:
- Tangens grafigida ikkita "adekvat" nuqtani toping: ularning koordinatalari butun son bo'lishi kerak. Bu nuqtalarni A (x 1 ; y 1) va B (x 2 ; y 2) deb belgilaymiz. Koordinatalarni to'g'ri yozing - bu yechimdagi asosiy nuqta va bu erda har qanday xato noto'g'ri javobga olib keladi.
- Koordinatalarni bilgan holda, Dx = x 2 − x 1 argumentining ortishi va Dy = y 2 − y 1 funksiyasining o‘sishini hisoblash oson.
- Nihoyat, hosila D = Dy/Dx qiymatini topamiz. Boshqacha qilib aytganda, funktsiyaning o'sishini argumentning o'sishiga bo'lish kerak - va bu javob bo'ladi.
Yana bir bor eslatib o'tamiz: A va B nuqtalarni ko'pincha sodir bo'lganidek f(x) funksiya grafigidan emas, balki aniq tangensdan izlash kerak. Tangens chizig'i majburiy ravishda kamida ikkita bunday nuqtani o'z ichiga oladi - aks holda muammo to'g'ri shakllantirilmaydi.
A (−3; 2) va B (−1; 6) nuqtalarini ko‘rib chiqing va o‘sishlarni toping:
Dx = x 2 - x 1 = -1 - (-3) = 2; Dy = y 2 - y 1 = 6 - 2 = 4.
Hosilaning qiymati topilsin: D = Dy/Dx = 4/2 = 2.
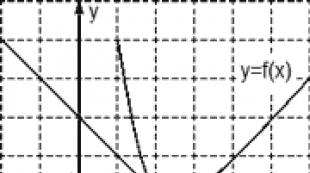
Vazifa. Rasmda y = f(x) funksiyaning grafigi va abtsissa x 0 nuqtada unga teginish ko'rsatilgan. f(x) funksiyaning x 0 nuqtadagi hosilasi qiymatini toping.
A (0; 3) va B (3; 0) nuqtalarini ko'rib chiqing, o'sishlarni toping:
Dx = x 2 - x 1 = 3 - 0 = 3; Dy = y 2 - y 1 = 0 - 3 = -3.
Endi hosilaning qiymatini topamiz: D = Dy/Dx = -3/3 = -1.
Vazifa. Rasmda y = f(x) funksiyaning grafigi va abtsissa x 0 nuqtada unga teginish ko'rsatilgan. f(x) funksiyaning x 0 nuqtadagi hosilasi qiymatini toping.
A (0; 2) va B (5; 2) nuqtalarini ko'rib chiqing va o'sishlarni toping:
Dx = x 2 - x 1 = 5 - 0 = 5; Dy = y 2 - y 1 = 2 - 2 = 0.
Hosilaning qiymatini topish qoladi: D = Dy/Dx = 0/5 = 0.
Oxirgi misoldan biz qoidani shakllantirishimiz mumkin: agar tangens OX o'qiga parallel bo'lsa, teginish nuqtasida funktsiyaning hosilasi nolga teng. Bunday holda, siz hatto hech narsani hisoblashingiz shart emas - shunchaki grafikaga qarang.
Maksimal va minimal ballarni hisoblash
Ba'zan B9 masalada funktsiya grafigi o'rniga hosila grafigi beriladi va funktsiyaning maksimal yoki minimal nuqtasini topish talab etiladi. Bunday vaziyatda ikki nuqtali usul foydasiz, ammo boshqa, undan ham oddiyroq algoritm mavjud. Birinchidan, terminologiyani aniqlaymiz:
- x 0 nuqtasi f(x) funksiyaning maksimal nuqtasi deyiladi, agar bu nuqtaning qaysidir qo'shnisida quyidagi tengsizlik bajarilsa: f(x 0) ≥ f(x).
- x 0 nuqtasi f(x) funksiyaning minimal nuqtasi deyiladi, agar shu nuqtaning qaysidir qo'shnisida quyidagi tengsizlik bajarilsa: f(x 0) ≤ f(x).
Hosil grafigidan maksimal va minimal nuqtalarni topish uchun quyidagi amallarni bajaring:
- Barcha keraksiz ma'lumotlarni olib tashlagan holda lotin grafigini qayta chizing. Amaliyot shuni ko'rsatadiki, keraksiz ma'lumotlar faqat qaror qabul qilishga xalaqit beradi. Shuning uchun biz koordinata o'qida lotinning nollarini belgilaymiz - va bu.
- Nollar orasidagi intervallardagi hosila belgilarini toping. Agar biron bir x 0 nuqtasi uchun f'(x 0) ≠ 0 ekanligi ma'lum bo'lsa, u holda faqat ikkita variant mumkin: f'(x 0) ≥ 0 yoki f'(x 0) ≤ 0. Hosilning belgisi: Dastlabki chizmadan aniqlash oson: hosilaviy grafik OX oʻqidan yuqorida joylashgan boʻlsa, f'(x) ≥ 0. Va aksincha, hosila grafik OX oʻqi ostida joylashgan boʻlsa, f'(x) ≤ 0 boʻladi.
- Biz lotinning nollarini va belgilarini yana tekshiramiz. Belgining minusdan plyusga o'zgarishi minimal nuqtadir. Aksincha, lotin belgisi ortiqcha dan minusga o'zgartirilsa, bu maksimal nuqtadir. Hisoblash har doim chapdan o'ngga amalga oshiriladi.
Ushbu sxema faqat uzluksiz funktsiyalar uchun ishlaydi - B9 muammosida boshqa yo'q.
Vazifa. Rasmda f(x) funksiyaning [−5 oraliqda aniqlangan hosilasining grafigi ko'rsatilgan; 5]. f(x) funksiyaning shu segmentdagi minimal nuqtasini toping.
Keling, keraksiz ma'lumotlardan xalos bo'laylik va faqat chegaralarni qoldiramiz [−5; 5] va hosila nollari x = -3 va x = 2,5. Shuningdek, biz belgilarga e'tibor qaratamiz:
Shubhasiz, x = −3 nuqtada hosilaning belgisi minusdan plyusga o'zgaradi. Bu minimal nuqta.
Vazifa. Rasmda f(x) funksiyaning [−3 oraliqda aniqlangan hosilasining grafigi ko'rsatilgan; 7]. f(x) funksiyaning shu segmentdagi maksimal nuqtasini toping.
Keling, faqat chegaralarni qoldirib, grafikni qayta chizamiz [−3; 7] va hosila nollari x = −1.7 va x = 5. Hosil boʻlgan grafikdagi hosilaning belgilarini qayd qilaylik. Bizda ... bor:
![]()
Shubhasiz, x = 5 nuqtada lotin belgisi ortiqcha dan minusga o'zgaradi - bu maksimal nuqta.
Vazifa. Rasmda f(x) funksiyaning [−6 oraliqda aniqlangan hosilasining grafigi ko'rsatilgan; 4]. f(x) funksiyaning [−4” segmentiga tegishli maksimal nuqtalari sonini toping; 3].
Masalaning shartlaridan kelib chiqadiki, grafikning faqat segment bilan chegaralangan qismini ko'rib chiqish kifoya [−4; 3]. Shuning uchun biz yangi grafik quramiz, unda biz faqat chegaralarni belgilaymiz [-4; 3] va uning ichidagi hosilaning nollari. Ya'ni, x = -3,5 va x = 2 nuqtalari. Biz quyidagilarni olamiz:
![]()
Bu grafikda faqat bitta maksimal nuqta x = 2. Aynan shu nuqtada hosilaning belgisi ortiqcha dan minusga o'zgaradi.
Butun son bo'lmagan koordinatali nuqtalar haqida kichik eslatma. Masalan, oxirgi masalada x = -3,5 nuqtasi ko'rib chiqildi, ammo xuddi shu muvaffaqiyat bilan biz x = -3,4 ni olishimiz mumkin. Agar muammo to'g'ri tuzilgan bo'lsa, bunday o'zgarishlar javobga ta'sir qilmasligi kerak, chunki "belgilangan yashash joyisiz" nuqtalar muammoni hal qilishda bevosita ishtirok etmaydi. Albatta, bu hiyla butun sonlar bilan ishlamaydi.
O'sish va kamayuvchi funktsiyalarning intervallarini topish
Bunday masalada maksimal va minimal nuqtalar kabi, funktsiyaning o'zi ortib yoki kamayadigan sohalarni topish uchun hosilaviy grafikdan foydalanish taklif etiladi. Birinchidan, o'sish va kamayish nima ekanligini aniqlaymiz:
- Agar ushbu segmentning istalgan ikkita x 1 va x 2 nuqtalari uchun quyidagi fikr to'g'ri bo'lsa, f(x) funksiya segmentda ortib borayotgan deyiladi: x 1 ≤ x 2 ⇒ f(x 1) ≤ f(x 2) . Boshqacha qilib aytganda, argument qiymati qanchalik katta bo'lsa, funktsiya qiymati shunchalik katta bo'ladi.
- Agar ushbu segmentdagi x 1 va x 2 nuqtalar uchun quyidagi fikr to'g'ri bo'lsa, f(x) funksiya segmentda kamayuvchi deyiladi: x 1 ≤ x 2 ⇒ f(x 1) ≥ f(x 2) . Bular. Kattaroq argument qiymati kichikroq funktsiya qiymatiga mos keladi.
Keling, oshirish va kamaytirish uchun etarli shartlarni tuzamiz:
- Uzluksiz f(x) funksiya segmentda ortishi uchun uning segment ichidagi hosilasi musbat bo'lishi kifoya, ya'ni. f’(x) ≥ 0.
- Uzluksiz f(x) funksiya segmentida kamayishi uchun uning segment ichidagi hosilasi manfiy bo'lishi kifoya, ya'ni. f’(x) ≤ 0.
Keling, bu gaplarni dalilsiz qabul qilaylik. Shunday qilib, biz o'sish va pasayish intervallarini topish sxemasini olamiz, bu ko'p jihatdan ekstremum nuqtalarni hisoblash algoritmiga o'xshaydi:
- Barcha keraksiz ma'lumotlarni olib tashlang. Hosilning asl grafigida bizni birinchi navbatda funksiyaning nollari qiziqtiradi, shuning uchun biz faqat ularni qoldiramiz.
- Nol orasidagi oraliqda hosilaning belgilarini belgilang. f’(x) ≥ 0 bo’lgan joyda funksiya ortadi, f’(x) ≤ 0 bo’lsa, u kamayadi. Agar muammo x o'zgaruvchisiga cheklovlar qo'ygan bo'lsa, biz ularni qo'shimcha ravishda yangi grafikda belgilaymiz.
- Endi biz funktsiyaning xatti-harakati va cheklovlarni bilganimizdan so'ng, muammoda talab qilinadigan miqdorni hisoblash qoladi.
Vazifa. Rasmda f(x) funksiyaning [−3 oraliqda aniqlangan hosilasining grafigi ko'rsatilgan; 7.5]. f(x) funksiyaning kamayish oraliqlarini toping. Javobingizda ushbu intervallarga kiritilgan butun sonlar yig'indisini ko'rsating.
Odatdagidek, grafikni qayta chizamiz va chegaralarni belgilaymiz [−3; 7.5], shuningdek x = -1.5 va x = 5.3 hosilasining nollari. Keyin hosila belgilarini qayd etamiz. Bizda ... bor:
![]()
(− 1,5) oraliqda hosila manfiy bo‘lgani uchun bu funksiya kamayuvchi intervaldir. Bu oraliq ichidagi barcha butun sonlarni yig'ish uchun qoladi:
−1 + 0 + 1 + 2 + 3 + 4 + 5 = 14.
Vazifa. Rasmda [−10 oraliqda aniqlangan f(x) funksiya hosilasining grafigi ko'rsatilgan; 4]. f(x) funksiyaning ortish oraliqlarini toping. Javobingizda ulardan eng kattasining uzunligini ko'rsating.
Keling, keraksiz ma'lumotlardan xalos bo'laylik. Keling, faqat chegaralarni qoldiramiz [−10; 4] va hosilaning nollari, bu safar ulardan to‘rttasi bor edi: x = −8, x = −6, x = −3 va x = 2. Hosilning belgilarini belgilaymiz va quyidagi rasmni olamiz:
Biz funktsiyani oshirish intervallari bilan qiziqamiz, ya'ni. f’(x) ≥ 0. Grafikda ikkita shunday interval mavjud: (−8; −6) va (−3; 2). Keling, ularning uzunligini hisoblaylik:
l 1 = - 6 - (-8) = 2;
l 2 = 2 - (−3) = 5.
Intervallarning eng kattasining uzunligini topishimiz kerakligi sababli, javob sifatida l 2 = 5 qiymatini yozamiz.
Funksiya nuqtada va uning ba'zi qo'shnilarida aniqlansin. Argumentga shunday o'sish beraylikki, nuqta funktsiyani aniqlash sohasiga to'g'ri keladi. Shundan so'ng funktsiya oshiriladi.
TA’RIF. Funktsiyaning nuqtadagi hosilasi bu nuqtadagi funktsiya o'sishining argumentning o'sishiga nisbati chegarasi deb ataladi, at (agar bu chegara mavjud bo'lsa va cheklangan bo'lsa), ya'ni.
Belgilang: ,,,.
Funktsiyaning o'ngdagi nuqtadagi hosilasi (chap) chaqirdi
(agar bu chegara mavjud bo'lsa va cheklangan bo'lsa).
Belgilangan: , – o‘ngdagi nuqtada hosila,
, chapdagi nuqtadagi hosiladir.
Shubhasiz, quyidagi teorema to'g'ri.
TEOREMA. Funktsiya nuqtada hosilaga ega bo'ladi, agar shu nuqtada funktsiyaning o'ng va chap tomonidagi hosilalari mavjud bo'lsa va bir-biriga teng bo'lsa. Bundan tashqari
Quyidagi teorema funktsiyaning bir nuqtada hosilasi mavjudligi bilan funksiyaning shu nuqtadagi uzluksizligi o'rtasidagi bog'liqlikni o'rnatadi.
TEOREMA (funksiyaning bir nuqtada hosilasi mavjudligining zaruriy sharti). Agar funktsiya nuqtada hosilaga ega bo'lsa, u holda bu nuqtadagi funktsiya uzluksizdir.
ISLOV
U mavjud bo'lsin. Keyin
![]() ,
,
qaerda cheksiz kichik.
Izoh
funktsiyaning hosilasi va belgilang
funktsiyani farqlash .
GEOMETRIK VA Jismoniy manosi
1) Hosilning fizik ma'nosi. Agar funktsiya va uning argumenti fizik miqdorlar bo'lsa, hosila o'zgaruvchining nuqtadagi o'zgaruvchiga nisbatan o'zgarish tezligidir. Misol uchun, agar vaqt nuqtasi bosib o'tgan masofa bo'lsa, uning hosilasi vaqt momentidagi tezlikdir. Agar bir vaqtning o'zida o'tkazgichning kesishmasidan oqib o'tadigan elektr miqdori bo'lsa, u holda bir vaqtning o'zida elektr miqdorining o'zgarish tezligi, ya'ni. bir vaqtning o'zida joriy kuch.
2) Hosilning geometrik ma'nosi.
Qandaydir egri chiziq bo'lsin, egri chiziqdagi nuqta bo'lsin. 
Eng kamida ikkita nuqtani kesib o'tuvchi har qanday to'g'ri chiziq deyiladi sekant .
Bir nuqtadagi egri chiziqqa tangens Agar nuqta egri chiziq bo'ylab harakatlansa, sekantning chegara holati deb ataladi.
Ta'rifdan ko'rinib turibdiki, agar egri chiziqqa tegish nuqtada mavjud bo'lsa, u yagonadir.
Egri chiziqni (ya'ni, funktsiya grafigini) ko'rib chiqing. Bir nuqtada vertikal bo'lmagan tangensga ega bo'lsin. Uning tenglamasi: (nuqtadan o'tuvchi va burchak koeffitsientiga ega bo'lgan to'g'ri chiziq tenglamasi). 
Nishabning ta'rifi bo'yicha
to'g'ri chiziqning o'qqa moyillik burchagi qayerda.
Sekantning o'qga moyillik burchagi bo'lsin, bu erda. Chunki tangens, keyin qachon
Demak,
Shunday qilib, biz buni oldik – nuqtadagi funksiya grafigiga tegishning burchak koeffitsienti(nuqtadagi funksiya hosilasining geometrik ma'nosi). Shuning uchun bir nuqtadagi egri chiziqqa teginish tenglamasini shaklda yozish mumkin
Izoh . Nuqtadagi egri chiziqqa chizilgan tangensga perpendikulyar nuqtadan o'tuvchi to'g'ri chiziq deyiladi nuqtadagi egri chiziqqa normal . Perpendikulyar to'g'ri chiziqlarning burchak koeffitsientlari o'zaro bog'liqlik bilan bog'liq bo'lganligi sababli, bir nuqtadagi egri chiziqning normal tenglamasi ko'rinishga ega bo'ladi.
![]() , Agar .
, Agar .
Agar bo'lsa, u holda nuqtadagi egri chiziqqa tegish ko'rinishga ega bo'ladi
va normal.
TANGENT VA NORMAL TENGLAMALAR
Tangens tenglamasi
Funktsiya tenglama bilan berilgan bo'lsin y=f(x), tenglamani yozishingiz kerak tangens nuqtada x 0. Hosila ta’rifidan:
y/(x)=limD x→0Δ yΔ x
Δ y=f(x+Δ x)−f(x).
Tenglama tangens funktsiya grafigiga: y=kx+b (k,b=const). Hosilning geometrik ma'nosidan: f/(x 0)=tgα= k Chunki x 0 va f(x 0)∈ to'g'ri chiziq, keyin tenglama tangens quyidagicha yoziladi: y−f(x 0)=f/(x 0)(x−x 0), yoki
y=f/(x 0)· x+f(x 0)−f/(x 0)· x 0.

Oddiy tenglama
Oddiy- ga perpendikulyar tangens(rasmga qarang). Shu asosda:
tgβ= tg(2p−a)= ctg a=1 tg a=1 f/(x 0)
Chunki normalning qiyalik burchagi b1 burchak bo'lsa, bizda:
tg b1= tg(π−β)=− tg b=−1 f/(x).
nuqta ( x 0,f(x 0))∈ normal, tenglama quyidagi shaklni oladi:
y−f(x 0)=−1f/(x 0)(x−x 0).
ISLOV
U mavjud bo'lsin. Keyin
![]() ,
,
qaerda cheksiz kichik.
Lekin bu uning bir nuqtada uzluksiz ekanligini bildiradi (uzluksizlikning geometrik ta'rifiga qarang). ∎
Izoh . Funktsiyaning nuqtadagi uzluksizligi bu funksiyaning hosilasining nuqtada mavjudligi uchun yetarli shart emas. Masalan, funktsiya uzluksiz, lekin nuqtada hosilasi yo'q. Haqiqatan ham,
va shuning uchun mavjud emas.
Shubhasiz, yozishmalar ba'zi bir to'plamda aniqlangan funktsiyadir. Uni chaqirishadi funktsiyaning hosilasi va belgilang
Funksiyaning hosila funksiyasini topish operatsiyasi deyiladi funktsiyani farqlash .
Yig'indi va ayirmaning hosilasi
Bizga hosilalari ma’lum f(x) va g(x) funksiyalar berilsin. Misol uchun, siz yuqorida muhokama qilingan elementar funktsiyalarni olishingiz mumkin. Keyin ushbu funktsiyalarning yig'indisi va farqining hosilasini topishingiz mumkin:
(f + g) ' = f ' + g '
(f − g)’ = f ’ − g ’
Demak, ikki funktsiya yig‘indisining (farqining) hosilasi hosilalarning yig‘indisiga (farqiga) teng. Ko'proq shartlar bo'lishi mumkin. Masalan, (f + g + h)' = f' + g' + h'.
Qat'iy aytganda, algebrada "ayirish" tushunchasi yo'q. "Salbiy element" tushunchasi mavjud. Shuning uchun f - g farqini f + (−1) g yig'indisi sifatida qayta yozish mumkin va keyin faqat bitta formula qoladi - yig'indining hosilasi.
Maqolaning mazmuni
HOSILA– funksiyaning hosilasi y = f(x), ma'lum bir oraliqda berilgan ( a, b) nuqtada x bu oraliq funktsiya o'sish nisbati moyil bo'lgan chegara deb ataladi f bu nuqtada argumentning o'sishi nolga moyil bo'lganda, argumentning mos keladigan o'sishiga.
Hosil odatda quyidagicha ifodalanadi:
Boshqa belgilar ham keng qo'llaniladi:
Tezlik.
Nuqtaga ruxsat bering M to'g'ri chiziqda harakat qiladi. Masofa s harakatlanuvchi nuqta, ba'zi bir boshlang'ich pozitsiyasidan hisoblangan M 0 , vaqtga bog'liq t, ya'ni. s vaqt funksiyasi mavjud t: s= f(t). Bir vaqtning o'zida ruxsat bering t harakatlanuvchi nuqta M masofada edi s boshlang'ich pozitsiyasidan M 0 va keyingi daqiqada t+D t o'zini bir holatda topdi M 1 - masofada s+D s boshlang'ich pozitsiyasidan ( rasmga qarang.).
Shunday qilib, ma'lum vaqt ichida D t masofa s D miqdoriga o'zgartirildi s. Bunday holda, ular vaqt oralig'ida D t kattalik s qabul qilingan D s.
O'rtacha tezlik hamma hollarda nuqtaning harakat tezligini aniq tavsiflay olmaydi M bir vaqtning o'zida t. Agar, masalan, D intervalining boshida tana t juda tez harakatlanadi va oxirida juda sekin, keyin o'rtacha tezlik nuqta harakatining ko'rsatilgan xususiyatlarini aks ettira olmaydi va hozirgi vaqtda uning harakatining haqiqiy tezligi haqida tasavvurga ega bo'lmaydi. t. Haqiqiy tezlikni o'rtacha tezlikdan foydalangan holda aniqroq ifodalash uchun siz qisqaroq vaqt D vaqtini olishingiz kerak t. Hozirgi vaqtda nuqtaning harakat tezligini eng to'liq tavsiflaydi t o'rtacha tezlikning D da moyil bo'lgan chegarasi t® 0. Bu chegara joriy tezlik deb ataladi:
Shunday qilib, ma'lum bir momentdagi harakat tezligi yo'lning o'sish nisbati D chegarasi deb ataladi s vaqt o'sishiga D t, vaqt o'sishi nolga moyil bo'lganda. Chunki
Hosilning geometrik ma'nosi. Funksiya grafigiga teginish.
Tangens chiziqlarni qurish differensial hisobning paydo bo'lishiga olib kelgan muammolardan biridir. Differensial hisoblash bilan bog'liq birinchi nashr etilgan asar Leybnits tomonidan yozilgan Na kasr, na irratsional miqdorlar to'siq bo'lmaydigan maksimal va minimal, shuningdek tangenslarning yangi usuli va buning uchun hisobning maxsus turi..
Egri chiziq funksiyaning grafigi bo'lsin y =f(x) to'rtburchaklar koordinatalar tizimida ( sm. guruch.).
Qandaydir qiymatda x funktsiyasi muhim y =f(x). Bu qadriyatlar x Va y egri chiziqdagi nuqta mos keladi M 0(x, y). Agar argument bo'lsa x berish oshirish D x, keyin argumentning yangi qiymati x+D x yangi funksiya qiymatiga mos keladi y+ D y = f(x + D x). Egri chiziqning mos keladigan nuqtasi nuqta bo'ladi M 1(x+D x,y+D y). Agar siz sekant chizsangiz M 0M 1 va j bilan belgilanadi o'qning musbat yo'nalishi bilan ko'ndalang hosil bo'lgan burchak ho'kiz, bu rasmdan darhol ma'lum bo'ladi.
Agar hozir D x nolga intiladi, keyin nuqta M 1 nuqtaga yaqinlashib, egri chiziq bo'ylab harakatlanadi M 0 va burchak j D bilan o'zgaradi x. Da Dx® 0 j burchagi ma'lum a chegarasiga va nuqtadan o'tuvchi to'g'ri chiziqqa intiladi M 0 va x o'qining musbat yo'nalishi bo'lgan komponent, burchak a, kerakli tangens bo'ladi. Uning qiyaligi:
Demak, f´( x) = tga
bular. hosilaviy qiymat f´( x) berilgan argument qiymati uchun x funksiya grafigiga tangens hosil qilgan burchak tangensiga teng f(x) tegishli nuqtada M 0(x,y) musbat o'q yo'nalishi bilan ho'kiz.
Funksiyalarning differentsialligi.
Ta'rif. Agar funktsiya y = f(x) nuqtada hosilasi bor x = x 0 bo'lsa, bu nuqtada funktsiya differentsial bo'ladi.
Hosilasiga ega funksiyaning uzluksizligi. Teorema.
Agar funktsiya y = f(x) bir nuqtada farqlanadi x = x 0, u holda bu nuqtada uzluksiz bo'ladi.
Shunday qilib, funktsiya uzilish nuqtalarida hosilaga ega bo'lishi mumkin emas. Qarama-qarshi xulosa noto'g'ri, ya'ni. bir nuqtada ekanligidan x = x 0 funktsiyasi y = f(x) uzluksiz bo'lishi bu nuqtada farqlanishini anglatmaydi. Masalan, funktsiya y = |x| hamma uchun doimiy x(–H x x = 0 ning hosilasi yo'q. Bu nuqtada grafikning tangensi yo'q. O'ng va chap tangens bor, lekin ular bir-biriga mos kelmaydi.
Differensiallanuvchi funksiyalar haqidagi ba'zi teoremalar. Hosilning ildizlari haqidagi teorema (Rol teoremasi). Agar funktsiya f(x) segmentda uzluksiz [a,b], ushbu segmentning barcha ichki nuqtalarida va uchlarida farqlanadi x = a Va x = b nolga tushadi ( f(a) = f(b) = 0), keyin segment ichida [ a,b] kamida bitta nuqta bor x= Bilan, a c b, unda hosila fў( x) nolga tushadi, ya'ni. fў( c) = 0.
Chekli o'sish teoremasi (Lagranj teoremasi). Agar funktsiya f(x) [ oraliqda uzluksiz a, b] va bu segmentning barcha ichki nuqtalarida, keyin segmentning ichida [ [ a, b] kamida bitta nuqta bor Bilan, a c b bu
f(b) – f(a) = fў( c)(b– a).
Ikki funktsiyaning o'sish nisbati haqidagi teorema (Koshi teoremasi). Agar f(x) Va g(x) – segmentda uzluksiz ikkita funksiya [a, b] va ushbu segmentning barcha ichki nuqtalarida differensiallanadi va gў( x) bu segment ichida, keyin segment ichida [ hech qanday joyda yo'qolmaydi. a, b] shunday nuqta bor x = Bilan, a c b bu
Turli tartibli hosilalar.
Funktsiyaga ruxsat bering y =f(x) ba'zi bir intervalda differensiallanadi [ a, b]. Hosil qiymatlar f ў( x), umuman olganda, bog'liq x, ya'ni. hosila f ў( x) ning funksiyasi hamdir x. Bu funksiyani differensiallashda biz funktsiyaning ikkinchi hosilasi deb ataladigan narsani olamiz f(x), bu bilan belgilanadi f ўў ( x).
Hosil n- Funktsiya tartibi f(x) hosilaning (birinchi tartibli) hosilasi deyiladi n- 1- th va belgisi bilan belgilanadi y(n) = (y(n– 1))o.
Turli xil buyurtmalarning farqlari.
Funktsional differentsial y = f(x), Qayerda x- mustaqil o'zgaruvchi, ha dy = f ў( x)dx, dan ba'zi funksiyalar x, lekin dan x faqat birinchi omil bog'liq bo'lishi mumkin f ў( x), ikkinchi omil ( dx) mustaqil o‘zgaruvchining o‘sish ko‘rsatkichidir x va bu o'zgaruvchining qiymatiga bog'liq emas. Chunki dy dan funksiya mavjud x, keyin bu funksiyaning differentsialini aniqlashimiz mumkin. Funksiya differensialining differensiali bu funksiyaning ikkinchi yoki ikkinchi tartibli differensiali deyiladi va belgilanadi. d 2y:
d(dx) = d 2y = f ўў( x)(dx) 2 .
Differensial n- birinchi tartibli differensialning birinchi differensiali deyiladi n- 1- tartib:
d n y = d(d n–1y) = f(n)(x)dx(n).
Qisman hosila.
Agar funktsiya bitta emas, balki bir nechta argumentlarga bog'liq bo'lsa x i(i 1 dan farq qiladi n,i= 1, 2,… n),f(x 1,x 2,… x n), keyin differentsial hisobda qisman hosila tushunchasi kiritiladi, bu faqat bitta argument o'zgarganda bir nechta o'zgaruvchilar funksiyasining o'zgarish tezligini tavsiflaydi, masalan, x i. ga nisbatan 1-tartibli qisman hosila x i oddiy hosila sifatida aniqlanadi va bundan mustasno barcha argumentlar deb faraz qilinadi x i, doimiy qiymatlarni saqlang. Qisman hosilalar uchun yozuv kiritiladi
Shu tarzda aniqlangan 1-tartibli qisman hosilalar (bir xil argumentlarning funktsiyalari sifatida) o'z navbatida qisman hosilalarga ham ega bo'lishi mumkin, bular ikkinchi tartibli qisman hosilalar va boshqalar. Turli argumentlardan olingan bunday hosilalar aralash deyiladi. Bir xil tartibdagi uzluksiz aralash hosilalar differentsiallanish tartibiga bog'liq emas va bir-biriga teng.
Anna Chugainova
(\large\bf funktsiyaning hosilasi)
Funktsiyani ko'rib chiqing y=f(x), intervalda ko'rsatilgan (a, b). Mayli x- intervalning istalgan sobit nuqtasi (a, b), A Dx- qiymatga ega bo'lgan ixtiyoriy raqam x+Dx intervalga ham tegishli (a, b). Bu raqam Dx argument ortishi deb ataladi.
Ta'rif. Funktsiyaning o'sishi y=f(x) nuqtada x, argument o'sishiga mos keladi Dx, raqamga qo'ng'iroq qilaylik
Dy = f(x+Dx) - f(x).
Biz bunga ishonamiz Dx ≠ 0. Berilgan belgilangan nuqtada ko'rib chiqing x bu nuqtadagi funktsiya o'sishining mos keladigan argument o'sishiga nisbati Dx
Bu munosabatni farq munosabati deb ataymiz. Qiymatidan beri x biz sobit deb hisoblaymiz, farq nisbati argumentning funktsiyasidir Dx. Bu funksiya barcha argument qiymatlari uchun aniqlanadi Dx, nuqtaning etarlicha kichik mahallasiga tegishli Dx=0, nuqtaning o'zi bundan mustasno Dx=0. Shunday qilib, biz belgilangan funktsiyaning chegarasi mavjudligi haqidagi savolni ko'rib chiqishga haqlimiz Dx → 0.
Ta'rif. Funktsiyaning hosilasi y=f(x) ma'lum bir belgilangan nuqtada x limiti deb ataladi Dx → 0 farq nisbati, ya'ni
Agar bu chegara mavjud bo'lsa.
Belgilanish. y'(x) yoki f'(x).
Hosilning geometrik ma'nosi: Funktsiyaning hosilasi f(x) ayni paytda x eksa orasidagi burchakning tangensiga teng ho'kiz va tegishli nuqtada ushbu funktsiya grafigiga teginish:
f'(x 0) = \tga.
Hosilning mexanik ma'nosi: Yo'lning vaqtga nisbatan hosilasi nuqtaning to'g'ri chiziqli harakati tezligiga teng:
Chiziqga teguvchi tenglama y=f(x) nuqtada M 0 (x 0 ,y 0) shaklni oladi
y-y 0 = f'(x 0) (x-x 0).
Qaysidir nuqtada egri chiziqning normali xuddi shu nuqtadagi tangensga perpendikulyar hisoblanadi. Agar f'(x 0)≠ 0, keyin normalning chiziqqa tenglamasi y=f(x) nuqtada M 0 (x 0 ,y 0) shunday yozilgan:

Funksiyaning differentsialligi tushunchasi
Funktsiyaga ruxsat bering y=f(x) ma'lum bir oraliqda aniqlanadi (a, b), x- bu oraliqdan ba'zi sobit argument qiymati, Dx- argumentning qiymati argumentning har qanday o'sishi x+Dx ∈ (a, b).
Ta'rif. Funktsiya y=f(x) berilgan nuqtada differentsiallanuvchi deb ataladi x, agar ortib borsa dy nuqtada bu funktsiya x, argument o'sishiga mos keladi Dx, shaklida ifodalanishi mumkin
Dy = A Dx +aDx,
Qayerda A- ba'zi bir raqamdan mustaqil Dx, A α - argument funktsiyasi Dx da cheksiz kichik bo'lgan Dx→ 0.
Ikki cheksiz kichik funktsiyaning mahsuloti bo'lgani uchun adx dan yuqori tartibli cheksiz kichikdir Dx(3 ta cheksiz kichik funktsiyaning xossasi), u holda yozishimiz mumkin:
Dy = A Dx +o(Dx).
Teorema. Funktsiyani bajarish uchun y=f(x) ma'lum bir nuqtada farqlanishi mumkin edi x, bu nuqtada uning cheklangan hosilasi bo'lishi zarur va etarli. Qayerda A=f′(x), ya'ni
Dy = f'(x) Dx +o(Dx).
Hosilni topish operatsiyasi odatda differentsiallash deb ataladi.
Teorema. Agar funktsiya y=f(x) x, keyin bu nuqtada uzluksiz bo'ladi.
Izoh. Funksiyaning uzluksizligidan y=f(x) ayni paytda x, umuman olganda, funksiyaning differentsialligi kuzatilmaydi f(x) ayni paytda. Masalan, funktsiya y=|x|- bir nuqtada uzluksiz x=0, lekin hosilasi yo'q.
Differensial funksiya haqida tushuncha
Ta'rif. Funktsiya differensial y=f(x) bu funktsiyaning hosilasi va mustaqil o'zgaruvchining o'sish ko'paytmasi deyiladi x:
dy = y′ Dx, df(x) = f′(x) Dx.
Funktsiya uchun y=x olamiz dy=dx=x′Dx = 1· Dx= Dx, ya'ni dx=Dx- mustaqil o'zgaruvchining differensialligi ushbu o'zgaruvchining o'sishiga teng.
Shunday qilib, biz yozishimiz mumkin
dy = y′ dx, df(x) = f′(x) dx
![]()
Differensial dy va oshirish dy funktsiyalari y=f(x) ayni paytda x, ikkalasi ham bir xil argument o'sishiga mos keladi Dx, umuman olganda, bir-biriga teng emas.
Differensialning geometrik ma'nosi: Argument oshirilganda funksiyaning differensialligi ushbu funksiya grafigiga teginish ordinatasining ortishiga teng. Dx.
Farqlash qoidalari
Teorema. Funktsiyalarning har biri bo'lsa u(x) Va v(x) ma'lum bir nuqtada farqlanadi x, so'ngra bu funktsiyalarning yig'indisi, farqi, mahsuloti va qismi (ko'rsatkich bo'lsa v(x)≠ 0) bu nuqtada ham farqlanadi va formulalar quyidagilarni o'z ichiga oladi:

Murakkab funktsiyani ko'rib chiqing y=f(ph(x))≡ F(x), Qayerda y=f(u), u=ph(x). Ushbu holatda u chaqirdi oraliq argument, x - mustaqil o'zgaruvchi.
Teorema. Agar y=f(u) Va u=ph(x) argumentlarining differensiallanuvchi funksiyalari, keyin esa kompleks funksiyaning hosilasi y=f(ph(x)) mavjud va bu funktsiyaning oraliq argumentga nisbatan mahsulotiga va mustaqil o'zgaruvchiga nisbatan oraliq argumentning hosilasiga teng, ya'ni.
![]()
Izoh. Uch funktsiyaning superpozitsiyasi bo'lgan murakkab funktsiya uchun y=F(f(ph(x))), farqlash qoidasi shaklga ega
y' x = y' u u' v v' x,
funktsiyalari qayerda v=ph(x), u=f(v) Va y=F(u)- ularning argumentlarining differentsial funksiyalari.
Teorema. Funktsiyaga ruxsat bering y=f(x) oshadi (yoki kamayadi) va nuqtaning ba'zi qo'shnilarida uzluksizdir x 0. Bundan tashqari, ushbu funktsiya ko'rsatilgan nuqtada differentsial bo'lsin x 0 va bu nuqtada uning hosilasi f'(x 0) ≠ 0. Keyin tegishli nuqtaning ba'zi mahallalarida y 0 =f(x 0) uchun teskarisi aniqlanadi y=f(x) funktsiyasi x=f -1 (y), va ko'rsatilgan teskari funktsiya mos keladigan nuqtada differentsiallanadi y 0 =f(x 0) va bu nuqtada uning hosilasi uchun y formula haqiqiydir

Hosilalar jadvali

Birinchi differentsial shaklining o'zgarmasligi
Kompleks funktsiyaning differentsialini ko'rib chiqamiz. Agar y=f(x), x=ph(t)- ularning argumentlarining funktsiyalari differentsial bo'ladi, keyin funktsiyaning hosilasi y=f(ph(t)) formula bilan ifodalanadi
y' t = y' x x' t.
A-prior dy=y′ t dt, keyin olamiz
dy = y′ t dt = y′ x · x′ t dt = y′ x (x′ t dt) = y′ x dx,
dy = y' x dx.
Shunday qilib, biz isbotladik
Funktsiyaning birinchi differentsial shaklining o'zgarmaslik xususiyati: argument bo'lganda bo'lgani kabi x mustaqil o'zgaruvchidir va argument bo'lgan holatda x o'zi yangi o'zgaruvchining differentsial funksiyasi, differentsialdir dy funktsiyalari y=f(x) bu funksiya hosilasining argumentning differentsialiga ko‘paytirilganiga teng dx.
Differensialni taxminiy hisoblarda qo'llash
Differensial ekanligini ko'rsatdik dy funktsiyalari y=f(x), umuman olganda, o'sishga teng emas dy bu funksiya. Biroq, kichiklikning yuqori tartibidagi cheksiz kichik funktsiyagacha Dx, taxminiy tenglik amal qiladi
Dy ≈ dy.
Nisbatan bu tenglik tengligining nisbiy xatosi deyiladi. Chunki Dy-dy=o(Dx), keyin bu tenglikning nisbiy xatosi kamayishi bilan kerakli darajada kichik bo'ladi |Dx|.
Shuni hisobga olib Dy=f(x+d x)-f(x), dy=f'(x)Dx, olamiz f(x+d x)-f(x) ≈ f′(x)Dx yoki
f(x+d x) ≈ f(x) + f'(x)Dx.
Bu taxminiy tenglik xato bilan ruxsat beradi o(Dx) funktsiyasini almashtiring f(x) nuqtaning kichik bir mahallasida x(masalan, kichik qiymatlar uchun Dx) argumentning chiziqli funksiyasi Dx, o'ng tomonda turgan.
Yuqori tartibli hosilalar
Ta'rif. Funktsiyaning ikkinchi hosilasi (yoki ikkinchi tartibli hosilasi). y=f(x) birinchi hosilasining hosilasi deyiladi.
Funktsiyaning ikkinchi hosilasi uchun belgi y=f(x):
Ikkinchi hosilaning mexanik ma'nosi. Agar funktsiya y=f(x) to'g'ri chiziqdagi moddiy nuqtaning harakat qonunini, keyin ikkinchi hosilani tasvirlaydi f″(x) harakatlanuvchi nuqtaning vaqt momentidagi tezlanishiga teng x.
Uchinchi va to'rtinchi hosilalar xuddi shunday aniqlanadi.
Ta'rif. n th lotin (yoki hosila n-chi tartib) funktsiyalari y=f(x) uning hosilasi deyiladi n-1 th hosilasi:
y (n) =(y (n-1))′, f (n) (x)=(f (n-1) (x))′.
Belgilar: y″', y IV, y V va hokazo.
Hosilning geometrik ma'nosi
|
Egri chiziqqa TANGENTINING TA’RIFI Egri chiziqqa tangens y=ƒ(x) nuqtada M nuqta orqali o'tkazilgan sekantning chegaralanish pozitsiyasi deyiladi M va unga tutash nuqta M 1 nuqta bo'lishi sharti bilan egri chiziq M 1 nuqtaga egri chiziq bo'ylab cheksiz yaqinlashadi M. HOSULAMANING GEOMETRIK MA'NOSI Funktsiyaning hosilasi y=ƒ(x) nuqtada X 0 son jihatdan o'qga moyillik burchagi tangensiga teng Oh egri chiziqqa tangens y=ƒ(x) nuqtada M (x 0; ƒ(x 0)). |
VARIATION DOTIC TO CURVE Egri chiziqqa nuqta y=ƒ(x) aynan M nuqtadan o'tkazilgan chiziqning chegara pozitsiyasi deyiladi M va u bilan keyingi nuqta M 1 qiyshiq, aqldan tashqari, qanday nuqta M 1 egri chiziq muqarrar ravishda nuqtaga yaqinlashadi M. GEOMETRIK ZMIST POKHIDNOI Shunga o'xshash funktsiyalar y=ƒ(x) aynan x 0 son jihatdan qiyalikning o‘qga tangensiga teng Oh dotic, egri chiziqqa olib borilgan y=ƒ(x) aynan M (x 0; ƒ(x 0)). |
Hosilning amaliy ma’nosi
Keling, ma'lum bir funktsiyaning hosilasi sifatida topgan kattalik amaliy jihatdan nimani anglatishini ko'rib chiqaylik.
Eng avvalo, hosila- bu funktsiyaning berilgan nuqtadagi o'zgarish tezligini tavsiflovchi differentsial hisobning asosiy tushunchasi.
"O'zgarish tezligi" nima? Funktsiyani tasavvur qilaylik f(x) = 5. Argumentning (x) qiymatidan qat'i nazar, uning qiymati hech qanday tarzda o'zgarmaydi. Ya'ni, uning o'zgarish tezligi nolga teng.
Endi funktsiyani ko'rib chiqing f(x) = x. X ning hosilasi birga teng. Darhaqiqat, (x) argumentidagi har bir o'zgarish uchun funktsiyaning qiymati ham bittaga oshishini sezish oson.
Olingan ma'lumotlar nuqtai nazaridan, endi oddiy funksiyalarning hosilalari jadvalini ko'rib chiqamiz. Shunga asoslanib, funktsiyaning hosilasini topishning fizik ma'nosi darhol aniq bo'ladi. Bu tushunish amaliy muammolarni hal qilishni osonlashtirishi kerak.
Shunga ko‘ra, hosila funksiyaning o‘zgarish tezligini ko‘rsatsa, qo‘sh hosila tezlanishni ko‘rsatadi.
2080.1947