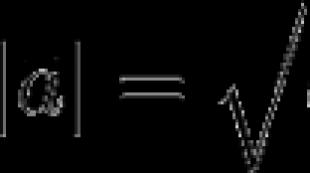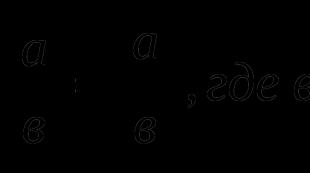Sagor

Vektor längd formel. Hitta längden på en vektor med koordinater. Formeln för att bestämma koordinaterna för en vektor för rumsliga problem

Låt oss hitta längden på vektorn genom dess koordinater (i ett rektangulärt koordinatsystem), genom koordinaterna för punkterna i början och slutet av vektorn och av cosinussatsen (2 vektorer och vinkeln mellan dem anges).

Vektor är ett riktat linjesegment. Längden på detta segment bestämmer vektorns numeriska värde och kallas vektorlängd eller vektormodul.

1. Beräkna längden på en vektor från dess koordinater

Om vektorkoordinaterna ges i ett platt (tvådimensionellt) rektangulärt koordinatsystem, d.v.s. a x och a y är kända, då kan längden på vektorn hittas av formeln

I fallet med en vektor i rymden läggs en tredje koordinat till

I MS EXCEL uttryck =ROT(SUMSQ(B8:B9)) låter dig beräkna vektorns modul (det antas att vektorkoordinatorerna anges i cellerna B8:B9, se exempelfil ).

Funktionen SUMSQ() returnerar summan av kvadraterna av argumenten, dvs. i detta fall, motsvarande formeln =B8*B8+B9*B9 .

Exempelfilen beräknar också längden på vektorn i rymden.

En alternativ formel är uttrycket =ROT(SUMMAPRODUKT(B8:B9,B8:B9)).

2. Hitta längden på en vektor genom punkternas koordinater

Om vektorn ges genom koordinaterna för dess start- och slutpunkter, kommer formeln att vara annorlunda =ROT(SUMDIFF(C28:C29;B28:B29))

Formeln förutsätter att koordinaterna för start- och slutpunkterna anges i intervallen C28:C29 Och B28:B29 respektive.

Fungera SUMMQVAR() in Returnerar summan av kvadrerade skillnader mellan motsvarande värden i två arrayer.

Faktum är att formeln först beräknar vektorns koordinater (skillnaden mellan motsvarande koordinater för punkterna), beräknar sedan summan av deras kvadrater.

3. Hitta längden på en vektor med hjälp av cosinussatsen

Om du vill hitta längden på en vektor med hjälp av cosinussatsen, så anges vanligtvis 2 vektorer (deras moduler och vinkeln mellan dem).

Hitta längden på vektorn med hjälp av formeln =ROT(SUMQ(B43:C43)-2*B43*C43*COS(B45))

I celler B43:B43 innehåller längderna av vektorerna a och b, och cellen B45 - vinkeln mellan dem i radianer (i bråkdelar av talet PI() ).

Om vinkeln anges i grader, kommer formeln att vara något annorlunda. =ROOT(B43*B43+C43*C43-2*B43*C43*COS(B46*PI()/180))

Notera: för tydlighetens skull, i en cell med ett vinkelvärde i grader, kan du använda , se till exempel artikeln

Oxy

HANDLA OM A OA.

, var OA .

Således, .

Tänk på ett exempel.

Exempel.

Lösning.

Svar:

Oxyz i rymden.

A OA kommer att vara en diagonal.

I det här fallet (eftersom OA OA .

Således, vektor längd .

Exempel.

Beräkna vektorlängd

Lösning.

, därav,

Svar:

Rak linje på ett plan

Allmän ekvation

Axe + By + C ( > 0).

Vektor = (A; B)är en normal linjevektor.

I vektorform: + C = 0, där är radievektorn för en godtycklig punkt på en rät linje (Fig. 4.11).

Speciella fall:

1) Med + C = 0- rät linje parallell med axeln Oxe;

2) Ax+C=0- rät linje parallell med axeln Oj;

3) Axe + By = 0- linjen går genom origo;

4) y=0- axel Oxe;

5) x=0- axel Oj.

Ekvation för en rät linje i segment

Var a, b- storleken på segmenten avskurna av en rät linje på koordinataxlarna.

Normalekvationen för en rät linje(Bild 4.11)

var är vinkeln som bildas normalt mot linjen och axeln Oxe; sidär avståndet från koordinaternas ursprung till linjen.

Att föra den allmänna ekvationen för en rät linje till normal form:

Här är den normaliserade faktorn för den direkta linjen; tecknet väljs mitt emot tecknet C, if och godtyckligt, if C=0.

Hitta längden på en vektor med koordinater.

Längden på vektorn kommer att betecknas med . På grund av denna notation kallas längden på en vektor ofta till som vektorns modul.

Låt oss börja med att hitta längden på vektorn på planet genom koordinaterna.

Vi introducerar ett rektangulärt kartesiskt koordinatsystem på planet Oxy. Låt en vektor ges i den och den har koordinater. Låt oss få en formel som låter dig hitta längden på vektorn genom koordinaterna och .

Sätt åt sidan från utgångspunkten för koordinaterna (från punkten HANDLA OM) vektor . Beteckna punktens projektioner A på koordinataxlarna som och respektive och betrakta en rektangel med en diagonal OA.

I kraft av Pythagoras sats, jämlikheten , var . Från definitionen av koordinaterna för en vektor i ett rektangulärt koordinatsystem kan vi hävda att och , och genom konstruktion, längden OAär lika med längden på vektorn, därför .

Således, formel för att hitta längden på en vektor i sina koordinater på planet har formen .

Om vektorn representeras som en sönderdelning i koordinatvektorer , sedan beräknas dess längd med samma formel , eftersom i detta fall koefficienterna och är koordinaterna för vektorn i det givna koordinatsystemet.

Tänk på ett exempel.

Exempel.

Hitta längden på vektorn i kartesiska koordinater.

Lösning.

Använd omedelbart formeln för att hitta vektorns längd med koordinater :

Svar:

Nu får vi en formel för att hitta längden på en vektor genom sina koordinater i ett rektangulärt koordinatsystem Oxyz i rymden.

Lägg vektorn åt sidan från origo och beteckna punktens projektioner A på koordinataxlarna samt . Då kan vi bygga på sidorna och en rektangulär parallellepiped där OA kommer att vara en diagonal.

I det här fallet (eftersom OAär diagonalen för en rektangulär parallellepiped), varifrån . Genom att bestämma koordinaterna för vektorn kan vi skriva likheterna och längden OAär lika med den önskade längden på vektorn, därför .

Således, vektor längd i rymden är lika med kvadratroten av summan av kvadraterna av dess koordinater, det vill säga hittas av formeln .

Exempel.

Beräkna vektorlängd , var är orterna för det rektangulära koordinatsystemet.

Lösning.

Vi ges expansionen av en vektor i form av koordinatvektorer för formen , därav, . Sedan, enligt formeln för att hitta längden på en vektor med koordinater, har vi .

På abskissan och ordinatan kallas axlar koordinater vektor. Vektorkoordinaterna anges vanligtvis i formuläret (x, y), och själva vektorn som: = (x, y).

Formeln för att bestämma koordinaterna för en vektor för tvådimensionella problem.

Vid ett tvådimensionellt problem, en vektor med känd punktkoordinater A(x 1; y 1) Och B(x 2 ; y 2 ) kan beräknas:

\u003d (x 2 - x 1; y 2 -y 1).

Formeln för att bestämma koordinaterna för en vektor för rumsliga problem.

I fallet med ett rumsligt problem, en vektor med känd punktkoordinater A (x 1; y 1;z 1 ) och B (x 2 ; y 2 ; z 2 ) kan beräknas med formeln:

= (x 2 - x 1 ; y 2 - y 1 ; z 2 - z 1 ).

Koordinaterna ger en omfattande beskrivning av vektorn, eftersom det är möjligt att konstruera själva vektorn från koordinaterna. Genom att känna till koordinaterna är det lätt att beräkna och vektor längd. (Egenskap 3 nedan).

Vektorkoordinategenskaper.

1. Alla lika vektorer i ett enda koordinatsystem har lika koordinater.

2. Koordinater kolinjära vektorer proportionell. Förutsatt att ingen av vektorerna är lika med noll.

3. Kvadraten på längden av en vektor är lika med summan av dess kvadrater koordinater.

4.När operationen vektormultiplikationer på riktigt nummer var och en av dess koordinater multipliceras med detta tal.

5. Under driften av vektoraddition beräknar vi summan av motsvarande vektorkoordinater.

6. Skalär produkt av två vektorer är lika med summan av produkterna av deras respektive koordinater.

Längden på vektorn a → kommer att betecknas med a → . Denna notation liknar modulen för ett tal, så längden på en vektor kallas också modulen för en vektor.

För att hitta längden på en vektor på planet genom dess koordinater, måste man betrakta ett rektangulärt kartesiskt koordinatsystem O x y . Låt den innehålla någon vektor a → med koordinaterna a x ; ett y. Vi introducerar en formel för att hitta längden (modulen) av vektorn a → i termer av koordinaterna a x och a y .

Lägg undan vektorn OA → = a → från origo. Låt oss definiera motsvarande projektioner av punkten A på koordinataxlarna som A x och A y . Betrakta nu en rektangel O A x A A y med diagonal O A .

Från Pythagoras sats följer likheten O A 2 = O A x 2 + O A y 2 , varav O A = O A x 2 + O A y 2 . Från den redan kända definitionen av koordinaterna för en vektor i ett rektangulärt kartesiskt koordinatsystem får vi att OA x 2 = a x 2 och O A y 2 = a y 2 , och genom konstruktion är längden av OA lika med längden på vektor OA → , därför OA → = OA x 2 + O A y 2.

Därför visar det sig att formel för att hitta längden på en vektor a → = a x; a y har motsvarande form: a → = a x 2 + a y 2 .

Om vektorn a → ges som en expansion i koordinatvektorerna a → = a x i → + a y j → , så kan dess längd beräknas med samma formel a → = a x 2 + a y 2 , i detta fall är koefficienterna a x och a y som koordinaterna för vektorn a → i det givna koordinatsystemet.

Exempel 1

Beräkna längden på vektorn a → = 7 ; e , givet i ett rektangulärt koordinatsystem.

Lösning

För att hitta längden på en vektor använder vi formeln för att hitta längden på en vektor genom koordinaterna a → = a x 2 + a y 2: a → = 7 2 + e 2 = 49 + e

Svar: a → = 49 + e.

Formel för att hitta längden på en vektor a → = a x ; ett y; a z av dess koordinater i det kartesiska koordinatsystemet Oxyz i rymden, härleds på samma sätt som formeln för fallet på planet (se figuren nedan)

I det här fallet, OA 2 \u003d OA x 2 + O A y 2 + OA z 2 (eftersom OA är diagonalen för en rektangulär parallellepiped), därav OA \u003d OA x 2 + OA y 2 + O A z 2. Från definitionen av vektorns koordinater kan vi skriva följande likheter O A x = a x ; O A y = a y; OAz = az; , och längden på OA är lika med längden på vektorn vi letar efter, därför OA → = OA x 2 + O A y 2 + OA z 2 .

Det följer att längden på vektorn a → = a x ; ett y; a z är lika med a → = a x 2 + a y 2 + a z 2 .

Exempel 2

Beräkna längden på vektorn a → = 4 i → - 3 j → + 5 k → , där i → , j → , k → är enhetsvektorerna för det rektangulära koordinatsystemet.

Lösning

Givet en nedbrytning av en vektor a → = 4 i → - 3 j → + 5 k → är dess koordinater a → = 4 , - 3 , 5 . Med formeln ovan får vi a → = a x 2 + a y 2 + a z 2 = 4 2 + (- 3) 2 + 5 2 = 5 2 .

Svar: a → = 5 2 .

Längden på en vektor i termer av koordinaterna för dess start- och slutpunkter

Ovan härleddes formler som låter dig hitta längden på en vektor genom dess koordinater. Vi har övervägt fall på planet och i tredimensionellt utrymme. Låt oss använda dem för att hitta vektorns koordinater genom koordinaterna för dess start- och slutpunkter.

Så, givna punkter med givna koordinater A (a x; a y) och B (b x; b y), därför har vektorn A B → koordinater (b x - a x; b y - a y), vilket betyder att dess längd kan bestämmas med formeln: A B → = ( b x - a x) 2 + (b y - a y) 2

Och om punkter ges med givna koordinater A (a x; a y; a z) och B (b x; b y; b z) i tredimensionellt rymd, så kan längden på vektorn A B → beräknas med formeln

A B → = (b x - a x) 2 + (b y - a y) 2 + (b z - a z) 2

Exempel 3

Hitta längden på vektorn A B → om i ett rektangulärt koordinatsystem A 1 , 3 , B - 3 , 1 .

Lösning

Med hjälp av formeln för att hitta vektorlängden från koordinaterna för start- och slutpunkterna på planet får vi A B → = (b x - a x) 2 + (b y - a y) 2: A B → = (- 3 - 1) 2 + (1 - 3) 2 = 20 - 2 3 .

Den andra lösningen innebär tillämpning av dessa formler i sin tur: A B → = (- 3 - 1; 1 - 3) = (- 4; 1 - 3) ; A B → = (- 4) 2 + (1 - 3) 2 = 20 - 2 3 . -

Svar: A B → = 20 - 2 3 .

Exempel 4

Bestäm för vilka värden längden på vektorn A B → är lika med 30 om A (0 , 1 , 2) ; B (5, 2, X2).

Lösning

Låt oss först skriva längden på vektorn A B → enligt formeln: A B → = (b x - a x) 2 + (b y - a y) 2 + (b z - a z) 2 = (5 - 0) 2 + (2 - 1) 2 + (λ 2 - 2) 2 = 26 + (λ 2 - 2) 2

Sedan likställer vi det resulterande uttrycket med 30, härifrån hittar vi det önskade λ:

26 + (λ 2 - 2) 2 = 30 26 + (λ 2 - 2) 2 = 30 (λ 2 - 2) 2 = 4 λ 2 - 2 = 2 och l och λ 2 - 2 = - 2 λ 1 = -2, X2 = 2, X3 = O.

Svar: λ 1 \u003d - 2, λ 2 \u003d 2, λ 3 \u003d 0.

Hitta längden på en vektor med hjälp av cosinuslagen

Tyvärr är koordinaterna för en vektor inte alltid kända i uppgifter, så låt oss överväga andra sätt att hitta längden på en vektor.

Låt längden på två vektorer A B → , A C → och vinkeln mellan dem (eller vinkelns cosinus) anges, och det krävs att man hittar längden på vektorn B C → eller C B → . I det här fallet ska du använda cosinussatsen i triangeln △ A B C , beräkna längden på sidan B C , som är lika med den önskade längden på vektorn.

Låt oss överväga ett sådant fall i följande exempel.

Exempel 5

Längden på vektorerna A B → och A C → är lika med 3 respektive 7, och vinkeln mellan dem är lika med π 3 . Beräkna längden på vektorn B C → .

Lösning

Längden på vektorn B C → i detta fall är lika med längden på sidan B C i triangeln △ A B C . Längden på sidorna A B och A C i triangeln är kända från villkoret (de är lika med längden på motsvarande vektorer), vinkeln mellan dem är också känd, så vi kan använda cosinussatsen: B C 2 = A B 2 + A C 2 - 2 A B A C cos ∠ (AB , → A C →) = 3 2 + 7 2 - 2 3 7 cos π 3 = 37 ⇒ B C = 37 Alltså B C → = 37 .

Svar: Bc^ = 37.

Så för att hitta längden på en vektor med koordinater finns följande formler a → = a x 2 + a y 2 eller a → = a x 2 + a y 2 + a z 2, enligt koordinaterna för punkterna i början och slutet av vektorn A B → = (b x - a x) 2 + ( b y - a y) 2 eller A B → = (b x - a x) 2 + (b y - a y) 2 + (b z - a z) 2, i vissa fall cosinussatsen borde användas.

Om du märker ett fel i texten, markera det och tryck på Ctrl+Enter

6.4. Vissa tillämpningar av dot-produkten

11. Uttryck av skalärprodukten av en vektor i termer av faktorernas koordinater. Sats.

12. Längd på en vektor, längd på ett segment, vinkel mellan vektorer, villkor för vinkelräthet av vektorer.

13. Vektorprodukt av vektorer, dess egenskaper. Arean av ett parallellogram.

14. Blandad produkt av vektorer, dess egenskaper. Villkoret för vektorkomplanaritet. Volymen av parallellepipeden. Pyramidens volym.

15. Metoder för att sätta en rät linje på ett plan.

16. Normalekvation för en rät linje på ett plan (derivation). Koefficienternas geometriska betydelse.

17. Ekvationen för en rät linje på ett plan i segment (slutsats).

Reduktion av den allmänna ekvationen för planet till ekvationen för planet i segment.

18. Ekvationen för en rät linje i ett plan med en lutning (utgång).

19. Ekvation för en rät linje på ett plan som går genom två punkter (slutsats).

20. Vinkel mellan räta linjer på ett plan (slutsats).

21. Avstånd från en punkt till en rät linje på ett plan (utgång).

22. Villkor för parallellitet och vinkelräthet hos räta linjer på ett plan (slutsats).

23. Planets ekvation. Planets normala ekvation (härledning). Koefficienternas geometriska betydelse.

24. Planets ekvation i segment (slutsats).

25. Ekvation för ett plan som passerar genom tre punkter (utgång).

26. Vinkel mellan plan (utgång).

27. Avstånd från en punkt till ett plan (utgång).

28. Villkor för parallellitet och vinkelräta plan (slutsats).

29. Ekvationer för en rät linje i r3. Ekvationer för en rät linje som går genom två fasta punkter (derivation).

30. Kanoniska ekvationer av en rät linje i rymden (derivation).

Sammanställning av kanoniska ekvationer för en rät linje i rymden.

Särskilda fall av kanoniska ekvationer av en rät linje i rymden.

Kanoniska ekvationer av en rät linje som går genom två givna punkter i rymden.

Övergång från kanoniska ekvationer av en rät linje i rymden till andra typer av ekvationer av en rät linje.

31. Vinkel mellan raka linjer (utgång).

32. Avstånd från en punkt till en rät linje på ett plan (utgång).

Avstånd från en punkt till en rät linje på ett plan - teori, exempel, lösningar.

Det första sättet att hitta avståndet från en given punkt till en given rät linje på ett plan.

Den andra metoden, som låter dig hitta avståndet från en given punkt till en given linje på planet.

Lösa problem med att hitta avståndet från en given punkt till en given rät linje på ett plan.

Avstånd från en punkt till en rät linje i rymden - teori, exempel, lösningar.

Det första sättet att hitta avståndet från en punkt till en linje i rymden.

Den andra metoden, som låter dig hitta avståndet från en punkt till en rak linje i rymden.

33. Villkor för parallellitet och vinkelräta linjer i rymden.

34. Inbördes arrangemang av raka linjer i rymden och en rak linje med ett plan.

35. Den klassiska ekvationen för en ellips (avledning) och dess konstruktion. Den kanoniska ekvationen för en ellips har formen där finns dessutom positiva reella tal Hur bygger man en ellips?

36. Den klassiska ekvationen för en hyperbel (avledning) och dess konstruktion. Asymptoter.

37. Kanonisk ekvation av en parabel (avledning) och konstruktion.

38. Funktion. Grundläggande definitioner. Grafer över grundläggande elementära funktioner.

39. Nummerföljder. Gränsen för den numeriska sekvensen.

40. Oändligt små och oändligt stora mängder. Satsen om sambandet mellan dem, egenskaper.

41. Satser om åtgärder på variabler med ändliga gränser.

42. Nummer e.

Innehåll

Metoder för att bestämma

Egenskaper

Berättelse

Uppskattningar

43. Definition av gränsen för en funktion. Avslöjande av osäkerheter.

44. Anmärkningsvärda gränser, deras slutsats. Motsvarande oändliga mängder.

Innehåll

Första underbara gränsen

Den andra underbara gränsen

45. Ensidiga gränser. Kontinuitet och diskontinuiteter av funktion. Ensidiga gränser

Vänster och höger gränser för en funktion

Diskontinuitetspunkt av det första slaget

Diskontinuitetspunkt av det andra slaget

Brytpunkt

46. Definition av ett derivat. Geometrisk betydelse, mekanisk betydelse av derivatan. Tangent- och normalekvationer för en kurva och en punkt.

47. Satser om derivatan av de inversa, komplexa funktionerna.

48. Derivater av de enklaste elementära funktionerna.

49. Differentiering av parametriska, implicita och exponentiella funktioner.

21. Differentiering av implicita och parametriskt definierade funktioner

21.1. Implicit funktion

21.2. Funktion definierad parametriskt

50. Derivat av högre ordning. Taylor formel.

51. Differential. Tillämpning av differentialen för ungefärliga beräkningar.

52. Satser av Rolle, Lagrange, Cauchy. L'Hopitals regel.

53. Sats om nödvändiga och tillräckliga villkor för en funktions monotoni.

54. Bestämning av max, minimum av en funktion. Satser om nödvändiga och tillräckliga villkor för existensen av ett extremum av en funktion.

Sats (nödvändigt extremumvillkor)

55. Konvexitet och konkavitet av kurvor. Böjningspunkter. Satser om nödvändiga och tillräckliga förutsättningar för förekomsten av böjningspunkter.

Bevis

57. Bestämningsfaktorer för den n:e ordningen, deras egenskaper.

58. Matriser och åtgärder på dem. Matrix rang.

Definition

Relaterade definitioner

Egenskaper

Linjär transformation och matrisrang

59. Invers matris. Sats om förekomsten av en invers matris.

60. Linjära ekvationssystem. Matrislösning av linjära ekvationssystem. Cramers regel. Gauss metod. Kronecker-Capelli-satsen.

Lösa system av linjära algebraiska ekvationer, lösningsmetoder, exempel.

Definitioner, begrepp, beteckningar.

Lösning av elementära system av linjära algebraiska ekvationer.

Lösa linjära ekvationssystem med Cramers metod.

Lösa system av linjära algebraiska ekvationer med matrismetoden (med invers matris).

Lösa linjära ekvationssystem med Gauss-metoden.

Lösa system av linjära algebraiska ekvationer av allmän form.

Kronecker-Capelli-satsen.

Gauss metod för att lösa system av linjära algebraiska ekvationer av allmän form.

Registrering av den allmänna lösningen av homogena och inhomogena linjära algebraiska system med hjälp av vektorerna för det fundamentala lösningssystemet.

Lösning av ekvationssystem som reducerar till slough.

Exempel på problem som reducerar till att lösa system av linjära algebraiska ekvationer.

12. Längd på en vektor, längd på ett segment, vinkel mellan vektorer, villkor för vinkelräthet av vektorer.

Vektor - det är ett riktat segment som förbinder två punkter i rymden eller i ett plan. Vektorer betecknas vanligtvis antingen med små bokstäver eller med start- och slutpunkter. Ovan är vanligtvis ett streck.

Till exempel en vektor riktad från en punkt A till poängen B, kan betecknas a ,

Noll vektor 0 eller 0 - är en vektor vars start- och slutpunkter är desamma, dvs. A = B. Härifrån, 0 = – 0 .

Längd (modul) av vektorna är längden på segmentet som representerar det AB, betecknad med |a | . I synnerhet | | 0 | = 0.

Vektorerna kallas kolinjär om deras riktade segment ligger på parallella linjer. Kolinjära vektorer a Och b är utsedda a || b .

Tre eller flera vektorer kallas i samma plan om de ligger i samma plan.

Tillägg av vektorer. Eftersom vektorer är riktad segment, så kan deras tillägg utföras geometriskt. (Algebraisk addition av vektorer beskrivs nedan, i stycket "Ortogonala enhetsvektorer"). Låt oss låtsas som det

a = AB och b = CD,

sedan vektorn __ __

a + b = AB+ CD

är resultatet av två operationer:

a)parallell överföring en av vektorerna så att dess startpunkt sammanfaller med slutpunkten för den andra vektorn;

b)geometriskt tillägg, dvs. konstruera den resulterande vektorn som går från startpunkten för den fixerade vektorn till slutpunkten för den translaterade vektorn.

Subtraktion av vektorer. Denna operation reduceras till den föregående genom att ersätta den subtraherade vektorn med den motsatta: a – b =a + (– b ) .

Lagarna för addition.

jag. a + b = b + a (V erabel lag).

II. (a + b ) + c = a + (b + c ) (Kombinerad lag).

III. a + 0 = a .

IV. a + (– a ) = 0 .

Lagar för multiplikation av en vektor med ett tal.

jag. 1 · a = a , 0 · a = 0 , m· 0 = 0 , (– 1) · a = – a .

II. ma = a m,| ma | = | m | · | en | .

III. m(na ) = (m n)a . (Kombinerad

multiplikationens lag).

IV. (m+n) a = ma +na , (Distributör

m(a + b ) = ma + mb . multiplikationens lag).

Skalär produkt av vektorer. __ __

Vinkel mellan vektorer som inte är noll AB Och CDär den vinkel som bildas av vektorerna under deras parallella överföring tills punkterna är inriktade A Och C. Punktprodukt av vektorera Och b kallas ett tal lika med produkten av deras längder med cosinus för vinkeln mellan dem:

Om en av vektorerna är noll, är deras skalära produkt, i enlighet med definitionen, noll:

(en , 0 ) = ( 0 , b ) = 0 .

Om båda vektorerna inte är noll, beräknas cosinus för vinkeln mellan dem med formeln:

Skalär produkt ( a, a ) lika med | a | 2 kallas skalär kvadrat. Vektor längd a och dess skalära kvadrat är relaterade till:

Punktprodukt av två vektorer:

- positivt om vinkeln mellan vektorerna kryddad;

- negativ om vinkeln mellan vektorerna trubbig.

Skalärprodukten av två icke-nollvektorer är då noll och endast om vinkeln mellan dem är rätt, d.v.s. när dessa vektorer är vinkelräta (ortogonala):

Egenskaper hos den skalära produkten. För alla vektorer en , före Kristus och valfritt nummer m följande relationer är giltiga:

jag. (en , b ) = (b, a ) . (V erabel lag)

II. (men , b ) = m(en , b ) .

III.(a + b, c ) = (en , c ) + (b, c ). (Distributiv lag)

Enhet ortogonala vektorer. I vilket rektangulärt koordinatsystem som helst kan du gå in enhet parvisa ortogonala vektoreri , j Och k associerade med koordinataxlarna: i - med axel X, j - med axel Y Och k - med axel Z. Enligt denna definition:

(i , j ) = (i , k ) = (j , k ) = 0,

| jag | =| j | =| k | = 1.

Vilken vektor som helst a kan uttryckas i termer av dessa vektorer på ett unikt sätt: a = xi + yj+ zk . En annan form av skrivande: a = (x, y, z). Här x, y, z-koordinater vektor a i detta koordinatsystem. I enlighet med den sista relationen och egenskaperna hos enhets ortogonala vektorer I j , k den skalära produkten av två vektorer kan uttryckas olika.

Låta a = (x, y, z); b = (u, v, w). Sedan ( en , b ) = xi +yv +zw.

Skalärprodukten av två vektorer är lika med summan av produkterna av motsvarande koordinater.

Längd (modul) av vektorn a = (x, y, z ) är lika med:

Dessutom kan vi nu algebraisk operationer på vektorer, nämligen addition och subtraktion av vektorer kan utföras med koordinater:

ett + b= (x + u, y + v, z + w) ;

a – b= (x–u, y– v, z–w) .

Vektorprodukt av vektorer. vektor konst [en, b ] vektorera Ochb (i den ordningen) kallas en vektor:

Det finns en annan formel för längden på vektorn [ a, b ] :

| [ a, b ] | = | a | | b | synd( a, b ) ,

dvs. längd ( modul ) korsprodukt av vektorera Ochb är lika med produkten av längderna (modulerna) av dessa vektorer och sinus för vinkeln mellan dem. Med andra ord: vektorns längd (modul).[ a, b ] numeriskt lika med arean av parallellogrammet byggt på vektorerna a Ochb .