Att upprätthålla din integritet är viktigt för oss. Av denna anledning har vi tagit fram en integritetspolicy som beskriver hur vi använder och lagrar din information. Läs igenom vår sekretesspraxis och låt oss veta om du har några frågor.

Insamling och användning av personlig information

Med personuppgifter avses uppgifter som kan användas för att identifiera eller kontakta en specifik person.

Du kan bli ombedd att lämna din personliga information när som helst när du kontaktar oss.

Nedan finns några exempel på de typer av personlig information vi kan samla in och hur vi kan använda sådan information.

Vilken personlig information samlar vi in:

• När du skickar in en ansökan på webbplatsen kan vi samla in olika uppgifter, inklusive ditt namn, telefonnummer, e-postadress, etc.

Hur vi använder din personliga information:

• De personuppgifter vi samlar in gör att vi kan kontakta dig med unika erbjudanden, kampanjer och andra evenemang och kommande evenemang.
• Från tid till annan kan vi använda din personliga information för att skicka viktiga meddelanden och kommunikationer.
• Vi kan även använda personuppgifter för interna ändamål, såsom att utföra revisioner, dataanalyser och olika undersökningar för att förbättra de tjänster vi tillhandahåller och ge dig rekommendationer angående våra tjänster.
• Om du deltar i en prisdragning, tävling eller liknande kampanj kan vi använda informationen du tillhandahåller för att administrera sådana program.

Utlämnande av information till tredje part

Vi lämnar inte ut informationen från dig till tredje part.

Undantag:

• Om nödvändigt - i enlighet med lagen, rättsliga förfaranden, i rättsliga förfaranden och/eller på grundval av offentliga förfrågningar eller förfrågningar från statliga myndigheter på Ryska federationens territorium - att avslöja din personliga information. Vi kan också komma att avslöja information om dig om vi fastställer att ett sådant avslöjande är nödvändigt eller lämpligt för säkerhets-, brottsbekämpande eller andra offentliga ändamål.
• I händelse av en omorganisation, sammanslagning eller försäljning kan vi komma att överföra den personliga information vi samlar in till tillämplig efterträdande tredje part.

Skydd av personlig information

Vi vidtar försiktighetsåtgärder - inklusive administrativa, tekniska och fysiska - för att skydda din personliga information från förlust, stöld och missbruk, såväl som obehörig åtkomst, avslöjande, ändring och förstörelse.

Respektera din integritet på företagsnivå

För att säkerställa att din personliga information är säker kommunicerar vi sekretess- och säkerhetsstandarder till våra anställda och tillämpar strikt sekretesspraxis.

I den här artikeln hittar du egenskaper för bisektrisen och medianen för en triangel som kan vara användbara för att lösa problem.

Bisektorer.

1. Skärningspunkten mellan halvledarna i en triangel är mitten av triangelns inskrivna cirkel.

Bevis.

Faktum är att punkter som ligger på bisektrisen av en vinkel är lika långt från vinkelns sidor. Följaktligen är skärningspunkten för bisektrarna lika långt från alla sidor av triangeln, det vill säga den är mitten av den inskrivna cirkeln.

2. Halslinjen i en triangel delar den motsatta sidan i segment som är proportionella mot de intilliggande sidorna:

Bevis.

Låt oss göra ytterligare konstruktioner. Låt oss dra en linje parallell med punkten

Skärningspunkten för en rät linje och en rät linje:

∠1=∠2, eftersom - bisektris ∠

∠2=∠3 liggande korsvis, som av konstruktion.

Därför, ∠1=∠3 och triangeln är likbent, och .

därav,

3. Längden på bisektrisen beräknas med följande formler:

Låt oss bevisa den andra formeln.

Låt oss presentera följande notation:

Låt oss likställa uttrycken för arean av triangeln:

4. Låt O vara mitten av cirkeln och vara bisektrisen av triangelns vinkel:

Då gäller förhållandet:

Bevis:

Tänk på en triangel:

Halvled av en vinkel, alltså genom egenskapen för en triangels bisektrik

Låt det vara då

Låt oss uttrycka det. Enligt egenskapen för bisektrisen i en triangel:

Härifrån

I vissa problem är det bekvämt att förlänga bisektrisen av en triangel till skärningen med den omskrivna cirkeln.

Lemma om trefoten.

Givet en triangel. Punkt - skärningspunkten för vinkelhalveringslinjen med triangelns omringade cirkel. Låt vara mitten av cirkeln inskriven i triangeln. Sedan

Bevis.

Inskrivna vinklar som bildar lika bågar är lika. Notera de lika inskrivna vinklarna:

Härifrån.

Mitten av incirkeln är därför vinkelns bisektrik.

Från en triangel

Sedan från triangeln

Fick.

Det vill säga triangeln är likbent.

Härifrån.

Bevisade det

Låt oss bevisa formel (1) från punkt 3:

Bevis:

Låt oss fortsätta med bisektrisen tills den skär den omslutna cirkeln. Tänk på trianglar och . Låt oss markera lika vinklar:

En triangel liknar en triangel i två vinklar. Härifrån:

Genom egenskapen för segment av korsande ackord

Låt oss ersätta (3) med (2) och använda (4):

Låt oss uttrycka längderna på segmenten i vilka halveringslinjen delar triangelns sida i termer av längderna på triangelns sidor. Låt oss presentera följande notation:

Vi får systemet:

Medianer.

1. Medianerna för en triangel divideras med skärningspunkten i förhållandet 2:1, räknat från vertex:

2. Låt vara en punkt inuti triangeln så att följande relation gäller: , då är skärningspunkten för triangelns medianer.

Bevis.

Låt oss bevisa ett hjälpteorem.

Lemma.

För en godtycklig punkt inuti en triangel gäller följande relation:

Låt oss falla från punkterna och vinkelräta till :

Från likheten mellan trianglar får vi:

Om vi ​​betraktar trianglar med en gemensam bas , då får vi relationen:

På samma sätt får vi

Lägger vi till dessa jämlikheter får vi:

Vi använder detta lemma för att bevisa påstående 2.

Om jämställdheten håller (1), sedan jämställdheten (2) och av lemma följer att i likhet (2) är varje bråktal lika med .

Låt oss bevisa att i detta fall segmenten är medianer.

Om , då får vi . Låt oss rita raka linjer parallella med och genom punkten och betrakta två par liknande trianglar: och:

Härifrån får vi

Från likheten mellan trianglar får vi, det vill säga punkten är mitten av segmentet. Härifrån.

Därför är medianen för triangeln.

3. Medianerna för en triangel, som skär varandra, delar den i 6 lika trianglar.

Bevis.

Låt oss bevisa det

därför att ,

därför att ,

Därav,

höjder.

1. Linjerna som innehåller triangelns höjder skär varandra vid en punkt. I fallet med en spetsig triangel, skär själva höjderna vid en punkt.

2. Skärningspunkten för en triangels höjder har följande egenskap: summan av kvadraten på avståndet från triangelns vertex och kvadraten på den motsatta sidan är densamma för alla vertex:

Bevis.

Låt oss bevisa den första delen av jämlikheten:

Låt oss skriva om det i formen:

Enligt Pythagoras sats: (från trianglar och)

(från triangel)

(från triangel)

Genom att ersätta dessa uttryck med (1) får vi:

Låt oss öppna parenteserna och få:

Vi har en identitet. Den andra delen av jämlikheten bevisas på liknande sätt.

3. Om vi ​​beskriver en cirkel runt en triangel och förlänger triangelns höjder tills de skär denna cirkel,

för varje höjd av en triangel är avståndet från höjdens bas till skärningspunkten för fortsättningen av höjden med cirkeln lika med avståndet från höjdens bas till skärningspunkten för höjderna:

Eller så här: Punkter som är symmetriska till skärningspunkten för triangelns höjder i förhållande till triangelns sidor ligger på triangelns omringade cirkel.

Bevis.

Låt oss bevisa det.

För att göra detta, överväg trianglar och , och bevisa det :

Låt oss använda tecknet att trianglar är lika längs en sida och två intilliggande vinklar. - allmän sida. Låt oss bevisa likheten mellan två vinklar.

Låt oss bevisa att ∠ ∠

Låt ∠, sedan får vi det från triangeln

∠. Därför får vi det från triangeln

Men ∠ och ∠ vilar på samma båge, därför ∠ ∠ ∠

På samma sätt finner vi att ∠ ∠

4. I en triangel är punkterna och baserna för de höjder som dras från hörnen och. Bevisa att en triangel liknar en triangel och att likhetskoefficienten är lika med .

Bevis:

Mitten av den omskrivna cirkeln i en rätvinklig triangel ligger i mitten av hypotenusan . Poängen ligger på denna cirkel eftersom - hypotenusa av en rätvinklig triangel:

Som inskrivna vinklar baserade på en båge.

från triangeln:

Härifrån. Vinkel är den vanliga vinkeln för trianglar och. Därför liknar en triangel en triangel. Likhetskoefficienten är lika med förhållandet mellan liknande sidor, det vill säga sidor som ligger mitt emot lika vinklar:

Cevas sats

Släpp in en triangel

Segment skär varandra vid en punkt om och endast om

Bevis.

Låt oss bevisa att om segmenten skär varandra vid en punkt, så är relation (1) uppfylld.

Det är lätt att kontrollera att om , då håller

Låt oss tillämpa denna proportionsegenskap:

Likaså:

Cevas sats kan skrivas så här:

Om segmenten skär varandra vid en punkt, gäller följande relation:

Att bevisa Cevas sats i form av sinus, det räcker att i den andra delen av likhet (2) istället för arean av trianglarna ersätta arean av varje triangel med formeln .

Från föreläsningar av Nazar Khangeldyevich Agakhanov och Vladimir Viktorovich Trushkov, KPK MIPT.

En triangel är en polygon med tre sidor, eller en sluten streckad linje med tre länkar, eller en figur som bildas av tre segment som förbinder tre punkter som inte ligger på samma räta linje (se fig. 1).

Grundläggande element i triangeln abc

Toppar – punkterna A, B och C;

Fester – segmenten a = BC, b = AC och c = AB som förbinder hörnen;

Vinklar – α, β, γ bildade av tre par sidor. Vinklar betecknas ofta på samma sätt som hörn, med bokstäverna A, B och C.

Vinkeln som bildas av en triangels sidor och som ligger i dess inre område kallas en inre vinkel, och den intill den är triangelns intilliggande vinkel (2, s. 534).

En triangels höjder, medianer, bisektrar och mittlinjer

Förutom huvudelementen i en triangel övervägs även andra segment med intressanta egenskaper: höjder, medianer, bisektrar och mittlinjer.

Höjd

Triangelhöjder- dessa är vinkelräta vinkelräta från triangelns hörn till motsatta sidor.

För att rita höjden måste du utföra följande steg:

1) rita en rak linje som innehåller en av triangelns sidor (om höjden är ritad från spetsen av en spetsig vinkel i en trubbig triangel);

2) från spetsen som ligger mittemot den ritade linjen, rita ett segment från punkten till denna linje och gör en vinkel på 90 grader med den.

Punkten där höjden skär triangelns sida kallas höjd bas (se fig. 2).

Egenskaper för triangelhöjder

I en rätvinklig triangel delar höjden från spetsen av den räta vinkeln den i två trianglar som liknar den ursprungliga triangeln.

I en spetsig triangel skär dess två höjder av liknande trianglar från den.

Om triangeln är spetsig, hör alla höjdernas baser till triangelns sidor, och i en trubbig triangel faller två höjder på fortsättningen av sidorna.

Tre höjder i en spetsig triangel skär varandra vid en punkt och denna punkt kallas ortocenter triangel.

Median

Medianer(från latin mediana - "mitten") - dessa är segment som förbinder triangelns hörn med mittpunkterna på de motsatta sidorna (se fig. 3).

För att konstruera medianen måste du utföra följande steg:

1) hitta mitten av sidan;

2) koppla ihop punkten som är mitten av sidan av triangeln med motsatt vertex med ett segment.

Egenskaper för triangelmedian

Medianen delar en triangel i två trianglar med lika stor yta.

Medianerna i en triangel skär varandra i en punkt, som delar var och en av dem i förhållandet 2:1, räknat från vertex. Denna punkt kallas tyngdpunkt triangel.

Hela triangeln delas med sina medianer i sex lika stora trianglar.

Bisektris

Bisektorer(från latin bis - två gånger och seko - skär) är de raka linjesegmenten inneslutna i en triangel som delar dess vinklar (se fig. 4).

För att konstruera en bisektrik måste du utföra följande steg:

1) konstruera en stråle som kommer ut från vinkelns spets och dela den i två lika delar (vinkelns bisektrik);

2) hitta skärningspunkten för halveringslinjen för triangelns vinkel med motsatt sida;

3) välj ett segment som förbinder triangelns spets med skärningspunkten på motsatt sida.

Egenskaper för triangelhalveringslinjer

Halslinjen för en vinkel i en triangel delar den motsatta sidan i ett förhållande som är lika med förhållandet mellan de två intilliggande sidorna.

Halvledarna för de inre vinklarna i en triangel skär varandra i en punkt. Denna punkt kallas mitten av den inskrivna cirkeln.

Bisektorerna för de inre och yttre vinklarna är vinkelräta.

Om halveringslinjen för en yttre vinkel av en triangel skär förlängningen av den motsatta sidan, då ADBD=ACBC.

Halvledarna för en inre och två yttre vinklar i en triangel skär varandra i en punkt. Denna punkt är mitten av en av de tre cirklarna i denna triangel.

Baserna för halveringslinjen för två inre och en yttre vinkel i en triangel ligger på samma räta linje om den yttre vinkelns halveringslinje inte är parallell med den motsatta sidan av triangeln.

Om halvledarna för de yttre vinklarna i en triangel inte är parallella med motsatta sidor, ligger deras baser på samma räta linje.

När du studerar vilket ämne som helst i en skolkurs kan du välja ett visst minimum av problem, och efter att ha bemästrat metoderna för att lösa dem kommer eleverna att kunna lösa alla problem på nivån för programkraven för ämnet som studeras. Jag föreslår att du överväger problem som gör att du kan se sambanden mellan enskilda ämnen i skolans matematikkurs. Därför är det sammanställda systemet med uppgifter ett effektivt sätt att repetera, generalisera och systematisera utbildningsmaterial under förberedelserna för studenterna för tentamen.

För att klara provet kommer det att vara användbart att ha ytterligare information om några av elementen i triangeln. Låt oss överväga egenskaperna hos medianen i en triangel och problem med att lösa vilka dessa egenskaper som kan användas. De föreslagna uppgifterna genomför principen om nivådifferentiering. Alla uppgifter är villkorligt uppdelade i nivåer (nivån anges inom parentes efter varje uppgift).

Låt oss komma ihåg några egenskaper hos medianen för en triangel

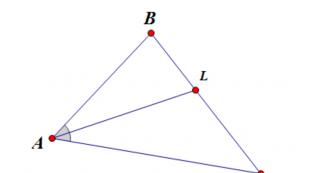
Fastighet 1. Bevisa att medianen för en triangel ABC, ritad från vertexet A, mindre än halva summan av sidorna AB Och A.C..

Bevis

https://pandia.ru/text/80/187/images/image002_245.gif" alt="$\displaystyle (\frac(AB + AC)(2))$" width="90" height="60">.!}

Fastighet 2. Medianen skär triangeln i två lika stora områden.

Bevis

Låt oss rita från vertex B i triangeln ABC medianen BD och höjden BE..gif" alt="Area" width="82" height="46">!}

Eftersom segmentet BD är medianen, alltså

Q.E.D.

https://pandia.ru/text/80/187/images/image008_96.gif" alt="Median" align="left" width="196" height="75 src=">!} Fastighet 4. Medianerna i en triangel delar upp triangeln i 6 lika stora trianglar.

Bevis

Låt oss bevisa att arean av var och en av de sex trianglarna som medianerna delar triangeln ABC i är lika med arean av triangeln ABC. För att göra detta, överväg till exempel triangeln AOF och släpp en vinkelrät AK från vertex A till linje BF.

På grund av fastighet 2,

https://pandia.ru/text/80/187/images/image013_75.gif" alt="Median" align="left" width="105" height="132 src=">!}

Fastighet 6. Medianen i en rätvinklig triangel dragen från spetsen på den räta vinkeln är lika med halva hypotenusan.

Bevis

https://pandia.ru/text/80/187/images/image015_62.gif" alt="Median" width="273" height="40 src="> что и требовалось доказать.!}

Konsekvenser:1. Mitten av en cirkel omskriven om en rätvinklig triangel ligger i mitten av hypotenusan.

2. Om längden på medianen i en triangel är lika med halva längden på sidan till vilken den är ritad, så är denna triangel rätvinklig.

UPPGIFTER

Vid lösning av varje efterföljande problem används beprövade egenskaper.

№1 Ämnen: Fördubbling av medianen. Svårighetsgrad: 2+

Tecken och egenskaper hos ett parallellogram Betyg: 8,9

Skick

På fortsättning av medianen A.M. triangel ABC per poäng M segmentet uppskjutet M.D., likvärdig A.M.. Bevisa att fyrhörningen ABDC- parallellogram.

Lösning

Låt oss använda ett av tecknen på ett parallellogram. Diagonaler av en fyrhörning ABDC skära vid en punkt M och dela den på mitten, så fyrhörningen ABDC- parallellogram.

Det finns ett teorem som Medianerna i en triangel skär varandra i en punkt, och denna punkt delar varje median i förhållandet 2:1, där 2 motsvarar segmentet från spetsen från vilket medianen dras till skärningspunkten för medianerna, och 1 motsvarar segmentet från skärningspunkten för medianerna till mitten av sidan till vilken medianen dras.

För att bevisa detta teorem, överväg triangeln ABC med medianerna AE, BF, CD. Det vill säga punkterna D, E, F delar sidorna AB, BC, CA, respektive.
Vi vet inte om alla medianer skär varandra vid en punkt (detta måste fortfarande bevisas). Däremot kommer vilka två medianer som helst att skära varandra vid en punkt, eftersom de inte kan vara parallella. Låt medianerna AE och BF skära varandra i punkt O.

Median BF delar upp median AE i två segment AO och EO. Låt oss dra en linje parallell med BF genom punkt E. Denna linje kommer att skära sidan AC vid en viss punkt L. Vi kommer också att dra en annan linje parallellt med BF genom mitten av segment AB (punkt D). Den kommer att skära AC vid punkt K.

Enligt Thales sats, om vi på ena sidan av en vinkel från dess vertex lägger ut successivt lika segment och drar parallella linjer genom ändarna av dessa segment som skär den andra sidan av vinkeln, då kommer dessa parallella linjer också att skära av lika segment på andra sidan av vinkeln.

Låt oss titta på vinkeln BCA för denna triangel. Segmenten BE och EC är lika med varandra, linjerna BF och EL är parallella med varandra. Då, enligt Thales sats, CL = LF.
Om vi ​​tittar på vinkeln BAC, eftersom AD = BD och DK || BF, sedan AK = KF.

Eftersom segmenten AF och CF är lika med varandra (eftersom de bildas av medianen) och var och en av dem är uppdelad i två lika stora segment, så är alla fyra segmenten på sidan AC lika med varandra: AK = KF = FL = LC.

Tänk på vinkeln EAC. Parallella linjer dras genom ändarna av tre lika stora segment av sidan AC. Följaktligen skär de av lika segment på sidan AE. Segmentet AO innehåller två sådana segment och EO endast ett. Således har vi bevisat att minst en median av en triangel, vid skärningspunkten med en annan median, är uppdelad i två segment, vars längder är relaterade till 2:1.

Betrakta nu skärningspunkten mellan median AE och median CD. Låt dem skära varandra vid punkt P.

I likhet med den föregående är det bevisat att parallella linjer FM, CD, EN delar sidan AB i lika delar. I sin tur delar de in AE i tre lika stora segment. Dessutom, från vertex A till skärningspunkten mellan medianerna finns det två sådana segment, och efter det finns det ett.

Ett och samma segment kan inte delas upp i tre lika delar så att de med ett uppdelningsalternativ har samma storlek och med ett annat - ett annat. Därför måste punkterna O och P sammanfalla. Det betyder att alla tre medianerna i trianglarna skär varandra i en punkt.

För att bevisa att de andra två medianerna är dividerade med skärningspunkten i förhållandet 2: 1 kan du, på samma sätt som den föregående, dra parallella linjer till sidorna AB och BC.