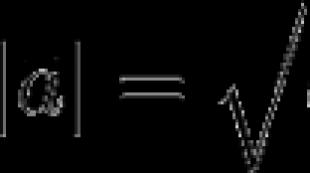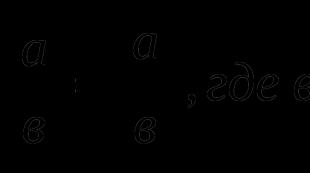Formula dolžine vektorja. Iskanje dolžine vektorja po koordinatah. Formula za določanje koordinat vektorja za prostorske probleme
Poiščimo dolžino vektorja po njegovih koordinatah (v pravokotnem koordinatnem sistemu), po koordinatah točk začetka in konca vektorja ter po kosinusnem izreku (podana sta 2 vektorja in kot med njima).
Vektor je usmerjena daljica. Dolžina tega segmenta določa numerično vrednost vektorja in se imenuje vektorska dolžina ali vektorski modul.
1. Izračunavanje dolžine vektorja iz njegovih koordinat
Če so vektorske koordinate podane v ravnem (dvodimenzionalnem) pravokotnem koordinatnem sistemu, tj. znana sta a x in a y, potem lahko dolžino vektorja poiščemo s formulo
V primeru vektorja v prostoru se doda še tretja koordinata
V MS EXCEL izrazu =ROOT(SUMSQ(B8:B9)) omogoča izračun modula vektorja (predpostavlja se, da so koordinatorji vektorjev vneseni v celice B8:B9, glejte primer datoteke ).
Funkcija SUMSQ() vrne vsoto kvadratov argumentov, tj. v tem primeru enakovredno formuli =B8*B8+B9*B9 .
Primer datoteke izračuna tudi dolžino vektorja v prostoru.
Alternativna formula je izraz =KOREN(SUMPROIZVOD(B8:B9,B8:B9)).
2. Iskanje dolžine vektorja skozi koordinate točk
Če vektor podana s koordinatami svoje začetne in končne točke, potem bo formula drugačna =KOREN(SUMDIFF(C28:C29;B28:B29))
Formula predvideva, da so koordinate začetne in končne točke vnesene v obsege C28:C29 in B28:B29 oz.
funkcija SUMMQVAR() in Vrne vsoto kvadratov razlik ustreznih vrednosti v dveh nizih.
Pravzaprav formula najprej izračuna koordinate vektorja (razlika med ustreznimi koordinatami točk), nato pa izračuna vsoto njihovih kvadratov.
3. Iskanje dolžine vektorja z uporabo kosinusnega izreka
Če želite najti dolžino vektorja s kosinusnim izrekom, sta običajno podana 2 vektorja (njihovi moduli in kot med njima).
Poiščite dolžino vektorja s pomočjo formule =KOREN(SUMQ(B43:C43)-2*B43*C43*COS(B45))
V celicah B43:B43 vsebuje dolžini vektorjev a in b ter celico B45 - kot med njima v radianih (v ulomkih števila PI() ).
Če je kot podan v stopinjah, bo formula nekoliko drugačna. =ROOT(B43*B43+C43*C43-2*B43*C43*COS(B46*PI()/180))
Opomba: zaradi jasnosti lahko v celici z vrednostjo kota v stopinjah uporabite , glejte na primer članek
Oxy
O A OA.
, kje 
OA 
.
torej 
.
Razmislite o primeru.
Primer.
rešitev.
:
odgovor:
Oxyz v vesolju.
A OA bo diagonala.
V tem primeru (ker OA 
OA 
.
torej vektorska dolžina 
.
Primer.
Izračunajte dolžino vektorja 
rešitev.
, torej, 
odgovor:
Premica na ravnini
Splošna enačba
Ax + By + C (> 0).
Vektor = (A; B) je vektor normalne črte.
V vektorski obliki: + C = 0, kjer je radij vektor poljubne točke na premici (slika 4.11).
Posebni primeri:
1) Z + C = 0- ravna črta, vzporedna z osjo Ox;
2) Ax+C=0- ravna črta, vzporedna z osjo Oj;
3) Ax + By = 0- premica poteka skozi izhodišče;
4) y=0- os Ox;
5) x=0- os Oj.
Enačba ravne črte v segmentih
Kje a, b- velikost segmentov, odrezanih z ravno črto na koordinatnih oseh.
Normalna enačba premice(Slika 4.11)
kjer je kot, ki ga tvori normalno na premico in os Ox; str je razdalja od izhodišča koordinat do črte.
Prenos splošne enačbe ravne črte v normalno obliko:
Tukaj je normaliziran faktor neposrednega voda; znak je izbran nasproti znaka C, če in poljubno, če C=0.
Iskanje dolžine vektorja po koordinatah.
Dolžino vektorja bomo označili z . Zaradi tega zapisa se dolžina vektorja pogosto imenuje modul vektorja.
Začnimo z iskanjem dolžine vektorja na ravnini po koordinatah.
Na ravnini uvedemo pravokotni kartezični koordinatni sistem Oxy. Naj bo v njem podan vektor in ima koordinate . Dobimo formulo, ki vam omogoča, da poiščete dolžino vektorja prek koordinat in .
Odmaknite se od izhodišča koordinat (od točke O) vektor. Označimo projekciji točke A na koordinatnih oseh kot in oziroma ter upoštevajte pravokotnik z diagonalo OA.
Na podlagi Pitagorovega izreka je enakost , kje . Iz definicije koordinat vektorja v pravokotnem koordinatnem sistemu lahko trdimo, da in , in po konstrukciji dolžina OA je enaka dolžini vektorja , torej .
torej formula za iskanje dolžine vektorja v svojih koordinatah na ravnini ima obliko .
Če je vektor predstavljen kot razčlenitev v koordinatnih vektorjih , potem se njegova dolžina izračuna po isti formuli , saj sta v tem primeru koeficienta in koordinate vektorja v danem koordinatnem sistemu.
Razmislite o primeru.
Primer.
Poiščite dolžino vektorja, podanega v kartezičnih koordinatah.
rešitev.
Takoj uporabite formulo za iskanje dolžine vektorja s koordinatami :
odgovor:
Zdaj dobimo formulo za iskanje dolžine vektorja s svojimi koordinatami v pravokotnem koordinatnem sistemu Oxyz v vesolju.
Odmaknite vektor od izhodišča in označite projekcije točke A na koordinatnih oseh kot tudi . Potem lahko gradimo na straneh in pravokotni paralelepiped, v katerem OA bo diagonala.
V tem primeru (ker OA je diagonala pravokotnega paralelopipeda), od koder je . Določitev koordinat vektorja nam omogoča, da zapišemo enakosti , in dolžino OA je enak želeni dolžini vektorja, torej .
torej vektorska dolžina v prostoru je enaka kvadratnemu korenu vsote kvadratov svojih koordinat, to je, najdemo s formulo .
Primer.
Izračunajte dolžino vektorja , kjer so orti pravokotnega koordinatnega sistema.
rešitev.
Podana nam je ekspanzija vektorja v smislu koordinatnih vektorjev oblike , torej, . Potem imamo po formuli za iskanje dolžine vektorja po koordinatah .
Na abscisni in ordinatni osi se imenujejo koordinate vektor. Koordinate vektorja so običajno navedene v obrazcu (x, y), sam vektor pa kot: = (x, y).
Formula za določanje koordinat vektorja za dvodimenzionalne probleme.
V primeru dvodimenzionalnega problema je vektor z znano koordinate točke A(x 1; y 1) in B(x 2 ; l 2 ) se lahko izračuna:
\u003d (x 2 - x 1; y 2 - y 1).
Formula za določanje koordinat vektorja za prostorske probleme.
V primeru prostorskega problema vektor z znanim koordinate točke A (x 1; y 1;z 1 ) in B (x 2 ; l 2 ; z 2 ) se lahko izračuna po formuli:
= (x 2 - x 1 ; l 2 - l 1 ; z 2 - z 1 ).
Koordinate dajejo izčrpen opis vektorja, saj je mogoče iz koordinat sestaviti sam vektor. Poznavanje koordinat je enostavno izračunati in vektorska dolžina. (Lastnost 3 spodaj).
Lastnosti vektorskih koordinat.
1. Kateri koli enaki vektorji v enem samem koordinatnem sistemu imajo enake koordinate.
2. Koordinate kolinearni vektorji sorazmerno. Pod pogojem, da nobeden od vektorjev ni enak nič.
3. Kvadrat dolžine poljubnega vektorja je enak vsoti njegovih kvadratov koordinate.
4. Ko je operacija vektorska množenja na realno število vsaka njegova koordinata je pomnožena s tem številom.
5. Med operacijo vektorskega seštevanja izračunamo vsoto ustreznih vektorske koordinate.
6. Skalarni produkt dveh vektorjev je enaka vsoti produktov njunih ustreznih koordinat.
Dolžino vektorja a → bomo označili z a → . Ta zapis je podoben modulu števila, zato dolžino vektorja imenujemo tudi modul vektorja.
Da bi našli dolžino vektorja na ravnini z njegovimi koordinatami, je treba upoštevati pravokotni kartezični koordinatni sistem O x y . Naj vsebuje nek vektor a → s koordinatami a x ; a y . Uvedemo formulo za iskanje dolžine (modula) vektorja a → glede na koordinate a x in a y .
Odmaknite vektor O A → = a → od izhodišča. Definirajmo ustrezni projekciji točke A na koordinatni osi kot A x in A y . Zdaj razmislite o pravokotniku O A x A A y z diagonalo O A .
Iz Pitagorovega izreka sledi enakost O A 2 = O A x 2 + O A y 2 , od koder je O A = O A x 2 + O A y 2 . Iz že znane definicije koordinat vektorja v pravokotnem kartezičnem koordinatnem sistemu dobimo O A x 2 = a x 2 in O A y 2 = a y 2 , po konstrukciji pa je dolžina O A enaka dolžini vektorja. vektor O A → , torej O A → = O A x 2 + O A y 2.
Zato se izkaže, da formula za iskanje dolžine vektorja a → = a x ; a y ima ustrezno obliko: a → = a x 2 + a y 2 .
Če je vektor a → podan kot ekspanzija v koordinatnih vektorjih a → = a x i → + a y j → , potem lahko njegovo dolžino izračunamo z isto formulo a → = a x 2 + a y 2 , v tem primeru sta koeficienta a x in a y kot koordinate vektorja a → v danem koordinatnem sistemu.
Primer 1
Izračunaj dolžino vektorja a → = 7 ; e , podan v pravokotnem koordinatnem sistemu.
rešitev
Za iskanje dolžine vektorja bomo uporabili formulo za iskanje dolžine vektorja po koordinatah a → = a x 2 + a y 2: a → = 7 2 + e 2 = 49 + e
odgovor: a → = 49 + e .
Formula za iskanje dolžine vektorja a → = a x ; a y ; a z s svojimi koordinatami v kartezičnem koordinatnem sistemu Oxyz v prostoru, se izpelje podobno kot formula za primer na ravnini (glej sliko spodaj)
V tem primeru je O A 2 \u003d O A x 2 + O A y 2 + O A z 2 (ker je OA diagonala pravokotnega paralelepipeda), torej O A \u003d O A x 2 + O A y 2 + O A z 2. Iz definicije koordinat vektorja lahko zapišemo naslednje enačbe O A x = a x ; O A y = a y ; O A z = a z ; , dolžina OA pa je enaka dolžini vektorja, ki ga iščemo, torej O A → = O A x 2 + O A y 2 + O A z 2 .
Iz tega sledi, da je dolžina vektorja a → = a x ; a y ; a z je enako a → = a x 2 + a y 2 + a z 2 .
Primer 2
Izračunajte dolžino vektorja a → = 4 i → - 3 j → + 5 k → , kjer so i → , j → , k → enotski vektorji pravokotnega koordinatnega sistema.
rešitev
Glede na dekompozicijo vektorja a → = 4 i → - 3 j → + 5 k → so njegove koordinate a → = 4, - 3, 5 . Z uporabo zgornje formule dobimo a → = a x 2 + a y 2 + a z 2 = 4 2 + (- 3) 2 + 5 2 = 5 2 .
odgovor: a → = 5 2 .
Dolžina vektorja glede na koordinate njegove začetne in končne točke
Zgoraj so bile izpeljane formule, ki vam omogočajo, da poiščete dolžino vektorja po njegovih koordinatah. Upoštevali smo primere na ravnini in v tridimenzionalnem prostoru. Uporabimo jih za iskanje koordinat vektorja s koordinatami njegove začetne in končne točke.
Torej, podane točke z danimi koordinatami A (a x; a y) in B (b x; b y), torej ima vektor A B → koordinate (b x - a x; b y - a y), kar pomeni, da lahko njegovo dolžino določimo s formulo: A B → = ( b x - a x) 2 + (b y - a y) 2
In če so podane točke z danimi koordinatami A (a x; a y; a z) in B (b x; b y; b z) v tridimenzionalnem prostoru, potem lahko dolžino vektorja A B → izračunamo po formuli
A B → = (b x - a x) 2 + (b y - a y) 2 + (b z - a z) 2
Primer 3
Poiščite dolžino vektorja A B → če je v pravokotnem koordinatnem sistemu A 1, 3, B-3, 1.
rešitev
Z uporabo formule za iskanje dolžine vektorja iz koordinat začetne in končne točke na ravnini dobimo A B → = (b x - a x) 2 + (b y - a y) 2: A B → = (- 3 - 1) 2 + (1 - 3) 2 = 20 - 2 3 .
Druga rešitev pomeni uporabo teh formul po vrsti: A B → = (- 3 - 1; 1 - 3) = (- 4; 1 - 3) ; A B → = (- 4) 2 + (1 - 3) 2 = 20 - 2 3 . -
odgovor: A B → = 20 - 2 3 .
Primer 4
Ugotovite, za katere vrednosti je dolžina vektorja A B → enaka 30, če je A (0 , 1 , 2) ; B (5 , 2 , λ 2) .
rešitev
Najprej zapišimo dolžino vektorja A B → po formuli: A B → = (b x - a x) 2 + (b y - a y) 2 + (b z - a z) 2 = (5 - 0) 2 + (2 - 1) 2 + (λ 2 - 2) 2 = 26 + (λ 2 - 2) 2
Nato dobljeni izraz enačimo s 30, od tu najdemo želeni λ:
26 + (λ 2 - 2) 2 = 30 26 + (λ 2 - 2) 2 = 30 (λ 2 - 2) 2 = 4 λ 2 - 2 = 2 in l in λ 2 - 2 = - 2 λ 1 = - 2, λ 2 = 2, λ 3 = 0.
odgovor: λ 1 \u003d - 2, λ 2 \u003d 2, λ 3 \u003d 0.
Iskanje dolžine vektorja z uporabo kosinusnega zakona
Žal, koordinate vektorja niso vedno znane v nalogah, zato razmislimo o drugih načinih iskanja dolžine vektorja.
Naj sta podani dolžini dveh vektorjev A B → , A C → in kot med njima (oz. kosinus kota) ter najti dolžino vektorja B C → ali C B → . V tem primeru bi morali uporabiti kosinusni izrek v trikotniku △ A B C , izračunati dolžino stranice B C , ki je enaka želeni dolžini vektorja.
Oglejmo si tak primer v naslednjem primeru.
Primer 5
Dolžini vektorjev A B → in A C → sta enaki 3 oziroma 7, kot med njima pa je enak π 3 . Izračunaj dolžino vektorja B C → .
rešitev
Dolžina vektorja B C → je v tem primeru enaka dolžini stranice B C trikotnika △ A B C . Iz pogoja sta znani dolžini strani A B in A C trikotnika (enaki sta dolžini ustreznih vektorjev), znan je tudi kot med njima, zato lahko uporabimo kosinusni izrek: B C 2 = A B 2 + A C 2 - 2 A B A C cos ∠ (A B , → A C →) = 3 2 + 7 2 - 2 3 7 cos π 3 = 37 ⇒ B C = 37 Torej je B C → = 37 .
odgovor: B C → = 37 .
Torej, da bi našli dolžino vektorja s koordinatami, obstajajo naslednje formule a → = a x 2 + a y 2 ali a → = a x 2 + a y 2 + a z 2, glede na koordinate točk začetka in konca vektorja A B → = (b x - a x) 2 + ( b y - a y) 2 ali A B → = (b x - a x) 2 + (b y - a y) 2 + (b z - a z) 2, v nekaterih primerih kosinusni izrek je treba uporabiti.
Če v besedilu opazite napako, jo označite in pritisnite Ctrl+Enter
12. Dolžina vektorja, dolžina odseka, kot med vektorji, pogoj pravokotnosti vektorjev.
Vektor - je usmerjeni odsek, ki povezuje dve točki v prostoru ali ravnini. Vektorje običajno označujemo z malimi črkami ali z začetno in končno točko. Zgoraj je običajno pomišljaj.
Na primer vektor, usmerjen iz točke A do točke B, lahko označimo a ,
Ničelni vektor 0 ali 0 - je vektor, katerega začetna in končna točka sta enaki, tj. A = B. Od tod, 0 = – 0 .
Dolžina (modul) vektorjaa je dolžina segmenta, ki ga predstavlja AB, označeno z |a | . Zlasti | | 0 | = 0.
Vektorji se imenujejo kolinearniče njihove usmerjene odseke ležijo na vzporednih premicah. Kolinearni vektorji a in b so določeni a || b .
Imenujejo se trije ali več vektorjev komplanarenče ležijo v isti ravnini.
Seštevanje vektorjev. Ker so vektorji usmeril segmentov, potem lahko izvedemo njihovo dodajanje geometrijsko. (Algebraično seštevanje vektorjev je opisano spodaj, v odstavku "Enotski ortogonalni vektorji"). Pretvarjajmo se, da
a = AB in b = CD,
potem vektor __ __
a + b = AB+ CD
je rezultat dveh operacij:
a)vzporedni prenos enega od vektorjev tako, da njegova začetna točka sovpada s končno točko drugega vektorja;
b)geometrijski dodatek, tj. konstruiranje nastalega vektorja, ki poteka od začetne točke fiksnega vektorja do končne točke prevedenega vektorja.
Odštevanje vektorjev. Ta operacija se zmanjša na prejšnjo z zamenjavo odštetega vektorja z nasprotnim: a – b =a + (– b ) .
Zakoni dodajanja.
JAZ. a + b = b + a (Veljavno pravo).
II. (a + b ) + c = a + (b + c ) (Združeno pravo).
III. a + 0 = a .
IV. a + (– a ) = 0 .
Zakoni množenja vektorja s številom.
JAZ. 1 · a = a , 0 · a = 0 , m· 0 = 0 , (– 1) · a = – a .
II. ma = a m,| ma | = | m | · | a | .
III. m(na ) = (m n)a . (Združeno
zakon množenja).
IV. (m+n) a = ma +na , (Distributer
m(a + b ) = ma + mb . zakon množenja).
Skalarni produkt vektorjev. __ __
Kot med vektorji, ki niso nič AB in CD je kot, ki ga tvorita vektorja med njunim vzporednim prenosom, dokler se točki ne poravnata A in C. Točkovni produkt vektorjeva in b imenovano število, ki je enako zmnožek njihovih dolžin s kosinusom kota med njima:
Če je eden od vektorjev enak nič, potem je njihov skalarni produkt v skladu z definicijo enak nič:
(a , 0 ) = ( 0 , b ) = 0 .
Če oba vektorja nista nič, se kosinus kota med njima izračuna po formuli:
Skalarni produkt ( a , a ) enako | a | 2 se imenuje skalarni kvadrat. Dolžina vektorja a in njegov skalarni kvadrat sta povezana z:
Pikčasti produkt dveh vektorjev:
- pozitivnoče je kot med vektorji začinjeno;
- negativnoče je kot med vektorji Top.
Skalarni produkt dveh neničelnih vektorjev je potem enak nič in le, če je kot med njima pravi, tj. ko so ti vektorji pravokotni (ortogonalni):
Lastnosti skalarnega produkta. Za vse vektorje a , b, c in poljubno število m veljajo naslednje relacije:
JAZ. (a , b ) = (b, a ) . (Veljavno pravo)
II. (ma , b ) = m(a , b ) .
III.(a + b , c ) = (a , c ) + (b, c ). (Distributivni zakon)
Enotski ortogonalni vektorji. V kateri koli pravokotni koordinatni sistem lahko vnesete enota po paru pravokotni vektorjijaz , j in k povezana s koordinatnimi osemi: jaz - z osjo X, j - z osjo Y in k - z osjo Z. Po tej definiciji:
(jaz , j ) = (jaz , k ) = (j , k ) = 0,
| jaz | =| j | =| k | = 1.
Kateri koli vektor a lahko izrazimo s temi vektorji na edinstven način: a = xjaz + lj + zk . Druga oblika pisanja: a = (x, y, z). Tukaj x, l, z-koordinate vektor a v tem koordinatnem sistemu. V skladu z zadnjo relacijo in lastnostmi enotskih ortogonalnih vektorjev jaz, j , k skalarni produkt dveh vektorjev lahko izrazimo različno.
Pustiti a = (x, y, z); b = (u, v, š). Potem ( a , b ) = xi +yv +zw.
Skalarni produkt dveh vektorjev je enak vsoti produktov ustreznih koordinat.
Dolžina (modul) vektorja a = (x, l, z ) je enako:
Poleg tega smo zdaj sposobni algebrski operacije na vektorjih, in sicer seštevanje in odštevanje vektorjev, se lahko izvajajo s koordinatami:
a + b= (x + u, y + v, z + w) ;
a – b= (x–u, y– v, z–w) .
Vektorski produkt vektorjev. vektorska umetnost [a, b ] vektorjia inb (v tem vrstnem redu) imenujemo vektor:
Obstaja še ena formula za dolžino vektorja [ a, b ] :
| [ a, b ] | = | a | | b | greh( a, b ) ,
tj. dolžina ( modul ) navzkrižni produkt vektorjeva inb je enak produktu dolžin (modulov) teh vektorjev in sinusa kota med njima. Z drugimi besedami: dolžina (modul) vektorja[ a, b ] numerično enaka površini paralelograma, zgrajenega na vektorjih a inb .
Lastnosti vektorskega izdelka.
JAZ. Vektor [ a, b ] je pravokotna (ortogonalno) oba vektorja a in b .
(Dokažite, prosim!) .
II.[ a , b ] = – [b, a ] .
III. [ ma , b ] = m[a , b ] .
IV. [ a + b , c ] = [ a , c ] + [ b, c ] .
v. [ a , [ b, c ] ] = b (a , c ) – c (a , b ) .
VI. [ [ a , b ] , c ] = b (a , c ) – a (b, c ) .
Potreben in zadosten pogoj za kolinearnost vektorji a = (x, y, z) In b = (u, v, š) :
Nujen in zadosten pogoj za komplanarnost vektorji a = (x, y, z), b = (u, v, š) In c = (p, q, r) :
PRIMER Dani vektorji: a = (1, 2, 3) in b = (– 2 , 0 ,4).
Izračunajte njihove pikčaste in vektorske produkte ter kot
med temi vektorji.
Rešitev Z uporabo ustreznih formul (glej zgoraj) dobimo:
a). skalarni produkt:
(a , b ) = 1 (– 2) + 2 0 + 3 4 = 10;
b). vektorski izdelek:
| " |
